2. 广东工业大学 机电工程学院, 广东 广州 510006
2. School of Electromechanical Engineering, Guangdong University of Technology, Guangzhou 510006, China
现实生活中,求解答案是绝对的“是”与“否”、“对”与“错”的问题是少量的,大量存在的是一些目标和问题领域相对确定,边界条件可以拓展的问题,将其定义为开放性问题(ill-defined problems) 。这类开放性问题在管理实践中更为普遍、更有价值,但其缺少训练样本数据,难以用知识推理、知识图谱、机器学习等智能技术解决。求解这类开放性问题需要具有完备性的知识,特别是跨领域的知识[1-10]。虽然多源、异构、海量数据与复杂的知识网络体系中蕴含着解决开放性问题的知识,但如何对开放性问题求解所需的知识进行智能化拓展,挖掘相关的隐性知识并识别知识内在的关联,达到问题求解所需知识的完备状态,仍缺乏有效的方法。对此,国外学者提出研究方向需要有所改变,即重新从理论开始,而不是从数据开始[11]。
王小彬[12]基于与或图指出知识的完备性是指对于被认为是目标的命题存在一条规则可以导出此命题。桂修文[13]基于知识库中的规则指出对于某一个目标,用知识库中的知识无法推导出该目标的属性值,则该知识库中的规则知识是不完备的。陈雪龙[14]认为在问题解决时保证有包含解决问题所需要的全部知识,即达到了知识的完备性。Paul Leemans[15]认为知识的完备性就是所有有效的知识都能产生的理想结论,知识不完备均是由知识库中存在间隙或者规则缺失引起的。
中国原创学科可拓学中的特有方法可拓创新方法,是以形式化和定量化相结合的可拓模型[16],研究创新和矛盾问题处理的有效方法,在问题求解领域应用广泛。李兴森[17]以可拓学中的基元理论与因素空间为基础,构建基元−因素空间模型研究面向矛盾问题的智能算法。梁梓源[18]以可拓创新方法中矛盾问题的可拓模型构建方法和求解方法为基础,提出了开放性问题的初始可拓模型的构建方法以及利用拓展分析方法与可拓变换方法对单目标开放性问题进行求解的方法。李苏洋[19]运用可拓创新方法中的“转换桥”方法解决消灭肿瘤并不损伤健康组织的对立问题,得到了使两对立目标在现有条件下能同时实现的思路和方法。通过文献分析可见,借助可拓创新方法进行开放性问题求解研究具有可行性。
本文研究构建开放性问题求解过程中的完备知识网络,通过以描述性知识和方法论知识相互交织,结合领域知识,构建知识网络,为开放性问题求解提供充分条件。
1 知识完备性对于开放性问题而言,其难以求解的原因,通常是未能认识和还原客观事物的全貌及复杂性所致,找出隐含的、不明显的、甚至是隐藏很深的因素知识,往往使原先看似不可求解的问题得到解决。这类问题求解的完备知识通常包含着问题求解的原料描述性知识、策略生成工具的方法论知识以及问题所处领域的领域知识。描述性知识是基础,和原问题密切相关,可以明确开放性问题现有的资源环境;恰当的方法论知识是策略生成工具,可以对描述性知识进行拓展,同时对领域知识提出需求,将隐性知识进行显化,或者能够从更高维空间上去思考较低维空间的问题求解方案,领域知识与原问题目标和条件息息相关,为方法论知识的拓展提供真实的信息。
知识是否完备往往在问题解决后才有明确结论,不同领域、不同类型的问题知识完备性可能存在差异。但当问题求解人具备开放性问题的原料以及掌握合适的方法论知识,并结合问题所处领域的领域知识,就能够对该开放性问题缺失的知识进行拓展与挖掘,构建出问题求解的完备性知识网络,生成该开放性问题求解的策略。
2 完备性知识网络的构建层次分明的知识网络能帮助知识拓展与关联。大数据环境下,基于互联网各类数据资源及信息的公开性、广泛性和海量性,知识的数量早已呈指数形式增长,然而知识之间形成的网络还未能满足求解开放性问题的需求。这不仅是基于知识的多源异构情况,更多的原因在于缺乏方法论知识。方法论知识在知识拓展、知识关联,甚至是对于问题理解方面都有着举足轻重的作用,能够对知识进行拓展、变换等操作,由此也能形成知识网络。
因此,以描述性知识为主的策略生成原料、方法论知识为主的策略生成工具以及领域知识的相互关联,搭建知识网络,探索将该知识网络模型应用于开放性问题求解领域,将隐性知识显化,充分挖掘开放性问题求解的充分条件、必要条件,实现开放性问题求解的知识完备性网络构建。
2.1 知识种类的划分完备知识网络结构主要由描述性知识为主的开放性问题原料、方法论知识为主的问题求解工具和领域知识相互关联而成,以增加知识粒度、挖掘隐性知识、明确关键知识等。描述性知识为方法论知识提供知识加工、推理、融合的原材料,方法论知识反过来从处理方法、对象等角度对缺失的描述性知识提出需求,领域知识与问题本身息息相关,借助领域知识对问题类型进行判断,为方法论知识的应用提供充分的原料信息。
描述性知识是对客观规律、事实、原理等的客观反映和描述,是开放性问题策略生成的原料知识,包含着事实、原理、功能、结构等认知知识。描述性知识主要有两类来源:一类是通过人类社会实践获得的经验知识(包括直接经验和间接经验,以人为主),另一类是通过数据挖掘等技术手段从数据或海量信息资料中获取隐含的规律并显性化为智能知识[20,21]。在大数据时代描述性知识的获取或许足够方便,此时,如何利用这些信息和知识进行加工、延展成为问题求解的关键因素。
方法论知识是建立在实践分析结果之上的、具有规律性的方法体系,是研究方式、方法的综合,是一套完整的实践引导体系知识,能指导知识加工和实践应用的方法、技能、流程等。它包含程序性知识,是运用知识产生创意和决策,进而解决问题的知识。如果在开放性问题求解时不具备系统方法论知识体系,就会造成即使处于知识数量早已呈指数形式增长、知识与信息资源丰富的环境下,仍然无法有效地运用大数据资源和信息资源生成解决开放性问题的创新策略。
领域知识对于开放性问题求解是不可或缺的,与开放性问题息息相关,是个体对于问题领域判断的前提知识,开放性问题的目标和领域是相对确定的,这需要依靠领域知识判断开放性问题的涉及领域,同时也需要借助领域知识判断该问题是单目标开放性问题,还是双目标开放性问题。
2.2 描述性知识的提取描述性知识是开放性问题求解策略生成的原料知识,其完备性直接影响到策略的优度。故此,对开放性问题中的描述性知识需提取完整,只有在充分提取情况下,后续才能充分地运用方法论知识进行拓展与变换,以解决问题。
依据可拓创新方法体系中可拓模型的构建规范,对描述性知识进行提取主要从开放性问题题干中所涉及的物、事、关系(包含物与物、物与事、事与事之间的关系)出发,分别提取出物、事、关系中所对应的特征与量值。以物为例,其特征通常包含着实义特征(长度、宽度、质量、材质等)、性质特征(导电率、可燃度、可靠度、稳定度等)、功能特征(产能、运输能力、续航能力等)等,事和关系的特征参见文献[22]。
2.3 方法论知识——可拓创新方法体系可拓创新方法体系[16]是一种基于可拓学理论的流程化方法体系,在该体系中,为了能够形式化表达万事万物和问题,建立了形式化表达物、事和关系的基本元——物元、事元和关系元,统称为基元。对于复杂事物和关系,还可以利用基元的算数运算和逻辑运算、复合元及其算术运算和逻辑运算等进行形式化表达。基于基元和复合元,建立了将数学模型拓广的可拓模型,以形式化表示问题及其解决过程,可以在信息统一表达与存储的基础上进行系统拓展和创新,从而作为处理矛盾问题的形式化工具。因此,本文中采取的方法论知识为可拓创新方法体系。
2.3.1 开放性问题的初始可拓模型对描述性知识建立可拓模型,是开放性问题求解的第一步。对于开放性问题,由于其边界条件是不确定的或者是不足的,所以问题表达不清晰、目标难以实现。故此需要进一步认识和还原客观事物的全貌及复杂性,找出隐含的、不明显的、甚至是隐藏很深的因素知识,使原先看似不可求解的问题得到解决。因此需要借助方法论知识从处理方法、对象等角度对缺失的描述性知识提出需求,结合领域知识对描述性知识进行拓展、延伸,从而满足问题求解的充分条件、必要条件。
可拓创新流程化方法体系认为问题都是由目标和条件构成。目标可以由事元、复合元或其运算形式化表示,构成目标的可拓模型;并从问题目标的数量角度,分为单目标问题的可拓模型、双目标问题的可拓模型和多目标问题的可拓模型[22]。对于开放性问题而言,问题目标领域是相对确定的,而条件是不确定或者是不足的,其边界是可以进行拓展的。开放性问题可分为单目标、双目标和多目标开放性问题。根据可拓学中问题的可拓模型[22]建立方法,建立开放性问题的初始可拓模型:
(1) 单目标开放性问题的初始可拓模型[18]:
| $ P = {G_1}*( {{L_1} \wedge {L_2} \wedge \cdots \wedge {L_q}} ) $ |
式中:
(2) 双目标开放性问题的初始可拓模型:
| $ P = ( {{G_1} \odot {G_2}} ) *( {{L_1} \wedge {L_2} \wedge \cdots \wedge {L_s}} ) $ |
式中:
(3) 多目标开放性问题的初始可拓模型:
| $ P = ( {{G_1} \odot {G_2} \odot \cdots \odot {G_n}} ) *( {{L_1} \wedge {L_2} \wedge \cdots \wedge {L_m}} ) $ |
式中:
可拓创新方法体系中蕴含着独特的知识拓展方法,将开放性问题中的描述性知识建立可拓模型之后,运用可拓推理对描述性知识进行拓展与变换推理,并结合领域知识,将知识之间进行关联,形成知识网络。利用可拓推理,以开放性问题中描述性知识为基础,对所建立的可拓模型进行拓展与变换,从问题所涉及物的物质性、结构性、动态性和对立性四个方面进行分析,从虚实、软硬、潜显和正负八个角度对物进行拓展与变换,为知识的智能化拓展提供方向,构成开放性问题求解的知识网络。可拓推理规则包括:拓展推理规则、传导推理规则、共轭推理规则。下面简要介绍各种推理规则,详见文献[23]。
1) 拓展推理规则
对由描述性知识构建的基元或复合元模型进行拓展分析,即运用可拓推理中的拓展推理规则(发散规则、相关规则、可扩规则、蕴含规则等),是构成开放性问题求解的知识网络的关键。下面简要介绍常用的几种拓展推理规则。
(1) 发散规则是根据物、事、关系的发散性,对开放性问题的初始可拓模型中的基元进行拓展的推理规则,以某个初始条件基元Li的发散规则为例,发散规则知识式为
| $ \begin{split} &{L}_{i}=({O}_{i},{c}_{j},{v}_{k}) \dashv ({O}_{q},{c}_{r},{v}_{l}) ,q=\mathrm{1,2},\cdots ,n\\ &\qquad r=\mathrm{1,2},\cdots ,m,\;\;l=\mathrm{1,2},\cdots ,s\end{split}$ | (1) |
(2) 相关规则是根据物、事、关系的相关性,对基元与基元之间进行相关关系的建立。以多个初始条件的动态基元
| $ L(t) \widetilde{\leftarrow }({L}_{1}(t) \wedge {L}_{2}(t) \wedge {\cdots \wedge L}_{n}(t) ) $ | (2) |
建立相关规则之前,首先要针对开放性问题的初始模型中的目标与条件的可拓模型,建立相应的一般可拓模型,然后再根据领域知识,获取具有相关关系的一维基元的量值之间的函数关系,进而建立相关规则。
(3) 蕴含规则是根据物、事、关系的蕴含性,形式化表示基元与基元之间的因果关系和存在关系的规则。以某个初始目标基元的或因果蕴含规则为例,
| $ {G}_{1}\vee {G}_{2}\Rightarrow G $ | (3) |
2) 传导推理规则
事物之间普遍存在相关性与蕴含性,当对某个基元实施主动可拓变换时,不可避免会对其他相关基元或者蕴含基元产生相应的影响,导致发生传导变换。以某2个条件基元
基于主动变换和传导变换的推理规则,称为传导推理规则。以上述一阶传导变换为例,其传导推理规则可表示为
| $ (\varphi {L}_{1}={L}'_{1}) \wedge ({L}_{1}\widetilde{\rightarrow }{L}_{2}) \models ({}_{\varphi }{}^{}T{L}_{2}={L}'_{2}) $ | (4) |
并且多次传导会形成可拓变换蕴含系,在很多情形中,可通过传导推理规则对问题进行求解。复合元也有类似的传导推理规则[24],当开放性问题的初始可拓模型中包含复合元时,可通过复合元的传导推理规则对问题进行求解。
3) 共轭推理规则
对物进行共轭分析可知,任何物都有4对共轭部,在一定条件下,物的某一共轭部的变化会导致与其相关的对应共轭部发生传导变换。共轭推理规则包括:虚实共轭推理规则、软硬共轭推理规则、浅显共轭推理规则、正负共轭推理规则。
基于上述可拓模型和可拓推理规则,生成开放性问题求解策略的一般步骤为:对描述性知识进行提取,建立问题的初始可拓模型,并结合领域知识对初始目标与条件进行界定之后,进一步对初始目标或下位目标进行相关分析,建立初始目标或下位目标相关网;基于相关网,对相关的初始条件进行发散分析,建立起发散树,最后结合发散树、相关网中的知识,以传导推理规则生成问题求解策略。若未达到初始目标,则进一步以领域知识对初始目标进行蕴含分析,建立初始目标的蕴含系,最后结合发散树、相关网、蕴含系中的知识,以传导推理规则生成问题求解策略。限于篇幅,此处不详述,参见文献[18,22]。
2.3.3 知识网络完备性的判断基于上述知识,对开放性问题的条件及条件与目标的关系进行拓展分析与可拓变换,然后判断开放性问题的目标是否能够实现,如果能实现,则认为求解该开放性问题的知识是完备的;如果不能实现,则要进一步利用蕴含规则获取该开放性问题的目标的下位目标,再判断下位目标是否能实现,如果能实现,认为求解该开放性问题的知识是完备的;如果不能实现,则认为该开放性问题为矛盾问题,需要利用关联函数建立矛盾度函数,再利用矛盾问题的求解方法[22]对下位问题进行求解,当矛盾度大于0时,说明下位目标可以实现,此时认为求解该开放性问题的知识是完备的。在多个知识完备性网络积累到一定程度后,可进一步挖掘知识完备性判断的基本规律以指导后续实践。
2.4 完备知识网络的构建步骤在掌握该开放性问题原料的描述性知识、开放性问题求解策略生成工具的方法论知识、开放性问题针对性求解策略生成的领域知识后,可构建问题求解的知识网络,并通过初始目标能否实现验证知识网络的完备性,开放性问题求解的完备性知识网络的构建步骤如图1所示。

|
图 1 构建完备知识网络的一般流程 Figure 1 Basic steps for constructing complete knowledge network |
开放性问题求解的完备知识网络中,以基元为最小单元,描述性知识以及领域知识作为主要的知识内容,方法论知识作为描述性知识与领域知识、领域知识与领域知识拓展的路径,为知识之间的推理提供了路径。以某种单目标开放性问题的完备性知识网络构建为例,结构示例如图2所示。

|
图 2 单目标开放性问题求解的知识网络结构示例 Figure 2 Example of knowledge network structure for solving single-goal ill-defined problems |
双目标与多目标开放性问题的完备性知识网络构建流程与单目标开放性问题类似,但更复杂,限于篇幅,将另文介绍。
3 案例分析某人因工学椅设计公司,有款面向工作环境(写、绘图、打字等)的座椅产品D0,市场反馈其使用舒适度不足,需要对该款产品进行重新设计。座椅相关部件有坐面、坐垫、腰靠面、腰靠垫、扶手,分别用符号D01、D02、D03、D04、D05表示。
根据公司调研结果发现座椅使用舒适度评价主要来源于使用座椅时使用者腰椎椎间盘E01、坐骨E02、脚部E03、腘窝E04、肩部肌肉E05方面的舒适程度,用z1、z2、z3、z4、z5分别表示各部位的舒适度。因此,选择该5个方面的舒适度情况作为评价座椅整体舒适度的评价指标,并结合文献[25-26]确定指标权重,具体如表1所示。
| 表 1 座椅舒适度评价指标权重 Table 1 Weight of the seat comfort evaluation index |
根据领域知识可以知道,该问题目标领域是确定的,然而其条件是不足的需要拓展分析。由于该问题的目标个数为一个,因此该问题是单目标开放性问题。以此单目标开放性问题为例,运用前文中的完备知识网络构建方法,构建该问题求解的完备知识网络。
3.1 初始可拓模型的建立首先提取开放性问题原料——描述性知识,以座椅设计的领域知识对目标和条件进行界定:以提升该座椅D0的使用者E0的舒适度作为目标,目前该座椅的设计参数,以及使用者相关状态作为初始条件。基于此建立开放性问题的初始可拓问题模型。目标的初始可拓模型为
由于本产品主要面对成年人群体,依据GB/T 10000—1988中坐姿人体尺寸数据,为符合广大用户的舒适性要求,最大值采取男性95百分数,最小值采取女性10百分数,用符号E0表达该类群体。数据如表2所示(数据来源于文献[25]):
目标的初始可拓模型为
| $ { {G}_{0}=\left[\begin{array}{ccc}提升,& 支配对象,& 舒适度\\ & 接受对象,& {E}_{0}\\ & 程度,\;\;\;\;\;\;\;\;\;\;& 30\text{%}\end{array}\right]} $ |
根据现有座椅产品
| $ {{L}_{01}=\left[\begin{array}{ccc}{D}_{0},& 使用者,\;\;\;\;\;\;& {E}_{0}\\ & 使用场景,& 办公\end{array}\right]} $ |
| ${ {L}_{011}=\left[\begin{array}{ccc}{D}_{01},& 高度,& [400,520]\text{ mm}\\ & 倾角,& 0^\circ \\ & 深度,& 500\text{ mm}\\ & 宽度,& 480\text{ mm}\\ & 材质,& 人造皮革\end{array}\right]=\left[\begin{array}{c}{L}_{0111}\\ {L}_{0112}\\ {L}_{0113}\\ {L}_{0114}\\ {L}_{0115}\end{array}\right]} $ |
| $ {{L}_{012}=\left[\begin{array}{ccc}{D}_{02},& 厚度,\;\;\;\;\;& \text{40 mm}\\ & 填充物,& 低回弹海绵\end{array}\right]=\left[\begin{array}{c}{L}_{0121}\\ {L}_{0122}\end{array}\right]} $ |
| ${ {L}_{013}=\left[\begin{array}{ccc}{D}_{03},& 高度,& \text{150 mm}\\ & 宽度,& \text{460 mm}\\ & 厚度,& \text{80 mm}\\ & 倾角\;\;\;\;\;& 97^\circ \\ & 材质,& 人造皮革\end{array}\right]=\left[\begin{array}{c}{L}_{0131}\\ {L}_{0132}\\ {L}_{0133}\\ {L}_{0134}\\ {L}_{0135}\end{array}\right] }$ |
| ${ {L}_{014}=\left[\begin{array}{ccc}{D}_{04},& 厚度,\;\;\;\;\;\;& \text{80 mm}\\ & 填充物,& 低回弹海绵\end{array}\right]=\left[\begin{array}{c}{L}_{0141}\\ {L}_{0142}\end{array}\right] }$ |
| ${ {L}_{015}=\left[\begin{array}{ccc}{D}_{05},& 高度,& \text{200 mm}\\ & 材质,& \text{PP}\end{array}\right]=\left[\begin{array}{c}{L}_{0151}\\ {L}_{0152}\end{array}\right] }$ |
根据使用目前座椅产品D0的使用者身体状况,构建初始条件的可拓模型如下:
| $ { {L}_{02}=\left[\begin{array}{ccc}{E}_{0},& 位置,\;\;\;\;\;\;& {D}_{0}上\\ & 姿势,\;\;\;\;\;\;& 坐姿\\ & 舒适度,& 56\text{%}\end{array}\right]=\left[\begin{array}{c}{L}_{02}^{1}\\ {L}_{02}^{2}\\ {L}_{02}^{3}\end{array}\right]} $ |
| $ { {L}_{021}=(\begin{array}{ccc}{E}_{01},& 压力,& 中等\end{array})} $ |
| $ { {L}_{022}=(\begin{array}{ccc}{E}_{02},& 压力,& 中等\end{array}) }$ |
| $ {{L}_{023}=(\begin{array}{ccc}{E}_{03},& 支撑力,& 中等\end{array})} $ |
| $ {{L}_{024}=(\begin{array}{ccc}{E}_{04},& 压力,& 中等\end{array})} $ |
| $ {{L}_{025}=(\begin{array}{ccc}{E}_{05},& 状况,& 比较紧张\end{array}) }$ |
则原问题的初始可拓模型为
| $ {P}_{0}={G}_{0}*({L}_{01}\wedge {L}_{011}\wedge \cdots \wedge {L}_{02}\wedge {L}_{021}\cdots \wedge {L}_{025}) $ |
根据领域知识,该问题是初始条件与目标、初始条件与初始条件之间关系不确定导致无法求解。故需要对初始条件与目标、初始条件与初始条件之间进行相关分析。根据领域知识文献[25-29],要实现提高坐在座椅D0上工作者舒适度这一目标,该目标相关的初始条件有腰椎椎间盘压力大小、坐骨压力大小、肩部肌肉的紧张程度等。同时,初始条件与初始条件之间也存在相关关系。
根据方法论知识中的相关规则知识,以初始目标G0对应的一般可拓模型G与初始条件对应的一般可拓模型L1,L11,L12,···,L2,L21,…,L25为基础,基于领域知识和相关规则知识,得知目标G与条件L21,L22,L23,L24,L25之间存在相关关系,相关关系为
| $ {\begin{split} &G=\left[\begin{array}{ccc}提升,& 支配对象,& 舒适度\\ & 接受对象,& E\\ & 程度,\;\;\;\;\;\;\;\;\;\;& z-56\text{%}\end{array}\right]\\ &\widetilde{\leftarrow } {L}_{2}^{3}=(\begin{array}{ccc}E,& 舒适度,& z\end{array}) \\ &\xleftarrow{{\wedge}} \left\{\begin{array}{l}{L}_{21}=(\begin{array}{ccc}{E}_{1},& 压力,& y{}_{1}\end{array}) \\ {L}_{22}=(\begin{array}{ccc}{E}_{2},& 压力,& y{}_{2}\end{array}) \\ {L}_{23}=(\begin{array}{ccc}{E}_{3},& 支撑力,& {y}_{3}\end{array}) \\ {L}_{24}=(\begin{array}{ccc}{E}_{4},& 压力,& {y}_{4}\end{array}) \\ {L}_{25}=(\begin{array}{ccc}{E}_{5},& 状况,& {y}_{5}\end{array}) \end{array}\right.\end{split}} $ |
其中用z表示重新设计后的座椅使用舒适度,并且
| $ { {z}_{1}={f}_{1}({y}_{1}) =\left\{\begin{aligned} &100\text{%},\text{ }{y}_{1}=较小\\ &60\text{%},\text{ }{y}_{1}=中等\\ &0,\text{ }{y}_{1}=较大\end{aligned}\right.} $ |
| $ {{z}_{2}={f}_{2}({y}_{2}) =\left\{\begin{aligned} &100\text{%},\text{ }{y}_{2}=很小\\ &80\text{%},\text{ }{y}_{2}=较小\\ &60\text{%},\text{ }{y}_{2}=中等\\ &30\text{%},\text{ }{y}_{2}=较大\\ &0,\text{ }{y}_{2}=很大\end{aligned}\right.} $ |
| $ { {z}_{3}={f}_{3}({y}_{3}) =\left\{\begin{aligned} &100\text{%},\text{ }{y}_{3}=较大\\ &60\text{%},\text{ }{y}_{3}=中等\\ &0,\text{ }{y}_{3}=较小\end{aligned}\right.} $ |
| $ {{z}_{4}={f}_{4}({y}_{4}) =\left\{\begin{aligned} &100\text{%},\text{ }{y}_{4}=较小\\ &50\text{%},\text{ }{y}_{4}=中等\\ &0,\text{ }{y}_{4}=较大\end{aligned}\right.} $ |
| $ { {z}_{5}={f}_{5}({y}_{5}) =\left\{\begin{aligned} &100\text{%},\text{ }{y}_{5}=自然放松\\ &50\text{%},\text{ }{y}_{5}=比较紧张\\ &0,{y}_{5}=很紧张\end{aligned}\right.} $ |
根据上述对G的相关分析可知,要实现目标G0,需要对初始条件L021、L022、L023、L024、L025实施变换,而根据领域知识可知,初始条件L021、L022、L023、L024、L025是无法直接进行变换的。因此,需进一步寻找条件之间的相关关系,基于领域知识和相关规则可知,L21、L22、L23、L24、L25与L11、L12、L13、L14、L15相关,相关关系为
| $ { {L}_{21}=(\begin{array}{ccc}{E}_{1},& 压力,& {y}_{1}\end{array}) \stackrel{\wedge }{\leftarrow }\left\{\begin{array}{l}{L}_{131}=(\begin{array}{ccc}{D}_{3},& 高度,& {x}_{131}\end{array}) \\ {L}_{134}=(\begin{array}{ccc}{D}_{3},& 倾角,& {x}_{134}\end{array}) \end{array}\right.} $ |
| $ {\begin{aligned} &{y}_{1}={f}_{11}({x}_{131},{x}_{134}) =\\ &\qquad \left\{\begin{aligned} &较小,{x}_{131}\in (165,200) \text{ mm},{x}_{132}\in (100^\circ ,110^\circ ) \\ &中等,{x}_{131}\in [150,165]\text{ mm}\cup [200,225]\text{ mm},\\ &\qquad\quad {x}_{132}\in [90^\circ ,100^\circ ]\cup [110^\circ ,115^\circ ]\\ &较大,{x}_{131}\notin [150,225]\text{ mm},{x}_{132}\notin [90^\circ ,115^\circ ]\end{aligned}\right.\end{aligned}} $ |
| $ {{L}_{22}=(\begin{array}{ccc}{E}_{2}, & 压力,& {y}_{2}\end{array}) \stackrel{\wedge }{\leftarrow }\left\{\begin{aligned} &{L}_{111}=(\begin{array}{ccc}{D}_{1},& 高度,& {x}_{111}\end{array}) \\ &{L}_{112}=(\begin{array}{ccc}{D}_{1},& 倾角,& {x}_{112}\end{array}) \\ &{L}_{115}=(\begin{array}{ccc}{D}_{1},& 材质,& {x}_{115}\end{array}) \\ &{L}_{122}=(\begin{array}{ccc}{D}_{2},& 填充物,& {x}_{122}\end{array}) \end{aligned}\right.} $ |
| $ {\begin{aligned} &{y}_{2}={f}_{21}({x}_{111},{x}_{112},{x}_{115},{x}_{122}) =\\ &\qquad \left\{\begin{aligned} &很小,{x}_{111}\in (360,480) \text{ mm},{x}_{112}\in (1^\circ ,5^\circ ) ,\\ &\qquad\quad {x}_{115}=聚酰胺制长毛绒,{x}_{122}=高回弹海绵\\ &较小,{x}_{111}\in (360,480) \text{ mm},{x}_{112}\in (2^\circ ,4^\circ ) ,\\ &\qquad\quad {x}_{115}=网布,{x}_{122}=高回弹海绵\\ &中等,{x}_{111}\in (360,480) \text{ mm},{x}_{112}\in (0^\circ ,1^\circ ) ,\\ &\quad\qquad {x}_{115}=人造皮革,{x}_{122}=低回弹海绵\\ &较大,{x}_{111}\notin (360,480) \text{ mm},{x}_{112}\in (0^\circ ,1^\circ ) ,\\ &\qquad\quad {x}_{115}=人造皮革,{x}_{122}=低回弹海绵\\ &很大,{x}_{111}\notin (360,480) \text{ mm},{x}_{112}\notin (0^\circ ,5^\circ ) ,\\ &\qquad\quad {x}_{115}=人造皮革,{x}_{122}=低回弹海绵\end{aligned}\right.\end{aligned}} $ |
| $ {\begin{aligned} &{L}_{23}=(\begin{array}{ccc}{E}_{3},& 支撑力,& {y}_{3}\end{array}) \widetilde{\leftarrow }{L}_{111}=(\begin{array}{ccc}{D}_{1},& 高度,& {x}_{111}\end{array}) \\ &{y}_{3}={f}_{31}({x}_{111}) =\left\{\begin{aligned} &较大,{x}_{111}\in (300,380) \text{ mm}\\ &中等,{x}_{111}\in [380,500) \text{ mm}\\ &较小,{x}_{111}\in [500,600) \text{ mm}\end{aligned}\right.\end{aligned}} $ |
| $ {{L}_{24}=(\begin{array}{ccc}{E}_{4},& 压力,& {y}_{4}\end{array}) \stackrel{\wedge }{\leftarrow }\left\{\begin{aligned} &{L}_{111}=(\begin{array}{ccc}{D}_{1},& 高度,& {x}_{111}\end{array}) \\ &{L}_{113}=(\begin{array}{ccc}{D}_{1},& 深度,& {x}_{113}\end{array}) \end{aligned}\right.} $ |
| $ {\begin{aligned} &{y}_{4}={f}_{41}({x}_{111},{x}_{113}) =\\ &\qquad \left\{\begin{aligned} &较小,{x}_{111}\in (360,480) \text{ mm},{x}_{113}\in (360,390) \text{ mm}\\ &中等,{x}_{111}\in (360,480) \text{ mm},{x}_{113}\in [390,520) \text{ mm}\\ &较大,{x}_{111}\notin (360,480) \text{ mm},{x}_{113}\notin (360,520) \text{ mm}\end{aligned}\right.\end{aligned}} $ |
| $ {{L}_{25}=(\begin{array}{ccc}{E}_{5},& 状况,& {y}_{5}\end{array}) \widetilde{\leftarrow }{L}_{151}=(\begin{array}{ccc}{D}_{5},& 高度,& {x}_{151}\end{array})} $ |
| $ {{y}_{5}={f}_{51}({x}_{151}) =\left\{\begin{aligned} &自然放松,{x}_{151}\in (210,250) \text{ mm}\\ &比较紧张,{x}_{151}\in (190,210]\text{ mm}\\ &很紧张,{x}_{151}\notin (190,250) \text{ mm}\end{aligned}\right.}$ |
根据领域知识和相关规则知识,对初始问题的目标与初始条件所对应的一般可拓模型进行相关分析后,可构建该问题的相关网,如式(5)所示。
| $ { G\widetilde{\leftarrow }L_{2}^{3}\overset{\wedge }{\mathop{\leftarrow }}\,\left\{ \begin{aligned} &{{L}_{21}}\overset{\wedge }{\mathop{\leftarrow }}\,\left\{\begin{aligned} & {{L}_{131}} \\ & {{L}_{134}} \\ \end{aligned} \right. \\ & {{L}_{22}}\overset{\wedge }{\mathop{\leftarrow }}\,\left\{ \begin{aligned} & {{L}_{111}} \\ & {{L}_{112}} \\ & {{L}_{115}} \\ & {{L}_{122}} \\ \end{aligned} \right. \\ & {{L}_{23}}\widetilde{\leftarrow }\text{ }{{L}_{111}} \\ & {{L}_{24}}\overset{\wedge }{\mathop{\leftarrow }}\,\left\{ \begin{aligned} & {{L}_{111}} \\ & {{L}_{113}} \\ \end{aligned} \right. \\ & {{L}_{25}}\widetilde{\leftarrow }\text{ }{{L}_{151}}\end{aligned} \right.} $ | (5) |
完成相关分析后,再根据发散规则和领域知识,对相关网中的叶基元对应的初始条件基元进行如下发散分析:
| $ { {L}_{0131}{\text{┫}} \left\{\begin{aligned} &{L}_{0131}^{1}=(\begin{array}{ccc}{D}_{3},& 高度,& (140\text{ },160) \text{ mm}\end{array}) \\ &{L}_{0131}^{2}=(\begin{array}{ccc}{D}_{3},& 高度,& [160\text{ },180) \text{ mm}\end{array}) \\ &{L}_{0131}^{3}=(\begin{array}{ccc}{D}_{3},& 高度,& [180\text{ },200) \text{ mm}\end{array})\end{aligned}\right.} $ |
| $ { {L}_{0134}{\text{┫}}\left\{\begin{aligned} &{L}_{0134}^{1}=(\begin{array}{ccc}{D}_{3},& 倾角,& (90^\circ ,100^\circ ) \end{array}) \\ &{L}_{0134}^{2}=(\begin{array}{ccc}{D}_{3},& 倾角,& [100^\circ ,110^\circ ) \end{array}) \\ &{L}_{0134}^{3}=(\begin{array}{ccc}{D}_{3},& 倾角,& [100^\circ ,120^\circ ) \end{array}) \end{aligned}\right.} $ |
| $ {{L}_{0111}{\text{┫}}\left\{\begin{aligned} &{L}_{0111}^{1}=(\begin{array}{ccc}{D}_{1},& 高度,& (300,360) \text{ mm}\end{array}) \\ &{L}_{0111}^{2}=(\begin{array}{ccc}{D}_{1},& 高度,& [360,480) \text{ mm}\end{array}) \\ &{L}_{0111}^{3}=(\begin{array}{ccc}{D}_{1},& 高度,& [480,600) \text{ mm}\end{array}) \end{aligned}\right.} $ |
| $ {{L}_{0112}{\text{┫}}\left\{\begin{aligned} &{L}_{0112}^{1}=(\begin{array}{ccc}{D}_{1},& 倾角,& (0^\circ \text{ },\text{ }1^\circ ) \end{array}) \\ &{L}_{0112}^{2}=(\begin{array}{ccc}{D}_{1},& 倾角,& (2^\circ \text{ },\text{ }4^\circ ) \end{array}) \\ &{L}_{0112}^{3}=(\begin{array}{ccc}{D}_{1},& 倾角,& [1^\circ \text{ },\text{ }5^\circ ]\end{array}) \end{aligned}\right.} $ |
| $ {{L}_{0115}{\text{┫}}\left\{\begin{aligned} &{L}_{0115}^{1}=(\begin{array}{ccc}{D}_{1},& 材质,& 网布\end{array}) \\ &{L}_{0115}^{2}=(\begin{array}{ccc}{D}_{1},& 材质,& 聚酰胺制长毛绒\end{array}) \\ &{L}_{0115}^{3}=(\begin{array}{ccc}{D}_{1},& 材质,& 特拉纶长毛绒\end{array}) \\ &{L}_{0115}^{4}=(\begin{array}{ccc}{D}_{1},& 材质,& 聚酰胺丝绒\end{array}) \end{aligned}\right.} $ |
| $ {{L}_{0122}{\text{┫}}\left\{\begin{aligned} &{L}_{0122}^{1}=(\begin{array}{ccc}{D}_{2},& 填充物,& 高回弹海绵\end{array}) \\ &{L}_{0122}^{2}=(\begin{array}{ccc}{D}_{2},& 填充物,& 乳胶\end{array}) \\ &{L}_{0122}^{3}=(\begin{array}{ccc}{D}_{2},& 填充物,& 木材\end{array}) \\ &{L}_{0122}^{4}=(\begin{array}{ccc}{D}_{2},& 填充物,& 金属\end{array}) \end{aligned}\right. }$ |
| $ {{L}_{0113}{\text{┫}}\left\{\begin{aligned} &{L}_{0113}^{1}=(\begin{array}{ccc}{D}_{1},& 深度,& [360,390) \text{ mm}\end{array}) \\ &{L}_{0113}^{2}=(\begin{array}{ccc}{D}_{1},& 深度,& [390,520]\text{ mm}\end{array}) \end{aligned}\right.} $ |
| $ {{L}_{0151}{\text{┫}}\left\{\begin{aligned} &{L}_{0151}^{1}=(\begin{array}{ccc}{D}_{5},& 高度,& (190,210) \text{ mm}\end{array}) \\ &{L}_{0151}^{2}=(\begin{array}{ccc}{D}_{5},& 高度,& [210,250) \text{ mm}\end{array}) \\ &{L}_{0151}^{3}=(\begin{array}{ccc}{D}_{5},& 高度,& ]250,280) \text{ mm}\end{array}) \end{aligned}\right.} $ |
结合上述知识,要实现目标G0,必须要改变初始条件L021、L022、L023、L024、L025,而初始条件L021、L022、L023、L024、L025的改变需要通过变换初始条件L011、L012、L013、L014、L015来实现。因此,首先对条件L011、L012、L013、L014、L015实施可拓变换,再利用传导推理规则生成问题求解策略。
根据相关网式(5)和上述发散规则,实施可拓变换:
| $ {{\varphi }_{0131}{L}_{0131}={{L}^{\prime }}_{0131}=(\begin{array}{ccc}{{D}^{\prime }}_{03},& 高度,& [160\text{ },180) \text{ mm}\end{array})} $ |
| $ {{\varphi }_{0132}{L}_{0132}={{L}^{\prime }}_{0132}=(\begin{array}{ccc}{{D}^{\prime }}_{03},& 倾角,& [100^\circ ,110^\circ ) \end{array})} $ |
| $ {{\varphi }_{0111}{L}_{11}={{L}^{\prime }}_{0111}=(\begin{array}{ccc}{{D}^{\prime }}_{01},& 高度,& [360\text{ },\text{ }480) \text{ mm}\end{array})} $ |
| $ {{\varphi }_{0112}{L}_{0112}={{L}^{\prime }}_{0112}=(\begin{array}{ccc}{{D}^{\prime }}_{01},& 倾角,& (2^\circ \text{ },\text{ }4^\circ ) \end{array})} $ |
| $ {{\varphi }_{0115}{L}_{0115}={{L}^{\prime }}_{0115}=(\begin{array}{ccc}{{D}^{\prime }}_{01},& 材质,& 网布\end{array})} $ |
| $ {{\varphi }_{0122}{L}_{0122}={{L}^{\prime }}_{0122}=(\begin{array}{ccc}{{D}^{\prime }}_{02},& 填充物,& 高回弹海绵\end{array})} $ |
| $ {{\varphi }_{0113}{L}_{0113}={{L}^{\prime }}_{0113}=(\begin{array}{ccc}{{D}^{\prime }}_{01},& 深度,& [360\text{ },\text{ }390) \text{ mm}\end{array}) }$ |
| $ {{\varphi }_{0151}{L}_{0151}={{L}^{\prime }}_{0151}=(\begin{array}{ccc}{{D}^{\prime }}_{05},& 高度,& [210\text{ },\text{ }250) \text{ mm}\end{array})} $ |
对座椅D0的部件进行上述可拓变换后,可获得一种新座椅
记
| $ {{}_{{\psi }_{1}}T{L}_{021}={{L}^{\prime }}_{021}=(\begin{array}{ccc}{{E}^{\prime }}_{01},& 压力,& 较小\end{array})} $ |
| $ { {}_{{\psi }_{2}}T{L}_{022}={{L}^{\prime }}_{022}=(\begin{array}{ccc}{{E}^{\prime }}_{02},& 压力,& 较小\end{array})} $ |
| $ { {}_{{\varphi }_{0111}}T{L}_{023}={{L}^{\prime }}_{023}=(\begin{array}{ccc}{{E}^{\prime }}_{023},& 支撑力,& 中等\end{array})} $ |
| $ { {}_{{\psi }_{3}}T{L}_{024}={{L}^{\prime }}_{024}=(\begin{array}{ccc}{{E}^{\prime }}_{024},& 压力,& 较小\end{array}) }$ |
| $ {{}_{{\varphi }_{0151}}T{L}_{025}={{L}^{\prime }}_{025}=(\begin{array}{ccc}{{E}^{\prime }}_{024},& 压力,& 自然放松\end{array})} $ |
记
| $ { {}_{\psi }T{L}_{02}^{3}={({L}_{02}^{3}) }^{\prime }=(\begin{array}{ccc}{{E}^{\prime }}_{0},& 舒适度,& 90\text{%}\end{array})} $ |
再根据相关网式(5)可知,通过对座椅D0实施上述一系列的主动可拓变换及所引起的传导变换,会导致用户E0的舒适度提升了90%−56%=34%。显然,也超过了目标G0中提高30%舒适度的要求。进而得知目标G0在目前掌握的知识网络中是可以实现的,即说明由上述知识构成的知识网络是完备的。
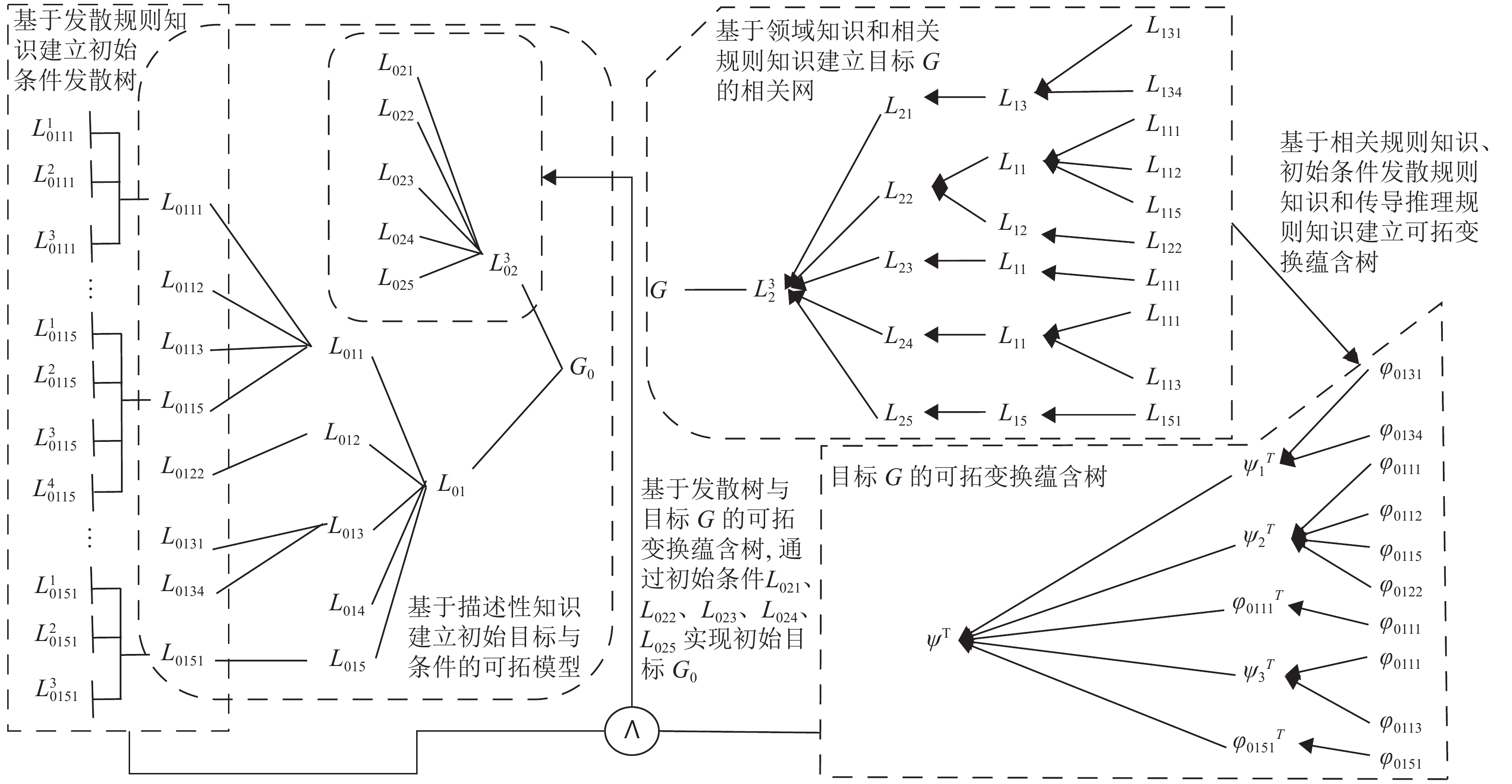
3.4 知识网络的建立基于2.4节完备性知识网络的构建步骤,建立出该开放性问题的完备知识网络。对该开放性问题中描述性知识进行提取,并依据领域知识对初始目标与条件进行界定,通过方法论知识建立该开放性问题的初始可拓模型。以描述性知识为起点,结合领域知识,基于可拓推理规则对初始目标和条件进行拓展分析,在3种知识之间建立联系,形成知识网络。经过上述验证,生成的策略能够实现该开放性问题的初始目标,即证明掌握的知识对于该开放性问题求解是完备的,该开放性问题的完备知识网络如图3所示。
|
图 3 开放性问题求解的完备知识网络 Figure 3 Complete knowledge network for solving the ill-defined problem |
开放性问题求解具有广泛的实践应用背景,其关键是具有完备性的知识网络。要构建完备的知识网络至少需要3类知识:描述性知识、方法论知识、领域知识。可拓学以矛盾问题为研究对象,在应用中总结形成了可拓创新方法体系,为开放性问题求解提供了基本的方法论知识。利用该方法论知识,对描述性知识与领域知识进行拓展分析,以双螺旋结构拓展与挖掘关联知识和潜在知识,从而建立问题求解的完备知识网络。通过设计案例证明,这种方法是有效的。该研究为人工智能环境下开放性问题求解的知识完备性研究提供一条新路径。
开放性问题的智能化求解难度大、价值高,具有问题处理、知识管理和人工智能多学科交叉的特点,在实际生活中大量存在,后续还应对知识网络的完备程度进行定量化分析,为开放性问题求解策略的智能生成提供更加可靠的评价依据。
| [1] |
杨春燕, 李兴森. 可拓学40年发展历程及研究进展[J].
广东工业大学学报, 2023, 40(6): 1-11.
YANG C Y, LI X S. Development and research progress of extenics over the past 40 years[J]. Journal of Guangdong University of Technology, 2023, 40(6): 1-11. DOI: 10.12052/gdutxb.kanshouyu. |
| [2] |
李兴森, 许立波, 刘海涛, 等. 因素空间与可拓学的互补性分析及问题处理融合模型[J].
智能系统学报, 2022, 17(5): 990-998.
LI X S, XU L B, LIU H T, et al. A complementary analysis of factor space and extenics and a fusion model for solving problems[J]. CAAI Transactions on Intelligent Systems, 2022, 17(5): 990-998. DOI: 10.11992/tis.202106016. |
| [3] |
李兴森, 石勇, 张玲玲. 从信息爆炸到智能知识管理[M]. 北京: 科学出版社, 2010.
|
| [4] |
李兴森, 洪振挺, 王昊, 等. 可拓学与知识管理交叉研究视角下的问题智能化处理[J].
包装工程, 2021, 42(12): 51-58.
LI X S, HONG Z T, WANG H, et al. Intelligent problem solving from the perspective of extenics and knowledge management[J]. Packaging Engineering, 2021, 42(12): 51-58. |
| [5] |
ZHUANG Y T, WU F, CHEN C, et al. Challenges and opportunities: from big data to knowledge in AI2.0[J], Frontiers of Information Technology & Electronic Engineering, 2017, 18(1): 3-14
|
| [6] |
FUNKE J. Complex problem solving in search for complexity[J].
Journal of Dynamic Decision Making, 2019, 5(10): 1-2.
|
| [7] |
JOKSIMOVIC S. Opportunities of artificial intelligence for supporting complex problem-solving: findings from a scoping review[J].
Computers and Education: Artificial Intelligence, 2023(4): 100138.
|
| [8] |
MONTAG S, MAERTZ J. Searching outside the box in creative problem solving: the role of creative thinking skills and domain knowledge[J].
Journal of Business Research, 2017, 81: 1-10.
DOI: 10.1016/j.jbusres.2017.07.021. |
| [9] |
PARKER A, TIPPMANN E, KRATOCHVIL R. Accessing diverse knowledge for problem solving in the MNC: a network mobilization perspective[J].
Global Strategy Journal, 2019, 9(3): 423-452.
DOI: 10.1002/gsj.1311. |
| [10] |
ARS J, KARIM L. Marginality and problem-solving effectiveness in broadcast search[J].
Organization Science, 2010, 21(5): 1016-1033.
DOI: 10.1287/orsc.1090.0491. |
| [11] |
BECKMANN J. Heigh-Ho: CPS and the seven questions-some thoughts on contemporary complex problem solving research[J].
Journal of Dynamic Decision Making, 2019, 5(12): 1-5.
|
| [12] |
王小彬, 屈梁生. 专家系统中知识一致性和完备性检验的一种方法[J].
计算机工程与应用, 1989(9): 63-66.
|
| [13] |
桂修文, 丁洪, 杨叔子, 等. 知识库的一致性与完备性检验[J].
华中理工大学学报, 1991(S2): 33-39.
GUI X W, DING H, YANG S Z, et al. Consistency and completeness verification of the knowledge base[J]. Journal of Huazhong University of Science and Technology, 1991(S2): 33-39. |
| [14] |
陈雪龙, 镇培. 知识网络的知识完备性测度方法研究[J].
情报学报, 2014, 33(5): 465-480.
CHEN X L, ZHEN P. Measure of knowledge completeness in knowledge network[J]. Journal of the China Society for Scientific and Technical Information, 2014, 33(5): 465-480. DOI: 10.3772/j.issn.1000-0135.2014.05.002. |
| [15] |
PAUL L, JAN T, MARK W. A semantical perspective on verification of knowledge[J].
Data & Knowledge Engineering, 2002, 40: 33-70.
|
| [16] |
杨春燕. 可拓创新方法[M]. 北京: 科学出版社, 2017.
|
| [17] |
李兴森, 许立波, 刘海涛. 面向问题智能处理的基元-因素空间模型研究[J].
广东工业大学学报, 2019, 36(1): 1-9.
LI X S, XU L B, LIU H T. A research on problem oriented intelligent processing model by basic-element and factor space[J]. Journal of Guangdong University of Technology, 2019, 36(1): 1-9. DOI: 10.12052/gdutxb.180135. |
| [18] |
梁梓源, 杨春燕. 基于可拓学的单目标开放性问题求解方法研究[J].
广东工业大学学报, 2023, 40(5): 1-7.
LIANG Z Y, YANG C Y. The method for solving single-goal ill-defined problems based on extenics[J]. Journal of Guangdong University of Technology, 2023, 40(5): 1-7. DOI: 10.12052/gdutxb.220193. |
| [19] |
李苏洋, 杨杰, 周金平, 等. 应用TRIZ理论“脸谱法”和可拓学解决矛盾问题[J].
机械工程师, 2017(3): 30-32.
LI S Y, YANG J, ZHOU J P, et al. Solving contradiction problem based on facebook method of triz theory and extenics[J]. Mechanical Engineer, 2017(3): 30-32. DOI: 10.3969/j.issn.1002-2333.2017.03.014. |
| [20] |
许立波, 李兴森, 郭研. 三参数区间数下非线性可拓关联度决策方法[J].
控制与决策, 2019, 34(10): 2203-2212.
XU L B, LI X S, GUO Y. Nonlinear extension dependent degree method to three-parameter interval number decision making[J]. Control and Decision, 2019, 34(10): 2203-2212. |
| [21] |
YANG C Y, WANC G H, LI Y, et al. Study on knowledge reasoning based on extended formulas[C]//International Conference on AIAI. New York: Springer, 2005.
|
| [22] |
杨春燕, 蔡文, 汤龙. 可拓学[M]. 2版. 北京: 科学出版社, 2024.
|
| [23] |
蔡文, 杨春燕, 何斌. 可拓逻辑初步[M]. 北京: 科学出版社, 2003.
|
| [24] |
杨春燕, 廖升平, 葛标标. 复合元变换的传导规则及其在创意生成中的应用[J]. 机械设计, 2023, 40(12): 156-162.
YANG C Y, LIAO S P, GE B B. Conductive rules of compound-element transformations and its application in ideas generation[J]. Journal of Meching Design, 2023, 40(12): 156-162. |
| [25] |
阮宝湘, 刘永翔, 董明明. 工业设计人机工程[M]. 3版. 北京: 机械工业出版社, 2016.
|
| [26] |
王金, 支锦亦, 向泽锐, 等. 基于座椅人机参数的列车座椅舒适度评价方法[J].
西南交通大学学报, 2019, 54(6): 1342-1348.
WANG J, ZHI J Y, XIANG Z R. Evaluation method of seat comfort for high-speed trains based on seat ergonomic parameters[J]. Journal of Southwest Jiaotong University, 2019, 54(6): 1342-1348. |
| [27] |
蒋祖华, 赖朝安, 王东勃, 等. 人因工程[M]. 北京: 科学出版社, 2011.
|
| [28] |
吕荣丰, 姜芹, 张莹, 等. 人体工程学[M]. 重庆: 重庆大学出版社, 2014.
|
| [29] |
芦国桢, 熊先青. 办公座椅设计对用户舒适度的影响[J].
家具, 2022, 43(5): 54-58.
|
 2025, Vol. 42
2025, Vol. 42

