在医学成像领域中,锥束计算机断层扫描(Cone Beam Computed Tomography, CBCT) 和单光子发射计算机断层扫描(Single Photon Emission Computed Tomography, SPECT) 是两种广泛使用的成像方式。CBCT以其高分辨率的三维成像能力,在牙科和骨科等领域中发挥着重要作用。而SPECT则通过使用放射性示踪剂和专用探测器提供人体器官和组织的功能性成像,有效提高了疾病诊断和治疗监测的精确性。然而,这两种成像技术在为医学诊断提供宝贵信息的同时,也可能对人体造成辐射伤害。过量的辐射不仅增加了患者患癌的风险,还可能对身体造成其他影响。为了降低上述潜在的伤害,研究者们探索了减少投影角度和降低射线强度等策略,以期在保证成像质量的前提下减少辐射剂量。
在CBCT和SPECT的图像重建领域,主要使用两大类传统方法:解析法和迭代法。解析法通过直接对投影数据进行数学变换来重建图像,其中FDK(Feldkamp-Davis-Kress) 算法[1]在CBCT重建中被广泛应用,而滤波反投影(Filtered Back Projection, FBP) 算法[2]则是SPECT以及其他断层成像技术中的经典重建方法。相较之下,迭代法[3-4]通过一个逐步逼近的过程来优化和提高图像质量,它不断调整图像以更好地符合投影数据,从而实现更精确的重建效果。尽管这两大方法各有优势,但在投影角度不足的情况下都面临着一定的缺陷。解析法在处理稀疏数据时往往会导致图像中的伪影和噪声增多,使得图像质量下降。迭代法虽然在处理稀疏数据和降噪方面表现更好,但计算过程相对复杂且耗时,这在需要高分辨率和高质量重建的医学应用中尤为明显。因此,针对稀疏视角条件下的重建问题,传统方法的局限性促使研究者寻求更高效且质量更优的重建算法。
近年来,深度学习技术在医学影像处理等领域被广泛应用[5-9],特别是神经辐射场(Neural Radiance Fields, NeRF) [10]技术的出现和发展,为三维场景的理解和新视角合成提供了新的思路。这种隐式神经表达(Implicit Neural Representation, INR) 技术通过神经网络模型学习场景的连续体积密度和颜色,从而能够从新视角合成高质量的图像。它对三维场景深入学习和合成新视图的能力,与稀疏视角医学影像重建的研究目标高度契合。
尽管基于NeRF的方法在三维场景重建和新视图合成方面已经取得显著成就,但在计算机视觉及医学影像的3D重建研究中,大部分现有方法仍旧采用多层感知器(Multi-Layer Perceptron, MLP) 来表征有界场。这种方法在本质上采取的是对单个点进行独立学习的策略,通过逐点查询逼近真实的三维场景。然而,这种点级查询的方式忽略了采样点之间的内在联系,从而限制了NeRF技术的巨大潜能。为了克服这一缺点,Wang等[11]采用了Transformer而非MLP作为查询网络,通过Transformer的自注意力机制,捕捉同一射线上所有采样点之间的内在联系,从而实现了更优的重建效果。然而这种同时学习整条射线上的采样点的方法并不适用于医学影像重建工作,因为在人体内同一射线上相距较远的采样点间的关联性较弱,这可能会削弱自注意力机制的学习效果。只有相邻采样点(沿同一射线或相邻射线) 才具有强关联性。
为了充分利用人体内相邻采样点之间的强关联性,并将点级查询扩展至多条射线级查询,本文提出了一种专为稀疏视角断层重建设计的新型自监督方法。本文的主要贡献如下:
(1) 利用Transformer网络的自注意力机制,捕捉二维邻域采样点之间的内在联系,极大地挖掘了INR方法的潜力。此外,在锥束和平行光束成像几何结构上进行了数值实验,展示了所提方法的鲁棒性和广泛适用性。
(2) 在稀疏视角CBCT投影重建图像中,展现了卓越的性能,特别是在整体精度、图像空间分辨率和噪声抑制方面,显著超过了当前先进的自监督INR方法。
(3) 首次将INR技术应用于SPECT模态的稀疏视角重建,并通过数值实验验证了其性能优于传统的SPECT重建方法。
1 相关工作 1.1 隐式神经表示技术近年来,应用神经网络来表征场景的形状与外观,已成为学术研究的热点。这类方法属于INR技术的一种应用。尤其是NeRF技术,它通过MLP参数化的连续函数,有效地将三维坐标和观测方向映射至体积密度和颜色值,因此受到广泛关注。它的成功应用激发了一系列后续扩展,以适用于不同的场景。
在训练视角受限方面,Rematas等[12]提出了一种基于单张图像的神经场表示方法,可以用于估计物体的几何形状和辐射场,并且能够生成具有几何一致性的新视图。Yu等[13]通过引入一种全卷积方式在图像输入上调节NeRF的架构,让网络能够从稀疏视图集以前馈方式执行新视图合成。
在加速训练方面,Reiser等[14]通过利用数千个小型的MLP代替单一大型的MLP,从而加速NeRF的渲染速度,同时不影响渲染质量。肖祎龙等[15]通过引入自适应的编码方式作为位置特征编码并设计一个体密度估计网络,加快模型收敛的同时还提高了体渲染计算效率。
另外,在稀疏视角医学影像重建方面,Zha等[16]通过三维空间坐标的连续函数表示目标的衰减系数,并采用基于学习的编码器进行哈希编码,不仅提高了模型重建的精度,还显著减少了计算时间。Xian等[17]通过加入频率正则化直接控制神经网络输入中的可见频段,减少过拟合的同时有效地平衡了高频信息和低频信息,从而提高模型重建精度。Fang等[18]通过训练神经衰减场来进行稀疏视角CBCT重建,并提出了一种结合去模糊网络的视图增强策略克服来自稀疏输入视图的挑战,有效提升了重建质量。
1.2 Transformers模型Transformers最初被设计用于机器翻译,并彻底革新了许多自然语言处理任务[19-20]。近期,基于Transformer的方法在计算机视觉领域也取得了显著进展。Dosovitskiy等[21]将图像分成多个块,将上述图像块的线性嵌入序列直接输入到Transformer中进行分类,这种方法不仅在性能上与卷积神经网络相当,还有效减少了计算资源的消耗。Li等[22]通过开发Tokens-to-Token模块,逐步将图像结构化为令牌,有效地建模了图像的局部结构信息,这一方法显著提升了在中等规模数据集上的训练效率和性能表现。Xie等[23]将Transformer与轻量级MLP解码器相结合,在避免了位置编码插值的同时,还通过结合局部注意力和全局注意力,实现了一个简单、高效且功能强大的语义分割框架。Dai等[24]采用了一种名为随机查询补丁检测的先验任务,该任务通过预测原始图像中的随机查询补丁来预训练模型的Transformer部分,从而提高目标检测性能。
在医学图像处理任务中,Chen等[25]提出了一种新的医学图像分割框架,该框架结合了 Transformer和U-Net,通过恢复局部空间信息从而增强了细节表现。Zhang等[26]将低剂量的 LDCT图像分解为高低频特征,然后使用 Transformer 对高频特征进行精细处理,从而实现高质量的低剂量LDCT图像恢复。
在将Transformer应用于INR技术的研究中,范国玉[27]将Transformer与对抗生成网络结合,优化了隐式神经表达模型的处理能力,使其能有效处理高分辨率图像,并显著提升了图像生成的效果。Wang等[28]提出一个通用的视图插值函数,该函数可广泛应用于新场景,其中卷积神经网络在颜色预测中起到关键作用,且预测过程遵循点级查询的原则。相较之下,本文提出了一种完全基于Transformer的方法,它通过局部区域查询来预测成像物理量,并通过跳跃连接增强原始位置信息,实现高质量图像渲染。
2 本文方法 2.1 背景NeRF通过MLP将场景表示为一个连续的神经辐射场f,该场用于预测颜色和密度。具体而言,它将三维位置坐标X = (x, y, z) 和观察方向d = (θ, ϕ) 作为输入,并输出相应的颜色c和密度σ:f (X, d) = (c, σ) 。通过在一条光线路径上查询共N个采样点,能够获取这些点的颜色值ci和密度值σi,进而计算该光线渲染后的像素颜色。像素渲染的计算见式(1)。
| $ \begin{split} & {\overset{\frown} c} =\sum\limits_{i = 1}^N {{T_i}} (1 - \exp ( - {\sigma _i}{\delta _i}) ) {c_i}{\text{, }} \\ & {\text{ where }}{T_i} = \exp \big( - \sum\limits_{j = 1}^{i - 1} {{\sigma _j}{\delta _j}} \big) \end{split} $ | (1) |
式中:δi 为相邻采样点之间的距离,ci为采样点的颜色值,σi为采样点的密度值,Ti为采样点沿射线的透射率。通过对MLP进行W×H×N次查询,能够渲染出具有W×H像素的二维图像,最终通过最小化真实像素与相应渲染像素之间的均方误差来优化网络参数。关于NeRF的更多信息详见文献[10]。
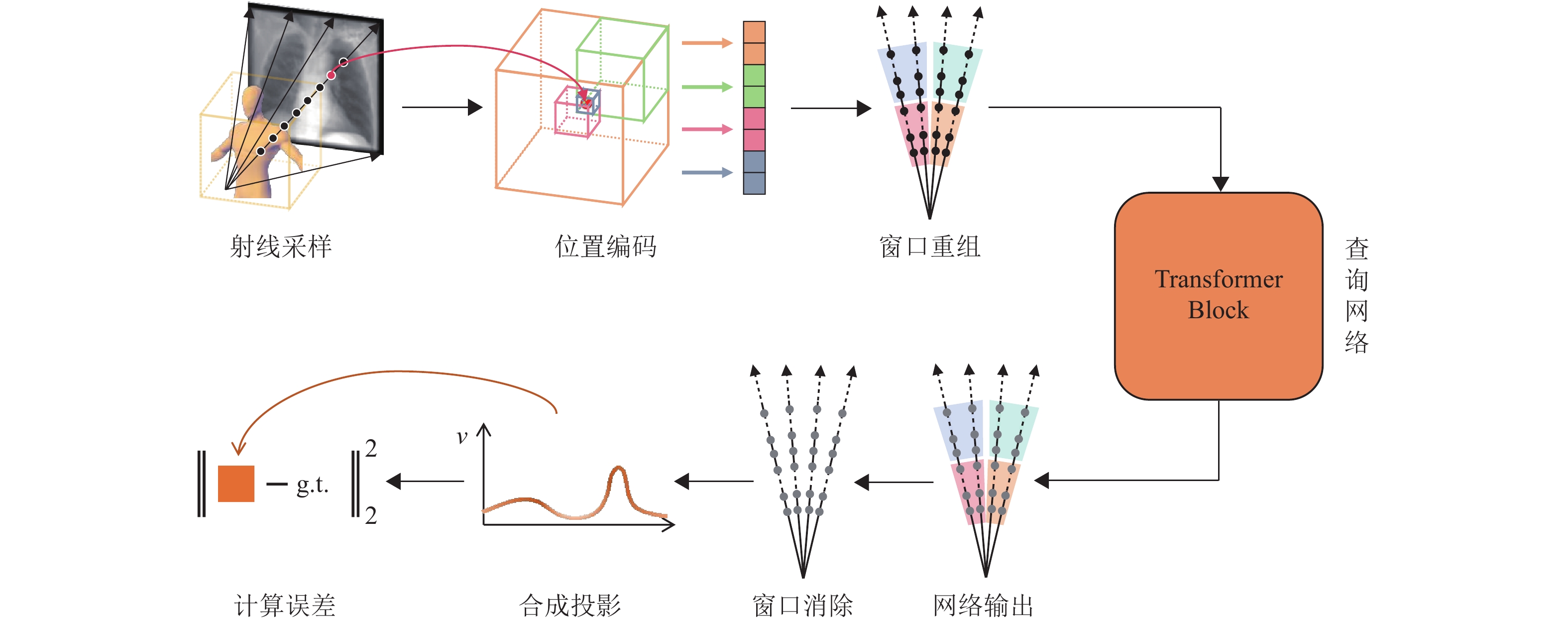
2.2 总体框架本文的训练迭代流程如图1所示。首先,在三维图像空间中依据特定的成像几何(锥束或平行光束) 生成1 024条射线,每条射线上均匀采样N个点,并将所有采样点按其空间位置顺序排列。接着通过多分辨率哈希编码[29]对采样点进行位置编码,关于多分辨率哈希编码的更多信息详见文献[29]。位置编码后的采样点顺序不发生改变,随后将局部邻域内的采样点重新组织为一系列感兴趣窗口。上述窗口被输入到查询网络中,经过处理后最终输出相应的一维物理量,代表采样点处的衰减系数μ(CBCT成像模态) 或示踪剂活性分布λ(SPECT成像模态) 。最后通过撤销窗口将采样点恢复到原始顺序,并沿既定射线合成投影图像,模型通过最小化合成投影与真实投影之间的均方误差进行学习。
|
图 1 方法训练迭代流程框架 Figure 1 The basic training iteration procedure of the proposed method |
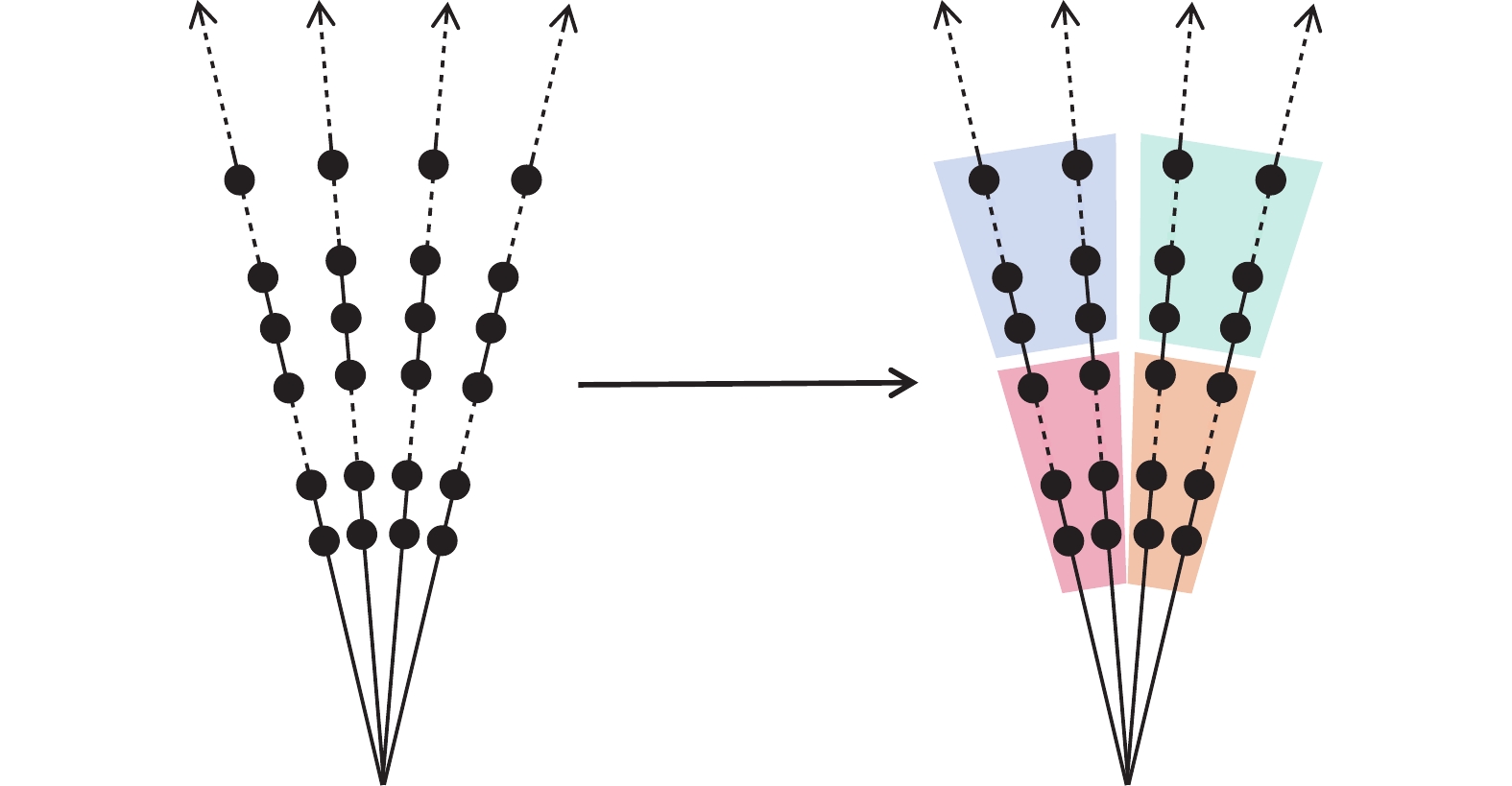
医学图像因其分段平滑的特性,衰减系数μ或示踪剂活性分布λ在局部邻域内通常表现出相似性。因此,相邻射线上的邻近采样点之间存在较强的关联性。为了有效学习上述采样点之间的内在联系,本文将它们重新组织成相应的感兴趣窗口以便输入到网络中。如图2所示,首先将每条光线上的采样点等量划分为Q个段,其中每个段包含N/Q个采样点;然后定义一个感兴趣窗口,该窗口涵盖R条相邻射线上的R个段,每条射线对应一个段。在锥束几何配置中,这R个段具有相同的径向距离;在平行光束几何配置中,这R个段与探测器表面保持相同的深度。通过这种方式进行窗口重组后,每个感兴趣窗口包含了R×N/Q个采样点。此外,上述感兴趣窗口被设计为互不重叠,因此整个空间可以被划分为1 024×Q/R个独立的感兴趣窗口。
|
图 2 窗口重组示意图 Figure 2 Diagram of window reorganization |
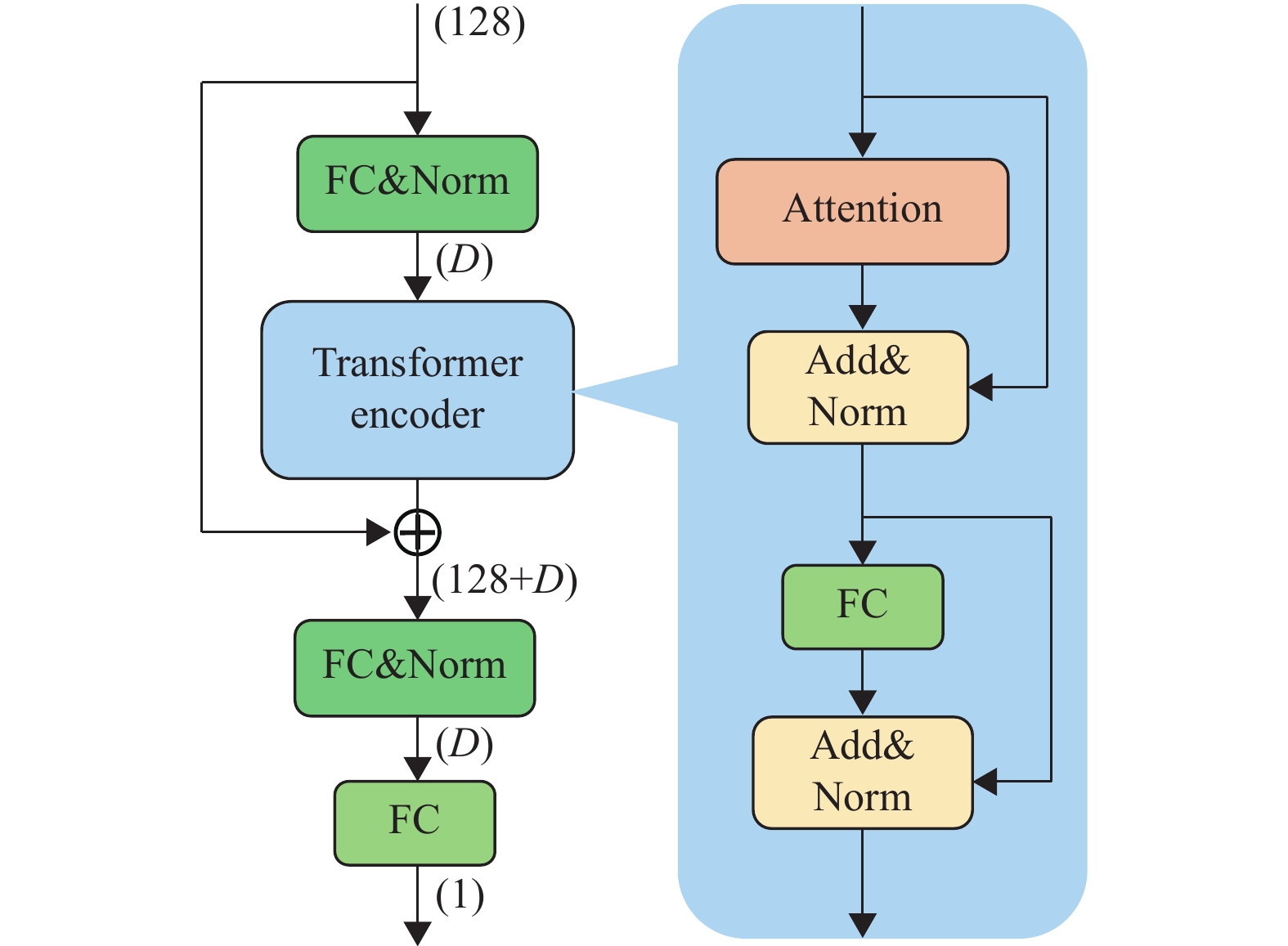
如图3所示,本文构建了一个基于Transformer的网络模型,专门用于表征三维场景。该模型由1个Transformer编码器和3个全连接(Fully Connected, FC) 层构成,其中Transformer编码器包含1个自注意力模块和1个MLP模块。将所有收集到的感兴趣窗口输入到网络后,可以通过Transformer的自注意力机制学习每个感兴趣窗口内采样点之间的内在联系。此外,受文献[10]模型结构的启发,本文采用了一种跳跃连接策略。这种策略通过将位置编码的输出与Transformer模块的输出相连接,从而增强了每个采样点的原始位置信息。因此,经过跳跃连接处理后的输出表达式定义为式(2)。
|
图 3 Transformer网络结构示意图 Figure 3 Architecture of the Transformer network |
| $ {C_{{\text{out}}}}={T_{{\text{out}}}} \oplus \gamma (X) $ | (2) |
式中:Tout为经过Transformer编码器后的输出,
经网络处理后,所有采样点的特征信息已通过自注意力机制得到增强。为了进行后续的投影合成步骤,需要撤销感兴趣窗口的设置,从而恢复采样点的原始空间顺序。这一过程实质上是窗口重组的逆过程,有效地将采样点从感兴趣窗口中解放,并将它们重新分配回其在三维域中相应的原始射线上。
2.3.4 合成投影为了计算与真实投影之间的均方误差,将根据CBCT或平行光束SPECT的数据采集原理,通过在神经表示模型中使用相应采样点的衰减系数μ或示踪剂活性分布λ来生成合成投影。
CBCT:根据比尔−朗伯定律,X射线的出射强度相对于其入射强度呈指数衰减。该过程的数学描述见式(3)。
| $ I = {I_0}\exp \big( - \sum\limits_{i = 1}^N {{\mu _i}{\delta _i}} \big) $ | (3) |
式中:I0为X射线的入射强度,μi为网络输出的采样点的衰减系数,δi为相邻点之间的距离,N为每条射线上的采样点个数。
SPECT:SPECT成像中的简化投影过程可通过拉东变换进行数学描述,该变换用于表示在特定伽马射线路径上,放射性示踪剂活性的累积效应。据此,伽马射线出射的累积值的计算公式见式(4)。
| $ I = \sum\limits_{i = 1}^N {{\lambda _i}{\delta _i}} $ | (4) |
式中:λi为网络输出的采样点示踪剂活性分布,δi为相邻点的距离,N为每条射线上的采样点个数。
在图像上的所有射线完成投影计算后,将生成预测的投影图,随后通过最小化真实图像与合成投影之间的均方误差来对模型进行优化。
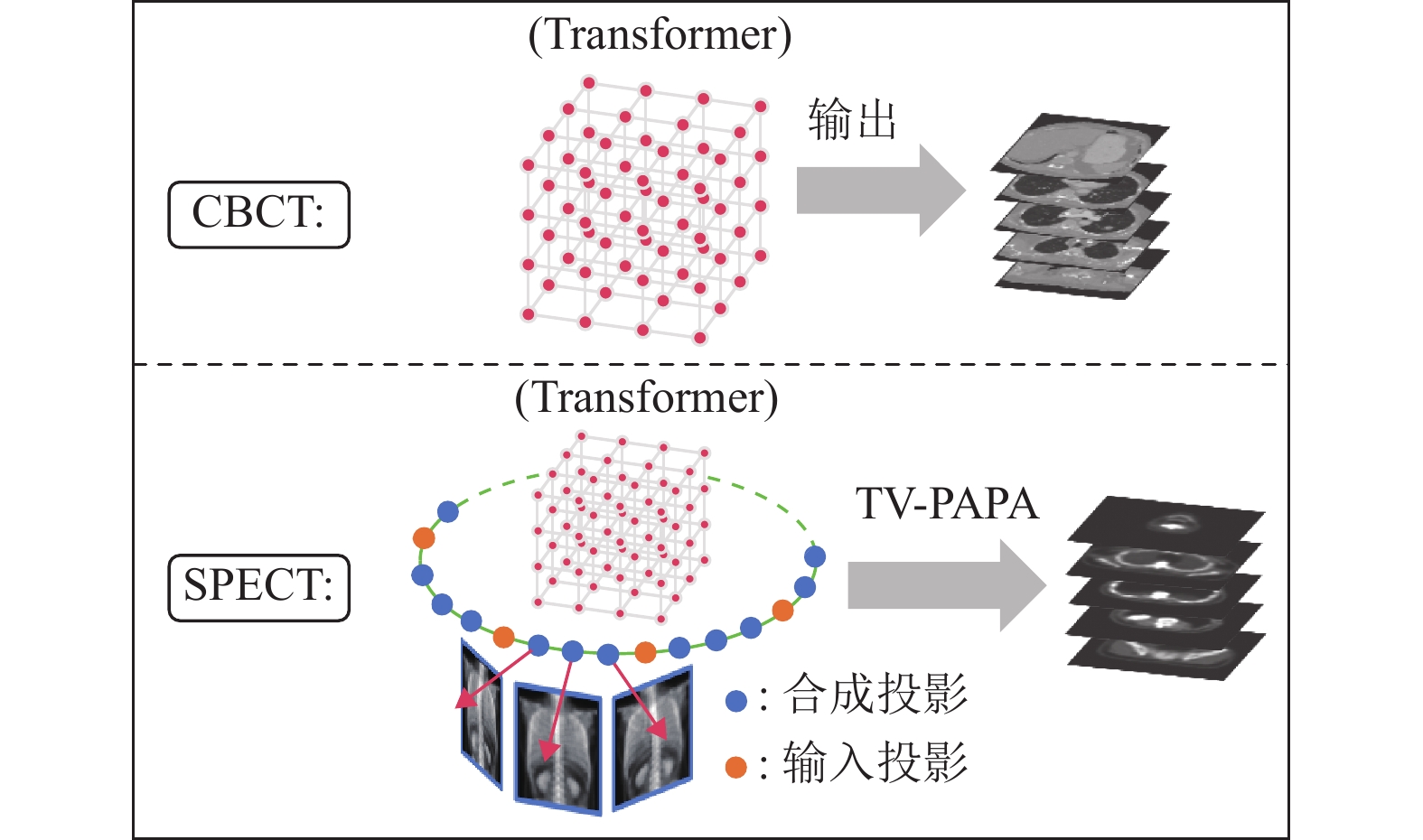
2.4 模型重建如图4所示,本文采用了不同的策略来重建CBCT和SPECT的稀疏视角投影图像。
|
图 4 CBCT和SPECT的重建策略示意图 Figure 4 Reconstruction diagrams of the CBCT and SPECT |
对于CBCT数据集,三维衰减场被离散化为一个均匀的网格,每个体素对应一个采样点。训练完成后的Transformer网络以所有采样点的坐标为输入,直接预测每个采样点的衰减系数μ,并基于上述预测值直接输出重建图像。
对于SPECT数据集,使用训练完成的Transformer网络来合成新视角下的投影;随后通过结合真实投影和合成投影的组合数据,采用TV-PAPA重建算法[4]进一步处理,以生成SPECT的重建图像。
3 实验结果与分析 3.1 数据集本文在4个CBCT数据集和4个平行光束SPECT数据集上进行了数值实验,以验证所提方法在稀疏视角断层重建中的有效性。相关数据集的具体细节见表1。
| 表 1 实验数据集详情 Table 1 Details of datasets used in the experiments |
CBCT数据集:本文采用与NAF[16]相同的公开人体器官CT扫描数据集来进行数值实验,上述数据集涵盖胸部、颌部、足部和腹部区域。其中,胸部数据来源于LIDC-IDRI数据集[30],其余数据集则选自开放科学可视化数据集[31]。本文使用断层成像工具箱TIGRE生成了50个投影,以上投影共覆盖180°的范围,每个投影中包含3%的高斯噪声。本文的方法根据上述投影数据进行训练,并以原始的三维CT数据作为基准进行比较评估。
SPECT数据集:SPECT投影数据集是通过使用蒙特卡罗模拟软件SIMIND[32]和XCAT数字模体[33]生成的仿真模体数据集。具体来说,本文模拟了4个用于骨骼SPECT研究的仿真模体数据集,使用了放射性示踪剂Tc-99m-MDP,并覆盖了360°的范围。初始的稀疏视角投影数据包括30个由SIMIND软件模拟的投影图像,以上图像用于自监督训练以确定INR模型。基于优化后的INR模型,合成了90个新视角的投影,并使用TV-PAPA重建算法重建了120个组合视角的投影数据。最终,重建结果与真实的三维仿真模体数据进行了比较评估。
3.2 对比方法为了验证本文方法的有效性,本文将所提方法与迭代重建方法和基于INR的深度学习方法进行了对比,以此评估其性能。对于CBCT数据集,本文选择同时代数重建技术(Simultaneous Algebraic Reconstruction Technique, SART)[3]作为对比的迭代重建方法;对于SPECT数据集,选择了迭代重建方法TV-PAPA[4]作为对比的迭代重建方法。此外,本文还分别在这两种模态下与INR方法:NAF, NeXT和Freq-NAF进行了比较,以评估本文方法在CBCT和SPECT这两种模态上的性能。
3.3 实验设置和评价指标本文的所有实验均在配备PyTorch框架的NVIDIA RTX 3090Ti GPU上进行。在实验中,使用Adam优化器对参数进行优化,初始学习率设定为10−3,随后在实验的后期降低至10−4。实验训练迭代次数为3 000次。实验批大小设定为1 024条射线,每条射线上的采样点数量N则依据被训练断层图像的分辨率确定。例如,在处理分辨率为128×128×128像素的胸部CT图像时,选择在每条射线上采样192个点。网络中的MLP激活函数为LeakyReLU函数。在执行窗口重组的过程中,射线数量R和分段数量Q是2个重要参数,不同取值对实验结果的影响将在第3.5节进行详细讨论。
为了全面评估不同重建方法的性能,本文采用了3种图像质量评价指标:峰值信噪比(Peak Signal-to-Noise Ratio, PSNR)、结构相似性指数(Structural Similarity Index Measure, SSIM) 和感知图像质量评分(Learned Perceptual Image Patch Similarity, LPIPS)。
PSNR是衡量图像重建质量的常用量化指标,主要评估重建图像与原始图像间的绝对误差;通常情况下,更高的PSNR值意味着更低的像素级误差。
SSIM专注于图像的视觉感知特性,通过模拟人眼对亮度、对比度和结构的感知来评价图像质量;更高的SSIM值表示图像的结构、亮度和对比度与原始图像更为接近。
LPIPS利用深度学习方法来衡量图像间的感知差异,通过在特征空间中比较图像的差异来评估视觉相似度;更低的LPIPS分数表明图像间的感知差异更小,即重建图像在视觉上更贴近原图。
3.4 实验结果 3.4.1 CBCT数据集表2列出了5种重建方法在4个CBCT数据集上的PSNR、SSIM和LPIPS结果。定量分析结果显示,所提方法在大部分评估的数据集中明显优于其他4种方法,表现出最高的PSNR和SSIM值,同时在LPIPS值上也显示出良好的结果。特别是在胸部数据集上,所提方法的PSNR值比排名次之的方法Freq-NAF高0.45 dB。
| 表 2 5种重建方法在4个CBCT数据集上的PSNR/SSIM/LPIPS测量结果1) Table 2 PSNR/SSIM/LPIPS measurements of five reconstruction methods on four CBCT datasets |
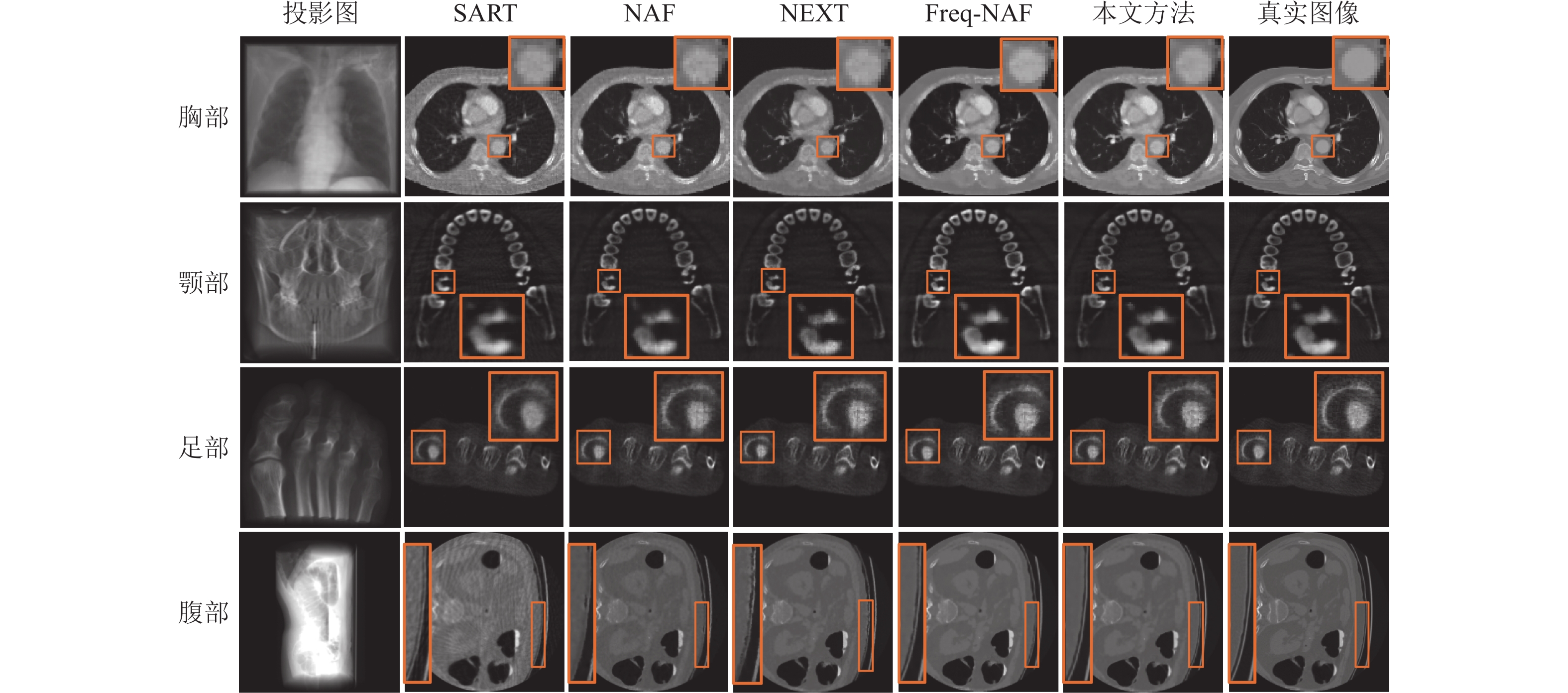
图5对5种重建方法进行了视觉对比。由于投影视角不足,迭代方法SART重建的图像出现了明显的条纹伪影,且呈现较高的噪声水平和较低的对比度。INR方法NAF有效地抑制了条纹伪影,然而,其重建的人体内部区域如胸部和颌部数据集的感兴趣区域仍出现轻微噪声。此外,在腹部数据集放大的感兴趣区域,重建图像边缘的空间分辨率有所下降。上述重建图像的评估显示,传统的MLP学习网络未能有效地区分重要的高频信息(如边缘和边界)与不需要的信息(如图像噪声)。INR方法NeXT通过利用Transformer的自注意力机制,在减少噪声和提高分辨率方面相较于NAF方法取得了一定的改善。然而,总体图像质量的提升仍然有限。这表明在处理关联性较低的采样点时,自注意力机制无法充分发挥其学习效果。INR方法Freq-NAF通过引入频率正则化,进一步提高了重建图像的清晰度和降低了噪声水平,然而观察胸部和腹部切片放大的感兴趣区域,其视觉效果与本文方法相比仍存在肉眼可见的差距。相较之下,本文方法借助自注意力机制学习二维窗口内相邻采样点的内在联系,在不牺牲空间分辨率的情况下,显著提高了重建图像的对比度并降低了噪声水平,从而生成了细节丰富、边缘清晰且噪声最小的重建图像。
|
图 5 5种CBCT重建方法的定性结果 Figure 5 Qualitative results of five CBCT reconstruction methods |
本文对4个仿真模体数据集进行了数值实验,表3展示了5种重建方法在仿真模体数据集上的PSNR、SSIM和LPIPS结果。在仅有30个投影视角的条件下,本文方法展现了最优的定量效果,其PSNR、SSIM和LPIPS值明显优于其他对比方法。在SPECT成像模态中,相比于TV-PAPA,NAF、NeXT和Freq-NAF在提升图像质量方面的效果有限,其SSIM值甚至低于迭代方法TV-PAPA。相较之下,本文方法在这3个指标上均展示了卓越的性能,充分体现了其鲁棒性和广泛的适用性。
| 表 3 5种重建方法在4个SPECT仿真模体上的PSNR/SSIM/LPIPS测量结果1) Table 3 PSNR/SSIM/LPIPS measurements of five reconstruction methods on four SPECT phantoms |
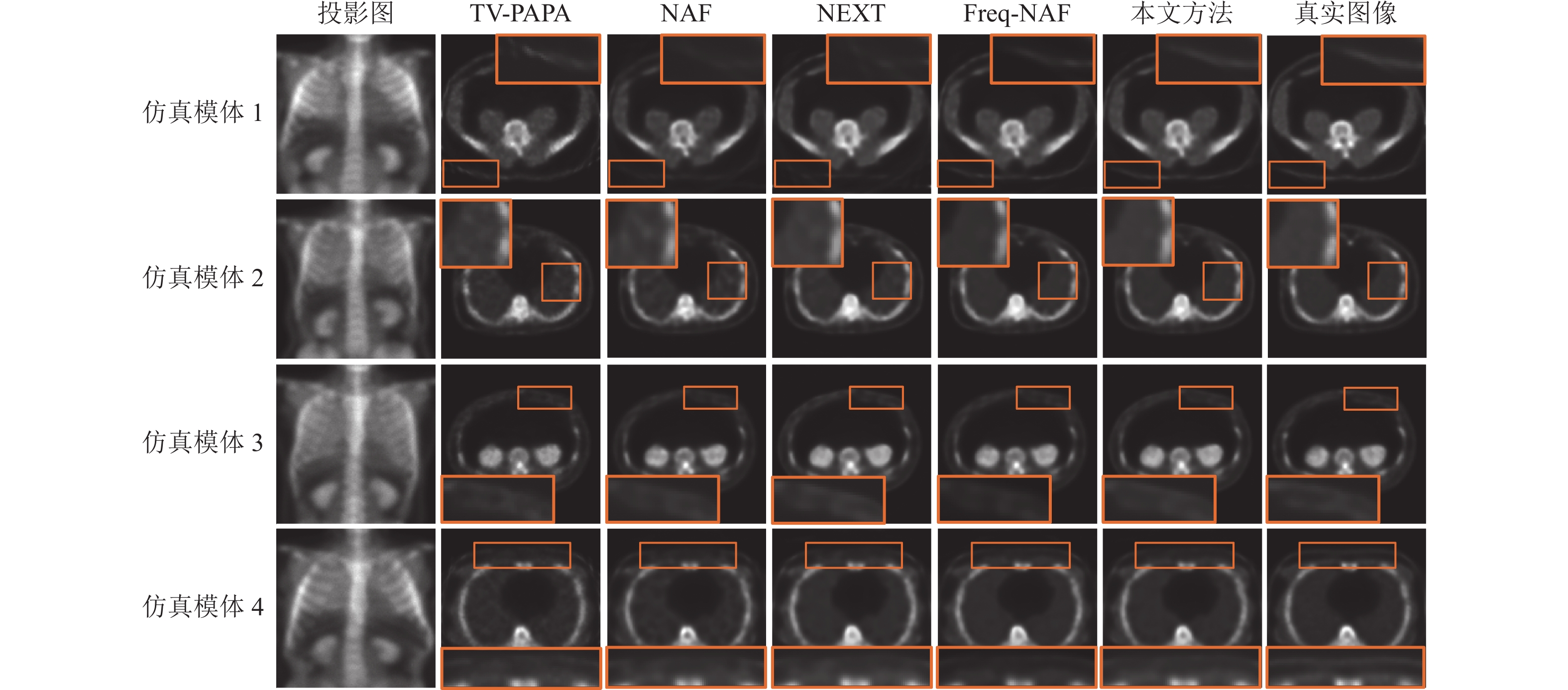
图6展示了从每个SPECT仿真模体中选取的最具代表性的一张重建切片,以此展现5种SPECT重建方法的视觉效果。观察放大的感兴趣区域显示,相比于TV-PAPA、NAF、NeXT和Freq-NAF,本文方法在噪声抑制和对比度恢复方面表现更为突出。
|
图 6 5种SPECT重建方法的定性结果 Figure 6 Qualitative results of five SPECT reconstruction methods |
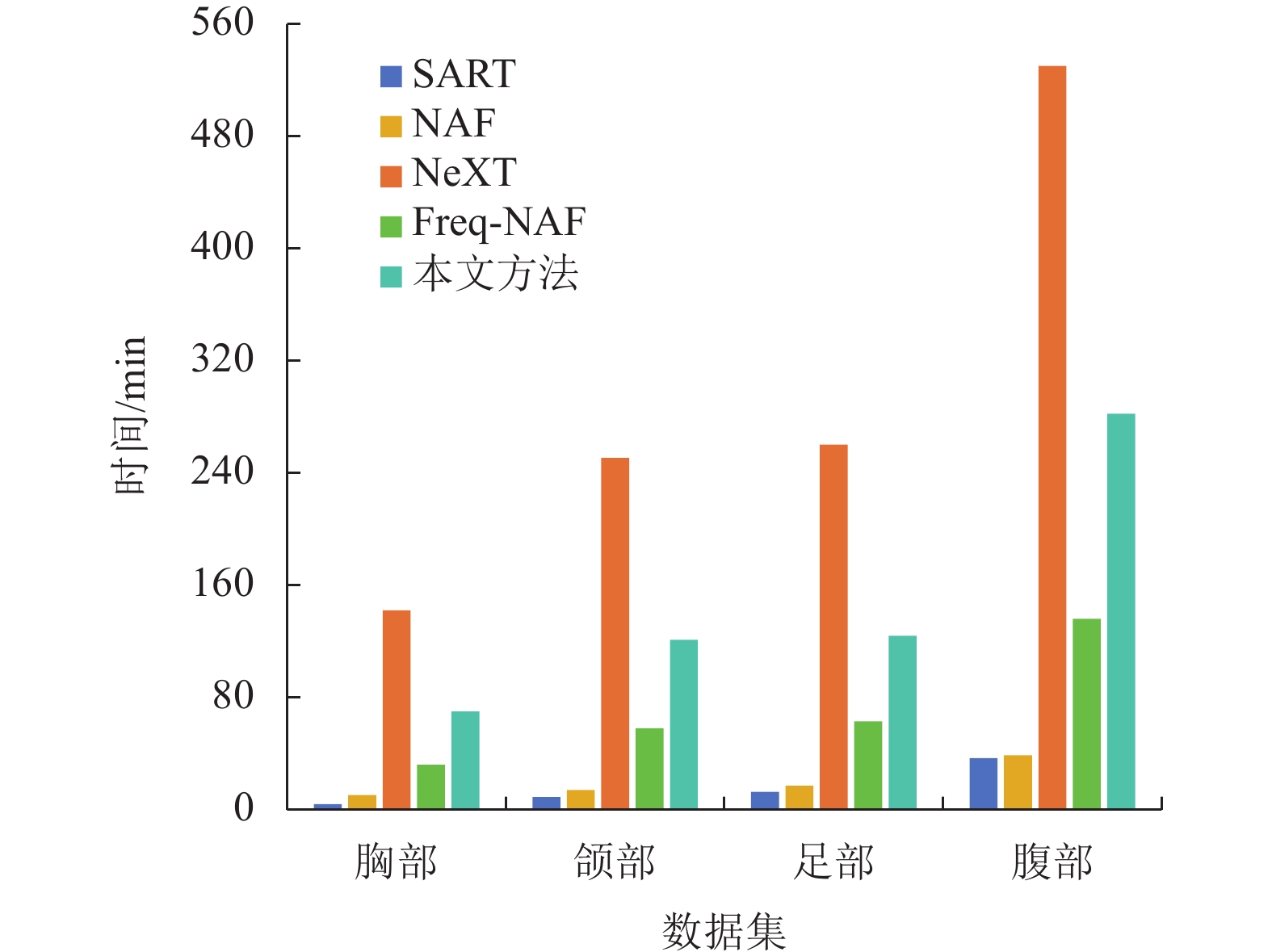
图7记录了几种重建方法在不同CBCT数据集上的运行或训练时间。总体来看,随着数据集投影数据尺寸的增大,所有方法所需的时间均呈现增加趋势。不同方法在相同数据集上的运行或训练时间差异显著,按从长到短的顺序为:NeXT、本文方法、Freq-NAF、NAF和SART。NAF方法采用多分辨率哈希编码,并使用轻量级的MLP网络,因此其训练时间与迭代方法SART相近。NeXT方法则依赖于复杂的Transformer网络模型,并结合傅里叶编码与正弦编码作为位置编码方式,使得其训练时间在所有方法中最长。Freq-NAF方法在NAF的基础上引入频率正则化,虽然该技术不会显著增加训练时间,但Freq-NAF扩大了MLP网络的深度和宽度,导致其训练时间比NAF增加了2至3倍。本文方法同样采用了复杂的Transformer网络模型,但利用多分辨率哈希编码作为位置编码方式,将训练时间缩短至Freq-NAF的2倍。
|
图 7 5种CBCT重建方法收敛到稳定结果所需的运行时间 Figure 7 The running time required by five CBCT reconstruction methods when they converge |
为了研究构成感兴趣窗口大小的2个关键参数:每个窗口覆盖的射线数量R和每条射线的分段数量Q对所提方法性能的影响,本文在胸部数据集上进行了一系列数值实验,探索了R和Q分别取1、2、4和8时的不同组合效果。表4显示了在不同R和Q配置下,所提方法的PSNR、SSIM和LPIPS的结果。定量分析表明,在保持Q值不变的情况下,当R=2时,方法性能达到最优;相反,R值保持恒定,当Q=4时,性能表现最佳。在所有测试组合中,当R=2且Q=4时,本文方法展示出了最优越的性能,具体体现为PSNR和SSIM最高,以及LPIPS最低。此外,本文采用了与胸部数据集相同的实验设计方法,以确定所有数据集的最佳R-Q组合策略。
| 表 4 不同R(射线数量) 和Q(分段数量) 值在胸部数据集上的PSNR/SSIM/LPIPS测量结果 Table 4 PSNR/SSIM/LPIPS measurements of the proposed method versus different R (number of rays) and Q (number of partitions) values on the chest dataset |
本文提出一种针对稀疏视角断层重建的新型自监督方法。该方法通过把三维图像域内的采样点组织成一系列感兴趣窗口,从而将传统的点对点学习方式扩展到INR背景下的二维窗口学习方式。随后感兴趣窗口被输入到一个带有跳跃连接的Transformer查询网络中进行处理,该网络通过利用自注意力机制学习每个感兴趣窗口内采样点之间的内在联系。最终,基于训练完成的Transformer网络预测衰减系数μ或示踪剂活性分布λ。该方法在具有锥束几何的CT数据集和具有平行光束几何的SPECT数据集上均达到了最优的性能,为INR技术在断层重建中的应用拓展,及在稀疏视角场景下提高重建图像质量提供了新的可能性。在未来的工作中,研究重点将是把邻近采样点的依赖性学习从二维窗口式推广到三维锥体式或立方体式。
| [1] |
FELDKAMP L A, DAVIS L C, KRESS J W. Practical cone-beam algorithm[J].
Journal of the Optical of America A, 1984, 1(6): 612-619.
DOI: 10.1364/JOSAA.1.000612. |
| [2] |
RONCHETTI M. Torchradon: fast differentiable routines for computed tomography[EB/OL]. arXiv: 2009.14788(2020-09-29) [2024-09-24]. https://arxiv.org/abs/2009.14788.
|
| [3] |
ANDERSEN A H, KAK A C. Simultaneous algebraic reconstruction technique (SART): a superior implementation of the ART algorithm[J].
Ultrasonic Imaging, 1984, 6(1): 81-94.
DOI: 10.1177/016173468400600107. |
| [4] |
LI S, ZHANG J, KROL A, et al. Effective noise‐suppressed and artifact‐reduced reconstruction of SPECT data using a preconditioned alternating projection algorithm[J].
Medical Physics, 2015, 42(8): 4872-4887.
DOI: 10.1118/1.4926846. |
| [5] |
叶文权, 李斯, 凌捷. 基于多级残差U-Net的稀疏SPECT图像重建[J].
广东工业大学学报, 2023, 40(1): 61-67.
YE W Q, LI S, LING J. Sparse-view SPECT image reconstruction based on multilevel-residual U-Net[J]. Journal of Guangdong University of Technology, 2023, 40(1): 61-67. DOI: 10.12052/gdutxb.220016. |
| [6] |
夏皓, 蔡念, 王平, 等. 基于多分辨率学习卷积神经网络的磁共振图像超分辨率重建[J].
广东工业大学学报, 2020, 37(6): 26-31.
XIA H, CAI N, WANG P, et al. Magnetic resonance image super-resolution via multi-resolution learning[J]. Journal of Guangdong University of Technology, 2020, 37(6): 26-31. DOI: 10.12052/gdutxb.200011. |
| [7] |
梁宇辰, 蔡念, 欧阳文生, 等. 基于切片关联信息的慢性阻塞性肺疾病CT诊断[J].
广东工业大学学报, 2024, 41(1): 27-33.
LIANG Y C, CAI N, OUYANG W S, et al. CT diagnosis of chronic obstructive pulmonary disease based on slice correlation information[J]. Journal of Guangdong University of Technology, 2024, 41(1): 27-33. |
| [8] |
郑煜, 蔡念, 欧阳文生, 等. 基于深度关联机制的肝胆管超分辨率分割[J].
广东工业大学学报, 2023, 40(5): 41-46.
ZHENG Y, CAI N, OUYANG W S, et al. Super-resolution segmentation of hepatobiliary ducts based on deep correlation mechanism[J]. Journal of Guangdong University of Technology, 2023, 40(5): 41-46. DOI: 10.12052/gdutxb.220197. |
| [9] |
曾安, 陈旭宙, 姬玉柱, 等. 基于自注意力和三维卷积的心脏多类分割方法[J].
广东工业大学学报, 2023, 40(6): 168-175.
ZENG A, CHEN X Z, JI Y Z, et al. Cardiac multiclass segmentation method based on self-attention and 3D convolution[J]. Journal of Guangdong University of Technology, 2023, 40(6): 168-175. DOI: 10.12052/gdutxb.230131. |
| [10] |
MILDENHALL B, SRINIVASAN P P, TANCIK M, et al. NeRF: representing scenes as neural radiance fields for view synthesis[J].
Communications of the ACM, 2021, 65(1): 99-106.
|
| [11] |
WANG Y, LI Y, LIU P, et al. NeXT: towards high quality neural radiance fields via multi-skip transformer[C]//European Conference on Computer Vision. Cham: Springer Nature Switzerland, 2022: 69-86.
|
| [12] |
REMATAS K, MARTIN-BRUALLA R, FERRARI V. ShaRF: shape-conditioned radiance fields from a single view[EB/OL]. arXiv: 2102.08860(2021-06-23) [2024-09-24]. https://arxiv.org/abs/2102.08860.
|
| [13] |
YU A, YE V, TANCIK M, et al. Pixelnerf: neural radiance fields from one or few images[C]//Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition. Nashville: IEEE, 2021: 4578-4587.
|
| [14] |
REISER C, PENG S, LIAO Y, et al. KiloNeRF: speeding up neural radiance fields with thousands of tiny mlps[C]//Proceedings of the IEEE/CVF International Conference on Computer Vision. Montreal: IEEE, 2021: 14335-14345.
|
| [15] |
肖祎龙, 邓伊琴, 陈志刚. 面向动态三维人体重建的神经辐射场加速方法[EB/OL]. (2024-06-14) [2024-09-24]. https://doi.org/10.19678/ j.issn.1000-3428.0069317.
|
| [16] |
ZHA R, ZHANG Y, LI H. NAF: neural attenuation fields for sparse-view CBCT reconstruction[C]//International Conference on Medical Image Computing and Computer-Assisted Intervention. Cham: Springer Nature Switzerland, 2022: 442-452.
|
| [17] |
XIAN J M, ZHU J, LIAO H L, et al. Frequency-regularized neural representation method for sparse-view tomographic reconstruction[EB/OL]. arXiv: 2409.14394 (2024-09-24) [2024-09-24]. https://arxiv.org/abs/2409.14394.
|
| [18] |
FANG Y, MEI L, LI C, et al. SNAF: sparse-view CBCT reconstruction with neural attenuation fields[EB/OL]. arXiv: 2211.17048 (2022-11-30) [2024-09-24]. https://arxiv.org/abs/2211.17048.
|
| [19] |
VASWANI A, SHAZEER N, PARMAR N, et al. Attention is all you need[C]//Advances in Neural Information Processing Systems. Long Beach: Curran Associates, 2017: 5998–6008.
|
| [20] |
DEVLIN J, CHANG M W, LEE K, et al. BERT: Pre-training of deep bidirectional transformers for language understanding[C]//Proceedings of the 2019 Conference of the North American Chapter of the Association for Computational Linguistics: Human Language Technologies(NAACL-HLT) . Minneapolis: ACL, 2019: 4171-4186.
|
| [21] |
DOSOVITSKIY A, BEYER L, KOLESNIKOV A, et al. An image is worth 16×16 words: transformers for image recognition at scale[C]// Proceeding of the 9th International Conference on Learning Representations. Vienna: OpenReview. net, 2021: 1-21.
|
| [22] |
YUAN L, CHEN Y, WANG T, et al. Tokens-to-token ViT: training vision transformers from scratch on imagenet[C]//Proceedings of the IEEE/CVF International Conference on Computer Vision. Montreal: IEEE, 2021: 558-567.
|
| [23] |
XIE E, WANG W, YU Z, et al. SegFormer: simple and efficient design for semantic segmentation with transformers[J].
Advances in Neural Information Processing Systems, 2021, 34: 12077-12090.
|
| [24] |
DAI Z, CAI B, LIN Y, et al. UP-DETR: unsupervised pre-training for object detection with transformers[C]//Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition. Nashville: IEEE, 2021: 1601-1610.
|
| [25] |
CHEN J, LU Y, YU Q, et al. TransUNet: transformers make strong encoders for medical image segmentation[EB/OL]. arXiv: 2102.043 06 (2021-02-08) [2024-09-24]. https://arxiv.org/abs/2102.04306.
|
| [26] |
ZHANG Z, YU L, LIANG X, et al. TransCT: dual-path transformer for low dose computed tomography[C]//Medical Image Computing and Computer Assisted Intervention. Strasbourg: Springer, 2021: 55-64.
|
| [27] |
范国玉. 基于transformer和生成对抗网络的3D人脸生成和重建研究[D]. 南京: 南京邮电大学, 2023.
|
| [28] |
WANG Q, WANG Z, GENOVA K, et al. IBRNet: learning multi-view image-based rendering[C]//Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition. Nashville: IEEE, 2021: 4690-4699.
|
| [29] |
MÜLLER T, EVANS A, SCHIED C, et al. Instant neural graphics primitives with a multiresolution hash encoding[J].
ACM Transactions on Graphics (TOG), 2022, 41(4): 1-15.
|
| [30] |
ARMATO III S G, MCLENNAN G, BIDAUT L, et al. The lung image database consortium (LIDC) and image database resource initiative (IDRI): a completed reference database of lung nodules on CT scans[J].
Medical Physics, 2011, 38(2): 915-931.
DOI: 10.1118/1.3528204. |
| [31] |
KLACANSKY P. Open scientific visualization datasets[EB/OL]. (2024-05-16) [2024-09-24]. https://klacansky.com/open-scivis-datasets/.
|
| [32] |
LJUNGBERG M, STRAND S E, KING M A. Monte Carlo calculations in nuclear medicine: applications in diagnostic imaging[M]. Boca Raton, FL: CRC Press, 2012: 287-312.
|
| [33] |
SEGARS W P, STURGEON G, MENDONCA S, et al. 4D XCAT phantom for multimodality imaging research[J].
Medical Physics, 2010, 37(9): 4902-4915.
DOI: 10.1118/1.3480985. |
 2025, Vol. 42
2025, Vol. 42

