2. 广东省第二人民医院 神经外科, 广东 广州 510317;
3. 南方医科大学珠江医院 关节骨病外科, 广东 广州 510280;
4. 湖南省药品审核查验中心, 湖南 长沙 410000
2. Department of Neurosurgery, Second People's Hospital of Guangdong Province, Guangzhou 510317, China;
3. Department of Arthropathy, Zhujiang Hospital, Southern Medical University, Guangzhou 510280, China;
4. Hunan Drug Inspection Center, Changsha 410000, China
半月板是位于股骨髁和胫骨平台之间的独特软骨结构,是稳定膝关节和分配负荷的关键生物组织,并在膝关节的营养和润滑方面发挥一定的作用[1]。当膝关节发生创伤性或退行性半月板撕裂时,若治疗不当,则很容易造成半月板退化或早期骨关节炎[2]。当前的主要治疗方案是用组织工程半月板生物复合植入物(即人工半月板)替代生物体半月板[3]。但是,目前对于生物半月板周向纤维三维微观结构的研究较为匮乏,导致人工半月板几乎不能模拟生物体半月板的微观结构,进而很难获得与生物体半月板相同的力学性能[4]。为此,有必要深入探索和研究半月板周向纤维的三维微观结构,为半月板的力学分析、损伤后的治疗奠定基础。
在半月板微观结构的研究中,Karjalainen等[5]通过微计算机断层扫描技术(Micro Computed Tomography,MicroCT)扫描,定量分析了半月板样本,发现胶原微观结构紊乱是半月板退化的重要原因。Petersen等[6]通过扫描电子显微镜观察半月板横截面,发现半月板上胶原蛋白纤维的分布状况与主要路径呈现3个不同的层次。Fox等[7]同样指出半月板内的胶原蛋白由3个部分组成,并给出了半月板内胶原纤维超微结构和取向的假想图。然而以上研究均局限于人工观察的方法。Tack等[8]提出一种从磁共振图像中自动分割膝关节半月板的新方法,通过算法实现了研究效率的大幅度提升,但其分割对象只是内外侧半月板的轮廓,研究内容并没有深入到半月板的具体微观结构。
深度学习在医学图像分割领域中发挥着独特的优势,基于深度学习的图像分割方法近年来取得了很大成就。全卷积神经网络(Fully Convolutional Networks,FCN)使用卷积层替代了经典卷积神经网络模型的最后一层,达到了准确分割的效果[9]。但这种算法的分割精度不够,并且对图像中的细节不敏感,缺乏空间一致性。U型网络(U-Net)是FCN网络的一个变体,结构简单,采用了与FCN不同的特征融合方式,能够更好地利用全局信息,但是对物体边界的分割精度不够[10]。TransUNet网络是将Transformer和U-Net进行融合后得到的一个网络模型,它是一个具有很强的固有的自我注意机制的医学图像分割框架[11]。实践表明,TransUNet网络在医学图像分割领域取得了比其他网络模型更加优异的性能。
MicroCT图像能够清晰显示半月板内部的微观组织结构,但由于微观组织复杂,当前主要通过人工实现半月板内部结构的分割[12]。人工分割存在效率低下、分割标准不一致等问题。因此,为解决这一困境,在完成人体半月板MicroCT图像获取的基础上,本文提出了一种改进TransUNet算法的半月板MicroCT图像分割模型,文章主要包括以下工作:(1) 在原始算法模型中引入图像块相对位置编码(image Relative Position Encoding,iRPE)并改进损失函数,根据MicroCT图像特点提出了一种全新的图像扩增方法;(2) 设计分割实验,验证改进策略的有效性、图像分割结果的准确性以及模型的泛化能力;(3) 利用改进模型对半月板周向纤维进行分割并完成三维重建。
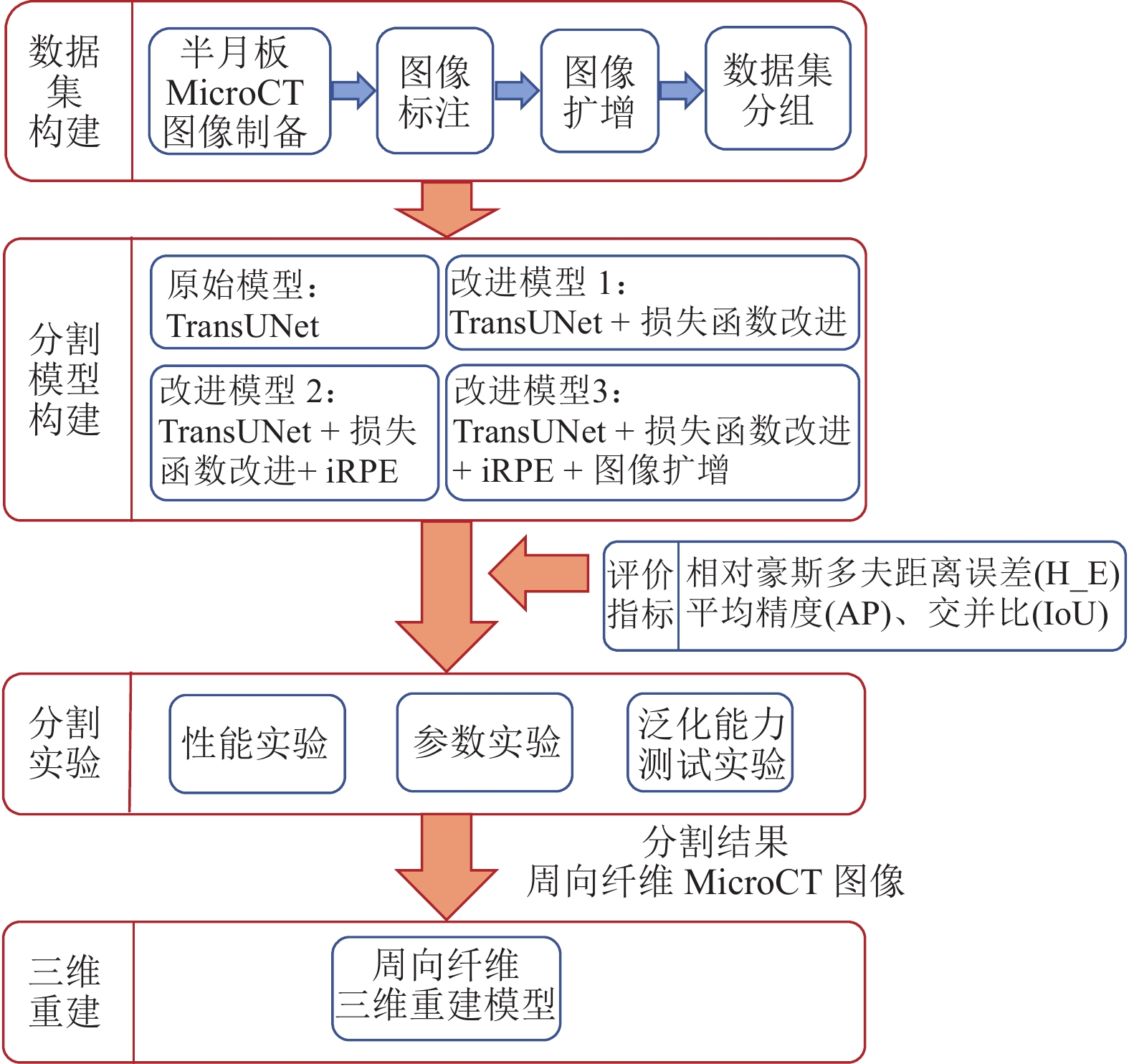
1 研究架构本文的总体研究框架如图1所示,主要包括数据集构建、分割模型构建、评价指标、分割实验和三维重建5部分。
|
图 1 总体研究框架 Figure 1 Overall research framework |
数据集构建部分介绍了半月板MicroCT图像数据集的制备流程、标注方法,同时结合MicroCT图像的特点进行了图像扩增,并且将本文涉及的所有数据集进行了分组。
在分割模型构建部分中,本文进行了2个方面的改进:引入iRPE算法和改进损失函数。
评价指标用于模型性能的评估,为了多角度准确分析模型性能,本文使用了如下3个指标:平均精度、相对豪斯多夫距离误差和交并比。
在分割实验部分中,本文设计了3组实验来分析模型性能:(1) 性能实验用于准确测试模型的分割效果以及探究改进策略的可行性;(2) 参数实验用于探究关键参数对模型性能的影响;(3) 泛化能力测试实验用来测试改进模型的泛化能力。
最后,采用3D Slicer平台对图像中周向纤维的分割结果进行三维建模,得到周向纤维的三维模型[13]。
2 材料由于人体半月板材料获取难度较大,本文并无公共数据集可用,因此本文的数据集为自行构建得到。
2.1 图像制备从两位膝关节置换患者身上获取切除的半月板标本,洗净后冷冻干燥,得到一块冻干的人体半月板组织。取无明显半月板撕裂的部分使用MicroCT扫描仪进行扫描,相关参数见文献[14],得到医学数字成像和通信(Digital Imaging and Communications in Medicine,DICOM)格式图像。
2.2 图像扩增观察标本的原始图像发现,影响图像中目标区域分割的主要因素是背景噪声和“冻干伤”。样本的“冻干伤”是指在前期半月板材料制备过程中,由于水分蒸发和物质浓缩,造成的半月板组织结构变形或损伤。图像扩增流程如图2所示。按照该方法,每张原始图像可得到4张不同于原图的新增图像。

|
图 2 图像扩增流程 Figure 2 Image amplification process |
对DICOM格式图像进行数据预处理,然后使用LabelMe工具对每张半月板MicroCT图像进行人工分割、标注标签[15]。根据本文的研究目的及半月板的微观组织结构,标注的目标区域共分为4类,分别是松散结缔组织、周向纤维、毛细状纤维和背景[16]。图像标注结果如图3所示。

|
图 3 图像标注结果 Figure 3 Results of image annotation |
本文的数据集分组如下:
(1) 半月板数据集A:来自患者1,共310张。按照4:1的比例划分为训练集A1(248张)与测试集A2(62张),分别用于实验部分模型的训练与测试。
(2) 半月板数据集B:由数据集A1扩增得到,共
(3) 半月板数据集C:来自患者2,共50张。按照2:3的比例划分为训练集C1(20张)和验证集C2(30张),分别用于分割模型的二次训练和泛化能力的验证。
3 方法 3.1 网络结构如图4所示,TransUNet在U-Net基础上进行改进,将CNN和Transformer结合共同构成模型的编码器。CNN由于受到卷积运算感受野小的局限而很难利用全局信息,但它可以提取图像的低级定位细节信息,而Transformer结构能很好地把握全局信息。因此CNN和Transformer的结合可以充分发挥二者的优势,使得模型可以提取到更全面且准确的图像特征信息。

|
图 4 改进的TransUNet模型结构图 Figure 4 Improved TransUNet model structure diagram |
TransUNet原始模型采用绝对位置编码,该方法忽视了图像块间的空间位置联系。由于半月板各组织间的边界特征极为相似,模型需要具备极高的边缘分割能力才能完成分割,因此为了提高分割精度,本文在分块嵌入模块中引入了iRPE算法[17-18],如图4所示。
图像块的位置方向包含了大量的图像信息,因此本文引入的iRPE算法采用交叉法计算相对位置编码向量,在水平和垂直方向上分别计算编码,最后进行汇总。通过交叉法的计算,可以将图像的相对位置信息编码到向量
| $ {{\boldsymbol{r}}_{ij}} = {\boldsymbol{p}}_{{I^{\tilde x}}{\text{(}}i,j{\text{) }}}^{\tilde x} + {\boldsymbol{p}}_{{I^{\tilde y}}{\text{(}}i,j{\text{) }}}^{\tilde y} $ | (1) |
| $ {{\boldsymbol{z}}_i} = \sum\limits_{j{\text{ = }}1}^N {{a_{ij}}{\text{(}}{{\boldsymbol{x}}_j}{{\boldsymbol{W}}^{\text{V}}} + {\boldsymbol{r}}_{ij}^{\text{V}}{\text{) }}} $ | (2) |
| $ {a_{ij}} = \frac{{{\text{exp(}}{e_{ij}}{\text{) }}}}{{\sum\limits_{k{\text{ = }}1}^N {{\text{exp(}}{e_{ik}}{\text{) }}} }} $ | (3) |
| $ {e_{ij}} = \frac{{{\text{(}}{{\boldsymbol{x}}_j}{{\boldsymbol{W}}^{\text{Q}}} + {\boldsymbol{r}}_{ij}^{\text{Q}}{\text{) (}}{{\boldsymbol{x}}_j}{{\boldsymbol{W}}^{\text{K}}} + {\boldsymbol{r}}_{ij}^{\text{K}}{{\text{) }}^{\rm{T}}}}}{{\sqrt {{d_z}} }} $ | (4) |
式(1)~(4)中:p为编码方式,
本文在分块嵌入模块中引入iRPE算法,实际处理的对象也并不是原始图像,而是特征图。相较于改进前,改进模型对于特征图的位置信息感知更准确,提高了对边缘分割的准确率。
3.3 损失函数原始TransUNet算法使用的损失函数是组合损失函数,包括戴斯损失函数[19]和交叉熵损失函数[20]两部分。本文对于半月板MicroCT图像的分割更关注周向纤维部分,而在大部分图像中周向纤维在整幅图像中的占比不足10%。因此本文在交叉熵损失函数的基础上引入权重因子wc,使模型能较好地处理不均衡样本。同时调整组合损失函数L的权重分配,改进后的损失函数如式(5)~(6)所示,式中LWCE为带权交叉熵损失函数,LDice为戴斯损失函数,λ为组合损失函数L的权重因子,yc为标签值,pc为预测值,c表示不同类别,M为类别数。
| $ L = \lambda {L_{{\text{WCE}}}} + {\text{(}}1 - \lambda {\text{) }}{L_{{\text{Dice}}}} $ | (5) |
| $ {L_{{\text{WCE}}}} = - \sum\limits_{c = 1}^M {{w_c}{y_c}{\text{l}}{{\text{n}}}{p_c}} $ | (6) |
LWCE的权重因子的计算采取动态调整策略:开始时根据不同类别像素点数量使用反向赋权的方法对权重因子进行初始化。后续权重因子的更新方法如式(7) 所示,在每轮训练后计算出各类别的F1分数值,取其倒数和上一次的权重因子进行等比例加权求和,这样可以使权重因子在相邻的迭代中保持一定的连续性和平滑过渡,减少因偶然情况导致的权重变化对模型训练的干扰。如此循环,直到模型收敛。
| $ {w_{{\text{c\_new}}}} = 0.5{w_{{\text{c\_old}}}} + \frac{{0.5}}{{{F_{\text{1}}}}} $ | (7) |
| $ {F_1} = \frac{{{\text{2}}PR}}{{P + R}} $ | (8) |
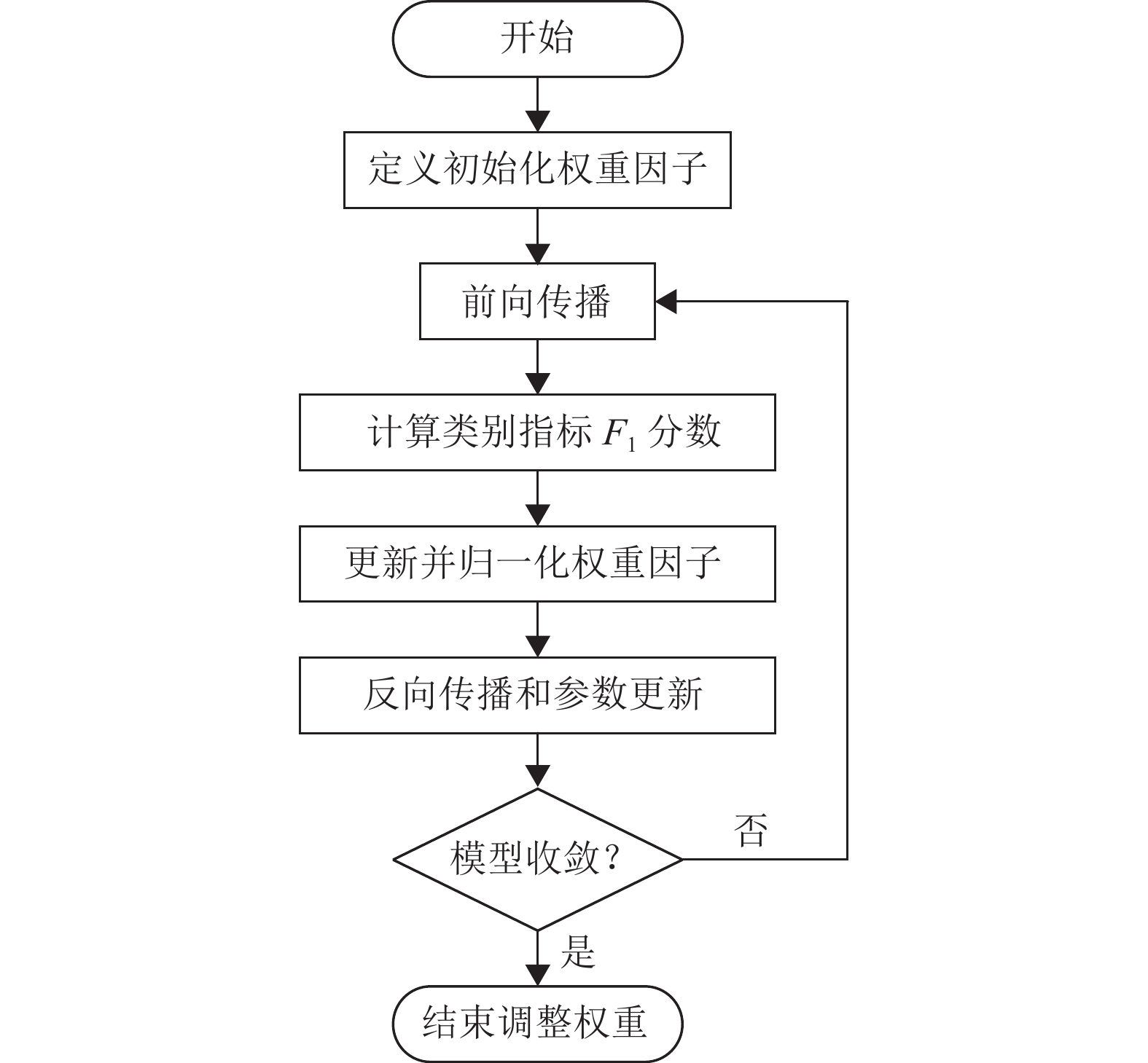
式(8)的F1分数是动态调整策略中的关键指标,它综合考虑了精确度(Precision, P)和召回率(Recall, R),用于评估模型的综合性能。因此在本文中用它计算每个类别的权重因子,使模型更好地处理类别不均衡的情况。权重因子wc动态调整算法流程如图5所示。
|
图 5 权重因子动态调整算法流程图 Figure 5 Flowchart of dynamic adjustment algorithm for weight factors |
本文实验软硬件环境如下:医学图像处理平台3D Slicer(5.0.3,美国),Python集成开发环境Pycharm(2022.1,JetBrains Inc.,捷克),中央处理器(Intel(R) Core(TM) i7-3770 CPU @ 3.40 GHz,Intel Inc.,美国),图形处理器(NVIDIA GeForce GTX1070,NVIDIA,美国)。
4.2 评价指标为了从多个角度全面衡量各分割模型在半月板MicroCT数据集上的表现,本文采用了3个性能指标作为评价标准,分别是平均精度(Average Precision, AP)、相对豪斯多夫距离误差[21](Relative Hausdorff Distance Error, H_E)和交并比[22](Intersection over Union, IoU)。
AP由精确度与召回率共同决定,如式(9) 所示。
| $ {\text{AP}} = \int_0^1 {P{\text{(}}R{\text{) d}}R} $ | (9) |
H_E的定义如式(10)所示,其中C为真实区域的周长,d(a,b)为a、b两点的欧几里得距离。在本文中,由于分割区域较大,因此要求H_E不高于1%。
| $ {\text{H\_E}} = \frac{{{\text{max}}\left\{ {\mathop {{\text{max}}}\limits_{a \in {\boldsymbol{A}}} \mathop {{\text{min}}}\limits_{b \in {\boldsymbol{B}}} d\left( {a,b} \right) ,\mathop {{\text{max}}}\limits_{b \in {\boldsymbol{B}}} \mathop {{\text{min}}}\limits_{a \in {\boldsymbol{A}}} d\left( {a,b} \right) } \right\}}}{C} $ | (10) |
IoU的定义如式(11) 所示,其中A、B分别表示预测结果和真实结果。
| $ {\text{IoU}} = \frac{{{\boldsymbol{A}} \cap {\boldsymbol{B}}}}{{{\boldsymbol{A}} \cup {\boldsymbol{B}}}} $ | (11) |
本实验除了对比TransUNet模型与其他分割模型的效果,还设计了消融实验,验证本文对于TransUNet模型改进方法的有效性。本实验所构建的分割模型如下。
(1) 原始模型:TransUNet;(2) 对比模型1:Mask R-CNN;(3) 对比模型2:U-Net;(4) 对比模型3:SwinUNet;(5) 改进模型1:TransUNet+改进损失函数;(6) 改进模型2:TransUNet+改进损失函数+iRPE;(7) 改进模型3:TransUNet+改进损失函数+iRPE+图像扩增。
先将以上分割模型的所有参数在ImageNet21K数据集上进行大规模预训练,然后将其作为初始参数进行半月板MicroCT图像的分割模型训练,模型训练时的参数设置统一为:学习率0.01,迭代次数150次,图片分辨率512×512 pixels,优化器为SGD。
训练结束后,使用相同的测试集(测试集A2)进行测试,得到的模型评价结果如表1所示。各模型的可视化分割结果如图6所示。
| 表 1 不同分割模型的评价指标结果 Table 1 Evaluation results of different segmentation models |

|
图 6 不同模型的可视化分割结果 Figure 6 Visual segmentation results of different models |
从表1的结果可以看出:
(1) 在AP指标上,① Mask R-CNN模型的得分不超过91%,而其他模型的得分均在95%以上,说明U-Net机制在图像分割任务中有着更加显著的优势,其编码器和解码器结构能够更好地处理图像的细节信息。② 原始模型的周向纤维类得分比平均得分低0.07%,而改进模型1的周向纤维类得分比平均得分高0.16%,说明损失函数的改进提高了模型对周向纤维的关注度,进而提高了分割准确率。
(2) 在H_E指标上,① 其他模型得分均在0.2‰以上,但改进模型2和3的指标得分降到了0.2‰以下,说明iRPE算法的引入可以显著提高模型对于边缘细节的分割效果。② 相比于原始模型,改进模型1的周向纤维类得分提高了0.035‰,说明损失函数的改进使模型边缘分割的能力减弱,但在可接受范围内。
(3) 在IoU指标上,① Mask R-CNN模型的得分依旧是所有模型中最低的,与AP指标呈现相同的趋势。② 改进模型1与原始模型的周向纤维类得分差别不大,说明损失函数的改进对提高模型宏观上的分割精度没有帮助,但也不会使模型性能变差。③ 除改进模型2和3外,其他模型的周向纤维类得分均比平均得分低2%~3%,但是改进模型2和3却将这个差距缩至了0.5%,这充分说明iRPE算法的引入可以使模型对于不同类别的分割能力达到均衡。
综上所述,损失函数的改进可以使模型提高对小样本类别(周向纤维)的关注度,进而提高对不同区域的识别能力和分割精度,但对边缘细节的把握变差;iRPE算法的引入能够提高模型对于边缘细节的把握,有效提升边缘分割能力;基于MicroCT图像特点提出的图像扩增方法有效解决了数据集不足的问题,使模型的各个指标获得了不同程度的提升。
在本文的分割任务中,半月板周向纤维和毛细状纤维在边界处的特征极为相似,若模型没有学习到足够特征,便很难对边界区域做出准确分割。图6中使用橙色曲线勾画的区域便属于较难分割的部分,因为它的特征与周向纤维和毛细状纤维都很接近,但实际上它属于毛细状纤维。
从分割结果可以明显看出:
(1) Mask R-CNN模型的分割结果最差,它对于边界的分割存在极大的失误,各类别的边界处均存在分割不彻底的情况。相比之下,带有U-Net机制的其他模型均可以做到完整分割,但是对于橙色区域的分割结果却都达不到要求的准确率。
(2) 对于橙色区域的分割,原始TrasnUNet模型仅能够将小部分区域正确分割;改进模型1相比于原始模型有了一些改进,正确分割的比例增大,但仍达不到100%;改进模型2和3的效果最好,基本上能对橙色区域完整正确分割,说明iRPE算法的引入对于边缘分割发挥了重要作用。
综合模型评价指标数据和可视化分割结果,本文提出的两项改进策略能帮助模型捕获更精确的特征,提升周向纤维分割的准确率,此外,独特的图像扩增方法也使得模型性能进一步得到提升。
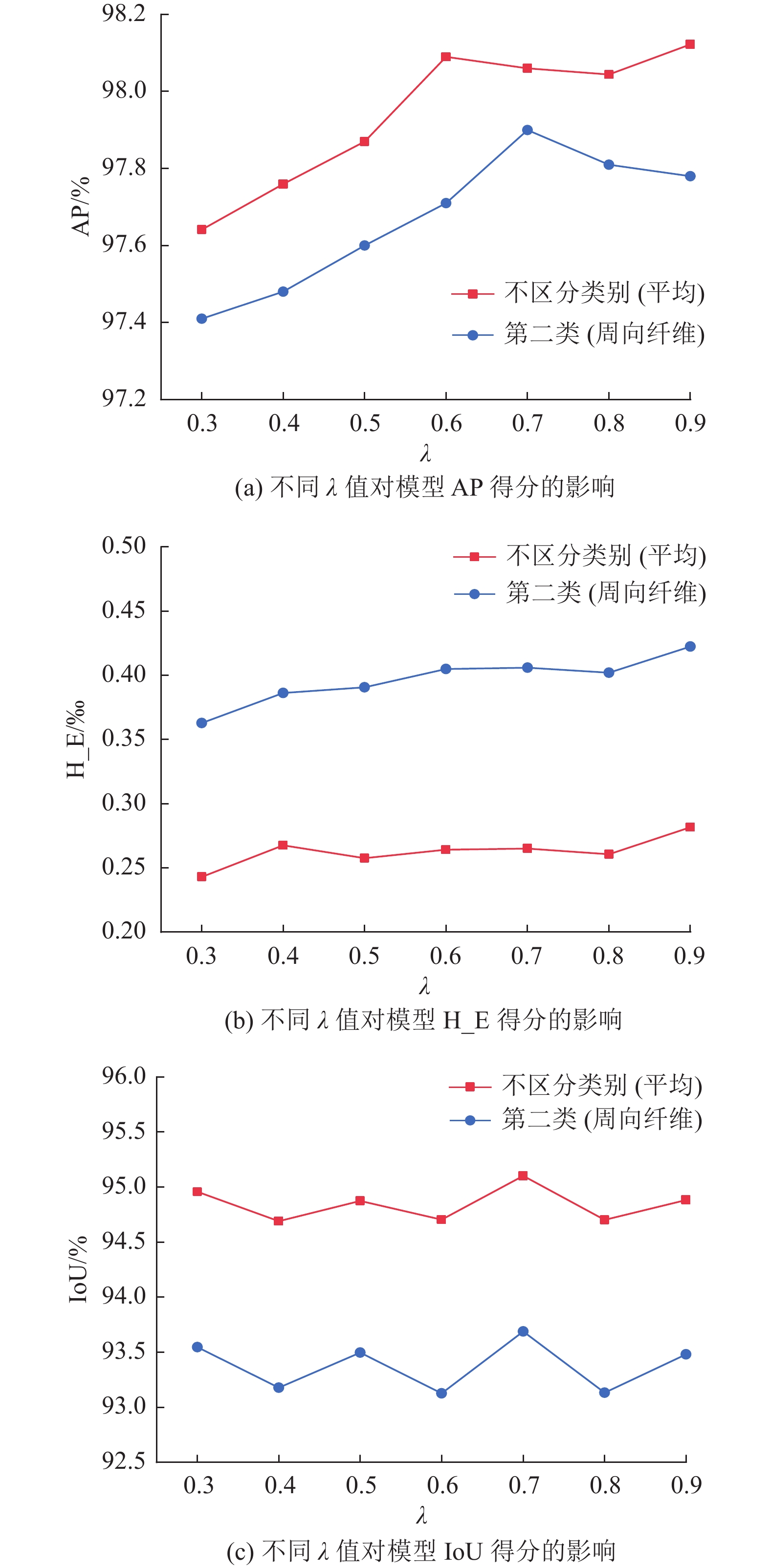
4.3.2 实验2:探究不同λ值下的组合损失函数对分割模型性能的影响(关键参数影响实验)为了探索不同λ值下的组合损失函数的性能以及对分割模型的影响,本文分别对λ值为0.3、0.4、0.5、0.6、0.7、0.8、0.9的改进损失函数的TransUNet模型进行训练,实验相关配置与实验1相同,并对训练结果进行对比和分析。训练结果如图7所示。
|
图 7 不同λ值对模型性能的影响 Figure 7 Influence of different λ values on model performance |
从图7可知,(1) 随着λ的增大,模型AP得分呈现先增大再减小的趋势,虽然周向纤维类的得分一直小于平均得分,但是二者的差距在不断缩小。当λ取值为0.7时,二者相差最小,且此时周向纤维类的AP得分最高。(2) 随着λ的增大,模型的H_E得分基本呈现递增的趋势,说明损失函数的改进对于模型边缘分割能力是有影响的,这与实验1的结论一致。(3) 随着λ的增大,模型的IoU得分呈现波动的趋势,但波动的幅度很小,在0.005以内。当λ取值为0.7时,IoU得分取得极大值,也是所有结果的最大值。
综上所述,当λ=0.7时,模型分割周向纤维的AP和IoU得分取得最佳结果,虽然此时H_E得分相比于原始状态有些升高,但提升的效果远大于带来的劣势,模型表现出最优的性能。本文以此作为最优参数。
4.3.3 实验3:泛化性能实验为验证本文所改进的TransUNet模型的泛化能力,按照下列方法进行两次测试,模型测试的评价指标结果如表2所示,分割结果如图8所示。
| 表 2 泛化能力测试实验结果 Table 2 Experimental results of generalization ability test |

|
图 8 泛化能力测试实验分割结果 Figure 8 Segmentation results of generalization ability test experiment |
(1) 直接使用训练好的改进TransUNet模型对验证集C2进行测试;
(2) 将训练好的改进TransUNet模型作为预训练权重,使用训练集C1对改进模型继续训练,在训练150次迭代后对验证集C2进行测试,本文将其命名为二次训练后分割。
从图8(a)可以看出,数据集C与数据集A存在较大差别,除了图像主体的位置变化外,最大的差别在于毛细状纤维的图像特征。数据集C的毛细状纤维基本上全部存在“冻干伤”,而且占比很大,从图像上很难看到毛细状纤维应有的“毛细状”特征。这种情况的出现会导致分割结果的不准确,最直接的影响是造成周向纤维的错误分割。因此直接分割验证集C2时,分割结果存在多处错误,毛细状纤维被误分割为周向纤维,且边界分割也不准确。而二次训练后的分割结果与手动标注的结果十分接近,未出现明显的错误分割现象,边界分割也较为准确。
根据表2的结果,得知:
(1) 当直接分割验证集C2时,周向纤维的AP得分为91.52%,具有较高的分割准确率;且H_E得分为0.34%,符合本文要求的1%的标准,该结果说明模型具有较强的泛化能力。但是毛细状纤维的指标结果却极不理想,这与图8的分割结果是一致的,它的错误分割还在一定程度上影响了周向纤维的IoU得分。
(2) 当二次训练后分割验证集C2时,毛细状纤维的分割得到了极大提升,其中AP和IoU得分分别提升了33.81%和36.91%;同时它的正确分割也使得其对周向纤维影响减小。周向纤维类的IoU得分从80.75%提升至91.62%,并且其他指标也得到了不同程度的提升。以上结果说明改进模型能够迅速提取特征,在二次训练后适应新图像的特点,克服分割难点,对各个类实现精准分割。
通过以上两项测试可以发现,将改进模型在数据集A上预训练后,对于一个全新的半月板数据集:(1) 可直接对图像中的周向纤维进行分割,并且能够达到十分高的分割精度;(2) 当图像质量存在一些问题,导致周向纤维分割效果不理想时,通过小规模训练后分割,便可得到较高精度的分割结果。因此模型具备良好的泛化能力,这使其对其他半月板MicroCT数据集中周向纤维的分割也广泛适用。
4.3.4 实验4:半月板周向纤维的三维重建对分割获得的半月板周向纤维MicroCT图像,借助3D Slicer软件进行三维重建,结果如图9所示。

|
图 9 周向纤维三维重建模型 Figure 9 Three-dimensional reconstruction model of circumferential fibers |
从图9(a)可以看出,周向纤维在延伸一定距离后会出现分裂的情况,并且周向纤维的分裂主要分为两种情况,分别是一分为二和一分为三,未发现一分为四及以上的分裂情况出现。
此外从数据上看,图中共有10根周向纤维,其中未见分裂的个数为2,一分为二的个数为6,一分为三的个数为2。说明一分为二的分裂情况最多,未见分裂和一分为三的情况较少且占比接近。以上两种分裂的三维模型分别如图9(b)和(c)所示。
5 结论周向纤维是半月板受力的关键区域。构建周向纤维的三维微观结构对于半月板损伤的治疗和人工半月板的研发具有重要意义。当前主要通过人工分割MicroCT图像中半月板的周向纤维。由于半月板微观组织复杂,人工分割存在效率低下、分割标准不一致等问题。为此,本文提出了一种改进TransUNet算法分割MicroCT图像中的半月板周向纤维,并进行了周向纤维的三维重建。
本文的主要贡献有:(1) 提出了一种实现MicroCT图像中半月板周向纤维高精度分割的通用方法;(2) 发现了半月板周向纤维存在分裂现象。
实验结果表明:(1) 本文改进的分割模型能够精确完成半月板MicroCT图像中周向纤维的分割;(2) iRPE算法的引入提升了模型对于边缘细节分割的能力,损失函数的改进提升了模型对于小样本类别的关注度,进而提高了分割精度;(3) 改进模型具有良好的泛化能力,可广泛适用于其他半月板MicroCT图像中周向纤维的分割;(4) 周向纤维存在分裂的情况,以一分为二为主,存在少量一分为三的情况,未发现一分为四及以上的分裂情况。
下一步,将在此基础上从影像组学角度对半月板周向纤维做进一步研究。
| [1] |
ZIHNA G, TOPUZ B, GÜNAL G, et al. Preparation of hybrid meniscal constructs using hydrogels and acellular matrices[J].
Journal of Biomaterials Science, Polymer Edition, 2023, 34(5): 587-611.
DOI: 10.1080/09205063.2022.2135078. |
| [2] |
PRENDERGAST M E, HEO S J, MAUCK R L, et al. Suspension bath bioprinting and maturation of anisotropic meniscal constructs[J].
Biofabrication, 2023, 15(3): 035003.
DOI: 10.1088/1758-5090/acc3c3. |
| [3] |
BILGEN B, JAYASURIYA C T, OWENS B D. Current concepts in meniscus tissue engineering and repair[J].
Advanced Healthcare Materials, 2018, 7(11): 1701407.
DOI: 10.1002/adhm.201701407. |
| [4] |
朱爽, 梁敏娟, 赖剑强. 基于Micro-CT技术的半月板微观结构分析和三维重建[J].
现代医用影像学, 2021, 30(8): 1432-1434.
DOI: 10.3969/j.issn.1006-7035.2021.08.013. |
| [5] |
KARJALAINEN V P, KESTILÄ I, FINNILÄ M A, et al. Quantitative three-dimensional collagen orientation analysis of human meniscus posterior horn in health and osteoarthritis using micro-computed tomography[J].
Osteoarthritis and Cartilage, 2021, 29(5): 762-772.
DOI: 10.1016/j.joca.2021.01.009. |
| [6] |
PETERSEN W, TILLMANN B. Collagenous fibril texture of the human knee joint menisci[J].
Anatomy and Embryology, 1998, 197: 317-324.
DOI: 10.1007/s004290050141. |
| [7] |
FOX A J S, BEDI A, RODEO S A. The basic science of human knee menisci: structure, composition, and function[J].
Sports Health, 2012, 4(4): 340-351.
DOI: 10.1177/1941738111429419. |
| [8] |
TACK A, MUKHOPADHYAY A, ZACHOW S. Knee menisci segmentation using convolutional neural networks: data from the osteoarthritis initiative[J].
Osteoarthritis and Cartilage, 2018, 26(5): 680-688.
DOI: 10.1016/j.joca.2018.02.907. |
| [9] |
SHELHAMER E, LONG J, DARRELL T. Fully convolutional networks for semantic segmentation[J].
IEEE Trans Pattern Anal Mach Intell, 2017, 39(4): 640-651.
DOI: 10.1109/TPAMI.2016.2572683. |
| [10] |
RONNEBERGER O, FISCHER P, BROX T. U-net: convolutional networks for biomedical image segmentation[EB/OL]. arXiv: 1505.04597 (2015-05-18) [2023-09-15]. https://doi.org/10.48550/arXiv.1505.04597.
|
| [11] |
STEGMANN H, WERKMEISTER R M, PFISTER M, et al. Deep learning segmentation for optical coherence tomography measurements of the lower tear meniscus[J].
Biomedical Optics Express, 2020, 11(3): 1539-1554.
DOI: 10.1364/BOE.386228. |
| [12] |
CHEN J H, LU Y Y, YU Q H, et al. TransUNet: Transformers make strong encoders for medical image segmentation[EB/OL]. arXiv: 2102.04346 (2021-02-08) [2023-09-15]. https://doi.org/10.48550/arXiv.2102.04306.
|
| [13] |
FEDOROV A, BEICHEL R, KALPATHY-CRAMER J, et al. 3D Slicer as an image computing platform for the quantitative imaging network[J].
Magnetic Resonance Imaging, 2012, 30(9): 1323-1341.
DOI: 10.1016/j.mri.2012.05.001. |
| [14] |
ZHU S, GE T, XIANG J P, et al. Microstructure analysis and reconstruction of a meniscus[J].
Orthopaedic Surgery, 2021, 13(1): 306-313.
DOI: 10.1111/os.12899. |
| [15] |
RUSSELL B C, TORRALBA A, MURPHT K P, et al. LabelMe: a database and web-based tool for image annotation[J].
International Journal of Computer Vision, 2008, 77: 157-173.
DOI: 10.1007/s11263-007-0090-8. |
| [16] |
WOODMASS J M, LAPRADE R F, SGAGLIONE N A, et al. Meniscal repair: reconsidering indications, techniques, and biologic augmentation[J].
The Journal of Bone and Joint surgery. American Volume, 2017, 99(14): 1222-1231.SS.
|
| [17] |
WU K, PENG H, CHEN M, et al. Rethinking and improving relative position encoding for vision transformer[EB/OL]. arXiv: 2107.14222 (2021-07-29) [2023-09-15]. https://doi.org/10.48550/arXiv.2107.14222.
|
| [18] |
SHAW P, USZKOREIT J, VASWANI A. Self-attention with relative position representations[EB/OL]. arXiv: 1803.02155 (2018-04-12) [2023-09-15]. https://doi.org/10.48550/arXiv.1803.02155.
|
| [19] |
MILLETARI F, NAVAB N, AHMADI S A. V-Net: fully convolutional neural networks for volumetric medical image segmentation[EB/OL]. arXiv: 1606.04797 (2016-06-15) [2023-09-15]. https://doi.org/10.48550/arXiv.1606.04797.
|
| [20] |
ROTH H R, ODA H, ZHOU X, et al. An application of cascaded 3D fully convolutional networks for medical image segmentation[J].
Computerized Medical Imaging and Graphics, 2018, 66: 90-99.
DOI: 10.1016/j.compmedimag.2018.03.001. |
| [21] |
孙思语, 钟映春, 郑海阳, 等. MicroCT图像中周围神经束轮廓的建模[J].
计算机仿真, 2022, 39(1): 258-262.
SUN S Y, ZHONG Y C, ZHENG H Y, et al. Modeling of contour of peripheral fasciculi in MicroCT images[J]. Computer Simulation, 2022, 39(1): 258-262. |
| [22] |
GOMALAVALLI R, MUTTAN S, SAI P M V. Boundary detection of renal using contour segmentation[J].
International Journal of Biomedical Engineering and Technology, 2018, 28(1): 53-66.
DOI: 10.1504/IJBET.2018.094428. |
 2025, Vol. 42
2025, Vol. 42

