NAND闪存依靠其高容量、高密度、高吞吐量和低功耗的优点,正逐渐成为计算机系统、移动设备等领域的主要存储介质。NAND闪存早期为2D平面结构,最初的2D NAND只有32 MB的容量,芯片厂家为了更大的容量不断提高存储密度和缩小存储单元尺寸。然而过小的存储单元尺寸导致单元间的干扰越来越严重,其可靠性与寿命也不断降低。3D NAND于2014年提出,通过垂直堆叠的方式提高闪存存储容量,与2D NAND对比单元间干扰降低了83%,编程时间减少50%,可靠性与寿命大幅提升[1]。
3D NAND发展至今,许多厂家采取多级存储单元技术提高存储单元的位数,以实现存储容量的倍数增加。于2023年市场上已推出232层四级存储单元3D NAND闪存芯片,存储密度可达19.8 Gb/mm2。然而随着存储密度的增加,研究人员发现3D NAND的数据可靠性问题也在不断恶化。
数据可靠性问题主要体现在数据保持性和耐用性方面,前者指的是不重新擦写情况下数据的最大保留时间,后者是闪存芯片可承受的最大擦/写循环(Program/Erase Cycles, PEC) 次数。闪存芯片的寿命与PEC次数有关,随着编程次数的增加闪存的可用寿命逐渐降低,原始错误比特率(Raw Bit Error Rate,RBER) 逐渐升高。RBER是指实际读取数据与实际写入数据之间未经过纠错的错误率,当错误率超过一定限制时闪存芯片不能继续正常使用。
为了延长闪存芯片的寿命,厂家在SSD产品中使用了许多技术。在实际SSD产品的软件层中会加入纠错码(Error Correcting Code, ECC),采用特殊的编码规则对读出的原始数据进行纠错,从而间接延长闪存芯片的寿命,但受限于存储空间的限制,其纠错能力被大大降低。厂家还采用了磨损均衡技术,通过平衡每个闪存块间的PEC次数[2],延后闪存块因频繁擦写被判为坏块的时间,间接延长闪存块的寿命,然而闪存总会存在冷热数据导致的不均衡,该技术还可以进一步优化。Read-Retry技术通过修改读电压的方法减少数据错误,但会增加冗余时间,使闪存芯片的读写性能降低。SSD软件层中的数据刷新机制[3]会将长时间未更新的数据进行读取、校正和重新写入,以消除积累的干扰错误。刷新机制可间接延长SSD的寿命,但会造成额外的写放大。
闪存可靠性研究的真正难题在于耐久性,也就是芯片寿命的不确定性,闪存厂商因同类型闪存颗粒寿命存在的巨大差异,在芯片出厂的寿命标称值规定得相对保守,这会导致寿命的极大浪费。即使考虑到刷新机制和垃圾回收造成的额外损耗,寿命标称值与实际寿命相比仍然存在数倍的差异。此外,闪存芯片的寿命检测对芯片本身是破坏性的,而且过程十分耗时,例如使用的测试设备进行一次PEC需要3 s,进行寿命检测实验会耗费数小时之久。
利用机器学习算法进行闪存芯片寿命预测已成为解决可靠性难题的重要手段,本文中将采用支持向量机算法(Support Vector Machine, SVM) 进行寿命预测。
目前使用机器学习算法预测闪存芯片寿命已有不少研究。Barry Fitzgerald等[4]观察到多级存储单元闪存中的字线数、页类型和页奇偶校验会影响码字错误率、编程和擦除时间,利用该特征提出了一种基于误差概率密度函数的采样方法,构建了8个不同的两类机器学习模型。但该论文忽略了样本平衡问题,导致模型精度的可靠性不足。Ruixiang Ma等[5]认为预测模型会因闪存使用环境的变化而失去有效性,因此采用耐力参数的增量变化来更新预测模型,以适应不同环境的变化。Haichun Zhang等[6]基于SVM算法构造了一个多分类预测模型并对比了不同核函数的预测精度,以页面错误比特数、PEC次数和块内擦除耗时作为输入特征。以上两篇文章都没有考虑到不同闪存芯片之间存在错误特性的差异,即使是同型号同批次的芯片,其错误特性也存在一定差异。同时在文献[6]中作者提出写入的原始数据的差异性和随机性会导致阵列干扰现象对不同页的影响程度不同,局部差异非常显著,严重影响预测精度。
为解决以上问题,本文提出一种控制编程内容的方法,通过加速电荷泄漏的速度激发数据保留错误,使数据保留错误这种错误机制变得可控且稳定,最大程度上避免了因闪存芯片自身错误特性不同导致的低寿命预测精度。同时本文提出的方法可以减少等待数据保留错误到达目标水平的时间,经实验验证本文的方法可使预测实验耗时减少90.9%,寿命预测准确度提高33.3个百分点。
1 3D NAND闪存简介本章节将叙述3D NAND闪存的基本结构、3D NAND闪存类型和3D NAND闪存常见的错误类型。
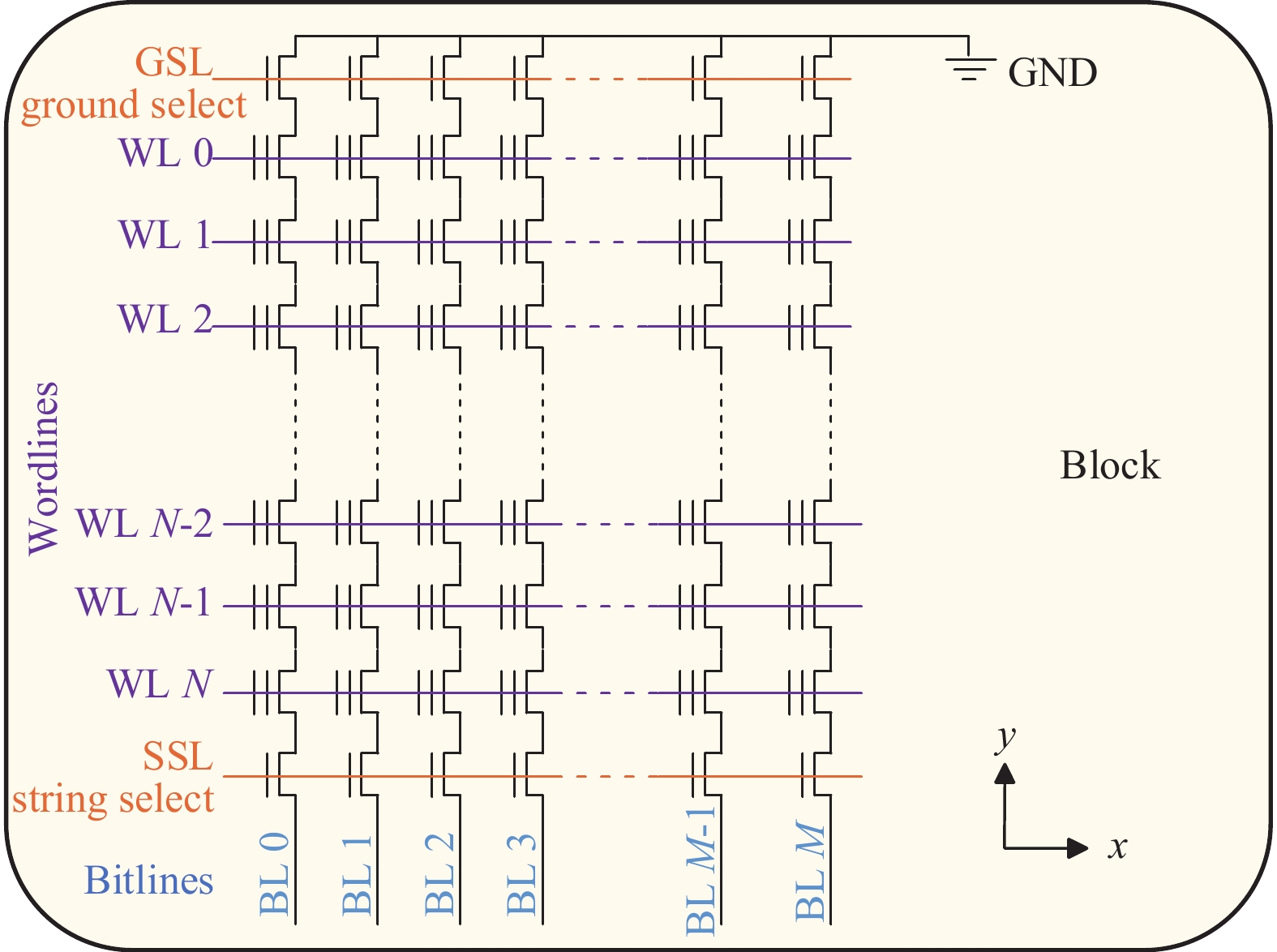
1.1 3D NAND闪存的基本结构3D NAND闪存的内部结构如图1所示,图中是一个闪存块(Block) 的基本结构。图中的MOS管是闪存存储单元(Cell),Cell是存储的最小单位,根据电荷存储层的材料可区分为浮栅(Floating Gate, FG)型和电荷捕获(Charge Trap, CT)型,其中FG型采用导体的浮栅材料,而CT型则是绝缘的电荷陷阱材料,因材料的不同这两种类型的某些错误特性也不同。在x方向上共用一个控制极的Cell称为字线(Wordlines, WL);y方向上共用一个位线(Bitlines, BL) 的Cell称为串(String);由所有字线和串组成的叫闪存块(Block),所有闪存块组成一个逻辑单元号(Logical Unit Number, LUN)。
|
图 1 闪存块的内部结构 Figure 1 The internal structure of a Flash NAND block |
闪存芯片除了按材料不同分成CT型和FG型,还分为单级存储单元(Single-Level Cell, SLC) 和多级存储单元(Multi-Level Cell, MLC)。SLC一个存储单元可存储单比特数据,而MLC一个存储单元可存储多比特数据,后者的存储容量是前者的数倍。MLC可细分为三级存储单元(Triple-Level Cell, TLC) 和四级存储单元(Quad-Level Cell, QLC),现在更多级的存储单元闪存芯片也在研究当中。
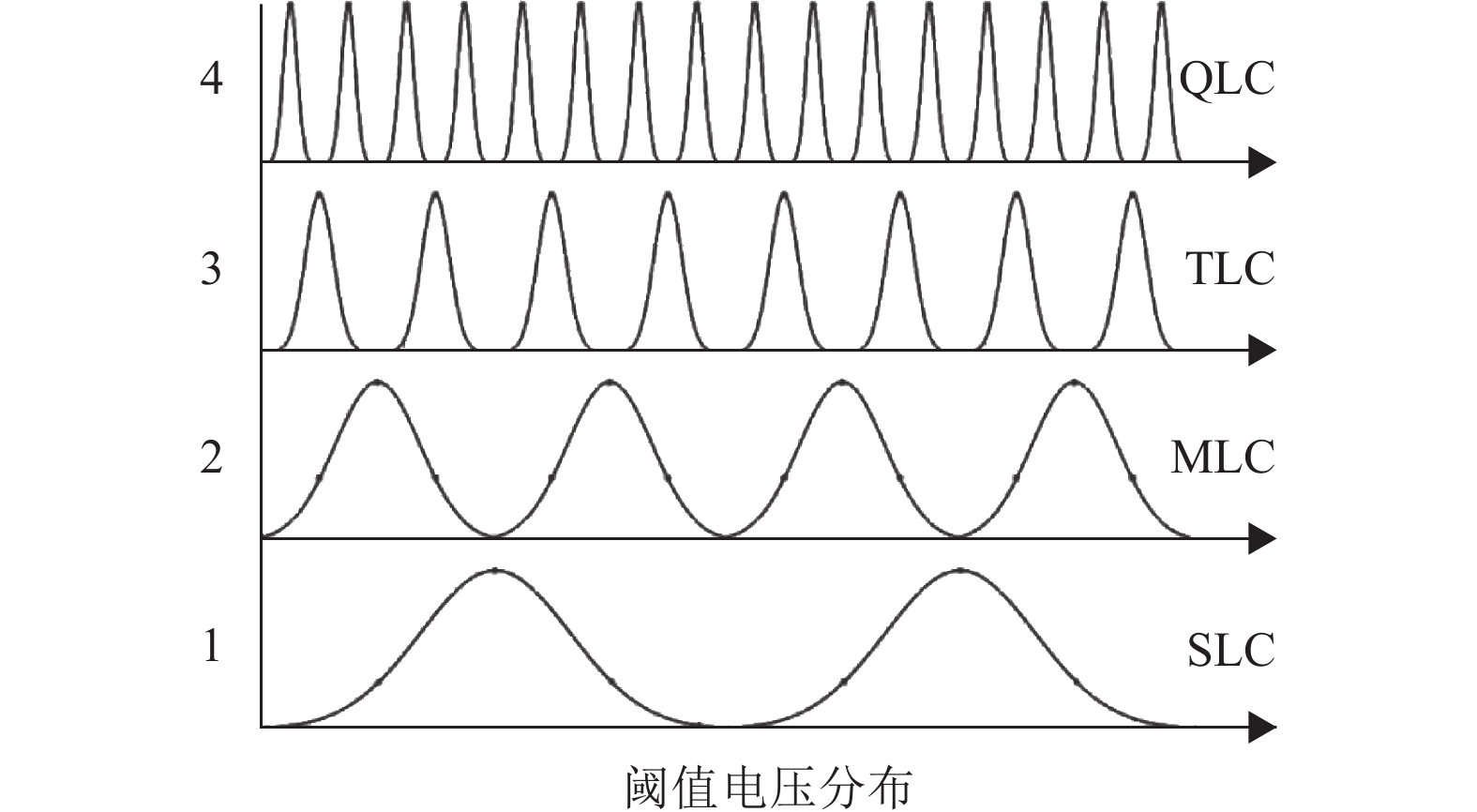
SLC有擦除态和编程态两种状态,而MLC随着可存储比特数的增加其状态数呈指数关系增加,TLC和QLC分别有8种状态和16种状态,图2为SLC到QLC的阈值电压状态。所示每个波峰代表一个状态,需要划分的状态数越多意味着每个状态窗口越窄,过窄的阈值电压窗口导致面临干扰时存储单元的电压水平很容易跨状态转移,读取数据的时候发生错误,因此从SLC到QLC的芯片性能、寿命和可靠性是不断降低的。
|
图 2 SLC到QLC的阈值电压分布 Figure 2 Threshold voltage of SLC to QLC |
NAND错误是指原始数据被编程到存储单元的过程中和编程完成后,受到某些干扰导致再次读取时数据与原始数据不同的错误。本文主要使用的错误是PEC错误和数据保留错误(Retention, RET),除这两种错误以外还有编程错误(Program Disturb, PD)、单元间干扰错误(Cell-to-Cell Interference, CCI) 和读干扰错误(Read Disturb, RD)。
PEC错误是对存储单元进行编程操作时,目标单元所在字线控制极需要施加一个写电压;对存储单元进行擦除操作时,在衬底施加一个擦除电压。为使电子可以通过隧穿效应穿过氧化层进入到存储层,这两个电压通常都非常高,反复施加高电压会对氧化层造成不可逆的损伤使得氧化层隔离电子的能力变弱,也就是可用寿命降低。
RET错误发生在对存储单元编程后,在保持数据过程中随时间的增长存储在单元内的电荷发生泄漏,RET错误是闪存错误的主要来源[7]。闪存单元的氧化层经过的损耗越严重,电荷泄漏的速度越快,一个存储单元的电荷泄漏到一定程度后会发生跨电压状态转移,导致读取时发生读取错误。
PD错误发生在对闪存页编程的过程中,当对一个目标单元编程时,所在字线施加一个写电压,其相邻BL为保持截止在控制极也会施加一个电压,导致对目标单元附近的存储单元造成轻微写[8],这些存储单元的电压水平会略微升高。
CCI错误是因为FG型闪存芯片存储电荷的介质是导体,同时存储单元间的距离很小,导致存储单元之间存在耦合电容[9],对存储在单元内的电荷产生影响从而引发数据读取错误。CT型闪存芯片的CCI错误影响较小。
RD错误发生在数据读取的过程中。在读取一个闪存页时,相邻闪存页为保持导通其控制极会施加一个正电压,当快速连续读取时反复施加的电压会对相邻闪存页造成轻微写[10],使相邻闪存页的电压水平略微升高。
2 实验思路及步骤 2.1 实验思路首先本文使用5颗相同型号的闪存芯片进行了寿命预测实验,使用PEC过程的RBER作为输入特征,发现预测精度非常低。接着通过分析RBER曲线发现芯片间的错误特性不一致的问题,因为生产工艺差异导致PEC次数相同的情况下某些芯片具有更高的RBER。而且发现RBER和PEC次数并不是呈线性关系,在PEC次数达到某个区间时闪存芯片的RBER会出现不同幅度的下降,机器学习模型在构建寿命模型时受到这些数据的干扰导致预测精度降低。
本文考虑使用别的错误特征来代替PEC进行寿命预测,设计实验分析了先前叙述的常见闪存错误机制。PD错误与CCI错误影响大小取决于写入内容,而写入内容是随机生成的具有不稳定因素。通过对一条字线使用快速读指令,然后读取其相邻字线的RBER分析RD错误,发现其RBER与PEC次数关系不密切且变化不具有规律,由此不采用以上3种错误机制。决定采用RET错误进行寿命预测,因其RBER稳定且好量化,而且经实验发现RET的RBER大小与PEC有极强的关联性。从错误机制原理方面来说,在PEC过程中对氧化层的损耗越多电荷流失的速度越快,RET错误正是因电荷流失引起的,因此RET错误可以很好地表征当前PEC次数。然而RET实验需要非常长的时间,而且不同PEC次数间的RBER大小差异不足。
为了解决耗时问题和提高数据抗干扰能力,本文提出使用特定内容编程方法激励字线间干扰,结合RET错误进行寿命预测。电荷流失速度与相邻字线的写入内容有关[11],本文的实验中将两条相邻字线通过编程特定内容使它们具有一定的电压差,相当于形成电场加速了电荷的流失。而一个存储单元受到的最大单元间干扰来自于处于同一位线的相邻字线的存储单元[12],特定的编程内容可以有效激励字线间干扰,使RET的RBER放大,从而放大不同PEC次数间的RBER差异,最终使得RBER具有一定的空间冗余,最大程度上减少工艺差异对寿命预测精度的影响。具体实验数据会在后续内容给出。
2.2 实验步骤本文使用了基于FPGA平台的NanoCycler闪存芯片测试仪作为3D NAND闪存测试设备,此设备支持目前大部分市场主流厂商的芯片,支持封装为BGA132和BGA152,可并行实验6个芯片,可以对闪存芯片进行编程、擦除、PEC老化循环、读取RBER和加热芯片等操作。使用芯片为64层FG型3D TLC NAND闪存芯片,一个闪存块具有384条字线,单页大小为16 384字节。
在RET实验中,本文使用阿伦尼乌斯公式计算加热时间。在进行数据保留实验过程中,往往需要将数据保留较长的时间,耗费的时间成本是巨大的。通过加热芯片的方法可以加速电荷的流失速度,从而减少实际的数据保留时间[13]。阿伦尼乌斯公式如式(1)所示,其中AF(Acceleration Factor) 称为加速因子,Ea为分子活化能,取为1.1 eV,t1和t2是实际加热时间和模拟放置时间,T1和T2为加热温度和室温,k为玻尔兹曼常数。经过此公式可以计算出在特定温度下需要模拟的放置时间对应的实际加热时间。
| $ {\rm{AF}} = \frac{{{t_1}}}{{{t_2}}} = \exp \left(\frac{{{E_{\rm{a}}}}}{k} \times \left(\frac{1}{{{T_1}}} - \frac{1}{{{T_2}}}\right) \right) $ | (1) |
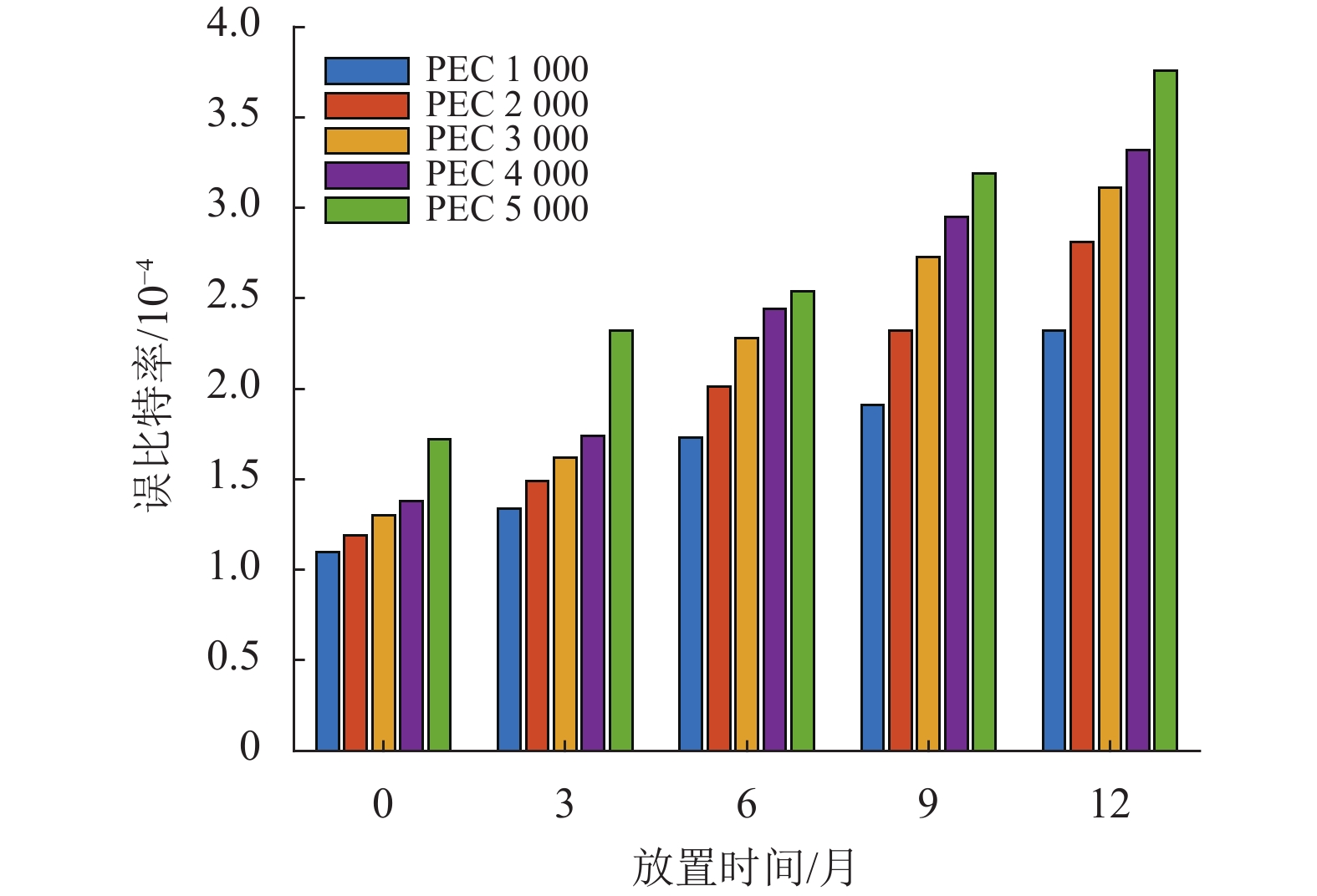
首先构建了PEC-RET模型来寻找PEC次数与RET的RBER之间的关系。使用5组闪存块,每组闪存块各自进行1 000~5 000次PEC老化循环,随后使用随机生成的数据将其编程后放置一共12个月的时间,每隔3个月读取一次RBER水平,其RBER和放置时间关系如图3所示。
|
图 3 PEC-RET模型 Figure 3 Model of the PEC-RET |
可见图3中每个时间刻度的组间RBER水平与其PEC次数呈现正关系,因此可以使用RET的RBER水平来表征闪存块的PEC次数。但是从图3里看到RET时间至少达到12个月的组间RBER才呈现比较明显的分级,使用80 ℃高温加热的方式模拟12个月的放置时间也需要加热11 h,在实际使用中使用如此长的时间进行数据采集是不实际的。而且图中的PEC1 000和PEC5 000的RBER差异只有1.5×10−4,如此小的差异导致SVM模型在划分超平面时不准确,影响寿命预测准确性。
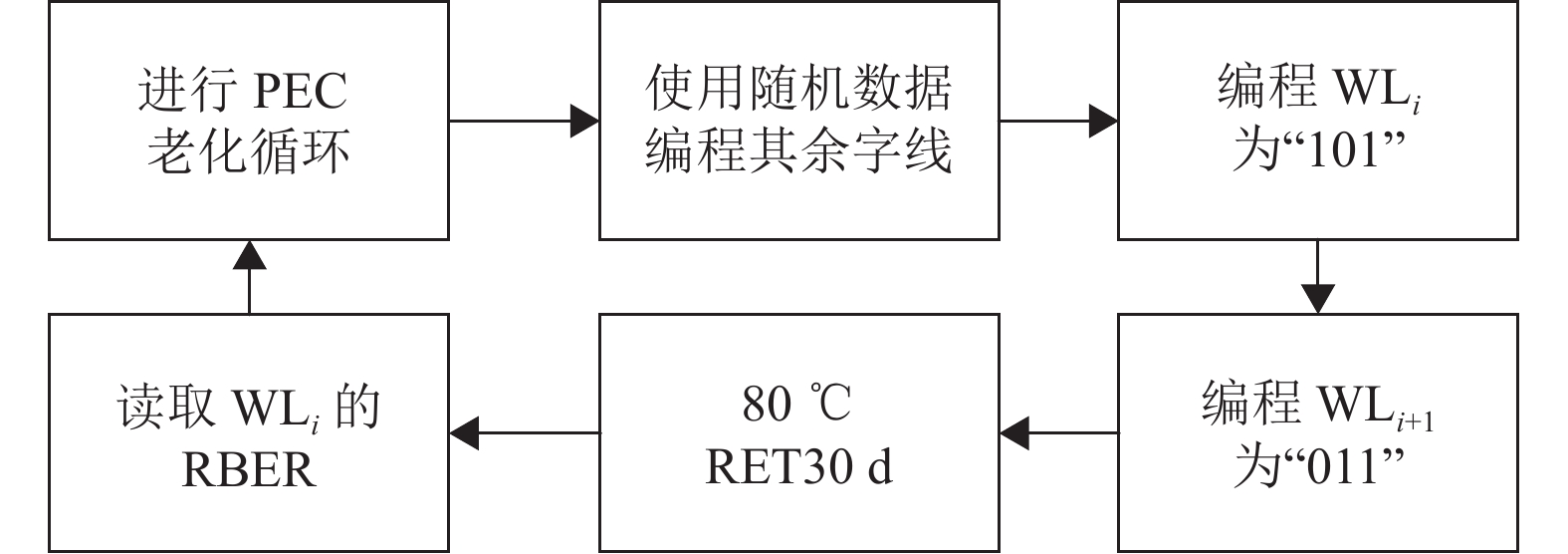
2.2.2 激励字线间干扰实验步骤激励字线间干扰实验步骤如图4所示,先将闪存芯片的闪存块分组进行PEC老化循环。从闪存块中挑选两条相邻的字线,为避免边缘效应[14]挑选了处于内部位置的字线,将其编号为WLi和WLi+1。TLC单个存储单元可存储3个比特数据,分别对应高、中、低位,3个比特数据组合起来对应8个电压状态。将WLi的存储单元全部编程为“101”,其对应最高电压状态;将WLi+1的存储单元全部存储为“011”,其对应除擦除态外最低电压状态。
|
图 4 实验步骤 Figure 4 Experimental procedure |
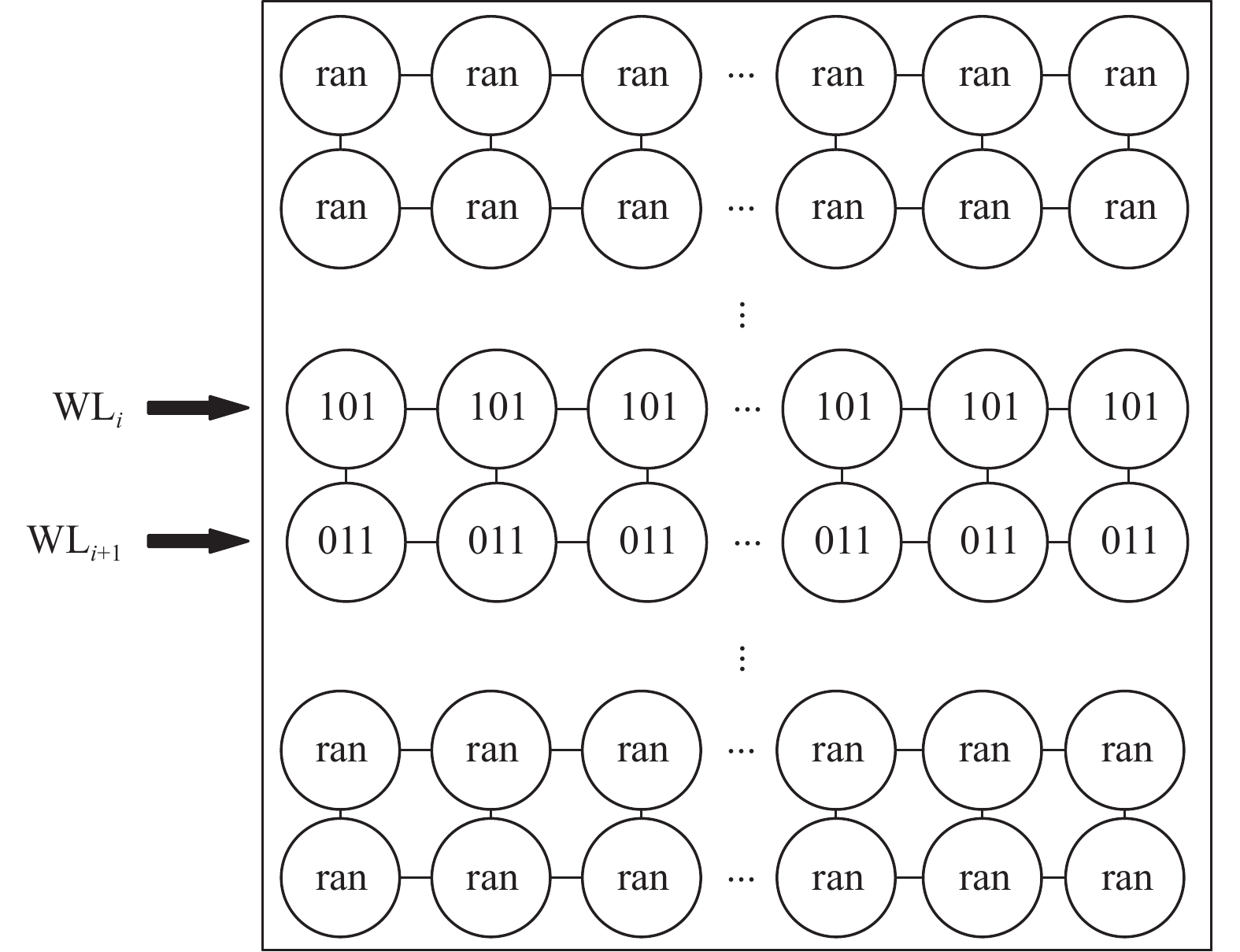
图5为内部编程状态示意图,为最大程度避免其余字线的电压干扰,闪存块中除了WLi和WLi+1外的所有字线使用随机生成的数据编程,经过测试,WLi和WLi+1的存储单元具有3.5 V左右的电压差。编程完毕后RET30 d,经过阿伦尼乌斯公式计算80 ℃下的加热时间不到1 h,加热完成读取WLi的RBER后重复实验。
|
图 5 激励字线间干扰实现方法 Figure 5 Realization of stimulating word-line interference |
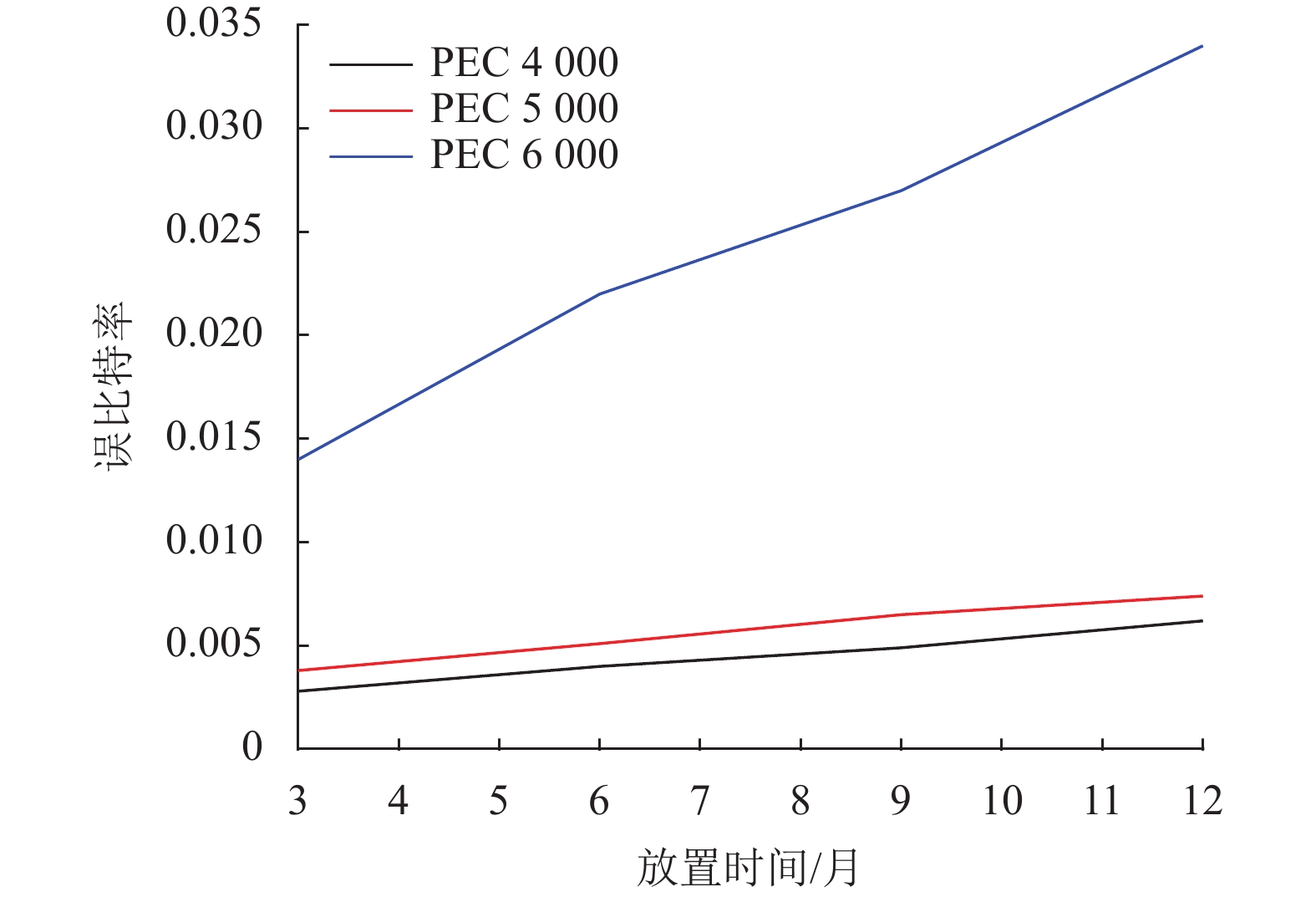
在实际SSD的使用中主控会通过磨损均衡技术使各闪存块的磨损水平接近,依此用闪存块的寿命表征芯片的寿命。参考JEDEC协议的JESD218B[15],消费级颗粒的物理块写入数据后在30 ℃环境放置1年的RBER若超过10−2则判定此物理块为坏块,以此标准判定所使用闪存芯片的寿命。图6为不同PEC次数的RBER随放置时间的变化曲线,闪存块PEC次数为4 000次和5 000次放置12个月的RBER尚未达到10−2,而6 000次的3个月时就达到了10−2以上。
|
图 6 4 000~6 000次PEC的RBER对比 Figure 6 RBER’s comparison of the PEC with 4 000-6 000 times |
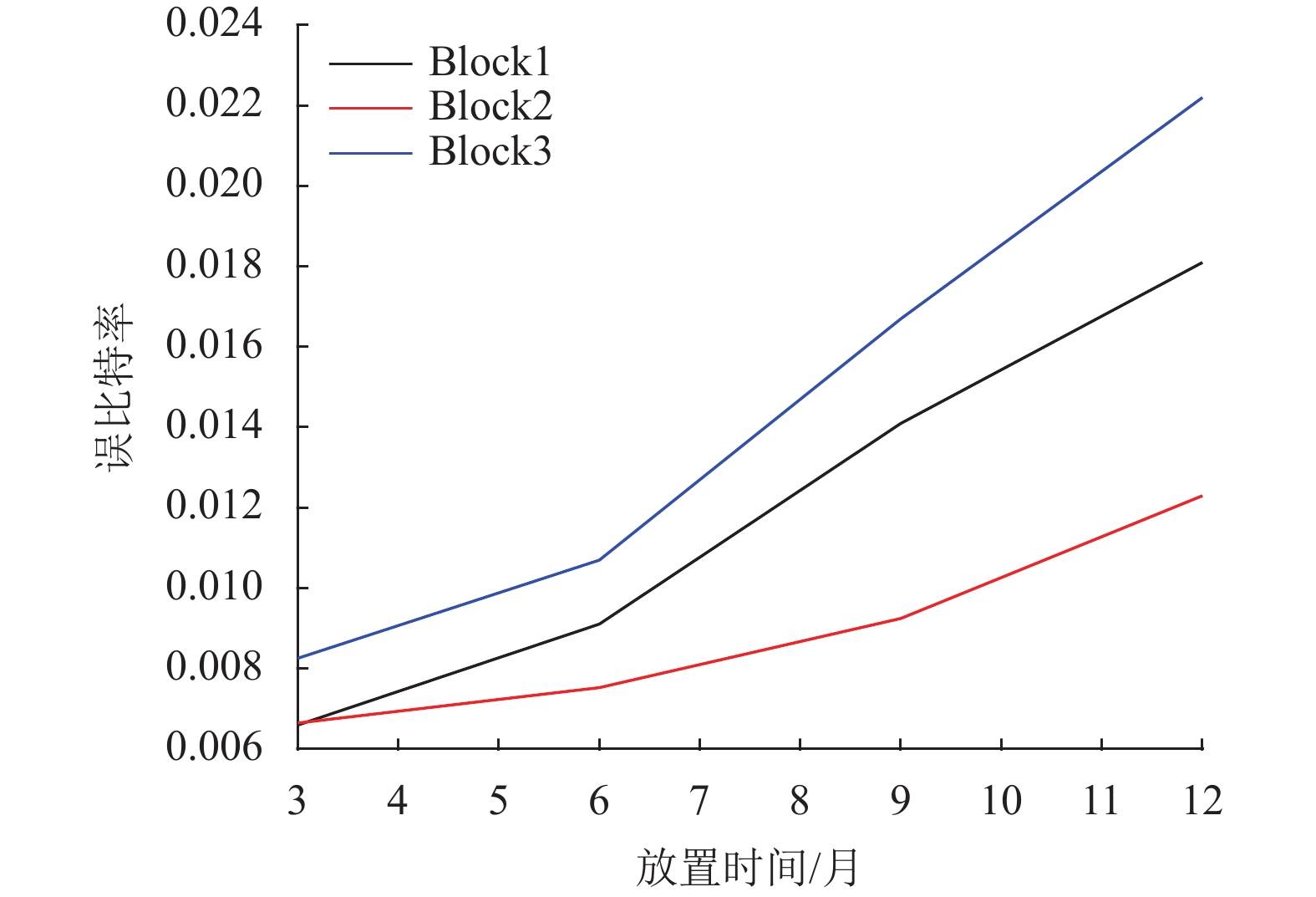
随后使用中间值5 500次PEC次数的3个物理块放置1年观察其RBER变化,结果如图7所示。
|
图 7 5 500次PEC的RBER变化 Figure 7 RBER changes of the PEC with 5 500 times |
3个闪存块的RBER分别在7个月、10个月和5个月达到了10−2。虽然3个块达到坏块标准的时间不同,但都在12个月前超过了JEDEC的标准。而图6中PEC5 000的RBER在12个月时达到了8×10−3,考虑到闪存块间寿命水平存在起伏,将5 000次PEC定为实验使用颗粒的最大寿命。
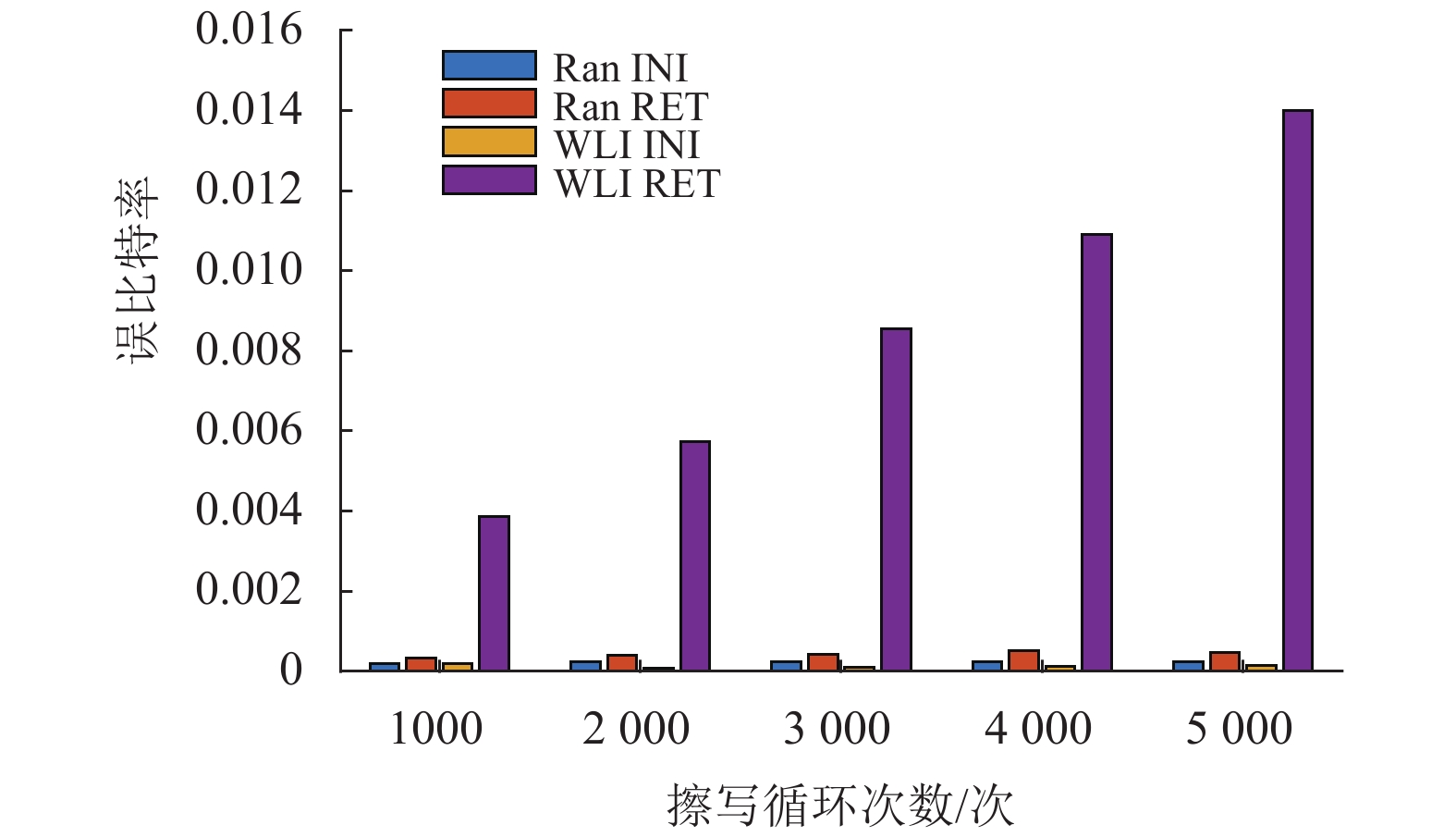
3.2 随机写入与激励写入对比通过对比实验对比随机写入模式和激励写入模式下RET错误的RBER水平。使用经过老化的闪存块和挑选好的字线,随机写入模式编程完毕后读取其初始误比特率,命名为Ran INI(Random Initial,表示随机写入的初始RBER)。80 ℃加热模拟一个月的放置时间后读取其误比特率Ran RET(Random RET,表示随机写入经过RET的RBER)。激励写入模式重复以上操作获得误比特率WLI INI(WL Interference Initial,表示激励写入的初始RBER)与WLI RET(WL Interference RET,表示激励写入经过RET后的RBER),结果如图8所示。因激励写入的所有单元被编程至最高态,其初始RBER比随机写入更低;同时因相邻字线干扰,放置一个月的时间RBER差异能达到1.2×10−2,并且与PEC有较强相关性。
|
图 8 随机写入和激励写入的误比特率对比 Figure 8 RBER comparison between random and stimulated programming |
机器学习领域中通常使用以下指标评估模型的预测效果:(1) 准确率:准确率指预测正确的结果占总样本的百分比,但在正负样本均衡的情况下才可作为衡量指标。(2) 精确率:精确率指所有被预测为正的样本中实际为正的样本的概率。(3) 召回率:召回率指实际为正的样本中被预测为正样本的概率,也称为查全率。(4) F1分数:精确率和召回率这两个指标呈反比关系,为了综合两者的表现在两者之间有一个平衡点,也就是F1分数,计算公式如下:F1分数=2×精确率×召回率/(精确率+召回率)。
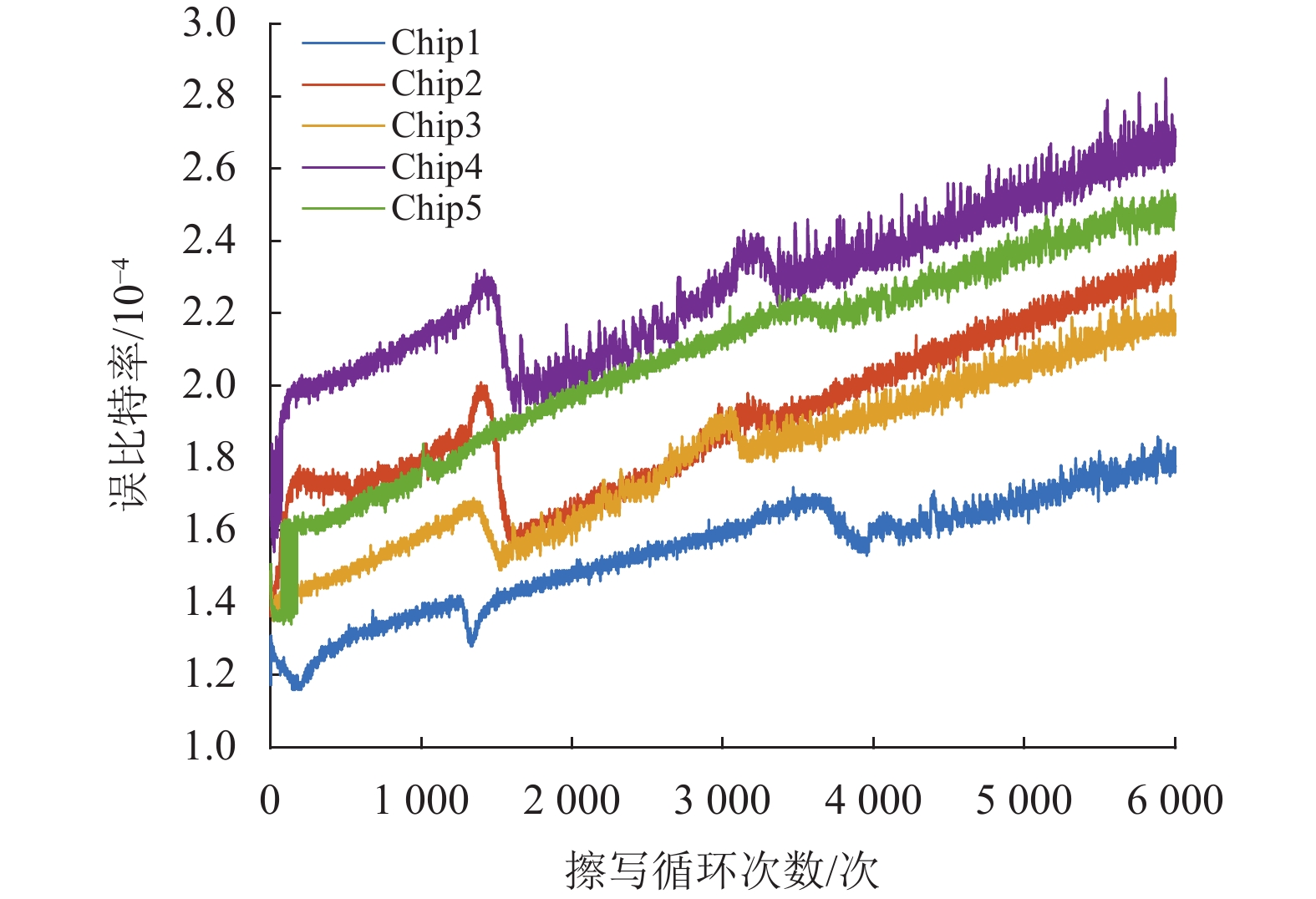
使用5颗同型号同批次的闪存芯片,每个芯片使用相同编号的闪存块进行PEC老化循环,每次PEC都记录一次RBER,RBER结果如图9所示。
|
图 9 芯片错误特性不同导致的误比特率差异 Figure 9 RBER’s difference caused by different error characteristic |
通过图9可知3D NAND闪存芯片即使是同一批次的错误特性也有一定的差距。在PEC次数较少的时候2号、4号和5号芯片的RBER激增,而1号芯片的RBER反而降低。在PEC达到1 500次时除了5号芯片以外的芯片的RBER出现了不同幅度的下降,PEC次数在3 000到4 000次的区间内所有芯片的RBER有不同幅度的下降,PEC4 000次以上时RBER上下波动明显,而且不同芯片间的RBER差异较大,很明显RBER并不是随着PEC次数线性增长的。
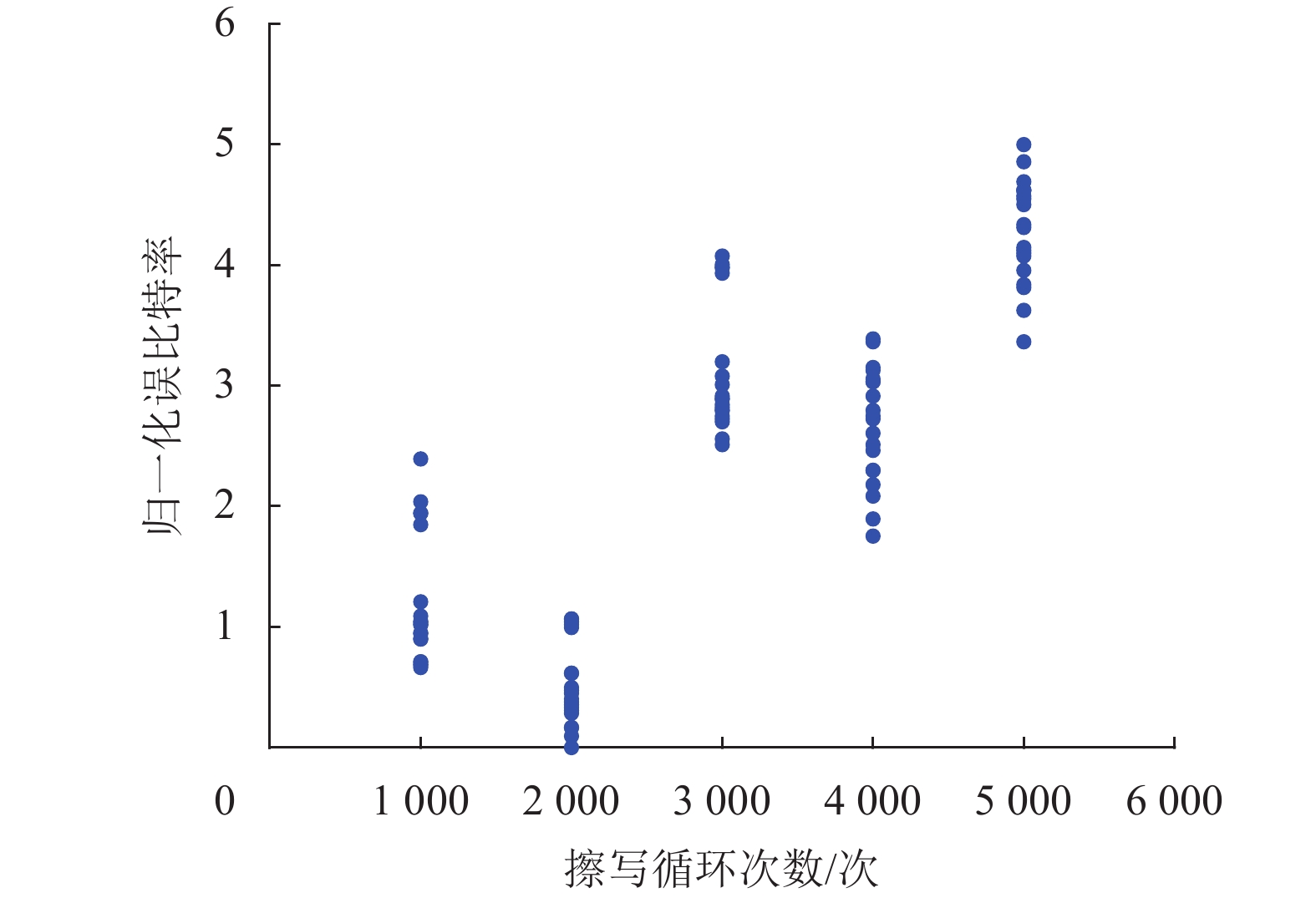
按照PEC次数将数据分成5组,把次数作为对应组的标签,进行20次重复实验后将得到的RBER归一化处理,RBER随PEC次数的分布如图10所示。可见组内的误比特率分布范围宽,组间的重合区间较大。
|
图 10 随机写入下不同PEC次数的RBER分布 Figure 10 RBER distribution of different PEC times under random programming |
把以上获得的数据(见表1)输入到SVM预测模型中进行寿命预测,测试集大小为0.7。计算机预测模型输出显示训练集的准确率为71.42%,测试集的准确率为53.33%,每个标签组的评估得分如表2所示,除了PEC为5 000次的外,其他组的精准率、召回率和F1分数都是比较低的。因此使用PEC单特征进行寿命预测的方法是不可靠的或者无法适用所有芯片。
| 表 1 随机写入模式数据集 Table 1 Dataset of the random programming mode |
| 表 2 随机写入模式预测结果 Table 2 Predict results of the random programming mode |
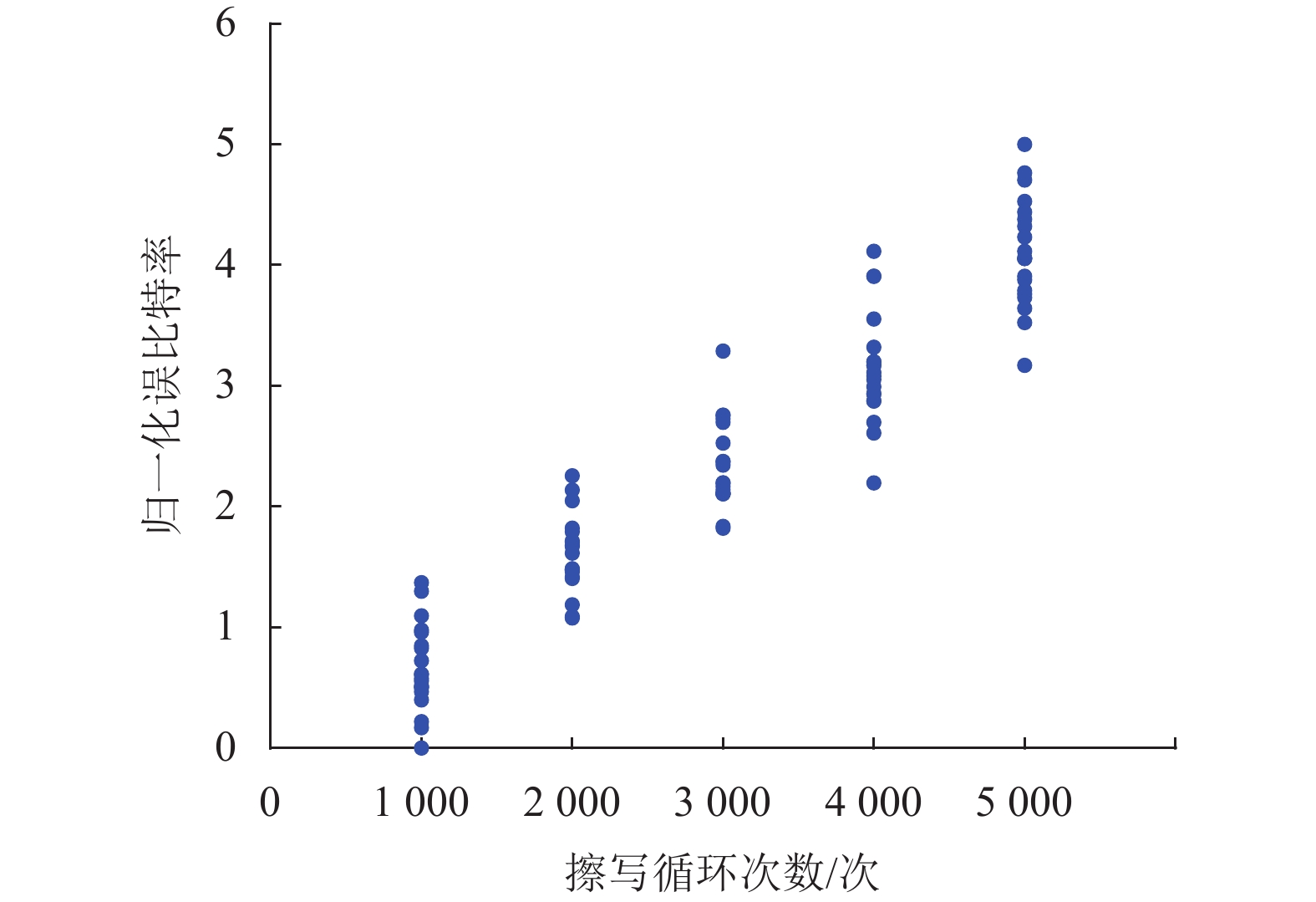
将3.2节中获得的数据RBERWLI归一化后,RBER分布如图11所示,每组PEC的RBER分布与其对应的PEC次数呈现一个正相关的关系。将表3的数据集输入到SVM模型中进行预测,计算机预测模型输出显示训练集准确率达到79.00%,测试集准确率达到80.00%。每个标签组的评估得分如表4所示。可以看到图11中还具有一定的重合区间和数据奇异点,这是由工艺差异导致错误特性不同引起的,而准确率的提高说明本文方法具有一定的抗干扰能力和泛化能力。
|
图 11 激励写入下不同PEC次数的RBER分布 Figure 11 RBER distribution of different PEC times under stimulating programming |
结合PEC的误比特率RBERPEC和激励写入的误比特率RBERWLI作为输入特征进行寿命预测,结果如表5所示。预测模型输出显示训练集准确率达到了81.42%,测试集准确率达到了86.67%,各标签组评估得分如表6所示,各标签的各项指标都有了很大的提升。
| 表 3 激励写入模式数据集 Table 3 Dataset of the stimulated programming mode |
| 表 4 激励写入模式预测结果 Table 4 Predict results of the stimulate programming mode |
| 表 5 数据混合后的数据集 Table 5 Dataset of mixed data |
| 表 6 数据混合后的预测结果 Table 6 Predict results of the mixed data |
本文使用了几种常见的机器学习分类算法进行对比,使用支持向量机、决策树(DT) 和K邻近(KNN) 算法,数据集和训练集大小相同,其中支持向量机的准确度是最高的。各项指标如表7所示,可见KNN算法表现相对较差,SVM的精确度比DT算法高4.8%左右。
| 表 7 机器学习算法对比 Table 7 Comparison of machine learning algorithms |
3D NAND闪存芯片因工艺的差异导致不同芯片间的错误特性有一定的不同,这种差异导致对闪存芯片进行寿命预测时具有不确定性。本文通过NAND测试平台实验发现数据保留错误可以表征当前PEC次数,提出一种特殊写入模式激励字线间干扰效应,可大大减少等待数据保留错误达到目标水平的时间,在本文实验中可节约接近90.91%的时间。同时本文方法可以放大不同PEC次数下数据保留错误的RBER差异水平,使用放大后的RBER通过SVM进行寿命预测准确率可提高33.3个百分点。
然而本文只使用了一种型号的芯片进行实验,提出的方法可能具有一定的局限性。而且只使用了单边的字线间干扰效应,双边的字线间干扰效应可能可以达到更短的时间和更高的准确率。本文方法理论上可以加速和数据保留错误有关的实验,不过需要构建对应的模型,还具有很大的研究空间。
| [1] |
YOON C W. The fundamentals of NAND flash memory: technology for tomorrow’s fourth industrial revolution[J].
IEEE Solid-State Circuits Magazine, 2022, 14(2): 56-65.
DOI: 10.1109/MSSC.2022.3166466. |
| [2] |
MURUGAN M, DU D H. Rejuvenator: a static wear leveling algorithm for NAND flash memory with minimized overhead[C]//2011 IEEE 27th Symposium on Mass Storage Systems and Technologies (MSST) . Denver, USA: IEEE, 2011: 1-12.
|
| [3] |
CAI Y, GHOSE S, HARATSCH E F, et al. Error characterization, mitigation, and recovery in flash-memory-based solid-state drives[J].
Proceedings of the IEEE, 2017, 105(9): 1666-1704.
DOI: 10.1109/JPROC.2017.2713127. |
| [4] |
FITZGERALD B, HOGAN D, RYAN C, et al. Endurance prediction and error reduction in NAND flash using machine learning[C]//2017 17th Non-Volatile Memory Technology Symposium (NVMTS) . Aachen, Germany: IEEE, 2017: 1-8.
|
| [5] |
MA R, WU F, ZHANG M, et al. RBER-aware lifetime prediction scheme for 3D-TLC NAND flash memory[J].
IEEE Access, 2019, 7: 44696-44708.
DOI: 10.1109/ACCESS.2019.2909567. |
| [6] |
ZHANG H, WANG J, CHEN Z, et al. An SVM-based NAND flash endurance prediction method[J].
Micromachines, 2021, 12(7): 746.
DOI: 10.3390/mi12070746. |
| [7] |
KIM S, LEE K, WOO C, et al. Analysis of failure mechanisms during the long-term retention operation in 3-D NAND flash memories[J].
IEEE Transactions on Electron Devices, 2020, 67(12): 5472-5478.
DOI: 10.1109/TED.2020.3028349. |
| [8] |
YOO H, CHOI E, OH J, et al. Modeling and optimization of the chip level program disturbance of 3D NAND Flash memory[C]//2013 5th IEEE International Memory Workshop. Monterey, USA: IEEE, 2013: 147-150.
|
| [9] |
PARK M, KIM K, PARK J H, et al. Direct field effect of neighboring cell transistor on cell-to-cell interference of NAND flash cell arrays[J].
IEEE Electron Device Letters, 2008, 30(2): 174-177.
|
| [10] |
CAI Y, LUO Y, GHOSE S, et al. Read disturb errors in MLC NAND flash memory: characterization, mitigation, and recovery[C]//2015 45th Annual IEEE/IFIP International Conference on Dependable Systems and Networks. Rio de Janeiro, Brazil: IEEE, 2015: 438-449.
|
| [11] |
LUO Y, GHOSE S, CAI Y, et al. Improving 3D NAND flash memory lifetime by tolerating early retention loss and process variation[J].
Proceedings of the ACM on Measurement and Analysis of Computing Systems, 2018, 2(3): 1-48.
|
| [12] |
PARK S K, MOON J. Characterization of inter-cell interference in 3D NAND flash memory[J].
IEEE Transactions on Circuits and Systems I: Regular Papers, 2021, 68(3): 1183-1192.
DOI: 10.1109/TCSI.2020.3047484. |
| [13] |
WEI D, FENG H, QIAO L, et al. Experimental verification and analysis of the acceleration factor model for 3-D NAND flash memory[J].
IEEE Transactions on Computer-Aided Design of Integrated Circuits and Systems, 2021, 41(10): 3543-3547.
|
| [14] |
WEI D, FENG H, LIU M, et al. Edge word-Line reliability problem in 3-D NAND flash memory: observations, analysis, and solutions[J].
IEEE Transactions on Very Large Scale Integration (VLSI) Systems, 2023, 31(6): 861-873.
DOI: 10.1109/TVLSI.2023.3249183. |
| [15] |
JEDEC, JC-64.8. SSD requirements and endurance test method: JESD218B[S]. USA: JEDEC Solid State Technology Association, 2010.
|
 2024, Vol. 41
2024, Vol. 41

