2. 广东工业大学 集成电路学院, 广东 广州 510006
2. School of Integrated Circuits, Guangdong University of Technology, Guangzhou 510006, China
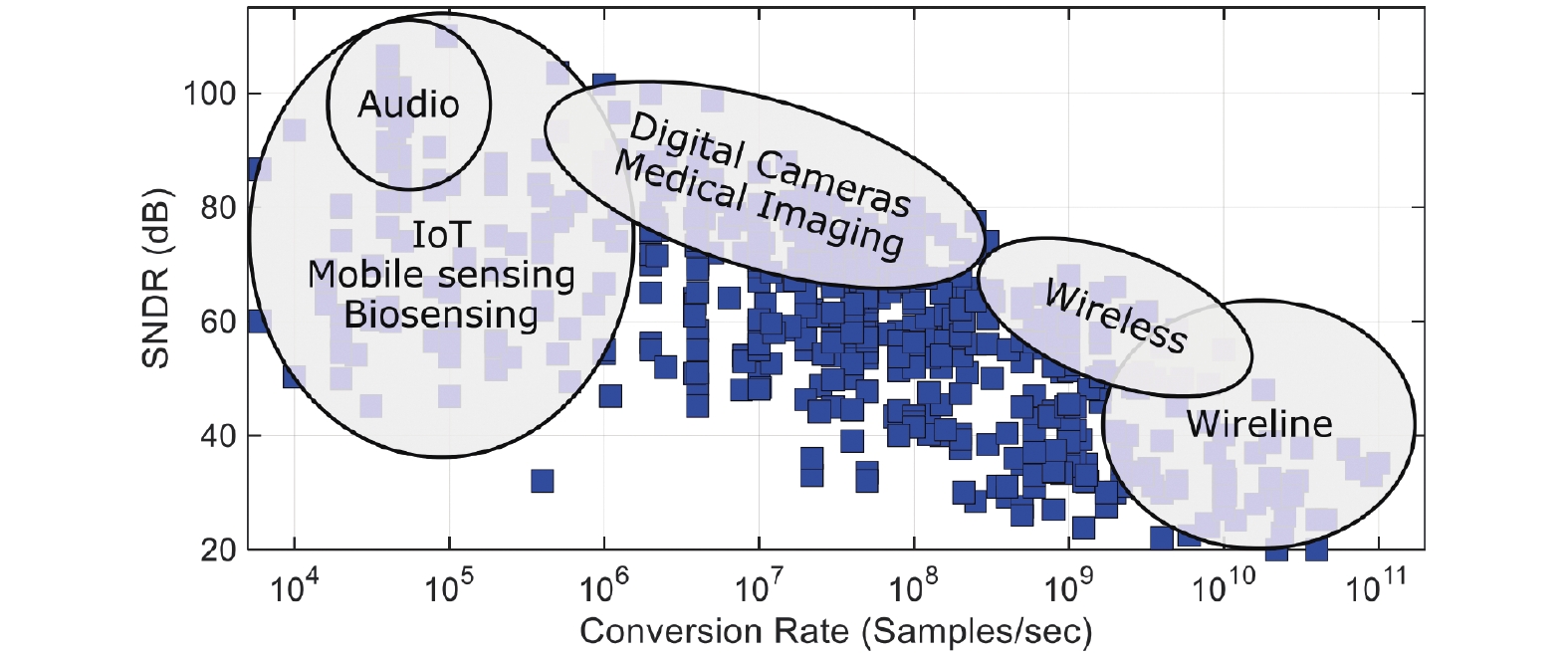
近年来,随着集成电路设计和制造技术的不断进步,无线通信、物联网(Internet of Things, IoT)和可穿戴设备等领域蓬勃发展。模拟/数字转换器(Analog to Digital Converter, ADC)是各类传感器的关键部分,担负着连接模拟世界与数字世界的桥梁作用,其各项性能指标不断取得突破,不同的应用场景对ADC的性能提出了不同的要求[1],总结如图1所示。
音频信号处理是高精度ADC的一个典型应用场景,高性能的音频信号采集设备要求其中的ADC具有非常高的精度,如20 bit;由于人耳的听觉范围为20 Hz~20 kHz,音频设备对ADC的转换速率要求不高,常见的规格为48 kS/s、96 kS/s等[2]。而在物联网、便携传感和生物传感设备等领域,需求的转换速率可能在数kS/s至数百kS/s级别,一些设备对ADC精度的要求同样很高;而有一些设备需要在电池供电下长时间工作,对ADC提出了低功耗的要求[3]。一些应用领域中对ADC精度和转换速度的要求比较均衡,例如在数字摄影、医学影像领域既追求成像质量,也追求成像速度;图像传感器往往会在多个像素间复用ADC[4],为了避免“果冻效应”,对其中的ADC的转换速度提出了更高的要求。近年来,在无线通信领域,5G、WiFi-7等技术飞速发展,一些通信设备对ADC转换速率的要求已经达到数GS/s至数十GS/s级别[5];而在有线通信、材料探查等领域,一些先进设备中的ADC已经具有数百GS/s级别的转换速度[6]。
本文由以下几个部分组成:首先介绍ADC在不同应用场景下的需求;第1节对ADC进行分类,并以图表总结它们的发展现状;第2节介绍高速ADC的原理、电路设计和发展趋势,主要聚焦于SAR ADC与Pipelined-SAR ADC;第3节中介绍了多种类型的高精度ADC,包括Delta-Sigma ADC、Zoom ADC和NS-SAR ADC;最后总结本文内容。
1 ADC的分类和发展现状根据采样定理[7],在模拟信号到数字信号的转换过程中,若采样率至少模拟信号带宽的2倍,采样后的信号可以完整保留原始信号的全部信息,保证采样信号不失真的最小频率(2倍信号带宽)称为奈奎斯特频率。根据信号带宽和采样率的关系,可以将ADC分为奈奎斯特型ADC和过采样型ADC两类[8]。
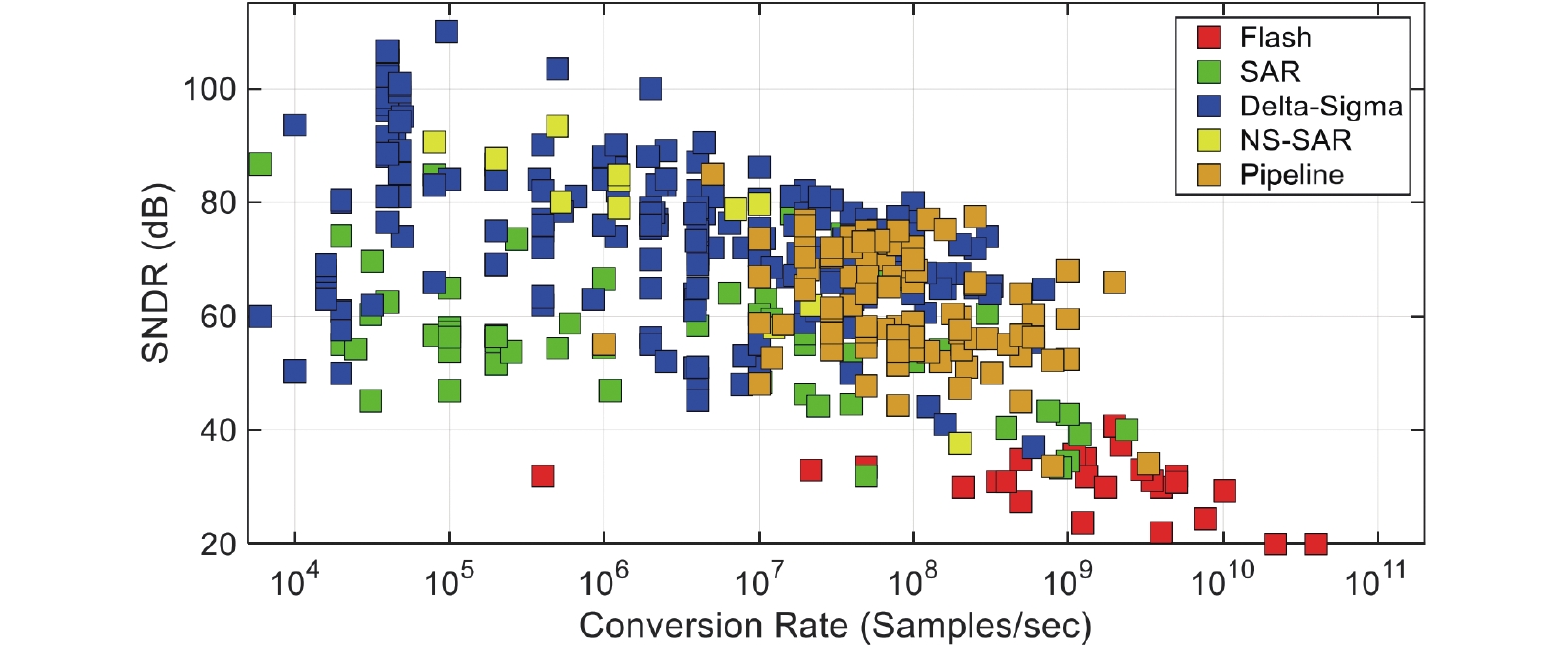
而根据ADC的结构和工作方式,可以分为多种不同的类型,如SAR ADC[9]、Delta-Sigma ADC[10]等,一些经典的ADC结构仍在不停发展,推陈出新。Murmann总结了1997至2022年发表在学术会议ISSCC和VLSI的ADC[1],图2将它们的性能以SNDR-转换速率的形式表示,并分别标注ADC的类型。
奈奎斯特型ADC往往偏向于高速方向。其中Flash ADC[11]主要应用在转换速度要求极高的场景,对应于前文中的高速通信领域。而Pipeline ADC[12]在速度较快的同时也能够取得中高精度,其广泛应用于无线通信和一些图像传感领域;普通的SAR ADC[9]具有中等精度和较快的速度,其主要优势是图中未体现的能源效率,适合物联网、便携和生物传感等领域;而由SAR ADC构成的Pipelined-SAR ADC[13]则可以在保持较快速度的同时提高转换精度,拓展了其应用场景。
过采样型ADC往往偏向于高精度方向。Delta-Sigma ADC[10]是典型的过采样型ADC,其在高精度领域极具优势,但带宽有限和能效较差,适合应用于前文提到的音频信号处理设备中;Zoom ADC[14]通过结合Delta-Sigma ADC与SAR ADC,以较小的面积和功耗开销同样能实现高精度转换;NS-SAR ADC[15]是一种基于SAR ADC的过采样ADC,相比于Delta-Sigma ADC更偏向于提高带宽,在精度、带宽和功耗间取得良好的权衡,在图像传感和通信领域都有所应用。
ADC的主要性能指标分为静态指标和动态指标,包括分辨率(Resolution)、积分/微分非线性(INL/DNL)、信噪失真比(SNDR)、动态范围(DR)、信号带宽(BW)和功耗(Power)等多种[8],不同种类的ADC具有不同的技术特点。Rabii和Wooley提出了一种评价ADC性能的指标[16],能够比较综合地比较ADC的精度和能效表现,称为Schreier品质因数(Figure of Merit, FoM),表达式为
| $ {\text{FO}}{{\text{M}}_{\mathrm{S}}} = {\text{DR}} + {\text{10}} \cdot {\text{lg}}\left( {\frac{{{\text{BW}}}}{{{\text{Power}}}}} \right) $ |
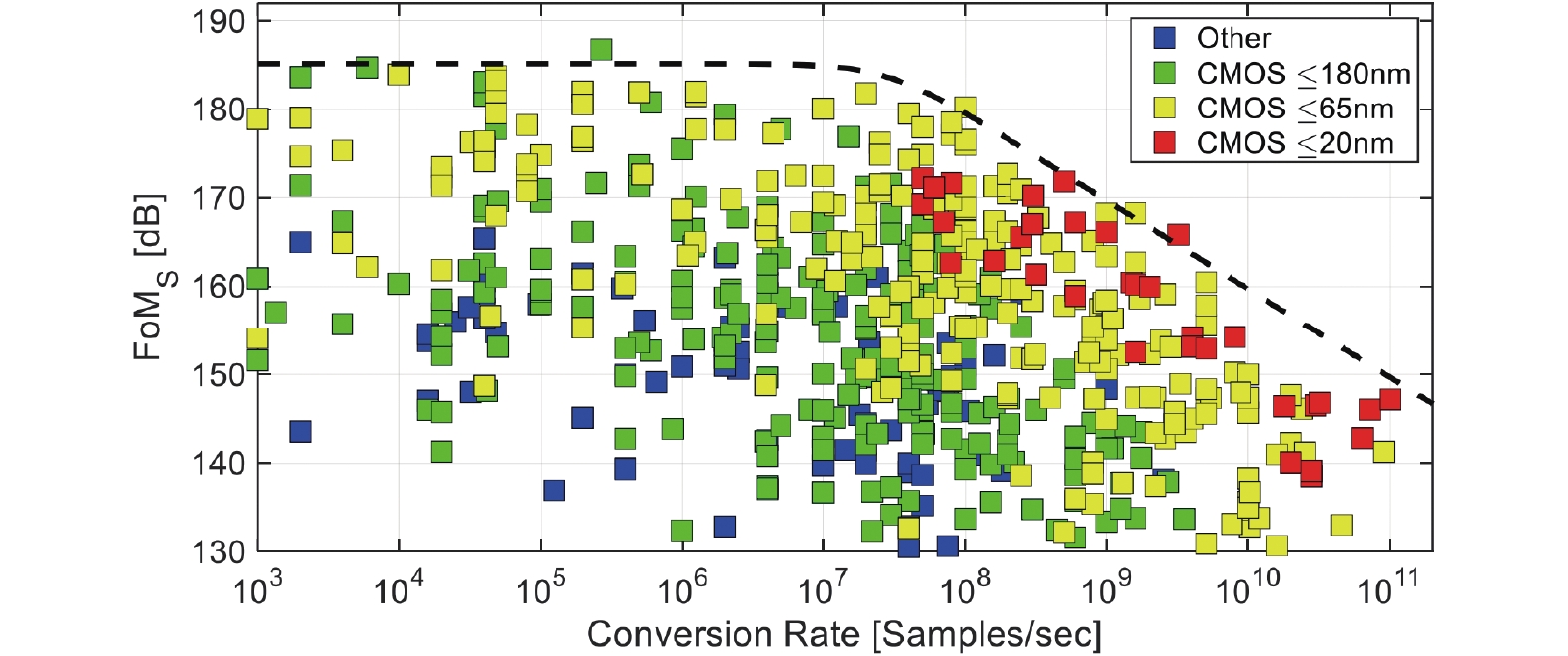
这个值随着ADC的动态范围、带宽的增加一同增大,而ADC功耗的上升则会引起FoMS下降。随着集成电路制造技术的发展,模拟集成电路的特征尺寸也已经达到20 nm以下,根据FoMS,可以对比不同工艺节点下ADC的性能变化趋势。图3总结了1997至2022年发表在学术会议ISSCC和VLSI上关于ADC的FoMS[1],并分别标注它们的制造工艺。
在65 nm以前,180 nm工艺是模拟设计领域一个经典的节点,得益于较高的电源电压和良好的晶体管性能,以及稳定的制造水平,一些出色的ADC设计,尤其是高精度ADC正是基于180 nm工艺设计的[17]。但较大的特征尺寸带来较大的寄生,限制了ADC在高速方向的发展。65 nm是一个比较均衡的工艺节点,既有FoMS达到185 dB左右的高精度ADC设计,也有转换速率达到100 GS/s的高速ADC设计。近年来随着工艺改进达到20 nm以内,ADC进一步向高速方向发展,一些ADC已经具有数百GS/s的转换速度[18]。但集成电路特征尺寸的减小伴随着晶体管本征增益和电源电压的降低,导致放大器的高增益设计遇到困难,另外信号功率相较于热噪声、参考噪声的比例降低,给高精度ADC的设计带来挑战。从FoMS上限近似曲线可以看出,随着采样率的增加,ADC的精度和能效性能面临越来越大的挑战。
2 高速模数转换器近年来,通信、接口、图像传感等技术快速发展,这些场景下对高速ADC的速度要求也越来越高。常见的高速ADC有Flash ADC、SAR ADC和Pipeline ADC等,它们在速度、功耗和面积方面各有优劣。其中,SAR ADC是一类结构简单的ADC,受益于先进的制造工艺和设计技术,其具有较快的速度,且面积小、能源效率非常高,其自然产生量化残差的特点还使其十分适合应用于流水线结构中[19]。上述优点使SAR ADC和包含它的混合架构ADC成为高速ADC领域的研究热点。本节将聚焦于单通道的SAR ADC和Pipelined-SAR ADC,介绍其基本原理和近期发展。
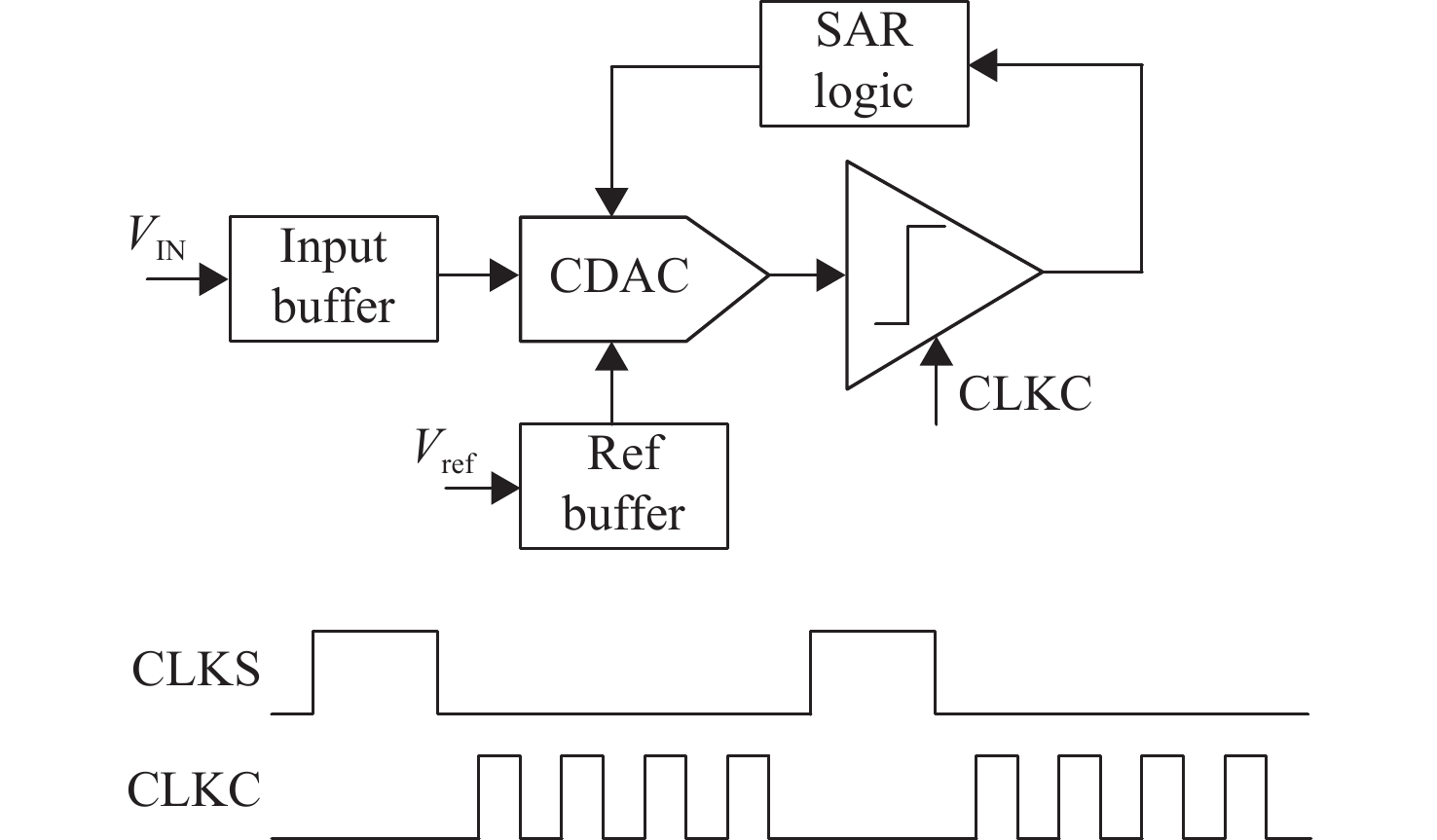
2.1 逐次逼近型(SAR)ADC 2.1.1 SAR ADC的基本结构与工作过程SAR ADC的基本结构如图4所示,主要包括3个部分:电容型数模转换器(Capactive Digital-to-Analog Convertor, CDAC)、比较器和SAR逻辑电路。此外,SAR ADC中还可以引入输入缓冲器以确保采样过程的高驱动能力和高线性度,以及引入参考电压缓冲器提供稳定、低噪声的反馈参考电压[20]。
|
图 4 SAR ADC的基本结构和工作时序 Figure 4 Structure and timing diagrams of the SAR ADC |
SAR ADC的工作过程可以分为采样和逐次比较两个阶段[9]。在采样阶段,未知的输入信号VIN通过采样开关采样到CDAC上;而在逐次比较阶段,SAR ADC通过二进制搜索算法,逐次比较VIN与CDAC反馈的电压值并调整反馈电压,最终获得N bit的量化结果。
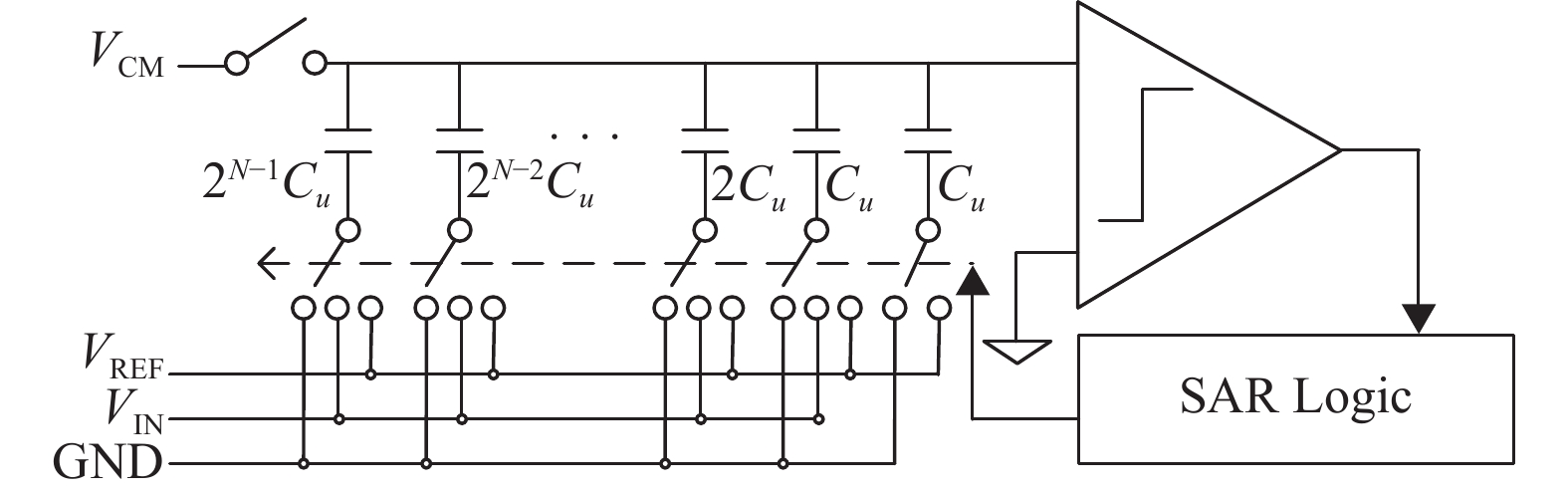
SAR ADC的经典电路实现如图5所示,最早在1975年由McCreary和Gary提出[21],这是一种下极板采样的SAR ADC结构,电路中的CDAC由2N个单位电容Ci以二进制权重构成。在采样阶段,CDAC中所有单位电容下级板采样输入信号VIN,同时上级板接地,使得CDAC获得总电荷量QTOT=−VIN×2N×Ci。在逐次比较阶段,所有单位电容上级板与地断开,最高位2N−1×Ci的下级板连接至高参考电压VREFP,其余单位电容下级板连接至低参考电压VREFN。CDAC上级板节点(即比较器正向输入节点)VCPP此时处于悬空状态而保持电荷守恒,因此
|
图 5 SAR ADC的经典电路结构 Figure 5 Clasic circuit structure of the SAR ADC |
| $ {V_{{\text{CPP}}}} = \frac{{\left( {{V_{{\text{REFP}}}} - {V_{{\text{REFN}}}}} \right) }}{{\text{2}}} - {V_{{\text{IN}}}} $ |
比较器将正向输入节点电压VCPP与接地的反相输入节点电压VCPN进行对比,得到反映SAR ADC输入信号VIN与CDAC反馈电压(VREFP−VREFN) /2的比较结果。根据比较结果,控制最高位SAR逻辑置“1”或“0”,使得CDAC中的(2N−1)×Ci下级板固定地连接至VREFP或VREFN,完成当前比较周期。接下来,次高位重复上述工作过程,直到SAR ADC完成N次比较过程,得到全部N bit转换结果。
2.1.2 SAR ADC中CDAC、开关控制方法的优化技术SAR ADC利用单一的比较器实现模拟信号到数字信号的转换,结构中不存在大功耗的运放,由此获得了很高的能源效率,适合应用于低功耗场景中。SAR ADC中大部分电路为数字电路或MOS管堆叠有限的模拟电路,受电压变化影响小,随着先进工艺特征尺寸的减小,SAR ADC进一步表现出了速度较快、面积较小的优势[20]。然而,随着设计所需的位数N的提高,传统SAR ADC也会出现一些问题。
单位电容间的失配是限制SAR ADC线性度的关键因素,较高的位数N同时会要求ADC有较高的线性度,从而限制了单位电容Ci的最小尺寸。同时,CDAC的单位电容数量随位数N增加而指数上升,这使得SAR ADC中的电容面积迅速增大,从而显著增大了芯片面积消耗。高位电容大小的指数增加,使其充放电所需时间也显著增加,严重降低了SAR ADC的转换速度[9]。此外,SAR ADC的转换过程是串行、循环的,所需的工作周期也随位数 N 增加而线性上升,进一步限制了其转换速度。尽管可以通过失配校准技术抑制单位电容间失配的影响[22-24],但需要复杂的校准电路和时序设计,这依然会损失SAR ADC低功耗、小面积的优势。
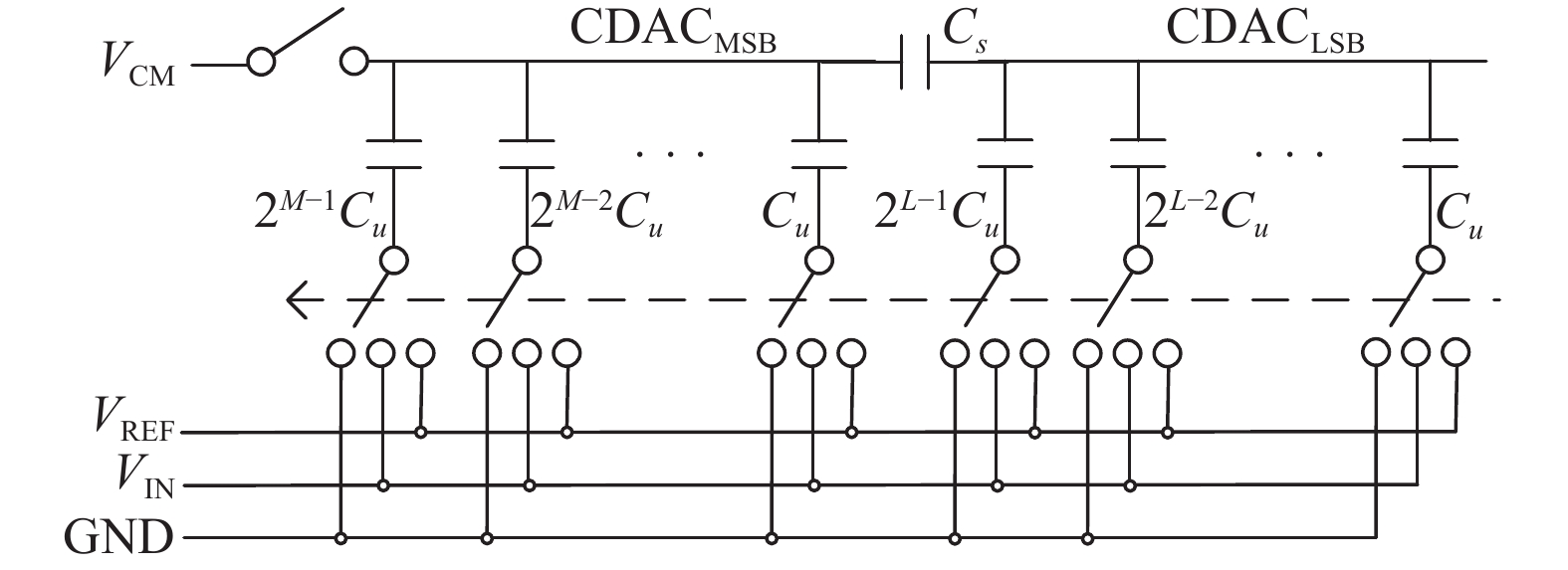
通过采用分段式CDAC可以有效地减小SAR ADC中CDAC的面积[25]。如图6所示,两个二进制权重子CDAC以一个桥接电容Cs串联起来。这种技术还使得SAR ADC在功耗和面积方面获得了一定优化。然而添加的桥接电容Cs可能是单位电容Ci的非整数倍,带来额外的失配问题。C-2C式CDAC可以进一步减少单位电容数量[26],但这种电容结构对寄生十分敏感,往往需要引入额外的校准电路。
|
图 6 分段式CDAC Figure 6 Segmented CDAC |
另一方面,采样热噪声、比较器噪声也是限制SAR ADC精度的重要因素,随着设计位数N的提高,CDAC总面积、比较器功耗的提高仍然会使得SAR ADC丢失原有的低功耗、小面积优势。因此,在不采用复杂的校准电路或热噪声消除电路的情况下,SAR ADC的精度被限制为10 bit左右[20]。设计者在设计ADC的过程中,一个有意义的设计方向是进一步发扬某类ADC的固有优势,而不是通过较大的代价有限地抑制原有劣势。近年来围绕着进一步降低功耗、提高转换速度、减小面积消耗的研究方向,一些新的技术被引入到SAR ADC的设计中。
在SAR ADC中,SAR逻辑电路的功耗可以通过采用动态逻辑电路降低[27],其面积也可以随着制造工艺进步而缩小。而CDAC的总面积受kT/C噪声限制,其中k为玻尔兹曼常数,T为开尔文温度,C为采样电容大小,不能随工艺进步而缩小,需要额外的设计优化以减小功耗。
前文提到的经典SAR ADC采用了下极板采样的传统开关控制方法[21],一个N位的SAR ADC需要CDAC中的单位电容数量为2N个。这种开关控制方法中输入信号VIN并不直接采样至比较器的输入端,而需要一个额外的相位和电荷转移。尽管下极板采样存在不受电荷注入影响、寄生不敏感的优势,但对于SAR ADC常应用的中等精度、较高速场景,这些因素往往并不是限制性能的主要因素。而下极板采样的预设−比较−置位过程却消耗了不必要的功耗[20]。
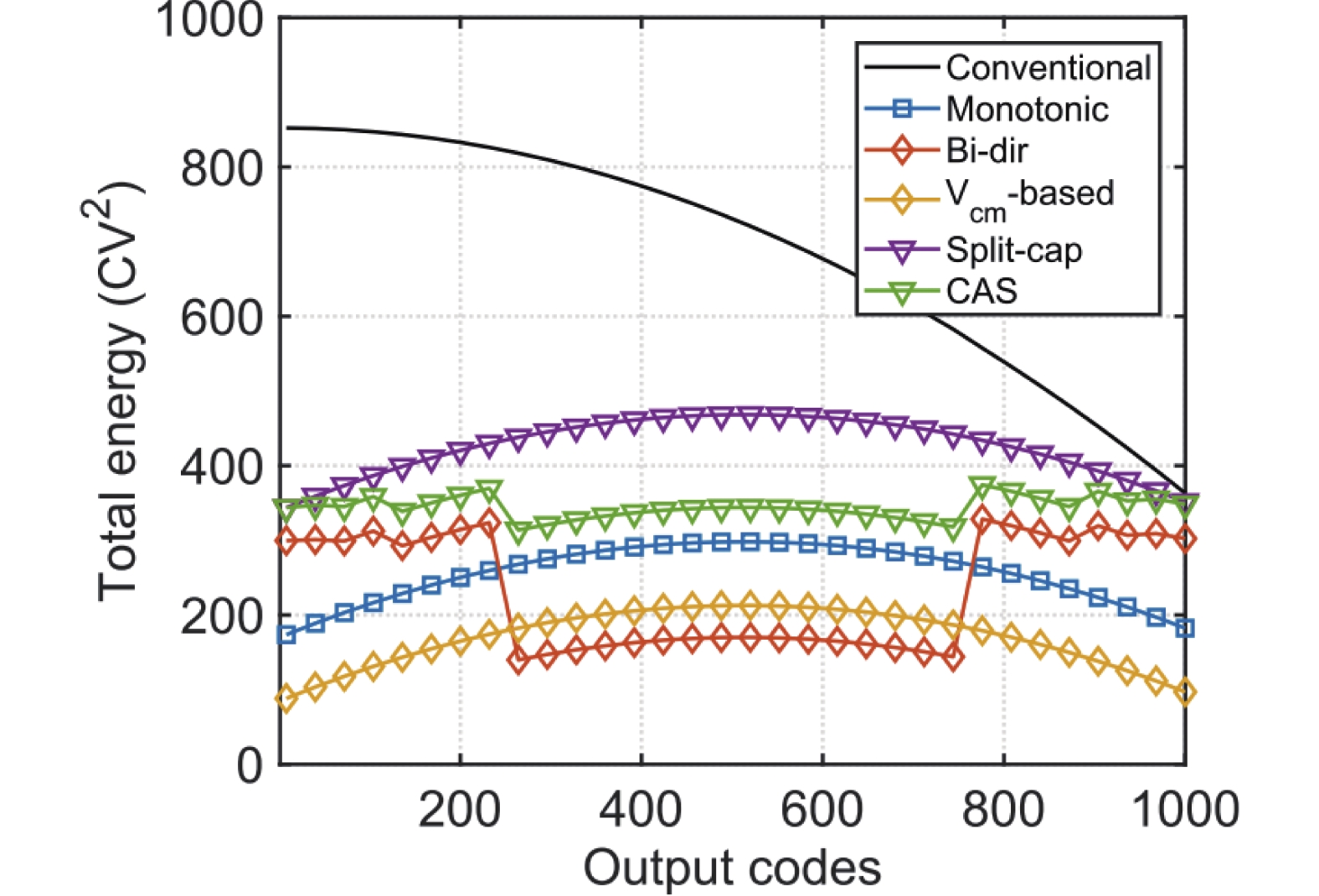
为了减少开关切换过程中的功耗,并避免额外的电荷转移相位,Liu等[28]提出了一种上级板采样的Monotonic开关控制方法。得益于上级板采样时输入信号VIN直接采样至比较器的输入端,在SAR ADC的逐次比较阶段一开始就能直接得到最高位转换结果,节省了额外的电荷转移相位,同时CDAC的单位电容数量也由2N个减小至2N−1个。相较于传统开关控制方法,功耗降低了63%。然而,由于Monotonic开关控制方法下所有单位电容的下级板只能由VREFP有选择地切换至VREFN,使得电容上级板,即比较器输入端的共模电压下降,有可能导致比较器的速度、噪声等性能发生变化,甚至无法正常工作。
为了避免比较器输入共模电平的变化,Ginsburg等[29]在中提出了split-cap开关控制方法。这种控制方法下,CDAC中每个单位电容被分为两个1/2大小的小电容,并在SAR ADC的复位阶段分别连接至VREFP和VREFN,从而保证转换过程中比较器输入共模电平的稳定。相较于传统开关控制方法,功耗降低了37%。然而由于电容的切分,CDAC中小电容的数量又由2N-1个增加至2N个,为版图设计带来困难,不适合高精度设计。
为了避免切分单位电容,Zhu等[30]提出了VCM-Based开关控制方法。在SAR ADC的复位阶段,所有单位电容的下级板连接至VREFP、VREFN以外的第3个基准电压VCM。相较于传统开关控制方法,功耗降低了75%。对于SAR ADC常作为子ADC的场景,一个额外的基准电压VCM并不是难以接受的代价,但能效的提升是显著的。
2022年,Jian等[31]在VCM-Based开关控制方法的基础上,提出了可逆VCM-based开关控制方法(Reversible VCM-based Controlling, RVC),使得功耗进一步降低了62.3%。通过分段的方式,CDAC中的单位电容数量由2N−1个减少至2N−8个,由此节省了75%的电容面积,并有效提高了SAR ADC的转换速度。
图7总结了这些CDAC开关控制方法的功耗曲线。其中,split-cap开关控制方法则因为其快速的建立速度,常应用于高速设计中;而VCM-Based开关控制方法凭借其极高的能源效率,在低功耗应用中十分受欢迎。
2.1.3 SAR ADC中比较器的优化技术比较器是SAR ADC中的关键模块,由预放大级和锁存器组成。在逐次比较阶段,比较器对CDAC上级板的残差电压进行多次比较,产生每个bit的数字结果,其功耗、速度和噪声等非理想因素直接影响了SAR ADC的整体性能。传统的SAR ADC采用静态预放大级,这种结构虽然能提供较大的增益,但存在很大的静态功耗[20]。
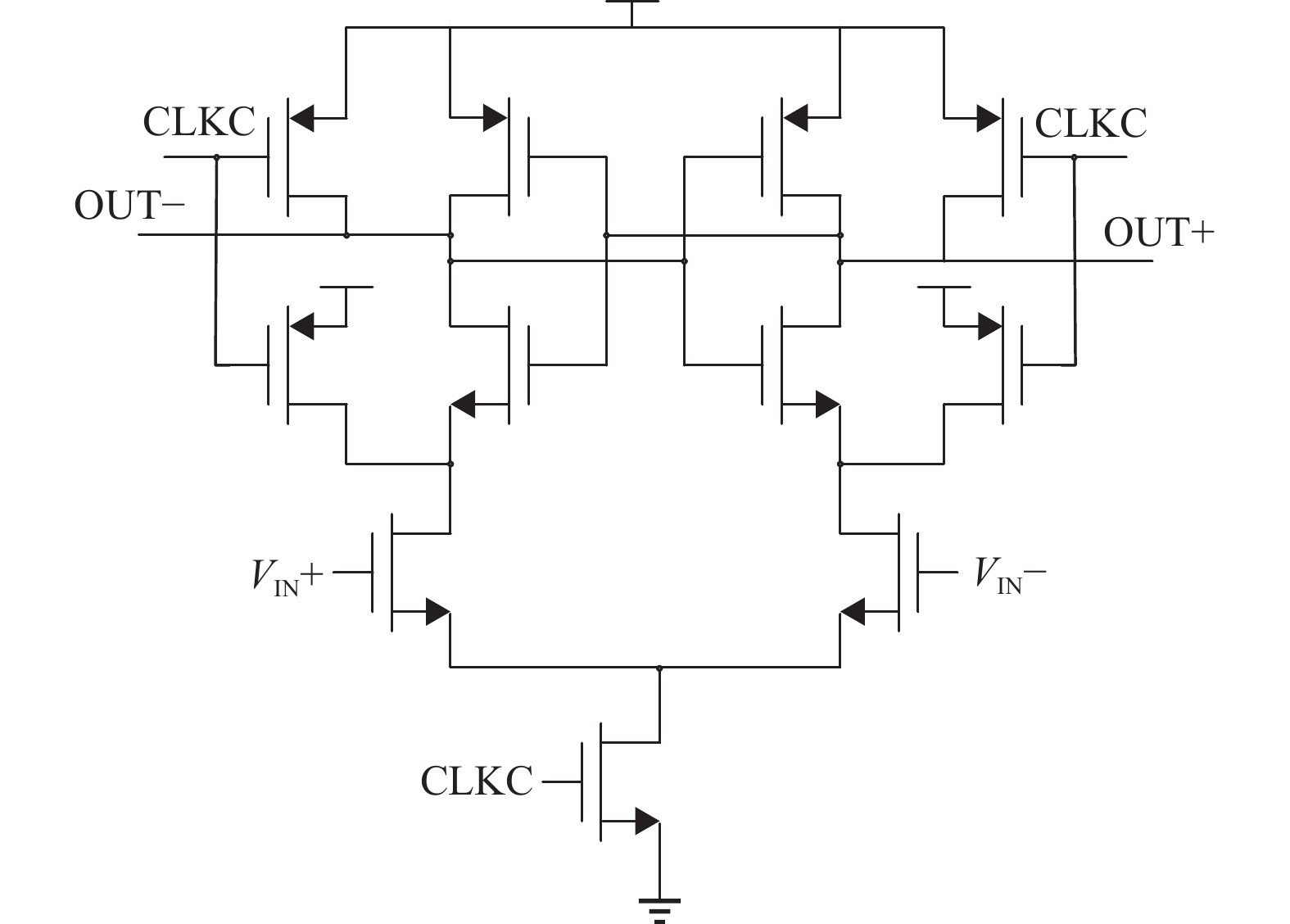
Strong-Arm型比较器[32]是一种动态比较器,其结构如图8所示,为单级结构,输入对管等效为预放大级,顶部交叉耦合的对管等效为锁存级。Strong-Arm型比较器具有速度较快、功耗较低、输出全摆幅的优点,在SAR ADC中被广泛采用。然而,电源到地之间过多堆叠的MOS管导致Strong-Arm型比较器的输入共模范围较小,不适合低电源电压下工作;单级结构使得锁存级的回踢(Kick-back)噪声问题比较严重,对SAR ADC的精度和建立速度有不利影响。
|
图 8 Strong-Arm型比较器 Figure 8 Strong-Arm latch comparator |
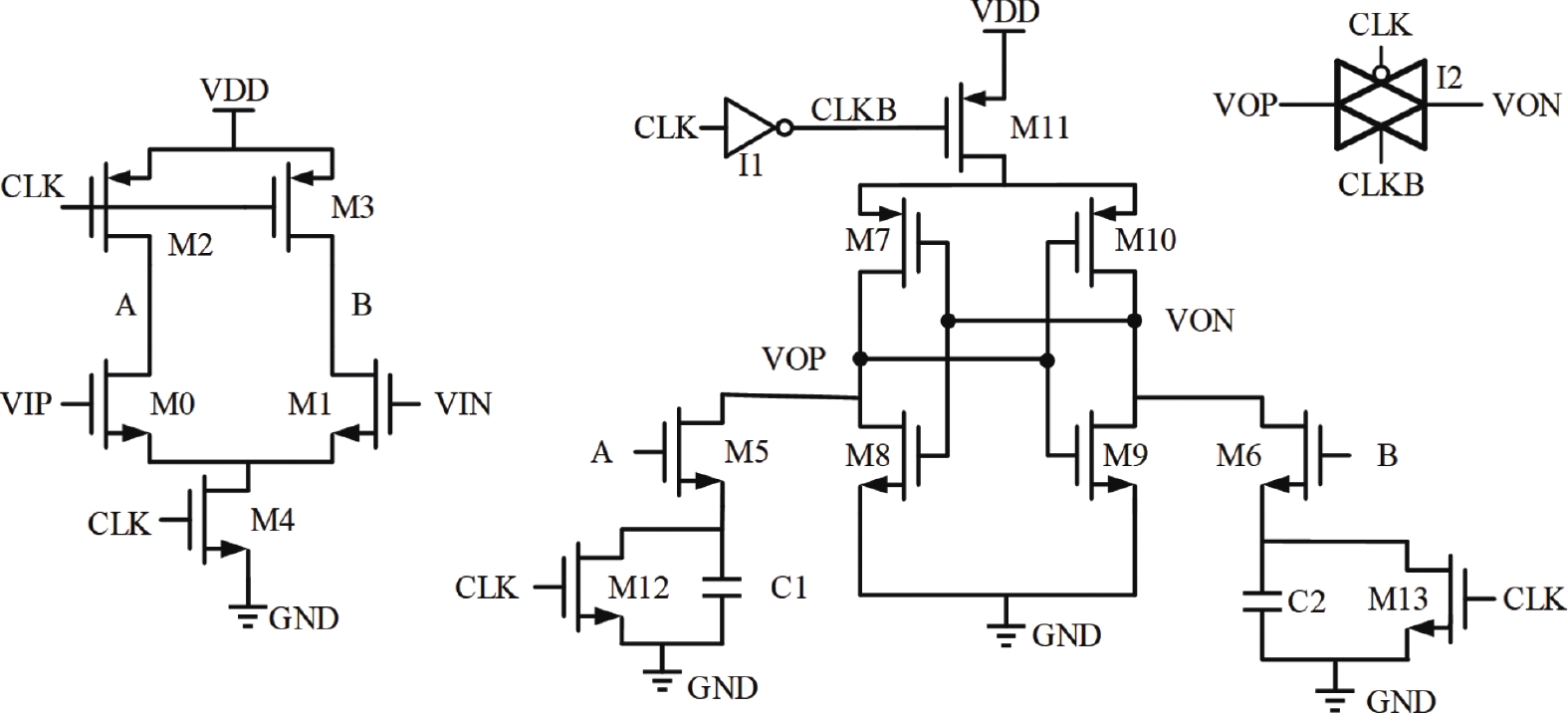
Double-Tail型比较器[33]是另一种SAR ADC中常采用的比较器类型,通过分离预放大级和锁存级,实现了更快的比较速度、更大的输入共模范围,以及对回踢噪声的有效抑制。在文献[34]中,Bindra等在Double-Tail型比较器的基础上,提出了Dynamic-Bias型比较器,通过在预放大级添加额外的电容,动态地控制输入对管的工作状态,实现了2.5倍的能源效率。在文献[35]中,杨德旺等设计了一种具有低输入共模电压的比较器,适合应用于SAR ADC中。在文献[36]中,简明朝等进一步优化了比较器的锁存级,其电路结构如图9所示,通过控制锁存级输入对管的预充电和提前关断,进一步降低了比较器30%的动态功耗,并提高了比较器的速度。
除了在电压域进行比较,时间域比较器也被应用在了SAR ADC当中[37-38]。首先由电压−时间转换器(Voltage-to-Time Convertor, VTC)转换为两个相位差与输入电压正相关的信号,再由时间−数字转换器(Time-to-Digital Convertor,TDC)得到比较结果。时间域比较器受工艺和电源电压影响较小,在SAR ADC中表现出了十分优秀的能效和噪声表现,具有良好的发展前景。
2.1.4 高速SAR ADC设计技术SAR ADC作为一种速度较快、面积和功耗较小的ADC,非常适合作为混合架构ADC的子ADC。传统SAR ADC的逐次比较过程完全由外部时钟控制,例如一个N bit的同步时序SAR ADC需要至少N个相位的外部时钟才能完成转换。虽然工作稳定,但控制时序复杂,不利于集成。在文献[39]中,Chen等提出了一种异步时序SAR ADC,在逐次比较阶段,通过内部环振产生比较器控制时钟,并在完成N bit转换后自动停止。异步SAR ADC仅需要外部输入一个单相位的时钟用于控制采样,实现了外部控制时钟的简化,有利于作为子ADC应用于混合架构ADC中。
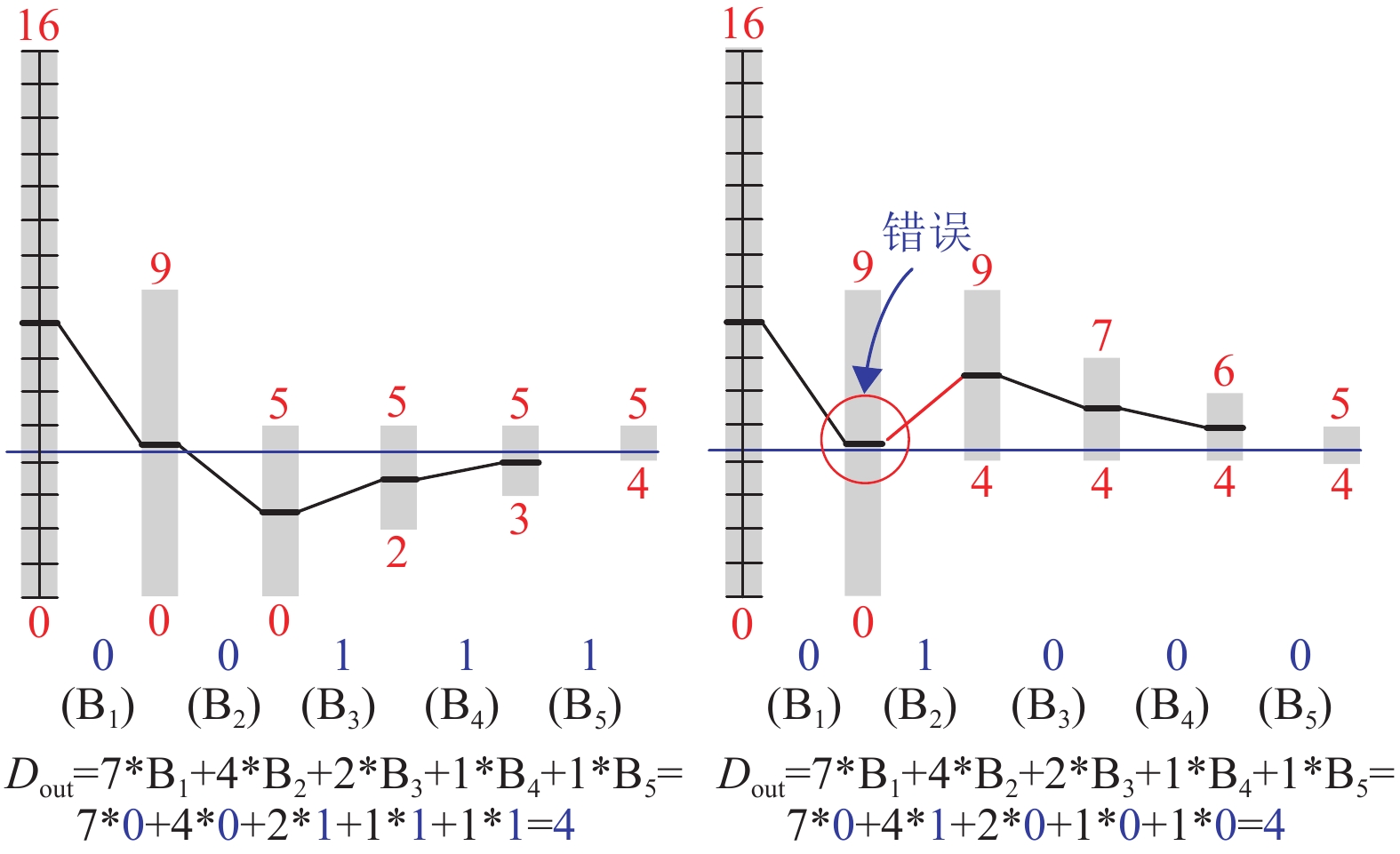
异步SAR ADC需要给每位设置足够等待时间,以保证CDAC上电压的完整建立,这拖慢了SAR ADC的转换速度。这是因为对于普通的二进制权重CDAC阵列,高位的建立误差会在后续比较过程中累积,影响SAR ADC的精度。通过引入非二进制冗余技术[40],高位的建立误差可以在后续比较过程中被纠正,如图10所示。采用非二进制冗余技术的SAR ADC每位转换都存在冗余的码字空间,能够容忍一定范围的建立误差,因此允许为SAR ADC的每一位分配更少的建立时间。尽管引入冗余位可能会增加SAR ADC的总转换次数,但高位节约的建立时间带来的速度优势更大,SAR ADC的整体转换速度得到了很大的提升[41-44]。
理想情况下,异步SAR ADC的速度只受限于CDAC中电压的建立和比较器的比较延时,这两部分耗时可以通过前文提到的冗余和高速比较器技术降低。然而在实际电路中,比较器的复位、SAR逻辑的建立延时等因素都会限制SAR ADC的速度。为了进一步提高SAR ADC的速度,在文献[44]中,通过采用2 bit flash量化器,SAR ADC在每个时钟周期完成2 bit转换,以功耗为代价换得采样率的有效提高。在文献[45]中,通过交替使用两个比较器,可以有效规避比较器复位阶段的耗时,实现超过1 GS/s的采样率。
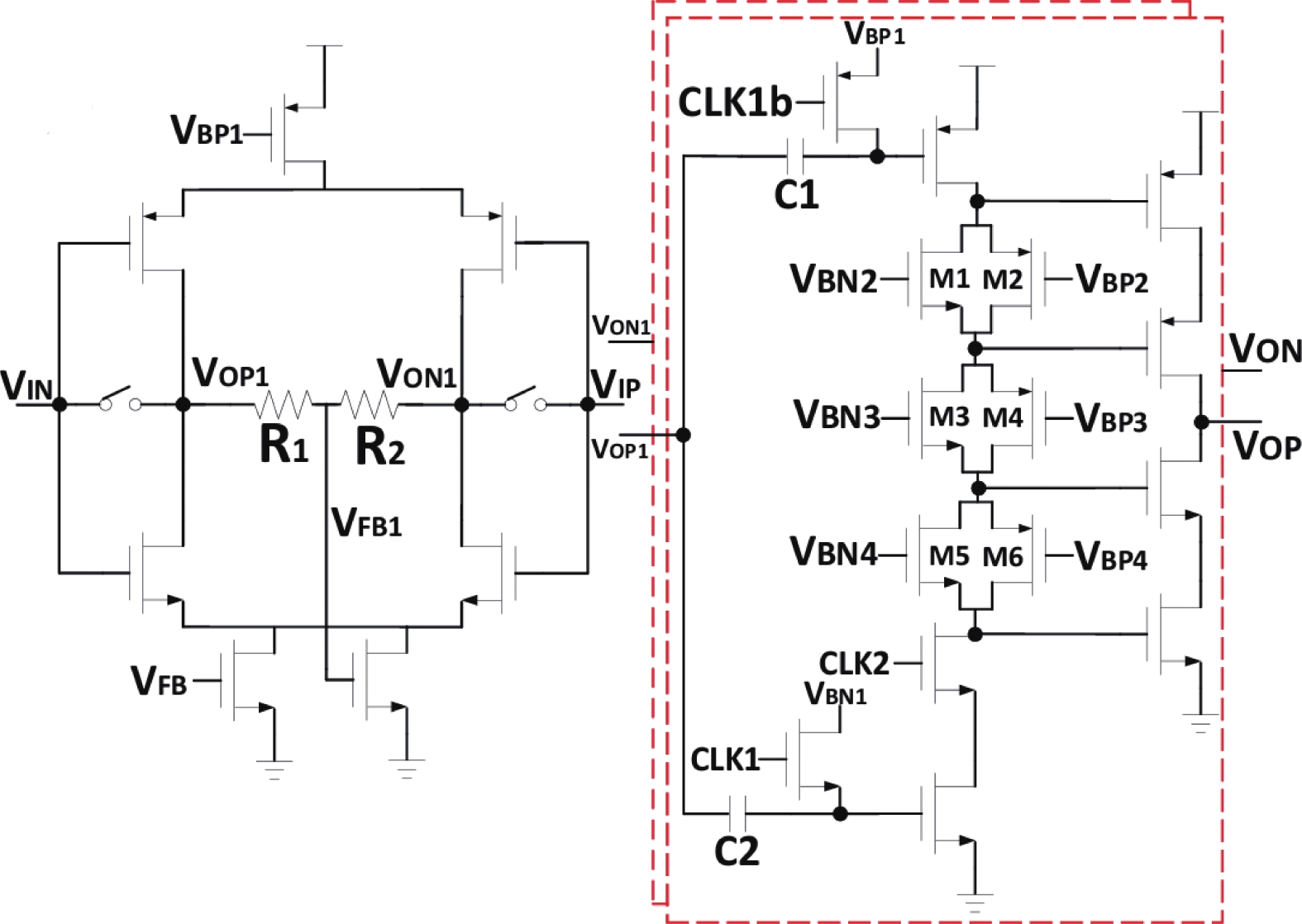
在文献[46]中,Jiang等为进一步提高转换速度提出了一种环路展开型(Loop-Unrolled, LU)SAR ADC,如图11所示。LU-SAR ADC不是循环使用同一个比较器,而是采用N个比较器依次完成N bit转换。在采样阶段,每个比较器只被复位一次;而在逐次比较阶段,每个比较器只完成一次比较,随后锁存各自bit的结果以控制CDAC,无需额外的SAR逻辑电路[47]。LU-SAR ADC避免了比较器复位和SAR逻辑建立所需的时间,使得SAR ADC的转换速度几乎被优化到极限,近些年的高速ADC设计中,LU-SAR ADC和包含它的单通道ADC已经可以实现超过1 GS/s的采样率[48-50]。
|
图 11 环路展开型SAR ADC的电路结构 Figure 11 Structure diagram of the Loop-unrolled SAR ADC |
对于一个常规的SAR ADC,由于其逐次比较并反馈的工作原理,在完成所有数字位的转换后,在SAR ADC中CDAC的上级板自然得到了量化残差,无需任何额外的电路。而对于Flash ADC等其他奈奎斯特型ADC,则需要在完成转换后,由数字输出控制一个额外的CDAC,并从ADC输入信号中减去CDAC反馈电压,才能重建这个量化残差。得益于SAR ADC自然产生量化残差的特性,它非常适合作为各类混合架构ADC的子ADC。
对于一个N bit奈奎斯特型ADC,若对其量化残差做进一步处理,构成混合架构ADC,可以得到超过N bit的量化结果,或转换为ADC其他性能的提升。例如将这个残差(进行放大后)送入另一个ADC中进一步量化,就构成了Two-Step ADC[51](或Pipelined ADC),直接对输入信号进行转换的称为粗量化子ADC,而进一步转换残差的称为细量化子ADC。而将这个残差(进行放大后)直接送回这个ADC本身再次量化,就构成了Cyclic ADC[52]。
上述几种混合架构ADC每次采样输入信号后转换得到一组数字结果,仍为奈奎斯特型ADC。而另一种处理残差的方法是将其送入一组环路滤波器中,并影响之后SAR ADC的比较过程,实现类似于Delta-Sigma ADC的噪声整形效果,称为Noise-Shaping SAR ADC[15],这部分内容将在后续章节介绍。
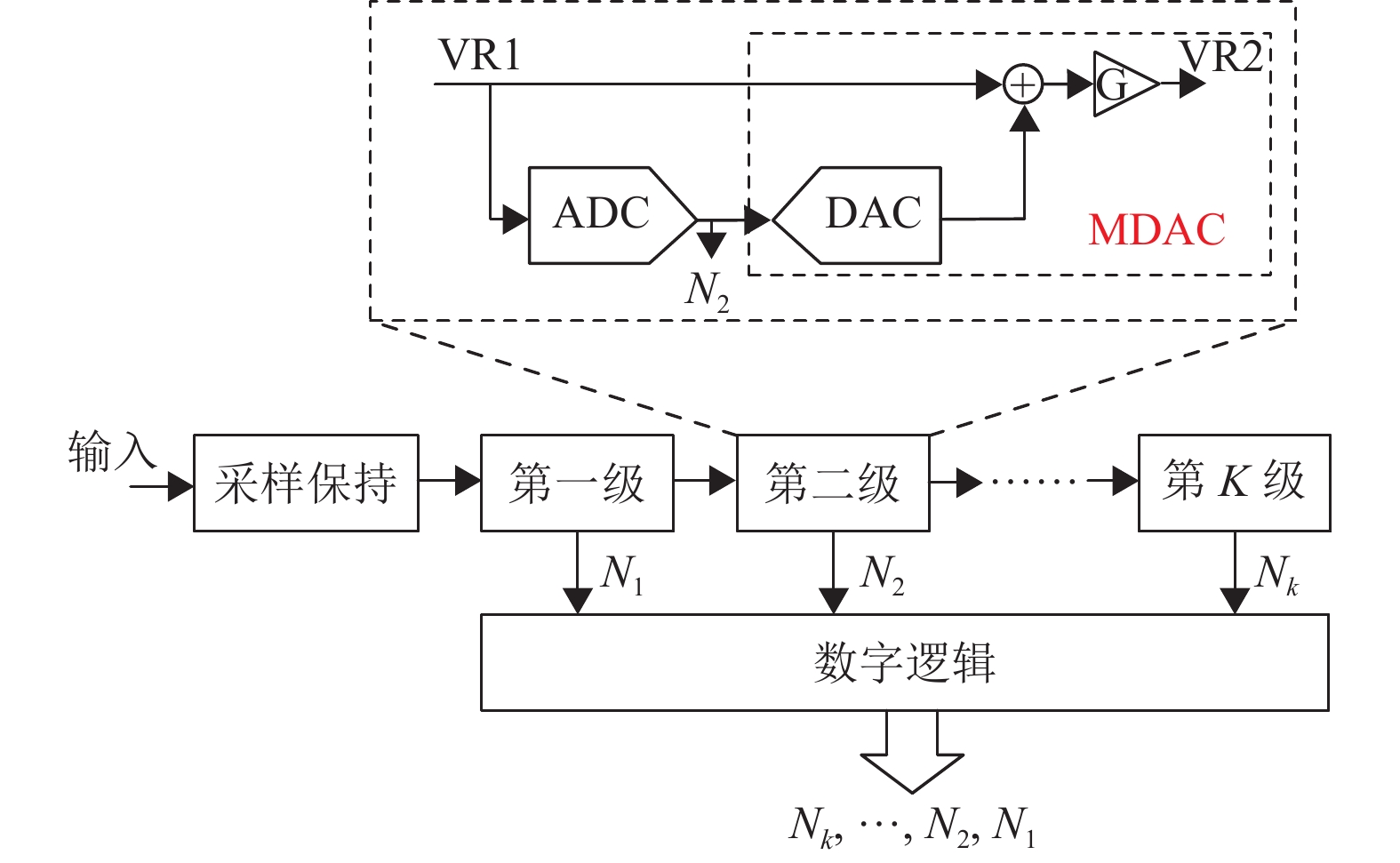
2.2 流水线型(Pipelined)-SAR ADC 2.2.1 Pipelined-SAR ADC基本原理流水线型(Pipeline)ADC[12]是一类奈奎斯特型ADC,图12展示了一个K级Pipeline ADC的基本结构,每级包含1个子ADC、1个DAC和1个残差放大器,其工作过程为:采样保持后第一级子ADC对输入信号进行转换,随后控制DAC从输入信号减去该级量化结果对应的模拟电压,得到量化残差;这个残差经残差放大器放大特定倍数后,送入下一级子ADC进行进一步的细量化;各级子ADC按顺序以流水线的形式工作,直到完成全部bit位的转换。对于每一级子ADC,残差送入下一级后,本级会继续工作,量化下一个输入信号或残差。由于Pipeline ADC中多级子ADC串行的数据传输和并行工作的特点,这类ADC能够实现非常快的工作速度,适合应用于大信号带宽场景[19]。
|
图 12 Pipeline ADC基本结构 Figure 12 Structure diagram of the Pipeline ADC |
传统Pipeline ADC中各级子ADC的量化残差需要一个额外的DAC来产生,ADC与DAC之间的失配限制了Pipeline ADC的精度;残差产生还需要专门的时钟相位[19]。传统Pipeline ADC中子ADC常采用传统Flash ADC,其比较器数量随ADC位数增加而指数上升,导致非常大的面积和功耗。
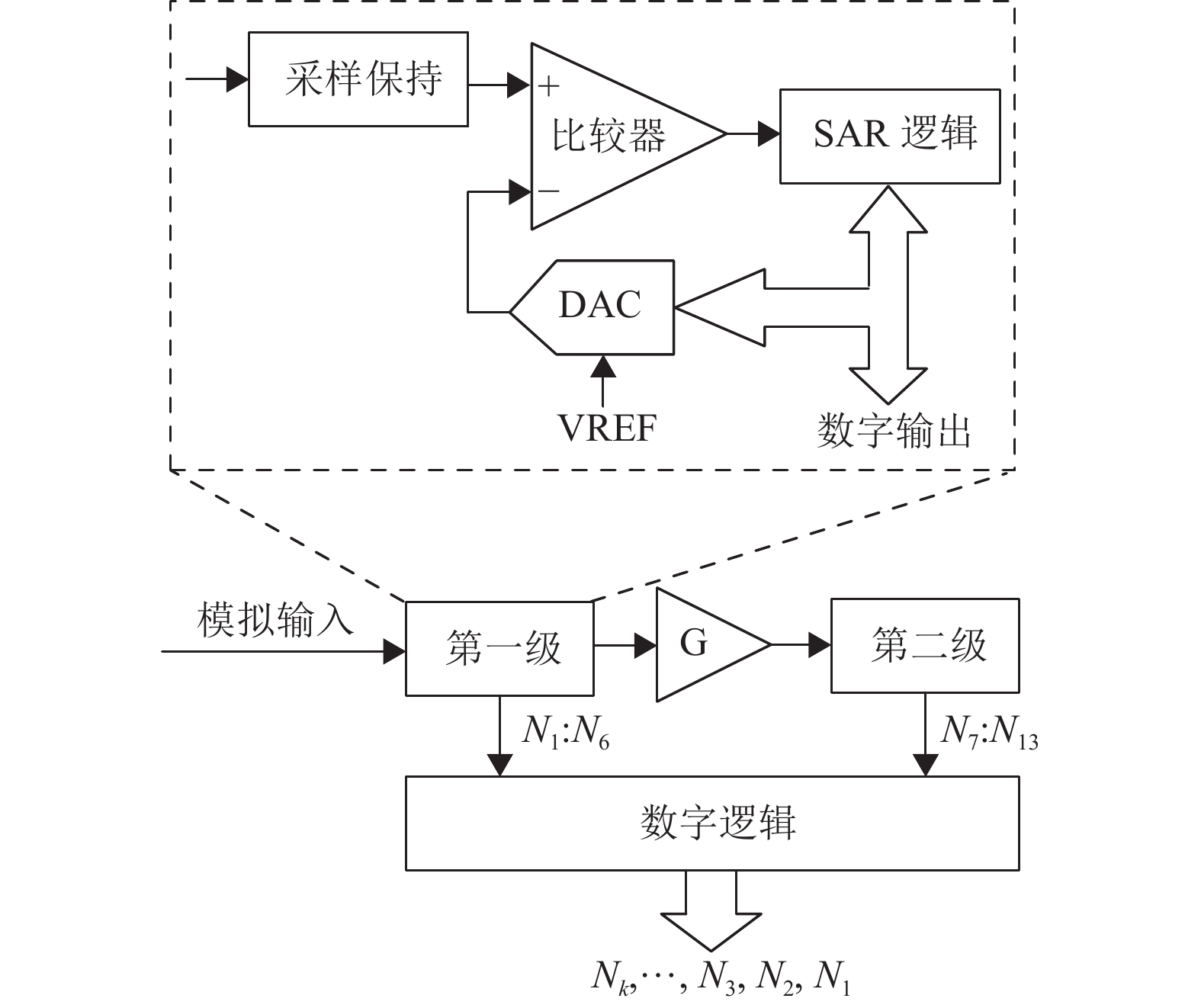
2002年,Li等在文献[13]中第一次提出了Pipelined-SAR ADC,这种将高能效的SAR ADC与高速的Pipeline ADC结合的混合架构ADC在当时实现了先进的性能水平,成为ADC领域的研究热点。相较于Flash ADC,SAR ADC单级就可以采用接近10 bit的位数,因此Pipelined-SAR ADC的级数往往较少,残差放大器数量的减少有利于节省功耗。一个经典的两级Pipelined-SAR ADC基本结构如图13所示,由2个子SAR ADC和1个残差放大器构成。得益于SAR ADC在转换后自有量化残差的优点,Pipelined-SAR ADC的第一级不需要额外的DAC,这有效地节省了面积,且避免了ADC与DAC间失配对ADC精度的限制,不需要专门的残差建立相位则有利于提高速度。相比于传统Pipeline ADC,Pipelined-SAR ADC的速度较慢,但在精度、功耗和设计复杂度等方面具有显著的优势。
|
图 13 Pipelined-SAR ADC基本结构 Figure 13 Structure diagram of the Pipelined-SAR ADC |
Pipelined-SAR ADC的非理想因素既有来自于子ADC的部分,也有来自于极间残差放大的部分。前文提到的电路模块、开关时序、冗余和环路展开等SAR ADC的优化技术也可以应用在Pipelined-SAR ADC的子ADC中。而两极间的残差放大过程则会引入极间失调等非理想因素。极间失调主要来源于残差放大器和前级比较器的输入失调,这会导致残差放大曲线偏移。尽管可以通过调整器件尺寸、版图匹配一定程度上减少极间失调,但残差放大后仍有可能超出后级量程。
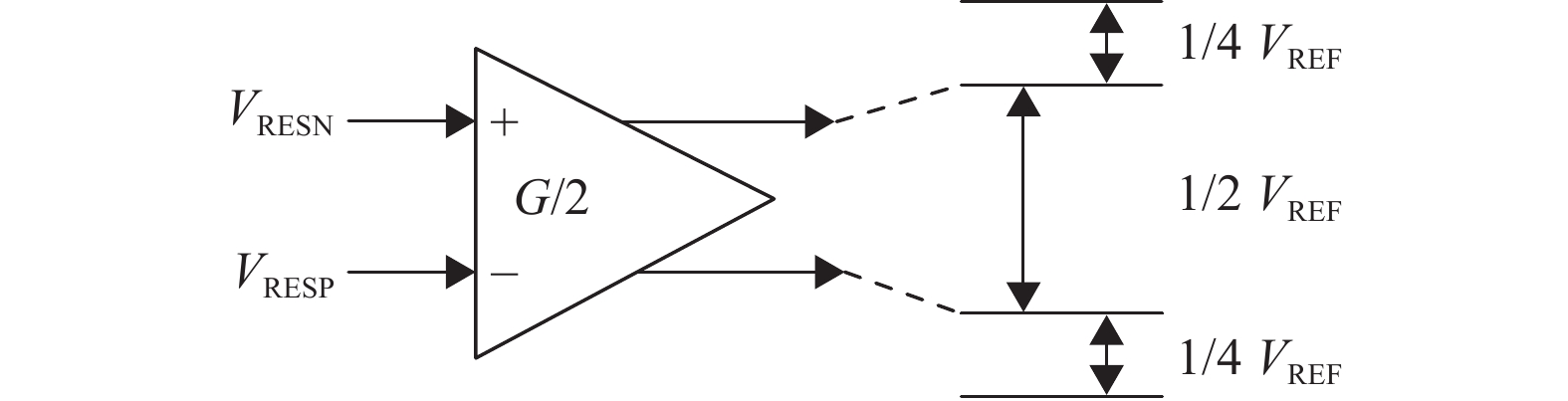
极间冗余技术是来源于Pipeline ADC的技术,也适用于Pipelined-SAR ADC中,通过减小极间残差放大的倍数,以确保放大后的残差在后级的量程以内[19]。图14展示了带有1 bit极间冗余的非理想残差放大过程,前级残差放大倍数被减半,残差放大后的波动范围恰为后级量程的一半。以1 bit分辨率损失为代价,只要极间失调在±0.5 bit以内,Pipelined-SAR ADC仍然能够得到正确的转换结果。
|
图 14 带有1 bit极间冗余的残差放大过程 Figure 14 Residual amplification with 1 bit redundancy |
近年来,一些设计者结合SAR ADC的设计技术,优化Pipelined-SAR ADC中的子ADC,取得了一些设计成果。例如,文献[53]中在Pipelined-SAR ADC的第一级子ADC中采用了环路展开型结构,有效避免了比较器和SAR逻辑复位的时间消耗,还引入了MDAC技术,以65 nm工艺制造,可以工作在300 MS/s的采样率下并具有63.6 dB的SNDR。而在文献[54]中,Pipelined-SAR ADC的第一级子ADC采用了非二进制冗余技术,能够容忍一定的建立误差,有效提高了逐次转换的速度,后仿真显示其在125 MS/s的采样率下实现了70.34 dB的SNDR。
Pipelined-SAR ADC中的残差放大器可以分为开环和闭环两种结构。开环放大器没有反馈环路,具有很快的建立速度,但其增益线性度较差,对PVT变化十分敏感。闭环残差放大结构主要基于开关电容反馈的闭环放大器,增益线性度高,鲁棒性好,但建立速度受限于其中静态放大器的输出能力。近年来,一些新型的动态放大器被设计出来,动态偏置允许放大器在不同的输出阶段具有不同的带宽和输出电流,具有出色的输出能力和能效表现,被广泛地应用于Pipelined-SAR ADC中[54-57]。在文献[55]中,Guo等提出了一种基于反相器的动态放大器,以简单的电路实现了较大的带宽,且PVT稳定性好;结合三态SAR逻辑技术,该Pipelined-SAR ADC能够在625 MS/s的高采样率下工作,FoMW达到10.5 fJ/cov。环形放大器(Ring Amplifier)由三级反相器级联构成,文献[54]中提出了一种新型的环形放大器,如图15所示,采用增益增强的输出级;该放大器应用于一个两级Pipelined-SAR ADC中,得益于残差放大阶段良好的增益线性度,ADC实现了63.6 dB的SNDR。
除了对SAR子ADC和残差放大过程的优化,还有一个设计方向是结合其他种类ADC的优点,以流水线形式构成性能更加优秀的混合架构ADC,称为SAR-assisted Pipeline ADC。2021年,Oh等[50]提出了一种8 bit的新型流水线结构ADC,由高速的环路展开型SAR ADC与插值型Flash ADC组成,且在2个子ADC中复用8个比较器,该ADC的采样率达到1 GS/s,而功耗仅为2.55 mW。2023年,Zhao等[58]利用SAR压缩时间域ADC的输入信号摆幅,构成了一种新型流水线结构ADC,可以工作在0.8 V的低电源电压下并具有极高的能效,实现了优异的4.27 fJ/cov的FoMW。
3 高精度模数转换器高精度ADC一般指分辨率超过14 bit的ADC,常应用于音频、测量、生物医疗等领域。Delta-Digma ADC是一类经典的高精度ADC,凭借过采样和噪声整形技术实现了良好的信噪比和动态范围[59]。近年来,芯片制造工艺不断进步,先进工艺使得数字芯片的速度、功耗等表现有了长足的进步,而伴随着特征尺寸的减小,电源电压也逐渐下降,高精度ADC的设计迎来新的挑战。单一的Delta-Sigma ADC越来越难以满足高精度、低功耗的要求,由此一些包含Delta-Sigma ADC的混合架构ADC逐渐成为热门的研究方向,如Zoom ADC、NS-SAR ADC等,在精度、带宽、能效和芯片面积等方面表现出了各自的优势。本节将介绍这3种ADC的基本原理和近期发展。
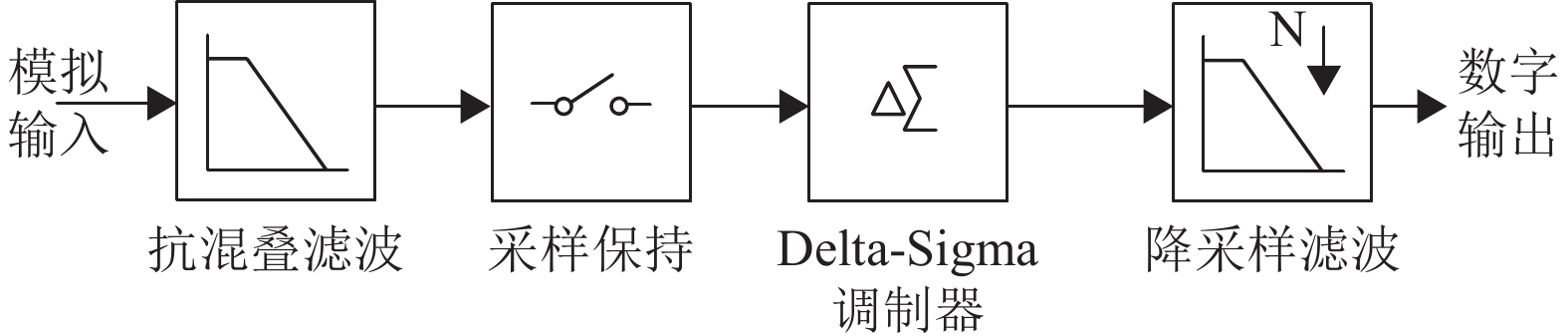
3.1 误差积分型(Delta-Sigma)ADC 3.1.1 Delta-Sigma ADC的基本结构与工作原理Delta-Sigma ADC的基本结构如图16所示,主要包括3个部分:抗混叠滤波器、Delta-Sigma调制器(Delta-Sigma Modulator,DSM)以及数字抽取滤波器[10]。其中Delta-Sigma调制器是Delta-Sigma ADC的核心部分,通过过采样和噪声整形技术,实现ADC精度和动态范围的有效提高。
|
图 16 Delta-Sigma ADC整体结构 Figure 16 Block diagram of the Delta-Sigma ADC |
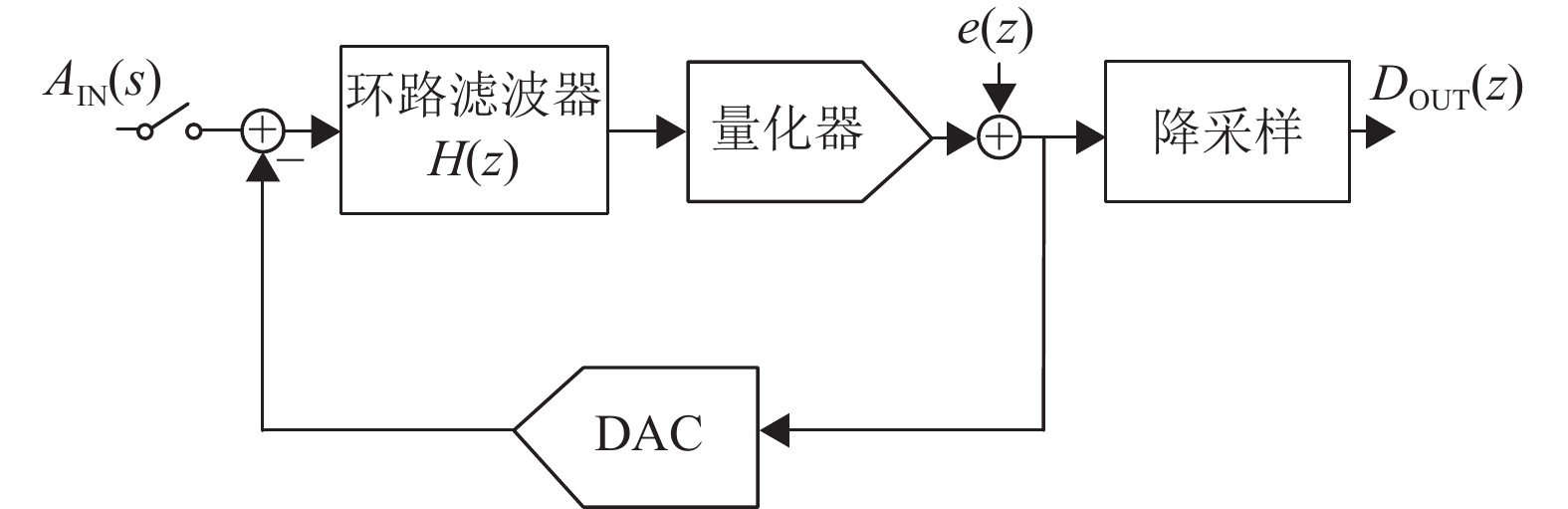
离散时间型(Discrete-Time,DT)Delta-Sigma调制器的基本结构图17所示,由环路滤波器(Loop-Filter)、量化器(Quantizer)、电容型模数转换器(CDAC)构成[59]。其中CDAC与采样开关构成采样保持电路(Sampling/Hold,S/H),它以远高于信号带宽FB的时钟频率FS对输入信号VIN进行采样,称为过采样技术。采样结果在每个时钟周期与上一周期量化结果控制的反馈电压在CDAC的电荷转移过程中相减,并送入环路滤波器。量化器对环路滤波器的输出进行数字化,最终得到当前周期Delt-Sigma调制器的量化结果。Delt-Sigma调制器输出的高速数字码流需经过后续的数字抽取滤波器,完成低通滤波和降采样,以奈奎斯特速率输出转换结果,由此构成了完整的Delta-Sigma ADC。
|
图 17 离散时间型Delta-Sigma调制器基本结构 Figure 17 Structure diagram of the DT Delta-Sigma Modulator |
以经典的单bit一阶Delta-Sigma ADC为例,其量化器为一个简单的比较器,环路滤波器为一个简单的开关电容积分器,传递函数为
| $ H\left( z \right) = \frac{{{z^{{{ - }}1}}}}{{{{1}} - {z^{{{ - 1}}}}}} $ |
而一阶Delta-Sigma调制器的信号传递函数(Signal Transfer Function, STF)和噪声传递函数(Noise Transfer Function, NTF)分别为
| $ {\text{STF}}\left( z \right) = {z^{{{ - }}1}},\;\; {\text{NTF}}\left( z \right) = {{1}} - {z^{{{ - 1}}}} $ |
其中,输入信号仅经过了一个时钟周期的延时,而量化噪声却经过了高通滤波。图18绘制了归一化频率内的STF和NTF[60]。可以看到,噪声整形使得原本在广泛频率内均匀分布的量化噪声由带内推向带外,但不影响输入信号。量化器引入的其他非理想因素,如比较器噪声、失调等也会与量化噪声一同被NTF整形[10]。经过低通滤波后,输入信号在带内被完整保留,而量化噪声则在带内被显著衰减,有效地提高了Delta-Sigma ADC的信噪比(SNR)及有效位数(ENOB)。

|
图 18 归一化的STF与NTF Figure 18 Normalized STF and NTF |
一阶噪声整形对Delta-sigma的精度提升有限,为了获得更高的信噪比,可以采用二阶或更高阶的环路滤波器。理想情况下,一个L阶单环Delta-Sigma调制器的信噪比为[10]
| $ \begin{split} {\text{SNDR}} =& {{6}}{{.02}}N + 1.76 + \left( {20L + 10} \right) \log \left( {{\text{OSR}}} \right) - \\ &10\log \left( {\frac{{{{\text{π}}^{{{2}}L}}}}{{2L + 1}}} \right) \end{split}$ |
对于二阶Delta-Sigma调制器,过采样率OSR每增加一倍,可以获得15 dB信噪比或2.5 bit有效位数的提升。二阶Delta-Sigma调制器的固有稳定性使得它在精度和电路规模、设计难度间取得了良好的权衡,被广泛地应用于各类高精度ADC中,时至今日仍有新的设计出现[61-62]。
三阶及以上的Delta-Sigma调制器对于极其微小的输入就可能发生过载,这是因为其NTF在高频的增益过大。若要保持环路滤波器稳定,需要细致地设计NTF的零极点,以减小其高频增益,代价是无法获得理想的噪声整形效果[10]。此外,高阶环路滤波器还会导致额外的能量和面积消耗。虽然存在上述问题,但在Delta-Sigma ADC发展的早期阶段,通过提高环路滤波器的阶数获得更好的噪声整形效果,仍然是一个常见的设计方向。例如在文献[63]中,Roh等设计了一款四阶CRFF结构的Delta-Sigma ADC,通过在三、四级加入谐振回路,优化了NTF的带内表现,并确保调制器稳定,最终在20 kHz带宽内实现了73.1 dB的SNDR。
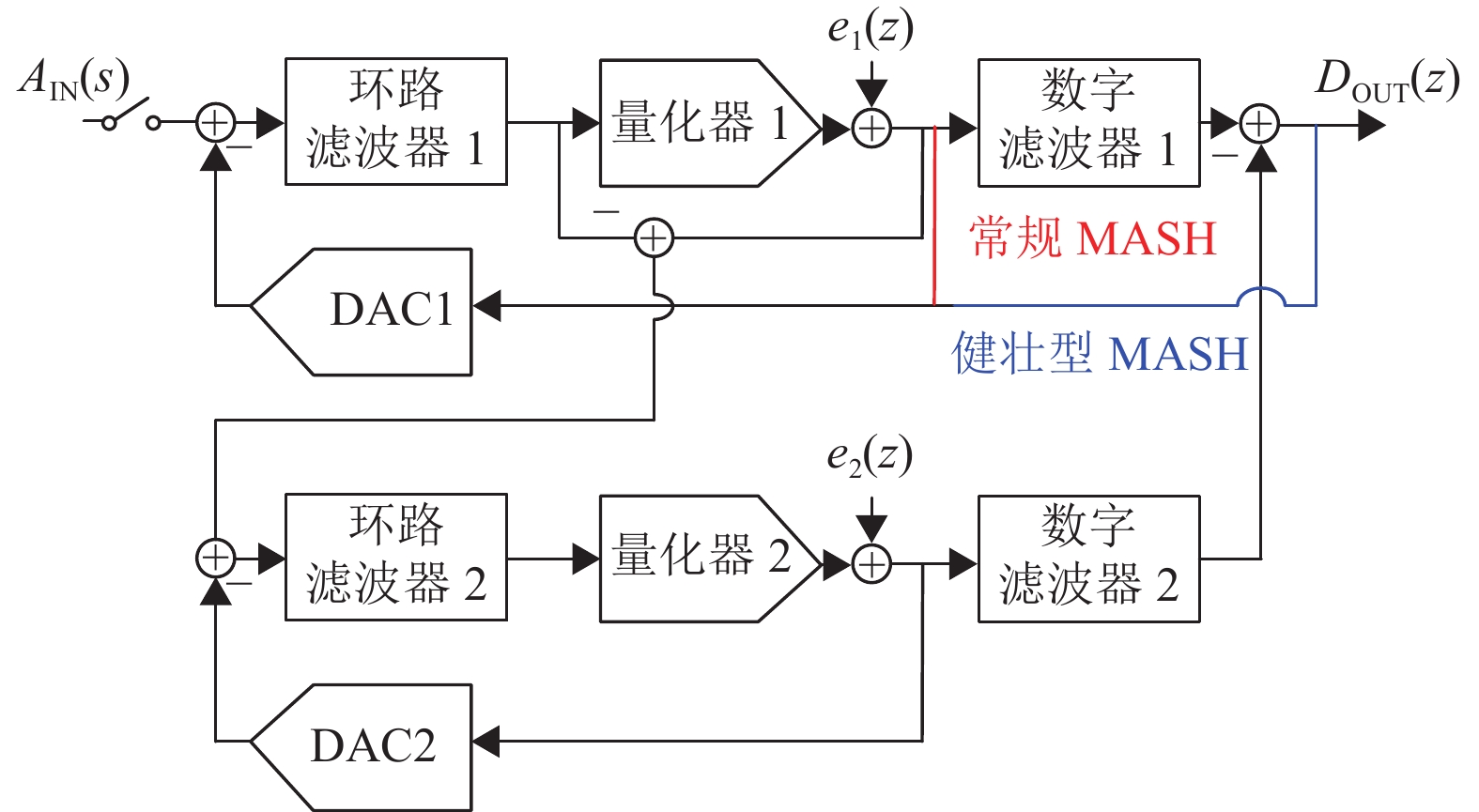
为了在提高Delta-Sigma调制器阶数的同时保证稳定性,多级噪声整形(Multi-Stage Noise-Shaping,MASH)Delta-Sigma ADC被设计出来[64]。通过拆分单个高阶环路滤波器为多个低阶环路滤波器,并在数字域以特定规则组合,实现了高阶噪声整形并规避了稳定性问题。两级MASH型Delta-Sigma ADC的基本结构如图19所示。
|
图 19 常规/健壮型MASH ADC Figure 19 Conventional/Sturdy MASH ADC |
当数字滤波器的传递函数H1=STF2,H2=NTF1时,ADC的传递函数为
| $ {D_{{\text{OUT}}}}\left( z \right) = {\text{ST}}{{\text{F}}_{\text{1}}}{\text{ST}}{{\text{F}}_{\text{2}}}{A_{{\text{IN}}}}\left( z \right) - {\text{NT}}{{\text{F}}_{\text{1}}}{\text{NT}}{{\text{F}}_{\text{2}}}{e_{\text{2}}}\left( z \right) $ |
理想情况下,输入信号被完整保留,第一级的量化误差e1被完全消除,第二级的量化误差e2则经过了高阶的噪声整形。MASH型Delta-Sigma ADC表现出了优异的信噪比和动态范围性能,被广泛应用于各类高精度ADC设计中[65-67]。
对于一般的MASH ADC,由于寄生、失配和制造偏差,各级环路滤波器的STF和NTF易发生变化,导致数字滤波器难以完全滤除第一级量化误差,称为噪声泄露[60]。在文献[68]中,Maghari等提出了一种健壮型MASH ADC,其基本结构如图19所示。健壮型MASH ADC的第二级输出也会耦合入第一级环路滤波器,且不再需要数字滤波器,有效地降低了模拟与数字电路之间传递函数的匹配要求,从而避免噪声泄露。
近些年来,随着先进制程下电源电压逐渐下降,热噪声限制了ADC精度的进一步提高,MASH型Delta-Sigma ADC的设计方向逐渐转向提高信号带宽。例如在文献[69]中,Tan等设计了一款0-4 MASH ADC,可以工作在400 MS/s的采样率下,对10 MHz带宽的信号实现76.7 dB的SNDR。
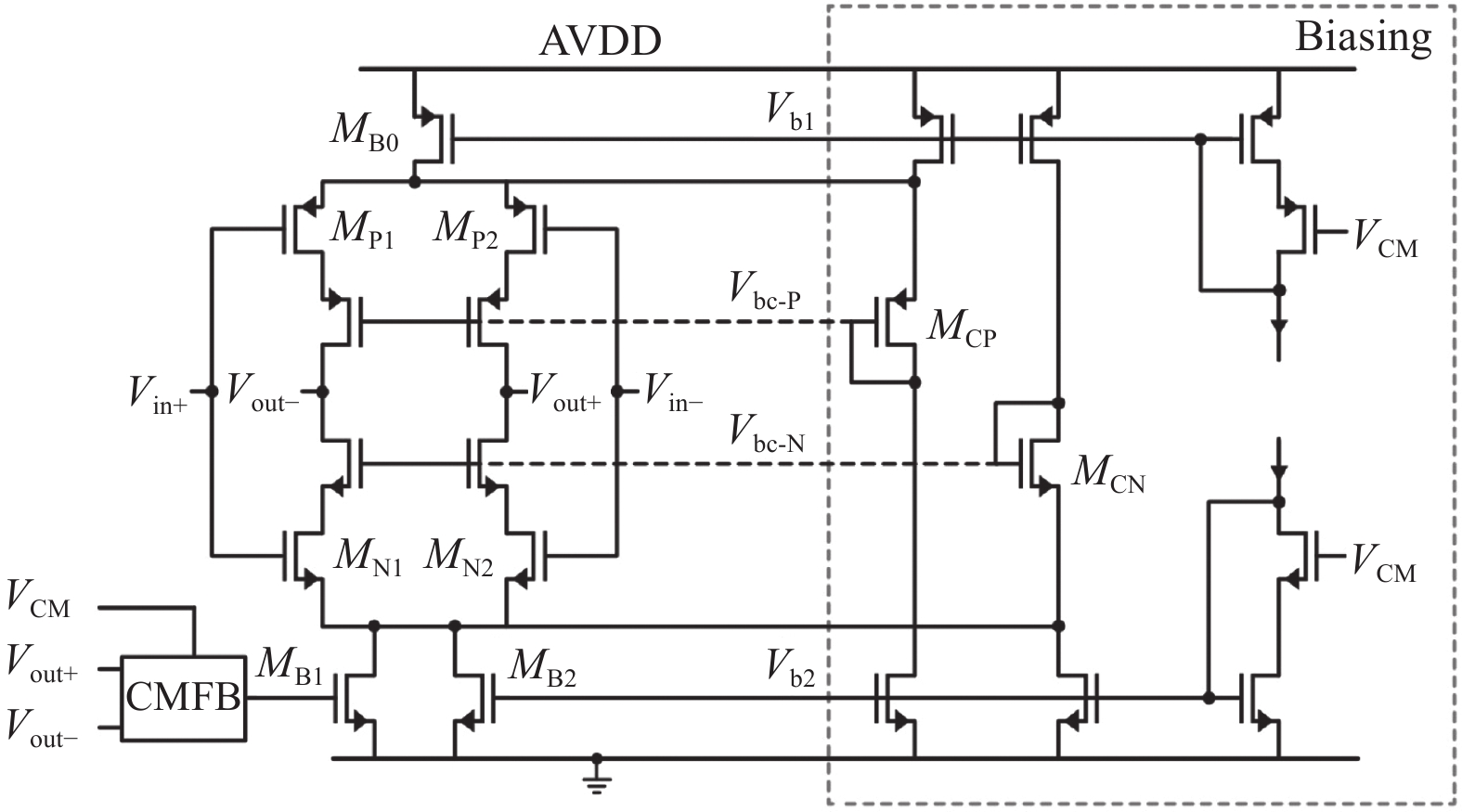
开关电容积分器是环路滤波器的核心,高性能Delta-Sigma ADC要求其中的运放具有高增益、大带宽和摆率的特点。传统静态运放,如折叠式共源共栅放大器、两级米勒补偿放大器等,它们易于设计、工作稳定、控制方法简单,但往往静态功耗较大。基于反相器的放大器[70]、电流复用放大器[62](如图20所示)等是常应用于Delta-Sigma ADC中的新型静态运放,得益于同时工作的NMOS与PMOS输入对,其具有更高的能效;但它们对寄生和PVT变化更敏感。动态放大器,如环形放大器(Ring Amplifier)[55]、基于反相器的放大器(Floating Inverter-based Amplifier, FIA)[71]等,它们只在特定的时钟相位下工作,具有优异的能效表现,十分适合应用于DT Delta-Sigma ADC中。其中,FIA由一个预充电的大电容驱动,具有稳定的输出共模电压,文献[72]进一步引入CLS和体偏置技术,提升其直流增益和输出摆幅,设计了一款2-0 MASH型Delta-Sigma ADC,在1 kHz的带宽下实现了94.0 dB的SNDR,且功耗仅为2.87 μW。
由于DT Delta-Sigma ADC的采样过程发生在环路滤波器之前,其采样误差直接加载在输入信号上而不会被噪声整形,因此采样开关的线性度直接影响ADC的性能。传统CMOS传输门的导通电阻随输入信号变化,会导致严重的采样非线性[10],不适合应用在高精度Delta-Sigma ADC中。栅压自举开关[73],通过开关电容固定导通管的栅源电压VGS,确保其导通电阻不随输入信号变化,实现了高线性度的采样。文献[74]通过进一步增大导通管的VGS,减小了自举开关的导通电阻,取得了更小的导通电阻。
3.1.3 增量型Delta-Sigma ADC前文介绍了连续转换的DT Delta-Sigma ADC的原理和优化技术,作为一类非奈奎斯特带宽型ADC,某次采样对环路滤波器、降采样滤波器的影响将持续影响后续采样和转换的过程。这种“记忆效应”不利于其作为子ADC应用于混合架构ADC中。
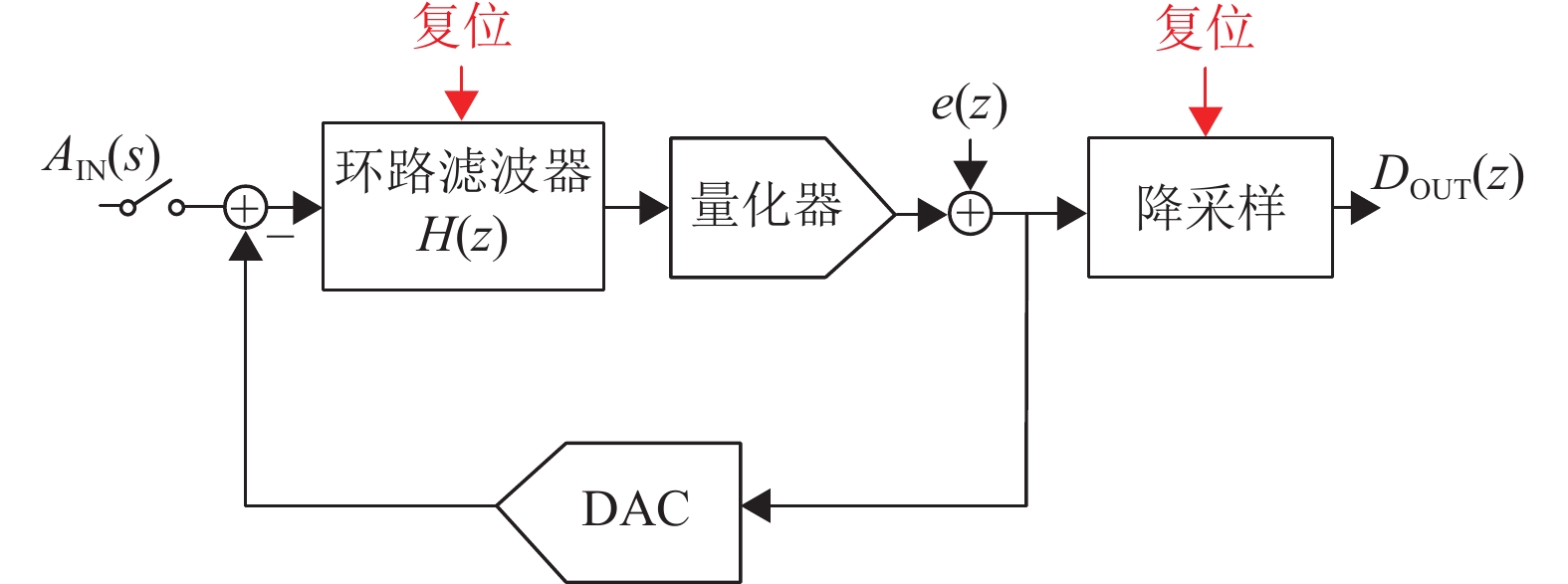
增量型(Incremental)DT Delta-Sigma ADC的基本结构如图21所示,与持续工作的DT Delta-Sigma ADC相比,其环路滤波器、降采样滤波器会进行周期性的复位,以消除上一周期的残留影响[60]。I-DT Delta-Sigma ADC在每个复位周期中对输入信号进行数次采样,转换结果仅取决于当前周期内采样到的模拟信号,最终降采样得到一个N bit数字输出。
|
图 21 增量型Delta-Sigma调制器基本结构 Figure 21 Structure diagram of the I-Delta-Sigma Modulator |
周期性复位消除了记忆效应,使得I-DT Delta-Sigma ADC表现出奈奎斯特ADC的特性,它还可以作为一个独立的电路模块进行复用。持续工作的DT Delta-Sigma ADC存在空闲音的问题[75],在频谱中表现为与输入直流量相关的杂散;而I-DT Delta-Sigma ADC的周期性复位避免了空闲音的产生。此外,I-DT Delta-Sigma ADC的数字部分只需要采用简单的计数器就可以完成降采样,且缩短了转换延时。这些优点使得I-DT Delta-Sigma ADC非常适合作为子ADC应用于混合架构ADC中[76]。
然而,Incremental Delta-Sigma ADC的周期性复位打断了环路滤波器工作的连续性,由此带来了一些缺点。为实现N bit的分辨率,一阶噪声整形的I-DT Delta-Sigma ADC需要在一个复位周期内完成2N次采样,这严重限制了ADC的带宽。对于持续工作的DT Delta-Sigma ADC,可以通过提高环路滤波器的阶数获得更好的噪声整形效果;而对于I-DT Delta-Sigma ADC,高阶的环路滤波器会导致采样样本权重逐渐衰减,以及输入信号相较于热噪声的损失。对于一阶、二阶、三阶和四阶I-DT Delta-Sigma ADC,输入信号功率相较于热噪声功率分别损失了1、1.3、1.8和2.3倍[77]。
采用有限脉冲响应(Finite Impulse response, FIR)反馈路径可以降低高阶I-DT Delta-Sigma ADC中的信号功率损失[78-79],并缩小环路滤波器输入摆幅,放宽积分器中运放的设计需求。而在文献[80]中,Wang等采用了两步linear-exponential混合式I-DT Delta-Sigma ADC,其中指数积分阶段可以补偿样本权重的衰减,显著降低了输入信号相较于热噪声和失配的损失,使ADC可以在更短的时间周期内实现更高的转换精度。文献[81]进一步提出了一种噪声耦合技术,其中量化误差被提取并经过放大和延时后送入环路滤波器中,同样实现了指数积分效果,最终在500 kHz的带宽下实现了14 bit的有效位数。
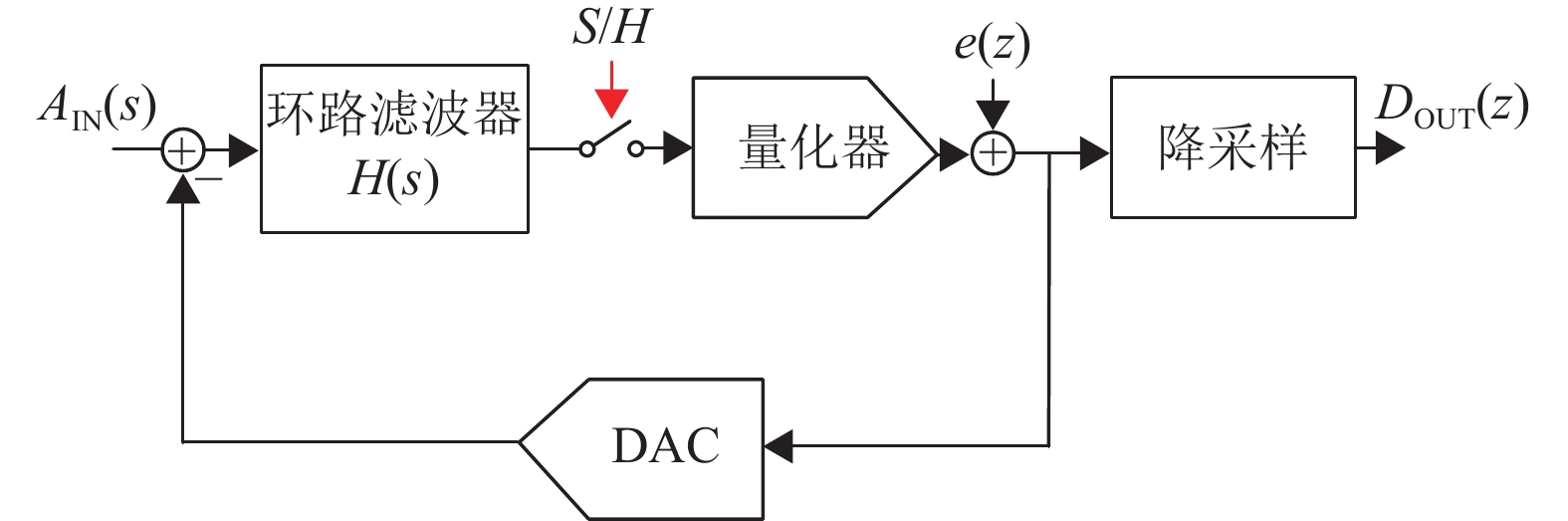
3.1.4 连续时间型Delta-Sigma ADC伴随着先进制程下电源电压的降低,DT Delta-Sigma ADC的性能逐渐失去优势,而人们对高精度传感器的带宽的要求逐渐提高,因此连续时间型(Continuous-Time,CT)Delta-Sigma ADC得到了越来越广泛的应用。CT Delta-Sigma ADC基本结构如图22所示,与DT Delta-Sigma ADC相比,电路中的环路滤波器为连续时间有源RC滤波器而不是开关电容滤波器[60]。
|
图 22 连续时间型Delta-Sigma调制器基本结构 Figure 22 Structure diagram of the CT Delta-Sigma Modulator |
DT Delta-Sigma ADC对模拟信号的采样过程发生在环路滤波器之前,采样开关的非理想因素直接加载在输入信号中[10]。而CT Delta-Sigma ADC中对模拟信号的采样过程发生在环路滤波器之后,因此采样器的非理想因素会与量化噪声一同被NTF整形,显著降低了采样开关的设计要求。有源RC滤波器本身具有的低通特性,使得CT Delta-Sigma ADC固有抗混叠特性;而连续工作的环路滤波器具有阻性输入阻抗,易于驱动。以上3个因素使得CT Delta-Sigma ADC可以采用很简单的前端电路[82]。
相较于开关电容积分器,连续工作的有源RC积分器具有更快的转换速度,使得CT Delta-Sigma ADC可以工作在更高的时钟频率下,有利于提高精度和信号带宽,在一些设计中CT Delta-Sigma ADC已经能够工作在800 MS/s的采样率下,实现25 MHz的信号带宽[83]。
然而,连续工作的环路滤波器也存在一些缺陷[76]。首先,DAC的输出误差会持续地输入环路滤波器中,导致CT Delta-Sigma ADC对时钟抖动和DAC非线性比较敏感。此外,有源RC滤波器的传递函数由RC的乘积比例决定,而不是匹配良好的电容比例决定,因此CT Delta-Sigma ADC的噪声整形效果受工艺、电源和温度变化(Process, Voltage, Temperature, PVT)影响较大,有时需要引入额外的调谐电路以获得准确的NTF。
近些年来,为提高线性度和稳定性、降低功耗,一些新型的CT Delta-Sigma ADC优化技术被提出来。传统CT Delta-Sigma ADC中的有源RC滤波器的噪声直接加载在输入信号上,需要很大的功耗以实现足够低的噪声水平。采用FIR-DAC可以有效地降低运放噪声[84],但电路中需要添加大尺寸的电阻,其寄生电容可能会影响噪声整形效果。
在文献[85]中,Jang等提出了Negative-R技术,在第一级积分器中运放的虚地点引入负阻,放宽了运放的设计要求,能够降低ADC的噪声和功耗。这种方法中运放的噪声衰减量取决于负阻与实际电阻之间的匹配程度,额外的1/f 噪声可以通过斩波技术消除。采用Negative-R技术,文献[86]中的CT Delta-Sigma ADC在2 MS/s的采样率下实现了97 dB的SFDR。
3.2 缩放型(Zoom)ADCDelta-Sigma ADC凭借过采样和噪声整形技术,可以取得较高的信噪比,适合应用于高精度ADC中。为了进一步提高Delta-Sigma ADC的精度,可以采用高阶环路滤波器,但会导致额外的功耗和面积,且存在稳定性问题;若采用多bit量化器,一方面也会消耗额外的功耗和面积,另一方面其增益误差也会影响ADC的性能。
ZoomADC是一类混合架构ADC,它在高精度的Delta-Sigma ADC基础上,引入了高能效的SAR ADC,无需高阶环路滤波器就可以实现很高的精度和动态范围,在精度、功耗和设计难度间取得了良好的权衡[87]。
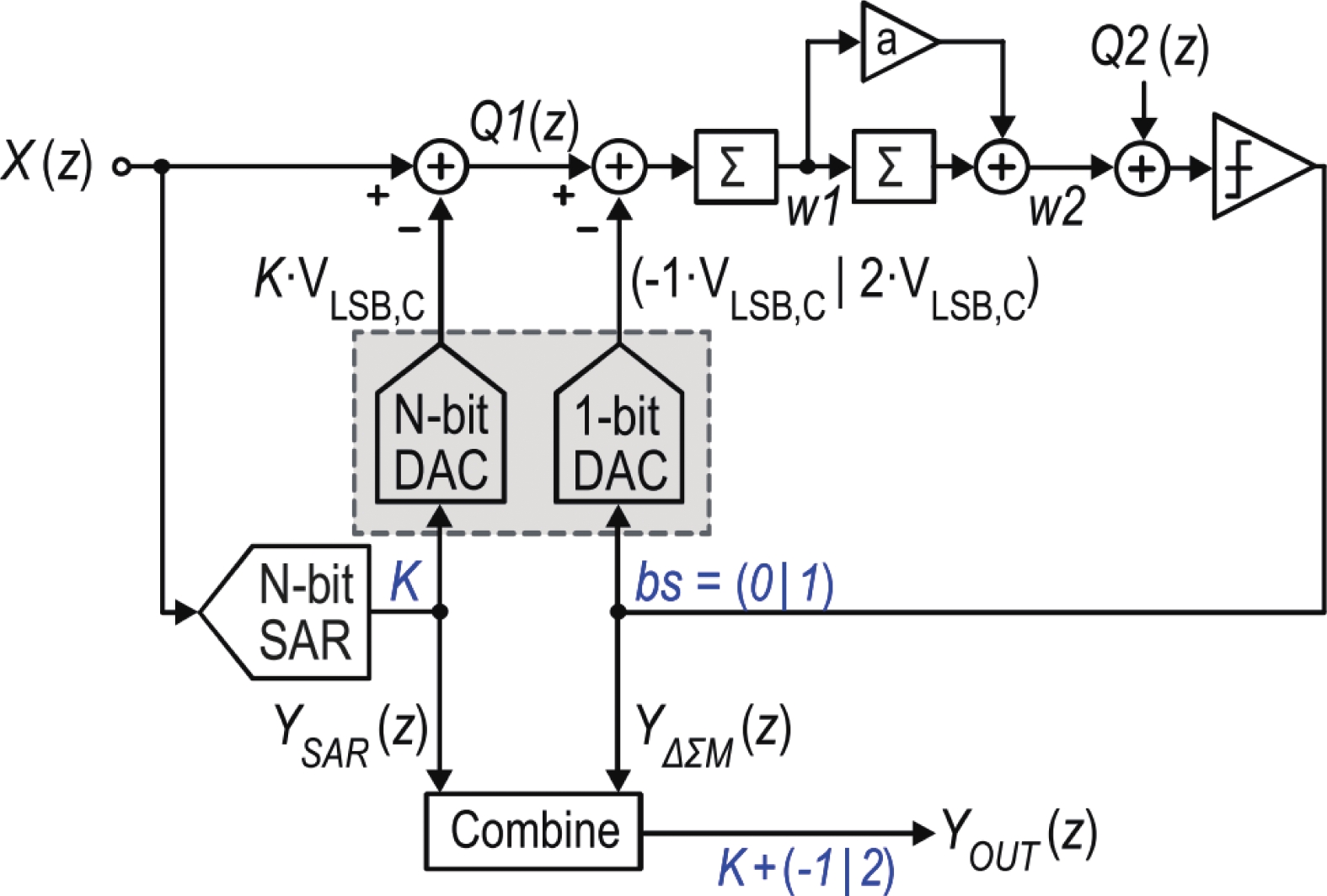
3.2.1 增量型与动态型Zoom ADCZoom ADC最早于2011年由Souri等在文献[88]中提出,应用于一款性能优异的温度传感器中。电路中环路滤波器周期性复位,为Incremental型Delta-Sigma。Incremental Zoom ADC的电路结构如图23所示,它由一个N bit的SAR ADC与一个单bit的Delta-Sigma ADC组成,2个子ADC交替工作,并共用CDAC。
SAR ADC首先对输入信号进行粗量化,得到N bit粗量化结果K,与Delta-Sigma调制器的单bit细量化结果B在数字模块中以特定的规则组合后;组合后的数字信号控制CDAC的反馈电压,ADC输入信号VIN与反馈电压相减后送入环路滤波器。理想情况下,Zoom ADC的传输函数为
| $ {D_{{\text{OUT}}}} = {V_{{\text{IN}}}}\left( z \right) - {Q_{{\text{SAR}}}}\left( z \right) \cdot \left( {{\text{STF}} - 1} \right) + {Q_{{\text{DSM}}}}\left( z \right) {\text{NTF}} $ |
若STF=1,则粗量化误差e1被完全滤除,使得Zoom ADC中可以以一个简单的单bit低阶Delta-Sigma ADC,实现与多bit量化的高阶Delta-Sigma ADC可比拟的精度。此外,环路滤波器的输入电压摆幅很小,也放宽了其中OTA的设计需求。
在2013年,Chae等在文献[14]中详细分析了Incremental Zoom ADC的工作原理,电路中采用系统级斩波技术和基于反相器的低功耗放大器,实现了高达20 bit的精度和182.7 dB的FoMS。然而,受限于SAR ADC与Delta-Sigma ADC的交替工作,该Incremental Zoom ADC的带宽只有30 Hz左右。
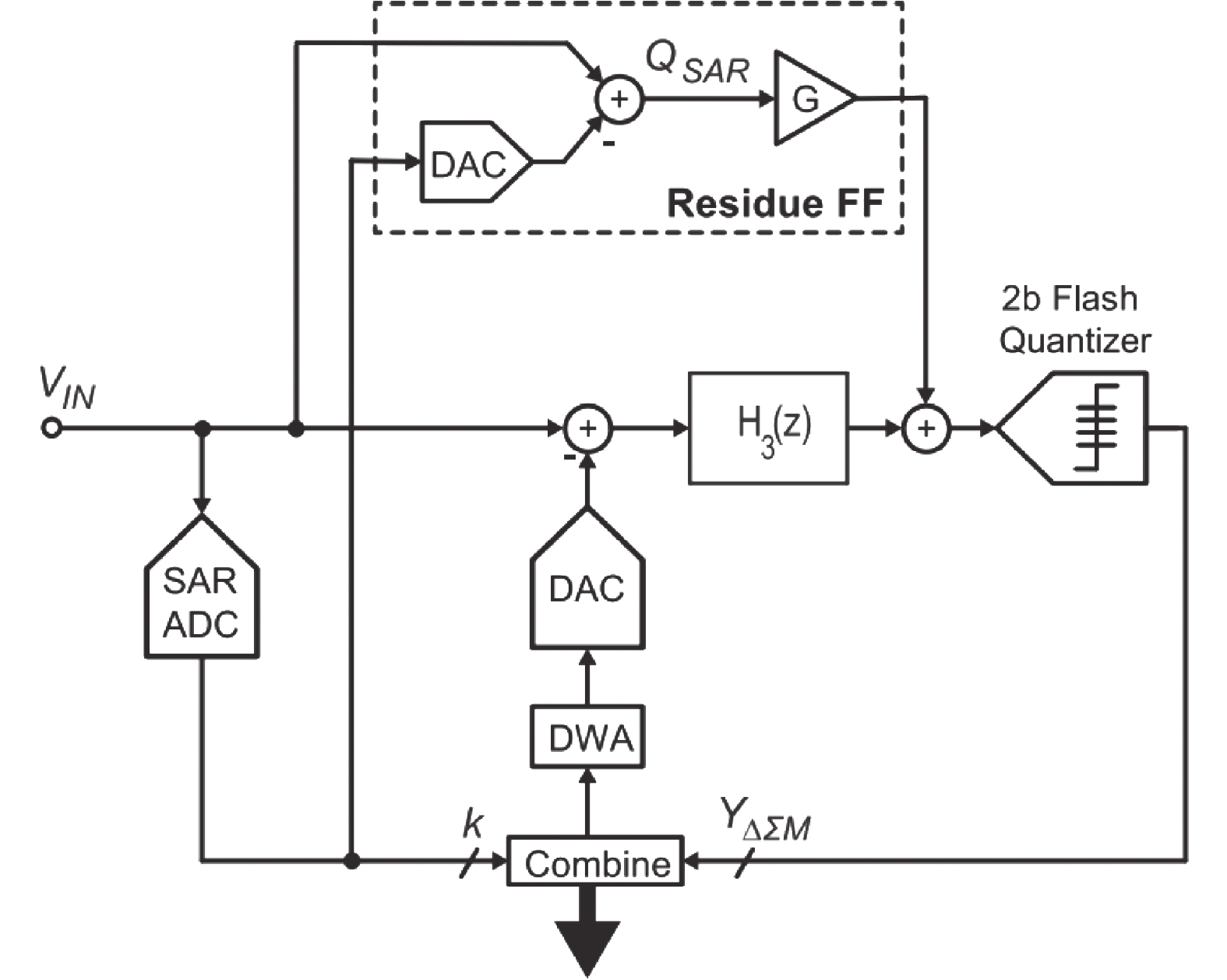
为了提高Zoom ADC所能处理的信号带宽,在2017年,Gonen等提出了动态型(Dynamic)Zoom ADC[89],其结构如图24所示。电路中SAR ADC不再与Delta-Sigma ADC共用CDAC和比较器,2个子ADC并行工作且不再周期性复位,粗量化结果动态地控制细量化过程的参考电压,大大地提高了Dynamic Zoom ADC能处理的信号带宽。该ADC能够应用于音频场景,在20 kHz带宽下实现了103 dB的SNDR。
在Zoom ADC中,SAR ADC的跟踪能力有限,快速变化的输入信号超出反馈电压的范围,使得环路滤波器过载。Over-Ranging技术通过扩大了参考电平的覆盖范围,确保环路滤波器稳定,但代价是损失一定的SQNR。在文献[62]中,Karmakar等采用了异步时序SAR ADC,显著提高了SAR ADC的跟踪能力。该ADC最终在1 kHz的带宽下实现了高达119.1 dB的SNDR,且功耗仅为280 μW,ADC的FoMS达到了185.8 dB。
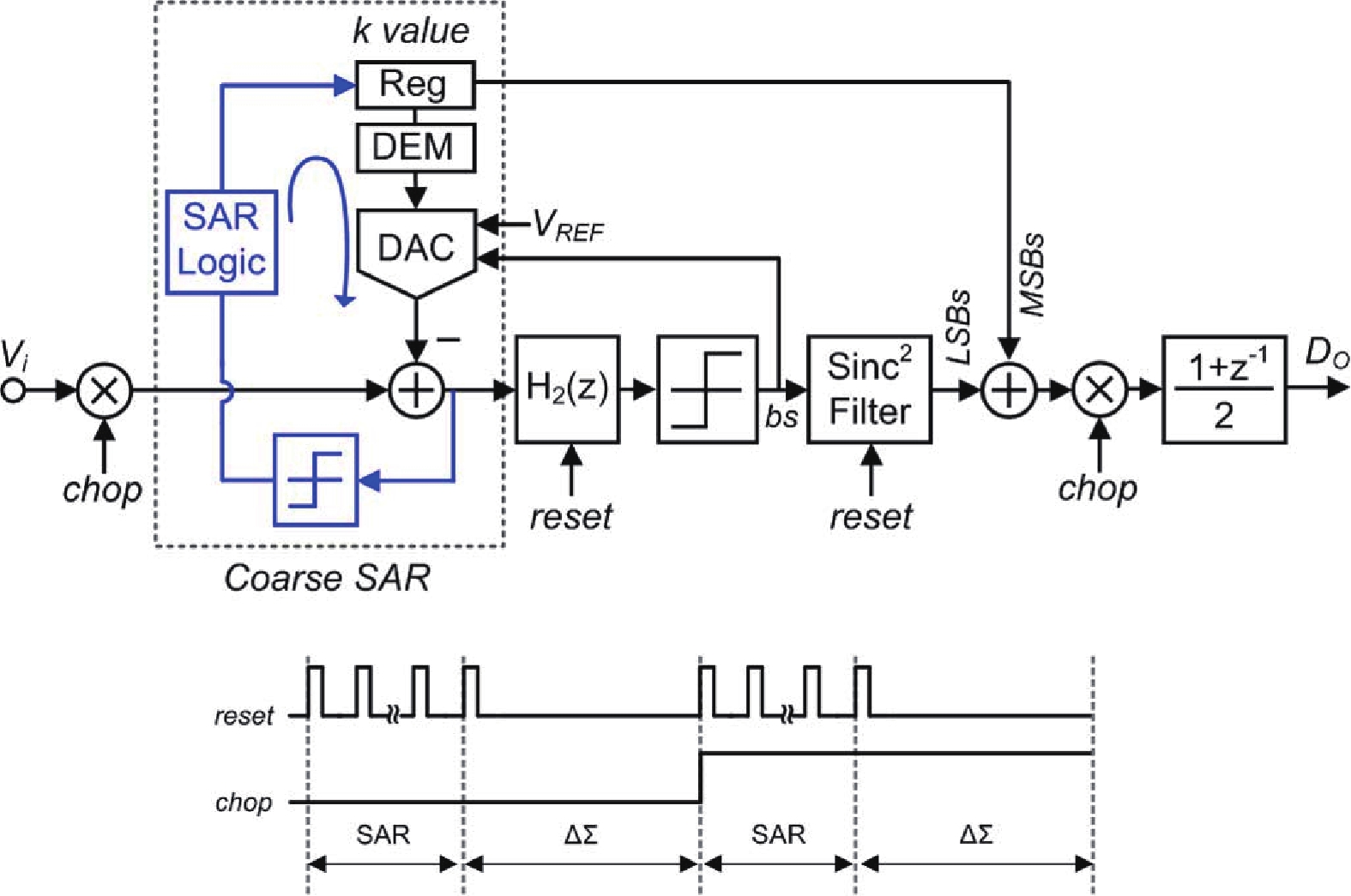
3.2.2 Zoom ADC近期发展近些年来,随着研究者们对Zoom ADC理论研究的逐渐深入,Zoom ADC的设计有了一些新的发展。由于传统Zoom ADC中缺少从ADC输入到环路滤波器输出的前馈通路,其STF并不完全等于1,导致出现了类似于MASH ADC中的噪声泄露问题,在ADC输出频谱中表现为带外杂波[87]。文献[62]通过在SAR ADC输出后添加传递函数等同于STF的数字滤波器,在数字域抵消了泄露的噪声。而在文献[17]中,Eland等通过引入额外的CDAC和前馈通路,使得STF严格地等于1,在模拟域解决了噪声泄露的问题。该ADC的电路结构如图25所示,其中环路滤波器为3阶CRFF结构,通过二三级间的谐振环路优化了NTF,最终在20 kHz的带宽下实现了106.5 dB的SNDR,并具有目前Zoom ADC中最优的186.4 dB的FoMS。
Over-Ranging技术扩大了参考电平范围,同时引起Delta-Sigma调制器的量化误差增大,会造成Zoom ADC的SQNR损失。在文献[17]和[90]中,设计者分别采用了2 bit和2.25 bit量化器,在扩大的参考电平之间进一步精细量化,在理论上完全避免了SQNR损失。
除了调整Zoom ADC的整体架构以外,优化积分器中的运放也是一个常见的设计方向。在文献[91]中,Ma等提出了一种基于浮动反相器的放大器(Floating Inverter-based Amplifier, FIA),这是一种由电容供电的动态放大器结构,具有出色的能源效率。在文献[90]和[92]中,设计者分别提出了2种新型的FIA设计,均有效地提高了FIA的直流增益和输出摆幅,使得ADC取得了良好的FoMS。Zoom ADC的积分器还可以通过引入CLS技术提高建立精度[92]。
在一些低功耗、集成度高的传感器中,ADC可能在不同的转换需求下复用,这要求ADC具有可调节的精度或带宽,以避免不必要的功耗。文献[93]中通过调节环路滤波器中的电容大小,其噪声整形效果在不同过采样率下取得最优化,使得Zoom ADC能在精度可调节的同时保持高能效。文献[92]则根据SEFIA的带宽和功耗在广泛频率范围正相关的特点,以几乎恒定的能效实现了10 Hz~12.5 kHz的可调带宽。
3.3 噪声整形(Noise-Shaping)-SAR ADC 3.3.1 Noise-Shaping SAR ADC基本原理得益于逐次比较并反馈的工作过程,在完成所有数字位的转换后,SAR ADC能够自然地在CDAC上级板获得量化误差,而无需任何额外的电路。如前文所描述的,电路设计者们利用SAR ADC的这个特点构成了Pipelined SAR ADC,前级SAR ADC的残差经放大后由下一级采样并进一步精细转换,在几乎不影响ADC速度的情况下实现了精度的提高,或转换为ADC其他性能的提升。然而受限于信号建立、比较和残差放大过程的非理想因素,即使引入一定的校准模块和算法,Pipelined SAR ADC的精度仍被限制为最高14 bit左右[19]。
过采样和噪声整形是Delta-Sigma ADC能够取得很高精度的关键技术,并能够放宽量化器和环路滤波器后级的设计要求。随着集成电路工艺制程的进步,SAR ADC的工作速度有了长足的进步,且能够保持高能效的优点;而先进工艺下电源电压和器件本征增益的降低,导致传统Delta-Sigma ADC的性能提高遇到困难。文献[94]提出了这样一种设计思路,即在SAR ADC中引入噪声整形技术,提取上一次转换的残差并影响下一次转换过程,以提高SAR ADC的精度。这成为了一个有意义的研究方向,并启发Flynn等在2012年正式提出并命名了Noise-Shaping(NS)-SAR ADC[15]。
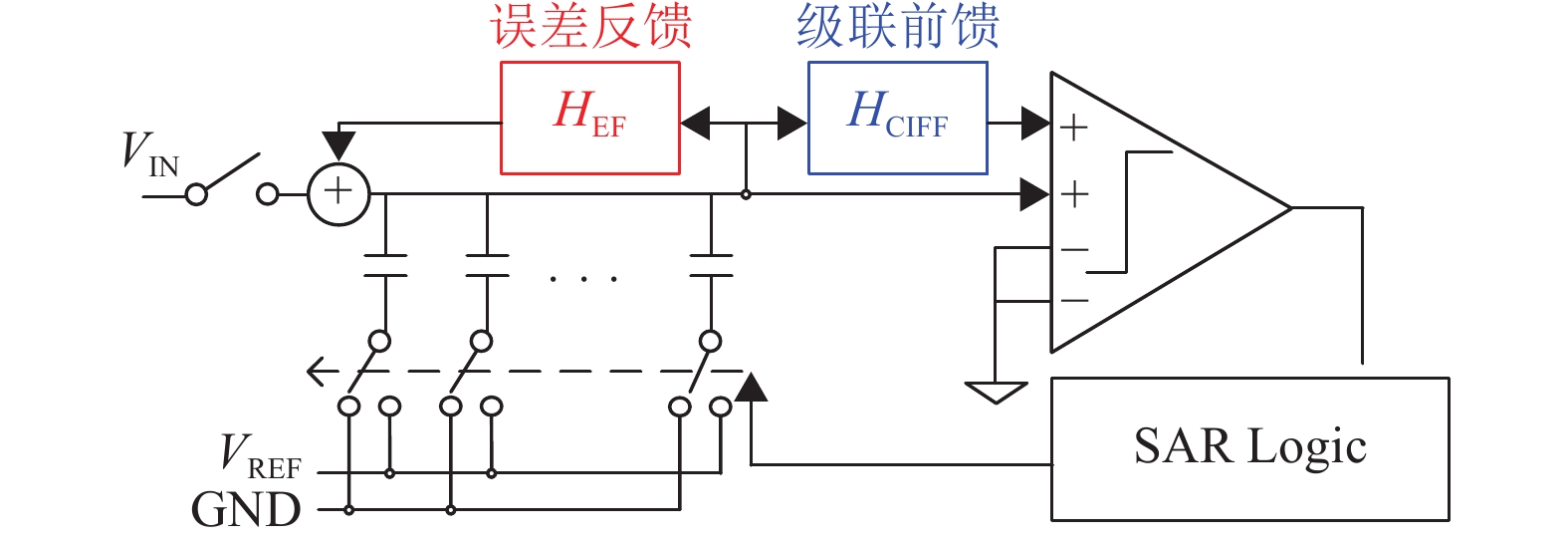
NS-SAR ADC可以看作是包含SAR ADC和Delta-Sigma ADC的一类混合架构ADC,主要有Cascaded Integrator Feed-Forward(CIFF)与Error Feedback(EF)两种结构[95],如图26所示,由1个SAR ADC、1组环路滤波器组成。其中SAR ADC完成量化并自然产生量化残差VRES,环路滤波器采样并处理VRES,并影响SAR ADC之后的转换过程。在CIFF结构中,环路滤波器的输出会前馈入SAR ADC中比较器之前的节点,作为偏移量影响比较结果,其经典实现方式是由CDAC上级板、环路滤波器的各级输出控制分别多输入比较器的不同输入对[15]。而在EF结构中,环路滤波器的输出会影响CDAC的反馈电压,进而影响SAR ADC的采样结果[96]。
|
图 26 NS-SAR ADC电路结构 Figure 26 Structure diagram of the NS-SAR ADC |
CIFF和EF结构NS-SAR ADC不同的信号处理方式使得它们具有不同的噪声整形效果,对应的噪声传递函数分别为[95]
| $ {\text{NT}}{{\text{F}}_{{\text{CIFF}}}}\left( z \right) = \frac{{{1}}}{{{{1}} + {H_{{\text{CIFF}}}}\left( z \right) \cdot {z^{{{ - 1}}}}}} $ |
| $ {\text{NT}}{{\text{F}}_{{\text{EF}}}}\left( z \right) = 1 - {H_{{\text{EF}}}}\left( z \right) \cdot {z^{{{ - 1}}}} $ |
式中:HCIFF和HEF分别为两种结构的NS-SAR ADC中环路滤波器的传递函数。
若想实现良好的噪声整形效果,ADC的NTF应在带内趋近于0,而在带外可以较大,即对量化噪声高通滤波。对于CIFF结构NS-SAR ADC,HCIFF在NTF的分母中,实现高通滤波需要HCIFF在带内具有很大的增益,环路滤波器需要采用积分器或IIR滤波器,往往具有比较高的功耗和电路复杂度;而对于EF结构NS-SAR ADC,HEF在NTF的分子中,实现高通滤波需要HEF在带内具有单位增益,环路滤波器可以通过一个简单的FIR滤波器实现。然而,EF结构要求HEF在带内严格为1,对环路滤波器参数变化十分敏感,易受不匹配和PVT变化影响;而CIFF结构仅要求HCIFF在带内尽可能地大,无需精确地匹配,鲁棒性较高[97]。
NS-SAR ADC具有与传统Delta-Sigma ADC相似的信号流图,且天然地具有输入到量化器的前馈通路,使得环路滤波器只需要处理量化残差;N bit的SAR ADC可以等效为Delta-Sigma ADC中的N bit量化器,这个bit数远高于传统多bit Delta-Sigma ADC,使得环路滤波器具有非常小的输入摆幅。以上优点都放宽了NS-SAR ADC中环路滤波器的设计要求,使得它可以采用低增益甚至无源的环路滤波器[98],可以保持SAR ADC高能效、小面积的优点。
3.3.2 Noise-Shaping SAR ADC近期发展尽管NS-SAR ADC具有高能效、小面积,且速度较快的优点,但受限于较小的过采样率,难以达到与传统Delta-Sigma ADC相当的精度。为了提高NS-SAR ADC的性能,一些设计者通过结合CIFF与EF结构的优势,增强噪声整形的效果。文献[99]中提出了一种低硬件开销的高阶环路滤波方法,使用一个放大器就构成了3阶CIFF+EF混合结构NS-SAR ADC,在625 kHz的带宽内实现了84.8 dB的SNDR,且功耗仅为119 μW。在文献[100]中同样采用CIFF+EF混合结构,通过一个单位增益缓冲器实现良好的NTF,在2.5 MHz的带宽下实现了75 dB的SNDR,且具有177.2 dB的FoMS。
MASH型Delta-Sigma ADC通过级联环路滤波器实现稳定的高阶噪声整形,这个设计思想也可以被应用于NS-SAR ADC中。在文献[101]中,Jie等设计了一个4阶噪声整形NS-SAR ADC,由两组2阶环路滤波器级联而成,在100 kHz的带宽内实现了88 dB的SNDR。文献[102]中,Liu等进一步设计了一个由4组1阶环路滤波器级联而成的NS-SAR ADC,在250 kHz的带宽内实现了93 dB的SNDR,其FoMS达到了优异的182 dB。
除了量化噪声以外,NS-SAR ADC的性能还受限于CDAC中单位电容间的失配和采样过程的kT/C噪声。CDAC失配可以通过数字方法进行校准,例如在文献[102]中应用前台校准算法实现了105 dB的SFDR,但这种方法需要一个额外的相位。动态元件匹配(Dynamic Elements Matching, DEM)技术是一种有效地消除CDAC失配的方法,其中数据加权平均(DWA)[103]技术常应用于多bit Delta-Sigma ADC中,通过循环选取单位电容实现对CDAC失配的一阶整形。由于DWA电路的规模随位数增加而指数上升,文献[104]中只在MSB应用了DWA技术,并实现了112 dB的SFDR。在文献[105]中,Shu等提出了一种失配误差整形(MES)技术,在模拟域采样LSB的失配并在ADC采样前置位CDAC,无需数字校准就实现了105 dB的SFDR。文献[99]中提出了一种适用于NS-SAR ADC的kT/C噪声消除技术,仅采用0.4 pF的采样电容就实现了85 dB的SNDR。
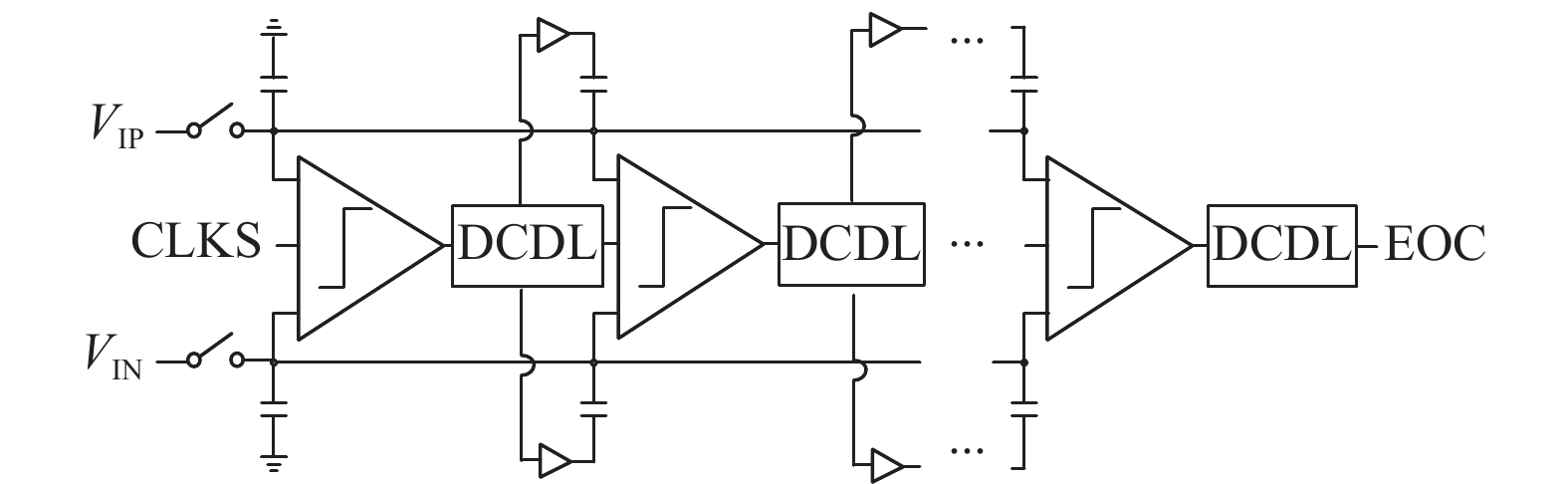
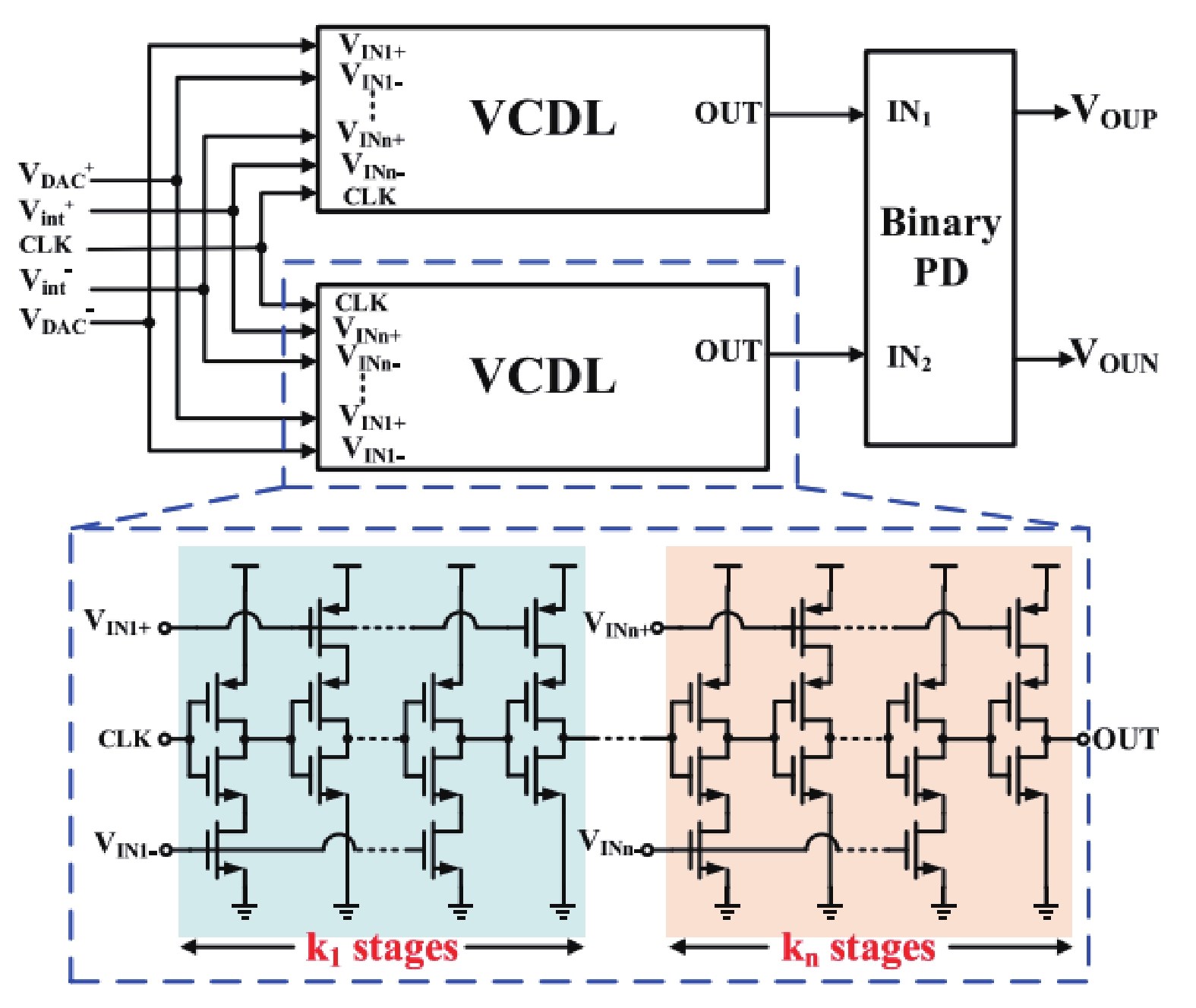
CIFF结构的NS-SAR ADC需要采用多输入比较器以完成信号求和,常规的电压域比较器的等效输入噪声随着输入对数量的增加而变大,影响了ADC的性能。2024年,Jian等在文献[106]中提出了一种基于时间域比较器的NS-SAR ADC,其电路结构如图27所示。这种新型多输入时间域比较器的等效输入噪声随其中VCDL级数增加而变小,具有低噪声、设计简单和易于缩放的优点。该NS-SAR ADC在250 kHz的带宽下实现了73 dB的SNDR,且功耗仅为94 μW。
|
图 27 应用于NS-SAR ADC的多输入时间域比较器[106] Figure 27 Multi-input time-domian comparator in the NS-SAR ADC[106] |
近年来,设计者们还在尝试从整体结构上设计新型的NS-SAR ADC。2023年,Li等设计了一种连续时间型NS-SAR ADC[107],由DT SAR和CT环路滤波器组成,具有77.3 dB的SNDR和13.5 μW的低功耗。流水线技术也被引入到NS-SAR ADC中[108],由一个1阶NS-SAR ADC和一个2阶NS-SAR以流水线工作的方式组成,且通过复用运放降低功耗,最终在4 MHz的大带宽内实现了78.2 dB的SNDR。
4 总结本文分别聚焦于高速和高精度场景,阐述了多种类型ADC的基本原理和关键技术。首先介绍了SAR ADC和Delta-Sigma ADC,它们分别是高速和高精度ADC的经典类型,具有不同的特点:SAR ADC速度较快、能效良好,但精度有限;Delta-Sigma ADC精度较高,但速度受限、功耗较大。随着集成电路制造工艺的进步,数据处理、物联网、通信和传感技术都在飞速发展,无论是高速还是高精度方向,传统的单结构ADC都逐渐难以满足各个应用场景下新的性能要求。因此本文进一步介绍了多种不同类型的混合架构ADC,它们结合了不同类型的ADC,能够实现子ADC的优势互补:例如Pipelined-SAR ADC能够在保持高速的基础上实现精度的提高,Zoom ADC可以以较低的功耗和面积实现高精度转换,而NS-SAR ADC则在速度、精度和功耗间取得了良好的权衡。时间域ADC具有速度快、工艺适应性好的优点,适合应用于混合架构ADC中,是一个新兴的研究方向。对于每种类型的ADC,本文最后总结了近期该领域的研究成果和发展趋势。
| [1] |
MURMANN B, et al. ADC performance survey 1997-2022[EB/OL]. (2023-10-03) [2024-11-10]. https://github.com/bmurmann/ADC-survey.
|
| [2] |
张军, 何方, 徐海宁, 等. 高性能音频模数转换器TLV320ADC6140的应用技术研究[J].
电子世界, 2020(15): 31-33.
|
| [3] |
EUN J P , HA Y H , KYOON D J. A 0.4-to-1 V voltage scalable Delta Sigma ADC with two-step hybrid integrator for iot sensor applications in 65-nm LP CMOS[J]. IEEE Transactions on Circuits and Systems II: Express Briefs, 2017, 64(12): 1417-1421
|
| [4] |
郭仲杰, 苏昌勖, 许睿明, 等. 基于粗细量化并行与TDC混合的CMOS图像传感器列级ADC设计方法[J].
电子学报, 2024, 52(2): 486-499.
GUO Z J, SU C X, XU R M, et al. Column level ADC design method of CMOS image sensor based on coarse and fine quantization parallel and TDC hybrid[J]. Acta Electronica Sinica, 2024, 52(2): 486-499. DOI: 10.12263/DZXB.20220744. |
| [5] |
LIU J, LUO Z, XIONG X. Low-resolution ADCs for wireless communication: a comprehensive survey[J].
IEEE Access, 2019, 7: 91291-91324.
DOI: 10.1109/ACCESS.2019.2927891. |
| [6] |
华玉, 冯伟, 曹俊诚. 6G技术愿景与太赫兹通信电路研究进展[J].
移动通信, 2023, 47(5): 7-13.
HUA Y, FENG W, CAO J C. Advancements in terahertz communication circuits for 6G technology vision[J]. Mobile Communications, 2023, 47(5): 7-13. |
| [7] |
NYQUIST H. Certain topics in telegraph transmission theory[J].
Transactions of the American Institute of Electrical Engineers, 1928, 47(2): 617-644.
DOI: 10.1109/T-AIEE.1928.5055024. |
| [8] |
MALOBERTI F. Data converters specifications[M]. Berlin: Springer, 2007.
|
| [9] |
朱樟明, 杨银堂. 低功耗CMOS逐次逼近型模数转换器[M]. 北京: 科学出版社, 2015.
|
| [10] |
PAVAN S, SCHREIER R, TEMES G C. Understanding delta-sigma data converters[M]. Hoboken, NJ, USA: Wiley, 2017.
|
| [11] |
PETERSON J G. A monolithic video A/D converter[J].
IEEE Journal of Solid-State Circuits, 1979, 14(6): 932-937.
DOI: 10.1109/JSSC.1979.1051300. |
| [12] |
LEWIS S H, GRAY P R. A pipelined 5-Msample/s 9 bit analog-to-digital converter[J].
IEEE Journal of Solid-State Circuits, 1987, 22(6): 954-961.
DOI: 10.1109/JSSC.1987.1052843. |
| [13] |
LI J, MALOBERTI F. Pipeline of successive approximation converters with optimum power merit factor[C]//9th International Conference on Electronics, Circuits and Systems. Dubrovnik: IEEE, 2002, 1: 17-20.
|
| [14] |
CHAE Y, SOURI K, MAKINWA K A A. A 6.3 µW 20 bit incremental zoom-ADC with 6 ppm INL and 1 µV offset[J].
IEEE Journal of Solid-State Circuits, 2013, 48(12): 3019-3027.
DOI: 10.1109/JSSC.2013.2278737. |
| [15] |
FREDENBURG J A, FLYNN M P. A 90-MS/s 11-MHz-bandwidth 62-dB SNDR noise-shaping SAR ADC[J].
IEEE Journal of Solid-State Circuits, 2012, 47(12): 2898-2904.
DOI: 10.1109/JSSC.2012.2217874. |
| [16] |
RABII S, WOOLEY B A. A 1.8-V digital-audio sigma-delta modulator in 0.8-µm CMOS[J].
IEEE Journal of Solid-State Circuits, 1997, 32(6): 783-796.
DOI: 10.1109/4.585245. |
| [17] |
ELAND E, KARMAKAR S, GÖNEN B, et al. A 440-µW, 109.8-dB DR, 106.5-dB SNDR discrete-time zoom ADC with a 20-kHz BW[J].
IEEE Journal of Solid-State Circuits, 2021, 56(4): 1207-1215.
DOI: 10.1109/JSSC.2020.3044896. |
| [18] |
ZHANG Y, QIAO D. Energy efficiency of indoor THz communication systems with finite bit DACs/ADCs under minimum rate constraints[C]//2022 IEEE/CIC International Conference on Communications in China (ICCC). Sanshui: IEEE, 2022: 1044-1049.
|
| [19] |
ALI A M A. High speed data converters[M]. London: Institution of Engineering and Technology, 2016.
|
| [20] |
TANG X, LIU J, SHEN Y, et al. Low-power SAR ADC design: overview and survey of state-of-the-art techniques[J].
IEEE Transactions on Circuits and Systems I: Regular Papers, 2022, 69(6): 2249-2262.
DOI: 10.1109/TCSI.2022.3166792. |
| [21] |
MCCREARY J L, GRAY P R. All-MOS charge redistribution analog-to-digital conversion techniques. I[J].
IEEE Journal of Solid-State Circuits, 1975, 10(6): 371-379.
DOI: 10.1109/JSSC.1975.1050629. |
| [22] |
刘伟, 郭尚尚, 商世广. 用于CZT探测器前端的数字自校准SAR-ADC设计[J].
电子测量与仪器学报, 2022, 36(9): 167-173.
LIU W, GUO S S, SHANG S G. Design of SAR-ADC with digital self-calibration for CZT detectors front-ends[J]. Journal of Electronic Measurement and Instrumentation, 2022, 36(9): 167-173. |
| [23] |
ZHOU Y, XU B, CHIU Y. A 12-b 1-GS/s 31.5-mW time-interleaved SAR ADC with analog HPF-assisted skew calibration and randomly sampling reference ADC[J].
IEEE Journal of Solid-State Circuits, 2019, 54(8): 2207-2218.
DOI: 10.1109/JSSC.2019.2915583. |
| [24] |
HASSAN A W, ZHOU D, SILVA-MARTINEZ J. Matrix-based digital calibration technique for high-performance SAR and pipeline ADCs[J].
IEEE Transactions on Circuits and Systems I: Regular Papers, 2024, 71(1): 20-28.
DOI: 10.1109/TCSI.2023.3322633. |
| [25] |
WEI H, CHAN C H, CHIO U F, et al. An 8-b 400-MS/s 2-b-per-cycle SAR ADC with resistive DAC[J].
IEEE Journal of Solid-State Circuits, 2012, 47(11): 2763-2772.
DOI: 10.1109/JSSC.2012.2214181. |
| [26] |
FURUTA M, NOZAWA M, ITAKURA T. A 10 bit, 40-MS/s, 1.21 mW pipelined SAR ADC using single-ended 1.5 bit/cycle conversion technique[J].
IEEE Journal of Solid-state Circuits, 2011, 46(6): 1360-1370.
DOI: 10.1109/JSSC.2011.2126390. |
| [27] |
庞稼玺, 李强. 一种单通道7 bit 1.25 GS/s高速低功耗SAR ADC[J/OL]. 微电子学 (2024-09-03) [2024-11-29]. https://doi.org/10.13911/j.cnki.1004-3365.240013.
|
| [28] |
LIU C C, CHANG S J, HUANG G Y, et al. A 10 bit 50-MS/s SAR ADC with a monotonic capacitor switching procedure[J].
IEEE Journal of Solid-State Circuits, 2010, 45(4): 731-740.
DOI: 10.1109/JSSC.2010.2042254. |
| [29] |
GINSBURG B P, CHANDRAKASAN A P. 500-MS/s 5 bit ADC in 65-nm CMOS with split capacitor array DAC[J].
IEEE Journal of Solid-State Circuits, 2007, 42(4): 739-747.
DOI: 10.1109/JSSC.2007.892169. |
| [30] |
ZHU Y, CHAN C H, CHIO U F, et al. A 10 bit 100-MS/s reference-free SAR ADC in 90 nm CMOS[J].
IEEE Journal of Solid-State circuits, 2010, 45(6): 1111-1121.
DOI: 10.1109/JSSC.2010.2048498. |
| [31] |
JIAN M C, ZHENG J W, KONG X J, et al. A 12 bit SAR ADC with a reversible VCM-based capacitor switching scheme[J].
Microelectronics Journal, 2022, 129: 105588.
DOI: 10.1016/j.mejo.2022.105588. |
| [32] |
RAZAVI B. The StrongARM latch[J].
IEEE Solid-State Circuits Magazine, 2015, 7(2): 12-17.
DOI: 10.1109/MSSC.2015.2418155. |
| [33] |
SCHINKEL D, MENSINK E, KLUMPERINK E, et al. A double-tail latch-type voltage sense amplifier with 18ps setup+hold time[C]//2007 IEEE International Solid-state Circuits Conference. Digest of technical papers. San Francisco: IEEE, 2007: 314-605.
|
| [34] |
BINDRA H S, LOKIN C E, SCHINKEL D, et al. A 1.2-V dynamic bias latch-type comparator in 65-nm CMOS with 0.4-mV input noise[J].
IEEE Journal of Solid-State Circuits, 2018, 53(7): 1902-1912.
DOI: 10.1109/JSSC.2018.2820147. |
| [35] |
杨德旺, 张春华, 郭春炳. 一种超低输入共模电压的动态比较器电路设计[J].
电子技术应用, 2021, 47(10): 48-52.
YANG D W, ZHANG C H, GUO C B. Design of a dynamic comparator circuit for ultra-low input common-mode voltage[J]. Application of Electronic Technique, 2021, 47(10): 48-52. |
| [36] |
简明朝, 张春华, 符业聪, 等. 一种低功耗动态比较器: CN116488622B[P]. 2024-02-02.
|
| [37] |
HSIEH S E, KAO C C, HSIEH C C. A 0.5-V 12 bit SAR ADC using adaptive time-domain comparator with noise optimization[J].
IEEE Journal Solid-State Circuits, 2018, 53(10): 2763-2771.
DOI: 10.1109/JSSC.2018.2862880. |
| [38] |
LEE S K, PARK S J, PARK H J, et al. A 21 fJ/conversion-step 100 kS/s 10 bit ADC with a low-noise time-domain comparator for low-power sensor interface[J].
IEEE Journal of Solid-State Circuits, 2011, 46(3): 651-659.
DOI: 10.1109/JSSC.2010.2102590. |
| [39] |
CHEN S W M, BRODERSEN R W. A 6 bit 600-MS/s 5.3-mW Asynchronous ADC in 0.13-µm CMOS[J].
IEEE Journal of Solid-State Circuits, 2006, 41(12): 2669-2680.
DOI: 10.1109/JSSC.2006.884231. |
| [40] |
KUTTNER F. A 1.2V 10b 20MSample/s non-binary successive approximation ADC in 0.13 µm CMOS[C]//2002 IEEE International Solid-State Circuits Conference. Digest of Technical Papers (Cat. No. 02CH37315). San Francisco: IEEE, 2002: 176-177.
|
| [41] |
KIRAN S, CAI S, LUO Y, et al. A 52-Gb/s ADC-based PAM-4 receiver with comparator-assisted 2 bit/stage SAR ADC and partially unrolled DFE in 65-nm CMOS[J].
IEEE Journal of Solid-State Circuits, 2018, 54(3): 659-671.
|
| [42] |
刘宇航, 曹晓东, 张雪莲, 等. 基于整数权重的非二进制SAR ADC及其校准算法的设计[J].
北京交通大学学报, 2022(2): 46.
LIU Y H, CAO X D, ZHANG X L, et al. Design of integer-weight-based non-binary SAR ADC and calibration algorithm[J]. Journal of Beijing Jiaotong University, 2022(2): 46. DOI: 10.11860/j.issn.1673-0291.20220012. |
| [43] |
陈晓青, 叶凡. 非二进制SAR ADC的电容失配校正方法[J].
计算机工程与设计, 2018, 39(6): 7.
CHEN X Q, YE F. Calibration for capacitor weight error of non-binary SAR ADC[J]. Computer Engineering and Design, 2018, 39(6): 7. |
| [44] |
CAO Z, YAN S, LI Y. A 32 mW 1.25 GS/s 6b 2b/step SAR ADC in 0.13 µm CMOS[J].
IEEE Journal Solid-State Circuits, 2009, 44(3): 862-873.
DOI: 10.1109/JSSC.2008.2012329. |
| [45] |
KULL L, TOIFL T, SCHMATZ M, et al. A 3.1 mW 8b 1.2 GS/s single-channel asynchronous SAR ADC with alternate comparators for enhanced speed in 32 nm digital SOI CMOS[J].
IEEE Journal of Solid-State Circuits, 2013, 48(12): 3049-3058.
DOI: 10.1109/JSSC.2013.2279571. |
| [46] |
JIANG T, LIU W, ZHONG F Y, et al. Single-channel, 1.25-GS/s, 6 bit, loop-unrolled asynchronous SAR-ADC in 40nm-CMOS[C]//IEEE Custom Integrated Circuits Conference 2010. San Jose: IEEE, 2010: 1-4.
|
| [47] |
LIU S, RABUSKE T, PARAMESH J, et al. Analysis and background self-calibration of comparator offset in loop-unrolled SAR ADCs[J].
IEEE Transactions on Circuits and Systems I: Regular Papers, 2017, 65(2): 458-470.
|
| [48] |
LEE E, PYO C, LEE S, et al. A 1.5-GS/s 6 bit single-channel loop-unrolled SAR ADC with speculative CDAC switching control technique in 28-nm CMOS[J].
IEEE Transactions on Circuits and Systems I: Regular Papers, 2022, 69(10): 3954-3964.
DOI: 10.1109/TCSI.2022.3185677. |
| [49] |
BUHR S, MATTHUS C D, KHAFAJI M M, et al. A 1.38-mW 7 bit 1.7-GS/s single-channel loop-unrolled SAR ADC in 22-nm FD-SOI with 8.85 fJ/Conv. -step for GHz mobile communication and radar systems[J]. IEEE Transactions on Microwave Theory and Techniques, 2023, 71(9): 3841-3851.
|
| [50] |
OH D R, MOON K J, LIM W M, et al. An 8 bit 1-GS/s asynchronous loop-unrolled SAR-flash ADC with complementary dynamic amplifiers in 28-nm CMOS[J].
IEEE Journal of Solid-State Circuits, 2020, 56(4): 1216-1226.
|
| [51] |
郭仲杰, 王杨乐, 许睿明, 等. 应用于CMOS图像传感器的高速全差分两步式ADC设计方法[J].
电子与信息学报, 2023, 45(9): 3410-3419.
GUO Z J, WANG Y L, XU R M, et al. High-speed fully differential two-step ADC design method for CMOS image sensor[J]. Journal of Electronics & Information Technology, 2023, 45(9): 3410-3419. DOI: 10.11999/JEIT221420. |
| [52] |
卢新民, 侯文杰, 谢凌霄. 一个转换时间280 ns的10 bit两级流水线式循环ADC设计[J].
固体电子学研究与进展, 2020, 40(5): 378-383.
LU X M, HOU W J, XIE L X. Design of a 10 bit 280 ns conversion time two-stage pipelined cyclic ADC[J]. Research & Progress of SSE, 2020, 40(5): 378-383. |
| [53] |
WU C, YUAN J. A 12 bit, 300-MS/s single-channel pipelined-SAR ADC with an open-loop MDAC[J].
IEEE Journal of Solid-State Circuits, 2019, 54(5): 1446-1454.
DOI: 10.1109/JSSC.2018.2886327. |
| [54] |
FU Y, JIAN M, ZHENG J, et al. A 100ms/s 12 bit SAR-assisted pipeline ADC with gain-enhanced fully differential ring amplifier[C]//2023 IEEE MTT-S International Wireless Symposium (IWS). Qingdao: IEEE, 2023: 1-3.
|
| [55] |
GUO X, CHEN R, CHEN Z, et al. A 13b 600-675MS/s tri-state pipelined-SAR adc with inverter-based open-loop residue amplifier[J].
IEEE Journal of Solid-State Circuits, 2022, 58(3): 624-633.
|
| [56] |
KWON Y, KIM T, SUN N, et al. A 348-µW 68.8-dB SNDR 20-MS/s pipelined SAR ADC with a closed-loop two-stage dynamic amplifier[J].
IEEE Solid-State Circuits Letters, 2021, 4: 166-169.
DOI: 10.1109/LSSC.2021.3114318. |
| [57] |
李树明. 基于新型环形放大器的低功耗Pipelined SAR ADC[J].
中国集成电路, 2024, 33(5): 50-56.
LI S M. Low power consumption Pipelined SAR ADC based on a novel ring amplifier[J]. China lntegrated Circuit, 2024, 33(5): 50-56. DOI: 10.3969/j.issn.1681-5289.2024.05.009. |
| [58] |
ZHAO H, DAI F F. A 12 bit 260-MS/s pipelined-SAR ADC with ring-TDC-based fine quantizer for automatic cross-domain scale alignment[J].
IEEE Journal of Solid-State Circuits, 2023, 58(10): 2883-2896.
DOI: 10.1109/JSSC.2023.3272640. |
| [59] |
RAZAVI B. The delta-sigma modulator[J].
IEEE Solid State Circuits Mag., 2016, 8(2): 10-15.
DOI: 10.1109/MSSC.2016.2543061. |
| [60] |
VERREAULT A, CICEK P V, ROBICHAUD A. oversampling ADC: a review of recent design trends[J].
IEEE Access, 2024, 12: 121753-121779.
DOI: 10.1109/ACCESS.2024.3452589. |
| [61] |
王阁藩, 李恺, 刘博, 等. 一种新型的高精度Sigma_Delta调制器结构[J].
电子测量技术, 2022, 45(12): 1-5.
WANG G F, LI K, LIU B, et al. A new high-precision Sigma_Delta modulator structure[J]. Electronic Measurement Technology, 2022, 45(12): 1-5. |
| [62] |
KARMAKAR S, GÖNEN B, SEBASTIANO F, et al. A 280 µW dynamic zoom ADC with 120 dB DR and 118 dB SNDR in 1 kHz BW[J].
IEEE Journal of Solid-State Circuits, 2018, 53(12): 3497-3507.
DOI: 10.1109/JSSC.2018.2865466. |
| [63] |
ROH J, BYUN S, CHOI Y, et al. A 0.9-V 60-μW 1 bit fourth-order delta-sigma modulator with 83-dB dynamic range[J].
IEEE Journal of Solid-State Circuits, 2008, 43(2): 361-370.
DOI: 10.1109/JSSC.2007.914266. |
| [64] |
HAYASHI T, INABE Y, UCHIMURA K, et al. A multistage delta-sigma modulator without double integration loop[C]//1986 IEEE International Solid-State Circuits Conference. Digest of Technical Papers. Anaheim: IEEE, 1986: 182-183.
|
| [65] |
FUKAZAWA M, OSHIMA T, FUJIWARA M, et al. A CT 2-2 MASH ΔΣ ADC with multi-rate LMS-based background calibration and input-insensitive quantization-error extraction[J].
IEEE Journal of Solid-State Circuits, 2021, 56(10): 2943-2955.
DOI: 10.1109/JSSC.2021.3082943. |
| [66] |
HUANG J S, KUO S C, CHEN C H. A multistep multistage fifth-order incremental delta sigma analog-to-digital converter for sensor interfaces[J].
IEEE Journal of Solid-State Circuits, 2023, 58(10): 2733-2744.
DOI: 10.1109/JSSC.2023.3288198. |
| [67] |
彭蠡霄, 汪东, 李振涛, 等. 一种级间运放共享的MASH结构Σ-Δ调制器[J].
微电子学, 2024, 54(1): 38-44.
PENG L X, WANG D, LI Z T, et al. A MASH structure interstage op-amp sharing Σ-Δ modulator[J]. Microelectronics, 2024, 54(1): 38-44. |
| [68] |
MAGHARI N, KWON S, MOON U K. 74 dB SNDR multi-loop sturdy-mash delta-sigma modulator using 35 dB open-loop opamp gain[J].
IEEE Journal of Solid-State Circuits, 2009, 44(8): 2212-2221.
DOI: 10.1109/JSSC.2009.2022302. |
| [69] |
TAN G, TAN G, QIN X, LIU Y, et al. A 10 MHz-BW 85 dB-DR CT 0-4 mash delta-sigma modulator achieving +5 dBFS MSA[J].
IEEE Transactions on Circuits and Systems I: Regular Papers, 2023, 70(12): 4781-4792.
DOI: 10.1109/TCSI.2023.3299931. |
| [70] |
CHAE Y, HAN G. Low voltage, low power, inverter-based switched-capacitor delta-sigma modulator[J].
IEEE Journal of Solid-State Circuits, 2009, 44(2): 458-472.
DOI: 10.1109/JSSC.2008.2010973. |
| [71] |
ZHANG C, JIAN M, YUAN M, et al. A Σ-Δ modulator based on an inverter-based integrator with dynamic current switch[J].
Journal of Physics: Conference Series, 2023, 2477(1): 012086.
DOI: 10.1088/1742-6596/2477/1/012086. |
| [72] |
MENG L, HU Y, ZHAO Y, et al. A 1.2-V 2.87-µW 94.0-dB SNDR discrete-time 2-0 MASH delta-sigma ADC[J].
IEEE Journal of Solid-State Circuits, 2022, 58(6): 1636-1645.
|
| [73] |
RAZAVI B. The bootstrapped switch[J].
IEEE Solid-State Circuits Magazine, 2015, 7(3): 12-15.
DOI: 10.1109/MSSC.2015.2449714. |
| [74] |
高钧达, 郭春炳, 陆维立, 等. 一种具有低导通电阻的高速自举开关: CN113098455B[P]. 2022-05-10.
|
| [75] |
刘晓为, 刘云涛, 姜一鸣, 等. 四阶Sigma-Delta微加速度计系统设计与分析[J].
哈尔滨工业大学学报, 2011, 43(7): 38-41.
LIU X W, LIU Y T, JIANG Y M, et al. System level design and anaysis of fourth-order sigma-delta micromachined accelerometer[J]. Journal of Harbin Institute of Technology, 2011, 43(7): 38-41. DOI: 10.11918/j.issn.0367-6234.2011.07.008. |
| [76] |
JIANG D, SIN S W, QI L, et al. Recent advances in high-resolution hybrid discrete-time noise-shaping ADCs[J].
IEEE Open Journal of the Solid-State Circuits Society, 2021, 1: 129-139.
DOI: 10.1109/OJSSCS.2021.3118668. |
| [77] |
KAESSER P, ISMAIL O, RUDORF C, et al. Linear-exponential I-DS ADCs: analysis, limitations and higher order[C]//2023 IEEE International Symposium on Circuits and Systems (ISCAS). Monterey: IEEE, 2023. 1-5.
|
| [78] |
MOKHTAR M A, VOGELMANN P, ABDELAAL A, et al. FIR DACs in CT incremental delta-sigma modulators[C]//2020 IEEE International Symposium on Circuits and Systems (ISCAS). Seville: IEEE, 2020: 1-5.
|
| [79] |
PAVAN S, HALDER T, KANNAN A. continuous-time incremental delta-sigma modulators with FIR feedback[J].
IEEE Transactions on Circuits and Systems I: Regular Papers, 2021, 68(8): 3222-3231.
DOI: 10.1109/TCSI.2021.3080379. |
| [80] |
WANG B, SIN S W, SENG-PAN U, et al. A 1.2 V 86dB SNDR 500 kHz BW linear-exponential multi bit incremental ADC using positive feedback in 65 nm CMOS[C]//2019 IEEE Asian Solid-State Circuits Conference (A-SSCC). Macau: IEEE, 2019: 117-120.
|
| [81] |
WANG B, SIN S W, U S P, et al. A 550-μW 20-kHz BW 100.8-dB SNDR linear-exponential multi bit incremental ΣΔ ADC with 256 clock cycles in 65-nm CMOS[J].
IEEE Journal of Solid-State Circuits, 2019, 54(4): 1161-1172.
DOI: 10.1109/JSSC.2018.2888872. |
| [82] |
孙奥运, 温培旭, 邵淮先, 等. 高精度音频Sigma-Delta调制器综述[J].
电子与信息学报, 2024, 46(5): 1874-1887.
SUN A Y, WEN P X, SHAO H X, et al. A review of high-resolution audio sigma-delta modulator[J]. Journal of Electronics & Information Technology, 2024, 46(5): 1874-1887. DOI: 10.11999/JEIT231208. |
| [83] |
CHAE H, FLYNN M P. A 69 dB SNDR, 25 MHz BW, 800 MS/s continuous-time bandpass Δ-Σ modulator using a duty-cycle-controlled DAC for low power and reconfigurability[J].
IEEE Journal of Solid-State Circuits, 2016, 51(3): 649-659.
DOI: 10.1109/JSSC.2016.2514442. |
| [84] |
BILLA S, SUKUMARAN A, PAVAN S. Analysis and design of continuous-time delta-sigma converters incorporating chopping[J].
IEEE Journal of Solid-State Circuits, 2017, 52(9): 2350-2361.
DOI: 10.1109/JSSC.2017.2717937. |
| [85] |
JANG M, LEE C, CHAE Y. A 134-μW 99.4-dB SNDR audio continuous-time delta-sigma modulator with chopped negative-R and Tri-level FIR-DAC[J].
IEEE Journal of Solid-State Circuits, 2021, 56(6): 1761-1771.
DOI: 10.1109/JSSC.2020.3032152. |
| [86] |
MOKHTAR M A, ABDELAAL A, SPORER M, et al. A 0.9-V calibration-free 97 dB-SFDR 2-MS/s continuous time incremental delta-sigma ADC utilizing variable bit width quantizer in 28 nm CMOS[C]//2021 IEEE Custom Integrated Circuits Conference (CICC). Austin: IEEE, 2021. 1-2.
|
| [87] |
YUAN M, JIAN M, ZHENG J, et al. Behavioral modeling and circuit design of high precision low power dynamic zoom ADC[J]. Journal of Physics: Conference Series, 2023, 2477(1): 012074.
|
| [88] |
SOURI K, MAKINWA K A A. A 0.12 mm2 7.4 μW micropower temperature sensor with an inaccuracy of ±0.2 ℃ (3σ) from −30 ℃ to 125 ℃[J].
IEEE Journal of Solid-State Circuits, 2011, 46(7): 1693-1700.
DOI: 10.1109/JSSC.2011.2144290. |
| [89] |
GÖNEN B, SEBASTIANO F, QUAN R, et al. A dynamic zoom ADC with 109-dB DR for audio applications[J].
IEEE Journal of Solid-State Circuits, 2017, 52(6): 1542-1550.
DOI: 10.1109/JSSC.2017.2669022. |
| [90] |
CHOI Y, LEE W, PARK S, et al. A 101.6-dB-SNDR fully dynamic zoom adc using miller-compensated floating inverter amplifiers[J].
IEEE Transactions on Circuits and Systems II: Express Briefs, 2024, 71(9): 4141-4145.
|
| [91] |
MA T, YUAN M, WANG Z, et al. A 180 µW dynamic zoom adc with 110 dB SNDR in 2 kHz BW[C]//2023 IEEE MTT-S International Wireless Symposium (IWS). Qingdao: IEEE, 2023: 1-3.
|
| [92] |
ZHAO Y, ZHAO M, TAN Z. Fully dynamic zoom-adc based on improved swing-enhanced FIAs using CLS technique with 1250× bandwidth/power scalability[J].
IEEE Transactions on Circuits and Systems II: Express Briefs, 2023, 70(6): 1901-1905.
|
| [93] |
LIANG Y, REN J, CHEN L, et al. A reconfigurable 12-to-18 bit dynamic zoom ADC with pole-optimized technique[J].
IEEE Transactions on Circuits and Systems I: Regular Papers, 2023, 70(5): 1940-1948.
DOI: 10.1109/TCSI.2023.3247434. |
| [94] |
KIM K S, KIM J, CHO S H. Nth-order multi bit ΣΔ ADC using SAR quantiser[J].
Electronics Letters, 2010, 46(19): 1315-1316.
DOI: 10.1049/el.2010.1554. |
| [95] |
SALGADO G M, O’HARE D, O’CONNELL I. Recent advances and trends in noise shaping SAR ADCs[J].
IEEE Transactions on Circuits and Systems II: Express Briefs, 2020, 68(2): 545-549.
|
| [96] |
LI S, QIAO B, GANDARA M, et al. A 13-ENOB second-order noise-shaping SAR ADC realizing optimized NTF zeros using the error-feedback structure[J].
IEEE Journal of Solid-State Circuits, 2018, 53(12): 3484-3496.
DOI: 10.1109/JSSC.2018.2871081. |
| [97] |
JIE L, TANG X, LIU J, et al. An overview of noise-shaping SAR ADC: from fundamentals to the frontier[J].
IEEE Open Journal of the Solid-State Circuits Society, 2021, 1: 149-161.
DOI: 10.1109/OJSSCS.2021.3119910. |
| [98] |
CHEN Z, MIYAHARA M, MATSUZAWA A. A 9.35-ENOB, 14.8 fJ/conv. -step fully-passive noise-shaping SAR ADC[C]//2015 Symposium on VLSI Circuits (VLSI Circuits). Kyoto: IEEE, 2015: C64-C65.
|
| [99] |
WANG T H, WU R, GUPTA V, et al. A 13.8-ENOB fully dynamic third-order noise-shaping SAR ADC in a single-amplifier EF-CIFF structure with hardware-reusing kT/C noise cancellation[J].
IEEE Journal of Solid-State Circuits, 2021, 56(12): 3668-3680.
DOI: 10.1109/JSSC.2021.3108620. |
| [100] |
ZHANG H, WANG X, LI N, et al. A 2.5-mhz bw, 75-dB SNDR noise-shaping SAR ADC with a 1st-order hybrid EF-CIFF structure assisted by unity-gain buffer[J].
IEEE Transactions on Very Large Scale Integration (VLSI) Systems, 2022, 30(12): 1928-1932.
DOI: 10.1109/TVLSI.2022.3213365. |
| [101] |
JIE L, ZHENG B, CHEN H W, et al. A cascaded noise-shaping SAR architecture for robust order extension[J].
IEEE Journal of Solid-State Circuits, 2020, 55(12): 3236-3247.
DOI: 10.1109/JSSC.2020.3019487. |
| [102] |
LIU J, LI D, ZHONG Y, TANG X, et al. A 250 kHz-BW 93 dB-SNDR 4th-order noise-shaping SAR using capacitor stacking and dynamic buffering[C]//2021 IEEE International Solid-State Circuits Conference (ISSCC). San Francisco: IEEE, 2021. 369-371.
|
| [103] |
BAIRD R T, FIEZ T S. Linearity enhancement of multibit Δ-Σ A/D and D/A converters using data weighted averaging[J].
IEEE Transactions on Circuits and Systems II: Analog and Digital Signal Processing, 1995, 42(12): 753-762.
DOI: 10.1109/82.476173. |
| [104] |
OBATA K, MATSUKAWA K, MIKI T, et al. A 97.99 dB SNDR, 2 kHz BW, 37.1 µW noise-shaping SAR ADC with dynamic element matching and modulation dither effect[C]//2016 IEEE Symposium on VLSI Circuits (VLSI-Circuits). Honolulu: IEEE, 2016. 1-2.
|
| [105] |
SHU Y S, KUO L T, LO T Y. An oversampling SAR ADC with DAC mismatch error shaping achieving 105 dB SFDR and 101 dB SNDR over 1 kHz BW in 55 nm CMOS[J].
IEEE Journal of Solid-State Circuits, 2016, 51(12): 2928-2940.
DOI: 10.1109/JSSC.2016.2592623. |
| [106] |
JIAN M, ZHENG J, KONG X, et al. A 73-dB-SNDR 2nd-Order noise-shaping SAR with a low-noise time-domain comparator[J].
IEEE Transactions on Circuits and Systems II: Express Briefs, 2024, 71(8): 3645-3649.
|
| [107] |
LI H, SHEN Y, CANTATORE E, et al. A 77.3-dB SNDR 62.5-kHz bandwidth continuous-time noise-shaping SAR ADC with duty-cycled Gm-C integrator[J].
IEEE Journal of Solid-State Circuits, 2023, 58(4): 939-948.
DOI: 10.1109/JSSC.2022.3227678. |
| [108] |
OH S, OH Y, LEE J, et al. An 85 dB DR 4 MHz BW pipelined noise-shaping SAR ADC with 1-2 MASH structure[J].
IEEE Journal of Solid-State Circuits, 2021, 56(11): 3424-3433.
DOI: 10.1109/JSSC.2021.3086853. |
 2024, Vol. 41
2024, Vol. 41