随着电力需求的日益增长,变电站作为电力系统的核心节点,其定期巡检的重要性愈发凸显。然而,传统的变电站巡检主要依赖于人工操作,但在复杂电磁环境和部分恶劣的自然条件下,人工巡检不仅面临安全风险,而且在效率上也难以满足现代电力系统的要求。鉴于此,机器人作为一种新兴的巡检工具应运而生,它们不仅能够显著提高巡检效率,降低巡检成本,还能在保障巡检人员安全的同时,有效减少人力资源的消耗。因此,巡检机器人在变电站巡检中的应用具有广阔的前景和巨大的潜力[1-3]。
巡检机器人的路径规划是确保其能够全天候在规定的时间和位置高效完成巡检的关键。当前,巡检建图方法主要包括拓扑地图法和栅格网络法。拓扑地图法通过构建巡检场景的拓扑关系,利用图论[4]和枚举法[5]进行路径规划,但它在应对设备检测要求的差异化和巡检任务动态变化方面存在局限性,且求解效率有待提升。而栅格网络法则能更精确地构建变电站巡检环境,通过改进蚁群算法[6]和粒子群算法[7]等方法增强路径规划的鲁棒性。尽管已有研究将Dijkstra最短路径与改进蚁群算法相结合,实现了实时巡检路径规划与自动避障,但在监测点众多的情况下,其效率仍显不足。这些研究主要聚焦于巡检点与机器人工作站之间的经典路径规划问题,未充分考虑用电高峰期间的检测时间窗约束、设备等级异质性以及机器人电池容量限制。因此,现有的路径规划方法尚不能满足变电站巡检的差异化需求。为实现更高效、精准的巡检,需要综合考虑多种因素,提出适应性更强的路径规划算法,以确保巡检机器人能够在复杂多变的变电站环境中稳定、高效地运行。
在用电高峰期,变电设备因运行负荷剧增,故障风险显著提升,因此,设置合理的时间窗口进行巡检至关重要。本文将巡检任务建模为带时间窗口的车辆路径问题(Vehicle Routing Problem with Time Windows, VRPTW),以应对用电高峰时段的挑战。然而,VRPTW是典型的NP-hard问题,随着巡检点数量增加,可行路径的数量呈指数级上升,使得求解变得极为复杂。传统的启发式算法,如迭代局部搜索法、遗传算法、禁忌搜索法和自适应领域搜索法等,在解决此类问题上发挥了重要作用,但在面对节点规模扩大和约束条件增多时,这些算法往往难以在有限的时间内找到全局最优解,且容易陷入局部最优的困境。
近年来,深度学习(Deep Learning, DL)和强化学习(Reinforcement Learning, RL)的快速发展为复杂组合优化问题的求解提供了新的思路。深度强化学习(Deep Reinforcement Learning, DRL)结合了深度学习的特征表示能力和强化学习的决策优化能力,成为解决多目标组合优化问题的有力工具。分层强化学习和多智能体强化学习[8-9]在大规模路径规划问题上展现出了高效的性能,为解决VRPTW问题提供了新的方向。此外,巡检机器人硬件的不断升级也为巡检路径规划的实施提供了有力保障。更先进的传感器、更高效的处理器以及更稳定的运动控制系统使得巡检机器人能够在复杂多变的变电站环境中稳定运行,确保巡检任务的顺利完成[10-12]。
针对智能变电站巡检任务,巡检机器人的路径规划算法无疑是提升检测效率的关键所在。本文深入考虑了变电设备的检验等级差异、用电高峰期对设备稳定性的影响,以及待检测设备数量的实时变动,进而构建了基于带时间窗的车辆路径问题的巡检模型。这一模型不仅能够精准反映巡检任务的复杂性和动态性,还能为机器人提供科学的巡检路径规划。为有效求解这一复杂模型,本文提出了一种融合强化学习与多智能体注意力机制的求解方法。强化学习使得机器人能够在与环境的交互中不断优化自身的行为策略,而多智能体设计则能够充分利用多个机器人的协同能力,提高整体巡检效率。更为重要的是,注意力机制的引入使得机器人在多变的巡检场景中能够精确识别并重点关注当前最为关键的任务或信息,从而大大提高巡检的针对性和效率。
1 巡检规划建模 1.1 问题描述与定义变电站巡检机器人的路径规划,借鉴车辆路径问题(Vehicle Routing Problem, VRP)或其衍生模型的设计原理,要求机器人从工作站出发,在设定时间内有效地完成所有巡检点,确保服务的精准性。然而,变电站巡检任务的特殊性在于,机器人受到电池容量的严格限制,因此,规划过程中必须确保每个机器人所分配的巡检任务在其电池耗尽前能够顺利完成。
模型设定中,每台机器人的电池容量限制设置为
变电站巡检策略的优化必须充分考虑到变电站内部设备检测等级的差异性。变电站作为电力系统的核心组成部分,负责不同电压级别的升降压工作,涉及的电力设备种类繁多,包括变压器、电力电缆、输电线路、断路开关、隔离开关以及互感器等。鉴于不同设备可能出现的故障类型和发生概率存在显著差异,巡检工作应当侧重于故障率较高的设备,赋予其较高的检测优先级,以便及时识别并处理潜在的故障问题。基于文献[13]对变电站设备等级的评定和文献[14]中提出的电网设备差异化检测策略,进一步简化了变电站的检测区域划分,将其主要划分为主变区、馈电线区和开关控制区三大部分,并为每个区域设定了相应的检测优先级。具体而言,主变区作为变电站的核心区域,其设备故障可能对整个系统造成严重影响,因此被设定为一级检测优先级;馈电线区负责电能的传输与分配,其故障率虽相对较低,但仍需保持较高的警惕,故设定为二级检测优先级;而开关控制区则主要负责电路的开合控制,其故障影响相对较小,因此被设定为三级检测优先级。通过这种差异化巡检策略的制定与实施,可以更加精准地锁定潜在故障较高的设备,优先进行检测,从而提高巡检工作的效率和针对性。
为了确保巡检路径规划能够充分满足变电站巡检任务的实际需求,本文将机器人所处的巡检环境抽象为一个有向图
| 表 1 符号定义 Table 1 Symbol definition |
在巡检路径规划中,鉴于每台机器人拥有独立的巡检路线,总共将生成M条巡检路线。本模型旨在寻求最优解决方案
| $ \begin{split} {\rm{Cost}}\left(r\left[1,M\right]\right) =&{d}_{\mathrm{s}\mathrm{u}\mathrm{m}}\left(r\left[1,M\right]\right) +{p}_{\mathrm{s}\mathrm{u}\mathrm{m}}\left(r\left[1,M\right]\right) +\\ &{I}_{\mathrm{s}\mathrm{u}\mathrm{m}}\left(r\left[1,M\right]\right) \end{split} $ | (1) |
| $ {d}_{\mathrm{s}\mathrm{u}\mathrm{m}}\left(r\left[1,M\right]\right) = \sum _{m=1}^{M}\sum _{t=1}^{\left|r\left[m\right]\right|-1}\mathrm{D}\mathrm{i}\mathrm{s}\mathrm{t}\mathrm{a}\mathrm{n}\mathrm{c}\mathrm{e}({v}_{r\left[m\right]\left[t\right]},{v}_{r\left[m\right]\left[t+1\right]}) $ | (2) |
| $ \begin{split} {p}_{\mathrm{s}\mathrm{u}\mathrm{m}}\left(r\left[1,M\right]\right) =&\sum _{m=1}^{M}\sum _{i=1}^{K}[{I}_{{e}_{i} > {{\tilde t}}_{i}} \times {\alpha }_{i} \times \left({e}_{i}-{\widetilde {t}}_{i}\right) +\\ &{I}_{{ {\tilde t}}_{i} > {l}_{i}} \times {\beta }_{i} \times \left({\widetilde {t}}_{i}-{l}_{i}\right) ] \end{split} $ | (3) |
| $ {I}_{\mathrm{s}\mathrm{u}\mathrm{m}}\left(r\left[1,M\right]\right) = {\sum }_{m=1}^{M}{\sum }_{t=1}^{\left|r\left[m\right]\right|-1}\mathrm{G}\mathrm{r}\mathrm{a}\mathrm{d}\mathrm{e}\left({v}_{r\left[m\right]\left[t\right]},{v}_{r\left[m\right]\left[t+1\right]}\right) $ | (4) |
式中,
巡检机器人路径规划模型作为经典VRP问题的延伸,不仅包括了基本的路径规划需求,还整合了时间窗约束、机器人电池容量以及巡检设备的优先级等多重约束。传统的启发式算法在解决这类问题时,往往难以在复杂的约束条件下精确找到最优解。鉴于此,本文将注意力机制[15]与多智能体强化学习[16]相结合,设计了一种基于编码器−解码器结构的多智能体注意力模型(Multi-agent Attention Model,MAAM)。该模型通过智能体协同学习和注意力机制提升路径规划的精确性和效率,以在复杂约束下定位最优巡检路径。
1.3.1 MAAM强化学习形式环境(Environment)和智能体(Agent)构建了强化学习的二元基础结构。本文采用马尔可夫决策过程(Markov Decision Process,MDP)定义MAAM强化学习环境,该环境包括状态、动作、概率转移和奖励机制。在此框架中,智能体特指巡检机器人,它们通过与环境的交互来学习如何有效地执行巡检任务。
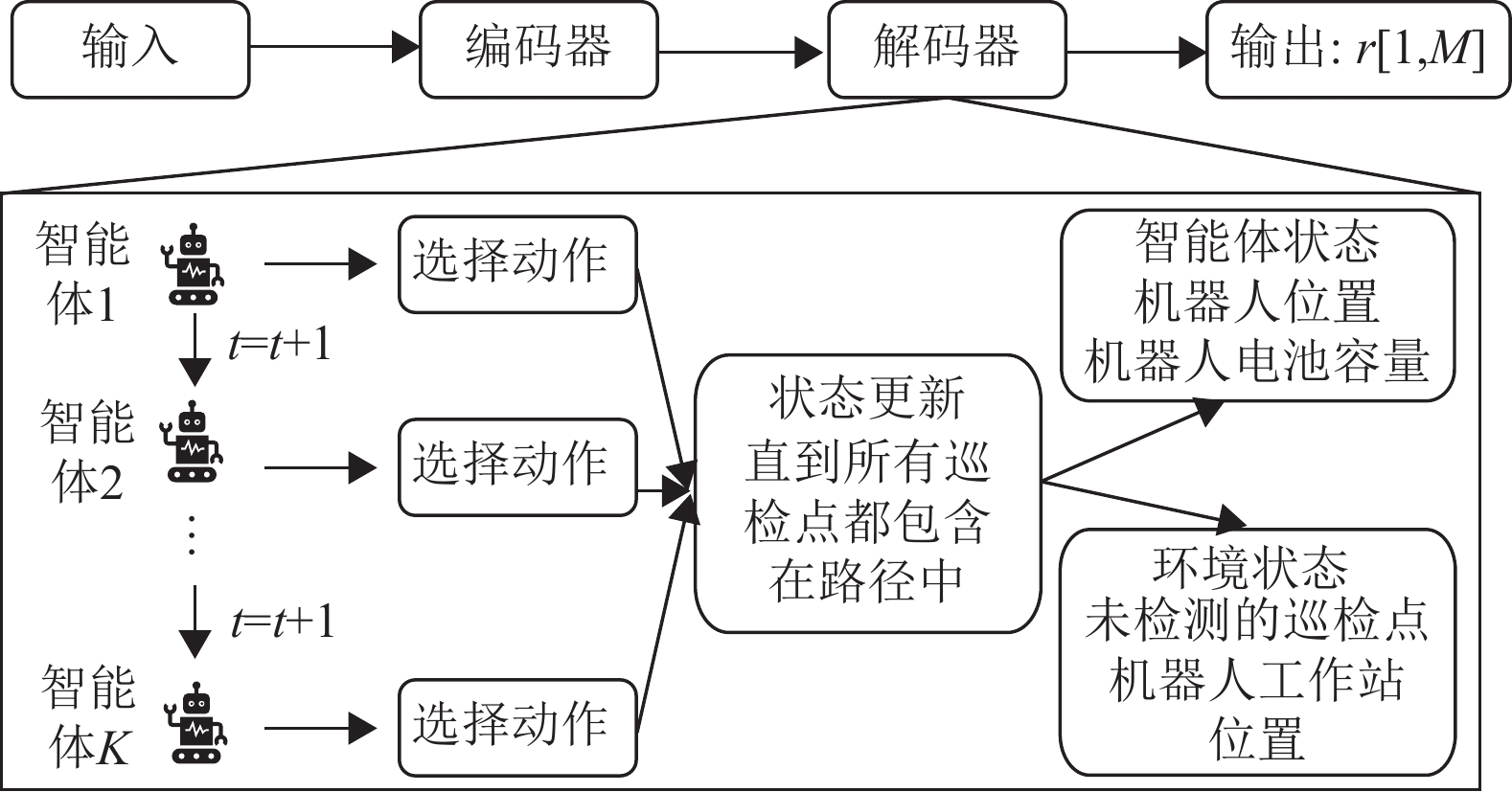
如图1所示,MAAM模型框架的核心是其解码器的多智能体结构设计。编码器首先处理来自机器人工作站和巡检点的信息,并输出高维特征表示。解码器结合高维特征、约束掩码和上下文嵌入,生成路径集
|
图 1 多智能体注意力模型 Figure 1 Multi-agent attention model |
每台机器人的路径规划过程可视为一个从当前巡检点出发,逐步选择下一个未访问巡检点的序列决策问题。为了实现这一点,本文定义了一个条件概率函数
| $ {p}_{{\boldsymbol{\theta }}}\left(r\left[1,M\right]|{S}\right) ={\prod }_{t=1}^{n}{p}_{{\boldsymbol{\theta }}}\left(r\left[{m}\left(t\right) \right]\left[t\right]|{S},c\left[t-1\right]\right) $ | (5) |
式中,
利用随机策略的方法无需为每个问题实例单独训练策略,而是可以从给定随机分布(通过离线训练获得)生成可行的实时解决方案。因此,本文通过随机策略方式生成高质量的解决方案,避免了在短时间内模型对每个新问题进行重复训练。
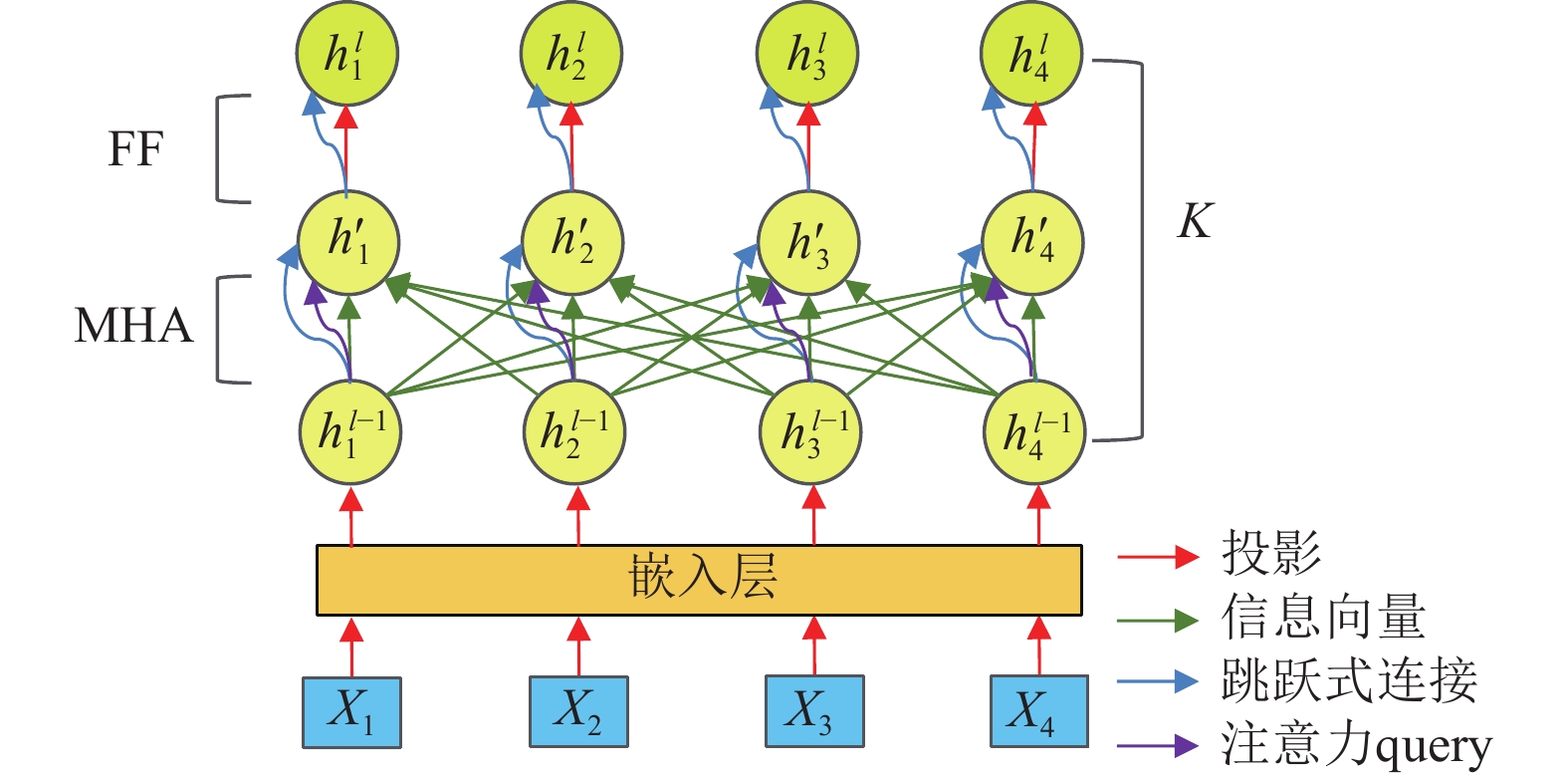
1.3.2 编码器编码器旨在将低维信息转化为高维表示。以4个待检测的巡检点为例,其编码器结构详见图2。
|
图 2 编码器框架 Figure 2 Encoder framework |
在此过程中,信息向量首先投影到嵌入层(Embedding Layer, EL),随后经过一系列参数相互独立的注意力模块进行深度处理。每个模块均融合了多头注意力层(Multi-head Attention, MHA)与前反馈层(Feed Forward, FF),并通过残差连接和批归一化技术优化性能。
| $ {h}_{i}^{0}={W}^{i}{X}_{i}+{b}^{i} $ | (6) |
注意力机制是一种带权池化方法,输入由询问(query)和键值对(key-value)组成,可以理解为巡检点之间的加权消息传递[17]。key用于计算注意力分布,value则生成选择信息。在本文中,以
| ${u}_{i,j}=\frac{{\boldsymbol{q}}_{{i}}^{\mathrm{T}}{k}_{j}}{\sqrt{{d}_{k}}} $ | (7) |
| $ {h}_{i'}={\rm{softmax}}\left({u}_{i,j}\right) {v}_{j}={\sum }_{j}\frac{{e}^{{u}_{i,j}}}{{\sum }_{{j'}}{e}^{{u}_{i,j'}}}{v}_{j} $ | (8) |
式中,
利用MHA层进行特征增强,模型对不同参数的注意力值
| ${F}_{i}\left({h}_{1}^{0},{h}_{2}^{0},\cdots ,{h}_{n}^{0}\right) ={\sum }_{z=1}^{Z}{W}_{Z}^{i}{h'}_{iz} $ | (9) |
| $ {{\widehat h}_{l}}={h}_{i}^{0}+{{F}}_{i}\left({h}_{1}^{0},{h}_{2}^{0},\cdots ,{h}_{n}^{0}\right) $ | (10) |
| ${h}_{i}^{1}={{\widehat h}_{l}}+\varphi \left({{\widehat h}_{l}}\right) $ | (11) |
其中,式(11)
| $\varphi \left({{\widehat h}_{l}}\right) ={W}_{1}^{f}{\rm{ReLu}}\left({W}_{2}^{f}{{\widehat h}_{l}}+{b}_{0}^{f}\right) +{b}_{1}^{f} $ | (12) |
利用式(9)~(11)经过
| $ {{\overline h}}^{K}=\frac{1}{K}{\sum }_{i=1}^{K}{h}_{i}^{\eta } $ | (13) |
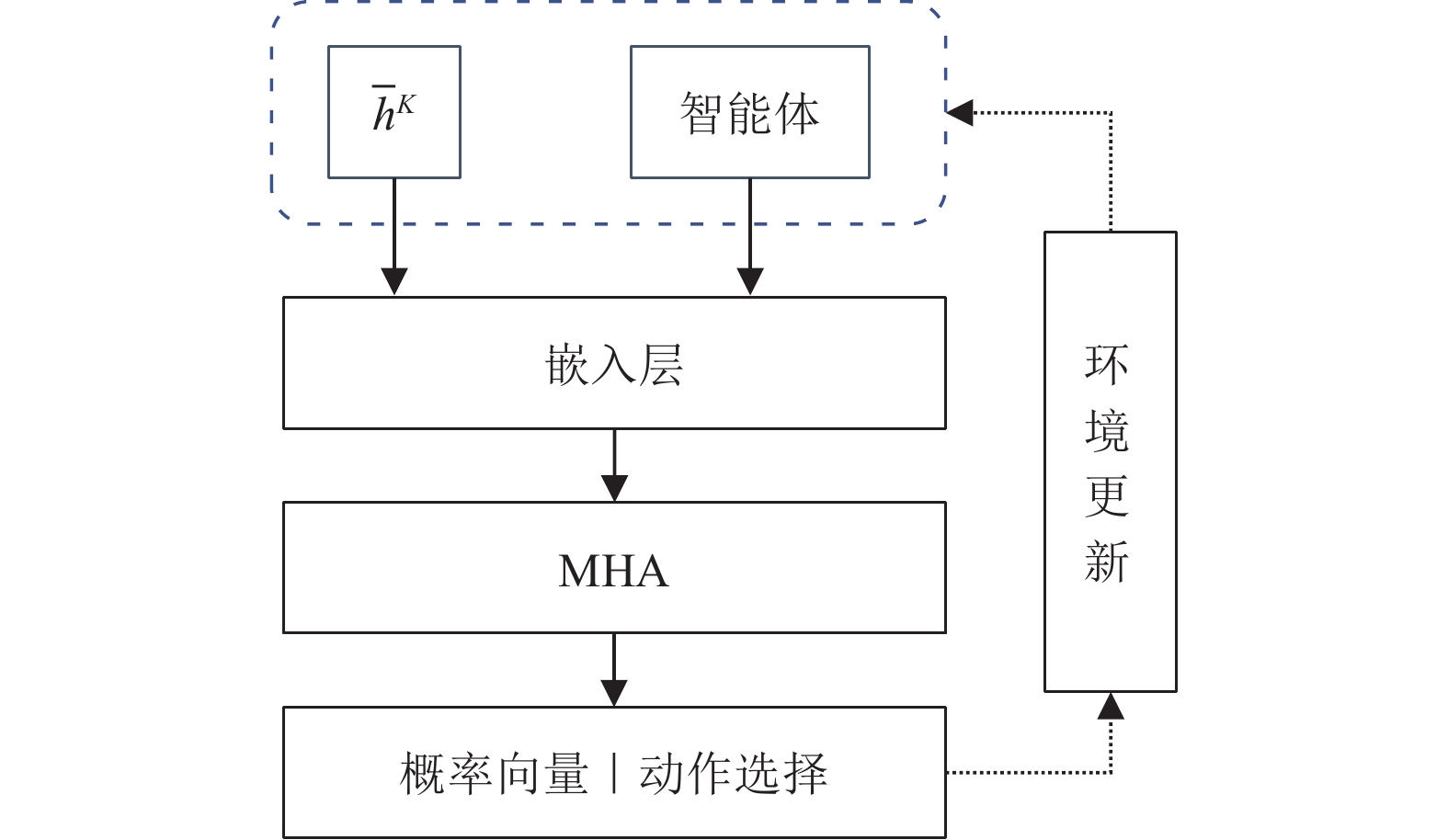
解码器负责设定状态、动作和奖励,并通过深度神经网络训练智能体。智能体通过感知环境与彼此状态,生成有序动作序列。这些动作不仅影响环境,还改变智能体的状态。如图3所示,解码器基于编码器的嵌入和前一步输出,在第t时间步选择下一个巡检点。智能体的核心目标是选择一系列动作,直至达到目标状态,从而最大化随时间累积的奖励函数值。通过状态与动作的映射[18],解码器协助智能体制定有效的决策策略,直至所有巡检点检测完毕。
|
图 3 解码器框架 Figure 3 Decoder framework |
(1) 状态。在多智能体注意力模型中,全局状态可以分为环境状态和智能体状态。环境状态包含待检测巡检点的高维嵌入
| $ {\widehat{w}}_{m,t}=\mathrm{max}\left(0,{\widehat{w}}_{m,t-1}-{\delta d}_{i}\right) $ | (14) |
在第
| ${h}_{t}^{c}=\left[{{\overline h}}^{K};{h}_{{r}_{t-1},1}^{K};{\widehat{w}}_{1,t};{h}_{{r}_{t-1},2}^{K};{\widehat{w}}_{2,t};\cdots ;{h}_{{r}_{t-1},M}^{K};{\widehat{w}}_{M,t}\right] $ | (15) |
(2) 动作。每台机器人的动作表示在第
| $ {h}_{t}^{c'}={\rm{MHA}}\left({h}_{t}^{c}\right) $ | (16) |
| $ {\boldsymbol{q}}_{{c}}={W}^{Q_v}{{h}_{t}^{c'}}$ | (17) |
| ${k}_{i}={W}^{K}{h}_{i}^{\lambda } $ | (18) |
| $ {u}_{i,m,t}=\mathrm{tanh}\left(\frac{{\boldsymbol{q}}_{{c}}^{\mathrm{T}}{k}_{i}}{\sqrt{{d}_{k}}}\right) $ | (19) |
最后,通过
| $ {p}_{i,m,t}={\rm{softmax}}\left({u}_{i,m,t}\right) =\frac{{e}^{{u}_{i,m,t}}}{{\sum }_{{j'}}{e}^{{u}_{i,m,t}}} $ | (20) |
根据概率
(3) 奖励。奖励函数定义了强化学习的目标。在变电站巡检调度中,由巡检成本与智能体数量成本定义奖励函数,目标是巡检路径总成本最小。
| $ R\left(r\left[1,M\right]\right) =-{\rm{Cost}}\left(r\left[1,M\right]\right) -\partial M$ | (21) |
其中,
利用向量
| $ \begin{split} {\nabla }_{{\boldsymbol{\theta }}}L\left(\boldsymbol{\theta }|S\right) =&-{E}_{r \sim {p}_{\boldsymbol{\theta }}\left(.|{S}\right) }[(R(r[1,{M}]-\\ &R({r}^{{\rm{BL}}}\left[1,M\right]) ) {\nabla }_{\boldsymbol{\theta }}\mathrm{l}\mathrm{n}({p}_{\boldsymbol{\theta }}(r\left[1,M\right]|{S}) ) ] \end{split} $ | (23) |
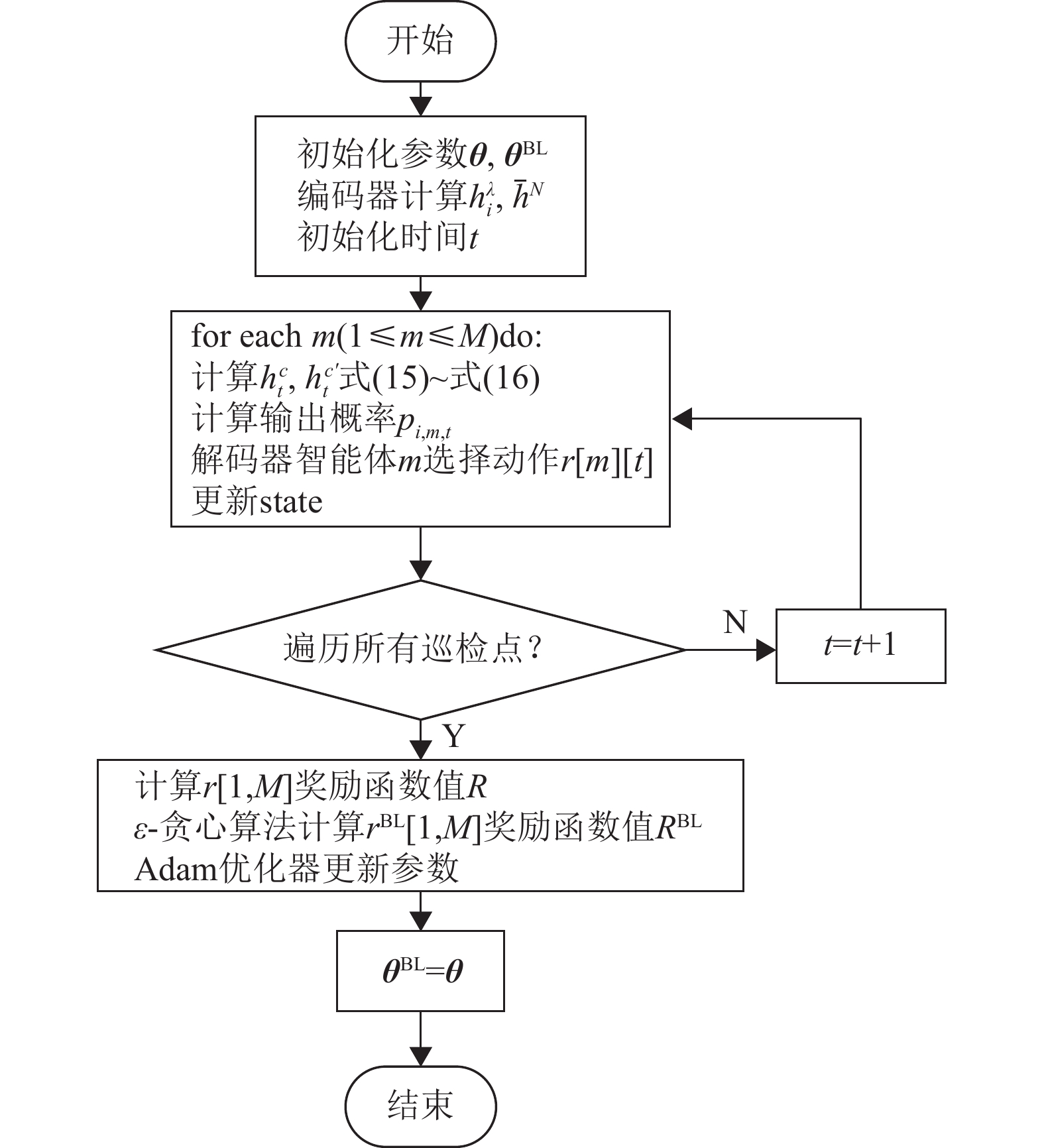
式中,
|
图 4 训练流程图 Figure 4 Training process |
如图5所示,本文以南方电网某变电站集群作为实验场景,评价路径巡检方法的性能,其中0节点表示机器人工作站,其他数字代表巡检点,巡检机器人运行在变电站可行区域内。以机器人工作站作为起点和终点,每个时段都要派出一定数量的机器人到每个巡检点进行检测。一个巡检点需要检测的设备数量、设备等级以及时间窗可以按照决策者的决策动态而变化。本文对巡检点的设置如表2所示。时间窗惩罚系数
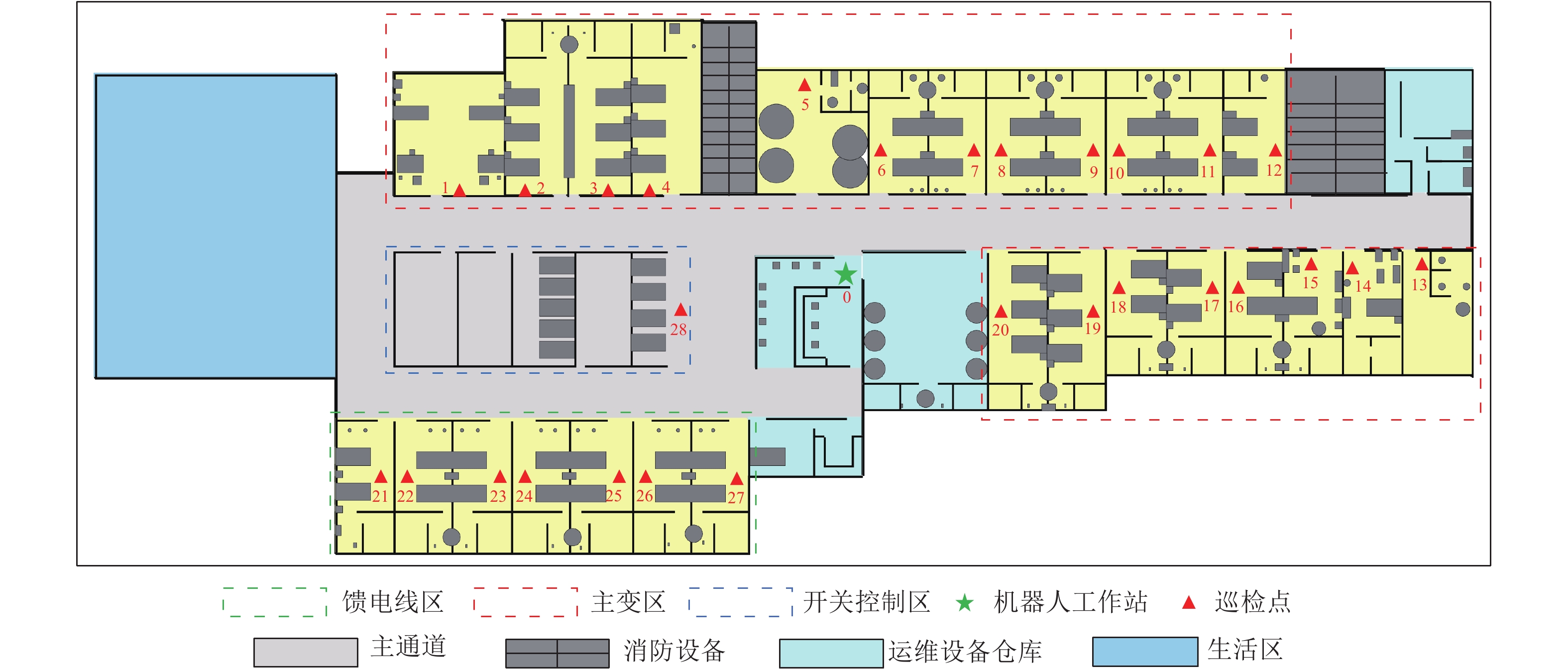
|
图 5 变电站布局图 Figure 5 The layout of the studied substation |
| 表 2 巡检点属性表 Table 2 Inspection point attributes |
以4个机器人为例,对有巡检时间窗约束的巡检点进行巡检路线规划,分别对比本文算法、遗传算法、HVNS算法以及APMMEAS算法,结果如图6所示。对比其他算法,本文提出的多智能体强化学习算法在综合考虑路径总距离、时间窗偏移以及设备重要性条件下规划的巡检路径更加合理,机器人巡检效率更高。
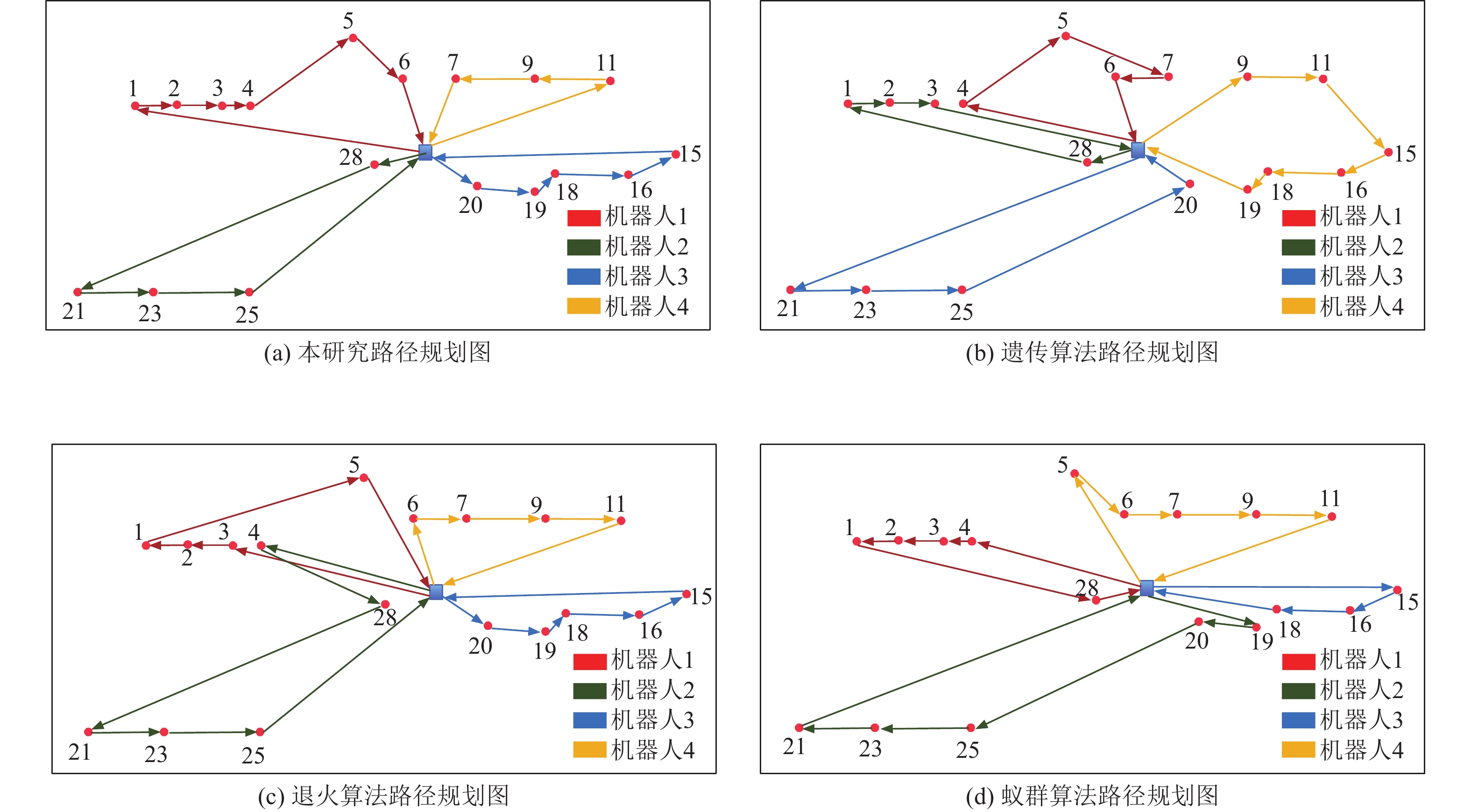
|
图 6 巡检路径图 Figure 6 Inspection path |
考虑到本文选取的变电站规模较小,因此将智能体数量设置为1~4个以考察算法运行效果。每个智能体之间初始参数是完全相同的,本文比较单个智能体以独立方式执行搜索的场景与多个智能体以合作方式搜索的场景。如图7所示,多智能体合作的情况比单智能体效率更高。在强化学习过程中,奖励函数会在智能体遍历解决方案时诱导智能体向更优的方向搜索。
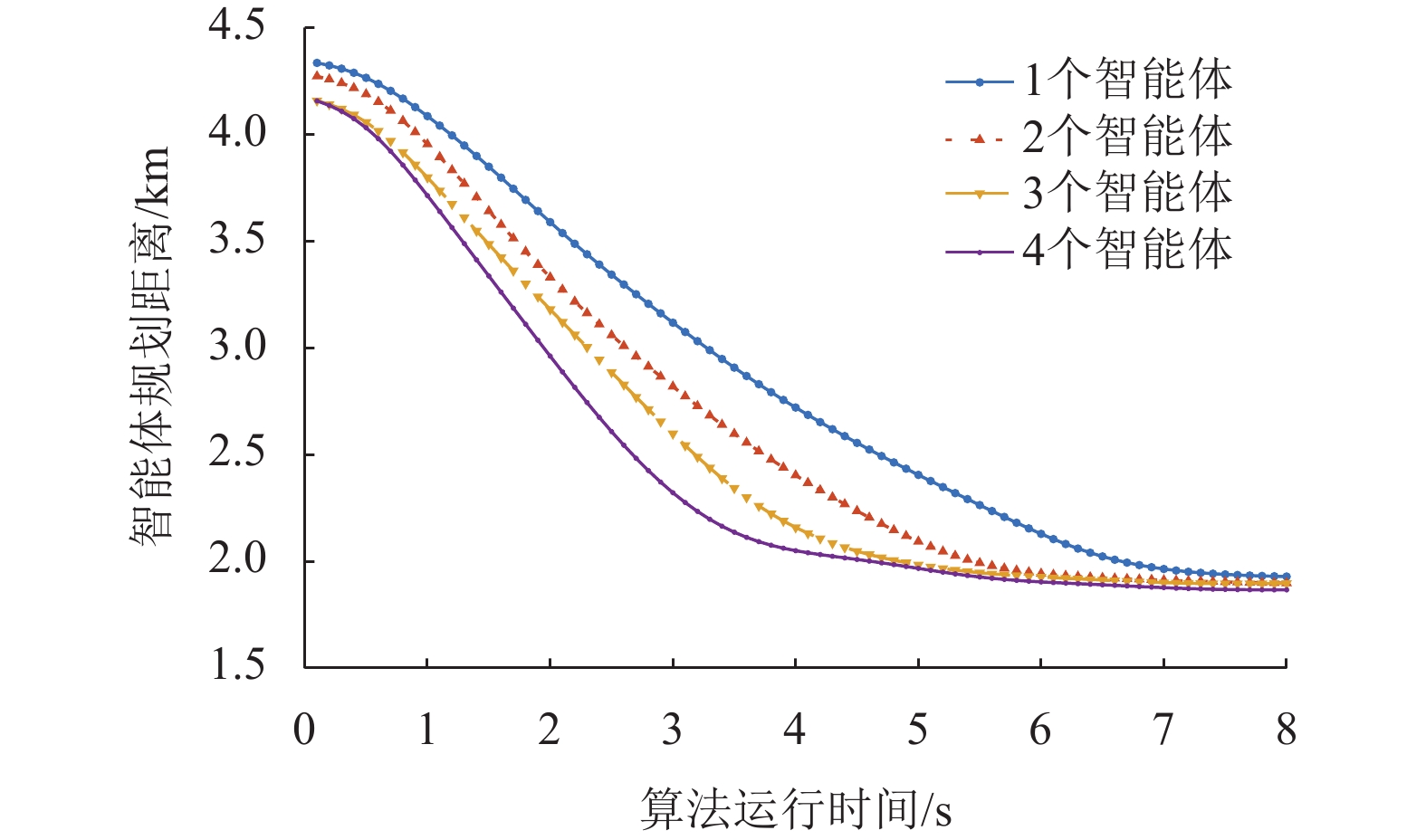
|
图 7 智能体数量与算法收敛关系 Figure 7 Agent quantity and algorithm convergence |
另外,每个智能体以合作的方式共存,因此多智能体遍历的方式能进一步提高效率。智能体数量越多,算法的收敛速度越快,巡检任务则需增加相应数量的机器人完成。然而,对于本案例,并非一昧增加智能体数量就能实现以最少的成本完成巡检任务,原因是奖励函数中需要考虑每个智能体的成本问题。
巡检机器人与人工巡检之间的成本比较是评估其优势的一个重要方面。然而,仅仅通过短期成本的对比无法完全体现巡检机器人的优势。因此,在考虑巡检机器人的使用寿命期间内,本文将人工巡检与机器巡检的成本进行了详细对比。人工巡检任务由6名技术员负责,每天上班8 h,信息来源于南方电网公开材料。同时,采购了4台SMP Robotics的S3.2型号巡检机器人,购买成本共计20万元。此外,每年还需要购买相应的维护耗材。图8展示了对比结果。图中人工累计成本于第3年超过机器人成本[5],机器人完成变电站巡检任务累计成本降低33.33%。
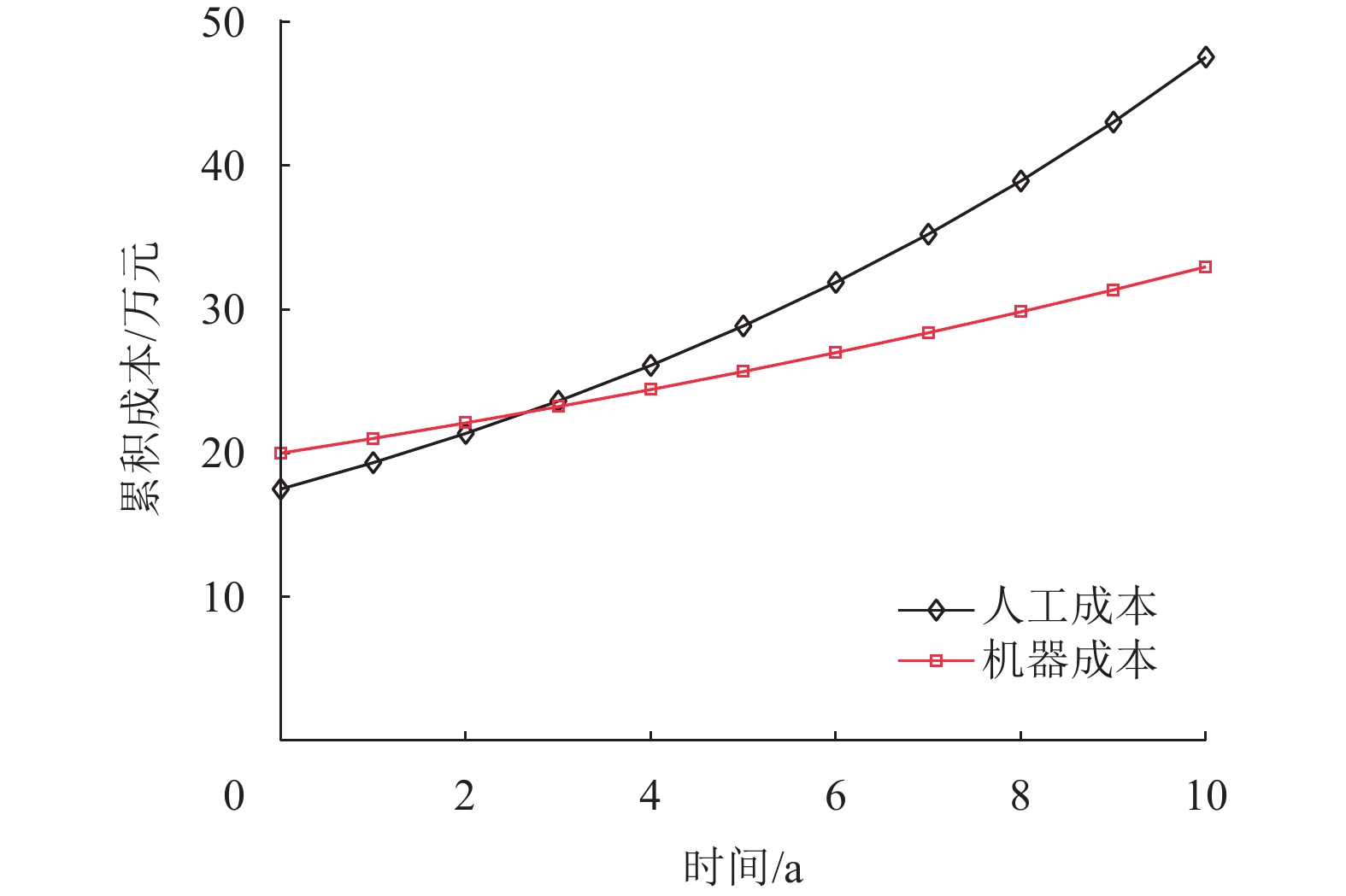
|
图 8 成本对比 Figure 8 Cost comparison |
为了全面评估本文提出的基于强化学习的多智能体注意力模型在智能巡检路径规划方面的效率,本文将之与遗传算法、HVNS算法以及APMMEAS算法进行了对比分析。
遗传算法作为一种模拟生物进化过程的优化方法,擅长在广泛的搜索空间内寻找最优解,适用于解决复杂的路径规划问题。然而,其需要大量的迭代计算,可能导致计算成本较高,且在局部最优解处可能陷入停滞,影响求解效率。
HVNS算法作为变邻域搜索的一种扩展,通过多层次的邻域搜索机制来优化解的质量,特别适用于处理具有多个约束条件的路径规划问题。然而,其效率受邻域结构设计的影响,需要复杂的邻域定义,并可能导致较长的计算时间。
APMMEAS算法结合了蚁群算法和局部搜索策略的优势,通过并行化和自适应机制提高搜索效率和解的质量。在变电站巡检路径规划中,该算法能有效地搜索多条可能的路径,并快速适应任务需求的变化。然而,其并行化和自适应机制的设计复杂度较高,需要精细调整以获得最佳性能。
相比之下,本文提出的基于强化学习的多智能体注意力模型在路径规划方面展现出了显著的优势。通过利用注意力机制捕捉巡检点之间的相关性,模型能够更准确地指导智能体的决策过程。同时,强化学习的应用使得模型能够根据实际反馈进行自适应调整,提高了解的质量和效率。此外,模型的并行处理能力也使其在处理大规模巡检任务时具有更高的效率。
变电站巡检路径规划问题的算法参数设置如表3所示,算法收敛时间与规划路径距离如表4所示。在路径规划质量方面,本文算法相较于遗传算法、HVNS算法和APMMEAS算法,分别缩短了3.31%、1.24%和1.73%的机器人行驶距离,显著降低了运维成本和能耗。在计算效率方面,本算法较遗传算法加快了17.06%的算法收敛时间;较HVNS算法加快了16.22%;较APMMEAS算法加快了13.89%。这一优异的效率不仅源于注意力机制的高效关注约束,更得益于多智能体并行搜索和强化学习序列决策的创新融合,为实时动态调度奠定基础。在成本控制方面,本文算法分别较遗传算法、HVNS算法和APMMEAS算法降低了21.22%、6.86%和9.14%的单次巡检总成本。究其原因,一方面规划出更优的低成本路径,另一方面则是有效避免了时间窗口和优先级违约而产生的高额罚金,最大限度实现了经济高效运维。通过上述对比,本文算法在路径质量、计算效率和成本控制等多个关键维度上的卓越性能和优越性得到了充分验证,从理论和实践层面为变电站巡检调度等复杂约束优化问题提供了创新高效的解决方案。
| 表 3 算法参数设置 Table 3 Algorithm parameter setting |
| 表 4 算法对比 Table 4 Algorithm contrast |
综合考虑了巡检点等级差异性以及高峰期用电时间窗对设备故障的影响建立机器人巡检路径方案,提出了基于多智能体注意力模型的VRPSTW问题解决方案。该模型能根据监测点动态变化的待检设备数量进行机器人调度,实现变电站设备短时抽检,确保设备稳定运行。
在模型构建方面,本文采用了编码器−解码器框架,通过注意力层生成高效的巡检路径。编码器负责将巡检点的信息转化为高维表示,而解码器则根据这些表示和先前的决策来生成下一步的动作。这种结构使得模型能够充分利用巡检点之间的相关信息,提高路径规划的准确性和效率。
为了训练模型,本文采用了无监督神经网络方法。这种方法无需大量的标注数据,而是利用模型自身的结构特性进行自学习。这不仅降低了数据收集的成本,还提高了算法的泛化能力。
在与其他算法的对比中,本文提出的方法展现出了显著的优势。与遗传算法、HVNS算法和APMMEAS算法相比,本文的规划路径平均缩短了2.09%,算法运行时间平均缩短了15.72%,成本也平均减少了12.41%。这些结果充分证明了多智能体注意力模型在解决VRPSTW问题上的有效性和高效性。
然而,机器人自动巡检路径规划这一领域仍然有诸多待完善之处。本文采用的是策略梯度下降法进行网络训练,这种方法虽然取得了一定的效果,但在效率方面仍有进一步提升的空间。因此,未来研究可以尝试采用更为先进、目标指向性更强的算法来优化训练过程,以期实现更高的路径规划效率。
此外,考虑到高压输电线路的覆盖面积广、线路长,需要众多巡检机器人进行并行作业。这不仅增加了巡检成本,也对机器人的协调和管理提出了更高的要求。为了降低机器人成本,同时保证巡检工作的全面性和高效性,可以考虑将本文的模型应用于高压和非高压输电设备的混合抽样巡检中。通过这种方式,可以根据设备的重要性和风险等级,合理调配巡检机器人的数量和巡检频率,减少单次检测的设备数量,缩短检测周期,从而在保证巡检质量的同时,有效降低巡检成本。
| [1] |
傅惠, 伍乃骐, 胡刚. 城市交通系统管理与优化研究综述[J].
工业工程, 2016, 19(1): 10-15.
FU H, WU N Q, HU G. An overview of management and optimization of urban transportation systems[J]. Industrial Engineering Journal, 2016, 19(1): 10-15. |
| [2] |
王建邦, 袁智勇, 陈波, 等. 变电站巡检机器人数据驱动无模型自适应控制[J].
电测与仪表, 2019, 56(19): 114-120.
WANG J B, YUAN Z Y, CHEN B, et al. Data driven model free adaptive control for substation inspection robots[J]. Electric Measurement and Instrumentation, 2019, 56(19): 114-120. |
| [3] |
黄金魁. 智能变电站三维实景无人值守感知系统的应用研究[J].
电测与仪表, 2020, 57(4): 87-92.
HUANG J K. Research on the application of three-dimensional real scene unattended sensing systems in intelligent substations[J]. Electric Measurement and Instrumentation, 2020, 57(4): 87-92. |
| [4] |
张永涛, 李博, 张甲, 等. 基于图论的变电站巡检机器人全局路径规划[J].
山东电力技术, 2020, 47(9): 45-49.
ZHANG Y T, LI B, ZHANG J, et al. Global path planning of substation inspection robots based on graph theory[J]. Shandong Electric Power Technology, 2020, 47(9): 45-49. DOI: 10.3969/j.issn.1007-9904.2020.09.009. |
| [5] |
张永涛, 于倩倩, 肖智彬, 等. 基于枚举法的变电站巡检机器人巡视路线优化[J].
浙江电力, 2021, 40(1): 12-17.
ZHANG Y T, YU Q Q, XIAO Z B, et al. Optimization of inspection routes for substation inspection robots based on enumeration method[J]. Zhejiang Electric Power, 2021, 40(1): 12-17. |
| [6] |
薛阳, 俞志程, 吴海东, 等. 基于IACO-ABC 算法的变电站巡检机器人路径规划[J].
浙江电力, 2019, 38(11): 10-15.
XUE Y, YU Z C, WU H D, et al. Path planning for substation inspection robots based on the IACO-ABC algorithm[J]. Zhejiang Electric Power, 2019, 38(11): 10-15. |
| [7] |
刘胜, 晏齐忠, 张志鑫, 等. 基于ACO-PSO算法的变电站巡检机器人路径规划研究[J].
浙江电力, 2021, 40(1): 29-35.
LIU S, YAN Q Z, ZHANG Z X, et al. Study on path planning for substation inspection robots using the ACO-PSO algorithm[J]. Zhejiang Electric Power, 2021, 40(1): 29-35. |
| [8] |
宋涛, 李丹, 路宁. 基于分层强化学习的数字化输电线路路径规划研究[J].
电测与仪表, 2022, 59(4): 91-97.
SONG T, LI D, LU N. Study on path planning for digital transmission lines using hierarchical reinforcement learning[J]. Electric Measurement and Instrumentation, 2022, 59(4): 91-97. |
| [9] |
王万良, 陈浩立, 李国庆, 等. 基于深度强化学习的多配送中心车辆路径规划[J].
控制与决策, 2022, 37(8): 2101-2109.
WANG W L, CHEN H L, LI G Q, et al. Path planning for vehicles at multiple distribution centers using deep reinforcement learning[J]. Control and Decision, 2022, 37(8): 2101-2109. |
| [10] |
YANG Q, MA S, ZHANG G, et al. A new assistance navigation method for substation inspection robots to safely cross grass areas[J].
Sensors, 2023, 23(22): 9201.
DOI: 10.3390/s23229201. |
| [11] |
NING X, LIU Z, LI Y. Autonomous obstacle crossing method for substation inspection robots based on locust optimization algorithm[C]//3rd International Conference on Artificial Intelligence, Automation, and High-Performance Computing. Wuhan: SPIE, 2023: 1271702.
|
| [12] |
傅惠, 金诚谦, 牛张哲, 等. 网联自动驾驶货车编队规划与控制研究综述[J].
工业工程, 2024, 27(1): 25-35.
FU H, JIN C Q, NIU Z Z, et al. A comprehensive review of platoon planning and control research for networked automated driving trucks[J]. Industrial Engineering, 2024, 27(1): 25-35. |
| [13] |
YANG Z, SHEN Y, ZHOU R, et al. A transfer learning fault diagnosis model of distribution transformer considering multi-factor situation evolution[J].
IEEJ Transactions on Electrical and Electronic Engineering, 2020, 15(1): 30-39.
DOI: 10.1002/tee.23024. |
| [14] |
YANG Z C, SHEN Y, FAN Y, et al. Research on differentiation inspection strategy of distribution networks[C]//Proceedings of the 2019 IEEE 2nd International Conference on Electronics and Communication Engineering. Xi'an: IEEE, 2019: 331-335.
|
| [15] |
KOOL W, VAN HOOF H, WELLING M. Attention, learn to solve routing problems![C]// International Conference on Learning Representations. New Orleans: ICLR, 2019: 1-25.
|
| [16] |
ZHANG K, HE F, ZHANG Z, et al. Multi-vehicle routing problems with soft time windows: a multi-agent reinforcement learning approach[J].
Transportation Research Part C: Emerging Technologies, 2020, 121: 102861.
DOI: 10.1016/j.trc.2020.102861. |
| [17] |
VASWANI A, SHAZEER N, PARMAR N, et al. Attention is all you need[C]//Proceedings of the 31st International Conference on Neural Information Processing Systems. LongBeach, California: NIPS'17, 2017: 6000-6010.
|
| [18] |
AREL I, LIU C, URBANIK T, et al. Reinforcement learning-based multi-agent system for network traffic signal control[J].
IET Intelligent Transport Systems, 2010, 4(2): 128-135.
DOI: 10.1049/iet-its.2009.0070. |
| [19] |
AGARWAL A, HENAFF M, KAKADE S, et al. PC-PG: policy cover directed exploration for provable policy gradient learning[J].
Advances in Neural Information Processing Systems, 2020, 33: 13399-13412.
|
| [20] |
WILLIAMS R J. Simple statistical gradient-following algorithms for connectionist reinforcement learning[J].
Machine Learning, 1992, 8(3): 229-256.
|
| [21] |
MIRJALILI S. Genetic algorithm[M]// Evolutionary Algorithms and Neural Networks. Cham: Springer, 2019: 43-55.
|
| [22] |
EUCHI J, YASSINE A. A hybrid metaheuristic algorithm to solve the electric vehicle routing problem with battery recharging stations for sustainable environmental and energy optimization[J]. Energy Systems, 2023, 14(1): 243-267.
|
| [23] |
YAN X, LI W, HUANG Y, et al. An adaptive parameter for max-min elite ant system to solve CVRP problem[C]// 17th International Conference on Computational Intelligence and Security.Chengdu: IEEE, 2021: 580-584.
|
 2024, Vol. 41
2024, Vol. 41

