2. 广东电网有限责任公司 江门供电局, 广东 江门 529000
2. Jiangmen Power Supply Bureau, Guangdong Power Grid Corporation Limited, Jiangmen 529000, China
在实施“双碳”战略的背景下,随着风电场大规模接入电力系统,构成了高比例可再生能源和高比例电力电子设备并存的系统[1]。由此诱发次/超同步控制相互作用、谐波谐振以及变流器驱动稳定性等问题对电力系统的安全运行产生了重大影响[2]。
根据现有研究,文献[3]和文献[4]根据次同步振荡参与对象的不同,对目前风电场接入引起的次同步振荡主要分为3类:次同步谐振(Sub-synchronous Resonance, SSR)、装置引起次同步振荡(Sub-Synchronous Control, SSTI)、次同步控制互作用(Sub-synchronous Control Interaction, SSCI)。
当双馈异步风机(Doubly fed Induction Generator, DFIG) 转子变流器经串补线路连接到电网时,可能会在某个特定的频率范围内转子控制策略与系统产生的电气振荡模式相互作用,导致双馈风机在并网运行过程中发生次同步谐振(SSR) [5-6] 。
DFIG在运行过程中会面临多种SSR问题,分析这类问题的方法较为复杂,在学术界受到了广泛关注以及深入研究。文献[7]研究表示,适当的环流控制能够有效提升多电平换流器的稳定性。文献[8]指出增加串补度和减小风速可能引起感应电机效应,而电流环控制器的比例系数和积分系数增大可能引起SSCI。文献[9]表明即使在传输系统的补偿度降低至仅为6.67%这一较低水平下,SSR事件依然有可能发生。文献[10]揭示了双馈风机串补互联系统中次同步振荡的主要诱因是风机变流器的控制器产生的负阻尼效应,针对这一问题,设计了一种附加阻尼控制抑制方法。文献[11]表明机侧电流控制内环的参数对系统稳定性有最显著的影响,尤其是比列系数越大,SSCI现象越明显。文献[12]进一步证实了比列系数增大是导致SSCI的重要原因,并且设计了阻尼控制器减缓SSCI的发生。文献[13]聚焦于双馈异步风机未经串联补偿线路直接连接到电力系统中引发的SSI问题。当在复平面上 DFIG的开环次同步振荡(Subsynchronous Oscillation, SSO) 模式接近系统其余部分的开环SSO模式,可能导致闭环SSO模式的阻尼降低。文献[14]提出了一种开环模式分析方法,揭示了开环模态耦合如何导致闭环模态的排斥,以及这种排斥对系统SSO事件产生的影响。文献[15]揭示了双馈风电无串补并网系统中,网侧变流器电流控制内环、锁相控制以及机侧变流器电流控制内环主导的振荡场景。文献[16]提出解析惯量模型分析永磁直驱风机内部控制模态交互作用以及内部谐振的作用机理。文献[17]通过振荡模式调整进行了模态相互作用优化,防止了潜在的系统模态谐振,增强了系统阻尼,证明了优化模态相互作用有利于提高电力系统谐振稳定性。文献[18] 研究了不同风电渗透水平和动态交互条件,基于功率敏感性的功率调度方法,增强稳定性边界并更新了电力系统机组组合问题解决方案。文献[19]提出了一种基于模态叠加理论的新型模态控制策略,用于减电力系统中的低频振荡问题。文献[20]提出了一种基于相量测量单元的在线协调策略,用于减轻全转换器在风电和电网之间的模态共振。文献[21]设计了辅助谐振控制器的详细参数,并通过多目标粒子群优化算法进行了参数优化,以改善电力系统与风电之间的模态交互作用。
本文以双馈异步风机(DFIG) 并网系统为研究对象,探究其控制模态的交互作用以及内部谐振的产生机理,并对其控制参数进行设计优化以达到抑制内部谐振效果,使得系统能够安全稳定运行。
1 双馈异步风机系统数学模型DFIG并网结构如图1所示,主要包括风轮机、齿轮箱、感应发电机、机侧换流器、直流母线、网侧换流器及换流器的控制系统。双馈异步风力发电机是以定子和转子两部分能与外部电网连接并输送电能为特征的一种特殊类型的绕线式异步发电机,故名“双馈”。其特点是将两个背靠背的换流器分别接在定子侧经升压变压器上接入电网,再通过滤波器接入电网。
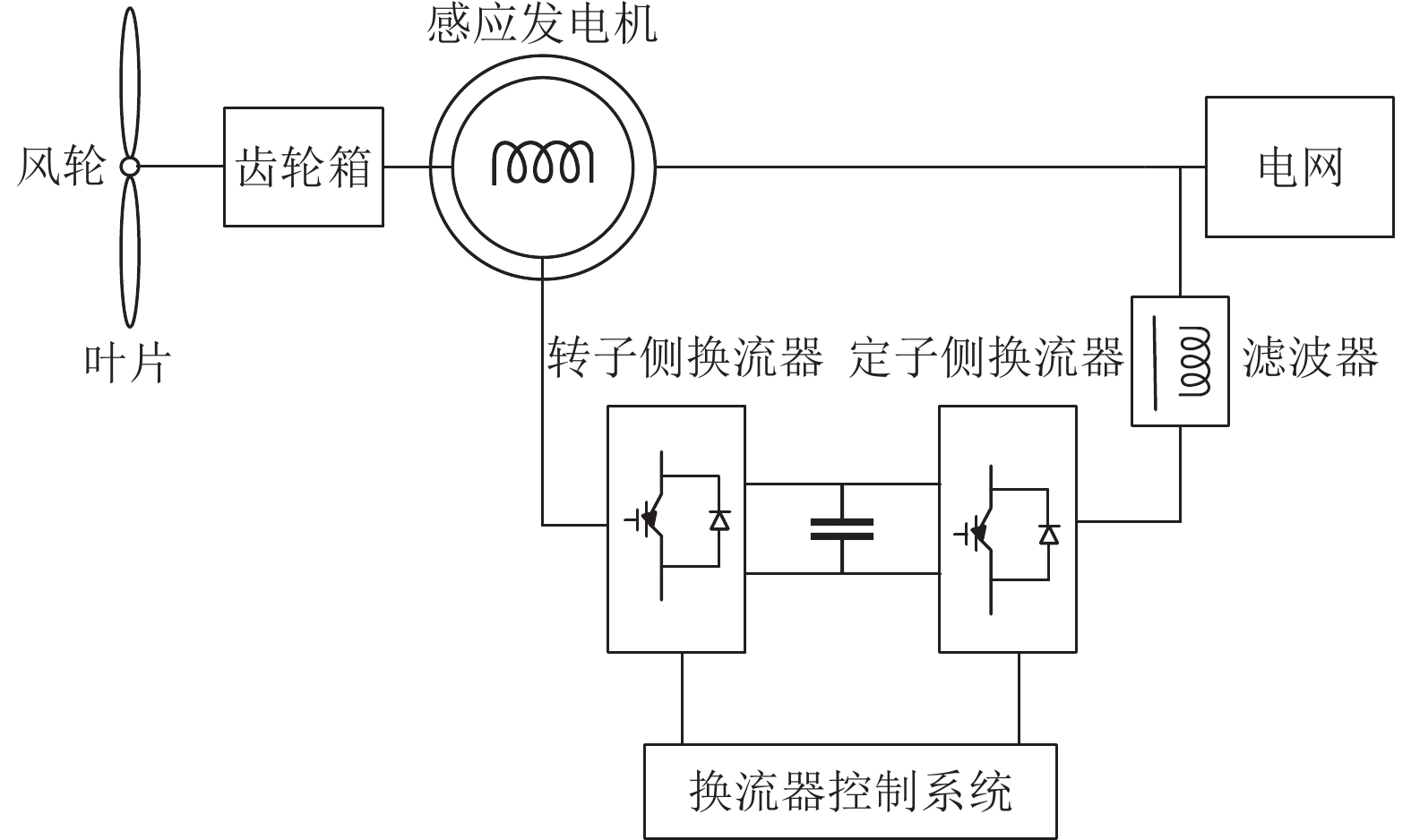
|
图 1 双馈异步风机并网结构示意图 Figure 1 Schematic diagram of the grid-connected structure of DFIG |
采用定子电压定向,双馈异步风机在dq旋转坐标轴下的数学模型为
| $ \left\{ \begin{gathered} {u_{{\mathrm{s}}d}} = {R_{\mathrm{s}}}{i_{{\mathrm{s}}d}} + \frac{{\mathrm{d}}}{{{\mathrm{d}}t}}{\psi _{{\mathrm{s}}d}} - {\omega _{\mathrm{s}}}{\psi _{{\mathrm{s}}q}} \\ {u_{{\mathrm{s}}q}} = {R_{\mathrm{s}}}{i_{{\mathrm{s}}q}} + \frac{{\mathrm{d}}}{{{\mathrm{d}}t}}{\psi _{{\mathrm{s}}q}} - {\omega _{\mathrm{s}}}{\psi _{{\mathrm{s}}d}} \\ {u_{{\mathrm{r}}d}} = {R_{\mathrm{r}}}{i_{{\mathrm{r}}d}} + \frac{{\mathrm{d}}}{{{\mathrm{d}}t}}{\psi _{{\mathrm{r}}d}} - \Delta \omega {\psi _{{\mathrm{r}}q}} \\ {u_{{\mathrm{r}}q}} = {R_{\mathrm{r}}}{i_{{\mathrm{r}}q}} + \frac{{\mathrm{d}}}{{{\mathrm{d}}t}}{\psi _{{\mathrm{r}}q}} - \Delta \omega {\psi _{{\mathrm{r}}d}} \\ \Delta \omega = {\omega _{\mathrm{s}}} - {\omega _{\mathrm{r}}} \\ \end{gathered} \right. $ | (1) |
磁链方程为
| $ \left\{ \begin{gathered} {\psi _{{\mathrm{s}}d}} = {L_{\mathrm{s}}}{i_{{\mathrm{s}}d}} + {L_m}{i_{{\mathrm{r}}d}} \\ {\psi _{{\mathrm{s}}q}} = {L_{\mathrm{s}}}{i_{{\mathrm{s}}q}} + {L_m}{i_{{\mathrm{r}}q}} \\ {\psi _{{\mathrm{r}}d}} = {L_{\mathrm{r}}}{i_{{\mathrm{r}}d}} + {L_m}{i_{{\mathrm{s}}d}} \\ {\psi _{{\mathrm{r}}q}} = {L_{\mathrm{r}}}{i_{{\mathrm{r}}q}} + {L_m}{i_{{\mathrm{s}}d}} \\ \end{gathered} \right. $ | (2) |
式(1)中:urd、urq、usd、usq分别为转子电压d轴分量、转子电压q轴分量、定子电压d轴分量、定子电压q轴分量;ψrd、ψrq、ψsd、ψsq分别为转子磁链d轴分量、转子磁链q轴分量、定子磁链d轴分量、定子磁链q轴分量;ird、irq、isd、isq分别为转子电流d轴分量、转子电流q轴分量、定子电流d轴分量、定子电流q轴分量;Rr、Rs分别为转子绕组阻值和定子绕组阻值;Δω、ωs、ωr分别为转差角速度、定子同步角速度以及转子角速度。
双馈风机定子侧有功功率、无功功率表示为
| $ \left\{ \begin{gathered} {P_{\mathrm{s}}} = \frac{3}{2}\left( {{u_{{\mathrm{s}}d}}{i_{{\mathrm{s}}d}} + {u_{{\mathrm{s}}q}}{i_{{\mathrm{s}}q}}} \right) \\ {Q_{\mathrm{s}}} = \frac{3}{2}\left( {{u_{{\mathrm{s}}d}}{i_{{\mathrm{s}}q}} - {u_{{\mathrm{s}}q}}{i_{{\mathrm{s}}d}}} \right) \\ \end{gathered} \right. $ | (3) |
当定子侧与外部电网相连后,定子侧的电压就等于电网电压,即定子侧的电压在dq轴坐标系下的电压矢量Us是恒定的,同时可以认为定子磁链是保持不变的。对于电网侧而言,定子绕组上的电阻压降很小,可以忽略不计,那么就有
| $ \frac{{{\mathrm{d}}{\psi _{{\mathrm{s}}d}}}}{{{\mathrm{d}}t}} = 0,\frac{{{\mathrm{d}}{\psi _{{\mathrm{s}}q}}}}{{{\mathrm{d}}t}} = 0,{R_{\mathrm{s}}} = 0 $ | (4) |
采用定子电压矢量定向在d轴上,即
| $ \left\{ \begin{gathered} {u_{{\mathrm{s}}d}} = {{\boldsymbol{U}}_{\mathrm{s}}} \\ {u_{{\mathrm{s}}q}} = 0 \\ \end{gathered} \right. $ | (5) |
联立式(3)与式(5),可得
| $ \left\{ \begin{gathered} {P_{\mathrm{s}}} = \frac{3}{2}{{\boldsymbol{U}}_{\mathrm{s}}}{i_{{\mathrm{s}}d}} \\ {Q_{\mathrm{s}}} = \frac{3}{2}{{\boldsymbol{U}}_{\mathrm{s}}}{i_{{\mathrm{s}}q}} \\ \end{gathered} \right. $ | (6) |
双馈异步风机机侧变流器的控制目标是有功和无功功率。机侧变流器通常采用定子磁链定向或者定子电压定向控制方法。理论上,磁链定向能够实现完全解耦控制,但在实际工程中,因电压定向法操作简便且容易实现,所以常采用电压定向控制方法。主要通过控制q轴和d轴的励磁电压从而实现独立解耦控制。用图2表示机侧变流器的控制结构。
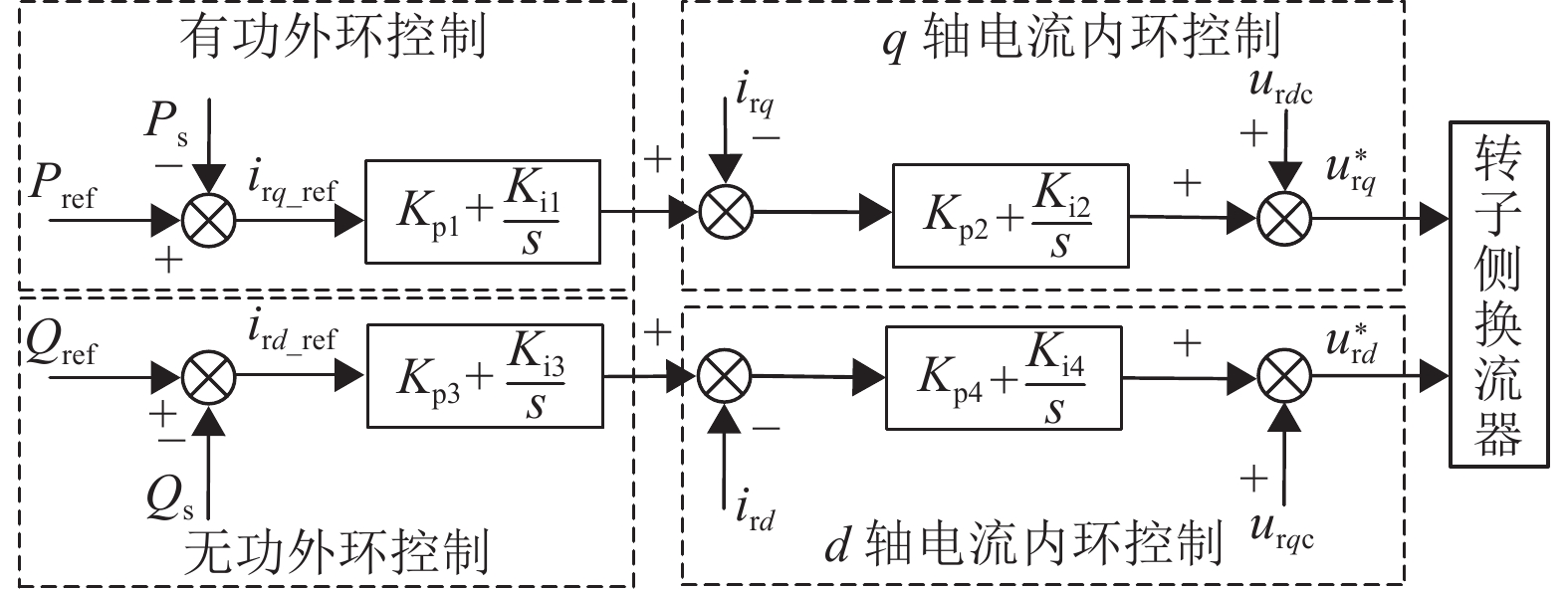
|
图 2 双馈异步风机机侧变流器控制框图 Figure 2 Control block diagram of rotor-side converter for DFIG |
主要工作原理如下:通过准确采集定子侧的有功和无功功率值,精确计算出机侧q轴和d轴电流的参考值。根据实时电流分量,进一步计算出q轴和d轴的电压分量。最终通过控制dq轴励磁电压,实现有功功率与无功功率的解耦控制。
2.2 网侧变流器控制系统网侧变流器的主要目的是维持直流侧电压稳定,使直流母线电压跟随给定值,通过调整网侧变流器的电流与电压方向,可实现能量的双向流动与回馈。如图3双馈异步风机网侧变流器控制框图所示,分别为电压控制外环以及电流控制内环,均采用PI控制器。
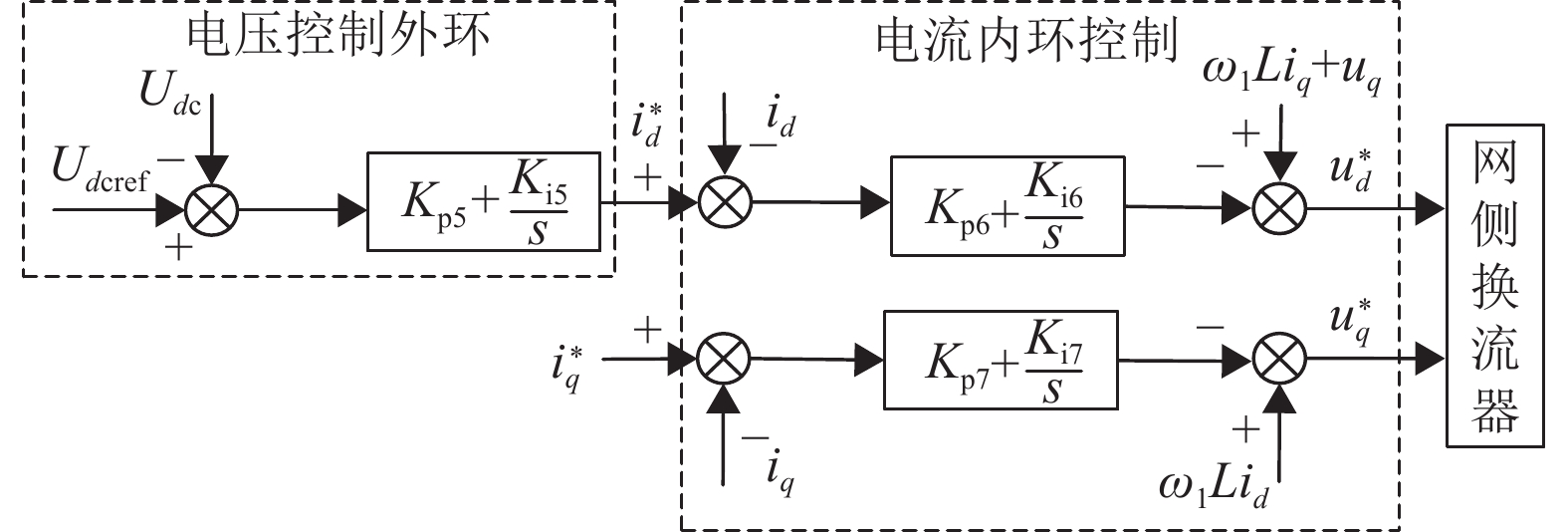
|
图 3 双馈异步风机网侧变流器控制框图 Figure 3 Control block diagram of grid-side converter for DFIG |
其控制原理如下:运行中的直流母线电压与预设电压Udcref会产生电压偏差,通过实时计算输出电流内环的d轴电流参考值
基于Matlab/Simulink软件平台搭建图1所示的双馈异步风机并网系统模型。发电机定子侧通过变比为
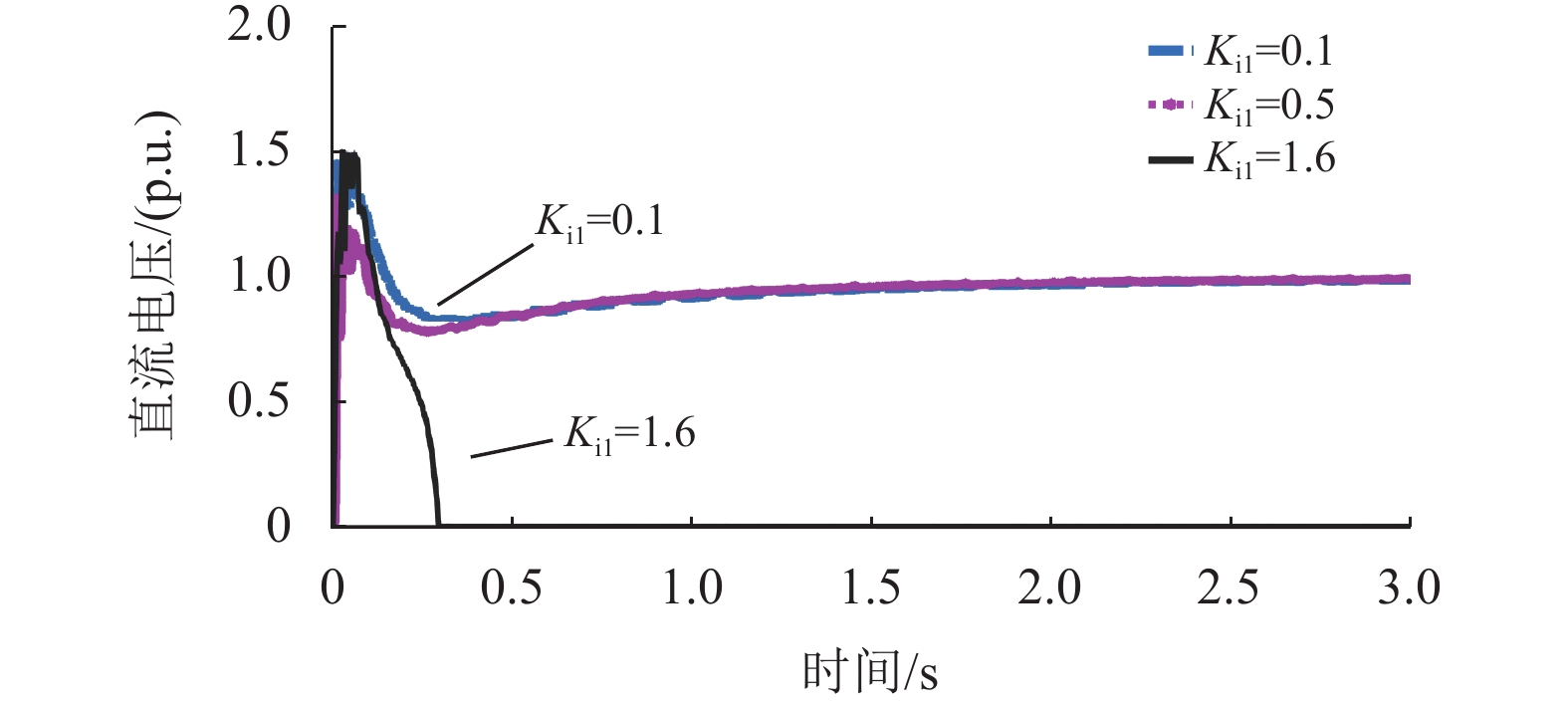
采用控制变量的方法进行探究,保持其他控制参数固定,仅改变PI控制器的单一控制参数进行探究。通过图4可发现,仅改变有功功率外环比例系数Kp1的参数时,比例系数逐渐增大,超调量会逐渐变小,最终到达稳定的时间大致相同。如图5所示,仅改变积分系数Ki1的参数,当积分系数逐渐增大,超调量也会相应地变大,最终到达稳定的时间大致相同。在本文系统中,有功功率控制外环的比例系数Kp1为
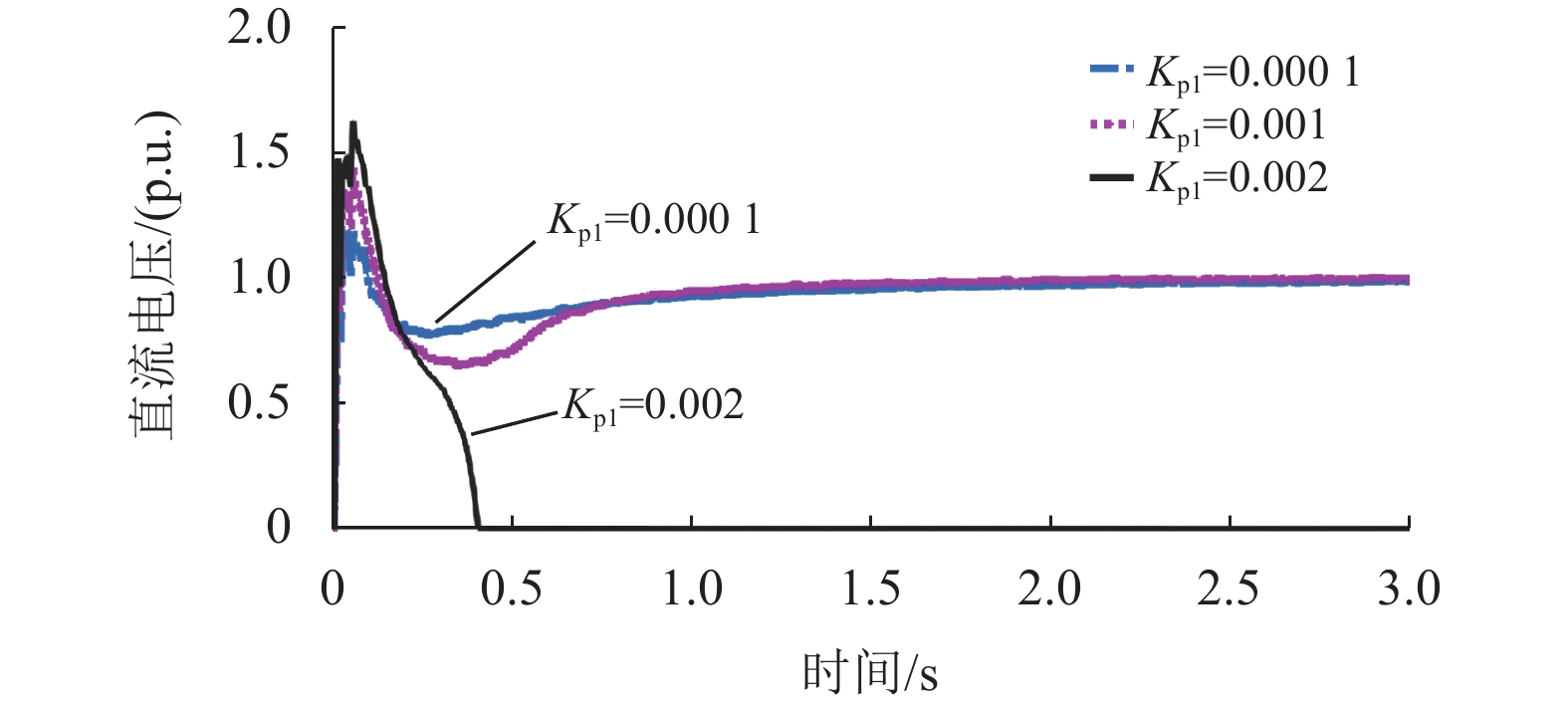
|
图 4 直流母线电压随有功外环比例系数Kp1变化波形 Figure 4 Waveform of DC bus voltage variation with active outer loop scale factor Kp1 |
|
图 5 直流母线电压随有功外环积分系数Ki1变化波形 Figure 5 Waveform of DC bus voltage variation with active outer loop integration factor Ki1 |
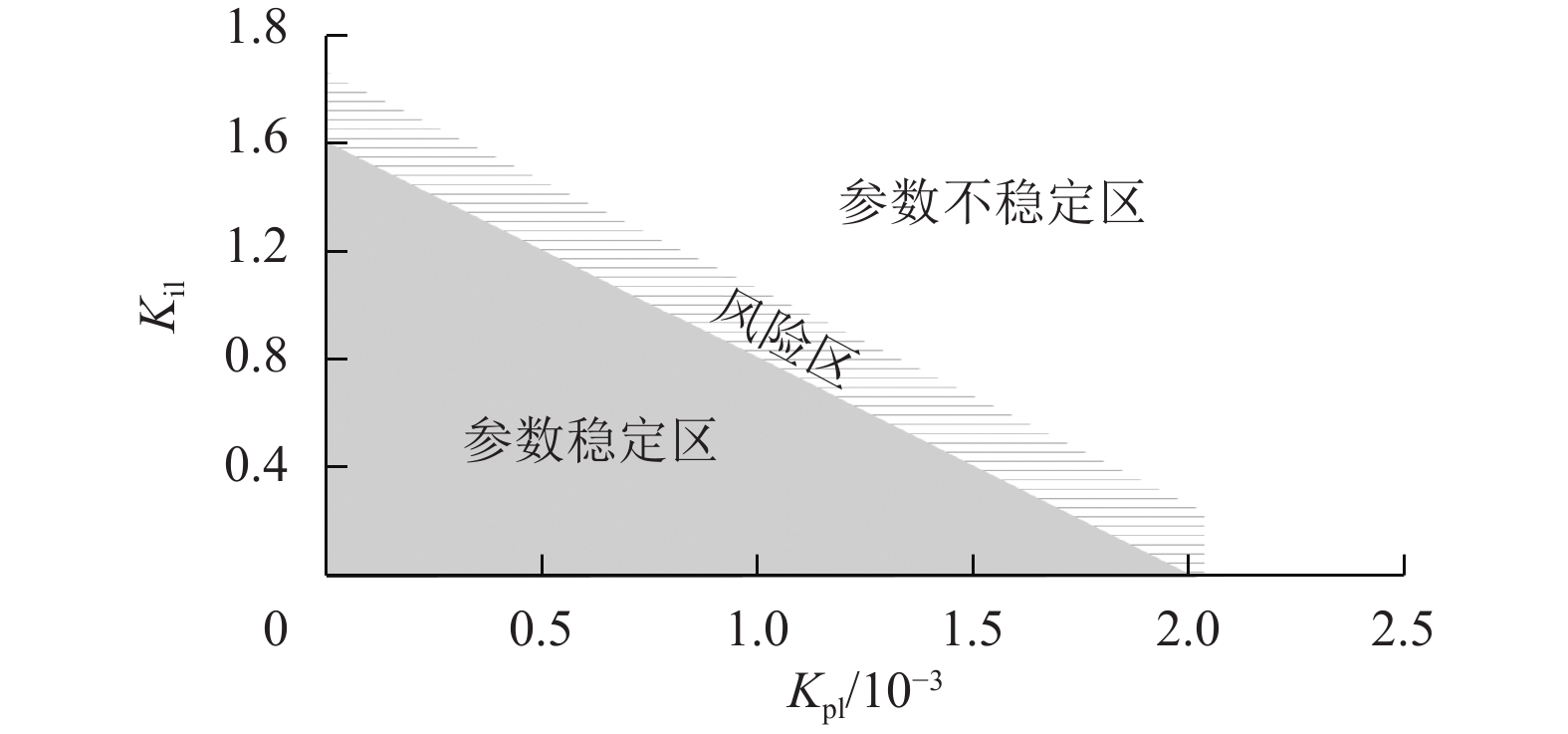
按照一定的步长,以Kp1为横轴,Ki1为纵轴观察其直流电压母线波形是否稳定,当两者同时改变时,在Matlab上作出大致的参数稳定区与不稳定区如图6所示。在直线的右上平面为参数不稳定区,直线的左下平面为参数稳定区,介于两者之间存在着参数风险区。
|
图 6 有功功率控制外环参数稳定区与不稳定区 Figure 6 Stable and unstable regions of active power control outer loop parameters |
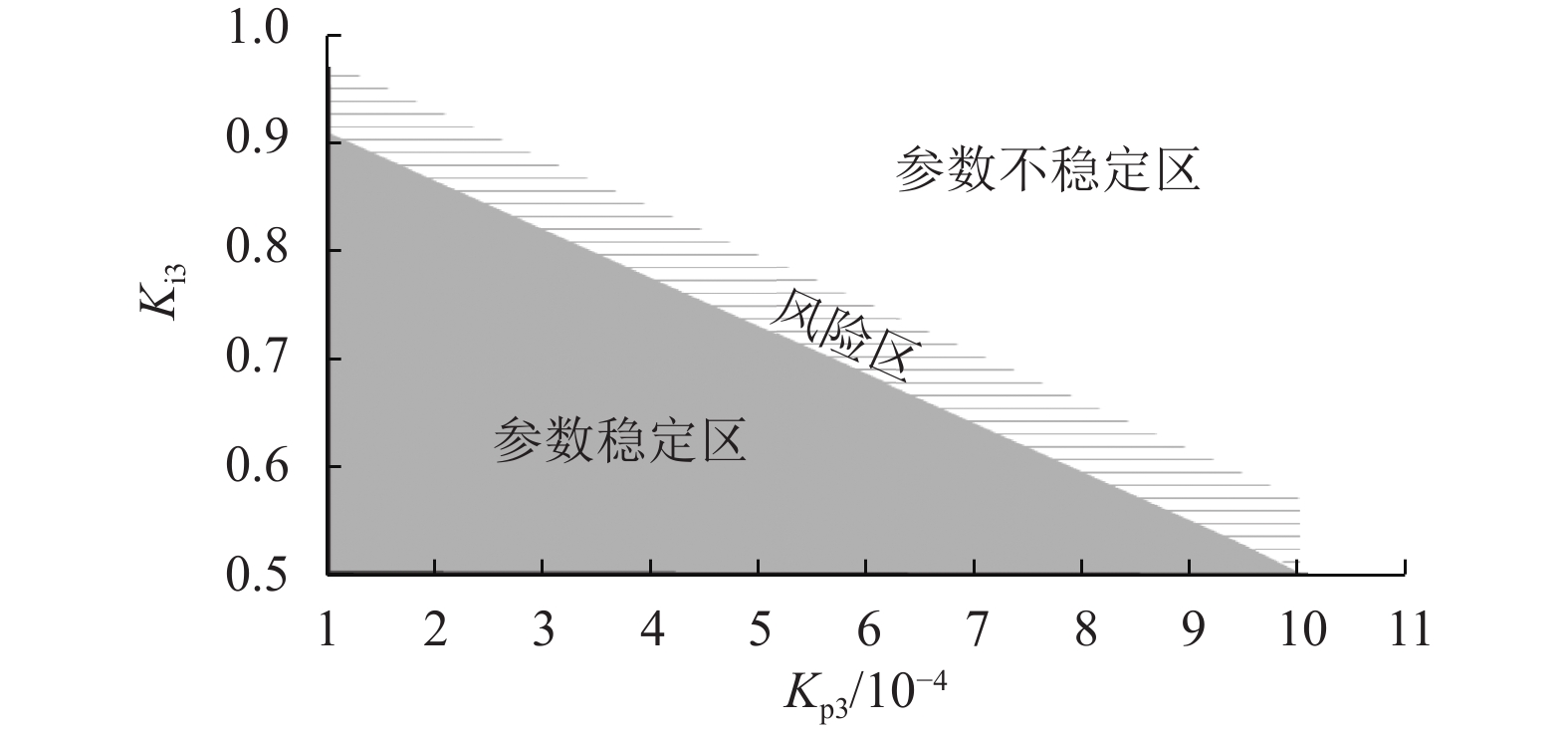
使用同样的方法对无功功率控制外环进行探究。无功功率控制外环参数稳定区如图7所示。在直线的右上平面为参数不稳定区,直线的左下平面为参数稳定区,介于两者之间存在着参数风险区。
|
图 7 无功功率控制外环参数稳定区与不稳定区 Figure 7 Stable and unstable regions of reactive power control outer loop parameters |
现对直流电压控制外环的PI控制器进行调参研究。采用上述相同的研究方法,采用控制变量法多次改变其积分系数Ki5,研究其稳定区与不稳定区,再探究两个参数的变化趋势。
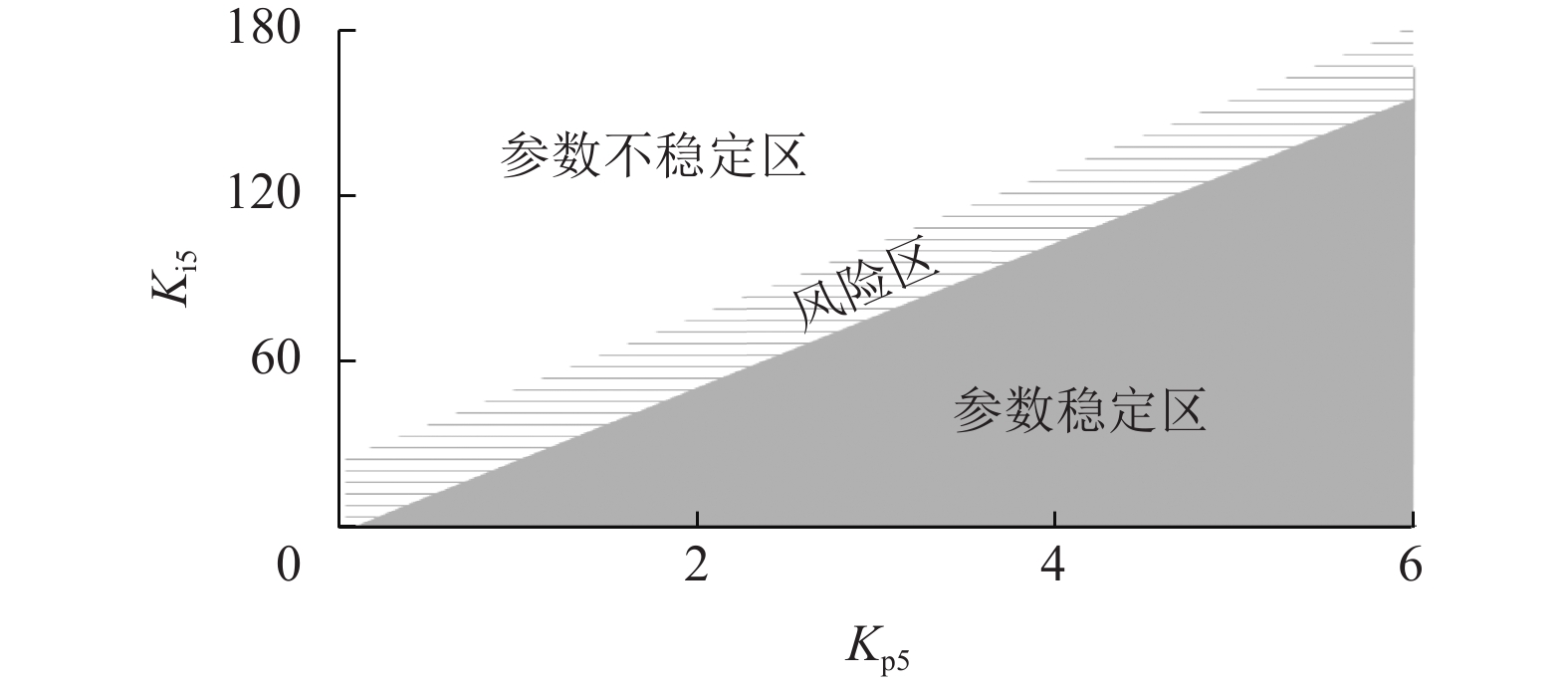
当Ki5为0.1时,电压控制外环的比例系数Kp5的稳定范围为0.1到6,当Kp5为6时,积分系数Ki5的稳定范围为0.1到170。在Matlab上以Kp5为横轴,Ki5为纵轴,作出直流电压控制外环的参数稳定区与不稳定区变化趋势如图8所示。可以发现在直线的左上平面为参数不稳定区,直线的右下平面为参数稳定区,介于两者之间存在着参数风险区,即网侧变流器控制参数稳定区呈正相关。
|
图 8 直流电压控制外环参数稳定区与不稳定区 Figure 8 Stable and unstable regions of DC voltage control outer loop parameters |
当并网系统稳定运行后,模拟不同的运行工况对系统稳定性进行分析。工况1:风速保持额定风速11.5 m/s;工况2:风速突降至8 m/s;工况3:风速突升至12.6 m/s。控制环节参数如表1所示。
| 表 1 控制环节初始参数 Table 1 Control link initial parameters |
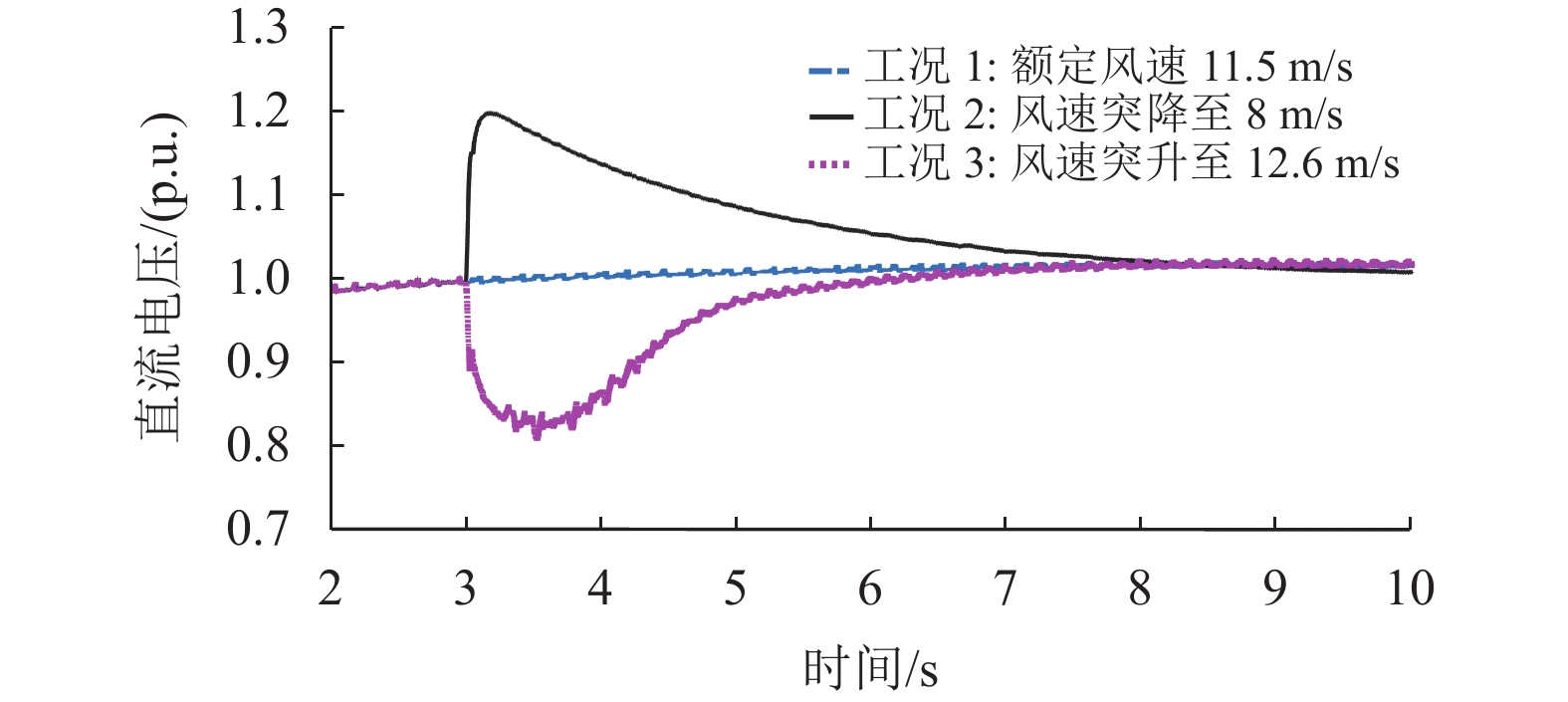
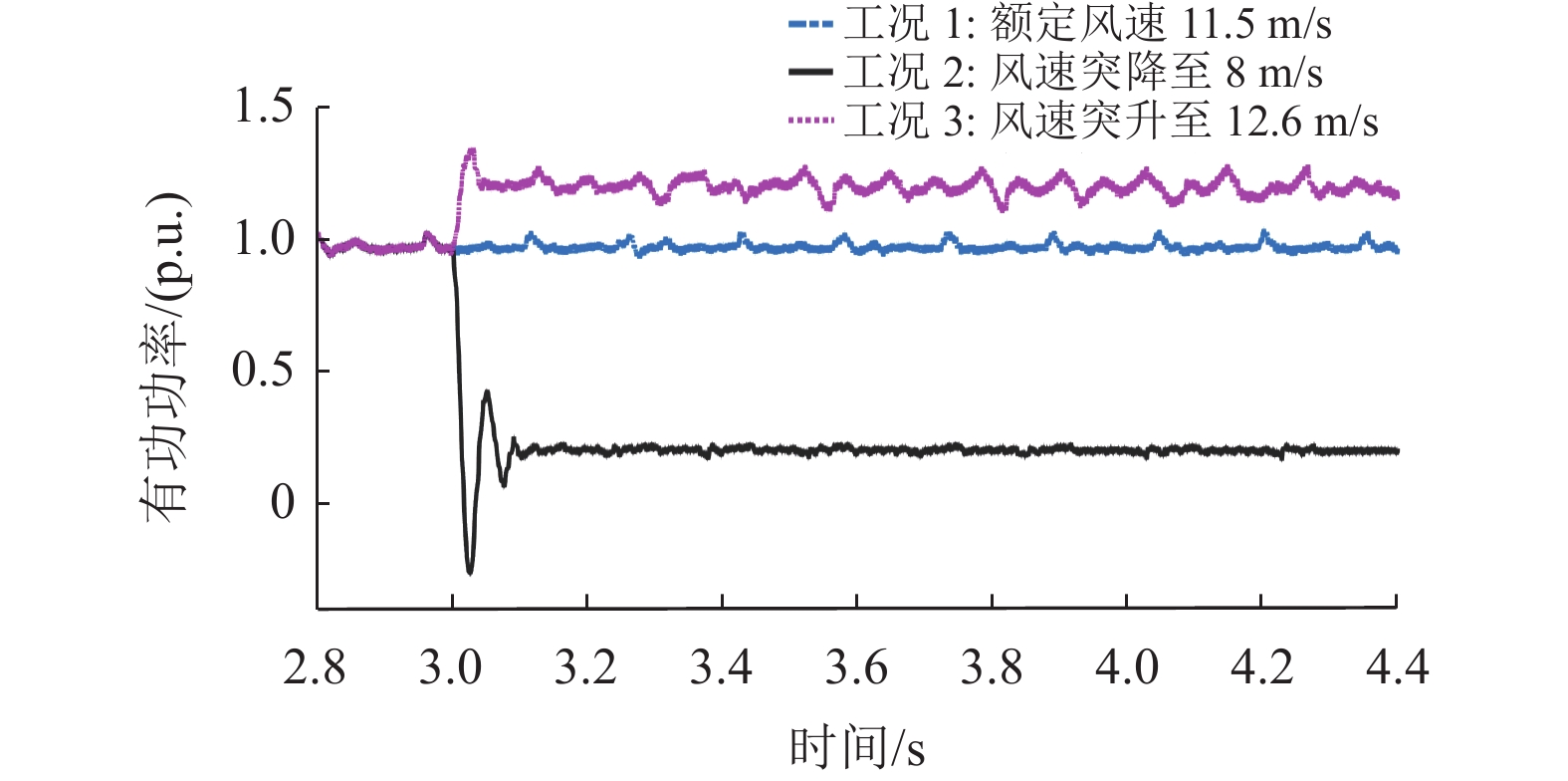
图9以及图10清晰地展示了在不同工况下,系统直流母线电压和有功功率的变化情况。在工况2中,直流母线电压在0.1 s内升至1.2 p.u.,大约5 s后才缓慢恢复到原来直流母线额定工作的预设电压;通过比较有功功率发现:当风速突降至8 m/s,有功功率会出现1.5个周期的振荡,在0.1 s后稳定在0.2 p.u.附近运行。通过观察工况3:风速突升至12.6 m/s波形,直流母线电压在0.8 s后降低到最小值,约为0.8 p.u.,约经历2.5 s后恢复至预设电压值附近运行,较工况2恢复时间较快;通过比较有功功率波形,工况3在受到干扰的0.1 s内出现振荡峰值,最大值升至1.4 p.u.,在0.1 s后逐渐恢复到1.2 p.u.处运行。无论是工况2还是工况3,在受到小干扰后都会经历较大的振荡并且需要较长的恢复时间。
|
图 9 初始参数不同工况下直流母线电压波形 Figure 9 DC bus voltage waveforms under different working conditions of initial parameters |
|
图 10 初始参数不同工况下有功功率波形 Figure 10 Active power waveforms under different operating conditions with initial parameters |
如果系统中的扰动模式与固有模式相似,或者开环与闭环状态下的多个固有模式相互趋近,它们之间将会产生强烈的动态相互作用,这种相互作用会导致系统发生谐振。这种谐振现象定义为广义模式谐振。为了深入探究双馈异步风机控制系统中各PI控制器的交互作用,现对网侧变流器的控制参数进行调整,寻找PI控制器之间的强交互作用,并逐渐往风险区范围进行参数调整,探究双馈异步风机并网系统内部谐振的产生机理。调整后控制参数如表2所示。
| 表 2 控制环节调整后参数 Table 2 Control link adjusted parameters |
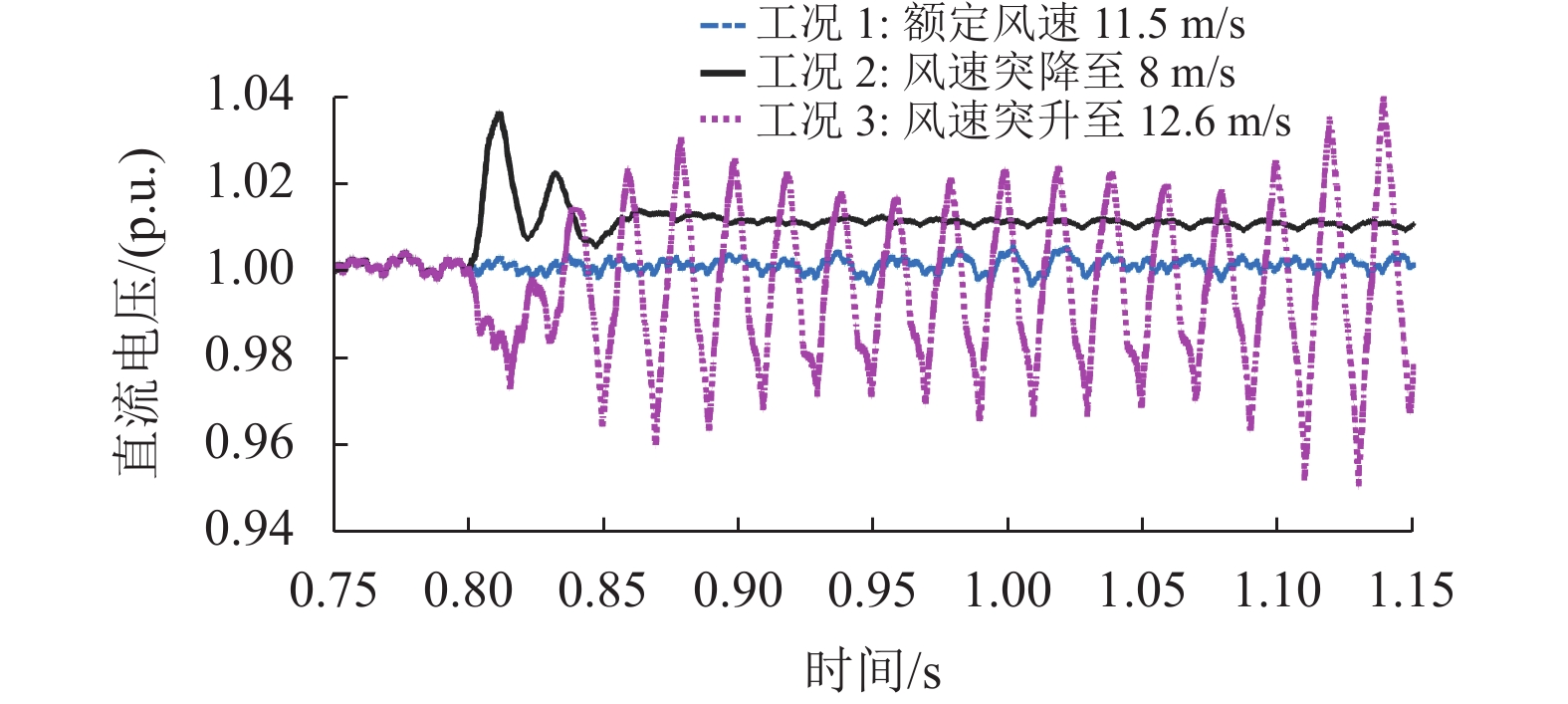
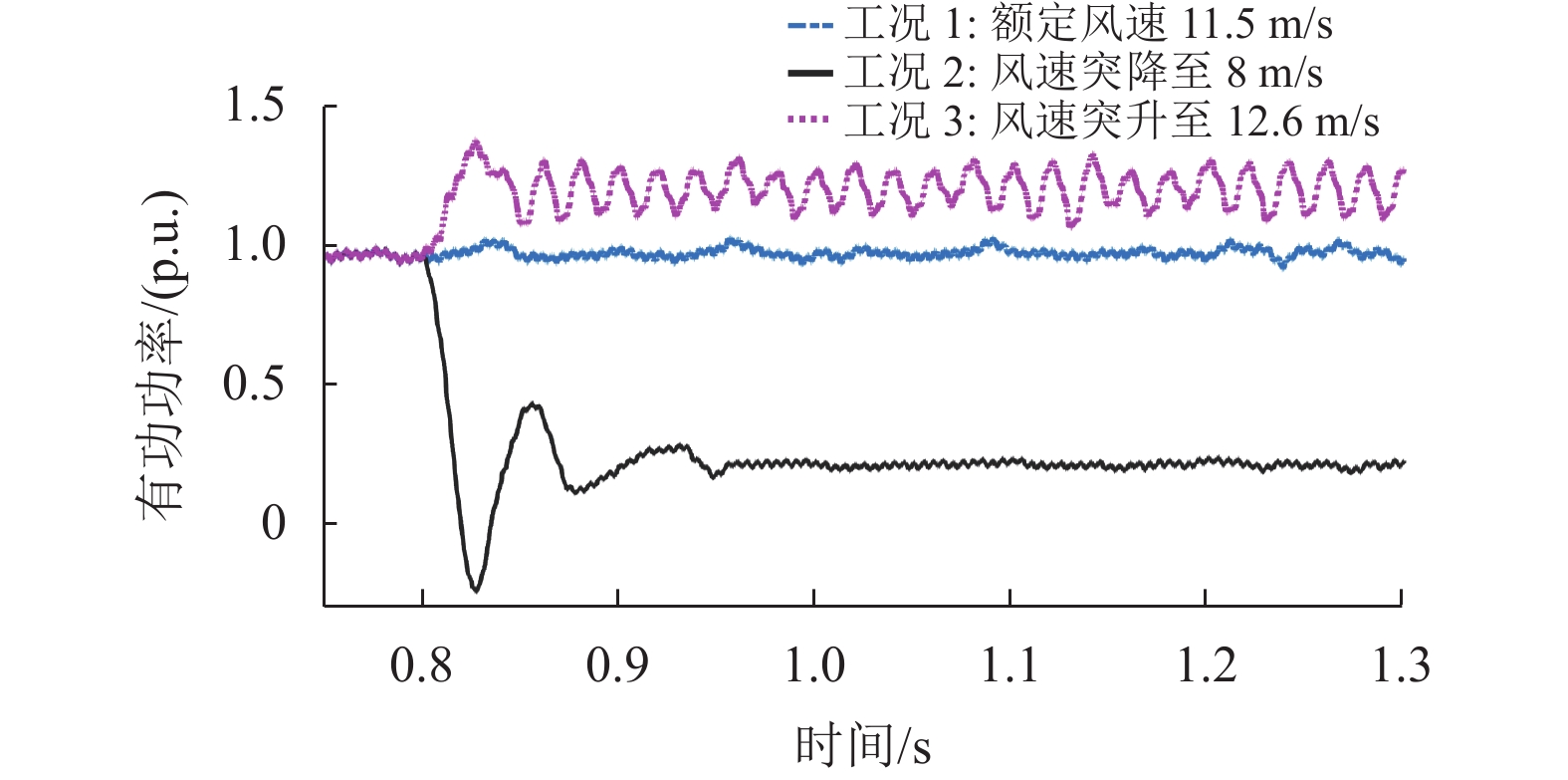
同样在3种设定的模拟工况下进行仿真验证,在3种不同工况下的时域仿真波形如图11与图12所示。
|
图 11 调整参数后不同工况下直流母线电压波形 Figure 11 DC bus voltage waveforms under different working conditions after adjusting parameters |
|
图 12 调整参数后不同工况下有功功率波形 Figure 12 Active power waveforms under different working conditions after adjusting parameters |
通过对比分析调整参数前后的直流母线电压波形和有功功率波形可以得到:调整网侧变流器控制参数后,在工况1的运行状态下,直流母线能够更快、更准确地进入到预设的直流工作电压;在工况2的运行状态下,调整参数后的波动幅度从1.2 p.u.降低到了1.04 p.u.,重新进入稳定运行的时间也大大缩短,有功功率波形经过大约2个周期的振荡就稳定在0.2 p.u.附近运行。但在工况3的运行状态下,调整参数后出现了谐振现象,谐振的幅度呈现逐渐放大的趋势,对系统的长时间运行会产生不利的影响,当超越一定的振幅,系统可能失去稳定性。有功功率谐振频率与直流母线电压的谐振频率也十分接近。
当直流母线控制外环的比例系数Kp5、积分系数Ki5以及电流内环PI控制器的比例系数Kp6、Kp7和积分系数Ki6、Ki7同时增大时,对于各控制器本身都是增强系统的阻尼,目的都是增强系统的稳定性,但是由于多个控制器之间的强交互作用,它们之间在某个运行状态下产生了相互排斥的作用,各控制器的阻尼效果叠加后产生了负作用,导致系统产生了内部谐振的现象,导致系统失去稳定。
4.2 内部谐振抑制策略网侧变流器直流电压控制外环采用表3所示参数设计A、B的控制参数,工况3的运行状态对系统的稳定性带来巨大挑战,为了验证参数设计A、B对于抑制内部谐振的有效性,在工况3的运行状态下对该参数设计进行验证。
| 表 3 直流电压控制外环参数设计 Table 3 Parameterization of DC voltage control outer loop |
图13表示调整直流电压控制外环参数前后的直流母线电压波形,在工况3下比较调参前后的直流母线电压波形。当直流电压控制外环的比例系数与积分系数都在原有基础上进行一定幅度的减小,直流母线电压在0.8 s处受到风速突升至12.6 m/s时,在经历3个周期的振荡后便稳定下来,可以达到抑制内部谐振现象作用。
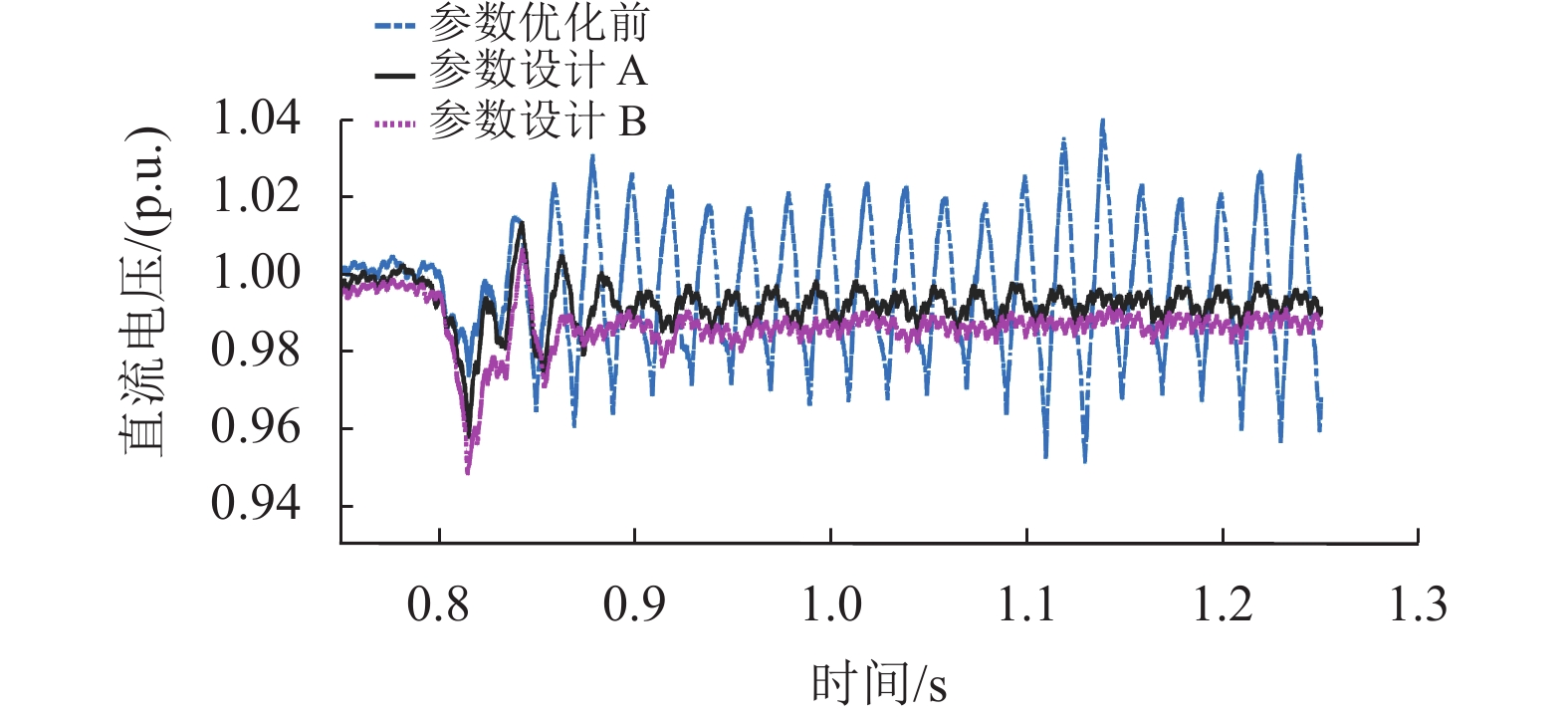
|
图 13 参数调整前、参数设计A和B的直流电压波形图 Figure 13 DC voltage waveforms before parameter adjustment, parameter designs A and B |
网侧变流器电流控制内环参数设计如表4所示,并在工况3的运行状态下对该参数进行验证。
| 表 4 网侧电流控制内环参数设计 Table 4 Current control inner loop parameterization |
如图14所示,参数设计C下,调整参数后的电压波形较调整前在前半个周期的电压降幅更大,往后的0.1 s内,经历了4个周期衰减振荡后便稳定在0.998 p.u.附近运行。参数设计D下,前3个周期与发生内部谐振现象十分相似,在之后的3到4个周期中,出现振幅逐渐变小的收敛性振荡,最后经历了0.27 s的振荡后恢复到稳定运行状态。
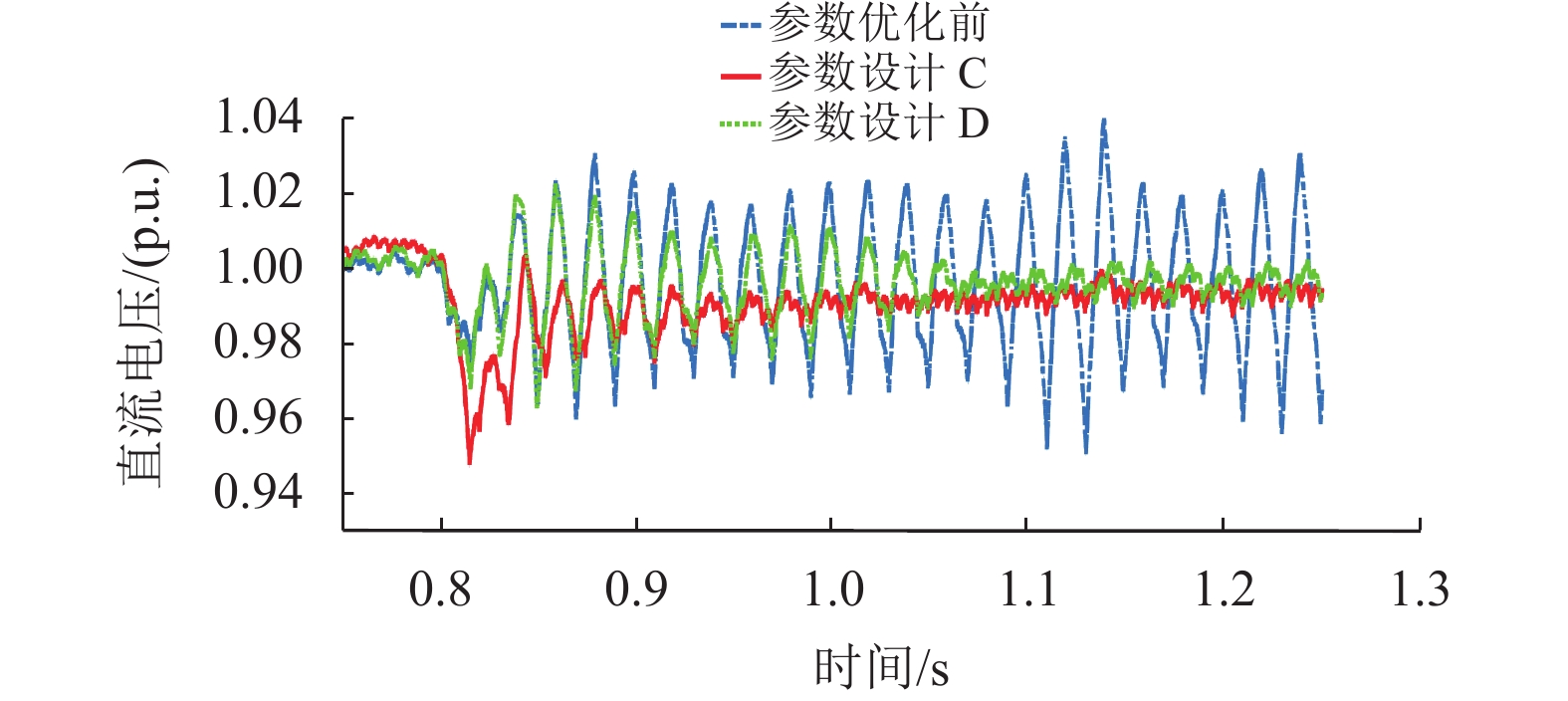
|
图 14 参数调整前、参数设计C和D的直流电压波形图 Figure 14 DC voltage waveforms before parameter adjustment, parameter designs C and D |
通过适度降低网侧变流器的控制外环或控制内环的参数,降低它们之间的强烈交互作用,都能达到抑制内部谐振的效果。现探究同时改变网侧变流器控制外环以及控制内环的控制参数对系统运行稳定性的影响。通过排列组合的方式,表5展示了参数设计A+C、参数设计A+D、参数设计B+C、参数设计B+D的控制参数。采用上述4种控制参数,再次模拟工况3风速突升至12.6 m/s的运行状态,验证抑制内部谐振的有效性。
| 表 5 综合参数设计 Table 5 Integrated parameter design |
图15表示调整参数前与参数设计A+C、A+D的直流电压波形,通过比较分析可以得到:在综合电压外环以及电流内环的参数调整后都能达到抑制内部谐振的效果。参数设计A+C情况下,电压幅值差最大为0.04 p.u.,参数设计A+D情况下为0.06 p.u.,当引入电流控制内环的参数调整后,其电压幅值差与参数设计A的十分接近,参数设计A+D的曲线在前2个周期的降幅较大,但其两个周期之后的振幅明显小于参数设计A+C,且其到达稳定运行的时间较快,从风速突升到稳定仅需要0.1 s。
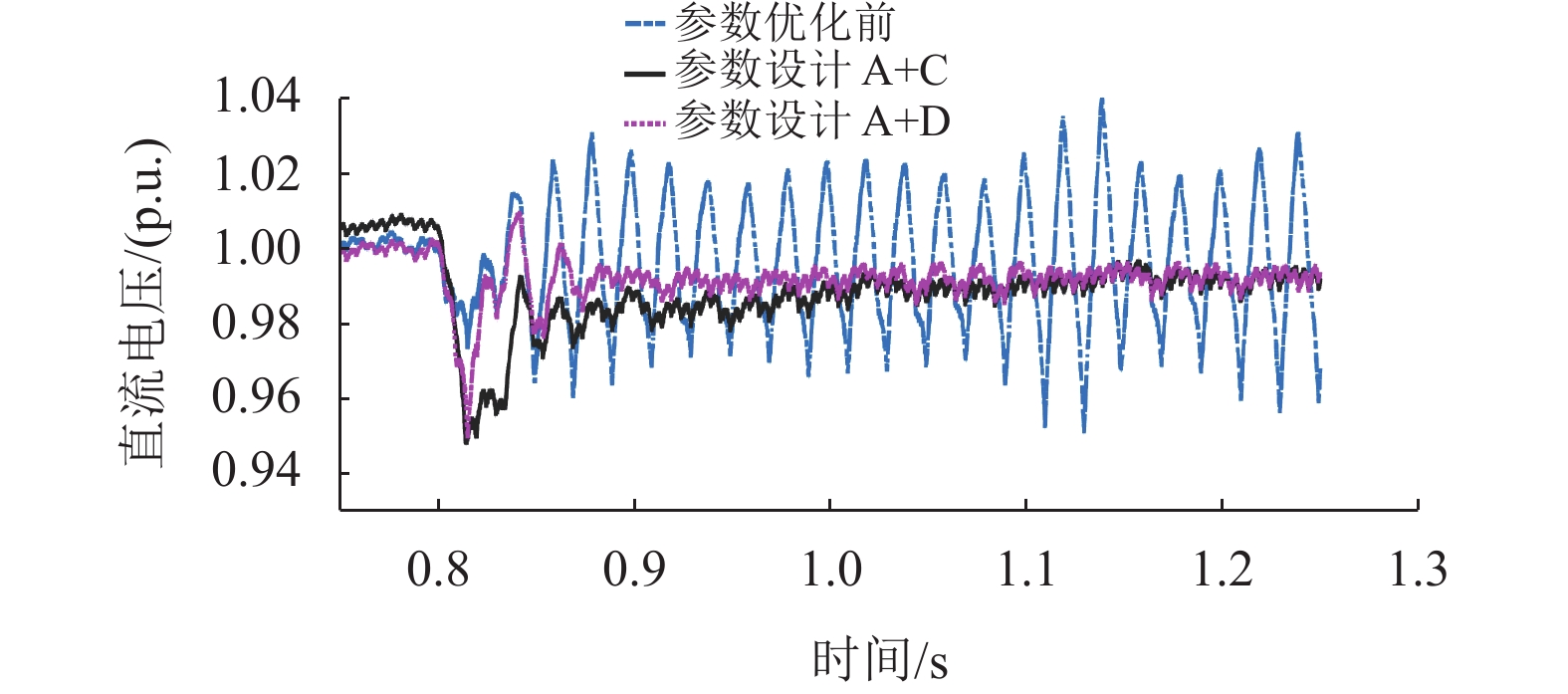
|
图 15 参数设计A+C和A+D前后直流母线电压波形 Figure 15 DC bus voltage waveforms before and after parameter designs A+C and A+D |
为了获得更好的控制效果以及动态性能,将粒子群优化算法(Particle Swarm Optimization, PSO) 与双馈异步风机网侧变换器的控制系统相结合,利用PSO算法对参数进行优化。经优化后的控制参数如表6所示。
| 表 6 PSO优化后控制参数 Table 6 Optimized control parameters |
通过观察图16,可以发现经PSO优化控制参数后同样能够达到抑制内部谐振作用。通过比较参数设计B+D,PSO优化后的超调量明显变小了,可以观察到在前半个周期的振荡现象消失了,并且其振荡幅值减小了0.02 p.u.,减幅达到40%。仔细对比稳定后的直流电压幅值可以得出,从原先稳定值再0.99 p.u.附近优化到了1.00 p.u.附近,这说明了经PSO优化后恢复速度更快,振荡幅度更小,稳态值更精确。
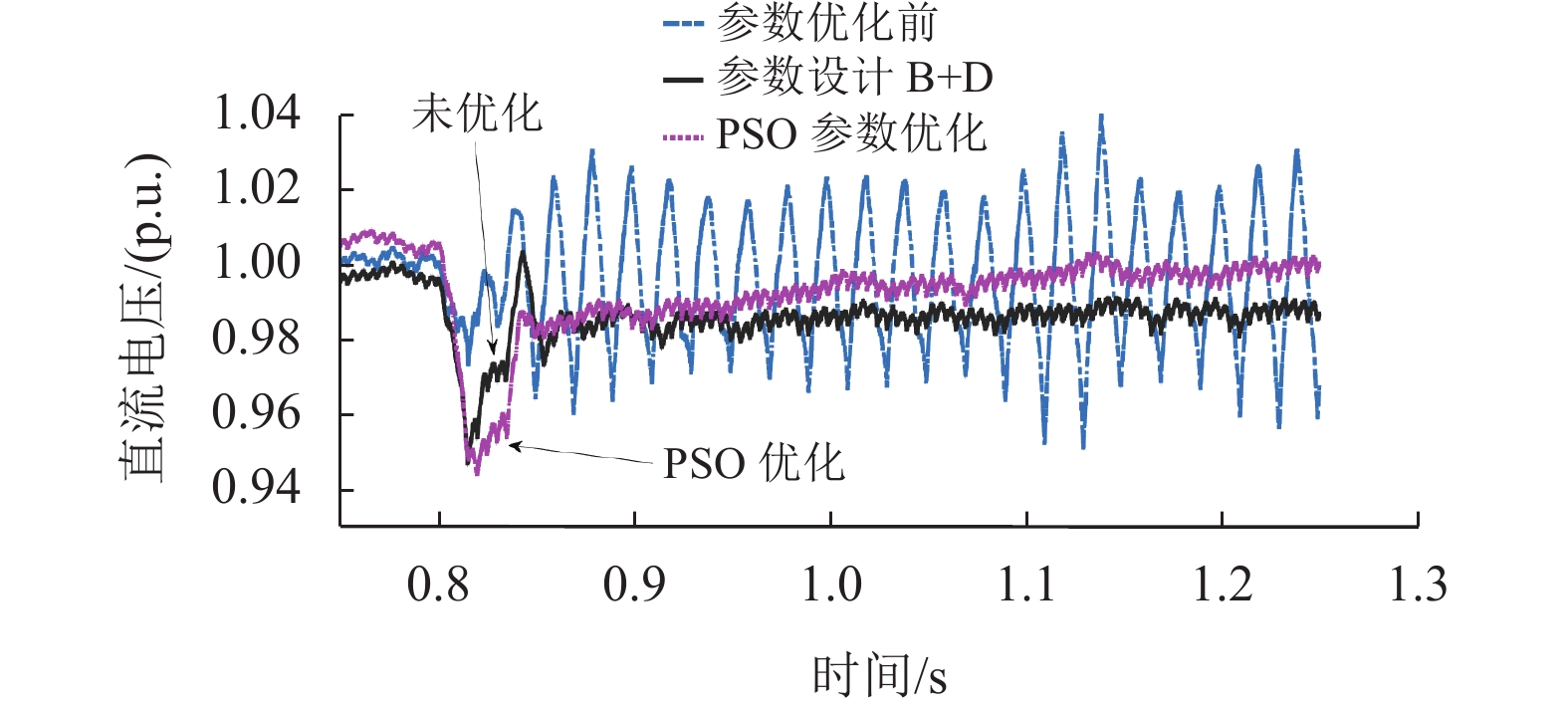
|
图 16 工况3下参数设计B+D与PSO优化直流电压波形 Figure 16 Parametric designs B+D and PSO optimized waveforms of DC voltage under operating condition 3 |
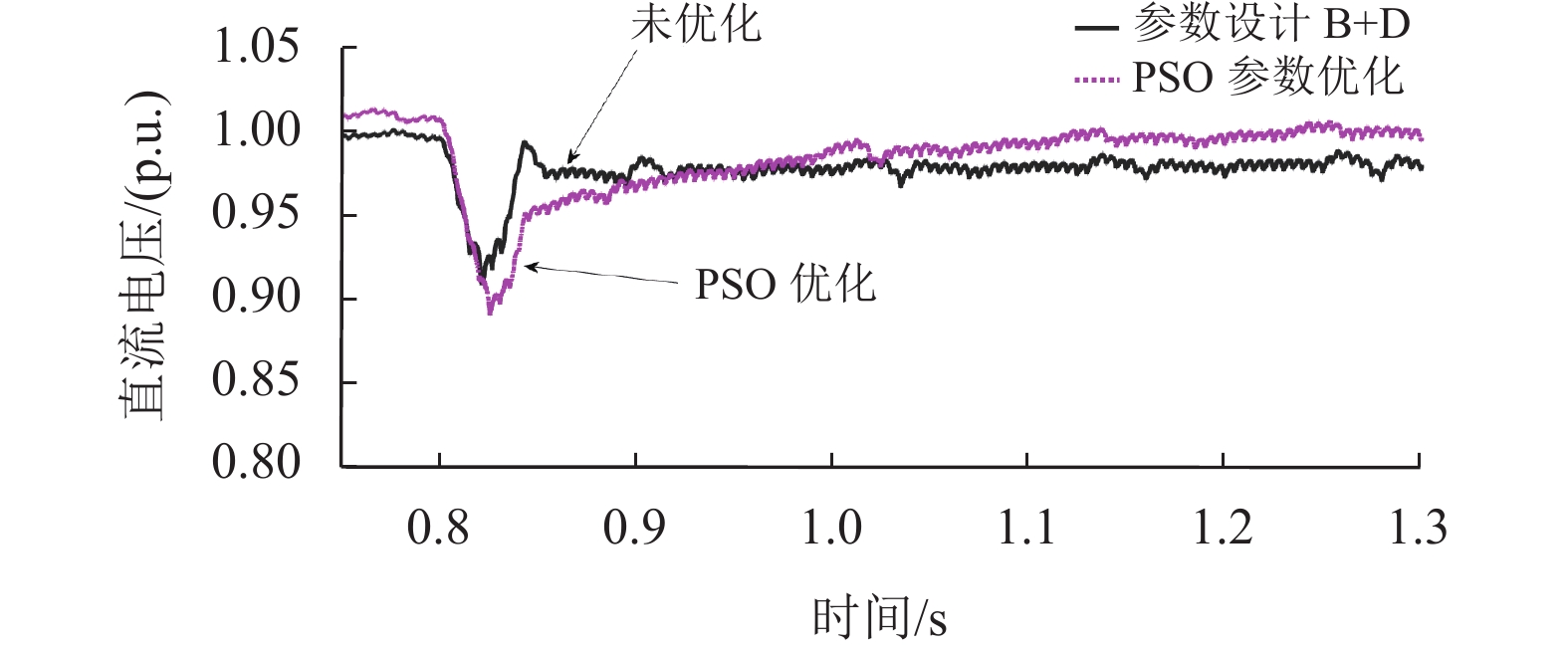
为了深入分析PSO优化控制参数在恶劣运行条件下的表现,设计了工况4的模拟实验。该工况模拟了风速急剧上升至13.1 m/s的情景,以反映自然界中可能遭遇的突发性强烈风事件。在这种恶劣工况下,对PSO优化控制参数进行测试,验证其在面对极端风速变化时的稳定性。
通过图17可以观察到未优化时最大电压振幅为0.09 p.u.,PSO优化后的最大振幅为0.06 p.u.,性能提升约为33%,优化后的稳定时间较未优化略长0.1 s,但是带来了更加准确的稳定值,优化后基本稳定在1.0 p.u.运行,未优化则是在0.99 p.u.附近运行。综上所述,经过PSO优化控制参数能够降低电压振幅,减少振荡周期,减小超调量,提供更稳定准确的响应能力。
|
图 17 工况4下PSO优化前后直流电压波形 Figure 17 DC voltage waveforms before and after PSO optimization under operating condition 4 |
探究了双馈异步风机机侧变流器和网侧变流器控制外环的比例系数和积分系数对并网系统的影响。以比例系数为横轴,积分系数为纵轴,有功控制外环跟无功控制外环呈现的稳定区域为负相关,电压控制外环呈现的稳定区域为正相关。研究发现:当网侧变流器控制外环与控制内环参数都增大到一定程度时,它们之间会产生强烈的交互作用,导致系统产生内部谐振的现象。采用PSO算法对网侧变流器的PI控制器参数进行优化,经优化后不仅能够抑制内部谐振现象,且直流电压恢复时间更短,超调量更小。
深入分析控制内环各个控制器带来的控制效果以及参数稳定区域变化同样具有研究价值。对于机侧变流器控制器以及机侧与网侧控制器之间是否会出现内部谐振现象同样值得深入研究。
| [1] |
谢小荣, 贺静波, 毛航银, 等. “双高”电力系统稳定性的新问题及分类探讨[J].
中国电机工程学报, 2021, 41(2): 461-474.
XIE X R, HE J B, MAO H Y, et al. New issues and classification of power system stability with high shares of renewables and power electronics[J]. Proceedings of the CSEE, 2021, 41(2): 461-474. |
| [2] |
高本锋, 刘晋, 李忍, 等. 风电机组的次同步控制相互作用研究综述[J].
电工技术学报, 2015, 30(16): 154-161.
GAO B F, LIU J, LI R, et al. Studies of sub-synchronous control interaction in wind turbine generators[J]. Transactions of China Electrotechnical Society, 2015, 30(16): 154-161. DOI: 10.3969/j.issn.1000-6753.2015.16.020. |
| [3] |
王伟胜, 张冲, 何国庆, 等. 大规模风电场并网系统次同步振荡研究综述[J].
电网技术, 2017, 41(4): 1050-1060.
WANG W S, ZHANG C, HE G Q, et al. Overview of research on subsynchronous oscillations in large-scale wind farm integrated system[J]. Power System Technology, 2017, 41(4): 1050-1060. |
| [4] |
陈晨, 杜文娟, 王海风. 风电场接入引发电力系统次同步振荡机理综述[J].
南方电网技术, 2018, 12(1): 84-93.
CHEN C, DU W J, WANG H F. Review on mechanism of sub-synchronous oscillations caused by grid-connected wind farms in power systems[J]. Southern Power System Technology, 2018, 12(1): 84-93. |
| [5] |
VARMA R K, MOHARANA A. SSR in Double-cage induction generator-based wind farm connected to series-compensated transmission line[J].
IEEE Transactions on Power Systems, 2013, 28(3): 2573-2583.
DOI: 10.1109/TPWRS.2013.2246841. |
| [6] |
王亮, 谢小荣, 姜齐荣, 等. 大规模双馈风电场次同步谐振的分析与抑制[J].
电力系统自动化, 2014, 38(22): 26-31.
WANG L, XIE X R, JIANG Q R, et al. Analysis and mitigation of SSR problems in large-scale wind farms with doubly-fed wind turbines[J]. Automation of Electric Power Systems, 2014, 38(22): 26-31. DOI: 10.7500/AEPS20131010016. |
| [7] |
吕敬, 蔡旭, 张占奎, 等. 海上风电场经MMC-HVDC并网的阻抗建模及稳定性分析[J].
中国电机工程学报, 2016, 36(14): 3771-3780.
LYU J, CAI X, ZHANG Z K, et al. Impedance modeling and stability analysis of MMC-based HVDC for offshore wind farms[J]. Proceedings of the CSEE, 2016, 36(14): 3771-3780. |
| [8] |
栗然, 卢云, 刘会兰, 等. 双馈风电场经串补并网引起次同步振荡机理分析[J].
电网技术, 2013, 37(11): 3073-3079.
LI R, LU Y, LIU H L, et al. Mechanism analysis on subsynchronous oscillation caused by grid-integration of doubly fed wind power generation system via series compensation[J]. Power System Technology, 2013, 37(11): 3073-3079. |
| [9] |
WANG L, XIE X, JIANG Q, et al. Investigation of SSR in practical DFIG-based wind farms connected to a series-compensated power system[J].
IEEE Transactions on Power Systems, 2015, 30(5): 2772-2779.
DOI: 10.1109/TPWRS.2014.2365197. |
| [10] |
胡应宏, 邓春, 谢小荣, 等. 双馈风机−串补输电系统次同步谐振的附加阻尼控制[J].
电网技术, 2016, 40(4): 1169-1173.
HU Y H, DENG C, XIE X R, et al. Additional damping control of DFIG series compensated transmission system under sub-synchronous resonance[J]. Power System Technology, 2016, 40(4): 1169-1173. |
| [11] |
OSTADI A, YAZDANI A, VARMA R K. Modeling and stability analysis of a DFIG-based wind-power generator interfaced with a series-compensated line[J].
IEEE Transactions on Power Delivery, 2009, 24(3): 1504-1514.
DOI: 10.1109/TPWRD.2009.2013667. |
| [12] |
IRWIN G D, JINDAL A K, ISAACS A L. Sub-synchronous control interactions between type 3 wind turbines and series compensated AC transmission systems[C]//2011 IEEE Power and Energy Society General Meeting. Detroit, MI: IEEE, 2011: 1-6.
|
| [13] |
DU W, CHEN C, WANG H. Subsynchronous interactions induced by DFIGs in power systems without series compensated lines[J].
IEEE Transactions on Sustainable Energy, 2018, 9(3): 1275-1284.
DOI: 10.1109/TSTE.2017.2781289. |
| [14] |
DU W, FU Q, WANG H, et al. Concept of modal repulsion for examining the subsynchronous oscillations caused by wind farms in power systems[J].
IEEE Transactions on Power Systems, 2019, 34(1): 518-526.
DOI: 10.1109/TPWRS.2018.2862883. |
| [15] |
熊浩清, 何鹏飞, 孙冉, 等. 双馈风电场无串补并网振荡场景及关键影响因素研究[J].
高电压技术, 2024, 50(2): 660-672.
XIONG H Q, HE P F, SUN R, et al. Oscillation scenarios of grid integrated wind farm with DFIGs without series compensation and effects of key factors[J]. High Voltage Engineering, 2024, 50(2): 660-672. |
| [16] |
LUO J, TONG N, BU S, et al. Internal modal resonance analysis for full converter-based wind generation using analytical inertia model[J].
IEEE Transactions on Power Systems, 2024, 39(2): 3509-3522.
DOI: 10.1109/TPWRS.2023.3287914. |
| [17] |
LUO J, BU S, ZHU J, et al. Modal shift evaluation and optimization for resonance mechanism investigation and mitigation of power systems integrated with FCWG[J].
IEEE Transactions on Power Systems, 2020, 35(5): 4046-4055.
DOI: 10.1109/TPWRS.2020.2975631. |
| [18] |
LUO J, TENG F, BU S, et al. Converter-driven stability constrained unit commitment considering dynamic interactions of wind generation[J].
International Journal of Electrical Power & Energy Systems, 2023, 144: 108614.
|
| [19] |
LUO J, BU S, TENG F. An optimal modal coordination strategy based on modal superposition theory to mitigate low frequency oscillation in FCWG penetrated power systems[J].
International Journal of Electrical Power & Energy Systems, 2020, 120: 105975.
|
| [20] |
LUO J, BU S, ZHU J. A novel PMU-based adaptive coordination strategy to mitigate modal resonance between full converter-based wind generation and grids[J].
IEEE Journal of Emerging and Selected Topics in Power Electronics, 2021, 9(6): 7173-7182.
DOI: 10.1109/JESTPE.2020.3024759. |
| [21] |
LUO J, BU S, CHUNG C Y. Design and comparison of auxiliary resonance controllers for mitigating modal resonance of power systems integrated with wind generation[J].
IEEE Transactions on Power Systems, 2021, 36(4): 3372-3383.
DOI: 10.1109/TPWRS.2021.3051252. |
 2024, Vol. 41
2024, Vol. 41

