综合能源系统(Integrated Energy System, IES)[1]耦合了电、热、气等不同能源形式的子系统,可实现不同能源系统之间的协调规划、优化运行,提高能源利用效率,是实现“双碳”目标的有效途径。多能流(Multi-energy Flow, MEF)计算是实现综合能源系统稳态分析与优化调度的基础[2],是当前研究的热点。
国内外学者针对电−热−气综合能源系统多能流计算模型的建立[3-6]和求解[7-9]已有大量研究成果发表。文献[3]建立了电−热−气综合能源系统的直接求解模型,将各子系统的多能流计算模型合并求解,但在计算雅克比矩阵过程中需对耦合单元的数学模型进行求导,计算复杂且效率低;文献[4]对各子系统的能量流进行解耦,根据各子系统的特点分别采用全纯嵌入法、图论法和牛拉法求解电、热、气子系统能流,建立了电−热−气互联系统的顺序求解模型,提升了计算效率;文献[5]深入分析电−热−气互联系统的直接求解模型和基于牛拉法形成的雅克比矩阵,对直接求解模型进行解耦和近似,并通过变换得到常数雅克比矩阵,有效缩短计算时间。然而,文献[3-5]仅针对工作在定压缩比模式下的压缩机进行建模,而在实际工况下压缩机存在多种工作模式,不同工作模式会对多能流结果产生不同的影响。文献[6]将通过压缩机的流量等效为天然气节点负荷,建立了压缩机多种工作模式下的等效负荷模型,但该方法需将压缩机管道以及不含压缩机的网络分开建模,使得多能流计算模型过于复杂且无法建立统一的多能流表征矩阵。因此,如何在考虑压缩机不同工作模式下建立统一的多能流计算模型有待进一步研究。
针对模型求解,文献[7]在直接求解模型的基础上,提出基于梯度下降的迭代算法,相较于非梯度下降算法有更高的计算效率;文献[8]探讨了基于牛拉法的多能流计算方法,通过迭代过程中自适应调节步长因子来解决初值敏感性问题;文献[9]针对天然气系统压力初值选取困难的问题,提出利用粒子群算法对压力初值进行优选,改善了计算效率和收敛性。上述文献[7-9]均从确定性多能流计算角度展开研究,但忽略了不确定性因素对能流分布的影响。
随着大规模可再生能源的接入以及需求侧能源设备的多样化[10],综合能源系统中不确定性因素对能流分布的影响日益显著,传统的确定性多能流计算难以满足工程实践需求。为克服这一问题,从概率多能流(Probabilistic Multi-energy Flow, PMEF)的角度对综合能源系统进行分析备受工程技术人员与学者关注。文献[11]将电力系统概率潮流计算推广至电−气互联系统,采用蒙特卡洛模拟法计算概率多能流,精度高但计算速度慢;文献[12]基于多元线性化蒙特卡洛模拟法求解电−气互联系统的概率多能流,相较于传统蒙特卡洛模拟法具有更高的计算效率;文献[13]结合半不变量法和最大熵原理,实现对电−气互联系统概率多能流的高效计算,并解决了GC级数拟合中概率密度为负的问题;文献[14]基于拉丁超立方采样求解冷−热−电−气互联系统的概率多能流,并分析了平衡节点对能流分布的影响。上述文献[11-14]均基于物理模型计算概率多能流,计算过程存在收敛性差和计算效率低的问题。
数据驱动方法通过处理历史数据,建立输入到输出的映射关系,通过映射关系可直接由输入得到对应输出,无需迭代也无需依赖具体的物理模型,可有效解决收敛性差和计算效率低的问题,为多能流求解提供新的思路,在电力系统潮流计算和概率潮流计算中已得到广泛应用[15-16]。文献[15]基于支持矩阵回归,分析潮流计算中各变量的关系,构建节点有功无功注入与节点电压幅值和相角的非线性回归模型;文献[16]基于高斯过程回归,构建负荷及可再生能源出力与节点电压幅值和相角的非线性回归模型,并使用该回归模型计算概率潮流。由于电网、热网和气网模型具有相似之处[17-18],有学者将数据驱动方法应用于综合能源系统确定性多能流计算。文献[19]基于偏最小二乘回归构建电网和热网的线性化潮流回归模型,并分析了热网管道长度和训练规模对回归精度的影响,但对具有高阶非线性关系的供热系统节点温度的计算精度不高;文献[20]在文献[19]的基础上提出模型与数据混合驱动的建模方法,但系统建模比较复杂,计算效率不高。且电−热−气综合能源系统的耦合关系比电−热综合能源系统更复杂,因此需要进一步针对电−热−气综合能源系统研究有效的概率能流计算方法。
为此,本文针对考虑压缩机不同工作模式的电−热−气综合能源系统的统一稳态能量流建模与概率多能流有效计算问题展开研究,提出一种基于数据驱动的考虑压缩机多种工作模式的概率多能流计算方法。首先提出一种适用于压缩机不同工作模式的天然气系统稳态能量流模型;同时构建电力、供热系统稳态能量流模型,使用牛拉法进行重复顺序求解,构建数据样本集;其次,考虑到综合能源系统多能流计算模型为非线性方程组,且热网节点温度与管道流量间具有高阶非线性函数关系[21],将支持向量回归(Support Vector Regression, SVR)应用于电−热−气综合能源系统,构建电、热、气网络的多能流非线性回归模型,并将训练后的回归模型应用于概率多能流计算,提出基于数据驱动的概率多能流计算方法;最后,通过IES14-14-10节点电−热−气综合能源测试系统验证所提压缩机模型和数据驱动算法的正确性与有效性。
1 综合能源系统与随机变量建模电−热−气综合能源系统由电力系统、供热系统、天然气系统和耦合单元组成。系统中不同节点类型的已知量和待求量不同,节点分类如表1所示。
| 表 1 IES节点类型及变量 Table 1 Node type and variables of IES |
表1中P、Q、V、θ分别为电力系统节点有功功率、无功功率、电压幅值、相角;Ts、Tr、m、Φ分别为供热系统中节点供热温度、回热温度、管道流量和节点热功率,To为热负荷节点输出温度;f、p分别为天然气系统中节点注入天然气流量和压力。
1.1 电力系统潮流模型IES中采用交流潮流模型描述电力系统的潮流方程。节点功率平衡方程为
| $ \left\{ \begin{gathered} \Delta {P_i} = {P_i} - {V_i}\sum\limits_{j \in i} {{V_j}({G_{ij}}\cos {\theta _{ij}} + {B_{ij}}\sin {\theta _{ij}}) = 0} \\ \Delta {Q_i} = {Q_i} - {V_i}\sum\limits_{j \in i} {{V_j}({G_{ij}}\sin {\theta _{ij}} - {B_{ij}}\cos {\theta _{ij}}) = 0} \\ \end{gathered} \right. $ | (1) |
式中:
供热系统管道各个节点均满足水流量连续性方程[17]、节点功率平衡方程和温度混合方程;在环网闭合回路中,各管道压头损失之和为0。供热系统的能量流模型如式(2)所示。
| $ \left\{ \begin{gathered} \Delta {{\boldsymbol{\varPhi }}_{{\text{Load}}}} = {C_{\mathrm{p}}}{{\boldsymbol{A}}_{{\text{H,Load}}}}{\boldsymbol{m}}\left( {{{\boldsymbol{T}}'_{{\text{s,Load}}}} - {{\boldsymbol{T}}'_{\text{o}}}} \right) - {{\boldsymbol{\varPhi}} _{{\text{Load}}}} = 0 \\ \Delta {{\boldsymbol{\varPhi}} _{{\mathrm{Source}}}} = {C_{\text{p}}}{{\boldsymbol{A}}_{{\text{H,Source}}}}{\boldsymbol{m}}\left( {{{\boldsymbol{T}}'_{{\text{s,Source}}}} - {{\boldsymbol{T}}'_{{\text{r,Source}}}}} \right) - {{\boldsymbol{\varPhi}} _{{\mathrm{Source}}}} = 0 \\ \Delta {{\boldsymbol{h}}_{\text{f}}} = {{\boldsymbol{B}}_{\mathrm{H}}}{{\boldsymbol{K}}_{\text{H}}}{\boldsymbol{m}}\left| {\boldsymbol{m}} \right| = 0 \\ \Delta {{\boldsymbol{T}}'_{{\text{s,Load}}}} = {{\boldsymbol{C}}_{\mathrm{s}}}{{\boldsymbol{T}}'_{{\text{s,Load}}}} - {{\boldsymbol{b}}_{\mathrm{s}}} = 0 \\ \Delta {{\boldsymbol{T}}'_{{\text{r,Load}}}} = {{\boldsymbol{C}}_{\mathrm{r}}}{{\boldsymbol{T}}'_{{\text{r,Load}}}} - {{\boldsymbol{b}}_{\mathrm{r}}} = 0 \\ {{{T}}'_{{{{\mathrm{r}}i,{\mathrm{Source}}}}}} = \frac{{\displaystyle\sum\nolimits_j {{m_{ji}}{T'_{{\mathrm{r}}j,{\mathrm{Load}}}}{{\text{e}}^{ - \tfrac{{\lambda {L_{\text{H}}}}}{{{C_{\text{p}}}{m_{ji}}}}}}} }}{{{m_{{\mathrm{q}}i}}}} \\ \end{gathered} \right. $ | (2) |
式中:第1~2行为节点热功率平衡方程,第3行为压头损失平衡方程,第4~5行为热负荷节点供、回热温度不平衡方程,第6行为热源节点回热温度方程;
天然气系统由气源、压缩机、输气管道和天然气负荷构成,系统模型主要包括管道流量方程、节点流量平衡方程和压缩机工作方程。
(1) 管道流量方程:天然气管道流量
| $ {f_{{\mathrm{G}}ij}} = {s_{ij}}{\left( {\frac{{{s_{ij}}\left( {p_i^{\text{2}} - p_j^2} \right) }}{{{K_{{\mathrm{G}}ij}}}}} \right) ^{\tfrac{1}{{1.854}}}} $ | (3) |
式中:
(2) 节点流量平衡方程:在天然气系统中,经天然气管道和压缩机流入节点的流量等于天然气负荷消耗的流量,如式(4)所示。
| $ {{\boldsymbol{A}}_{\text{G}}}{{\boldsymbol{f}}_{\mathrm{G}}} + {{\boldsymbol{B}}_{\text{G}}}{{\boldsymbol{f}}_{\text{c}}} = {{\boldsymbol{f}}_{{\text{Load}}}} $ | (4) |
式中:
(3) 压缩机工作方程:实际工况下,压缩机一般有恒定压缩比、恒定流量和恒定出口压力等工作模式[6];可采用式(5)对压缩机的不同工作模式进行建模。
| $ {{\boldsymbol{C}}_1}{{\boldsymbol{\varPi}} _{\text{I}}} + {{\boldsymbol{C}}_2}{{\boldsymbol{\varPi}} _{\text{O}}} + {{\boldsymbol{C}}_3}{{\boldsymbol{f}}_{\text{c}}} = {\boldsymbol{d}} $ | (5) |
定义p的平方为
| 表 2 压缩机不同工作模式参数 Table 2 Parameters of different compressor working modes |
由式(3)~(5)得到天然气系统能量流模型为
| $ \left\{ \begin{gathered} \Delta {\boldsymbol{f}} = {{\boldsymbol{A}}_{\text{G}}}{{\boldsymbol{f}}_{\mathrm{G}}} + {{\boldsymbol{B}}_{\text{G}}}{{\boldsymbol{f}}_{\text{c}}} - {{\boldsymbol{f}}_{{\text{Load}}}} = {\bf{0}} \\ \Delta {\boldsymbol{d}} = {{\boldsymbol{C}}_1}{{\boldsymbol{\varPi}} _{\text{I}}} + {{\boldsymbol{C}}_2}{{\boldsymbol{\varPi}} _{\text{O}}} + {{\boldsymbol{C}}_3}{{\boldsymbol{f}}_{\text{c}}} - {\boldsymbol{d}} = {\bf{0}} \\ \end{gathered} \right. $ | (6) |
将式(4)改写为与式(5)相同的表达形式[22],如式(7)所示。
| $ \left\{ \begin{gathered} {{\boldsymbol{G}}_{\mathrm{G}}}{\boldsymbol{\varPi}} + {{\boldsymbol{B}}_{\text{G}}}{{\boldsymbol{f}}_{\text{c}}} + {{\boldsymbol{f}}_{{\text{Load}}}} = {\bf{0}} \\ {{\boldsymbol{G}}_{\mathrm{G}}} = {{\boldsymbol{A}}_{\text{G}}}{{\boldsymbol{\varLambda}} ^{ {{ - 1}}}}{\boldsymbol{A}}_{\text{G}}^{\text{T}} \\ \end{gathered} \right. $ | (7) |
式中:Λ为对角线矩阵。第k条管道对应的值
| $ {\varLambda _k} = {K_{{\mathrm{G}}k}}{\left| {{f_k}} \right|^{0.854}} $ | (8) |
将天然气系统中非平衡节点划分为压缩机出口节点和非出口节点,可将式(7)改写为
| $ \left[ {\begin{array}{*{20}{c}} {{{\boldsymbol{G}}_{{\text{G1}}}}}&{{{\boldsymbol{G}}_{{\mathrm{G}}2}}}&{{{\boldsymbol{B}}_{{\text{GI}}}}} \\ {{\boldsymbol{G}}_{{\text{G2}}}^{\text{T}}}&{{{\boldsymbol{G}}_{{\mathrm{G}}3}}}&{{{\boldsymbol{B}}_{{\text{GO}}}}} \end{array}} \right]\left[ {\begin{array}{*{20}{c}} {{{\boldsymbol{\varPi}} _{\text{I}}}} \\ {{{\boldsymbol{\varPi}} _{\text{O}}}} \\ {{{\boldsymbol{f}}_{\text{c}}}} \end{array}} \right] + \left[ {\begin{array}{*{20}{c}} {{{\boldsymbol{f}}_{{\text{LI}}}}} \\ {{{\boldsymbol{f}}_{{\text{LO}}}}} \end{array}} \right] = {\bf{0}} $ | (9) |
式中:
综上所述,可得到考虑压缩机不同工作模式的天然气系统能量流统一模型为
| $ \left[ {\begin{array}{*{20}{c}} {\Delta {{\boldsymbol{f}}_{{\text{LI}}}}} \\ {\Delta {{\boldsymbol{f}}_{{\text{LO}}}}} \\ {\Delta {\boldsymbol{d}}} \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} {{{\boldsymbol{G}}_{{\text{G1}}}}}&{{{\boldsymbol{G}}_{{\mathrm{G}}2}}}&{{{\boldsymbol{B}}_{{\text{GI}}}}} \\ {{\boldsymbol{G}}_{{\text{G2}}}^{\text{T}}}&{{{\boldsymbol{G}}_{{\mathrm{G}}3}}}&{{{\boldsymbol{B}}_{{\text{GO}}}}} \\ {{{\boldsymbol{C}}_1}}&{{{\boldsymbol{C}}_2}}&{{{\boldsymbol{C}}_3}} \end{array}} \right] \left[ {\begin{array}{*{20}{c}} {{{\boldsymbol{\varPi}} _{\text{I}}}} \\ {{{\boldsymbol{\varPi}} _{\text{O}}}} \\ {{{\boldsymbol{f}}_{\text{c}}}} \end{array}} \right] + \left[ {\begin{array}{*{20}{c}} {{{\boldsymbol{f}}_{{\text{LI}}}}} \\ {{\boldsymbol{f}}_{{\text{LO}}}} \\ - {\boldsymbol{d}} \\ \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} {\bf{0}} \\ {\bf{0}} \\ {\bf{0}} \end{array}} \right] $ | (10) |
电−热−气综合能源系统的耦合单元主要包括燃气发电机(Gas-fired Generator,GG)、燃气锅炉(Gas-fired Boiler,GB)、热电联产机组(Combined Heat and Power,CHP)、循环泵(Circulation Pump,CP)和电驱动压缩机。燃气发电机数学模型参考文献[23]、燃气锅炉和热电联产机组数学模型参考文献[7]、循环泵和电驱动压缩机数学模型参考文献[3]。
将电力系统中风机出力与电、热、气负荷作为系统输入的随机变量。用Weibull分布描述风速的不确定性[24],用正态分布描述负荷的波动性[14]。随机变量间的相关性包括风速和电、热、气负荷的自相关性,采用皮尔逊相关系数进行描述。
2 基于数据驱动的概率多能流计算多能流计算本质是通过已知量求解方程未知量。本文采用顺序求解法重复求解基于物理模型的综合能源系统确定性多能流,并将计算结果作为数据样本集;使用数据驱动方法处理数据样本,构建已知量到未知量的回归模型,并用回归模型代替多能流计算模型进行概率多能流计算。
2.1 基于数据驱动的确定性多能流计算综合能源系统多能流计算模型为非线性方程组,且热网节点温度与管道流量间具有高阶非线性函数关系,而支持向量回归(Support Vector Regression,SVR)能通过核函数将低维空间中的非线性关系映射为高维空间中的线性关系,从而更好地捕捉变量间的非线性关系[25],故本文使用SVR构建多能流非线性回归模型。
2.1.1 状态变量分类将IES中各子系统的不同节点类型用不同的下标表示以便分类,如表3所示。
| 表 3 IES节点下标定义 Table 3 Definition of subscript characters of IES node |
根据表1,将多能流计算模型中的已知量和未知量分类为
| $ \begin{array}{*{20}{c}} \begin{array}{l} {{\boldsymbol{P}}_{\rm{N}}} = {[{\boldsymbol{P}}_{{{\mathrm{Slack}}}}]^{\rm{T}}}\\ {{\boldsymbol{Q}}_{\rm{N}}} = {[{\boldsymbol{Q}}_{{\rm{Source}}},{\boldsymbol{Q}}_{\mathrm{Slack}}]^{\rm{T}}}\\ {{\boldsymbol{V}}_{\rm N}} = {[{\boldsymbol{V}}_{{\rm{Load}}}]^{\rm{T}}}\\ {{\boldsymbol{\theta }}_{\rm N}} = {[{\boldsymbol{\theta }}_{{\rm{Load}}},{\boldsymbol{\theta }}_{{\rm{Source}}}]^{\rm{T}}}\\ {{\boldsymbol{\varPhi }} _{\rm N}} = {[{{{\boldsymbol{\varPhi }} }}_{\mathrm{Slack}}]^{\rm{T}}}\\ {{\boldsymbol{T}}_{{\rm{s,}}{\rm N}}} = {[{\boldsymbol{T}}_{{\rm{s,Load}}}]^{\rm{T}}}\\ {{\boldsymbol{T}}_{{\rm{r,}}{\rm N}}} = {[{\boldsymbol{T}}_{{\rm{s,Load}}},{\boldsymbol{T}}_{{\rm{r,Source}}},{\boldsymbol{T}}_{{\rm{r,Slack}}}]^{\rm{T}}}\\ {{\boldsymbol{m}}_{\rm N}} = {[{\boldsymbol{m}}_{{\rm{Load}}},{\boldsymbol{m}}_{{\rm{Source}}},{\boldsymbol{m}}_{\mathrm{Slack}}]^{\rm{T}}}\\ {{\boldsymbol{f}}_{\rm N}} = {[{\boldsymbol{f}}_{\mathrm{Slack}}]^{\rm{T}}}\\ {{\boldsymbol{p}}_{\rm N}} = {[{\boldsymbol{p}}_{{\rm{Load}}}]^{\rm{T}}} \end{array} & \begin{array}{l} {{\boldsymbol{P}}_{\rm K}} = {[{\boldsymbol{P}}_{{\rm{Load}}},{\boldsymbol{P}}_{{\rm{Source}}}]^{\rm{T}}}\\ {{\boldsymbol{Q}}_{\rm K}} = {[{\boldsymbol{Q}}_{{\rm{Load}}}]^{\rm{T}}}\\ {{\boldsymbol{V}}_{\rm K}} = {[{\boldsymbol{V}}_{{\rm{Source}}},{\boldsymbol{V}}_{\mathrm{Slack}}]^{\rm{T}}}\\ {{\boldsymbol{\theta }}_{\rm K}} = {[{\boldsymbol{\theta }}_{\mathrm{Slack}}]^{\rm{T}}}\\ {{\boldsymbol{\varPhi }} _{\rm K}} = {[{{{\boldsymbol{\varPhi }} }}_{{\rm{Load}}},{{{\boldsymbol{\varPhi }} }}_{{\rm{Source}}}]^{\rm{T}}}\\ {{\boldsymbol{T}}_{{\rm{s,{\rm K}}}}} = {[{\boldsymbol{T}}_{{\rm{s,Source}}},{\boldsymbol{T}}_{{\rm{s,Slack}}}]^{\rm{T}}}\\ {{\boldsymbol{f}}_{\rm K}} = {[{\boldsymbol{f}}_{{\rm{Load}}}]^{\rm{T}}}\\ {{\boldsymbol{p}}_{\rm K}} = {[{\boldsymbol{p}}_{\mathrm{Slack}}]^{\rm{T}}} \end{array} \end{array}$ | (11) |
式中:下标N、K分别为未知量和已知量。
2.1.2 SVR算法原理由式(11)可划分多能流计算模型中输入变量
SVR在高维空间中的线性回归模型为
| $ f\left( {\boldsymbol{x}} \right) = {{\boldsymbol{\omega}} ^{\mathrm{T}}}\phi \left( {\boldsymbol{x}} \right) + \beta $ | (12) |
式中:ω为权重向量,
根据结构风险最小化原则构建损失函数,得到下述优化目标为
| $ \left\{ {\begin{array}{*{20}{l}} \mathop {\min }\limits_{\omega ,\;\beta ,\;{\xi _i},\;\xi _i^*} &\dfrac{1}{2}{\left\| {\boldsymbol{\omega }}\right\|^2} + U\displaystyle\sum\limits_{i = 1}^n {\left( {{\xi _i} + \xi _i^*} \right)} \\ {\mathrm{s.t.}}& f\left( {{{\boldsymbol{x}}_i}} \right) - {y_i} \le o + {\xi _i}, \\ & {y_i} - f\left( {{{\boldsymbol{x}}_i}} \right) \le o + \xi _i^*, \\ & {\xi _i} \ge 0,\xi _i^* \ge 0,i = 1,2,\cdots,n \end{array}} \right.$ | (13) |
式中:U为惩罚系数,
引入拉格朗日乘子
| $ \left\{ \begin{array}{l} \mathop {\min }\limits_{{{\ell }},\,{{{\ell }}^*}} \quad \dfrac{1}{2}\displaystyle\sum\limits_{i = 1}^n {\displaystyle\sum\limits_{j = 1}^n {\left( {\ell _i^* - {\ell _i}} \right)} \left( {\ell _j^* - {\ell _j}} \right)\kappa \left( {{{\boldsymbol{x}}_i},{{\boldsymbol{x}}_j}} \right)} +\\ \qquad o\displaystyle\sum\limits_{i = 1}^n {\left( {\ell _i^* + {\ell _i}} \right) - \displaystyle\sum\limits_{i = 1}^n {{y_i}\left( {\ell _i^* - {\ell _i}} \right)} } \\ {\mathrm{s.t.}}\quad \displaystyle\sum\limits_{i = 1}^n {\left( {\ell _i^* - {\ell _i}} \right) = 0且0 \le {\ell _i},\ell _i^* \le U} \end{array} \right.$ | (14) |
式中:κ(xi, xj) 为核函数,κ(xi, xj) = ϕ(xi) T ϕ(xj) 。
求解式(14)得到最优支持向量回归函数为
| $ f{\left( {\boldsymbol{x}} \right) _{{\mathrm{best}}}} = \sum\limits_{i = 1}^n {\left( {\ell _i^* - {\ell _i}} \right) \kappa \left( {{\boldsymbol{x}},{{\boldsymbol{x}}_i}} \right) } + \beta $ | (15) |
核函数的选取对支持向量回归的表现至关重要,常用的核函数有线性核、多项式核、高斯核等。本文选取具有较好高维映射性能和泛化能力的高斯核作为核函数[26],表达式为
| $ \kappa \left( {{{\boldsymbol{x}}_i},{{\boldsymbol{x}}_j}} \right) = \exp \left( { - \frac{{{{\left\| {{{\boldsymbol{x}}_i} - {{\boldsymbol{x}}_j}} \right\|}^2}}}{{2{\delta ^2}}}} \right) $ | (16) |
式中:δ为高斯核的带宽,δ > 0。
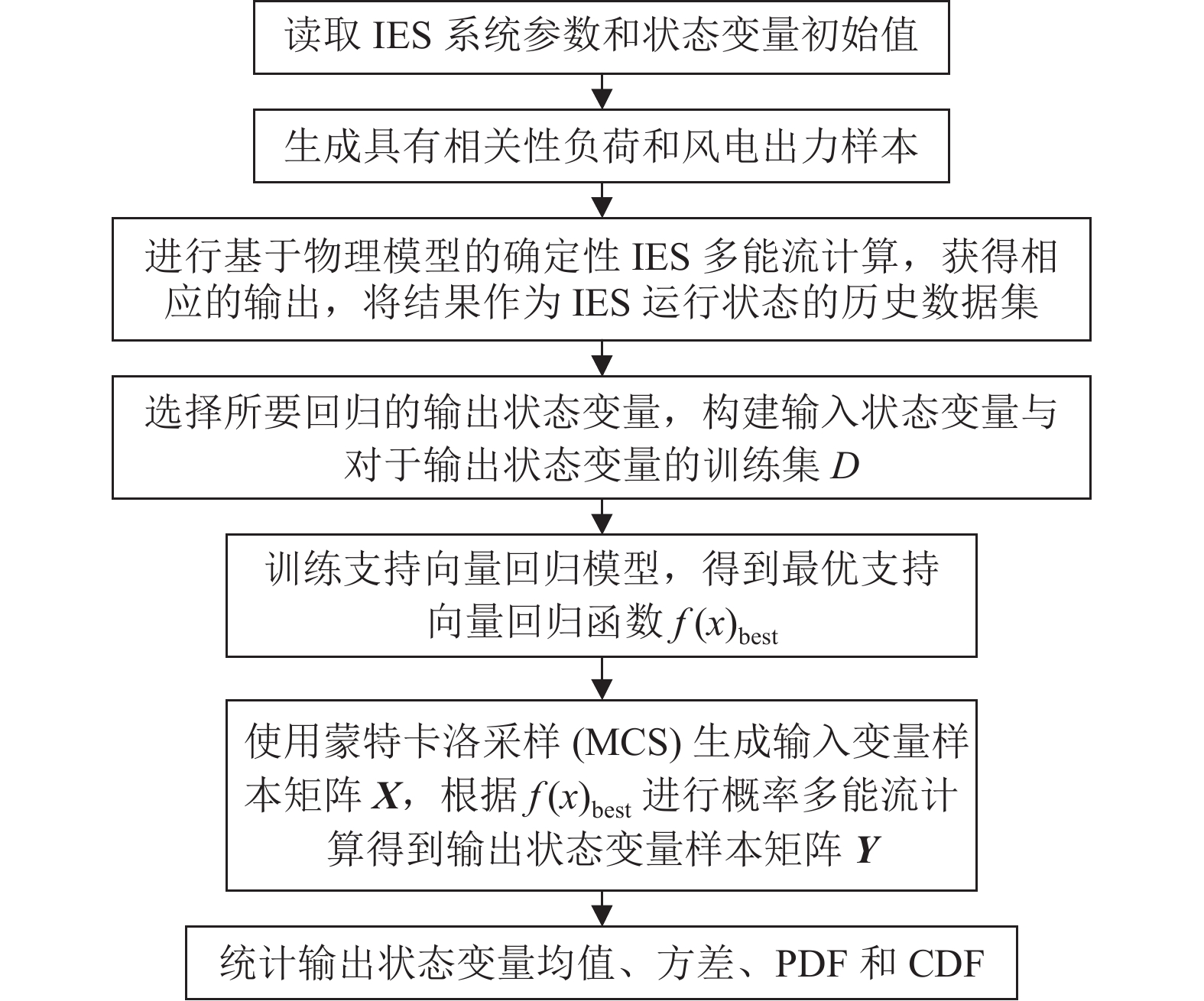
2.2 基于SVR的概率多能流计算通过上述方法得到最优支持向量回归函数f (x)best,并应用于概率多能流计算,提出基于SVR的概率多能流计算方法。该方法计算思路与蒙特卡洛模拟法相同,即针对每个输入都进行一次确定性多能流计算,得到对应的输出变量,最后统计输出变量的均值、方差等。不同点在于传统蒙特卡洛模拟法基于物理模型进行确定性多能流计算,而本文所提方法基于f (x)best进行确定性多能流计算,在每次计算中无需迭代,可极大提高计算效率和收敛性。基于SVR的概率多能流计算分为两个阶段:模型训练和概率多能流计算。具体步骤如下。
(1) 根据负荷和风速概率模型,通过蒙特卡洛采样和Nataf变换得到n组具有相关性的负荷和风电出力样本,作为输入样本。
(2) 基于本文所提考虑压缩机不同工作模式的多能流计算模型进行确定性多能流计算,得到与输入样本对应的n组输出样本;将输入样本和输出样本合并,作为综合能源系统运行状态的历史数据集
(3) 选择要回归的输出变量,如节点供热温度Ts;构建输入变量与输出变量的训练集
(4) 将训练集数据归一化,根据式(12)~(14)训练支持向量回归模型,得到最优回归函数f (x)best。
(5) 重复步骤1生成20 000组相关性输入样本X=[x1, x2,···, x20 000]。
(6) 使用f (x)best计算X中的所有样本,得到对应输出变量Y=[f (x1)best , f (x2)best ,···, f (x20 000)best],统计输出变量的均值、方差,通过核密度估计获取输出变量的概率密度函数。
综上所述,基于数据驱动的概率多能流计算方法流程如图1所示。
|
图 1 基于数据驱动的概率多能流计算流程 Figure 1 Flowchart of PMEF calculation based on data-driven |
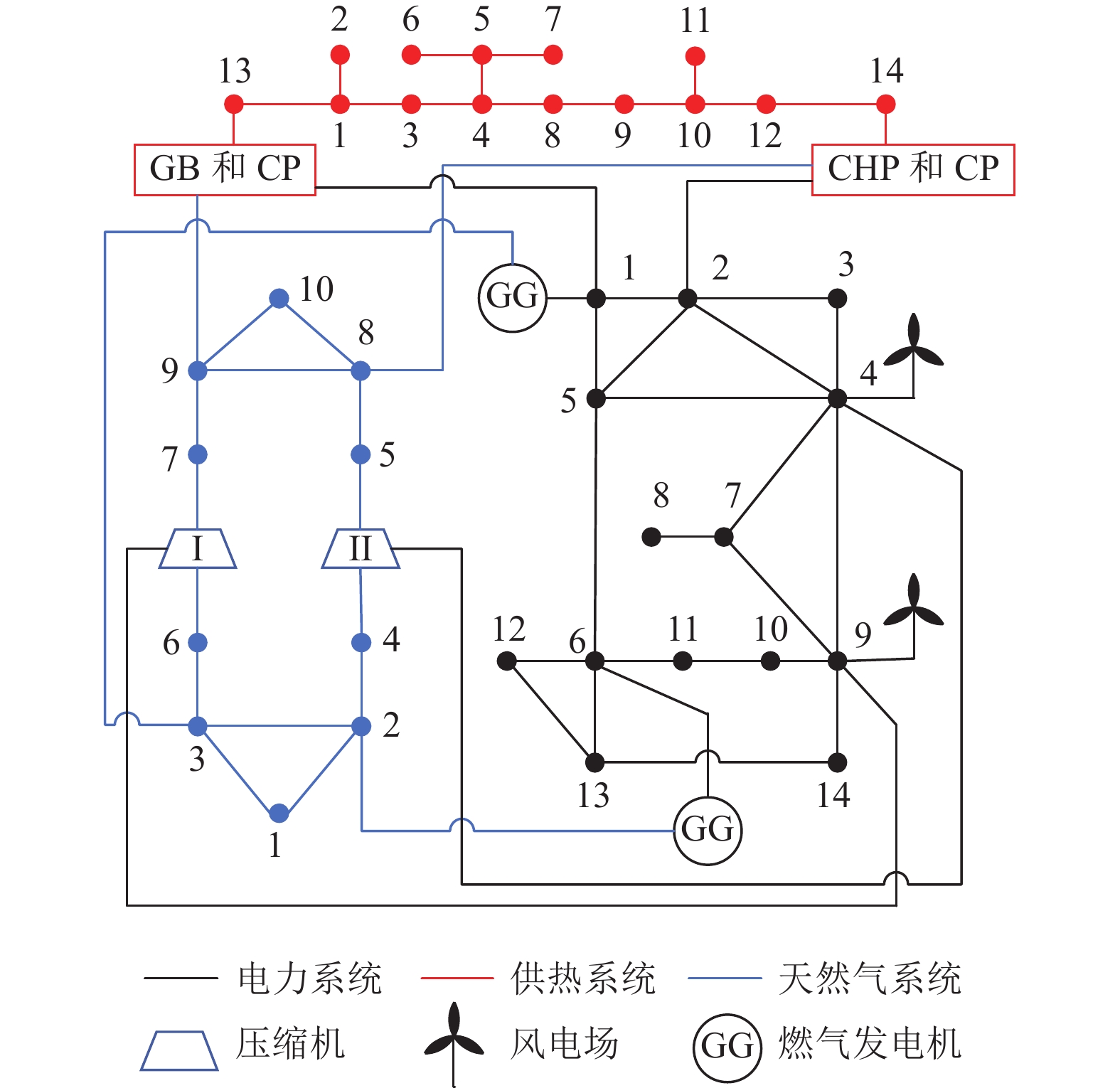
采用标准IEEE14节点电力系统、文献[7]中14节点供热系统、文献[22]中10节点天然气系统构成IES14-14-10节点综合能源测试系统,系统结构如图2所示。
|
图 2 综合能源测试系统拓扑图 Figure 2 Topology diagram of integrated energy test system |
风电场额定容量为25 MW,风速概率模型参数参考文献[27];供热系统节点13所接燃气锅炉输出热功率为80 MW;电力系统节点6所接燃气发电机输出电功率为100 MW;为使各子系统功率匹配,将电力系统节点3负荷缩小至原负荷的1/10。与多能流计算相关的参数参考文献[3]。算例分析在CPU为AMD Ryzen 7 5800H、主频为3.2 GHz的计算机上进行;在Matlab R2022b平台上编程。
| 表 4 供热系统管道参数 Table 4 Pipe parameters of heating system |
| 表 5 供热系统热负荷参数 Table 5 Heat load parameters of heating system |
| 表 6 天然气系统管道参数 Table 6 Pipe parameters of natural gas system |
| 表 7 天然气系统气负荷参数 Table 7 Gas load parameters of natural gas system |
耦合单元参数如表8所示。
| 表 8 耦合单元参数 Table 8 Parameters of coupling units |
采用蒙特卡洛法生成500组电、热、气负荷数据和风电场出力数据,基于上文提出的多能流计算模型进行求解,获得IES稳态运行的数据集,并作为历史数据,构建训练集。其中,电有功负荷均值采用IEEE14节点系统中节点负荷的给定值,热、气负荷均值采用表5和表7中的给定值,电、热、气负荷的标准差分别为均值的10%、5%和10%,电无功负荷由有功负荷乘[0.15,0.25]间的随机数得到[20];假设同类型负荷及风速之间的相关系数为0.7。
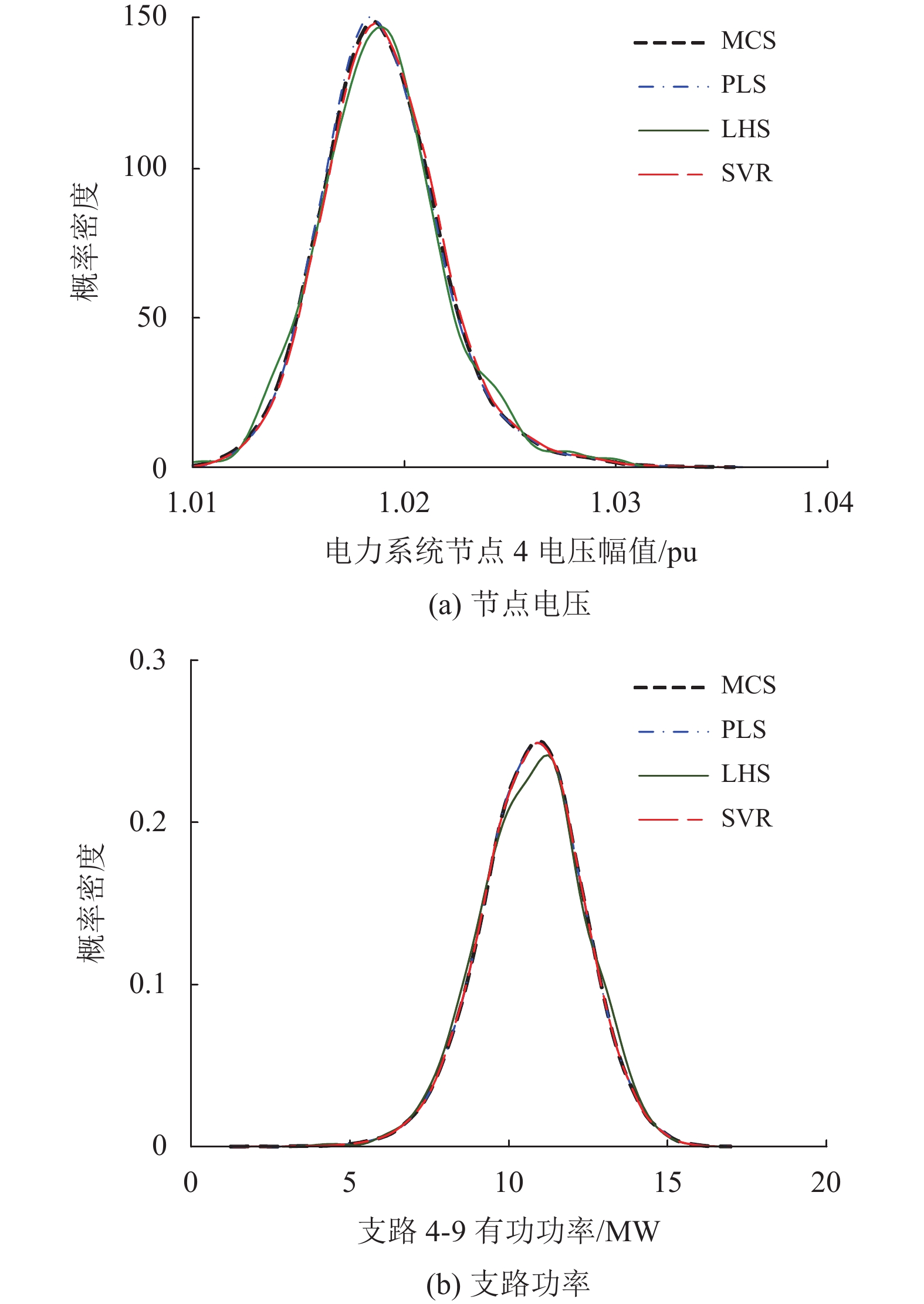
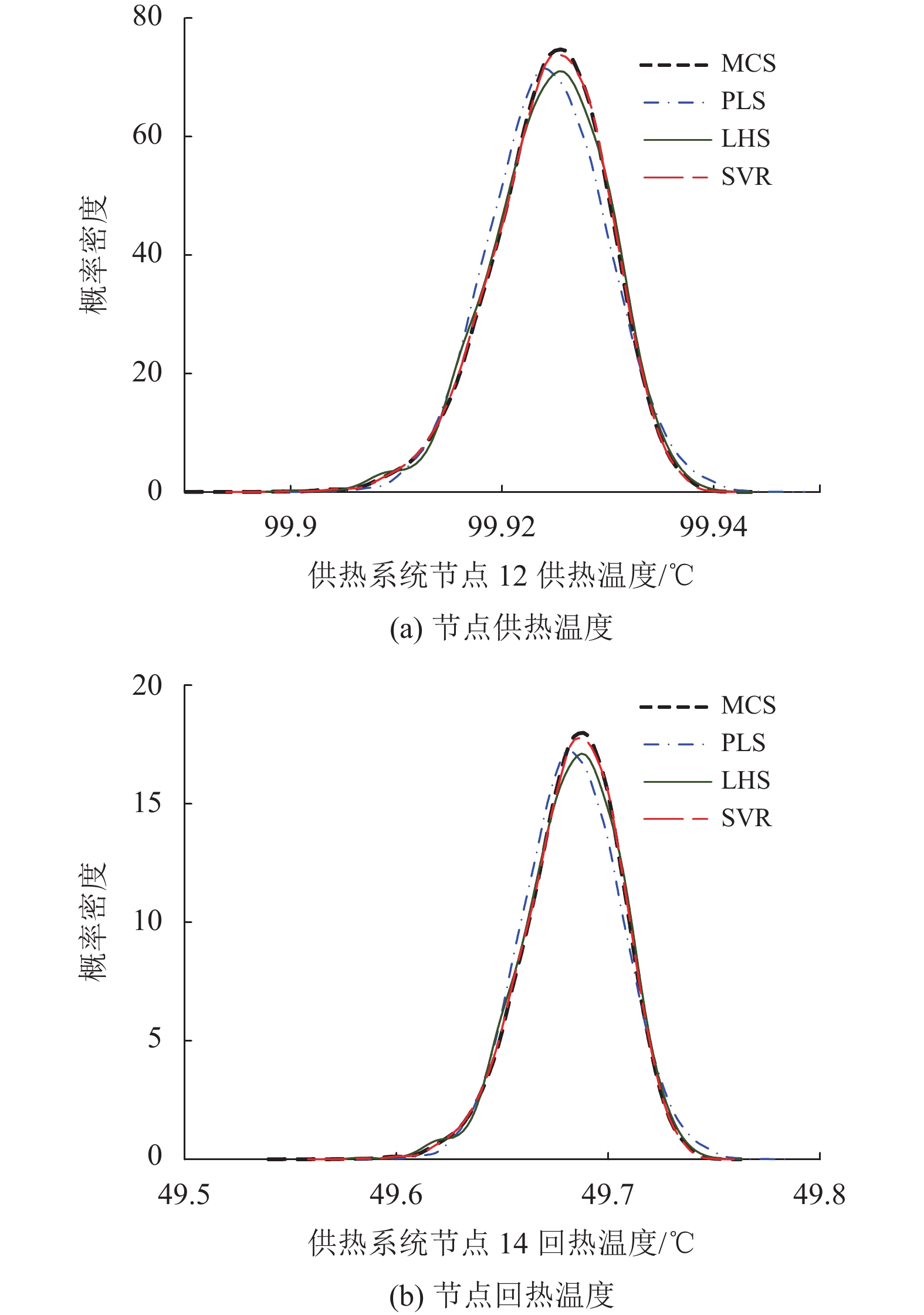
3.1.2 算法有效性验证为验证所提基于SVR的概率多能流计算方法的有效性,将该方法与基于蒙特卡洛模拟(Monte Carlo Simulation ,MCS)、拉丁超立方采样(Latin Hypercube Sampling,LHS)、偏最小二乘(Partial Least Squares,PLS)的概率多能流计算结果进行对比。本节以采样规模为
|
图 3 电力系统部分状态变量概率密度 Figure 3 PDFs of partial state variables in power system |
|
图 4 供热系统部分状态变量概率密度 Figure 4 PDFs of partial state variables in heating system |
|
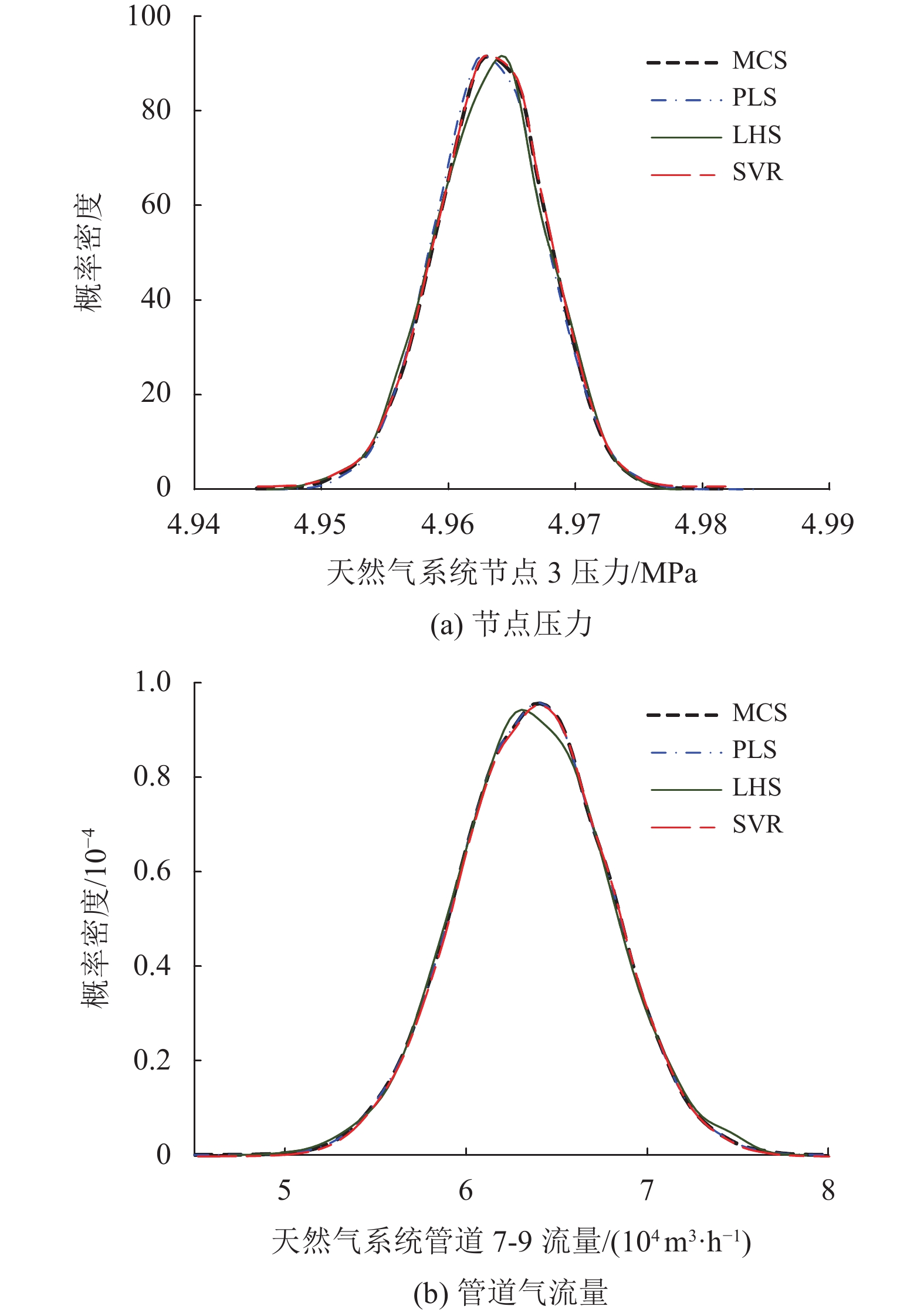
图 5 天然气系统部分状态变量概率密度 Figure 5 PDFs of partial state variables in nature gas system |
由图3~图5可知,SVR算法计算得到的电力系统节点电压、支路功率,供热系统节点供、回热温度和管道水流量,天然气系统节点压力和管道气流量的概率密度曲线与蒙特卡洛法得到的概率密度曲线基本重合,具有较高的计算精度。PLS算法对于供热系统中的供、回热温度计算精度不佳,而对于其他状态变量具有较高计算精度。LHS算法得到的各状态变量概率密度曲线,在均值附近拟合效果较差,在尾部则具有较高拟合精度。
本文从误差的角度进一步分析SVR算法的有效性。各状态变量的均值相对误差
| $ {\varepsilon _{{\text{μ}},{{M}}}} = \frac{{\left| {{\mu _{{M}}} - {\mu _{{\text{MCS}}}}} \right|}}{{{\mu _{{\text{MCS}}}}}} \times 100\% $ | (17) |
| $ {\varepsilon _{{\text{σ}},{{M}}}} = \frac{{\left| {{\sigma _{{M}}} - {\sigma _{{\text{MCS}}}}} \right|}}{{{\sigma _{{\text{MCS}}}}}} \times 100\% $ | (18) |
式中:
由于IES输出状态变量较多,本文采用同一类输出状态变量的均值和方差的相对误差的平均值,即
| 表 9 SVR、PLS和LHS相对误差对比 Table 9 Related errors comparison of SVR、PLS and LHS |
表9中PF和QF分别表示电力系统支路传输的有功功率和无功功率。由表9可知,PLS算法对于供热系统的节点供、回热温度的方差平均相对误差分别达到2.5%和4.58%,计算精度较低,对于其他状态变量仍保持较高计算精度;LHS算法在供热系统节点供、回热温度的计算精度上优于PLS算法,但在其他状态变量的计算精度上不如PLS算法;SVR算法对于各类状态变量的
这是因为电力系统中节点电压幅值和相角与支路功率、支路功率与节点注入功率、供热系统的管道水流量与节点水流量、天然气系统的管道气流量与节点气流量间为近似一阶线性化关系,天然气系统节点压力与管道气流量之间为近似二阶函数关系,而供热系统节点供、回热温度与管道水流量之间为高阶非线性关系。PLS作为一种线性回归算法,能对具有近似一阶线性化和二阶函数关系的状态变量进行有效计算,但无法有效捕捉变量间的高阶非线性关系;LHS作为一种分层抽样算法,基于模型进行重复的确定性多能流计算,其计算精度受采样规模影响,与变量间的函数关系无关,因此,当采样规模较小时,对于具有近似一阶线性化和二阶函数关系的状态变量LHS计算精度不如PLS,而对于具有高阶非线性关系的节点供、回热温度,LHS计算精度高于PLS;而SVR作为一种核方法,能通过核函数将低维空间中的非线性关系映射为高维空间中的线性关系,从而更好地捕捉变量间的非线性关系,实现对各状态变量的有效计算。上述算例仿真结果表明,所提SVR算法具有较高精度,能有效应用于综合能源系统概率多能流计算。
3.1.3 计算效率对比本节对比了计算规模为20 000的MCS、PLS、SVR和采样规模为
| 表 10 计算耗时比较 Table 10 Comparisons of computational time |
由表10可知,本文所提SVR算法相较于MCS算法节省了99.98%的计算时间,相较于LHS算法节省了99.48%的计算时间。结果表明,所提SVR算法能够在保持较高计算精度的同时大幅度提高计算效率。
3.2 压缩机不同工作模式对概率多能流影响分析综合能源系统运行过程中,压缩机一般有3种工作模式:(1) 给定压缩比;(2) 给定出口压力;(3) 给定流经压缩机流量。将这3种模式分别记为模式A、模式B、模式C。
为验证考虑压缩机不同工作模式的多能流计算模型的可行性,同时分析压缩机不同工作模式对概率多能流的影响,本节设计3种场景:(1) 压缩机I、II都工作在模式A,压缩比为1.2。(2) 压缩机I工作在模式A,压缩比为1.2;压缩机II工作在模式B,出口压力为6 MPa。(3) 压缩机I工作在模式A,压缩比为1.2;压缩机II工作在模式C,给定流量为67 000 m3/h。
首先,不考虑风机接入与负荷波动,对3种场景进行基于物理模型的确定性多能流计算,结果如表11所示。
| 表 11 3种场景下天然气系统节点压力 Table 11 Node pressure in natural gas system in three scenarios |
由表11可知,考虑压缩机不同工作模式的多能流计算模型在3种场景下均能收敛,验证了所提模型的可行性,且压缩机在不同工作模式下多能流计算结果不同。
接着,考虑风机接入与负荷波动,对上述3种场景进行基于SVR的概率多能流计算和分析,所有场景均考虑同类型随机变量间相关性ρ = 0.7。
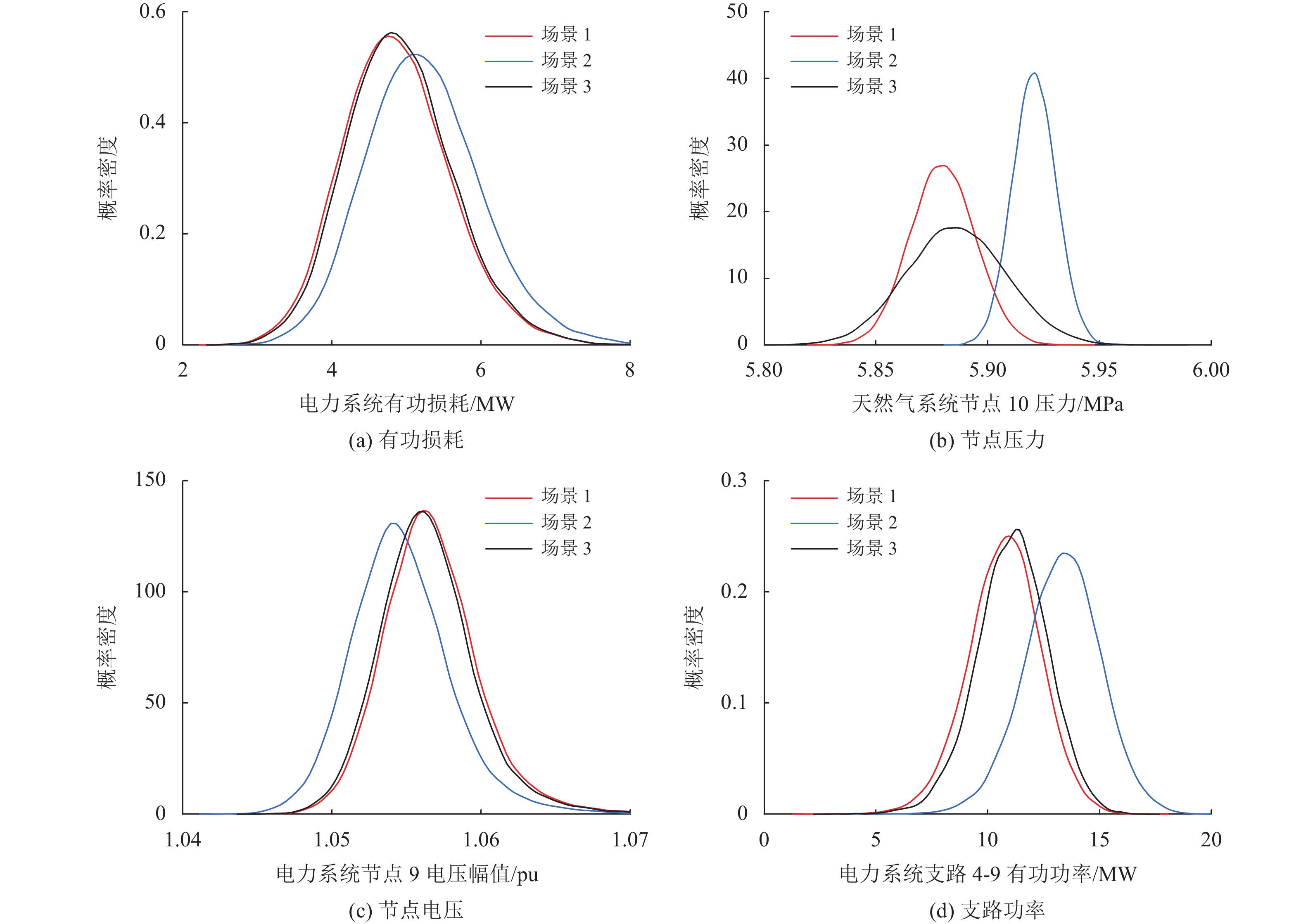
3种场景下电力系统有功损耗、天然气系统末端节点10压力、与压缩机II相连的电力系统节点9电压幅值、电力系统支路4-9有功功率的概率密度曲线如图6所示。
|
图 6 3种场景下IES部分状态变量概率密度 Figure 6 PDFs of partial state variables in IES in three scenarios |
由图6可知,当压缩机工作模式变化时,概率多能流计算结果也会随之变化,且场景2的计算结果变化最大。场景2中电力系统有功损耗最多、天然气系统节点10压力最高、电力系统节点9电压最低、电力系统支路4-9传输有功功率最高。这是因为在场景2中压缩机II工作在模式B,且设置出口压力为6 MPa,而在场景1或3中,压缩机II的出口压力小于6 MPa,所以场景2提高了压缩机II出口节点压力,进而提高了天然气系统末端节点10的压力;电驱动压缩机通过消耗电功率来提升压缩机出口节点压力,当出口节点压力越高时,压缩机消耗的电功率越多,故场景2中压缩机II消耗的电功率最多;压缩机II消耗的电功率作为电负荷接入电力系统节点9,故场景2中电力系统节点9所带负荷最大,使得节点9的电压最低,支路4-9传输的电功率最高,进而导致线路有功损耗的增加。
上述结果表明,压缩机不同工作模式会影响综合能源系统的能流分布。压缩机在提升天然气系统节点压力的同时,会增加电力系统的线路损耗。在实际工况中,需根据综合能源系统的运行状态切换压缩机的工作模式,来平衡天然气系统节点压力与电力系统线路损耗二者之间的关系。本文所提考虑压缩机不同工作模式的多能流计算模型适用于压缩机不同的工作模式,且各种工作模式间的切换过程简洁明了,可满足实际工况需求,具有一定的工程意义。
4 结论本文针对电−热−气综合能源系统,提出了一种考虑压缩机不同工作模式的多能流计算模型;在此基础上,进一步提出一种基于支持向量回归的概率多能流计算方法。通过对IES14-14-10综合能源测试系统进行算例仿真分析,得出如下结论。
(1) 本文提出的考虑压缩机不同工作模式的综合能源系统多能流计算统一模型,在不同压缩机工作模式下计算均能收敛,验证了该模型的有效性。
(2) 压缩机在提升天然气系统节点压力的同时,会增加电力系统中的线路损耗。在实际工况中,需根据综合能源系统的运行状态切换压缩机的工作模式,来平衡天然气系统节点压力与电力系统线路损耗之间的关系。本文所提多能流计算模型可满足实际工况中切换压缩机工作模式的需求,且各种工作模式间的切换过程简洁明了,对工程实践具有指导意义。
(3) 基于支持向量回归的概率多能流计算方法可实现对综合能源系统概率能流的有效计算,其计算得到的各类状态变量方差的平均相对误差均保持在0.42%以下;相比于PLS与LHS的概率多能流计算方法,支持向量回归的概率多能流计算方法在具有高阶非线性关系的节点供热温度的计算精度方面分别提升了94%与80.52%,回热温度的计算精度方面分别提升了90.83%与51.16%,且计算时间在0.8 s内,能够有效地改善概率多能流的计算精度与效率。
| [1] |
孙宏斌, 潘昭光, 郭庆来. 多能流能量管理研究: 挑战与展望[J].
电力系统自动化, 2016, 40(15): 1-8.
SUN H B, PAN Z G, GUO Q L. Energy management for multi-energy flow: challenges and prospects[J]. Automation of Electric Power Systems, 2016, 40(15): 1-8. |
| [2] |
王舒萍, 张沈习, 程浩忠, 等. 考虑天然气系统初值优化的综合能源系统改进多能流计算方法[J].
电力自动化设备, 2022, 42(1): 28-36.
WANG S P, ZHANG S X, CHENG H Z, et al. Improved multi-energy flow calculation method for integrated energy system considering initial value optimization of natural gas system[J]. Electric Power Automation Equipment, 2022, 42(1): 28-36. |
| [3] |
SHABANPOUR-HAGHIGHI A, SEIFI A R. An integrated steady-state operation assessment of electrical, natural gas, and district heating networks[J].
IEEE Transactions on Power Systems, 2016, 31(5): 3636-3647.
DOI: 10.1109/TPWRS.2015.2486819. |
| [4] |
MASSRUR H R, NIKNAM T, AGHAEI J, et al. Fast decomposed energy flow in large-scale integrated electricity-gas-heat energy systems[J].
IEEE Transactions on Sustainable Energy, 2018, 9(4): 1565-1577.
DOI: 10.1109/TSTE.2018.2795755. |
| [5] |
CHEN Y, ZHAO J, MA J. Fast decoupled multi-energy flow calculation for integrated energy system[J].
Journal of Modern Power Systems and Clean Energy, 2020, 8(5): 951-960.
DOI: 10.35833/MPCE.2018.000598. |
| [6] |
王英瑞, 曾博, 郭经, 等. 电−热−气综合能源系统多能流计算方法[J].
电网技术, 2016, 40(10): 2942-2950.
WANG Y R, ZENG B, GUO J, et al. Multi-energy flow calculation method for integrated energy system containing electricity, heat and gas[J]. Power System Technology, 2016, 40(10): 2942-2950. |
| [7] |
LI J H, HUANG Y J, ZHU M S. Gradient descent iterative method for energy flow of integrated energy system considering multiple modes of compressors[J].
Energy Conversion and Management, 2020, 207: 112534.
DOI: 10.1016/j.enconman.2020.112534. |
| [8] |
钟俊杰, 李勇, 曾子龙, 等. 综合能源系统多能流准稳态分析与计算[J].
电力自动化设备, 2019, 39(8): 22-30.
ZHONG J J, LI Y, ZENG Z L, et al. Quasi-steady-state analysis and calculation of multi-energy flow for integrated energy system[J]. Electric Power Automation Equipment, 2019, 39(8): 22-30. |
| [9] |
闵庆久, 马兆兴, 马英姿. 基于PSO-Newton法的电−气综合能源系统能流计算[J].
电力工程技术, 2021, 40(1): 33-39.
MIN Q J, MA Z X, MA Y Z. Energy flow calculation of integrated power-gas energy system based on PSO-newton method[J]. Electric Power Engineering Technology, 2021, 40(1): 33-39. |
| [10] |
SHABANPOUR-HAGHIGHI A, SEIFI A R. Simultaneous integrated optimal energy flow of electricity, gas, and heat[J].
Energy Conversion and Management, 2015, 101: 579-591.
DOI: 10.1016/j.enconman.2015.06.002. |
| [11] |
陈胜, 卫志农, 孙国强, 等. 电−气混联综合能源系统概率能量流分析[J].
中国电机工程学报, 2015, 35(24): 6331-6340.
CHEN S, WEI Z N, SUN G Q, et al. Probabilistic energy flow analysis in integrated electricity and natural-gas energy systems[J]. Proceedings of the CSEE, 2015, 35(24): 6331-6340. |
| [12] |
CHEN S, WEI Z N, SUN G Q, et al. Multi-linear probabilistic energy flow analysis of integrated electrical and natural-gas systems[J].
IEEE Transactions on Power Systems, 2017, 32(3): 1970-1979.
DOI: 10.1109/TPWRS.2016.2597162. |
| [13] |
张儒峰, 姜涛, 李国庆, 等. 基于最大熵原理的电−气综合能源系统概率能量流分析[J].
中国电机工程学报, 2019, 39(15): 4430-4441.
ZHANG R F, JIANG T, LI G Q, et al. Maximum entropy based probabilistic energy flow calculation for integrated electricity and natural gas systems[J]. Proceedings of the CSEE, 2019, 39(15): 4430-4441. |
| [14] |
杨家豪. 区域综合能源系统冷−热−电−气概率多能流计算[J].
电网技术, 2019, 43(1): 74-83.
YANG J H. Probabilistic multi-energy flow calculation for regional integrated energy system containing cooling, heating, electricity and gas[J]. Power System Technology, 2019, 43(1): 74-83. |
| [15] |
YUAN J, WENG Y. Support matrix regression for learning power flow in distribution grid with unobservability[J].
IEEE Transactions on Power Systems, 2021, 37(2): 1151-1161.
|
| [16] |
XU Y, HU Z, MILI L, et al. Probabilistic power flow based on a gaussian process emulator[J].
IEEE Transactions on Power Systems, 2020, 35(4): 3278-3281.
DOI: 10.1109/TPWRS.2020.2983603. |
| [17] |
LIU X. Combined analysis of electricity and heat networks[D]. Cardiff: Cardiff University, 2013.
|
| [18] |
LI Q, AN S, GEDRA T W. Solving natural gas loadflow problems using electric load flow techniques [C]//Proceedings of the North American Power Symposium. Rolla: NAPS, 2003: 1-7.
|
| [19] |
卫志农, 仲磊磊, 薛溟枫, 等. 基于数据驱动的电-热互联综合能源系统线性化潮流计算[J].
电力自动化设备, 2019, 39(8): 31-37.
WEI Z N, ZHONG L L, XUE M F, et al. Linearization flow calculation for integrated electricity-heat energy system based on data-driven[J]. Electric Power Automation Equipment, 2019, 39(8): 31-37. |
| [20] |
TIAN H, ZHAO H, LIU C, et al. A dual-driven linear modeling approach for multiple energy flow calculation in electricity-heat system[J].
Applied Energy, 2022, 314: 118872.
DOI: 10.1016/j.apenergy.2022.118872. |
| [21] |
陈乾, 张沈习, 程浩忠, 等. 基于径向基函数随机响应面法的综合能源系统概率能流计算[J].
中国电机工程学报, 2022, 42(22): 8075-8089.
CHEN Q, ZHANG S X, CHENG H Z, et al. Probabilistic energy flow calculation for integrated energy systems based on radial basis function-stochastic response surface method[J]. Proceedings of the CSEE, 2022, 42(22): 8075-8089. |
| [22] |
江茂泽, 徐羽镗, 王寿喜, 等. 输配气管网的模拟与分析[M]. 北京: 石油工业出版社, 1995: 205-219.
|
| [23] |
ZENG Q, FANG J K, LI J H, et al. Steady-state analysis of the integrated natural gas and electric power system with bi-directional energy conversion[J].
Applied Energy, 2016, 184: 1483-1492.
DOI: 10.1016/j.apenergy.2016.05.060. |
| [24] |
LI Y Z, WU Q H. Downside risk constrained probabilistic optimal power flow with wind power integrated[J].
IEEE Transactions on Power Systems, 2015, 31(2): 1649-1650.
|
| [25] |
魏步晗, 鲍刚, 李振华. 基于支持向量回归预测模型考虑天气因素和分时电价因素的短期电力负荷预测[J].
电网与清洁能源, 2023, 39(11): 9-19.
WEI B H, BAO G, LI Z H. Short-term electricity load forecasting based on support vector regression forecasting model considering weather factors and time-of-use tariff factors[J]. Power System and Clean Energy, 2023, 39(11): 9-19. |
| [26] |
朱宇迪. 基于数据驱动的潮流非线性回归建模及其灵敏度解析[D]. 吉林: 东北电力大学, 2024.
|
| [27] |
LI Y, LI W, YAN W, et al. Probabilistic optimal power flow considering correlations of wind speeds following different distributions[J].
IEEE Transactions on Power Systems, 2014, 29(4): 1847-1854.
DOI: 10.1109/TPWRS.2013.2296505. |
 2024, Vol. 41
2024, Vol. 41

