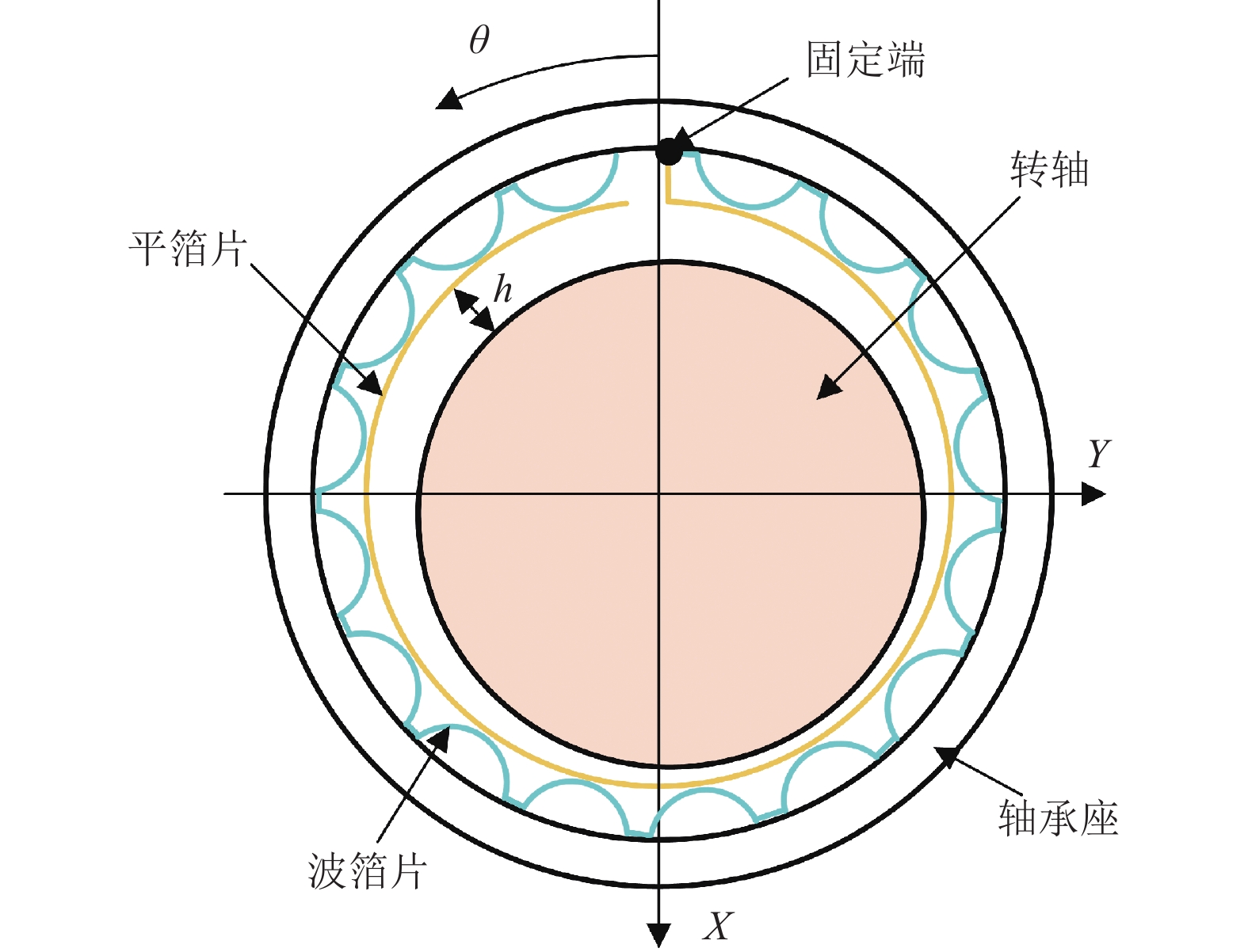
具有柔性结构的气体箔片轴承,比刚性气体轴承运行速度更高、不对中公差更大、运行稳定性更好,已经广泛应用于各种紧凑型、高要求的涡轮机械中[1-2]。第一代气体箔片轴承的结构如图1所示,它包括光滑的平箔片和由一系列箔段组成的波箔片,当气体动压加载在平箔片的表面上时,波箔片发生周向和径向位移,这种柔性结构具有一定的弹性,轴承具有更强的负载能力[3],波箔片与平箔片之间、波箔片与轴承套之间的相对运动会产生热量,轴承结构趋于稳定。但箔片结构之间的摩擦是不连续的,对其进行模拟是难点。
|
图 1 第一代气体箔片轴承 Figure 1 The first generation of gas foil bearings |
目前已经有多种分析模型被用来预测气体箔片轴承的性能。Heshmat 等[4-5]为气体箔片轴承开发了一种弹性基础模型,其中波箔片被构建为分离的弹簧。假设结构刚度是线性的、均匀分布且与载荷无关,求解静态雷诺方程,得到压力分布。该模型简单,已在其他研究中广泛应用[6-8],但由于忽略了箔片之间的相互作用,所以它预测的结构刚度较低。Ku 和 Heshmat [9]提出了考虑摩擦以及箔片之间相互作用的理论模型。他们发现波箔片的刚度随着不同的负载分布而变化。
Le 等[10]开发了一种多自由度模型,其中每个波箔片被简化为3个互连的弹簧,每个箔片与其相邻的箔片连接,并将该模型与有限元(Finite Element ,FE)模拟[11]进行了比较。自由度模型还被扩展应用到动态分析中[12],使用 Petrov 和 Ewins [13]的摩擦模型可计算出摩擦力。在多自由度模型的基础上,Osmanski 等[14]建立了全耦合模型,实现了联立求解,Arghir 和 Benchekroun [15-16]开发了利用增广拉格朗日法和罚函数法的简化模型计算法向接触力和摩擦力。Mahner 等[17]首先采用增广拉格朗日法对箔片轴承进行接触建模,并且使用了正则化库仑摩擦定律。后来,这两种方法也被用于全耦合热弹气动力轴承模型[18]。
Lee 等[19-20]提出了考虑摩擦滞后行为的箔片结构的有限元模型。与之前假设摩擦方向与水平位移相反的模型不同,该模型将摩擦方向与位移路径相关联。对于相同的载荷,在不同的加载或卸载情况下,可以获得箔片结构的各种偏转。研究了摩擦的影响和能量耗散特性。
Feng 等[21-22]提出了波箔片的连杆弹簧模型,平箔片被视为外壳。每个箔片都被简化为2个刚性连杆和一个水平弹簧。这2个连杆通过顶部的接头和底部的弹簧连接。考虑了波箔片的刚度、箔片之间的相互作用、平箔片的摩擦和偏转。Hoffman等[23-24]使用该模型对箔片轴承进行动态分析,并且使用了Petrov和Ewins[13]的摩擦模型。
大多数分析模型都假设箔片结构的刚度在轴向方向上是均匀的,因此忽略了轴向变化。然而,根据 Ruscitto 等的实验[25],在运行时轴承边缘处的最小气膜厚度小于中截面处的最小气膜厚度。San Andres 和 Kim [26]使用了与文献[21]类似的模型,只是弹簧被轴向方向上的几个独立的连杆弹簧模型取代,但结果与实验数据不太吻合。Lee 等[27]考虑到了轴承的三维形状,用壳单元对平箔片和波箔片进行了建模,然而,箔片结构之间的相对运动没有被考虑。
目前,对于箔片轴承的研究,大多数都是使用二维的分析模型,没有考虑轴向性能差异,这无法分析转子不对中情况下的轴承性能,且现有的三维模型不够全面,例如,有些模型忽略平箔片并将波箔片与弹簧等价,而有些模型忽略箔片结构之间的摩擦作用。为了能更好地模拟气体箔片轴承,本文建立一种考虑轴向变化的三维有限元模型,同时考虑箔片结构之间的相对运动,研究转子不对中对箔片轴承静态性能的影响。
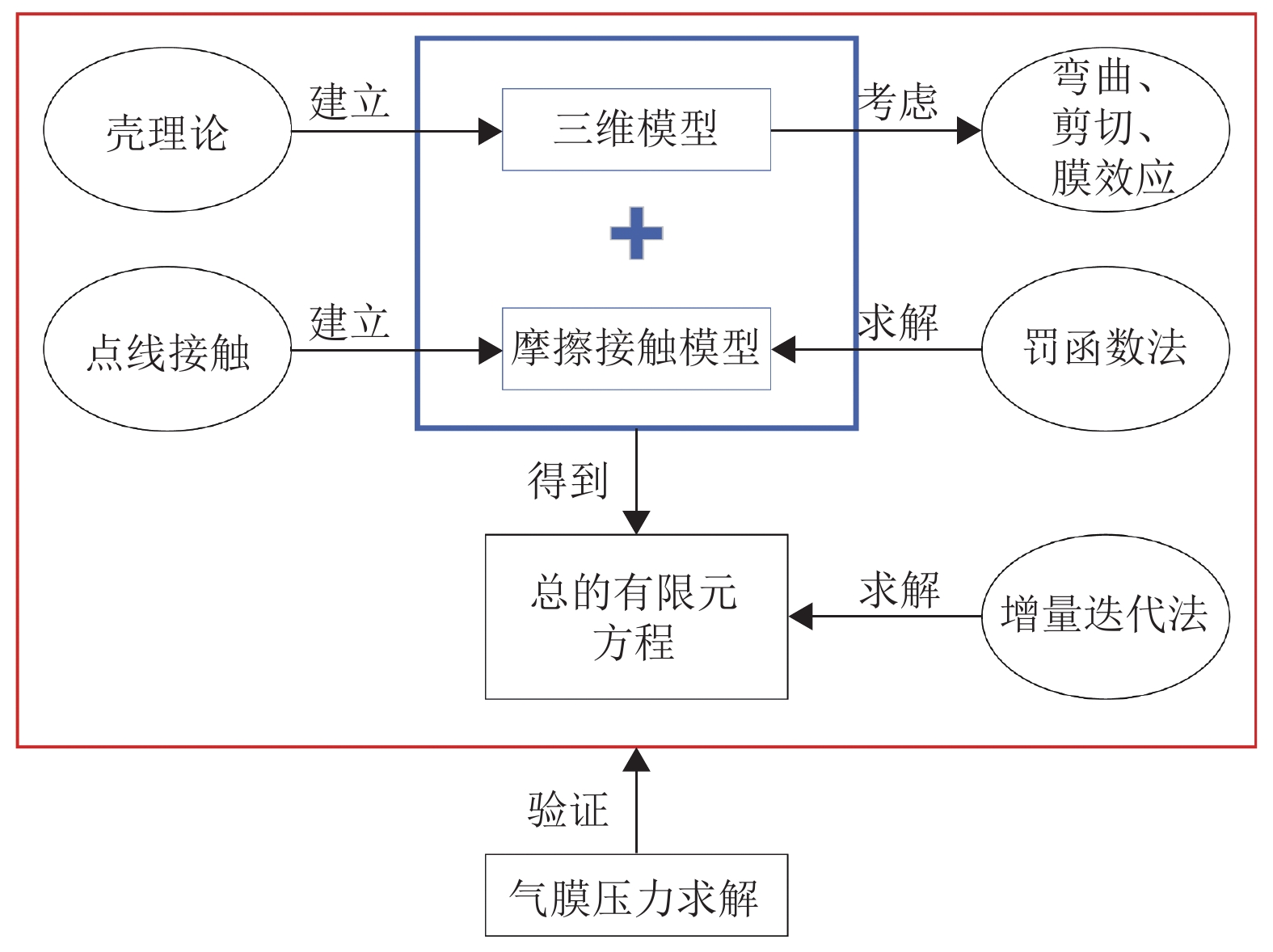
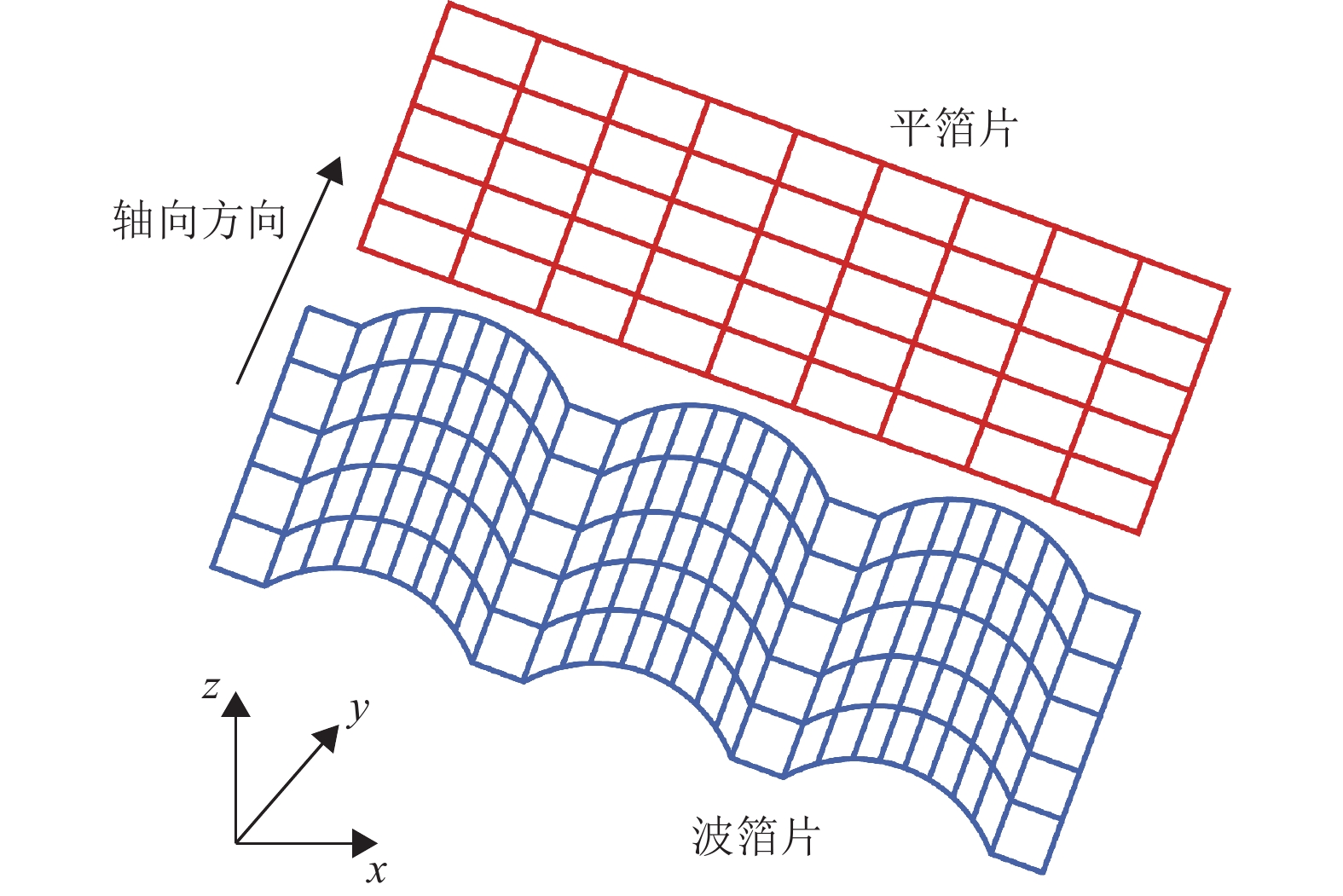
1 理论模型 1.1 箔片轴承的三维模型理论模型的总体示意图如图2所示。将箔片轴承的箔片结构三维模型沿周向方向展开,叠加平铺在同一个平面上,如图3所示。在进行模型分析时,为了更方便地将气膜力转换为结点力,需要将箔片结构合理地划分单元;在轴向上,平箔片与波箔片被划分为相同的单元数,这样有利于摩擦接触分析。在周向上,各个波箔被划分为8个单元,每个波箔对应的一段平箔片被划分为3个单元,这样的单元划分不仅能让程序有不错的精度,还能有较好的收敛性。
|
图 2 总体示意图 Figure 2 Overall diagram |
|
图 3 箔片结构的平面展开 Figure 3 The plane development of the foil structure |
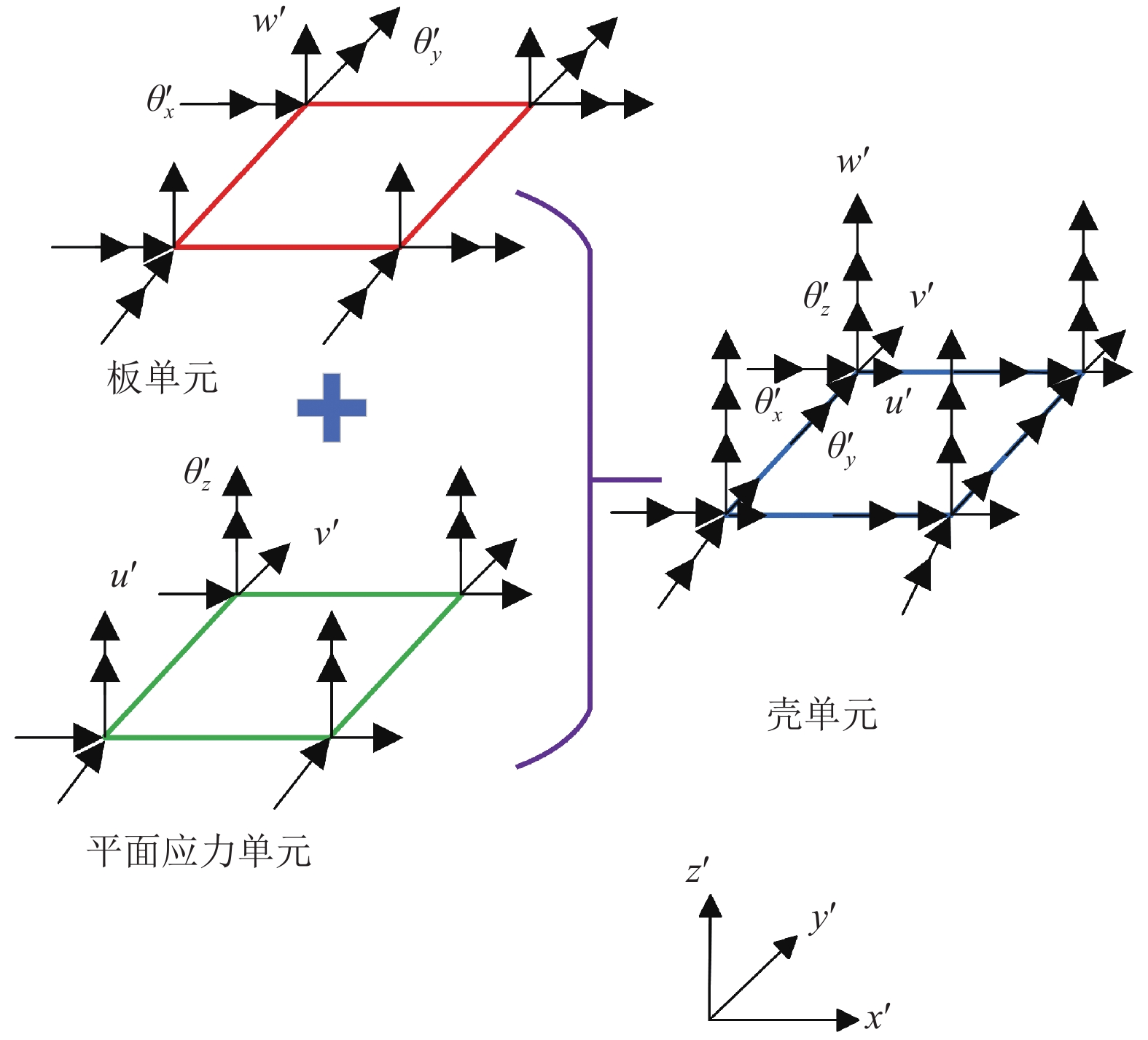
使用壳理论对箔片结构进行离散,如图4所示,板单元和平面应力单元相加,将其中的自由度叠加,每一个板单元和平面应力单元都有4个节点,每个节点都具有3个自由度;其中,板单元的每个节点具有一个垂直位移自由度
|
图 4 壳单元的组成 Figure 4 Composition of shell element |
所以,组装后的壳单元的每个节点具有
| $ \left[ {\begin{array}{*{20}{c}} {{{\boldsymbol{k}}_{\text{m}}}}&{}&{} \\ {}&{{{\boldsymbol{k}}_{{\text{ba}}}} + {{\boldsymbol{k}}_{\text{s}}}}&{} \\ {}&{}&0 \end{array}} \right]\left[ {\begin{array}{*{20}{c}} {{{\boldsymbol{u}}_{\text{m}}}} \\ {{{\boldsymbol{u}}_{{\text{ba}}}} + {{\boldsymbol{u}}_{\text{s}}}} \\ 0 \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} {{{\boldsymbol{f}}_{\text{m}}}} \\ {{{\boldsymbol{f}}_{{\text{ba}}}} + {{\boldsymbol{f}}_{\text{s}}}} \\ 0 \end{array}} \right] $ | (1) |
式中:km为平面应力单元刚度矩阵;kba为板单元弯曲效应刚度矩阵;ks为板单元剪切效应刚度矩阵。
对于式(1),壳单元是在局部坐标中定义得到的,它的刚度矩阵由3个矩阵叠加,最后需要转换到整体坐标系中。其中,各单元刚度矩阵的形函数均为
| $ \left\{ {\begin{array}{*{20}{c}} {{N_1}\left( {\xi ,\eta } \right) = \dfrac{1}{4}\left( {1 - \xi } \right) \left( {1 - \eta } \right) } \\ {{N_2}\left( {\xi ,\eta } \right) = \dfrac{1}{4}\left( {1 + \xi } \right) \left( {1 - \eta } \right) } \\ {{N_3}\left( {\xi ,\eta } \right) = \dfrac{1}{4}\left( {1 + \xi } \right) \left( {1 + \eta } \right) } \\ {{N_4}\left( {\xi ,\eta } \right) = \dfrac{1}{4}\left( {1 - \xi } \right) \left( {1 + \eta } \right) } \end{array}} \right. $ | (2) |
式中:N1~N4为形函数;η为无量纲参考坐标;ξ为无量纲参考坐标。
将平箔片和波箔片离散为壳单元时,每一个壳单元都由矩形组成。由于壳单元是建立在局部坐标系中的,所以局部坐标
| $ \xi = \frac{{x' - {{x}'_{\text{c}}}}}{a},\eta = \frac{{y' - {{y}'_{\text{c}}}}}{b},{\text{d}}x' = a{\text{d}}\xi ,{\text{d}}y' = b{\text{d}}\eta $ | (3) |
式中:
通过位移−应变关系式,平面单元应变可用单元结点位移表达为
| $ \begin{split} {\boldsymbol{\varepsilon}} =\;& {\boldsymbol{Lu}} = {\boldsymbol{LN}}{{\boldsymbol{u}}_{\text{e}}} = {{\boldsymbol{B}}_{\text{m}}}{{\boldsymbol{u}}_{\text{e}}} = \\ &\left[ {\begin{array}{*{20}{c}} {{{\boldsymbol{B}}_1}}&{{{\boldsymbol{B}}_2}}&{{{\boldsymbol{B}}_3}}&{{{\boldsymbol{B}}_4}} \end{array}} \right]{\left[ {\begin{array}{*{20}{c}} {{{\boldsymbol{u}}_1}}&{{{\boldsymbol{u}}_2}}&{{{\boldsymbol{u}}_3}}&{{{\boldsymbol{u}}_4}} \end{array}} \right]^{\text{T}}} \end{split}$ | (4) |
| $ {\boldsymbol{L}} = \left[ {\begin{array}{*{20}{c}} {\dfrac{\partial }{{\partial x}}}&0 \\ 0&{\dfrac{\partial }{{\partial y}}} \\ {\dfrac{\partial }{{\partial y}}}&{\dfrac{\partial }{{\partial x}}} \end{array}} \right],{{\boldsymbol{B}}_{{\text{m}}i}} = {\boldsymbol{L}}{N_i} = \left[ {\begin{array}{*{20}{c}} {\dfrac{{\partial {N_i}}}{{\partial x}}}&0 \\ 0&{\dfrac{{\partial {N_i}}}{{\partial y}}} \\ {\dfrac{{\partial {N_i}}}{{\partial y}}}&{\dfrac{{\partial {N_i}}}{{\partial x}}} \end{array}} \right] $ | (5) |
式中:L为算子矩阵;Bmi为应变矩阵。
要计算矩阵Bmi需要计算形函数对物理坐标(x,y) 的导数,而形函数Ni是定义在自然坐标系下的。因为所有的壳单元是矩形的,长宽都不变,通过链式求导法则得到:
| $ {{\boldsymbol{B}}_{{\text{m}}i}} = \left[ {\begin{array}{*{20}{c}} {\dfrac{{\partial {N_i}}}{{a\partial \xi }}}&0 \\ 0&{\dfrac{{\partial {N_i}}}{{g\partial \eta }}} \\ {\dfrac{{\partial {N_i}}}{{g\partial \eta }}}&{\dfrac{{\partial {N_i}}}{{a\partial \xi }}} \end{array}} \right],(i = 1,2,3,4) $ | (6) |
通过位移−应力关系式,平面单元应力可用单元结点位移表达为
| $ \begin{split} {\boldsymbol{ \sigma}} =\;& {{\boldsymbol{D}}_{\text{m}}}{\boldsymbol{\varepsilon }}= {{\boldsymbol{D}}_{\text{m}}}{{\boldsymbol{B}}_{\text{m}}}{{\boldsymbol{u}}_{\text{e}}} = {\boldsymbol{S}}{{\boldsymbol{u}}_{\text{e}}} = \\ & \left[ {\begin{array}{*{20}{c}} {{{\boldsymbol{S}}_1}}&{{{\boldsymbol{S}}_2}}&{{{\boldsymbol{S}}_3}}&{{{\boldsymbol{S}}_4}} \end{array}} \right] = {\left[ {\begin{array}{*{20}{c}} {{{\boldsymbol{u}}_1}}&{{{\boldsymbol{u}}_2}}&{{{\boldsymbol{u}}_3}}&{{{\boldsymbol{u}}_4}} \end{array}} \right]^{\text{T}}} \end{split} $ | (7) |
| $ {{\boldsymbol{D}}_{\text{m}}} = \frac{{Et}}{{1 - {v^2}}}\left[ {\begin{array}{*{20}{c}} 1&v&0 \\ v&1&0 \\ 0&0&{\dfrac{{1 - v}}{2}} \end{array}} \right] $ | (8) |
式中:Dm为弹性矩阵;E为弹性模量;ν为泊松比;t为单元厚度(m)。
平面单元刚度矩阵公式可从单元应变能表达式中推导出来,刚度矩阵表达为
| $ {{\boldsymbol{k}}_{\text{m}}} = ab\int_{ - 1}^1 {\int_{ - 1}^1 {{\boldsymbol{B}}_{\text{m}}^{\text{T}}} } {{\boldsymbol{D}}_{\text{m}}}{{\boldsymbol{B}}_{\text{m}}}{\text{d}}\xi {\text{d}}\eta $ | (9) |
板单元考虑了弯曲效应和剪切效应,通过与平面应力单元类似的推导,板单元刚度矩阵分为弯曲效应的刚度矩阵kba和剪切效应的刚度矩阵ks,表达为
| $ {{\boldsymbol{k}}_{{\text{ba}}}} = ab\int_{ - 1}^1 {\int_{ - 1}^1 {{\boldsymbol{B}}_{\text{b}}^{\text{T}}} } {{\boldsymbol{D}}_{\text{b}}}{{\boldsymbol{B}}_{\text{b}}}{\text{d}}\xi {\text{d}}\eta $ | (10) |
| $ {{\boldsymbol{k}}_{\text{s}}} = ab\int_{ - 1}^1 {\int_{ - 1}^1 {{\boldsymbol{B}}_{\text{s}}^{\text{T}}} } {{\boldsymbol{D}}_{\text{s}}}{{\boldsymbol{B}}_{\text{s}}}{\text{d}}\xi {\text{d}}\eta $ | (11) |
| $ \begin{split} &{{\boldsymbol{B}}_{{\text{b}}i}} = \left[ {\begin{array}{*{20}{c}} 0&0&{\dfrac{{\partial {N_i}}}{{a\partial \xi }}} \\ 0&{ - \dfrac{{\partial {N_i}}}{{b\partial \eta }}}&0 \\ 0&{ - \dfrac{{\partial {N_i}}}{{a\partial \xi }}}&{\dfrac{{\partial {N_i}}}{{b\partial \eta }}} \end{array}} \right],\\ &{{\boldsymbol{D}}_{\text{b}}} = \frac{{E{t^3}}}{{12(1 - {v^2}) }}\left[ {\begin{array}{*{20}{c}} 1&v&0 \\ v&1&0 \\ 0&0&{\dfrac{{1 - v}}{2}} \end{array}} \right] \end{split} $ | (12) |
| $ {{\boldsymbol{B}}_{{\text{s}}i}} = \left[ {\begin{array}{*{20}{c}} {\dfrac{{\partial {N_i}}}{{a\partial \xi }}}&0&{{N_i}} \\ {\dfrac{{\partial {N_i}}}{{b\partial \eta }}}&{ - {N_i}}&0 \end{array}} \right],{{\boldsymbol{D}}_{\text{s}}} = \frac{{5Et}}{{12(1 + v) }}\left[ {\begin{array}{*{20}{c}} 1&0 \\ 0&1 \end{array}} \right] $ | (13) |
式(10)~(11)中:Bb、Bs为应变矩阵;Db、Ds为弹性矩阵。
由板单元与平面应力单元得到的壳单元需要将单元矩阵及向量组装成系统整体矩阵及向量,需要将单元局部坐标下的结点自由度转换为整体坐标下的结点自由度,得到
| $ {{\boldsymbol{k}}_{\text{e}}} = {{\boldsymbol{T}}^{\text{T}}}{{\boldsymbol{k}}'_{\text{e}}}{\boldsymbol{T}} $ | (14) |
其中
| $ {\boldsymbol{T}} = \left[ {\begin{array}{*{20}{c}} {{{\boldsymbol{T}}_{\text{d}}}}&{}&{}&{} \\ {}&{{{\boldsymbol{T}}_{\text{d}}}}&{}&{} \\ {}&{}&{{{\boldsymbol{T}}_{\text{d}}}}&{} \\ {}&{}&{}&{{{\boldsymbol{T}}_{\text{d}}}} \end{array}} \right] $ | (15) |
| $ {{\boldsymbol{T}}_{\text{d}}} = \left[ {\begin{array}{*{20}{c}} {{\text{cos}}\phi }&0&{ - \sin \phi }&0&0&0 \\ 0&1&0&0&0&0 \\ {\sin \phi }&0&{\cos \phi }&0&0&0 \\ 0&0&0&{\cos \phi }&0&{ - \sin \phi } \\ 0&0&0&0&1&0 \\ 0&0&0&{\sin \phi }&0&{\cos \phi } \end{array}} \right] $ | (16) |
式(14)~(16)中:ke为总体刚度矩阵;T为坐标转换矩阵;
根据每个单元结点对应的编号,将平箔片的单元刚度矩阵组装为Kto,将波箔片的单元刚度矩阵组装为Kb;然后将平箔片和波箔片的刚度矩阵叠加,得到了三维箔片结构的整体刚度矩阵
| $ {\boldsymbol{K}} = \left[ {\begin{array}{*{20}{c}} {{{\boldsymbol{K}}_{\text{b}}}}&0 \\ 0&{{{\boldsymbol{K}}_{{\text{to}}}}} \end{array}} \right] $ | (17) |
所以,考虑了接触力的有限元方程
| $ {\boldsymbol{Ku}} - {{\boldsymbol{Q}}_{\text{c}}} = {{\boldsymbol{F}}_{\text{L}}} $ | (18) |
式中:u为所有单元节点的位移矢量;Qc为接触力矢量;FL为外力矢量。
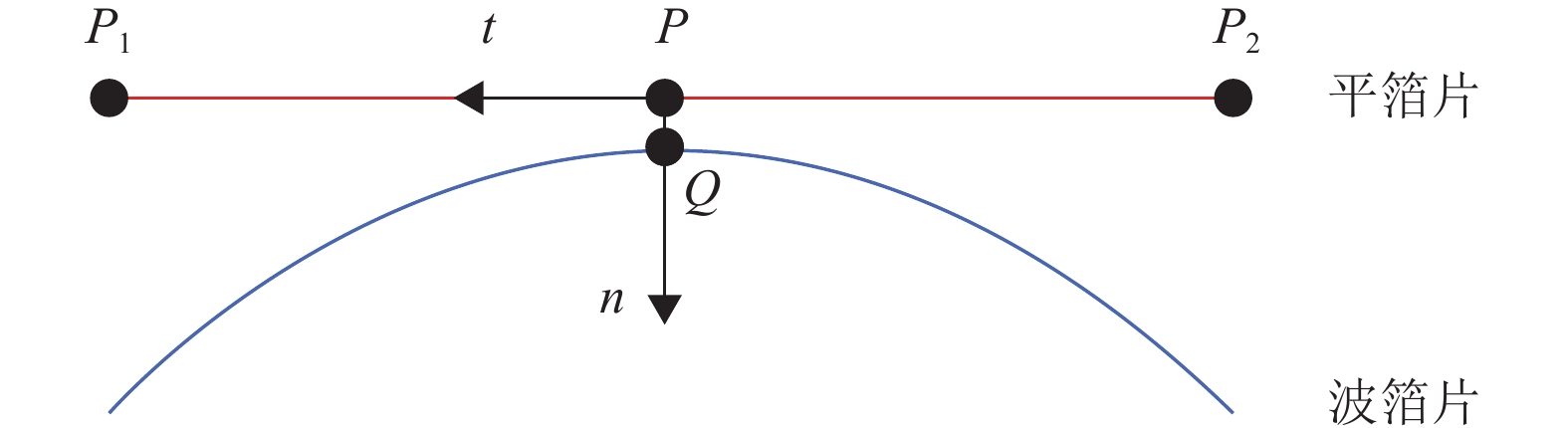
1.2 箔片轴承的摩擦接触模型采用点线接触方案和罚函数法,建立箔片轴承内部结构的摩擦接触模型,以图5中的平箔片和波箔片之间的接触对为例;平箔片为主体,波箔片为从体,波箔片的顶点定义为接触节点Q,其在平箔片上的投影点为P,P所在的单元由节点P1和P2定义,在P点建立局部坐标系。当主体与从体相互接触的时候,从体上的Q点处的法向接触力为
|
图 5 点线接触 Figure 5 Point-line contact |
| $ F_{\text{N}}^Q = - \alpha (u_{\text{N}}^Q - u_{\text{N}}^P + {g_0}) $ | (19) |
式中:α为罚因子;uN为法向位移;g0为初始法向间隙。
由于假设平箔片和波箔片的接触一开始是闭合的,即g0=0,施加到节点Q的法向接触力简化为
| $ F_{\text{N}}^Q = \left\{ {\begin{array}{*{20}{c}} { - \alpha (u_{\text{N}}^Q - u_{\text{N}}^P) ,}&{u_{\text{N}}^Q - u_{\text{N}}^P \leqslant 0} \\ {0,}&{u_{\text{N}}^Q - u_{\text{N}}^P > 0} \end{array}} \right. $ | (20) |
式中:α取值为1011 N/m时,既能得到足够精确的结果,又能使算法收敛。
由于该模型采用的库伦摩擦定律是非线性的,为了对其进行平滑处理,采用arctan函数,则施加到Q点处的切向接触力为
| $ F_{\text{T}}^Q = - \mu F_{\text{N}}^Q\frac{2}{{\text{π }}}\arctan \frac{{u_{\text{T}}^Q - u_{\text{T}}^P - u_{{{\text{T}}_{\text{0}}}}^{QP}}}{{{c_{\text{t}}}}} $ | (21) |
式中:
为了在保证收敛性能的同时实现库仑摩擦的良好近似,ct选择为105。接触点P的位移通过P1和P2的插值得到:
| $ \left\{ {\begin{array}{*{20}{c}} {{u^P}} \\ {{w^P}} \end{array}} \right\} = \left[ {\begin{array}{*{20}{c}} {{N_5}}&{} \\ {}&{{N_5}} \end{array}} \right]\left\{ {\begin{array}{*{20}{c}} {{u^{{P_1}}}} \\ {{w^{{P_1}}}} \end{array}} \right\} + \left[ {\begin{array}{*{20}{c}} {{N_6}}&{} \\ {}&{{N_6}} \end{array}} \right]\left\{ {\begin{array}{*{20}{c}} {{u^{{P_2}}}} \\ {{w^{{P_2}}}} \end{array}} \right\} $ | (22) |
其中
| $ \left\{ {\begin{array}{*{20}{c}} {{N_5} = {N_1}({\xi ^p}, - 1) = \dfrac{1}{2}(1 - {\xi ^P}) } \\ {{N_6} = {N_2}({\xi ^p}, - 1) = \dfrac{1}{2}(1 + {\xi ^P}) } \end{array}} \right. $ | (23) |
式中:u为周向位移;w为径向位移;
将P的位移转换到总体坐标系中可以得到
| $ \left\{ {\begin{array}{*{20}{c}} {u_{\text{T}}^Q - u_{\text{T}}^P} \\ {u_{\text{N}}^Q - u_{\text{N}}^P} \end{array}} \right\} = {{\boldsymbol{A}}^{\text{T}}}\left\{ {\begin{array}{*{20}{c}} {{u^Q} - {u^P}} \\ {{w^Q} - {w^P}} \end{array}} \right\} = {{\boldsymbol{A}}^{\text{T}}}\left\{ {\begin{array}{*{20}{c}} {{u^{QP}}} \\ {{w^{QP}}} \end{array}} \right\} $ | (24) |
其中
| $ \left\{ {\begin{array}{*{20}{c}} {{u^{QP}}} \\ {{w^{QP}}} \end{array}} \right\} = \left\{ {\begin{array}{*{20}{c}} { - {N_5}{u^{{P_1}}} - {N_6}{u^{{P_2}}} + {u^Q}} \\ { - {N_5}{w^{{P_1}}} - {N_6}{w^{{P_2}}} + {w^Q}} \end{array}} \right\} $ | (25) |
| $ {\boldsymbol{A}} = \left[ {\begin{array}{*{20}{c}} {{{\boldsymbol{e}}_{{\text{Ta}}}}}&{{{\boldsymbol{e}}_{\text{N}}}} \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} {{e_{{\text{Ta}}x}}}&{{e_{{\text{N}}x}}} \\ {{e_{{\text{Ta}}z}}}&{{e_{{\text{N}}z}}} \end{array}} \right] $ | (26) |
式中:A为变换矩阵,eTa和eN分别是矩阵A的切向分量和法向分量,根据箔片结构的接触方向,A=−I2×2或A=I2×2。所以式(24)可以简化为
| $ \left\{ {\begin{array}{*{20}{c}} {u_{\text{T}}^Q - u_{\text{T}}^P} \\ {u_{\text{N}}^Q - u_{\text{N}}^P} \end{array}} \right\} = J\left\{ {\begin{array}{*{20}{c}} {{u^{QP}}} \\ {{u^{QP}}} \end{array}} \right\},J = \pm 1 $ | (27) |
将式(20)、(21)、(27)联立得到节点Q的总接触力为
| $ {{\boldsymbol{F}}^Q} = \left\{ {\begin{array}{*{20}{c}} {F_{\text{T}}^Q} \\ {F_{\text{N}}^Q} \end{array}} \right\} = \alpha J{w^{QP}}\left[ {\begin{array}{*{20}{c}} {\dfrac{{2\mu }}{{\text{π}}}\arctan \dfrac{{J{u^{QP}} - u_{{{\text{T}}_{\text{0}}}}^{QP}}}{{{c_{\text{t}}}}}} \\ { - 1} \end{array}} \right] $ | (28) |
点Q与点P为一对节点,点Q与点P上的接触力相反,施加到点P的接触力应转换为施加到节点P1和节点P2的节点力,所以接触力Qc写为
| $ \begin{split} {{\boldsymbol{Q}}_{\text{c}}} = \;&{\boldsymbol{N}}_{\text{c}}^{\text{T}}{\boldsymbol{L}}{{\boldsymbol{F}}^Q} = {\boldsymbol{N}}_{\text{c}}^{\text{T}}\left[ {\begin{array}{*{20}{c}} {{{\boldsymbol{e}}_{\text{T}}}}&{{{\boldsymbol{e}}_{\text{N}}}} \end{array}} \right]{{\boldsymbol{F}}^Q} = \\ &\alpha J{w^{QP}}{\boldsymbol{N}}_{\text{c}}^{\text{T}}\left(\frac{{2\mu }}{{\text{π}}}\arctan \frac{{J{u^{QP}} - u_{{{\text{T}}_{\text{0}}}}^{QP}}}{{{c_{\text{t}}}}}{{\boldsymbol{e}}_{\text{T}}} - {{\boldsymbol{e}}_{\text{N}}}\right) \end{split} $ | (29) |
式中:
| $ {{\boldsymbol{N}}_{\text{c}}} = \left[ {\begin{array}{*{20}{c}} { - {N_5}}&0&{ - {N_6}}&0&1&0 \\ 0&{ - {N_5}}&0&{ - {N_6}}&0&1 \end{array}} \right] $ | (30) |
波箔片和轴承套之间的接触建模可以用类似的方式实现。由于轴承套是刚性的,即忽略其变形,因此建模过程更简单,此处省略。
1.3 增量迭代法由于上述的模型直接计算会产生发散的情况,因此,采用增量迭代法进行求解。在每一个增量步中的计算中应用牛顿−拉夫森迭代法,此时式(18)改写为
| $ ({\boldsymbol{K}} + {}^{t + \Delta t}{\boldsymbol{K}}_{\text{c}}^{(l) }) \Delta {{\boldsymbol{u}}^{(l) }} = {}^{t + \Delta t}{{\boldsymbol{F}}_{\text{L}}} - {}^{t + \Delta t}{{\boldsymbol{F}}^{(l) }} $ | (31) |
其中
| $ \begin{split} &{}^{t + \Delta t}{\boldsymbol{K}}_{\text{c}}^{(l) } = - \frac{{\partial {{\boldsymbol{Q}}_{\text{c}}}}}{{\partial {{\boldsymbol{u}}_{\text{c}}}}}|{{\boldsymbol{u}}_{\text{c}}} = - {}^{t + \Delta t}{\boldsymbol{u}}_{\text{c}}^{(l) }, \\ &\Delta {{\boldsymbol{u}}^{(l) }} = {}^{t + \Delta t}{{\boldsymbol{u}}^{(l + 1) }} - {}^{t + \Delta t}{{\boldsymbol{u}}^{(l) }}, \\ &{}^{t + \Delta t}{{\boldsymbol{F}}^{(l) }} = {{\boldsymbol{K}}^{t + \Delta t}}{{\boldsymbol{u}}^{(l) }} - {}^{t + \Delta t}{\boldsymbol{Q}}_{\text{c}}^{(l) }, \\ &{{\boldsymbol{u}}_{\text{c}}} = {\left[ {\begin{array}{*{20}{c}} {{u^{{P_1}}}}&{{w^{{P_1}}}}&{{u^{{P_2}}}}&{{w^{{P_2}}}}&{{u^Q}}&{{w^Q}} \end{array}} \right]^{\text{T}}} \end{split} $ | (32) |
在每一个增量步的迭代计算过程中,根据式(33)的条件来判断是否满足要求,重复计算直到满足再进行下一个增量步的计算。
| $ {\rm{er}} = \frac{{\left\| {{}^{t + \Delta t}{{\boldsymbol{F}}_{\text{L}}} - {}^{t + \Delta t}{{\boldsymbol{F}}^{(l) }}} \right\|_2^2}}{{1 + \left\| {{}^{t + \Delta t}{{\boldsymbol{F}}_{\text{L}}}} \right\|_2^2}} < {10^{ - 6}} $ | (33) |
式中:er为迭代残差;|| ||2为2-范数。
1.4 气膜压力求解为了获得箔片轴承的气膜压力分布情况,需要迭代求解雷诺方程,为方便进行对比,采用与文献[25]中相对应的参数。摩擦系数μ取0.1,能够有效地考虑箔片之间的摩擦力,箔片轴承的参数如表1所示。对于等温可压缩流体,雷诺方程表示为
| 表 1 箔片轴承结构参数 Table 1 Structural parameters of the foil bearing |
| $ \frac{1}{{{R^2}}}\frac{\partial }{{\partial \theta }}(p{h^3}\frac{{\partial p}}{{\partial \theta }}) + \frac{\partial }{{\partial y}}(p{h^3}\frac{{\partial p}}{{\partial y}}) = 6{\mu _{\text{a}}}\omega \frac{\partial }{{\partial \theta }}(ph) $ | (34) |
气膜厚度与箔片结构的变形相关,因此,膜厚h可表示为
| $ h = C + e\cos (\theta - \phi ) + {w_{\text{t}}} $ | (35) |
式中:C为名义间隙;e为转子的偏心距;ϕ为偏位角;θ为周向角度;wt为平箔片的径向变形。
使用有限差分法求解方程(34),在压力的迭代计算过程中,随着压力逐渐增加到目标值,wt在每一步中都会变化。在获得新的wt值后,将其代入式(35)中,得到新的h,然后用新的h代入式(34)中重新求解,这个过程重复进行。当偏心率变大时,解的收敛变得更加困难。为了解决这个问题,这里使用松弛迭代法,具体为
| $ {p^n} = {p^{n - 1}} + \gamma (\bar p - {p^{n - 1}}) $ | (36) |
式中:n为压力计算的第n步,γ为松弛因子,pn为根据方程(34)在第n步中计算的压力。为了提高算法的收敛性,γ应小于1。当偏心率增大时,需要较小的γ值。在文献[28]中,采用连续方法,在迭代过程中轴的角速度从小值开始,逐步增加到最终值,以提高数值解的收敛性,这里使用类似的方法。
通常认为箔片轴承的边缘以及箔片结构固定端和自由端的气压等于环境压力,因此,边界条件表示为
| $ \left\{ {\begin{array}{*{20}{c}} {p = {p_{\text{a}}},y = 0{\text{ or }}y = L} \\ {p = {p_{\text{a}}},\theta = 0{\text{ or }}\theta = 2{\text{π }}} \end{array}} \right. $ | (37) |
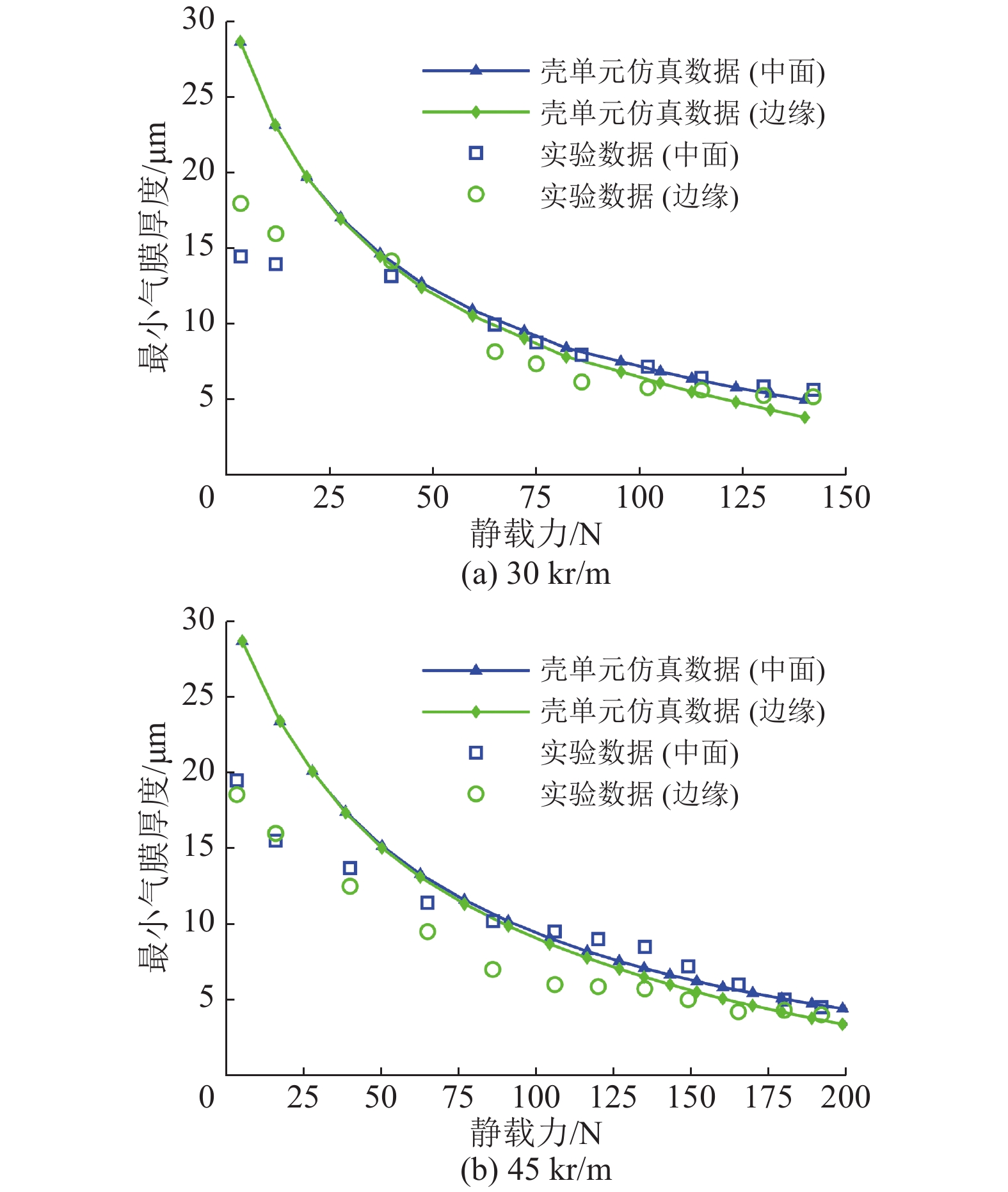
图6表明,当载荷比较小时,仿真数据比文献[25]的实验结果高出许多;但当载荷增加到一定值时,本模型的仿真数据与实验结果基本吻合,这证明了该模型的正确性。低载荷情况下本模型的误差较大,原因可能是在低载荷时,箔片结构的相互运动不太明显,只有小部分箔片产生了位移,本模型高估了低载荷下箔片结构的作用。
|
图 6 转速为30 kr/m、45 kr/m时最小气膜厚度与静载力的关系 Figure 6 Minimum film thickness versus static load for the operation at rotational speeds equal to 30 kr/m, 45 kr/m |
无论是仿真结果还是实验结果,轴承中截面均大于边缘,这可能是气体泄漏造成的,所以此处的箔片变形相对于边缘处要更大,最小气膜厚度更大。
在有限元求解的过程中,对有限单元数目的划分是一项重要的步骤,单元数目划分得越精细,计算结果就越接近真实值,但同时也会使计算过程变得复杂,应合理安排。在箔片轴承的仿真过程中,在周向上,平箔片被划分为78个单元数,波箔片的每个箔段被划分为8个单元,这样的划分在一般的二维模型中都能够得到很好的结果。在轴向上,单元数目的微小增加,就会使整体的计算规模变得巨大,数值求解可能会变得复杂。在能够得到比较准确的结果的前提下,对轴向单元数目的划分应该尽量精简。
表2为当转子转速为30 kr/m,偏心率为1时,第13个波箔片在中截面处和边缘处的变形量,其中,轴向单元数目分别选为10,14和18个时,得到了不同的结果。对比表中的3个轴向单元数目得到的结果,发现3种计算结果之间的差异不是很大。例如,取轴向单元数目为10时得到的结果与取18时得到的结果之间相差不到1%,所以轴向单元数目选10的时候就能很好地满足计算要求。
| 表 2 波箔的变形量对比 Table 2 Comparison of deflection of the bump μm |
在轴承−转子系统中,转子与轴承之间的错位很难避免,常常出现转子不对中的现象,其原因包括装配安装误差、热变形和制造误差等。这种转子不对中会导致气体箔片轴承和气体动压轴承的气膜压力分布发生变化,影响转子的稳定运行和轴承的承载能力。特别是在气体箔片轴承中,由于气膜厚度较小,即使微小的转子不对中也会改变气膜压力分布,使气膜压力在轴承轴向上分布不均匀,导致转子扰动和轴承承载力降低。此外,转子不对中还会导致气膜厚度减小,从而导致转子与轴承接触,造成箔片结构损坏。
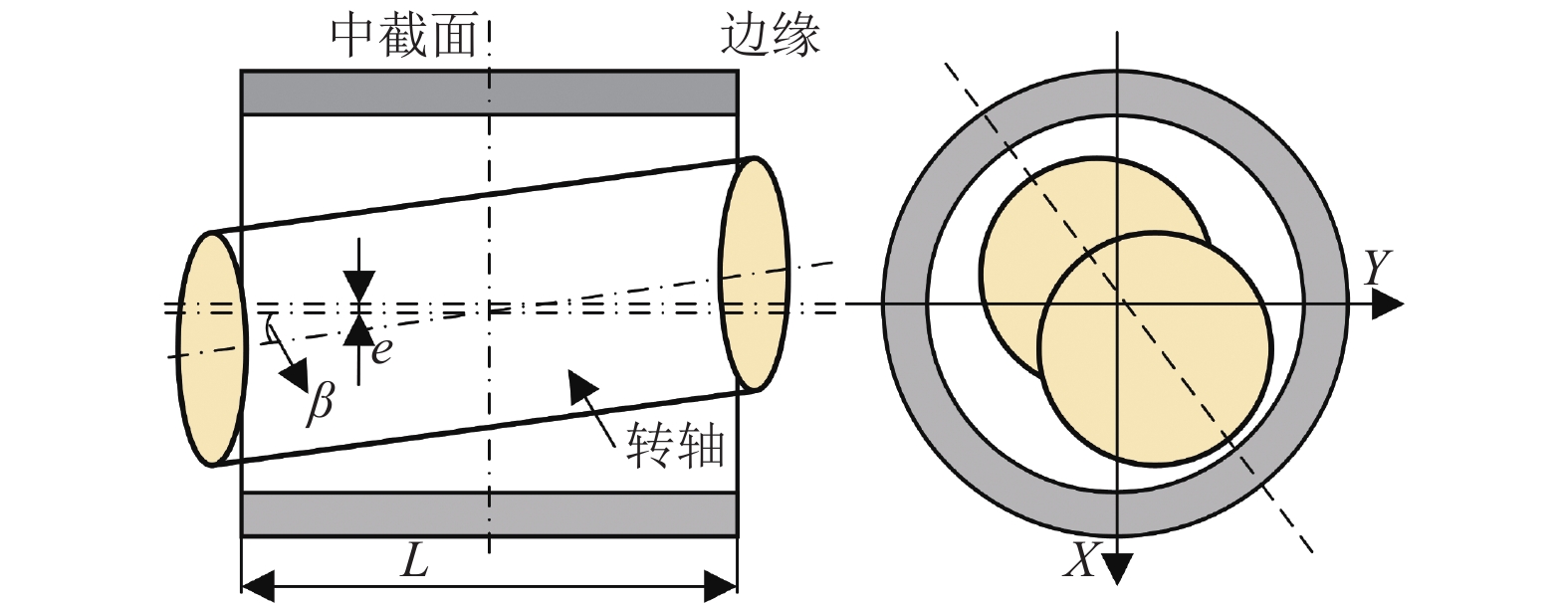
转子不对中主要分为轴向不对中和扭曲不对中,轴向不对中主要关注轴向方向上的偏移,而扭曲不对中则涉及转子轴的整体形变和形状不规则,本文主要研究轴向不对中。转子发生轴向不对中时,如图7所示,转子与轴承中心线之间的偏移量不为零,即转子在轴向上偏离了轴承的中心位置,此时,不对中的无量纲气膜厚度表示为
|
图 7 转子轴向不对中示意图 Figure 7 Rotor axial misalignment diagram |
| $ H = 1 + \frac{{e + (z - 0.5L) \tan \beta }}{C}\cos (\theta - \phi ) + \frac{{{w_{\text{t}}}}}{C} $ | (38) |
式中:β为倾斜角,θ为周向角度。
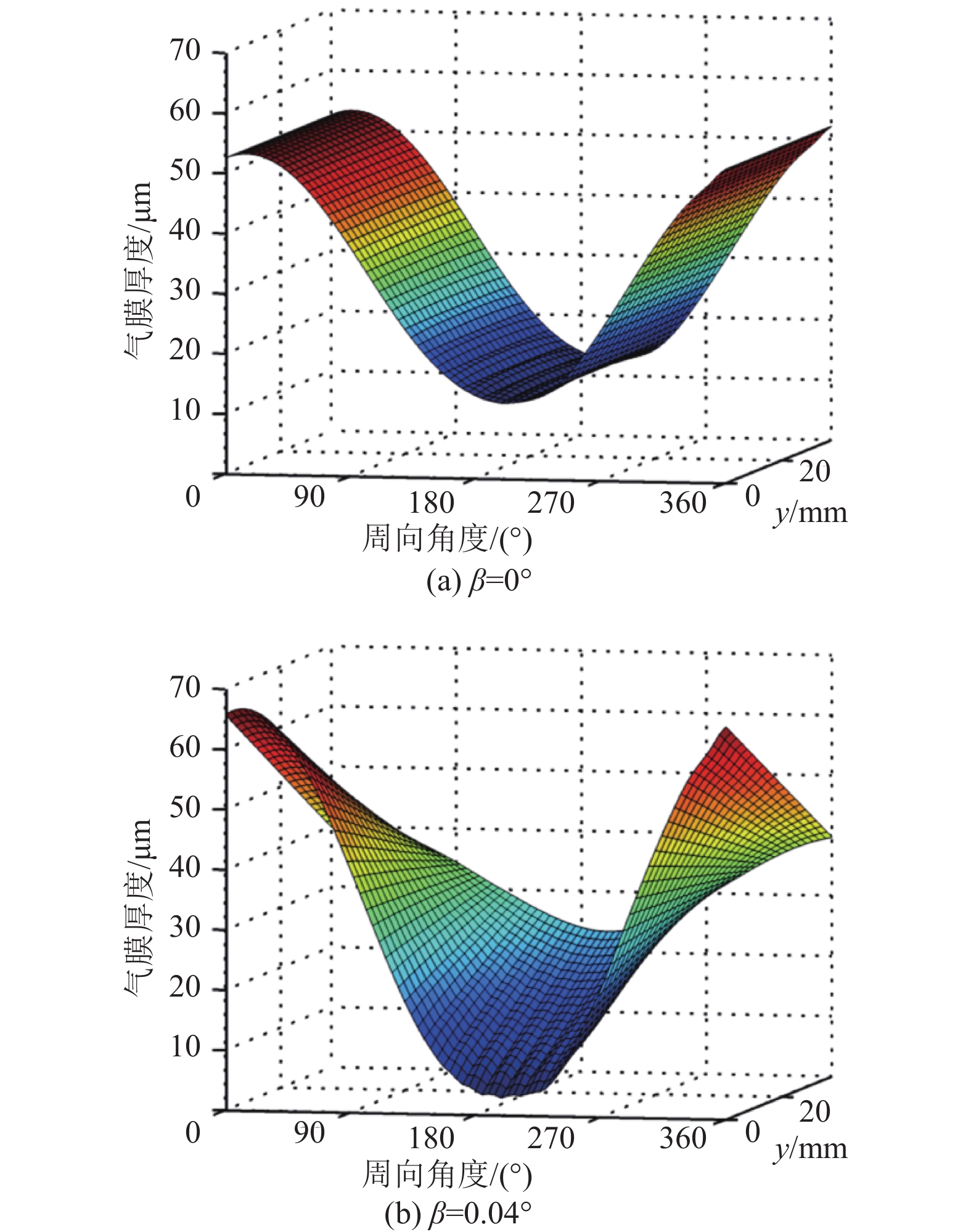
2.2.1 倾斜角对气膜分布的影响图8为转子−轴承正常配合(倾斜角为0°)和转子不对中(倾斜角为0.04°)时箔片轴承的气膜厚度分布示意图,仿真结果为当转子转速为30 kr/m、轴承承载力为41 N时得到。对比发现,当转子正常对中时,气膜厚度在整体上分布比较均匀,在轴向上气膜厚度关于轴承中截面对称,且在轴向上中截面处的气膜厚度要略大于轴承边缘处。而当转子发生不对中,即倾斜角为0.04°时,气膜厚度的分布不规则,此时在轴向上,轴承的一端的气膜厚度急剧减小接近零,而另一端的气膜厚度增大比较明显,两端的气膜厚度差异将会导致轴承的承载力下降,从而使轴承转子系统失稳。
|
图 8 气膜厚度分布 Figure 8 Film thickness distribution |
对于气体箔片轴承来说,最小气膜厚度与轴承承载能力息息相关。正常情况下,第一代气体箔片轴承的最小气膜厚度一般分布在轴承轴向上的两端边缘,但是当发生转子不对中的情况后,最小气膜厚度将会倾向于轴承的一端边缘。
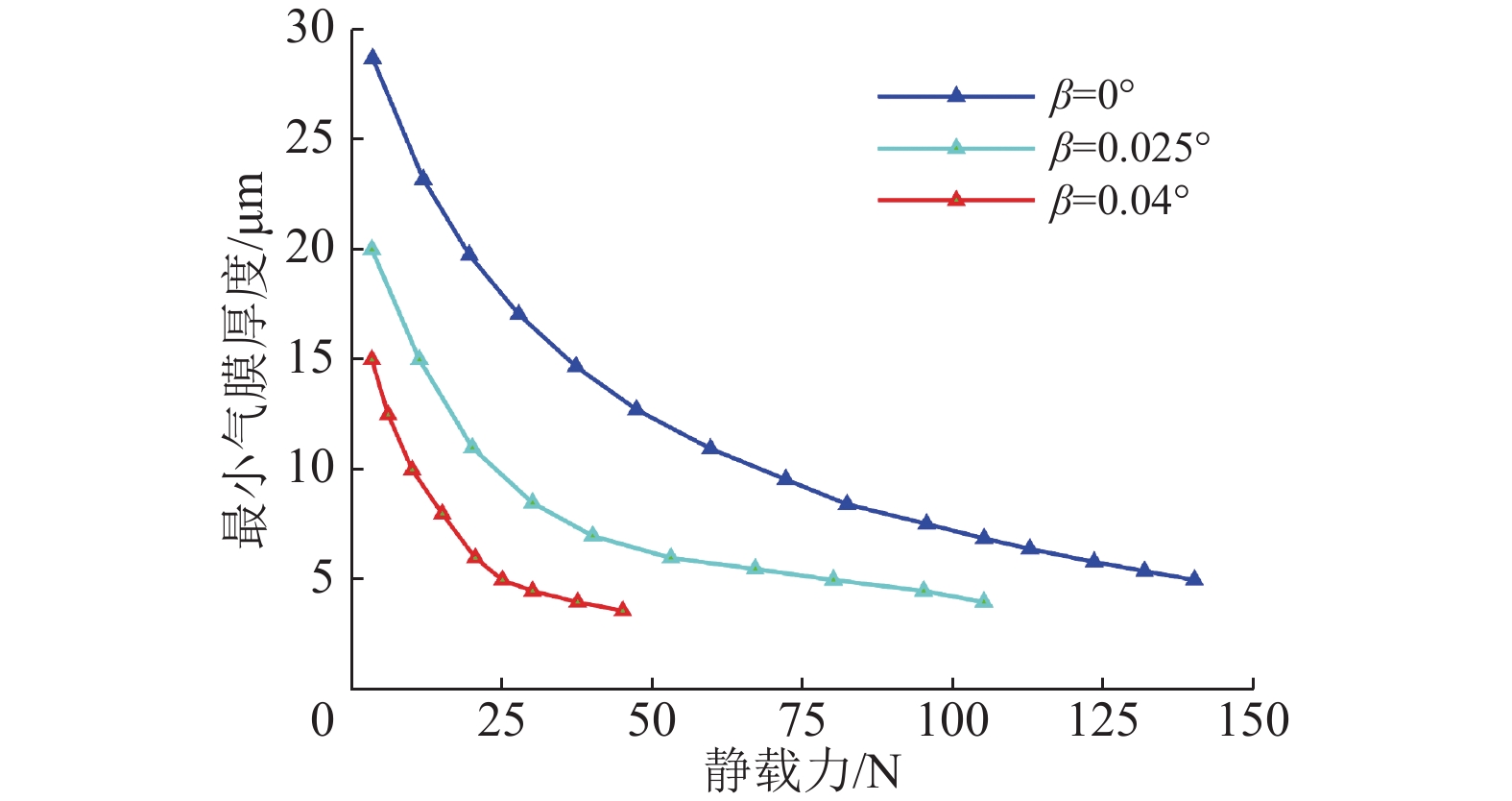
2.2.2 倾斜角对最小气膜厚度的影响图9为轴承最小气膜厚度与承载力的关系图。
|
图 9 不同倾斜角时箔片轴承的最小气膜厚度曲线 Figure 9 Minimum film thickness with the different tilt angles |
图9中转子转速为30 kr/m,倾斜角分别为0°、0.025°、0.04°。从图中可以看到,对于相同的承载力,不同的倾斜角的最小气膜厚度不同,倾斜角越大,最小气膜厚度就越小,随着承载力的增加,最小气膜厚度逐渐减小,且倾斜角越大,最小气膜厚度减小的趋势越快。例如,当承载力大概为41 N时,倾斜角为0.04°和0°下的最小气膜厚度分别为2.95 μm和12.67 μm,过小的气膜厚度会使轴承的承载能力下降,同时容易使转子与轴承边缘发生碰撞,从而损坏轴承结构,所以应该尽量避免转子不对中的发生。
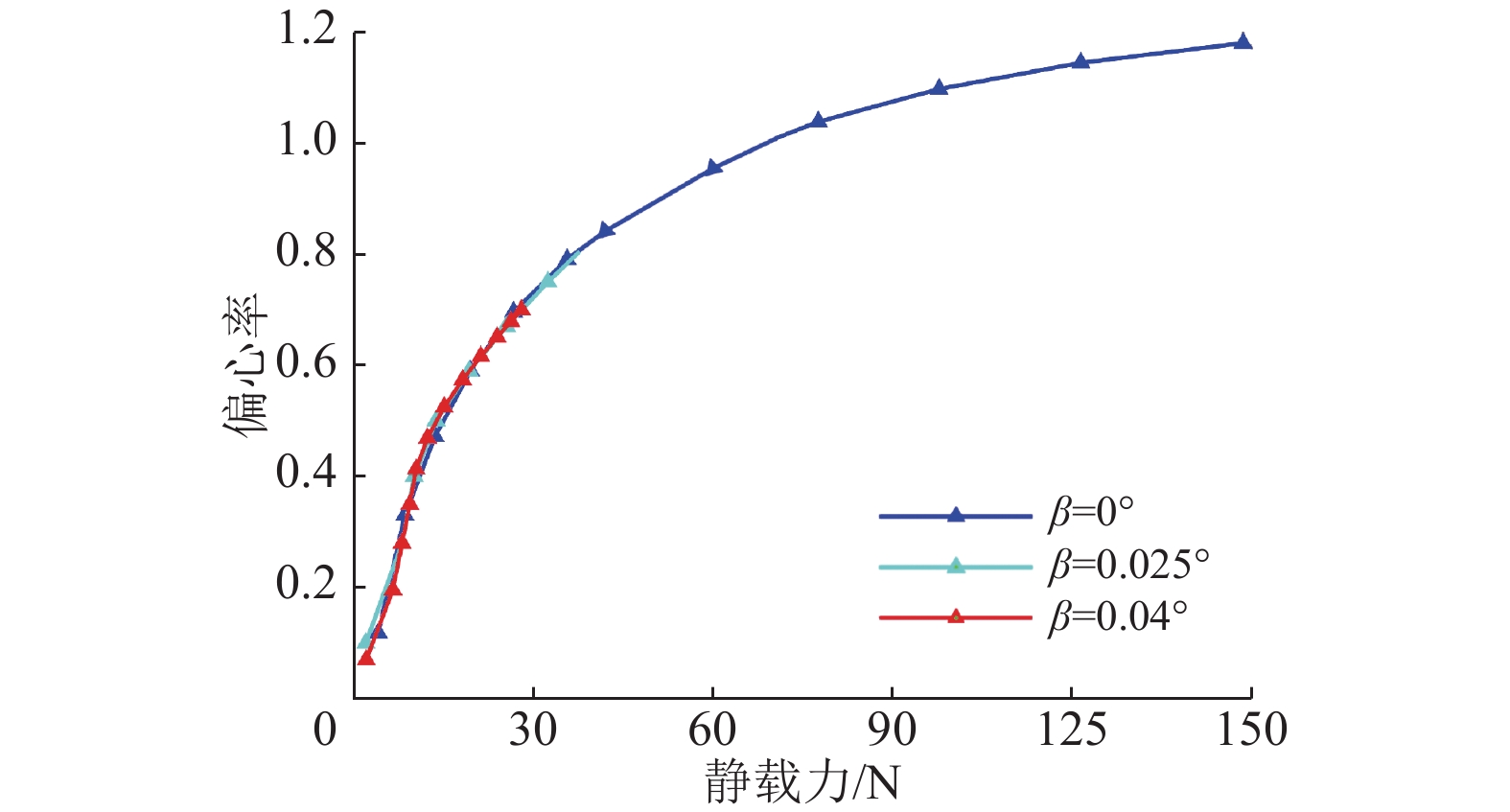
2.2.3 倾斜角对转子偏心率的影响由图8(b)可知,当转子发生不对中的时候,气膜厚度在轴向上会分布不均匀,不再关于中截面对称,此时转子在轴向上一端高另一端低。在相同的运行条件下,对比不同的倾斜角时转子偏心率与轴承承载力的关系,如图10所示。从图中可以发现,随着承载力的增大,不同倾斜角下的偏心率均一致,3条曲线几乎重合,说明不同的倾斜角对转子偏心率并没有影响,即转子不对中不会影响偏心率。原因是当发生转子不对中时,在轴向上,轴承一端的气膜厚度增大另一端相对减小,承载力在轴承的两端也是如此,总的承载力未发生变化,所以转子的偏心率也不会发生改变。
|
图 10 不同倾斜角时转子偏心率随承载力变化曲线 Figure 10 Eccentricity of the rotor versus static load with the different tilt angles |
图11为当倾斜角分别为0°与0.025°时,箔片轴承平箔片的径向位移的三维分布图,转子转速为30 kr/m,承载力为100 N。从图中可以看到,平箔片的变形不平滑,为锯齿状。这是因为从固定端到自由端,每一段平箔片的刚度都不一样,在与波箔片接触的那一部分平箔片刚度较大,变形较小,在每两段波箔片之间的那一部分平箔片刚度较大,变形量相对较大。当倾斜角为0°时,箔片轴承的平箔片的变形在轴向上关于中截面对称,且边缘处的变形量相对于中截面处要小。当倾斜角为0.025°时,箔片轴承的变形变得不均匀,其中,一端边缘的变形很小,另一端要大得多。因此,在相同运行条件下,转子不对中会使箔片结构的变形变得不规则。
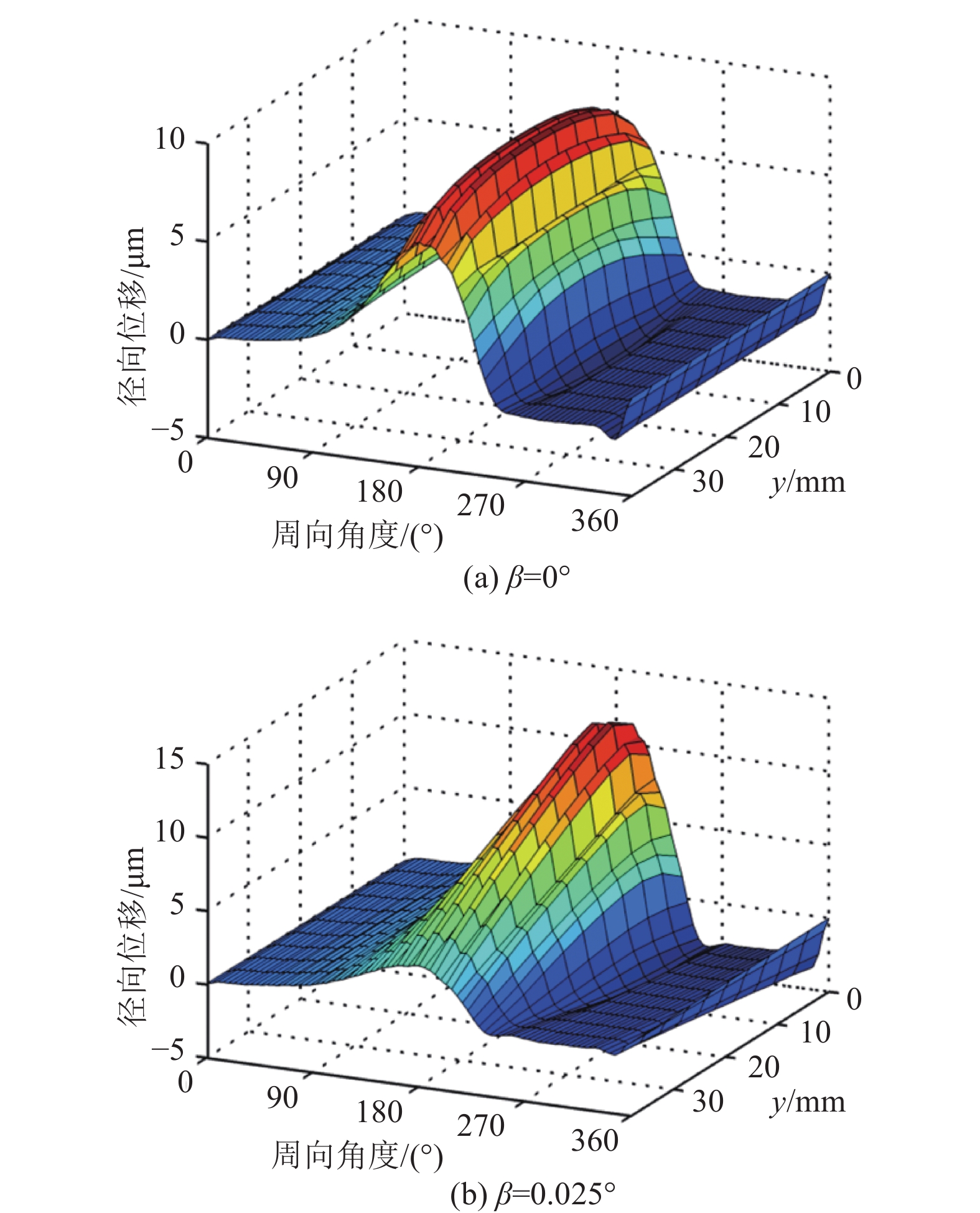
|
图 11 平箔片的变形 Figure 11 Deflections of the top foil |
建立了一种考虑轴向不对中情况下的气体箔片轴承的三维有限元模型,平箔片和波箔片采用壳单元建模,壳单元由平面应力单元和板单元组合而成,考虑了平箔片的变形效应和箔片结构之间的相互作用,能够很好地模拟轴承结构轴向上的刚度变化情况。为了对箔片结构的摩擦接触进行建模,使用罚函数方法并对库仑摩擦定律进行正则化以实现稳定的数值程序算法,解释了如何将摩擦接触集成到有限元方程中,由于摩擦接触的非线性,采用增量迭代法求解方程。
仿真模型表明,在正常的情况下,预测的轴承中截面处最小气膜厚度大于边缘处,这与实验结果一致,验证了模型的正确性。当发生转子不对中的情况时,最小气膜厚度将会倾向于轴承的一端边缘,当承载力约为41 N时,倾斜角为0°和0.04°下的最小气膜厚度分别为12.67 μm和2.95 μm,下降超过75%,过小的气膜厚度会使轴承的承载能力下降,且随着倾斜角的增大,最小气膜厚度减小的趋势越快,这使转子系统不稳定。然而,对于不同程度不对中的相同静载荷,偏心率是相同的,这意味着不对中对箔片轴承转子系统总体刚度的影响可以忽略不计。正常情况下平箔片的最大变形量大约为7 μm,且轴向上变形均匀,当发生不对中现象时,在轴向上,平箔片一端的变形超过10 μm,而另一端的变形在2 μm左右,两端相差太大,这会使轴承的承载能力下降,应尽量避免转子不对中现象。
| [1] |
WALTON J F, HOOSHANG H, TOMASZEWSKI M J. Testing of a small turbocharger/turbojet sized simulator rotor supported on foil bearings[J].
Journal of Engineering for Gas Turbines and Power, 2008, 130(3): 320-326.
|
| [2] |
KIM K S, LEE I. Vibration characteristics of a 75 kW turbo machine with air foil bearings[J].
Journal of Engineering for Gas Turbines and Power, 2007, 129(3): 843-849.
DOI: 10.1115/1.2718220. |
| [3] |
DELLACORTE C, VALCO M J. Load capacity estimation of foil air journal bearings for oil-free turbomachinery applications[J].
Tribology Transactions, 2000, 43(4): 795-801.
DOI: 10.1080/10402000008982410. |
| [4] |
HESHMAT H, WALOWIT J, PINKUS O. Analysis of gas-lubricated foil journal bearings[J].
Journal of Lubrication Technology, 1983, 105(4): 647-655.
DOI: 10.1115/1.3254697. |
| [5] |
HESHMAT H, WALOWIT J A, PINKUS O. Analysis of gas-lubricated compliant thrust bearings[J].
Journal of Lubrication Technology, 1983, 105(4): 638-646.
DOI: 10.1115/1.3254696. |
| [6] |
PENG J P, CARPINO M. Calculation of stiffness and damping coefficients for elastically supported gas foil bearings[J].
Journal of Tribology, 1993, 115(1): 20-27.
DOI: 10.1115/1.2920982. |
| [7] |
PENG Z C, KHONSARI M M. Hydrodynamic analysis of compliant foil bearings with compressible air flow[J].
Journal of Tribology, 2004, 126(3): 542-546.
DOI: 10.1115/1.1739242. |
| [8] |
LI Y, LEI G, SUN Y, et al. Effect of environmental pressure enhanced by a booster on the load capacity of the aerodynamic gas bearing of a turbo expander[J].
Tribology International, 2017, 105: 77-84.
DOI: 10.1016/j.triboint.2016.09.027. |
| [9] |
KU C P R, HESHMAT H. Compliant foil bearing structural stiffness analysis: part I–theoretical model including strip and variable bump foil geometry[J].
Journal of Tribology, 1992, 114(2): 394-400.
DOI: 10.1115/1.2920898. |
| [10] |
LE LEZ S, ARGHIR M, FRENE J. A new bump-type foil bearing structure analytical model[J].
Journal of Engineering for Gas Turbines and Power, 2007, 129(4): 1047-1057.
DOI: 10.1115/1.2747638. |
| [11] |
LE LEZ S, ARGHIR M, FRENE J. Static and dynamic characterization of a bump-type foil bearing structure[J].
Journal of Tribology, 2007, 129: 75-83.
DOI: 10.1115/1.2390717. |
| [12] |
LE LEZ S, ARGHIR M, FRENE J. Nonlinear numerical prediction of gas foil bearing stability and unbalanced response[J].
Journal of Engineering for Gas Turbines and Power, 2009, 131(1): 012503.
DOI: 10.1115/1.2967481. |
| [13] |
PETROV E P, EWINS D J. Generic friction models for time-domain vibration analysis of bladed disks[J].
Journal of Turbomachinery, 2004, 126(4): 184-192.
|
| [14] |
OSMANSKI V S, LARSEN J S, SANTOS I F. A fully coupled air foil bearing model considering friction-theory & experiment[J].
Journal of Sound and Vibration, 2017, 400: 660-679.
DOI: 10.1016/j.jsv.2017.04.008. |
| [15] |
ARGHIR M, BENCHEKROUN O. A simplified structural model of bump-type foil bearings based on contact mechanics including gaps and friction[J].
Tribology International, 2019, 134: 129-144.
DOI: 10.1016/j.triboint.2019.01.038. |
| [16] |
ARGHIR M, BENCHEKROUN O. A new structural bump foil model with application from start-up to full operating conditions[J].
Journal of Engineering for Gas Turbines and Power, 2019, 141(10): 101017.
DOI: 10.1115/1.4044685. |
| [17] |
MAHNER M, LI P, LEHN A, et al. Numerical and experimental investigations on preload effects in air foil journal bearings[J].
Journal of Engineering for Gas Turbines and Power, 2018, 140(3): 032505.
DOI: 10.1115/1.4037965. |
| [18] |
MAHNER M, BAUER M, SCHWEIZER B. Numerical analyzes and experimental investigations on the fully-coupled thermo-elasto-gasdynamic behavior of air foil journal bearings[J].
Mechanical Systems and Signal Processing, 2020, 149: 107221.
|
| [19] |
LEE D H, KIM Y C, KIM K W. The dynamic performance analysis of foil journal bearings considering coulomb friction: rotating unbalance response[J].
Tribology Transactions, 2009, 52(2): 146-156.
DOI: 10.1080/10402000802192685. |
| [20] |
LEE D H, KIM Y C, KIM K W. The effect of Coulomb friction on the static performance of foil journal bearings[J].
Tribology International, 2010, 43(5-6): 1065-1072.
DOI: 10.1016/j.triboint.2009.12.048. |
| [21] |
FENG K, KANEKO S. Analytical model of bump-type foil bearings using a link-spring structure and a finite-element shell model[J].
Journal of Tribology, 2010, 132(2): 021706.
DOI: 10.1115/1.4001169. |
| [22] |
FENG K, ZHAO X, HUO C, et al. Analysis of novel hybrid bump-metal mesh foil bearings[J].
Tribology International, 2016, 103: 529-539.
DOI: 10.1016/j.triboint.2016.08.008. |
| [23] |
HOFFMANN R, MUNZ O, PRONOBIS T, et al. A valid method of gas foil bearing parameter estimation: a model anchored on experimental data[J].
Proceedings of the Institution of Mechanical Engineers, Part C:Journal of Mecha; nical Engineering Science, 2018, 232(24): 4510-4527.
DOI: 10.1177/0954406216667966. |
| [24] |
HOFFMANN R, LIEBICH R. Experimental and numerical analysis of the dynamic behaviour of a foil bearing structure affected by metal shims[J].
Tribology International, 2017, 115: 378-388.
DOI: 10.1016/j.triboint.2017.04.040. |
| [25] |
RUSCITTO D, MCCORMICK J, GRAY S. Hydrodynamic air lubricated compliant surface bearing for an automotive gas turbine engine.1. Journal bearing performance[R/OL]. (1978-04-01)[2023-08-30]. https://doi.org/10.2172/7095892.
|
| [26] |
SAN ANDRES L, KIM T H. Improvements to the analysis of gas foil bearings: integration of top foil 1D and 2D structural models.[J].
American Society of Mechanical Engineers Digital Collection, 2007, 47942: 779-789.
|
| [27] |
LEE D H, KIM Y C, KIM K W. The static performance analysis of foil journal bearings considering three-dimensional shape of the foil structure[J].
Journal of Tribology, 2008, 130(3): 031102.
DOI: 10.1115/1.2913538. |
| [28] |
LEHN A, MAHNER M, SCHWEIZER B. Elasto-gasdynamic modeling of air foil thrust bearings with a two-dimensional shell model for top and bump foil[J].
Tribology International, 2016, 100: 48-59.
DOI: 10.1016/j.triboint.2015.11.011. |
 2024, Vol. 41
2024, Vol. 41

