压缩感知(Compressed Sensing，CS) 是一种有效的信息采集技术^[1-2]，奈奎斯特采样定理要求信号的采样频率必须大于其最高频率的两倍以上才能保证完全重构原始信号，而压缩感知可以使用测量矩阵以远低于奈奎斯特采样特理论要求的采样率从测量值中重构出原始信号。压缩感知理论的出现不仅降低了信号采集的难度，而且减少了存储空间的消耗。压缩感知技术被应用于核磁共振成像^[3]，雷达成像^[4]，视频压缩^[5]等领域。

压缩感知重构是压缩感知理论的核心问题之一，目标是从降维的测量值中重构出被采样的原始信号。传统的压缩感知重构方法专注于探索有理论保证的结构稀疏先验信息，再利用迭代优化的方法求解。这类方法具有较高的计算复杂性，并且要求较高的参数微调能力。

近年来，卷积神经网络在图像恢复方面取得较大成功。文献[6]提出一个非迭代的基于卷积神经网络的CS重构方法，证实了基于神经网络的CS重构的可行性，但逐块重构的方式导致出现许多块状伪影。文献[7]提出联合学习采样矩阵和重构进程的网络，有效抑制了伪影。为了实现网络的可扩展性，Shi W Z等^[8]提出SCSNet，通过一个模型处理多个采样率任务。一些研究者提出了基于深度学习的展开CS方法。基于迭代收缩阈值算法^[9]，Zhang J等^[10]将其展开为更灵活的网络，名为ISTA-Net，文献[11]进一步提出ISTA-Net⁺⁺网络，能够灵活处理多个采样率和多场景的任务。

除了网络结构和优化算法设计，采样率分配也被学者所关注。根据人类视觉系统的特性，Yu Y等^[12]提出分配更少采样率给非显著块，显著块分配更多采样率的策略。文献[13]也基于显著性设计了一个多通道的网络来分配不同的采样率给不同块，重构精度更高,但是手工设计的显著性检测方法适应性差。基于采样矩阵的约束等距性质^[14](Restricted Isometry Property，RIP)，Qiu C X等^[15]提出一个自适应和级联的卷积网络名为ACCSNet，依靠级联架构实现了采样率的自适应分配，但是级联架构只能针对特定采样率训练，缺乏灵活性。

本文基于测量域的误差估计图像块重构难度，提出有效的分配策略，保证了低采样率下的重构效果。通过掩码生成特定采样率的采样矩阵，实现了一个模型处理多个采样率任务，降低了存储消耗。提出跨阶段的通道连接和双支路的特征融合模块，增强了上下文信息的交互，并自适应调整不同支路权重，提高了网络的重构能力。

1 相关工作

图像压缩感知方法可以分为两类，一类是基于优化理论的方法，第二类是基于网络的方法。

1.1 压缩感知重构方法 1.1.1 基于优化理论的方法

压缩感知理论指出，假设一个原始信号$ {\boldsymbol{x}}_{N\times 1} $是可压缩的，则采样进程描述为：$ {\boldsymbol{y}} = {\boldsymbol{\varPhi x}} $，式中观测值y为M×1维向量。Φ为M×N维观测矩阵，采样率为M/N，(M 一般远小于N) 。从y中恢复x这种病态逆问题可以转化为下面的优化问题，这个优化问题通常被假设是凸的。

$ \hat {\boldsymbol{x}} = \mathop {\arg \min }\limits_x \frac{1}{2}\left\| {{\boldsymbol{\varPhi x}} - {\boldsymbol{y}}} \right\|_2^2 + \lambda \psi \left( {\boldsymbol{x}} \right) $

(1)

式中：$\psi \left( {\boldsymbol{x}} \right) $表示正则函数，$\lambda $是正则参数。各种计算成本较低的迭代方法被用来求解此问题，如迭代硬阈值算法^[9]、近似消息传递算法^[16]和交替方向乘子法^[17]等。

1.1.2 基于网络的方法

文献[6]最早提出利用卷积网络从观测值中重构图像块。在文献[9]和文献[16]的基础上，文献[18]和文献[19]分别被提出，进一步探索块间关系和增强采样矩阵的性能，提高了重构质量。文献[20]提出COAST网络，增强了对任意采样矩阵的适用性。文献[21]提出了一个特征优化启发网络，在特征空间分阶段实现信息流，获得了好的重构效果。

1.2 误差钳制原理

Candes E J提出约束等距性质^[14]，理论指出：当观测矩阵Φ满足约束等距性质，则有

$ (1 - \delta ) \left\| {\boldsymbol{x}} \right\|_2^2 \leqslant \left\| {{\boldsymbol{\varPhi x}}} \right\|_2^2 \leqslant (1 + \delta ) \left\| {\boldsymbol{x}} \right\|_2^2 $

(2)

式中：$\delta $$ \in $(0,1) 。在缺乏真实图像的情况下，如何去评估重构误差$\left\| {\Delta {\boldsymbol{x}}} \right\|_2^2$的大小。根据观测矩阵Φ和重构结果$\hat {\boldsymbol{x}}$的关系，可以通过式(3)计算观测值的误差。

$ {{\Delta }}{\boldsymbol{y}} = {\boldsymbol{\varPhi}} {{\Delta }}{\boldsymbol{x}} = {\boldsymbol{\varPhi}} \left( {{\boldsymbol{x}} - \hat {\boldsymbol{x}}} \right) = {\boldsymbol{y}} - {\boldsymbol{\varPhi}} \hat {\boldsymbol{x}} $

(3)

式中：x表示真实图像，y表示观测值。由限制等距性质得到下列不等式

$ \frac{{\left\| {{{\Delta }}{\boldsymbol{y}}} \right\|_2^2}}{{(1 + \delta ) }} \leqslant \left\| {{{\Delta }}{\boldsymbol{x}}} \right\|_2^2 \leqslant \frac{{\left\| {{{\Delta }}{\boldsymbol{y}}} \right\|_2^2}}{{(1 - \delta ) }} $

(4)

式中：$\delta $$ \in $(0,1) 。RIP性质提供了$\left\| {{{\Delta }}{\boldsymbol{x}}} \right\|_2^2$的双边钳制，因此，可以总结得到，如果$\left\| {{{\Delta }}{\boldsymbol{y}}} \right\|_2^2$相对较大，则$\left\| {{{\Delta }}{\boldsymbol{x}}} \right\|_2^2$可能也较大，反之亦然。

2 算法设计 2.1 网络框架

本文设计的网络框架如图1所示，包含4个子网：误差预测子网(Error Prediction Subnet，EPSNet) 、采样子网、初始化子网、恢复子网。原始图像先输入误差预测子网来评估图像块的重构难度，以此指导后续的采样和初始化，生成初始重构图像，再经过深度重构网络增强后输出重构图像。

2.2 误差预测子网

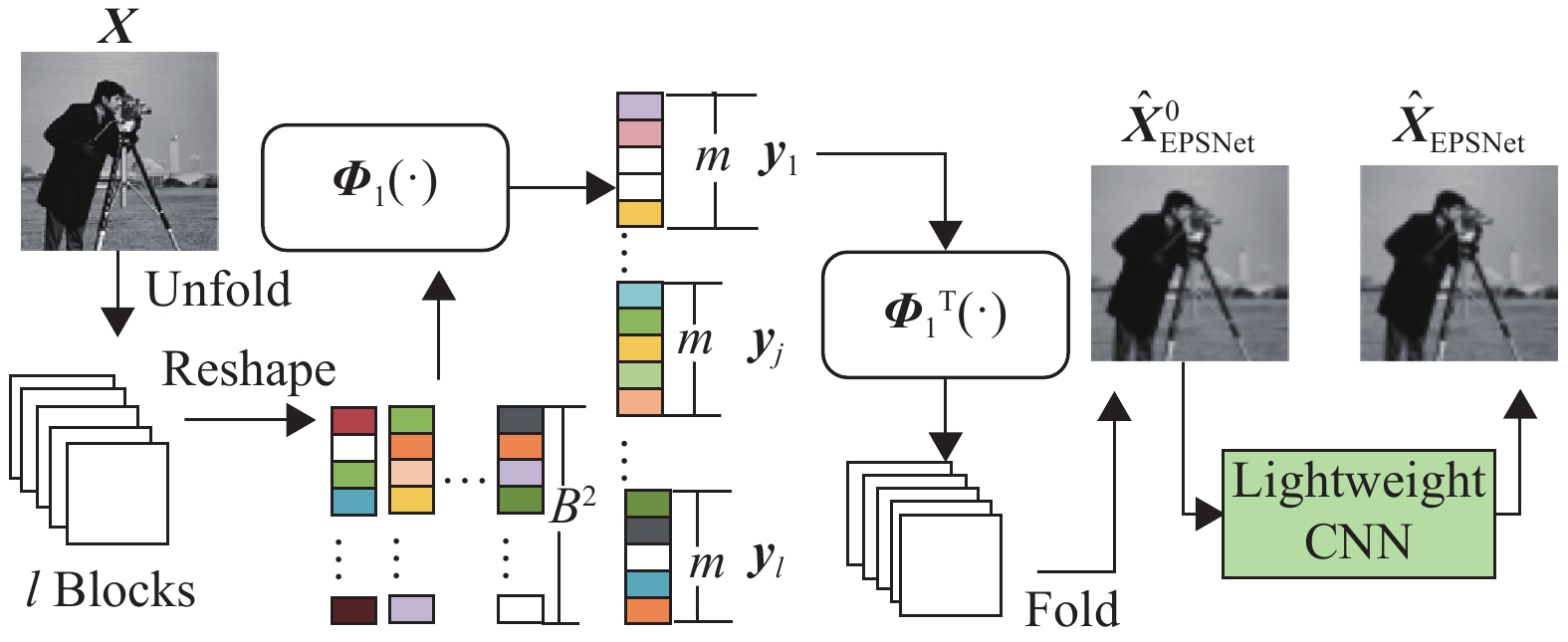
误差预测子网的框架如图2所示，包含采样、初始化、轻量化重构和误差估计等4个进程。

为了更好地表述4个进程,假设输入图像$ {\boldsymbol{X}}_{H\times W} $，图像被展开为l块大小为B×B的块$\{ {{\boldsymbol{x}}_j}\} _{j = 1}^l$。可学习的观测矩阵$ {\boldsymbol{\varPhi }}_{N\times N} $，其中N=B² ，采样率为M/N。通过公式Φ₁ = Φ[1:M,1:N ]生成Φ₁，进行均匀采样，第j块的采样进程可以描述为$ {\boldsymbol{y}}_j^1 = {{\boldsymbol{\varPhi}} _1}{{\boldsymbol{x}}_j} $，初始化进程可以描述为$ \hat {\boldsymbol{x}}_j^1 = {\boldsymbol{\varPhi}} _1^{\rm{T}}{\boldsymbol{y}}_j^1 $。$ {\boldsymbol{\varPhi}} _1^{\rm{T}} $表示$ {{\boldsymbol{\varPhi}} _1} $的转置矩阵，这些块被折叠得到初始化结果$ \hat {\boldsymbol{X}}_{{\text{EPSNet}}}^0 $。经过包含两个残差块的轻量化残差卷积网络得到重构结果$ \hat {\boldsymbol{X}}_{{\text{EPSNet}}}^{} $，通过式(5)计算第j块的观测值误差。

$ {{\Delta }}{\boldsymbol{y}}_j^1 = {\boldsymbol{y}}_j^1 - {{\boldsymbol{\varPhi}} _1}\hat {\boldsymbol{x}}_j^1 $

(5)

式中：$ \hat {\boldsymbol{x}}_j^1 $为$ \hat {\boldsymbol{X}}_{{\text{EPSNet}}}^{} $展开后的第j个图像块，$ {\boldsymbol{y}}_j^1 $表示误差预测子网初始化阶段对应第j块的观测值。用$\left\| {{{\Delta }}{\boldsymbol{y}}_j^1} \right\|_2^2$来评估$\left\| {{{\Delta }}{\boldsymbol{x}}_j^1} \right\|_2^2$的误差大小，误差比例信息用V表示，则通过式(6)评估第j个子块的V_j。

$ {V_j} = \left\| {{{\Delta }}{\boldsymbol{y}}_j^1} \right\|_2^2\bigg/\sum \left\| {{{\Delta }}{\boldsymbol{y}}_j^1} \right\|_2^2 $

(6)

算法1展示了采样率sr分配的过程。为了保证低采样率下块的测量值不会太小，本文设置了γ 来控制分配的基础测量值和自适应采样测量值的比例。在低采样率时，可以最大程度保留图像的基本信息；高采样率时，可以提高自适应采样资源分配的比例，来获得更好的重构质量。

$ \gamma =\left\{ {\begin{array}{*{20}{l}} 0.8, & {\rm{sr}}\le 0.1 \\ 0.95-{\rm{sr}}, & 0.1 < {\rm{sr}}\le 0.5\end{array}} \right. $

(7)

算法1　采样率自适应分配策略

1) 输入：图像大小为H×W，块大小为B×B，采样率为sr，误差比例信息为V。

(a) 块的数量用l表示：l = (H/B) ×(W/B) ；

(b) 全部的像素数用total表示：total = H×W×sr；

(c) 基础采样数用base表示：base = sr × B² × γ；

(d) for j = 1：l do

　　　m_j = base + round ( total×V_j ) ×( 1－γ)

　　 end for

2) 输出：每个块分配测量值的数量m_j。

为了体现自适应分配采样率的优点，图3展示了两张图像“摄影师”和“鹦鹉”的测量数分布。图像块内的数字表示分配到的测量数。从图3可以看到，细节更多的块分配了更多的测量资源。例如“摄影师”图片中的相机和“鹦鹉”的眼睛周围有更多复杂的结构和纹理，这些块更难重构，所以被分配了更多测量资源。

2.3 采样子网

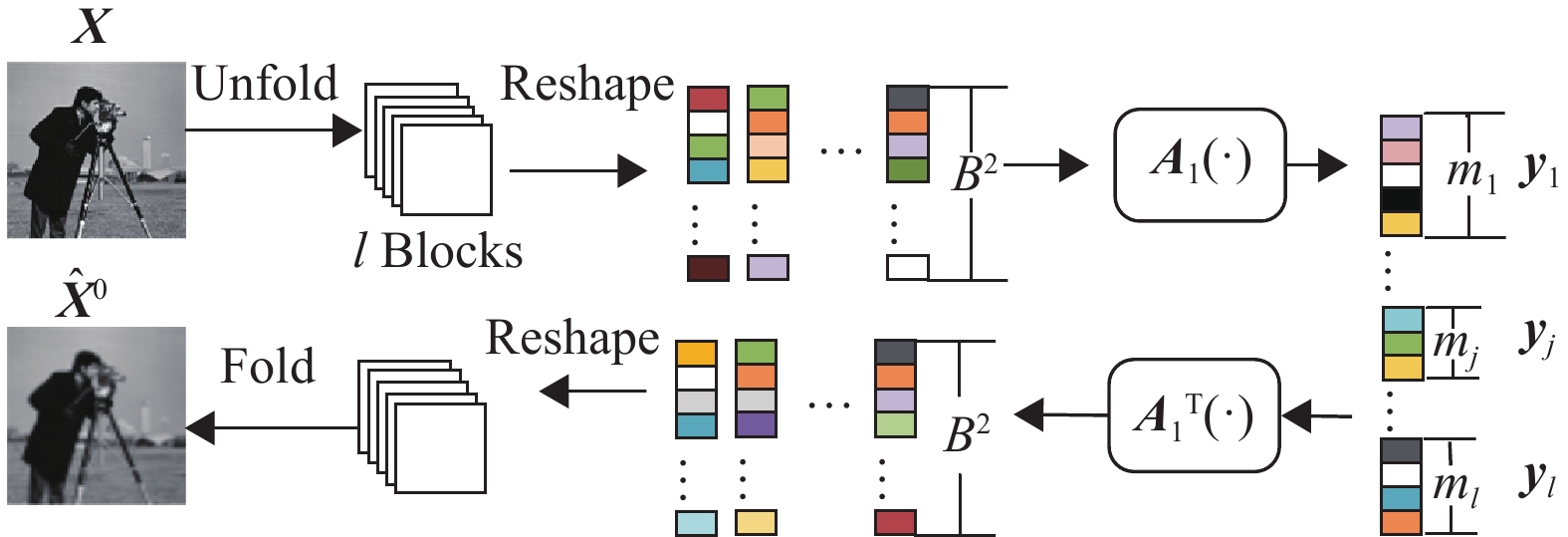
如图4所示，原始图像被展开成l块大小为B×B的块，块x_j的采样过程为：$ {{\boldsymbol{y}}}_{j}={{\boldsymbol{A}}}_{1}{{\boldsymbol{x}}}_{j} $，其中A₁是块x_j分配的测量数m_j对应的采样矩阵。若使用不同的采样率所对应的观测矩阵，将会大量消耗存储空间。使用观测矩阵$ {\boldsymbol{A}}_{N\times N} $乘以掩码矩阵M来生成新观测矩阵A₁，进程描述为$ {{\boldsymbol{A}}}_{1}={\boldsymbol{A}}\otimes {\boldsymbol{M}} $，其中M[1:m_j,:]=1, M[m_j+1:B²_,:]=0，$ \otimes $表示逐元素相乘。

2.4 初始化子网

初始化进程如图4所示，每个块独立进行初始化，y_j初始化的进程可以描述：$\hat {\boldsymbol{x}}_j^0 = {({{\boldsymbol{A}}_1}) ^{\rm{T}}}{{\boldsymbol{y}}_j}$ ，然后所有的块被折叠以形成原图像大小的初始化结果${\hat {\boldsymbol{X}}^0}$。

2.5 恢复子网

本文通过展开传统的近似梯度下降(Proximal Gradient Descent，PGD) ，利用公式(8)～(9)的迭代更新解决等式(1) 的问题。

$ {{\boldsymbol{z}}^k} = {\hat {\boldsymbol{x}}^{k - 1}} - \rho {{\boldsymbol{\varPhi}} ^{\rm{T}}}\left( {{\boldsymbol{\varPhi}} {{\hat {\boldsymbol{x}}}^{k - 1}} - {\boldsymbol{y}}} \right) $

(8)

$ {\hat {\boldsymbol{x}}^k} = \mathop {\arg \min }\limits_x \frac{1}{2}\left\| {\boldsymbol{x}} \right. - \left. {{{\boldsymbol{z}}^k}} \right\|_2^2 + \lambda \psi ({\boldsymbol{x}}) $

(9)

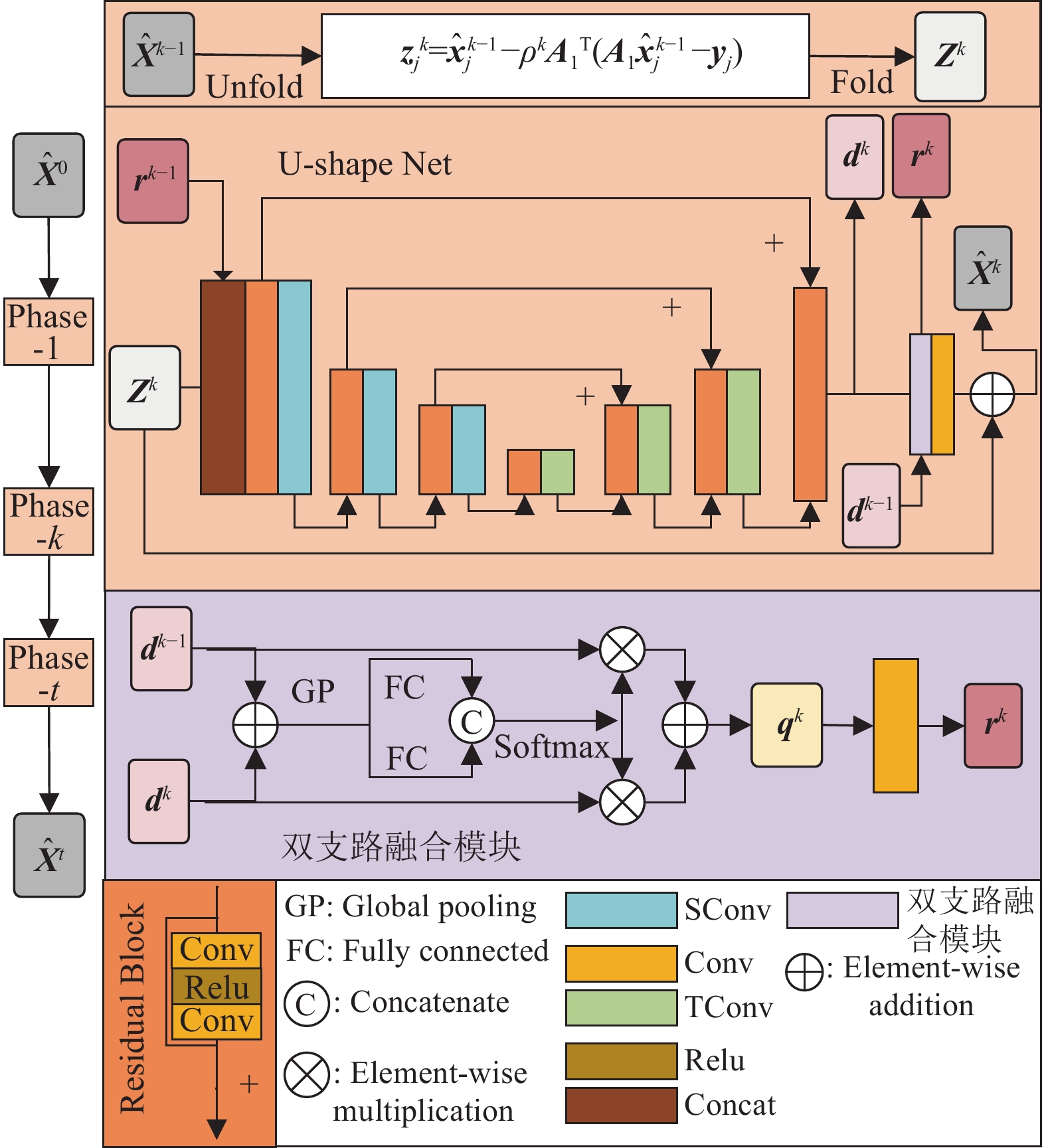
如图5所示，恢复子网包括t个阶段，每个阶段内包含2个进程：块梯度下降和记忆增强的近端映射，这与前面的2个公式迭代过程相对应。

2.5.1 块梯度下降

首先，映射PGD的第一步迭代，根据等式(8) 进行逐块的块梯度下降，第j块的更新公式如下

$ {\boldsymbol{z}}_j^k = \hat {\boldsymbol{x}}_j^{k - 1} - {\rho ^k}{\boldsymbol{A}}_1^{\rm{T}}\left( {{{\boldsymbol{A}}_1}\hat {\boldsymbol{x}}_j^{k - 1} - {{\boldsymbol{y}}_j}} \right) $

(10)

式中：z表示更新后的子块，$ \rho $是可学习的步长。如图5所示，第k−1阶段的重构结果${\hat {\boldsymbol{X}}^{k{{-}}1}}$被展开成l块，块$ \hat {\boldsymbol{x}}_j^{k{\text{-}}1} $独立更新得到$ {\boldsymbol{z}}_j^k $,然后所有子块$\{ {\boldsymbol{z}}_j^{k - 1}\} _{j = 1}^l$被折叠形成与原图像大小一致的${{\boldsymbol{Z}}^k}$。

2.5.2 记忆增强的近端映射

本文设计了记忆增强映射网络来解等式(9) ，为了减少阶段间的信息丢失，上一个阶段的中间特征$ {{\boldsymbol{r}}^{{k - 1}}} $与块梯度下降的结果${{\boldsymbol{Z}}^k}$拼接作为U形网络^[22]$ f_{{\rm{UNet}}}^k $的输入。

$ {{\boldsymbol{d}}^k} = f_{{\rm{UNet}}}^k\left( {\left[ {{{\boldsymbol{Z}}^k}\mid {{\boldsymbol{r}}^{k - 1}}} \right]} \right) $

(11)

式中：$\left[ | \right]$表示Concat操作。如图5所示，$ f_{{\rm{UNet}}}^k $网络包含了4个尺度，输入通过三层编码器，其使用步长为2×2的卷积进行特征下采样操作，特征图的分辨率从上到下逐渐降低。解码器使用步长为2的转置卷积进行上采样，在执行上采样或下采样之前，先使用一个残差块来提取图像的特征信息，并且对应尺度编解码器之间存在跳跃连接。

除了跨阶段的特征拼接，受到SKNet^[23]的启发，本文设计了双支路特征融合模块，上一阶段中间特征${{\boldsymbol{d}}^{k - 1}}$经过双层卷积后和这一个阶段的${{\boldsymbol{d}}^k}$进行特征融合，w_k和w_k−1代表2个阶段的权重，由2个全连接层$ {\cal H}_{{\rm{FC}}}^{\;1} $和$ {\cal H}_{{\rm{FC}}}^{\;2} $学习得到。

$ \left\{ {\begin{array}{*{20}{l}} {{\boldsymbol{v}} = {\rm{GP}}({{\boldsymbol{d}}^k} + {\rm{Conv}}({\rm{Conv}}({{\boldsymbol{d}}^{k{{-}}1}}) ) ) } \\ {{{\boldsymbol{w}}_k},{{\boldsymbol{w}}_{k - 1}} = {\rm{softmax}}([{\cal H}_{{\rm{FC}}}^{\;1}({\boldsymbol{v}}) ,{\cal H}_{{\rm{FC}}}^{\;2}({\boldsymbol{v}}) ]) } \\ {{{\boldsymbol{q}}^k} = {{\boldsymbol{d}}^k} \cdot {{\boldsymbol{w}}_k} + ({\rm{Conv}}({\rm{Conv}}({{\boldsymbol{d}}^{k - 1}}) ) ) \cdot {{\boldsymbol{w}}_{k - 1}}} \end{array}} \right. $

(12)

$ {{\boldsymbol{r}}^k} = {\rm{Conv}}({{\boldsymbol{q}}^k}) $

(13)

$ {\hat {\boldsymbol{X}}^k} = {\rm{Conv}}({\boldsymbol{r}}^k) + {{\boldsymbol{Z}}^k} $

(14)

式中：GP表示自适应全局池化操作，通过这两种方式，更多信息被保留到下一个阶段，且注意机制自适应调整不同支路的权重，可以强化重要特征的表达，提高网络性能。

2.6 损失函数

与其他基于深度学习的CS方法一样，均方误差函数被设为损失函数。损失函数包括4个部分：L₁，L₂,L₃，L₄，$ \{ {{\boldsymbol{X}}_k}\} _{k = 1}^{{N_{\rm{b}}}} $表示数据集，计算输入图像和对应的重构图像的误差如式(15)所示。

$ {L_1} = \frac{1}{{2{N_{\rm{b}}}}}\mathop \sum \nolimits_{k = 1}^{{N_{\text{b}}}} \left\| {{{\hat {\boldsymbol{X}}}_k} - {{\boldsymbol{X}}_k}} \right\|_2^2 $

(15)

式中：${\hat {\boldsymbol{X}}_k}$表示第k张图像的重构图像，N_b为图像数量。另外，本文提出了正交约束来增强观测矩阵的正交性。其中N为采样矩阵的维度, E为N维单位矩阵。

$ {L_2} = \frac{1}{{{N^2}}}\left\| {{\boldsymbol{A}}{{\boldsymbol{A}}^{\rm{T}}} - {\boldsymbol{E}}} \right\|_2^2 $

(16)

本文对误差预测子网重构结果也做出了损失约束。

$ {L_3} = \frac{1}{{2{N_{\rm{b}}}}}\mathop \sum \nolimits_{k = 1}^{{N_{\text{b}}}} \left\| {{f_{{\rm{EPSNet}}}}{\text{(}}{{\boldsymbol{X}}_k}) - {{\boldsymbol{X}}_k}} \right\|_2^2 $

(17)

式中：$ {f_{{\rm{EPSNet}}}}{\text{(}}{{\boldsymbol{X}}_k}) $表示误差预测子网的重构结果。好的初始化结果能够提高误差预测的准确性，于是增加了对误差预测子网初始化结果的误差约束。

$ {L_4} = \frac{1}{{2{N_{\rm{b}}}}}\mathop \sum \nolimits_{k = 1}^{{N_{\text{b}}}} \left\| {f_{{\rm{EPSNet}}}^0{\text{(}}{{\boldsymbol{X}}_k}) - {{\boldsymbol{X}}_k}} \right\|_2^2 $

(18)

式中：$ f_{{\rm{EPSNet}}}^0{\text{(}}{{\boldsymbol{X}}_k}) $表示第k张图像在误差预测子网中的初始化结果。最后，总损失函数定义为

$ L = {L_1} + {\mu _1}{L_2} + {\mu _2}{L_3} + {\mu _3}{L_4} $

(19)

式中：$ \mu $为正则权重，根据经验，设置$ {\mu _1} $、$ {\mu _2} $、$ {\mu _3} $为0.01、0.001、0.001。

3 实验 3.1 实验设置和训练数据

实验的训练平台为Windows10系统，CPU为Intel(R) Core(TM) i7-9700, GPU为NVIDA GeForce RTX2080 Ti，内存为32 GB。实验基于Pytorch深度学习框架，使用Adam对损失函数进行优化，总共训练70个epoch，前30个epoch的学习率为0.0001，后面的学习率变为0.00001.训练时，[0.01,0.5]之间的随机数被设置成采样率，阶段数t被设为9。

本文的数据集有291张图像，其中包括T91的91张和Train400中的200张图像，与文献[7]、[18]一样，这些图像经过了随机旋转对数据进行增广，例如原图、旋转90°、旋转180°等。将训练图片裁剪成128×128的子图像，设置块大小B=32，N=1024，随机抽取了25600张子图像作为训练数据。常见的基准数据集Set11、CBSD68和BSD100作为测试集，在图像的Y通道上使用PSNR和SSIM来评估重构结果。

3.2 消融实验

本文通过消融实验来验证不同模块对网络重构性能的影响，测试集为Set11。由表1可见，自适应采样和记忆增强模块都不添加时，进行均匀采样，纹理块缺乏采样，而平滑块采样资源冗余，阶段间信息丢失严重，导致重构质量不佳。只采用自适应采样模块时，PSNR平均提升0.41 dB；只采用记忆增强模块时，PSNR提升0.13 dB。说明两者都可以提升重构质量，且自适应采样提升作用更大。两者同时添加比只添加自适应采样模块仍有性能提升，说明记忆增强模块能进一步提高网络重构能力。当未采用数据增广时，其性能降低较大，PSNR平均降低了约0.48 dB，可见模型训练仍需要一定量的数据。

3.3 实验结果对比

本文对比了其他8种不同的基于深度学习的CS方法包括ReconNet^[6]、ISTA-Net^++[11]、SCSNet^[8]、CSNet^+[7]、OPINE-Net^+[18]、AMP-Net^[19]、BCSNet^[13]、ACCSNet^[15]和COAST^[20]，实验代码来自作者的主页。

表2列举了不同方法实现的功能、参数量以及重构时间，其重构时间是指在统一平台下重构一帧256×256图像所需时间。表3给出了本文与ACCSNet和COAST方法的性能对比。表4列举了这些方法在基准数据集Set11、CBSD68和BSD100上不同采样率下的平均PSNR和SSIM表现。从表2～6来看，ReconNet采用高斯矩阵作为采样矩阵，网络简单参数少，但是重构质量不佳。CSNet⁺、OPINE-Net⁺和AMPNet等方法在Set11数据集上平均PSNR比本文方法分别低2.72 dB、1.57 dB、1.61 dB，均匀分配采样率限制了这些方法重构质量的提高。受益于采样率自适应分配的优势，BCSNet重构质量大大提高，但是多通道的框架缺乏灵活性且导致更长的重构时间。其他可伸展网络的方法ISTA-Net⁺⁺和SCSNet,分别通过分层卷积和贪婪算法实现网络可扩展性，但只支持{0.1、0.2、0.3、0.4、0.5}几个采样比例，在CBSD68数据集上分别比本文方法的平均PSNR分别低2.69 dB、1.13 dB，SSIM分别低0.059、0.019。COAST需要训练数千个不同比例的可学习采样矩阵，训练成本高昂。从表3来看，其在0.1的采样率下比本文方法的平均PSNR低1 dB。本文方法通过掩码生成特定采样率的采样矩阵，结构更合理，支持[0,0.5]之间的任意采样率且在重构性能上更为优秀。从表1、2来看，在阶段共享的情况下，参数量降低了约64%，但PSNR平均只降低了约0.15 dB，说明网络的结构有效。图6、图7列出了不同方法的重构图像，本文重构图像的PSNR和SSIM最高，且纹理与原图最接近，有效抑制了块状伪影并恢复了更多的细节和锐利的边缘。

如表3所见，ACCSNet在Set11数据集上平均PSNR和SSIM分别比本文方法低1.27 dB和0.0138，级联的框架导致只训练了常见的采样率，缺乏普适性，而且非迭代网络的方法也缺乏好的可解释性。

4 结论

本文提出了一种新的自适应采样与记忆增强的压缩感知重构算法。本文基于测量域的重构误差估计块的重构难度，设计了有效的分配策略来自适应分配采样率，并引入掩码矩阵，以实现特定采样率下的图像块采样。另外，本文增加了双支路的特征融合模块，来自适应聚合不同支路的信息，通过注意机制调整不同支路的权重，提高了网络的重构能力。实验表明，本文提出的算法比多个现有深度学习重构算法有更高的图像重构质量。