聚类是根据数据的相似性度量,将数据集分成若干个簇的无监督方法,它使得在同一簇内的样本间尽可能显示出高的相似性,在不同簇的样本间显示出较低的相似性。聚类广泛应用于数据挖掘、文档检索、图像分割和模式识别[1-4]。
根据用于聚类的数据集视角是否为多个,可以将聚类分为单视角聚类与多视角聚类[5]。在大数据时代,数据从不同角度观察得到,这些数据被称为多视角数据。由于不同视角数据之间的多样性,基于单视角的聚类方法不能有效利用多视角综合信息。多视角聚类通过利用多个视角之间潜在的互补和一致信息,在不同视角中搜索一致的聚类[5-7]。
在多视角聚类中,不同视角的数据维度往往不同。基于图的谱聚类算法能够对任意形状的数据进行聚类,是目前最流行的多视角方法之一。在多视角谱聚类中,人们通过求共识相似度矩阵或求共识特征矩阵的方法统一不同视角的信息。
2016年Lee等[8]通过学习一个增广视角,并在由各个视角的拉普拉斯矩阵的特征向量形成的信息矩阵的谱分解中构造其相应的相似度矩阵。2020年Kang等[9]同时执行图融合和谱聚类算法。该方法得到近似于每个单独视角的原始图,但保持了显式的聚类结构的融合图。值得注意的是,有些方法关注于利用高阶信息。2020年Hao等[10]构造了包含数据点之间高阶关系的超图拉普拉斯矩阵,以提高互补信息的使用。2020年Liang等[11]和Zhou等[12]同时搜索一阶和高阶基本拉普拉斯矩阵的线性组合的邻域来生成最优的拉普拉斯矩阵,更好地利用了隐藏的高阶连接信息。2021年Jing等[13]结合超图嵌入和稀疏回归的优点来选择重要的特征,将超图拉普拉斯算子建模为格拉斯曼流形上的点,通过学习一致相似图的方法融合视角。为避免不可靠图对局部流形信息的影响,2021年Hao等[14]构造一个动态的局部表示,通过强加一个融合项来最大化局部表示和全局表示的共同结构。同时,有方法利用张量提取视角内和视角间的关系。2021年Jia等[15]在张量的正面和水平切片上施加对称的低秩约束和结构化稀疏低秩约束来分别表征视角内和视角间的关系,将多视角谱聚类表示为一个凸的低秩张量恢复问题。2022年Zhao等[16]提出使用张量
2011年Kumar等[18]提出两种共正则化方法组合不同视角的信息来学习共识谱嵌入矩阵。2014年Huang等[19]通过约束不同视角谱嵌入矩阵之间的相关性,获得共识矩阵。文献[20-21]通过使用成对约束信息将多视角谱聚类方法扩展为半监督方法。2016年Lu等[20]结合了稀疏子空间表示和成对约束,正则化了成对约束。2019年Chen等[21]通过对统一的谱嵌入矩阵施加成对固定约束来利用成对信息。2020年Xu等[22]提出一种加权张量核范数方法,考虑奇异值的先验信息,在公共谱嵌入矩阵中嵌入高阶相关性和空间结构。此外,有些方法关注对不完整数据的处理。2020年Zhuge等[23]提出一种不完全图多视角谱聚类方法,它将谱嵌入和相似度矩阵补全连在一个过程,使用公共表示矩阵和对应视角的表示矩阵相乘的方式恢复相似度矩阵的缺失项,再基于补全后的相似度矩阵学习表示矩阵。同时,有些方法也利用非负嵌入的优势。2022年 Hajjar等[24]使用与数据空间相关联的图的聚类标签相关性来构建一个额外的图,并利用非负嵌入的平滑性约束对聚类标签矩阵进行约束。Hajjar等[25]在文献[24]的基础上增加了对聚类标签矩阵的正交性约束。2023年Yang等[26]通过使用L1范数得到各个视角的高质量图,然后在高质量图中学习公共非负特征矩阵。然而,文献[26]等没有利用到共识相似图的一致性信息,不能同时利用多视角谱嵌入矩阵的共识特征关系和相似关系,这很大程度上影响了聚类性能。
本文专注于多视角谱聚类问题,设计了一个双共识约束和放松的正交约束将谱嵌入矩阵约束到所需的解决方案。基于Ding等[27]工作中的分析,本文在谱聚类模型中添加谱嵌入矩阵的共识特征约束项和共识相似约束项,利用了不同视角间的谱嵌入矩阵共识特征关系和相似关系。因此,学习到的一致性矩阵更适合聚类。此外,为了便于计算和更好地利用双共识约束,放松了单位正交约束。通过使用这些约束,开发了双共识约束的多视角谱聚类方法,称为双共识多视角谱聚类,以实现对谱聚类模型的优化。为了求解所提出的约束模型,使用基于梯度的方法更新谱嵌入矩阵,同时也得到2个共识矩阵的闭式解。
本文结构如下:第1节回顾了经典的谱聚类模型,描述了所提出的模型,得到了相应的算法,并分析了算法的计算复杂度;第2节给出了3个真实世界数据集的实验结果;第3节给出了结论。
1 双共识多视角谱聚类本文使用的主要符号如表1所示。
| 表 1 符号及其描述 Table 1 Notations and their descriptions |
在谱聚类中,原始信息以相似度图G=(R,E) 的形式表示,其中R是一组顶点,E是顶点之间的一组边。这里每个顶点ri表示一个数据点,E的每条边表示2个数据点之间的相似性。然后用一个相似度矩阵W来描述G,其中W={Wij},i, j=1,
经典谱聚类模型可以表述为
| $ \begin{split} &\mathop {\min }\limits_{{{\boldsymbol{H}}}} {\text{Tr}}({{\boldsymbol{H}}^{\rm{T}}}{\boldsymbol{L}}{\boldsymbol{H}}) ,\\ &{\text{s}}{\text{.t}}{\text{.}}{\kern 1pt} {\kern 1pt} {\kern 1pt} {{\boldsymbol{H}}^{\rm{T}}}{\boldsymbol{H}} = {\boldsymbol{I}} \\ \end{split} $ | (1) |
式中:H∈Rn×k是一个包含k个标准正交向量的谱嵌入矩阵,I是单位矩阵,归一化图的拉普拉斯矩阵L=D−1(D−W) ,D=diag(d1, d2, ···, dn) 是满足
为了计算方便,本文将谱聚类方法中的谱嵌入矩阵的单位正交约束放松,得到以下模型:
| $ \mathop {\min }\limits_{\boldsymbol{H}} {\text{Tr}}({{\boldsymbol{H}}^{\rm{T}}}{\boldsymbol{LH}}) + \frac{\gamma }{2}\| {{{\boldsymbol{H}}^{\rm{T}}}{\boldsymbol{H}} - {\boldsymbol{I}}} \|_F^2 $ | (2) |
式中:
为了得到一个共同的谱嵌入矩阵结果,基于多视角数据中不同视角的相同样本应分配给同一簇的特点,本方法将从不同的视角中学习到的谱嵌入矩阵约束为一个共识谱嵌入矩阵。对共识谱嵌入矩阵H*施加行归一化,以使H*稀疏,这增强了高可靠值,削弱了低值。同时,行归一化的方法保持了各个视角谱嵌入矩阵Hv一定的多样性信息。最后,行归一化也避免了矩阵大小对最终聚类效果的影响。因此,本文提出新的多视角谱聚类模型为
| $\begin{split} \mathop {\min }\limits_{{{\boldsymbol{H}}^v},{\kern 1pt} {{\boldsymbol{H}}^*}} J =& \sum\limits_{v = 1}^V {({\text{Tr}}({{({{\boldsymbol{H}}^v}) }^{\text{T}}}{{\boldsymbol{L}}^v}{{\boldsymbol{H}}^v}) } + \beta \| {{{\boldsymbol{H}}^v} - {{\boldsymbol{H}}^*}} \|_F^2 + \\ & \dfrac{\gamma }{2}\| {{{({{\boldsymbol{H}}^v}) }^{\rm{T}}}{{\boldsymbol{H}}^v} - {\boldsymbol{I}}} \|_F^2) ,\\ & {\text{s}}{\text{.t}}{\text{.}}{\kern 1pt} {\kern 1pt} {\kern 1pt} \| {{{({{\boldsymbol{H}}^*}) }_i}} \|_2^2 = 1 \end{split} $ | (3) |
式中:(H*)i表示共识谱嵌入矩阵的第i行,J是目标函数。
对于第v个视角的数据矩阵Xv,使用余弦相似度
| $ \begin{split} {{\boldsymbol{H}}^v} = & \mathop {\min }\limits_{{{\boldsymbol{H}}^v}} \| {{{\boldsymbol{H}}^v}{{({{\boldsymbol{H}}^v}) }^{\text{T}}} - {{\boldsymbol{Z}}^*}} \|_F^2 = \\ & \mathop {\min } \limits_{{{\boldsymbol{H}}^v}} (\| {{{\boldsymbol{Z}}^*}} \|_F^2 - 2{\text{Tr}}({({{\boldsymbol{H}}^v}) ^{\text{T}}}{{\boldsymbol{Z}}^*}{{\boldsymbol{H}}^v}) + \| {{{({{\boldsymbol{H}}^v}) }^{\text{T}}}{{\boldsymbol{H}}^v}} \|_F^2) = \\ & \mathop {\min }\limits_{{{\boldsymbol{H}}^v}} ( - 2{\text{Tr}}({({{\boldsymbol{H}}^v}) ^{\text{T}}}{{\boldsymbol{Z}}^*}{{\boldsymbol{H}}^v}) + \| {{{({{\boldsymbol{H}}^v}) }^{\rm{T}}}{{\boldsymbol{H}}^v}} \|_F^2) \end{split} $ | (4) |
可以看出,多视角谱嵌入矩阵的成对约束是为了得到所有视角的共识相似度矩阵。共识相似度矩阵Z*保证不同视角谱嵌入矩阵具有相同的相似关系。
本方法使用共识相似约束和共识谱嵌入约束,同时利用谱嵌入矩阵的共识相似关系和特征关系,提出了以下用于多视角谱聚类的新模型:
| $ \begin{split} \mathop {\min }\limits_{{{\boldsymbol{H}}^v},{\boldsymbol{Z}},{{\boldsymbol{H}}^*}} J = & \sum\limits_{v = 1}^V {({\text{Tr}}({{({{\boldsymbol{H}}^v}) }^{\text{T}}}{{\boldsymbol{L}}^v}{{\boldsymbol{H}}^v}) } + \frac{\alpha }{2}\| {{{\boldsymbol{H}}^v}{{({{\boldsymbol{H}}^v}) }^{\text{T}}} - {{\boldsymbol{Z}}^*}} \|_F^2 + \\ & \beta \| {{{\boldsymbol{H}}^v} - {{\boldsymbol{H}}^*}} \|_F^2 + \frac{\gamma }{2}\| {{{({{\boldsymbol{H}}^v}) }^{\rm{T}}}{{\boldsymbol{H}}^v} - {\boldsymbol{I}}} \|_F^2), \\ & {\text{s}}{\text{.t}}{\text{.}} \| {{{({{\boldsymbol{H}}^*}) }_i}} \|_2^2 = 1\\[-10pt] \end{split} $ | (5) |
式中:α是共识相似约束的权重系数。Z*为共识相似度矩阵,用于约束不同视角谱嵌入矩阵的相似关系。H*为共识谱嵌入矩阵,用于减少谱嵌入矩阵之间的分布差异。同时,H*的行归一化限制了Hv的行和大小,使得HHT更加接近相似度矩阵。
1.2 算法优化过程为了便于优化,将模型(5) 替换为
| $ \begin{split} \mathop {\min }\limits_{{{\boldsymbol{H}}^v},{\kern 1pt} {\boldsymbol{Z}},{{\boldsymbol{H}}^*}} J =& \displaystyle \sum\limits_{v = 1}^V {(J_1^v + \frac{\alpha }{2}J_2^v + \beta J_3^v + \frac{\gamma }{2}J_4^v) } ,\\ &{\text{s}}{\text{.t}}{\text{.}}\| {{{({{\boldsymbol{H}}^*}) }_i}} \|_2^2 = 1 \end{split} $ | (6) |
式中:
为了解决模型(6)中的优化问题,利用交替迭代更新方案逐一优化矩阵,即当一个矩阵被优化时,其他矩阵是固定的。本文算法所涉及的矩阵更新规则如下。
(1) 更新Hv: J相对于Hv的梯度由式(7)~(12)导出
| $ \begin{gathered} \frac{{\partial J_1^v}}{{\partial {{\boldsymbol{H}}^v}}} = \frac{{\partial ({\text{Tr}}({{({{\boldsymbol{H}}^v}) }^{\text{T}}}{{\boldsymbol{L}}^v}{{\boldsymbol{H}}^v}) ) }}{{\partial {{\boldsymbol{H}}^v}}} = ({{\boldsymbol{L}}^v} + {({{\boldsymbol{L}}^v}) ^{\text{T}}}) {{\boldsymbol{H}}^v} = 2{{\boldsymbol{L}}^v}{{\boldsymbol{H}}^v} \end{gathered} $ | (7) |
| $ \begin{split} \frac{{\partial J_2^v}}{{\partial {{\boldsymbol{H}}^v}}} =& \frac{{\partial {\text{Tr(}}{{({{\boldsymbol{H}}^v}{{({{\boldsymbol{H}}^v}) }^{\rm{T}}} - {{\boldsymbol{Z}}^*}) }^{\text{T}}}({{\boldsymbol{H}}^v}{{({{\boldsymbol{H}}^v}) }^{\rm{T}}} - {{\boldsymbol{Z}}^*}) ) }}{{\partial {{\boldsymbol{H}}^v}}} = \\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} & \frac{{\partial {\text{Tr}}({{\boldsymbol{H}}^v}{{({{\boldsymbol{H}}^v}) }^{\rm{T}}}{{\boldsymbol{H}}^v}{{({{\boldsymbol{H}}^v}) }^{\rm{T}}} - 2{{\boldsymbol{H}}^v}{{({{\boldsymbol{H}}^v}) }^{\rm{T}}}{{\boldsymbol{Z}}^*}) }}{{\partial {{\boldsymbol{H}}^v}}} = \\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} & 4{{\boldsymbol{H}}^v}{({{\boldsymbol{H}}^v}) ^{\rm{T}}}{{\boldsymbol{H}}^v} - 4{{\boldsymbol{Z}}^*}{{\boldsymbol{H}}^v} \\ \end{split} $ | (8) |
| $ \begin{split} \frac{{\partial J_3^v}}{{\partial {{\boldsymbol{H}}^v}}} =& \frac{{\partial {\text{Tr(}}{{({{\boldsymbol{H}}^v} - {{\boldsymbol{H}}^*}) }^{\text{T}}}({{\boldsymbol{H}}^v} - {{\boldsymbol{H}}^*}) ) }}{{\partial {{\boldsymbol{H}}^v}}} = \\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} & \frac{{\partial {\text{Tr}}({{({{\boldsymbol{H}}^v}) }^{\rm{T}}}{{\boldsymbol{H}}^v} - 2{{({{\boldsymbol{H}}^v}) }^{\rm{T}}}{{\boldsymbol{H}}^*}) }}{{\partial {{\boldsymbol{H}}^v}}} = \\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} &2{{\boldsymbol{H}}^v} - 2{{\boldsymbol{H}}^*} \\[-20pt] \end{split}\qquad\qquad\qquad $ | (9) |
| $ \begin{split} \frac{{\partial J_4^v}}{{\partial {{\boldsymbol{H}}^v}}} =& \frac{{\partial {\text{Tr(}}{{({{\boldsymbol{H}}^v}{{({{\boldsymbol{H}}^v}) }^{\rm{T}}} - {\boldsymbol{I}}) }^{\text{T}}}({{\boldsymbol{H}}^v}{{({{\boldsymbol{H}}^v}) }^{\rm{T}}} - {\boldsymbol{I}}) ) }}{{\partial {{\boldsymbol{H}}^v}}} = \\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt}& \frac{{\partial {\text{Tr}}({{\boldsymbol{H}}^v}{{({{\boldsymbol{H}}^v}) }^{\rm{T}}}{{\boldsymbol{H}}^v}{{({{\boldsymbol{H}}^v}) }^{\rm{T}}} - 2{{\boldsymbol{H}}^v}{{({{\boldsymbol{H}}^v}) }^{\rm{T}}}) }}{{\partial {{\boldsymbol{H}}^v}}} = \\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt}& 4{{\boldsymbol{H}}^v}{({{\boldsymbol{H}}^v}) ^{\rm{T}}}{{\boldsymbol{H}}^v} - 4{{\boldsymbol{H}}^v} \\ \end{split} $ | (10) |
然后,综合所有梯度:
| $ \begin{split} \frac{{\partial J}}{{\partial {{\boldsymbol{H}}^v}}} =& \frac{{\partial J_1^v}}{{\partial {{\boldsymbol{H}}^v}}} + \frac{\alpha }{2}\frac{{\partial J_2^v}}{{\partial {{\boldsymbol{H}}^v}}} + \beta \frac{{\partial J_3^v}}{{\partial {{\boldsymbol{H}}^v}}} + \frac{\gamma }{2}\frac{{\partial J_4^v}}{{\partial {{\boldsymbol{H}}^v}}} = \\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} & 2{\boldsymbol{L}}{{\boldsymbol{H}}^v} + 2\alpha ({{\boldsymbol{H}}^v}{({{\boldsymbol{H}}^v}) ^{\rm{T}}} - {{\boldsymbol{Z}}^*}) {{\boldsymbol{H}}^v} + \\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} & 2\beta ({{\boldsymbol{H}}^v} - {{\boldsymbol{H}}^*}) + 2\gamma {{\boldsymbol{H}}^v}({({{\boldsymbol{H}}^v}) ^{\rm{T}}}{{\boldsymbol{H}}^v} - {\boldsymbol{I}}) \end{split} $ | (11) |
通过使用基于梯度的方法,Hv更新为
| $ {{\boldsymbol{H}}^v} \leftarrow {{\boldsymbol{{\boldsymbol H}}}^v} - \lambda \frac{{\partial J}}{{{{\boldsymbol{{\boldsymbol H}}}^v}}} $ | (12) |
(2) 更新Z*:固定了除Z*之外的所有变量后,得到关于Z*的子问题:
| $ \mathop {\min }\limits_{\boldsymbol{Z}} J' = \sum\limits_{v = 1}^V {J_2^v} = \sum\limits_{v = 1}^V {\| {{{\boldsymbol{H}}^v}{{({{\boldsymbol{H}}^v}) }^{\text{T}}} - {{\boldsymbol{Z}}^*}} \|_F^2} $ | (13) |
设置推导
| $ 2\sum\limits_{v = 1}^V {({{\boldsymbol{H}}^v}{{({{\boldsymbol{H}}^v}) }^{\text{T}}} - {{\boldsymbol{Z}}^*}) } = 0 $ | (14) |
因此,Z*有一个闭式解:
| $ {{\boldsymbol{Z}}^*} = \frac{1}{V}\sum\limits_{v = 1}^V {{{\boldsymbol{H}}^v}{{({{\boldsymbol{H}}^v}) }^{\text{T}}}} $ | (15) |
(3) 更新H*:固定除H*之外的所有变量后,得到对应于H*的子问题:
| $ \begin{split} \mathop {\min }\limits_{{{\boldsymbol{H}}^*}} J'' =& \displaystyle \sum\limits_{v = 1}^V {J_3^v} = \sum\limits_{v = 1}^V {(\| {{{\boldsymbol{H}}^v} - {{\boldsymbol{H}}^*}} \|_F^2) } ,\\ &{\text{s}}{\text{.t}}{\text{.}}{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \| {{{({{\boldsymbol{H}}^*}) }_i}} \|_F^2 = 1 \end{split} $ | (16) |
将矩阵展开,然后利用拉格朗日乘子法,将问题转化为无约束最小化问题为
| $ \begin{split} \varDelta = &\sum\limits_{v = 1}^V {\sum\limits_{i = 1}^n {\sum\limits_{j = 1}^{{k_n}} {{{({{({{\boldsymbol{H}}^v}) }_{ij}} - {{({{\boldsymbol{H}}^*}) }_{ij}}) }^2}} } } + \\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt}& \mu \sum\limits_{i = 1}^n {(\sum\limits_{j = 1}^{{k_n}} {{{({{({{\boldsymbol{H}}^*}) }_{ij}}) }^2} - 1) } } \\[-10pt] \end{split} $ | (17) |
式中:kn为谱嵌入矩阵Hv的行维度。
最优的H*应满足以下方程组:
| $ \left\{ {\begin{array}{*{20}{l}} {\displaystyle \frac{{\partial \varDelta }}{{\partial {{({{\boldsymbol{H}}^*}) }_{ij}}}} = \displaystyle\sum\limits_{v = 1}^V {(2{{({{\boldsymbol{H}}^*}) }_{ij}} - 2{{({{\boldsymbol{H}}^v}) }_{ij}}) } + 2\mu {{({{\boldsymbol{H}}^*}) }_{ij}} = 0} \\ {\displaystyle \frac{{\partial \varDelta }}{{\partial \mu }} = \displaystyle \sum\limits_{j = 1}^{{k_n}} {{{({{({{\boldsymbol{H}}^*}) }_{ij}}) }^2} - 1 = 0} } \end{array}} \right. $ | (18) |
因此,得到H*的最优解为
| $ {({{\boldsymbol{H}}^*}) _{ij}} = \frac{{\displaystyle \sum\nolimits_{v = 1}^V {{{({{\boldsymbol{H}}^v}) }_{ij}}} }}{{\sqrt {\displaystyle \sum\nolimits_{j = 1}^{{k_n}} {{{(\sum\nolimits_{v = 1}^V {{{({{\boldsymbol{H}}^v}) }_{ij}}} ) }^2}} } }} $ | (19) |
到目前为止,本文已经提出了整个总体目标函数的交替优化程序,整个优化过程总结为算法1。
关于上述算法中的初始化,为充分利用多视角的相似度矩阵信息,本文使用对图拉普拉斯矩阵求特征向量的方式初始化谱嵌入矩阵Hv,然后用Hv初始化H*和Z*。对于停止准则,本文利用一般条件,如迭代次数、相对误差等。获得最优的H*后,通过使用典型的k-means方法将其最终聚类为k类,以完成多视角聚类的整个工作。
算法1 双共识多视角谱聚类算法。
(1) 输入:多视角特征矩阵Xv,谱嵌入矩阵的行维度kn,超参数α、β和γ,迭代次数t。
(2) 初始化:
(a) 计算图拉普拉斯矩阵Lv;
(b) 对Lv取kn个特征值最小的特征向量作为Hv;
(c) 用式(19) 和式(15) 初始化H*和Z*。
(3) 矩阵迭代:
(a) 更新Hv:固定Z*和H*不变,使用式(12) 计算Hv;
(b) 更新Z*: 固定H*和Hv不变,使用式(15) 计算Z*;
(c) 更新H*:固定Z*和Hv不变,使用式(19) 计算H*;
(d) 对式(5) 计算目标函数值。
(e) i=i+1。
(4) 直到i=t或目标函数值收敛。
(5) 输出:谱嵌入矩阵
本方法的计算复杂度主要在于更新
本文在3个数据集上进行了广泛的实验,以验证所提出的双共识多视角谱聚类方法的性能,并与现有多视角谱聚类算法进行了比较。所涉及的数据集包括人脸图像和文档。所有方法都是用MATLAB R2021b 实现的,并在Inter Core i5-12400 2.5 GHz CPU和16 GB RAM的PC上进行。
2.1 数据集本文选择了广泛使用的3个数据集作为测试数据。具体如下:
BBCSports:它是运动新闻文章数据集,包括5个主题领域,相当于5个类 (田径、板球、足球、橄榄球和网球),总共544个文档。每个文档由2个视角进行描述,它们的特征大小分别为3 183和
MSRCv1:它由来自7个不同主题的210张图片组成。根据提取特征 (CM(Colour Moment)特征、GIST特征、HOG(Histogram of Oriented Gradients)特征、CENT(Centrist)特征和LBP(Local Binary Pattern)特征) 的不同生成5个视角的数据集。
3-SOURCES:它是一个新闻文档数据集,包括6个主题,每个文章根据新闻来源(BBC、路透社和卫报)不同分为3个不同的视角。
3个数据集的统计数据如表2所示。
| 表 2 测试数据集的统计数据 Table 2 The Statistical information |
为了验证所提方法的优越性,在实验中与5个多视角谱聚类方法进行对比。
S-MVSC[28]:该方法使用L1范数从多个视角学习具有稀疏结构的一致相似度矩阵,再对一致相似度矩阵进行谱聚类。
NESE[29]:该方法将非负嵌入和谱嵌入集成到统一框架中。
GFSC[9]:该方法通过为接近共识图的视角分配较大的动态权重来集成多视角信息,再对共识图进行谱聚类。
UOMVSC[30]:该方法将谱嵌入和k均值方法集成到一个统一的框架中,以一步策略获得离散的聚类标签。
AGLMF[26]:该方法使用L1范数自适应地从每个视角的原始相似度图中学习高质量图,同时学习谱嵌入和非负嵌入。模型结合了基于图的方法和矩阵分解方法的优点。
2.3 参数设置与评估指标根据对应方法的论文介绍,本文为每个方法设置最优参数。对于S-MVSC,最近邻设置为10,约束项参数从[0.02:0.22]中选择。对于NESE,因为模型无参数,所以本文不设置参数取值范围。对于GFSC,其超参数α,β和γ在[10−7:107]选择。对于AGLMF,参数在[10−6:10−3]选择。对于UOMVSC,参数从[0:0.05:1]选择。对于本文提出的方法,参数α、β和γ分别在[10−5, 10−4, 10−3, 10−2], [0.01, 0.1, 1, 10]和[10−5, 10−4, 10−3, 10−2] 中选择,最近邻参数设置为9,固定迭代步长λ设置为0.15。
此外,本文采用了3个评估指标,包括准确度 (Accuracy, ACC)、标准化互信息 (Normalized Mutual Information, NMI)、调整兰德系数 (Adjusted Rand Index, ARI) 来评估性能。
2.4 实验结果表3~5中报告了在3个数据集上通过所有方法得到的3个评估聚类性能的指标。
| 表 3 不同方法在BBCSports数据集中的聚类性能 Table 3 Different methods’ clustering performance on BBCSports datasets |
| 表 4 不同方法在MSRCv1数据集中的聚类性能 Table 4 Different methods’ clustering performance on MSRCv1 datasets |
| 表 5 不同方法在3-SOURCES数据集中的聚类性能 Table 5 Different methods' clustering performance on 3-SOURCES datasets |
本文方法的聚类结果显著优于比较方法。以3−SOURCES数据集为例,其ACC、ARI和NMI分别超过S-MVSC11.24%、20.11%和13.69%,这验证了本文方法的优势和有效性。主要原因是:本文所提出的方法对谱嵌入矩阵Hv施加了公共相似约束和公共谱嵌入约束,同时利用相似信息和特征信息,提高了一致性矩阵的聚类能力。
本文提出的方法优于多步的谱聚类方法S−MVSC和GFSC,不仅使用了共识相似约束,还使用了共识谱嵌入约束,比其他方法更多地利用了一致性信息。
本文提出的方法优于单步的谱聚类方法NESE、AGLMF和UOMVSC。NESE和AGLMF结合非负嵌入与谱嵌入对不同视角的相似度矩阵进行学习,直接得到标签信息。UOMVSC通过结合谱嵌入与k-means对统一的相似度矩阵进行学习,直接得到标签信息。结果表明,考虑不同视角谱嵌入矩阵的双共识关系(特别是共识相似关系)可以保留更多一致性信息,减少第二步k-means聚类的信息损失。
2.5 模型分析(1) 参数敏感度:本文所提出的方法由3个参数组成,即α、β和γ。通过网格搜索策略在[10−5, 10−4, 10−3, 10−2]、[0.01, 0.1, 1, 10]和[10−5, 10−4, 10−3, 10−2]中选择α、β和γ。
图1~3表示每个数据集对参数的敏感度,可以看出BBCSports、MSRCv1和3-SOURCES的α、β和γ的最佳参数分别为{10−3, 10, 10−3}、{10−3, 10, 10−2}、{10−3, 10, 10−3}。对于这3个数据集而言,本文方法设定的最佳参数基本相同。本方法在α取最优值,且β和γ均取较大值时,聚类的准确度较高且表现出较好的稳定性。当β取最优值,且α和γ均取较大值时,聚类的准确度较高且表现出较好的稳定性。当γ取最优值的时候,α对聚类准确度表现稳定,准确度随β增大而增大。

|
图 1 BBCSports的聚类ACC随α、β和γ变化 Figure 1 Clustering ACC v.s. parameters α, β and γ on the BBCSports |

|
图 2 MSRCv1的聚类ACC随α、β和γ变化 Figure 2 Clustering ACC v.s. parameters α, β and γ on the MSRCv1 |

|
图 3 3-SOURCES的聚类ACC随α、β和γ变化 Figure 3 Clustering ACC v.s. parameters α, β and γ on the 3-SOURCES |
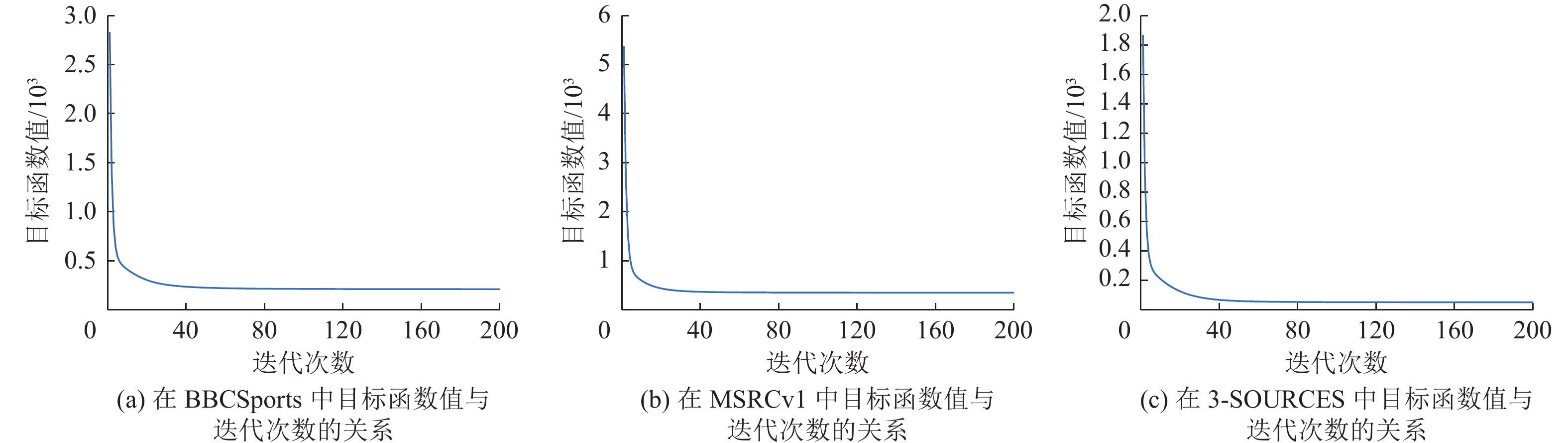
(2) 实验收敛性:图4展示了在3个数据集中本文方法的目标函数值收敛曲线。结果表明,3个数据集的目标函数值在60次迭代内基本达到稳定值。因此,该方法具有稳定的收敛性。
|
图 4 在BBCSports、MSRCv1与3-SOURCES中目标函数值与迭代次数的关系 Figure 4 Objective function value versus the number of iterations on the BBCSports, MSRCv1 and 3-SOURCES |
本文提出了一种新的多视角谱聚类方法,称为双共识多视角谱聚类算法。具体而言,该方法旨在通过联合学习公共相似度矩阵和公共谱嵌入矩阵,利用不同视角谱嵌入矩阵的共识特征关系和相似关系,更好地保留每个视角谱嵌入矩阵的多种一致性信息,来减少不同视角之间的分布差异。此外,为了便于计算和更好地利用双共识约束,本方法放松正交约束以建立多视角谱聚类模型。在基准数据集上进行的几项实验表明,与最近的谱聚类方法相比,本文的方法具有最佳的聚类性能。结果表明,综合多共识约束有助于挖掘更多的多视角一致性信息。
| [1] |
JAIN A K, MURTY M N, FLYNN P J. Data clustering: a review[J].
ACM Computing Surveys (CSUR), 1999, 31(3): 264-323.
DOI: 10.1145/331499.331504. |
| [2] |
XU R, WUNSCH D. Survey of clustering algorithms[J].
IEEE Transactions on Neural Networks, 2005, 16(3): 645-678.
DOI: 10.1109/TNN.2005.845141. |
| [3] |
FOWLKES C, BELONGIE S, CHUNG F, et al. Spectral grouping using the nystrom method[J].
IEEE Transactions on Pattern Analysis and Machine Intelligence, 2004, 26(2): 214-225.
DOI: 10.1109/TPAMI.2004.1262185. |
| [4] |
XU D, TIAN Y. A comprehensive survey of clustering algorithms[J].
Annals of Data Science, 2015, 2: 165-193.
DOI: 10.1007/s40745-015-0040-1. |
| [5] |
FU L, LIN P, VASILAKOS A V, et al. An overview of recent multi-view clustering[J].
Neurocomputing, 2020, 402: 148-161.
DOI: 10.1016/j.neucom.2020.02.104. |
| [6] |
YANG Y, WANG H. Multi-view clustering: a survey[J].
Big Data Mining and Analytics, 2018, 1(2): 83-107.
DOI: 10.26599/BDMA.2018.9020003. |
| [7] |
CHAO G, SUN S, BI J. A survey on multiview clustering[J].
IEEE Transactions on Artificial Intelligence, 2021, 2(2): 146-168.
DOI: 10.1109/TAI.2021.3065894. |
| [8] |
LEE C K, LIU T L. Guided co-training for multi-view spectral clustering[C]//2016 IEEE International Conference on Image Processing (ICIP) . [S.l.]: IEEE, 2016: 4042-4046.
|
| [9] |
KANG Z, SHI G, HUANG S, et al. Multi-graph fusion for multi-view spectral clustering[J].
Knowledge-Based Systems, 2020, 189: 105102.
DOI: 10.1016/j.knosys.2019.105102. |
| [10] |
HAO W, PANG S, ZHU J, et al. Self-weighting and hypergraph regularization for multi-view spectral clustering[J].
IEEE Signal Processing Letters, 2020, 27: 1325-1329.
DOI: 10.1109/LSP.2020.3011599. |
| [11] |
LIANG W, ZHOU S, XIONG J, et al. Multi-view spectral clustering with high-order optimal neighborhood laplacian matrix[J].
IEEE Transactions on Knowledge and Data Engineering, 2020, 34(7): 3418-3430.
|
| [12] |
ZHOU S, LIU X, LIU J, et al. Multi-view spectral clustering with optimal neighborhood Laplacian matrix[J]. Proceedings of the AAAI Conference on Artificial Intelligence. 2020, 34(4) : 6965-6972.
|
| [13] |
JING P, SU Y, LI Z, et al. Learning robust affinity graph representation for multi-view clustering[J].
Information Sciences, 2021, 544: 155-167.
DOI: 10.1016/j.ins.2020.06.068. |
| [14] |
HAO W, PANG S, CHEN Z. Multi-view spectral clustering via common structure maximization of local and global representations[J].
Neural Networks, 2021, 143: 595-606.
DOI: 10.1016/j.neunet.2021.07.020. |
| [15] |
JIA Y, LIU H, HOU J, et al. Multi-view spectral clustering tailored tensor low-rank representation[J].
IEEE Transactions on Circuits and Systems for Video Technology, 2021, 31(12): 4784-4797.
DOI: 10.1109/TCSVT.2021.3055039. |
| [16] |
ZHAO Y, YUN Y, ZHANG X, et al. Multi-view spectral clustering with adaptive graph learning and tensor schatten p-norm[J].
Neurocomputing, 2022, 468: 257-264.
DOI: 10.1016/j.neucom.2021.09.052. |
| [17] |
SHI S, NIE F, WANG R, et al. Self-weighting multi-view spectral clustering based on nuclear norm[J].
Pattern Recognition, 2022, 124: 108429.
DOI: 10.1016/j.patcog.2021.108429. |
| [18] |
KUMAR A, RAI P, DAUME H. Co-regularized multi-view spectral clustering[J]. Advances in Neural Information Processing Systems, 2011, 24. 1413-1421.
|
| [19] |
HUANG L, LU J, TAN Y P. Co-learned multi-view spectral clustering for face recognition based on image sets[J].
IEEE Signal Processing Letters, 2014, 21(7): 875-879.
DOI: 10.1109/LSP.2014.2319817. |
| [20] |
LU C, YAN S, LIN Z. Convex sparse spectral clustering: single-view to multi-view[J].
IEEE Transactions on Image Processing, 2016, 25(6): 2833-2843.
DOI: 10.1109/TIP.2016.2553459. |
| [21] |
CHEN C, QIAN H, CHEN W, et al. Auto-weighted multi-view constrained spectral clustering[J].
Neurocomputing, 2019, 366: 1-11.
DOI: 10.1016/j.neucom.2019.06.098. |
| [22] |
XU H, ZHANG X, XIA W, et al. Low-rank tensor constrained co-regularized multi-view spectral clustering[J].
Neural Networks, 2020, 132: 245-252.
DOI: 10.1016/j.neunet.2020.08.019. |
| [23] |
ZHUGE W, LUO T, TAO H, et al. Multi-view spectral clustering with incomplete graphs[J].
IEEE Access, 2020, 8: 99820-99831.
DOI: 10.1109/ACCESS.2020.2997755. |
| [24] |
HAJJAR E, DORNAIKA F, ABDALLAH F. One-step multi-view spectral clustering with cluster label correlation graph[J].
Information Sciences, 2022, 592: 97-111.
DOI: 10.1016/j.ins.2022.01.017. |
| [25] |
HAJJAR E, DORNAIKA F, ABDALLAH F. Multi-view spectral clustering via constrained nonnegative embedding[J].
Information Fusion, 2022, 78: 209-217.
DOI: 10.1016/j.inffus.2021.09.009. |
| [26] |
YANG W, WANG Y, TANG C, et al. One step multi-view spectral clustering via joint adaptive graph learning and matrix factorization[J].
Neurocomputing, 2023, 524: 95-105.
DOI: 10.1016/j.neucom.2022.12.023. |
| [27] |
DING C, HE X, SIMON H D. On the equivalence of nonnegative matrix factorization and spectral clustering[C]//Proceedings of the 2005 SIAM International Conference on Data Mining. [S.l.] : Society for Industrial and Applied Mathematics, 2005: 606-610.
|
| [28] |
HU Z, NIE F, CHANG W, et al. Multi-view spectral clustering via sparse graph learning[J].
Neurocomputing, 2020, 384: 1-10.
DOI: 10.1016/j.neucom.2019.12.004. |
| [29] |
HU Z, NIE F, WANG R, et al. Multi-view spectral clustering via integrating nonnegative embedding and spectral embedding[J].
Information Fusion, 2020, 55: 251-259.
DOI: 10.1016/j.inffus.2019.09.005. |
| [30] |
TANG C, LI Z, WANG J, et al. Unified one-step multi-view spectral clustering[J].
IEEE Transactions on Knowledge and Data Engineering, 2022, 35(6): 6449-6460.
|
 2024, Vol. 41
2024, Vol. 41

