由于无人机具有移动性可控、灵活部署以及视距通信等特点，无人机可为物联网边缘应用提供服务^[1-3]，例如无人机可以作为空中基站(Base Station, BS) 或者中继节点，实现地面智能终端无处不在的连接。因此，无人机网络通过协调多个无人机通信，可以实现自主的空中网络，已受到学术界和工业界广泛关注。然而，随着无人机网络中地面智能终端设备激增、多场景多业务动态叠加、网络规模持续扩大以及无人机快速移动等特征，无人机网络优化和管理越来越复杂。数字孪生采用建模工具构建无人机网络中地面BS、地面智能终端、空中无人机以及无线传输信道等物理实体的高保真数字模型(即数字孪生体) 。在未来6G无人机网络时代，大量无人机网络数字孪生体将被部署在网络边缘服务器上，通过虚实交互，保持无人机网络物理实体和数字孪生体状态同步更新和协同演化，最终形成无人机数字孪生边缘网络，并采用分布式智能算法，为无人机网络优化和管理提供智能化决策，更加高效地应对无人机网络复杂挑战^[4-6]。

然而，无人机数字孪生边缘网络在协同边缘服务器上的数字孪生体进行智能化决策时，边缘服务器需要获取海量异构数据，这些数据涉及智能终端敏感信息，例如生物特征识别信息、车辆自动驾驶控制信息等。多个互不信任的数字孪生体协同计算，容易泄露智能终端敏感信息，导致无人机数字孪生边缘网络安全问题。联邦学习作为一种新兴的分布式机器学习架构，智能终端在本地训练机器学习模型，并将训练好的本地模型参数上传到中心云服务器聚合，而不用上传原始数据，从而可有效保护智能终端数据安全和隐私^[7]。目前，联邦学习已经应用于计算机视觉、自然语言处理、汽车自动驾驶、智能家居等领域^[8]。当前联邦学习应用于无人机数字孪生边缘网络，仍面临严峻挑战。无人机有限的计算资源、存储能力、能量资源、高速移动性，以及动态时变的无线传输环境，将导致联邦学习模型参数传输出错的概率增大，进而使联邦学习性能下降^[9]。Song 等^[10]提出基于非正交多接入技术的无人机网络联邦学习架构，通过联合优化上行非正交多接入传输时延、下行广播时延以及无人机的计算时延，实现最小化联邦学习时延的目标。Cheng 等^[11]研究无人机网络多任务联邦学习激励机制，提出使用拍卖博弈算法激励无人机和智能终端参与联邦学习模型训练。Sun等^[12]提出采用数字孪生辅助无人机网络联邦学习激励机制和斯塔克伯格算法，激励地面智能终端贡献资源参与联邦学习模型训练，提高联邦学习准确率。

考虑无人机数字孪生边缘网络动态时变的无线传输环境，当前大部分研究将深度强化学习(Deep Reinforcement Learning, DRL)算法和无人机网络的孪生网络模型结合，DRL算法可以从孪生网络模型中获取反映真实无人机网络状态的信息，并利用这些状态信息进行模型训练。同时，孪生网络模型实时获取真实无人机网络状态变化信息，且连续地更新模型参数，以对真实无人机网络的性能优化做出最优决策。Li等 ^[13]提出采用数字孪生辅助无人机网络边缘计算任务卸载，将数字孪生和双层深度Q网络(Double Deep Q-Network，DDQN)算法结合，求解智能终端最优关联和无人机最优飞行轨迹，实现最小化无人机网络边缘计算能耗的目标。Chen等 ^[14]提出无人机网络智能终端任务卸载调度策略，将数字孪生和DRL算法结合，在构建的孪生网络模型中训练智能终端任务卸载调度决策模型，实现最大化无人机网络地面智能终端平均效用的目标。这些工作聚焦于无人机数字孪生边缘网络中计算任务卸载策略设计，然而在无人机数字孪生边缘网络的联邦学习中，如何应对复杂变化的网络环境，并协同多个无人机提升联邦学习性能仍存在极大挑战。与现有工作不同，本文在无人机数字孪生边缘网络中，设计无人机多智能体协作调度策略，以降低联邦学习时延，同时保证学习准确率和损失的优越性。因此本文主要贡献如下：

(1) 提出基于无人机数字孪生边缘网络的联邦学习资源调度策略。首先，采用数字孪生技术在地面BS构建无人机网络的孪生网络模型，对无人机网络运行状态进行模拟和仿真。考虑多个无人机作为联邦学习模型参数的聚合器，对地面智能终端训练的本地模型参数进行聚合，在保护地面智能终端原始数据安全的前提下提供分布式机器学习服务。

(2) 进一步将无人机数字孪生边缘网络联邦学习资源分配问题建模为马尔科夫决策过程，建立联合无人机飞行距离、飞行角度以及无线网络频谱资源分配的自适应资源优化模型，实现最小化联邦学习时延的目标。提出基于孪生网络模型的多智能体深度确定性策略梯度(Multi-Agent Deep Deterministic Policy Gradient，MA-DDPG) 的资源分配优化算法，求解自适应资源优化模型。

(3) 仿真结果表明，本文算法具有良好的收敛性。与其他算法对比，本文算法可显著降低联邦学习时延性能，同时保证了联邦学习训练损失和准确率性的优越性。

1 系统模型

本文构建的无人机数字孪生边缘网络联邦学习架构如图1所示，由真实无人机网络模型和孪生网络模型组成。真实无人机网络模型中，$ N $个智能终端部署在区域$ \mathcal{A} $中。同时，考虑集合$ \mathcal{M}=\left\{\mathrm{1,2},\cdots,M\right\} $的无人机配备有边缘服务器，地面智能终端向无人机发送辅助计算需求。在无人机对地面智能终端计算服务需求充分认知的情况下，为地面用户提供高质量计算服务，如车辆自动驾驶预警、导航等。每个无人机的覆盖区域用$ {\mathcal{A}}_{m} $表示，且对于任意$ m,m'\in \mathcal{M} $，$ m\ne m' $，存在$ {\cup }_{\forall m\in \mathcal{M}}{\mathcal{A}}_{m}=\mathcal{A} $且$ {\mathcal{A}}_{m}\cap {\mathcal{A}}_{m'}=\mathrm{\varnothing } $。在无人机$ m $的区域$ {\mathcal{A}}_{m} $中，分布有$ {N}_{m} $个智能终端，用集合$ {\mathcal{N}}_{m}= \left\{\mathrm{1,2},\cdots,{N}_{m}\right\} $表示。因此，区域$ \mathcal{A} $中分布的所有智能终端集合为$ \mathcal{N}=\left\{\mathrm{1,2},\cdots,N\right\} $，且$ \mathcal{N}={\cup }_{m\in \mathcal{M}}{\mathcal{N}}_{m} $。为了提高计算服务质量，每个无人机只为覆盖区域内的智能终端提供计算服务。由于无人机的电池能量有限，设每个无人机最大服务时长为$ T $，设其在满电状态且亏电前不补充电量前提下的最大飞行距离为$ {d}_{m}^{\mathrm{m}\mathrm{a}\mathrm{x}} $。设在无人机提供计算服务过程中，始终保持在高度为$ H $的水平面上。

在时刻$ t\in \left\{\mathrm{0,1},2,\cdots,T\right\} $，考虑智能终端n的数据表示为$ {\mathcal{D}}_{n}=\left\{\left({x}_{n1},{y}_{n1}\right) ,\cdots,({x}_{n{D}_{n}},{y}_{n{D}_{n}}) \right\} $，且无人机的数据表示为$ {\mathcal{D}}_{m}=\left\{\left({x}_{m1},{y}_{m1}\right) ,\cdots,({x}_{m{D}_{m}},{y}_{m{D}_{m}}) \right\} $。其中，$ {D}_{n} $表示智能终端$ n $的数据大小，$ {D}_{m} $表示无人机$ m $的数据大小。地面BS连续地采集服务区域$ \mathcal{A} $内智能终端和无人机的数据，以构建包含智能终端、无人机、网络拓扑及环境的孪生网络模型。智能终端$ n $和无人机$ m $在地面BS的孪生模型分别表示为$\mathrm{D}{\mathrm{T}}_{{n}}=\big\{{\mathcal{M}}_{n},{\mathcal{D}}_{n}, {S}_{n,t}, {S}_{n,t+1}\big\}$和$ \mathrm{D}{\mathrm{T}}_{m}=\left\{{\mathcal{M}}_{m},{\mathcal{D}}_{m},{S}_{m,t},{\mathrm{S}}_{m,t+1}\right\} $。其中，$ {\mathcal{M}}_{n} $和$ {\mathcal{M}}_{m} $分别表示智能终端$ n $和无人机$ m $的行为模型，$ {S}_{n,t} $和$ {S}_{m,t} $分别表示智能终端$ n $和无人机$ m $的实时状态，$ {S}_{n,t+1} $和$ {S}_{m,t+1} $分别表示智能终端$ n $和无人机$ m $的更新状态。地面BS通过生成的孪生网络模型对无人机网络运行状态进行模拟和仿真，并使用合适的智能算法设计无人机边缘计算方案，以满足地面用户的计算服务性能需求。

在本文提出的系统模型中，无人机充当联邦学习的聚合器，聚合维护具体计算任务的全局模型参数。地面智能终端从服务区域的无人机获得全局模型参数，在全局模型的基础上使用本地数据训练本地模型；然后智能终端通过上行信道将训练后的本地模型参数上传到服务区域的无人机，由无人机对智能终端本地模型参数进行聚合以更新全局模型参数。

1.1 联邦学习模型

用$ {w}_{m} $表示第$ m $个无人机的全局模型参数，用$ {w}_{n} $表示第$ n $个智能终端的本地模型参数，用$ f({w}_{m},{x}_{n,i},{y}_{n,i}) $表示关于数据样本$ ({x}_{n,i},{y}_{n,i}) $和参数$ {w}_{m} $的损失函数，则智能终端$ n $的本地模型参数训练损失可以表示为

$ {f}_{n}\left({w}_{m}\right) =\frac{1}{{D}_{n}}{\sum }_{i\in {\mathcal{D}}_{n}}f({w}_{m},{x}_{n,i},{y}_{n,i}) $

(1)

第$ m $个无人机的全局模型参数训练损失表示为

$ f\left({w}_{m}\right) =\frac{1}{{D}_{m}}{\sum }_{n\in {\mathcal{N}}_{m}}{\sum }_{i\in {\mathcal{D}}_{n}}f({w}_{m},{x}_{n,i},{y}_{n,i}) $

(2)

第$ m $个无人机执行联邦学习，寻找最优模型参数，以最小化全局模型训练损失。

$ {w}_{m}^{*}={\mathrm{a}\mathrm{r}\mathrm{g}\mathrm{m}\mathrm{i}\mathrm{n}}_{{w}_{n}}f\left({w}_{m}\right) $

(3)

1.2 通信模型

每一轮联邦学习训练过程中，考虑智能终端采用正交频分多址接入技术，通过上行信道将训练的本地模型参数上传到服务区域的无人机。区域$ \mathcal{A} $中有K个上行子信道，表示为$ \mathcal{K}=\left\{\mathrm{1,2},\cdots,K\right\} $ 。N个智能终端复用K个上行子信道。此时，第m个无人机将收到复用相同子信道的其他区域内智能终端干扰。因此，在时刻$ t $，第$ n $个智能终端与第$ m $个无人机在子信道$ k $上的信干噪比可以表示为

$ {\mathrm{S}\mathrm{I}\mathrm{N}\mathrm{R}}_{n,m,k}^{m}=\frac{{P}_{n,k}^{\mathrm{u}\mathrm{p}}{g}_{n,m}}{\sum _{{n}'\in \mathcal{N},{n}'\ne n}{P}_{{n}',k}^{{\rm{up}}}{g}_{{n}',m}+{\sigma }^{2}} $

(4)

式中：$ {P}_{n,k}^{\mathrm{u}\mathrm{p}} $为智能终端$ n $在子信道$ k $上的发送功率，$ {\sigma }^{2} $是高斯噪声功率，$ \sum _{{n}'\in \mathcal{N},{n}'\ne n}{P}_{{n}',k}^{{\rm{up}}}{g}_{{n}',m} $表示来自其他区域智能终端在子信道$ k $的干扰；$ {g}_{n,m}\left(t\right) $为智能终端$ n $和无人机$ m $之间的信道增益

$ {g}_{n,m}\left(t\right) =\frac{\beta }{{d}_{n,m}^{2}\left(t\right) +{H}^{2}} $

(5)

式中：$ {d}_{n,m}\left(t\right) =\sqrt{{({X}_{m}\left(t\right) -{x}_{n}) }^{2}+{({Y}_{m}\left(t\right) -{y}_{n}) }^{2}} $为智能终端$ n $和无人机$ m $之间的水平投影距离。无人机$ m $在时刻$ t $的物理位置为$ {\psi }_{m}\left(t\right) =({X}_{m}\left(t\right) ,{Y}_{m}\left(t\right) ,H) $，智能终端$ n $的物理位置为$ {\omega }_{n}\left(t\right) =({x}_{n},{y}_{n}) $，考虑M个无人机的飞行高度均为$ H $。因此，在时刻$ t $，智能终端$ n $在子信道$ k $上的数据传输速率表示为

$ {R}_{n,m}\left(t\right) =B{\sum }_{k=1}^{K}{\phi }_{n,m,k}\left(t\right) {\mathrm{l}\mathrm{o}\mathrm{g}}_{2}(1+\mathrm{S}\mathrm{I}\mathrm{N}{\mathrm{R}}_{n,m,k}^{m}) $

(6)

式中：$ B $为子信道的带宽，$ {\phi }_{n,m,k}\left(t\right) $为子信道$ k $分配决策变量，且$ {\phi }_{n,m,k}\in \left(\mathrm{0,1}\right) $。当$ {\phi }_{n,m,k}=1 $时，表示智能终端$ n $选择子信道$ k $上传本地模型参数，否则$ {\phi }_{n,m,k}=0 $。

1.3 计算模型

在联邦学习训练过程中，地面智能终端$ n $根据本地数据样本训练本地模型参数，贡献的计算资源表示为$ {f}_{n}^{\mathrm{C}\mathrm{P}\mathrm{U}} $，即CPU周期频率。训练一个数据样本需要的CPU周期频率表示为$ {c}_{n} $，则在本地训练过程中，智能终端$ n $本地训练的计算时延表示为

$ {T}_{n,\mathrm{l}\mathrm{o}\mathrm{c}}=\frac{{D}_{n}{c}_{n}}{{f}_{n}^{\mathrm{c}}} \text{，} \forall n\in \mathcal{N} $

(7)

本地模型参数训练完成后，智能终端将本地模型参数无线传输到服务区域的无人机，本地模型参数上传时延表示为

$ {T}_{n,m,\mathrm{u}\mathrm{p}}\left(t\right) =\frac{\left|{w}_{m}\right|}{{R}_{n,m}\left(t\right) } \text{，} \forall n\in \mathcal{N} $

(8)

式中：$ \left|{w}_{m}\right| $为本地模型参数大小，$ {R}_{n,m}\left(t\right) $为智能终端$ n $的数据上传速率。

每轮联邦学习训练总时延由本地模型训练时延、本地模型上传时延、全局模型聚合时延和全局模型广播时延组成。考虑无人机配备的边缘服务器有充足的计算资源，且无人机使用专门的信道进行全局模型参数广播。与本地模型训练和上传时延相比，无人机全局模型聚合时延和全局模型广播时延较小。因此，第$ n $个智能终端参与一轮联邦学习训练的时延表示为

$ {T}_{n}\left(t\right) ={T}_{n,\mathrm{l}\mathrm{o}\mathrm{c}}+{T}_{n,m,\mathrm{u}\mathrm{p}}\left(t\right) \text{，} \forall n\in \mathcal{N} $

(10)

每轮联邦学习训练总时延由所有终端参与此轮联邦学习的最大时延决定，表示为

$ {T}_{m}\left(t\right) =\mathrm{max}{T}_{n}\left(t\right) ,\forall n\in \mathcal{N},m\in \mathcal{M} $

(11)

为此，通过优化无人机的飞行距离、飞行角度、子信道分配，设计式(11)最小化无人机数字孪生边缘网络联邦学习时延的优化问题

$ \underset{\alpha ,d,\phi ,}{\mathrm{min}}\frac{1}{T}\sum _{t=1}^{T}{T}_{m}\left(t\right) ,\forall m\in \mathcal{M} $

$ {\rm{s}}.{\rm{t}}.\left\{ \begin{array}{l} {\rm{C}}1: 0\le {X}_{m}\left(t\right) \le {X}_{\mathrm{m}\mathrm{a}\mathrm{x}} ,\; 0\le {Y}_{m}\left(t\right) \le {Y}_{\mathrm{m}\mathrm{a}\mathrm{x}},\\ \qquad\quad \forall m\in \mathcal{M} , \\ {\rm{C}}2: 0\le {d}_{m}\left(t\right) \le {d}_{m}^{\mathrm{m}\mathrm{a}\mathrm{x}} ,\; 0\le {\varphi }_{m}\left(t\right) \le \text{2π},\forall m\in \mathcal{M} ,\\ {\rm{C}}3: {d}_{m,{m}'}\left(t\right) \ge {d}_{\mathrm{m}\mathrm{i}\mathrm{n}},\;\forall m\in \mathcal{M}, \\ {\rm{C}}4: {d}_{n,m}\left(t\right) \le {R}_{\mathrm{m}\mathrm{a}\mathrm{x}},\;\forall n\in \mathcal{N},\;\forall m\in \mathcal{M} ,\\ {\rm{C}}5: \sum _{n\in {N}_{m}}\sum _{k\in K}{\phi }_{n,m,k}\left(t\right) \le K,{\phi }_{n,m,k}\left(t\right) \in \left\{\mathrm{0,1}\right\},\\ \qquad\quad \forall n\in \mathcal{N},\;\forall m\in \mathcal{M} \end{array} \right.$

(12)

式中：C1表示无人机不能飞出服务区域$ \mathcal{A} $；C2表示无人机在$ t $时刻执行决策的飞行距离$ {d}_{m}\left(t\right) $不能超过最大飞行距离$ {d}_{m}^{\mathrm{m}\mathrm{a}\mathrm{x}} $，且飞行角度$ {\varphi }_{m}\left(t\right) $不能超过最大飞行角度$ \text{2π} $；C3表示无人机$ m $ 和$ m' $之间的距离$ {d}_{m,{m}'}\left(t\right) = \sqrt{{({X}_{m}\left(t\right) -{X}_{m'}\left(t\right) ) }^{2}+{({Y}_{m}\left(t\right) -{Y}_{m'}\left(t\right) ) }^{2}} $需大于最小碰撞距离$ {d}_{\mathrm{m}\mathrm{i}\mathrm{n}} $；C4为地面智能终端到无人机的水平投影距离小于无人机的覆盖区域半径$ {R}_{\mathrm{m}\mathrm{a}\mathrm{x}} $；C5为子信道最大分配数量约束。

2 无人机数字孪生边缘网络联邦学习资源自适应优化算法设计

由于无人机数字孪生边缘网络无线传输环境的随机性，以及网络边缘计算、通信等资源的动态时变性，用传统的优化方法较难求解优化问题(11)。MA-DDPG中每个智能体结合全部智能体的策略进行参数更新，从而更适合用于处理多个智能体的复杂协作问题，并具有较高鲁棒性。此外，MA-DDPG采用中心化训练、去中心化执行框架，允许智能体使用其他智能体的策略信息来增强自身的训练效果，而在实际应用或测试时不需要全局信息也能做出有效决策。Ryan等^[15]通过与已有算法在协作和竞争场景下的比较，证明了MA-DDPG算法性能优越性。

本文设计基于孪生网络模型的MA-DDPG优化算法，以求解无人机数字孪生边缘网络联邦学习时延优化问题(11)。如图2所示，在设计的优化算法中，MA-DDPG算法的运行环境由本地BS维护的孪生网络模型组成，包括无人机、地面智能终端以及无线传输信道的孪生模型。本文所提模型的具体流程如下：

步骤1：无人机网络中的地面智能终端和无人机将状态更新信息上传给本地BS维护的孪生网络模型，保持虚实同步更新。

步骤2：本地BS从孪生网络模型中观测无人机和地面智能终端的状态以及系统返回的即时报酬。

步骤3：将步骤2新观测到的状态输入MA-DDPG决策模型求解优化问题(11) ，获得输出决策。该决策会与状态和报酬等信息一起保存到MA-DDPG的经验缓存池中。当经验缓存池内的经验数据达到一定数量后，MA-DDPG开始迭代训练更新自身的网络参数。

步骤4：将MA-DDPG输出的决策应用到孪生网络模型中进行测试，孪生网络模型更新自身状态并计算即时报酬。

步骤5：将经过测试的优化决策反馈给无人机和地面智能终端的物理实体执行。

相比传统MA-DDPG算法，本文设计的基于孪生网络模型的MA-DDPG算法，本地BS 从孪生网络模型中获取状态信息，可减少MA-DDPG算法训练过程中无人机和地面智能终端交互的资源开销。

2.1 基于孪生网络模型的MA-DDPG优化算法

本文提出的基于孪生网络模型的MA-DDPG优化算法中，将决策问题构造成马尔可夫决策过程，其中，状态空间、动作空间和报酬函数分别定义如下。

(1) 状态空间。在决策时刻$ t $，$ t\in \left\{\mathrm{0,1},\cdots ,T\right\} $，本地BS维护的孪生网络模型状态空间包括：无人机$ m $的位置$ {\psi }_{m}\left(t\right) $，无人机 $ m $ 和无人机$ m' $之间的距离$ {d}_{m,{m}'}\left(t\right) $，地面智能终端$ n $的位置$ {\omega }_{n}\left(t\right) $，地面智能终端联邦学习的本地模型参数$ {w}_{n}\left(t\right) $，以及地面智能终端$ n $和无人机$ m $之间的信道增益$ {g}_{n,m}\left(t\right) $，其中，$n\in \mathcal{N},\;m\in \mathcal{M} $。因此，状态空间可以表示为

$ {S}_{m,t}=\left\{{\psi }_{m}\left(t\right) ,{d}_{m,{m}'}\left(t\right) ,{\omega }_{n}\left(t\right) ,{w}_{n}\left(t\right) ,{g}_{n,m}\left(t\right) \right\} $

(13)

(2) 动作空间。为了最小化无人机数字孪生边缘网络联邦学习时延，需要调整决策变量以适应网络环境的动态时变性。本地BS需要调整的决策变量包括：无人机在第$ t $时刻的飞行距离$ {d}_{m}\left(t\right) $，无人机飞行角度$ {\varphi }_{m}\left(t\right) $，地面智能终端n的子信道分配决策$ {\phi }_{n,m,k}\left(t\right) $。其中，$ {d}_{m}\left(t\right) $和$ {\varphi }_{m}\left(t\right) $可以调整无人机的位置以降低式(4)中无人机与地面智能终端交互时的信噪比$ {\mathrm{S}\mathrm{I}\mathrm{N}\mathrm{R}}_{n,m,k}^{m} $，$ {\phi }_{n,m,k}\left(t\right) $通过子信道的分配情况来调整式(6)中地面智能终端上传模型的速率$ {R}_{n,m}\left(t\right) $。上述3个决策变量相互配合可降低式(8)中所有地面智能终端本地模型参数的上传时间$ {T}_{n,m,\mathrm{u}\mathrm{p}}\left(t\right) $，降低式(10)中的无人机$ m $服务的$ {T}_{m}\left(t\right) $。所有无人机执行上述决策配合训练，每个无人机均实现其服务的联邦学习训练总时延$ {T}_{m}\left(t\right) $最小化，进而解决本文的优化问题(11)。因此，在决策时刻$ t $，优化无人机数字孪生边缘网络联邦学习时延的动作空间表示为

$ {A}_{m,t}=\left\{{d}_{m}\right(t) ,{\varphi }_{m}(t) ,{\phi }_{n,m,k}\left(t\right) \} $

(14)

(3) 报酬函数。考虑到强化学习以最大化长期平均报酬为目标，而本文需要最小化联邦学习的训练时延，因此设计如下即时报酬函数$ {r}_{m,t} $

$ {r}_{m,t}=\frac{l}{{T}_{m}\left(t\right) } $

(15)

式中：$ l $为大于0的常数。MA-DDPG智能体的优化目标是最大化长期平均报酬

$ \mathcal{R}=\mathrm{m}\mathrm{a}\mathrm{x}\mathbb{E}\left[{\sum }_{t=0}^{T-1}{\sum }_{m=1}^{M}\gamma \cdot {r}_{m,t}({S}_{m,t},{A}_{m,t}) \right] $

(16)

式中：$ \gamma $是折扣因子。

2.2 MA-DDPG算法原理

DDPG采取确定性策略，以第$ m $个无人机智能体为例，其Actor作为策略网络，以环境状态$ {S}_{m,t} $作为输入，输出一个确定性动作$ {A}_{m,t} $。为保证神经网络的泛化能力且防止过拟合，DDPG会在策略网络Actor输出动作时添加随机噪声$ \mathcal{o} $，增加智能体尝试探索潜在最优策略的概率，即$ {A}_{m,t}={\mu }_{{\theta }_{m}^{{\rm{Actor}}}}({S}_{m,t}) +\mathcal{o} $，其中$ {\mu }_{{\theta }_{m}^{\mathrm{Actor}}}({S}_{m,t}) $是Actor网络的输入与输出的关系表示, $ {\theta }_{m}^{{\rm{Actor}}} $是Actor网络的参数。第$ t $时刻M个无人机智能体所处的环境状态集合表示为$ {S}_{t}=\{{S}_{1,t},{S}_{2,t},\cdots ,{S}_{M,t}\} $，动作集合表示为$ {A}_{t}=\{{A}_{1,t},{A}_{2,t},\cdots ,{A}_{M,t}\} $，即时报酬集合表示为$ {r}_{t}=\{{r}_{1,t},{r}_{2,t},\cdots ,{r}_{M,t}\} $。Target Actor是一个与Actor具有相同结构但不同参数的缓慢更新网络，将下一时刻的环境状态$ {S}_{m,t+1} $作为输入，输出与$ {A}_{m,t} $具有相同形状的动作$ {A'}_{m,t+1} $，但该输出仅用于更新价值网络Critic。MA-DDPG中每个智能体的价值网络Critic的作用是拟合状态−动作值函数$ {Q}_{m}({S}_{t},{A}_{m,t}) $，以M个无人机智能体的环境状态集合$ {S}_{t} $和对应第$ m $个智能体的策略动作$ {A}_{m,t} $为输入，输出该动作于当前状态的价值$ q{\text{-}}\mathrm{v}\mathrm{a}\mathrm{l}\mathrm{u}\mathrm{e} $。同样地，Target Critic与Critic具有相同的网络结构，以$ {S}_{t+1}\mathrm{、}{A'}_{m,t+1} $为输入，生成对Target Actor网络输出$ {A'}_{m,t+1} $的评估价值$ {Q}_{m}^{\mathrm{T}\mathrm{a}\mathrm{r}\mathrm{g}\mathrm{e}\mathrm{t}}({S}_{t+1}, {A'}_{m,t+1}) $。DDPG借鉴了深度Q网络(Deep Q Network, DQN) 的经验回放的技巧，同样会把$ ({S}_{t},{A}_{t},{r}_{t},{S}_{t+1}) $存储到经验回放池。DDPG每次训练并更新网络参数时，会从经验回放池随机采样一个minibatch大小的经验作为本次训练的数据样本。

MA-DDPG的基本思想是中心化训练、去中心化执行。每个无人机智能体可利用全局信息，包括其他无人机智能体所处的环境状态及对应的策略动作等信息。对Critic进行训练，但在其进行决策时只需局部信息(该智能体自身所处的环境状态)，就可得到确定性策略。第$ m $个无人机智能体会独立地学习集中式的状态−动作值函数$ {Q}_{m}({S}_{t},{A}_{m,t}) $，因此可通过为每个智能体设置不同报酬函数来实现不同智能体间的协作。

价值网络Critic采用基于TD-error的梯度下降更新方法，该网络需要结合环境的真实收益$ {r}_{m,t} $和$ {Q}_{m}^{\mathrm{T}\mathrm{a}\mathrm{r}\mathrm{g}\mathrm{e}\mathrm{t}}({S}_{t+1},{A'}_{m,t+1}) $来学习如何对策略网络Actor的动作价值做出准确的评价。本文所提出的优化方案中，所有无人机智能体之间是相互协作的关系，目标是使所有无人机智能体的平均报酬最大化。因此，第$ m $个无人机智能体的Critic网络损失函数表示为

$ \begin{split} {L}_{m}^{\mathrm{C}\mathrm{r}\mathrm{i}\mathrm{t}\mathrm{i}\mathrm{c}}\left({\theta }_{m}^{{\rm{Critic}}}\right) =&\mathrm{M}\mathrm{S}\mathrm{E}\left({Q}_{m}\right({S}_{t},{A}_{m,t}) , \frac{1}{M}{\sum }_{m=1}^{M}{r}_{m,t}+\\ &\gamma {Q}_{m}^{\mathrm{T}\mathrm{a}\mathrm{r}\mathrm{g}\mathrm{e}\mathrm{t}}({S}_{t+1},{A'}_{m,t+1}) ) \end{split} $

(17)

策略网络Actor的目标是找到当前环境状态下的最优策略动作，优化策略网络Actor就需要最大化价值网络输出$ {Q}_{m}({S}_{t},{A}_{m,t}) $。因此，Actor网络采用梯度上升的更新方法，第$ m $个无人机智能体的损失函数表示为

$ {L}_{m}^{\mathrm{A}\mathrm{c}\mathrm{t}\mathrm{o}\mathrm{r}}=-{Q}_{m}({S}_{t},{A}_{m,t}) $

(18)

第m个无人机智能体的累计期望报酬

$ J\left({\theta }_{m}^{\mathrm{Actor}}\right) ={E}_{{S}_{m,t},{A}_{m,t} \sim {\mu }_{{\theta }_{m}^{{\rm{Actor}}}}}\left[{\sum }_{t=0}^{\infty }\gamma \cdot \frac{1}{M}{\sum }_{m=1}^{M}{r}_{m,t}\right] $

(19)

对应第$ m $个无人机智能体的确定性策略$ {\mu }_{{\theta }_{m}^{{\rm{Actor}}}} $，其梯度为

$ {{\nabla }_{{\theta }_{m}^{\mathrm{Actor}}}J\left({\mu }_{{\theta }_{m}^{\mathrm{Actor}}}\right) = {E}_{{S}_{m,t},{A}_{m,t} \sim D}\left[{\nabla }_{{\theta }_{m}^{\mathrm{Actor}}}{\mu }_{{\theta }_{m}^{\mathrm{Actor}}}\left({S}_{m,t}\right) {\nabla }_{{A}_{m,t}}{Q}_{m}\left({S}_{t},{A}_{m,t}\right) \right] }$

(20)

式中：D为元素$ ({S}_{t},{A}_{t},{r}_{t},{S}_{t+1}) $组成的经验回放池。

Target Actor的网络参数$ {\theta '}_{m}^{{\rm{Actor}}} $以及Target Critic的网络参数$ {\theta '}_{m}^{{\rm{Critic}}} $则分别按下式进行更新

$ {\theta '}_{m}^{\mathrm{Actor}}=\tau {\theta }_{m}^{\mathrm{Actor}}+(1-\tau ) {\theta '}_{m}^{\mathrm{Actor}} $

(21)

$ {\theta '}_{m}^{\mathrm{Critic}}=\tau {\theta }_{m}^{\mathrm{Critic}}+(1-\tau ) {\theta '}_{m}^{\mathrm{Critic}} $

(22)

其中$ \tau $用于调节Target网络更新时的参数占比。算法1给出了本文提出的MA-DDPG 算法原理。

算法1　MA-DDPG算法原理

输入　状态$ {{S}_{1},{S}_{2},\cdots ,{S}_{T} }$

输出　对应时刻t所有无人机代理的决策$ { {A}_{1},{A}_{2},\cdots ,{A}_{T} }$

(1) 当episode=1,2,···，循环1：

(2) 对于t=1,2,···,T，循环2：

(3) M个无人机分别从孪生网络模型中获取当前时刻t的状态$ { {S}_{m,t},m\in \mathcal{M}} $，并输入各自的Actor网络得到决策$ {{A}_{m,t}={\mu }_{{\theta }_{m}^{{\rm{Actor}}}}({S}_{m,t}) +\mathcal{o},m\in \mathcal{M} }$

(4) M个无人机分别在各自的孪生网络模型中执行决策，并得到各自的实时报酬及下一时刻的状态

(5) 存储$ { ({S}_{t},{A}_{t},{r}_{t},{S}_{t+1}) }$到经验回放池

(6) 对于代理=1,2,···, $ {\mathcal{M}} $，循环3：

(7) 从经验回放池中随机采样一个minibatch大小的经验

(8) 根据式(17)、(19)分别更新参数$ { {\theta }_{m}^{\mathrm{Actor}}、{\theta }_{m}^{\mathrm{Critic}} }$

(9) 根据式(20)、(21)分别更新参数$ { {\theta '}_{m}^{\mathrm{Actor}}、{\theta '}_{m}^{\mathrm{Critic}} }$

(10) 结束循环3

(11) 结束循环2

(12) 结束循环1

3 仿真结果

本节通过实验验证提出的基于孪生模型的MA-DDPG优化算法的性能。利用Pytorch神经网络框架搭建MA-DDPG优化算法。考虑在长和宽均为500 m的正方形区域$ \mathcal{A} $内部署4架无人机，无人机的飞行高度保持100 m，覆盖区域为半径$ {R}_{\mathrm{m}\mathrm{a}\mathrm{x}}=10\;\mathrm{m} $的圆形，每次的最大飞行距离$ {d}_{m}^{\mathrm{m}\mathrm{a}\mathrm{x}}=10\;\mathrm{m} $，飞行速度为10 m/s。区域$ \mathcal{A} $内上行子信道数量K=50，每个子信道的上传带宽为10 MHz。区域$ {\mathcal{A}}_{m} $内的地面智能终端数量$ {\mathcal{N}}_{m}\in \left[\mathrm{20,60}\right] $，第$ n $个终端设备可贡献的计算资源$ {f}_{n}^{{\rm{CPU}}}\in \left[1.5-3.0\right]\mathrm{G}\mathrm{H}\mathrm{z} $，用于计算长期平均报酬的折扣因子$ \gamma =0.97 $。在MA-DDPG算法实现过程中，设置Actor和Critic网络分别由1个输入层，2个隐藏层和1个输出层构成。此外，本文还利用真实的数据集CIFAR10^[16]验证无人机数字孪生边缘网络联邦学习的性能，CIFAR10数据集由10种类别的60 000张图像组成，包括50 000张训练图像和10 000张测试图像。在进行仿真验证时，CIFAR10数据集被随机分配给地面智能终端。本文采用卷积神经网络作为联邦学习的机器学习模型。

图3对比了不同算法下无人机智能体的平均报酬。从图中可以看出，随着训练次数增加，不同算法下无人机智能体的平均报酬均能上升并趋于收敛。由于MA-DDQN算法适合处理离散变量，而本文研究场景中表征无人机移动的飞行距离和飞行角度属于连续变量，因此，MA-DDQN算法需先对这些连续变量进行离散化处理后再执行迭代训练，而这限制了获得的无人机飞行距离和飞行角度的准确性。尽管MA-DDQN算法最终也能收敛至一个稳定区间，但其在报酬优化和收敛方面都逊于本文方案算法。这一结果充分证明了本文方案算法在提出的无人机数字孪生边缘网络中的优势。

图4对比了不同学习率下无人机智能体的平均报酬。从图中可以看出，随着训练次数增加，不同学习率下无人机智能体的平均报酬都能增加并收敛至稳定值，证明了提出的基于孪生网络模型的MA-DDPG优化算法可以通过探索不同的动作策略，如无人机$ m $在第$ t $时刻的飞行距离$ {d}_{m}\left(t\right) $，无人机飞行角度$ {\varphi }_{m}\left(t\right) $，子信道分配决策$ {\phi }_{n,m,k}\left(t\right) $，从而实现最大化无人机平均报酬的目标。此外，当Actor神经网络参数的学习率$a={10}^{-4}$，Critic 神经网络参数的学习率$c={10}^{-4}$时，获得的无人机平均报酬最大。其次，当Actor神经网络参数的学习率$ a={10}^{-5} $，Critic神经网络参数的学习率$ c={10}^{-5} $时，获得的无人机平均报酬最小。这说明设置较大的学习率，可以获得较好的收敛性能。

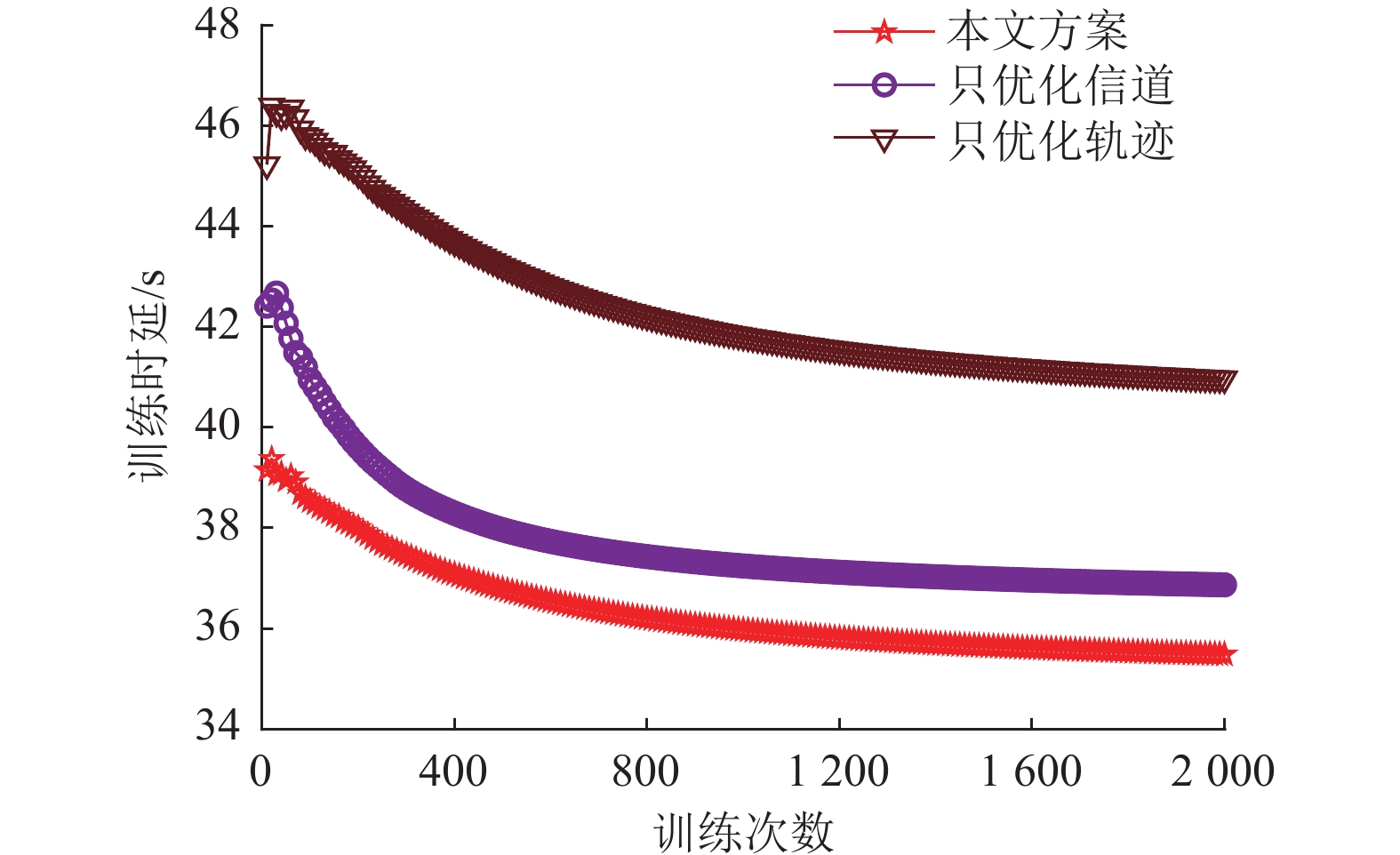
图5展示了本文提出的方案与只优化信道和只优化轨迹的两种方案在联邦学习训练延迟方面的对比。根据报酬函数(见式(14))，联邦学习的训练延迟是计算报酬时的一个关键因素，其最小化是实现报酬最大化的必要条件，这与本文旨在最小化联邦学习训练延迟的目标相吻合。从图中可以观察到，随着训练迭代次数的增加，3种优化方案的训练延迟都有所下降，并最终趋于稳定。本文提出的方案在降低联邦学习训练延迟方面表现出了最佳的性能，这一优势源自于对无人机的飞行距离、飞行角度以及子信道分配3个关键变量的综合优化。当且仅当这3个变量同时得到优化时，才能取得最佳效果。仿真结果证实了，相较于其他对照方案，本文提出的方案更有效地降低了联邦学习的训练延迟。

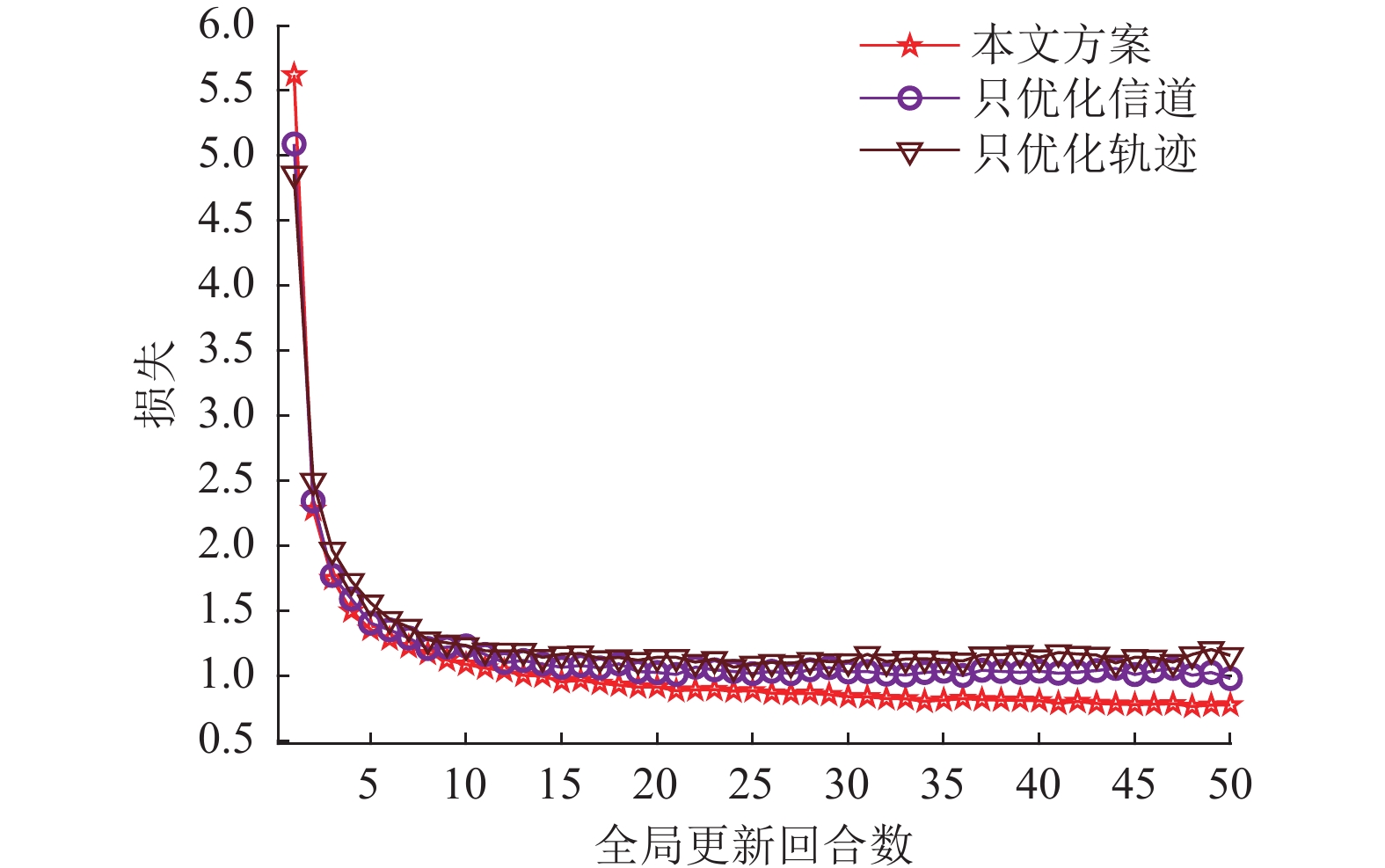
图6对比了3种优化方案实现的无人机数字孪生边缘网络联邦学习训练损失。从图中可以看出，随着联邦学习全局训练回合数增加，3种优化方案的联邦学习训练损失都能逐渐减小并趋于稳定值。其次，本文方案可以获得最小的联邦学习训练损失。这是因为提出的方案通过联合优化无人机飞行距离、无人机飞行角度和子信道分配3个优化变量，无人机可以聚合更多地面智能终端的本地模型参数，从而使全局模型参数训练损失快速降低。而在只优化子信道分配的优化方案中，无人机悬停于固定位置，无法采集服务区域内所有地面智能终端的本地模型参数，因而该方案的损失比本文方案大。在只优化无人机轨迹的优化方案中，子信道随机分配给地面智能终端，无法保证所有地面智能终端被分配足够子信道传输本地模型参数，因而该方案的损失最大。

图7对比了3种优化方案实现的无人机数字孪生边缘网络联邦学习训练准确率。从图中可以看出，随着联邦学习全局训练回合数增加，3种优化方案的联邦学习训练准确率都能逐渐增加并趋于稳定值。其次，本文方案可以获得最大的全局模型准确率。与图6的分析一致，只优化子信道分配的方案中全局模型的准确率低于本文方案，而只优化无人机轨迹的方案中全局模型的准确率最低。

4 结论

本文采用联邦学习，提出基于无人机数字孪生边缘网络的联邦学习资源调度机制。考虑无人机数字孪生边缘网络环境的动态时变性，建立联合无人机飞行距离、飞行角度以及无线网络子信道分配的联邦学习自适应资源优化模型，实现最小化无人机数字孪生边缘网络联邦学习时延的目标。提出基于孪生网络模型的MA-DDPG算法，求解联邦学习自适应资源优化模型。仿真结果表明，本文方案可显著降低联邦学习时延性能，同时保证联邦学习损失函数和准确率的优越性。下一步工作将研究无人机数字孪生边缘网络中集成联邦学习与现有隐私保护技术，例如差分隐私技术，并将设计新的隐私保护框架和资源优化机制。