随着网络技术的不断发展，多智能体系统的一致性问题愈发受到学者的重视，并广泛运用于无人车系统^[1]、无人机编队^[2]、传感器网络^[3]等领域。在实现一致性的各种控制中，脉冲控制^[4]因其强鲁棒性和容易执行的特点，在过去20年得到了广泛的研究。例如，文献[5]研究了二阶多智能体系统的脉冲一致性算法；文献[6]研究了多智能体系统在脉冲控制受到攻击时实现一致性的问题。然而，这些结果中的脉冲都是基于时间触发的，它们要求事先设置出现的频率，因而控制成本居高不下^[7]。此外，尽管事件触发控制是通过设置一个临界值来判断系统控制信息是否更新，但是其控制方式还是连续的，控制成本仍然较高^[8]。

为了进一步降低控制的成本，事件触发脉冲控制被提出^[9-11]。它是事件触发策略和脉冲控制的结合，可实现按需控制与离散控制。一般地，它可分为静态和动态事件触发策略两大类。其中，静态事件触发策略是指触发函数仅与系统相关状态变量有关，而动态事件触发策略则包含额外的动态变量。近年来，动态事件触发策略得到了大量的研究，如文献[12]指出动态事件触发策略的最小触发间隔(任意两个相邻触发时刻间的最小时间间隔) 不小于其对应的静态触发策略的最小触发间隔；文献[13]提出了新颖的动态事件触发策略实现多智能体系统一致性；文献[14-15]则分别考虑了随机噪声和脉冲攻击对动态事件触发脉冲控制实现系统镇定的影响。

值得注意的是，上述文献都忽略了外部干扰或恶意攻击(如虚假数据注入攻击会破坏系统数据的完整性与准确性) 的存在，也就是说这些策略都对运行环境十分敏感。因此，考虑事件触发策略的抗干扰能力就显得十分重要。文献[16]提出了一种分布式脉冲控制器，研究了由虚假数据注入引起的有界同步问题。文献[17]进一步放宽了文献[18]中关于触发机制中参数的限制。文献[19]基于事件触发脉冲控制研究了具有时变延迟的随机复杂网络在欺骗攻击下的稳定性。文献[20]提出了一种基于观测者的一致性协议，利用局部观测者同时估计系统状态和攻击信号，从而保证系统能达到一致。文献[21]研究了随机网络控制系统在随机网络攻击下的事件触发脉冲控制问题。然而，它们的触发策略都是静态的，所以如何拓展到动态的形式值得进一步研究。

基于上述分析，本文旨在设计一个新颖的动态事件触发策略，并结合脉冲控制实现多智能体系统的拟一致性。本文主要贡献如下：

(1) 提出了可抗干扰的动态事件触发策略。芝诺行为可由策略参数的选择排除，且文献[14-15]中需要事先指定的最小触发间隔在此并不需要。

(2) 基于构造的动态事件触发策略，本文给出了系统同时遭受外部干扰和虚假数据注入攻击时实现拟一致性的充分条件。

符号说明　$ \mathbb{R},{\mathbb{N}^ + } $分别为实数集和正整数集；$ {\mathbb{R}^n},{\mathbb{R}^{n \times m}} $分别为$ n $维欧几里得空间和$ n \times m $维全体实矩阵集。对任意实对称矩阵$ {\boldsymbol{Q}},{\lambda _{\max }}\left( {\boldsymbol{Q}} \right) , $$ {\lambda _{\min }}\left( {\boldsymbol{Q}} \right) $分别为其最大特征值与最小特征值。对任意分段连续函数$ p:\mathbb{R} \to \mathbb{R}, $令$ p({t^ + }) = \lim {_{h \to {0^ + }}}p(t + h) $与$ p({t^ - }) = \lim {_{h \to {0^ - }}}p(t + h) $，其右上迪尼导数定义如下：$ {D^ + }p(t) = \lim {\mathrm{sup}}{_{s \to {0^ + }}}\left( {p(t + s) - p(t) } \right) /s $。$ \left| {\boldsymbol{v}} \right| $为向量$ {\boldsymbol{v}} $的欧几里得范数或矩阵$ {\boldsymbol{v}} $的诱导范数。此外，$ {\text{diag}}\left\{ \cdot \right\} $为对角矩阵，*为对称矩阵的对称项。

1 模型构造与预备知识 1.1 图论

多智能体系统可使用图论来描述。一般地，一个无向图可用$ G = (\overline V,\overline E,\overline {\boldsymbol{A}}) $表示，其中$\overline V$为节点集，而$\overline E$和$ \overline {\boldsymbol{A}} = {[{a_{ij}}]_{N \times N}} $则分别为其边集和连接矩阵，其中$N$为跟随者智能体的个数。$\overline E$反映了智能体之间的连接关系，如果智能体$i$和智能体$j$存在连接边，则有${a_{ij}} = {a_{ji}} > 0$，否则为0；同时，给定${a_{ii}} = 0$。图$ G $的拉普拉斯矩阵表示为${\boldsymbol{L}} = {[{l_{ij}}]_{N \times N}}$，其中$ {l_{ii}} = {a_{i1}} + {a_{i2}} + \cdots + {a_{iN}} $与$ {l_{ij}} = - {a_{ij}},i \ne j $；另外，令领导者智能体的标签为0，并令对角矩阵${\boldsymbol{D}} = {\text{diag}}\{ {d_1},{d_2}, \cdots ,{d_N}\} $表示领导者智能体和跟随者智能体的连接关系。若有信息从领导者智能体定向流动到跟随者智能体$i$，则有$ {d_i} > 0 $，否则${d_i} = 0$。此外，令$ {\boldsymbol{H}} = {\boldsymbol{L}} + {\boldsymbol{D}} $。

1.2 模型描述

考虑由一个领导智能体和$ N $个跟随智能体组成的多智能体系统。该系统的动态特性描述为

$ \left\{ \begin{array}{l} {\dot{{\boldsymbol{x}}}}_{i}(t) ={\boldsymbol{A}}{{\boldsymbol{x}}}_{i}(t) +{\boldsymbol{Bf}}({{\boldsymbol{x}}}_{i}(t) ) +{\boldsymbol{C}}{{\boldsymbol{\omega }}}_{i}(t) +\\ \qquad\quad {{\boldsymbol{u}}}_{i}(t) ,t\ge{t}_{0}\\ {\dot{{\boldsymbol{x}}}}_{0}(t) ={\boldsymbol{A}}{{\boldsymbol{x}}}_{0}(t) +{\boldsymbol{Bf}}({{\boldsymbol{x}}}_{0}(t) ) ,t\ge{t}_{0} \end{array} \right.$

(1)

式中：$ {{\boldsymbol{x}}_i}(t) \in {\mathbb{R}^n} $和$ {{\boldsymbol{x}}_0}(t) \in {\mathbb{R}^n} $分别为跟随者$ i $和领导者的系统状态变量；$ {{\boldsymbol{\omega}} _i}(t) \in {\mathbb{R}^w} $为跟随者$ i $的外部扰动；$ {{\boldsymbol{u}}_i}(t) \in {\mathbb{R}^n} $为跟随者$ i $的控制输入。$ {\boldsymbol{A}},{\boldsymbol{B}},{\boldsymbol{C}} \in {\mathbb{R}^{n \times n}} $为常数矩阵。$ {\boldsymbol{f}}:{\mathbb{R}^n} \to {\mathbb{R}^n} $描述系统的非线性特性，且满足$ {\boldsymbol{f}}({\bf{0}}) \equiv {\bf{0}} $。假设系统(1) 的初始时刻是$ {t_0} $,跟随者$ i $和领导者的初始状态分别为$ {{\boldsymbol{x}}_i}({t_0}) $和$ {{\boldsymbol{x}}_0}({t_0}) $。

为确保系统能够实现拟一致性，本文考虑如下脉冲控制协议：

$ \begin{split} {{\boldsymbol{u}}_i}(t) =& \sum\limits_{k = 1}^{ + \infty } {\bigg\{ {\boldsymbol{K}}\sum\limits_{j = 1}^N {({a_{ij}}({{\boldsymbol{x}}_i}(t) - {{\boldsymbol{x}}_j}(t) ) + } } \\ &{d_i}({{\boldsymbol{x}}_i}(t) - {{\boldsymbol{x}}_0}(t) ) ) + {{\boldsymbol{K}}_{\mathrm{s}}}{\zeta _i}(t) \bigg\} \delta (t - {t_k}) \end{split} $

(2)

式中：$ {\boldsymbol{K}} \in {\mathbb{R}^{n \times n}},{{\boldsymbol{K}}_{\mathrm{s}}} \in {\mathbb{R}^{n \times n}} $分别为脉冲控制增益矩阵和虚假数据注入攻击的强度矩阵，$ \delta (t) $为用于描述脉冲作用的狄拉克函数，$ {\zeta _i}(t) \in {\mathbb{R}^n} $为智能体$ i $所遭受的攻击信号。此外，令$ \{ {t_k},k \in {\mathbb{N}^ + }\} $为由事件触发机制所产生的脉冲序列，$ N(t,{t_0}) $为在$ ({t_0},t) $中脉冲触发次数。设系统状态变量在脉冲时刻是右连续的，即有$ {{\boldsymbol{x}}_i}(t_k^ + ) = {{\boldsymbol{x}}_i}({t_k}) $。

定义系统误差变量$ {{\boldsymbol{e}}_i}(t) = {{\boldsymbol{x}}_i}(t) - {{\boldsymbol{x}}_0}(t) $，以及$ \tilde {\boldsymbol{f}}({{\boldsymbol{e}}_i}(t) ) = {\boldsymbol{f}}({{\boldsymbol{x}}_i}(t) ) - {\boldsymbol{f}}({{\boldsymbol{x}}_0}(t) ) $。则由系统(1)~(2)可得如下误差系统：

$ \left\{ \begin{array}{l} {\dot{{\boldsymbol{e}}}}_{i}(t) ={\boldsymbol{A}}{{\boldsymbol{e}}}_{i}(t) +{\boldsymbol{B}}\tilde{{\boldsymbol{f}}}({{\boldsymbol{e}}}_{i}(t) ) + {\boldsymbol{C}}{{\boldsymbol{\omega }}}_{i}(t) \text{, }t\text{ }\ge{t}_{\text{0}}\text{, }t\ne {t}_{k},\text{ }k\in {\mathbb{N}}^+\\ \Delta {{\boldsymbol{e}}}_{i}({t}_{k}) ={\boldsymbol{K}}({\displaystyle \sum _{j=1}^{N}{a}_{ij}}({{\boldsymbol{e}}}_{i}({t}_{k}^-) -{{\boldsymbol{e}}}_{j}(\text{ }{t}_{k}^-) ) +\\ \qquad\qquad{d}_{i}{\boldsymbol{e}}({t}_{k}^-) ) +{{\boldsymbol{K}}}_{{\mathrm{s}}}{\zeta }_{i}({t}_{k}^-) ,t\ge{t}_{\text{0}}\text{, }t\ne {t}_{k},\text{ }k\in {\mathbb{N}}^+ \end{array} \right.$

(3)

式中：$ \Delta {{\boldsymbol{e}}_i}({t_k}) = {{\boldsymbol{e}}_i}(t_k^ + ) - {{\boldsymbol{e}}_i}(t_k^ - ) $。

令${\boldsymbol{ \varGamma }}({\boldsymbol{e}}(t) ) = {({\tilde {\boldsymbol{f}}^{\mathrm{T}}}({{\boldsymbol{e}}_1}(t) ) ,{\tilde {\boldsymbol{f}}^{\mathrm{T}}}({{\boldsymbol{e}}_2}(t) ) , \cdots ,{\tilde {\boldsymbol{f}}^{\mathrm{T}}}({{\boldsymbol{e}}_N}(t) ) ) ^{\mathrm{T}}} $，$ {\boldsymbol{e}}(t) = {({\boldsymbol{e}}_1^{\mathrm{T}}(t) ,{\boldsymbol{e}}_2^{\mathrm{T}}(t) , \cdots ,{\boldsymbol{e}}_N^{\mathrm{T}}(t) ) ^{\mathrm{T}}} $，${\boldsymbol{\omega }}(t) \;=\; ({\boldsymbol{\omega}} _1^{\mathrm{T}}(t) ,{\boldsymbol{\omega}} _2^{\mathrm{T}}(t), \cdots ,{\boldsymbol{\omega}} _N^{\mathrm{T}}(t) {) ^{\mathrm{T}}} $和$ \zeta (t) = {(\zeta _1^{\mathrm{T}}(t) ,\zeta _2^{\mathrm{T}}(t) , \cdots ,\zeta _N^{\mathrm{T}}(t) ) ^{\mathrm{T}}} $。利用克罗内克积的性质，误差系统(3)可被改写为

$ \left\{ \begin{array}{l} \dot{{\boldsymbol{e}}}(t) =({{\boldsymbol{I}}}_{N}\otimes {\boldsymbol{A}}) {\boldsymbol{e}}(t) +({{\boldsymbol{I}}}_{N}\otimes {\boldsymbol{B}}) {\boldsymbol{\varGamma}} ({\boldsymbol{e}}(t) ) +\\ \qquad ({{\boldsymbol{I}}}_{N}\otimes {\boldsymbol{C}}) {\boldsymbol{\omega }}(t) \text{, }t\ge{t}_{\text{0}},t\ne {t}_{k},\text{ }k\in {\mathbb{N}}^+\\ \Delta {\boldsymbol{e}}(t) =({\boldsymbol{H}}\otimes {\boldsymbol{K}}) {\boldsymbol{e}}({t}_{k}^-) + ({{\boldsymbol{I}}}_{N}\otimes {{\boldsymbol{K}}}_{s}) \zeta ({t}_{k}) \text{,}t={t}_{k}\end{array} \right.$

(4)

1.3 定义、引理与假设

定义1^[22]　对任意给定的初始状态$ {{\boldsymbol{x}}_i}({t_0}) $和$ {{\boldsymbol{x}}_0}({t_0}) $，如果存在常数$ E > 0 $使得当$ t \to + \infty $时，$ {\boldsymbol{e}}(t) $收敛到如下有界集：

$ \mathcal{C}=\left\{{\boldsymbol{e}}\in {\mathbb{R}}^{Nn}:\left|{\boldsymbol{e}}\right|\le E\right\} $

则受控领导跟随多智能体系统(1)~(2)可实现领导跟随拟一致性，而$ E $则被称为误差上界。此外，如果$ E = 0 $，则系统(1)~(2)可实现领导跟随一致性。

引理1^[23]　对于任意$ {\boldsymbol{u}} \in {\mathbb{R}^q} $，$ \beta > 0 $，$ {\boldsymbol{v}} \in {\mathbb{R}^l} $和$ {\boldsymbol{M}} \in {\mathbb{R}^{q \times l}} $，总存在正定矩阵$ {\boldsymbol{G}} \in {\mathbb{R}^{l \times l}} $，使得下述不等式成立：

$ 2\boldsymbol{u}^{\mathrm{T}}\boldsymbol{Mv}\le \beta\boldsymbol{u}^{\mathrm{T}}\boldsymbol{MGM}^{\mathrm{T}}\boldsymbol{u}+\beta^{-1}\boldsymbol{v}^{\mathrm{T}}\boldsymbol{G}^{-1}\boldsymbol{v} $

假设1　对于任意$ {\boldsymbol{x}},{\boldsymbol{y}} \in {\mathbb{R}^n} $，系统(1) 中的非线性函数$ {\boldsymbol{f}}:{\mathbb{R}^n} \to {\mathbb{R}^n} $满足如下不等式:

$ \left|\boldsymbol{f}(\boldsymbol{x})-\boldsymbol{f}(\boldsymbol{y})\right|\le L_f\left|\boldsymbol{x}-\boldsymbol{y}\right| $

假设2　系统(1)的通信拓扑具有一颗以领导者智能体为根节点的有向生成树。

假设3　外部扰动$ {{\boldsymbol{\omega }}_i}(t) $与攻击信号$ {\zeta _i}(t) $均是可测且有界的,分别满足$ {\mathrm{sup}}_{{t \geqslant {t_0}}}\left| {{\boldsymbol{\omega}} (t) } \right| \leqslant \varpi < + \infty $与$ {\mathrm{sup}}_{t\ge {t}_{0}}\left|\zeta (t) \right|\le \overline{\zeta } < +\infty $。

2 主要结果 2.1 动态事件触发机制的设计

本文考虑如下动态事件触发机制：

$ \left\{ \begin{array}{l} {t}_{k}=\mathrm{min}\left\{{t}_{k}^{*},{t}_{k-1}+\tau \right\},k\in {\mathbb{N}}^+\\ {t}_{k}^{*}=\mathrm{inf}\left\{t > {t}_{k-1}:J(t) \ge xi (t) \right\}\end{array} \right.$

(5)

式中：$\tau > 0$为满足某些条件的事先给定的最大的脉冲间隔。$ J(t) {\text{ = }}{\theta _{\text{1}}}|\varUpsilon (t) {|^2} - {\theta _2}|{\boldsymbol{e}}({t_{k - 1}}) {|^2} - {\theta _3}{\varpi ^2} $，其中$ \varUpsilon \left( t \right) = {\boldsymbol{e}}\left( t \right) - {\boldsymbol{e}}\left( {{t_{k - 1}}} \right) $，$ {\theta _1},{\theta _2},{\theta _3} \in {\mathbb{R}^{\text{ + }}} $是一些待定的参数。机制(5)中动态变量$ \xi \left( t \right) $的构造为

$ \left\{ \begin{gathered} \dot \xi (t) = \upsilon \xi (t) - J(t) ,{\text{ }}t \ne {t_k},{\text{ }}k \in {\mathbb{N}^{\text{ + }}} \\ \xi (t) = \gamma \xi (t_k^ - ) ,{\text{ }}t = {t_k} \\ \end{gathered} \right. $

(6)

式中：$ \upsilon \in \left( { - \infty ,1} \right) $，$ \gamma \in (0,1) $，且满足$ \xi \left( {{t_0}} \right) > 0 $。此外，假设$ \xi (t) $在脉冲时刻是右连续的，即$ \xi (t_k^ + ) = \xi ({t_k}) $。

注释1　如图1所示，领导跟随多智能体系统(1) 通过传感器进行采样，并将相关状态信息传输到事件触发机制(5)中以判断是否更新控制信息。倘若在时间间隔$ \tau $内触发新的事件，则通过条件事件(由$ {t_k} = t_k^* $触发的事件) 更新脉冲控制信息；否则，通过强制事件(由$ {t_k} = {t_{k - 1}} + \tau $触发的事件) 更新。由于环境干扰或人为恶意攻击，更新的控制信息会受到虚假数据注入攻击，此后将受到攻击后的控制信息传输到执行器，并由执行器反馈到系统(1) 中。

注释2　目前关于动态事件触发脉冲控制的研究并不多。例如，文献[14-15]均要求事件触发间隔同时具有指定的上限和下限，这一定程度上限制了应用的场景。此外，为实现系统的指数收敛，文献[7]需要用到触发间隔的上限一般难以甚至不可获取，故加入额外的周期检测机制(即强制事件) 是合理的。对比上述文献，本文设计的机制(5)仅需要触发间隔的上限，而下限则由机制中的参数所决定，以排除芝诺行为。

注释3　不同于非脉冲系统中动态事件触发机制中的动态变量，机制(5)的动态变量$ \xi \left( t \right) $应该同时具有用于描述连续特性的微分方程和用于描述脉冲跳跃的差分方程，这与文献[14-15]是一致的。类似于非脉冲系统中的分析，动态变量$ \xi \left( t \right) $一般需要参与到李雅普诺夫函数的设计中。因此，为了确保动态变量$ \xi \left( t \right) $的非负性，需要进一步约束该变量的初始值。

引理2　若$ \xi ({t_0}) > 0 $，则方程(6)恒有正解，即$ \xi (t) > 0 $。

证明　对任意的$ t \in \left[ {{t_{k - 1}},{t_k}} \right) ,k \in {\mathbb{N}^ + } $，由式(5)可知有$ J(t) < \xi (t) $。故有$ \dot \xi \left( t \right) > - \left( {1 - \upsilon } \right) \xi \left( t \right) $和

$ \xi (t) > \exp ( - (1 - \upsilon ) (t - {t_{k - 1}}) ) \xi ({t_{k - 1}}) $

(7)

故对任意的$ t \in \left[ {{t_{\text{0}}},{t_{\text{1}}}} \right) $，由式(7)可知

$ \xi \left( t \right) > \exp ( - (1 - \upsilon ) (t - {t_0}) ) \xi ({t_0}) $

(8)

而对$ t = {t_1} $，从式(6)可知

$ \xi (t) > \gamma \exp ( - (1 - \upsilon ) (t - {t_0}) ) \xi ({t_0}) $

(9)

通过迭代，可以得到对于任意的$ t \in \left[ {{t_{k - 1}},{t_k}} \right) ,k \in {\mathbb{N}^ + }$有

$ \xi (t) > {\gamma ^{k - 1}}\exp ( - (1 - \upsilon ) (t - {t_0}) ) \xi ({t_0}) > 0 $

(10)

2.2 一致性分析

定理1　如果存在正定矩阵$ {\boldsymbol{P}},{{\boldsymbol{Q}}_1},{{\boldsymbol{Q}}_2} $，常数$ a > 0$, $ \mu > \theta /{\theta _1} + \upsilon $, $ \sigma \in (0,1/(1 + a) ) $以及$ \vartheta \ge 0 $使得$ {\eta _1} = \max \{ (1 + a) \sigma ,\gamma \} $满足$ \kappa = \ln {\eta _{\text{1}}}/\tau + \mu < 0 $和下述不等式成立：

$ \left( {\begin{array}{*{20}{c}} {{\boldsymbol{PA}} + {{\boldsymbol{A}}^{\mathrm{T}}}{\boldsymbol{P}} + L_f^2{{\boldsymbol{Q}}_1} + \theta {{\boldsymbol{I}}_n} - \mu {\boldsymbol{P}}}&{{{\boldsymbol{B}}^{\mathrm{T}}}{\boldsymbol{P}}}&{\boldsymbol{P}} \\ *&{ - {{\boldsymbol{Q}}_1}}&0 \\ *&*&{ - {{\boldsymbol{Q}}_2}} \end{array}} \right) < 0 $

(11)

$ \left( {\begin{array}{*{20}{c}} { - {{\boldsymbol{I}}_N} \otimes \sigma {\boldsymbol{P}}}&{{{\boldsymbol{I}}_{Nn}} + {\boldsymbol{H}} \otimes {\boldsymbol{K}}} \\ *&{ - {{({{\boldsymbol{I}}_N} \otimes {\boldsymbol{P}}) }^{ - 1}}} \end{array}} \right) < 0 $

(12)

$ \left( {\begin{array}{*{20}{c}} { - {{\boldsymbol{I}}_N} \otimes \vartheta {\boldsymbol{P}}}&{{{\boldsymbol{I}}_N} \otimes {{\boldsymbol{K}}_{\mathrm{s}}}} \\ *&{ - {{({{\boldsymbol{I}}_N} \otimes {\boldsymbol{P}}) }^{ - 1}}} \end{array}} \right) < 0 $

(13)

式中：$ \theta = 2{\theta _1}{\theta _2}/({\theta _1} - 2{\theta _2}) ,{\theta _1} > 2{\theta _2} > 0 $。则在动态事件触发机制(5)和脉冲控制协议(2)下，受扰领导跟随多智能体系统(1)可实现拟一致，且其误差上界

$ \begin{split} &E=\sqrt{({\rho }_{0}{\varpi }^{2}/({\eta }_{1}\left|\kappa \right|) +{\eta }_{2}{\overline{\zeta }}^{2}/(1-{e}^{\kappa \tau }) ) /{\lambda }_{\mathrm{min}}({\boldsymbol{P}}) }\\ &{\rho }_{0}={\lambda }_{\mathrm{max}}({{\boldsymbol{C}}}^{{\mathrm{T}}}{{\boldsymbol{Q}}}_{2}{\boldsymbol{C}}) +{\theta }_{\text{1}}{\theta }_{3}/({\theta }_{\text{1}} - \text{2}{\theta }_{\text{2}}) ,{\eta }_{2}=(1+{a}^{-1}) \vartheta \end{split} $

证明　选择候选李雅普诺夫函数

$ V({\boldsymbol{e}}(t) ,\xi (t) ) = {{\boldsymbol{e}}^{\mathrm{T}}}(t) ({{\boldsymbol{I}}_N} \otimes {\boldsymbol{P}}) {\boldsymbol{e}}(t) + \xi (t) $

对任意$ t \in [{t_{k - 1}},{t_k}) $沿着误差系统(4)来进行求导，可得

$ \begin{split} &{D}^+V({\boldsymbol{e}}(t) ,\xi (t) ) =2{{\boldsymbol{e}}}^{{\mathrm{T}}}(t) ({{\boldsymbol{I}}}_{N}\otimes {\boldsymbol{P}}) \dot{{\boldsymbol{e}}}(t) +\\ &\quad \dot{\xi }(t) ={\boldsymbol{e}}^{{\mathrm{T}}}(t) ({{\boldsymbol{I}}}_{N}\otimes ({\boldsymbol{PA}}+{{\boldsymbol{A}}}^{{\mathrm{T}}}{\boldsymbol{P}}) ) {\boldsymbol{e}}(t) +\\ &\quad \dot{\xi }(t) +2{\boldsymbol{e}}^{{\mathrm{T}}}(t) ({{\boldsymbol{I}}}_{N}\otimes {\boldsymbol{P}}) {\boldsymbol{C\omega }}(t) +\\ &\quad {2}{\boldsymbol{e}}^{{\mathrm{T}}}(t) ({{\boldsymbol{I}}}_{N}\otimes {\boldsymbol{P}}) {\boldsymbol{B\varGamma }}(t,{\boldsymbol{e}}(t) ) \le \upsilon \xi (t) +\\ &\quad {\boldsymbol{e}}^{{\mathrm{T}}}(t) ({{\boldsymbol{I}}}_{N}\otimes ({\boldsymbol{PA}}+{{\boldsymbol{A}}}^{{\mathrm{T}}}{\boldsymbol{P}}) ) \boldsymbol{e}(t) \text+{\theta }_{3}{\varpi }^{2}+\\ &\quad {\boldsymbol{e}}^{{\mathrm{T}}}(t) ({{\boldsymbol{I}}}_{N}\otimes ({\boldsymbol{P}}{{\boldsymbol{Q}}}_{2}^{-1}{\boldsymbol{P}}) ) {\boldsymbol{e}}(t) +{\theta }_{2}{\left|{\boldsymbol{e}}({t}_{k-1}) \right|}^{2}+\\ &\quad {{\boldsymbol{\omega }}}^{{\mathrm{T}}}(t) ({{\boldsymbol{I}}}_{N}\otimes ({{\boldsymbol{C}}}^{{\mathrm{T}}}{{\boldsymbol{Q}}}_{2}{\boldsymbol{C}}) ) {\boldsymbol{\omega}} (t) -{\theta }_{\text{1}}{\left|\varUpsilon (t) \right|}^{2}+\\ &\quad {\boldsymbol{e}}^{{\mathrm{T}}}(t) ({{\boldsymbol{I}}}_{N}\otimes ({{\boldsymbol{B}}}^{{\mathrm{T}}}{\boldsymbol{P}}{{\boldsymbol{Q}}}_{1}{}^{-1}{\boldsymbol{PB}}+{L}_{f}^{2}{{\boldsymbol{Q}}}_{1}) ) {\boldsymbol{e}}(t) \end{split} $

(14)

由式(5)可知对任意$ t \in [{t_{k - 1}},{t_k}) $$ J(t) < \xi \left( t \right) $，且$ {\boldsymbol{e}}\left( {{t_{k - 1}}} \right) = {\boldsymbol{e}}(t) - \varUpsilon \left( t \right) $，故

$ |\varUpsilon (t) {|^2} < \frac{1}{{{\theta _1} - 2{\theta _2}}}\left( {2{\theta _2}|{\boldsymbol{e}}(t) {|^2} + \xi (t) + {\theta _3}{\varpi ^2}} \right) $

(15)

把式(15)代入到式(14)中，且由式(11)~(12)可以推导出对于任意的$ t \in \left[ {{t_{k - 1}},{t_k}} \right) ,k \in {\mathbb{N}^ + }$有

$ \begin{split} &{D}^+V({\boldsymbol{e}}(t) ,\xi (t) ) \le \left({\lambda }_{\mathrm{max}}\text{(}{{\boldsymbol{C}}}^{{\mathrm{T}}}{{\boldsymbol{Q}}}_{2}{\boldsymbol{C}}\text{) +}\frac{{\theta }_{\text{1}}{\theta }_{3}}{{\theta }_{\text{1}} - \text{2}{\theta }_{\text{2}}}\right) {\varpi }^{2}+\\ &\quad {\boldsymbol{e}}^{{\mathrm{T}}}(t) ({{\boldsymbol{I}}}_{N}\otimes ({\boldsymbol{PA}}+{{\boldsymbol{A}}}^{{\mathrm{T}}}{\boldsymbol{P}}+{{\boldsymbol{B}}}^{{\mathrm{T}}}{\boldsymbol{P}}{{\boldsymbol{Q}}}_{1}{}^{-1}{\boldsymbol{PB}}+\\ &\quad {L}_{f}^{2}{{\boldsymbol{Q}}}_{1}+{\boldsymbol{P}}{{\boldsymbol{Q}}}_{2}^{-1}{\boldsymbol{P}}+\theta {{\boldsymbol{I}}}_{n}) ) \boldsymbol{e}(t) +\\ &\quad \left(\frac{\text{2}{\theta }_{\text{2}}}{{\theta }_{\text{1}} - \text{2}{\theta }_{\text{2}}}+\upsilon \right) \xi (t) \le \mu V({\boldsymbol{e}}(t) ,\xi (t) ) +{\rho }_{0}{\varpi }^{2} \end{split} $

(16)

式中：$ \mu > \theta /{\theta _1} + \upsilon $。

另一方面，对于任意$ t = {t_k},k \in {\mathbb{N}^ + } $，从式(4)和式(6)以及定理1可知

$ \begin{split} & V(\boldsymbol{e}(t_k), \xi(t_k))=\boldsymbol{e}^{\mathrm{T}}(t_k)(\boldsymbol{I}_N \otimes \boldsymbol{P}) \boldsymbol{e}(t_k)+ \xi(t_k)=\\ &\quad (\boldsymbol{e}^{\mathrm{T}}(t_k^{-})(\boldsymbol{I}_{N n}+\boldsymbol{H} \otimes \boldsymbol{K})^{\mathrm{T}}+\gamma \xi(t_k^{-})+ \\ &\quad \zeta^{\mathrm{T}}(t_k^{-})(\boldsymbol{I}_N \otimes \boldsymbol{K}_{\mathrm{s}})^{\mathrm{T}})(\boldsymbol{I}_N \otimes \boldsymbol{P})((\boldsymbol{I}_{N n}+ \\ &\quad \boldsymbol{H} \otimes \boldsymbol{K}) \boldsymbol{e}(t_k^{-})+(\boldsymbol{I}_N \otimes \boldsymbol{K}_{\mathrm{s}}) \zeta(t_k^{-}))= \\ &\quad \boldsymbol{e}^{\mathrm{T}}(t_k^{-})(\boldsymbol{I}_{N n}+\boldsymbol{H} \otimes \boldsymbol{K})^{\mathrm{T}}(\boldsymbol{I}_N \otimes \boldsymbol{P})(\boldsymbol{I}_{N n}+\boldsymbol{H} \otimes \boldsymbol{K}) \times \\ &\quad \boldsymbol{e}(t_k^{-})+\boldsymbol{e}^{\mathrm{T}}(t_k^{-})(\boldsymbol{I}_{N n}+\boldsymbol{H} \otimes \boldsymbol{K})^{\mathrm{T}}(\boldsymbol{I}_N \otimes \boldsymbol{P} \boldsymbol{K}_{\mathrm{s}}) \zeta(t_k^{-})+ \\ &\quad \zeta^{\mathrm{T}}(t_k^{-})(\boldsymbol{I}_N \otimes \boldsymbol{K}_{\mathrm{s}})^{\mathrm{T}}(\boldsymbol{I}_N \otimes \boldsymbol{P})(\boldsymbol{I}_{N n}+\boldsymbol{H} \otimes \boldsymbol{K}) \boldsymbol{e}(t_k^{-})+ \\ &\quad \zeta^{\mathrm{T}}(t_k^{-})(\boldsymbol{I}_N \otimes \boldsymbol{K}_{\mathrm{s}} \boldsymbol{P})(\boldsymbol{I}_N \otimes \boldsymbol{K}_{\mathrm{s}}) \zeta(t_k^{-})+\gamma \xi(t_k^{-}) \leqslant \\ &\quad (1+a) \boldsymbol{e}^{\mathrm{T}}(t_k^{-})(\boldsymbol{I}_{N n}+\boldsymbol{H} \otimes\boldsymbol{K})^{\mathrm{T}}(\boldsymbol{I}_N \otimes \boldsymbol{P})(\boldsymbol{I}_{N n}+ \\ &\quad \boldsymbol{H} \otimes \boldsymbol{K}) \boldsymbol{e}(t_k^{-})+\gamma \xi(t_k^{-})+(1+a^{-1}) \zeta^{\mathrm{T}}(t_k^{-})(\boldsymbol{I}_N \otimes \\ &\quad \boldsymbol{K}_{\mathrm{s}} \boldsymbol{P})(\boldsymbol{I}_N \otimes \boldsymbol{K}_{\mathrm{s}}) \zeta(t_k^{-}) \leqslant \eta_1 V(\boldsymbol{e}(t_k^{-}), \xi(t_k^{-}))+\eta_2 \bar{\zeta}^2 \end{split} $

对任意$ t \in [{t_{k - 1}},{t_k}) ,k \in {\mathbb{N}^ + } $以及任意足够小的$ \phi > 0 $，构造如下的微分方程组。

$ \left\{ \begin{gathered} \dot y(t) = \mu y(t) + {\rho _0}{\varpi ^2} + \phi \\ y({t_{k - 1}}) = V({\boldsymbol{e}}({t_{k - 1}}) ,\xi ({t_{k - 1}}) ) \\ \end{gathered} \right. $

(17)

求解式(17)可知：当$ \phi \to 0 $时，可得其解为

$ y(t) = \exp (\int_{{t_{k - 1}}}^t {\mu {\mathrm{d}}s} ) y({t_{k - 1}}) + {\rho _0}{\varpi ^2}\int_{{t_{k - 1}}}^t {\exp (\int_s^t {\mu {\mathrm{d}}v} ) {\mathrm{d}}s} $

由比较原理可知：

$ \begin{split} V({\boldsymbol{e}}(t) ,\xi (t) )\le &{\rho }_{0}{\varpi }^{2}{\displaystyle {\int }_{{t}_{k-1}}^{t}\mathrm{exp}(\mu (t-s) ) {\mathrm{d}}s}+\\ &\mathrm{exp}(\mu (t-{t}_{k-1}) ) V({\boldsymbol{e}}({t}_{k-1}) ,\xi ({t}_{k-1}) ) \end{split}$

(18)

接下来，验证对任意$ t \in [{t_{k - 1}},{t_k}) ,k \in {\mathbb{N}^ + } $总有不等式(19)成立。

$\begin{split} & V(\boldsymbol{e}(t), \xi(t)) \leqslant \eta_1^{k-1} \exp \left(\mu\left(t-t_0\right)\right) V\left(\boldsymbol{e}\left(t_0\right), \xi\left(t_0\right)\right)+ \\ & \rho_0 \varpi^2 \int_{t_{k-1}}^t \exp (\mu(t - s)) \mathrm{d} s + \sum_{i=1}^{k-1} \eta_1^{k-1-i} \eta_2 \exp \left(\mu\left(t - t_i\right)\right) \bar{\zeta}^2 \;\; \end{split}$

(19)

对任意$ t \in [{t_0},{t_1}) $，从式(18)得出

$\begin{split} V(\boldsymbol{e}(t), \xi(t)) \leqslant & \rho_0 \varpi^2 \int_{t_0}^t \exp (\mu(t-s)) \mathrm{d} s+ \\ & \exp \left(\mu\left(t-t_0\right)\right) V\left(\boldsymbol{e}\left(t_0\right), \xi\left(t_0\right)\right) \end{split} $

(20)

则式(19)对任意$ t \in [{t_0},{t_1}) $成立。假设式(19)适用任意的$ t \in [{t_{p - 1}},{t_p}) ,p \in {\mathbb{N}^ + },p > 1 $。由于$ V({\boldsymbol{e}}({t_p}) ,\xi ({t_p}) ) \leqslant $$ {\eta _1}V({\boldsymbol{e}}(t_p^ - ) ,\xi (t_p^ - ) ) + {\eta _2}{\overline \zeta ^2} $，则对于任意$ t \in [{t_p},{t_{p + 1}}) $，从式(18)得到

$ \begin{split} &V(\boldsymbol{e}(t), \xi(t)) \leqslant \varpi^2 \int_{t_0}^t \rho_0 \exp (\mu(t-s)) \mathrm{d} s+ \\ &\quad \exp (\mu(t-t_p)) V(\boldsymbol{e}(t_p), \xi(t_p)) \leqslant \\&\quad \eta_1 \exp (\mu(t-t_p)) V(\boldsymbol{e}(t_p^{-}), \xi(t_p^{-}))+ \\&\quad \rho_0 \varpi^2 \int_{t_0}^t \exp (\mu(t-s)) \mathrm{d} s+\eta_2 \bar{\zeta}^2 \leqslant \\&\quad \eta_1^p \exp (\mu(t-t_0)) V(\boldsymbol{e}(t_0), \xi(t_0))+ \\&\quad \rho_0 \varpi^2 \int_{t_0}^t \eta_1^{N(t, s)} \exp (\mu(t-s)) \mathrm{d} s+ \\&\quad \sum_{i=1}^{p-1} \eta_1^{p-1-i} \eta_2 \exp (\mu(t-t_i)) \bar{\zeta}^2+\eta_2 \bar{\zeta} \leqslant \\&\quad \eta_1^p \exp (\mu(t-t_0)) V(\boldsymbol{e}(t_0), \xi(t_0))+ \\&\quad \rho_0 \varpi^2 \int_{t_0}^t \eta_1^{N(t, s)} \exp (\mu(t-s)) \mathrm{d} s+ \\&\quad \sum_{i=1}^p \eta_1^{p-i} \eta_2 \exp (\mu(t-t_i)) \bar{\zeta}^2 \end{split}$

(21)

则式(19)中适用于任意的$ t \in [{t_p},{t_{p + 1}}) $。因此，由数学归纳法，可以得到式(19)适用于任意$ t \in [{t_{k - 1}},{t_k}) , k \in {\mathbb{N}^ + } $。

因为$ {\eta _1} \in \left( {0,1} \right) ,N\left( {t,{t_0}} \right) = k - 1, $$ N\left(t,{t}_{0}\right) \ge $$ (t - {t_0}) /\tau - 1 $，对任意$ t \in [{t_{k - 1}},{t_k}) ,k \in {\mathbb{N}^ + } $，从式(19)得到

$\begin{split} & V(\boldsymbol{e}(t), \xi(t)) \leqslant \rho_0 \varpi^2 \int_{t_p}^t \eta_1^{N(t, s)} \exp (\mu(t-s)) \mathrm{d} s+ \\ &\quad \eta_1^{k-1} \exp \left(\mu\left(t-t_0\right)\right) V\left(\boldsymbol{e}\left(t_0\right), \xi\left(t_0\right)\right)+ \\ &\quad \sum_{i=1}^{k-1} \eta_1^{k-1-i} \eta_2 \exp \left(\mu\left(t-t_i\right)\right) \bar{\zeta}^2 \leqslant \\ &\quad \dfrac{1}{\eta_1} \exp \left(\kappa\left(t - t_0\right)\right) V\left(\boldsymbol{e}\left(t_0\right), \xi\left(t_0\right)\right) + \\ &\quad \dfrac{\rho_0 \sigma^2}{\eta_1|\kappa|}(1 - \exp \left(\kappa\left(t - t_0\right)\right))+ \frac{1-\eta_1^{k-2} \exp (\mu \tau(k-2))}{1-\eta_1 \exp (\mu \tau)} \eta_2 \bar{\zeta}^2 \end{split}$

(22)

式中：$ \kappa = \mu + \ln {\eta _1}/\tau < 0 $，故有

$ \limsup _{t \rightarrow \infty}|\boldsymbol{e}(t)| \leqslant \sqrt{\frac{\rho_0 \varpi^2}{\lambda_{\text {min }}(\boldsymbol{P}) \eta_1|\kappa|}+\frac{\eta_2 \bar{\zeta}^2}{\lambda_{\text {min }}(\boldsymbol{P})\left(1-e^{\kappa \tau}\right)}}:=E $

因此，在动态事件触发机制(5)和脉冲控制下，具有外界干扰的多智能体系统(1)可以达到跟随拟一致性，且其误差上界可估量为$ E $。证毕。

2.3 芝诺行为的排除

定理2　如果存在正定矩阵$ {{\boldsymbol{S}}_1},{{\boldsymbol{S}}_2},{{\boldsymbol{S}}_3} $和常数$ \overline \mu > 0 $满足

$ \left(\begin{array}{cccc}2\left(\boldsymbol{S}_1+L_f^2 \boldsymbol{S}_2\right)-\bar{\mu} \boldsymbol{I}_n & \boldsymbol{A} & \boldsymbol{B} & \boldsymbol{C} \\ * & -\boldsymbol{S}_1 & 0 & 0 \\ * & * & -\boldsymbol{S}_2 & 0 \\ * & * & * & -\boldsymbol{S}_3\end{array}\right) \lt 0$

(23)

则在动态事件触发控制(5)下，系统(1)不存在芝诺行为。

证明　根据动态事件触发的形式，证明由3部分组成。

情形1　$ {t_k} - {t_{k - 1}} \equiv \tau ,k \in {\mathbb{N}^ + } $。芝诺行为就会自然地被排除在外。

情形2　$ {t_k} = t_k^*,k \in {\mathbb{N}^ + } $。设$ W\left( t \right) = {\varUpsilon ^{\mathrm{T}}}\left( t \right) \varUpsilon \left( t \right) , $那么对任意$ t \in [{t_{k - 1}},{t_k}) $，由式(4)有

$ \begin{split} &{D}^+W(t) =2{\varUpsilon }^{{\mathrm{T}}}(t) ({{\boldsymbol{I}}}_{N}\otimes {\boldsymbol{A}}) {\boldsymbol{e}}(t) +\\ &\quad 2{\varUpsilon }^{{\mathrm{T}}}(t) ({{\boldsymbol{I}}}_{N}\otimes {\boldsymbol{B}}) {\boldsymbol{\varGamma}} ({\boldsymbol{e}}(t) ) +2{\varUpsilon }^{{\mathrm{T}}}(t) ({{\boldsymbol{I}}}_{N}\otimes \\&\quad {\boldsymbol{C}}) {\boldsymbol{\omega}} (t) \le {\varUpsilon }^{{\mathrm{T}}}(t) ({{\boldsymbol{I}}}_{N}\otimes ({\boldsymbol{A}}{{\boldsymbol{S}}}_{1}^{-1}{{\boldsymbol{A}}}^{{\mathrm{T}}}+{\boldsymbol{B}}{{\boldsymbol{S}}}_{2}^{-1}{{\boldsymbol{B}}}^{{\mathrm{T}}}+\\ &\quad {\boldsymbol{C}}{{\boldsymbol{S}}}_{3}^{-1}{{\boldsymbol{C}}}^{{\mathrm{T}}}) ) \varUpsilon (t) +{{\boldsymbol{e}}}^{{\mathrm{T}}}(t) ({{\boldsymbol{I}}}_{N}\otimes {{\boldsymbol{S}}}_{1}) {\boldsymbol{e}}(t) +\\ &\quad {{\boldsymbol{\varGamma}} }^{{\mathrm{T}}}({\boldsymbol{e}}(t) ) ({{\boldsymbol{I}}}_{N}\otimes {{\boldsymbol{S}}}_{2}) {\boldsymbol{\varGamma}} ({\boldsymbol{e}}(t) ) +{{\boldsymbol{\omega }}}^{{\mathrm{T}}}(t) ({{\boldsymbol{I}}}_{N}\otimes \\ &\quad {{\boldsymbol{S}}}_{3}) {\boldsymbol{\omega }}(t) \le {\varUpsilon }^{{\mathrm{T}}}(t) ({{\boldsymbol{I}}}_{N}\otimes ({\boldsymbol{A}}{{\boldsymbol{S}}}_{1}^{-1}{{\boldsymbol{A}}}^{{\mathrm{T}}}+{\boldsymbol{B}}{{\boldsymbol{S}}}_{2}^{-1}{{\boldsymbol{B}}}^{{\mathrm{T}}}+\\ &\quad {\boldsymbol{C}}{{\boldsymbol{S}}}_{3}^{-1}{{\boldsymbol{C}}}^{{\mathrm{T}}}) ) \varUpsilon (t) +{{\boldsymbol{\omega }}}^{{\mathrm{T}}}(t) ({{\boldsymbol{I}}}_{N}\otimes {{\boldsymbol{S}}}_{3}) {\boldsymbol{\omega}} (t) +\\ &\quad 2{\varUpsilon }^{{\mathrm{T}}}(t) ({{\boldsymbol{I}}}_{N}\otimes ({L}_{f}^{2}{{\boldsymbol{S}}}_{2}+{{\boldsymbol{S}}}_{1}) ) \varUpsilon (t) +2{{\boldsymbol{e}}}^{{\mathrm{T}}}({t}_{k-1}) \times \\ &\quad ({{\boldsymbol{I}}}_{N}\otimes ({L}_{f}^{2}{{\boldsymbol{S}}}_{2}+{{\boldsymbol{S}}}_{1}) ) {\boldsymbol{e}}({t}_{k-1}) \le \overline{\mu }W\left(t\right) +\\ &\quad {\rho }_{1}|{\boldsymbol{e}}\left({t}_{k-1}\right) {|}^{2}+{\rho }_{2}{{\boldsymbol{\omega }}}^{{\mathrm{T}}}(t) {\boldsymbol{\omega}} \left(t\right) \end{split} $

(24)

式中：第1个不等式用到了引理1，第2个不等式用到了$ {\boldsymbol{e}}(t) = {\boldsymbol{e}}({t_{k - 1}}) + \varUpsilon (t) $，最后一个不等式用到了式(23)，且$ {\rho }_{1}=2{\lambda }_{\max}({{\boldsymbol{S}}}_{1}+{L}_{f}^{2}{{\boldsymbol{S}}}_{2}) $，$ {\rho _{\text{2}}} = {\lambda _{\max}}({{\boldsymbol{S}}_3}) $。

注意到$ \varUpsilon ({t_{k - 1}}) = 0 $，运用比较原理，类似地可知对于任意的$ t \in [{t_{k - 1}},{t_k}) $有

$ |\varUpsilon \left(t\right) {|}^{2}\le {\varepsilon }_{k}{\displaystyle {\int }_{{t}_{k-1}}^{{t}_{k}}\mathrm{exp}(\overline{\mu }({t}_{k}-s) ) {\mathrm{d}}s} $

(25)

式中：$ {\varepsilon _k} = {\rho _1}|e({t_{k - 1}}) {|^2} + {\rho _2}{\varpi ^2} $。

另外，由式(5)可知对于任意的$ t = {t_k},k \in {\mathbb{N}^ + } $有

$ |\varUpsilon ({t_k}) {|^2} = \frac{1}{{{\theta _1}}}( {{\theta _2}|{\boldsymbol{e}}({t_{k - 1}}) {|^2} + \xi ({t_k}) + {\theta _3}{\varpi ^2}} ) $

(26)

将式(25)代入式(26)，并化简可得

$ \int_{t_{k-1}}^{t_k} \exp \left(\bar{\mu}\left(t_k-s\right)\right) \mathrm{d} s \geqslant \frac{\left(\min \left\{\theta_2, \theta_3\right\}+\dfrac{\xi\left(t_k\right)}{\left|e\left(t_{k-1}\right)\right|^2+\rho_2 \varpi^2}\right)}{\theta_1 \max \left\{\rho_1, \rho_2\right\}} $

(27)

则有

$ {t_k} - {t_{k - 1}} > \frac{1}{{\overline \mu }}\ln \left( {\frac{{\overline \mu \min \{ {\theta _2},{\theta _3}\} }}{{{\theta _1}\max \{ {\rho _1},{\rho _2}\} }} + 1} \right) > 0 $

(28)

由此可知，情景2下并不存在芝诺行为。

情景3　$ {t_k} $不是单纯地由$ {t_{k - 1}} + \tau $或者$ t_k^* $触发的。在这种情况下，假设其存在芝诺行为，并且有$ {\lim _{k \to + \infty }}{t_k} = {T_1} $。考虑区间$ \left[ {{T_0},{T_1}} \right) $，其中$ {T_0} = ({T_1} - \tau /2) > {t_0} $，那么在这个区间里面会有无限多个事件。则假设其中有且只有一个由$ {t_k} = {t_{k - 1}} + \tau $所触发的事件，并记这个时刻为$ {t^*} $，则区间$ ({t^*},{T_1}) $中的事件均由事件$ {t_k} = t_k^* $触发的。从情景2中，可以知道其没有芝诺行为。因此在情景3中芝诺行为也被排除。

因此，上述3种情景均不存在芝诺行为。证毕。

注释4　为了实现系统的拟一致性，定理1需要对机制(6)中的参数$ {\theta _{\text{1}}},{\theta _{\text{2}}} $施加额外的约束，而这在排除芝诺行为中是不需要的。对比文献[15]在强制触发脉冲的帮助下仅可实现渐近性收敛，本文的结果可实现系统指数收敛，更具有时效性。此外，对比文献[15]，本文所得结果的验证条件更简便。

注释5　令$ \xi ({t_k}) = 0 $，式(27)可由式(26)得到，但$ \xi (t) $总是正的。因此，动态事件触发机制(6)中非强制触发的最小触发时间间隔总会不小于其所简化得到的静态触发机制(详见式(29))。

上述定理分别实现了系统(1) 的拟一致性和排除了芝诺行为。为了方便验算，可将两者联合，结果如定理3所示。因为推导过程类似，故在此省略。

定理3　如果存在维度合适的正定对角矩阵$ \overline {\boldsymbol{P}} \in {\mathbb{R}^{n \times n}}, $正定矩阵$ \overline {\boldsymbol{Y}} \in {\mathbb{R}^{n \times n}} $以及正常数$ \overline \sigma ,\overline \vartheta ,{\overline \varepsilon _i},i = $$1,2,3,{\varepsilon _l},l = 1,2 $，以及常数$ {\mu _1} > 2{\theta _2}/({\theta _1} - 2{\theta _2}) $$ + \upsilon $和$ {\mu _2} $满足$\; \overline \kappa = \ln {\eta _1}/\tau + {\mu _2} < 0 $和

$ \left( {\begin{array}{*{20}{c}} { - \exp ( - \overline \sigma ) {{\boldsymbol{I}}_N} \otimes \overline {\boldsymbol{P}}}&{\overline {\boldsymbol{Y}}} \\ *&{ - {{\boldsymbol{I}}_N} \otimes \overline {\boldsymbol{P}}} \end{array}} \right) < 0 $

$ \left( {\begin{array}{*{20}{c}} { - \vartheta \overline {\boldsymbol{P}}}&{{{\boldsymbol{K}}_{\mathrm{s}}}} \\ *&{ - {{\overline {\boldsymbol{P}}}^{ - 1}}} \end{array}} \right) < 0 $

$ \left( {\begin{array}{*{20}{c}} {{\varXi _1}}&{{{\boldsymbol{B}}^{\mathrm{T}}}\overline {\boldsymbol{P}}}&{\overline {\boldsymbol{P}}} \\ *&{ - {\varepsilon _1}\overline {\boldsymbol{P}}}&0 \\ *&*&{ - {\varepsilon _2}\overline {\boldsymbol{P}}} \end{array}} \right) < 0 $

$ \left( {\begin{array}{*{20}{c}} {{\varXi _2}}&{\boldsymbol{A}}&{\boldsymbol{B}}&{\boldsymbol{C}} \\ *&{ - {{\overline \varepsilon }_1}\overline {\boldsymbol{P}}}&0&0 \\ *&*&{ - {{\overline \varepsilon }_2}\overline {\boldsymbol{P}}}&0 \\ *&*&*&{ - {{\overline \varepsilon }_3}\overline {\boldsymbol{P}}} \end{array}} \right) < 0 $

式中，$ {\varXi _1} = \overline {\boldsymbol{PA}}{\text{ + }}{{\boldsymbol{A}}^{\mathrm{T}}}\overline {\boldsymbol{P}}{\text{ + }}{\varepsilon _1}L_f^2\overline {\boldsymbol{P}}{\text{ + }}\theta {{\boldsymbol{I}}_n} - {\mu _2}\overline {\boldsymbol{P}},{\varXi _2} = 2 \times $$ ({\overline \varepsilon _1}\overline {\boldsymbol{P}} + L_f^2{\overline \varepsilon _2}\overline {\boldsymbol{P}}) - {\mu _1}{{\boldsymbol{I}}_n} $。则系统(1)在机制(5)和脉冲控制(2)的控制下可实现拟一致性，其中脉冲增益矩阵满足$ {\boldsymbol{H}} \otimes {\boldsymbol{K}} = {{\boldsymbol{I}}_N} \otimes ({\overline {\boldsymbol{P}}^{ - 1}}{\overline {\boldsymbol{Y}}^{\mathrm{T}}} - {{\boldsymbol{I}}_n}) $，误差上界估量为$ E =\sqrt {({\rho _0}{\varpi ^2}/({\eta _1}|\overline \kappa |) + {\eta _2}{{\overline \zeta }^2}/(1 - {e^{\overline \kappa \tau }}) ) /{\lambda _{\min }}({\boldsymbol{P}}) } $，$ {\rho _0} = {\varepsilon _2}{\lambda _{\max }}({\boldsymbol{P}}) + {\theta _1}{\theta _3}/({\theta _1} - 2{\theta _2}) $。与此同时，芝诺行为也可以排除。

3 数值仿真

考虑由一个领导者和4个跟随者组成的领导跟随多智能体系统，其动力学特性如系统(1)所描述，而其通信拓扑描述为

$ {\boldsymbol{L}} = \left[ {\begin{array}{*{20}{c}} 2&{ - 1}&{ - 1}&0 \\ { - 1}&2&0&{ - 1} \\ { - 1}&0&1&0 \\ 0&{ - 1}&0&1 \end{array}} \right],{\boldsymbol{D}} = \left[ {\begin{array}{*{20}{c}} 1&0&0&0 \\ 0&0&0&0 \\ 0&0&1&0 \\ 0&0&0&0 \end{array}} \right] $

假设$ f({x}_{i}(t) ) =0.18 \tanh ({x}_{i}(t) ) $，则$ {L_f} = 0.18 $。此外，选择如下参数：

$ \begin{split} & \left[ {{{\boldsymbol{\omega }}_1}(t) ,{{\boldsymbol{\omega }}_2}(t) ,{{\boldsymbol{\omega }}_3}(t) ,{{\boldsymbol{\omega }}_4}(t) } \right] = \\ & \left[ {\begin{array}{*{20}{c}} {0.5\sin \left( t \right) }&{1.1\cos \left( t \right) }&{1.3\sin \left( t \right) }&{\sin \left( t \right) } \\ {1.1\sin \left( t \right) }&{ - 0.5\cos \left( t \right) }&{\sin \left( t \right) }&{ - 0.8\sin \left( t \right) } \\ {0.4\cos \left( t \right) }&{1.3\sin \left( t \right) }&{0.4\sin \left( t \right) }&{0.8\cos \left( t \right) } \end{array}} \right] \\ & {\boldsymbol{A}} = \left[ {\begin{array}{*{20}{c}} {0.17}&0&0 \\ 0&{0.1}&0 \\ 0&0&{0.25} \end{array}} \right],{\boldsymbol{B}} = \left[ {\begin{array}{*{20}{c}} {0.51}&0&0 \\ 0&{0.42}&0 \\ 0&0&{0.45} \end{array}} \right] \\ &{\boldsymbol{C}} = \left[ {\begin{array}{*{20}{c}} { - 0.875}&0&0 \\ 0&{0.51}&0 \\ 0&0&{0.4} \end{array}} \right] \end{split} $

虚假数据注入攻击的攻击信号选择如下：$ {\zeta _1}(t) =\; {\zeta _2}(t) = \;{[0.41, - 1.11,0.25]^{\mathrm{T}}}\sin (t) $, ${\zeta _3}(t) =\; {\zeta _4}(t) \;= {[0.41, - 1.11,0.25]^{\mathrm{T}}}\cos (t) , $有$ \varpi = 2.315 $，$ \overline \zeta = 1.710 $。另一方面，选择动态事件触发控制机制(5)中参数如下：$ {\theta _1} = 6.5,{\theta _2} = 0.2,{\theta _3} = 0.65 $和$ \upsilon = 0.25,\gamma = 0.55 $。显然满足定理(1) 中的条件$ {\theta _1} > 2{\theta _2} > 0 $。

根据定理3选择系数：$ {\varepsilon }_{1}=0.12,{\varepsilon }_{2}=0.52 $，$ {\overline{\varepsilon }}_{1}= 0.14,{\overline{\varepsilon }}_{2}=4.12,{\overline{\varepsilon }}_{3}=10.53,{\mu }_{2}=10.816 $。选择参数$ \alpha = 0.1 $，则$ {\eta _1} = (1 + \alpha ) \sigma = 0.607 $，取$ {\mu _1} = 1.056 > \theta /{\theta _1} + \upsilon = 0.316 $，$ \tau = 0.25 $有$ \kappa $$ = {\mu _1} + {\mathrm{ln}}{\eta _1}/\tau {\text{ = }} - {\text{0}}{\text{.954}} < 0 $满足定理1中的条件。则定理3中的线性矩阵不等式可以用MATLAB来求解，可得：$ {\boldsymbol{P}} = {\text{diag}}\{ 1.302, 1.313, 1.301 \} $和$ \;{\boldsymbol{K}} = {\text{diag}}\left\{ { - 0.330, - 0.330, - 0.330} \right\} $。

此外令$ {{\boldsymbol{K}}_{\mathrm{s}}} = 0.45{{\boldsymbol{I}}_3} $，由式(13)可知$ \vartheta = 0.203 $，则$ {\eta _2} = 2.228 $。由定理3可知$ {\rho _0} = 1.375 $，所以可知其误差上界$ E = 5.778 $。此时由式 (24) 可求得$ {\rho _1} = 3.475, {\rho _2} = 15.227 $，所以可求得其触发间隔$ {t_k} - {t_{k - 1}} > 0.006 $。因此，定理1和2中的所有条件均满足，系统(1) 在设计的触发机制(5)下是可以达到拟一致的，同时也排除了芝诺行为。

令$ {t_0} = 0,\xi ({t_0}) = 10 $，各个多智能体的初始状态设置为

$ \begin{gathered} \left( {{{\boldsymbol{x}}_0}({t_0}) ,{{\boldsymbol{x}}_1}({t_0}) ,{{\boldsymbol{x}}_2}({t_0}) ,{{\boldsymbol{x}}_3}({t_0}) ,{{\boldsymbol{x}}_4}({t_0}) } \right)= \\ \left[ {\begin{array}{*{20}{c}} {1.5}&{0.5}&{ - 0.5}&{ - 1.5}&{2.5} \\ { - 1}&2&{ - 1}&{ - 2}&{ - 1.5} \\ 2&{ - 2.5}&{2.5}&2&1 \end{array}} \right] \\ \end{gathered} $

当系统无控制时，其仿真结果如图2所示。易知系统误差随着时间的增长而变大，此时系统无法实现拟一致性。根据系统的受扰情况，进一步考虑如下4种情况。

情况1　无外部干扰与虚假数据注入攻击，仿真结果如图3所示。可知此时系统可实现一致性，因为$ |{e_i}(t) | $最终能够趋于0。同时，芝诺行为可被排除。

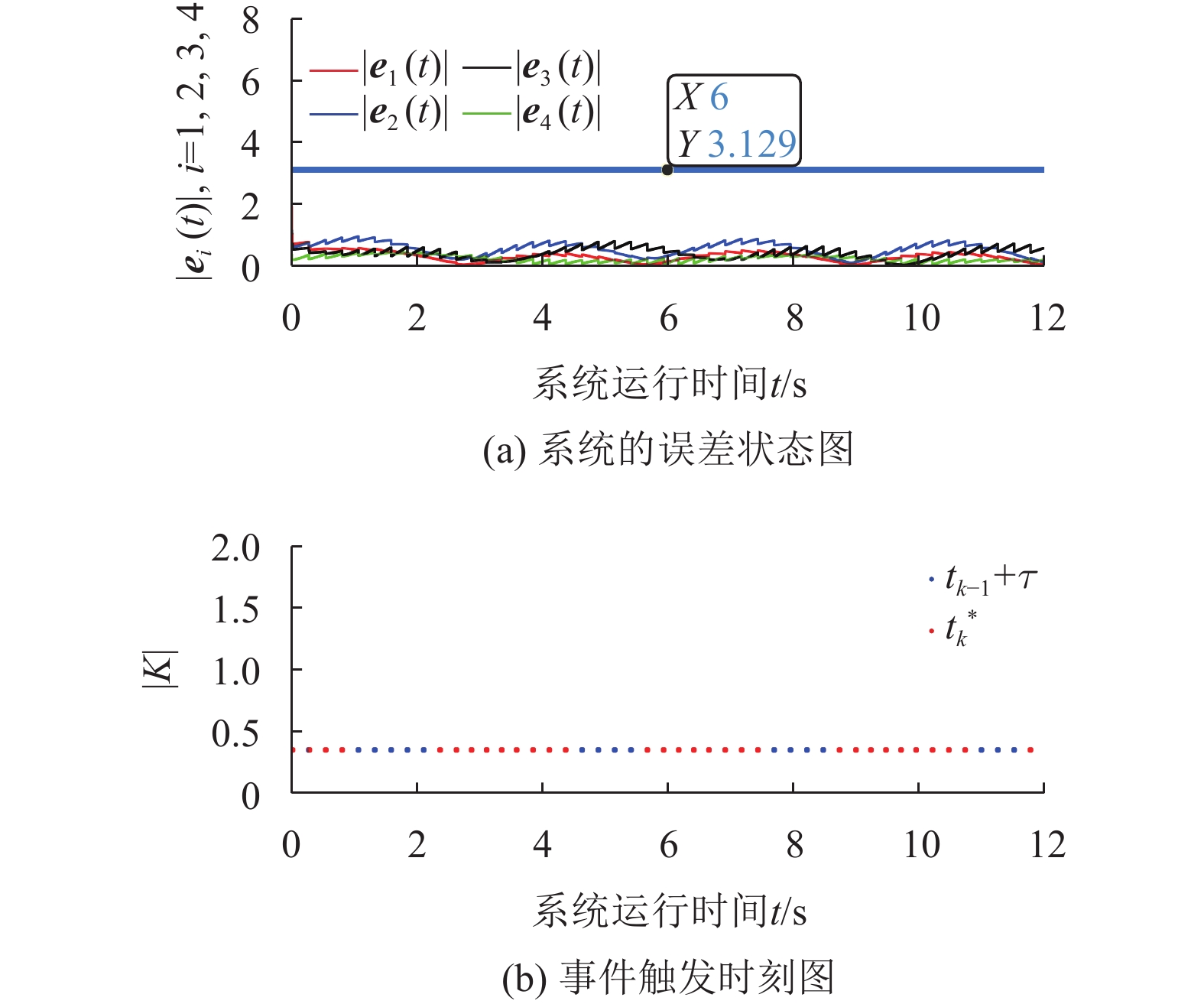
情况2　仅受到外部干扰影响时，仿真结果如图4所示。此时$ |{e_i}(t) | $随着时间的增长而不断波动，但始终保持在误差上界$ {E_1} = 3.129 $内，即系统仅可实现拟一致性。由图4(b)可知芝诺行为可被排除。

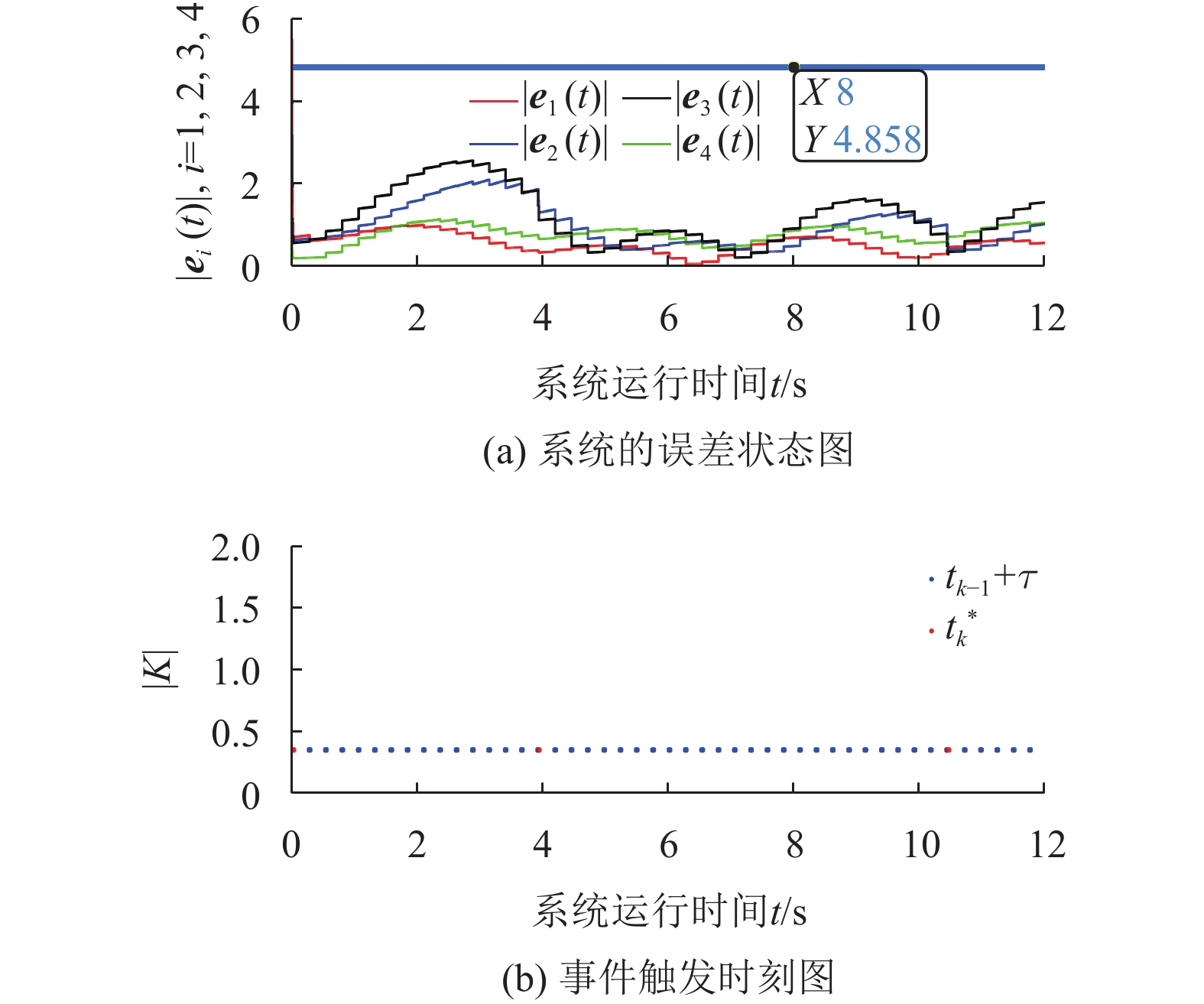
情况3　仅受到虚假数据注入攻击影响时，仿真结果如图5所示。类似于情况2，此时$ |{e_i}(t) | $在误差上界$ {E_2} = 4.858 $内随着时间的增长而波动，故根据定义1可知系统可实现拟一致性。通过观察图5(b)可知，芝诺行为也可被排除。

情况4　同时受到外部干扰与虚假数据注入攻击的影响时，仿真结果如图6所示。类似地可知，系统此时仍可实现领导跟随拟一致，其误差上界为$ E = 5.778 $。因为同时受到外部干扰与虚假数据注入攻击的影响，故其误差上界更大。

此外，为了突出所设计的动态事件触发机制(5) 的优点，考虑如下由机制(5) 简化所得到的静态事件触发机制：

$ \left\{ \begin{array}{l} {t}_{k}=\mathrm{min}\left\{{t}_{k}^{*},{t}_{k-1}+\tau \right\},k\in {\mathbb{N}}^+\\ {t}_{k}^{*}=\mathrm{inf}\left\{t > {t}_{k-1}:J(t) \ge 0\right\} \end{array} \right.$

(29)

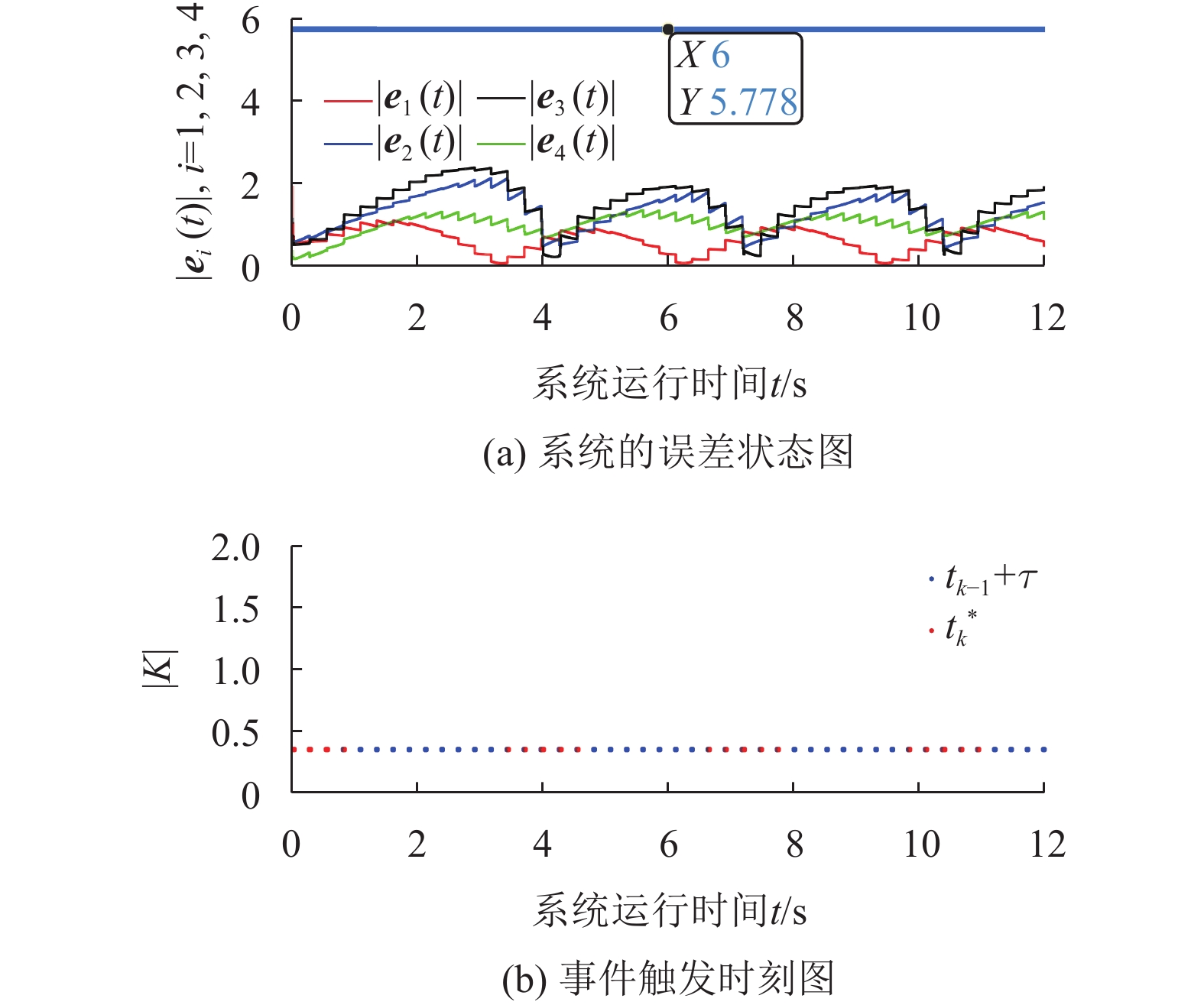
从图6和图7可知，系统在动态事件触发机制(5)的协调下和静态事件触发机制(29)的协调下均可实现拟一致性；但对比图6和图7可知，动态事件触发机制(5)比静态事件触发机制(29)所触发的次数更少，故其所需的控制资源更少。

4 结论

本文设计了一种新颖的可抗干扰的动态事件触发机制，其芝诺行为可由自身参数排除。借助于该机制和脉冲控制，本文进一步研究了一类受扰受虚假数据注入攻击的非线性多智能体系统的领导跟随拟一致性，并给出了相应的充分条件。最后，通过一个数值仿真实验验证了上述理论的有效性。注意到触发机制有可能存在执行时滞，如何描述这类时滞和分析该时滞影响下的系统拟一致性值得进一步研究。