近年来,随着人工智能、传感器网络、计算机科学等学科的发展,多智能体系统作为一门跨领域的学科已经成为研究热点,引起了学术界和工业界的广泛关注[1-5]。多智能体系统广泛应用于故障检测[6-8]、网络协作[9]、智能交通控制[10-11]等领域。其目的是通过控制通信网络连接的一组多智能体系统,以实现动态一致性[12-14]。一致性可分为连续时间一致性和离散时间一致性,Olfati sabera等[15-16]提出了传统的一致性协议框架,并分别建立了连续时间和离散时间的一致性模型。在固定网络拓扑、切换网络拓扑和带时延的固定网络拓扑中,分别设计了一致性协议,并证明了网络邻接矩阵的第二小特征值代表了网络的连通性,也决定了智能体系统的收敛速度。Moreau[17]通过大量仿真实验发现,智能体的邻居过多,会减缓系统的收敛速度。Khateri等[18]在对多智能体系统的研究中,设计了一种维护各智能体局部连通性的方法,在通信延迟的情况下可以更好地保护系统的连通性。考虑到时间限制,Kan等[19]设计了一个可以在预定的有限时间内达成一致的协议。郑军等[20]证明了在无向切换拓扑中,调整因子只需满足在某一个区间内,系统就会完成收敛。Lu等[21]研究了二阶异构多智能体系统一致性,并提出了一种输入饱和与输入非饱和算法使系统达到一致性。Gomez等[22]提出了一种可扩展的方法用来解决有向拓扑和无向拓扑结构的大规模智能体系统一致性,通过研究由少量降低复杂度的拟多项式组成的集合,保证了多智能体系统的一致性。
对于多智能体系统,收敛速度和收敛簇数是评估多智能体系统一致性的一项重要指标。对于一个智能体来说,过多的邻居不仅会增加通信负载,还会削弱一致性。对于这种情况,合理选择邻居进行通信可以有效地减少这种情况的发生。Jadbabaie等[23]首先提出了最近邻选择规则,并对收敛性给出了理论解释。Masoud等[24]提出了一种最近邻控制协议,该协议保证收敛到空间中的一个公共点,即使每个智能体仅限于与单个最近邻通信。Xie等[25]提出了大规模高密度拓扑结构下的快速收敛一致性算法。在先前的研究中,多数学者只考虑在特定密度范围内进行研究和实验,没有考虑不同密度范围对算法和模型的影响,而这些影响可能会导致收敛过慢、稳定性变弱等结果,针对这一类因素,本文着重于解决不同密度范围导致的一致性减弱的问题。本文从多智能体系统中每个智能体的邻居角度出发,研究了多智能体系统在混合密度状态下加快收敛速度的问题,主要贡献如下:
(1) 提出了一种分层邻域选择算法LNS,将邻域层次均等划分后选取每个层次的代表邻居进行通信,并设计了层次调整策略LMO(Layer Modify Optimize) 和层次融合策略LNO(Layer Number Optimize) 两种策略,保证可与每个层次的邻居进行通信,减少了智能体的通信代价,加快了系统收敛速度,对一致性起到一定的增强作用。
(2) 通过LNS构造邻居集合,并在此基础上设计了一种新的邻域选择一致性协议,在传统的一致性协议基础上对邻居进行层次划分并选择具有代表的智能体作为通信邻居,使系统在稳定的条件下达到一致性的效果。
(3) 通过李雅普诺夫函数法证明了分层邻域选择一致性协议的稳定性和收敛性,最后通过仿真实验对智能体的收敛进行演示和结果统计,验证了协议对一致性增强的有效性。
1 预备知识 1.1 图论和矩阵论在本文中,使用图
| $ {a_{ij}}(k) = \left\{ {\begin{array}{*{20}{l}} {1,}&{({v_i},{v_j}) \in E} \\ {0,}&{{\text{otherwise}}} \end{array}} \right. $ | (1) |
图
在离散时间切换拓扑结构下的多智能体系统中,传统的一致性协议为
| $ {x_i}(k + 1) = {x_i}(k) + \alpha \sum\limits_{j \in {N_i}(k) }^{} {({x_j}(} k) - {x_i}(k) ) $ | (2) |
式中:
| $ \mathop {\lim }\limits_{x \to + \infty } ||{x_i}(k) - {x_j}(k) || = 0 $ | (3) |
则称系统达到收敛,即智能体系统达到了一致性。
在传统的离散模型下,每个智能体的邻居集
在邻域选择一致性协议中,智能体的邻居集合被具体地划分为几个子集部分,具体协议如式(4) 所示。
| $ {u_i}(k) = \alpha \bigg(\sum\limits_{j \in {A_i}(k) }^{} {({x_j}(} k) - {x_i}(k) ) + \sum\limits_{j \in {P_i}(k) ,j \notin {A_i}k) } {({x_j}(k) - {x_i}(k) ) \bigg) } $ | (4) |
式中:
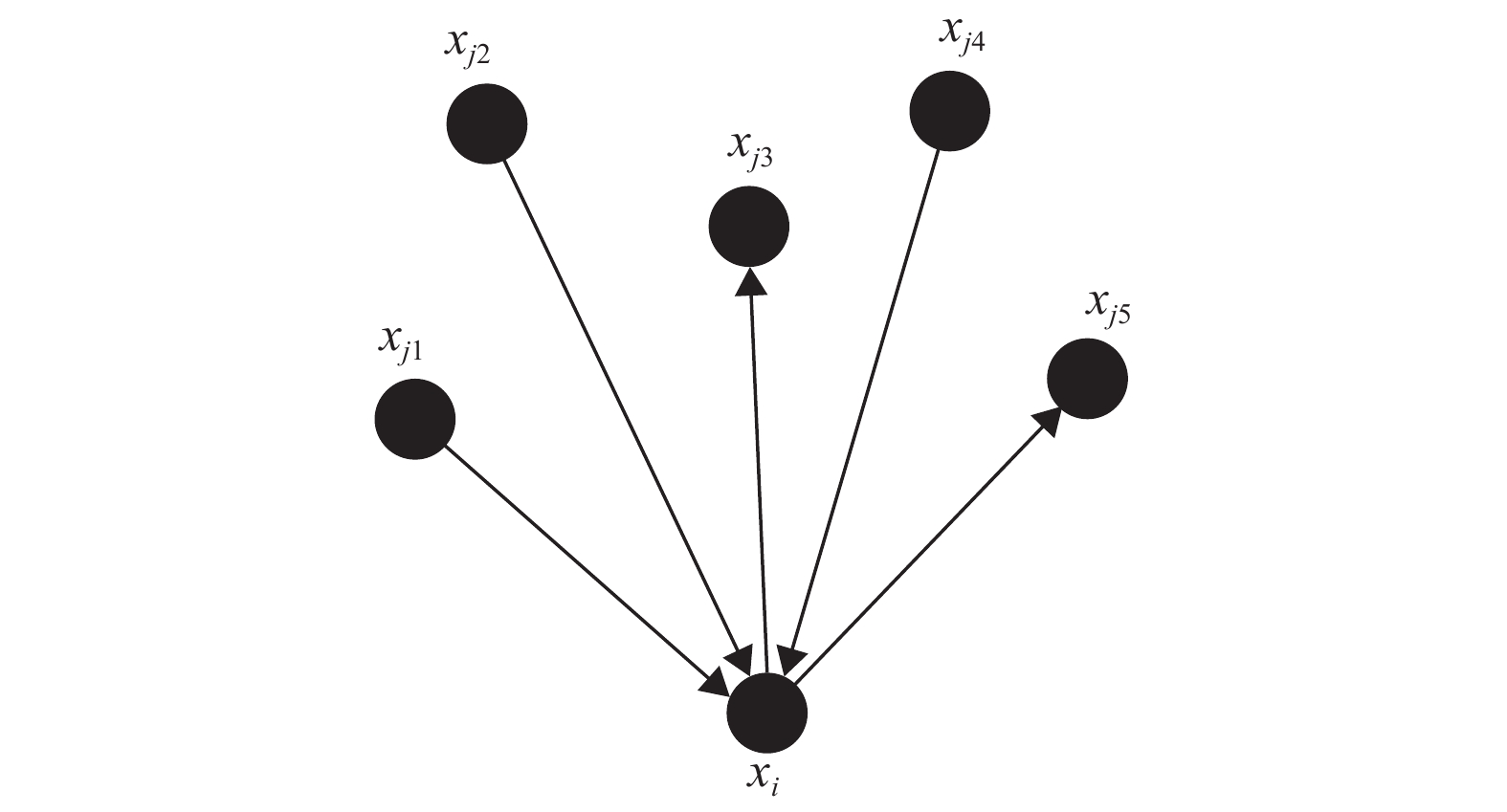
|
图 1 智能体i的请求和接收信号 Figure 1 Request and received signals of the agent i |
在社会学对密度的研究中[26],将系统的平均密度定义为
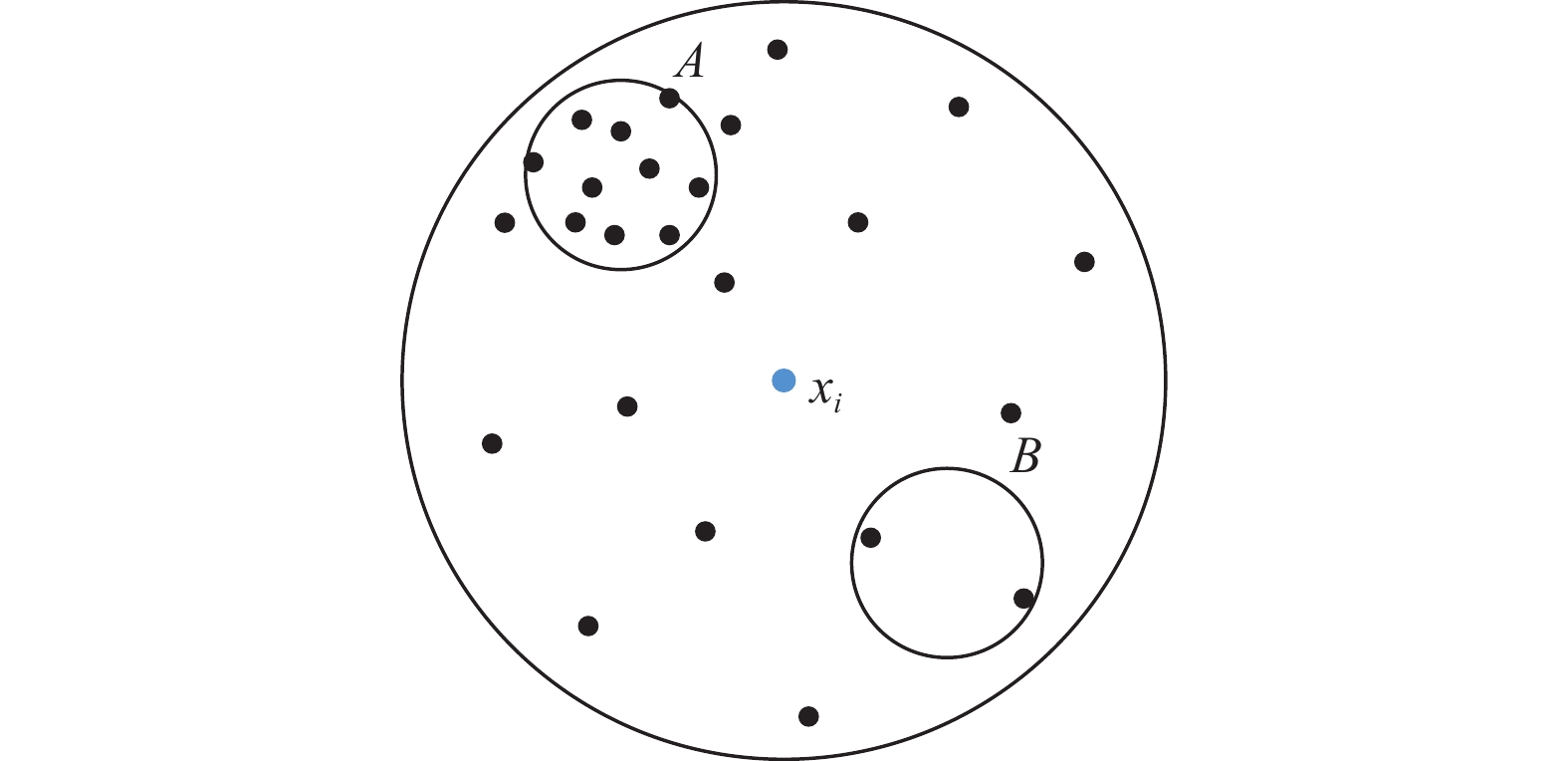
|
图 2 拥挤和非拥挤图例 Figure 2 The illustration of crowded and non-crowded |
网络的拓扑结构在多智能体系统一致性中起重要作用。在离散时间模型中,由于智能体初始数量与拓扑结构的不确定性,过多或过少的邻居都会抑制一致性的效果。在收敛过程中,感知密度也随时间变化,包括出现拥挤和非拥挤的状态,甚至出现拥挤与非拥挤的混合密度状态,这些都会抑制一致性的效果。因此,主要问题是如何在离散时间切换拓扑下设计分布式一致性协议,该协议能有效适应混合密度的状态,在系统稳定的条件下有效提高收敛速度。分层邻域选择能够将高密度、复杂信息等减少,将低密度智能体联系更加紧密,且通过分层的方法可以不破坏整个系统的结构,提取更有价值的邻域信息,保证系统不会因为邻居数量减少而使模型稳定性遭到破坏,一定程度上加强了一致性的效果。
2 基于分层邻域选择一致性协议本章主要介绍了LNS的设计过程,并给出LNS中层次的调整策略,根据LNS来构造新的分层邻域选择一致性协议,并详细介绍其构造过程,最后对一致性协议的稳定性进行理论分析和证明。
2.1 分层邻域选择算法传统的邻域选择算法,每个智能体只考虑与最近的邻居进行通信和状态更新,忽略不同状态差值的邻居对收敛结果的影响,导致收敛速度慢和收敛簇数过多的问题。在分层邻域选择中,考虑所有状态差值下的邻居后并对其进行均等划分,减少了智能体的通信代价,加快了系统的收敛速度。
多智能体系统中每个智能体的通信半径是有限的,本文中,将智能体的通信半径设为
| $ d = \frac{{{\text{max}}({N_i}(k) ) - {\text{min}}({N_i}(k) ) }}{m} $ | (5) |
其中,若
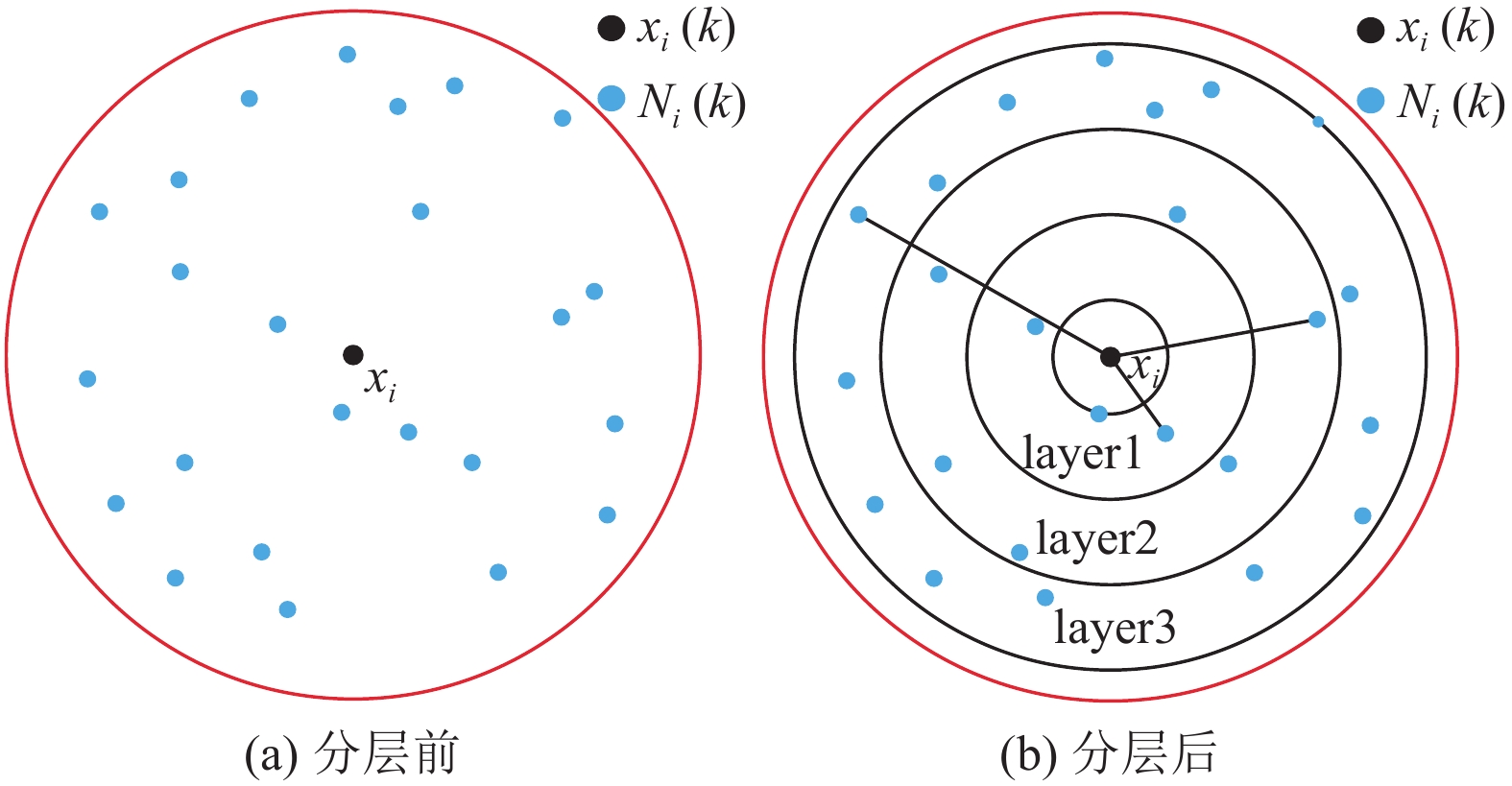
|
图 3 分层模型的图例 Figure 3 The illustration of layered model |
这是一个构造新的邻居集合的过程,通过该算法构建出了一个新的邻居集
算法1 分层邻域选择算法
输入:
输出:
a) 循环遍历
b) 令
c) 再对
d) 结束循环,求出并集
通过算法1得到的邻居集
| $ {u_i}(k) = \lambda \bigg[\sum\limits_{f({i^\omega }) \in {A_i}(k) } {({x_{f({i^\omega }) }}(k) - {x_i}(k) ) } + \sum\limits_{j \in {P_i}(k) ,j \notin {A_i}(k) } {({x_j}(k) - {x_i}(k) ) \bigg]} $ | (6) |
式中:
针对混合密度拓扑结构,考虑到每个智能体的邻居数量不同,对邻域进行层次调整,使得邻域中的每个层次都有与自身进行通信的邻居,保证了一致性的准确性。
在这一部分中,优化了LNS中抑制一致性效果的问题。首先,当智能体
策略1 层次调整策略:
a) 设初始智能体
b) 循环遍历每一层的邻居集,结束条件为
c) 层数
针对EL现象,本文还提出了一种对空层现象进行合并的层次融合策略2(LMO) ,该策略将出现的空层相邻层进行融合。首先,智能体
策略2 层次融合策略:
a) 设初始智能体
b) 循环遍历每一层的邻居集,结束条件为
c) 如果
在本节中,分析了分层邻域选择一致性协议的收敛性,并证明了系统的稳定性。
首先,将式(6)的控制输入代入一致性协议(2),得到完整的分层邻域选择一致性协议,转换为矩阵的形式可以表示为
| $ \begin{split} {\boldsymbol{M}}(k + 1) =& {\boldsymbol{M}}(k) + \lambda [{{\boldsymbol{L}}_1}(k) {\boldsymbol{M}}(k) + {{\boldsymbol{L}}_2}(k) {\boldsymbol{M}}(k) ]= \\ & [{\boldsymbol{I}} + \lambda ({{\boldsymbol{L}}_1}(k) + {{\boldsymbol{L}}_2}(k) ) ]{\boldsymbol{M}}(k) \end{split} $ | (7) |
式中:
引理1[27] 负半定矩阵的充要条件是实对称矩阵
引理2[27] 对于一个系统
引理3[27] 设矩阵
| $ \begin{split} &{\sigma }_{i}\in S=\bigcup\limits_{i = 1}^n {{S_i}} (i=1,2,3,\cdots,n) \\ &{S}_{i}=\left\{z\in C:|z-{a}_{ii}| \le {R}_{i}={\displaystyle \sum _{j\ne 1}|}{a}_{ij}|\right\} \end{split} $ | (8) |
式中:
定理1[27] 随时间
证明 将李雅普诺夫函数设置为
| $ F({\boldsymbol{M}}(k) ) = {{\boldsymbol{M}}^{\text{T}}}(k) \cdot {\boldsymbol{M}}(k) $ | (9) |
对李雅普诺夫函数进行作差得
| $ \begin{split} &F({\boldsymbol{M}}(k + 1) ) - F({\boldsymbol{M}}(k) ) = \\ & {{\boldsymbol{M}}^{{\mathrm{T}}}}(k + 1) \cdot {\boldsymbol{M}}(k + 1) - {{\boldsymbol{M}}^{{\mathrm{T}}}}(k) \cdot {\boldsymbol{M}}(k)= \\ & {{\boldsymbol{M}}^{{\mathrm{T}}}}(k) {[{\boldsymbol{I}} + \lambda ({{\boldsymbol{L}}_1}(k) + {{\boldsymbol{L}}_2}(k) ) ]^{{\mathrm{T}}}} \times \\ & [{\boldsymbol{I}} + \lambda ({{\boldsymbol{L}}_1}(k) + {{\boldsymbol{L}}_2}(k) ) ] \cdot {\boldsymbol{M}}(k) - {{\boldsymbol{M}}^{{\mathrm{T}}}}(k) {\boldsymbol{M}}(k) = \\ & {{\boldsymbol{M}}^{{\mathrm{T}}}}(k) {[{\boldsymbol{I}} + \lambda ({{\boldsymbol{L}}_1}(k) + {{\boldsymbol{L}}_2}(k) ) ]^2}{\boldsymbol{M}}(k) - {{\boldsymbol{M}}^{{\mathrm{T}}}}(k) {\boldsymbol{M}}(k) = \\ & {{\boldsymbol{M}}^{{\mathrm{T}}}} \cdot [2\lambda ({{\boldsymbol{L}}_1}(k) + {{\boldsymbol{L}}_2}(k) ) + {\lambda ^2}{({{\boldsymbol{L}}_1}(k) + {{\boldsymbol{L}}_2}(k) ) ^2}] \cdot {\boldsymbol{M}}(k) = \\ & 2\lambda {{\boldsymbol{M}}^{{\mathrm{T}}}} \cdot [({{\boldsymbol{L}}_1}(k) + {{\boldsymbol{L}}_2}(k) ) + \frac{\lambda }{2}{({{\boldsymbol{L}}_1}(k) + {{\boldsymbol{L}}_2}(k) ) ^2}] \cdot {\boldsymbol{M}}(k) \end{split} $ | (10) |
在这里将矩阵
| $ {\boldsymbol{H}}(k) = ({{\boldsymbol{L}}_1}(k) + {{\boldsymbol{L}}_2}(k) ) + \frac{\lambda }{2}{({{\boldsymbol{L}}_1}(k) + {{\boldsymbol{L}}_2}(k) ) ^2} $ | (11) |
式中:
| $ {h_{ii}}(k) = \frac{\lambda }{2}[{({n_1}(k) + {n_2}(k) ) ^2} + {n_1}(k) + {n_2}(k) ] - ({n_1}(k) + {n_2}(k) ) $ | (12) |
从引理3可得,
| $ |\lambda -{h}_{ij}| \le {\displaystyle \sum _{j\ne i}{b}_{ij}} $ | (13) |
由于智能体的邻居数量总是要小于除智能体自身外的所有智能体的数量,即
| $ \begin{split} & h_{i i}(k) = \frac{\lambda}{2}\left[\left(n_1(k) + n_2(k)\right)^2 + \right. \left.n_1(k) + n_2(k)\right] - \left(n_1(k) + n_2(k)\right) \leqslant\\ & \frac{1}{n_1 + n_2 + 1}\left[\left(n_1(k) + n_2(k)\right)^2 + \right. \left.n_1(k) + n_2(k)\right] - \left(n_1(k) + n_2(k)\right) \leqslant 0 \\ \end{split}$ | (14) |
因此,圆心
综上所述,系统最终将达到李雅普诺夫渐进稳定,证毕。
3 仿真实验与分析本节对分层邻域选择一致性协议进行验证,分别用不同密度状态下的拓扑结构进行实验,根据实验的结果对参数进行调整,使得系统的一致性效果达到最优。
3.1 收敛性验证本节将智能体的数量设置为10~1 000,低密度下增量设为10,高密度下增量设为100。这样设置目的是为了验证高密度差值下收敛效果提升更加明显。每个智能体的拓扑结构如图4所示,初始状态随机生成。在2.3节中,证明了收敛因子
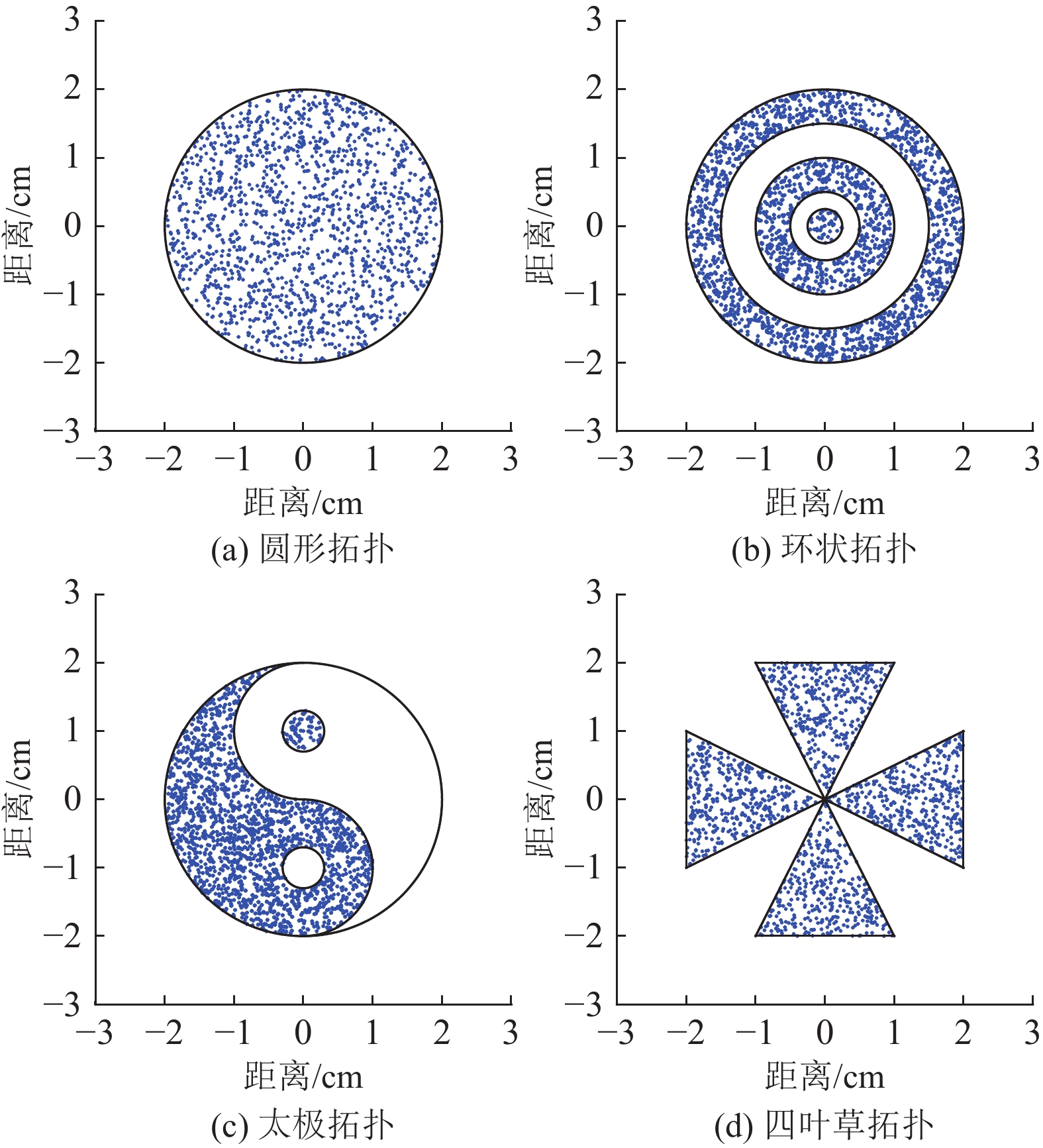
|
图 4 不同初始状态的拓扑结构图 Figure 4 Topological structure diagram of different initial states |
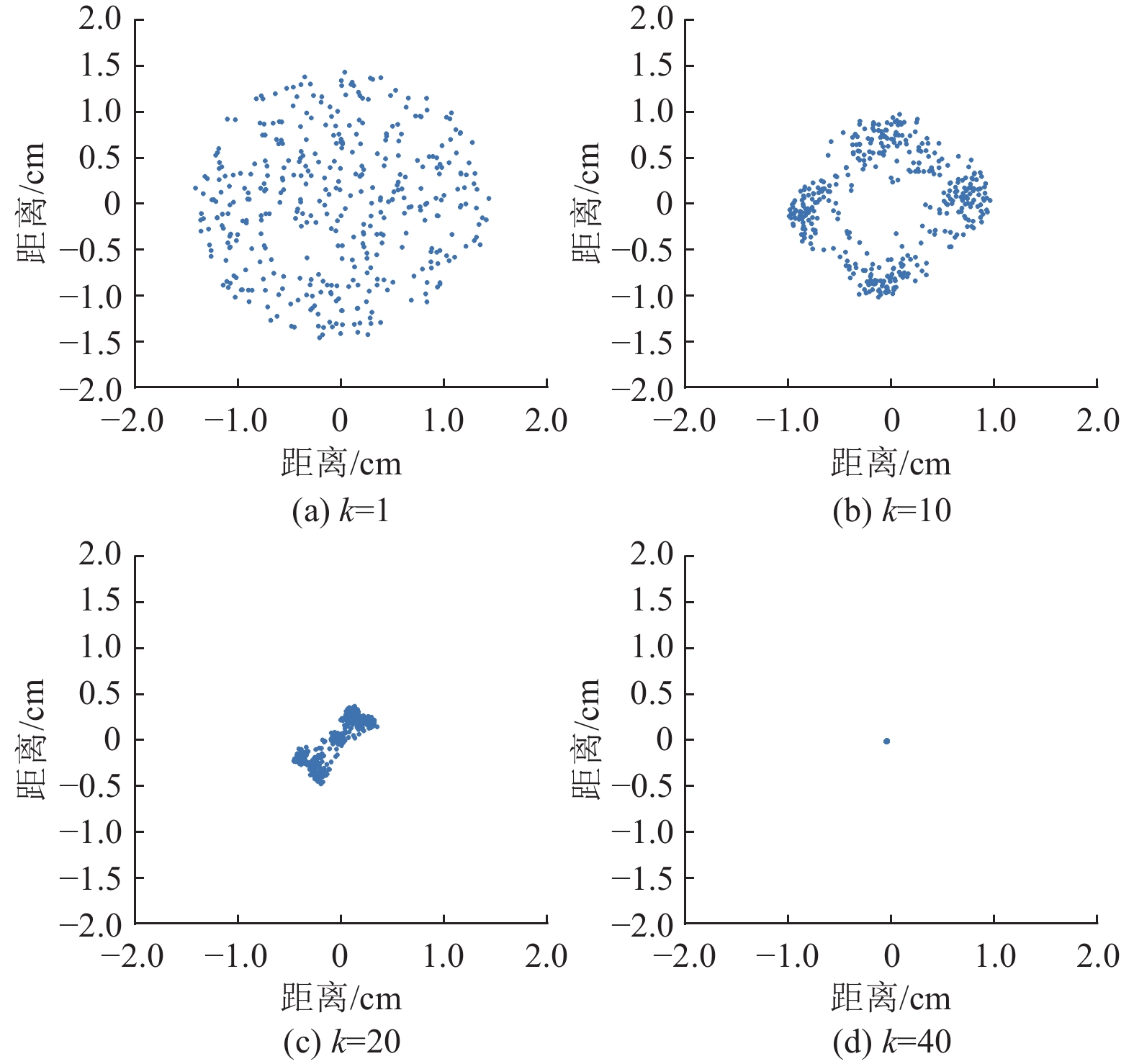
|
图 5 智能体数量为500的收敛演化图 Figure 5 Convergence diagram with 500 agents |
为了验证实验的有效性,选取了收敛过程中大量出现混合密度状态的拓扑结构进行2 000次实验,其实验结果数据见表1和表2。其中SAN为文献[15]中的传统的一致性算法;NSM为文献[28]中提出的邻域选择算法,该算法选择特征向量大于1的邻居作为通信邻居来进行状态更新;SNN算法为文献[24]中提出的算法,该算法将每个智能体的最近邻居作为通信邻居,且最近的邻居必须位于一个预先确定的优先级区域之外。经过重复实验验证了LNS算法可以在有限的时间内实现快速一致性。并且从结果数据的比较可以看出,LNS在收敛的迭代次数方面要优于其他一致性算法。
| 表 1 低密度下不同算法收敛的平均迭代次数 Table 1 Iterations for convergence of different algorithms in low density |
| 表 2 高密度下不同算法收敛的平均迭代次数 Table 2 Iterations for convergence of different algorithms in high density |
在文献[26]对社会学的密度研究中,作者通过大量实验,在同一社区环境下不同居民数量中,统计其达到密度阈值的次数,并定义次数最多的为该社区的密度阈值。本文参考其密度划分的思想,也对多智能体系统的密度进行划分,在本文的研究中,分别在智能体数量为10~1 000且其他参数相同的情况下进行实验,当数量超过某一个阈值时,系统则将不会收敛,本文通过大量仿真实验发现其阈值在90~110区间内,即系统在超过该阈值时发散。如图6所示,实验数量为2 000次,当智能体数量为100时统计数量最多,远大于其周围情况。因此,在本文的研究中将智能体系统高低密度的阈值设为100。
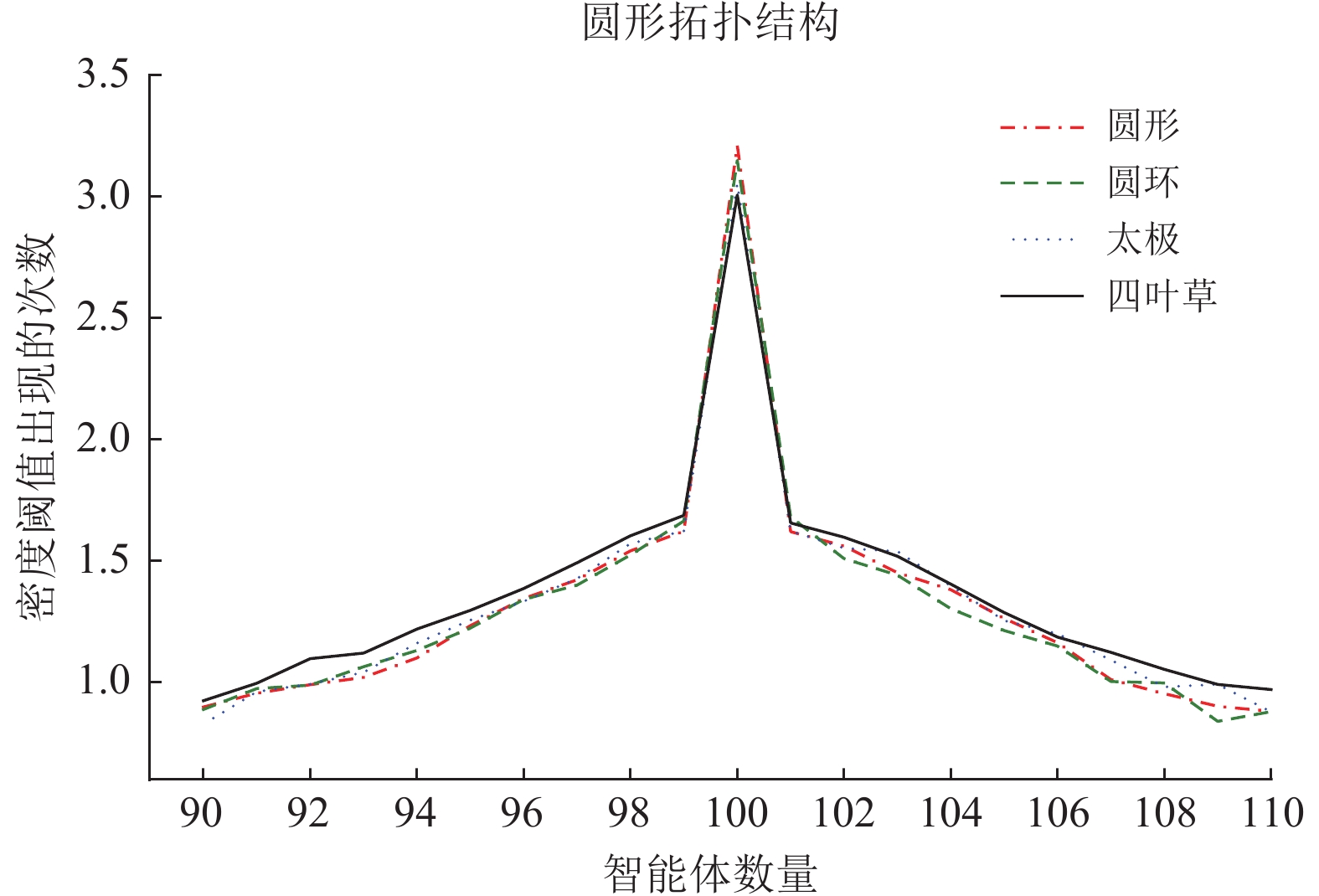
|
图 6 智能体数量在区间90~110内出现断层现象的次数 Figure 6 The frequency faults occur for the agents of 90~110 |
在分层邻域选择一致性协议中,可调参数
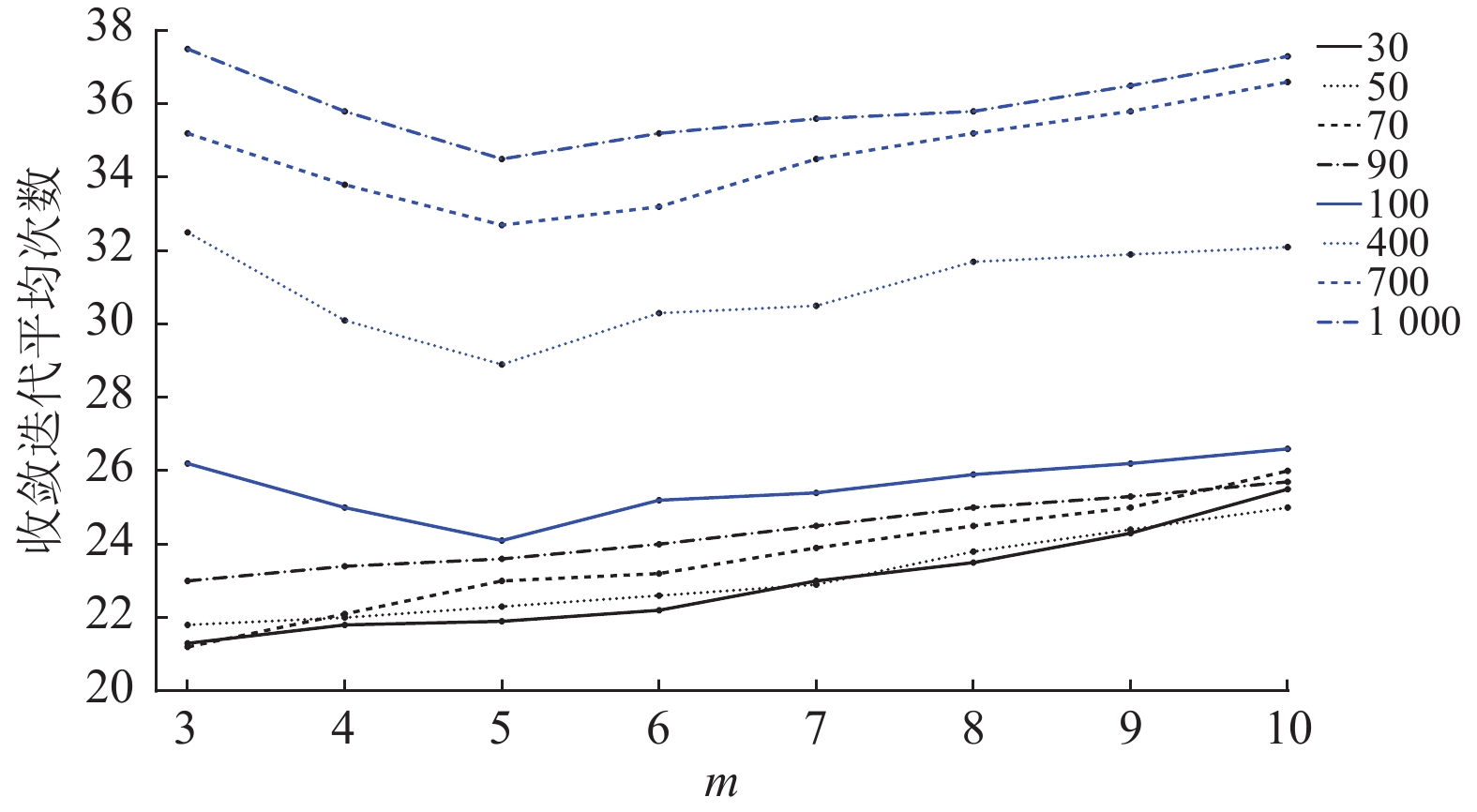
|
图 7 不同m下收敛迭代次数 Figure 7 Number of iterations under different parameter m |
由于层数
(1) 智能体数量小于100,
(2) 智能体数量大于等于100,
对本文提出的算法和近来研究的一致性算法的收敛速度进行比较,然后通过给定特定的混合密度拓扑结构进行实验,比较了2种优化策略的效果。实验中,在低密度下智能体数量以差值为10增加,在高密度下智能体的数量成倍数级增加,如图8所示,将智能体数量取对数作为横坐标,然后对每种数量的拓扑结构分别进行2 000次实验,结果取平均值。由图8的实验结果可知,LNS算法收敛的迭代次数均小于其他算法,并且在高密度下表现更佳。
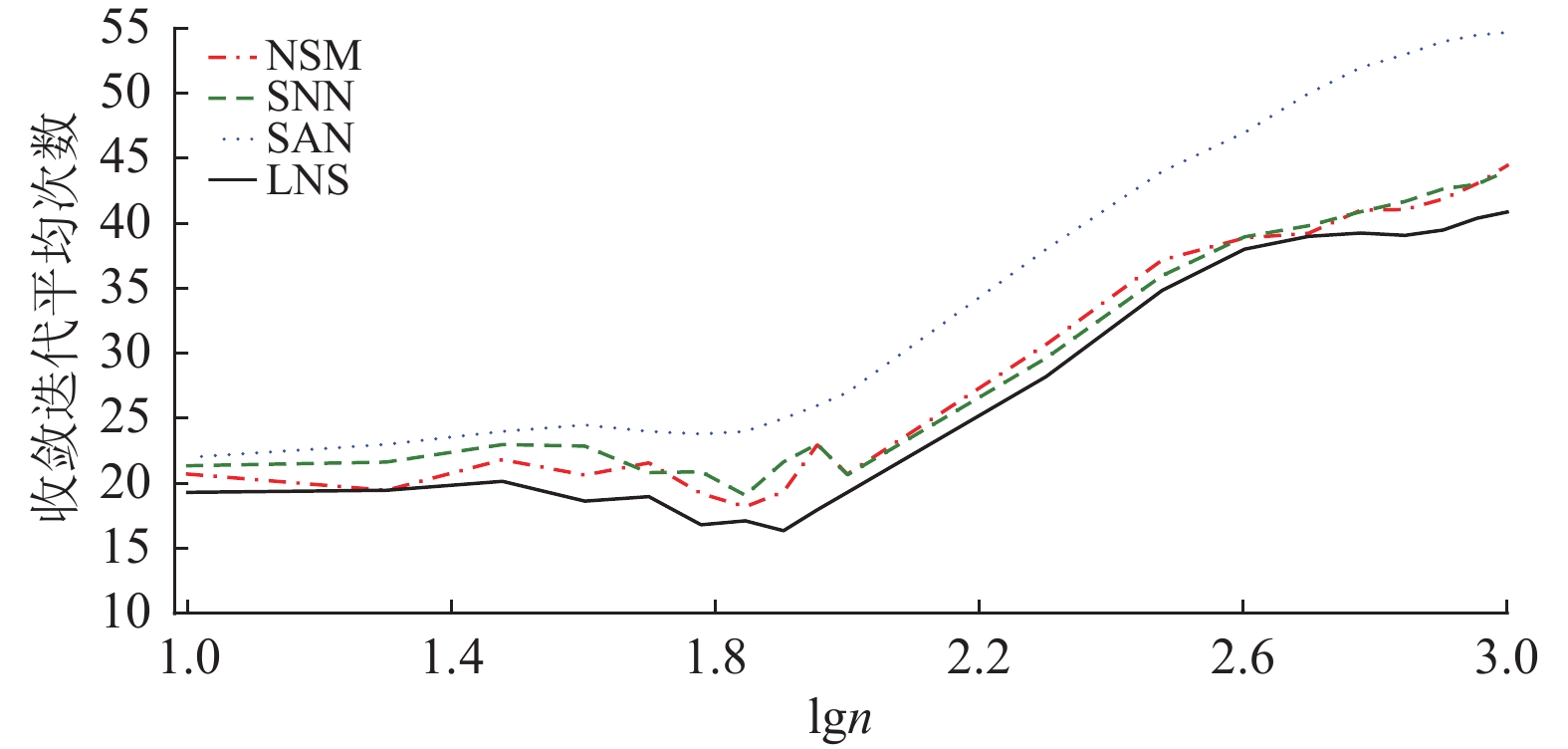
|
图 8 几种算法的收敛平均迭代次数比较 Figure 8 Comparison of convergence average iteration times |
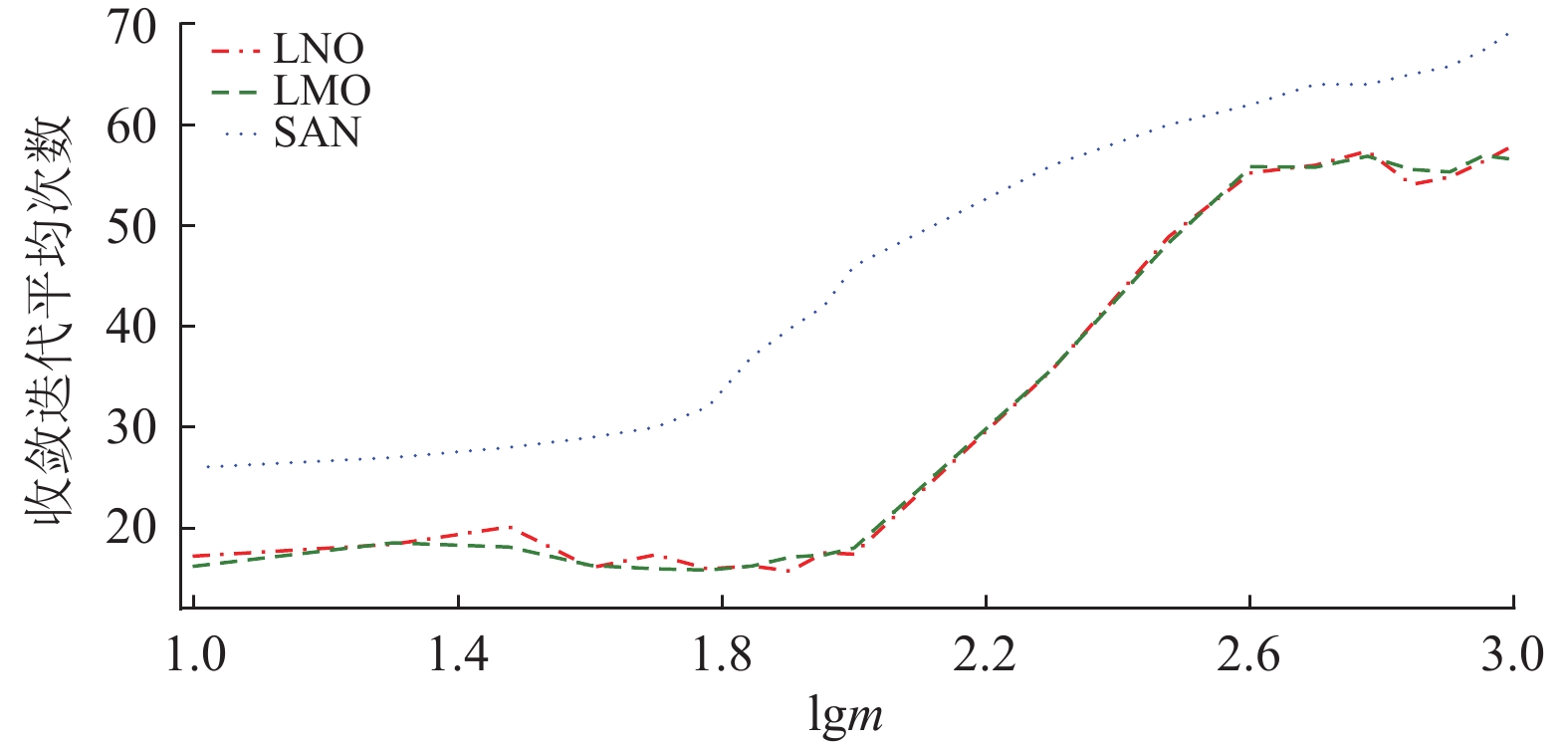
根据不同的拓扑结构特性,选取了混合密度状态的拓扑结构进行对比实验,如图9所示,横坐标为出现EL次数的对数形式,纵坐标为收敛的平均迭代次数。从实验结果可以看出,在出现不同次数EL现象的情况下,两种基于层次优化策略后的LNS对收敛的速度都有所提升,且对于EL现象不敏感。总的来说,LNO与LMO在具体应用场景中,无论是否出现EL现象,收敛速度较传统的一致性算法都有所提升。
|
图 9 不同数量EL现象下的优化策略比较 Figure 9 Comparison of optimization strategies under different EL |
本文主要研究了无向切换拓扑下的多智能体一致性问题,不仅考虑了初始拓扑密度对收敛的影响,还考虑了收敛过程中出现的混合密度状态如拥挤和非拥挤对收敛结果产生的影响,并通过理论分析证明了一致性协议的稳定性,最后通过仿真实验验证了一致性协议的有效性与优异性。与传统的研究方法不同,本文扩展了应用场景,提出了一种分层邻域选择算法LNS和2种层次优化策略,并设计了一种新的分层邻域选择一致性协议。新的算法与一致性协议具有以下优点:
(1) 基于密度信息设计了一致性协议,能够适应不同密度拓扑结构对一致性的影响,且保证系统在稳定的基础上提升收敛速度
(2) 2种策略优化后,能够在EL现象下有效提升收敛速度,与传统的一致性算法相比,本文提出的算法效果都有所提升。
未来将进一步研究在切换拓扑下的混合密度信息与分层之间的关系以及密度阈值与系统收敛的对应关系。
| [1] |
AMIRKHANI A, BARSHOOI A H. Consensus in multi-agent systems: a review[J].
Artificial Intelligence Review, 2021, 55(5): 1-39.
|
| [2] |
CAO X, ZHANG C, ZHAO D, et al. Guaranteed cost positive consensus for multi-agent systems with multiple time-varying delays and MDADT switching[J].
Nonlinear Dynamics, 2022, 107(4): 3557-3572.
DOI: 10.1007/s11071-021-07157-w. |
| [3] |
孙彧, 曹雷, 陈希亮, 等. 多智能体深度强化学习研究综述[J].
计算机工程与应用, 2020, 56(5): 13-24.
SUN Y, CAO L, CHEN X L, et al. Overview of multi-agent deep reinforcement learning[J]. Computer Engineering and Applications, 2020, 56(5): 13-24. DOI: 10.3778/j.issn.1002-8331.1912-0100. |
| [4] |
LIU C, JIANG B, ZHANG K, et al. Distributed fault-tolerant consensus tracking control of multi-agent systems under fixed and switching topologies[J].
IEEE Transactions on Circuits and Systems I: Regular Papers, 2021, 68(4): 1646-1658.
DOI: 10.1109/TCSI.2021.3049347. |
| [5] |
DAS A, GERVET T, ROMOFF J, et al. Tarmac: targeted multi-agent communication[C]//International Conference on Machine Learning. LA: PMLR, 2019: 1538-1546.
|
| [6] |
KASHYAP N, YANG C W, SIERLA S, et al. Automated fault location and isolation in distribution grids with distributed control and unreliable communication[J].
IEEE Transactions on Industrial Electronics, 2014, 62(4): 2612-2619.
|
| [7] |
DAVOODI M R, KHORASANI K, TALEBI H A, et al. Distributed fault detection and isolation filter design for a network of heterogeneous multiagent systems[J].
IEEE Transactions on Control Systems Technology, 2013, 22(3): 1061-1069.
|
| [8] |
DAVOODI M, MESKIN N, KHORASANI K. Simultaneous fault detection and consensus control design for a network of multi-agent systems[J].
Automatica, 2016, 66: 185-194.
DOI: 10.1016/j.automatica.2015.12.027. |
| [9] |
PALAU A S, DHADA M H, BAKLIWAL K, et al. An industrial multi agent system for real-time distributed collaborative prognostics[J].
Engineering Applications of Artificial Intelligence, 2019, 85: 590-606.
DOI: 10.1016/j.engappai.2019.07.013. |
| [10] |
LI Y, TANG C, LI K, et al. Consensus-based cooperative control for multi-platoon under the connected vehicles environment[J].
IEEE Transactions on Intelligent Transportation Systems, 2018, 20(6): 2220-2229.
|
| [11] |
LI Y, CHEN W, PEETA S, et al. Platoon control of connected multi-vehicle systems under V2X communications: design and experiments[J].
IEEE Transactions on Intelligent Transportation Systems, 2019, 21(5): 1891-1902.
|
| [12] |
RUAN X, FENG J, XU C, et al. Observer-based dynamic event-triggered strategies for leader-following consensus of multi-agent systems with disturbances[J].
IEEE Transactions on Network Science and Engineering, 2020, 7(4): 3148-3158.
DOI: 10.1109/TNSE.2020.3017493. |
| [13] |
JIANG F, XIE D, CAO M. Dynamic consensus of double-integrator multi-agent systems with aperiodic impulsive protocol and time-varying delays[J].
IET Control Theory & Applications, 2017, 11(16): 2879-2885.
|
| [14] |
YI X, LIU K, DIMAROGONAS D V, et al. Dynamic event-triggered and self-triggered control for multi-agent systems[J].
IEEE Transactions on Automatic Control, 2018, 64(8): 3300-3307.
|
| [15] |
OLFATI-SABER R, MURRAY R M. Consensus problems in networks of agents with switching topology and time-delays[J].
IEEE Transactions on Automatic Control, 2004, 49(9): 1520-1533.
DOI: 10.1109/TAC.2004.834113. |
| [16] |
SABER R O, MURRAY R M. Consensus protocols for networks of dynamic agents[C]//Proceedings of the 2003 American Control Conference. Toronto: IEEE, 2003: 951-956.
|
| [17] |
MOREAU L. Stability of multiagent systems with time-dependentcommunication links[J].
IEEE Transactions on Automatic Control, 2005, 50(2): 169-182.
DOI: 10.1109/TAC.2004.841888. |
| [18] |
KHATERI K, POURGHOLI M, MONTAZERI M, et al. A comparison between decentralized local and global methods for connectivity maintenance of multi-robot networks[J].
IEEE Robotics and Automation Letters, 2019, 4(2): 633-640.
DOI: 10.1109/LRA.2019.2892552. |
| [19] |
KAN Z, YUCELEN T, DOUCETTE E, et al. A finite-time consensus framework over time-varying graph topologies with temporal constraints[J].
Journal of Dynamic Systems, Measurement, and Control, 2017, 139(7): 071012.
DOI: 10.1115/1.4035612. |
| [20] |
郑军, 颜文俊. 多主体汇聚问题离散算法的稳定性[J].
浙江大学学报: 工学版, 2007, 41(10): 1684-1687.
ZHENG J, YAN W J. Sufficient condition on stability of multi-agent rendezvous discrete algorithm[J]. Journal of Zhejiang University (Engineering Science), 2007, 41(10): 1684-1687. |
| [21] |
LU M, WU J, ZHAN X, et al. Consensus of second-order heterogeneous multi-agent systems with and without input saturation[J].
ISA Transactions, 2022, 126: 14-20.
DOI: 10.1016/j.isatra.2021.08.001. |
| [22] |
GOMEZ M A, RAMIREZ A. A scalable approach for consensus stability analysis of a large-scale multi-agent system with single delay[J].
IEEE Transactions on Automatic Control, 2022, 68(7): 4375-4382.
|
| [23] |
JADBABIE A, LIN J, MORSE A S. Coordination of groups of mobile autonomous agents using nearest neighbor rules[J].
IEEE Transactions on Automatic Control, 2003, 48(6): 988-1001.
DOI: 10.1109/TAC.2003.812781. |
| [24] |
MASOUD A A. Nearest neighbor-based rendezvous for sparsely connected mobile agents[J].
Journal of Dynamic Systems, Measurement, and Control, 2015, 137(12): 121002.
DOI: 10.1115/1.4031248. |
| [25] |
XIE G, XU H, LI Y, et al. Fast distributed consensus seeking in large-scale and high-density multi-agent systems with connectivity maintenance[J].
Information Sciences, 2022, 608: 1010-1028.
DOI: 10.1016/j.ins.2022.06.079. |
| [26] |
CHURCHMAN A. Disentangling the concept of density[J].
Journal of Planning Literature, 1999, 13(4): 389-411.
DOI: 10.1177/08854129922092478. |
| [27] |
HORN R A, JOHNSON C R. Matrix analysis[M]. London: Cambridge University Press, 2012.
|
| [28] |
CHEN L, DUAN H, ZENG Z. Fast convergent tracking control of networked UAVs over a dynamic interaction topology[J].
IEEE Transactions on Circuits and Systems II: Express Briefs, 2022, 69(12): 4884-4888.
|
 2024, Vol. 41
2024, Vol. 41

