科技咨询机构ICV TAnK的《Global intelligent driving forecast-2022》指出,到2026年全球L1及以上智能驾驶汽车市场渗透率将达到94.24%,总数预计将达到
在混合交通环境中,通过控制一辆领航CAV迫使跟随的HDVs形成间距较小的混合编队,具有提高交通吞吐量和燃油经济性等潜在优势[2]。近年来,混合编队作为CAVs与HDVs相互共享道路的一种新兴形式,受到了广泛的研究和关注[3-7]。尽管当前研究成果丰富,但它们主要聚焦于单车道场景,而忽略了更为复杂的多车道环境,这与城市道路和高速公路的实际情况存在偏差。此外,现有研究表明,道路通行能力随着编队的规模增大而增加[8]。因此,存在研究多车道混合编队的必要性。在探讨多车道混合编队的形成过程中,多辆领航CAVs的换道行为是一个复杂的关键问题。针对智能网联汽车换道问题,已经提出了基于规则、基于离散选择、基于人工智能以及基于博弈论的换道决策方法[9]。这些方法各有优势和局限。
基于规则的换道策略方法简单易懂,但对于复杂和不确定的交通环境存在一些局限性。例如,文献[10]的节流控制策略能有效应对快速路瓶颈问题,在初始化换道过程中,使用以CAVs的空间位置先后顺序指定目标车道的规则,但忽略CAVs初始车道的随机性和执行换道的安全性。而基于离散选择的换道决策模型只能考虑有限的选择,执行优化目标下的结果,而在实际换道决策时仍可能存在其他选项。如胡祥旺等[11]以优化车道流量分布为目标,实时决策匝道上游CAVs的向左、向右或保持车道的换道行为,但缺少考虑连续变量及其对换道效率的影响。受混合交通流中HDVs驾驶随机性影响,Gong等[12]和Wang等[13]分别提出基于深度强化学习的CAV换道决策模型,综合考虑安全性和效率,前者改进后的DDPG(Deep Deterministic Policy Gradient)算法在不同场景下平均换道成功率为96.15%,后者经过训练SAC(Soft Actor-critic)算法在highD测试数据集中实现90%的换道成功率。然而,这些强化学习模型为了拓展应用场景需要大量训练数据和成本,在实际应用中受环境和设备影响较大。而基于博弈论的换道决策方法能模拟人类自然竞争和合作行为的过程,相比于其他传统方法,能揭示更真实的驾驶行为[14]。不过,目前的研究仍面临一些挑战。
在混合交通中,CAVs与HDVs在换道过程中被视为博弈换道,涉及到两者信息不对称、策略独立性和目标优化的差异。作为研究CAVs与HDVs之间交互行为的博弈理论,能够为自动驾驶车辆换道过程中提供足够的安全性和公平性[15]。为了研究CAV换道决策行为,Zheng等[16]构建了3种决策博弈函数来定量换道收益,Qu等[17]通过量化车辆换道意图以分析换道决策行为。通过仿真验证,与LC2013换道模型相比,这两种博弈换道模型都能够提高交通系统的通行效率和安全性。但是,上述两种博弈换道模型实验对象仅为CAVs,且面向CAVs自由换道决策,难以解决混合交通流下CAVs协同换道问题。Fu等[18]提出了一种网联混合交通环境下基于联盟博弈(Coalition Game)多CAVs协同换道决策模型。虽然该模型能在保证混合交通流安全的同时,提高CAVs的换道效率,但是并不满足本文领航CAVs多车道分布这一特征。
基于以上背景,本文针对多车道混合编队中领航CAVs换道决策的问题,提出了一种面向混合编队领航CAVs的博弈换道决策模型。具体而言,该模型建立数学优化与博弈论相结合的换道决策机制,考虑CAVs初始车道的随机性,以最小化CAVs换道次数为目标,建立领航CAVs目标车道初始化流程,并依据CAVs博弈换道收益,更新领航CAVs目标车道,实现混合编队多车道分布。其中,基于博弈论建立CAVs与HDVs非合作博弈矩阵,综合考虑换道效率和安全性,分别设计时间和安全收益函数,量化CAVs换道决策的风险。本文贡献可总结如下:
(1) 提出了一种结合数学优化与博弈论的换道决策机制,在保证换道次数较低情况下,有效提高了多车道混合编队完成率。
(2) 构建了一种基于博弈论的领航CAVs换道决策模型,与基准模型相比,显著提升了CAVs换道效率和安全性。
1 基于博弈论的领航CAVs换道模型 1.1 模型基本假设条件为了在交通系统中实现本文所提的博弈换道决策模型,需要满足以下基本假设条件:
(1) 交通系统中仅考虑CAVs和HDVs两类车型,其中CAVs可获取周边车况信息(车距、车速等)并执行系统的换道决策,同时不考虑信息传输等延迟。
(2) CAVs和HDVs的到达车流服从泊松分布,且到达车辆随机分布于不同车道。
1.2 领航CAVs目标车道初始化在形成多车道分布的混合编队过程中,需考虑领航CAVs初始车道的随机性,以最小化每组领航CAVs的换道次数,优化领航CAVs的目标车道,即领航CAV目标车道初始流程。这是本文所提的换道决策机制的数学优化部分。
假设CAVs按顺序且随机地从不同车道驶入编队区域,以与车道数相同数量的CAVs为一组,并逐个初始化每辆领航CAV目标车道。假设车道数为n,车道编号数据集N=[0, 1, 2, ···, n−1],某一组领航CAVs编号数据集C=[i, i+1, i+2, ···, i+n−1]。同时,第i辆领航CAV所在车道编号表示为
算法1 领航CAVs目标车道数学优化算法
1) 输入:N, C = [i, i+1, i+2, ···, i+n−1],
2) 赋值并创建空列表:
(a) 判断车辆j所在车道
若成立,删除
否则,将
同时删除
(b)
3) 直至
4) 输出:领航CAVs目标车道R
1.3 领航CAVs博弈换道决策在初始化领航CAVs目标车道后,由于周边HDVs的干扰,CAVs可能无法快速且安全地换到目标车道,同时需要在各车道形成混合编队。图1展示了每3辆CAVs博弈换道决策的典型情况。情况1是3辆领航CAVs在同一车道行驶。在情况2中,有2辆领航CAVs在同一车道上。情况3中,CAVs分布在不同的车道上。在情况1和2中,同一车道上的领航CAVs可以通过博弈更新其目标车道并执行换道决策。在情况3中,由于每个车道上都有充当混合编队的领航车的CAV,则不需要进行博弈换道。针对以上情况,本文建立领航CAVs博弈换道决策模型。该模型设计安全效益和时间收益函数,比较CAVs的换道收益,并通过协调更新领航CAVs的目标车道实现车辆换道。这一模型旨在平衡安全性和时间收益,使得领航CAVs能够在周边车辆的影响下,高效而安全地完成换道过程。
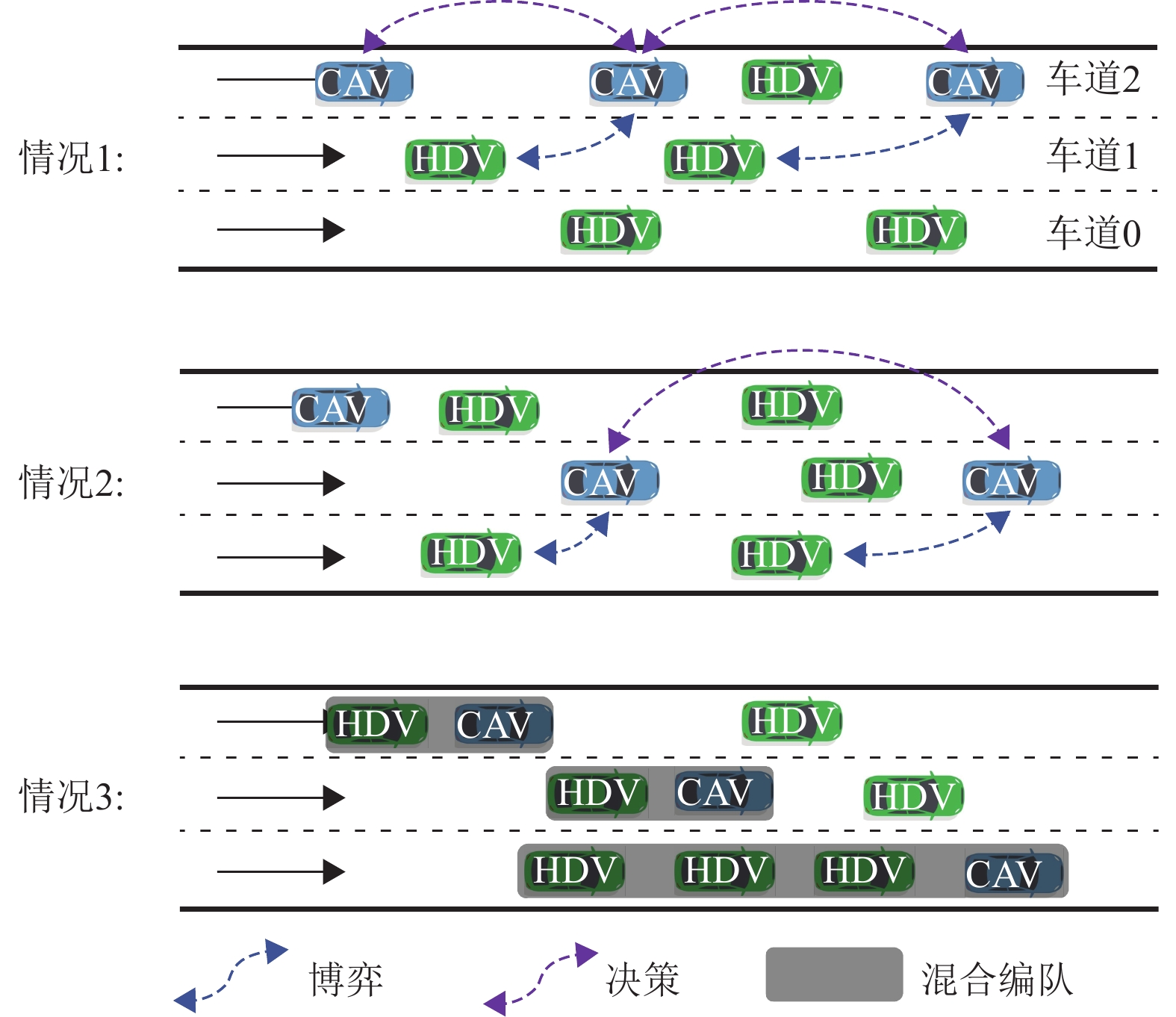
|
图 1 每3辆CAVs博弈换道决策典型案例 Figure 1 Typical example of lane-changing decision in a game between every 3 CAVs |
换道CAV与目标车道后方HDV之间的博弈为非合作博弈。假设CAV执行换道概率为p,其车道保持的概率为1−p,而HDV以一定的概率随机选择不同的驾驶策略。其中,假设HDV减速让行的概率为q,加速通过的概率为1−q。为了量化CAV换道收益,引入时间收益T和安全收益S,用
| 表 1 CAV与HDV非合作博弈收益矩阵 Table 1 Payoff matrix for non-cooperative game between CAV and HDV |
由表1可知,CAV期望收益为
| $\begin{split} {{E}}_{{{\rm{CAV}}}}{(}{p}{,}{q}) =\;&{pq}{\varphi T}+{p}{(1}{-q}{) }{(}-{\varphi T}- \omega S{) }-\\& {(1-}{p}{) }{q}{\varphi T}{-(1-}{p}{) }{(1}{-q}{) }{\varphi T} \end{split} $ | (1) |
考虑目标车道前后车辆与换道CAV车道纵向距离,安全收益Si(t) 在t时刻被定义为第i辆换道CAV的安全收益函数。这一函数可以通过换道CAV与目标车道前后车辆的实时距离和安全距离之差的总和构成,表示为
| $ {{S}}_{{i}}{(}{t}{) }={{D}}_{{i}}^{{{\rm{L}}}}{(}{t}{) }-{{D}}_{{i}{,{\rm{min}}}}^{{{\rm{L}}}}{(}{t}{) }+{{D}}_{{i}}^{{{\rm{F}}}}{(}{t}{) }-{{}{D}}_{{i}{,{\rm{min}}}}^{{{\rm{F}}}}{(}{t}{) } $ | (2) |
式(2)中,如图2所示,以单侧换道为例,

|
图 2 换道CAV与目标车道前后车辆的实时距离与安全距离 Figure 2 Real-time distance and safety distance between lane-changing CAV and vehicles in target lane |
时间收益T定义为Ti(t) ,为t时刻第i辆换道CAV的时间收益函数,与换道CAV从当前速度vi(t) 到期望速度vi,req(t) 的响应时间
| $\widetilde T(t) = \left\{ {\begin{array}{*{20}{l}} \begin{array}{l} {\Delta t,}\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\; D_i^{\rm{L}}(t) \ge D_{i,\min }^{\rm{L}}(t) 且D_i^{\rm{F}}(t) \ge D_{i,\min }^{\rm{F}}(t) \end{array}\\ {\max \left\{ {\Delta t,\dfrac{{{v_i}(t) - {v_{i,{\rm{req }}}}(t)}}{{{b_{\max }}}}} \right\},}\begin{array}{c} \;\;\;\;\;\;\;D_i^{\rm{L}}(t) < D_{i,\min }^{\rm{L}}(t)\\ \;\;\;且D_i^{\rm{F}}(t) \ge D_{i,\min }^{\rm{F}}(t) \end{array}\\ {\max \left\{ {\Delta t,\dfrac{{{v_{i,{\rm{req }}}}(t) - {v_i}(t)}}{{{a_{\max }}}}} \right\},}\begin{array}{c} \;\;\;\;\;\;\;D_i^{\rm{L}}(t) \ge D_{i,\min }^{\rm{L}}(t)\\ \;\;\;且D_i^{\rm{F}}(t) < D_{i,\min }^{\rm{F}}(t) \end{array}\\ {\infty ,}\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;{其他} \end{array}} \right. $ | (3) |
式中:
t时刻第i辆换道CAV与目标车道前后车辆的安全距离
| $\left\{ {\begin{array}{*{20}{l}} {D_{i,\min }^{\rm{L}}(t) = \dfrac{{v_i^2(t)}}{{2{b_{\max }}}} + {v_i}(t) \cdot {t_i} + g_{\min }^i - \dfrac{{{{\left[ {v_i^{\rm{L}}(t)} \right]}^2}}}{{2b_{i,\max }^{\rm{L}}}}}\\ {D_{i,\min }^{\rm{F}}(t) = \dfrac{{{{\left[ {v_i^{\rm{F}}(t)} \right]}^2}}}{{2b_{i,\max }^{\rm{F}}}} + v_i^{\rm{F}}(t) \cdot t_i^{\rm{F}} + g_{i,\min }^{\rm{F}} - \dfrac{{v_i^2(t)}}{{2{b_{\max }}}}}\\ {{v_{i,{\rm{req}}}}(t) = {b_{\max }} \left[ { - {t_i} + \sqrt {t_i^2 - \dfrac{2}{{{b_{\max }}}} \left( {g_{\min }^i - \dfrac{{{{\left[ {v_i^{\rm{L}}(t)} \right]}^2}}}{{2b_{i,\max }^L}} - D_i^{\rm{L}}(t)} \right)} } \;\right]} \end{array}} \right. $ | (4) |
在式(4) 中,
假设在每组领航CAVs中t时刻第i辆CAV执行换道(即p=1)时,与之博弈的HDV减速让行或加速行驶的概率q = 0.5[19]。由式(1) 可得换道CAV收益为
| $E_i^{\mathrm{CAV}}(t)=E_i^{\mathrm{CAV}}(1,0.5, t)=\varphi T_i(t)+\frac{1}{2} \omega S_i(t) $ | (5) |
在每组领航CAVs中,在1.2节数学优化算法结果的基础上,根据式(6)协同更新博弈换道的CAVs的目标车道,实现决策换道机制。例如,在图1的情况1中,初始目标车道为[(0, 0) , (1, 1) , (2, 2) ]。假设根据式(6)计算得I=2,即车辆2需向右换道至目标车道1,与目标车道冲突的车辆1互换,则更新后的结果为[(0, 0) , (1, 2) , (2, 1) ]。
| $I=\operatorname{argmax}_i\left\{E_i^{\mathrm{CAV}} \mid E_i^{\mathrm{CAV}} > 0\right\} $ | (6) |
式中:I为需要换道的车辆编号。
若在某个时刻t,
本文选择SUMO(Simulation of Urban MObility) 作为仿真工具,该开源微观仿真软件可以实现HDVs和CAVs混合交通,并提供基于Python语言的在线交互接口TraCI(Traffic Control Interface) 以支持用户的二次开发。为了模拟混合交通环境,实验仿真参考文献[20-21],设置HDVs和CAVs的跟驰模型,具体参数如表2所示。此外,实验中所有车辆均使用SUMO默认的LC2013换道模型。实验环境配置为AMDr7-5800@3.40 GHz处理器,32 G内存,Windows操作系统,Python 3.9 + SUMO 1.14.1实验平台。
| 表 2 不同车辆类型的参数值 Table 2 Parameter values for different vehicle types |
实验场景以2 km的单向3车道高速路为例。依据我国《公路路线设计规范》(JTG D20—2017)在时速80 km/h下二级服务水平的最大服务交通量为1 100 pcu/(h·ln),其中,pcu为标准车的当量数。因此,对HDVs和CAVs的混合交通量从2 000 pcu/h到4 000 pcu/h的不同交通需求进行仿真实验。参考文献[22-23]的研究结果,表明30%的CAVs渗透率能有效提高交通效率,因此本文设置混合交通量的CAVs渗透率为30%。仿真的时长为3 600 s,仿真步长
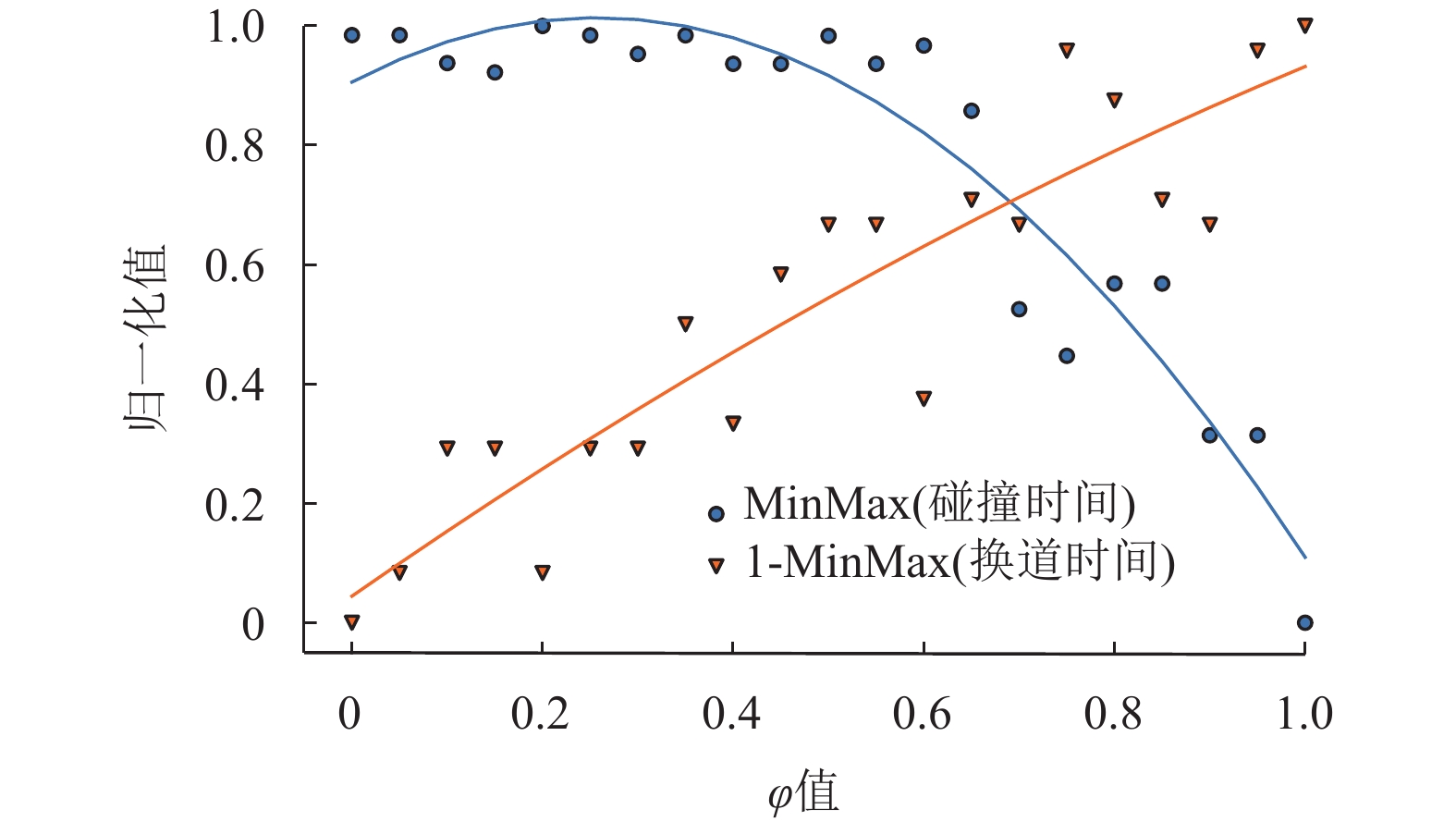
为了评估CAVs换道行为的效率和安全性,并确认最佳权重参数
如图3所示,1-MinMax(换道时间)随
|
图 3 不同 |
本文将文献[10]所用的换道规则(以下简称为依次换道)和文献[11]所提的优化方法(以下简称为优化换道)作为基准模型,与本文所提的方法(以下简称为博弈换道)作对比。为了确保实验结果的可靠性,每种策略均执行10次仿真实验,取其结果的平均值进行分析。
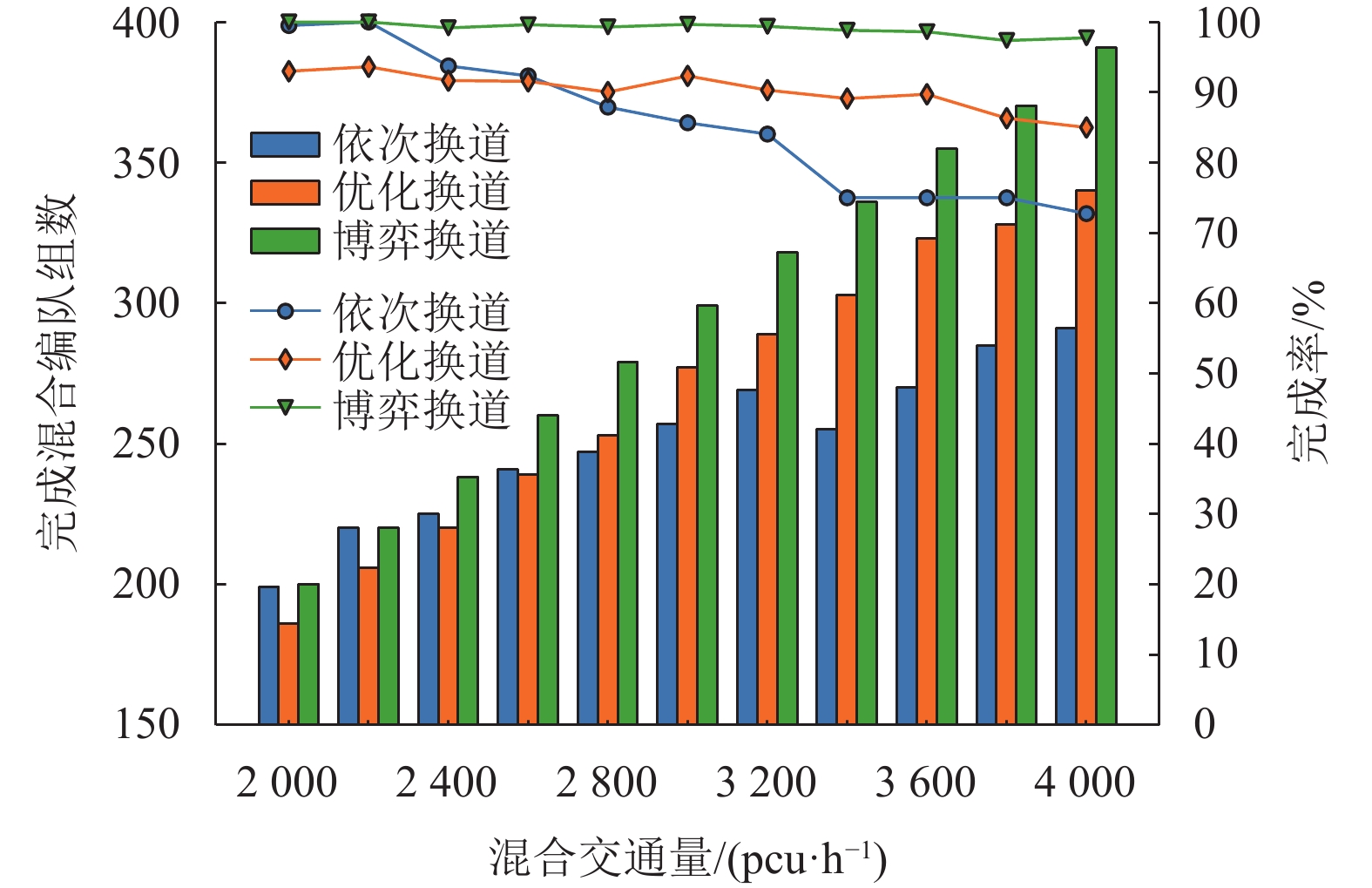
假设HDVs和CAVs的混合交通量为F。在仿真1 h中,以每3辆CAVs为一组,因此依次换道和博弈换道策略都需要完成混合编队组数(即领航CAVs组数)为
|
图 4 混合交通量对完成混合编队组数及完成率的影响 Figure 4 The effect of mixed traffic volume on the number and completion rate of mixed formation groups |
具体而言,随着混合交通量从2 000 pcu/h增加至4 000 pcu/h(每次增加200 pcu),优化换道和博弈换道策略的完成混合编队组数稳步上升,而依次换道策略的完成混合编队组数变化出现振荡,尤其在混合交通量为3 400 pcu/h时。然而,当混合交通量低于2 200 pcu/h时,依次换道和博弈换道策略的效果相差无几,而优化换道策略的效果差于依次换道策略。同时,相比于完成率呈现明显下降趋势的依次换道策略,优化换道策略的完成率下降至85%,而博弈换道策略的完成率都能保持在97%以上。这表明博弈换道策略能够更好地应对混合交通环境中HDVs非合作行为的干扰,使得领航CAVs高效换道,与跟随的HDVs形成多车道分布的混合编队。
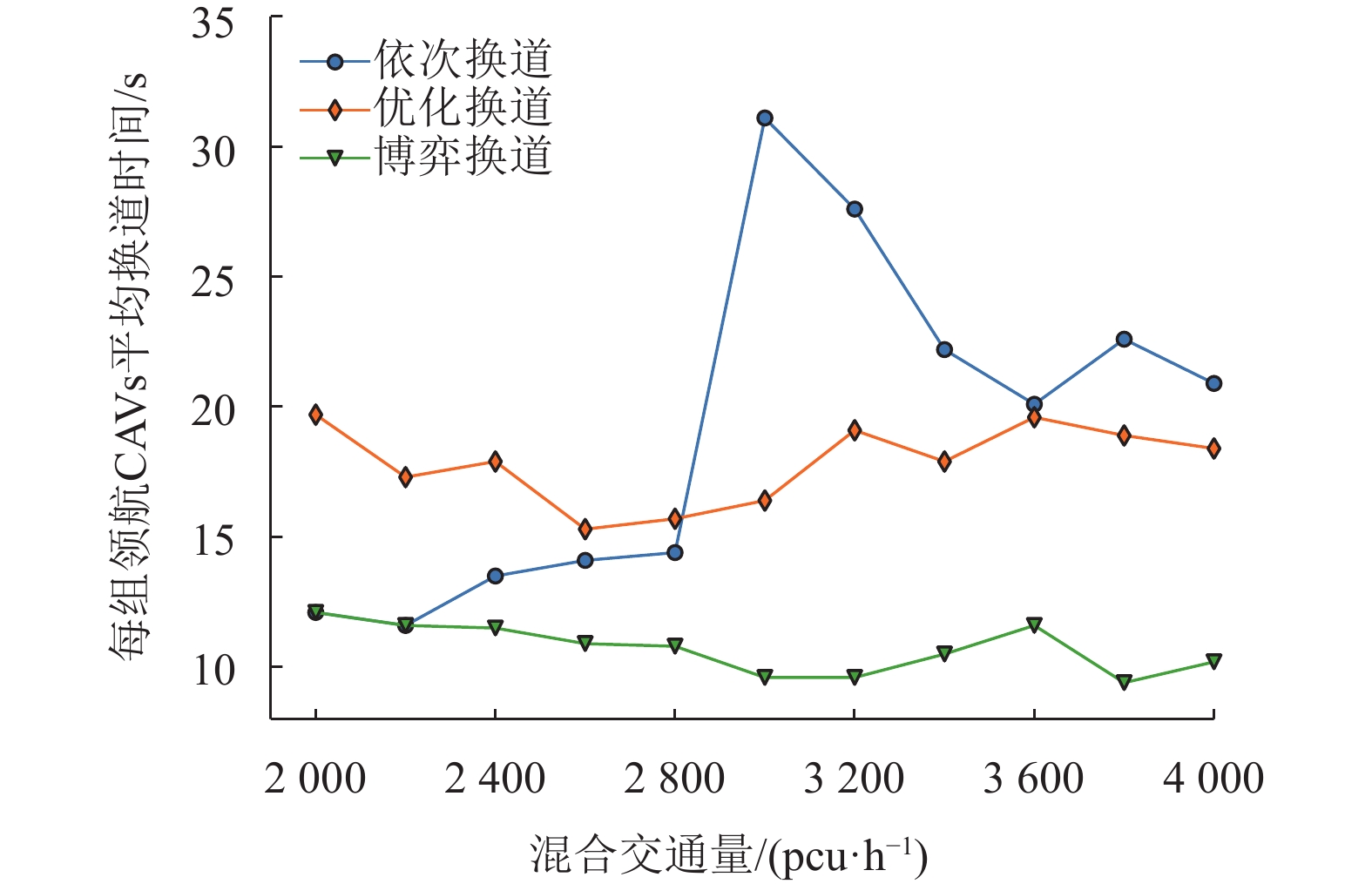
同时,实验进一步统计每组完成混合编队的领航CAVs换道时间,即每组第1辆CAV开始换道与第3辆CAV完成换道的时间间隔。图5展示了混合交通量对每组领航CAVs平均换道时间的影响。与依次换道和优化换道策略相比,博弈换道策略在换道时间方面也表现出显著的效果。随着混合交通量的增加,30%渗透率的CAVs车辆数也相应增加,意味着每组第1辆和第3辆CAVs到达编队区域的时间间隔更短。受此影响,博弈换道策略的每组领航CAVs平均换道时间从12.1 s降低至约9.8 s,说明该策略在不同混合交通量的条件下仍保持较高的换道效率和稳定性能。
|
图 5 混合交通量对每组领航CAVs平均换道时间的影响 Figure 5 The effect of mixed traffic volume on the average lane-changing time for each group of leading CAVs |
相比之下,优化换道策略的平均换道时间较长,维持在15 ~ 20 s之间。而依次换道策略的每组领航CAVs平均换道时间差距从2 200 pcu/h开始逐渐拉大,尤其在交通量为3 000 pcu/h时,平均换道时间激增至31.1 s,是博弈换道策略的3.2倍,涨幅接近116%。由此判定,在2 km场景下依次换道策略的每组领航CAVs平均换道时间的极大值所对应的交通量在3 000 pcu/h左右。随着混合交通量持续增加,使得原本在低密度车流能换道的CAVs需要更长时间执行换道,因换道区域长度限制,导致这部分CAVs在未完成编队情况下驶离换道区域且未被纳入统计。因此,依次换道策略的平均换道时间呈现出先上升后下降的现象。总体而言,完成混合编队的每组3辆领航CAVs平均换道时间从依次换道和优化换道策略的19.11 s和17.87 s减少至博弈换道策略的10.71 s,减少了约44.0%和40.1%。
综上所述,相较于依次换道和优化换道策略,本文提出的博弈换道策略在确保车辆换道安全性的同时,不仅能有效提高混合编队的形成数量,而且能显著缩短领航CAVs在形成混合编队过程中的换道时间。
为了进一步验证本文提出的策略的有效性,统计仿真中领航CAVs的换道次数,如图6所示。3种换道策略的CAVs换道车辆数与换道次数成反比。从图6(d)可知,与依次换道策略相比,在不同混合交通量下,优化换道和博弈换道策略的领航CAVs平均换道次数明显减少。然而,博弈换道策略的平均换道次数略高于优化换道策略的平均换道次数。原因在于博弈换道策略为了更高的混合编队完成率,使得部分CAVs通过积极换道达到这一目标。
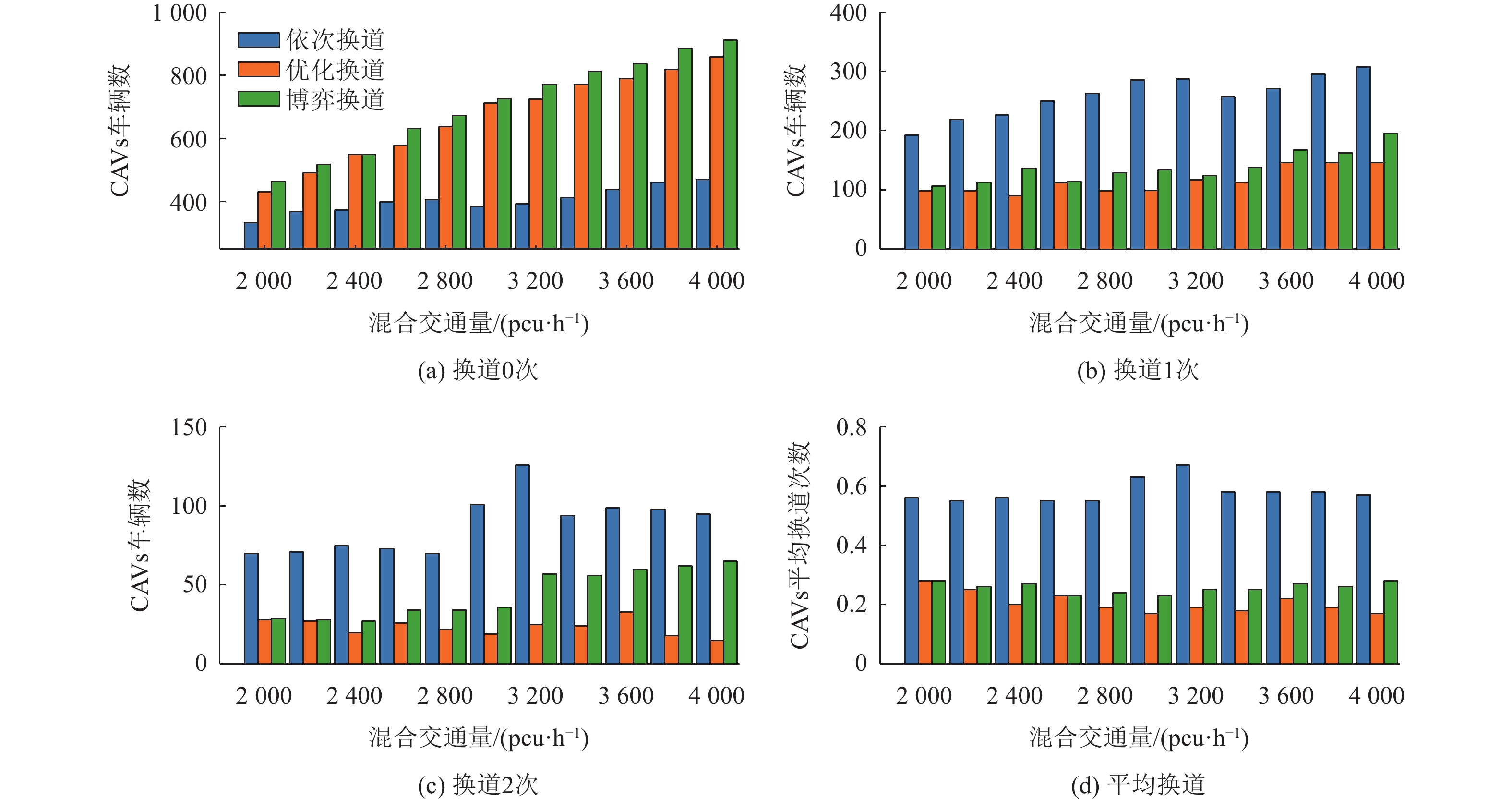
|
图 6 不同混合交通量下各换道策略的领航CAVs换道次数分布 Figure 6 Distribution of lane-changing frequencies for leading CAVs with different lane-changing strategies under various mixed traffic volumes |
由图6(a)和(b)可知,3种策略换道0次和1次的CAVs车辆数随着混合交通量增加而呈现上升趋势,而依次换道策略与其余策略之间的差距也随之增大。相比之下,图6(c)中依次换道策略换道2次的CAVs车辆数波动较大。当混合交通量为3 000 pcu/h和3 200 pcu/h时,依次换道策略换道2次的车辆数较高,这也解释该策略平均换道时间激增的现象。
总体而言,已知在博弈换道策略完成率远大于依次换道和优化换道策略完成率的情况下,总体领航CAVs平均换道次数仍能从依次换道策略的0.58降低至0.27,约减少53.4%,与优化换道策略平均换道次数相差约0.05。以上证实本文提出的博弈换道策略在提高混合编队数量的同时,能在一定程度上减少混合编队形成过程中的换道次数,从而降低碰撞风险。
3 结语本文提出数学优化与博弈论相结合的换道决策机制,并综合考虑换道效率和安全性,建立基于博弈论的换道决策模型。通过仿真实验证实,相比于依次换道和优化换道策略,本文提出的博弈换道策略在不同混合交通量下都能保持较高的混合编队完成率,同时缩短领航CAVs的换道时间和保持较低的换道次数,有效保障行车安全,降低碰撞风险。这为自动驾驶技术逐步应用的过渡场景提供了可行的解决方案。下一步研究方向包括验证博弈换道策略在更加复杂的道路环境中的适用性,考虑不同类型自动驾驶车辆的协同性,以更全面地推动智能交通系统的演进。
| [1] |
GONG S, DU L. Cooperative platoon control for a mixed traffic flow including human drive vehicles and connected and autonomous vehicles[J].
Transportation Research Part B: Methodological, 2018, 116: 25-61.
DOI: 10.1016/j.trb.2018.07.005. |
| [2] |
MAHBUB A M I, LE V A, MALIKOPOULOS A A. A safety-prioritized receding horizon control framework for platoon formation in a mixed traffic environment[J].
Automatica, 2023, 155: 111115.
DOI: 10.1016/j.automatica.2023.111115. |
| [3] |
ORKI O, AROGETI S. Control of mixed platoons consist of automated and manual vehicles[C]//2019 IEEE International Conference on Connected Vehicles and Expo (ICCVE) . Graz: IEEE, 2019: 1-6.
|
| [4] |
KATO S, KUNIBE M, YAMAZAKI R, et al. Group formation for cooperative highway merging considering undetected vehicles in mixed traffic[C]//2021 IEEE Vehicular Networking Conference (VNC). Ulm: IEEE, 2021: 68-71.
|
| [5] |
HUA Z, ZHAN J, ZHANG L. Decentralized tube model predictive control for arbitrarily mixed vehicle platoons with HDV uncertainties[C]//2022 41st Chinese Control Conference (CCC) . Hefei: IEEE, 2022: 5429-5434.
|
| [6] |
MAHBUB A M I, MALIKOPOULOS A A. A platoon formation framework in a mixed traffic environment[J].
IEEE Control Systems Letters, 2022, 6: 1370-1375.
DOI: 10.1109/LCSYS.2021.3092188. |
| [7] |
王树凤, 王世皓, 王新凯. 基于改进跟驰模型的混合车辆编队研究[J].
公路, 2023, 68(6): 289-297.
WANG S F, WANG S H, WANG X K. Research on hybrid vehicle formation based on improved car-following[J]. Highway, 2023, 68(6): 289-297. |
| [8] |
YAO Z, MA Y, REN T, et al. Impact of the heterogeneity and platoon size of connected vehicles on the capacity of mixed traffic flow[J].
Applied Mathematical Modelling, 2024, 125: 367-389.
DOI: 10.1016/j.apm.2023.09.001. |
| [9] |
崔冰艳, 李贺, 崔哲, 等. 智能网联汽车换道决策安全性研究综述[J].
交通信息与安全, 2023, 41(4): 1-13.
CUI B Y, LI H, CUI Z, et al. A review of safety studies on lane change decision-makings for connected automated vehicles[J]. Journal of Transport Information and Safety, 2023, 41(4): 1-13. DOI: 10.3963/j.jssn.1674-4861.2023.04.001. |
| [10] |
赵杭, 赵敏, 孙棣华, 等. 面向快速路交通瓶颈的混合交通群体节流控制策略[J].
交通运输工程学报, 2022, 22(3): 162-173.
ZHAO H, ZHAO M, SUN D H, et al. Mixed traffic group throttling control strategy for traffic bottleneck of expressway[J]. Journal of Traffic and Transportation Engineering, 2022, 22(3): 162-173. |
| [11] |
胡祥旺, 倪颖, 孙剑. 车联网环境下匝道汇入区瓶颈换道优化[J].
同济大学学报(自然科学版), 2023, 51(9): 1424-1432.
HU X W, NI Y, SUN J. Freeway merging area lane changing advisory optimization under connected vehicles environment[J]. Journal of Tongji University (Natural Science), 2023, 51(9): 1424-1432. DOI: 10.11908/j.issn.0253-374x.22148. |
| [12] |
GONG B, XU Z, WEI R, et al. Reinforcement learning-based lane change decision for CAVs in mixed traffic flow under low visibility conditions[J].
Mathematics, 2023, 11(6): 1556.
DOI: 10.3390/math11061556. |
| [13] |
WANG Z, HUANG H, TANG J, et al. A deep reinforcement learning-based approach for autonomous lane-changing velocity control in mixed flow of vehicle group level[J].
Expert Systems with Applications, 2024, 238: 122158.
DOI: 10.1016/j.eswa.2023.122158. |
| [14] |
JI A, LEVINSON D. A review of game theory models of lane changing[J].
Transportmetrica A: Transport Science, 2020, 16(3): 1628-1647.
DOI: 10.1080/23249935.2020.1770368. |
| [15] |
陈华. 基于博弈论的自动驾驶车辆协同换道分析[EB/OL]. 武汉理工大学学报(交通科学与工程版) . (2023-07-04) [2024-03-09]. http://kns.cnki.net/kcms/detail/42.1824.U.20230704.1126.032.html.
CHEN H. Cooperative lane changing analysis of autonomous vehicles based on game theory [EB/OL]. Journal of Wuhan University of Technology (Transportation Science & Engineering) . (2023-07-04) [2024-03-09]. http://kns.cnki.net/kcms/detail/42.1824.U.20230704.1126.032.html. |
| [16] |
ZHENG Y, DING W, RAN B, et al. Coordinated decisions of discretionary lane change between connected and automated vehicles on freeways: a game theory-based lane change strategy[J].
IET Intelligent Transport Systems, 2020, 14(13): 1864-1870.
DOI: 10.1049/iet-its.2020.0146. |
| [17] |
QU D, ZHANG K, SONG H, et al. Analysis and modeling of lane-changing game strategy for autonomous driving vehicles[J].
IEEE Access, 2022, 10: 69531-69542.
DOI: 10.1109/ACCESS.2022.3187431. |
| [18] |
FU M, LI S, GUO M, et al. Cooperative decision-making of multiple autonomous vehicles in a connected mixed traffic environment: a coalition game-based model[J].
Transportation Research Part C: Emerging Technologies, 2023, 157: 104415.
DOI: 10.1016/j.trc.2023.104415. |
| [19] |
GUERIAU M, DUSPARIC I. Quantifying the impact of connected and autonomous vehicles on traffic efficiency and safety in mixed traffic[C]//2020 IEEE 23rd International Conference on Intelligent Transportation Systems (ITSC) . New York: IEEE, 2020: 1-8.
|
| [20] |
SONG L, FAN W (David) , LIU P. Exploring the effects of connected and automated vehicles at fixed and actuated signalized intersections with different market penetration rates[J].
Transportation Planning and Technology, 2021, 44(6): 577-593.
DOI: 10.1080/03081060.2021.1943129. |
| [21] |
YAO Z, WANG Y, LIU B, et al. Fuel consumption and transportation emissions evaluation of mixed traffic flow with connected automated vehicles and human-driven vehicles on expressway[J].
Energy, 2021, 230: 120766.
DOI: 10.1016/j.energy.2021.120766. |
| [22] |
YE L, YAMAMOTO T. Modeling connected and autonomous vehicles in heterogeneous traffic flow[J].
Physica A: Statistical Mechanics and its Applications, 2018, 490: 269-277.
DOI: 10.1016/j.physa.2017.08.015. |
| [23] |
DING J, PENG H, ZHANG Y, et al. Penetration effect of connected and automated vehicles on cooperative on-ramp merging[J].
IET Intelligent Transport Systems, 2020, 14(1): 56-64.
DOI: 10.1049/iet-its.2019.0488. |
 2024, Vol. 41
2024, Vol. 41

