2. 广东工业大学 高性能工具全国重点实验室, 广东 广州 510006;
3. 利物浦大学 电气与电子工程学院, 利物浦 L69 3GJ
2. National Key Laboratory of High Performance Tools, Guangdong University of Technology, Guangzhou 510006, China;
3. Department of Electrical Engineering & Electronics, University of Liverpool, Liverpool L69 3GJ, The United Kingdom of Great Britain and Northern Ireland
随着科学技术的不断发展,在微纳加工、微机电系统封装、生物医学以及航空航天等领域中对高精度微位移定位技术需求与日俱增。其中,精密致动器是发展高精度微位移定位技术的核心机构。例如,半导体集成电路加工、微电子设备封胶、生物细胞的穿刺和航天器飞行姿态调整等都需要在微纳米数量级别上进行操作[1-4]。传统的致动器受限于实现原理以及结构设计等因素,已难以满足如此高精度的要求。
近年来,形状记忆材料、超磁致伸缩材料以及压电材料等智能材料陆续被研究人员发现并应用到致动器中[5-7]。其中,研究基于压电材料制作的致动器最为广泛。压电致动器利用压电材料的逆效应输出纳米级别的位移精度,并且具有体积小、响应快、驱动负载能力强、可多自由度输出以及不受电磁干扰等优点,在高精度微位移定位致动机构中得到大量应用。虽然压电致动器具有诸多的优点,但是压电致动器所使用的压电材料在外加电场的作用下会产生非线性特征,不仅对压电致动器的性能带来不良影响,甚至导致系统的不稳定。因此,研究压电致动器的非线性特征及其控制策略对于高精度微位移定位技术的发展具有重要的研究意义。
当前,国内外学者致力于研究压电致动器中迟滞和蠕变非线性特征,主要的研究方法是通过建立不同的数学模型对压电致动器非线性特征进行精确的描述,并且结合不同的控制策略进行补偿。
本文对压电致动器的非线性特征进行概述,重点回顾了迟滞模型和蠕变模型的发展历程,介绍了压电致动器的控制补偿策略及研究进展,最后对压电致动器控制技术的未来发展方向进行讨论与展望。
1 压电致动器非线性特征概述压电致动器中的陶瓷材料在外加电场的极化作用下,陶瓷材料内部的电畴方向与外加电场的方向趋近。由于电畴自行恢复的能力较弱,在外加电场停止工作后,大部分电畴却无法在短时间内恢复到原来的方向上,这种现象称为剩余极化,剩余极化是造成压电致动器存在非线性特征的根本原因[8]。根据压电致动器非线性特征的具体表现,分为迟滞非线性以及蠕变非线性。
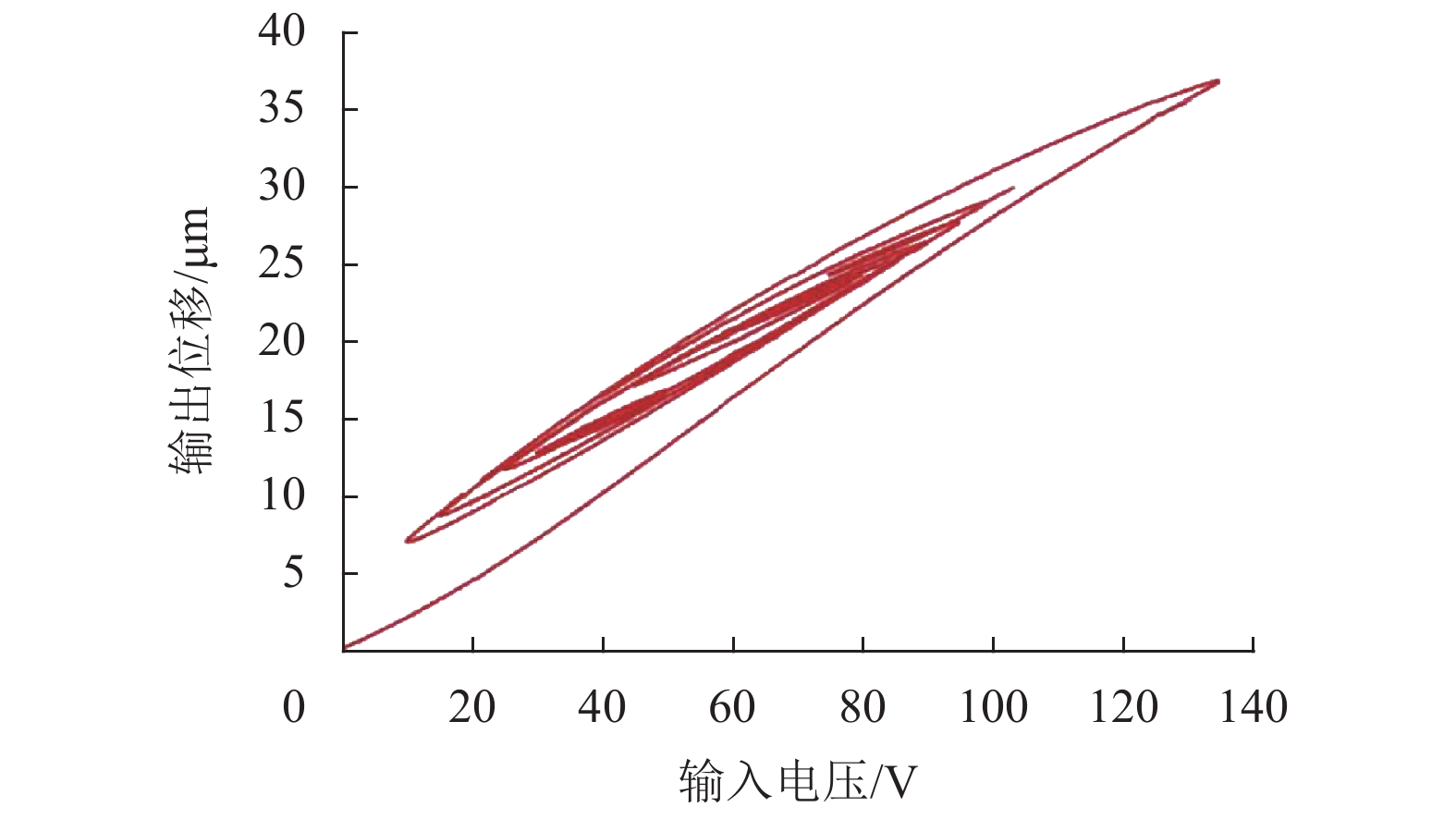
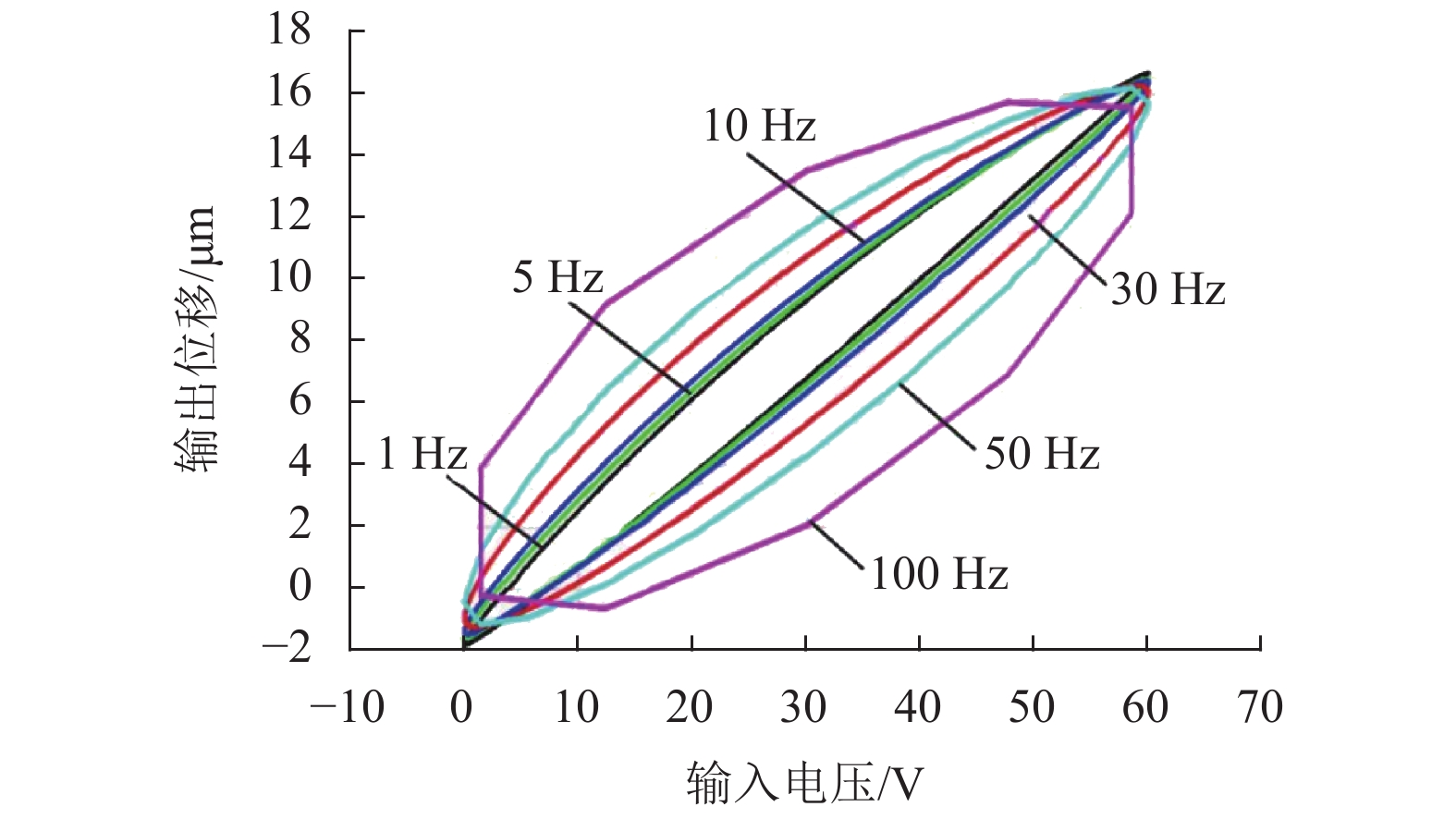
1.1 迟滞非线性迟滞非线性是指压电致动器的输入电压与输出位移呈现出复杂的非线性关系。根据是否考虑输入频率,迟滞特性可分为静态频率无关迟滞特性和动态频率相关迟滞特性[9]。静态频率无关迟滞特性侧重于研究低频电压输入与位移输出之间的关系。图1所示的静态频率无关迟滞特性使压电致动器的输出具有历史记忆特性:既与输入信号的当前值有关,又与前一时刻的系统状态相关。另外,当不参考历史系统状态时,相同的输入信号将对应多个输出值,表现出多值映射特性。图2反映了压电致动器的动态频率相关迟滞特性,即输出位移不仅依赖于输入信号的幅值,还与输入信号的频率有关,随着输入信号频率的增加,迟滞环曲线有明显的变化。
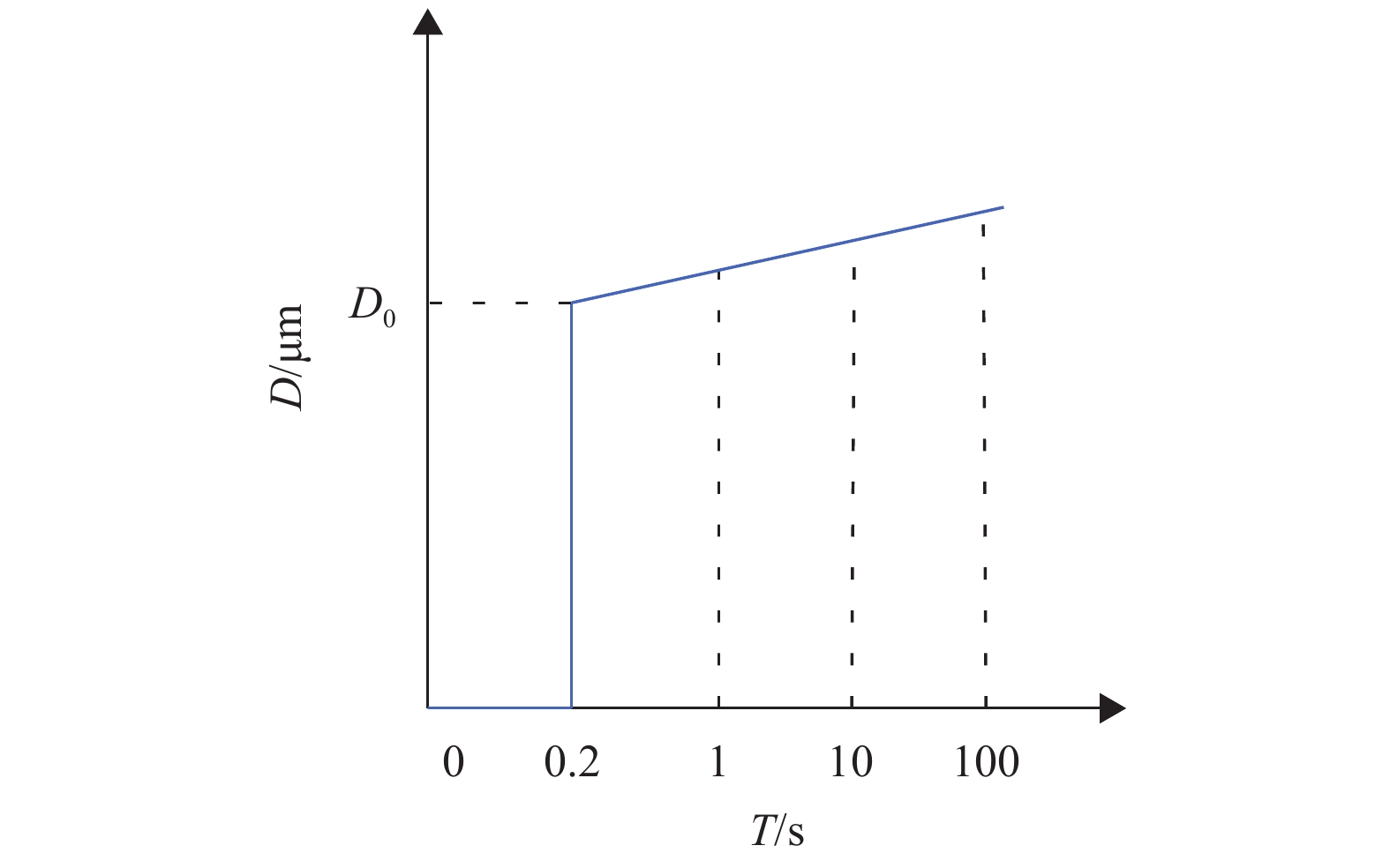
1.2 蠕变非线性压电致动器输出的位移,随着时间的延长仍然缓慢增加,称为蠕变非线性[10]。如图3所示,蠕变现象在外加电场刚接入时,压电致动器快速响应并上升到D0值,但并未结束进程。然后,在恒定的外加电场作用下,压电致动器输出的位移仍然在缓慢增加,且在较长时间后输出位移值才达到稳定状态。因此,蠕变非线性会影响压电致动器输出位移的绝对精度。
|
图 3 蠕变非线性特征 Figure 3 Characteristic of creep nonlinear |
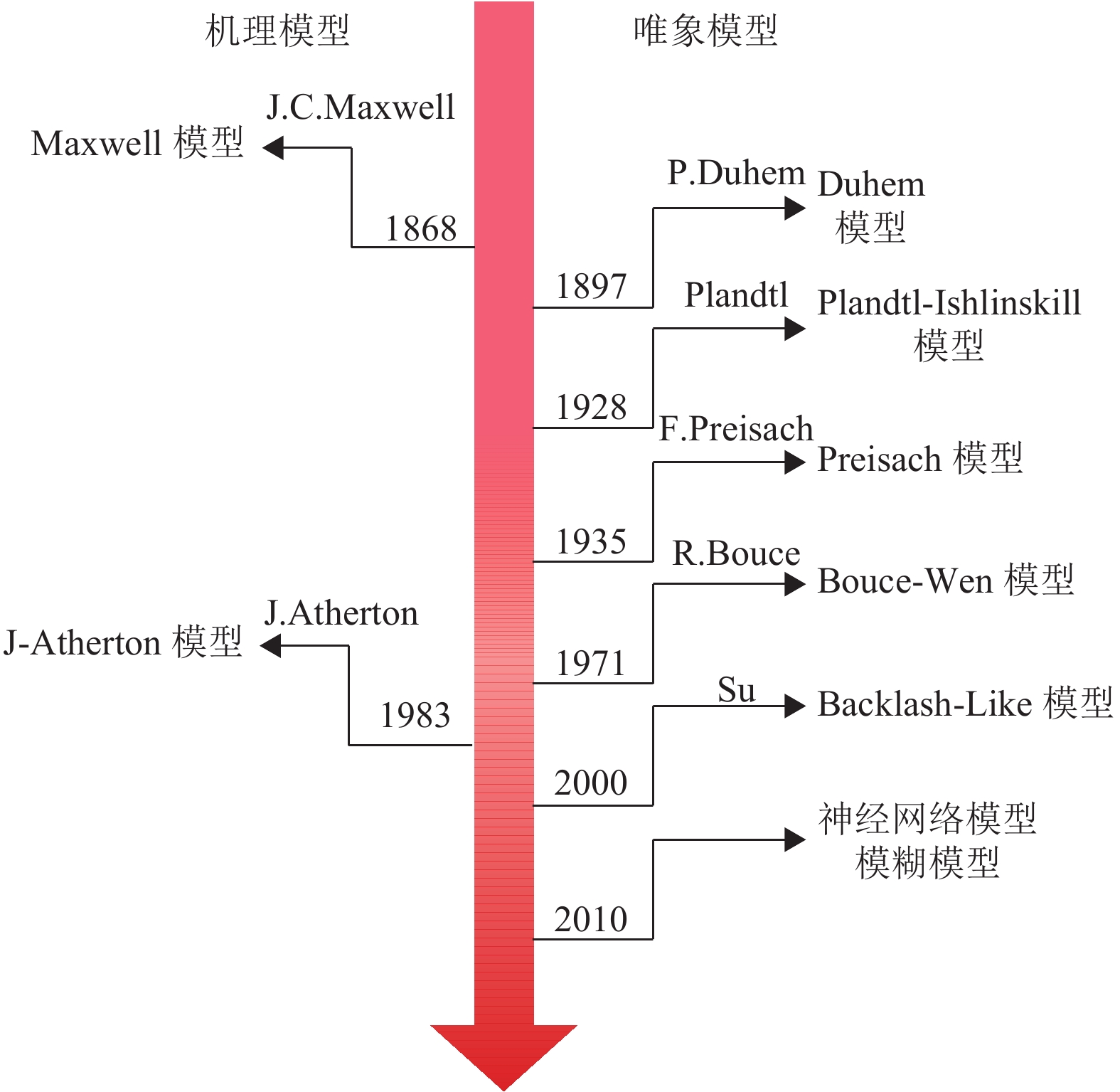
从1868年至今,许多学者都提出了具有重要意义的迟滞模型,如图4所示。于志亮[11]根据迟滞模型建立本质的不同,将其分为机理和唯象迟滞模型两大类。机理模型是通过应力−应变或能量−位移等物理关系来推导迟滞模型,唯象模型直接采用数学模型来表征迟滞现象。唯象模型凭借建模精度高、灵活性强的优点,成为目前研究迟滞模型最常用的建模手段。此外,随着计算机技术的发展,部分学者利用计算机强大的计算能力研究迟滞模型,这是未来研究迟滞模型的热点方向。
|
图 4 迟滞模型的发展历程 Figure 4 Development of the hysteresis model |
机理迟滞模型是基于材料所表现的机理性质推导的迟滞模型[12],常见有Maxwell模型和Jiles-Atheron模型两类。
(1) Maxwell模型:经典的Maxwell模型是由多个弹性单元组合而成,其中每个弹性单元由一个无质量的滑块与一个无质量的线性弹簧组成[13]。该模型表达式如式(1)所示。
若
| $ F_{i}=k_{i}\left(x-x_{i}\right) $ | (1) |
否则,滑块处于滑动状态,则有
| $ \left\{\begin{array}{l} F_{i}=\operatorname{sgn}\left(x-x_{i}\right) \cdot f_{{i}} \\ x_{i}=x-\dfrac{f_{i}}{k_{i}} \operatorname{sgn}\left(x-x_{i}\right) \cdot f_{\bar{i}} \end{array}\right. $ | (2) |
式中:x为位移输入值,Fi为输出力值,k为弹簧刚度值,fi为最大静摩擦力值,xi为第i个弹性单元滑块初始位置。
由此可见,Maxwell模型不考虑输入信号的频率或速率,属于静态率无关迟滞模型。单个弹性单元无法建立精确的迟滞模型,可通过增加弹性滑动单元的数目,并且相互并联的方式使得输出的迟滞曲线趋向平滑,提高模型的精度,同时模型的阶数不会增加。此时,Maxwell模型的公式可以表示为
| $ F=\sum_{i=1}^{n} F_{i} $ | (3) |
但是,随着弹性单元数目的增加,迟滞模型的计算量也随之增大,使得参数识别过程更加复杂。为此,Liu等[14]提出一种分布式参数麦克斯韦滑移(Distributed Parameter Maxwell-slip,DPMS)模型,弹性单元的属性由饱和变形函数和刚度函数描述,仅需几个参数即可控制DPMS模型产生的滞后现象。DPMS模型与传统的模型相比,迟滞非线性下降了81.5%。另外基于Maxwell模型的混合模型都可以有效降低迟滞非线性,Xie等[15]提出一种Maxwell-slip与最小二乘支持向量机混合模型,通过实验结果表明,该模型的逆模型可以使建模误差小于0.66%,补偿系统的跟踪误差小于1.2%。
(2) Jile-Atherton模型:Jile-Atherton模型简称J-A模型,是一种基于铁磁材料特性开发的迟滞模型[16]。J-A模型通过可逆磁化Mrev与不可逆磁化Mirr两个分量描述总磁化强度M,表达式为
| $ M=M_{\mathrm{rev}}+M_{\mathrm{irr}} $ | (4) |
J-A模型最大的优点是能够清楚地反映出材料的物理性质,但是其建立迟滞模型的形式较为复杂,且具有较强的独立性,导致普遍性较差。
Savoie等[17]对J-A模型的参数获取方式进行了研究,通过随机选择产生迟滞曲线的参数对J-A模型进行蒙特卡罗实验,其产生的数据显示了参数空间的趋势,可用于进一步缩小参数选择的空间,对压电致动器的迟滞特性进行精确建模。Zhang等[18]提出了一种基于标量静态滞后J-A模型的新方法,该方法利用了卷积法求解,大大减少了数值问题,且该方法可以在一个非常大的频率带宽中获得正确的仿真结果。
2.2 唯象迟滞模型唯象迟滞模型是基于数学原理推导的迟滞模型,可分为微分方程迟滞模型、算子迟滞模型和其他模型[19]。
1) 微分方程迟滞模型
微分方程迟滞模型是通过构建微分方程来描述迟滞特性[20]。微分方程迟滞模型结构紧凑,便于结合动力学模型来进行控制器设计。常见的微分方程迟滞模型有Duhem模型、Backlash-Like模以及Bouc-Wen模型。
(1) Duhem模型:Duhem模型于1897年由Duhem提出[21]。微分表达式为
| $ \dot{y}=\alpha|\dot{u}|[f(u) -y]+\dot{u} g(u) $ | (5) |
式中:y和u分别为输出位移和输入电压信号,α为模型参数,f(u)和g(u)为输入电压的函数。
从表达式可以看出,Duhem模型的输出与输入u的导数密切相关,这表明了该模型属于动态率相关模型。
在Duhem模型的实际应用中,f(u)和g(u)必须满足特定条件,因此选取合适的函数具有比较大的难度,这导致该模型应用时受到一定限制,且经典Duhem模型需要利用Weierstrass第一定理分别对分段函数f(u)和g(u)进行多项式逼近,过程复杂且精度较低。为此,孙涛等[22]将传统Duhem模型分为上下2个半环,利用样条曲线和神经网络对模型进行参数识别,得到精确的Duhem迟滞模型及其逆模型,并且结合PID控制器组成复合控制,实验结果表明,压电致动器输出平均绝对误差为0.053 9 μm,有效提高了定位精度。贺一丹等[23]提出了一种基于单输入输出关系的改进Duhem模型,利用差分进化算法识别模型参数。实验结果表明,在1,20,60,100 Hz的输入频率下,改进Duhem模型建模误差相比于传统Duhem模型分别降低了46%、50%、50%、47%,证明了该模型的有效性。针对Duhem模型求逆计算十分复杂的问题,高源蓬等[24]提出了对Duhem模型中的微分方程进行变换,直接建立Duhem非对称逆迟滞模型作为迟滞前馈补偿器的方法,并利用了免疫差分进行算法辨识模型参数,该模型可对频率为0.5 Hz的压电非对称曲线进行精确拟合,拟合均方根误差为0.635 9 V,相对误差为0.79%。
(2) Backlash-Like模型:Su等[25]在2000年提出Backlash-Like模型,这是在Duhem模型的基础上得到的动态模型。该模型表达式为
| $ \dot{y}=\alpha|\dot{u}|[\beta u-y]+\gamma \dot{u} $ | (6) |
相比于Duhem模型,Backlash-Like模型的形式更加简单明了,且该模型可把迟滞非线性描述为有界干扰,十分适合迟滞补偿的鲁棒控制器设计条件[26]。
杨晓京等[27]提出了一种基于Backlash-Like的Hammerstein率相关迟滞模型,采用改进的Backlash-Like分段辨识模型对压电微定位台的静态非线性特征进行描述,并结合了ARX(Auto Regressive eXogenous)模型,对压电微定位台率相关动态特性进行描述。同时提出了一种具有交叉变异策略的改进型粒子群算法对模型进行参数辨识。实验数据表明,压电微定位台在输入电压60 V,频率为30,60,90 Hz单频信号的条件下,与Backlash-Like分段辨识模型的相比,Hammerstein率相关迟滞模型的均方根误差由0.393~0.701 μm下降到0.054~0.190 μm,相对误差由1.721%~3.087%下降到0.236%~0.831%,验证了新模型具有较好的频率泛化能力,并提高了压电微定位台的精度。Chen等[28]针对一类未知Backlash-Like迟滞和具有未知外部干扰的n阶非线性系统,提出了一种基于反推法的鲁棒自适应控制方法,该方法拥有很好的稳定性。Li等[29]针对现有的Backlash-Like模型主要集中描述单环迟滞效应,不能用于描述蝶形迟滞效应的问题,开发了一种扭曲机制,将单环间隙滞回模型转化为能够表示蝴蝶滞回的模型,且将分数阶表达式集成在模型中,提高了模型精度。
(3) Bouc-Wen模型:Bouc-Wen模型起初是由Bouc提出的物理模型,随后由Wen对其进行了完善和推广,改进后的模型受到推广运用[30]。该模型可以表示为
| $ \left\{\begin{array}{l} y(t) =k_{0}-x(t) +h(t) \\ \dot h(t) =A \dot x(t) -B \dot x(t) |h(t) |^{n}- C|\dot{x}(t) \| h(t) |^{n-1} h(t) \end{array}\right. $ | (7) |
式中:A、B、C、n为模型的参数,k为权重系数,x(t)和h(t)分别为线性分量以及滞后分量。
从式(7)中可以发现,输出位移y(t)与输入电压x(t)的导数有密切关系,说明Bouc-Wen模型为一个动态率相关模型。针对Bouc-Wen模型参数辨识复杂,无法准确地描述复杂的迟滞现象,而且其难以求得逆模型的问题,Wang等[31]用Bouc-Wen模型来描述压电致动器迟滞特性时,利用了最小二乘法辨识得到模型参数。Rakotondrabe等[32]首次提出级乘构造Bouc-Wen模型的逆模型,并建立了相应的补偿控制器。Zablotskaya[33]将模型的基本参数进行了详细的研究和分类,并根据研究提出了有效的参数范围。Aboura[34]研究了压电陶瓷驱动器的Bouc-wen迟滞回线与模型参数的关系。Hu等[35]引入一个新的输入函数来描述压电致动器的不对称迟滞,并将输入电压的频率引入到迟滞模型中。然后,利用差分进化算法对改进的Bouc-Wen模型参数进行辨识。Saleem等[36]提出了一种新的基于信号峰值和低谷误差的优化适应度函数,并利用该适应度函数和粒子群优化技术对Bouc-Wen模型参数进行估计,实验和仿真结果表明,这种选择的适应度函数在峰值和低谷提高了90%的性能。Minh等[37]提出了一种改进的Bouc-Wen模型,并与自适应控制技术相结合来控制PEA。与传统的控制方法相比,该方法有效地线性化了滞后非线性。
2) 算子类迟滞模型
算子类迟滞模型是通过对非线性算子加权叠加来对迟滞非线性进行描述,在与微分方程迟滞非线性模型的对比中,算子迟滞非线性模型能更加准确描述主环和次环的细节,且参数辨识简单,便于构造逆模型[38]。算子类迟滞模型可按照算子的差异,主要有Preisach模型、Prandtl-ishlinskii模型。
(1) Preisach模型:Preisach模型于1935年由Preisach F提出,最初用于对铁磁材料迟滞现象进行描述,因其具有广泛适用性,已逐步应用于压电系统迟滞模型建立方法中[39]。由于该模型输入信号不影响输出信号,因此该模型属于静态率无关迟滞模型。
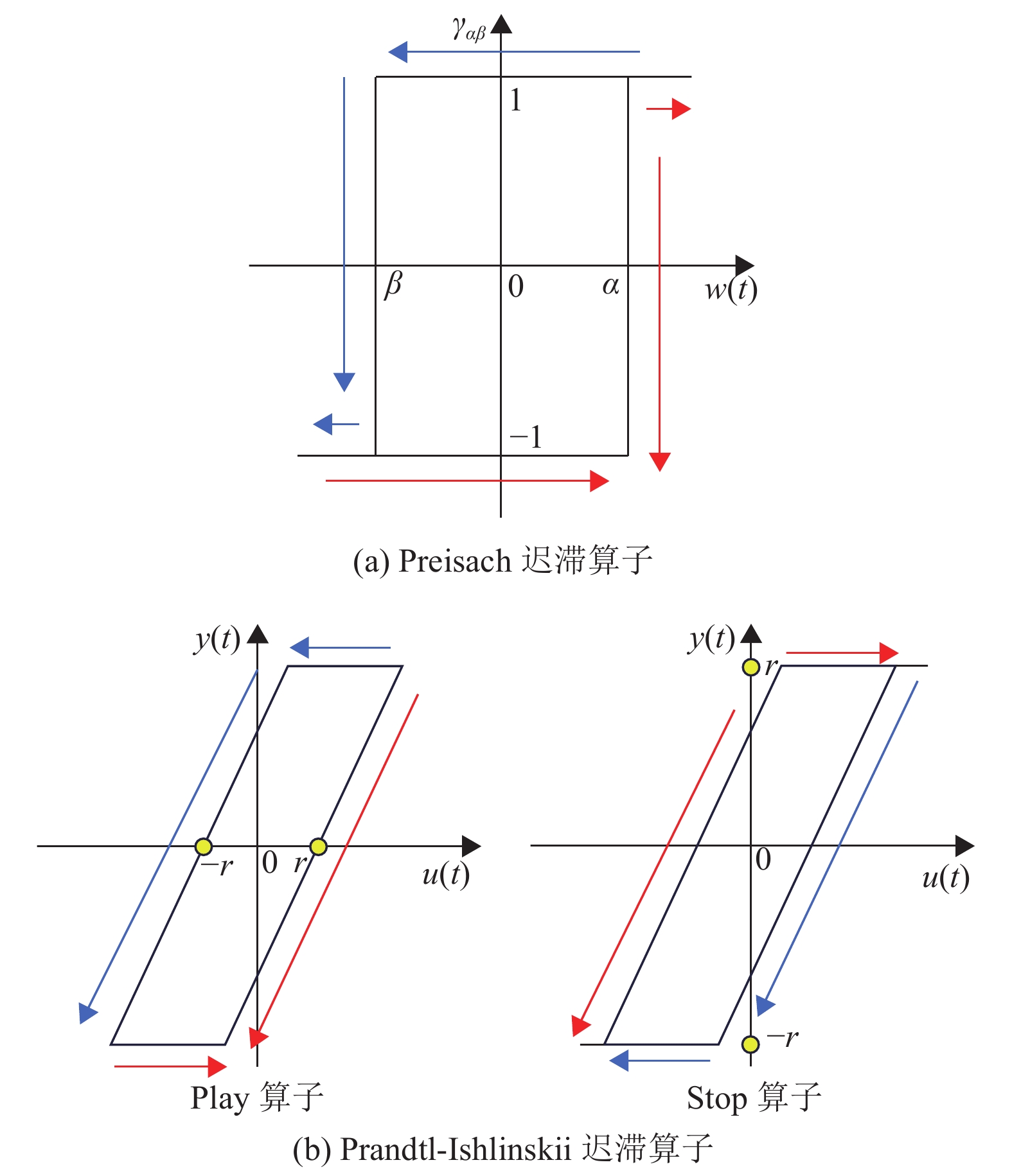
Preisach模型的基本单位为Relay算子[40]。如图5(a)所示,Relay算子在输入输出平面表示为一个矩形的迟滞环,有−1和1两种状态,表示一种开关切换特性。当输入电压值大于α时,Relay算子输出从−1上升到1;当输入电压值小于β时,Relay算子输出从1下降到−1。Relay算子的输出表达式为
|
图 5 算子模型示意图 Figure 5 Schematic diagram of the operator model |
| $ \gamma_{\alpha \beta }[w(t) ]=\left\{\begin{array}{ll} 1, & w(t) >\alpha \\ \theta, & \beta<w(t) <\alpha \\ -1, & w(t) <\beta \end{array}\right. $ | (8) |
该模型可通过若干个Relay算子的加权叠加描述压电致动器的迟滞非线性特征。经典的Preisach模型可用以下表达式表示:
| $ y(t) =\iint_{\alpha >\beta} \mu(\alpha, \beta) \gamma_{\alpha \beta}[w(t) ] \mathrm{d} \alpha \mathrm{d} \beta $ | (9) |
式中:w(t)和y(t)分别为输入与输出,α和β为开关阈值,且满足α>β。μ(α,β) 为密度函数,θ为满足θ∈{−1,1}的变量参数。
经典的Preisach模型具有次环一致特性,压电致动器迟滞特性不满足其特性。范青武等[41]提出一种改进型Preisach模型,推导出离散化计算方法,其数值实现采用三线性插值法。武毅男等[42]提出了一种基于Preisach模型的深度学习网络迟滞模型,提高了迟滞模型的精度与泛化能力。陈彬等[43]提出了一种基于R-L型分数阶导数的动态解析逆Preisach模型的方法,并验证了其有效性。
(2) Prandtl-Ishlinskii模型:Prandtl-Ishlinskii模型简称P-I模型,其用作描述弹塑性变形现象[44]。P-I模型与Preisach模型类似,区别在于P-I模型是由多个Play算子或Stop算子加权叠加得到[45]。如图5(b) 所示,两个算子在本质上非常相似,区别在于表达方式,因此可利用Play算子来描述经典的P-I迟滞模型,表达式为
| $ y(t) =q u(t) +\int p(r) F r[u](t) {\rm{d}} r $ | (10) |
式中:y(t)和u(t)分别为输出位移和输入电压,q为常数,p(r) 为密度函数,Fr[u](t) 为Play算子。
从式(10)中可以发现,该模型不考虑输入信号的频率,属于静态率无关迟滞模型。因为P-I模型的基本单元Play算子为对称结构,故P-I模型只能描述对称迟滞现象,存在局限性。为此,许多研究人员对传统P-I模型进行改进。Xie等[46]提出了一种改进的非对称广义Prandtl-Ishlinskii模型,该模型采用级联算子来描述气动肌肉执行器的非对称迟滞特性。Ko等[47]提出了一种基于识别的广义P-I逆模型构建方法,以促进基于逆模型的非对称迟滞非线性前馈补偿。钟云等[48]针对周期正弦输入信号,提出了一种改进增强型P-I模型,与传统的模型相比更具有优势。
总体来说,P-I模型数学表达式简单,计算量少,并且具有解析逆模型的表达形式,便于设计迟滞补偿器。
3) 其他迟滞模型
随着计算机技术的发展,越来越多学者利用计算机强大的处理数据能力来研究迟滞模型,该模型具有更高的精度,较为典型的有人工神经网络模型和模糊模型。
(1) 人工神经网络模型:人工神经网络能够对非线性模型的输入和输出数据之间的非线性行为进行近似计算及预估,且无需事先了解这些数据,因此备受关注[49]。在理论上,多层的前反馈型神经网络能以任意精度逼近非线性函数,因此在非线性的系统识别上有着广泛地应用。
熊永程等[50]利用神经网络可用于拟合任意非线性曲线的特点,将经过深度学习的神经网络迟滞模型应用到压电致动器的前馈补偿。实验结果表明,应用神经网络前馈补偿后,压电致动器的最大误差降低到80 nm,稳态误差为±20 nm。Wang等[51]提出一种基于长短期记忆模型和具有外部输入的非线性自回归神经网络模型的新型混合模型,该混合模型比传统的迟滞模型具有更高的精度以及适用性。Cheng等[52]提出了一种非线性模型预测控制方法,利用了多层神经网络实现了压电致动器的迟滞模型建立,这种方法不需要建立迟滞逆模型,避免了迟滞模型反演时的误差问题。
(2) 模糊模型:美国加州大学教授Zadch L A于1965年提出表达事物模糊性的重要概念:隶属函数,为模糊理论奠定了基础[53]。除了依靠专家经验进行的模糊推理外,还有基于数据驱动的T-S模糊模型,而且理论上T-S模糊模型可以以任意精度逼近非线性系统[54]。
陈圣鑫[55]在基于动态迟滞算子上提出了T-S模糊模型。通过引入动态迟滞算子,将迟滞非线性输入输出中的多支映射问题转化为一一对应的关系,使得迟滞非线性特性能够更有效地辨别。张伟等[56]利用模糊树方法逼近非线性系统的内部模型以及逆模型,将两者相结合后,提出了一种基于模糊树模型的非线性系统内模控制方法,该方法不仅跟踪精度高,并且具有较强的鲁棒性。Li等[57]开发了一种简化的IT2模糊系统,用于压电致动器的迟滞建模和建模控制。Yang等[58]针对压电致动器的控制精度在振动控制领域内易受噪声点影响的问题,提出了一种改进的T-S模糊建模方法。通过引入改进的回归聚类算法和超平面隶属函数,使得迟滞模型误差在5~100 Hz频率的条件下小于0.002 8 μm。
2.3 不同类型迟滞模型的基本特点表1为不同迟滞模型的特点对比。Preisach模型的优点是具有广泛适用性,且描述的迟滞特性精度较高,但是使用双重积分增加了计算的复杂性,导致后续出现参数识别困难以逆模型难以求解的情况。P-I模型的优点是计算量较小,能求出逆模型,但是传统的P-I模型只能对对称迟滞模型描述。B-W模型的优点是使用较少的参数便能描述大部分的复杂迟滞模型,有利于控制器的设计,但是需要对模型改进才能描述非对称迟滞模型;B-L模型的优点是数学表达式较为简洁,但是对于非对称模型难以求解,控制器的设计复杂。Duhem模型的优点是较为精确描述迟滞特性,缺点是逆模型的求解相对困难。J-A模型的优点是能较为完整地反映压电材料的物理性质,缺点是建模时较为复杂,且材料成分发生改变,模型必须重建,缺乏一般性。Maxwell模型优点是建立迟滞模型较为简单且能够反映出物理意义,但是其模型的精度较低,使得控制器的设计较为困难。人工神经网络模型的优点是能实现高精度逼近迟滞曲线,但是其只能一对一映射,需要与其他算法组成复合算法进行迟滞模型描述。模糊模型的优点是对于非线性系统具有较强的辨识能力,但是需要的数据量较大,在缺乏数据支持下,易出现误差。
| 表 1 迟滞模型特点对比 Table 1 Comparison of hysteresis model characteristics |
压电陶瓷在外加电场的恒定作用下,陶瓷内部晶粒发生缓慢的重新排列现象,其在这段时间内产生的位移称为蠕变[59]。蠕变非线性在高频率输入信号下不明显,一般在超低频信号或者阶跃信号下对其进行研究。蠕变非线性会对压电陶瓷产生定位点漂移,尤其是长时间的精密定位[60]。当前,主要用对数模型以及有限维线性时不变模型对蠕变非线性进行描述。
对数模型表达式为
| $ L(t, u) =L_{0}\left[1+\gamma(u) \lg \frac{t}{0.1}\right] $ | (11) |
有限维线性时不变模型表达式为
| $ G(s) =\frac{Y(s) }{U(s) }=\frac{1}{k_{0}}+\sum_{i=1}^{n} \frac{1}{c_{i} s+k_{i}} $ | (12) |
温盛军等[61]针对压电驱动微定位平台复杂的非线性特征,通过在Hammerstein模型上串联分数阶算子,改进出一种融合了迟滞、蠕变以及动力学的非线性数学模型。与传统的Hammerstein模型不考虑蠕变特性相比,该改进型模型在1~100 Hz的正弦波输入电压信号作用下,均方根误差指标降低了27%以上,相对误差指标下降了50%,试验结果表明了该模型的有效性。作者在该有效模型的基础上设计了前馈补偿,并利用PID控制算法实施闭环调节,达到了良好的跟踪效果。赵学良等[62]针对蠕变的动态特性展开研究,为了达到抑制动态蠕变的效果,首先对双向小峰值电压尖峰的抑制作用展开研究,并利用PI复合控制器对不同离散化作用下的动态蠕变抑制作用,最后在压电执行器是本质分数阶对象的特点的基础上,分析了分数阶复合控制器的抑制效果。试验结果表明,当
为了能减少压电致动器的迟滞非线性特征对于整体系统的影响,国内外学者纷纷提出了相应的控制策略。根据目前对压电致动器的致动方式分类,国内外对于迟滞非线性特征的控制策略研究主要分为电荷控制与电压控制两大方向[63]。其中,对于电压控制的研究主要分为迟滞逆模型控制方法和无迟滞逆模型的控制方法[64]。
4.1 电荷控制方法1981年,Comstok[65]设计了一种用于减少压电致动器迟滞效应的电荷控制电路,这是电荷控制方法首次在压电致动器上运用。电荷控制的原理:首先电容传感器对流过压电致动器电路中的电荷量进行检测,其次经过缓冲放大器后电荷作为反馈信号传输到运算放大器的反向输入端,然后运算放大器根据同向输入端以及电压输入控制信号的差值输出一个电压信号,最后作用到压电致动器,达到调节压电致动器的电荷量的目的。此后,不断有学者在此原理上研究和改进电荷控制方法。
余婷婷[66]基于OPA454高压运算放大器设计了一种新型的电荷控制电路,实验结果表明在该种电荷控制电路下,压电致动器的迟滞非线性减少了82%。喻奇志[67]采用电荷控制的方法控制压电变形镜,通过与电压控制方法的实验对比,结果表明,使用电荷控制方法的情况,整体迟滞约为1%,而在不同面型的重构实验当中,电荷控制方法的精度至少提高了70%。
4.2 电压控制方法虽然电荷控制在实现方法上较为简单且可达到一定程度上迟滞抑制,但是其有两大局限性。(1) 电荷控制补偿电路中的电荷放大器在结构上十分复杂,设计难度大,从而导致了此类器械设备十分昂贵。(2) 随着电荷密度的不断增加,压电陶瓷产生的形变量也会不断增加,所以在高频电压下电荷放大器才能较好地对迟滞非线性实现补偿,在低频电压下补偿效果较差。这两大局限性使得电荷控制方法难以在实际的工程当中得到运用。因此,对于压电致动器的控制方法以电压控制为主。
1) 基于迟滞逆模型控制方法
(1) 基于迟滞逆模型的前馈控制方法:基于迟滞逆模型的前馈控制方法是有效减小迟滞非线性的方法之一,其在利用迟滞模型反解出迟滞逆模型后,将其直接与压电致动器串联,可使得系统输入与输出线性化,补偿过程如图6所示。

|
图 6 基于迟滞逆模型的前馈补偿过程 Figure 6 The process of feed-forward compensation based on inverse hysteresis model |
王博文等[68]在经典P-I模型基础上得到改进P-I(Modified Prandtl-Ishilinskii,MPI) 模型,在得到基于率相关MPI逆模型后建立平台的前馈控制器,并对其展开阶跃响应以及正弦轨迹跟踪实验。在阶跃响应实验中,在无前馈控制器作用时,x、y和θz稳态误差分别为0.45 μm、0.79 μm和6.33 μrad,加入前馈控制器后,稳态误差分别下降到0.19 μm、0.41 μm和1.21 μrad。在1 Hz的正弦轨迹跟踪实验中,x、y和θz在前馈控制器的作用下,最大误差为0.26 μm、0.26 μm和2.11 μrad。当频率为20 Hz时,最大误差为0.32 μm、0.37 μm和2.60 μrad。实验数据表明所设计的前馈控制器对动态迟滞特性有一定抑制作用,提高了系统的稳定性。
赵建杰[69]同样对传统的P-I模型进行改进,主要是针对下降段算子的权值重新进行录取,得到非对称性P-I迟滞模型,在推导得到迟滞逆模型表达式并进行参数选取后,对压电致动器进行仿真实验,当输入一个期望位移为0.5的阶跃信号时,输出的实际位移为0.495 9,误差为0.82%,实验数据表明该前馈控制能有效补偿压电致动器的迟滞特性。
另外还有陈辉[70]运用最小二乘法辨识迟滞逆模型参数,用此开发前馈控制策略。韩少鹏[71]将4种不同迟滞模型的逆模型加入前馈控制,有效减少开环定位误差,其精度是传统开环的10倍左右。
总的来说,前馈控制方法有2方面的优点:一方面,建立的迟滞逆模型具有结构简单、适应性广的特点;另一方面,只要该迟滞逆模型的精度足够高,可以有效实现迟滞补偿的目的。但在实际运用中,迟滞模型参数摄动往往会使得控制精度比较低。
(2) 基于迟滞逆模型的前馈−反馈控制方法:基于迟滞逆模型的前馈控制简单易实现,并在一定程度上有效抑制迟滞非线性对系统的影响,但该方法属于开环控制,系统中没有反馈控制,无法对外部的振动、扰动等非迟滞因素造成的误差进行及时的补偿修正,只适用于低速稳定的系统。因此有必要设计闭环控制系统实现高精度定位和位置跟踪。基于迟滞逆模型的前馈−反馈主要组件和基本流程如图7所示。

|
图 7 基于迟滞逆模型的前馈−反馈补偿过程 Figure 7 The process of feed-forward-feedback compensation based on inverse hysteresis model |
将PID控制器与逆迟滞模型相结合组成的前馈−反馈控制器是目前应用最广泛、最有效的控制方法。郭兴旺[72]提出一种改进的PID控制算法,并与P-I模型结合实现闭环控制实现迟滞补偿。于文慧[73]提出在基于椭圆迟滞逆模型上,结合经典PID控制,实现系统的闭环控制。Li等[74]将经典的FxLMS算法和传统的PID控制器相结合,运用到提高压电悬臂梁的振动控制效率。Wang等[75]提出一种新的控制器,利用PID控制与子区间维法得到闭环系统的特定相应区间,完成不确定性传播分析。
自适应控制方法具有较强的鲁棒性,其能够自行修正模型参数,减少外界的干扰,将自适应控制器与迟滞逆模型相结合的控制方法可有效降低压电迟滞现象。杜建周等[76]在自适应控制方法的基础上设计一款压电驱动电源,相比于在无控制条件下,其补偿效果有较大的提升。陆奇涛[77]提出了一款基于凸轮机构的压电步进驱动器方案,其采用自适应控制方法,通过对直接式以及间接式箝位进行实验,证明该方案具有可行性。Sun等[78]提出了一种增益可调的模型参考自适应控制方法,通过数值实验验证了模型自适应控制方案的有效性。Shi等[79]提出一种前馈/反馈联合控制方法,通过在反馈控制器中采用自适应控制算法减少外部干扰的影响。
滑模控制系统能够根据滑模面运动轨迹自动调整系统结构,其在达到滑模面后就会迅速收敛到期望值,具有较强的鲁棒性以及抗干扰能力。张毅[80]在基于Bouc-Wen逆模型的基础上,针对补偿误差以及系统外部扰动等问题,设计基于滑模观测器的滑模控制方法。通过仿真和实验,表明在期望信号1~50 Hz的频率内,实验的最大相差误差控制在5%以内,证明了闭环系统的稳定性。Ding等[81]提出了一种改进的滑模控制策略,主要是改进动态矩阵控制中的状态方程修正系数的设计方法,增强了控制器的跟踪能力。
2) 无逆迟滞模型控制方法
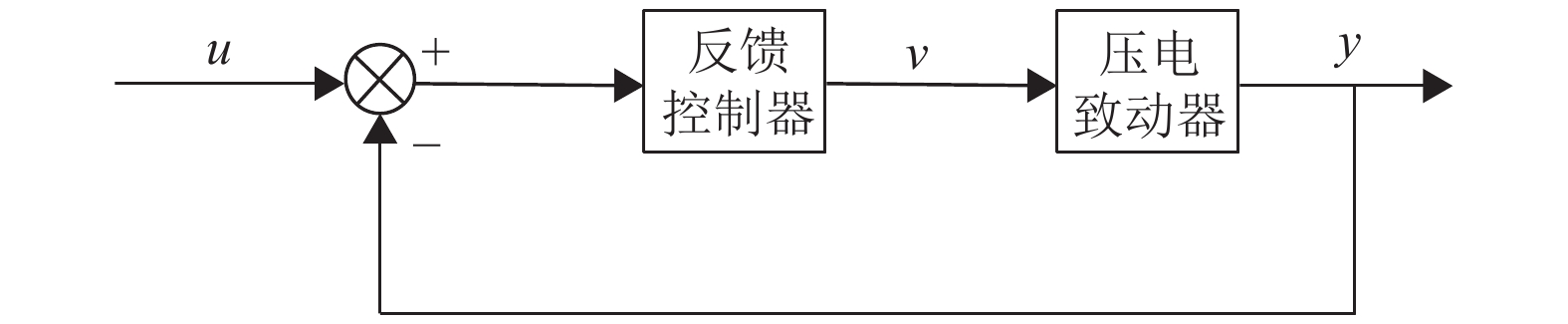
虽然基于逆迟滞模型的前馈−反馈控制方法在实际运用中能达到实时补偿迟滞的作用,但是该控制方法依然会受到模型精度的影响。因此,有学者开始研究无需建立迟滞逆模型的控制方法。如图8所示,该控制方法无需迟滞逆模型与被控制对象串联,直接采用反馈控制器对期望信号和反馈信号之间的差值进行调节。
|
图 8 无逆迟滞模型补偿过程 Figure 8 The process of compensation based on no-inverse hysteresis model |
由于PID控制器具有较高的稳定性和较广的适用范围,在工业控制领域中经久不衰。Shieh等[82]提出一种最优PID控制方法,该方法采用最优控制机制确定PID控制器的参数,摒弃了传统的试凑法,有效地降低了压电迟滞特性。
滑模控制器作为一种传统的控制器,被广泛运用到压电迟滞控制。Xu等[83]提出了一种分数阶滑模控制方法,将分数阶滑模面与一种新的双功率趋近律相结合,实现了不同载荷下压电纳米定位阶段的高精度跟踪控制。Chang等[84]对基于波纹管式液压位移放大机构的压电刀具支架进行研究,采用线性和非线性滑模控制方法对压电迟滞特性进行补偿,实现非轴对称非球面材料的加工。
自适应控制器无需被控制对象具有精确的模型,可省去建立精确模型的时间成本,被广泛地运用在压电致动器的控制。Zhang等[85]开发了一种预定义时间自适应神经控制方法,该方法可以在不违反输出约束的前提下,使得压电驱动运动在预定义的时间内达到控制效果。Wu等[86]为了减小压电作动器由于滞回非线性和未知外部干扰造成的定位误差,设计了一种基于神经网络的自适应控制器,实现了压电作动器的精确轨迹跟踪。Zhang等[87]提出无模型自适应控制策略,可有效补偿外界扰动对控制精度的影响,在长行程运动下的定位误差为30 nm。
5 总结与展望压电致动器易于实现微纳米级位移输出的特点,使其在高精度微位移机构的应用中具有较大的潜力,但其固有的迟滞与蠕变非线性特征限制了其发展,为了能够提高压电致动器位移输出精度,国内外研究者基本采用以下的控制策略:(1) 选取适当的迟滞模型精确描述压电迟滞现象,防止误差的扩大;(2) 求解迟滞模型的逆模型,达到初步控制与补偿效果;(3) 结合适当的控制策略再次对迟滞模型进行复合控制与补偿,形成闭环控制。此种控制策略能实现控制的精度很大程度取决于模型的精度,因此,随着计算机技术的进一步发展,研究无迟滞逆模型的控制策略对于压电致动器的普及应用具有重要意义。另外,从整体性上看,对于精密系统误差以及补偿控制策略的研究还是比较少。因此,在进行自由度较多、具有优异性能的精密系统设计时,不仅要考虑到压电致动器的非线性,更有必要将控制策略与系统的整体结构优化、误差补偿结合起来,对系统的控制策略进行更深入的研究,这也是未来微纳领域一个极其重要的研究方向。
| [1] |
谭久彬. 超精密测量是支撑光刻机技术发展的基石[J].
仪器仪表学报, 2023, 44(3): 1-7.
TAN J B. Ultra-precision measurement: the cornerstone of the lithography development[J]. Chinese Journal of Scientific Instrument, 2023, 44(3): 1-7. |
| [2] |
张威, 肖渊, 张津瑞, 等. 压电式微滴喷头电源驱动系统设计与实现[J].
西安工程大学学报, 2019, 33(3): 326-331.
ZHANG W, XIAO Y, ZHANG J R, et al. Design and imple- mentation of driven system for piezoelectric droplet sprinkler[J]. Journal of Xi'an Polytechnic University, 2019, 33(3): 326-331. |
| [3] |
DENG J, LIU S H, LIU Y X, et al. A 2-DOF needle insertion device using inertial piezoelectric actuator[J].
IEEE Transactions on Industrial Electronics, 2022, 69(4): 3918-3927.
DOI: 10.1109/TIE.2021.3073313. |
| [4] |
刘军. 用于航天控制力矩陀螺的行波型超声电机技术研究[D]. 南京: 南京航空航天大学, 2020.
|
| [5] |
HANGYEOL B, ABDUL M K, YOUNGSHIK K. A bidirectional rotating actuator by using a single shape memory alloy wire in adouble bend shape[J].
Sensors and Actuators: A. Physical, 2023, 360: 114526.
DOI: 10.1016/j.sna.2023.114526. |
| [6] |
AI K E, RAZZAGHI P, HURMUZLU Y. Feedback control of millimeter scale pivot walkers using magnetic actuation[J].
Robotics and Autonomous System, 2023, 168: 104496.
DOI: 10.1016/j.robot.2023.104496. |
| [7] |
李锐. 基于迟滞环对称性的压电陶瓷迟滞补偿算法研究[D]. 哈尔滨: 哈尔滨工业大学, 2018.
|
| [8] |
彭国祥. 压电驱动器输出力迟滞效应的建模与控制方法研究[D]. 哈尔滨: 哈尔滨工业大学, 2021.
|
| [9] |
GAN J Q, ZHANG X M. A review of nonlinear hysteresis modeling and control of piezoelectric actuators[J].
AIP Advances, 2019, 9: 040702.
DOI: 10.1063/1.5093000. |
| [10] |
李泽琨. 压电陶瓷作动器迟滞非线性建模与补偿控制研究[D]. 哈尔滨: 哈尔滨工业大学, 2022.
|
| [11] |
于志亮. 压电陶瓷执行器迟滞补偿与控制方法研究[D]. 哈尔滨: 哈尔滨工业大学, 2019.
|
| [12] |
徐瑞瑞. 基于Bouc-Wen模型的压电陶瓷驱动的运动平台迟滞建模与控制研究[D]. 武汉: 武汉工程大学, 2022.
|
| [13] |
甘金强. 微位移平台压电陶瓷驱动系统非线性建模与控制方法研究[D]. 广州: 华南理工大学, 2017.
|
| [14] |
LIU Y F, DU D S, QI N M, et al. A distributed parameter Maxwell-slip model for the hysteresis in piezoelectric actuators[J].
IEEE Transactions on Industrial Electronics, 2018, 66(9): 7150-7158.
|
| [15] |
XIE S B, NI C R, DUAN H Y, et al. Hybrid model based on the Maxwell-Slip model and a support vector machine for hysteresis in piezoelectric actuators[C] //2020 IEEE/ASME International Conference on Advanced Intelligent Mechatronics (AIM) . Boston: IEEE, 2020: 36-41.
|
| [16] |
段建东, 雷阳, 李浩, 等. 铁磁元件J-A模型的研究进展与趋势[J].
高压电器, 2020, 56(12): 16-23.
DUAN J D, LEI Y, LI H, et al. Review of ferromagnetic components J-A models[J]. High Voltage Apparatus, 2020, 56(12): 16-23. |
| [17] |
SAVOIE M, SHAN J J. Monte carlo study of Jiles-Atherton parameters on hysteresis area and remnant displacement[C]//2022 IEEE 31st International Symposium on Industrial Electronics (ISI E) . Anchorage: IEEE, 2022: 1017-1022.
|
| [18] |
ZHANG B, GUPTA B, DUCHARNE B, et al. Dynamic magneticscalar hysteresis lump model based on Jiles-Atherton quasistatichysteresis model extended with dynamic fractional derivativecontribution[J].
IEEE Transactions on Magnetics, 2018, 54(11): 1-5.
|
| [19] |
明敏. 压电微动平台迟滞补偿与运动控制研究[D]. 武汉: 武汉大学, 2021.
|
| [20] |
严秀权, 吴洪涛, 李耀, 等. 压电作动器的支持向量机迟滞模型[J].
仪器仪表学报, 2018, 39(9): 228-235.
YAN X Q, WU H T, LI Y, et al. Support vector machine-based hystersis model of piezoelectric actuator[J]. Chinese Journal of Scientific Instrument, 2018, 39(9): 228-235. |
| [21] |
IKHOUANE F. A survey of the hysteretic Duhem model[J].
Archives of Computational Methods in Engineering, 2018, 25(4): 965-1002.
DOI: 10.1007/s11831-017-9218-3. |
| [22] |
孙涛, 李国平, 孙浩益. 基于Duhem模型和逆模型的压电执行器精密定位及控制[J].
宁波大学学报(理工版), 2017, 30(1): 13-17.
SUN T, LI G P, SUN H Y. Accurate positioning and control of piezoelectric actuator based on Duhem model and inverse model[J]. Journal of Ningbo University (NSEE), 2017, 30(1): 13-17. |
| [23] |
贺一丹, 王贞艳, 何延超, 等. 压电陶瓷作动器的改进Duhem迟滞模型[J].
压电与声光, 2021, 43(3): 431-434.
HE Y D, WANG Z Y, HE Y C, et al. Improved Duhem hysteresis modeling of piezoelctric actuators[J]. Piezoelectrics & Acoustooptics, 2021, 43(3): 431-434. DOI: 10.11977/j.issn.1004-2474.2021.03.029. |
| [24] |
高源蓬, 张泉, 李清灵, 等. 压电陶瓷执行器迟滞非线性补偿与最优控制[J].
仪器仪表学报, 2022, 43(8): 163-172.
GAO Y P, ZHANG Q, LI Q L, et al. Hysteresis nonlinear compensation and optimal control of piezoelectric actuators[J]. Chinese Journal of Science Instrument, 2022, 43(8): 163-172. |
| [25] |
SU C Y, STEPANENKO Y, SVONODA J, et al. Robust adaptive control of a class of nonlinear systems with unknown backlash-like hysteresis[J].
IEEE Transactions on Automatic Control, 2000, 45(12): 2427-2432.
DOI: 10.1109/9.895588. |
| [26] |
ZHOU J, WEN C Y, ZHANG Y. Adaptive backstepping control of a class of uncertain nonlinear systems with unknown backlash-like hysteresis[J].
IEEE Transactions on Automatic Control, 2004, 49(10): 1751-1759.
DOI: 10.1109/TAC.2004.835398. |
| [27] |
杨晓京, 胡俊文, 李庭树. 压电微定位台的率相关动态迟滞建模及参数辨识[J].
光学精密工程, 2019, 27(3): 610-618.
YANG X J, HU J W, LI T S. Rate-dependent dynamic hysteresismodeling of piezoelectric micro platform and its parameter identification[J]. Optics and Precision Engineering, 2019, 27(3): 610-618. DOI: 10.3788/OPE.20192703.0610. |
| [28] |
CHEN Y Y, WANG Y , DONG Q, et al. Robust adaptive back-stepping control for nonlinear systems with unknown backlash-like hysteresis[C] //2021 IEEE International Conference on Mechatronics and Automation (ICMA) . Takamatsu: IEEE, 2021: 554-559.
|
| [29] |
LI Z, LI Z K, XU H Z, et al. Development of a butterfly fractional-order backlash-like hysteresis model for dielectric elastomer actuators[J].
IEEE Transactions on Industrial Electronics, 2022, 70(2): 1794-1801.
|
| [30] |
WEN Y K. Method for random vibration of hysteretic system[J].
Journal of the Engineering Mechanics Division, 1976, 102(2): 249-263.
DOI: 10.1061/JMCEA3.0002106. |
| [31] |
WANG D H, ZHU W. A phenomenological model for pre- stressed piezoelectric ceramic stack actuators[J].
Smart Materials & Structures, 2011, 20(3): 35018.
|
| [32] |
RAKOTONDRABE M. Bouc-Wen modeling and inverse multiplicative structure to compensate hysteresis nonlinearity in piezoelectric actuators[J].
IEEE Transactions on Automation Science & Engineering, 2010, 8(2): 428-431.
|
| [33] |
ZABLOTSKAYA T Y. Analyzing the classical and extended Bouc-Wen model parameters[C] //2020 2nd International Conference on Control Systems, Mathematical Modeling, Automation and Energy Efficiency (SUMMA) . Lipetsk: IEEE, 2020: 576-581.
|
| [34] |
ABOURA F. Modeling and analyzing Bouc-Wen hysteresis model[C] //2019 19th International Symposium on Electromagnetic Fields in Mechatronics, Electrical and Electronic Engineering (ISEF) . Nancy: IEEE, 2019: 1-2.
|
| [35] |
HU J Y, DONG R L, TAN Y H. A new improved Bouc-Wen model of piezoelectric ceramics actuators[C] //2021 40th Chinese Control Conference (CCC) . Shanghai: IEEE, 2021: 1-5.
|
| [36] |
SALEEM A, AL-RATROUT S, MESBAH M. A fitness function for parameters identification of Bouc-Wen hysteresis model for piezoelectric actuators[C] //2018 5th International Conference on Electrical and Electronic Engineering (ICEEE) . Istanbul: IEEE, 2018: 119-123.
|
| [37] |
MINH T V, TUNG T T, CHEN X K. Precision control of piezoelectric actuator using modified Bouc-Wen model[C] //2020 International Conference on Advanced Mechatronic Systems (ICAMS) . Hanoi: IEEE, 2020: 162-167.
|
| [38] |
赵博文. 压电陶瓷驱动平台的迟滞补偿控制方法研究[D]. 盐城: 盐城工学院, 2023.
|
| [39] |
PREISACH F. Über die magnetische Nachwirkung[J].
Zeitschrift Für Physik, 1935, 94(5): 277-302.
|
| [40] |
MGOLDFARB M, CELANOVIC N. Modeling piezoelectric stack actuators for control of micromanipulation[J].
IEEE Control Systems Magazine, 1997, 17(3): 69-79.
|
| [41] |
范青武, 张恒, 刘旭东, 等. 基于三线性插值法的Preisach模型及数值实现[J].
压电与声光, 2018, 40(5): 811-814.
FAN Q W, ZHANG H, LIU X D, et al. The Preisach model based on trilinear interpolation method and its numerical implementation[J]. Piezoelectrics & Acoustooptics, 2018, 40(5): 811-814. DOI: 10.11977/j.issn.1004-2474.2018.05.037. |
| [42] |
武毅男, 方勇纯. 基于Preisach模型的深度学习网络迟滞建模[J].
控制理论与应用, 2018, 35(6): 723-731.
WU Y N, FANG Y C. Hysteresis modeling with deep leaning network based on Preisach model[J]. Control Theory & Application, 2018, 35(6): 723-731. DOI: 10.7641/CTA.2017.70554. |
| [43] |
陈彬, 王斐然, 陈睿, 等. 基于R-L型分数阶导数的动态解析逆Preisach模型[J].
高压电技术, 2023, 49(9): 3918-3926.
CHEN B, WANG F R, CHEN R, et al. Dynamic analytical inverse Preisach model based on R-L fractional derivative[J]. High Voltage Engineering, 2023, 49(9): 3918-3926. |
| [44] |
MACKI J W, NISTRI P, ZECCA P. Mathematical models for hysteresis[J].
SIAM Review, 1993, 35(1): 94-123.
DOI: 10.1137/1035005. |
| [45] |
GU G Y, YANG M J, ZHU L M. Real-time inverse hysteresis compensation of piezoelectric actuators with a modified Prandtl-Ishlinskii mode[J].
Review of Scientific Instruments, 2012, 83(6): 065106.
DOI: 10.1063/1.4728575. |
| [46] |
XIE S, REN G, WANG B. A modified asymmetric generalized Prandtl-Ishlinskii model for characterizing the irregular asymmetrichysteresis of self-made pneumatic muscle actuators[J].
Mechanism and Machine Theory, 2020, 149: 103836.
DOI: 10.1016/j.mechmachtheory.2020.103836. |
| [47] |
KO Y R, CHUN S, KIM T H. Identification of inverse gen- eralized asymmetric Prandtl-Ishlinskii model for compensation of hysteresis nonlinearities[C] //2017 IEEE Conference on Control Technology and Applications (CCTA) . Maui: IEEE, 2017: 1183- 1188.
|
| [48] |
钟云, 黄楠, 曾俊海. 压电驱动器迟滞非线性的增强型Prandtl-Ishlinskii模型建模及实验验证[J].
机电工程技术, 2020, 49(10): 33-35.
ZHONG Y, HUANG N, ZENG J H. Enhanced Prandtl-Ishlinskii modeling and experimental verification of hysteresis nonlinearities in piezoelectric actuators[J]. Mechanical & Electrical Engineering Technology, 2020, 49(10): 33-35. DOI: 10.3969/j.issn.1009-9492.2020.10.008. |
| [49] |
张金, 张健滔, 宁艺文, 等. 基于神经网络的压电能量收集器性能预估模型[J].
振动, 测试与诊断, 2023, 49(1): 172-178.
ZHANG J, ZHANG J T, NING Y W, et al. Performance prediction model of piezoelectric energy harvester based on artificial neural network[J]. Journal of Vibration, Measurement & Diagnosis, 2023, 49(1): 172-178. |
| [50] |
熊永程, 贾文红, 张丽敏, 等. 基于深度神经网络(DNN) 的压电陶瓷前馈补偿研究[J].
压电与声光, 2022, 44(1): 35-41.
XIONG Y C, JIA W H, ZHANG L M, et al. Research on feedforward compensation of piezoelectric ceramics based on deep neural network[J]. Piezoelectrics & Acoustooptics, 2022, 44(1): 35-41. |
| [51] |
WANG G, YAO X M, CUI J J, et al. A novel piezoelectric hysteresis modeling method combining LSTM and NARX neural network[J].
Modern Physics Letters B, 2020, 34(28): 1-14.
|
| [52] |
CHENG L, LIU W C, HOU Z G, et al. Neural-network based nonlinear model predictive control for piezoelectric actuators[J].
IEEE Transactions on Industrial Electronics, 2015, 62(12): 7717-7727.
DOI: 10.1109/TIE.2015.2455026. |
| [53] |
ZADEH L A. Fuzzy sets[J].
Information and Control, 1965, 8(3): 338-353.
DOI: 10.1016/S0019-9958(65)90241-X. |
| [54] |
毛剑琴, 丁海山. 率相关迟滞非线性系统的智能化建模与控制[J].
中国科学, 2009, 39(3): 289-304.
|
| [55] |
陈圣鑫. 基于T-S模糊系统的压电执行器建模与控制[D]. 杭州: 浙江理工大学, 2021.
|
| [56] |
张伟, 毛剑琴. 基于模糊树模型的非线性系统内模控制[J].
控制理论与应用, 2013(4): 463-468.
ZHANG W, MAO J Q. Internal model control for nonlinear system based on fuzzy-tree method[J]. Control Theory & Application, 2013(4): 463-468. DOI: 10.7641/CTA.2013.20349. |
| [57] |
LI P Z, ZHANG D F, HU J Y, et al. Hysteresis modelling and feedforward control of piezoelectric actuator based on simplified interval type-2 fuzzy system[J].
Sensor, 2020, 20(9): 2587.
DOI: 10.3390/s20092587. |
| [58] |
YANG L, WANG Q T, XIAO Y Q, et al. Hysteresis modeling of piezoelectric actuators based on a T-S fuzzy model[J].
Electronics, 2022, 11(17): 2786.
DOI: 10.3390/electronics11172786. |
| [59] |
LIU G W, ÖZER A Ö, WANG M G. Longtime dynamics for a novel piezoelectric beam model with creep and thermo-viscoelasticeffects[J].
Nonlinear Analysis: Real World Application, 2022, 68: 103666.
DOI: 10.1016/j.nonrwa.2022.103666. |
| [60] |
范伟, 林瑜阳, 李钟慎. 基于BP神经网络的压电陶瓷蠕变预测[J].
计量学报, 2017, 38(4): 429-434.
FAN W, LIN Y Y, LI Z S. Prediction of the creep of piezoelectric ceramic based on BP neural network optimized by genetic algorithm[J]. Acta Metrologica Sinica, 2017, 38(4): 429-434. DOI: 10.3969/j.issn.1000-1158.2017.04.10. |
| [61] |
温盛军, 李亮, 喻俊, 等. 迟滞与蠕变耦合压电系统的建模及补偿方法[J].
振动与冲击, 2023, 42(7): 25-37.
WEN S J, LI L, YU J, et al. Modeling and compensation method of hysteresis-creep coupled piezoelectric system[J]. Journal of Vibration and Shock, 2023, 42(7): 25-37. |
| [62] |
赵学良. 低速大范围下压电执行器动态蠕变特性分析与控制方法研究[D]. 济南: 山东大学, 2016.
|
| [63] |
ZHONG J P, NISHIDA R, SHINSHI T. A digital charge control strategy for reducing the hysteresis in piezoelectric actuators: analysis, design and implementation[J].
Precision Engineering, 2021, 67: 370-382.
DOI: 10.1016/j.precisioneng.2020.10.006. |
| [64] |
GAN J Q, ZHANG X M. A review of nonlinear hysteresis modeling and control of piezoelectric actuators[J].
AIP Advance, 2019, 9(4): 1-10.
|
| [65] |
COMSTOCK R H. Charge control of piezoelectric actuators to reduce hysteresis effects: US4263527A[P]. 1981-4-21.
|
| [66] |
余婷婷. 基于电荷控制法的压电惯性摩擦驱动器的设计及控制研究[D]. 上海: 华东理工大学, 2023.
|
| [67] |
喻奇志. 基于电荷驱动的压电变形镜控制方法研究[D]. 宁波: 宁波大学, 2019.
|
| [68] |
王博文, 崔玉国, 谢启芳, 等. 基于率相关迟滞模型的压电微动平台前馈控制[J].
压电与声光, 2022, 44(6): 898-900.
WANG B W, CUI Y G, XIE Q F, et al. Feedforward control of piezoelectric micro-positioning stage based on rate-dependent hysteresis model[J]. Piezoelectric & Acoustooptics, 2022, 44(6): 898-900. |
| [69] |
赵建杰. 基于前馈控制算法的快速响应压电陶瓷模型设计[D]. 哈尔滨: 哈尔滨工业大学, 2020.
|
| [70] |
陈辉. 多维超精密定位系统建模与控制关键技术研究[D]. 南京: 东南大学, 2015.
|
| [71] |
韩少鹏. 压电陶瓷驱动器多段改进动态PI模型研究与精度控制[D]. 杭州: 杭州电子科技大学, 2019.
|
| [72] |
郭兴旺. 纳米定位与扫描平台模型辨识与控制算法研究[D]. 沈阳: 沈阳建筑大学, 2016.
|
| [73] |
于文慧. 二维压电平台迟滞动力学复合建模及其运动特性研究[D]. 哈尔滨: 哈尔滨工业大学, 2022.
|
| [74] |
LI W G, YANG Z C, LI K, et al. Hybrid feedback PID-FxLMSalgorithm for active vibration control of cantilever beam with piezoelectric stack actuator[J].
Journal of Sound and Vibration, 2021, 509: 116243.
DOI: 10.1016/j.jsv.2021.116243. |
| [75] |
WANG L, ZHAO Y Y, LIU J X, et al. Uncertainty-oriented optimal PID control design framework for piezoelectric structures based on subinterval dimension-wise method (SDWM) and non-probabilistic time-dependent reliability (NTDR) analysis[J].
Journal of Sound and Vibration, 2023, 549: 117588.
DOI: 10.1016/j.jsv.2023.117588. |
| [76] |
杜建周, 陈远晟, 刘绍娜, 等. 基于自适应逆控制的压电驱动电源[J].
压电与声光, 2022, 44(6): 901-906.
DU J Z, CHEN Y S, LIU S N, et al. Research on piezoelectric drive power with adaptive inverse control[J]. Piezoelectric & Acoustooptics, 2022, 44(6): 901-906. DOI: 10.11977/j.issn.1004-2474.2022.06.015. |
| [77] |
陆奇涛. 自驱动自适应压电步进驱动器的研究[D]. 杭州: 浙江师范大学, 2022.
|
| [78] |
SUN J F, CHEN W K, CHEN X S. Model reference adaptive control with adjustable gain for piezoelectric actuator[J].
European Journal of control, 2022, 67: 100712.
DOI: 10.1016/j.ejcon.2022.100712. |
| [79] |
SHI B C, SHI R, WANG F J. Design of an adaptive feedfor- ward feedback combined control for piezoelectric actuated micro positioning stage[J]. Precision Engineering, 2022, 78: 199-205.
|
| [80] |
张毅. 压电作动器的非线性建模及控制方法研究[D]. 哈尔滨: 哈尔滨理工大学, 2022.
|
| [81] |
DING Z A, YANG Z J, CHEN C H, et al. Improved sliding mode dynamic matrix control strategy: application on spindle loading and precision measuring device based on piezoelectric actuator[J].
Mechanical Systems and Signal Processing, 2022, 167: 108543.
DOI: 10.1016/j.ymssp.2021.108543. |
| [82] |
SHIEH H J, CHIU Y J, CHEN Y T. Optimal PID control system of a piezoelectric micropositioner[C] //2008 IEEE/SCIE International Symposium on System Integration, Nagoya: IEEE, 2008: 1-5.
|
| [83] |
XU R, WANG Z S, ZHOU M L, et al. A robust fractional-order sliding mode control technique for piezoelectric nanopositioning stage in Trajectory-tracking application[J].
Sensors and Actuators: A. Physical, 2023, 363: 114711.
DOI: 10.1016/j.sna.2023.114711. |
| [84] |
CHANG K M, CHEN J M, LIU Y T. Nonlinear sliding mode control for piezoelectric tool holder with bellow-type hydraulic displacement amplification mechanism[J].
Sensors and Actuators: A. Physical, 2023, 361: 114543.
DOI: 10.1016/j.sna.2023.114543. |
| [85] |
ZHANG C, YU Y W, ZHANG X Y, et al. Predefined-time adaptive control of a piezoelectric-driven motion system with time-varying output constraint[J].
IEEE Transactions on Circuits and Systems II: Express Briefs, 2023, 70(7): 2605-2609.
|
| [86] |
WU Y N, CHEN H, SUN N, et al. Neural network based adaptive control for a piezoelectric actuator with model uncertainty and unknown external disturbance[J].
International Journal of Robust and Nonlinear Control, 2023, 33(3): 2251-227.
DOI: 10.1002/rnc.6517. |
| [87] |
ZHANG Z G, DONG Y K, YU S, et al. Model-free adaptive positioning control of the bidirectional stick-slip piezoelectric actuator with coupled asymmetric flexure-hinge mechanisms[J].
Sensors, 2023, 23(18): 7795.
DOI: 10.3390/s23187795. |
 2024, Vol. 41
2024, Vol. 41