云计算能够为互联网提供弹性的资源调度和可拓展的计算服务，但是也给用户数据带来了严重安全威胁。通常云存储服务提供商(Cloud Service Provider, CSP) 被认为是诚实而又好奇的角色，即它诚实地执行既定协议,但又好奇地窃听用户数据^[1]。因此，云计算环境下通常使用允许数据拥有者自定义访问结构的密文属性加密(Ciphertext-policy Attribute-Based Encryption，CP-ABE)方案来加密和共享数据^[2]。

为了降低传统CP-ABE方案用户一侧的解密开销，Green等^[3]提出了一个支持外包解密计算的CP-ABE方案。该方案引入了解密代理实体，其职责是将密文转换为中间密文，随后用户再对中间密文进行解密，能够将繁重的双线性对运算转移到解密代理。虽然引入解密代理带来了额外的费用成本和时间成本，但是在资源受限的移动设备场景下，节省用户侧的计算资源更为重要。然而，该方案不能保证外包解密的可验证性。文献[4]提出了一种高效的可验证外包解密方案，利用了散列值来检查外包解密的正确性。文献[5]设计了两种密钥封装机制，让公共的ABE服务提供商执行加解密过程中的耗时操作。文献[6-7]将加解密外包的属性基加密运用到资源受限的边缘智慧医疗场景下。文献[8]构建了一个可验证外包的CP-ABE方案，并采用智能合约来保证解密外包结果的正确性。

传统CP-ABE方案还存在授权用户恶意分享私钥和属性授权机构违规发放私钥两类解密私钥泄露问题。为了解决授权用户恶意分享私钥的问题，文献[9]中的CP-ABE方案采用了叛逆追踪技术，但方案的密文和公钥较长。Liu等^[10]提出了支持任意单调访问结构的白盒可追踪CP-ABE方案，而且实现了标准模型下的适应性安全。Ning等^[11]提出了支持大属性域的可追踪CP-ABE方案，且采用秘密共享方案固定了追踪列表的存储开销。文献[12]利用承诺方案实现了完全安全的白盒可追踪CP-ABE方案。文献[13]使用二叉树叶节点值表示用户身份信息，并将其加密后嵌入在解密私钥中，用户的身份信息可以从泄露的解密私钥中得出。He等^[14]提出的CP-ABE方案同时支持白盒追踪和黑盒追踪，可以更有效地解决密钥追踪问题。

另一方面，即使系统追踪到了用户，恶意用户仍然可以宣称泄露的密钥是属性授权机构非法发放的，原因在于属性授权机构可以为任意属性集合的用户生成解密私钥。文献[15-16]采用离散对数知识的零知识证明方法，分别在合数阶群和素数阶群下实现了用户和属性授权机构可追责的CP-ABE方案。Zhang等^[17]通过多授权机构的方式避免单个授权机构拥有全部解密私钥，但引进了额外的实体和通信代价。文献[18]的多授权机构CP-ABE方案中，确保了只有在所有属性授权机构将密钥组件颁发给区块链后，才生成最终的解密私钥，从而在密钥泄露时通过追溯合约来实现公开定责。文献[19]同时实现了恶意用户追踪功能以及外包解密功能，但是属性授权机构非法颁发密钥给未授权用户的问题亟待解决。

以上所述的CP-ABE方案均无法同时支持对恶意用户的追责、对属性授权机构的追责以及可验证外包解密。为解决上述问题，本文提出了一种支持追责和可验证外包解密的属性基加密方案(Accountable and Verifiable Outsourced Decryption for CP-ABE，A-VO-CP-ABE)，该方案基于素数阶群构造，拥有标准模型下的选择性安全、可追责性和外包解密的可验证性。本文的主要贡献点如下：

(1) 本文提出的属性基加密方案实现了可验证外包解密，并且能够同时对恶意用户与属性授权机构追责。此外，本文方案支持大属性域的特性，因此无需在参数设置阶段固定系统表达能力的边界。

(2) 本文方案可以避免解密代理在提供解密服务时，获得数据用户的秘密信息。数据用户会在预处理原始密文和转换密钥之后，再将其发送至解密代理进行部分解密，并且预处理操作仅新增4个额外的指数操作。

(3) 本文方案中解密私钥中显式包含了用户ID，审计机构可以直接追踪到用户信息，追踪存储代价几乎为零。

1 预备知识 1.1 访问结构

令$P = \left\{ {{P_{\text{1}}},\cdots,{P_n}} \right\}$表示系统中的参与者集合，集合$ Q \subseteq {2^P} $是单调的当且仅当对于$ \forall E,F \subseteq P $，若$E \in Q$且$E \subseteq F$，则$F \in Q$。若Q为集合P的(单调) 非空子集，则Q是一个(单调) 访问结构。对于任一集合D，若$D \in Q$，则D为授权集合，否则为非授权集合。

1.2 线性秘密共享方案

令$P = \left\{ {{P_1},\cdots,{P_n}} \right\}$表示系统中的参与者集合，若定义在P上的秘密共享方案П满足以下条件，则称其为Z_p上线性的。

(1) 所有参与者所持有的秘密份额组成Z_p上的一个向量；

(2) 方案П对应一个l行n列秘密生成矩阵M，并且映射ρ把M的每一行映射到参与者集合P中，即$\rho :\left\{ {1,2,\cdots,l} \right\} \to P$。给定秘密值$s \in {Z_p}$，随机选取$ {z_{2}},\cdots,{z_n} \in {Z_p} $，构成一个列向量$ {\boldsymbol{z}} = {{(}s,{z_2},\cdots,{z_n}{) }^{{\rm{T}}}} $，则${\boldsymbol{M}}_{\boldsymbol{z}}$是秘密s的l个秘密份额，其中秘密份额$ {({\boldsymbol{M}}_{\boldsymbol{z}})_i} $属于参与者ρ(i) 。

LSSS方案具有线性重构性。对于访问结构Q的授权集$S \in Q$，令$I \subset \left\{ {1,\cdots,l} \right\}$定义为$ I = \left\{ {i:\rho \left( i \right) \in S} \right\} $，存在常数集合$ {\{ {\omega _i} \in {Z_p}\} _{i \in I}} $使得$ \displaystyle\sum\limits_{i \in I} {\omega _i}{\boldsymbol{M}} = \left( {1,0,\cdots,0} \right) $。使用该常数集合计算$\displaystyle\sum\limits_{i \in I} {\omega _i}{\boldsymbol{M}}_{\boldsymbol{z}} = \left( {1,0,\cdots,0} \right) {({s},{{z}_2},\cdots,{{z}_n}) ^{{\rm{T}}}}$，得出的计算结果即为秘密s。

2 系统定义和安全模型 2.1 系统模型

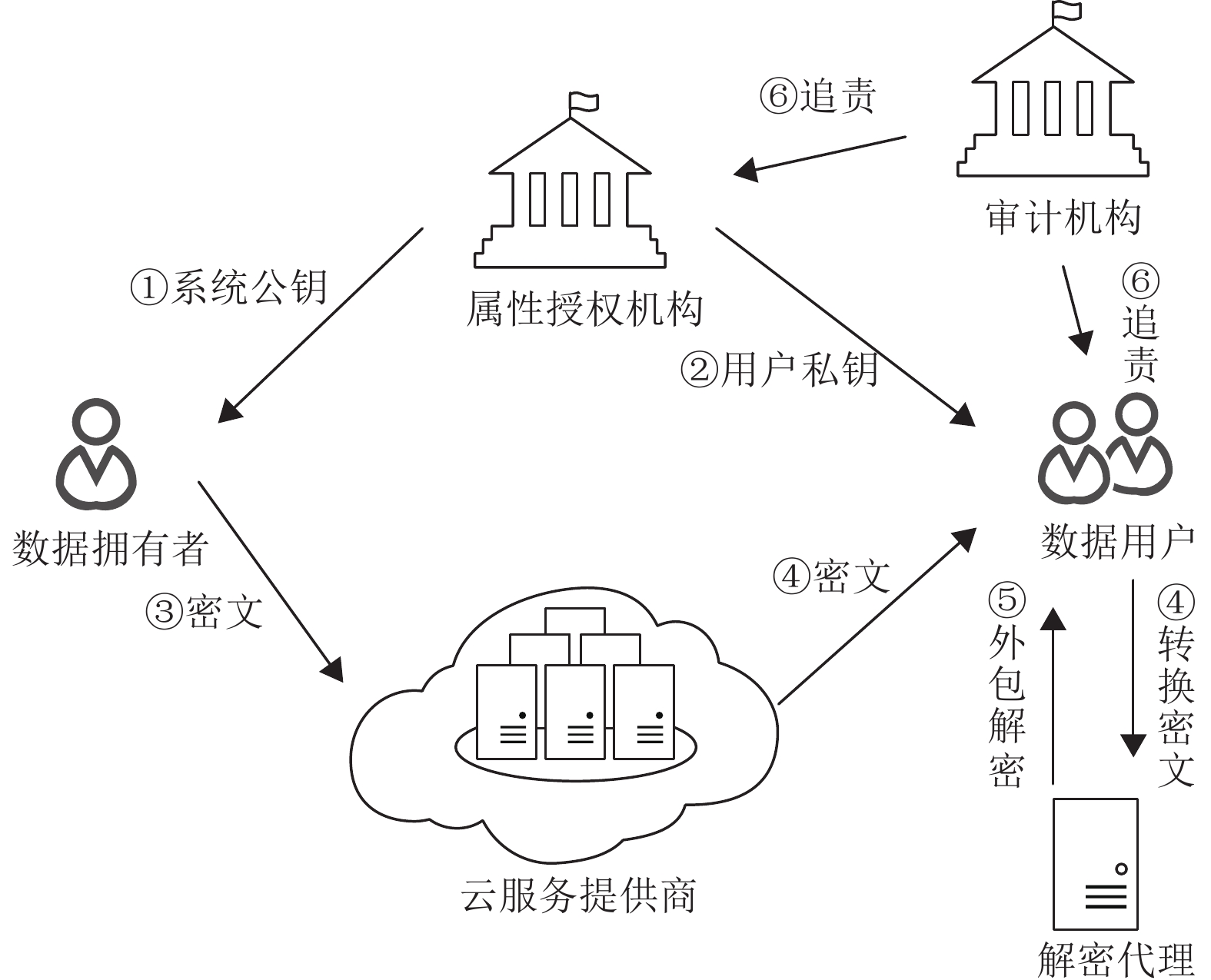
方案A-VO-CP-ABE的系统模型如图1所示。系统中包含六类实体：属性授权机构(Attribute Authority，AA)、云服务商(Cloud Service Provider，CSP)、解密代理(Decryption Agent，DA)、数据用户(Data User，DU)、数据拥有者(Data Owner，DO)和审计机构(Audit Authority)。AA负责生成系统公开密钥、主密钥和用户解密私钥；CSP提供云端存储服务；DA提供解密外包服务，DA可以是恶意的，即其尝试窥探用户数据隐私或者返回错误结果；DO依据访问结构加密数据，然后将密文上传到云端；DU执行预处理算法将脱敏后的密钥发送给DA，获取到部分解密密文并进行最终解密；审计机构可以根据格式正确的泄露密钥对AA和DU进行追责。

2.2 算法定义

A-VO-CP-ABE方案包括以下8种算法。

(1) $ {\text{Setup}}\left( \lambda \right) \to \left( {{\text{PK}},{\text{MSK}}} \right) $：输入安全参数λ，输出系统的公开密钥PK和主密钥MSK。

(2) $ {\text{Encrypt}}\left( {{\text{PK}},\left( {{\boldsymbol{M}},\rho } \right) ,m} \right) \to \left( {{\text{CT,VK}}} \right) $：输入公开密钥PK、访问结构(M, ρ) 和明文数据m，输出密文CT和验证密钥VK。

(3) $ {\text{KeyGen}}\left( {{\text{PK,MSK,ID}}{\text{,}}S} \right) \to \left( {{\text{TK,RK}}} \right) $：输入公开密钥PK、主密钥MSK、用户标识ID和用户属性集合S，输出转换密钥TK和取回密钥RK。

(4) $ {\text{Pre - Process}}\left( {{\text{CT,TK}}} \right) \to \left( {{\text{PCT,PTK}}} \right) $：输入密文CT和转换密钥TK，输出预处理后的密文PCT和转换密钥PTK。

(5) $ {\text{Transform}}\left( {{\text{PCT,PTK}}} \right) \to {\text{CT}}' $：输入预处理后的密文PCT和转换密钥PTK，若S满足(M, ρ) ，输出部分解密密文CT′ ；否则输出终止符⊥。

(6) ${\text{Decrypt}}\left( {{\text{PK}},{\text{CT}}',{\text{RK}},{\text{VK}}} \right) \to m$：输入部分解密密文CT′ 、取回密钥RK和验证密钥VK，若部分解密密文CT′ 有效，输出明文消息m；否则输出终止符⊥。

(7) ${\text{KeySantityCheck}}\left( {{\text{PK,TK,RK}}} \right) \to 1\;{\text{or}}\;0$：输入公开密钥PK、转换密钥TK和取回密钥RK，若TK和RK通过密钥完整性检查，则输出1，否则输出0。该算法用于检查解密私钥的合理性，判断是否需要进行追责。

(8) ${\text{Trace}}\left( {{\text{PK,TK,RK}}} \right) \to {\text{ID}}\;{\text{or}}\;{\text{AA}}$：输入公开密钥PK和泄露的解密私钥(TK,RK) ，若${\text{KeySantityCheck}} \left( {{\text{PK,TK,RK}}} \right) \to 1\;{\text{or}}\;0$，表示(TK,RK) 不是合理的解密私钥，输出终止符⊥；否则输出用户标识ID或者属性授权机构AA。

2.3 总体流程

本节介绍本文方案的总体流程，如图1所示，系统初始化环节，属性授权机构首先执行初始化算法Setup，生成系统公开密钥和主密钥，并且系统运行期间保持使用。

初始化环节后，数据用户携带用户标识ID和用户属性集合S向属性授权机构请求用户私钥，后者执行KeyGen算法生成转换密钥TK和取回密钥RK返回给数据用户。同时，数据拥有者本地执行Encrypt算法生成密文CT和验证密钥VK，并发送至云服务提供商进行存储。

解密过程中，数据用户从云服务提供商获取CT和VK，并执行Pre-Process算法对CT和TK进行预处理，并将预处理后的密文PCT和转换密钥PTK发送给解密代理。解密代理执行Transform算法，生成部分解密密文CT′ 。最后，数据用户取得CT′ 后，进行验证并解密出明文消息。

假设系统运行过程中出现密钥泄露问题，审计机构可以先执行KeySantityCheck算法检查解密私钥的合理性，若通过检查则执行Trace算法对数据用户和属性授权机构进行公开追责。

2.4 选择性安全模型

本节通过攻击者A和挑战者B之间的游戏来定义本文方案的安全模型，具体过程如下：

系统初始化：A将挑战访问结构(M^*, ρ^*) 发送给B。

参数设置阶段：B执行Setup算法，获得系统公开密钥PK和主密钥MSK，然后将PK发送给A。

密钥查询阶段1：B初始化空表T，空集合D和一个整数j=0。A可以对(ID,S) 进行以下询问。

(1) Create(S) ：B接收到(ID,S) 后，首先设置$j: = j + 1$，然后运行KeyGen算法获得关联用户标识ID和属性集合S的私钥SK=(TK,RK) ，最后将(j,S,SK,TK) 存储在表T中。然后把转换密钥TK返回给A。唯一的约束是S不满足(M^*, ρ^*) 。

(2) Corrupt(i) ：B验证第i个元组是否在表T中。若存在，设置$ D: = D \cup \left\{ S \right\} $并返回SK，否则返回终止符⊥。

挑战阶段：A提交两个等长的消息m₀和m₁，然后B随机选取${\mu } \in \left\{ {0,1} \right\}$，并基于挑战访问结构(M^*, ρ^*) 和消息m_μ执行Encrypt算法获得(CT^*,VK^*) 。最后，B输出挑战密文(CT^*,VK^*) 给A。

密钥查询阶段2：此阶段A继续按照密钥查询阶段1进行询问。

猜测阶段：A发送给B一个值$\mu ' \in \left\{ {0,1} \right\}$作为对μ的猜测。若$\mu ' = \mu $，则称A赢得了游戏。A在该游戏中的优势定义为$\left| {{\text{Pr}}\left[ {\mu = \mu '} \right] - \dfrac{1}{2}} \right|$。

定义1　若没有多项式时间内的攻击者能够以不可忽略的优势来攻破上述安全模型，则本文方案是选择性安全的。

2.5 可验证性安全模型

可验证性保证转换阶段执行正确与否，本节通过攻击者A和挑战者B之间的游戏来定义本文方案的可验证性，具体过程如下：

参数设置阶段：B执行Setup算法，获得系统公开密钥PK和主密钥MSK，然后将PK发送给A。

密钥查询阶段1：A按照上述密钥查询阶段1方式进行适应性询问。

挑战阶段：A提交一个消息m^*和挑战访问结构(M^*, ρ^*) ，然后B执行Encrypt算法获得(CT^*,VK^*) 。最后，B输出挑战密文(CT^*,VK^*) 给A。

密钥查询阶段2：此阶段A继续按照密钥查询阶段1进行询问。

猜测阶段：A输出满足条件$f( {({{\boldsymbol{M}}^*},{\rho ^*}) ,{S^{\text{*}}}} ) = 1$的属性集合S^*和部分解密密文CT′ 。若${\text{Decrypt}}\left( {\text{PK}},{\text{CT}}', {{\text{RK}}^{\text{*}}}{\text{,V}}{{\text{K}}^{\text{*}}} \right) \notin \left\{ {{m^{\text{*}}}, \bot } \right\}$，则称A赢得了游戏。A在该游戏中的优势定义为$ {\text{Adv}}_{\text{A}}^{\text{Ver}}\left(\lambda \right) :=\text{Pr}\left[\text{A}\text{wins}\right] $。

定义2　若没有多项式时间内的攻击者能够以不可忽略的优势来攻破上述安全模型，则本文方案具有可验证性。

2.6 可追责性

本文方案在文献[16]的基础上进行改动，涉及密钥生成算法KeyGen的改动对原追责模型的定义不造成影响，因此本文方案的可追责性安全模型和证明与文献[16]一致。

3 A-VO-CP-ABE方案 3.1 主要思想

本文的目标是在不损害安全和隐私的前提下实现高效的用户解密和可追责性。然而，如果以朴素的方式结合可验证解密外包CP-ABE方案和可追责CP-ABE方案，会将用户私密指数o泄露给解密代理，解密代理可以构造出能够通过密钥完整性检查算法的解密私钥，从而构陷用户或者属性授权机构泄露了私钥。因此，本文方案在请求解密代理进行外包解密前，先对转换密钥和密文进行脱敏的预处理操作。

3.2 具体构造

令G为素数p阶的循环群，g为群G的生成元。同时，令$e:G \times G \to {G_T}$表示双线性映射，身份ID和属性是$Z_p^*$中的元素。

(1) ${\text{Setup}}\left( \lambda \right) \to \left( {{\text{PK,MSK}}} \right) $：给定安全参数λ，调用群生成算法获取系统参数PP=(p, G, G_T, e) 。随机选取$ g,h,u,v,w \in G $和$ \alpha ,x,y \in Z_p $。选取两个抵抗冲突的哈希函数${\text{H}}{{\text{A}}_{\text{1}}}:{G_T} \to {\{ 0,1\} ^{{l_{{\text{H}}{{\text{A}}_{\text{1}}}}}}}$和${\text{H}}{{\text{A}}_{\text{2}}}:{\{ 0,1\} ^{\text{*}}} \to {\{ 0,1\} ^{{l_{{\text{H}}{{\text{A}}_{\text{2}}}}}}}$，选取密钥空间为${\{ 0,1\} ^{{l_{{\text{SE}}}}}}$的对称加密算法SE=(SE.KeyGen,SE.Encrypt,SE.Decrypt) ，从成对独立的哈希函数族$ H:{G_T} \to {\{ 0,1\} ^{{l_{{\text{SE}}}}}} $中选取私钥提取器HA₃。系统的主密钥MSK=(α, x, y) ，系统的公开密钥为

$ {\rm{PK}}=({\rm{PP}}, g, h, u, v, w, e(g, g)^{\alpha } ,g^{x},g^{y},{\rm{HA}}_{1},{\rm{HA}}_{2},{\rm{HA}}_{3},{\rm{SE}}) $

(2) ${\text{Encrypt}}\left( {{\text{PK}},\left( {{\boldsymbol{M}},\rho } \right) ,m} \right) \to \left( {{\text{CT,VK}}} \right) $：给定明文$ m \in \eta $和访问结构(M, ρ) ，其中M表示一个$l \times n$矩阵，ρ表示把M的每一行映射到相应属性的映射函数。

① DO选取随机向量${\boldsymbol{v}} = \left( {s,{v_2},\cdots,{v_n}} \right) \in Z_p^n$，对于$i \in \left[ {1,l} \right]$，计算$ {\lambda _i} = {\boldsymbol{v}} \cdot {{\boldsymbol{M}}_i} $，其中M_i是M的第i行。随机选取${t_1},\cdots,{t_l} \in {Z_p}$，$K \in {G_T}$，计算出关于K的密文

$ \begin{gathered} {C_K} = (C = K \cdot e{(g,g) ^{\alpha s}},{D_1} = {g^s},{D_2} = {g^{xs}},{D_3} = {g^{ys}}, \\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\{ {C_{i,1}} = {w^{{\lambda _i}}}{v^{{t_i}}},{C_{i,2}} = {({u^{\rho \left( i \right) }}h) ^{ - {t_i}}},{C_{i,3}} = {g^{{t_i}}}\} _{i \in \left[ {1,l} \right]}}) \\ \end{gathered} $

② DO计算TAG₁=HA₁(K) 和对称加密密钥SEK=HA₃(K) 。然后调用对称加密算法SE创建密文C_SE=SE.Encrypt(m, SEK) 和验证密钥${\text{VK}} = {\text{TA}}{{\text{G}}_2} = {\text{H}}{{\text{A}}_2}({\text{TA}}{{\text{G}}_1}||{C_{{\text{SE}}}}) $。最后，算法输出密文CT=(C_K,C_SE) 和密钥VK。

(3) ${\text{KeyGen}}\left( {{\text{PK,MSK,ID}},S} \right) \to \left( {{\text{TK,RK}}} \right) $：给定DU的身份标识ID和属性集合$ S = \left\{ {{S_1},\cdots,{S_k}} \right\} \subseteq {Z_p} $，AA与DU通过交互产生DU的解密私钥(TK,RK) 。

① 用户ID随机选取$o \in {Z_p}$，计算${w^o}$，用户发送${w^o}$以及一个${w^o}$相对于$w$的离散对数的零知识证明给AA；

② AA选取k+3个随机数$z,c,r,{r_1}, \cdots ,{r_k} \in {Z_p}$，得出DU的转换密钥，其中${N_3} = o$为DU私密拥有：

$ \begin{gathered} {\text{TK}} = (S,{K_1} = {g^{\tfrac{\alpha }{{z\left( {x + {\text{ID}} + yc} \right) }}}}{w^{or}},{L_1} = {g^r},{L_2} = {g^{xr}}, \\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {L_3} = {g^{yr}},{N_1} = {\text{ID}},{N_2} = c,{N_3} = o, \\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\{ {K_{i,2}} = {g^{{r_i}}},{K_{i,3}} = {( {{u^{{S_i}}}h} ) ^{{r_i}}}{v^{ - \left( {x + {\text{ID}} + yc} \right) r}}\} _{i \in \left[ {1,k} \right]}}) \\ \end{gathered} $

DU的取回密钥RK=z，算法输出解密私钥(TK,RK) 。

(4) ${\text{Pre - Process}}\left( {{\text{CT,TK}}} \right) \to \left( {{\text{PCT,PTK}}} \right) $：给定密文CT=(C_K,C_SE) 和转换密钥TK，用户ID分别对密文及密钥进行预处理。计算${L_4} = L_1^{{\text{ID}}}{L_2}L_3^c,{D_4} = D_{\text{1}}^{{\text{ID}}}{D_2}D_3^c$，输出预处理后的密文${\text{PCT}} = ((C,{D_4},{\{ {C_{i,1}},{C_{i,2}},{C_{i,3}}\} _{i \in \left[ {1,l} \right]}}) ,{C_{{\text{SE}}}}) $以及转换密钥${\text{PTK}} = ({K_1},{L_4},{\{ {K_{i,2}},{K_{i,3}}\} _{i \in \left[ {1,k} \right]}}) $。

(5) ${\text{Transform}}\left( {{\text{PCT,PTK}}} \right) \to {\text{CT}}'$：算法输入参数为关联属性集合S的预处理转换密钥PTK和关联访问结构(M, ρ) 的预处理密文PCT。假设S满足(M, ρ) ，令$I = \left\{ {i:\rho \left( i \right) \in S} \right\}$，则算法在多项式时间内可以计算出常数集合${\{ {\omega _i} \in {Z_p}\} _{i \in I}}$，使得$ \displaystyle\sum\limits_{i \in I} {\omega _i}{\lambda _i} = s $，其中{λ_i}是关于M的秘密值s的有效共享。因此，在S满足(M, ρ) 的情况下，解密代理DA可以计算出

$ \begin{split} E = \;&e\left( {{K_1},{D_4}} \right) = e{(g,g) ^{\alpha s}}e{(g,w) ^{\left( {x + {\text{ID}} + yc} \right) rso}}\\ F = \; &\mathop \prod \limits_{i \in I} {(e\left( {{L_4},{C_{i,1}}} \right) e\left( {{K_{i,2}},{C_{i,2}}} \right) e\left( {{K_{i,3}},{C_{i,3}}} \right) ) ^{{\omega _i}}} =\\ & e{(g,w) ^{\left( {x + {\text{ID}} + yc} \right) rs}} \end{split} $

最终输出部分解密密文${\text{CT}}' = \left( {E,F,{C_{{\rm{SE}}}}} \right)$。

(6) ${\text{Decrypt}}\left( {{\text{PK}},{\text{CT}}',{\text{RK}},{\text{VK}}} \right) \to m$：给定部分解密密文CT′ 、取回密钥RK和验证密钥VK，该算法首先计算$K = C/{(E/{F^o}) ^z}$，接着计算TAG₁=HA₁(K) 。若${\text{H}}{{\text{A}}_2}({\text{TA}}{{\text{G}}_1}||{C_{{\text{SE}}}}) \ne {\text{VK}}$，说明部分解密密文无法对应验证密钥，算法输出终止符⊥并停止。否则，计算SEK=HA₃(K) 并且恢复出明文m=SE.Decrypt(C_SE, K) 。

(7) ${\text{KeySantityCheck}}\left( {{\text{PK,TK,RK}}} \right) \to 1\;{\text{or}}\;0$：给定解密私钥(TK,RK) ，检查其是否满足以下5个条件：

① $ {\text{TK}} = (S,{K_1},{N_1},{N_2},{N_3},{L_1},{L_2},{L_3},{\{ {K_{i,2}},{K_{i,3}}\} _{i \in \left[ {1,k} \right]}}) $

且${N_1},{N_2},{N_3} \in {Z_p},{K_1},{L_1},{L_2},{L_3},{K_{i,2}},{K_{i,3}} \in G$

② ${\text{RK}} = z \in {Z_p}$

③ $e\left( {{L_1},{g^x}{g^y}} \right) = e\left( {{L_2}{L_3},g} \right) $

④ $e\left( {{K_1},{g^x}{g^{{N_1}}}{g^{y{N_2}}}} \right) = e{(g,g) ^{\alpha /z}}e{(w,L_1^{{N_1}}{L_2}L_3^{{N_2}}) ^{{N_3}}}$

⑤ 存在$i \in \left[ k \right]$，使得以下等式成立：

$ e\left( {{K_{i,3}},g} \right) e\left( {v,L_1^{{N_1}}{L_2}L_3^{{N_2}}} \right) = e({K_{i,2}},{u^{{S_i}}}h) $

SK若满足上述5个条件，则通过密钥完整性检查，算法输出1，否则输出0。

(8) $ {\text{Trace}}\left( {{\text{PK,TK,RK}}} \right) \to {\text{ID}}\;{\text{or}}\;{\text{AA}} $：给定解密私钥(TK,RK) ，如果${\text{KeySantityCheck}}\left( {{\text{PK,TK,RK}}} \right) \to 0$，则算法停止并输出⊥，表示(TK,RK) 不是合理的私钥；否则输出私钥中的N₁=ID和N₃=o。如果ID不存在，则输出AA，表示AA伪造了一个假的用户ID；否则比较o与标识为ID的有效用户的私钥家族号${o_{{\text{ID}}}}$是否相等。如果$o = {o_{{\text{ID}}}}$，则输出ID，表示用户ID泄露了解密私钥；否则输出AA，表示AA伪造了解密私钥。

4 安全性证明 4.1 选择性安全证明

定理1　若ZJL方案^[16]是选择性安全的，HA₃是从成对独立的散列函数族H中选取的，对称加密算法SE是语义安全的且涉及参数满足$ 0 < {l_{{\rm{SE}}}} \leqslant ({\rm{lb}}\left| \eta \right| - {l_{{\rm{H}}{{\rm{A}}_1}}}) - 2{\rm{lb}}\left( {1/{\varepsilon _H}} \right)$，那么本文所提A-VO-CP-ABE方案是选择性安全的。

证明　定义以下3个游戏：

Game₀：选择性安全游戏。sA挑选一个挑战访问策略(M^*,ρ^*) ，生成挑战密文和验证密钥$( {{\text{C}}{{\text{T}}^{\text{*}}}{\text{,V}}{{\text{K}}^{\text{*}}}} ) = ( {( {C_K^{\text{*}},C_{{\text{SE}}}^{\text{*}}} ) ,{\text{TA}}{{\text{G}}_2^*}} )$。明文${K^{\text{*}}} \in {G_T}$对应密文$C_K^{\text{*}}$，密文$C_{{\text{SE}}}^{\text{*}}$使用的对称密钥是SEK^*=HA₃(K) 。

Game₁：除了${\text{TAG}}_1^{\text{*}}$和SEK^*使用随机元素${R^{\text{*}}} \in {G_T}$替代生成，其他与Game₀相同。这里强调的是密文$C_K^{\text{*}}$对应的明文与${\text{TAG}}_1^{\text{*}}$,SEK^*使用的元素是随机且独立的。

Game₂：除了SEK^*使用随机串$R_{{\text{SE}}}^{\text{*}} \in {\{ 0,1\} ^{{l_{{\text{SE}}}}}}$进行替换，其他与Game₁相同。

由于ZJL方案^[16]是选择性安全的，那么在攻击者A的视角下，Game₀和Game₁是计算不可区分的。由于H是一个成对独立的哈希函数族，那么在A的视角下，Game₁和Game₂是统计不可区分的。由于SE是语义安全对称加密方案，那么A赢得Game₂的优势是可忽略的。因此，可以证明A-VO-CP-ABE方案是选择性安全的。

4.2 可验证性安全证明

定理2　若哈希函数HA₁和HA₂为拥有抗碰撞性，那么A-VO-CP-ABE方案拥有可验证性。

证明　若存在攻击者A可以攻破A-VO-CP-ABE方案的可验证性，那么能够构造一个仿真者B攻破哈希函数HA₁和HA₂的抗碰撞性。A选择2个挑战哈希函数${\text{HA}}_1^{\text{*}}$和${\text{HA}}_2^{\text{*}}$。仿真者B与攻击者A的交互如下：

参数设置阶段：B执行Setup算法，获得系统公开密钥PK和主密钥MSK，将PK中的哈希函数替换为${\text{HA}}_1^{\text{*}}$和${\text{HA}}_2^{\text{*}}$，然后将PK发送给A。

密钥查询阶段1：B使用主密钥MSK，回应A发起的解密私钥、转换密钥、解密和外包解密询问。

挑战阶段：A挑选一个消息m^*和挑战访问结构(M^*, ρ^*) ，然后B执行Encrypt算法，随机选取${K^{\text{*}}} \in {G_T}$，并计算关于K^*的密文$C_K^{\text{*}}$、${\text{TAG}}_1^{\text{*}} = {\text{HA}}_1^{\text{*}}\left( {{K^{\text{*}}}} \right) $和${\text{SE}}{{\text{K}}^{\text{*}}} = {\text{HA}}_3^{\text{*}}\left( {{K^{\text{*}}}} \right) $。接着计算出$C_{{\text{SE}}}^{\text{*}} = {\text{SE}}{\text{.Encrypt}}( {m,{\text{SE}}{{\text{K}}^{\text{*}}}} ) $和${\text{V}}{{\text{K}}^{\text{*}}} = {\text{TAG}}_2^{\text{*}} = {{\rm{HA}}} _2^{\text{*}}({\text{TAG}}_1^{\text{*}}||C_{{\text{SE}}}^{\text{*}}) $。最后，B输出挑战密文$( {{\text{C}}{{\text{T}}^{\text{*}}},{\text{V}}{{\text{K}}^{\text{*}}}} ) = ( {( {C_K^{\text{*}},C_{{\text{SE}}}^{\text{*}}} ) ,{\text{V}}{{\text{K}}^{\text{*}}}} ) $给A，并且留存VK^*、K^*和$C_{{\text{SE}}}^{\text{*}}$。

密钥查询阶段2：A按照密钥查询阶段1进行询问。

猜测阶段：A输出满足条件$f\left( {({{\boldsymbol{M}}^*},{\rho ^*}) ,{S^{\text{*}}}} \right) = 1$的属性集合S^*和部分解密密文$ {\text{CT}}' = \left( {E,F,{C_{{\text{SE}}}}} \right) $。

假设A可以攻破可验证性，B就可以通过Decrypt(PK,CT',RK^*,VK^*) 解密出消息$m \notin \left\{ {{m^{\text{*}}}, \bot } \right\}$。针对两种情形，分析A赢得游戏的可能性，首先根据CT和CT′ 可以计算出K和${\text{TA}}{{\text{G}}_1} = {\text{HA}}_1^{\text{*}}\left( K \right) $，若${\text{HA}}_2^{\text{*}}({\text{TA}}{{\text{G}}_1}||{C_{{\text{SE}}}}) \ne {\text{TAG}}_2^{\text{*}}$, 算法输出终止符⊥并停止。

(1) $\left( {{\text{TA}}{{\text{G}}_1},{C_{{\text{SE}}}}} \right) \ne \left( {{\text{TAG}}_1^{\text{*}},C_{{\text{SE}}}^{\text{*}}} \right) $，由于B知道$\left( {\text{TAG}}_1^{\text{*}}, C_{{\text{SE}}}^{\text{*}} \right)$，所以B可以攻破哈希函数${\text{HA}}_2^{\text{*}}$的抗碰撞性。

(2) $\left( {{\text{TA}}{{\text{G}}_1},{C_{{\text{SE}}}}} \right) = \left( {{\text{TAG}}_1^{\text{*}},C_{{\text{SE}}}^{\text{*}}} \right)$且$K \ne {K^{\text{*}}}$。由于${\text{TA}}{{\text{G}}_1} = {\text{HA}}_1^{\text{*}}\left( K \right) ,{\text{TAG}}_1^{\text{*}} = {\text{HA}}_1^{\text{*}}\left( {{K^{\text{*}}}} \right) $，且等式${\text{TA}}{{\text{G}}_1} = {\text{TAG}}_1^{\text{*}}$成立，故${\text{HA}}_1^{\text{*}}\left( K \right) = {\text{HA}}_1^{\text{*}}\left( {{K^{\text{*}}}} \right) $，可以攻破哈希函数${\text{HA}}_1^{\text{*}}$的抗碰撞性。

5 方案分析及实验验证 5.1 理论分析

本节从理论层面对比分析A-VO-CP-ABE方案与文献[4,16,19]的功能特性及计算开销。表1给出了功能特性方面的比较，可以看到本文方案同时拥有大属性域、可验证外包解密、用户和属性授权机构可追责多种特性，并且追责存储开销可以忽略不计。

令$\left| U \right|$代表属性全集数目，$\left| S \right|$代表数据用户属性集合的大小，$\left| I \right|$代表满足解密需求的属性集合的大小，l代表LSSS矩阵的行数，E和E_T分别代表G和G_T的模指数运算，P代表双线性映射运算，N代表系统中用户数量，${l_{{\text{H}}{{\text{A}}_2}}}$代表哈希函数HA₂的输出长度。表2给出了计算效率上的对比，可以看到本文方案将用户解密开销转移到了解密代理实体，在用户侧解密总共需要进行6次群指数运算，其中4次是在预处理过程中执行，适合计算资源受限的移动设备用户使用。

表3给出了存储开销上的对比。由于本文方案支持大属性域，不需要在公开参数中列出所有可能的属性，因此公开参数大小固定为常数。此外，与不支持外包解密的方案相比，本文方案需要额外的元素作为取回密钥，但是实现了解密开销的转移。

5.2 实验分析

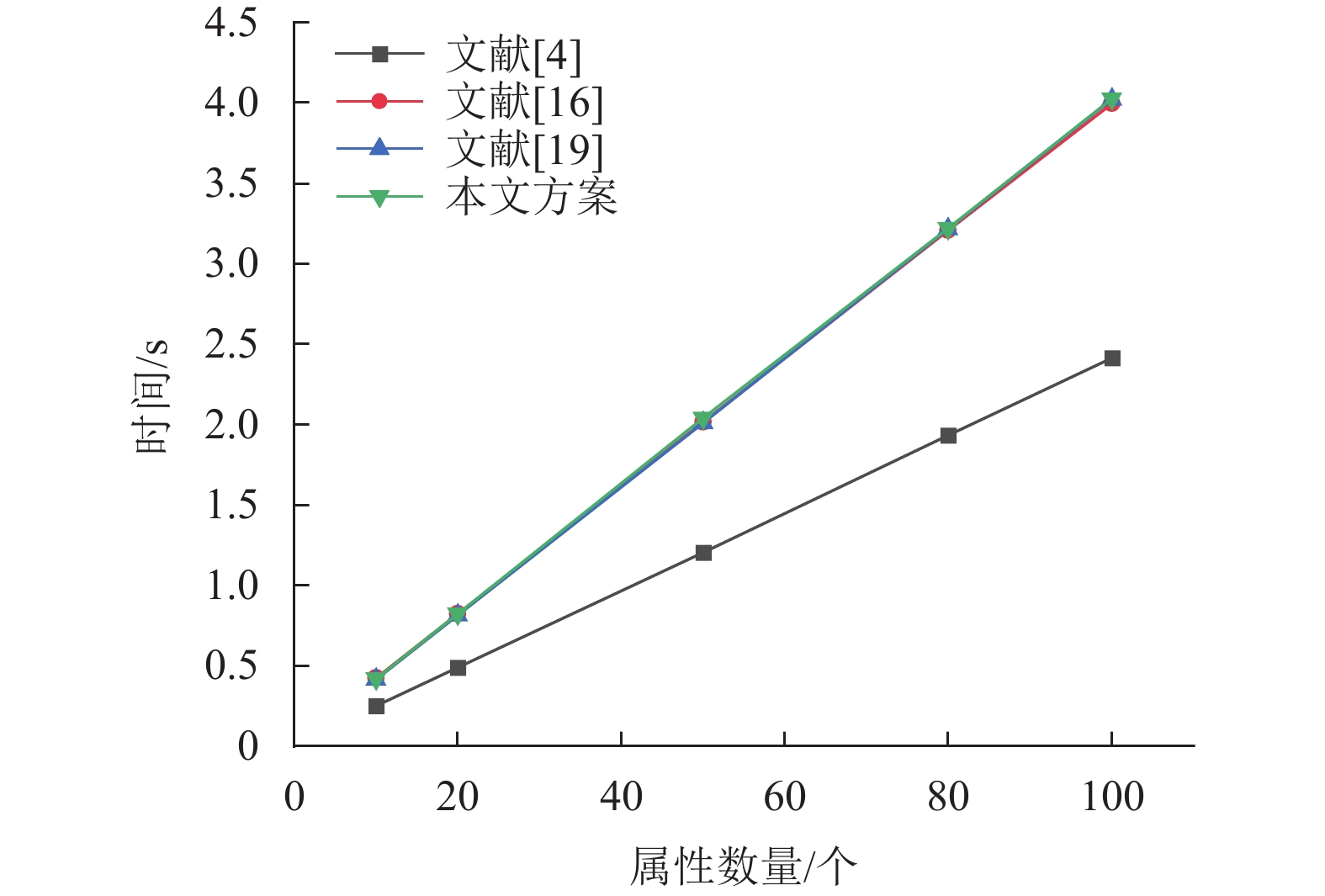
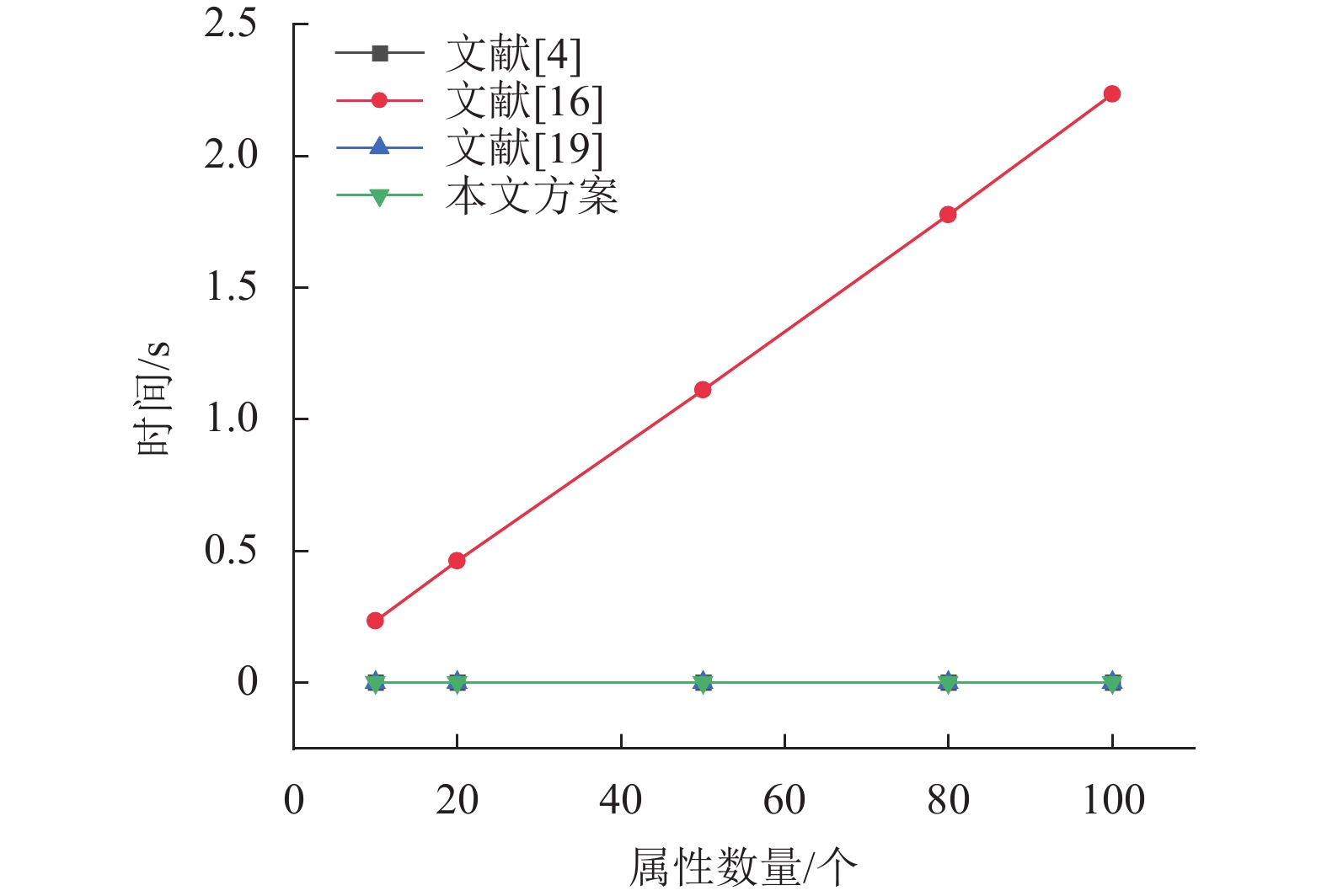
本节通过实验仿真来评估本文方案的性能。实验环境为操作系统Win10 64位，4核8线程处理器Intel(R) Core(TM) i7-7700 CPU @ 3.60 GHz，内存16 GB，同时使用了JPBC2.0库来实现椭圆曲线指数运算和双线性配对运算。性能评估主要从私钥生成、加密和解密3个方面进行对比。如图2～3所示，本文方案在私钥生成和加密阶段的时间开销与文献[16,19]基本一致，高于文献[4]，其时间开销源于实现可追责性引入的大量群指数运算。图4说明文献[16] 方案中用户侧承担了大部分解密开销，且解密开销与属性数量呈线性关系。然而文献[4,19]与本文方案均支持解密外包技术，使得用户侧的解密开销均为常数级，也因此在资源受限和不可信外包场景下能够较大提升系统性能。

6 结论

本文提出了一种采用素数阶群构造的可追责和可验证外包解密的属性基加密方案，该方案可以实现对恶意用户和属性授权机构的追踪，以确保泄露或者伪造密钥的一方得到惩罚，且追责存储开销可以忽略不计。此外，针对资源受限的设备及不可信外包场景，本文提供了可验证外包解密服务，减轻了用户侧解密负担。最后，证明了方案在标准模型下的选择性安全性、可追责性和外包解密的可验证性。目前本文方案追责和验证过程中若出现争议需要可信任第三方来解决争议并作出惩罚，下一步将研究如何利用区块链和公平支付的思想来移除可信任第三方，并实现健壮的公平性。