在电缆系统中，电缆中间接头主要用于电缆之间的相互连接。然而电缆接头受制作工艺、施工水平和运行环境等因素的影响，容易产生各种绝缘缺陷，导致电缆的绝缘性能逐渐下降，从而引发电缆故障。为保障电缆线路的稳定运行，有必要对电缆接头这一薄弱环节进行准确的状态评估^[1-3]。

电缆中间接头内部结构复杂，状态信息繁多且具有不确定性，国内外研究学者提出了多种智能算法对电缆接头绝缘状态进行评估。文献[4]揭示了电缆中间接头绝缘与其暂态电压传递函数之间的联系，并提出了对暂态电压传递函数曲线进行积分定量计算的方法，实现了对电缆中间接头绝缘状态的有效诊断，但评估时仅考虑了暂态电压因素，得到的结果并不全面；文献[5]对电缆接头的早期故障扰动波形信号特征进行定量分析，提出了基于暂态波形衰减因子刻画电缆接头早期故障发展的状态监测方法，但在确定衰减因子的阈值时依赖于相关经验准则，缺乏对电缆接头实际运行情况的考虑。而目前随着在线监测技术的发展，数据驱动技术在电缆接头状态监测中得到更为广泛的应用，如文献[6]基于电缆接头表面温度特征信息，构建了改进麻雀搜索算法优化的极限学习机模型，有效地预测了电缆接头的绝缘劣化程度；文献[7]运用改进的Wasserstein生成对抗网络训练电缆接头局部放电样本，有效提高了缺陷判别的准确率。但上述方法对于历史数据的要求较高，若数据不足或者质量较差，将影响预测模型的准确性。实际上电缆中间接头运行是不确定的动态过程，表征其运行状态的信息是时刻变化的，所以在线监测数据并不完全精确，通常会在某个区间范围内波动。在这种情况下，近些年发展起来的区间数理论和集对分析耦合方法可为解决由信息不确定性引起的数据波动问题提供新的研究思路。

鉴于以上分析，本文提出了基于区间数与集对分析耦合的电缆中间接头状态评估方法。首先采用区间数表示样本实测指标与评估等级标准，其次引入方差和均差来确定客观权重，并结合指标的趋势参数与劣化程度，构造惩罚性的状态变权向量对常权重进行修正而得到指标变权重，最后采用集对分析耦合方法，以综合联系期望最大值为度量标准，判断待评估样本的状态等级。

1 评估方法及理论 1.1 区间数理论

区间数理论是一种处理信息不确定性的数学方法。通过应用区间数理论，可将某个采样时间段内的测量数据表示为一个区间，而不仅仅是一个确定的数值。这个区间可以反映测量的不确定性范围，从而为研究对象提供更全面的信息。

区间数的定义如下^[8]：设R为实数域，对任意$ {x^{\rm{L}}},{x^{\rm{U}}} \in {\bf{R}} $且$ {x^{\rm{L}}} \leqslant {x^{\rm{U}}} $，则称[X]=[x^L，x^U]为二元区间数，其中x^L，x^U分别是区间数[X]的下、上界，并将区间中点作为区间数[X]的期望值，如式(1)所示。

$ {\text{E}}([X]) = \frac{{{x^{\rm{L}}} + {x^{\rm{U}}}}}{2} $

(1)

式(1)中：E ([X]) 为区间数[X]的期望值。

在描述电缆接头状态信息时，应用区间数表示评估样本的实测值与指标等级标准。为进一步确定评估样本与评估标准间的联系，进而构建评估模型的评定等级，本文将区间数与集对分析相结合，用以分析两个区间数之间的动态变化关系。

1.2 集对分析理论

集对分析理论是通过集对和联系度来描述研究对象之间的关系^[9-10]。对于2个具有一定联系的集合A和B可构成一个集对H(A，B) ，并可通过集对联系度来刻画这两个集合间的同异反关系，具体算式为

$ {\mu _{\left( {A,B} \right) }} = a + bz + cg $

(2)

式中：$ \mu \in [ - 1,{\text{ }}1] $为集对H(A，B) 的联系度；a、b和c分别为评估样本与指标标准等级之间的同一度、差异度和对立度，且a+b+c=1；z表示差异度系数，取值范围为[−1，1]；g为对立度系数，一般取值为−1。

对于动态不确定的评估问题，设有m组评估样本，每个评估对象有n个指标，在某阶段内的样本数据值可用区间数$ [{X_{ij}}] = [x_{ij}^{\rm{L}},x_{ij}^{\rm{U}}] $(i=1，2，···，m；j=1，2，···，n) 表示，并根据式(1)得到相应期望值为E ([X_ij])；将n项电缆接头状态评估指标全部划分为K个标准等级，其中第j个指标的第k(k=1，2，···，K) 个等级的标准分级阈值可以用区间数$ [{Y_{j,k}}] = [y_{j,k}^{\rm{L}},y_{j,k}^{\rm{U}}] $表示，相应期望值为E ([Y_j,k]) 。

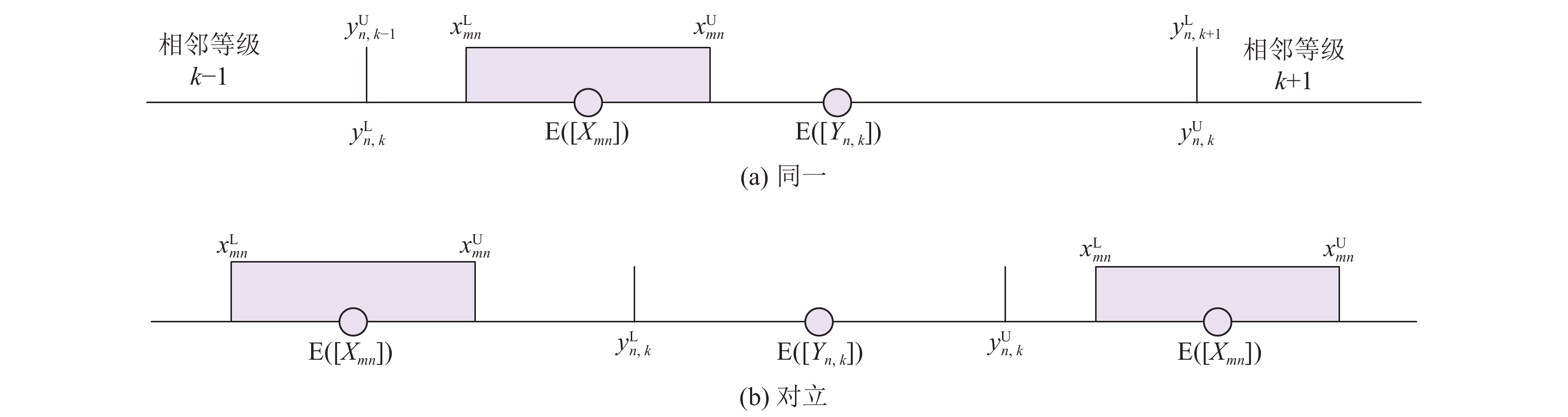
由样本数据值[X_ij]组成集合A_i，指标等级k的标准分级阈值[Y_j,k]组成集合B_k。将集合A_i、B_k构造集对H(A_i，B_k) ，并通过区间数期望间的关系来刻画该集对的同异反关系。相应的同异反评判准则定义为：若$ x_{ij}^{\rm{L}} \gt y_{j,k}^{\rm{L}} $且$ x_{ij}^{\rm{U}} \lt y_{j,k}^{\rm{U}} $时，则样本[X_ij]与等级[Y_n,k]为同一性关系；若$ x_{ij}^{\rm{L}} \gt y_{j,k}^{\rm{U}} $且$ x_{ij}^{\rm{U}} \lt y_{j,k}^{\rm{L}} $时，则样本[X_ij]与等级[Y_j,k]为对立性关系；其他情况下，样本[X_ij]与等级[Y_j,k]为差异性关系，具体关系如图1所示。

将电缆接头评估指标分为效益型指标和成本型指标，其中数值随等级增加而增大的指标为效益型指标，反之为成本型指标。基于以上分析，分别建立对应于效益型指标的联系期望计算式(3)和成本型指标的联系期望计算式(4)^[11]。

$ \begin{split} &\mu ([{X}_{ij}],[{Y}_{j,k}]) =\\ &\left\{ {\begin{array}{*{20}{l}}\dfrac{\text{E}([{X}_{ij}]) -{y}_{j,k}^{\rm{L}}}{{y}_{j,k}^{\rm{L}}-{y}_{j,k-1}^{\rm{L}}},&{y}_{j,k-1}^{\rm{L}}\le \text{E}([{X}_{ij}]) \lt {y}_{j,k}^{\rm{L}}\\ \dfrac{\text{E}([{X}_{ij}]) -{y}_{j,k}^{\rm{L}}}{\text{E}([{Y}_{j,k}]) -{y}_{j,k}^{\rm{L}}},&{y}_{j,k}^{\rm{L}}\le \text{E}([{X}_{ij}]) \lt \text{E}([{Y}_{j,k}]\text{) }\\ \dfrac{\text{E}([{X}_{ij}]) -{y}_{j,k}^{\rm{U}}}{\text{E}([{Y}_{j,k}]) -{y}_{j,k}^{\rm{U}}},&{\rm{E}}([{Y}_{j,k}]) \le \text{E}([{X}_{ij}]) \lt {y}_{j,k}^{\rm{U}}\\ \dfrac{{y}_{j,k}^{\rm{U}}-\text{E}([{X}_{ij}]) }{{y}_{j,k+1}^{\rm{U}}-{y}_{j,k}^{\rm{U}}},&{y}_{j,k}^{\rm{U}}\le \text{E}([{X}_{ij}]) \lt {y}_{j,k+1}^{\rm{U}}\\ -1,&其他\end{array}} \right. \end{split} $

(3)

$ \begin{split} &\mu ([{X}_{ij}],[{Y}_{j,k}]) =\\ &\left\{ {\begin{array}{*{20}{l}}\dfrac{\text{E}([{X}_{ij}]) -{y}_{j,k}^{\rm{L}}}{{y}_{j,k}^{\rm{L}}-{y}_{j,k+1}^{\rm{L}}},&{y}_{j,k+1}^{\rm{L}}\le \text{E}([{X}_{ij}]) \lt {y}_{j,k}^{\rm{L}}\\ \dfrac{\text{E}([{X}_{ij}]) -{y}_{j,k}^{\rm{L}}}{{\rm{E}}([{Y}_{j,k}]) -{y}_{j,k}^{\rm{L}}},&{y}_{j,k}^{\rm{L}}\le \text{E}([{X}_{ij}]) \lt \text{E}([{Y}_{j,k}]{) }\\ \dfrac{\text{E}([{X}_{ij}]) -{y}_{j,k}^{\rm{U}}}{\text{E}([{Y}_{j,k}]) -{y}_{j,k}^{\rm{U}}},&{{\rm{E}}}([{Y}_{j,k}]) \le \text{E}([{X}_{ij}]) \lt {y}_{j,k}^{\rm{U}}\\ \dfrac{{y}_{j,k}^{\rm{U}}-\text{E}([{X}_{ij}]) }{{y}_{j,k-1}^{\rm{U}}-{y}_{j,k}^{\rm{U}}},&{y}_{j,k}^{\rm{U}}\le \text{E}([{X}_{ij}]) \lt {y}_{j,k-1}^{\rm{U}}\\ {-1 },&其他\end{array}} \right. \end{split}$

(4)

式(3)~(4)中，μ ([X_ij]_, [Y_{j, k}]) 为评估样本i的第j个指标关于评估等级k的联系期望。

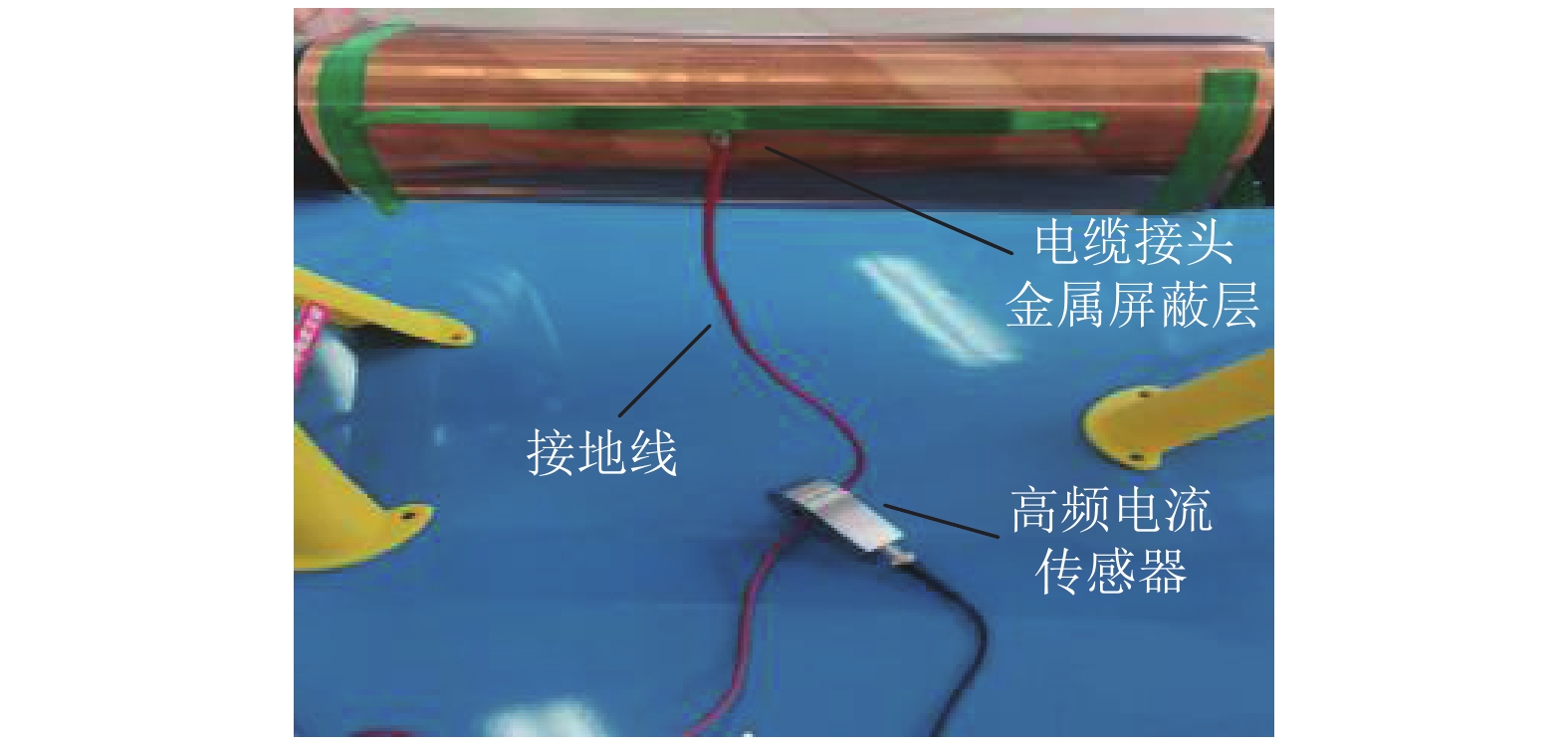
2 电缆接头状态评估指标

电缆接头状态量众多，要实时监测电缆接头的绝缘劣化情况，就需要选取合理的在线监测指标，从而构建科学的指标评估体系。目前，用于电缆接头的在线监测方法有温度监测法、护层电流法和局部放电(Partial Discharge，PD)在线监测法，其中局部放电在线监测方法的研究与实际应用较为成熟，是评估交联聚乙烯(Cross Linked Polyethylene，XLPE)电缆绝缘状态的最有效监测方法。考虑到现场监测的条件，本文采用高频电流法检测局部放电信号。如图2所示，该方法将高频电流传感器安装在电缆接头金属屏蔽层的接地线上以耦合局部放电信号。当局部放电发生时，产生的脉冲电流信号会通过同轴电缆传输进数据采集装置，经过滤波去噪、衰减放大、模数转换等步骤后，可从中提取得到PD统计特征参数。由相关文献可知，PD统计特征参数与电缆接头绝缘劣化程度具有单调相关性^[12-13]。为此，文中选取了4项PD统计特征参数作为表征电缆中间接头状态的量化指标，具体如下：

(1) 放电重复率R：指单位时间内出现的放电次数。放电重复率越高，表明局部放电发展越剧烈，电缆接头绝缘劣化情况越严重，计算模型如式(5)所示。

$ R = \frac{{50}}{M}\sum\limits_{s = 1}^M {{N_s}} $

(5)

式(5)中：M为检测工频周期总数；N_s为第s个检测工频周期的放电次数。

(2) 总放电能量W_total：指检测周期内局部放电所消耗能量的总和，计算模型为

$ {W_{{\text{total}}}} = \sum\nolimits_{i = 1} {{W_i}} $

(6)

式(6)中：W_i为t时间段内第i次放电脉冲的能量。设t时间段内第i次放电的视在放电量为q_i，起始放电电压为u_i，则放电能量为

$ {W_i} = \frac{1}{2}{q_i}{u_i} $

(7)

(3) 平均放电量Q_avg：指检测周期内局部放电量的算术平均值。该值反映了局部放电的发展变化水平，计算式如式(8)所示。

$ {Q_{{\rm{avg}}}} = \frac{{\displaystyle\sum\nolimits_{i = 1}^N {{q_i}} }}{N} $

(8)

式(8)中：q_i为第i次放电的视在放电量；N为检测周期内的局部放电次数。

(4) 最大放电量Q_max：指检测周期内局部放电量的最大值。该值反映了电缆接头绝缘损坏的严重程度，计算模型为

$ {Q_{\max}} = \max \{ {q_1},{q_2}, \cdots ,{q_i}\} $

(9)

式(9)中：q_i为第i次放电的视在放电量。

由于指标量纲不统一，导致指标间无法进行直接比较，所以需要对指标区间数据$ [{X_{ij}}] = [x_{ij}^{\rm{L}},x_{ij}^{\rm{U}}] $进行规范化处理，得到$ [{O_{ij}}] = [o_{ij}^{\rm{L}},o_{ij}^{\rm{U}}] $。由于上述指标均为效益型指标，采用式(10)进行规范化处理。

$ \left\{ \begin{gathered} o_{ij}^{\rm{L}} = \frac{{x_{ij}^{\rm{L}} - \mathop {\min }\limits_i \left\{ {x_{ij}^{\rm{L}}} \right\}}}{{\mathop {\max }\limits_i \left\{ {x_{ij}^{\rm{U}}} \right\} - \mathop {\min }\limits_i \left\{ {x_{ij}^{\rm{L}}} \right\}}} \\ o_{ij}^{\rm{U}} = \frac{{x_{ij}^{\rm{U}} - \mathop {\min }\limits_i \left\{ {x_{ij}^{\rm{L}}} \right\}}}{{\mathop {\max }\limits_i \left\{ {x_{ij}^{\rm{U}}} \right\} - \mathop {\min }\limits_i \left\{ {x_{ij}^{\rm{L}}} \right\}}} \\ \end{gathered} \right. $

(10)

式(10)中：$ o_{ij}^{\rm{L}} $为样本i的第j个指标的规范化数值的下界，$ o_{ij}^{\rm{U}} $为样本i的第j个指标的规范化数值的上界。

3 指标权重的确定 3.1 基于指标数据波动性的客观权重确定

客观权重是基于指标数值的大小，并通过一定的标准或逻辑规则，对指标进行定量化的赋值。从数据波动性的角度考虑，若指标数据波动性越大则应赋予其较大的权重。相反，若指标数据波动性越小则应赋予其较小的权重。为此，本文引入方差T 和均差V 来衡量指标数据的波动性，从而赋予指标的客观权重^[14]。

对于以区间数$ [{X_{ij}}] = [x_{ij}^{\rm{L}},x_{ij}^{\rm{U}}] $表示的电缆接头运行数据，可构成原始决策矩阵$ {\boldsymbol{X'}} = {\left( {[{X_{ij}}]} \right) _{m \times n}} $，对原始区间数指标值进行标准化处理，得标准化决策矩阵$ {\boldsymbol{P}} = \left( {\left[ {{P_{ij}}} \right]} \right) _{m \times n} = \left( {[p_{ij}^{\rm{L}},p_{ij}^{\rm{U}}]} \right) {}_{m \times n} $，其中

$ p_{ij}^{\rm{L}} = \frac{{x_{ij}^{\rm{L}}}}{{\sqrt {\displaystyle\sum\limits_{i = 1}^m {{{\left( {x_{ij}^{\rm{U}}} \right) }^2}} } }} $

(11)

$ p_{ij}^{\rm{U}} = \frac{{x_{ij}^{\rm{U}}}}{{\sqrt {\displaystyle\sum\limits_{i = 1}^m {{{\left( {x_{ij}^{\rm{L}}} \right) }^2}} } }} $

(12)

式(11)～(12)中：$ p_{ij}^{\rm{L}} $为标准化处理后区间指标数据的下界，$ p_{ij}^{\rm{U}} $为标准化处理后区间指标数据的上界。在区间数表示下，电缆接头各项指标的标准差T和平均差V定义为

$ \begin{split} {T_j} =& \frac{1}{m}{\sum\limits_{i = 1}^m {\left( {{w_j}[{p_{ij}}] - {w_j}\frac{1}{m}\sum\limits_{k = 1}^m {[{p_{kj}}]} } \right) } ^2} = \\ & {w_j}\frac{1}{m}\sum\limits_{i = 1}^m {{d^2}\left( {[{p_{ij}}],[{p_j}]} \right) } \end{split} $

(13)

$ \begin{split} {V_j} =& \frac{1}{m}\sum\limits_{i = 1}^m {\left( {{w_j}[{p_{ij}}] - {w_j}\frac{1}{m}\sum\limits_{k = 1}^m {[{p_{kj}}]} } \right) } = \\ & {w_j}\frac{1}{m}\sum\limits_{i = 1}^m {d\left( {[{p_{ij}}],[{p_j}]} \right) } \end{split} $

(14)

式中：$ [{p_j}] = \dfrac{1}{m}\displaystyle\sum\limits_{k = 1}^m {[{p_{kj}}]} $，$ d\left( {[{p_{ij}}],[{p_j}]} \right) $为各指标平均值$ [{p_j}] $与各区间指标值$ [{p_{ij}}] $的距离。其中记${\sigma _j} = \dfrac{1}{m}\displaystyle\sum\limits_{i = 1}^m {d^2}\left( [{p_{ij}}], [{p_j}] \right)$，$ {\delta _j} = \dfrac{1}{m}\displaystyle\sum\limits_{i = 1}^m {d\left( {[{p_{ij}}],[{p_j}]} \right) } $。

在求解各指标权重时，应满足所有评估指标的总标准差与总平均差之和$ F\left( w \right) $最大的条件。为此，构造如下目标函数

$ \max F\left( w \right) = \sum\limits_{j = 1}^n {\left( {\alpha {T_j} + \beta {V_j}} \right) } = {w_j}\sum\limits_{j = 1}^n {\left( {\alpha {\sigma _j} + \beta {\delta _j}} \right) } $

(15)

式(15)中：$ \alpha + \beta = 1 $，$ \alpha \geqslant 0 $，$ \beta \geqslant 0 $。求解该目标函数，得到第j个指标的权重w_j为

$ {w_j} = \left( {\alpha {\sigma _j} + \beta {\delta _j}} \right) /\sum\limits_{j = 1}^n {\left( {\alpha {\sigma _j} + \beta {\delta _j}} \right) } $

(16)

调整$ \alpha 、\beta $的值，即可求得各指标的客观权重。

3.2 基于指标劣化程度与趋势参数的变权重确定 3.2.1 变权理论基本原理

客观权重作为常权重主要用于衡量指标间的相对重要性，但并不能反映评估对象的数据变化特点。为此，文中引入变权理论对客观权重进行动态调整，使指标权重能更好反映状态量变化对评估结果的真实影响。设因素状态向量$ \overline {\boldsymbol{X}} = \left( {{{\overline x}_1},{{\overline x}_2}, \cdots ,{{\overline x}_n}} \right) $，并给出变权理论的基本定义^[15]。

定义1　一组n维变权是指n个映射：$ {w_j}\left( j = 1, 2, \cdots ,n \right) ,$ ${w_j} : {\left[ {0,1} \right]^n} \to \left[ {0,1} \right],\left. {\left( {{{\overline x}_1},{{\overline x}_2}, \cdots , {{\overline x}_n}} \right) } \right| \to {w_j}\left( {{\overline x}_1},{{\overline x}_2}, \cdots , {{\overline x}_n} \right) $，满足：

(1) 归一性：$\displaystyle\sum\limits_{j = 1}^n {{w_j}\left( {{{\overline x}_1},{{\overline x}_2}, \cdots, {{\overline x}_n}} \right) } = 1$

(2) 连续性：${w_j}\left( {{{\overline x}_1},{{\overline x}_2}, \cdots, {{\overline x}_n}} \right)$(其中，$ j = 1,2, \cdots ,n $)关于每个变元x_j连续。

(3) 单调性：${w_j}\left( {{{\overline x}_1},{{\overline x}_2}, \cdots, {{\overline x}_n}} \right)$(其中，$ j = 1,2, \cdots ,n $)关于每个变元x_j单调增加(激励性)或单调减小(惩罚性)。

设变权向量$ {\boldsymbol{W}}(\overline {\boldsymbol{X}}) = \left( {w({{\overline x}_1}) ,w({{\overline x}_2}) , \cdots ,w({{\overline x}_n}) } \right) $，则有如下定义。

定义2　1个n维惩罚性状态变权向量是指映射：$ S:\left[ {0,1} \right] \to \left[ {0,1} \right],\overline {\boldsymbol{X}} \to {\boldsymbol{S}}(\overline {\boldsymbol{X}}) = (s({\overline x_1}) ,s({\overline x_2}) , \cdots ,s({\overline x_n}) ) , $满足：

(1) 单调性：若$ {\overline x_i} \geqslant {\overline x_j} $，则$ s({\overline x_i}) \leqslant s({\overline x_j}) $。

(2) 连续性：$ s({\overline x_j}) $(其中，$ j = 1,2, \cdots ,n $) 对每个变元x_j连续。

(3) 任意的常权向量$ {{\boldsymbol{w}}^0} = \left( {w_1^0,w_2^0, \cdots, w_n^0} \right) $满足定义1中的归一性、连续性、单调性时，则

$ {\boldsymbol{W}}\left( {{\overline{\boldsymbol X}}} \right) = \frac{{{{\boldsymbol{w}}^0}{\boldsymbol{S}}\left( {{\overline{\boldsymbol X}}} \right) }}{{\displaystyle\sum\limits_{j = 1}^n {w_j^0s\left( {{{\overline x}_j}} \right) } }} = \frac{{\left( {w_1^0s\left( {{{\overline x}_1}} \right) ,w_2^0s\left( {{{\overline x}_2}} \right) , \cdots ,w_n^0s\left( {{{\overline x}_n}} \right) } \right) }}{{\displaystyle\sum\limits_{j = 1}^n {w_j^0s\left( {{{\overline x}_j}} \right) } }} $

(17)

式(17)中：$ {\boldsymbol{S}}(\overline {\boldsymbol{X}}) $表示由状态变权函数构成的变权向量；$ {\boldsymbol{W}}(\overline {\boldsymbol{X}}) $表示对应的变权向量。

3.2.2 状态函数的确定

目前，大多数文献将均衡函数引入而形成变权综合模式，但该模式并不符合电缆接头局部放电指标数据的变化特点。为此，本文对电缆接头典型缺陷的局部放电发展规律进行分析，从而构建相应的变权状态函数。

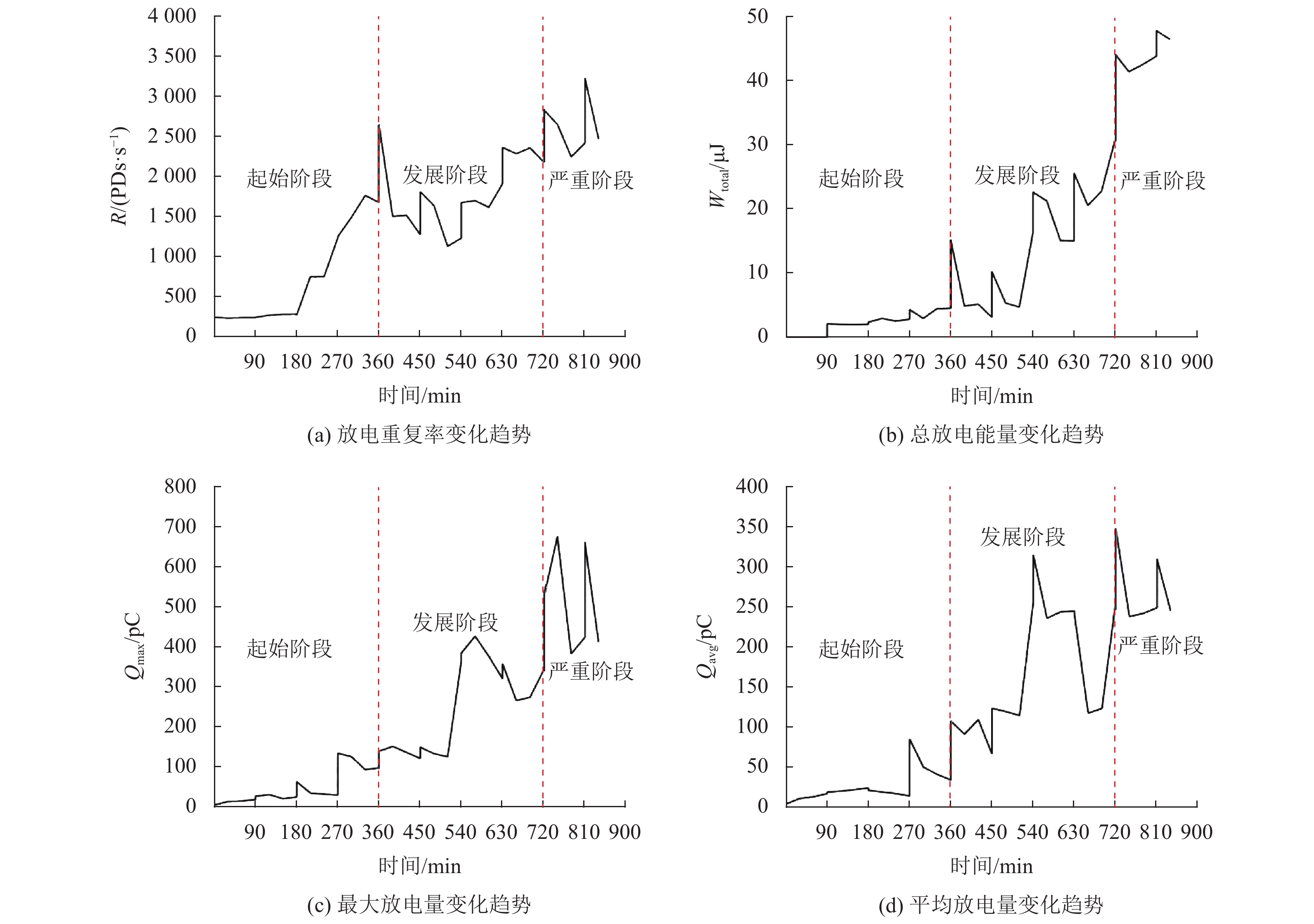
根据文献[16-17]的相关试验研究，可将电缆接头各绝缘缺陷下的PD发展过程分为起始、发展、严重3个阶段。局部放电起始阶段，PD统计特征参量在放电开始时均出现较明显的波动起伏，但很快变为平稳发展并维持相对稳定；局部放电发展阶段，电缆接头绝缘劣化程度不断加剧，PD统计特征参量均显著增大且呈近似线性增长的趋势；局部放电严重阶段，电缆接头绝缘濒临失效，PD统计特征参量幅值变化剧烈，呈非线性的变化趋势。以文献[16]中电缆接头气隙缺陷的绝缘加速劣化实验为例，各PD统计特征参量随加压时间的变化趋势见图3。由图3可知，在电缆接头绝缘劣化的过程中，PD特征量会随着时间的累积呈现阶段式的增长，但局部放电的客观不确定性会使指标区间数据具有波动性，导致实时数据无法充分反映电缆接头的具体绝缘状态。在这种情况下，对指标区间数据进行趋势分析能直观展现局部放电特征量的整体变化情况，从而更准确地反映电缆接头的实时运行状态。

基于上述分析，本文综合考量指标的劣化程度与趋势信息以构造相应的状态变权函数，从而对不同阶段的指标权重进行合理的修正，具体步骤如下：

1) 采集某时间范围内的电缆接头局部放电在线监测数据，以构造局部放电特征参量序列，并对其进行归一化处理。

2) 采用Mann-Kendall检验法对局部放电序列进行分析，定量计算各PD特征量的趋势参数UF_k，并将其作为指标权重修正的衡量标准之一。

Mann-Kendall检验法是一种非参数检验法，其优点是不需要样本遵循一定分布，也不受少数异常值干扰，可以很好揭示整体时间序列的突变情况与趋势变化。Mann-Kendall检验法的原理如下^[18]：

对于样本数为n₁的局部放电特征量序列h₁，h₂，···，h_n1，构造以下序列。

$ {S_k} = \sum\limits_{i = 1}^k {{r_i}} ,k = 2,3, \cdots ,{n_1} $

(18)

其中，

$ {r_i} = \left\{ \begin{gathered} 1,{h_i} \gt {h_j}{\text{ }}\left( {j = 1,2, \cdots ,i} \right) \\ 0,{h_i} \leqslant {h_j}{\text{ }}\left( {j = 1,2, \cdots ,i} \right) \\ \end{gathered} \right. $

(19)

式中：S_k是第i时刻数值大于第j个时刻数值个数的累计数。

在时间序列随机独立的假定下定义统计量

$ {\rm{U}}{{\rm{F}}_k} = \frac{{\left[ {{S_k} - M({S_k}) } \right]}}{{\sqrt {{{\rm{var}}} \left( {{S_k}} \right) } }},k = 1,2, \cdots ,{n_1} $

(20)

式中：S_k的均值和方差定义如下

$ M({S_k}) = \frac{{{n_1}({n_1} - 1) }}{4} $

(21)

$ {{\rm{var}}} ({S_k}) = \frac{{{n_1}({n_1} - 1) (2{n_1} + 5) }}{{72}} $

(22)

通过分析统计参量UF_k可以明确电缆接头局部放电特征序列数据的变化趋势。UF_k为标准正态分布，是按时间序列的顺序计算出的统计量序列。在给定显著性水平α后，如α=0.05，查正态分布表可以得到临界值$ {U_{0.05}} = \pm 1.96 $，若趋势参数UF_k ≥1.96或UF_k ≤−1.96，则表明上升或下降趋势显著。

3) 基于电缆接头典型缺陷的局部放电发展规律，综合考量指标的区间期望值大小与趋势信息，构造以下2种不同情况下局部放电指标的惩罚性状态变权函数，如式(23)～(24)所示。

(1) 在某个时间范围内，当指标整体上升趋势显著时，若指标区间期望值小于正常等级阈值，则无需对权重进行修正；若指标区间期望值超过正常值，则采用指数型函数对指标权重进行强惩罚。综上分析，指标的状态变权函数定义为

$ S({\text{E(}}\left[ {{O_{ij}}} \right]{\text{) }}) = \left\{ \begin{gathered} \exp (\lambda {\text{(E(}}\left[ {{O_{ij}}} \right]{\text{) }} - {a_1}{\text{) }}) {\text{, }}{a_1} \leqslant {\text{E(}}\left[ {{O_{ij}}} \right]{\text{) }} \\ {{1 ,0 }} \leqslant {\text{E(}}\left[ {{O_{ij}}} \right]{\text{) }} \lt {a_1} \\ \end{gathered} \right. $

(23)

(2) 在某个时间范围内，当指标整体上升趋势不显著时，若指标区间期望值小于正常等级阈值，则无需对权重进行修正；若指标区间期望值大于正常等级阈值且小于严重等级阈值，则采用线性函数对指标权重进行弱惩罚；若指标区间期望值超过严重等级阈值，则采用指数型函数对指标权重进行强惩罚。综上分析，指标的状态变权函数定义为

$ \begin{split} &S{\text{(E}}(\left[ {{O_{ij}}} \right]) {\text{) }} =\\ &\left\{ \begin{gathered} {c_2} + \lambda (\exp ({\text{E}}(\left[ {{O_{ij}}} \right]) - {a_2}) - 1) ,{\text{ }}{a_2} \leqslant {\text{E}}(\left[ {{O_{ij}}} \right]) \\ \frac{{{c_2} - {c_1}}}{{{a_2} - {a_1}}}{\text{E}}(\left[ {{O_{ij}}} \right]) + \frac{{{a_2}{c_1} - {a_1}{c_2}}}{{{a_2} - {a_1}}},{\text{ }}{a_1} \leqslant {\text{E}}(\left[ {{O_{ij}}} \right]) \lt {a_2} \\ {{1 ,0 }} \leqslant {\text{E}}(\left[ {{O_{ij}}} \right]) \lt {a_1} \\ \end{gathered} \right. \end{split} $

(24)

式(23)～(24)中，$ S{\text{(E}}(\left[ {{O_{ij}}} \right]) {\text{) }} $是样本i的第j个指标的状态变权函数；$ {\text{E}}(\left[ {{O_{ij}}} \right]) $是样本i的第j个指标区间期望的规范化数值；c₁、c₂为评价策略；a₁、a₂分别为第j个指标的正常和严重等级阈值；$ \lambda $为惩罚因子且大于0，主要影响指标的均衡性，当$ \lambda $越大时表明越不能容忍某些指标的严重畸变。考虑到电缆接头的设备特性，状态变权函数的各参数值可取为a₁=0.3、a₂=0.65、c₁=1、c₂=1.5、$ \lambda = 2 $。

4) 求得各指标的状态变权函数，并依据式(17)得到各项指标的变权权重。

4 电缆接头综合状态评估方法步骤

综上分析，建立基于变权与区间数−集对分析的电缆接头综合状态评估方法，具体步骤如下。

步骤1：确定电缆接头评估等级标准。依据相关导则将10 kV电缆中间接头状态划分为正常状态(Ⅰ)、注意状态(Ⅱ)、异常状态(Ⅲ)和严重状态(Ⅳ)4个等级。结合现场实际情况以及接头绝缘劣化的试验结果，得到各指标的分级标准，具体量化值见表1。

步骤2：对某阶段内的电缆接头指标数据进行区间表示，并通过式(2)分别计算评估样本和状态等级标准中各指标的区间数期望。

步骤3：构建待评估样本指标与评估等级间的集对，再基于联系期望的同异反准则计算单项指标与指标等级k间的联系期望。由于所选指标均为效益型指标，故根据式(3)进行计算。

步骤4：依据步骤2中的历史数据信息确定指标的常权重w⁰，并根据文中提出的变权理论求得各指标的变权重W_j。

步骤5：结合样本指标的变权重，得到待评估样本i与评估等级k间的综合联系期望$ {\mu _{i,k}} $为

$ {\mu _{i,k}} = \sum\limits_{j = 1}^n {{W_j}\mu \left( {\left[ {{X_{ij}}} \right],\left[ {{Y_{j,k}}} \right]} \right) } $

(25)

步骤6：确定电缆接头的状态等级。按照最大隶属度原则，将样本的最大综合联系期望值所对应的等级判断为该样本的状态等级k₀。

5 算例分析

为验证该状态评估方法的可行性和有效性，以某地10 kV电缆线路中3个电缆接头的局部放电监测数据为基础，进行电缆接头的状态评估。设置局部放电在线监测装置每隔1 h采集并储存1次数据。以3 d为1个阶段，对连续3个阶段共9 d的指标数据进行区间表示，如表2所示。

5.1 变权重计算 5.1.1 客观权重计算

根据3.1节提出的方法确定各指标的客观权重。取3个电缆接头在时间段t₁的监测数据，首先按式(11)和(12)进行指标值的规范化；其次计算各指标平均值与各区间指标值的距离，以求解式(15)的目标函数F(w) ；最后合理设置$ \alpha 、\beta $的值来使F(w) 最大，从而得到各指标的客观权重。

$ w^{0} =(0.247\text{，}0.250\text{，}0.255\text{，}0.248) $

5.1.2 变权权重计算

取各电缆接头在某时间段内的数据集构建局部放电特征序列，然后依据式(18)~(22)计算局部放电特征序列的趋势参数UF_k，并绘出相应的趋势变化曲线。根据曲线的变化可判断局部放电指标在该时间段内是否有显著的上升趋势，若趋势变化曲线在$ {U_{0.05}} = + 1.96 $临界线附近上下波动且多次超过临界线，则表明该指标的上升趋势显著，可依据式(23)确定指标的状态变权函数；其他情况下则依据式(24)确定状态变权函数。最后由式(17)计算该时间段内的各指标变权权重，计算结果如表3所示。

5.2 电缆接头的综合状态评估

以时间段t₁内的电缆接头C₁为例，取该阶段的指标区间数据，将指标数据与表1的指标等级区间组成集对，应用式(4)分别得到样本实测值与正常、注意、异常和严重等级标准间的联系期望，即μ([X_1j], [Y_j,1])=[0.9914, 0.885, −0.0375, −0.02]、μ([X_1j], [Y_j,2])=[−0.4957, −0.5575, 0.075, −0.51]、μ([X_1j], [Y_j,3])=[−1, −1, 0.0375, −1]、μ([X_1j],[Y_j,4])=[−1, −1, −1, −1]，进而结合各项指标的变权权重，依式(25)求得电缆接头C₁的综合联系期望μ_1,k=[0.4546, −0.3662, −0.7303, −1.000]，最后根据最大综合联系期望值判断该电缆接头的状态等级。各阶段的电缆接头状态评估结果如表4所示。从表4可以看出，本文评估结果与现场检修结果吻合度高，准确率可达88.9%。分析评估结果不吻合的电缆接头C₂可知，在时间段t₂内，放电重复率R落在等级Ⅰ，其他指标则落在等级Ⅱ。结合各项指标的变权重，将该电缆接头定为注意等级更为合理。究其原因，现场检修人员主要通过监测某项指标是否越限来判断电缆接头的状态等级，具有一定的局限性，而本文方法综合考虑了多项局部放电指标的影响，所得到的评估结果则更为准确。

5.3 不同评估方法对比

为进一步验证所提评估方法的先进性，采集了不同电缆接头的100组局部放电监测数据进行对比测试，其中15组局部放电数据由于远超过规定阈值被归结为故障数据，85组为正常数据。将局部放电数据分别代入传统集对分析法^[10]、常权与区间数−集对分析法以及本文方法进行分析计算，其中评估等级为正常和注意的都归结为正常状态。各方法的识别率对比如表5所示。

从表5可知，由传统集对分析法得到的评估结果与实际结果偏差最大。而相较于采用常权与区间数−集对分析法，本文方法的评估准确率则更高。综上所述，本文方法不仅解决了状态信息及等级边界的动态不确定性问题，而且综合考虑了指标幅值与趋势信息对指标权重的影响，优化了评估模型，提高了评估结果的客观性和可信度。

6 结论

(1) 针对电缆接头状态信息具有动态不确定性的特点，提出基于区间数与集对分析耦合的电缆接头状态评估方法。该方法分析了样本实测指标区间值与评估等级标准间的集对同异反关系，并以集对的综合联系期望最大值为依据，判断电缆接头的状态等级。

(2) 基于局部放电指标的劣化程度与趋势信息，构建了惩罚性状态变权函数对指标常权重进行动态修正，克服了传统变权函数忽略指标趋势变化影响的不足。

(3) 算例分析表明，提出的状态评估方法能够客观、准确地评估电缆接头的状态。对于电缆接头绝缘状态的在线监测具有应用价值。