新兴物联网技术正在推动许多新的计算需求和延迟敏感应用的发展，如自动驾驶汽车、人脸识别和虚拟/增强现实。由于通常不可预测的网络延迟和昂贵的带宽，传统的云计算无法满足延迟敏感型应用程序对时延的严格要求。移动边缘计算(Mobile Edge Computing, MEC) 将计算密集型或延迟敏感型任务的处理转移到靠近移动设备端侧的MEC服务器中，研究表明，MEC可以减小时间延迟和能量消耗^[1-3]。

现有的MEC系统架构能为用户设备提供服务，但通信信道处于深衰落时，无法保证通信质量，导致通信成本和计算复杂度高。因此，提高信道质量和抑制干扰等方面受到越来越多的关注。可重构智能反射面(又称智能反射面) (Reconfigurable Intelligent Surface，RIS) ，其面板由低成本、适应性强的反射单元组成，可以通过改变相移巧妙地反射入射信号。RIS通过信号增强和调节电磁波形，从而提高网络信道质量和传输功率效率，是一种有望改变无线电传播环境的最新技术^[4-6]。基于RIS辅助的边缘计算可以提高通信质量，以优化功率分配、服务器计算频率、执行时间和RIS相移等性能指标，国内外研究团队在这些方面已经进行了深入的研究。

此外，新兴物联网技术的另一个主要挑战是电源问题，为了延长电池的使用寿命和提高计算性能，文献[7-8]考虑了利用RIS来提高基于无线电力传输的MEC物联网网络的能量传输和通信效率。文献[9]考虑了能量采集无线供电传感器网络的资源管理与分配，可再生能量采集系统可以显著提高未来物联网设备电池的续航能力。文献[10]考虑了具有波束形成感知无线接入点的RIS辅助无线供电MEC网络，并提出了使系统的总计算速率最大化的优化问题。但是以上工作仅考虑了单RIS辅助无线通信的场景。

基于此，文献[11]提出了一种基于最小二乘交替信道估计方法，可以估计级联信道状态信息，且适当地放置反射单元数目，可以提高估计精度。文献[12]考虑了双RIS辅助下多输入单输出毫米波通信系统，通过联合优化主动波束形成和被动波束形成使加权速率最大化，但忽略了计算任务在本地计算的情况。文献[13-14]在双RIS辅助MEC系统下，通过联合优化用户的发射功率、卸载比例和RIS的相移，在有限的资源下最大限度地降低用户的能源消耗。文献[15]提出了在非完美信道的前提下双RIS辅助通信的情况，采用交替优化和凹凸过程算法对双RIS相移和发射波束进行联合优化设计，有效地减少系统能量消耗。文献[16]考虑了在双RIS辅助下行无线携能系统下，采用交替优化、半定松弛等算法，在保证信息传输安全和能量要求的前提下使总传输速率最大化。

基于以上讨论，现有的工作缺乏在MEC系统具有能量收集的场景下考虑双RIS辅助的情况。因此，本文考虑了在双RIS辅助的MEC系统中，多用户可以在同一个时隙进行能量收集，并以收集到的能量进行计算卸载和本地计算，在用户设备能量受限的情况下，使用户在有限的时间内加权计算比特数目最大化。此外，本文考虑了比文献[13]使用的半定松弛(Semidefinite Relaxation，SDR)更低复杂度的交替方向乘子法(Alternating Direction Method of Multipliers，ADMM)对RIS的相移进行求解，有效减少系统计算时间。

本论文的主要贡献概述如下：(1) 首先，提出基于双RIS辅助多用户能量采集移动边缘计算系统的计算吞吐量最大化问题。考虑将总时间周期T划分为N个时隙，用户设备可以在每个时隙内随机获取能量。(2) 其次，建立的计算吞吐量最大化问题，由于变量高度耦合导致其非凸，难以直接进行求解，所以需要将该非凸问题解耦为3个子问题分别进行优化。其中，双RIS的相移优化问题仍属于非凸问题，本文将采用ADMM算法对RIS的相移进行求解。(3) 最后实验仿真结果表明，在消耗较少系统计算时间的情况下，本文所提方案与基于SDR算法方案获得的系统性能增益相当，相较于其他基准方案，本文所提方案有显著的性能增益。

1 系统模型与问题建造

本文考虑了现实场景中用户设备与基站之间的通信，通常由于信道的时变衰落特性而使信号受到大幅度衰落。可以考虑通过部署RIS来提高信道质量，由于一个RIS的覆盖范围比较有限，为了扩大覆盖区域、用户设备可以选择更多的链路进行通信，本文考虑了一种基于双RIS辅助多用户能量采集MEC系统。系统由2个RIS、1个配备了服务器的基站(Base Station, BS) 和多个单天线用户设备所构成，系统模型如图1所示。

为了便于表达，记$ {{k}} \in \mathcal{K} \triangleq \left\{ {\left. {1, \cdots ,K} \right\}} \right. $为用户设备集合中的第k个用户设备，每个用户设备都可以进行能量采集和处理到达的计算任务；记$m \in {\mathcal{M}_j} \triangleq \left\{ {1, \cdots ,{M_j}} \right\}$，$ \forall j \in \left\{ {1,2} \right\} $为RIS j的反射单元集合中的第$m$个反射单元；配备了服务器的基站可以与$ K $台单天线用户设备进行通信，为用户设备提供计算服务。每一个用户设备处理计算任务的时间周期为$ T $，并将其划分为时隙长度相同的$ N $个时隙，时隙长度$ {\text{τ }} = T/N $，用$ n\in \mathcal{N}\triangleq \{1,\cdots ,N\} $表示第$n$个时隙。

1.1 用户本地计算模型

用$l_{k,n}^{{\rm{loc}}}$表示第k个用户设备在第n个时隙进行本地计算的任务输入比特数，第k个用户设备本地处理每比特计算任务所需要的CPU周期数目为$ {C_k} $。用户设备通过动态电压频率调节技术根据完成计算任务所需CPU周期数进行动态调节CPU速率$ {f_k} $，因此第k个用户设备在第n个时隙完成比特数目为$l_{k,n}^{{\rm{loc}}}$，通过公式${f_k} = \dfrac{{l_{k,n}^{{\rm{loc}}}{C_k}}}{\tau }$变换可得$l_{k,n}^{{\rm{loc}}} = \dfrac{{{f_k}\tau }}{{{C_k}}}$。用$ E_{k,n}^{{\rm{loc}}} $ 表示第k个用户设备在第n个时隙本地计算消耗的能量，建模本地计算消耗的能量模型^[1]为

$ E_{k,n}^{{\rm{loc}}} = {\zeta _k}{C_k}l_{k,n}^{{\rm{loc}}}\dfrac{{C_{k,}^2{{\left( {l_{k,n}^{{\rm{loc}}}} \right) }^2}}}{{{\tau ^2}}} = \dfrac{{{\zeta _k}C_k^3{{\left( {l_{k,n}^{{\rm{loc}}}} \right) }^3}}}{{{\tau ^2}}} $

(1)

式中：$ {\zeta _k} $为与用户设备的处理器芯片架构有关的电容系数。

1.2 用户计算卸载模型

本文考虑无源双RIS辅助通信，不支持在RIS处完成信道估计。可以考虑先关闭RIS 2，又由于信道估计通常需要一段时间信号的收集和处理，所以用户设备应在时隙n内发送信号到达RIS 1，RIS 1接收到信号并进行叠加，RIS 1将处理后的信号反射到达基站，基站接收叠加后的信号并进行信道估计。从而获得用户设备-RIS 1-基站的信道状态信息，同理可获得用户设备-RIS 2-基站的信道状态信息^[17-18]。由于无线信道路径损耗严重，本文不考虑RIS 1与RIS 2之间反射的情况^[15]。用$ {{\boldsymbol{u}}_{1,k,n}} \in {\mathbb{C}^{{M_1} \times 1}} $和$ {{\boldsymbol{u}}_{2,k,n}} \in {\mathbb{C}^{{M_2} \times 1}} $分别表示用户设备k在时隙n与RIS 1和RIS 2之间的信道增益，用$ {{\boldsymbol{g}}_{1,n}} \in {\mathbb{C}^{1 \times {M_1}}} $和$ {{\boldsymbol{g}}_{2,n}} \in {\mathbb{C}^{1 \times {M_2}}} $分别表示在第n个 时隙RIS 1和RIS 2与基站之间的信道增益。用${{\boldsymbol{\varTheta}} _{j,n}} = $ $ {\rm{diag}}\left( {{{\rm{e}}^{j{\theta _{j,1,n}}}}, \cdots ,{{\rm{e}}^{j{\theta _{j,{M_j},n}}}}} \right) \in {\mathbb{C}^{{M_j} \times {M_j}}} $表示第n个时隙RIS$ j $的对角相移矩阵，其中$ \forall m \in {\mathcal{M}_j} \triangleq \left\{ {1, \cdots ,{M_j}} \right\} $，$ {\theta _{j,m,n}} \in \left[ {0,2{\text{π }}} \right] $，$ \forall j \in \left\{ {1,2} \right\} $。则用户设备k在时隙n与基站之间通信的有效信道可以表示为^[15]

$ {h_{k,n}} = {{\boldsymbol{g}}_{2,n}}{{\boldsymbol{\Theta}} _{2,n}}{{\boldsymbol{u}}_{2,k,n}} + {{\boldsymbol{g}}_{1,n}}{{\boldsymbol{\Theta}} _{1,n}}{{\boldsymbol{u}}_{1,k,n}} $

(2)

建模第k个用户设备在时隙n的信噪比表示为

$ {\gamma _{k,n}} = \frac{{{p_{k,{{n}}}}{{\left| {{h_{k,n}}} \right|}^2}}}{{{\sigma ^2}}},\forall k \in \mathcal{K},\forall n \in \mathcal{N} $

(3)

式中：$ {\sigma ^2} $为接收机加性高斯白噪声的功率，$ {p_{k,{{n}}}} $为第k个用户设备在第n个时隙的发射功率。基于用户设备的信噪比，可以得到第k个用户设备在第n个时隙的上行链路传输速率^[3]：

$ {R}_{k,n}={B}_{k}{\rm{lo}}{{\rm{g}}}_{2}\left(1+{\gamma }_{k,n}\right) ={B}_{k}{\rm{lo}}{{\rm{g}}}_{2}\left(1+\dfrac{{p}_{k,{n}}{\left|{h}_{k,n}\right|}^{2}}{{\sigma }^{2}}\right) $

(4)

式中：$ {B_k} $为第k个用户设备在上行链路进行计算任务卸载时需要的传输频谱带宽。

用$ l_{{\text{k}},n}^{{\rm{off}}} $表示第k个用户设备在第n个时隙进行计算卸载时的计算任务输入比特数，则第k个用户设备在第n个时隙进行计算任务卸载的比特数为

$ {l}_{\text{k},n}^{{\rm{off}}}={R}_{k,n}\tau＝\tau {B}_{k}{\rm{lo}}{{\rm{g}}}_{2}\left(1+\dfrac{{p}_{k,{n}}{\left|{h}_{k,n}\right|}^{2}}{{\sigma }^{2}}\right) $

(5)

用$ E_{k,n}^{{\rm{off}}} $表示用户设备k在第n个时隙计算卸载消耗的能量，第k个用户设备在第n个时隙通过计算任务卸载所消耗的能量建模为

$ E_{k,n}^{{\rm{off}}} = \tau {p_{k,{{n}}}} $

(6)

1.3 用户能量因果约束模型

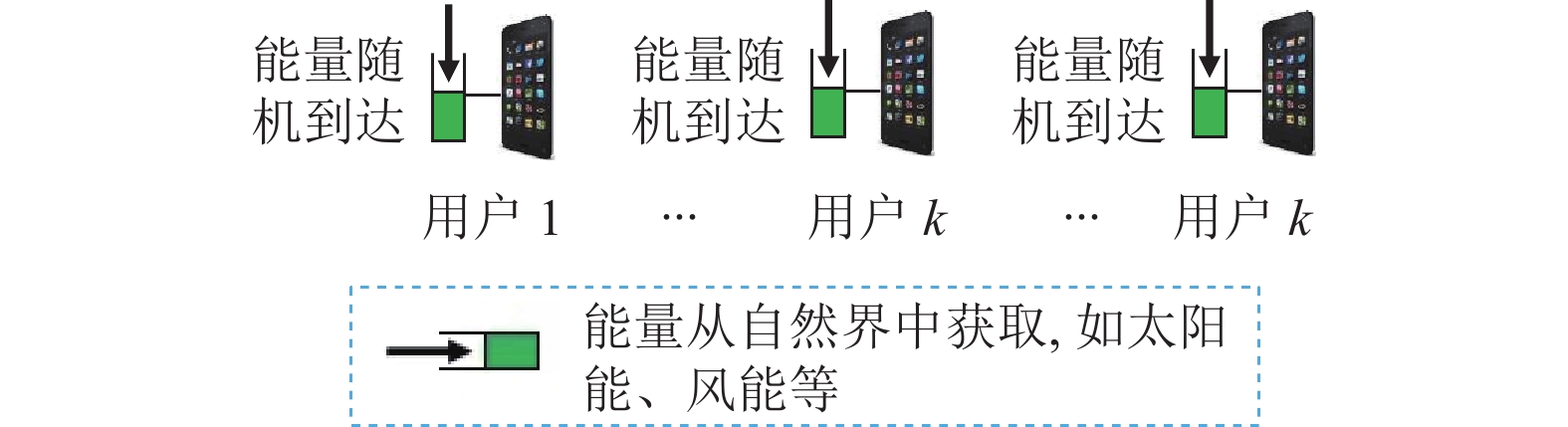
用户设备k通过能量采集装置获取动态能量^[3]，如图2所示。获取的能量来源于自然界中的太阳能、风能等；能量来源清单及其特征^[19]，如表1所示。

本文考虑用户设备的能量因果约束条件，即截止至第n个时隙，用户设备累计采集到的能量不小于用户设备累计消耗的能量，用户设备累计消耗的能量包括本地计算及计算卸载所消耗的能量。因此，用户设备的能量因果约束条件建模为

$ \begin{split}{\displaystyle {\sum }_{i=1}^{n}{E}_{k,i}^{{\rm{loc}}}}+{\displaystyle {\sum }_{{i}=1}^{n}{E}_{k,i}^{{\rm{off}}}}=& {\displaystyle {\sum }_{i=1}^{n}\frac{{\zeta }_{k}{C}_{k}^{3}{\left({l}_{k,i}^{{\rm{loc}}}\right) }^{3}}{{\tau }^{2}}}+\\ & {\displaystyle {\sum }_{i=1}^{n}\tau {p}_{k,i}}\le {\displaystyle {\sum }_{i=1}^{n}{E}_{k,\text{i}}}\text{，}\forall n\in \mathcal{N}\end{split} $

(7)

式中：$ k = 1, \cdots ,K $，$ {E_{k,n}} $为用户设备k在第n个时隙采集的能量。

1.4 优化问题构造

本文对用户设备上行链路发射功率，本地计算比特数目和双RIS的相移进行联合优化设计使系统的吞吐量最大化，构造如下基于双RIS辅助能量采集移动边缘计算资源分配优化问题。

$ \mathop {{\rm{max}}}\limits_{{\boldsymbol{p}}{{,}}{{\boldsymbol{l}}^{{\rm{loc}}}}{{,}}{{\boldsymbol{\theta }}_1},{{\boldsymbol{\theta }}_2}} \sum\nolimits_{k = 1}^K {\sum\nolimits_{n = 1}^N {\left( {{\boldsymbol{l}}_{k,{\text{n}}}^{{\rm{loc}}} + \tau {B_k}{\rm{lo}}{{\rm{g}}_2}\left( {1 + \frac{{{p_{k,{{n}}}}{{\left| {{h_{k,n}}} \right|}^2}}}{{{\sigma ^2}}}} \right) } \right) } }\tag{8a} $

(8a)

$ {\rm{s.t.}}　{\displaystyle {\sum }_{i=1}^{n}\frac{{\zeta }_{k}{C}_{k}^{3}{\left({{\boldsymbol{l}}}_{k,i}^{{\rm{loc}}}\right) }^{3}}{{\tau }^{2}}}+{\displaystyle {\sum }_{i=1}^{n}\tau {p}_{k,i}}\le {\displaystyle {\sum }_{i=1}^{n}{E}_{k,\text{i}}},\forall k\in \mathcal{K}\tag{8b} $

(8b)

$ {{\boldsymbol{l}}}_{k,n}^{{\rm{loc}}}\ge 0\text{，}{p}_{k,n}\ge 0,\forall k\in \mathcal{K},\forall n\in \mathcal{N}\tag{8c} $

(8c)

$ {\theta }_{j,m,n}\in \left[0,2{\text{π}} \right]　\forall m\in \mathcal {M}_{j},\forall j\in \left\{1,2\right\}\tag{8d} $

(8d)

式中：${\boldsymbol{p}} = \{ {p_{k,{{n}}}},\forall k \in \mathcal{K},\forall n \in \mathcal{N}\}$，${{\boldsymbol{l}}^{{\rm{loc}}}} = \{ l_{k,{{n}}}^{{\rm{loc}}},$ $ \forall k \in \mathcal{K},\forall n \in \mathcal{N}\} $，${{\boldsymbol{\theta}} _1} = \{ {\theta _{1,m,n}},\forall m \in {\mathcal{M}_1},\;\forall n \in \mathcal{N}\}$，${{\boldsymbol{\theta}} _2} = \{ {\theta _{2,m,n}}, \forall m \in {\mathcal{M}_2}, \;\forall n \in \mathcal{N}\}$。约束条件(8b) 为用户设备的能量因果约束条件，保证第k个用户设备进行本地计算和计算卸载时累计消耗的能量不超过该用户设备收集的能量；约束条件(8d) 为双RIS的相位调整范围。

2 问题优化分析与求解

针对计算系统最大吞吐量问题，由于优化变量${\boldsymbol{ p}}$、${{\boldsymbol{\theta}} _1}$和${{\boldsymbol{\theta}} _2}$三者存在耦合关系，所以本文采用交替迭代优化技术，将目标问题分为3个子问题，分别记为(P1) 、(P2) 和(P3) 。首先，子问题(P1) 是在给定${{\boldsymbol{\theta}} _1}$和${{\boldsymbol{\theta}} _2}$的情况下对${\boldsymbol{p}}$和${{\boldsymbol{l}}^{{\rm{loc}}}}$进行优化；然后，子问题(P2) 是在给定${\boldsymbol{p}}$、${{\boldsymbol{\theta}} _2}$和${{\boldsymbol{l}}^{{\rm{loc}}}}$的情况下，对${{\boldsymbol{\theta}} _1}$进行优化；最后，子问题(P3) 是在给定${\boldsymbol{p}}$、${{\boldsymbol{\theta}} _1}$和${{\boldsymbol{l}}^{{\rm{loc}}}}$的情况下，对${{\boldsymbol{\theta}} _2}$进行优化。依次迭代，得到本地计算的比特数目，双RIS的相移和用户设备发射功率的联合优化分配方案$\left( {{{\left( {{{\boldsymbol{l}}^{{\rm{loc}}}}} \right) }^*},{{\boldsymbol{p}}^*},{\boldsymbol{\theta}} _1^*,{\boldsymbol{\theta}} _2^*} \right)$。

在给定${{\boldsymbol{\theta}} _1}$和${{\boldsymbol{\theta}} _2}$的情况下，可以通过求解子问题(P1) 优化${\boldsymbol{p}}$和${{\boldsymbol{l}}^{{\rm{loc}}}}$，子问题(P1) 表示为

$ {\rm{(P1)}} \mathop {{\rm{max}}}\limits_{{\boldsymbol{p}}{{,}}{{\boldsymbol{l}}^{{\rm{loc}}}}} \sum\nolimits_{k = 1}^K {\sum\nolimits_{n = 1}^N {\left( {l_{k,{{n}}}^{{\rm{loc}}} + \tau {B_k}{\rm{lo}}{{\rm{g}}_2}\left( {1 + \frac{{{p_{k,{{n}}}}{{\left| {{h_{k,n}}} \right|}^2}}}{{{\sigma ^2}}}} \right) } \right) } } \tag{9a}$

(9a)

${\rm{ s.t.}}　{\displaystyle {\sum }_{i=1}^{n}\frac{{\zeta }_{k}{C}_{k}^{3}{\left({l}_{k,i}^{{\rm{loc}}}\right) }^{3}}{{\tau }^{2}}}+{\displaystyle {\sum }_{i=1}^{n}\tau {p}_{k,i}}\le {\displaystyle {\sum }_{i=1}^{n}{E}_{k,{i}}}\tag{9b} $

(9b)

$ {l}_{k,n}^{{\rm{loc}}}\ge 0\text{，}{p}_{k,n}\ge 0 \tag{9c}$

(9c)

式中：$ k = 1, \cdots ,K $，$ n = 1, \cdots ,N $，该子问题属于凸优化问题，可以借助凸优化软件(CVX)进行求解，得到最优解$ {\left( {{{\boldsymbol{l}}^{{\rm{loc}}}}} \right) ^*} $和$ {{\boldsymbol{p}}^*} $。

子问题(P2) 是在给定${\boldsymbol{p}}$、${{\boldsymbol{\theta}} _2}$和${{\boldsymbol{l}}^{{\rm{loc}}}}$的情况下，对${{\boldsymbol{\theta}} _1}$进行优化，子问题(P2) 表示为

$ ({\rm{P}}2) \mathop {{\rm{max}}}\limits_{{{\boldsymbol{\theta }}_1}} \sum\nolimits_{k = 1}^K {\sum\nolimits_{n = 1}^N {\left( {\tau {B_k}{\rm{lo}}{{\rm{g}}_2}\left( {1 + \frac{{{p_{k,{{n}}}}{{\left| {{h_{k,n}}} \right|}^2}}}{{{\sigma ^2}}}} \right) } \right) } } \;\,\, \tag{10a}$

(10a)

$ {\rm{s.t.}}　{\theta }_{1,m,n}\in \left[0,2\text{π} \right],\forall m\in \mathcal{M}_{1},\forall n\in \mathcal{N}\tag{10b} $

(10b)

令${{\boldsymbol{v}}_{1,n}} = {\left( {{v_{1,1,n}}, \cdots ,{v_{1,{M_1},n}}} \right) ^H} \in {\mathbb{C}^{{M_1} \times 1}}$，$ n = 1, \cdots ,N $其中$ {{{v}}_{1,m,n}} = {{\rm{e}}^{j{\theta _{1,m,n}}}} $，$ m = 1, \cdots ,{M_1} $，则原问题中的信道增益可以表示为：$|{h_{k,n}}{|^2} = |{{\boldsymbol{g}}_{2,n}}{{\boldsymbol{\varTheta}} _{2,n}}{{\boldsymbol{u}}_{2,k,n}}$ $+ {{\boldsymbol{g}}_{1,n}}{{\boldsymbol{\varTheta}} _{1,n}}{{\boldsymbol{u}}_{1,k,n}}{|^2} = |{\boldsymbol{v}}_{1,n}^H{{\boldsymbol{\varPhi}} _{1,k,n}} + {d_{2,k,n}}{|^2}$式中${{\boldsymbol{\varPhi}} _{1,k,n}} = {\rm{diag}}({{\boldsymbol{u}}_{1,k,n}}) {\boldsymbol{g}}_{1,n}^H \in {\mathbb{C}^{{M_1} \times 1}}$，$ {d_{2,k,n}} = $ ${{\boldsymbol{g}}_{2,n}}{{\boldsymbol{\varTheta}} _{2,n}}{{\boldsymbol{u}}_{2,k,n}}$。${\left| {{\boldsymbol{v}}_{1,n}^H{{\boldsymbol{\varPhi}} _{1,k,n}} + {d_{2,k,n}}} \right|^2}$进一步展开得到${\boldsymbol{v}}_{1,n}^H{{\boldsymbol{\varPhi}} _{1,k,n}}{\boldsymbol{\varPhi}} _{1,k,n}^H{{\boldsymbol{v}}_{1,n}} + {\boldsymbol{v}}_{1,n}^H{{\boldsymbol{\varPhi}} _{1,k,n}}{d_{2,k,n}} + {d_{2,k,n}}{\boldsymbol{\varPhi}} _{1,k,n}^H{{\boldsymbol{v}}_{1,n}} + {\left| {{d_{2,k,n}}} \right|^2}$。由于上述问题(P2) 仍属于非凸二次规划二次约束问题，故需要对其继续转化，令

$ {{\boldsymbol{R}}_{1,k,n}} = \left( {\begin{array}{*{20}{c}} {{{\boldsymbol{\varPhi}} _{1,k,n}}{\boldsymbol{\varPhi}} _{1,k,n}^H}&{{{\boldsymbol{\varPhi}} _{1,k,n}}{d_{2,k,n}}} \\ {{d_{2,k,n}}{\boldsymbol{\varPhi}} _{1,k,n}^H}&0 \end{array}} \right) {\kern 1pt}\tag{11} $

(11)

$ {{\boldsymbol{\bar v}}_{1,n}} = \left( {\begin{array}{*{20}{c}} {{{\boldsymbol{v}}_{1,n}}} \\ 1 \end{array}} \right) \,\tag{12} $

(12)

则子问题${\rm{(P2)}}$等价于

$ {\rm{(P2.1)}} \;\mathop {\max }\limits_{\{ {{\bar v}_{1,n}}\} } \;\;\sum\nolimits_{k = 1}^K {\sum\nolimits_{n = 1}^N {\tau {B_k}{{\log }_2}\left( {1 + \frac{{{p_{k,n}}\left( {{\boldsymbol{\bar v}}_{1,n}^H{{\boldsymbol{R}}_{1,k,n}}{{{\boldsymbol{\bar v}}}_{1,n}}} \right) }}{{{\sigma ^2}}}} \right) } } \; \tag{13a}$

(13a)

$ \text{ }{\rm{s.t.}}　　{\left|{v}_{1,m,n}\right|}^{2}=1 \tag{13b}$

(13b)

式中：$ n = 1, \cdots ,N $，本文提出低复杂度算法ADMM求解问题(P2.1) ，引入松弛变量$ {{\boldsymbol{w}}_{1,n}} $，则问题(P2.1) 等价于

$ \begin{split} & ({\rm{P2}}.{\rm{2}})\\ & \mathop {{\rm{min}}}\limits_{\left\{ {{{\overline {\boldsymbol{v}} }_{1,n}}}, \right\}\left\{ {{w_{1,n}}} \right\}} - \displaystyle\sum\nolimits_{K = 1}^K {\displaystyle\sum\nolimits_{{\rm{n}} = 1}^N {} } \tau {B_k}{\rm{lo}}{{\rm{g}}_2}\left( {1 + \dfrac{{{p_{k,n}}\left( {{\boldsymbol{\bar v}}_{1,n}^H{{\boldsymbol{R}}_{1,k,n}}{{\overline {\boldsymbol{v}} }_{1,n}}} \right)}}{{{\sigma ^2}}}} \right) \end{split} \tag{14a} $

(14a)

$ {\rm{s.t.}}　\left|{w}_{1,m,n}\right|=1\quad m=1,\cdots ,{M}_{1}+1\tag{14b} $

(14b)

$ \;\;{{\boldsymbol{w}}_{1,n}} = {{\boldsymbol{\bar v}}_{1,n}}\,\tag{14c} $

(14c)

式中：$ n = 1, \cdots ,N $，则问题(P2.2) 的增广拉格朗日函数表示为

$\begin{array}{l} L\left( {{{{\boldsymbol{\bar v}}}_{1,n}},{{\boldsymbol{w}}_{1,n}},{{\boldsymbol{z}}_{1,k,n}}} \right) = \;\quad \\ - \displaystyle\sum\nolimits_{k = 1}^K {\displaystyle\sum\nolimits_{n = 1}^N \tau {B_k}{\log _2} {\left( {1 + \dfrac{{{p_{k,n}}\left( {{\boldsymbol{\bar v}}_{1,n}^H{{\boldsymbol{R}}_{1,k,n}}{{{\boldsymbol{\bar v}}}_{1,n}}} \right)}}{{{\sigma ^2}}}} \right)} } +\\ \displaystyle\sum\nolimits_{n = 1}^N {\left( {{\rm{Re}}\left( {{\boldsymbol{z}}_{1,n}^H\left( {{{\boldsymbol{w}}_{1,n}} - {{{\boldsymbol{\bar v}}}_{1,n}}} \right)} \right) + \frac{\rho }{2}{{\left\| {{{\boldsymbol{w}}_{1,n}} - {{{\boldsymbol{\bar v}}}_{1,n}}} \right\|}^2}} \right)} \end{array}\tag{15}$

(15)

式中：$ n = 1, \cdots ,N $,${{\boldsymbol{z}}_{_{1,n}}} \in {\mathbb{C}^{({M_1} + 1) \times 1}}$ 为对应于(P2.2) 中约束的拉格朗日乘子，$ \rho \gt 0 $表示惩罚系数。设$ \left( {{\boldsymbol{w}}_{1,n}^0,{\boldsymbol{\bar v}}_{1,n}^0,{\boldsymbol{z}}_{1,k,n}^0} \right) $ 为初始原对偶变量，ADMM算法循环执行以下3个步骤^[20]。

$ {\boldsymbol{w}}_{1,n}^{i + 1} = \arg \;\mathop {\min }\limits_{{{\boldsymbol{w}}_{1,n}}} \;L\left( {{{\boldsymbol{w}}_{1,n}},{\boldsymbol{\bar v}}_{1,n}^i,{\boldsymbol{z}}_{1,n}^i} \right)\tag{16} $

(16)

${\boldsymbol{ \bar v}}_{1,n}^{i + 1} = \arg \;\mathop {\min }\limits_{{{{\boldsymbol{\bar v}}}_{1,n}}} \;L\left( {{\boldsymbol{w}}_{1,n}^{i + 1},{{{\boldsymbol{\bar v}}}_{1,n}},{\boldsymbol{z}}_{1,n}^i} \right)\tag{17} $

(17)

$ {\boldsymbol{z}}_{1,n}^{i + 1} = {\boldsymbol{z}}_{1,n}^i + \rho \left( {{\boldsymbol{w}}_{1,n}^{i + 1} - {\boldsymbol{\bar v}}_{1,n}^{i + 1}} \right)\tag{18} $

(18)

式中：$ n = 1, \cdots ,N $，可以容易地证明问题(16)存在闭合式形式解$ {\boldsymbol{w}}_{1,n}^{i + 1} = $ $ \angle \left( {{\boldsymbol{\bar v}}_{1,n}^i - {\rho ^{ - 1}}{\boldsymbol{z}}_{1,n}^i} \right) $ ，$\angle (\cdot)$为参数的相位向量。问题(17)是一个凸问题，可以通过对$ {{\boldsymbol{\bar v}}_{1,n}} $求一阶导并令其为零得到

$ \begin{split} & \displaystyle \sum\nolimits_{k = 1}^K {\dfrac{{2\tau {B_k}{p_{k,n}}{{\boldsymbol{R}}_{1,k,n}}{\boldsymbol{\bar v}}_{1,n}^{i + 1}}}{{\left( {{\sigma ^2} + {p_{k,n}}\left( {{{\left( {\bar v_{1,n}^{i + 1}} \right)}^H}{{\boldsymbol{R}}_{1,k,n}}{\boldsymbol{\bar v}}_{1,n}^{i + 1}} \right)} \right)\ln 2}}} - \\ & {\boldsymbol{z}}_{1,n}^i - \rho \left( {{\boldsymbol{w}}_{1,n}^{i + 1} - {\boldsymbol{\bar v}}_{1,n}^{i + 1}} \right) = 0 \end{split} \tag{19}$

(19)

通过化简问题(19)可以得到$ {\boldsymbol{\bar v}}_{1,n}^{i + 1} $；

通过问题(18)和问题(19)可以得到

$ {\boldsymbol{z}}_{1,n}^{i + 1} = \sum\nolimits_{k = 1}^K {\frac{{2\tau {B_k}{p_{k,n}}{{\boldsymbol{R}}_{1,k,n}}{\boldsymbol{\bar v}}_{1,n}^{i + 1}}}{{\left( {{\sigma ^2} + {p_{k,n}}\left( {{{\left( {{\boldsymbol{\bar v}}_{1,n}^{i + 1}} \right) }^H}{{\boldsymbol{R}}_{1,k,n}}{\boldsymbol{\bar v}}_{1,n}^{i + 1}} \right) } \right) \ln 2}}}\tag{20} $

(20)

通过多次迭代后可求得$ {\boldsymbol{v}}_{1,n}^* = \{ {[{\boldsymbol{\bar v}}_{1,n}^i({M_1} + 1) ]^{ - 1}}{\boldsymbol{\bar v}}_{1,n}^i $ $ (1: {M_1}) \} $，式中：$ \,\,n = 1, \cdots ,N $。

子问题(P3) 是在给定${\boldsymbol{p}}$、${{\boldsymbol{\theta}} _1}$和${{\boldsymbol{l}}^{{\rm{loc}}}}$的情况下，对${{\boldsymbol{\theta}} _2}$进行优化，子问题(P3) 表示为

$ {\rm{(P3) }}　\underset{{{\boldsymbol{\theta }}}_{2}}{{\rm{max}}}{\displaystyle {\sum }_{k=1}^{K}{\displaystyle {\sum }_{n=1}^{N}\left(\tau {B}_{k}{\rm{lo}}{{\rm{g}}}_{2}\left(1+\frac{{p}_{k,{n}}{\left|{h}_{k,n}\right|}^{2}}{{\sigma }^{2}}\right) \right) }}\tag{21a} $

(21a)

$ \text{}\text{ }{\rm{s.t.}}　{\theta }_{2,m,n}\in \left[0,2{\text{π}} \right],\forall m\in \mathcal {M}_{2} \tag{21b} $

(21b)

同理通过ADMM算法可求得${\boldsymbol{v}}_{2,n}^*$，从而求得 ${\boldsymbol{\theta}} _{2,n}^*$，式中：$ n = 1, \cdots ,N $。

算法1　交替优化算法

(a) 输入初始化可行解(${{\boldsymbol{w}}}_{1,n}^{\left(0\right) },{{\boldsymbol{z}}}_{1,k,n}^{\left(0\right) },{{\boldsymbol{\theta}} }_{1,n}^{(0)},{{\boldsymbol{\theta}} }_{2,n}^{(0)},$ $ \rho \gt 0 $)，最大迭代次数Q，式中：$ k = 1, \cdots ,K $ ，$ n = 1, \cdots ,N $；

(b) 根据${{{v}}_{j,m,n}} = {{\rm{e}}^{j{\theta _{j,m,n}}}}$关系，计算出$ {\boldsymbol{\bar v}}_{1,n}^{\left( 0 \right) } $ ，$ {\boldsymbol{\bar v}}_{2,n}^{\left( 0 \right) } $；

(c) 通过使用凸优化软件(CVX)可求解问题(9)，得到${\boldsymbol{p}}$ 和${{\boldsymbol{l}}^{{\rm{loc}}}}$；

(d) for i=0:Q

(e) 通过式(16)更新 ${\boldsymbol{w}}_{1,n}^{i + 1}$ ；

　 通过式(17)更新$ {\boldsymbol{\bar v}}_{1,n}^{i + 1} $；

　 通过式(18)更新${\boldsymbol{z}}_{1,k,n}^{i + 1}$；

(f) end

(g) 计算${\boldsymbol{v}}_{1,n}^* = \left\{ {{{\left[ {{\boldsymbol{\bar v}}_{1,n}^i\left( {{M_1} + 1} \right) } \right]}^{ - 1}}{\boldsymbol{\bar v}}_{1,n}^i\left( {1:{M_1}} \right) } \right\}$；

(h) 通过${\boldsymbol{v}}_{1,n}^*$得到${\boldsymbol{\theta}} _{1,n}^*$；

(i) 同理得到${{\boldsymbol{\theta}} _{2,n}}$的次优解${\boldsymbol{\theta}} _{2,n}^*$。

算法1复杂度分析：在算法1中问题(9) 含有NK个变量，使用凸优化软件(CVX) 进行求解，需要的时间复杂度不少于${ O}({N^{3.5}}{K^{3.5}})$^[21]；基于ADMM算法对双RIS的相移进行求解，进行了Q次迭代，需要的时间复杂度不少于${ O}(Q{N^2}K(M_1^3 +$ $M_2^3) ) $^[20]；故算法1需要的时间复杂度为${ O}({N^{3.5}}{K^{3.5}} + Q{N^2}K(M_1^3$ $ + M_2^3) ) $。

3 仿真结果分析与对比

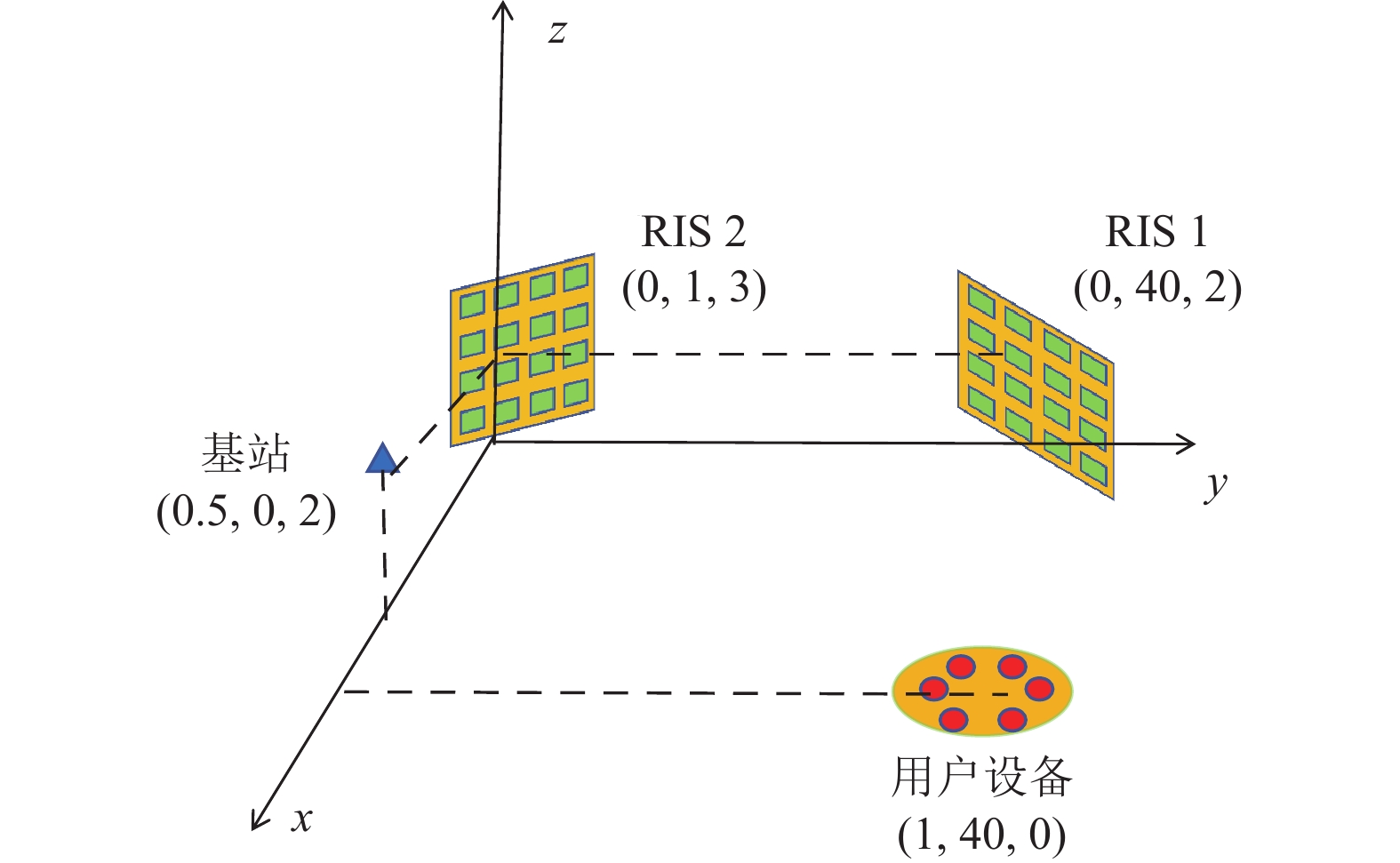
本节将提供实验结果来验证所考虑的双RIS辅助系统的性能。在三维笛卡尔坐标系下，假设BS、RIS 1、RIS 2和用户设备群的中心(参考) 点分别位于(0.5,0,2) 、(0,40,2) 、(0,1,3) 和(1,40,0) ，单位为m，如图3所示。

本文考虑莱斯衰落信道模型^[2],例如用户设备k与RIS 1之间的信道模型可以表示为：${u_{1,k,n}} = \sqrt {\dfrac{{{\beta _0}{\Omega _0}D_k^{ - \alpha }}}{{1 + {\beta _0}}}} {u_0} + \sqrt {\dfrac{{{\Omega _0}D_k^{ - \alpha }}}{{1 + {\beta _0}}}} u$，其式中：$ \alpha $ = 2.5，为路径损耗指数，${\Omega _0} = - 30\,\,{\text{dB}}$表示参考距离为1 m时的参考路径损耗，${\beta _0}$=10为莱斯因子，${D_k}$ 表示用户设备k与RIS 1之间的距离，${u_0}$=1表示视距因子，$u$表示小尺度信道衰落系数，且服从$ \mathcal{C}\mathcal{N}\left( {0,1} \right) $。对于通信和计算模型部分，在没有作额外说明时本文的参数设置如下：${B_k} = 10\,\, {\rm{MHz}}$, ${\sigma ^2} = $ $- 120\,\,{\text{d}}{\rm{Bw}}$，$ {\zeta _k} = {10^{ - 27}} $，$ {C_k} = 500 $，RIS反射单元数目$ {M_1} = {M_2} = 24 $，用户数量K=3，时隙个数N=10，时隙长度$ \tau = 0.1 $。

本文考虑了5种系统吞吐量最大化的基准方案，用于基于能量采集的多用户 MEC 系统性能比较。

(1) 基准方案 1−SDR算法方案^[13]

(2) 基准方案 2−单RIS方案^[6]：单RIS反射单元数$M = {M_1} + {M_2}$。

(3) 基准方案 3−随机相移方案：双RIS的相移随机产生。

(4) 基准方案 4−完全计算卸载方案：在双RIS辅助下，每个用户只进行计算卸载处理任务。

(5) 基准方案 5−完全本地计算方案：在没有RIS辅助的情况下每个用户只能进行本地计算。

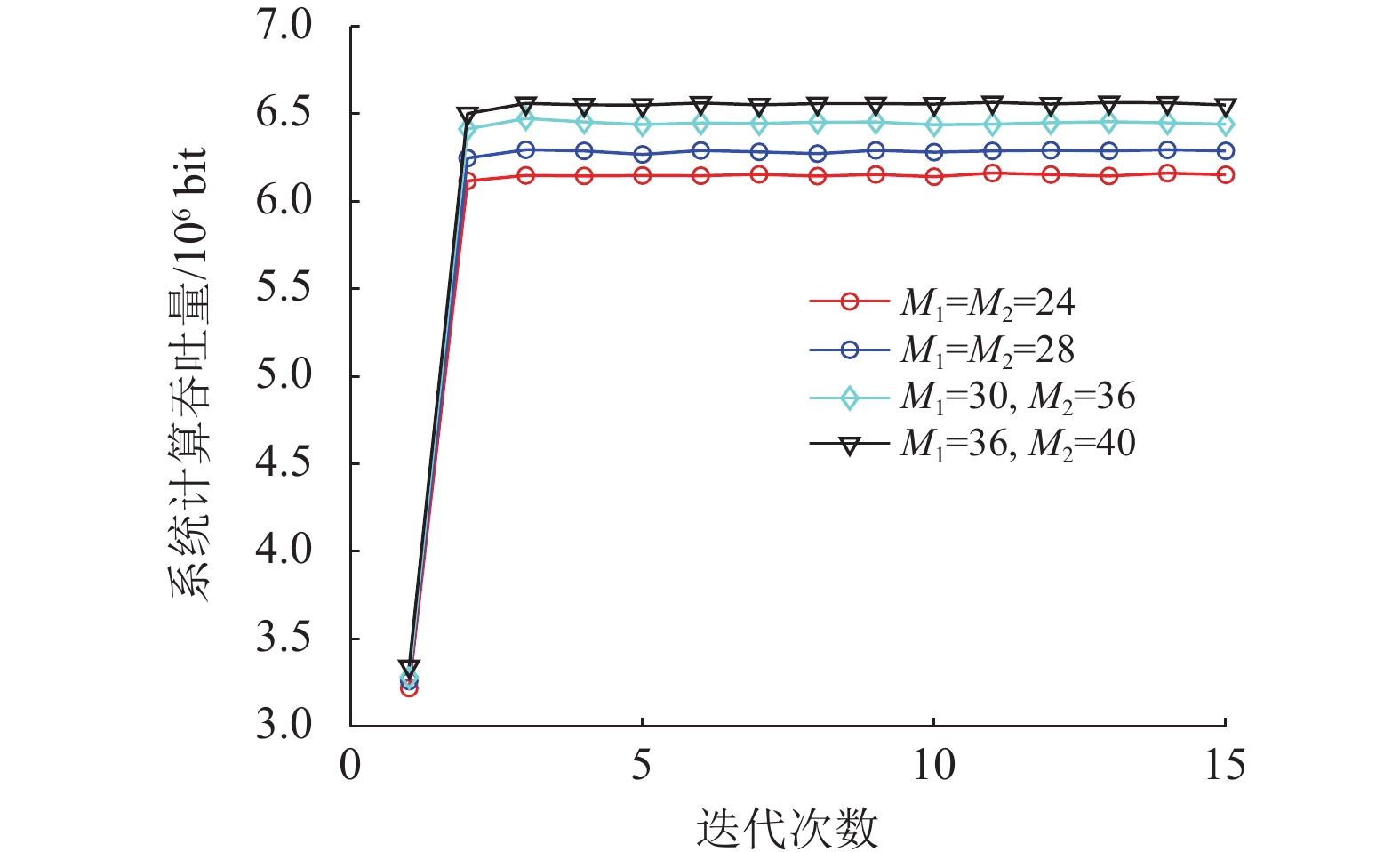
图4为不同RIS反射单元数目设置下系统总吞吐量的迭代收敛曲线图。可以看出通过本文所提算法获得系统总吞吐量首先随着迭代次数的增加单调递增，随后经过多次迭代后获得一个稳定的收敛值。并且即使在${M_1} \ne {M_2}$的情况下，同样获得稳定收敛值的效果，这体现了本文算法的有效性。此外，RIS反射元总数目越多，系统总吞吐量也在不同程度上递增。当${M_1} = 36$ , ${M_2} = 40$时，系统总吞吐量最大，这是因为增加反射单元数提高了系统空间自由度，增加了通信链路，有效地改善了通信信道，从而用户设备传输速率得到不断提升。

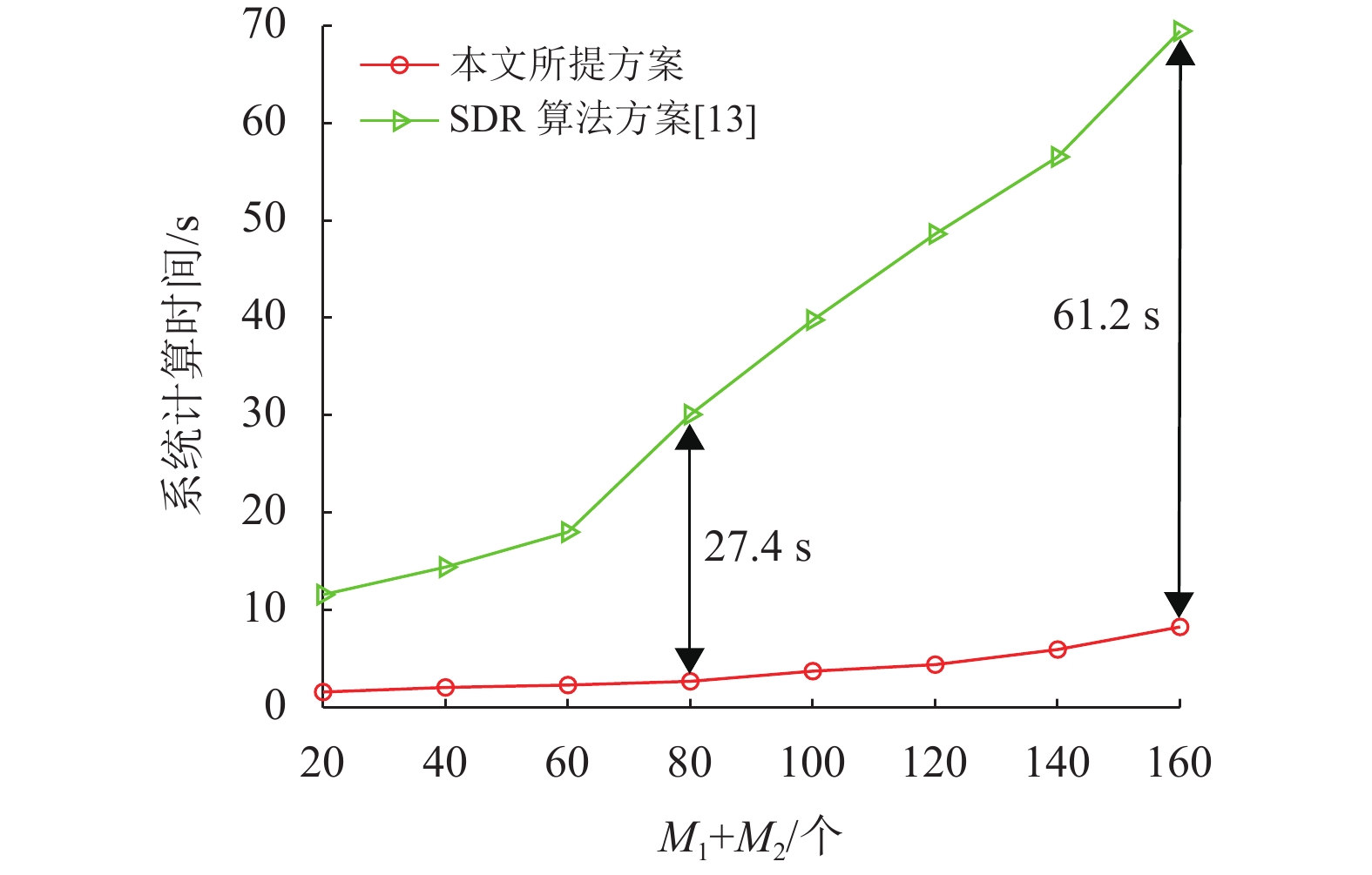
图5显示了不同反射单元数目下系统计算时间的性能曲线。当用户设备K=3，时隙数量N=5时，随着反射单元数的增加，本文提出的ADMM算法方案与基于SDR算法方案系统运行时间均增加，且本文所提方案系统运行时间明显优于SDR算法方案。这是因为计算同样多的相移，SDR算法需要调用CVX工具进行计算，需要花费大量的时间，本文所提方案可以节省这一步时间开销。随着反射单元数的增大，本文所提方案和SDR算法方案系统运行时间之间的差距也在增大。例如当反射单元数${M_1} + {M_2} = 80$时，本文所提方案节省27.4 s的系统计算时间，当反射单元总数${M_1} + {M_2} = 180$时，本文所提方案节省了61.2 s系统计算时间，显然本文所提方案具有显著的优越性，可以有效节约系统计算时间。

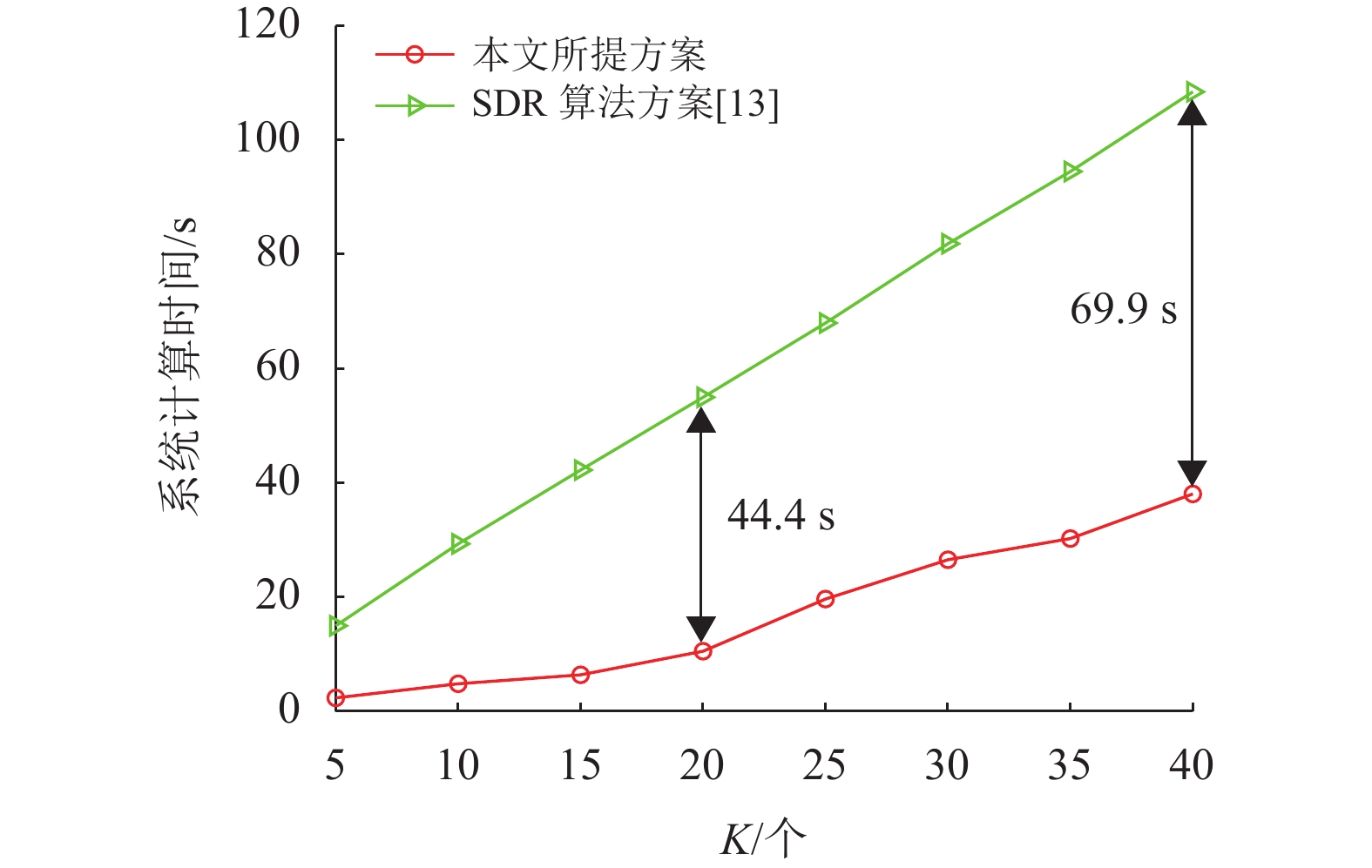
图6显示了不同用户设备数量下系统计算时间的性能曲线。当反射单元数$ {M_1} = {M_2} = 24 $，时隙数量N=3时，随着用户设备数量的增加，本文提出的ADMM算法方案与基于SDR算法方案系统运行时间均增加。对比本文所提方案与SDR算法方案性能曲线，本文所提方案系统计算时间明显优于SDR算法方案，且随着用户设备的增大，本文所提算法方案优势更加明显。例如K=20时，本文所提算法节省了44.4 s系统计算时间，当K=40时，本文所提算法节省了69.9 s系统计算时间，显然本文所提方案具有显著的优越性。

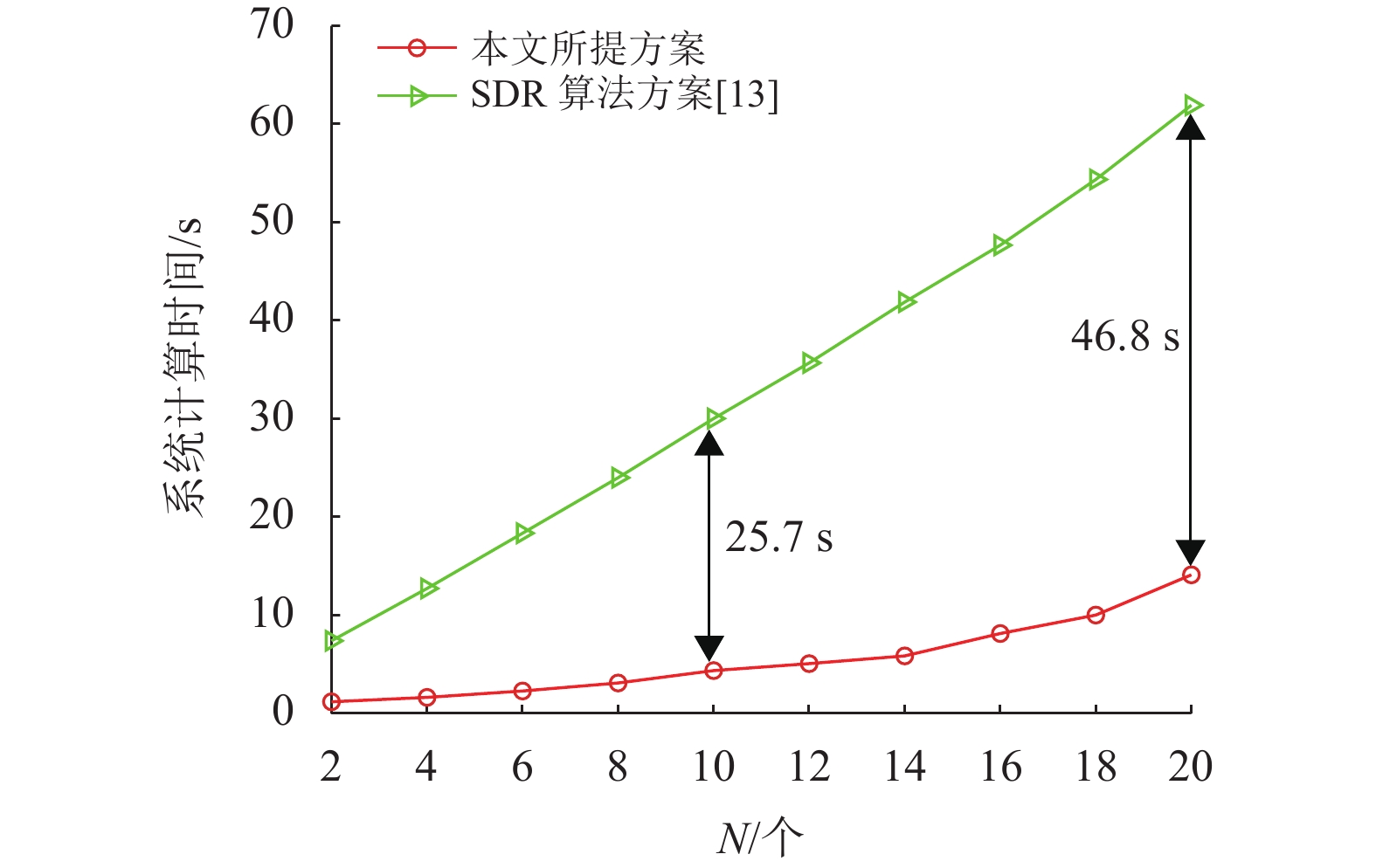
图7显示了不同时隙数量下系统计算时间的性能曲线。当反射单元数$ {M_1} = {M_2} = 24 $，时隙数量K=3时，随着时隙个数的增加，本文所提算法方案与基于SDR算法方案系统运行时间均增加。对比本文所提方案与SDR算法方案性能曲线，本文所提方案系统计算时间明显优于SDR算法方案。这是因为在N个时隙内计算同样多的相移，基于SDR算法方案需要使用CVX工具进行计算，导致消耗更多的时间。随着时隙个数的增大，本文所提算法方案优势更加明显。例如当时隙个数N=10时，本文所提方案节省了25.7 s的系统计算时间，当N=20时，本文所提方案节省了46.8 s的系统计算时间，显然本文所提方案具有显著的优越性。

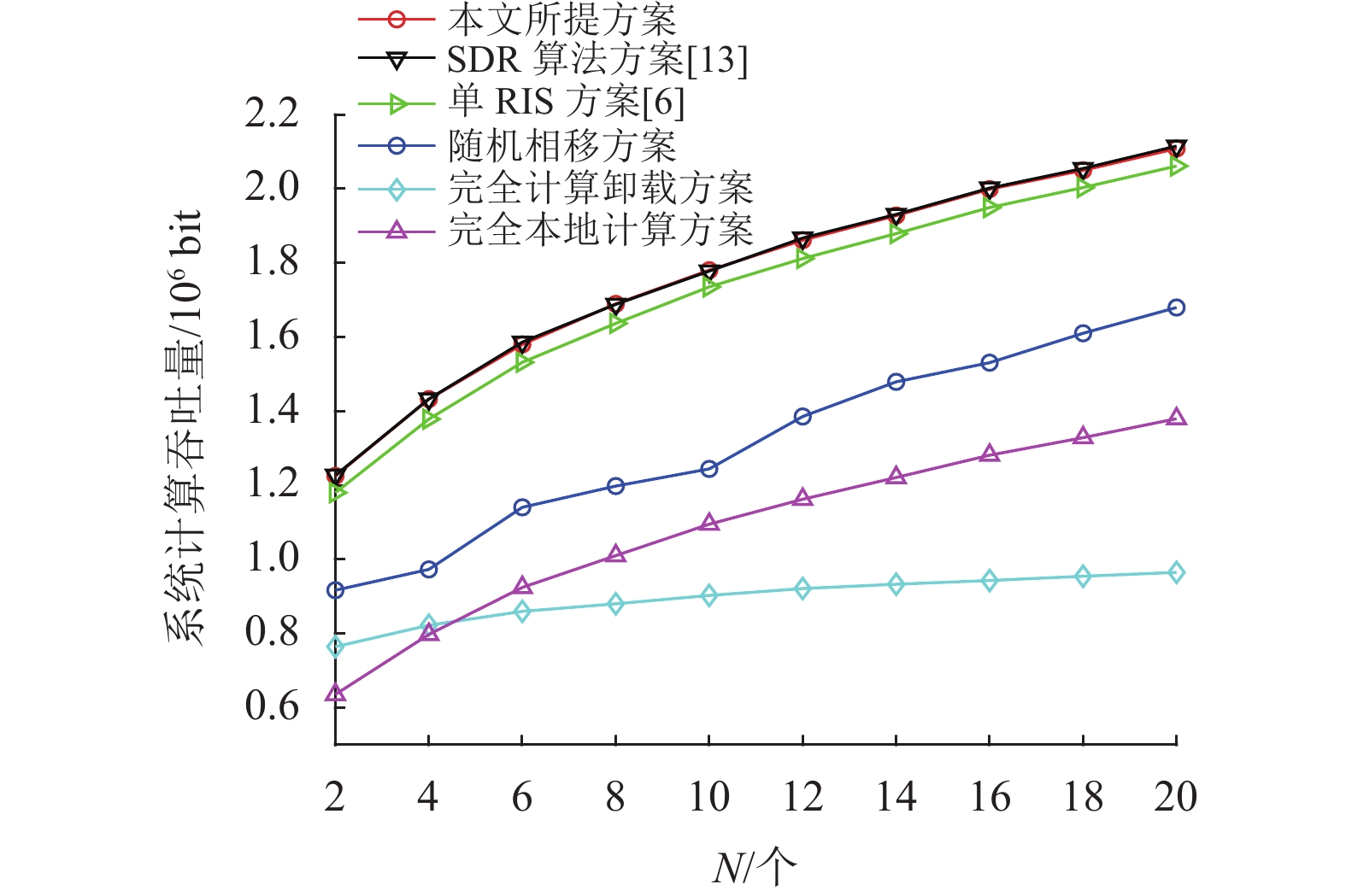
图8显示了不同时隙个数N下的系统计算吞吐量的性能曲线。其中用户个数K=3，时间周期T= 0.2 s，随着时隙个数N的增加，六种方案执行的任务输入比特总数单调递增。本文所提方案性能与基于SDR算法方案的性能相当，且与其他基准方案相比，本文所提方案获得了显著的性能增益。单RIS方案优于随机相移方案，说明了RIS相移优化对提高系统计算能力的重要性。此外，在较大的N值时，完全本地计算方案的性能优于完全计算卸载方案。

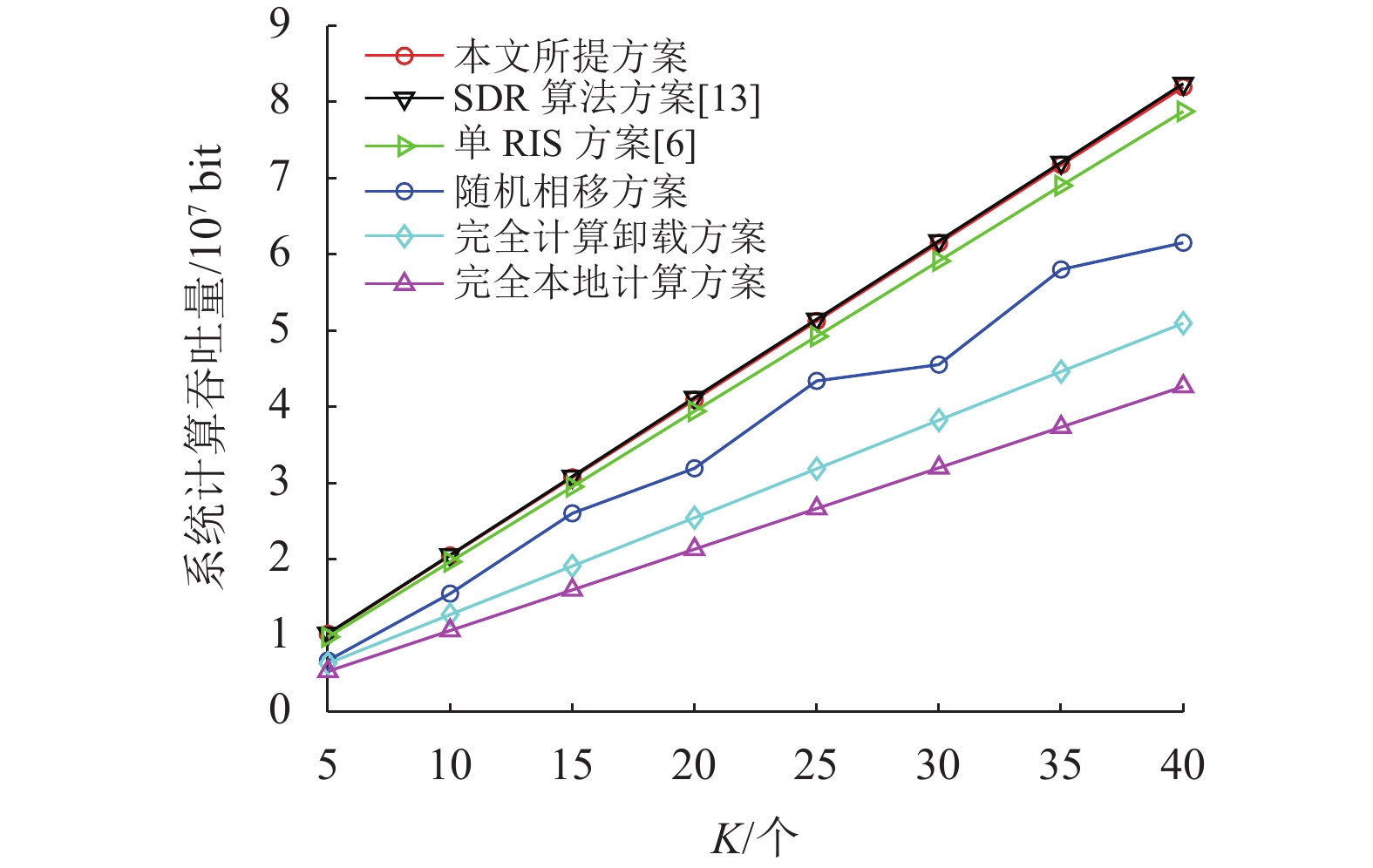
图9显示了系统计算总吞吐量与用户个数K的关系。其中时隙数目N = 10，时隙长度$ \tau = 0.1 $ s，可以观察到，随着用户数量K的增加，所有方案的计算比特数都在增加。对比本文所提方案与SDR算法方案的性能曲线，本文所提方案与SDR算法方案性能相当，且与其余4种基准方案相比，本文所提方案获得了显著的性能提升，特别是当K变大时，优势更加明显。

图10 显示了不同时隙长度τ下的系统计算吞吐量性能曲线。其中用户数量K=3，时隙数量N=10，本文所提的求解方案与基于SDR算法求解方案性能相当。且与其他基准方案相比，本文所提出的方案获得了显著的性能提升，随着时隙长度的增加，系统总吞吐量单调递增。当时隙长度$ \tau $变大(例如$ \tau > 0.04\,{\text{s}} $) 时，完全计算卸载方案优于完全本地计算方案。这意味着用户更倾向于将任务卸载到较大$ \tau $值的基站，以充分利用有限的能量。

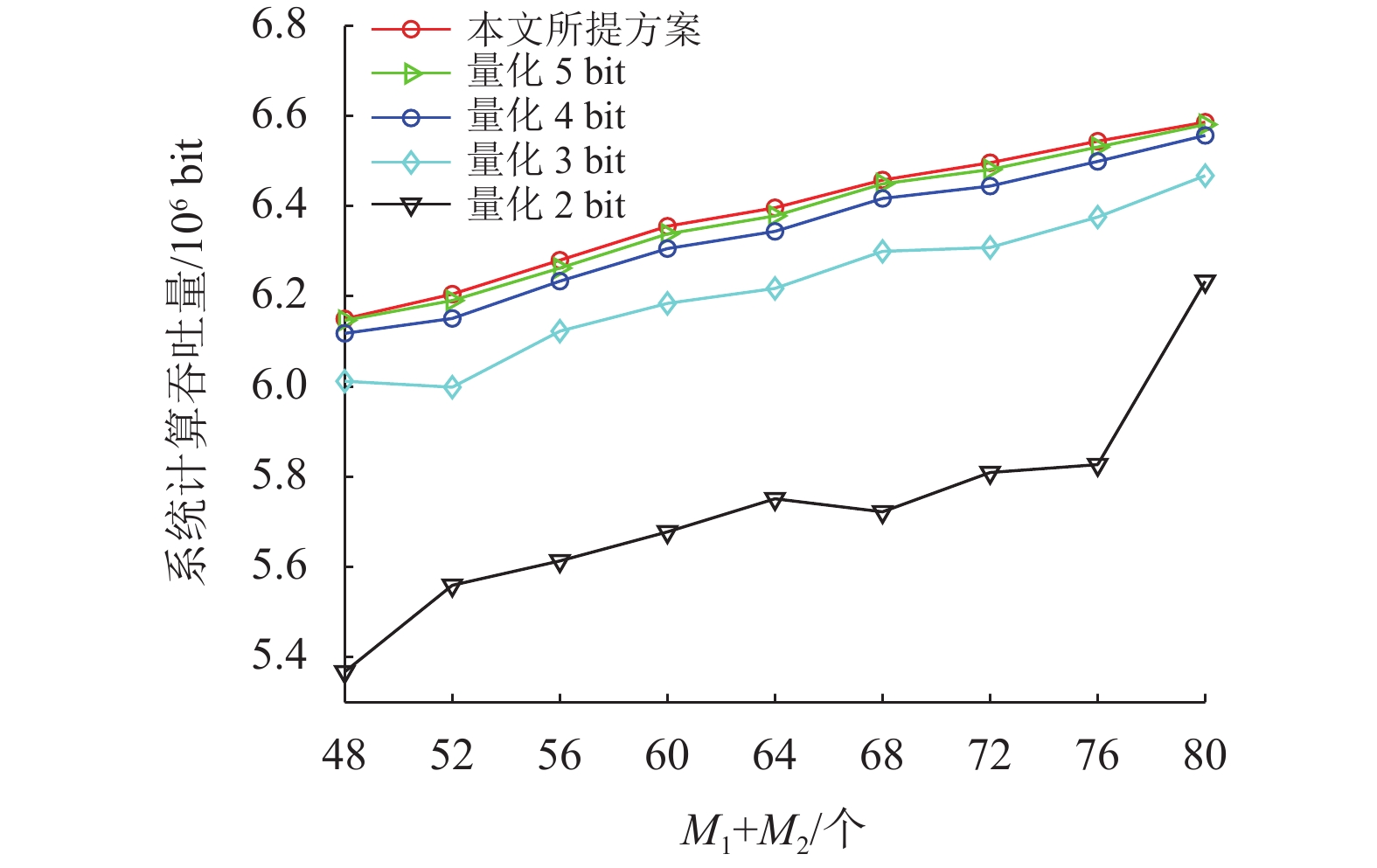
图11显示了连续、离散相位RIS与不同反射单元数量下的系统计算吞吐量性能曲线。经过优化的连续相位量化成离其最近的离散值，不同比特B量化后的离散值集合表示为$\{ 0,2{\text{π}} \times {2^{ - B}}, \cdots ,2{\text{π}} \times (1$ $ - {2^{ - B}}) \} $。在RIS反射元数目相同时，量化比特数越大系统总吞吐量越大，且越接近连续相位RIS的性能，这是因为量化后的相位已经靠近优化过的连续相位。从图中可以看出量化5 bit的离散相位RIS的性能已经逼近连续相位RIS的性能，量化2 bit的离散相位RIS性能远低于连续相位RIS性能。

4 结语

本文研究了双RIS辅助的多用户多时隙能量采集边缘计算优化配置问题，建立计算模型。该计算模型以系统总吞吐量最大化为目标，以用户随机收集的能量为约束条件，采用高效的交替优化、低复杂度ADMM等算法，对本地计算任务量、用户设备发射功率，以及RIS的相移进行联合优化设计。最后通过仿真实验验证了所提迭代算法的快速收敛特性与有效性。同时可以得出本文所提方案较于SDR算法方案具有低复杂度特性，与其他基准方案相比具有显著的计算吞吐量性能增益，并且离散相位RIS的量化比特数越大越接近连续相位RIS的性能。