可拓学^[1-2]中，建立了形式化描述物、事和关系的基本元，统称为基元，包括物元、事元和关系元，作为可拓学的基本模型。但是在进行复杂产品创新或解决复杂问题时，问题所涉及的对象往往不是单一的，而是物、事和关系复合而成的，仅用基元很难清晰地形式化描述出来，因此引入了复合元^[3]这一概念。多维复合元是由两个以上的多维基元相复合形成的、形式化表达复杂系统、产品功能与结构或矛盾问题的重要工具。多维复合元有多种不同的复合方式，两个不同复合方式的多维复合元，称为异类多维复合元(Heterogeneous Multi-dimensional Compound-elements，HMdCes)。在可拓学中，创新或解决矛盾问题的工具是可拓变换，所以研究复合元及其可拓变换是解决复杂矛盾问题的重要手段。文献[1-3]中介绍了基元的传导变换定义及传导规则；文献[4]以传导变换和传导效应为基础,规定了传导度和传导知识的定义与类型,为研究传导知识的挖掘奠定理论基础。文献[5]针对复杂基元相关网,提出了基元相关矩阵和基元相关函数的概念,为基元相关性的形式化表述提供了工具，进一步给出了复杂基元相关网下传导变换对象的判定规则及其传导效应的计算模型，文献[6]提出了以广义表作为数据结构表示复合元的方式，并在此方法下进行可拓变换等算法的实现。文献[7]研究了如何使用Web Ontology Language (OWL)本体，构建相应的复合元，为OWL本体映射到可拓学中的复合元提供了思路，从而建立解决矛盾问题的知识领域。文献[8]利用发散分析、相关分析和蕴含分析原理，对过程元之间的关系进行了分析。通过可拓推理方法寻找主动变换。文献[9]提出可拓学与数据挖掘相结合，挖掘包含传导知识、可拓分类知识等以解决矛盾问题。文献[10]针对前n次可拓变换未引起与之相关的信息元发生传导变换，而n+1次主动变换才能引起与之相关的信息元发生传导变换的实际问题。文献[11]确定产品技术系统中的流，结合动态复合元建立可拓流模型，识别有益流或有缺陷流。文献[12]利用可拓变换和传导效应，可以准确而详细地描述各种物理效应的主要内容，以便人们理解各物理效应产生的机理以及输入与输出量的转换关系，也为结合物理效应与可拓变换解决工程技术领域的矛盾问题提供依据和方法。文献[13]提出简单网络管理协议(Simple Network Management Protocol, SNMP)上消息的复合元表达。文献[14]介绍了可拓知识工程与知识转换的研究概况，也说明了复合元与传导变换在知识表示、知识推理与知识获取中的应用。文献[15]提出了一种基于复合元和传导变换形式化地表达技术系统演化规律中隐含的可拓知识的方法，清晰地表达技术系统演化规律的内涵和外延，从而为将这些规律应用于可拓智能设计铺平了道路。文献[16]重点研究了同类多维复合元间的传导规则及其在产品创意生成中的应用。文献[17]将复合元应用于移动运输机器人的可拓创新设计研究，建立了移动运输机器人的功能复合元与结构复合元，研究了它们的映射、拓展与变换，并用于生成了多个移动运输机器人结构可拓设计创意。文献[18]将复合元及可拓变换与多品种小批量存储自动化立体仓库的结构创新设计相结合，从而获得结构可拓设计创意的生成。文献[19]提出将可拓创新方法应用于Mobile Transport Robot (MTR)的结构设计研究，在MTR的结构设计创意优选中，将Robot Operating System (ROS)仿真技术与优度评价方法相融合，使得优选出的结构设计创意更有效。很多创新设计要素都要用异类复合元形式化表示，如功能复合元和结构复合元，就属于异类多维复合元，当对其中一个复合元实施主动可拓变换时，相应的结构复合元会发生传导变换，但目前还没有推理规则作为依据，因此也难以为可拓创新设计提供理论支持。文献[20]运用可拓设计方法对永磁发电机产品进行形式化研究，结合绿色设计方法和逆向设计方法，从现有产品出发进行深入剖析，建立相应的永磁发电机绿色设计属性的物元、事元和关系元模型,再依据绿色设计要求，通过拓展、变换，最终进行绿色度、综合优度的分级评价，选出满足绿色设计要求的产品创意，形成一种新的具有领域普适性的绿色可拓设计方法，为研究其他类型发电机或产品绿色设计提供参考，丰富了可拓设计方法体系。

综上可见，现有的文献中，研究复合元形式化表达的文献较多，同类多维复合元变换的传导规则已经建立，并有效应用于产品的可拓设计创意生成，但目前还没有关于HMdCes间的传导规则研究的文献。而在可拓创新设计研究中，很多创新设计要素都可以用多维复合元形式化表示，且很多都属于HMdCes，例如功能复合元和结构复合元，就属于HMdCes，它们之间存在着各种复杂的关系，目前还缺乏对这些HMdCes间的传导规则的研究。建立HMdCes间的传导规则，可以为可拓创新设计创意的生成提供更多推理依据。

为此，本文基于HMdCes的构成和基元的传导规则，以物元和事元形成的多维复合元与物元与关系元形成的多维复合元为例，研究建立两个HMdCes间的传导规则，并以ZDY系列一级减速器的功能与结构设计为例，验证这些传导规则的普适性和有效性。多个HMdCes间的传导规则有类似的结论。

1 HMdCes与基元变换的传导规则 1.1 HMdCes

HMdCes是不同复合形式的两个或多个多维复合元。例如，在两个多维复合元中，如果一个是由多维物元和多维事元复合而成的，另一个是由多维物元和多维关系元、或多维事元和多维关系元复合而成的，则称这两个多维复合元为HMdCes。而同类复合元是相同复合形式的两个或多个多维复合元^[16]。下面用模型说明几种常用的HMdCes。

对于如下一个多维物元$ {M_{01}} $与一个多维事元$ {A_0} $形成的多维复合元(1)和由一个多维物元$ {M_{02}} $与一个多维关系元$ {R_0} $构成的多维复合元(2)，这两个复合元属于HMdCes。

$ {A_0}({M_{01}}) = \left[ \begin{gathered} {A_{01}}({M_{01}}) \\ {A_{02}}\\[-8pt] \vdots \\[-4pt] {A_{0i}}\\[-8pt] \vdots \\[-8pt] {A_{{0}{n_1}}} \\ \end{gathered} \right] \text{，} {M_{01}} = \left[ \begin{gathered} {M_{011}} \\[-8pt] \vdots \\[-4pt] {M_{01{i_1}}} \\[-8pt] \vdots \\[-8pt] {M_{{01}{s_1}}} \\ \end{gathered} \right] $

(1)

$ {R_0}({M_{02}}) = \left[ \begin{gathered} {R_{01}}({M_{02}}) \\ {R_{02}} \\[-8pt] \vdots \\[-4pt] {R_{0j}} \\[-8pt] \vdots \\[-8pt] {R_{0{n_2}}} \\ \end{gathered} \right] \text{，} {M_{02}} = \left[ \begin{gathered} {M_{021}} \\[-8pt] \vdots \\[-4pt] {M_{02{i_2}}} \\[-8pt] \vdots \\[-8pt] {M_{02{s_2}}} \\ \end{gathered} \right] $

(2)

类似地，两个多维物元$ {M}_{01}和{M}_{02} $与一个多维事元A₀形成的多维复合元，也有多种不同的复合方式，如

$ {A_0}({M_{01}},{M_{02}}) = \left[ \begin{gathered} {A_{01}}({M_{01}}) \\ {A_{02}}({M_{02}}) \\[-8pt] \vdots \\[-8pt] {A_{0i}} \\[-8pt] \vdots \\[-8pt] {A_{0{n_1}}} \\ \end{gathered} \right] $

(3)

$ {A_0}({M_{01}} \wedge {M_{02}}) = \left[ \begin{gathered} {A_{01}}({M_{01}} \wedge {M_{02}}) \\ {A_{02}} \\[-8pt] \vdots \\[-8pt] {A_{0i}} \\[-8pt] \vdots \\[-8pt] {A_{0{n_1}}} \\ \end{gathered} \right] $

(4)

等。同样，两个多维物元$ {M}_{01}和{M}_{02} $与一个多维关系元R₀形成的多维复合元，也有多种不同的复合方式，如

$ {R_0}({M_{01}},{M_{02}}) = \left[ \begin{gathered} {R_{01}}({M_{01}}) \\ {R_{02}}({M_{02}}) \\[-8pt] \vdots \\[-8pt] {R_{0j}} \\[-8pt] \vdots \\[-8pt] {R_{0{n_2}}} \\ \end{gathered} \right] $

(5)

等，其他复合形式此略。

1.2 基元变换的传导规则

文献[1,3]给出了基元变换的一阶一次传导规则、一阶n次传导规则和m阶n次传导规则。本文主要基于基元变换的一阶一次传导规则和一阶n次传导规则开展研究。

若某初始基元$ {B_0} $对应的动态基元为$ B $，且已知$ B $与另一动态基元$ {B_1} $相关，即$ B\widetilde \to {B_1} $，则当$ \varphi {B_0}{\text{ = }}{B'_0} $时，必然导致$ {B_1} $对应的初始基元$ {B_{10}} $发生传导变换，即有如下一阶一次传导规则：

$ ( {\varphi {B_0}{\text{ = }}{{B}'_0}} ) \wedge ( {B\widetilde \to {B_1}} ) \vDash ( {{}_\varphi {T_{{B_{10}}}}{B_{10}} = {{B}'_{10}}} ) $

类似地，一阶n次传导规则的形式为

$ ( {\varphi {B_0}{\text{ = }}{{B}'_0}} ) \wedge ( {B\widetilde \to {B_1}\widetilde \to \cdots \widetilde \to {B_n}} ) \vDash ( {{}_{{B_{{\text{(}}n - 1{\text{) 0}}}}}{T_{{B_{n0}}}}{B_{n0}} = {{B}'_{n0}}} ) $

并且有如下传导变换蕴含系：

$ \varphi \Rightarrow {}_\varphi {T_{{B_{10}}}} \Rightarrow \cdots \Rightarrow {}_{{B_{{\text{(}}n - 1{\text{) 0}}}}}{T_{{B_{n0}}}} $

说明：基元是物元、事元、关系元的统称，在研究中需要区分时，用M表示物元，用A表示事元，用R表示关系元。

现实世界中的事、物和关系，往往是十分复杂的，它们之间存在各种复杂的复合关系和相关关系，要想准确地形式化描述所研究的对象，就需要采用事元、物元或关系元形成的各种类型的多维复合元进行表达。本文将依据基元变换的传导规则的形式，研究多个HMdCes间的传导规则。

2 HMdCes间的传导规则

下面以物元和事元形成的多维复合元(1)、(4)与物元和关系元形成的多维复合元(2)、(5)为例，给出HMdCes间的传导规则。两个物元和一个事元或一个关系元形成的复合元以及其他形式的复合元，有类似的传导规则，但更加复杂，限于篇幅，此不详述。

2.1 内部只包含单个基元的HMdCes间的传导规则

以HMdCes(1)和(2)为例，下面在不考虑复合元$ {A_0}({M_{01}}) $和$ {R_0}({M_{02}}) $内部由于其他相关因素导致的传导变换的情况下，研究这两个复合元间的传导规则。为了简化传导规则的表达式，下列传导规则都只写出最终的传导结果，如果有中间的传导过程，请看传导规则说明中的传导变换蕴含系。

传导规则1　若$ {M_{01}} = {M_{02}} = {M_0} $，则

$ ( {\varphi {M_0} = {{M}'_0}} ) \vDash\left( {{}_\varphi T_{{A_0}({M_0}) }}{A_0}({M_0}) =\right. $

$ \left. {{A}'_0}({{M}'_0}) \right) \wedge ( {{}_\varphi {T_{{R_0}({M_0}) }}{R_0}({M_0}) = {{R}'_0}({{M}'_0}) } ) $

该传导规则说明：若$ {M_{01}} = {M_{02}} = {M_0} $，则对$ {M_0} $实施主动变换$ \varphi {M_0} = {M'_0} $，必然同时引起$ {A_0}({M_0}) $和$ {R_0}({M_0}) $发生传导变换，即存在传导变换 $\varphi \Rightarrow {}_\varphi {T_{{A_0}({M_0}) }} \wedge {}_\varphi {T_{{R_0}({M_0}) }}$,使

$ {}_\varphi {T_{{A_0}({M_0}) }}{A_0}({M_0}) = {A'_0}({M'_0}) \text{，} {}_\varphi {T_{{R_0}({M_0}) }} {R_0}({M_0}) = {R'_0}({M'_0}) $

即在两个异类复合元之间，若存在相同物元，当对此物元实施主动变换时，必会导致两个异类复合元产生如上规则的传导变换。

同理，若两个异类复合元中存在相同的事元s或关系元，也会有如上的传导规则，本文不再赘述。

传导规则2　若$ {M_{01}} \ne {M_{02}} $，且$ {M_{01}} $对应的动态物元$ {M_1} $中任一维分物元都与$ {M_{02}} $对应的动态物元$ {M_2} $中的任一维物元不相关，则

$ ( {{\varphi _1}{M_{01}} = {{M}'_{01}}} ) \vDash ( {{}_\varphi {T_{{A_0}( {{M_{01}}} ) }}{A_0}( {{M_{01}}} ) = {{A}'_0}( {{{M}'_{01}}} ) } ) $

该传导规则说明：若$ {M_{01}} \ne {M_{02}} $，且这两个物元对应的动态物元间没有任何相关关系存在，则对$ {M_{01}} $实施主动变换$ \varphi {M_{01}} = {M'_{01}} $，不会导致另一个异类复合元发生传导变换。

传导规则3　若$ {M_{01}} \ne {M_{02}} $，且$ {M_{01}} $对应的动态物元$ {M_1} $中的某一维分物元$ {M_{1{i_1}}} $与$ {M_{02}} $对应的动态物元$ {M_2} $中的某一维分物元$ {M_{2{i_2}}} $相关，即$ {M_{1{i_1}}}\widetilde \to {M_{2{i_2}}} $，则

$ \begin{gathered} ( {{\varphi _1}{M_{01{i_1}}} = {{M}'_{01{i_1}}}} ) \wedge ( {{M_{1{i_1}}}\widetilde \to {M_{2{i_2}}}} ) \vDash\\ ( {{}_{{M_{01}}}{T_{{A_0}({M_{01}}) }}{A_0}( {{M_{01}}} ) = {{A}'_0}( {{{M}'_{01}}} ) } ) \wedge \\ ( {{}_{{M_{02}}}{T_{{R_0}({M_{02}}) }}{R_0}( {{M_{02}}} ) = {{R}'_0}( {{{M}'_{02}}} ) } ) \\ \end{gathered} $

该传导规则说明：在上述条件下，对$ {M_{01{i_1}}} $实施主动变换$ {\varphi _1}{M_{01{i_1}}} = {M'_{01{i_1}}} $，必然会引起$ {A_0}( {{M_{01}}} ) $和$ {R_0}( {{M_{02}}} ) $发生一系列传导变换，即存在传导变换蕴含系

$ {\varphi _1} \Rightarrow \left\{ \begin{gathered} {}_{{\varphi _1}}{T_{{M_{01}}}} \Rightarrow {}_{{M_{01}}}{T_{{A_0}({M_{01}}) }} \\ {}_{{\varphi _1}}{T_{{M_{02{i_2}}}}} \Rightarrow {}_{{M_{02{i_2}}}}{T_{{M_{02}}}} \Rightarrow {}_{{M_{02}}}{T_{{R_0}({M_{02}}) }} \\ \end{gathered} \right. $

使得

$ \begin{split} &{}_{{M_{01}}}{T_{{A_0}({M_{01}}) }}{A_0}( {{M_{01}}} ) = {A'_0}( {{{M}'_{01}}} )\\ &{}_{{M_{02}}}{T_{{R_0}({M_{02}}) }}{R_0}( {{M_{02}}} ) = {R'_0}( {{{M}'_{02}}} ) \end{split} $

传导规则4　若$ {M_{01}} \ne {M_{02}} $，且$ {M_{01}} $对应的动态物元$ {M_1} $中的某一维分物元$ {M_{1{i_1}}} $与另一维分物元$ {M_{1{{i}'_1}}} $相关，$ {M_{1{{i}'_1}}} $又与$ {M_{02}} $对应的动态物元$ {M_2} $中的某一维分物元$ {M_{2{i_2}}} $相关，即$ {M_{1{i_1}}}\widetilde \to {M_{1{{i}'_1}}}\widetilde \to {M_{2{i_2}}} $，则

$ \begin{gathered} ( {{\varphi _1}{M_{01{i_1}}} = {{M}'_{01{i_1}}}} ) \wedge ( {{M_{1{i_1}}}\widetilde \to {M_{1{{i}'_1}}}\widetilde \to {M_{2{i_2}}}} ) \vDash \\ ( {{}_{{M_{01}}}{T_{{A_0}({M_{01}}) }}{A_0}({M_{01}}) = {{A}''_0}({{M}''_{01}}) } )\wedge \\ ( {{}_{{M_{02}}}{T_{{R_0}({M_{02}}) }}{R_0}({M_{02}}) = {{R}''_0}({{M}'_{02}}) } ) \\ \end{gathered} $

该传导规则说明：在上述条件下，对$ {M_{01{i_1}}} $实施主动变换$ {\varphi _1}{M_{01{i_1}}} = {M'_{01{i_1}}} $，必然会引起复合元$ {A_0}( {{M_{01}}} ) $和$ {R_0}( {{M_{02}}} ) $发生传导变换，即存在传导变换蕴含系

$ {\varphi _1} \Rightarrow {}_{{\varphi _1}}{T_{{M_{01{{i}'_1}}}}}\mathop \Rightarrow \limits^ \wedge \left\{ \begin{gathered} \mathop {{}_{{M_{01{{i}'_1}}}}{T_{{M_{01}}}} \Rightarrow {}_{{M_{01}}} }{T_{{A_{0}}({M_{01}}) }} \\[-2pt] {}_{{M_{01{{i}'_1}}}}{T_{{M_{02{i_2}}}}} \Rightarrow {}_{{M_{02{i_2}}}}{T_{{M_{02}}}} \Rightarrow {}_{{M_{02}}}{T_{{R_{0}}({M_{02}}) }} \end{gathered} \right. $

使

$ \begin{split} &{}_{{M_{01}}}{T_{{A_0}({M_{01}}) }}{A_0}( {{M_{01}}} ) = {A'_0}( {{{M}'_{01}}} )\\ &{}_{{M_{02}}}{T_{{R_0}({M_{02}}) }}{R_0}( {{M_{02}}} ) = {R'_0}( {{{M}'_{02}}} ) \end{split}$

传导规则5　若$ {M_{01}} \ne {M_{02}} $，且$ {M_{01}} $对应的动态物元$ {M_1} $中的某一维分物元$ {M_{1{i_1}}} $与另一维分物元$ {M_{1{{i}'_1}}} $相关，$ {M_{1{{i}'_1}}} $又与$ {M_{02}} $对应的动态物元$ {M_2} $中的某一维分物元$ {M_{2{i_2}}} $相关,即$ {M_{1{i_1}}}\widetilde \to {M_{1{{i}'_1}}}\widetilde \to {M_{2{i_2}}} $，而$ {M_{1{{i}'_1}}} $又与$ {A_{0i}} $对应的动态分事元$ {A_i} $相关，$ {M_{2{i_2}}} $又与$ {R_{0j}} $对应的动态分关系元$ {R_j} $相关，则

$ \begin{gathered} ( {{\varphi _1}{M_{01{i_1}}} = {{M}'_{01{i_1}}}} ) \wedge ( {{M_{1{i_1}}}\widetilde \to {M_{1{{i}'_1}}}\widetilde \to {M_{2{i_2}}}} ) \wedge \\ ( {{M_{1{{i}'_1}}}\widetilde \to {A_i}} ) \wedge ( {{M_{2{i_2}}}\widetilde \to {R_j}} ) \vDash \\ ( {{}_{{A_{01}}({M_{01}}) \wedge {A_{0i}}}{T_{{A_0}({M_{01}}) }}{A_0}({M_{01}}) = {{A}''_0}({{M}''_{01}}) } )\wedge \\ ( {{}_{{R_{01}}({M_{02}}) \wedge {R_{0j}}}{T_{{R_0}({M_{02}}) }}{R_0}({M_{02}}) = {{R}''_0}({{M}'_{02}}) } ) \\ \end{gathered} $

该传导规则说明：在上述条件下，若对$ {M_{01{i_1}}} $实施主动变换$ {\varphi _1}{M_{01{i_1}}} = {M'_{01{i_1}}} $，必然会引起复合元$ {A_0}( {{M_{01}}} ) $和$ {R_0}( {{M_{02}}} ) $发生传导变换，即存在传导变换蕴含系

$ \begin{split} &{\varphi _1} \Rightarrow {}_{{\varphi _1}}{T_{{M_{01{{i}'_1}}}}}\mathop \Rightarrow \limits^ \wedge \\[-2pt] &\left\{ \begin{gathered} \left. \begin{gathered} {}_{{M_{01{{i}'_1}}}}{T_{{M_{01}}}} \Rightarrow {}_{{M_{01}}}{T_{{A_{01}}({M_{01}}) }} \\[-2pt] {}_{{M_{01{{i}'_1}}}}{T_{{A_{0i}}}} \\[-2pt] \end{gathered} \right\}\mathop \Rightarrow \limits^ \wedge {}_{{A_{01}}({M_{01}}) \wedge {A_{0i}}}{T_{{A_0}({M_{01}}) }} \\[-2pt] {}_{{M_{01{{i}'_1}}}}{T_{{M_{02{i_2}}}}}\mathop \Rightarrow \limits^ \wedge \left. {\left\{ \begin{gathered} {}_{{M_{02{i_2}}}}{T_{{R_{0j}}}} \\[-2pt] {}_{{M_{02{i_2}}}}{T_{{M_{02}}}} \Rightarrow {}_{{M_{02}}}{T_{{R_{01}}({M_{02}}) }} \\[-2pt] \end{gathered} \right.} \right\}\mathop \Rightarrow \limits^ \wedge {}_{{R_{01}}({M_{02}}) \wedge {R_{0j}}}{T_{{R_0}({M_{02}}) }} \\[-2pt] \end{gathered} \right. \end{split} $

使得

$ \begin{split} &{}_{{A_{01}}({M_{01}}) \wedge {A_{0i}}}{T_{{A_0}({M_{01}}) }}{A_0}({M_{01}}) = {A''_0}({M''_{01}}) \\[-2pt] &{}_{{R_{01}}({M_{02}}) \wedge {R_{0j}}}{T_{{R_0}({M_{02}}) }}{R_0}({M_{02}}) = {R''_0}({M'_{02}}) \end{split} $

同理可得复合元$ {A}_{0}({M}_{011}，{M}_{012}) $与${R}_{0} ({M}_{021}，{M}_{022})$间的传导规则，此略。

2.2 内部包含多个基元或基元运算的HMdCe间的传导规则

对于复合元内部包含两个基元或基元运算的异类复合元，如HMdCes(4)和(5)，它们之间的传导规则如下。

传导规则6　若$ {M_{01}} \ne {M_{02}} $，且$ {M_{01}} $对应的动态物元$ {M_1} $中的某一维分物元$ {M_{1{i_1}}} $与另一维分物元$ {M_{1{{i}'_1}}} $相关，且$ {M_{1{i_1}}} $又与$ {M_{02}} $对应的动态物元$ {M_2} $中的某一维分物元$ {M_{2{i_2}}} $相关，而${M_{2{{i}_2}}} $又与另一维分物元${M_{2{{i}'_2}}} $相关，即$ {M_{1{i_1}}}\widetilde \to {M_{1{{i}'_1}}} $，$ {M_{1{i_1}}}\widetilde \to {M_{2{i_2}}} \widetilde \to{M_{2{{i}'_2}}}$。而$ {M_{1{{i}'_1}}} $和$ {M_{2{{i}'_2}}} $又与$ {A_{0i}} $对应的动态分事元$ {A_i} $相关，$ {M_{1{i_1}}} $与$ {M_{2{i_2}}} $又与$ {R_{0j}} $对应的动态分事元$ {R_j} $相关，则

$ \begin{array}{l}({\varphi }_{1}{M}_{01{i}_{1}}={{M}^{\prime }} _{01{i}_{1}}) \wedge ({M}_{1{i}_{1}}\tilde{\to }{M}_{1{{i}^{\prime }}_{1}}) \wedge ({M}_{1{i}_{1}}\tilde{\to }{M}_{2{i}_{2}}\tilde{\to }{M}_{2{{i}^{\prime }}_{2}})\wedge \\[-2pt] ({M}_{1{i}'_{1}}\wedge {M}_{2{i}'_{2}}\tilde{\to }{A}_{i}) \wedge ({M}_{1{i}_{1}}\wedge {M}_{2{i}_{2}}\tilde{\to }{R}_{j})\models \\[-2pt] ({}_{{\psi }_{1}}T{}_{{A}_{0}({M}_{01}\wedge {M}_{02}) }{A}_{0}({M}_{01}\wedge {M}_{02}) ={{A}''_{0}}({{M}''_{01}}\wedge {{M}''_{02}}) )\wedge \\[-2pt] ({}_{{\psi }_{2}}T{}_{{R}_{0}({M}_{01}，{M}_{02}) }{R}_{0}({M}_{01}，{M}_{02}) ={{R}''_{0}}({{M}''_{01}}，{{M}{''} _{02}}) ) \end{array} $

该传导规则说明：在上述条件下，对$ {M_{01{i_1}}} $实施主动变换$ {\varphi _1}{M_{01{i_1}}} = {M'_{01{i_1}}} $，必然会引起复合元$ {A_0}( {{M_{01}} \wedge {M_{02}}} ) $发生一阶5次传导变换，且$ {R_0}( {{M_{01}},{M_{02}}} ) $发生一阶5次传导变换，即存在如下传导变换蕴含系

${\begin{array}{l} {\varphi _1}\mathop \Rightarrow \limits^ \wedge \left\{ \begin{array}{l} {}_{{\varphi _1}}{T_{{M_{01{{i}'_1}}}}}\mathop \Rightarrow \limits^ \wedge \left\{ \begin{array}{l} {}_{{M_{01{{i}'_1}}}}{T_{{M_{01}}}}\mathop \Rightarrow \limits^ \wedge \left\{ \begin{array}{l} {}_{{M_{01}}}{T_{{A_{01}}({M_{01}} \wedge {M_{02}})}}\\[-2pt] {}_{{M_{01}}}{T_{{R_{01}}({M_{01}})}} \end{array} \right.\\[-2pt] {}_{{M_{01{{i}'_1}}}}{T_{{A_{0i}}}} \end{array} \right.\\[-2pt] {}_{{\varphi _1}}{T_{{M_{02{i_2}}}}}\mathop \Rightarrow \limits^ \wedge \left\{ \begin{array}{l} {}_{{M_{02{i_2}}}}{T_{{M_{02{{i}'_2}}}}}\mathop \Rightarrow \limits^ \wedge \left\{ \begin{array}{l} {}_{{M_{02{{i}'_2}}}}{T_{{A_{0i}}}}\\[-2pt] {}_{{M_{02{{i}'_2}}}}{T_{{M_{02}}}}\mathop \Rightarrow \limits^ \wedge \left\{ \begin{array}{l} {}_{{M_{02}}}{T_{{A_{01}}({M_{01}} \wedge {M_{02}})}}\\[-2pt] {}_{{M_{02}}}{T_{{R_{02}}({M_{02}})}} \end{array} \right. \end{array} \right.\\[-2pt] {}_{{M_{02{i_2}}}}{T_{{R_{0j}}}} \end{array} \right.\\[-2pt] {}_{{\varphi _1}}{T_{{R_{0j}}}} \end{array} \right\}\mathop \Rightarrow \limits^ \wedge \\ \begin{array}{*{20}{c}} {} \end{array} \quad \left\{ \begin{array}{l} {}_{{\psi _1}}{T_{{A_0}({M_{01}} \wedge {M_{02}})}}\\[-2pt] {}_{{\psi _2}}{T_{{R_0}({M_{01}},{M_{02}})}} \end{array} \right. \end{array}}$

其中

$ {\psi _1} = {}_{{M_{01}}}{T_{{A_{01}}({M_{01}} \wedge {M_{02}})}} \wedge {}_{{M_{02}}}{T_{{A_{01}}({M_{01}} \wedge {M_{02}})}} \wedge {}_{{M_{01{{i}'_1}}}}{T_{{A_{0i}}}} \wedge {}_{{M_{02{{i}'_2}}}}{T_{{A_{0i}}}} $

${\psi _2} = {}_{{M_{01}}}{T_{{R_{01}}({M_{01}})}} \wedge {}_{{M_{02}}}{T_{{R_{02}}({M_{02}})}} \wedge {}_{{M_{02{{i}'_2}}}}{T_{{R_{0j}}}} \wedge {}_{{\varphi _1}}{T_{{R_{0j}}}} $

使得

$ \begin{split} &{}_{{\psi _1}}{T_{{A_0}({M_{01}} \wedge {M_{02}}) }}{A_0}({M_{01}} \wedge {M_{02}}) = {A''_0}({M''_{01}} \wedge {M''_{02}})\\[-2pt] &{}_{{\psi }_{2}}T{}_{{R}_{0}({M}_{01}，{M}_{02}) }{R}_{0}({M}_{01},{M}_{02}) ={{R}''_{0}}({{M}''_{01}},{{M}''_{02}}) \end{split} $

说明：上述传导规则都是只实施一个主动变换的情况，如果同时实施多个主动变换或按顺序实施多个主动变换，则传导规则更复杂，但都可以依据上述规则和可拓变换的运算规则获取，有兴趣的读者可以进一步研究。另外，多个异类多维复合元间的传导规则类似可得，限于篇幅，此不赘述。

3 案例分析

以ZDY系列单级减速器齿轮D₀的功能和结构关系为例，设现有两圆柱齿轮正确安装，顶隙为标准值、两齿侧间隙为零、分度圆相切，主动齿轮D₀₁与从动齿轮D₀₂的传动比为4:1，产噪量中等，减速效率低。下面利用事元和物元组成的功能复合事元与关系元与物元组成的结构复合关系元之间的传导规则，获取改善ZDY系列单级减速器齿轮D₀的设计创意，进而验证异类多维复合元传导规则的适用性。

建立ZDY系列单级减速器齿轮D₀的初始物元模型为

$ {\begin{split} & M_{D 0}=\\[-4pt] &\left[ \begin{array}{lll} \text { 减速器 } D_0, & \text { 类型, } & \mathrm{ZDY} \text { 系列 } \\[-4pt] & \text { 产噪量, } & \text {中 } \\[-4pt] & \text { 减速效率, } & \text {低 } \end{array}\right]=\left[\begin{array}{l} M_{D 01} \\[-4pt] M_{D 02} \\[-4pt] M_{D 03} \end{array}\right] \end{split} }$

待改善的功能和结构的初始复合元模型为

$ { \begin{aligned} & A_0(M_{01} \wedge M_{02})= \\[-4pt] & {\left[ \begin{array}{lll} \text { 传递, } & \text { 工具, } & M_{01} \wedge M_{02} \\[-4pt] & \text { 效率, } & \text {中 } \\[-4pt] & \text { 传动比, } & 4 / 1 \\[-4pt] & \text { 支配对象, } & \text {动力 } \end{array} \right]=\left[ \begin{array}{l} A_{01}(M_{01} \wedge M_{02}) \\[-4pt] A_{02} \\[-4pt] A_{03} \\[-4pt] A_{04} \\[-4pt] A_{05} \end{array} \right]} \end{aligned} }$

$ {\begin{aligned} & R_0(M_{01}, M_{02})= \\[-2pt] & {\left[\begin{array}{lll} \text { 啮合关系, } & \text { 前项, } & M_{01} \\[-2pt] & \text { 后项, } & M_{02} \\[-2pt] & \text { 类型, } & \text {平面啮合 } \end{array}\right]=\left[\begin{array}{l} R_{01}(M_{01}) \\[-2pt] R_{02}(M_{02}) \\[-2pt] R_{04} \end{array}\right]} \end{aligned}}$

其中，

$ {\begin{split} & M_{01} = \left[ \begin{array}{lll} \text { 主动轮 } D_{01}, & \text { 类型, } & \text {圆柱齿轮 } \\[-2pt] & \text { 模数, } & 3 \\[-2pt] & \text { 齿数/头数, } & 20 \\[-2pt] & \text { 重合度, } & 1.4 \\[-2pt] & \text { 压力角, } & 20^{\circ} \end{array} \right] = \left[ \begin{array}{l} M_{011} \\[-2pt] M_{012} \\[-2pt] M_{013} \\[-2pt] M_{014} \\[-2pt] M_{015} \end{array} \right] \\[-2pt] & M_{02} = \left[ \begin{array}{lll} \text { 从动轮 } D_{02}, & \text { 类型, } & \text {圆柱齿轮 } \\[-2pt] & \text { 模数, } & 3 \\[-2pt] & \text { 齿数/头数, } & 80 \\[-2pt] & \text { 重合度, } & 1.4 \\[-2pt] & \text { 压力角, } & 20^{\circ} \end{array} \right] = \left[ \begin{array}{l} M_{021} \\[-2pt] M_{022} \\[-2pt] M_{023} \\[-2pt] M_{024} \\[-2pt] M_{025} \end{array} \right] \end{split}} $

为案例分析简便起见，设ZDY系列单级减速器齿轮D₀的初始物元模型对应的动态物元模型为

$ {M_D=\left[ \begin{array}{lll} \text { 减速器 } D, & \text { 类型, } & \mathrm{ZDY} \text { 系列 } \\[-2pt] & \text { 产噪量, } & v_{m 2} \\[-2pt] & \text { 减速效率, } & v_{m 3} \end{array} \right] = \left[\begin{array}{l} M_{D 1} \\[-2pt] M_{D 2} \\[-2pt] M_{D 3} \end{array} \right] }$

并设功能和结构的初始复合元模型对应的动态复合元模型为

$ { \begin{split} & A(M_1 \wedge M_2) = \\[-2pt] &\left[ \begin{array}{lll} \text { 传递, } & \text { 工具, } & M_1 \wedge M_2 \\[-2pt] & \text { 效率, } & v_{a 2} \\[-2pt] & \text { 传动比, } & v_{a 3} \\[-2pt] & \text { 支配对象, } & v_{a 4} \\[-2pt] & \text { 稳定性, } & v_{a 5} \end{array} \right] = \left[ \begin{array}{l} A_1(M_1 \wedge M_2) \\[-2pt] A_2 \\[-2pt] A_3 \\[-2pt] A_4 \\[-2pt] A_5 \end{array} \right] \\[-2pt] & R(M_1, M_2)=\\[-2pt] &\left[\begin{array}{lll} \text { 啮合关系, } & \text { 前项, } & M_1 \\[-2pt] & \text { 后项, } & M_2 \\[-2pt] & \text { 类型, } & v_{r 3} \\[-2pt] & \text { 程度, } & v_{r 3} \end{array}\right]=\left[\begin{array}{l} R_1(M_1) \\[-2pt] R_2(M_2) \\[-2pt] R_3 \\[-2pt] R_4 \end{array}\right] \end{split} }$

式中：

$ {\begin{split} & M_1=\left[\begin{array}{lll} \text { 主动轮 } D_{11}, & \text { 类型, } & v_{m 11} \\[-3pt] & \text { 模数, } & v_{m 12} \\[-3pt] & \text { 齿数/头数, } & v_{m 13} \\[-3pt] & \text { 重合度, } & v_{m 14} \\[-3pt] & \text { 压力角, } & v_{m 15} \end{array}\right]=\left[\begin{array}{l} M_{11} \\[-3pt] M_{12} \\[-3pt] M_{13} \\[-3pt] M_{14} \\[-3pt] M_{15} \end{array}\right] \\[-3pt] & M_2=\left[\begin{array}{lll} \text { 从动轮 } D_2, & \text { 类型, } & v_{m 21} \\[-3pt] & \text { 模数, } & v_{m 22} \\[-3pt] & \text { 齿数/头数, } & v_{m 23} \\[-3pt] & \text { 重合度, } & v_{m 24} \\[-3pt] & \text { 压力角, } & v_{m 25} \end{array}\right]=\left[\begin{array}{l} M_{21} \\[-3pt] M_{22} \\[-3pt] M_{23} \\[-3pt] M_{24} \\[-3pt] M_{25} \end{array}\right] \end{split}} $

根据领域知识和相关网方法可知：

$ {M_{11}} \widetilde \to {M_{12}} \wedge {M_{13}} \wedge {M_{14}} \wedge {M_{21}} $

(6)

$ {M_{21}}\widetilde \to {M_{22}} \wedge {M_{23}} \wedge {M_{24}} $

(7)

$ {A_1}( {{M_1} \wedge {M_2}} ) \widetilde \to {A_2} \wedge {A_4} \wedge {A_5} $

(8)

$ {A_2} \widetilde \to {A_3} $

(9)

$ {A_2} \widetilde \to M_{D2}^{} \widetilde \to M_{D3}^{} $

(10)

$ {R_1}( {{M_1}} ) \wedge {R_2}( {{M_2}} ) \widetilde \to {R_3} \wedge {R_4} $

(11)

综合式(6)、(7)可得如下相关网

$ {M_{11}}\mathop \to \limits^ \wedge \left\{ \begin{gathered} \mathop \wedge \limits_{{j_1} = 2}^4 {M_{1{j_1}}} \\[-3pt] {M_{21}}\widetilde \to \mathop \wedge \limits_{{j_2} = 2}^4 {M_{2{j_2}}} \\ \end{gathered} \right. $

(12)

综合式(8)、(9)、(10)可得如下相关网：

$ {A_1}( {{M_1} \wedge {M_2}} ) \mathop \to \limits^ \wedge \left\{ \begin{gathered} {A_2}\mathop \to \limits^ \wedge \left\{ \begin{gathered} M_{D2}^{} \widetilde \to M_{D3}^{} \\ {A_3} \\ \end{gathered} \right. \\ \\ {A_4} \\ {A_5} \\ \end{gathered} \right. $

(13)

此例中，显然$ {M_{01}} \ne {M_{02}} $，根据传导规则6可得如下传导规则：

$ \begin{split} &\left( {{\varphi _1}{M_{011}} = {{M'} _{011}}} \right) \wedge \left( {{M_{11}}\mathop \to \limits^ \wedge \left\{ \begin{array}{l} \mathop \wedge \limits_{{j_1} = 2}^4 {M_{1{j_1}}}\\ {M_{21}}\widetilde \to \mathop \wedge \limits_{{j_2} = 2}^4 {M_{2{j_2}}} \end{array} \right.} \right)\wedge\\ & \left( {{A_1}\left( {{M_1} \wedge {M_2}} \right)\mathop \to \limits^ \wedge \left\{ \begin{array}{l} {A_2}\mathop \to \limits^ \wedge \left\{ \begin{array}{l} M_{D2}^{}\widetilde \to M_{D3}^{}\\ {A_3} \end{array} \right.\\ \\ {A_4}\\ {A_5} \end{array} \right.} \right)\wedge\\ & ( {{R_1}\left( {{M_1}} \right) \wedge {R_2}\left( {{M_2}} \right)\widetilde \to {R_3} \wedge {R_4}} )\vDash\\ & ( {{}_{{\psi _1}}{T_{{A_{0}}({M_{01}}\wedge M_{02})}}{A_{0}}({M_{01}}\wedge M_{02}) = {{A'} _{0}}({{M'} _{01}}\wedge{{M'} _{02}})} )\wedge\\ & ( {{}_{{\psi _2}}{T_{{R_{0}}({M_{01},M_{02}})}}{R_{0}}({M_{01},M_{02}}) = {{R'} _{0}}({{M'} _{01},{M'} _{02}})} )\\[-5pt] \end{split} $

(14)

根据可拓变换方法和领域知识，若对$ M_{011}^{} $实施各种不同的主动可拓变换$ {\varphi _1} $，再根据传导规则(14)和领域知识可知，经过一系列传导变换，可获得多种不同的新功能复合元和新结构复合元，从而获得多种不同的新功能和新结构设计创意。

限于篇幅，仅以对$ M_{011}^{} $实施如下主动可拓变换为例：

$ {\varphi }_{1}{M}_{011}=(\begin{array}{ccc}主动轮{{D}^{\prime }} _{01}^{},& 类型,& {\rm{ZA}}型蜗杆\end{array}) ={{M}^{\prime }} _{011}^{} $

根据传导规则(14)和领域知识，可获得一种如下新功能复合元和新结构复合元：

$ {A_0^{\prime}(M_{01}^{\prime} \wedge M_{02}^{\prime})=\left[\begin{array}{lll} \text { 传递, } & \text { 工具, } &\;\; M'_{01} \wedge M_{02}^{\prime} \\[-1pt] & \text { 效率, } & \text { 低 } \\[-1pt] & \text { 传动比, } & \;\;10 / 1 \\[-1pt] & \text { 支配对象, } & \text { 动力 } \\[-1pt] & \text { 稳定性, } & \text { 高 } \end{array}\right] }$

$ { R_0^{\prime}(M_{01}^{\prime}, M'_{02})=\left[\begin{array}{lll} \text { 啮合关系, } & \text { 前项, } & \;\;M_{01}^{\prime} \\[-1pt] & \text { 后项, } &\;\; M_{02}^{\prime} \\[-1pt] & \text { 类型, } & \text { 螺旋啮合 } \\[-1pt] & \text { 程度, } & \text { 紧固 } \end{array}\right] }$

其中，

$ { M_{01}^{\prime}=\left[\begin{array}{lll} \text { 主动轮 } D_{01}^{\prime}, & \text { 类型, } & \text { ZA 型蜗杆 } \\[-2pt] & \text { 模数, } & 4 \\[-2pt] & \text { 齿数/头数, } & 2 \\[-2pt] & \text { 重合度, } & 0.1 \\[-2pt] & \text { 压力角, } & 20^{\circ} \end{array}\right]} $

$ {M_{02}^{\prime}=\left[\begin{array}{lll} \text { 从动轮 } D_{02}^{\prime}, & \text { 类型, } & \mathrm{ZA} \text { 型蜗轮 } \\[-2pt] & \text { 模数, } & 0 \\[-2pt] & \text { 齿数/头数, } & 20 \\[-2pt] & \text { 重合度, } & 0.1 \\[-2pt] & \text { 压角, } & 20^{\circ} \end{array}\right] }$

$ {M_{D 0}^{\prime}=\left[\begin{array}{lll} \text { 减速器 } D_0^{\prime}, & \text { 类型, } & \text { ZDY系列 } \\[-1pt] & \text { 产噪量, } & \text { 低 } \\[-1pt] & \text { 减速效率, } & \text { 高 } \end{array}\right]} $

由此获得一种ZDY型减速器的新功能和新结构设计创意，通过更改ZDY型减速器的动力传递元件，使传动比由4:1变为了10:1，并且提高了传动之间的稳定性，也使主动轮和从动轮之间的结构关系更加稳固，从而提高了ZDY型减速器的减速效率，同时降低了传递过程中的产噪量。

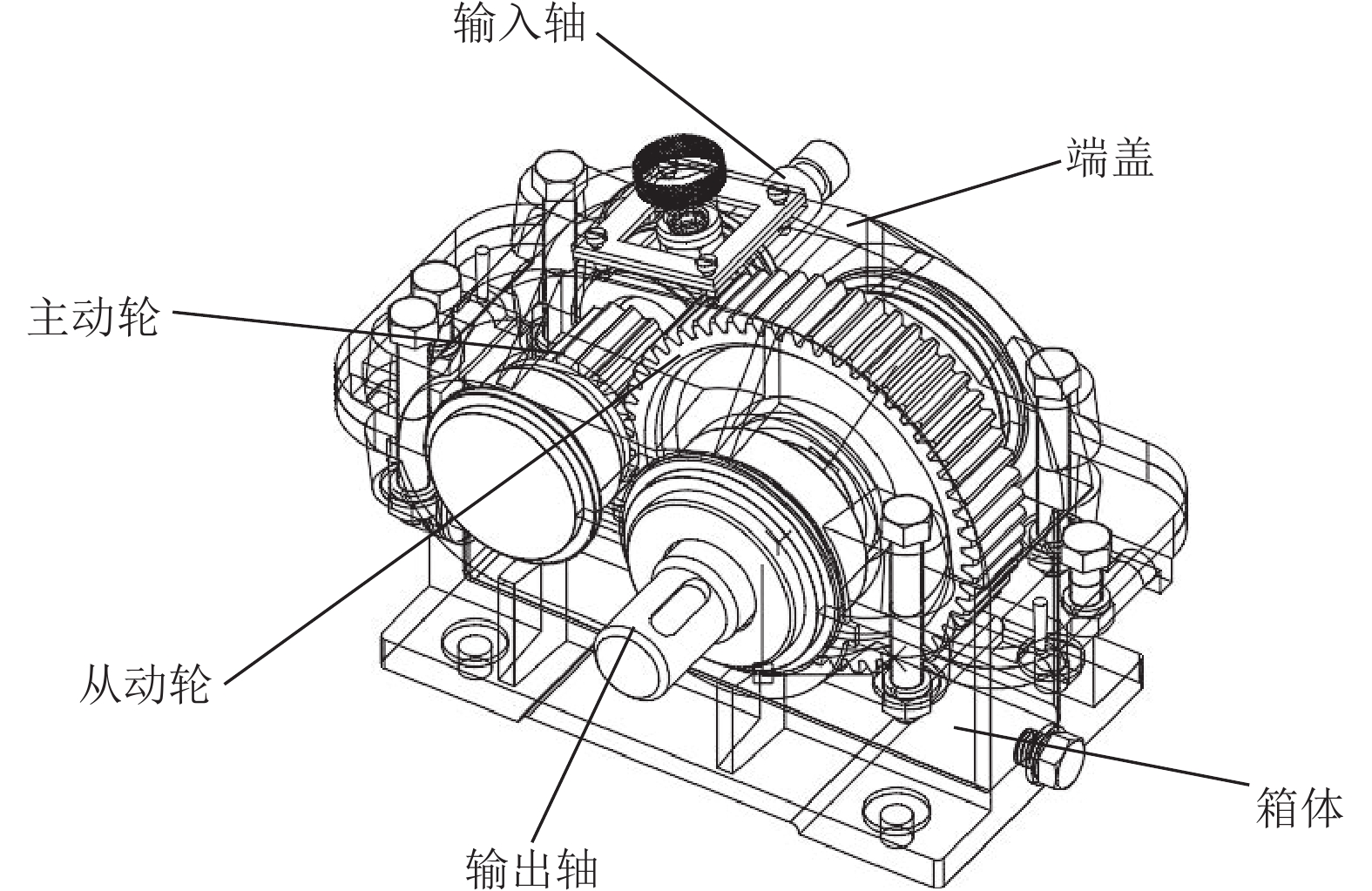
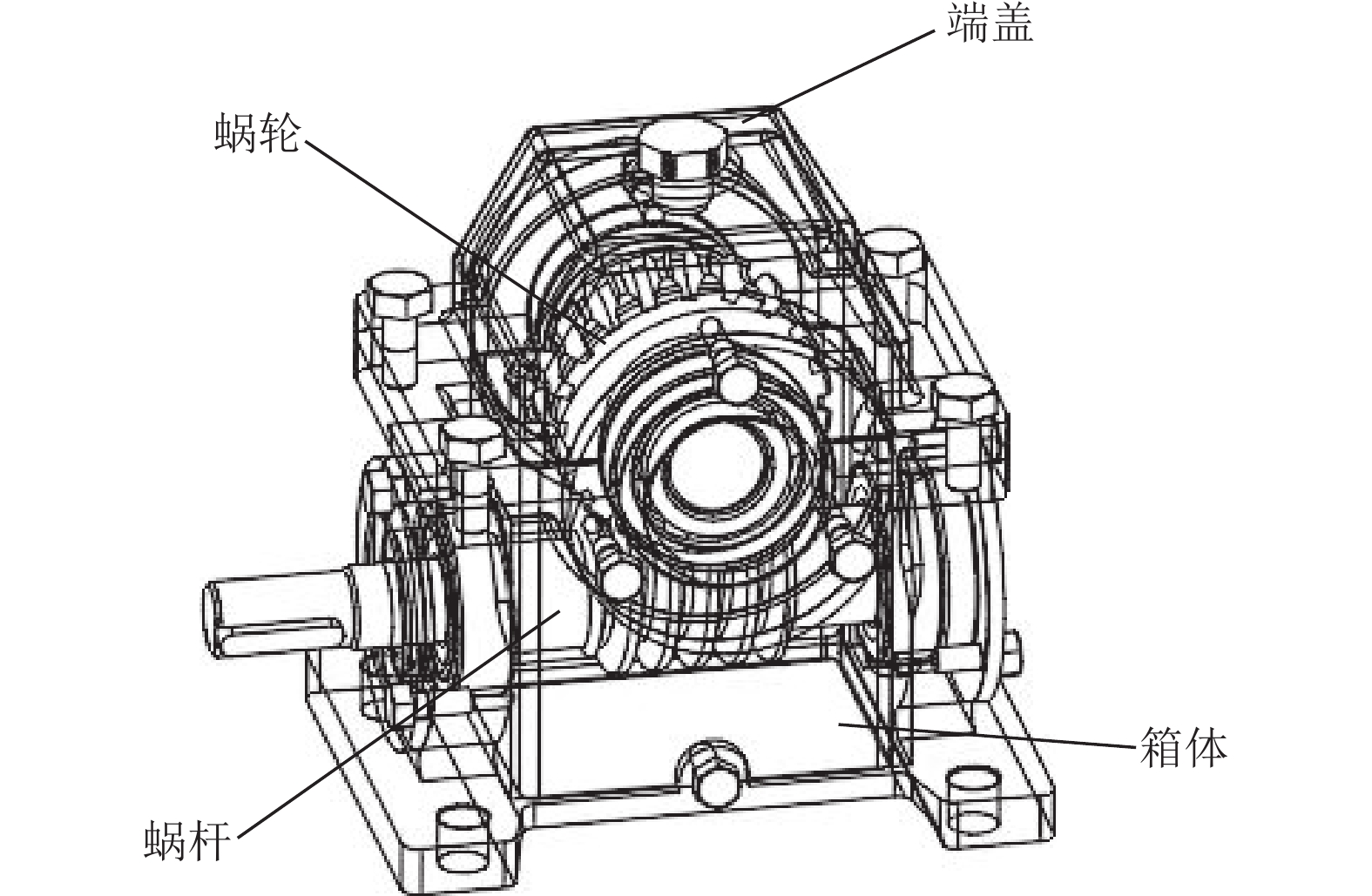
将该设计创意进一步具体化，可形成如图1和图2所示的设计方案。

4 结论

本文以物元和事元形成的复合元及物元和关系元形成的复合元为例，建立了异类多维复合元间的传导规则，填补了异类多维复合元变换的传导规则研究的空白，开辟了将异类多维复合元变换的传导规则应用于可拓创新设计的新方向，并以ZDY系列一级减速器的功能与结构设计为例，首先建立功能复合事元与结构复合关系元，并对其中的部件物元实施主动变换，根据所建立的传导规则，阐述传导变换的路径，并获得新功能复合元和新结构复合元，验证了异类多维复合元之间的传导规则的适用性。该研究为用形式化方法进行创新设计提供了推理依据，也为进一步研究可拓智能设计打下良好基础，具有重要的科学意义和实用价值。

异类多维复合元的复合类型有很多，不同基元之间组成的多维复合元变换的传导规则也有差异，本文只是给出了在可拓创新设计中应用较为广泛的异类多维复合元的传导规则，还需要更深入细致地研究各种异类多维复合元变换的传导规则，这是可拓推理的重要基础内容，可以为辅助人们进行矛盾问题的解决提供推理依据。异类多维复合元变换的传导规则在各领域矛盾问题求解中也有广阔的应用前景。