近年来，移动通信产业得到长足发展，智能手机、智能穿戴、便携平板电脑等网络边缘设备迅速普及，与此同时流量密集型网络应用随之产生。随着5G商用进程的快速推进，移动设备将会规模空前地应用于物联网之中^[1]。自动驾驶、增强现实等计算密集型和时延敏感型的应用，对计算能力和储能有限的移动设备提出了挑战^[2]。为了应对这种挑战，移动边缘计算成为了未来通信领域中一项引人注目的技术，它能够将用户设备的计算工作转移至边缘服务器，从而缓解用户设备的计算负荷，有效减少计算时延。然而，边缘计算服务器的位置通常是固定的，部分地区无法被无线网络覆盖，并且边缘服务器部署成本高昂^[2]，因此引入无人机(Unmanned Aerial Vehicle, UAV) 能有效支持移动边缘计算系统的应用。

无人机早期主要用于执行危险任务或作战打击中，随着技术的迭代更新发展，无人机因具有灵活性、按需部署和能与地面建立起高质量信道的优势而在无线通信领域备受青睐^[3-4]。无人机制造技术的进步，以及通信和计算设备的小型化，使得无人机通信和移动边缘计算系统的结合成为可能，进一步增强了任务的计算性能。相比于传统的固定通信基础设施的移动边缘计算系统，无人机移动边缘计算系统更具可移动性，能够向更广泛的用户设备提供按需服务^[5]。但是结合了移动边缘计算和无人机的物联网系统也面临着各种挑战，其中任务时延优化就是一个极为关键的问题。

随着物联网技术的快速发展，物联网需要支持具有严格时延要求和需要大量机器类型设备的实时应用^[6]，这促使国际电信联盟提出了超可靠低时延通信的5G通信目标，其中高可靠意味着网络需保持极高的稳定性，确保其他干扰不影响网络的通信过程，低时延则是要求传输极为迅速。为了保证URLLC的低时延，需要使用短数据包传输，而数据在有限块长度信道编码下不能实现无差错传输。目前大多数无线通信系统的设计建立在香农容量定理的基础之上，而在短包传输中，传统的香农容量已不再适用。如果直接采用香农容量表达式进行传输设计，会导致可靠性和时延的低估，无法保证服务质量^[7]。

针对无人机移动边缘计算系统的计算时延最小化问题，目前国内外已有不少学者对其进行了深入的探索。文献[2]研究了一个用于物联网设备计算卸载的无人机移动边缘计算系统，通过联合优化卸载调度、计算频率和无人机水平轨迹，分别以最小化无人机能耗和计算时延为目标，使用路径离散化技术解决问题，并提出了一种有效的交替迭代算法。文献[8]利用无人机充当移动边缘计算服务器，为任务计算量大的终端设备辅助计算，并作为中继将子任务传递到地面接入点执行。该作者以通信带宽、无人机传输功率、计算资源和无人机的三维位置为优化变量，研究了系统完成时间的最小化问题，并提出了一种基于连续凸逼近(Successive Convex Approximation, SCA) 的联合优化算法。文献[9]利用多辆无人机为海洋通信终端提供计算服务，通过优化无人机的轨迹设计和虚拟机的配置选择来研究系统时延最小化问题，并提出一种基于深度强化学习的深度Q网络和深度确定性策略梯度算法求解问题。文献[10]以最小化用户的平均业务延迟为目标，对多无人机轨迹、计算卸载和资源分配进行联合优化，并提出一种基于匹配博弈算法、块坐标下降(Block Coordinate Descent, BCD) 方法和SCA技术的优化算法，从而得到优化问题的次优解。

上述工作对计算任务卸载通信的考虑建立在香农容量定理上，即假设卸载通信的数据包足够长，不能满足低时延计算应用的要求。为了得到码长有限情况下的结果，需要采用URLLC(即短包通信)对任务卸载传输进行建模与分析。在2010年，文献[11]首次推导出了加性高斯白噪声信道下有限码长传输的速率近似表达式，该式为基于有限码长的数据传输研究和无线通信系统的设计提供了理论指导和支撑。文献[7]研究了URLLC场景下的安全任务关键型物联网通信系统，并考虑了两个优化问题：通过联合优化带宽单元和功率分配，实现加权吞吐量最大化和总传输功率最小化。文献[12] 研究工厂自动化场景中智能反射面辅助URLLC的系统，并对7种信道情况进行了全面的性能分析。文献[13]研究了一种具有URLLC要求的双向无人机中继系统，在前向链路的URLLC约束下，实现反向链路的平均通信速率最大化。然而，已有的研究工作缺少考虑无人机移动边缘计算系统中的URLLC计算任务卸载。

本文考虑了一个具有URLLC任务卸载的无人机移动边缘计算系统，其中地面设备将部分计算任务通过URLLC的方式卸载至无人机，无人机为地面设备提供MEC服务。为了平衡该系统的任务卸载通信能力和计算能力，优化计算性能，通过联合优化无人机的部署位置、任务卸载带宽和无人机与地面设备的CPU计算频率，最小化系统的整体计算时延。

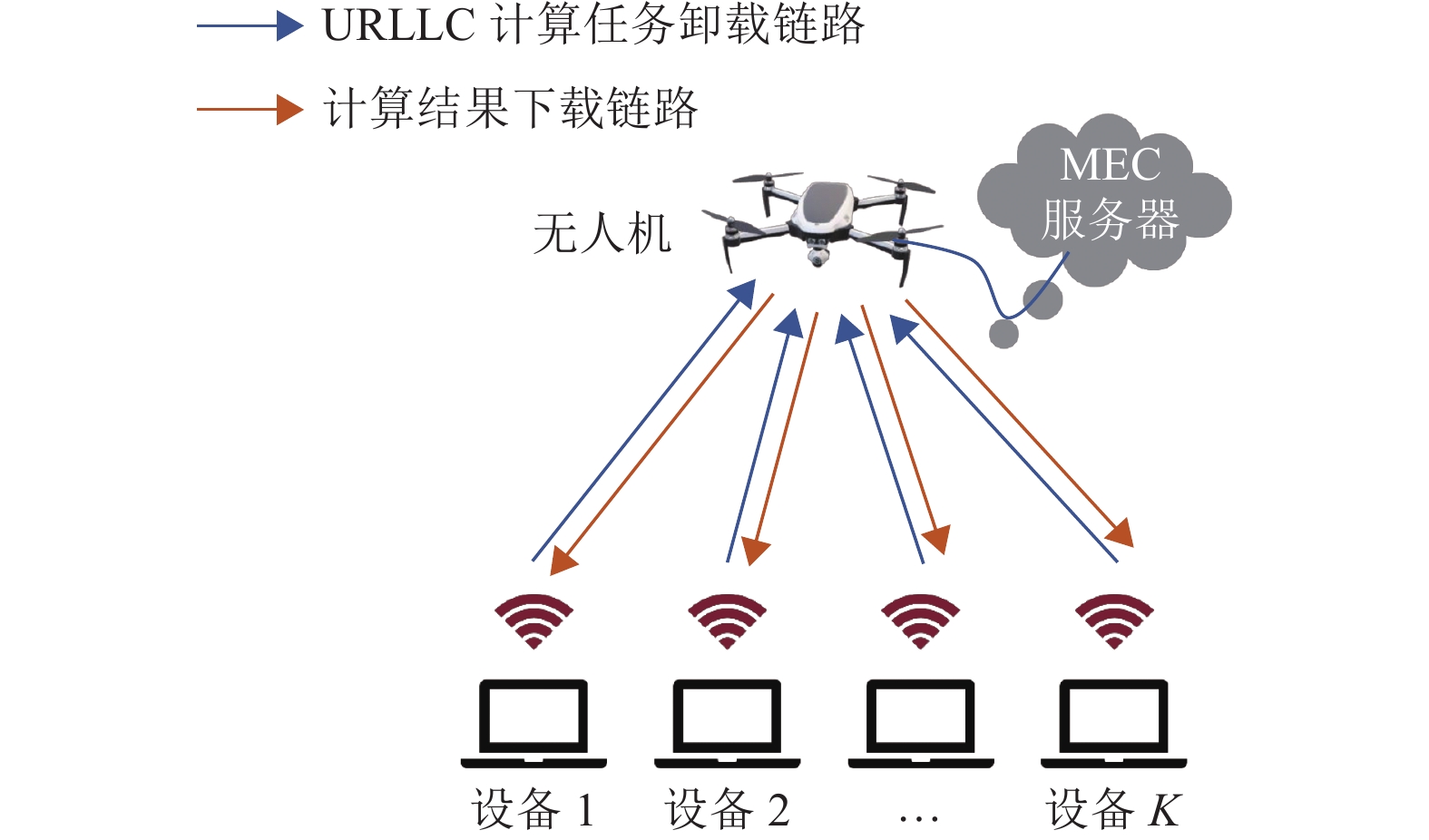
1 系统模型 1.1 通信模型

如图1所示，本文考虑一种无人机移动边缘计算系统：地面上有K个固定的设备以执行一些具有计算要求的任务(设备集合表示为$\mathcal{K} \triangleq \left\{ {1,2,\cdots,K} \right\}$)，一架配备边缘计算服务器的多旋翼无人机为多个地面设备提供边缘计算服务。假设地面设备随机分布在一个二维平面上，无人机的高度固定为H，并且无人机的位置在整个服务过程中保持不变。考虑一个三维的笛卡尔坐标系，地面设备k和无人机的水平位置坐标分别为${{\boldsymbol{q}}_k} = {[{x_k},{y_k}]^{\text{T}}},k \in K$和${{\boldsymbol{q}}_{\text{u}}} = {[{x_{\text{u}}},{y_{\text{u}}}]^{\text{T}}}$。

每个设备的计算任务可以划分为两部分，一部分在设备进行本地计算，另一部分卸载传输至无人机上的边缘服务器辅助计算^[14]，二者并行处理。

为保证低时延通信，设备向无人机传输的数据以短包形式传输。在短包通信的场景下，设备卸载一个数据包的时间一般不超过信道的相干时间。由于传输时间非常短，将任务周期划分为不同时隙给设备传输显然是不可行的，因此假设所有地面设备采用频分多址接入技术卸载数据，并假设所有设备的卸载传输时间相同，记为${T^{{\text{trans}}}}$。

考虑户外空旷环境的情况，无人机与设备之间的无线信道以视距链路为主导^[15]，无人机和设备之间的信道增益服从自由空间路径损耗模型。信道功率增益可表示为

${g_k} = {g_0}d_k^{ - 2} = \frac{{{g_0}}}{{{{\left\| {{{\boldsymbol{q}}_{\text{u}}} - {{\boldsymbol{q}}_k}} \right\|}^2} + {H^2}}},\forall k$

(1)

式中：${g_0}$为参考距离为1 m时的基准信道功率增益，${d_k} = {( {{{\left\| {{{\boldsymbol{q}}_{\text{u}}} - {{\boldsymbol{q}}_k}} \right\|}^2} + {H^2}} ) ^{1/2}}$为设备k和无人机的间距。设备k的传输功率为${P_k}$，分配给设备k的任务卸载带宽为${b_k}$，接收端的噪声功率谱密度为${\sigma ^2}$，则设备k的卸载信道的接收信噪比可表示为

${\gamma _k} = \frac{{{P_k}{g_k}}}{{{b_k}{\sigma ^2}}},\forall k$

(2)

地面设备卸载任务给无人机时采用的是有限块长度信道编码，而数据在有限块长度信道编码下不能实现无差错传输，因此接收器的解码错误概率是不可忽略的。设在给定信道数据包长度为${N_k} = {b_k}{T^{{\text{trans}}}}$时，设备k卸载数据时无人机接收数据的误码率为${\varepsilon _k} \in (0,1)$，则设备k卸载任务至无人机时的短包通信速率(bit·s⁻¹·Hz⁻¹)为^[11]

${R_k} \approx {\log _2}( {1 + {\gamma _k}} ) -\frac{{{Q^{ - 1}}({\varepsilon _k}) }}{{\ln 2}} \sqrt {\frac{{{V_k}}}{{{N_k}}}} ,\forall k$

(3)

式中：${V_k} = 1 - {( {1 + {\gamma _k}} ) ^{ - 2}}$为信道散度，${Q^{ - 1}}(x)$为$Q(x) = \displaystyle\int_x^\infty {\dfrac{1}{{\sqrt {2{\text{π}}} }}} \exp ( {{{ - {t^2}} / 2}} ) {\text{d}}t$的反函数。

1.2 计算模型

UAV和多设备间的任务卸载与计算分为3个阶段：设备本地计算、设备卸载传输数据和无人机边缘计算。假设任务计算结果的大小与卸载数据本身相比相对较小，因此无人机反馈计算结果所占据的时延可以忽略不计^[15]。

设设备k的CPU频率为${f_k}$，执行单位比特计算任务所需的CPU循环次数为${C_k}$，本地计算的数据量为$I_k^{{\text{local}}}$，则设备k的本地计算时延$t_k^{{\text{local}}}$可以表示为

$t_k^{{\text{local}}} = \frac{{I_k^{{\text{local}}}{C_k}}}{{{f_k}}},\forall k$

(4)

设无人机用于计算来自设备k的卸载任务的CPU运行频率为${f_{{\text{U}},k}}$，设备k的边缘计算数据量为$I_k^{{\text{UAV}}}$，则设备k的边缘计算时延 $t_k^{{\text{UAV}}}$可以表示为

$t_k^{{\text{UAV}}} = \frac{{I_k^{{\text{UAV}}}{C_k}}}{{{f_{{\text{U}},k}}}},\forall k$

(5)

因此设备k的计算时延取决于$t_k^{{\text{local}}}$和$t_k^{{\text{UAV}}} + {T^{{\text{trans}}}}$这两个数值的最大值，系统的总计算时延T可表示为所有设备中最大的计算时延，即

$T = \mathop {\max }\limits_{\forall k} \left\{ {\max \left\{ {t_k^{{\text{local}}},t_k^{{\text{UAV}}} + {T^{{\text{trans}}}}} \right\}} \right\}$

(6)

为了保证满足任务量要求，需要施加任务计算量约束条件。设设备k需要完成的任务计算量为${I_k}$，则设备k的任务计算量约束如下

$I_k^{{\text{local}}} + I_k^{{\text{UAV}}} \geqslant {I_k},\forall k$

(7)

对于地面设备的任务计算和卸载，应当施加设备的能耗约束。设备k的本地计算能耗为$E_k^{{\text{local}}} = t_k^{{\text{local}}}{\rho _k}{f_k}^3$，其中${\rho _k}$为设备k的有效电容系数。设备k卸载任务的能耗为$E_k^{{\text{trans}}} = {T^{{\text{trans}}}}{P_k}$。设设备k的能耗预算为$E_k^{\max }$，则设备k的能耗约束如下

$E_k^{{\text{local}}} + E_k^{{\text{trans}}} \leqslant E_k^{\max },\forall k$

(8)

由于短包通信中误码率不可忽略，因此无人机接收到的有效任务量必定小于设备卸载的任务量。设备k卸载的任务量为$I_k^{{\text{trans}}} = {N_k}{R_k} = {b_k}{T^{{\text{trans}}}}{R_k}$，当误码率为${\varepsilon _k}$时，无人机实际上接收到的有效任务量为$\left( {1 - {\varepsilon _k}} \right) I_k^{{\text{trans}}}$，因此需要施加以下的计算因果约束

$\left( {1 - {\varepsilon _k}} \right) I_k^{{\text{trans}}} \geqslant I_k^{{\text{UAV}}},\forall k$

(9)

1.3 问题描述

根据短包通信速率的表达式(3) ，URLLC无人机移动边缘计算系统的任务卸载通信能力由无人机的位置、卸载带宽和设备的发射功率决定；由前文讨论的计算模型可知，系统的计算能力由无人机和地面设备的CPU计算频率决定。为了平衡系统的通信能力和计算能力，从而优化其计算性能，本文研究联合优化无人机的部署位置、任务卸载带宽和无人机与地面设备的CPU计算频率，最小化所有设备的最大计算时延T。令${\mathcal{T}} \triangleq \{ t_k^{{\text{local}}},t_k^{{\text{UAV}}},\forall k\}$，${\mathcal{B}} \triangleq \{ {b_k},\forall k\}$，${\mathcal{F}} \triangleq \{ {f_{{\text{U}},k}},{f_k},\forall k\}$，则优化问题可以表述为

$\begin{array}{l} {\rm{P}}1:\mathop {\min }\limits_{\{ {{\boldsymbol{q}}_{\text{u}}},\mathcal{T},\mathcal{B},\mathcal{F}\} } \; T\\ {\text{s}}{\text{.t}}{\text{.}} \left\{ \begin{array}{l} \displaystyle\sum\limits_{k = 1}^K {{b_k} \leqslant {B^{\max }}}\qquad\qquad\qquad\qquad\qquad\qquad\;\;\,\;\,(10)\\ \displaystyle\sum\limits_{k = 1}^K {{f_{{\text{U}},k}} \leqslant f_{\text{U}}^{\max },{f_k} \leqslant f_k^{\max }}\qquad\qquad\qquad\qquad\;\;\,(11)\\ \dfrac{{{f_{{\text{U}},k}}}}{{{C_k}}}t_k^{{\text{UAV}}} + \dfrac{{{f_k}}}{{{C_k}}}t_k^{{\text{local}}} \geqslant {I_k},\forall k\qquad\qquad\qquad\qquad\,(12)\\ t_k^{{\text{local}}}{\rho _k}{f_k}^3 + {T^{{\text{trans}}}}{P_k} \leqslant E_k^{\max },\forall k\qquad\qquad\qquad\;\;\,(13)\\ \left( {1 - {\varepsilon _k}} \right) {b_k}{T^{{\text{trans}}}}{R_k} \geqslant \dfrac{{{f_{{\text{U}},k}}}}{{{C_k}}}t_k^{{\text{UAV}}},\forall k\qquad\qquad\quad\;\;\;(14) \end{array} \right. \end{array}$

式中：${B^{\max }}$为总卸载带宽，$f_{\text{U}}^{\max }$为无人机的最大CPU频率，$f_k^{\max }$为设备k的最大CPU频率。约束(10) 为设备的带宽分配约束；约束(11) 为设备和无人机的CPU计算频率约束；约束(12) 为任务计算量约束；约束(13) 为设备的能耗约束；约束(14) 为计算卸载的信息因果约束。由于问题P1存在非凸约束(12)~(14) ，使得问题P1的可行解集不是一个凸集，因此该问题是一个非凸优化问题^[16]。

2 问题求解

为了求解问题P1，可以使用BCD算法将原问题分解成两个可以交替循环迭代的子问题：子问题1给定卸载带宽和CPU频率，优化无人机部署的位置和计算时延；子问题2给定无人机部署的位置，优化卸载带宽、CPU频率和计算时延。

2.1 优化无人机部署位置和计算时延

当卸载带宽$\mathcal{B}$和CPU频率$\mathcal{F}$给定时，原问题中只与带宽和CPU频率有关的约束条件(10)和(11)可以删除，原问题P1将转换为

$\begin{array}{l} {\rm{P}}2: \mathop {\min }\limits_{\{ {{\boldsymbol{q}}_{\text{u}}},\mathcal{T}\;\} }\; T \\ \qquad{\text{s}}{\text{.t}}{\text{.}}\quad(12)\sim(14)\end{array}$

此时约束(14)不等式的左边是非凸的。为了处理约束(14)的非凸性，可以借鉴文献[17]中的定理3和定理4，使用对数函数去非线性近似短包通信速率的表达式。对于任意给定的信噪比初始值${\hat \gamma _k}$，存在${R_k}$的非线性下界为

$R_k^{{\text{lb}}} \triangleq {\dot {\rho }_k}{\log _2}\left( {{\gamma _k}} \right) + \frac{{{{\dot {\eta }}_k}}}{{\ln 2}}$

(15)

式中：${\dot \rho _k} = {\dddot \rho _k} - {\alpha _k}{\ddot \rho _k}$，${\alpha _k} = {{{Q^{ - 1}}({\varepsilon _k}) } / {\sqrt {{N_k}} }}$，${\ddot \rho _k} = \dfrac{{{{\hat \gamma }_k}}}{{\sqrt {{{\hat \gamma }_k}^2 + 2{{\hat \gamma }_k}} }} - \dfrac{{{{\hat \gamma }_k}\sqrt {{{\hat \gamma }_k}^2 + 2{{\hat \gamma }_k}} }}{{{{\left( {1 + {{\hat \gamma }_k}} \right) }^2}}}，$ ${\dddot \rho _k} = \dfrac{{{{\hat \gamma }_k}}}{{1 + {{\hat \gamma }_k}}}，$ ${\dot \eta _k} = {\dddot \eta _k} - {\alpha _k}{\ddot \eta _k}，$ ${\ddot \eta _k} = \sqrt {1 - \dfrac{1}{{{{\left( {1 + {{\hat \gamma }_k}} \right) }^2}}}} - {\ddot \rho _k}\ln \left( {{{\hat \gamma }_k}} \right)$，${\dddot \eta _k} = \ln \left( {1 + {{\hat \gamma }_k}} \right) - {\dddot \rho _k}\ln \left( {{{\hat \gamma }_k}} \right)$。当且仅当${\gamma _k} = {\hat \gamma _k}$时，${R_k} = R_k^{{\text{lb}}}$。

将式(15)代入约束条件(14)后化简，约束(14)可以改写为

${\gamma _k} \geqslant \exp \left( {\frac{{\ln 2}}{{{{\dot \rho }_k}}}\left( {\frac{{{f_{{\text{U}},k}}t_k^{{\text{UAV}}}}}{{\left( {1 - {\varepsilon _k}} \right) {b_k}{T^{{\text{trans}}}}{C_k}}} - \frac{{{{\dot \eta }_k}}}{{\ln 2}}} \right) } \right) ,\forall k$

(16)

此时问题P2可改写为

$\begin{array}{l} {\rm{P}}3: \mathop {\min }\limits_{\{ {{\boldsymbol{q}}_{\text{u}}},\mathcal{T}\;\} }\; T\\ \qquad{\text{s}}{\text{.t}}{\text{.}}\quad(12) , (13) ,(16) \end{array}$

不难发现，问题P3的可行解集是问题P2可行解集的子集，因此求解问题P3得到的目标函数值实际上是问题P2目标函数值的上界。

若定义常数${\omega _k} = {{{P_k}{g_0}} \mathord{\left/ {\vphantom {{{P_k}{g_0}} {({b_k}{\sigma ^2}}}} \right. } {({b_k}{\sigma ^2}}})$，则式(16) 可改写为

$\frac{{{\omega _k}}}{{{{\left\| {{{\boldsymbol{q}}_{\text{u}}} - {{\boldsymbol{q}}_k}} \right\|}^2} + {H^2}}} \geqslant \exp \left( {\frac{{\ln 2}}{{{{\dot \rho }_k}}}\left( {\frac{{{f_{{\text{U}},k}}t_k^{{\text{UAV}}}}}{{\left( {1 - {\varepsilon _k}} \right) {b_k}{T^{{\text{trans}}}}{C_k}}} - \frac{{{{\dot \eta }_k}}}{{\ln 2}}} \right) } \right)$

(17)

式(17)不等号的右边是凸的，而不等号左边关于${\left\| {{{\boldsymbol{q}}_{\text{u}}} - {{\boldsymbol{q}}_k}} \right\|^2} + {H^2}$是凸的。由于一个凸函数的一阶泰勒展开是它的凹下界^[16]，因此可以推导得到${\gamma _k}$的一个全局下界为

${\gamma _k} \geqslant \gamma _k^{{\text{lb}}} \triangleq \frac{{{\omega _k}}}{{{{\left\| {{{{\boldsymbol{\hat q}}}_{\text{u}}} - {{\boldsymbol{q}}_k}} \right\|}^2} + {H^2}}} - \frac{{{\omega _k}( {{{\left\| {{{\boldsymbol{q}}_{\text{u}}} - {{\boldsymbol{q}}_k}} \right\|}^2} - {{\left\| {{{{\boldsymbol{\hat q}}}_{\text{u}}} - {{\boldsymbol{q}}_k}} \right\|}^2}} ) }}{{{{\left( {{{\left\| {{{{\boldsymbol{\hat q}}}_{\text{u}}} - {{\boldsymbol{q}}_k}} \right\|}^2} + {H^2}} \right) }^2}}}$

(18)

式中：$\gamma _k^{{\text{lb}}}$为${\gamma _k}$的下界，${{\boldsymbol{\hat q}}_{\text{u}}}$为上一次的迭代值。式(18)中的等号当且仅当${{\boldsymbol{q}}_{\text{u}}} = {{\boldsymbol{\hat q}}_{\text{u}}}$时成立。

将${\gamma _k}$的凹下界(18)代入到约束(16)中，可以将问题P3近似为

${\begin{array}{l} {\rm{P}}4: \mathop {\min }\limits_{\{ {{\boldsymbol{q}}_{\text{u}}},\mathcal{T}\;\;\} }\; T \\ \qquad {\text{s}}{\text{.t}}{\text{.}} \quad \left\{ \begin{array}{l}\gamma _k^{{\text{lb}}} \geqslant \exp \left( {\dfrac{{\ln 2}}{{{{\dot \rho }_k}}}\left( {\dfrac{{{f_{{\text{U}},k}}t_k^{{\text{UAV}}}}}{{\left( {1 - {\varepsilon _k}} \right) {b_k}{T^{{\text{trans}}}}{C_k}}} - \dfrac{{{{\dot \eta }_k}}}{{\ln 2}}} \right) } \right) ,\forall k \\ (12),(13) \end{array} \right. \end{array}}$

(19)

此时的问题P4是一个标准的凸优化问题，可使用凸优化工具CVX有效求解，得到无人机的优化位置。由于问题P4的可行解集是问题P3的子集，因此求解问题P4得到的目标函数值实际上是问题P3目标函数值的上界。

2.2 优化卸载带宽、CPU频率和计算时延

不难证明，当第二个子问题取得最优解时，约束(12)将会取得等号，并且$t_k^{{\text{local}}} = T$和$t_k^{{\text{UAV}}} = T - {T^{{\text{trans}}}}$是$\mathcal{T}$的一个最优解，因此可以通过在任意给定T的情况下求解该子问题，然后使用二分法搜索$\eta = 1$时的计算时延T并得到最优的带宽与CPU频率分配。令${{\boldsymbol{q}}_{\text{u}}}$为求解子问题P4得到的无人机位置优化值，则原问题P1将转换为

$\begin{array}{l} {\rm{P}}5: \mathop {\max }\limits_{\{ \mathcal{B},\mathcal{F},\eta \} } \; \eta \\ {\text{s}}{\text{.t}}{\text{.}}\quad \left\{ \begin{array}{l}\dfrac{{\dfrac{{{f_{{\text{U}},k}}}}{{{C_k}}}\left( {T - {T^{{\text{trans}}}}} \right) + \dfrac{{{f_k}}}{{{C_k}}}T}}{{{I_k}}} \geqslant \eta ,\forall k \qquad\quad\,\;\;\;(20)\\ T{\rho _k}{f_k}^3 + {T^{{\text{trans}}}}{P_k} \leqslant E_k^{\max },\forall k\qquad\qquad\;\;\;\;\;(21)\\ \left( {1 - {\varepsilon _k}} \right) {b_k}{T^{{\text{trans}}}}{R_k} \geqslant \dfrac{{{f_{{\text{U}},k}}}}{{{C_k}}}\left( {T - {T^{{\text{trans}}}}} \right) ,\forall k\;\;\;(22)\\ (10) , (11) \end{array} \right. \end{array}$

此时，约束(22)不等式的左边相对于${b_k}$是非凸的，需要对其进行处理。若定义${a_k} = {{{P_k}{g_k}} \mathord{/ {\vphantom {{{P_k}{g_k}} {{\sigma ^2}}}} } {{\sigma ^2}}}$，则信噪比的表达式(2) 可以变形为

${\gamma _k} = \frac{{{P_k}{g_k}}}{{{b_k}{\sigma ^2}}} = \frac{{{a_k}}}{{{b_k}}},\forall k$

(23)

若定义${U_k} \triangleq {b_k}{V_k}$，则约束(22)不等式的左边可以表示为

$\left( {1 - {\varepsilon _k}} \right)\underbrace {\left({b_k}{T^{{\rm{trans}}}}{{\log }_2}\left( {1 + \frac{{{a_k}}}{{{b_k}}}} \right)\right.}_{{S_k}({b_k})} - \underbrace {\left.\sqrt {{U_k}{T^{{\rm{trans}}}}} \frac{{{Q^{ - 1}}({\varepsilon _k})}}{{\ln 2}}\right)}_{{Z_k}({b_k})}$

(24)

由于函数$f(x) = x{\log _2}\left( {1 + {1 \mathord{\left/ {\vphantom {1 x}} \right. } x}} \right)$是凹函数，因此${S_k}({b_k})$是一个关于${b_k}$的凹函数。

接下来讨论${Z_k}({b_k})$的凹凸性，先求得${U_k}$关于${b_k}$的一阶导数和二阶导数分别为

$\frac{{\partial {U_k}}}{{\partial {b_k}}} = \frac{{3{a_k}^2{b_k} + {a_k}^3}}{{{{\left( {{b_k} + {a_k}} \right) }^3}}}$

(25)

$\frac{{{\partial ^2}{U_k}}}{{\partial {b_k}^2}} = - \frac{{6{a_k}^2{b_k}}}{{{{\left( {{b_k} + {a_k}} \right) }^4}}}$

(26)

继而可以推导出${Z_k}({b_k})$的一阶导数和二阶导数分别为

$\frac{{\partial {Z_k}}}{{\partial {b_k}}} = \frac{1}{{2\sqrt {{U_k}} }}\left(\frac{{\partial {U_k}}}{{\partial {b_k}}}\right)\frac{{{Q^{ - 1}}({\varepsilon _k}) \sqrt {{T^{{\text{trans}}}}} }}{{\ln 2}}$

(27)

$\frac{{{\partial ^2}{Z_k}}}{{\partial {b_k}^2}} = \frac{{2\dfrac{{{\partial ^2}{U_k}}}{{\partial {b_k}^2}}{U_k} - {{\left( {\dfrac{{\partial {U_k}}}{{\partial {b_k}}}} \right) }^2}}}{{4{U_k}\sqrt {{U_k}} }}\left(\frac{{{Q^{ - 1}}({\varepsilon _k}) \sqrt {{T^{{\text{trans}}}}} }}{{\ln 2}}\right) \lt 0$

(28)

当${b_k} \geqslant 0$时，${Z_k}({b_k})$的二阶导数小于0，因此${Z_k}({b_k})$是一个关于 ${b_k}$ 的凹函数。

不难发现，约束(22)不等式的左边是2个凹函数之差，因此可以利用SCA方法对其进行处理。在给定的初始点${\hat b_k}$，对${Z_k}({b_k})$进行一阶泰勒展开，可以得到${Z_k}({b_k})$的上界函数为

$Z_k^{{\text{ub}}}({b_k}) \triangleq {Z_k}({\hat b_k}) + {\left. {\frac{{\partial {Z_k}}}{{\partial {b_k}}}} \right|_{{b_k} = {{\hat b}_k}}}( {{b_k} - {{\hat b}_k}} )$

(29)

当且仅当${b_k} = {\hat b_k}$时，存在${Z_k}({b_k}) = Z_k^{{\text{ub}}}({b_k})$。结合上述对${Z_k}({b_k})$的SCA操作，可以将子问题P5转换为

$\begin{array}{l} {\rm{P}}6: \mathop {\max }\limits_{\{ \mathcal{B},\mathcal{F},\eta \} }\; \eta \\ {\text{s}}{\text{.t}}{\text{.}} \left\{ \begin{array}{l} \left( {1 - {\varepsilon _k}} \right) ( {{S_k}({b_k}) - Z_k^{{\text{ub}}}({b_k}) } ) \geqslant \dfrac{{{f_{{\text{U}},k}}}}{{{C_k}}}\left( {T - {T^{{\text{trans}}}}} \right) ,\forall k\;\;\, (30)\\ (10) , (11) , (20) , (21) \end{array} \right. \end{array}$

此时问题P6是一个标准的凸优化问题，可以用CVX求解器有效求解。值得注意的是，问题P6的可行解集是问题P5可行解集的子集，因此求解问题P6得到的目标函数值实际上是问题P5目标函数值的下界。

2.3 联合优化算法

结合前文对2个子问题的处理，提出一种联合优化无人机部署的位置、任务卸载带宽和无人机与地面设备的CPU计算频率的交替优化算法，如算法1所示。

算法1　联合优化算法

(1) 初始化${\{ {\mathcal{B}^l},{\mathcal{F}^l},{\boldsymbol{q}}_{\text{u}}^l,{T^l}\} }$，令${l = 0}$，设置精确度阈值${\varepsilon }$。

(2) 重复：

　(a) 代入给定的${ \{ {\mathcal{B}^l},{\mathcal{F}^l}\} }$求解问题P4，得到优化解${ {\boldsymbol{q}}_{\text{u}}^{l + 1} }$。

　(b) 代入上一步求得的${ {\boldsymbol{q}}_{\text{u}}^{l + 1}}$求解问题P6，得到优化解${ \{ {\mathcal{B}\; ^ {l + 1}},{\mathcal{F} \;^ {l + 1}},{T^{l + 1}}\} }$。

　(c) 更新${l = l + 1}$。

(3) 直到达到收敛条件${{{| {{T^{l + 1}} - {T^l}} |} \mathord{/ {\vphantom {{| {{T^{l + 1}} - {T^l}} |} {{T^{l + 1}}}}} } {{T^{l + 1}}}} \leqslant \varepsilon }$。

(4) 输出最优解${\{ {\mathcal{B}\;^l},{\mathcal{F}\;^l},{\boldsymbol{q}}_{\text{u}}^l,{T^l}\} }$。

定义$T({\mathcal{B}\;^l},{\mathcal{F}\;^l},{\boldsymbol{q}}_{\text{u}}^l)$、${T^{\log }}({\mathcal{B}\;^l},{\mathcal{F}\;^l},{\boldsymbol{q}}_{\text{u}}^l)$、${T^{{\text{ub}}}}({\mathcal{B}\;^l},{\mathcal{F}\;^l},{\boldsymbol{q}}_{\text{u}}^l)$分别表示优化问题P2、P3、P4的目标函数值。在算法的第2(a)步中，存在以下的不等式关系：

$\begin{split} &T({\mathcal{B}\;^l},{\mathcal{F}\;^l},{\boldsymbol{q}}_{\text{u}}^l) \mathop = \limits^{{\text{(a) }}} {T^{\log }}({\mathcal{B}\;^l},{\mathcal{F}\;^l},{\boldsymbol{q}}_{\text{u}}^l) \mathop = \limits^{{\text{(b) }}} {T^{{\rm{ub}}}}({\mathcal{B}\;^l},{\mathcal{F}\;^l},{\boldsymbol{q}}_{\text{u}}^l) \mathop \geqslant \limits^{{\text{(c) }}} \\ &\qquad\qquad\quad {T^{{\rm{ub}}}}({\mathcal{B}\;^l},{\mathcal{F}\;^l},{\boldsymbol{q}}_{\text{u}}^{l + 1}) \mathop \geqslant \limits^{{\text{(d) }}} T({\mathcal{B}^l},{\mathcal{F}^l},{\boldsymbol{q}}_{\text{u}}^{l + 1}) \end{split}$

(31)

式中：等式(a)存在是因为使用对数函数近似短包通信速率表达式后，目标函数在${\boldsymbol{q}}_{\text{u}}^{} = {\boldsymbol{q}}_{\text{u}}^l$处数值相等。等式(b)存在是因为进行了一阶泰勒展开，目标函数在展开点处有同样的数值。不等式(c)存在是因为求解问题P4得到无人机优化位置，这样的操作让目标函数在迭代中保持非增。不等式(d)存在是因为求解问题P4得到的目标函数值是问题P3的上界，而求解问题P3得到的目标函数值是问题P2的上界。因此目标函数T在迭代求解的过程中是不递增的。

定义$\eta ({\mathcal{B}\;^l},{\mathcal{F}\;^l},{\boldsymbol{q}}_{\text{u}}^l)$、${\eta ^{{\text{lb}}}}({\mathcal{B}\;^l},{\mathcal{F}\;^l},{\boldsymbol{q}}_{\text{u}}^l)$分别为优化问题P5、P6的目标函数值。在算法的第2(b)步中，存在以下的不等式关系

$\begin{split} & \eta ({\mathcal{B}\;^l}, {\mathcal{F}\;^l} , {\boldsymbol{q}}_{\text{u}}^{l + 1}) \mathop = \limits^{{\text{(e) }}} {\eta ^{{{\rm{l}}} {\text{b}}}}({\mathcal{B}\;^l},{\mathcal{F}\;^l},{\boldsymbol{q}}_{\text{u}}^{l + 1}) \mathop \leqslant \limits^{{\text{(f) }}} \\ &\qquad {\eta ^{{{\rm{l}}} {\text{b}}}}({\mathcal{B}\;^{l + 1}},{\mathcal{F}\;^{l + 1}},{\boldsymbol{q}}_{\text{u}}^{l + 1}) \mathop \leqslant \limits^{{\text{(g) }}} \eta ({\mathcal{B}\;^{l + 1}},{\mathcal{F}\;^{l + 1}},{\boldsymbol{q}}_{\text{u}}^{l + 1}) \end{split}$

(32)

式中：等式(e)存在是因为进行了一阶泰勒展开，目标函数在展开点处有同样的数值。不等式(f)存在是因为求解问题P6得到卸载带宽和CPU频率的优化值，这样的操作让目标函数在迭代中保持非减。不等式(g)存在是因为求解问题P6得到的目标函数值是问题P5目标函数值的下界。因此目标函数$\eta$在迭代求解的过程中不递减且逐渐趋于1，保证计算时延、卸载带宽和无人机与地面设备的CPU计算频率分配取得局部最优解。

综上所述，由于受到任务计算量约束条件的限制，并且系统的计算时延是一个存在下界的有限值，因此联合优化算法在迭代过程中是收敛的。联合优化算法的计算复杂度为$\mathcal{O}({(KN) ^{3.5}}\log ({1 / \varepsilon }) )$，其中N为收敛所需的迭代次数。

3 仿真结果

考虑一个面积为800 m×400 m的矩形区域，设定一架配备MEC服务器的无人机处在固定的高度H=100 m，为地面上5个设备提供计算卸载服务。各设备的数据量分别设置为${I_1} = \overline I$、${I_2} = 1.1\overline I$、${I_3} = 1.5\overline I$、${I_4} = 1.3\overline I$和${I_5} = 1.2\overline I$，其中$\overline I$为仿真过程中具体设定的任务数据量数值。其他仿真参数如下：噪声功率谱密度${\sigma ^2} = - 169$ dBm/Hz，信道功率增益${g_0} = - 60$ dB，设备卸载传输任务的时间${T^{{\text{trans}}}} = 1$ ms，设备k的发射功率${P_k} = 0.5$ W，最大CPU频率$f_k^{\max } = 1$ GHz，能耗预算$E_k^{\max } = {10^{ - 3}}$ J，有效电容系数${\rho _k} = {10^{ - 28}}$，接收误码率${\varepsilon _k} = {10^{ - 9}}$，计算单位比特数据所需的CPU循环次数${C_k} = 1\;000$ cycle/bit，迭代阈值$\varepsilon = {10^{ - 8}}$。初始卸载带宽分配${b_k} = {{{B^{\max }}} \mathord{\left/ {\vphantom {{{B^{\max }}} K}} \right. } K}$，设备初始CPU频率分配${f_k} = f_k^{\max }$，无人机初始CPU频率分配${f_{{\text{U}},k}} = {{f_{\text{U}}^{{\text{max}}}} \mathord{\left/ {\vphantom {{f_{\text{U}}^{{\text{max}}}} K}} \right. } K}$。参数${g_0}$、${\rho _k}$、${C_k}$的设置与文献[2]一致，参数${T^{{\text{trans}}}}$、${b_k}$、${\varepsilon _k}$的设置符合第三代合作伙伴计划(3rd Generation Partnership Project, 3GPP) 标准中对URLLC的要求，即时延不超过1 ms，数据包长度不超过32 byte，误码率不高于${10^{ - 5}}$^[18]，其余参数均为根据实际场景合理设置。

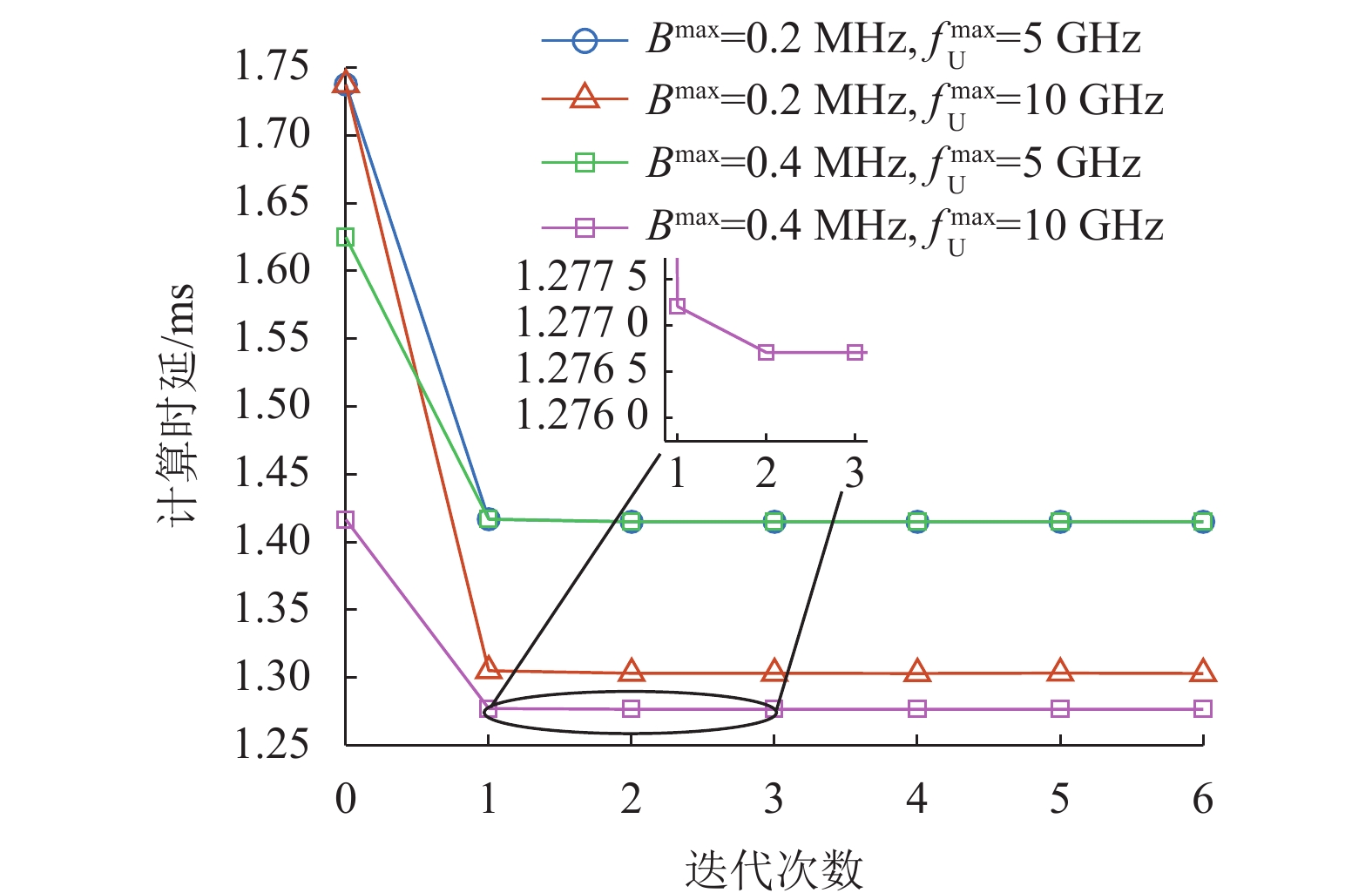
图2表明了不同参数时联合优化算法的收敛情况。目标函数值在第2次迭代之后收敛，可见算法可快速收敛。同时由于算法的收敛迭代次数较少，因此算法的复杂度较低。当改变总卸载带宽和无人机最大CPU频率时，也有相似的收敛情况，可见算法的稳定性较好。当$f_{\text{U}}^{{\text{max}}} = 5$ GHz时，无人机的计算资源有限，将总卸载带宽从0.2 MHz增大到0.4 MHz后，也无法进一步降低时延。

图3是无人机优化位置结果图。由图3(a)可知，随着任务数据量的增大，需要优化无人机位置以降低系统计算时延，又由于设备3的任务数据量最多，因此无人机优化位置逐渐向设备3靠近。由图3(b)可知，随着无人机最大CPU频率的增大，设备需要卸载更多的任务数据，同时需要更强的传输能力，因此无人机优化位置逐渐向设备3靠近，为数据量最多的设备3提供更强的卸载传输能力。由图3(c)可知，随着总卸载带宽的增大，设备的卸载传输能力逐渐增强，不必通过大幅度改变无人机位置来提高传输能力，因此无人机优化位置也越靠近初始位置。

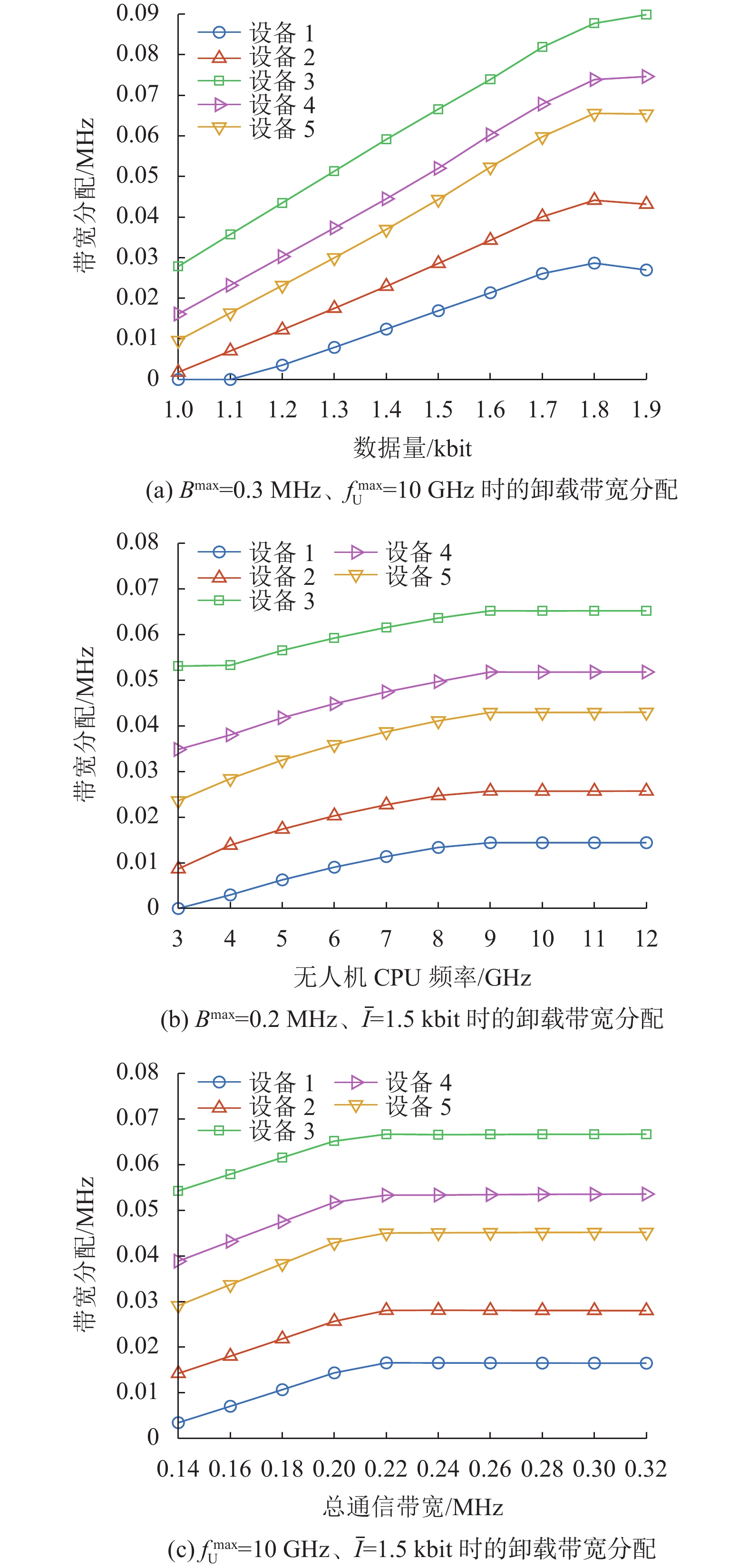
图4和图5分别是卸载带宽和无人机CPU频率分配结果图。在图4(a)和图5(a)中，当$\overline I \leqslant 1.1$ kbit时，设备1分配得到的卸载带宽和无人机CPU频率均为0，这是因为设备1的任务数据量较小，在本地就能计算全部任务数据且本地计算时延小于卸载传输时延${T^{{\text{trans}}}} = 1$ ms，不必卸载至无人机计算。由图4(a)可知，当$\overline I \leqslant 1.8$ kbit时，各设备分配得到的卸载带宽都随着$\overline I$的增大而增大，当$\overline I \gt 1.8$ kbit时，设备1、设备2和设备5分配得到的卸载带宽略微减少，设备3和设备4分配得到的卸载带宽仍在缓慢增大，这是因为带宽资源有限，而设备3和设备4的任务数据量最大，需要卸载至无人机计算的数据量也较大，因此需要为它们分配更多的卸载带宽。由图5(a)可知，随着$\overline I$的增大，分配给设备3的无人机CPU频率不断减少，分配给其他设备的无人机CPU频率先增加后减少，这是因为任务数据量较小时，部分设备选择本地计算，更多的计算资源分配给任务数据量大的设备，当任务数据量较大时，无人机的计算资源均衡分配。

由图4(b)和图5(b)可知，当$f_{\text{U}}^{{\text{max}}} \leqslant 9$ GHz时，各设备分配得到的卸载带宽和无人机CPU频率都随着$f_{\text{U}}^{{\text{max}}}$的增大而增大，这是因为增大无人机最大CPU频率后无人机计算能力更强，同时需要更多的带宽来卸载任务数据；当$f_{\text{U}}^{{\text{max}}} \gt 9$ GHz后，分配给各设备的卸载带宽和无人机CPU频率都趋于稳定，这是因为带宽资源已率先耗尽，没有更多的卸载带宽可供分配，无人机CPU频率即便有剩余也不会进一步分配。

由图4(c)和图5(c)可知，当${B^{\max }} \leqslant 0.22$ MHz时，各设备分配得到的卸载带宽和无人机CPU频率都随着${B^{\max }}$的增大而增大，这是因为增大总卸载带宽使得设备能够卸载更多的任务数据，同时也需要更多的计算资源；当${B^{\max }} > 0.22$ MHz时，各设备分配得到的卸载带宽和无人机CPU频率趋于稳定，这是因为无人机的计算资源有限，没有更多的无人机CPU频率可供分配，卸载带宽即便有剩余也不会进一步分配。

为了更加合理地评估算法的性能和效率，在此使用以下4种基准算法与所提出的联合优化算法进行性能对比。

(1) 仅优化卸载带宽和CPU频率：固定无人机的部署位置，优化卸载带宽和无人机与地面设备的CPU计算频率。

(2) 仅优化无人机部署位置：固定卸载带宽和无人机与地面设备的CPU计算频率，优化无人机的部署位置。

(3) 下界：将优化问题中的短包通信速率替换成香农容量公式，对无人机的部署位置、任务卸载带宽和无人机与地面设备的CPU计算频率进行联合优化，得到的时延结果作为所提算法的下界。

(4) 基于香农容量公式：将下界方案求得的无人机部署位置、任务卸载带宽和无人机与地面设备的CPU计算频率的优化值代入本文的URLLC系统模型中，得到基于香农容量公式方案的时延。

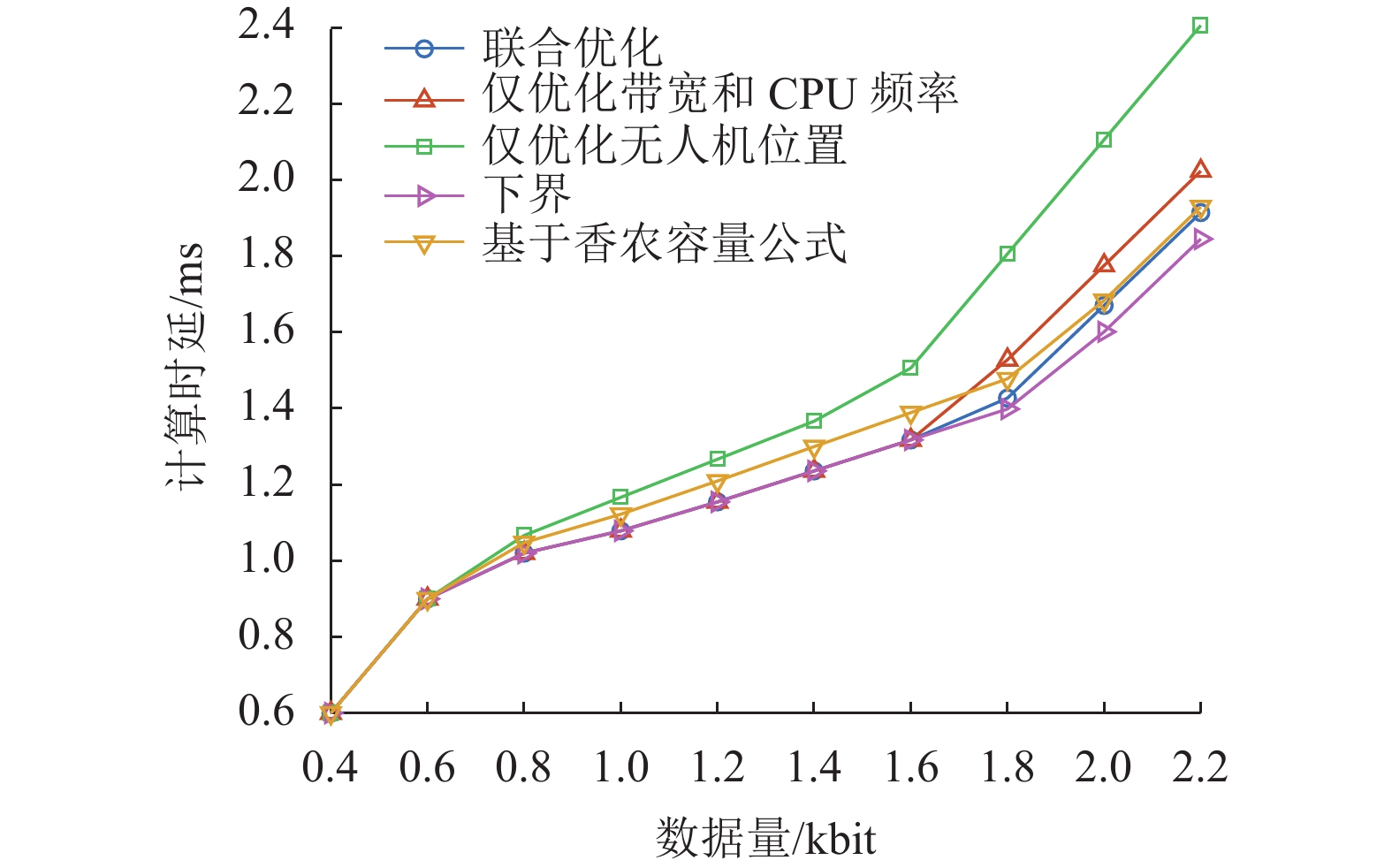
图6是不同任务量下不同方案的计算时延变化图。当$\overline I$较小时，所有任务在本地即可完成计算，不必卸载至无人机，此时本地计算时延小于${T^{{\text{trans}}}}$。随着$\overline I$的增大，计算时延增加的速度变缓，这是因为数据量较大时任务一部分在本地计算，另一部分卸载至无人机进行边缘计算，从而提高了系统的计算效率。但当$\overline I$增大到一定程度时，计算时延增加的速度再次变快，这是因为任务数据量更大时，受到总卸载带宽的限制，分配给各设备的卸载带宽都趋于稳定，无法将更多的任务数据卸载至无人机计算。不难发现，随着任务量的增大，联合优化方案逐渐优于仅优化卸载带宽和CPU频率、仅优化无人机部署位置以及基于香农容量公式3种方案，并接近于下界方案。当 $\overline I \leqslant 1.6$ kbit时，联合优化方案和仅优化卸载带宽和CPU频率方案的曲线重合，这是因为数据量不大时，需要卸载计算的任务数据量也不大，仅优化卸载带宽和CPU频率就能为设备提供足够的卸载计算能力。

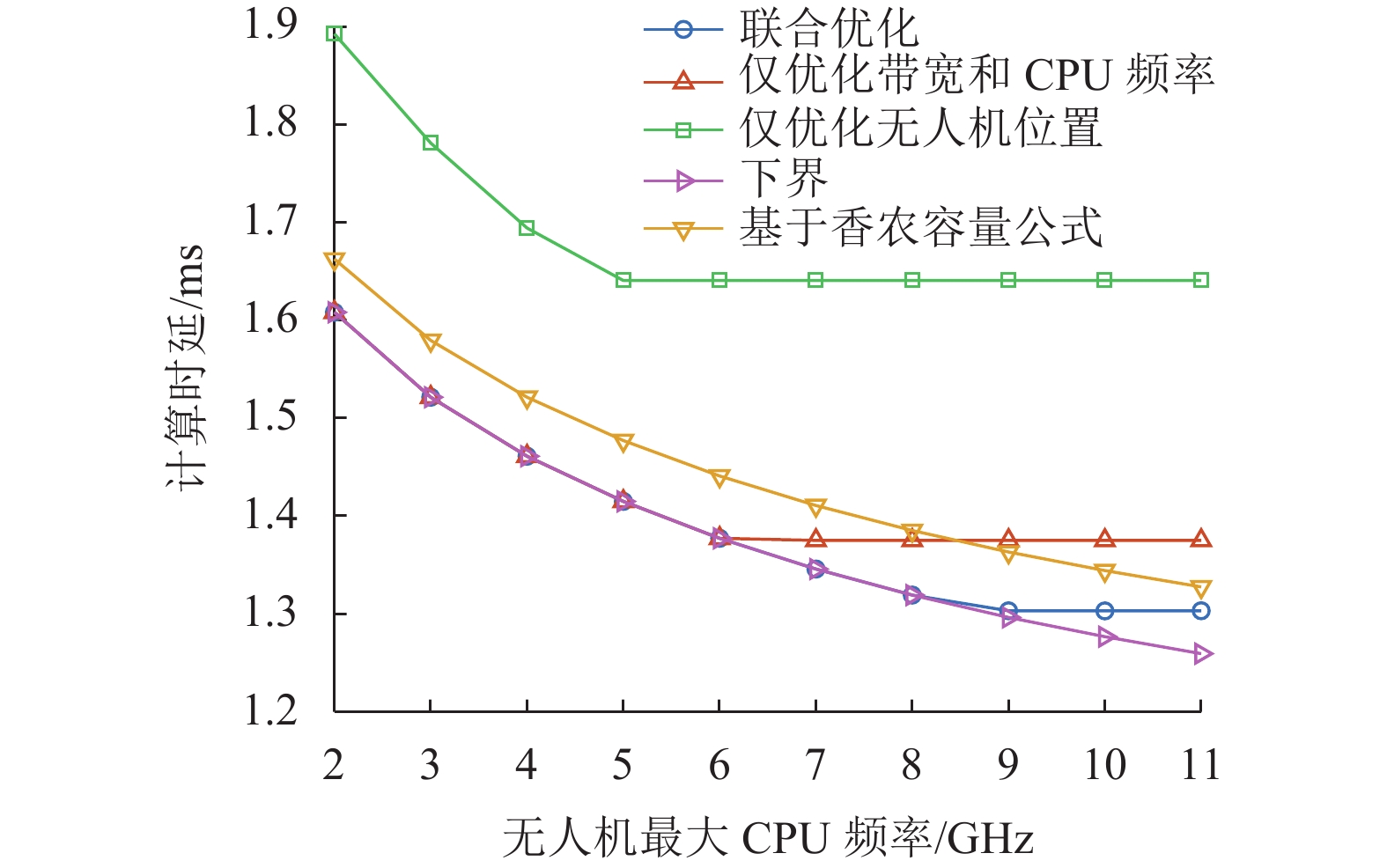
图7是不同无人机最大CPU频率下不同方案的计算时延变化图。当$f_{\text{U}}^{{\text{max}}}$较小时，随着$f_{\text{U}}^{{\text{max}}}$的增加，计算时延会逐渐降低，这是因为增大CPU频率提高了无人机的计算性能，从而减少了计算时延。当$f_{\text{U}}^{{\text{max}}}$增大到一定程度时，计算时延趋于稳定，这是因为受到了总卸载带宽的限制。不难发现，联合优化方案优于基于香农容量公式方案，并与下界方案相接近。随着无人机最大CPU频率的增大，联合优化方案逐渐优于仅优化卸载带宽和CPU频率以及仅优化无人机部署位置两种方案。当$f_{\text{U}}^{{\text{max}}} \leqslant 6$ GHz时，联合优化方案和仅优化卸载带宽和CPU频率方案的曲线重合，这是因为无人机CPU频率不大时，能够计算的任务数据量不大，需要的卸载传输能力较小，在初始位置处也能提供足够的卸载能力。

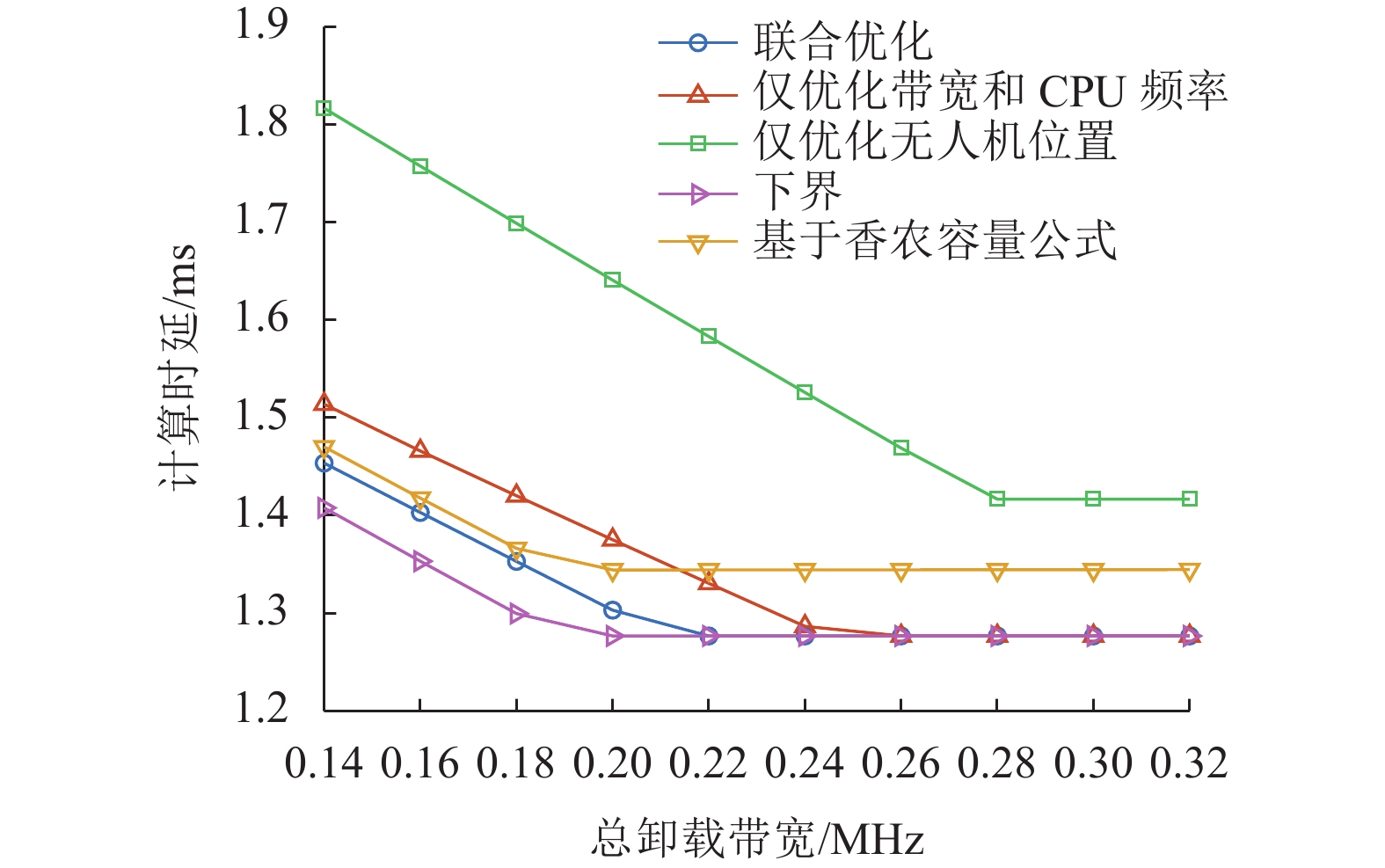
图8是不同卸载带宽下不同方案的计算时延变化图。当${B^{\max }}$较小时，增大总卸载带宽能够提高各设备的卸载传输能力，从而减少计算时延。当卸载带宽增大到一定程度时，计算时延趋于稳定，不再减少，这是因为受到了无人机计算能力的限制，在达到无人机计算频率上限时，即便将更多的任务卸载至无人机也无法更快完成计算。不难发现，联合优化方案优于基于香农容量公式方案，并接近于下界方案。当${B^{\max }} \leqslant 0.26$ MHz时，联合优化方案优于仅优化卸载带宽和CPU频率以及仅优化无人机部署位置两种方案。当${B^{\max }} \gt 0.26$ MHz时，联合优化方案和仅优化卸载带宽和CPU频率方案的曲线重合，这是因为在带宽资源比较充足的情况下，设备拥有较强的任务卸载传输能力，无需通过优化无人机位置提高卸载能力。

由图6~图8可知，联合优化算法的计算时延性能优于仅优化无人机位置以及仅优化卸载带宽和CPU频率两种方案，其中相较于仅优化卸载带宽和CPU频率方案性能最大提升约5%，相较于仅优化无人机部署位置方案性能最大提升约20%，由此验证了联合优化无人机部署的位置、卸载带宽和CPU计算频率的必要性。此外，与基于香农容量公式方案相比，所提算法的计算时延性能最大提升约5%，由此验证了URLLC系统中采用短包通信速率建立通信模型的必要性。

4 结论

本文研究了一个URLLC无人机移动边缘计算系统，考虑了地面设备的能耗预算、任务计算量约束以及计算卸载的信息因果约束，通过联合优化无人机的部署位置、任务卸载带宽和无人机与地面设备的CPU计算频率实现整个系统的计算时延最小化。为了求解该优化问题，本文采用BCD和SCA优化方法将原非凸问题转换为凸问题，并提出一种联合优化无人机位置、卸载带宽和CPU频率的交替优化算法。仿真结果表明，所提出的优化算法能够有效平衡系统的卸载通信能力和计算能力，从而减少计算时延，且计算时延性能明显优于仅优化无人机位置以及仅优化卸载带宽和CPU频率两种基准方案，验证了联合优化无人机部署的位置、卸载带宽和CPU计算频率的必要性。此外，联合优化算法的计算时延性能优于基于香农容量公式的方案，验证了URLLC系统模型中香农容量公式的不适用性。