内置式永磁同步电机(Interior Permanent Magnet Synchronous Motor, IPMSM) 交、直轴电感值不相等,这一特性使得IPMSM输出转矩更大,调速范围更宽,并且永磁同步电机具有功率密度大、体积小和可靠性高等优点[1],因此被广泛应用于机器人、电动汽车、风力发电等领域。IPMSM能在各领域充分发挥优势也得益于电机控制策略的迅速发展[2-3]。IPMSM控制系统控制环通常采用具有算法简单、易于实现等优点的比例积分(Proportional Integral, PI) 控制策略,但PI控制策略存在积分饱和、响应速度慢及抗扰能力差等问题,在IPMSM实际运行过程中,电机参数会发生摄动,电机运行情况会受到外部未知扰动影响,PI控制不能满足电机高性能控制要求[4]。
为了实现IPMSM高效控制,许多先进控制方法被应用于电机控制系统中,如模型预测控制[5]、滑模控制[6-7]、模型参考自适应控制[8-9]等,上述算法虽然能提高电机控制性能,但极度依赖精确的数学模型。然而电机是一个非线性、强耦合复杂系统,且电机运行过程中,电机参数会发生变化,IPMSM数学模型精准性很难保证。因此,参数摄动和外部扰动使得上述高度依赖数学模型的控制方法存在局限性,无法保证控制系统的鲁棒性。
为降低控制系统对电机数学模型精度的要求,无模型控制逐渐应用于永磁同步电机控制。无模型控制最早于20世纪70年代被提出并逐渐发展。学者侯忠生[10]给出无模型控制定义并将无模型控制与自适应控制相结合,使无模型理论得到创新。学者Michel Fliess[11]对无模型控制进行拓展,提出基于PI反馈控制器的超局部模型,为电机控制提供新思路。为增强无模型控制鲁棒性,强鲁棒性的滑模控制常与无模型控制结合应用。文献[12]提出无模型非奇异终端滑模控制,降低永磁体退磁对电机的影响,使PMSM具有永磁退磁故障容错控制功能。文献[13]将PI控制和超螺旋滑模控制结合起来作为无模型控制中的复合反馈控制器,控制系统鲁棒性得到增强。但上述传统滑模控制方法趋近过程不理想,存在较大抖振。为解决滑模抖振问题,改进滑模趋近律方法逐渐被应用在无模型控制中,文献[14]设计基于改进趋近律的无模型滑模控制,增强抗扰能力的同时减小系统抖振。
为进一步提高IPMSM无模型控制系统的鲁棒性及动静态性能。精确估计无模型控制中的未知复杂项也变得十分重要。文献[15]采用传统滑模观测器对未知项进行观测,该观测器能较精准地估计未知项,但存在抖振现象。文献[16]改进了传统滑模观测器,提出扩展滑模扰动观测器,该方法不仅提高了观测精度还抑制了滑模抖振,但仍不能解决滑模开关函数带来的固有抖振问题。文献[17]通过扩张状态观测器观测估计未知项来提高观测精度,但该方法参数整定较复杂。上述无模型未知项估计方法存在不足,而非线性干扰观测器(Nonlinear Disturbance Observer, NDOB) 能够很好地解决上述方法存在问题。文献[18]利用NDOB观测补偿机械臂系统扰动,降低了控制系统干扰上界。文献[19]利用干扰观测器精准估计反电动势,实现永磁同步电机无位置传感器高性能控制。文献[20]利用干扰观测器对永磁同步电机调速系统中的滑模速度环进行观测补偿,提高了系统的响应速度和鲁棒性。因此,通过干扰观测器来估计未知复杂项是一种行之有效的方法。
针对传统无模型滑模控制不能保证电机在参数摄动情况下高性能运行,本文提出一种基于非线性干扰观测器的永磁同步电机改进无模型滑模控制(Improved Model-free Sliding Mode Control,IMFSMC) 。首先,根据参数摄动时的IPMSM数学模型,建立新型超局部模型,新型超局部模型分离传统超局部模型可直接观测部分,减小观测器工作量。其次,采用改进滑模趋近律设计滑模控制器作为超局部模型中的反馈控制器来增强系统鲁棒性。最后,设计非线性干扰观测器观测超局部模型中的未知复杂项以减小传统无模型滑模控制中滑模观测器的抖振。仿真对比实验结果表明该控制方法提升了系统鲁棒性和抗扰能力。
1 IPMSM数学模型假设内置式永磁同步电机为理想电机,即忽略电机磁滞、损耗和磁路饱和,电机参数不发生变化,则在d-q坐标系下的数学模型为
| $ \left\{ {\begin{array}{*{20}{l}} {\dfrac{{{\rm{d}}{i_d}}}{{{\rm{d}}t}} = - \dfrac{{R{i_d}}}{{{L_d}}} + \dfrac{{{u_d}}}{{{L_d}}} + \dfrac{{{{{P}}_{\rm{n}}}{\omega _{\rm{m}}}{L_q}{i_q}}}{{{L_d}}}} \\ {\dfrac{{{\rm{d}}{i_q}}}{{{\rm{d}}t}} = - \dfrac{{R{i_q}}}{{{L_q}}} + \dfrac{{{u_q}}}{{{L_q}}} - \dfrac{{{{{P}}_{\rm{n}}}{\omega _{\rm{m}}}({L_d}{i_d} + {\psi _{\rm{f}}}) }}{{{L_q}}}} \\ {\dfrac{{{\rm{d}}{\omega _{\rm{m}}}}}{{{\rm{d}}t}} = - \dfrac{{B{\omega _{\rm{m}}}}}{J} + \dfrac{{{T_{\rm{e}}}}}{J} - \dfrac{{{T_{\rm{L}}}}}{J}} \end{array}} \right. $ | (1) |
式中:
永磁同步电机实际运行过程中,温度、永磁体磁路饱和及外部扰动等因素会使电机内部参数摄动。考虑IPMSM内部参数摄动,内置式永磁同步电机数学模型可写为
| $ \left\{ {\begin{array}{*{20}{l}} {\dfrac{{{\rm{d}}{i_d}}}{{{\rm{d}}t}} = - \dfrac{{R{i_d}}}{{{L_d}}} + \dfrac{{{u_d}}}{{{L_d}}} + \dfrac{{{P_{\rm{n}}}{\omega _{\rm{m}}}{L_q}{i_q}}}{{{L_d}}} + {f_{{d}}}} \\ {\dfrac{{{\rm{d}}{i_q}}}{{{\rm{d}}t}} = - \dfrac{{R{i_q}}}{{{L_q}}} + \dfrac{{{u_q}}}{{{L_q}}} - \dfrac{{{P_{\rm{n}}}{\omega _{\rm{m}}}({L_d}{i_d} + {\psi _{\rm{f}}}) }}{{{L_q}}} + {f_{{q}}}} \\ {\dfrac{{{\rm{d}}{\omega _{\rm{m}}}}}{{{\rm{d}}t}} = - \dfrac{{B{\omega _{\rm{m}}}}}{J} + \dfrac{{{T_{\rm{e}}}}}{J} - \dfrac{{{T_{\rm{L}}}}}{J} + {f_{\omega }}} \end{array}} \right. $ | (2) |
| $ \left\{ {\begin{array}{*{20}{l}} {{f_{{d}}} = - \dfrac{{\Delta R{i_{{d}}} + \Delta {L_{{d}}}{{\dot i}_{{d}}} - \Delta {L_{{q}}}{P_{\text{n}}}{\omega _{\text{m}}}{i_{{q}}}}}{{{L_{{d}}}}}} \\ {{f_{{q}}} = - \dfrac{{\Delta R{i_{{q}}} + \Delta {L_{{q}}}{{\dot i}_{{q}}} + {P_{\text{n}}}{\omega _{\text{m}}}(\Delta {L_{{d}}}{i_{{d}}} + \Delta {\psi _{\text{f}}}) }}{{{L_{{q}}}}}} \\ {{f_{\omega }} = - \dfrac{{\Delta B{\omega _{\text{m}}} + \Delta J{{\dot \omega }_{\text{m}}}}}{J}} \end{array}} \right. $ | (3) |
式中:
非线性、单输入单输出系统中,存在未知复杂项时,其超局部模型可写为
| $ \left\{ {\begin{array}{*{20}{l}} {{{\boldsymbol{y}}^{(V) }} = {\boldsymbol{\alpha}} {\boldsymbol{u}} + {\boldsymbol{F}}} \\ {{\boldsymbol{y}} = {\boldsymbol{x}}} \end{array}} \right. $ | (4) |
式中:
根据无模型理论可知IPMSM数学模型可写为
| $ {{\boldsymbol{{{\boldsymbol{\dot x}}}}}} = {{{\boldsymbol{\alpha}} {\boldsymbol{u}}}} + {\boldsymbol{F}} $ | (5) |
式中:
| $ {\boldsymbol{F}} = \left[ {\begin{array}{*{20}{l}} { - \dfrac{{R{i_d}}}{{{L_d}}} + \dfrac{{{P_{\rm{n}}}{\omega _{\rm{m}}}{L_q}{i_q}}}{{{L_d}}} + {f_{{d}}}} \\ { - \dfrac{{R{i_q}}}{{{L_q}}} - \dfrac{{{P_{\rm{n}}}{\omega _{\rm{m}}}({L_d}{i_d} + {\psi _{\rm{f}}}) }}{{{L_q}}} + {f_{{q}}}} \\ { - \dfrac{{B{\omega _{\rm{m}}}}}{J} - \dfrac{{{T_{\rm{L}}}}}{J} + {f_{\omega}}} \end{array}} \right] \qquad$ |
| $ {\boldsymbol{\alpha }} = \left[ {\begin{array}{*{20}{c}} {\dfrac{1}{{{L_{{d}}}}}}&{}&{} \\ {}&{\dfrac{1}{{{L_{{q}}}}}}&{} \\ {}&{}&{\dfrac{1}{J}} \end{array}} \right],{\boldsymbol{u}} = \left[ {\begin{array}{*{20}{c}} {{u_{{d}}}} \\ {{u_{{q}}}} \\ {{T_{{{\rm{e}}}}}} \end{array}} \right] $ |
将无模型控制与滑模控制结合起来,设计滑模控制器作为无模型反馈控制器,当
| $ {\boldsymbol{u}} = \frac{{ - {\boldsymbol{F}} + {{{{\dot {\boldsymbol{y}}}}}^{\boldsymbol{*}}} + {{\boldsymbol{u}}_{\rm{st}}}}}{{\boldsymbol{\alpha }}} $ | (6) |
式中:
根据式(4) 和式(6) 可得式(7) 。
| $ {{\boldsymbol{\dot y}}^{\boldsymbol{*}}} - {{\dot {\boldsymbol{y}}}} + {{\boldsymbol{u}}_{\rm{st}}} = \boldsymbol{0} $ | (7) |
定义各项误差
| $ {\boldsymbol{e}} = {{\boldsymbol{y}}^{\boldsymbol{*}}} - {\boldsymbol{y}} = \left[ {\begin{array}{*{20}{c}} {{e_d}} \\ {{e_q}} \\ {{e_\omega }} \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} {i_d^* - {i_d}} \\ {i_q^* - {i_q}} \\ {\omega _{\rm{m}}^* - {\omega _{\rm{m}}}} \end{array}} \right] $ | (8) |
选取积分滑模面
| $ {\boldsymbol{s}} = {{{\boldsymbol{e}}}} + {{{\boldsymbol{c}}}}\int {{{{\boldsymbol{e}}}}{\rm{d}}{{{{t}}}}} $ | (9) |
式中:
对式(9)所示积分滑模面求导,并结合式(7)、(8)得式(10)。
| $ {\boldsymbol{\dot s}} = {{{\boldsymbol{ce}}}} + {{\boldsymbol{\dot e}}} = {{{\boldsymbol{ce}}}} - {{{\boldsymbol{u}}}_{\rm{st}}} $ | (10) |
选取式(11)所示传统指数滑模趋近律
| $ {\boldsymbol{\dot s}} = - {\boldsymbol{\varepsilon}} {{\rm{sgn}}} ({\boldsymbol{s}}) - {\boldsymbol{qs}} $ | (11) |
通过式(10)和式(11)可得式(12)
| $ {{\boldsymbol{u}}_{\rm{st}}} = {\boldsymbol{ce}} + {\boldsymbol{\varepsilon }}{\rm{sgn}}({\boldsymbol{s}}) + {\boldsymbol{qs}} $ | (12) |
式中:
将式(12)代入式(6)最终得到无模型滑模控制器表达式(13)。
| $ {\boldsymbol{u}} = \frac{{ - {\boldsymbol{F}} + {{{\boldsymbol{\dot y}}}^{\boldsymbol{*}}} + {\boldsymbol{ce}} + {\boldsymbol{\varepsilon }}\,{\rm{sgn}}({\boldsymbol{s}}) + {\boldsymbol{qs}}}}{{\boldsymbol{\alpha }}} $ | (13) |
变量
| $ {\dot {\hat{\boldsymbol x}}} = {\boldsymbol{\alpha u}} + {\boldsymbol{k}}\,{\rm{sgn}}({\boldsymbol{y}} - {\hat{\boldsymbol y}}) $ | (14) |
式中:
令
| $ {{{{\hat {\boldsymbol{F}}}}}} = {{{\boldsymbol{k}}}}\,{\rm{sgn}}({{{{\boldsymbol{e}}}}_y}) $ | (15) |
将观测值
| $ {\boldsymbol{u}} = \dfrac{{ - {{\hat {\boldsymbol{F}}}} + {{{{\dot {\boldsymbol{y}}}}}^*} + {\boldsymbol{ce}} + {\boldsymbol{\varepsilon }}\,{\rm{sgn}}({\boldsymbol{s}}) + {\boldsymbol{qs}}}}{{\boldsymbol{\alpha }}} $ | (16) |
IPMSM传统无模型滑模控制(Model-free Sliding Mode Control,MFSMC) 框图如图1所示。

|
图 1 传统无模型滑模控制框图 Figure 1 Block diagram of traditional model-free sliding mode control |
传统无模型滑模控制方法,虽能保证较好控制性能,但存在滑模抖振严重、观测器工作量大、精度较低等问题。
3 基于NDOB的改进无模型滑模控制 3.1 IPMSM改进超局部模型非线性、单输入单输出系统的改进超局部数学模型为
| $ \left\{ {\begin{array}{*{20}{l}} {{{\boldsymbol{y}}^{(V) }} = {\boldsymbol{h}}({\boldsymbol{x}}) + {\boldsymbol{\alpha u}}} \\ {{\boldsymbol{y}} = {\boldsymbol{x}}} \end{array}} \right. $ | (17) |
式中:
IPMSM传统超局部模型中的未知复杂项
| $ {\boldsymbol{h}}({\boldsymbol{x}}) = {\boldsymbol{F}} = {\boldsymbol{Ax}} + {{\boldsymbol{F}}'} $ | (18) |
根据上述无模型理论可知IPMSM数学模型可改写为
| $ {\dot{\boldsymbol x}} = {\boldsymbol{\alpha u}} + {\boldsymbol{Ax}} + {{\boldsymbol{F}}'} $ | (19) |
| $ \begin{array}{l} \qquad {{\boldsymbol{F}}^\prime } = \left[ {\begin{array}{*{20}{c}} {\dfrac{{{P_{\rm{n}}}{\omega _{\rm{m}}}{L_q}{i_q}}}{{{L_d}}} + {f_{{d}}}}\\ { - \dfrac{{{P_{\rm{n}}}{\omega _{\rm{m}}}({L_d}{i_d} + {\psi _{\rm{f}}})}}{{{L_q}}} + {f_{{q}}}}\\ { - \dfrac{{{T_{\rm{L}}}}}{J} + {f_{{\omega}}}} \end{array}} \right]\\ {\boldsymbol{A}} = \left[ {\begin{array}{*{20}{c}} { - \dfrac{R}{{{L_{{d}}}}}}&{}&{}\\ {}&{ - \dfrac{R}{{{L_{{q}}}}}}&{}\\ {}&{}&{ - \dfrac{B}{J}} \end{array}} \right],{\boldsymbol{x}} = \left[ {\begin{array}{*{20}{c}} {{i_{{d}}}}\\ {{i_{{q}}}}\\ {{\omega _{{{\rm{m}}}}}} \end{array}} \right] \end{array}$ |
| $ {\boldsymbol{\alpha }} = \left[ {\begin{array}{*{20}{c}} {\dfrac{1}{{{L_{{d}}}}}}&{}&{} \\ {}&{\dfrac{1}{{{L_{{q}}}}}}&{} \\ {}&{}&{\dfrac{1}{J}} \end{array}} \right],{\boldsymbol{u}} = \left[ {\begin{array}{*{20}{c}} {{u_{{d}}}} \\ {{u_{{q}}}} \\ {{T_{{{\rm{e}}}}}} \end{array}} \right] $ |
设计滑模控制器作为无模型控制中的反馈控制器,得到IPMSM无模型控制器。
| $ {\boldsymbol{u}} = \frac{{ - {{\boldsymbol{F}}'} - {\boldsymbol{Ax}} + {{{\boldsymbol{\dot y}}}^*} + {{\boldsymbol{u}}_{\rm{st}}}}}{{\boldsymbol{\alpha }}} $ | (20) |
式中:
滑模控制器设计与上文相同,选取式(9)所示滑模面,趋近律选择式(21)所示新型滑模趋近律。
| $ \left\{ {\begin{array}{*{20}{l}} {\dot {\boldsymbol{s}} = - {{\boldsymbol{k}}_1}{{\left| {\boldsymbol{s}} \right|}^\eta }{{\rm{sgn}}} ({\boldsymbol{s}}) - {{\boldsymbol{k}}_2}{{\left| {\boldsymbol{s}} \right|}^\gamma }{{\rm{sgn}}} ({\boldsymbol{s}}) } \\ {{\boldsymbol{\eta}} = {\boldsymbol{\sigma}} - \dfrac{1}{{{\boldsymbol{\lambda}} + \left| {\boldsymbol{x}} \right|}}} \\ {\mathop {\lim }\limits_{t \to \infty } \left| {\boldsymbol{x}} \right| = 0} \end{array}} \right. $ | (21) |
式中:
对式(9)所示积分滑模面
| $ {{\boldsymbol{u}}_{\rm{st}}} = {{{\boldsymbol{ce}}}} + {{\boldsymbol{k}}_1}{\left| {\boldsymbol{s}} \right|^{\boldsymbol{\eta }}}{\rm{sgn}}({\boldsymbol{s}}) + {{\boldsymbol{k}}_2}{\left| {\boldsymbol{s}} \right|^{\boldsymbol{\gamma }}}{\rm{sgn}}({\boldsymbol{s}}) $ | (22) |
式中:
稳定性证明:以式(7)中的转速误差方程为例,定义Lyapunov函数
| $ {V_\omega } = \frac{1}{2}s_\omega ^2 $ | (23) |
对式(23)求导
| $ \begin{split} {{\dot V}_\omega } =& {s_\omega }[ - {k_{1\omega }}{\left| {{s_\omega }} \right|^{{\eta _\omega }}}{{\rm{sgn}}} ({s_\omega }) - {k_{2\omega }}{\left| {{s_\omega }} \right|^{{\gamma _\omega }}}{{\rm{sgn}}} ({s_\omega }) ] = \\ &- {k_{1\omega }}{\left| {{s_\omega }} \right|^{{\eta _\omega } + 1}} - {k_{2\omega }}{\left| {{s_\omega }} \right|^{{\gamma _\omega } + 1}} \leqslant 0 \end{split} $ | (24) |
分析式(24)可知当且仅当
将式(22)代入式(20)最终得到改进无模型滑模控制器表达式(25):
| $ \begin{gathered} {\boldsymbol{u}} = \dfrac{{ - {{\boldsymbol{F}}'} - {\boldsymbol{Ax}} + {{{\boldsymbol{\dot y}}}^*} + {\boldsymbol{ce}}}}{{\boldsymbol{\alpha }}} + \frac{{{{\boldsymbol{k}}_1}{{\left| {\boldsymbol{s}} \right|}^{\boldsymbol{\eta }}}{\rm{sgn}}({\boldsymbol{s}}) + {{\boldsymbol{k}}_2}{{\left| {\boldsymbol{s}} \right|}^{\boldsymbol{\gamma }}}{\rm{sgn}}({\boldsymbol{s}}) }}{{\boldsymbol{\alpha }}} \\ \end{gathered} $ | (25) |
由上文分析可知IPMSM的数学模型可以写为
| $ {\boldsymbol{\dot x}} = {\boldsymbol{\alpha u}} + {\boldsymbol{Ax}} + {{\boldsymbol{F}}'} $ | (26) |
假设扰动变化缓慢即
| $ {{{\dot {\boldsymbol{F}}}}'} = {\boldsymbol{0}} $ | (27) |
定义
| $ {{\boldsymbol{e}}_{{{\boldsymbol{F}}'}}} = {{\boldsymbol{F}}'} - {{{\hat {\boldsymbol{F}}}}'} $ | (28) |
干扰观测器设计为
| $ {{\dot {\hat{\boldsymbol F'}}}} = {\boldsymbol{L}}{(}{{\boldsymbol{F}}'} - {{{\hat {\boldsymbol{F}}}}'}) = - {\boldsymbol{L}}{{{\hat {\boldsymbol{F}}}}'} + {\boldsymbol{L}}({{\dot {\boldsymbol{x}}}} - {\boldsymbol{Ax}} - {\boldsymbol{\alpha u}}) $ | (29) |
式中:
定义辅助变量
| $ {\boldsymbol{z}} = {{{\hat {\boldsymbol{F}}}}'} - {\boldsymbol{Lx}} $ | (30) |
结合式(29)和式(30)得式(31)。
| $ \left\{ {\begin{array}{*{20}{l}} {{{\dot {\boldsymbol{z}}}} = - {\boldsymbol{Lz}} - {\boldsymbol{L}}({\boldsymbol{Lx}} + {\boldsymbol{Ax}} + {\boldsymbol{\alpha u}}) } \\ {{{{{\hat {\boldsymbol{F}}}}}'} = {\boldsymbol{z}} + {\boldsymbol{Lx}}} \end{array}} \right. $ | (31) |
对式(28)求导
| $ {\dot{{\boldsymbol{e}}}}_{{{\boldsymbol{F}}'}}={\dot{{\boldsymbol{F}}'}}-{\dot{\hat{{\boldsymbol{F}}'}}} $ | (32) |
将式(26)、(29)和(31)代入式(32)最终得式(33)。
| $ {{{\dot {\boldsymbol{e}}}}_{{{\boldsymbol{F}}'}}} = - {\boldsymbol {L}}{{\boldsymbol{e}}_{{{\boldsymbol{F}}'}}} $ | (33) |
设计
| $ {{\boldsymbol{\dot e}}_{{{\boldsymbol{F}}'}}}={\boldsymbol{ ce}}_{{{\boldsymbol{F}}'}}^{ - {\boldsymbol{Lt}}} $ | (34) |
用干扰观测器对未知量
| $ \begin{gathered} {\boldsymbol{u}} = \frac{{ - {{{{\hat {\boldsymbol{F}}}}}'} - {\boldsymbol{Ax}} + {{{{\dot {\boldsymbol{y}}}}}^*} + {\boldsymbol{ce}}}}{{\boldsymbol{\alpha }}} + \frac{{{{\boldsymbol{k}}_1}{{\left| {\boldsymbol{s}} \right|}^{\boldsymbol{\eta }}}{\rm{sgn}}({\boldsymbol{s}}) + {{\boldsymbol{k}}_2}{{\left| {\boldsymbol{s}} \right|}^{\boldsymbol{\gamma }}}{\rm{sgn}}({\boldsymbol{s}}) }}{{\boldsymbol{\alpha }}} \\ \end{gathered} $ | (35) |
本文所设计的改进无模型滑模控制(Improved model-free Sliding Mode Control,IMFSMC) 框图如图2所示。

|
图 2 改进无模型滑模控制框图 Figure 2 Block diagram of improved model-free sliding mode control |
为验证改进无模型滑模控制方法的可行性和有效性,用MATLAB/Simulink搭建模型并与传统无模型滑模进行仿真对比,采样时间为
| 表 1 电机参数 Table 1 Parameters of motor |

|
图 3 IPMSM控制框图 Figure 3 Block diagram of IPMSM control |
| 表 2 控制器参数 Table 2 Parameters of controller |
(1) 加减速仿真实验:电机在给定转速600 r/min情况下空载启动,在0.5 s时电机转速突增到1 000 r/min,1.2 s时转速突减到600 r/min。仿真对比实验如图4所示,控制性能数据对比见表3。

|
图 4 加减速转速波形Ⅰ Figure 4 The rotational speed waveforms of speed up and down Ⅰ |
| 表 3 参数正常加减速实验控制性能对比 Table 3 Comparison of control performance of speed up and down experiments with normal parameters |
结合图4和表3可知在参数正常情况下,IMFSMC控制方法的空载启动速度超调仅为MFSMC控制方法的57.4%,IMFSMC控制方法加减速速度超调分别为MFSMC控制方法的60%、42.8%。由此可知本文所提的改进无模型滑模控制在加减速实验中控制性能优于传统无模型滑模控制。
(2) 加减载仿真实验:电机在转速 1 000 r/min情况下启动,在0.6 s时突加10 N∙m,在1.3 s时负载突减为6 N∙m。仿真对比实验如图5、6、7所示,控制性能数据对比见表4。

|
图 5 加减载转速波形Ⅰ Figure 5 The rotational speed waveforms of loading and unloading Ⅰ |
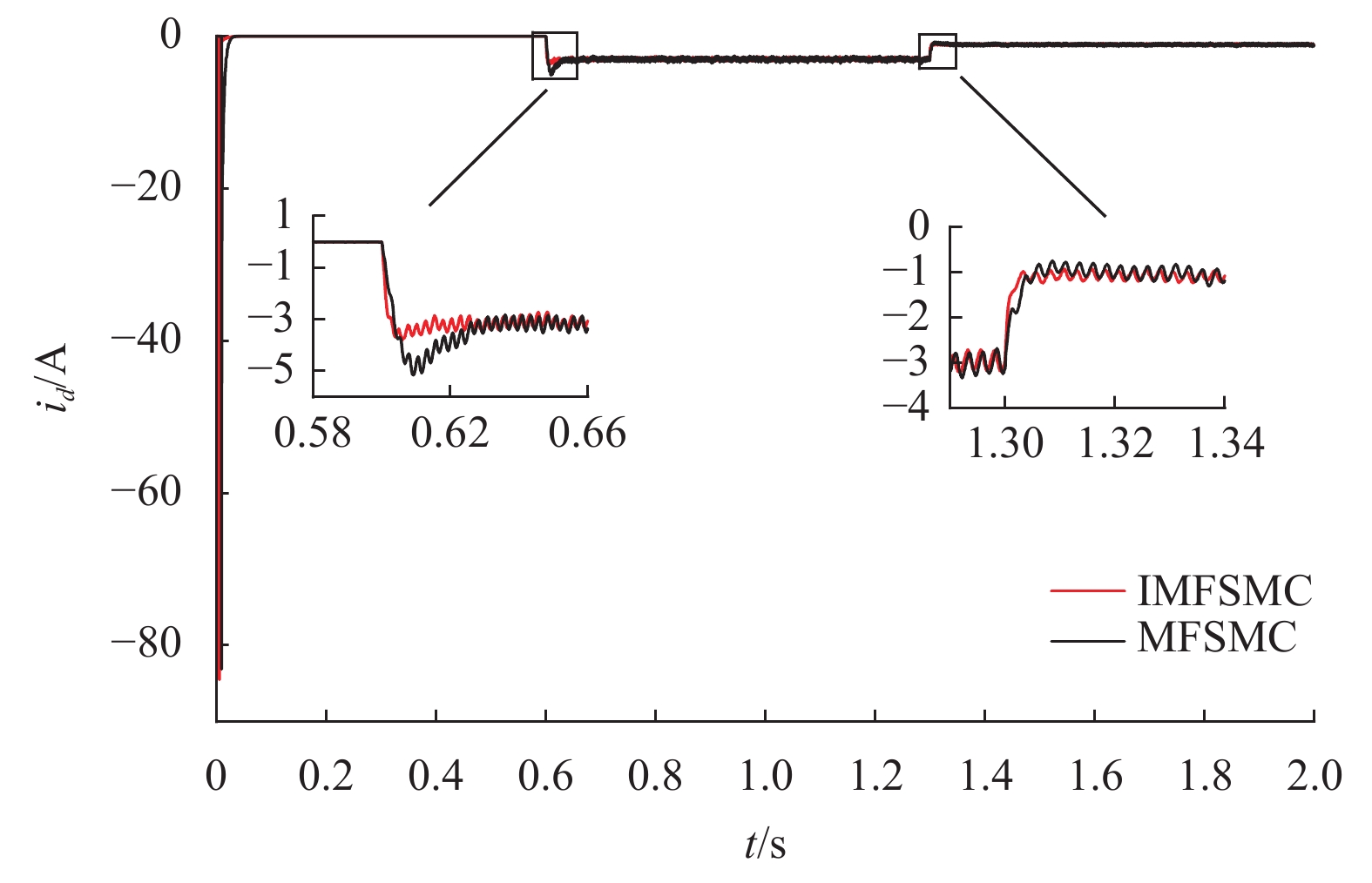
|
图 6 d轴电流波形Ⅰ Figure 6 The current waveforms of d-axis Ⅰ |
| 表 4 参数正常加减载实验控制性能对比 Table 4 Comparison of control performance of loading and unloading experiments with normal parameters |

|
图 7 q轴电流波形Ⅰ Figure 7 The current waveforms of q-axis Ⅰ |
结合图5、6、7和表4可知在参数正常情况下,在加减载仿真实验中IMFSMC控制方法的速度超调仅为MFSMC控制方法的67.2%,IMFSMC控制方法加减载速度变化分别为MFSMC控制方法的78.2%、80.6%,IMFSMC控制方法直轴电流
内置式永磁电机参数发生摄动,电阻变化为0.039 Ω,直轴电感
(1) 加减速仿真分析:电机在给定转速600 r/min情况下空载启动,在0.5 s时电机转速突增到1 000 r/min,1.2 s时转速突减到600 r/min。仿真对比实验如图8所示,控制性能数据对比见表5。
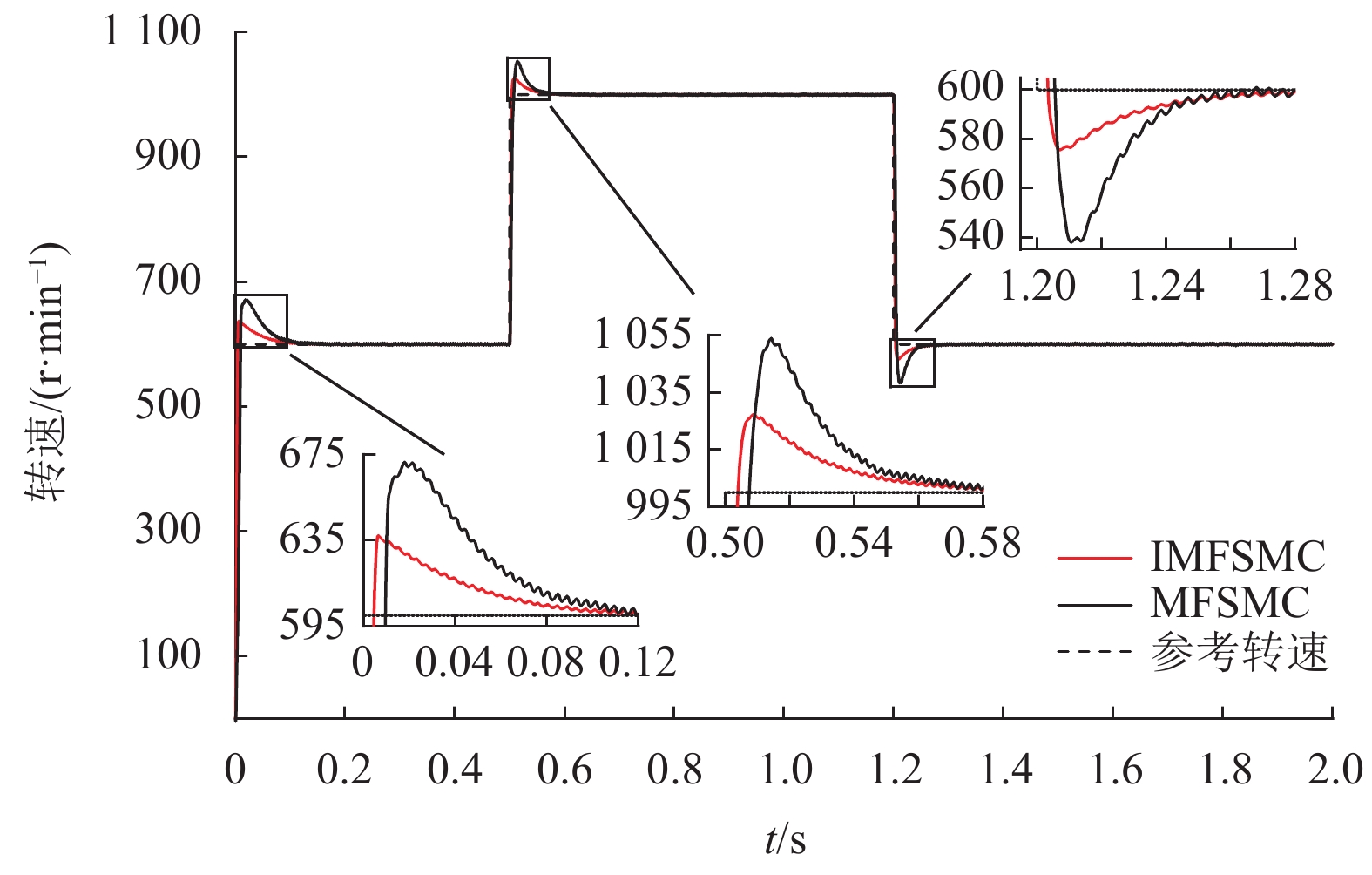
|
图 8 加减速转速波形Ⅱ Figure 8 The rotational speed waveforms of speed up and down Ⅱ |
结合图8和表5可知在参数发生摄动情况下,IMFSMC控制方法的空载启动速度超调仅为MFSMC控制方法的52.8%,IMFSMC控制方法加减速速度超调分别为MFSMC控制方法的50%、38.7%。
| 表 5 参数摄动加减速实验控制性能对比 Table 5 Comparison of control performance of speed up and down experiments with parameters perturbation |
(2) 加减载仿真分析:电机在转速1 000 r/min情况下启动,在0.6 s时突加10 N∙m,在1.3 s负载突减为6 N∙m。仿真对比实验如图9、10、11所示,控制性能数据对比见表6。
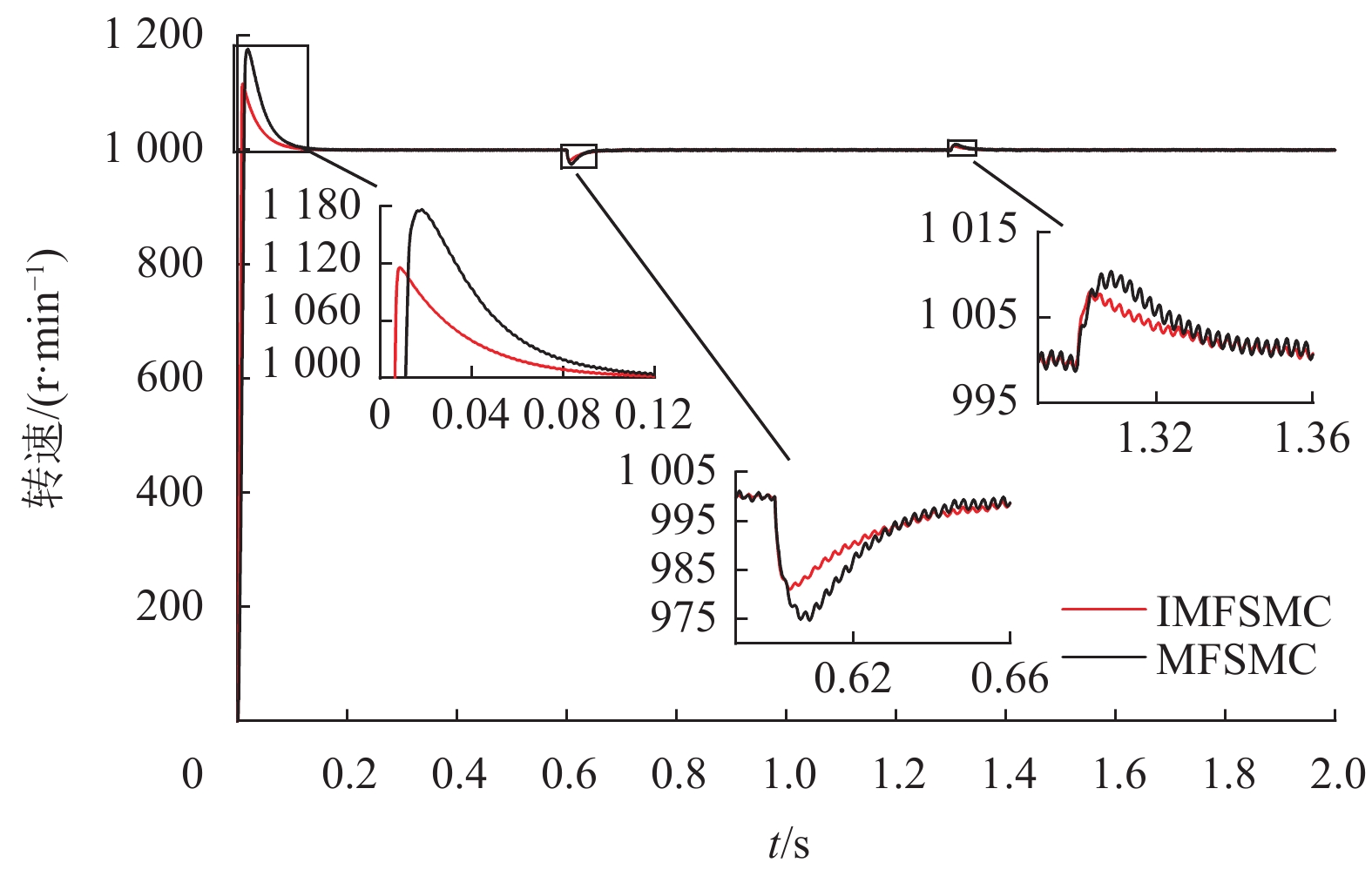
|
图 9 加减载转速波形Ⅱ Figure 9 The rotational speed waveforms of loading and unloading Ⅱ |

|
图 10 d轴电流波形Ⅱ Figure 10 The current waveforms of d-axis Ⅱ |
| 表 6 参数摄动加减载实验控制性能对比 Table 6 Comparison of control performance of loading and unloading experiments with parameters perturbation |

|
图 11 q轴电流波形Ⅱ Figure 11 The current waveforms of q-axis Ⅱ |
结合图9、10、11和表6可知在参数发生摄动情况下,在加减载仿真实验中IMFSMC控制方法的速度超调仅为MFSMC控制方法的65.9%,IMFSMC控制方法加减载速度变化分别为MFSMC控制方法的73.1%、77.9%,IMFSMC控制方法直轴电流
传统无模型滑模控制方法和改进无模型滑模控制方法电机参数摄动对电机运行影响具体对比数据见表7。
| 表 7 2种控制方法参数摄动对电机影响 Table 7 Influences of parameters perturbation of two control methods on motor |
结合上述实验和表7可知,加减速实验和加减载实验中,电机采用IMFSMC控制方法,转速超调增量、交直轴电流超调增量都比采用MFSMC控制方法小。由此可知,IMFSMC控制方法相比传统MFSMC控制方法,参数摄动对电机整体影响更小,电机在参数摄动情况下稳定性更好。
综上分析可得,本文所提IMFSMC控制方法具有抗扰能力强、鲁棒性好等优点。证明了IMFSMC算法的可行性和有效性。
5 结语为解决因IPMSM参数摄动而降低电机鲁棒性及影响电机运行性能等问题,本文提出基于非线性干扰观测器的改进无模型滑模控制方法。通过与传统无模型滑模控制方法仿真对比可知,本文所提IMFSMC控制方法有如下优点。
(1) 新型超局部模型分离了传统超局部模型中待观测项中的可直接观测部分,减小了观测器工作量,提高了观测精度。
(2) 超局部模型中的新型滑模反馈控制器相比传统滑模反馈控制器能减小滑模抖振,增强系统鲁棒性。
(3) 非线性干扰观测器能解决滑模观测器加剧系统抖振的问题。
(4) IMFSMC控制方法相比传统MFSMC控制方法能减小参数摄动对电机的影响,能保证电机在参数摄动情况高性能运行,整体提升电机控制系统鲁棒性和抗扰能力。
| [1] |
宋建国, 林强强, 牟蓬涛, 等. 内置式永磁同步电机MTPA和弱磁控制[J].
电力电子技术, 2017, 51(5): 84-86.
SONG J G, LIN Q Q, MOU P T, et al. MTPA and flux-weaken control for IPMSM[J]. Power Electronics Technology, 2017, 51(5): 84-86. |
| [2] |
马志林, 高梦迪, 刘从虎, 等. 内置式永磁同步电机低噪声控制策略研究[J].
控制工程, 2022, 29(1): 83-90.
MA Z L, GAO M D, LIU C H, et al. Research on low noise control strategy for interior permanent magnet synchronous motor[J]. Control Engineering, 2022, 29(1): 83-90. |
| [3] |
刘志刚, 李世华. 基于永磁同步电机模型辨识与补偿的自抗扰控制器[J].
中国电机工程学报, 2008(24): 118-123.
LIU Z G, LI S H. An active disturbance rejection controller based on permanent magnet synchronous motor model identification and compensation[J]. Chinese Journal of Electrical Engineering, 2008(24): 118-123. |
| [4] |
赵越, 刘斌. 基于滑模变结构的内置式永磁同步电机弱磁矢量控制[J].
信息与控制, 2017, 46(4): 428-436.
ZHAO Y, LIU B. Flux-weakening vector control of interior permanent magnet synchronous motor based on sliding mode variable structure controller[J]. Information and Control, 2017, 46(4): 428-436. |
| [5] |
陈文汉, 孙丹, 王铭泽. 断相故障下开绕组永磁同步电机模型预测控制容错控制策略研究[J].
电工技术学报, 2021, 36(1): 77-86.
CHEN W H, SUN D, WANG M Z. Research on fault-tolerant strategy based on model predictive control for open-winding pmsm system under open-phase fault[J]. Journal of Electrical Engineering Technology, 2021, 36(1): 77-86. |
| [6] |
康尔良, 陈健. 永磁同步电机改进滑模无位置传感器控制[J].
电机与控制学报, 2022, 26(10): 88-97.
KANG E L, CHEN J. Improved sliding mode sensorless control for permanent magnet synchronous motors[J]. Journal of Electrical Machinery and Control, 2022, 26(10): 88-97. |
| [7] |
彭思齐, 蒋雨函, 兰志勇, 等. 永磁同步电机新型指数型自适应滑模观测器无传感器控制[J].
电机与控制学报, 2022, 26(5): 104-114.
PENG S Q, JIANG Y H, LAN Z Y, et al. Sensorless control of new exponential adaptive sliding mode observer permanent magnet synchronous motors[J]. Journal of Electrical Machinery and Control, 2022, 26(5): 104-114. |
| [8] |
张兴华, 唐其太. 考虑参数和负载不确定性的内置式永磁同步电机自适应反步控制[J].
控制与决策, 2016, 31(8): 1509-1512.
ZHANG X H, TANG Q T. Adaptive backstepping control of interior permanent magnet synchronous motor considering parameter and load uncertainties[J]. Control and Decision Making, 2016, 31(8): 1509-1512. |
| [9] |
蒋学程, 彭侠夫, 何栋炜. 永磁同步电机模型自适应补偿速度控制[J].
电机与控制学报, 2011, 15(10): 69-74.
JIANG X C, PENG X F, HE D W. Permanent magnet synchronous motor model adaptive model compensation speed control[J]. Journal of Electrical Machinery and Control, 2011, 15(10): 69-74. |
| [10] |
侯忠生. 无模型自适应控制的现状与展望[J].
控制理论与应用, 2006, 23(4): 586-592.
HOU Z S. The status and prospects of model free adaptive control[J]. Control Theory and Applications, 2006, 23(4): 586-592. |
| [11] |
FLIESS M, JOIN C. Model-free control[J].
International Journal of Control, 2013, 86(12): 2228-2252.
DOI: 10.1080/00207179.2013.810345. |
| [12] |
ZHAO K H, YIN T H, ZHANG C F, et al. Robust model-free nonsingular terminal sliding mode control for PMSM demagnetization fault[J].
IEEE Access, 2019, 7: 15737-15748.
DOI: 10.1109/ACCESS.2019.2895512. |
| [13] |
GAO P, ZHANG G M, LYU X D. Model-free hybrid control with intelligent proportional integral and super-twisting sliding mode control of PMSM drives[J].
Electronics, 2020, 9(9): 1427.
DOI: 10.3390/electronics9091427. |
| [14] |
黄宜山, 唐润忠, 旷明秋, 等. 基于快速趋近律的永磁同步电机驱动系统改进无模型滑模控制[J].
机车电传动, 2022(3): 148-155.
HUANG Y S, TANG R Z, KUANG M Q, et al. Improved model-free sliding mode control for permanent magnet synchronous motor drive system based on quick reaching law[J]. Locomotive Electric Transmission, 2022(3): 148-155. |
| [15] |
赵凯辉, 殷童欢, 张昌凡, 等. 永磁同步电机无模型滑模控制方法研究[J].
电子测量与仪器学报, 2018, 32(4): 172-180.
ZHAO K H, YIN T H, ZHANG C F, et al. Research on model-free sliding mode control of permanent magnet synchronous motor[J]. Journal of Electronic Measurement and Instrumentation, 2018, 32(4): 172-180. |
| [16] |
赵凯辉, 戴旺坷, 周瑞睿, 等. 基于扩展滑模扰动观测器的永磁同步电机新型无模型滑模控制[J].
中国电机工程学报, 2022, 42(6): 2375-2386.
ZHAO K H, DAI W K, ZHOU R R, et al. Novel model free sliding mode control of permanent magnet synchronous motor based on extended sliding mode disturbance observer[J]. Chinese Journal of Electrical Engineering, 2022, 42(6): 2375-2386. |
| [17] |
侯利民, 何佩宇, 王巍, 等. 基于ESO的PMSM无模型自适应滑模控制研究[J].
控制工程, 2022, 29(11): 2082-2089.
HOU L M, HE P Y, WANG W, et al. Research on model-free adaptive sliding mode control for PMSM based on ESO[J]. Control Engineering, 2022, 29(11): 2082-2089. |
| [18] |
米根锁, 梁骅旗. 基于干扰观测器的机械臂非线性滑模控制[J].
系统仿真学报, 2019, 31(9): 1935-1941.
MI G S, LIANG H Q. Nonlinear sliding mode control for manipulator based on disturbance observer[J]. Journal of System Simulation, 2019, 31(9): 1935-1941. |
| [19] |
陆婋泉, 林鹤云, 韩俊林. 永磁同步电机的扰动观测器无位置传感器控制[J].
中国电机工程学报, 2016, 36(5): 1387-1394.
LU Y Q, LIN H Y, HAN J L. Position sensorless control of permanent magnet synchronous machine using a disturbance observer[J]. Chinese Journal of Electrical Engineering, 2016, 36(5): 1387-1394. |
| [20] |
李蕴倬, 侯利民, 王巍, 等. 基于NDOB的滑模速度调节PMSM的NLSEF电流控制[J].
控制工程, 2021, 28(6): 1093-1099.
LI Y Z, HOU L M, WANG W, et al. NLSEF current control of PMSM with sliding mode speed regulation based on NDOB[J]. Control Engineering, 2021, 28(6): 1093-1099. |
 2024, Vol. 41
2024, Vol. 41