近年来,无线通信技术的快速发展使得无线通信设备的数量急剧增加,而各种无线设备的数据都需要在一定的频谱上进行传输,频谱需求日益增长,传统的频谱固定分配政策已无法满足目前的频谱需求,这给稀缺的频谱资源带来了巨大的挑战[1-2]。认知无线电技术作为一种动态频谱接入技术[3-5],被认为在不干扰主用户正常通信的前提下,允许次用户共享授权给主用户的频谱,最大限度地提高频谱的利用率。目前常用的频谱共享方式可以分为覆盖(overlay)方式和衬底(underlay)方式[6-7]。在overlay频谱共享方式中,次用户可以使用主用户授权的空闲频谱资源,但是次用户需要帮主用户提高通信质量。在underlay频谱共享方式中,次用户需要保证其发射功率对主用户的干扰功率小于一个阈值,才可以与主用户共享频谱同时进行通信。另一方面,各种复杂的通信环境以及移动终端用户能量受限等问题暴露了传统供电方式的弊端。具体来说,传统的能量收集来源于太阳能、风能、热能等,但由于这些方法依赖于一些特定气候和环境,能量收集可能存在间歇性,无法可靠地提供永久的能源供应。为了延长无线通信网络的生命周期,人们发现环境中的射频信号可以携带能量信号,从射频信号中获取能量的无线能量传输技术被认为是一种有前途的解决方案[8-9]。随着射频信号能量采集电路的发展,能量采集效率不断提高,研究者们提出将无线信息传输和无线能量传输结合起来同时考虑,因此无线携能通信技术(Simultaneous Wireless Information and Power Transfer, SWIPT)[10]应运而生。
为了应对大规模无线设备数量激增和电池能量受限所带来的频谱和能量使用效率低下的问题,认知SWIPT技术由于其结合了认知无线电技术和无线携能通信技术的特点而受到了广大学者的关注[11-14]。具体来说,认知SWIPT既可以动态使用频谱资源又可以实现能量和信息的同时传输。文献[11]首次提出了利用主用户发射机的射频信号为次用户供能的通信模型,网络中次用户具有能量收集功能,可以从主用户传输的信号中收集并存储能量,当主用户空闲时,次用户再利用收集到的能量进行数据通信。文献[12]考虑了一种改进的认知无线携能通信模型,其中次用户可以从主用户收集能量,并以覆盖的共享方式接入主用户授权的频谱,以传输认知无线携能通信网络数据。文献[13]研究了一种次用户网络为主用户网络无线供电的认知无线电网络。在这网络中,次用户网络可以获得恒定的能量供应,并且为了获得更多的频谱接入机会,除了对主用户网络的无线充电外,还与主用户网络一起协同传输数据,从而增强了主用户网络的传输可靠性。因此,主用户网络可以忍受更多来自次用户网络的干扰,获得更多的能量,并以更高的功率进行传输。文献[14]考虑了在认知无线携能中继中,通过联合优化功率分割系数和中继的能量分配来最大化认知网络的吞吐量。
智能反射平面(Intelligent Reflecting Surfaces, IRS)被认为是实现无线智能网络和可重构信号传播环境的关键技术[15-18]。具体来说,IRS是由大量低成本的无源反射单元组成的超表面,这些反射单元可以独立地实现对反射信号相位及幅度的控制,从而有效地增强目标信号,抑制干扰信号。目前,已有很多关于IRS辅助的通信系统研究:文献[15]考虑了一种IRS辅助的多输入单输出无线携能通信系统,其中基站向不同的用户分别发送信息和能量,通过交替优化基站的发射波束和IRS的相移矩阵以最大化所有能量收集用户收集到的能量;文献[16]提出了一种基于半正定松弛(Semi-definite Relaxation, SDR)的算法,次用户网络与多个单天线主用户接收机共享频谱资源,通过联合优化次用户发射机的波束成形矢量和IRS的相移矩阵以最大限度地提高次用户接收机的数据传输速率;文献[17]研究了一个IRS辅助的多用户认知无线通信系统,其中部署IRS来改善信道环境,从而降低次用户对主用户的干扰信号强度,主要通过对基站处的波束成形矢量和IRS的相移矩阵进行了联合优化,使得次用户网络的和速率最大化;文献[18]考虑了一个IRS辅助的次用户多输入单输出无线携能通信模型,次用户网络以衬底方式与一个主用户网络共享频谱,仿真结果表明,IRS能有效抑制次用户网络通信时对主用户网络的干扰。然而,文献[15]并没有考虑到频谱资源稀缺的问题;文献[16-17]并没有考虑到无线能量传输的场景;文献[18]仅考虑在衬底方式下的频谱共享通信系统,而在这种模式下系统存在一个问题,为了尽可能的减少对主用户的干扰,受次用户发射功率的限制,会导致次用户网络的吞吐量较低。因此,对于衬底方式下的无线携能通信系统,可能存在能量需求和信息传输速率的难以权衡,系统结构难以设计的问题。与衬底系统不同的是,覆盖方式下的认知无线携能通信系统对于次用户的发射功率没有严格的限制,这有效地促进覆盖方式下的认知无线携能通信技术与其他关键技术的结合,提高了系统模型设计的灵活性。然而,文献[11]研究了一个覆盖方式下的认知无线电模型,但是还需要考虑各节点之间的距离以及主次网络范围和当前节点的状态,复杂度较高。文献[13]研究了一个特殊的认知无线携能通信网络,次用户为主用户供能并协助主用户传输信息,在该网络中要求次用户的发射功率尽可能大,才能保证主次用户网络通信质量要求,这给有限的能量资源带来了挑战。因此,这促使我们对覆盖方式下的认知无线携能通信系统展开进一步的研究。
为此,本文研究一个IRS辅助的认知无线携能通信网络,其中次用户网络以新颖的覆盖方式与主用户网络共享频谱资源。具体来说,次用户发射机以无线携能技术为主用户发射机供电的同时并与次用户接收机传输信息,主用户发射机再利用获得的功率传输自己的信息给主用户接收机,作为回报,主用户网络允许次用户网络占用空闲的频谱,其中次用户发射机有恒定的能量供应,主用户发射机为功率受限节点。传输过程中IRS通过动态调整反射相位来辅助主次用户网络进行通信,从而使得次用户网络在该种协作方式中提高了吞吐量和扩大了覆盖范围,同时为能量受限的主用户发射机提升了传输所需的能量。本文的主要研究工作如下:
(1) 针对认知无线携能通信网络中次用户网络吞吐量较低,模型设计复杂度高的问题,提出基于覆盖的频谱接入方式和IRS性能增强方案。
(2) 以最大化次用户网络的总吞吐量为研究目的,提出了联合优化次用户发射机的发射波束成形,传输时隙时间以及两个传输时间下IRS的相移矩阵的优化问题。考虑到该问题的非凸性,引入交替迭代算法将其分解为3个子问题。首先推导得出主用户传输阶段的IRS反射相位的闭式解,再采用半正定规划(Semidefinite Programming, SDP)、半正定松弛和连续凸逼近(Successive Convex Approximation, SCA)等方法将非凸优化问题转化为可解的凸优化问题,最后采用交替优化(Alternating Optimization, AO)和高斯随机法求得问题的高质量可行解。
(3) 为了降低求解问题的复杂度,提出了一种基于IRS反射单元分组的低复杂度算法。
仿真结果表明,本文所提算法获得的次用户发射机到次用户接收机的总吞吐量均优于其他的基准方案。
1 系统模型如图1所示,本文考虑一个由IRS辅助的多用户认知无线携能通信网络,它由一个次用户网络、一个主用户网络以及一个具有
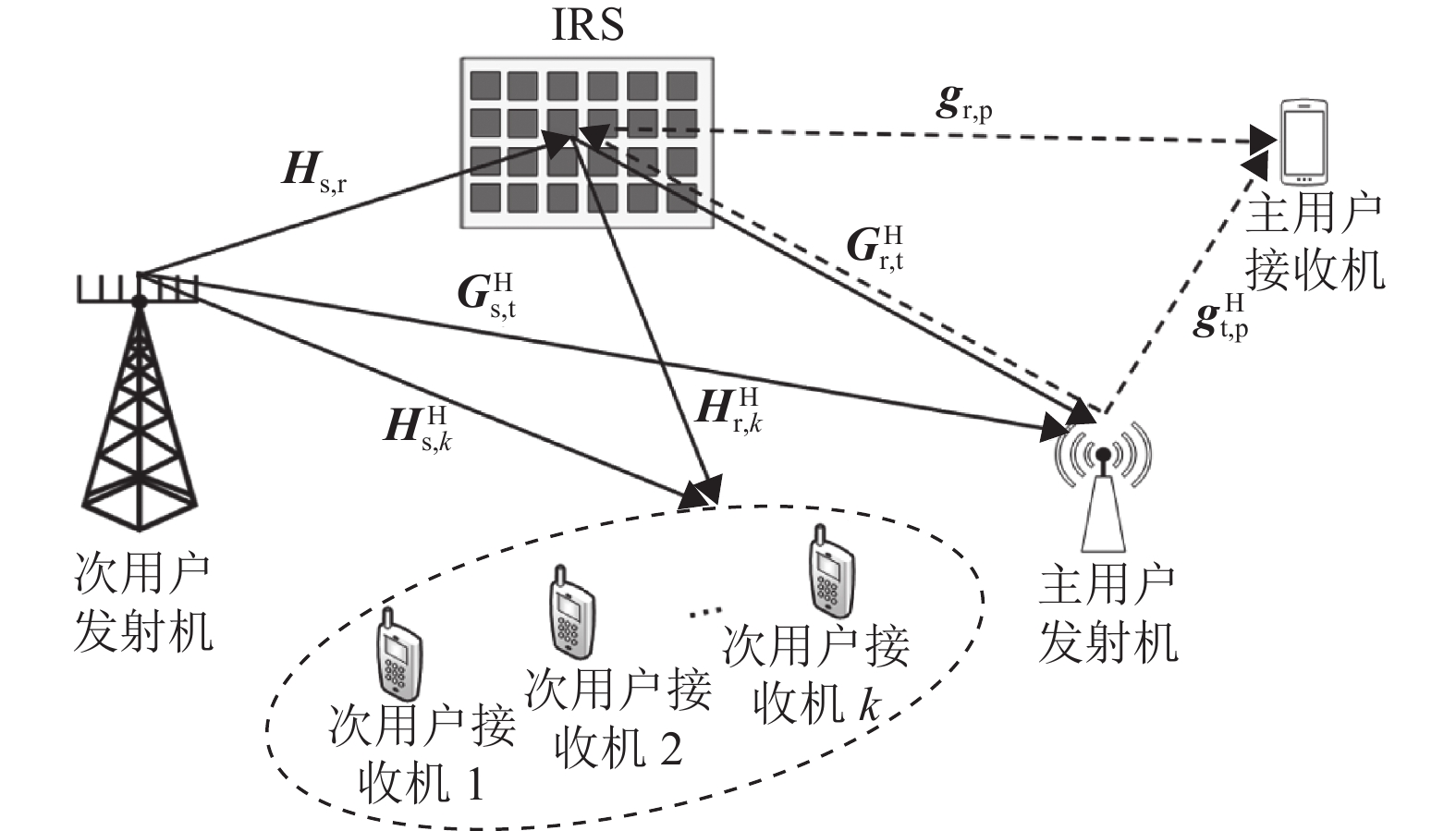
|
图 1 IRS辅助认知无线携能通信网络 Figure 1 An IRS-assisted cognitive SWIPT network |
如图2所示,
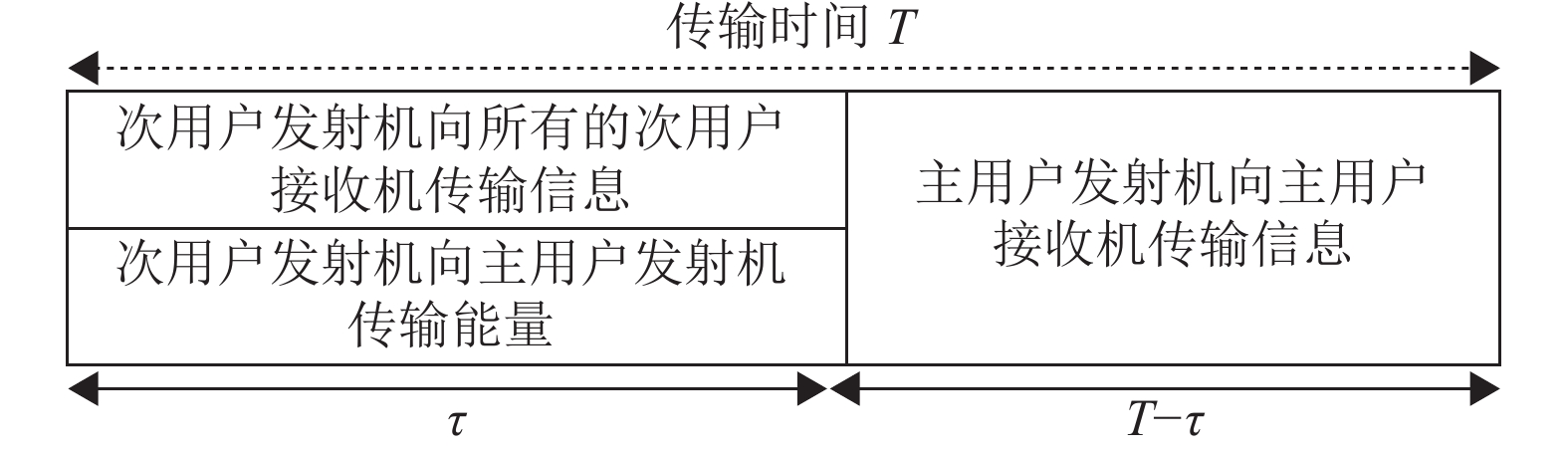
|
图 2 传输时隙图 Figure 2 Transmission time slot map |
定义次用户发射机到IRS、次用户接收机
在传输时隙
| $ {y_k} = ({\boldsymbol{H}}_{{\rm {s}},k}^{\rm {H}} + {\boldsymbol{H}}_{{\rm {r}},k}^{\rm {H}}{{\boldsymbol{\varTheta}} _1}{{\boldsymbol{H}}_{{\rm {s}},{\rm{r}}}}) {\boldsymbol{x}} + {n_k} $ | (1) |
式中,
| $ {{\rm{SINR}}_k} = \frac{{{{\left| {\left( {{\boldsymbol{H}}_{{\rm {s}},k}^{\rm {H}} + {\boldsymbol{H}}_{{\rm {r}},k}^{\rm {H}}{{\boldsymbol{\varTheta}} _1}{{\boldsymbol{H}}_{{\rm {s}},{\rm{r}}}}} \right) {\boldsymbol{v}}_k} \right|}^2}}}{{\displaystyle\sum\limits_{j \ne k}^K {{{\left| {\left( {{\boldsymbol{H}}_{{\rm {s}},k}^{\rm {H}} + {\boldsymbol{H}}_{{\rm {r}},k}^{\rm {H}}{{\boldsymbol{\varTheta}} _1}{{\boldsymbol{H}}_{{\rm {s}},{\rm{r}}}}} \right) {\boldsymbol{v}}_j} \right|}^2}} + \delta _{n,k}^2}} $ | (2) |
因此,在单位带宽下,次用户发射机到次用户接收机
| $ {R_{{\rm {s}},k}} = \tau {\log _2}\left( {1 +{ {\rm{SINR}}_k}} \right) $ | (3) |
在时隙
| $ {{{E}}_{{\rm{PT}}}} = \tau \eta \displaystyle\sum\limits_{k = 1}^K {{{\left| {({\boldsymbol{G}}_{{\rm {s}},{\rm{t}}}^{\rm {H}} + {\boldsymbol{G}}_{{\rm {r}},{\rm{t}}}^{\rm {H}}{{\boldsymbol{\varTheta}} _1}{{\boldsymbol{H}}_{{\rm {s}},{\rm{r}}}}) {{\boldsymbol{v}}_k}} \right|}^2}} $ | (4) |
式中,
忽略微小的能量损耗,主用户发射机将收集到的能量全部用于下行传输信息给主用户接收机。因此,在主用户传输时隙
| $ {P_{\rm{PT}}} = \frac{{{E_{\rm{PT}}}}}{{T - \tau }} $ | (5) |
在时隙
| $ {y_{\rm{PR}}} = \sqrt {{P_{\rm{PT}}}} \left( {{\boldsymbol{g}}_{{\rm {t}},{\rm{p}}}^{\rm {H}} + {\boldsymbol{G}}_{{\rm {r}},{\rm{t}}}^{\rm {H}}{{\boldsymbol{\varTheta}} _2}{{\boldsymbol{g}}_{{\rm {r}},{\rm{p}}}}} \right) {s_{\rm{pr}}} + {n_{\rm{pr}}} $ | (6) |
式中,
| $ {R_{\rm{PR}}} = \left( {T - \tau } \right) {\log _2}\left( {1 + \frac{{{P_{\rm{PT}}}{{\left| {{\boldsymbol{g}}_{{\rm {t}},{\rm{p}}}^{\rm {H}} + {\boldsymbol{G}}_{{\rm {r}},{\rm{t}}}^{\rm {H}}{{\boldsymbol{\varTheta}} _2}{{\boldsymbol{g}}_{{\rm {r}},{\rm{p}}}}} \right|}^2}}}{{\delta _{\rm{pr}}^2}}} \right) $ | (7) |
在单位带宽下,次用户网络总吞吐量定义为次用户发射机到所有次用户接收机的吞吐量之和,可以表示为
| $ R = \displaystyle\sum\limits_{k = 1}^K {{R_{{\rm {s}},k}}} $ | (8) |
为了提高次用户网络的总吞吐量,本文提出在保证满足次用户发射机的最小发射功率约束,次用户接收机的最小信干噪比约束,主用户网络的最小吞吐量约束、时隙时间约束以及不同时隙的IRS反射相位约束下,联合优化次用户发射机的发射波束成形矢量
| $ \mathop {\max }\limits_{\tau ,\left\{ {{{\boldsymbol{v}}_k}} \right\},{{\boldsymbol{\varTheta}} _1},{{\boldsymbol{\varTheta}} _2}} \displaystyle\sum\limits_{k = 1}^K {{R_{{\rm {s}},k}}} $ | (9) |
| $ {\rm{s.t.}} \displaystyle\sum\limits_{k = 1}^K {{{\left\| {{{\boldsymbol{v}}_k}} \right\|}^2}} \leqslant {P_{{\rm{ST}}}} $ | (10) |
| $ {{\rm{SINR}}_k} \geqslant {\gamma _k},\forall k $ | (11) |
| $ {R_{\rm{PR}}} \geqslant {\beta _{\rm{PR}}} $ | (12) |
| $ 0 \leqslant \tau \leqslant T $ | (13) |
| $ \left| {{q_{n,1}}} \right| = 1,\forall n \in \left\{ {1, \cdots ,N} \right\} $ | (14) |
| $ \left| {{q_{n,2}}} \right| = 1,\forall n \in \left\{ {1, \cdots ,N} \right\} $ | (15) |
式中,
为了方便求解,本节将原问题(P1) 转换为多个子问题进行求解。首先,考虑到在时隙
本节旨在优化主用户传输阶段的IRS相移矩阵,推导得出IRS反射相位的闭式解。首先,给定
| $ \mathop {\max }\limits_{{{\boldsymbol{\varTheta}} _2}} {\left| {{\boldsymbol{g}}_{{\rm {t}},{\rm{p}}}^{\rm {H}} + {\boldsymbol{G}}_{{\rm {r}},{\rm{t}}}^{\rm {H}}{{\boldsymbol{\varTheta}} _2}{{\boldsymbol{g}}_{{\rm {r}},{\rm{p}}}}} \right|^2} $ | (16) |
| $ {\rm{s.t.}} \left| {{q_{n,2}}} \right| = 1,\forall n \in \left\{ {1, \cdots ,N} \right\} $ | (17) |
由于恒模约束(17) 的存在,使得问题(P2) 是一个非凸问题,但可利用目标函数的特殊结构得到闭式解[23]。具体来说,问题(P2) 中的目标函数可以满足以下不等式:
| $ \left| {{\boldsymbol{g}}_{{\rm {t}},{\rm{p}}}^{\rm {H}} + {\boldsymbol{G}}_{{\rm {r}},{\rm{t}}}^{\rm {H}}{{\boldsymbol{\varTheta}} _2}{{\boldsymbol{g}}_{{\rm {r}},{\rm{p}}}}} \right| \leqslant \left| {{\boldsymbol{g}}_{{\rm {t}},{\rm{p}}}^{\rm {H}}} \right|{\text{ + }}\left| {{\boldsymbol{G}}_{{\rm {r}},{\rm{t}}}^{\rm {H}}{{\boldsymbol{\varTheta}} _2}{{\boldsymbol{g}}_{{\rm {r}},{\rm{p}}}}} \right| $ | (18) |
式中,当且仅当
| $ \mathop {\max }\limits_{{q_2}} \left| {{\boldsymbol{q}}_2^{\rm {H}}{\boldsymbol{h}}} \right| $ | (19) |
| $ {\rm{s.t.}}\; {\rm{arg}}\left( {{\boldsymbol{G}}_{{\rm {r}},{\rm{t}}}^{\rm {H}}{{\boldsymbol{\varTheta}} _2}{{\boldsymbol{g}}_{{\rm {r}},{\rm{p}}}}} \right) = \arg \left( {{\boldsymbol{g}}_{{\rm {t}},{\rm{p}}}^{\rm {H}}} \right) $ | (20) |
| $ \left| {{q_{n,2}}} \right| = 1,\forall n \in \left\{ {1, \cdots ,N} \right\} $ | (21) |
可以得到问题(P3) 的最优解
| $ \theta _{n,2}^{opt} = \arg \left( {{\boldsymbol{g}}_{{\rm {t}},{\rm{p}}}^{\rm {H}}} \right) - \arg \left( {{\boldsymbol{G}}_{{{\rm{r}}_n},{\rm{t}}}^{\rm {H}}} \right) - \arg \left( {{{\boldsymbol{g}}_{{{\rm{r}}_n},{\rm{p}}}}} \right) $ | (22) |
式中,
| $ {{G}}_{\rm{PR}}^* = {\left| {{\boldsymbol{g}}_{{\rm {t}},{\rm{p}}}^{\rm {H}} + {\boldsymbol{G}}_{{\rm {r}},{\rm{t}}}^{\rm {H}}{\boldsymbol{\varTheta}} _2^*{{\boldsymbol{g}}_{{\rm {r}},{\rm{p}}}}} \right|^2} $ | (23) |
那么问题(P1)可重新表述为联合优化
| $ \mathop {\max }\limits_{\tau ,\left\{ {{{\boldsymbol{v}}_k}} \right\},{{\boldsymbol{\varTheta}} _1}} \displaystyle\sum\limits_{k = 1}^K {\tau {{\log }_2}\left( {1 + \frac{{{{\left| {\left( {{\boldsymbol{H}}_{{\rm {s}},k}^{\rm {H}} + {\boldsymbol{H}}_{{\rm {r}},k}^{\rm {H}}{{\boldsymbol{\varTheta}} _1}{{\boldsymbol{H}}_{{\rm {s}},{\rm{r}}}}} \right) {\boldsymbol{v}}_k} \right|}^2}}}{{\displaystyle\sum\limits_{j \ne k}^K {{{\left| {\left( {{\boldsymbol{H}}_{{\rm {s}},k}^{\rm {H}} + {\boldsymbol{H}}_{{\rm {r}},k}^{\rm {H}}{{\boldsymbol{\varTheta}} _1}{{\boldsymbol{H}}_{{\rm {s}},{\rm{r}}}}} \right) {\boldsymbol{v}}_j} \right|}^2}} + \delta _{n,k}^2}}} \right) } $ | (24) |
| $ \begin{array}{c} {\rm{s.t.}}\; (10) ,(11) ,(13) ,(14) ,(15)\\ \left( {T - \tau } \right) {\log _2}\left( {1 + \dfrac{{\tau \eta \displaystyle\sum\limits_{k = 1}^K {{{\left| {({\boldsymbol{G}}_{{\rm {s}},{\rm{t}}}^{\rm {H}} + {\boldsymbol{G}}_{{\rm {r}},{\rm{t}}}^{\rm {H}}{{\boldsymbol{\varTheta}} _1}{{\boldsymbol{H}}_{{\rm {s}},{\rm{r}}}}) {{\boldsymbol{v}}_k}} \right|}^2}} {\boldsymbol{G}}_{\rm{PR}}^*}}{{\left( {T - \tau } \right) \delta _{\rm{pr}}^2}}} \right) \geqslant {\beta _{\rm{PR}}} \end{array}$ | (25) |
问题(P4) 为非凸问题,难以求解,于是本文采用交替优化的方法来解决问题(P4) 。具体来说,将问题(P4) 分成3个子问题:其中子问题1给定
在这一节中,给定优化变量
| $ \mathop {\max }\limits_{\left\{ {{{\boldsymbol{v}}_k}} \right\}} \displaystyle\sum\limits_{k = 1}^K {\tau {{\log }_2}\left( {1 + \frac{{{{\left| {\left( {{\boldsymbol{H}}_{{\rm {s}},k}^{\rm {H}} + {\boldsymbol{H}}_{{\rm {r}},k}^{\rm {H}}{{\boldsymbol{\varTheta}} _1}{{\boldsymbol{H}}_{{\rm {s}},{\rm{r}}}}} \right) {\boldsymbol{v}}_k} \right|}^2}}}{{\displaystyle\sum\limits_{j \ne k}^K {{{\left| {\left( {{\boldsymbol{H}}_{{\rm {s}},k}^{\rm {H}} + {\boldsymbol{H}}_{{\rm {r}},k}^{\rm {H}}{{\boldsymbol{\varTheta}} _1}{{\boldsymbol{H}}_{{\rm {s}},{\rm{r}}}}} \right) {\boldsymbol{v}}_j} \right|}^2}} + \delta _{n,k}^2}}} \right) } $ | (26) |
| $ {\rm{s.t.}}\; \displaystyle\sum\limits_{k = 1}^K {{{\left\| {{{\boldsymbol{v}}_k}} \right\|}^2}} \leqslant {P_{\rm{ST}}} $ | (27) |
| $ \frac{{{{\left| {\left( {{\boldsymbol{H}}_{{\rm {s}},k}^{\rm {H}} + {\boldsymbol{H}}_{{\rm {r}},k}^{\rm {H}}{{\boldsymbol{\varTheta}} _1}{{\boldsymbol{H}}_{{\rm {s}},{\rm{r}}}}} \right) {\boldsymbol{v}}_k} \right|}^2}}}{{\displaystyle\sum\limits_{j \ne k}^K {{{\left| {\left( {{\boldsymbol{H}}_{{\rm {s}},k}^{\rm {H}} + {\boldsymbol{H}}_{{\rm {r}},k}^{\rm {H}}{{\boldsymbol{\varTheta}} _1}{{\boldsymbol{H}}_{{\rm {s}},{\rm{r}}}}} \right) {\boldsymbol{v}}_j} \right|}^2}} + \delta _{n,k}^2}} \geqslant {\gamma _k},\forall k $ | (28) |
| $ \left( {T - \tau } \right) {\log _2}\left( {1 + \frac{{\tau \eta \displaystyle\sum\limits_{k = 1}^K {{{\left| {({\boldsymbol{G}}_{{\rm {s}},{\rm{t}}}^{\rm {H}} + {\boldsymbol{G}}_{{\rm {r}},{\rm{t}}}^{\rm {H}}{{\boldsymbol{\varTheta}} _1}{{\boldsymbol{H}}_{{\rm {s}},{\rm{r}}}}) {{\boldsymbol{v}}_k}} \right|}^2}} {\boldsymbol{G}}_{\rm{PR}}^*}}{{\left( {T - \tau } \right) \delta _{\rm{pr}}^2}}} \right) \geqslant {\beta _{\rm{PR}}} $ | (29) |
定义
| ${ \begin{split} & {\left| {\left( {{\boldsymbol{H}}_{{\rm {s}},k}^{\rm {H}} + {\boldsymbol{H}}_{{\rm {r}},k}^{\rm {H}}{{\boldsymbol{\varTheta}} _1}{{\boldsymbol{H}}_{{\rm {s}},{\rm{r}}}}} \right) {\boldsymbol{v}}_k} \right|^2} =\\ & {\rm{ Tr}}\left( {\left( {{\boldsymbol{H}}_{{\rm {s}},k}^{\rm {H}} + {\boldsymbol{H}}_{{\rm {r}},k}^{\rm {H}}{{\boldsymbol{\varTheta}} _1}{{\boldsymbol {H}}_{{\rm {s}},{\rm{r}}}}} \right) {{\boldsymbol{v}}_k}{\boldsymbol{v}}_k^{\rm {H}}{{\left( {{\boldsymbol{H}}_{{\rm {s}},k}^{\rm {H}} + {\boldsymbol{H}}_{{\rm {r}},k}^{\rm {H}}{{\boldsymbol{\varTheta}} _1}{{\boldsymbol {H}}_{{\rm {s}},{\rm{r}}}}} \right) }^{\rm {H}}}} \right) =\\ & {\rm{ Tr}}\left( {\left( {{\boldsymbol{H}}_{{\rm {s}},k}^{\rm {H}} + {\boldsymbol{\phi}}_1^{\rm {H}}{\rm{ diag}}({\boldsymbol{H}}_{{\rm {r}},k}^{\rm {H}}) {{\boldsymbol H}_{{\rm {s}},{\rm{r}}}}} \right) } \right. \left. {{{\boldsymbol{v}}_k}{\boldsymbol{v}}_k^{\rm {H}}{{\left( {{\boldsymbol{H}}_{{\rm {s}},k}^{\rm {H}} + {\boldsymbol{\phi}}_1^{\rm {H}}{\rm{ diag}}({\boldsymbol{H}}_{{\rm {r}},k}^{\rm {H}}) {{\boldsymbol {H}}_{{\rm {s}},{\rm{r}}}}} \right) }^{\rm {H}}}} \right) =\\ & {\rm{ Tr}}\left( {{\boldsymbol{H}}_{{\rm {s}},k}^{\rm {H}}{{\boldsymbol{v}}_k}{\boldsymbol{v}}_k^{\rm {H}}{{\boldsymbol {H}}_{{\rm {s}},k}} + {\boldsymbol{H}}_{{\rm {s}},k}^{\rm {H}}{{\boldsymbol{v}}_k}{\boldsymbol{v}}_k^{\rm {H}}{{\left( {{\rm{ diag}}({\boldsymbol{H}}_{{\rm {r}},k}^{\rm {H}}) {{\boldsymbol {H}}_{{\rm {s}},{\rm{r}}}}} \right) }^{\rm {H}}}{{\boldsymbol{\phi}}_1}} \right.+ \\ & {\boldsymbol{\phi}}_1^{\rm {H}}{\rm{ diag}}({\boldsymbol{H}}_{{\rm {r}},k}^{\rm {H}}) {{\boldsymbol {H}}_{{\rm {s}},{\rm{r}}}}{{\boldsymbol{v}}_k}{\boldsymbol{v}}_k^{\rm {H}}{{\boldsymbol {H}}_{{\rm {s}},k}}+ \\ & \left. { {\boldsymbol{\phi}}_1^{\rm {H}}{\rm{ diag}}({\boldsymbol{H}}_{{\rm {r}},k}^{\rm {H}}) {{\boldsymbol {H}}_{{\rm {s}},{\rm{r}}}}{{\boldsymbol{v}}_k}{\boldsymbol{v}}_k^{\rm {H}}{{\left( {{\rm{ diag}}({\boldsymbol{H}}_{{\rm {r}},k}^{\rm {H}}) {{\boldsymbol {H}}_{{\rm {s}},{\rm{r}}}}} \right) }^{\rm {H}}}{{\boldsymbol{\phi}}_1}} \right) =\\ & {\rm{ Tr}}\Bigg( \left[ \begin{gathered} {{\boldsymbol{\phi}}_1} \\ 1 \\ \end{gathered} \right]\left[ {{\boldsymbol{\phi}}_1^{\rm {H}}1} \right]\left[ \begin{gathered} {\rm{ diag}}({\boldsymbol{H}}_{{\rm {r}},k}^{\rm {H}}) {{\boldsymbol {H}}_{{\rm {s}},{\rm{r}}}} \\ {\boldsymbol{H}}_{{\rm {s}},k}^{\rm {H}} \Bigg.\\ \end{gathered} \right] \\ &\Bigg. {{\boldsymbol{v}}_k}{\boldsymbol{v}}_k^{\rm {H}}\left[ {\begin{array}{*{20}{c}} {{{\left( {{\rm{ diag}}({\boldsymbol{H}}_{{\rm {r}},k}^{\rm {H}}) {{\boldsymbol {H}}_{{\rm {s}},{\rm{r}}}}} \right) }^{\rm {H}}}} {{{\boldsymbol {H}}_{{\rm {s}},k}}} \end{array}} \right] \Bigg) =\\ & {\rm{ Tr}}\left( {{{\boldsymbol{Q}}_1}{{\boldsymbol{L}}_k}{{\boldsymbol{V}}_k}{\boldsymbol{L}}_k^{\rm {H}}} \right) \end{split}} $ | (30) |
同理可得
| $ {\left| {({\boldsymbol{G}}_{{\rm {s}},{\rm{t}}}^{\rm {H}} + {\boldsymbol{G}}_{{\rm {r}},{\rm{t}}}^{\rm {H}}{{\boldsymbol{\varTheta}} _1}{{\boldsymbol{H}}_{{\rm {s}},{\rm{r}}}}) {{\boldsymbol{v}}_k}} \right|^2} ={\rm{ Tr}}\left( {{{\boldsymbol{Q}}_1}{{\boldsymbol{JV}}_k}{{\boldsymbol{J}}^{\rm {H}}}} \right) $ | (31) |
根据等式(30) 、(31) 将问题(P5) 变形为问题 (P6):
| $ \mathop {\max }\limits_{\left\{ {{{\boldsymbol{V}}_k}} \right\}} \displaystyle\sum\limits_{k = 1}^K {\tau {{\log }_2}\left( {1 + \frac{{{\rm{Tr}}\left( {{{\boldsymbol{Q}}_1}{{\boldsymbol{L}}_k}{{\boldsymbol{V}}_k}{\boldsymbol{L}}_k^{\rm {H}}} \right) }}{{\displaystyle\sum\limits_{j \ne k}^K {{\rm{Tr}}\left( {{{\boldsymbol{Q}}_1}{{\boldsymbol{L}}_k}{{\boldsymbol{V}}_j}{\boldsymbol{L}}_k^{\rm {H}}} \right) } + \delta _{n,k}^2}}} \right) } $ | (32) |
| ${\rm{ s.t.}}\quad \displaystyle\sum\limits_{k = 1}^K {{\rm{Tr}}\left( {{{\boldsymbol{V}}_k}} \right) } \leqslant {P_{\rm{ST}}} $ | (33) |
| $ \frac{{{\rm{Tr}}\left( {{{\boldsymbol{Q}}_1}{{\boldsymbol{L}}_k}{{\boldsymbol{V}}_k}{\boldsymbol{L}}_k^{\rm {H}}} \right) }}{{\displaystyle\sum\limits_{j \ne k}^K {{\rm{Tr}}\left( {{{\boldsymbol{Q}}_1}{{\boldsymbol{L}}_k}{{\boldsymbol{V}}_j}{\boldsymbol{L}}_k^{\rm {H}}} \right) } + \delta _{n,k}^2}} \geqslant {\gamma _k},\forall k $ | (34) |
| $ \left( {T - \tau } \right) {\log _2}\left( {1 + \frac{{\tau \eta \displaystyle\sum\limits_{k = 1}^K {{\rm{Tr}}\left( {{{\boldsymbol{Q}}_1}J{{\boldsymbol{V}}_k}{J^{\rm {H}}}} \right) } {{G}}_{\rm{PR}}^*}}{{\left( {T - \tau } \right) \delta _{\rm{pr}}^2}}} \right) \geqslant {\beta _{\rm{PR}}} $ | (35) |
| $ {\rm{rank}}\left( {{{\boldsymbol{V}}_k}} \right) = 1,\forall k $ | (36) |
| $ {{\boldsymbol{V}}_k} \succcurlyeq 0,\forall k $ | (37) |
由于问题(P6) 的目标函数(32) 关于优化变量
| $\begin{split} & R = \displaystyle\sum\limits_{k = 1}^K {\tau {{\log }_2}\left( {1 + \frac{{{\rm{Tr}}\left( {{{\boldsymbol{Q}}_1}{{\boldsymbol{L}}_k}{{\boldsymbol{V}}_k}{\boldsymbol{L}}_k^{\rm {H}}} \right) }}{{\displaystyle\sum\limits_{j \ne k}^K {{\rm{Tr}}\left( {{{\boldsymbol{Q}}_1}{{\boldsymbol{L}}_k}{{\boldsymbol{V}}_j}{\boldsymbol{L}}_k^{\rm {H}}} \right) } + \delta _{n,k}^2}}} \right) } =\\ & \displaystyle\sum\limits_{k = 1}^K {\tau {{\log }_2}\left( {\displaystyle\sum\limits_{i = 1}^K {{\rm{Tr}}\left( {{{\boldsymbol{Q}}_1}{{\boldsymbol{L}}_k}{{\boldsymbol{V}}_i}{\boldsymbol{L}}_k^{\rm {H}}} \right) } + \delta _{n,k}^2} \right) } - \\ & \displaystyle\sum\limits_{k = 1}^K {\tau {{\log }_2}\left( {\displaystyle\sum\limits_{j \ne k}^K {{\rm{Tr}}\left( {{{\boldsymbol{Q}}_1}{{\boldsymbol{L}}_k}{{\boldsymbol{V}}_j}{\boldsymbol{L}}_k^{\rm {H}}} \right) } + \delta _{n,k}^2} \right) } =\\ & {F_1}\left( {\boldsymbol{V}} \right) + {F_2}\left( {\boldsymbol{V}} \right) \end{split} $ | (38) |
式中,
| $ {F_1}\left( { \boldsymbol{V}} \right) = \displaystyle\sum\limits_{k = 1}^K {\tau {{\log }_2}\left( {\displaystyle\sum\limits_{i = 1}^K {{\rm{Tr}}\left( {{{\boldsymbol{Q}}_1}{{\boldsymbol{L}}_k}{{\boldsymbol{V}}_i}{\boldsymbol{L}}_k^{\rm {H}}} \right) } + \delta _{n,k}^2} \right) } $ | (39) |
| $ {F_2}\left( { \boldsymbol{V}} \right) = - \displaystyle\sum\limits_{k = 1}^K {\tau {{\log }_2}\left( {\displaystyle\sum\limits_{j \ne k}^K {{\rm{Tr}}\left( {{{\boldsymbol{Q}}_1}{{\boldsymbol{L}}_k}{{\boldsymbol{V}}_j}{\boldsymbol{L}}_k^{\rm {H}}} \right) } + \delta _{n,k}^2} \right) } $ | (40) |
由于目标问题为最大化关于
| $\begin{split} & {F_2}\left( { \boldsymbol{V}} \right) \geqslant {F_2}\left( {{{\boldsymbol{V}}^{\left( t \right) }}} \right) + \displaystyle\sum\limits_{j \ne k}^K {{\rm{Tr}}} \left( {\nabla _{{{\boldsymbol{V}}_j}}^{\rm {H}}{F_2}\left( {{{\boldsymbol{V}}^{\left( t \right) }}} \right) \left( {{{\boldsymbol{V}}_j} - {\boldsymbol{V}}_j^{\left( t \right) }} \right) } \right) \triangleq\\ & F_2^{\rm{LB}}\left( {{\boldsymbol{V}},{{\boldsymbol{V}}^{\left( t \right) }}} \right) \end{split}$ | (41) |
式中,
| $ R \cong {F_1}\left( { \boldsymbol{V}} \right) + F_2^{\rm{LB}}\left( {{\boldsymbol{V}},{{\boldsymbol{V}}^{\left( t \right) }}} \right) $ | (42) |
由于
| $ \frac{1}{{{\gamma _k}}}{\rm{Tr}}\left( {{{\boldsymbol{Q}}_1}{{\boldsymbol{L}}_k}{{\boldsymbol{V}}_k}{\boldsymbol{L}}_k^{\rm {H}}} \right) - \displaystyle\sum\limits_{j \ne k}^K {{\rm{Tr}}\left( {{{\boldsymbol{Q}}_1}{{\boldsymbol{L}}_k}{{\boldsymbol{V}}_j}{\boldsymbol{L}}_k^{\rm {H}}} \right) } \geqslant \delta _{n,k}^2,\forall k $ | (43) |
然而,由于秩一约束(36)的存在,使得问题(P6)依然非凸。因此,采用半正定松弛技术,即忽略约束(36),得到(P6)松弛后的问题(P7)如式(44)~式(48)所示:
| $ \mathop {\max }\limits_{\left\{ {{{\boldsymbol{V}}_k}} \right\}} {F_1}\left( { \boldsymbol{V}} \right) + F_2^{\rm{LB}}\left( {{\boldsymbol{V}},{{\boldsymbol{V}}^{\left( t \right) }}} \right) $ | (44) |
| $ {\rm{s.t.}}\; \displaystyle\sum\limits_{k = 1}^K {{\rm{Tr}}\left( {{{\boldsymbol{V}}_k}} \right) } \leqslant {P_{\rm{ST}}} $ | (45) |
| $ \frac{1}{{{\gamma _k}}}{\rm{Tr}}\left( {{{\boldsymbol{Q}}_1}{{\boldsymbol{L}}_k}{{\boldsymbol{V}}_k}{\boldsymbol{L}}_k^{\rm {H}}} \right) - \displaystyle\sum\limits_{j \ne k}^K {{\rm{Tr}}\left( {{{\boldsymbol{Q}}_1}{{\boldsymbol{L}}_k}{{\boldsymbol{V}}_j}{\boldsymbol{L}}_k^{\rm {H}}} \right) } \geqslant \delta _{n,k}^2,\forall k $ | (46) |
| $ \left( {T - \tau } \right) {\log _2}\left( {1 + \frac{{\tau \eta \displaystyle\sum\limits_{k = 1}^K {{\rm{Tr}}\left( {{{\boldsymbol{Q}}_1}J{{\boldsymbol{V}}_k}{J^{\rm {H}}}} \right) } {\boldsymbol{G}}_{\rm{PR}}^*}}{{\left( {T - \tau } \right) \delta _{\rm{pr}}^2}}} \right) \geqslant {\beta _{\rm{PR}}} $ | (47) |
| $ {{\boldsymbol{V}}_k} \succcurlyeq 0,\forall k $ | (48) |
问题(P7) 是关于
给定优化变量
| $ \mathop {\max }\limits_{{{\boldsymbol{\varTheta}} _1}} \displaystyle\sum\limits_{k = 1}^K {\tau {{\log }_2}\left( {1 + \frac{{{{\left| {\left( {{\boldsymbol{H}}_{{\rm {s}},k}^{\rm {H}} + {\boldsymbol{H}}_{{\rm {r}},k}^{\rm {H}}{{\boldsymbol{\varTheta}} _1}{{\boldsymbol{H}}_{{\rm {s}},{\rm{r}}}}} \right) {\boldsymbol{v}}_k} \right|}^2}}}{{\displaystyle\sum\limits_{j \ne k}^K {{{\left| {\left( {{\boldsymbol{H}}_{{\rm {s}},k}^{\rm {H}} + {\boldsymbol{H}}_{{\rm {r}},k}^{\rm {H}}{{\boldsymbol{\varTheta}} _1}{{\boldsymbol{H}}_{{\rm {s}},{\rm{r}}}}} \right) {\boldsymbol{v}}_j} \right|}^2}} + \delta _{n,k}^2}}} \right) } $ | (49) |
| $ {\rm{s}}.{\rm{t}}. \frac{{{{\left| {\left( {{\boldsymbol{H}}_{{\rm {s}},k}^{\rm {H}} + {\boldsymbol{H}}_{{\rm {r}},k}^{\rm {H}}{{\boldsymbol{\varTheta}} _1}{{\boldsymbol{H}}_{{\rm {s}},{\rm{r}}}}} \right) {\boldsymbol{v}}_k} \right|}^2}}}{{\displaystyle\sum\limits_{j \ne k}^K {{{\left| {\left( {{\boldsymbol{H}}_{{\rm {s}},k}^{\rm {H}} + {\boldsymbol{H}}_{{\rm {r}},k}^{\rm {H}}{{\boldsymbol{\varTheta}} _1}{{\boldsymbol{H}}_{{\rm {s}},{\rm{r}}}}} \right) {\boldsymbol{v}}_j} \right|}^2}} + \delta _{n,k}^2}} \geqslant {\gamma _k},\forall k $ | (50) |
| $ \left( {T - \tau } \right) {\log _2}\left( {1 + \frac{{\tau \eta \displaystyle\sum\limits_{k = 1}^K {{{\left| {({\boldsymbol{G}}_{{\rm {s}},{\rm{t}}}^{\rm {H}} + {\boldsymbol{G}}_{{\rm {r}},{\rm{t}}}^{\rm {H}}{{\boldsymbol{\varTheta}} _1}{{\boldsymbol{H}}_{{\rm {s}},{\rm{r}}}}) {{\boldsymbol{v}}_k}} \right|}^2}} {\boldsymbol{G}}_{\rm{PR}}^*}}{{\left( {T - \tau } \right) \delta _{\rm{pr}}^2}}} \right) \geqslant {\beta _{\rm{PR}}} $ | (51) |
| $ \left| {{q_{n,1}}} \right| = 1,\forall n \in \left\{ {1, \cdots ,N} \right\} $ | (52) |
由于约束(52)为模一约束,难以求解。因此,根据3.2定义的变量,可知约束(52) 可以等价为式(53)~式(55):
| $ {{\boldsymbol{Q}}_{n,n,1}} = 1,\forall n \in \left\{ {1, \cdots ,N + 1} \right\} $ | (53) |
| $ {\rm{rank}}\left( {{{\boldsymbol{Q}}_1}} \right) = 1. $ | (54) |
| $ {{\boldsymbol{Q}}_1} \succcurlyeq 0 $ | (55) |
式中,
| $\begin{split} &\mathop {\max }\limits_{{{\boldsymbol{Q}}_1}} \displaystyle\sum\limits_{k = 1}^K {\tau {{\log }_2}\left( {1 + \frac{{{\rm{Tr}}\left( {{{\boldsymbol{Q}}_1}{{\boldsymbol{L}}_k}{{\boldsymbol{V}}_k}{\boldsymbol{L}}_k^{\rm {H}}} \right) }}{{\displaystyle\sum\limits_{j \ne k} {{\rm{Tr}}{{\left( {{{\boldsymbol{Q}}_1}{{\boldsymbol{L}}_k}{{\boldsymbol{V}}_j}{\boldsymbol{L}}_k^{\rm {H}}} \right) }^2} + \delta _{n,k}^2} }}} \right) }\\ &\qquad {\rm{s.t.}} \;\;(46) ,(47) ,(53) ,(54) ,(55) \end{split}$ | (56) |
然而,由于问题(P9) 中的目标函数关于优化变量
| $ \begin{split} & R = \displaystyle\sum\limits_{k = 1}^K {\tau {{\log }_2}\left( {1 + \frac{{{\rm{Tr}}\left( {{{\boldsymbol{Q}}_1}{{\boldsymbol{L}}_k}{{\boldsymbol{V}}_k}{\boldsymbol{L}}_k^{\rm {H}}} \right) }}{{\displaystyle\sum\limits_{j \ne k}^K {{\rm{Tr}}\left( {{{\boldsymbol{Q}}_1}{{\boldsymbol{L}}_k}{{\boldsymbol{V}}_j}{\boldsymbol{L}}_k^{\rm {H}}} \right) } + \delta _{n,k}^2}}} \right) } = \\ & \displaystyle\sum\limits_{k = 1}^K {\tau {{\log }_2}\left( {\displaystyle\sum\limits_{i = 1}^K {{\rm{Tr}}\left( {{{\boldsymbol{Q}}_1}{{\boldsymbol{L}}_k}{{\boldsymbol{V}}_i}{\boldsymbol{L}}_k^{\rm {H}}} \right) } + \delta _{n,k}^2} \right) } - \\ & \displaystyle\sum\limits_{k = 1}^K {\tau {{\log }_2}\left( {\displaystyle\sum\limits_{j \ne k}^K {{\rm{Tr}}\left( {{{\boldsymbol{Q}}_1}{{\boldsymbol{L}}_k}{{\boldsymbol{V}}_j}{\boldsymbol{L}}_k^{\rm {H}}} \right) } + \delta _{n,k}^2} \right) } = \\ & {D_1}\left( {{{\boldsymbol{Q}}_1}} \right) + {D_2}\left( {{{\boldsymbol{Q}}_1}} \right) \end{split}$ | (57) |
式中,
| $ {D_1}\left( {{{\boldsymbol{Q}}_1}} \right) = \displaystyle\sum\limits_{k = 1}^K {\tau {{\log }_2}\left( {\displaystyle\sum\limits_{i = 1}^K {{\rm{Tr}}\left( {{{\boldsymbol{Q}}_1}{{\boldsymbol{L}}_k}{{\boldsymbol{V}}_i}{\boldsymbol{L}}_k^{\rm {H}}} \right) } + \delta _{n,k}^2} \right) } $ | (58) |
| $ {D_2}\left( {{{\boldsymbol{Q}}_1}} \right) = - \displaystyle\sum\limits_{k = 1}^K {\tau {{\log }_2}\left( {\displaystyle\sum\limits_{j \ne k}^K {{\rm{Tr}}\left( {{{\boldsymbol{Q}}_1}{{\boldsymbol{L}}_k}{{\boldsymbol{V}}_j}{\boldsymbol{L}}_k^{\rm {H}}} \right) } + \delta _{n,k}^2} \right) } $ | (59) |
由于目标问题为最大化关于
| $ \begin{split} & {D_2}\left( {\boldsymbol{Q}} \right) \geqslant {D_2}\left( {{\boldsymbol{Q}}_1^{\left( t \right) }} \right) +{\rm{ Tr}}\left( {\nabla _{{{\boldsymbol{Q}}_1}}^{\rm {H}}{D_2}\left( {{\boldsymbol{Q}}_1^{\left( t \right) }} \right) \left( {{{\boldsymbol{Q}}_1} - {\boldsymbol{Q}}_1^{\left( t \right) }} \right) } \right) \triangleq\\ & D_2^{\rm{LB}}\left( {{{\boldsymbol{Q}}_1},{\boldsymbol{Q}}_1^{\left( t \right) }} \right) \end{split} $ | (60) |
式中,
| $ \nabla _{{{\boldsymbol{Q}}_1}}^{\rm {H}}{D_2}\left( {{\boldsymbol{Q}}_1^{\left( t \right) }} \right) = - \frac{1}{{\ln 2}}\frac{{\displaystyle\sum\nolimits_{j \ne k}^K {{{\boldsymbol{L}}_k}{{\boldsymbol{V}}_j}{\boldsymbol{L}}_k^{\rm {H}}} }}{{\displaystyle\sum\nolimits_{j \ne k}^K {{\rm{Tr}}\left( {{{\boldsymbol{Q}}_1}{{\boldsymbol{L}}_k}{{\boldsymbol{V}}_j}{\boldsymbol{L}}_k^{\rm {H}}} \right) } + \delta _{n,k}^2}} \text{,} $ |
| $ R = {D_1}\left( {{{\boldsymbol{Q}}_1}} \right) + D_2^{\rm{LB}}\left( {{{\boldsymbol{Q}}_1},{\boldsymbol{Q}}_1^{\left( t \right) }} \right) $ | (61) |
由于
| $ \mathop {\max }\limits_{{{\boldsymbol{Q}}_1}} {D_1}\left( {{{\boldsymbol{Q}}_1}} \right) + D_2^{\rm{LB}}\left( {{{\boldsymbol{Q}}_1},{\boldsymbol{Q}}_1^{\left( t \right) }} \right) $ | (62) |
| $ {\rm{s.t.}}\;\; (47) ,(48) ,(54) , (56)$ |
问题(P10) 是关于
给定优化变量
| $ \mathop {\max }\limits_\tau \displaystyle\sum\limits_{k = 1}^K {\tau {{\log }_2}\left( {1 + \frac{{{{\left| {\left( {{\boldsymbol{H}}_{{\rm {s}},k}^{\rm {H}} + {\boldsymbol{H}}_{{\rm {r}},k}^{\rm {H}}{{\boldsymbol{\varTheta}} _1}{{\boldsymbol{H}}_{{\rm {s}},{\rm{r}}}}} \right) {\boldsymbol{v}}_k} \right|}^2}}}{{\displaystyle\sum\limits_{j \ne k}^K {{{\left| {\left( {{\boldsymbol{H}}_{{\rm {s}},k}^{\rm {H}} + {\boldsymbol{H}}_{{\rm {r}},k}^{\rm {H}}{{\boldsymbol{\varTheta}} _1}{{\boldsymbol{H}}_{{\rm {s}},{\rm{r}}}}} \right) {\boldsymbol{v}}_j} \right|}^2}} + \delta _{n,k}^2}}} \right) } $ | (63) |
| $ {\rm{s.t.}} \;0 \leqslant \tau \leqslant T $ | (64) |
| $ \left( {T - \tau } \right) {\log _2}\left( {1 + \frac{{\tau \eta \displaystyle\sum\limits_{k = 1}^K {{{\left| {({\boldsymbol{G}}_{{\rm {s}},{\rm{t}}}^{\rm {H}} + {\boldsymbol{G}}_{{\rm {r}},{\rm{t}}}^{\rm {H}}{{\boldsymbol{\varTheta}} _1}{{\boldsymbol{H}}_{{\rm {s}},{\rm{r}}}}) {{\boldsymbol{v}}_k}} \right|}^2}} {{G}}_{\rm{PR}}^*}}{{\left( {T - \tau } \right) \delta _{\rm{pr}}^2}}} \right) \geqslant {\beta _{\rm{PR}}} $ | (65) |
由于目标函数是一个关于
综上所述,本文提出交替迭代求解问题(P4) 、问题(P10) 和问题(P11) 的方法,从而获得原问题的最优解。令目标函数
算法1 求解问题(P10) 的算法
1) 通过等式(22) 获得
2) 循环:
(a) 给定
(b) 给定
(c) 给定
(d) 令
3) 直到
4) 再利用高斯随机方法将
在算法1中,
为了降低整体算法的复杂度,提出一种基于IRS反射单元分组的低复杂度方法,即将相邻的IRS反射单元划分多个子组,每个子组中的所有反射单元被视为单个反射单元[25]。
基于IRS反射单元分组的方法,假设每个子组中的IRS发射单元数量相同,
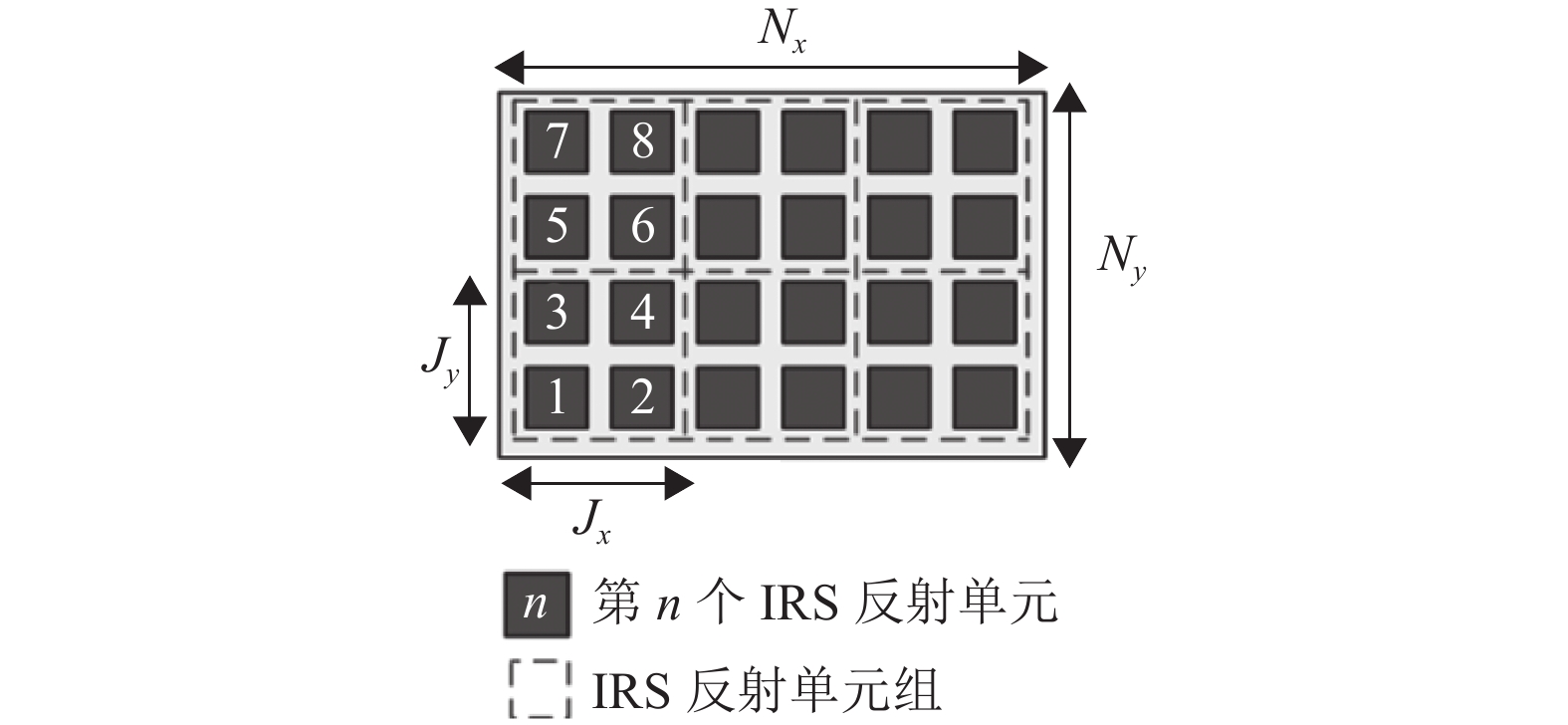
|
图 3 IRS反射单元分组的示意图 Figure 3 Illustration of IRS reflection unit grouping |
由于各子组中的IRS反射单元采用共同的反射系数,单个子组的IRS反射系数可以表示为
| $ {{\boldsymbol{\phi}}_1} = \tilde {{{\boldsymbol{\phi}}_1}} \otimes {1_{J \times 1}} $ | (66) |
| $ {{\boldsymbol{\phi}}_2} = \tilde {{{\boldsymbol{\phi}}_2}} \otimes {1_{J \times 1}} $ | (67) |
式中,
本文假设每个子组中的IRS反射单元索引是连续的,即第
综上,可以得到次用户发射机通过IRS到次用户接收机
| $ \begin{split} & {\hat {\boldsymbol{H}}_{{\rm {r}},k}} = {\boldsymbol{H}}_{{\rm {r}},k}^{\rm {H}}{{\boldsymbol{\varTheta}} _1}{{{\boldsymbol{ H}}}_{{\rm {s}},{\rm{r}}}} = {\left( {\tilde {{{\boldsymbol{\phi}}_1}} \otimes {1_{J \times 1}}} \right) ^{\rm {H}}}{\left[ {{{\wideparen{{\boldsymbol{h}}} }_{1,k}}^{\rm{T}}, \cdots ,{{\wideparen{{\boldsymbol{h}}} }_{N,k}}^{\rm{T}}} \right]^{\rm{T}}} = \\ & \tilde {{{\boldsymbol{\phi}}_1}}{\left[ {{{\tilde {\boldsymbol{h}}}_{1,k}}^{\rm{T}}, \cdots ,{{\tilde {\boldsymbol{h}}}_{B,k}}^{\rm{T}}} \right]^{\rm{T}}} = {\tilde {{{\boldsymbol{\phi}}_1}}^{\rm {H}}}{\tilde {\boldsymbol{H}}_{{\rm {r}},k}} \end{split} $ | (68) |
| $\begin{split} & {\hat {\boldsymbol{G}}_{{\rm {r}},{\rm{t}}}} = {\boldsymbol{G}}_{{\rm {r}},{\rm{t}}}^{\rm {H}}{{\boldsymbol{\varTheta}} _1}{{\boldsymbol{H}}_{{\rm {s}},{\rm{r}}}} = {\left( {\tilde {{{\boldsymbol{\phi}}_1}} \otimes {1_{J \times 1}}} \right) ^{\rm {H}}}{\left[ {{{\tilde {\boldsymbol{G}}}_{1,{\rm{t}}}}^{\rm{T}}, \cdots ,{{\tilde {\boldsymbol{G}}}_{N,{\rm{t}}}}^{\rm{T}}} \right]^{\rm{T}}} = \\ &\tilde {{{\boldsymbol{\phi}}_1}}{\left[ {{{\tilde {\boldsymbol{G}}}_{1,{\rm{t}}}}^{\rm{T}}, \cdots ,{{\tilde {\boldsymbol{G}}}_{B,{\rm{t}}}}^{\rm{T}}} \right]^{\rm{T}}} = {\tilde {{{\boldsymbol{\phi}}_1}}^{\rm {H}}}{\tilde {\boldsymbol{G}}_{{\rm {r}},{\rm{t}}}} \end{split} $ | (69) |
| $ \begin{split} & {\hat {\boldsymbol{G}}_{\rm{pr}}} = {\boldsymbol{G}}_{{\rm {r}},{\rm{t}}}^{\rm {H}}{{\boldsymbol{\varTheta}} _2}{{\boldsymbol{g}}_{{\rm {r}},{\rm{p}}}} = {\left( {\tilde {{{\boldsymbol{\phi}}_2}} \otimes {1_{J \times 1}}} \right) ^{\rm {H}}}{\left[ {{{\wideparen{{\boldsymbol{g}}} }_{1,{\rm{t}}}}^{\rm{T}}, \cdots ,{{\wideparen{{\boldsymbol{g}}} }_{N,{\rm{t}}}}^{\rm{T}}} \right]^{\rm{T}}} =\\ & \tilde {{{\boldsymbol{\phi}}_2}}{\left[ {{{\tilde {\boldsymbol{g}}}_{1,{\rm{t}}}}^{\rm{T}}, \cdots ,{{\tilde {\boldsymbol{g}}}_{B,{\rm{t}}}}^{\rm{T}}} \right]^{\rm{T}}} = {\tilde {{{\boldsymbol{\phi}}_2}}^{\rm {H}}}{\wideparen{{\boldsymbol{G}}} _{{\rm {r}},{\rm{p}}}} \end{split} $ | (70) |
与第4节算法类似,IRS反射单元分组算法也是基于交替优化算法,将原问题(P1) 分解为3个子问题进行迭代优化求解,直到收敛。
首先,根据等式(23) 和(70) 可将主用户传输阶段中主用户发射机到主用户接收机的最大信道增益重新表述为
| $ {\boldsymbol{G}}_{\rm{PR}}^* = {\left| {{\boldsymbol{g}}_{{\rm {t}},{\rm{p}}}^{\rm {H}} + {\wideparen{{\boldsymbol{G}}}_{{\rm {r}},{\rm{p}}}}} \right|^2} $ | (71) |
其次,令
| $ \begin{split} & {\left| {\left( {{\boldsymbol{H}}_{{\rm {s}},k}^{\rm {H}} + {\boldsymbol{H}}_{{\rm {r}},k}^{\rm {H}}{{\boldsymbol{\varTheta}} _1}{{\boldsymbol{H}}_{{\rm {s}},{\rm{r}}}}} \right) {\boldsymbol{v}}_k} \right|^2} = {\left| {\left( {{\boldsymbol{H}}_{{\rm {s}},k}^{\rm {H}} + {{\tilde {{{\boldsymbol{\phi}}_1}}}^{\rm {H}}}{{\tilde H}_{{\rm {r}},k}}} \right) {\boldsymbol{v}}_k} \right|^2} =\\ & {\rm{ Tr}}\left( {\left( {{\boldsymbol{H}}_{{\rm {s}},k}^{\rm {H}} + {{\tilde {{{\boldsymbol{\phi}}_1}}}^{\rm {H}}}{{\tilde H}_{{\rm {r}},k}}} \right) {{\boldsymbol{v}}_k}{\boldsymbol{v}}_k^{\rm {H}}{{\left( {{\boldsymbol{H}}_{{\rm {s}},k}^{\rm {H}} + {{\tilde {{{\boldsymbol{\phi}}_1}}}^{\rm {H}}}{{\tilde {\boldsymbol{H}}}_{{\rm {r}},k}}} \right) }^{\rm {H}}}} \right) =\\ & {\rm{ Tr}}\left( {\left[ \begin{gathered} \tilde {{{\boldsymbol{\phi}}_1}} \\ 1 \\ \end{gathered} \right]\left[ {\begin{array}{*{20}{c}} {{{\tilde {{{\boldsymbol{\phi}}_1}}}^{\rm {H}}}}&1 \end{array}} \right]\left[ \begin{gathered} {{\tilde {\boldsymbol{H}}}_{{\rm {r}},k}} \\ {\boldsymbol{H}}_{{\rm {s}},k}^{\rm {H}} \\ \end{gathered} \right]{{\boldsymbol{v}}_k}{\boldsymbol{v}}_k^{\rm {H}}\left[ {\tilde {\boldsymbol{H}}_{{\rm {r}},k}^{\rm {H}} {{\boldsymbol {H}}_{{\rm {s}},k}}} \right]} \right) =\\ & {\rm{ Tr}}\left( {{{\boldsymbol{Q}}_1}{{\widehat{\boldsymbol{ L}}}_k}{{\boldsymbol{V}}_k}\widehat {\boldsymbol{L}}_k^{\rm {H}}} \right) \end{split} $ | (72) |
同理可得到
| $ \begin{split} & {\left| {({\boldsymbol{G}}_{{\rm {s}},{\rm{t}}}^{\rm {H}} + {\boldsymbol{G}}_{{\rm {r}},{\rm{t}}}^{\rm {H}}{{\boldsymbol{\varTheta}} _1}{{\boldsymbol{H}}_{{\rm {s}},{\rm{r}}}}) {{\boldsymbol{v}}_k}} \right|^2} =\\ & {\rm{ Tr}}\left( {\left[ \begin{gathered} \tilde {{{\boldsymbol{\phi}}_1}} \\ 1 \\ \end{gathered} \right]\left[ {\begin{array}{*{20}{c}} {{{\tilde {{{\boldsymbol{\phi}}_1}}}^{\rm {H}}}}&1 \end{array}} \right]\left[ \begin{gathered} {{\tilde {\boldsymbol{G}}}_{{\rm {r}},{\rm{t}}}} \\ {\boldsymbol{G}}_{{\rm {s}},{\rm{t}}}^{\rm {H}} \\ \end{gathered} \right]{{\boldsymbol{v}}_k}{\boldsymbol{v}}_k^{\rm {H}}\left[ {\begin{array}{*{20}{c}} {\tilde {\boldsymbol{G}}_{{\rm {r}},{\rm{t}}}^{\rm {H}} }&{{{\boldsymbol{G}}_{{\rm {s}},{\rm{t}}}}} \end{array}} \right]} \right) =\\ & {\rm{ Tr}}\left( {{{\boldsymbol{Q}}_1}\widehat {\boldsymbol{J}}{{\boldsymbol{V}}_k}{{\widehat {\boldsymbol{J}}}^{\rm {H}}}} \right) \end{split} $ | (73) |
其中
求解(P7) 、(P10) 和(P11) 的算法实现与上文第4节类似,此处不再赘述。与此同时,可得到基于IRS反射单元分组算法的复杂度为
本节主要通过计算机仿真验证算法的性能。本文设置次用户发射机的天线数
| $ {\tilde {\boldsymbol{H}}_{{\rm {s}},{\rm{r}}}} = \sqrt {\frac{{{\beta _{{\rm {s}},{\rm{r}}}}}}{{1 + {\beta _{{\rm {s}},{\rm{r}}}}}}} \tilde {\boldsymbol{H}}_{{\rm {s}},{\rm{r}}}^{{\rm{Los}}} + \sqrt {\frac{1}{{1 + {\beta _{{\rm {s}},{\rm{r}}}}}}} \tilde {\boldsymbol{H}}_{{\rm {s}},{\rm{r}}}^{{\rm{NLos}}} $ | (74) |
式中,
(1) “上界”:交替求解去掉秩一约束的松弛问题(P7) 、问题(P10) 和问题(P11) ,以获得所提算法次用户网络的总吞吐量上界。
(2) “优化
(3) “固定
(4) “低复杂度算法(1/2) ”:IRS分组比为1/2,再进行迭代优化求解以获得次用户网络的总吞吐量。
(5) “低复杂度算法(1/4) ”:IRS分组比为1/4,再进行迭代优化求解以获得次用户网络的总吞吐量。
(6) “无IRS”:两个传输阶段的IRS相移矩阵设为全0矩阵,再进行迭代优化求解以获得次用户网络的总吞吐量。
以下结果是在200个随机生成的信道样本上进行计算机仿真后得到的平均结果。
如图4所示为次用户网络总吞吐量随主用户网络最小吞吐量阈值增大的变化趋势图。从图中可以看出,所有方案的次用户网络总吞吐量随着主用户最小吞吐量阈值的增大而下降,其中无IRS方案下降趋势最明显,其余6种方案下降趋势并不明显,这是因为随着主用户最小吞吐量阈值的增大,次用户发射机需要传输更多的能量信号给主用户发射机,从而降低了自己的传输数据性能。此外,本文所提算法的性能非常接近于上界方案,并显著优于其他5种对比方案,优化
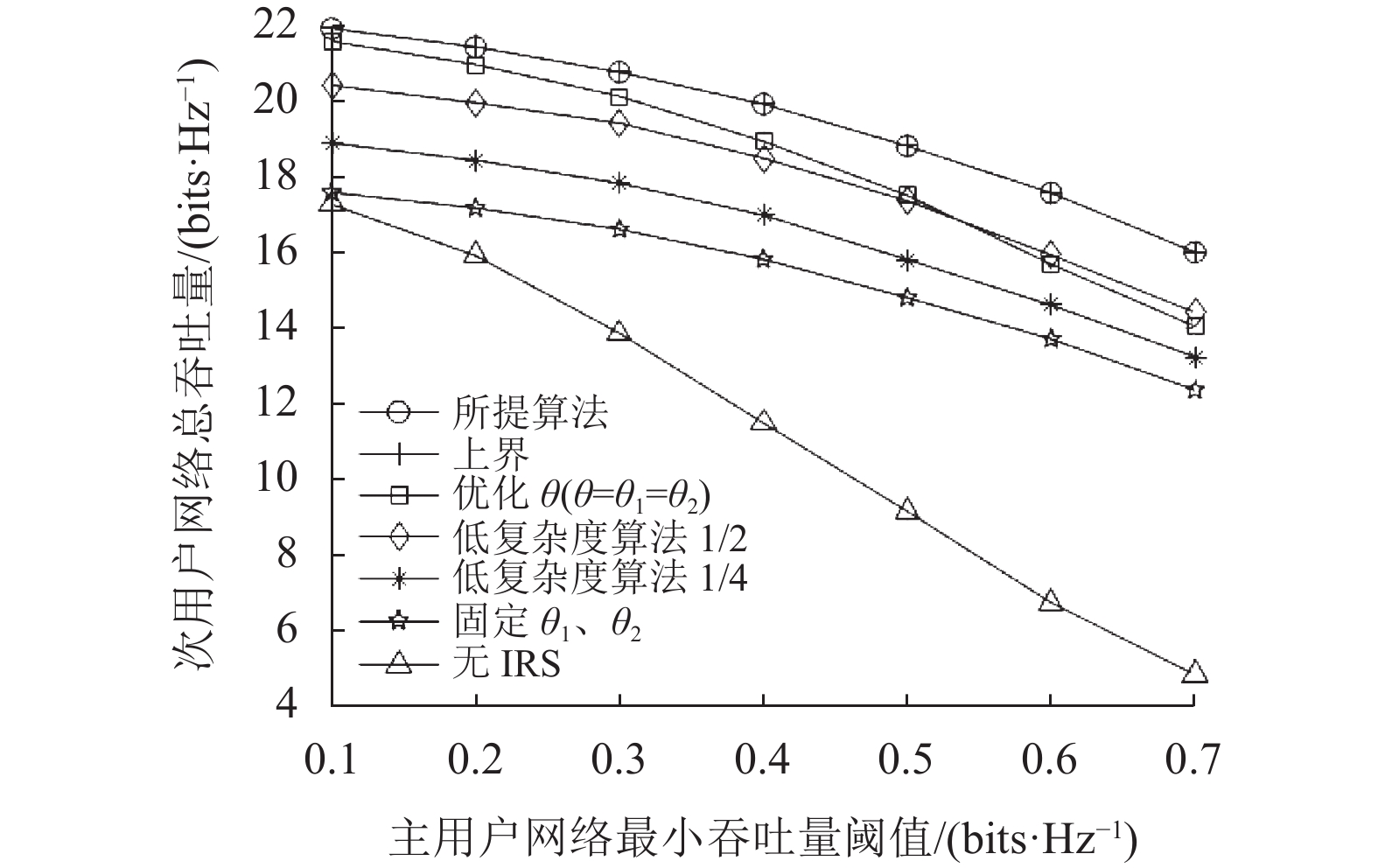
|
图 4 次用户网络总吞吐量随主用户网络最小吞吐量阈值变化的曲线 Figure 4 Curve of the total throughput of the secondary user network versus the minimum throughput threshold of the primary user network |
如图5所示为次用户网络的总吞吐量随IRS反射单元数量增加的变化趋势图。由图可知,本文所提算法非常接近于上界方案并远高于其他方案,体现出本文所提算法的优越性。除了无IRS方案的次用户网络总吞吐量随反射数量增加不变以外,其余6种方案的次用户网络总吞吐量随反射单元数量的增加而增加,这说明了部署IRS对提高系统性能是非常有效的,且随着IRS反射单元数量的增加,系统会获得更高的信道增益。此外,观察可知,两个传输时隙的IRS相移矩阵共用一个IRS相移矩阵进行相位优化的方案比固定两个传输时隙的IRS相移矩阵的方案要好,且随着反射单元数量增加,获得的信道增益越大,IRS提高系统性能的效果更明显。最后,可发现在相同的IRS反射单元数量下,所提出的低复杂度算法1/2、低复杂度算法1/4方案远高于无IRS方案,但低于本文所提算法,这表明本文所提出的低复杂度算法可以有效权衡系统性能与复杂度之间的关系。
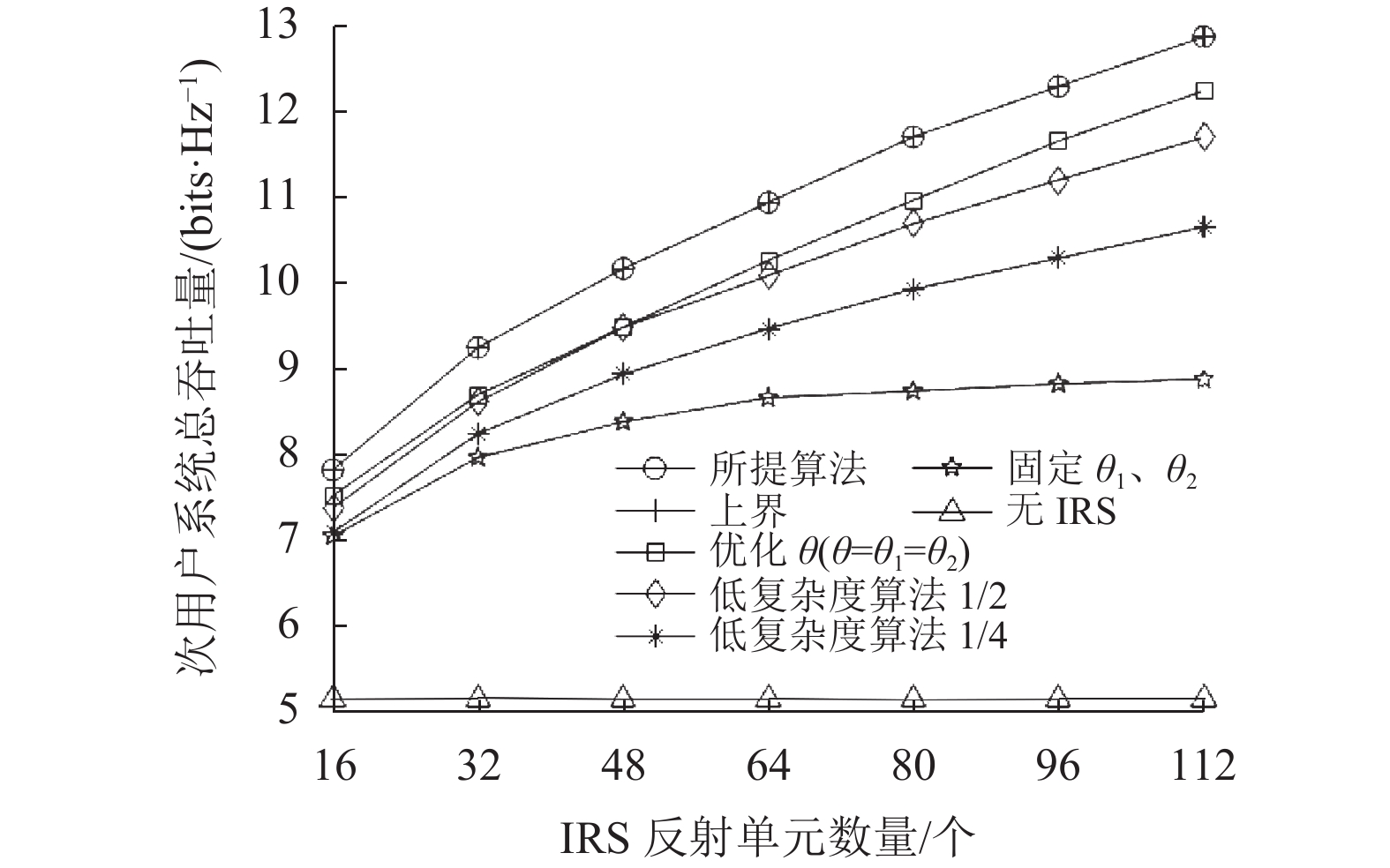
|
图 5 次用户网络总吞吐量随IRS反射单元数量变化的曲线 Figure 5 Curve of the total throughput of the secondary user network versus the number of reflective elements of the IRS. |
图6为次用户网络总吞吐量随次用户发射机的最大发射功率阈值增大的变化趋势图。从图中可以看出所有方案的次用户网络的总吞吐量随着次用户发射机最大发射功率阈值的增大而增大,其中本文所提算法的性能接近于上界方案,且显著优于其他5种方案,这说明了本文所提算法对发射波束成形、时隙时间以及两个传输时隙的IRS相移进行了合理的优化。此外,可发现随着最大发射功率阈值的增大,与无IRS方案相比,其余各方案提高总吞吐量的幅度逐渐降低,这是因为随着发射功率阈值的增大,次用户发射机带来的有源波束成形增益已经足够其满足各约束,因此通过部署IRS带来的无源增益对系统性能的提升并不显著,但却远优于无IRS方案。
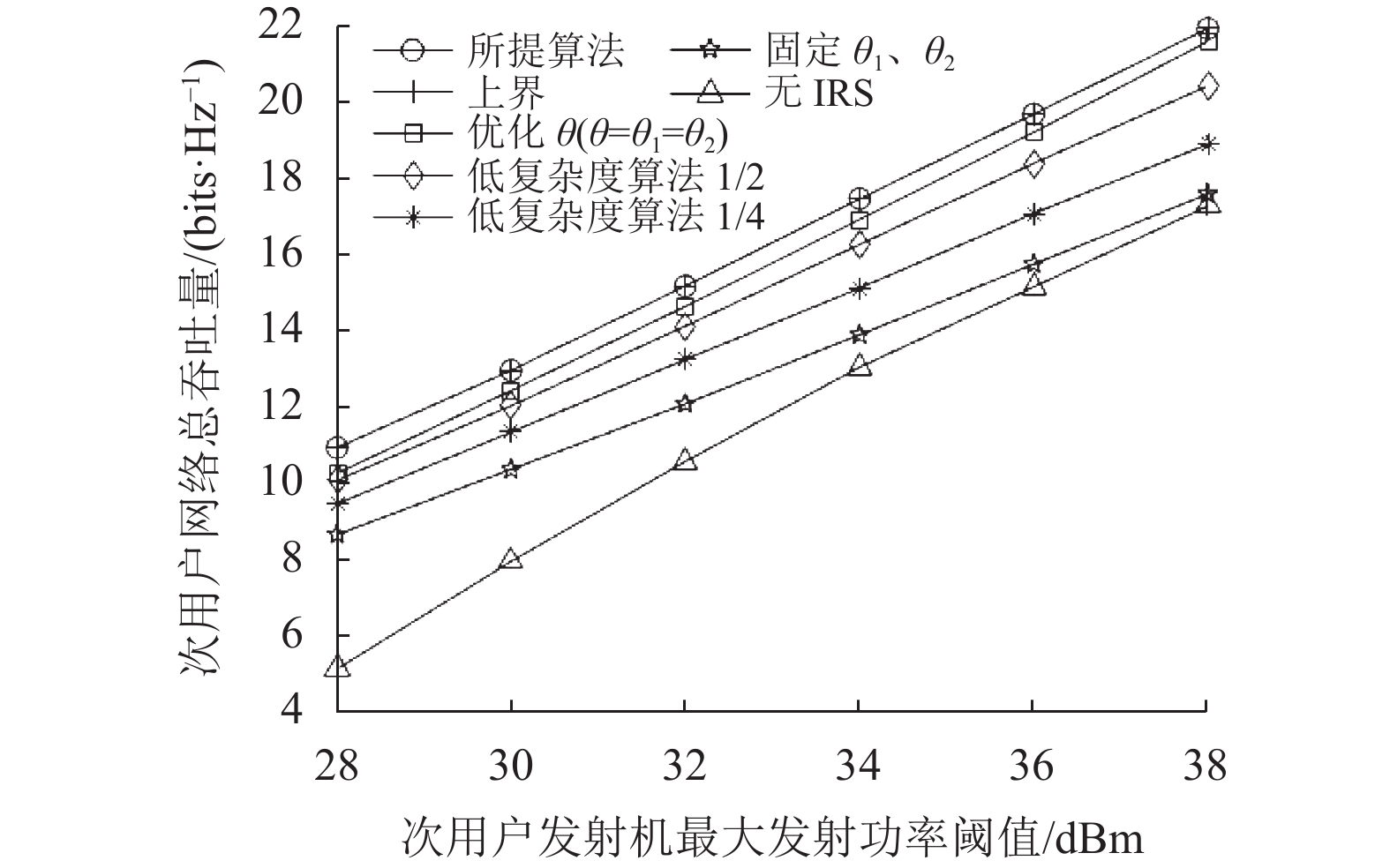
|
图 6 次用户网络总吞吐量随次用户发射机最大发射功率阈值变化的曲线 Figure 6 Curve of the total throughput of the secondary user network versus the maximum transmit power threshold of the secondary user transmitters. |
本文研究了一个IRS辅助的认知无线携能通信网络,其中次用户网络以覆盖方式与主用户网络共享频谱,次用户发射机同时为主用户发射机供能并传输自己的信息。通过联合优化次用户发射机的波束成形矢量,时隙时间和IRS的相移矩阵,最大化次用户网络的总吞吐量。针对难以直接求解的原非凸优化问题,首先通过将原问题转化为3个易于处理的子问题;其次采用引入松弛变量,一阶泰勒展开、高斯随机以及连续凸逼近等方法对各子问题进行求解;最后交替优化3个子问题求得原问题的高质量可行解。仿真结果表明,与其他基准方案相比,本文所提算法能够有效地增大次用户网络的总吞吐量。
| [1] |
WONG V W, SCHOBER R, NG D W K, et al. Key Technologies for 5G Wireless Systems [M]. Cambridge: Cambridge University Press, 2017.
|
| [2] |
DATLA D, WYGLINSKI A M, MINDEN G J. A spectrum surveying framework for dynamic spectrum access networks[J].
IEEE Transactions on Vehicular Technology, 2009, 58(8): 4158-4168.
DOI: 10.1109/TVT.2009.2021601. |
| [3] |
ZHANG W, WANG C X, GE X, et al. Enhanced 5G cognitive radio networks based on spectrum sharing and spectrum aggregation[J].
IEEE Transactions on Communications, 2018, 66(12): 6304-6316.
DOI: 10.1109/TCOMM.2018.2863385. |
| [4] |
HONG X, WANG J, WANG C X, et al. Cognitive radio in 5G: a perspective on energy-spectral efficiency trade-off[J].
IEEE Communications Magazine, 2014, 52(7): 46-53.
DOI: 10.1109/MCOM.2014.6852082. |
| [5] |
XIONG T, YAO Y D, REN Y, et al. Multiband spectrum sensing in cognitive radio networks with secondary user hardware limitation: random and adaptive spectrum sensing strategies[J].
IEEE Transactions on Wireless Communications, 2018, 17(5): 3018-3029.
DOI: 10.1109/TWC.2018.2805729. |
| [6] |
TORLAK M, NAMGOONG W. Sub-nyquist sampling receiver for overlay cognitive radio users[J].
IEEE Transactions on Signal Processing, 2018, 66(16): 4160-4169.
DOI: 10.1109/TSP.2018.2839611. |
| [7] |
TSENG F H, CHAO H, WANG J. Ultra-dense small cell planning using cognitive radio network toward 5G[J].
IEEE Wireless Communications, 2015, 22(6): 76-83.
DOI: 10.1109/MWC.2015.7368827. |
| [8] |
WU Q, ZHANG G, NG D W K, et al. Generalized wireless-powered communications: When to activate wireless power transfer?[J].
IEEE Transactions on Vehicular Technology, 2019, 68(8): 8243-8248.
DOI: 10.1109/TVT.2019.2924051. |
| [9] |
ZHANG G, XU J, WU Q, et al. Wireless powered cooperative jamming for secure OFDM system[J].
IEEE Transactions on Vehicular Technology, 2017, 67(2): 1331-1346.
|
| [10] |
ZHANG R, HO C K. MIMO broadcasting for simultaneous wireless information and power transfer[J].
IEEE Transactions on Wireless Communications, 2013, 12(5): 1989-2001.
DOI: 10.1109/TWC.2013.031813.120224. |
| [11] |
LEE S, ZHANG R, HUANG K. Opportunistic wireless energy harvesting in cognitive radio networks[J].
IEEE Transactions on Wireless Communications, 2013, 12(9): 4788-4799.
DOI: 10.1109/TWC.2013.072613.130323. |
| [12] |
YIN S, ZHANG E, QU Z, et al. Optimal cooperation strategy in cognitive radio systems with energy harvesting[J].
IEEE Transactions on Wireless Communications, 2014, 13(9): 4693-4707.
DOI: 10.1109/TWC.2014.2322972. |
| [13] |
ZHAI C, LIU J, LAN P, et al. Strive for the spectrum sharing by transferring energy and relaying data for the primary user[J].
Transactions on Emerging Telecommunications Technologies, 2017, 28(3): e2966.
DOI: 10.1002/ett.2966. |
| [14] |
LU X, XU W, LI S, et al. Simultaneous information and power transfer for relay-assisted cognitive radio networks[C]//2014 IEEE International Conference on Communications Workshops. Sydney: IEEE, 2014: 331-336.
|
| [15] |
WU Q, ZHANG R. Weighted sum power maximization for intelligent reflecting surface aided SWIPT[J].
IEEE Wireless Communications Letters, 2019, 9(5): 586-590.
|
| [16] |
YUAN J, LIANG Y C, JOUNG J, et al. Intelligent reflecting surface (IRS) -enhanced cognitive radio system[C]//ICC 2020-2020 IEEE International Conference on Communications. Dublin: IEEE, 2020: 1-6.
|
| [17] |
XU D, YU X, SCHOBER R. Resource allocation for intelligent reflecting surface-assisted cognitive radio networks[C]//2020 IEEE 21st International Workshop on Signal in Wireless Communications (SPAWC) . Atlanta: IEEE, 2020: 1-5.
|
| [18] |
NTOUGIAS K, KRIKIDIS I. Interference-Constrained IRS-aided SWIPT[C]//2021 IEEE 22nd International Workshop on Signal Processing Advances in Wireless Communications (SPAWC) . Lucca: IEEE, 2021: 116-120.
|
| [19] |
CUI M, ZHANG G, ZHANG R. Secure wireless communication via intelligent reflecting surface[J].
IEEE Wireless Communications Letters, 2019, 8(5): 1410-1414.
DOI: 10.1109/LWC.2019.2919685. |
| [20] |
ZHANG L, WANG Y, TAO W, et al. Intelligent reflecting surface aided MIMO cognitive radio systems[J].
IEEE Transactions on Vehicular Technology, 2020, 69(10): 11445-11457.
DOI: 10.1109/TVT.2020.3011308. |
| [21] |
ZHONG C, CUI M, ZHANG G, et al. Deep reinforcement learning-based optimization for IRS-assisted cognitive radio systems[J].
IEEE Transactions on Communications, 2022, 70(6): 3849-3864.
DOI: 10.1109/TCOMM.2022.3171837. |
| [22] |
ZHANG D, WU Q, CUI M, et al. Throughput maximization for IRS-assisted wireless powered hybrid NOMA and TDMA[J].
IEEE Wireless Communications Letters, 2021, 10(9): 1944-1948.
DOI: 10.1109/LWC.2021.3087495. |
| [23] |
WU Q, ZHANG R. Intelligent reflecting surface enhanced wireless network via joint active and passive beamforming[J].
IEEE Transactions on Wireless Communications, 2019, 18(11): 5394-5409.
DOI: 10.1109/TWC.2019.2936025. |
| [24] |
LUO Z Q, MA W K, SO A M C, et al. Semidefinite relaxation of quadratic optimization problems[J].
IEEE Signal Processing Magazine, 2010, 27(3): 20-34.
DOI: 10.1109/MSP.2010.936019. |
| [25] |
YYANG Y, ZHENG B, ZHANG S, et al. Intelligent reflecting surface meets OFDM: Protocol design and rate maximization[J].
IEEE Transactions on Communications, 2020, 68(7): 4522-4535.
DOI: 10.1109/TCOMM.2020.2981458. |
| [26] |
XU D, YU X, SUN Y, et al. Resource allocation for IRS-assisted full-duplex cognitive radio systems[J].
IEEE Transactions on Communications, 2020, 68(12): 7376-7394.
DOI: 10.1109/TCOMM.2020.3020838. |
 2024, Vol. 41
2024, Vol. 41

