锚索或内支撑(之后统称为支撑)与围护结构(如支护桩或地连墙等,之后用支护桩代表)组成的桩锚或桩撑式支护体系广泛应用于深基坑的支护工程中。该类支护体系施工过程的主要工况为:开挖基坑至拟设置支撑位置→设置支撑(对锚索还包括施加预应力)→继续开挖→继续设撑→所有支撑设置完毕→开挖至坑底设计高程等。
目前,考虑上述施工过程的基坑分析方法大致可分为弹性地基梁法[1-3]和有限单元法[4-8]两类,其中后者不仅能够模拟基坑的开挖、设撑等施工工况,而且还能反映基坑开挖对周围环境的影响,但计算方法比较复杂。
1 现有弹性地基梁分析法及其问题弹性地基梁法是将支护结构当作竖向放置的弹性地基梁,其外侧的水平向作用荷载为已知的主动土压力q(z),一般用朗肯土压力理论确定;内侧坑底以下土体作用的抗力p(x,z)通常按m法确定;支撑的作用力用线性弹簧模型确定。将上述作用力施加于梁(支护结构)上后,通过求解梁的挠曲微分方程,即可确定支护体系的变形及内力。与有限元法相比,该类方法计算简单,易于编程[9]。
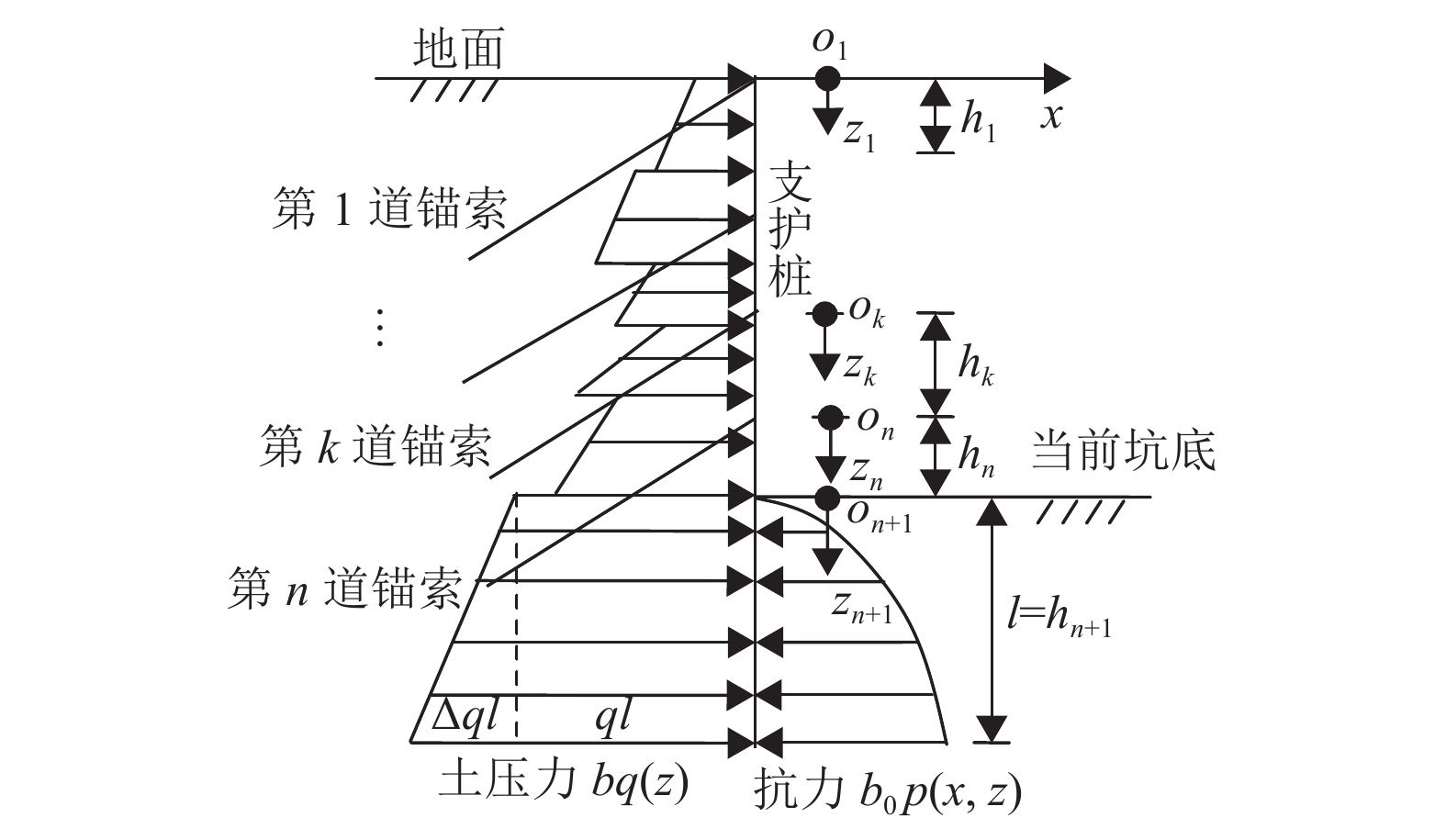
如图1所示,设某施工工况结束后当前坑底以上共设有n道支撑(锚索),则该类方法的主要计算步骤如下[1-2]:
|
图 1 弹性地基梁法对应某工况的计算模型 Figure 1 Model for some case by MBEF |
(1) 以每道支撑及坑底断面为分界面,将整个桩分割成(n+1)个桩段。即桩顶至第1道支撑之间为第1段,第1与第2道支撑之间为第2段,······,坑底以上至最后一道支撑之间为第n段,坑底以下至桩端之间为第(n+1)段。设第k(k=1~n+1)段的长度为hk,当前坑底以下最后一段的长度为hn+1=l。
(2) 以各分界面为坐标原点,各自建立一个局部坐标系ok-zk (k=1~n+1,0≤zk≤hk),其中zk沿桩中心竖直向下为正。
(3) 对第k个桩段,设zk处支护桩的水平位移(挠度)为
| $ EI \frac{{{{\rm{d}}^4}{x_{{z_k}}}}}{{{\rm{d}}\,{z_k^4}}} = bq{\kern 1pt} \,({z_k}) ,(k=1 \sim n) $ | (1) |
| $ EI \frac{{{{\rm{d}}^4}{x_{{z_k}}}}}{{{\rm{d}}\,{z_k^4}}} = - {b_0}p\,(x,{z_k}) + bq{\kern 1pt} \,({z_k}) ,(k=n+1) $ | (2) |
式中:EI为桩身抗挠曲刚度,E和I分别为桩的弹性模量和截面惯性矩;b和b0分别为荷载计算宽度和抗力计算宽度。
(4) 逐桩段求解方程(1)和(2),然后利用上、下桩段与支撑相交的分界面处的变形连续条件和受力平衡条件,推导待定参数方程并求解,之后再确定桩身位移和内力以及各道支撑力。
由于n个桩段必有(n−1)个交界面,每个交界面处有2个位移(水平位移和转角)和2个内力(弯矩和剪力)连续方程;此外,整个支护桩的桩顶和桩端通常也有4个已知边界条件(如桩顶弯矩和剪力已知、桩端自由时弯矩和剪力均为零等),这样,将共有4(n−1)+4=4n个已知条件;另一方面,由于求解4阶微分方程(1)和(2)必有4个积分常数,因此每个桩段将有4个待定参数{a}={a1 a2 a3 a4}T,n个桩段将有4n个待定参数。这样,待定参数与已知条件数相同,利用交界面处位移连续和受力平衡条件推出待定参数{a}方程并求解后,就可以确定本次施工结束后的桩身位移和内力以及各道支撑力。
(5) 对其后的每个开挖或加撑工况,重复上述计算步骤,直至完成所有工况。
从上述计算过程不难看出,该弹性地基梁法具有以下缺陷:(1) 计算过程繁杂,没有统一的计算公式。分析每个施工工况时,都需重新划分桩段并推导相应的待定参数方程,尚未形成一个统一的计算公式。(2) 待定参数方程有4n个未知数,求解相对不易。
2 弹性地基梁通用分析法 2.1 支护桩挠曲方程的求解如图1所示,设深度z处桩截面的水平位移(挠度)xz、转角Φz、弯矩Mz和剪力Qz构成的向量为{δz}={xz Φz Mz Qz}T,并且规定xz和Qz沿x轴正方向为正,Φz逆时针方向为正,Mz使桩的坑外侧纤维受拉时为正。
对当前坑底以上长度为hk的第k(1≤k≤n)个桩段,求解微分方程(1)可得
| $ \{{\boldsymbol{\delta }}_{z}\}=[{\boldsymbol{H}}(z) ]\{{\boldsymbol{a}}^{(k) }\}+\{{\boldsymbol{S}}(z) \}, (0 \leqslant z \leqslant h_{k}) $ | (3) |
式中:
| $ [{\boldsymbol{H}}(z) ] = \left[ {\begin{array}{*{20}{c}} 1&z&{{z^2}}&{{z^3}} \\ 0&1&{2z}&{3{z^2}} \\ 0&0&{2EI}&{6EI{\kern 1pt} z} \\ 0&0&0&{6EI} \end{array}} \right] ,\{ {\boldsymbol{S}}(z) \} = b\left\{ {\begin{array}{*{20}{c}} {\dfrac{{{X_q}(z) }}{{EI}}} \\ {\dfrac{{{\varPhi _q}(z) }}{{EI}}} \\ {{M_q}(z) } \\ {{Q_q}(z) } \end{array}} \right\} $ | (4) |
{S(z)}仅为第k桩段顶ok至z之间桩外侧分布荷载q(z)在深度z处产生的荷载函数,可按式(5)确定:
| $\tag{5{\rm{a}}} Q(z) = \int_{\,0}^{\,z} {\;q(z) \,{\rm{d}}z} $ |
| $\tag{5{\rm{b}}} M\,(z) = \int {\int_{\;0}^{\;z} {\,q(z) \,{{({\rm{d}}z) }^2} = \int_{\;0}^{\;z} {\,q(\xi ) (z - \xi ) \,{\rm{d}}\xi \quad } } } $ |
| $\tag{5{\rm{c}}} \varPhi (z) = \int {\int {\int_{\;0}^{\;z} {\;q(z) {{({\rm{d}}z) }^3} = \frac{1}{2}\int_{\;0}^{\;z} {\,q(\xi ) {{(z - \xi ) }^2}\,{\rm{d}}\xi } } } } $ |
| $\tag{5{\rm{d}}} X(z) = \int {\int {\int {\int_{\;0}^{\;z} {q(z) {{({\rm{d}}z) }^4} = \frac{1}{6}\int_{\;0}^{\;z} {q(\xi ) {{(z - \xi ) }^3}{\rm{d}}\xi } } } } } $ |
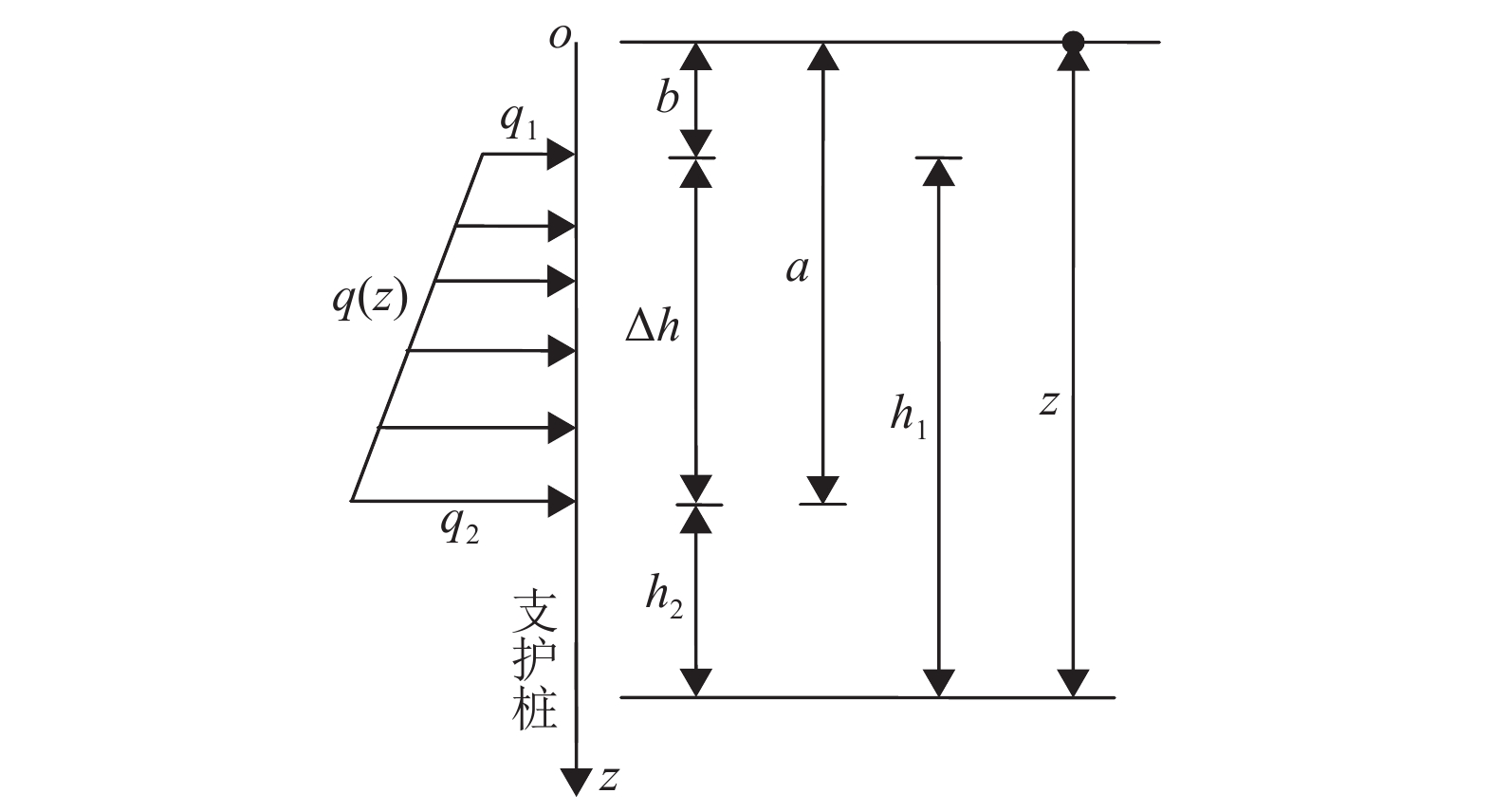
鉴于土压力q(z)一般随深度z呈分段线性分布(如图2所示),则利用式(5)可得:
|
图 2 分段荷载q(z) Figure 2 Segmented load q(z) |
(1) 如果0<z<b,因q(z)=0,故Xq(z)=Φq(z)= Mq(z)=Qq(z)=0。
(2) 如果b≤z≤a,则有
| $\tag{6{\rm{a}}} {Q_q}(z) = \Delta \,{h_z}[{q_1} + {q_2}(z) ]/2 $ |
| $\tag{6{\rm{b}}} {M_q}(z) = \Delta \;h_z^2[2{q_1} + {q_2}(z) ]/6 $ |
| $\tag{6{\rm{c}}} {\varPhi _q}\,(z) = \Delta \,h_z^3[3{q_1} + {q_2}(z) ]/24 $ |
| $\tag{6{\rm{d}}} {X_q}(z) = \Delta \,h_z^4[4{q_1} + {q_2}(z) ]/120 $ |
式中:
(3) 如果a<z≤a+h2,则有
| $\tag{7{\rm{a}}} Q_{q}(z) =\Delta h(q_{1}+q_{2}) /2 $ |
| $\tag{7{\rm{b}}} M_{q}(z) =\Delta h(q_{1}H_{1}+q_{2}H_{2}) /6 $ |
| $\tag{7{\rm{c}}} \varPhi_{q}(z) =\Delta h(q_{1}H_{3}+q_{2}H_{4}) /24 $ |
| $\tag{7{\rm{d}}} X_{q}(z) =\Delta h(q_{1}H_{5}+q_{2}H_{6}) /120 $ |
式中:H1=2h1+h2,H2=h1+2h2,H3=
另一方面,对当前坑底以下的第k=n+1个桩段,方程(2)中的抗力p(x,z)按m法确定,即
| $ p(x,z) =mzx_{z} $ | (8) |
式中:m为地基水平抗力系数的比例系数。此外,当坑外土压力按式(9)线性分布时,可求得该桩段挠曲方程(2)的解为式(10)[10]。
| $ q(z) =q_{l}+z\Delta q_{l}/l $ | (9) |
| $ \{{\boldsymbol{\delta }}_{z}\}=[{\boldsymbol{T}}(z) ] \{{\boldsymbol{\delta }}_{h0}\}+\{{\boldsymbol{R}}(z) \}, (0 \leqslant z \leqslant l) $ | (10) |
式中:
| $\tag{11{\rm{a}}} \begin{aligned}& [{\boldsymbol{T}}(z) ] = \left[ {\begin{array}{*{20}{c}} {{G_{11}}(z) }&{\dfrac{{{G_{21}}(z) }}{\alpha }}&{\dfrac{{{G_{31}}(z) }}{{{\alpha ^2}EI}}}&{\dfrac{{{G_{41}}(z) }}{{{\alpha ^3}EI}}} \\ {\alpha {\kern 1pt} {G_{12}}(z) }&{G{}_{22}(z) }&{\dfrac{{{G_{32}}(z) }}{{\alpha EI}}}&{\dfrac{{{G_{42}}(z) }}{{{\alpha ^2}EI}}} \\ {{\alpha ^2}{\kern 1pt} EI{G_{13}}(z) }&{\alpha {\kern 1pt} EI{G_{23}}(z) }&{{G_{33}}(z) }&{\dfrac{{{G_{43}}(z) }}{\alpha }} \\ {{\alpha ^3}{\kern 1pt} EI{G_{14}}(z) }&{{\alpha ^2}{\kern 1pt} EI{G_{24}}(z) }&{\alpha {\kern 1pt} {G_{34}}(z) }&{{G_{44}}(z) } \end{array}} \right] \\& {} \end{aligned}$ |
| $\tag{11{\rm{b}}} \{ {\boldsymbol{R}}(z) \} = \dfrac{{b{q_l}}}{\alpha }\left\{ {\begin{array}{*{20}{c}} {\dfrac{{{G_{51}}(z) }}{{{\alpha ^3}EI}}} \\ {\dfrac{{{G_{52}}(z) }}{{{\alpha ^2}EI}}} \\ {\dfrac{{{G_{53}}(z) }}{\alpha }} \\ {{G_{54}}(z) } \end{array}} \right\} + \dfrac{{b\Delta {\kern 1pt} \,{q_l}}}{{{\alpha ^2}l}}\left\{ {\begin{array}{*{20}{c}} {\dfrac{{{G_{61}}(z) }}{{{\alpha ^3}EI}}} \\ {\dfrac{{{G_{62}}(z) }}{{{\alpha ^2}EI}}} \\ {\dfrac{{{G_{63}}(z) }}{\alpha }} \\ {{G_{64}}(z) } \end{array}} \right\} $ |
系数Gij(z)(i=1~6,j=1~4)可统一按式(12)计算:
| $\tag{12{\rm{a}}} {G}_{ij}(z) ={G}_{ij0}(z) +{\displaystyle \sum _{k=1}^{\infty }{(-1) }^{k}\frac{{\displaystyle \prod _{s=k}^{1}(5s+i-j)}}{(5k+i-j) !}}{(\overline{z}) }^{(5k+i-j) } $ |
| $\tag{12{\rm{b}}} {G_{0\,i\,j}}(z) = \left\{ {\begin{array}{*{20}{c}} \dfrac{{{{(\bar z) }^{i - j}}}}{{(i - j) \,!}}&(i \gt j) \\ { 1 }& {(i = j) } \\ { 0 }& {(i \lt j) } \end{array}} \right.$ |
式中:
| $ \{{\boldsymbol{\delta }}_{h0}\}=[{\boldsymbol{V}}(l) ]\{{\boldsymbol{U}}\}-\{{\boldsymbol{W}}(l) \} $ | (13) |
式中:
| $ \{{\boldsymbol{W}}(l) \} = [{{\boldsymbol{T}}_s}(l) ]\{ {\boldsymbol{R}}(l) \},[{{\boldsymbol{T}}_s}(l) ] = {[{\boldsymbol{T}}(l) ]^{ - 1}} $ | (14) |
{U}={U1 U2}T为桩端的待求参数;[V(l)]为4×2矩阵,它们根据不同桩端约束条件取值为
(1) 桩端自由时:{U}={U1 U2}T={xG ΦG}T且
| $\tag{15{\rm{a}}} [{\boldsymbol{V}}(l) ] = \left[ {\begin{array}{*{20}{c}} {{V_{11}}}&{{V_{12}}} \\ {{V_{21}}}&{{V_{22}}} \\ {{V_{31}}}&{{V_{32}}} \\ {{V_{41}}}&{{V_{42}}} \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} {{T_{s11}}}&{{T_{s12}}} \\ {{T_{s21}}}&{{T_{s22}}} \\ {{T_{s31}}}&{{T_{s32}}} \\ {{T_{s41}}}&{{T_{s42}}} \end{array}} \right] $ |
(2) 桩端固定时: {U}={U1 U2}T={MG QG}T且
| $\tag{15{\rm{b}}} [{\boldsymbol{V}}(l) ] = \left[ {\begin{array}{*{20}{c}} {{V_{11}}}&{{V_{12}}} \\ {{V_{21}}}&{{V_{22}}} \\ {{V_{31}}}&{{V_{32}}} \\ {{V_{41}}}&{{V_{42}}} \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} {{T_{s13}}}&{{T_{s14}}} \\ {{T_{s23}}}&{{T_{s24}}} \\ {{T_{s33}}}&{{T_{s34}}} \\ {{T_{s43}}}&{{T_{s44}}} \end{array}} \right] $ |
(3) 桩端铰支时: {U}={U1 U2}T={ΦG QG}T且
| $\tag{15{\rm{c}}} [{\boldsymbol{V}}(l) ] = \left[ {\begin{array}{*{20}{c}} {{V_{11}}}&{{V_{12}}} \\ {{V_{21}}}&{{V_{22}}} \\ {{V_{31}}}&{{V_{32}}} \\ {{V_{41}}}&{{V_{42}}} \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} {{T_{s12}}}&{{T_{s14}}} \\ {{T_{s22}}}&{{T_{s24}}} \\ {{T_{s32}}}&{{T_{s34}}} \\ {{T_{s42}}}&{{T_{s44}}} \end{array}} \right] $ |
式中:Tsij为矩阵[Ts(l)]中的第i、j个元素。
2.2 各桩段待定参数之间的递推关系如图1所示,设某工况结束后坑底以上共设有n道锚索,则第k道锚索的拉力Rk可按式(16)确定:
| $ R_{k}=F_{k}+ K_{k} \cos \beta _{k}(u_{k}-u_{k0}) $ | (16) |
式中:Fk为第k道锚索施加的预应力;βk为其入射倾角;Kk为刚度系数;uk0为预应力施加完成时的水平初始位移;uk为当前时刻的水平位移。值得注意的是,如果第k道是水平内支撑(通常无需施加预应力),则其支撑力Rk仍可按式(16)确定,只不过应当令βk=0和Fk=0。
从式(3)可知,对坑底以上的每一个桩段,都有4个待定参数{a}={a1 a2 a3 a4}T。但相邻两个桩段的待定参数可以利用它们在交界处的位移连续条件和内力平衡条件互为递推确定。
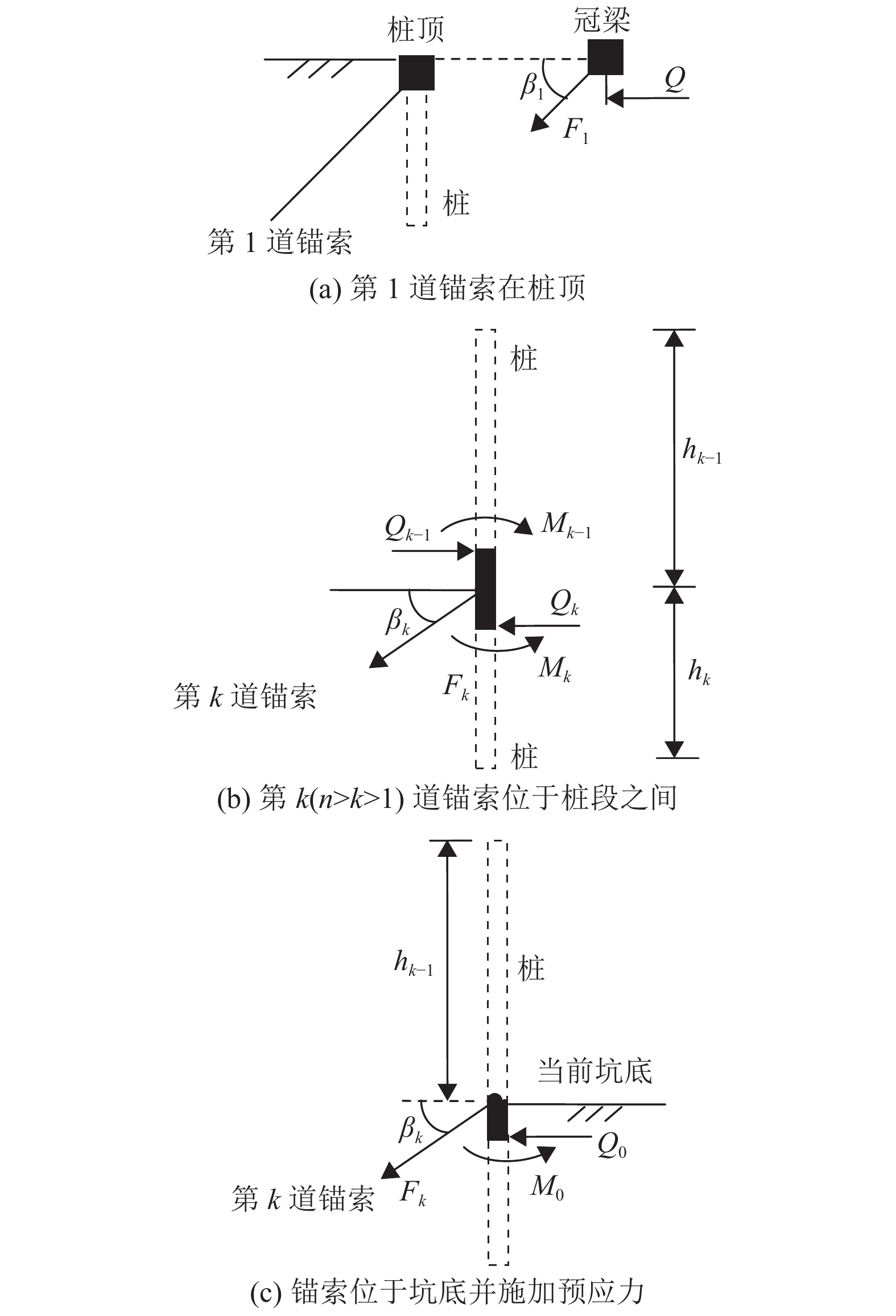
另一方面,从图1也不难看出,支撑与相邻桩段交界面的基本连接形式可归纳为图3所示的3种。有鉴于此,以下也只讨论这3种形式下相邻桩段间待定参数的递推公式。
|
图 3 锚索(支撑)与桩的3种基本连接形式 Figure 3 Three basic connection forms between support and pile-segment |
形式1:第1道支撑(锚索)交于桩顶。
如图3(a),设第1道锚索设置于z=0的桩顶,利用位移和内力连续条件及式(3)和式(16)有
| $ {{\{ }}{{\boldsymbol{a}}^{{{(1) }}}}{{\} }} = [{{\boldsymbol{C}}^{(1) }}]\;\left\{ {\begin{array}{*{20}{c}} {a_1^{(1) }} \\ {a_2^{(1) }} \end{array}} \right\} + \{ {{\boldsymbol{D}}^{(1) }}\} $ | (18) |
式中:
| $ [{{\boldsymbol{C}}^{(1) }}] = \left[ {\begin{array}{*{20}{c}} 1&0 \\ 0&1 \\ 0&0 \\ { - {\gamma _1}}&0 \end{array}} \right] ,\;\;\;\{ {{\boldsymbol{D}}^{(1) }}\} = \left\{ {\begin{array}{*{20}{c}} 0 \\ 0 \\ 0 \\ {{\gamma _1}{u_{10}} - {\rho _1}} \end{array}} \right\} $ | (19) |
式中:γ1=K1cos2β1/6EI,ρ1=F1cos β1/6EI。特别地,如果桩顶没有支撑(锚索),为便于计算,可在桩顶虚拟一道支撑,但应取γ1=ρ1=0。这样简单处理后,坑底以上桩段数就与支撑道数相同了。
形式2:支撑(锚索)位于中间桩段。
如图3(b)所示,设与第k道锚索相连的上、下桩段的长度分别为hk−1和hk,利用位移连续条件和内力平衡条件及式(3)和式(16)可得
| $ \{{\boldsymbol{a}}^{(k) }\}= [{\boldsymbol{C}}^{(k) }] \{{\boldsymbol{a}}^{(k-1) }\}+[D^{(k) }] ,(k > 1) $ | (20) |
式中:{a(1)}见式(18);
| $\tag{21{\rm{a}}} [{{\boldsymbol{C}}^{(k) }}]\; = \left[ {\begin{array}{*{20}{c}} 1&{{h_{k - 1}}}&{h_{k - 1}^2}&{h_{k - 1}^3} \\ 0&1&{2{h_{k - 1}}}&{3h_{k - 1}^2} \\ 0&0&1&{3{h_{k - 1}}} \\ { - {\gamma _k}}&{ - {\gamma _k}\,{h_{k - 1}}}&{ - {\gamma _k}\,h_{k - 1}^2}&{1 - {\gamma _k}\,h_{k - 1}^3} \end{array}} \right] $ |
| $\tag{21{\rm{b}}} \{ {{\boldsymbol{D}}^{(k) }}\} = \left\{ {\begin{array}{*{20}{c}} {\dfrac{{bX({h_{k - 1}}) }}{{EI}}} \\ {\dfrac{{b\varPhi ({h_{k - 1}}) }}{{EI}}} \\ {\dfrac{{bM({h_{k - 1}}) }}{{2EI}}} \\ {\dfrac{{bQ({h_{k - 1}}) }}{{6EI}} - \dfrac{{{\kern 1pt} bX({h_{k - 1}}) }}{{EI}}{\gamma _k} + {\delta _k}} \end{array}} \right\} $ |
式中:γk=Kkcos2βk/6EI,ρk=Fkcosβk/6EI,δk=γkuk0−ρk。
形式3:支撑(锚索)位于坑底。
如图3(c)所示,设当前坑底与第k道锚索相连,则根据该处桩身位移连续条件和内力平衡条件及式(3)、式(13)和式(16)可得
| $\tag{22{\rm{a}}} [{\boldsymbol{H}}({z_{k - 1}}) ]\{ {{\boldsymbol{a}}^{(k - 1) }}\} + \{ {\boldsymbol{S}}({z_{k - 1}}) \} = [{\boldsymbol{V}}]\{ U\} - (\,\{ {\boldsymbol{W}}(l) \} + \{ \Delta \,{\boldsymbol{W}}\} \,) $ |
式中:
| $\tag{22{\rm{b}}} \{\Delta {\boldsymbol{W}}\}=\{0\;\; 0 \;\;0\;\; F_{k}\cos \beta _{k}\}^{{\rm{T}}} $ |
在运用式(18)~(21)时应当注意:若该支撑(锚索)当前工况是施加预应力,则应令式中的刚度系数Kk=0;反之,若非施加预应力,则应令Fk=0。
2.3 确定待定参数方程对坑底以上全部n桩段采用递推公式(20)、对坑底以下桩段采用式(10)以及坑底截面处桩身位移和内力连续性条件,即可得到待定参数方程(23):
| $ [{\boldsymbol{A}}]\{{\boldsymbol{X}}\}=\{{\boldsymbol{B}}\} $ | (23) |
式中:
| $ [{\boldsymbol{A}}] = [ {\boldsymbol{E}}{-{\boldsymbol{V}}} ] = \left[ {\begin{array}{*{20}{c}} {{E_{11}}}&{{E_{12}}}&{ - {V_{11}}}&{ - {V_{12}}} \\ {{E_{21}}}&{{E_{22}}}&{ - {V_{21}}}&{ - {V_{22}}} \\ {{E_{31}}}&{{E_{32}}}&{ - {V_{31}}}&{ - {V_{32}}} \\ {{E_{41}}}&{{E_{42}}}&{ - {V_{41}}}&{ - {V_{42}}} \end{array}} \right]\, $ | (24) |
| $\tag{25{\rm{a}}} {[{\boldsymbol{E}}]_{4 \times 2}} = [{\boldsymbol{H}}({h_n}) ]\prod\limits_{k = n}^1 {[{{\boldsymbol{C}}^{(k) }}]} $ |
| $\tag{25{\rm{b}}} \begin{split} &{\{ {\boldsymbol{B}}\} _{4 \times 1}} = - \{ {\boldsymbol{W}}(l) \} - \{ {\boldsymbol{S}}({h_n}) \} - \\ &[{\boldsymbol{H}}({h_n}) ]\,\left( {[{{\boldsymbol{D}}^{(n) }}] + \sum\limits_{j = 1}^{n - 1} {\prod\limits_{p = n}^{j + 1} {[{{\boldsymbol{C}}^{(p) }}]\,[{{\boldsymbol{D}}^{(j) }}]\,} } } \right) \end{split} $ |
式中:Vi j为式(15)中矩阵[V(l)]内的第i、j个元素;而Eij为矩阵[E]内的第i、j个元素。应当注意:(1) 式(25b)中圆括号“( · )”内求和项只有当n>1时才存在;(2) 当基坑未开挖就对桩顶锚索施加预应力时,由式(10)可知,式(25)应替换为如下式(26)。
| $ [{\boldsymbol{E}}] = \left[ {\begin{array}{*{20}{c}} 1&0 \\ 0&1 \\ 0&0 \\ 0&0 \end{array}} \right],\;\;\; [{\boldsymbol{B}}] = \left\{ {\begin{array}{*{20}{c}} 0 \\ 0 \\ 0 \\ {{F_{1}}\cos {\beta _1}} \end{array}} \right\} $ | (26) |
方程(23)仅包含4个待定参数,它与之前包含4n个待定参数的传统方法相比,显然易于求解。
2.4 支护体系的变形和受力分析一旦求解方程(23)得到4个待定参数
(1) 根据支护体系的开挖和设撑情况,确定总的施工工况数以及支护结构的抗弯刚度EI。
特别注意:如果实际工程的桩顶没有支撑,为便于计算,可在桩顶虚拟一道支撑,但应取对应参数为零(如K1=F1=β1=0)。
(2) 对某工况,确定以下数据:
① 当前基坑深度h、坑底以下桩长l及桩长范围内土的抗力系数m、桩的变形系数α;坑底以上桩段数(支撑道数)n、第k(k=1~n)道支撑的刚度系数Kk、施加的预应力Fk和倾角βk;作用在桩外侧的土压力q(z)。
② 对坑底以下桩段:首先根据
③ 对当前坑底以上第k(k=1~n)桩段,计算z=hk处的相关矩阵。包括:根据q(z)和式(4)确定荷载函数{S(hk)};由式(19)和式(21)分别确定[C(k)]和[D(k)];依据式(4)确定[H(hn)]。
④ 由式(24)和(25)确定待定参数方程(23)中的矩阵[A]和{B},之后求解方程(23)得到4个参数{X}= {a1(k) a2(k) U1 U2}T。
⑤ 根据式(16)确定各道支撑力R。
⑥ 利用式(3),确定当前坑底以上第k(k=1~n)桩段各截面的位移和内力。
⑦ 利用式(10)确定坑底下桩段的位移和内力。
(3) 对其他工况,重复上述过程,直至结束。
显然,与现有的弹性地基梁分段法相比,本文所提方法具有如下优点:(1) 能够模拟桩锚(撑)式支护基坑开挖及设撑的全过程;(2) 对施工过程中的任意工况,使用统一的计算方法和计算公式。
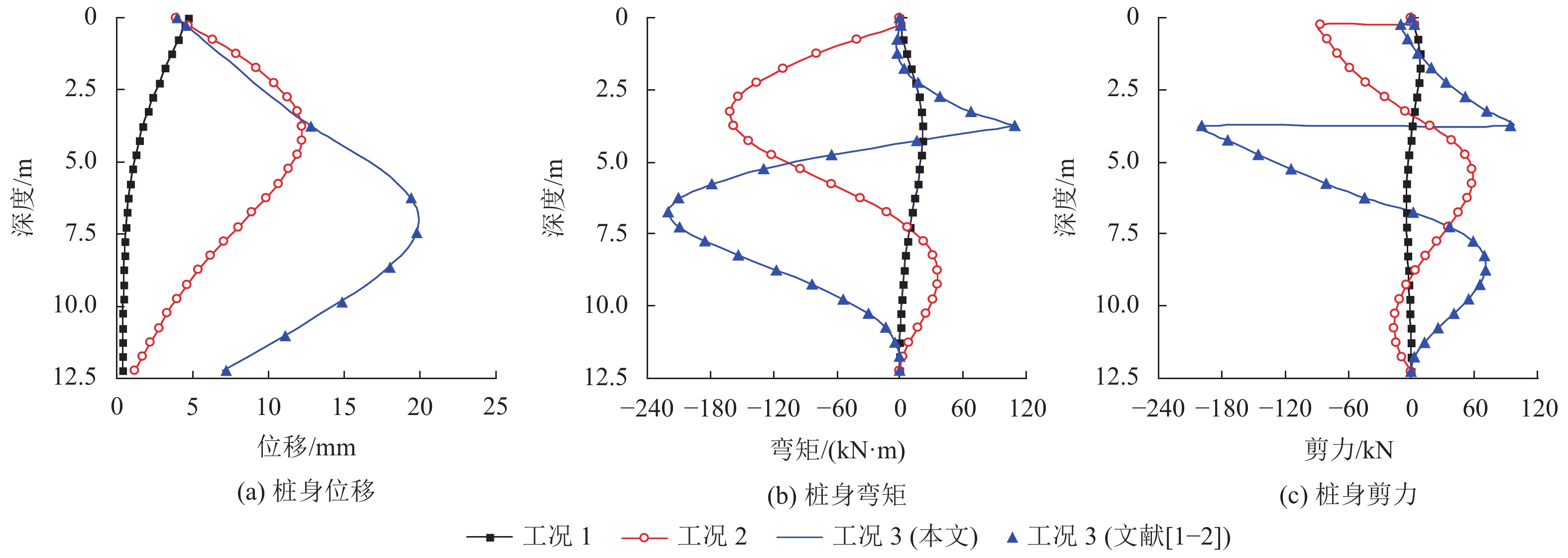
3 算例某基坑深7 m,支护桩长12.25 m,地表下0.75 m范围内采用放坡,1.0 m和4.5 m各设置一道内支撑,支撑刚度K=4.8×105 kN/m,桩身刚度EI=1.29×105 kN·m2。地基土忽略黏聚力后的等值内摩擦角φ=15°,重度γ=18 kN/m3,m=2 500 kN/m4,周围建筑在地表以下7 m平面上产生q=50 kPa的超载,假定桩端自由且b=b0=1 m[1,2]。按如下3个工况分析:
工况1:从地面开挖至预设第1道支撑处;
工况2:设置第1道支撑并继续开挖至预设第2道支撑处;
工况3:设置第2道支撑并继续开挖至最终坑底。
利用本文方法,上述3个工况下支护体系的变形和内力变化见图4。此外,针对工况3条件下的桩身位移(见图4(a))和其它重要物理量(见表1),比较了本文计算结果与文献[1]和[2]之间的差异,显然,两者几乎是相同的。
4 结论(1) 本文基于支撑与桩段交界面的3种基本连接形式,建立了相邻两个桩段之间待定参数的递推公式,由此形成的基坑分析方法不仅通用于内支撑和锚索支撑形式、任意支撑道数和开挖、设撑等施工工况,而且待定参数少于传统方法并易于确定。
(2) 文中算例结果与现有方法几乎是相同的,从而验证了本文方法的合理性和可行性。
| [1] |
肖宏彬, 蔡伟铭. 多支撑挡土结构考虑开挖过程的计算分析方法[J].
港口工程, 1992, 5: 25-37.
XIAO H B, CAI W M. A calculating method taking into account of staged excavation for multi-braced retaining structures[J]. Port Engineering, 1992, 5: 25-37. |
| [2] |
肖宏彬, 王永和, 王星华. 多支撑挡土结构考虑开挖过程的有限元分析方法[J].
岩土工程学报, 2004, 26(1): 47-51.
XIAO H B, WANG Y H, WANG X H. Finite element analysis of multi-braced retaining structures with consideration of the effect of staged excavation[J]. Chinese Journal of Geotechnical Engineering, 2004, 26(1): 47-51. |
| [3] |
莫品强, 刘尧, 黄子丰, 等. 复杂支护条件下深基坑支护桩−冠梁−支撑的变形协调及空间效应研究[J].
岩土力学, 2022, 43(9): 2592-2061.
MO P Q, LIU Y, HUANG Z F, et al. Compatibility of deformation and spatial effects for retaining pile, crown beam and braces under complex retaining conditions of deep foundation pit[J]. Rock and Soil Mechanics, 2022, 43(9): 2592-2061. |
| [4] |
崔宏环, 张立群, 赵国景. 深基坑开挖中双排桩支护的的三维有限元模拟[J].
岩土力学, 2006, 27(4): 662-666.
CUI H H, ZHANG L Q, ZHAO G J. Numerical simulation of deep foundation pit excavation with double-row piles[J]. Rock and Soil Mechanics, 2006, 27(4): 662-666. |
| [5] |
赖冠宙, 房营光, 史宏彦. 深基坑排桩支护结构空间共同变形分析[J].
岩土力学, 2007, 28(8): 1749-1750.
LAI G Z, FANG Y G, SHI H Y. Spatial mutual deformation analysis method for row of piles of deep excavation[J]. Rock and Soil Mechanics, 2007, 28(8): 1749-1750. |
| [6] |
邵权, 徐学连, 徐松, 等. 深基坑桩锚撑组合支护结构变形影响因素的三维数值分析[J].
岩土工程学报, 2014, 36(Supp.2): 87-91.
SHAO Q, XU X L, XU S, et al. Three-dimensional numerical analysis of factors affecting deformation of pile-anchor-support composite retaining structures for deep foundation pits[J]. Chinese Journal of Geotechnical Engineering, 2014, 36(Supp.2): 87-91. |
| [7] |
戴轩, 徐管应, 霍海峰, 等. 管廊隧道开挖对上覆在建深基坑影响的三维有限元分析[J].
岩土工程学报, 2019, 41(Supp.1): 21-24.
DAI X, XU G Y, HUO H F, et al. Three-dimensional finite element analysis of impact of utility tunnel construction on overlying deep excavations[J]. Chinese Journal of Geotechnical Engineering, 2019, 41(Supp.1): 21-24. |
| [8] |
秦会来, 黄俊, 李奇志, 等. 深厚淤泥地层深基坑变形影响因素分析[J].
岩土工程学报, 2021, 43(Supp.2): 23-26.
QIN H L, HUANG J, LI Q Z, et al. Influencing factors for deformation of deep foundation pits in thick mud stratum[J]. Chinese Journal of Geotechnical Engineering, 2021, 43(Supp.2): 23-26. |
| [9] |
BOWLES J E. 基础工程结构分析及程序[M]. 胡人礼, 陈太平, 林亚超, 等译. 北京: 中国铁道出版社, 1982, 101-243
|
| [10] |
范文田. 地下结构墙柱静力分析[J].
西南交通大学学报, 1978, 4: 73-83.
FAN W T. Static analysis of wall and columns of underground structures[J]. Journal of Southwest Jiaotong University, 1978, 4: 73-83. |
 2024, Vol. 41
2024, Vol. 41