2. 广东省第二人民医院 神经内科, 广东 广州 510317
2. Department of Neurology, Guangdong Second Provincial Hospital, Guangzhou 510317, China
在观察性研究中,推断某药物对患者预后情况的因果效应是一项常见而重要的课题。然而,在实际应用中,观察性数据中常伴随着未观测到的混杂变量,导致观察到的相关性往往不仅由因果关系引起,还受其他因素的干扰。因此,未观测到的混杂变量需要被特别考虑。当未观测变量对实验结果产生直接或间接的影响时,准确估计因果效应将变得复杂。例如,在试图估计药物治疗效果的观察性研究中,药物的分配方式受多种因素影响,其中一些因素(如社会经济地位)难以量化,成为无法观测的混杂因素。尽管随机对照试验是推断因果关系和计算因果效应的最有效方法,但其成本昂贵,时间消耗较大,且在伦理道德方面存在限制,因此观察性数据研究在研究变量之间的因果效应方面成为一种常见的替代方法。
目前,用于估计观察性数据中变量之间的因果效应的方法[1]包括但不限于以下几种:首先,基于分层[2]的方法,通过将研究群体根据混杂因素分层为不同子群,计算每个子群的平均效应;其次,基于拟群思想的方法,例如重加权方法[3]、匹配方法[4]、基于树的方法[5]、表征学习方法[6]和多任务学习方法[7]等;第三,采用仅基于观察性数据训练的潜在结果估计模型,然后校正由于选择偏差引起的估计误差,例如元学习方法[8]。然而,这些方法通常建立在无混淆假设上,即所有的混杂因素得到充分测量和控制,这在实际应用中往往难以实现。
处理未观测混杂因素的方法有2种:一是当偏差较小或可承受有偏、非一致性估计量的后果,可以选择忽略这些因素;二是在利用大规模数据时,采用代理变量来取代这些未观测的混杂因素。然而,当偏差无法忽略且难以找到合适的代理变量时,工具变量分析方法[9]成为一种值得考虑的选择。
工具变量(Instrumental Variables,IV)分析提供了一种绕过无混淆假设进行因果推断的方法,特别在流行病学研究中变得越来越普遍[10-11]。在临床试验数据中,通常缺乏与所研究的解释因素相关的混杂因素信息,从而在计算解释因素与预后结果之间的关系时会出现较大的偏差。而工具变量是可观测的变量,用于预测解释变量,但不直接或间接影响结果变量,并且与混杂变量独立。通常情况下,找到合适的工具变量具有挑战性,但如果找到了适当的工具变量,便可以得到更加无偏或接近真实值的结果。在流行病学背景下,医生的处方偏好可以作为工具变量来评估药物效果[12],与感兴趣的暴露变量相关的基因序列也可以作为工具变量[13],后者叫做孟德尔随机化[14]。工具变量的方法可以显著减少由于未观测混杂因素引起的偏差,在一定程度上解决混杂因素导致的伪关联问题。尽管该方法仍需要进一步完善,但它可以成为实验分析的有力工具之一。
本文运用工具变量法在急性缺血性卒中患者数据中进行了丁苯酞药物疗效的因果效应分析,并得出经校正后的因果效应。
1 基于工具变量的因果效应计算 1.1 问题定义和假设在回归模型中,当解释变量与误差项之间存在相关性时,工具变量法可以用来获得一致的估计量。这种方法的基本思想是引入一个额外的变量,称为工具变量,它与解释变量相关,但不与结果变量直接或间接相关,且仅通过解释变量影响结果变量。通过工具变量,就可以在观察数据中估计或确定解释变量对结果变量的因果效应,但为了得到可靠的结果,必须满足一些必要的假设[15]。
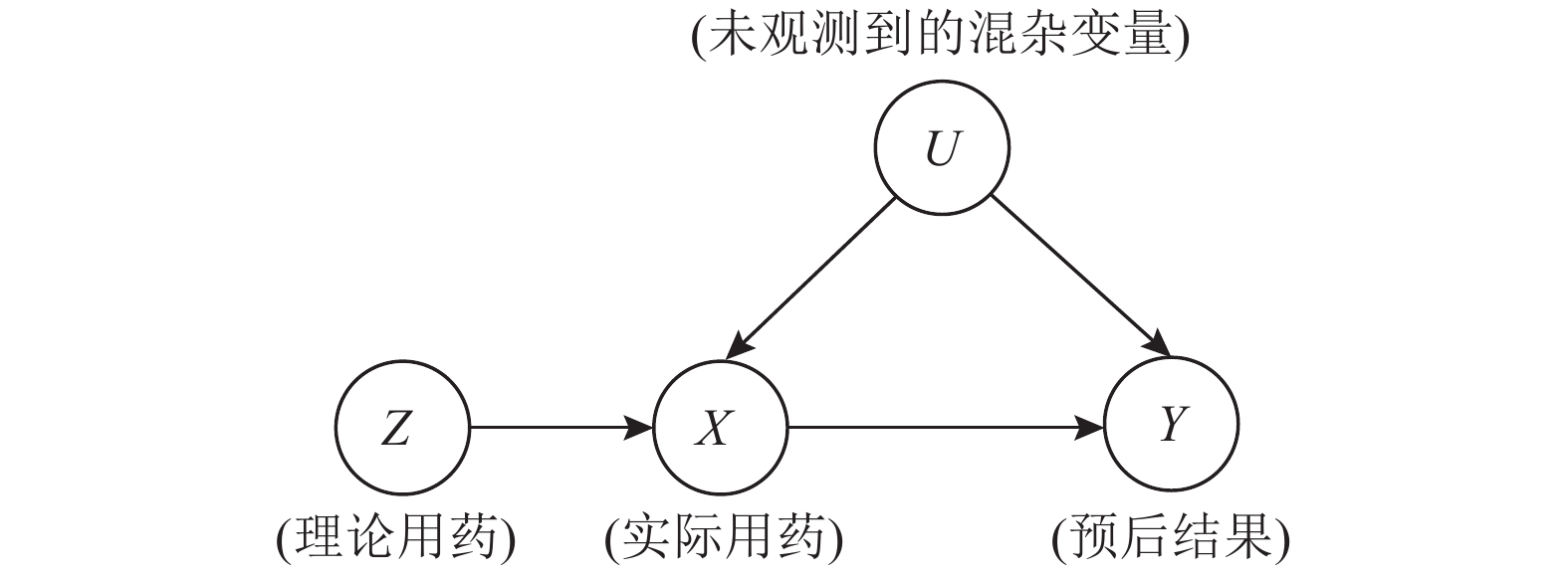
在本文中,用变量X表示实际接受的治疗(1表示用药,0表示不用药),变量Y表示结局事件(1表示康复,0表示未康复),变量Z表示随机分配指标(1表示分配到用药组,0表示分配到对照组)。可以观察到变量Z只与变量X相关,且不与结局事件直接或间接相关,因此变量Z为工具变量。变量U表示同时影响变量X和变量Y的所有变量的集合,即混杂变量。对于变量Z,必须满足以下3个基本假设(通常被称为3大基本假设):(i) Z与X相关;(ii) Z与U独立;(iii) 在给定X和U情况下,Z与Y独立。工具变量模型如图1所示。
|
图 1 工具变量模型 Figure 1 The model of instrumental variables |
需要注意的是,在工具变量的3大基本假设中,只有假设(i)是可验证的,它涉及到Z与X之间的直接相关性。只需证明Z跟X存在相关性,即
工具变量分析采用双阶最小二乘法来拟合线性模型以估计因果效应。在此模型中,自变量表示为X,个体i是否接受治疗为
| $ Y_i = \alpha + \beta X_i + \varepsilon _i $ | (1) |
式中:
假定
| $ {\rm{E}}\left( {\varepsilon _i} \right) = 0 $ | (2) |
| $ {\text{cov}}\left( {X_i,\varepsilon _i} \right) = 0 $ | (3) |
式(3)中的协方差为零的假设通常被称为“外生性”假定。在这一假定下,关于
| $ {\text{cov}}\left( {Y_i,X} \right) = \beta {\text{var}}\left( {X_i} \right) $ | (4) |
即
| $ \beta = {\text{cov}}\left( {Y_i,X_i} \right) /{\text{var}}\left( {X_i} \right) $ | (5) |
上述估计通常是最小二乘的解,如果将式(1)看作一个数据生成的机制,在式(2)、(3)的假定下,便可以估计出因果效应
问题的关键在于,式(3)往往不成立,即
此时,引入工具变量
此时,在线性模型式(1)两边关于
| $ {\text{cov}}\left( {Z_i,Y_i} \right) = \beta {\text{cov}}\left( {Z_i,X_i} \right) $ | (6) |
即
| $ \widehat \beta = {\text{cov}}\left( {Z_i,Y_i} \right) /{\text{cov}}\left( {Z_i,X_i} \right) $ | (7) |
给定x,y和z的样本数据,便可以得到式(6)中的IV估计量。式(1)中
| $ {\rm{E}}[ {{Y^{X = 1}}} ] - {\rm{E}}[ {{Y^{X = 0}}} ] = \frac{{{\rm{E}}\left[ {Y|Z = 1} \right] - {\rm{E}}\left[ {Y|Z = 0} \right]}}{{{\rm{E}}\left[ {X|Z = 1} \right] - {\rm{E}}\left[ {X|Z = 0} \right]}} $ | (8) |
式中:
式(7)中的分子表示Z对Y的影响,也被称为治疗意向效应;而分母表示Z对X的影响,表示被试个体的配合程度。如果被试个体完全配合研究人员,那么分母等于1,X对Y的影响就等于Z对Y的影响。如果配合程度较低,分母就会趋近于0,从而X对Y的影响大于Z对Y的影响。
1.3 IV估计量的置信区间计算当实际情况中治疗变量x与混杂因素u相关时,用工具变量进行估计实质上不是无偏的。在小样本情况下,工具变量估计量可能存在相当大的偏差,这就是为什么希望有大样本的一个原因。
为了对效应
| $ {\rm{E}}( {{u^2}|z} ) = {\sigma ^2} = {\rm{var}}\left( u \right) $ | (9) |
可以证明,
| $ \frac{{{\sigma ^2}}}{{n{\sigma _x^2}{\rho _{x,z}^2}}} $ | (10) |
式中:
为了估计
| $ \widehat u_i = y_i - \widehat \alpha - \widehat \beta x_i $ | (11) |
式中:
| $ {\sigma ^2} = \frac{1}{{n - 2}}\sum\nolimits_{i = 2}^n {{{\widehat u}_i}^2} $ | (12) |
可见,
OLS的渐进方差为
| $ \frac{{{\sigma ^2}}}{{n{\sigma _x^2}}} $ | (13) |
可见,
实验覆盖了2019年9月至2020年6月期间在卒中中心连续住院的123名急性缺血性卒中患者。数据集包括了基线人口统计学、临床和实验信息。该研究的主要结果是评估患者在接受治疗后的3个月内是否具有良好的预后,其中主要是使用改良Rankin量表(mRS)评分进行评估。当患者的评分小于等于2分时,被视为预后良好(记为1)。当患者的评分大于2时被视为预后不良好(记为0)。需要强调的是,数据集中包括了患者按理论安排的用药情况,丁苯酞对脑卒中患者来说并非指南推荐的治疗药物,故这种安排是随机的并符合伦理原则。同时,数据集还记录了患者实际用药(通过定期回访形式获得相关信息)以及最终的预后结果。
为了评估丁苯酞对急性缺血性卒中是否具有治疗效果,本文采用风险差(Risk Difference,RD)来衡量治疗效应[17]。在Wald估计方法中,最小二乘法计算的因果效应估计也可以被称为风险差估计[18]。风险差是干预组和对照组在解决事件发生概率上的绝对差值,也被称为归因危险度(Attributable Risk,AR)、绝对风险差(Absolute Risk Difference, ARD)和绝对风险降低率(Absolute Risk Reduction, ARR)。它反映了干预组中由于干预因素导致的净结局事件水平(从干预组角度考虑)。当风险差等于零时,表示两组之间没有差异。如果研究结局为不利事件时,当风险差小于零时,表示干预可以降低结局风险。风险差异的计算方式如下所示。
在表1的分组情况下,风险差异的点估计RD为
| 表 1 实验数据分组情况 Table 1 The grouping of experimental data |
| $ {\text{RD}} = \frac{{PO}}{{PO + PM}} + \frac{{CO}}{{CO + CM}} $ | (14) |
风险差异RD的抽样分布近似正态分布,具有标准误差SE:
| $ {\text{SE}}\left( {{\text{RD}}} \right) = \sqrt {\frac{{PO \times PM}}{{\mathop {\left( {PO + PM} \right) }\nolimits^3 }} + \frac{{CO \times CM}}{{\mathop {\left( {CO + CM} \right) }\nolimits^3 }}} $ | (15) |
则风险差异RD的置信区间(Confidence Interval, CI) 为
| $ {\text{CI}}_{1 - \partial }\left( {{\text{RD}}} \right) = {\text{RD}} \pm {\text{SE(RD) }} \times Z_{\partial }$ | (16) |
式中:
根据风险差的定义,可以直接计算未经任何调整的风险差,即计算干预组和对照组结局事件发生概率上的绝对差值。然而,由于数据集不是随机分配试验,患者实际接受的治疗(是否用药)取决于患者个体的决策。例如,选择不用药的患者可能对自身的预后有更乐观的态度,这间接地促进了良好预后的发生。这意味着数据中存在未观测到的混杂变量(数据集中并无衡量心理等因素相关的指标),且无法度量这些混杂变量。直接计算的效应将因此存在偏差,
本研究发现,理论用药满足工具变量的相关定义,因此,本文采用了工具变量来估计药效,并将未调整的药效估计、意向性分析(Intention-To-Treat Populaition, ITT)与工具变量估计进行了比较。下文将讨论该数据集在工具变量的假设下进行的药效估计。
2.2 数据集中的IV假设与验证本实验的数据集满足IV三大基本假设:Z表示治疗分配,X表示实际接受的治疗,Y表示结局事件。医生为患者提供的治疗方案对患者最终是否接受用药有一定的指导作用,即实际接受的治疗X受治疗分配Z的影响,但是不完全由Z决定,同时计算可得
由表2可见,在治疗分配后实际接受治疗的预后情况比仅仅根据治疗分配决定的预后情况更加乐观。这种差异很可能是由混淆因素U引起的,这也在一定程度上说明了在试图直接估计治疗X对结局Y的效应时,混杂因素的影响会导致结果出现偏差。
| 表 2 随机治疗分配下实际接受治疗的预后情况1) Table 2 Prognosis of actual treatment received under the randomized treatment assignment |
当患者由于一些与结局Y相关的原因U而不遵守分配时,即
这些问题引发了ITT[19]这类方法的需求。这一方法的主要目的是保持两组之间的基线特征均衡可比,通过随机化,将除了研究因素外的其他变量完全均衡和匹配,以便更好地观察干预结果。具体而言,如果某患者被随机分配到A组,那么在意向性分析中,该患者的数据必须始终与A组相关,即使在治疗过程中途退出,或者转到B组接受其他治疗,或者根本没有接受任何治疗。即仅根据治疗分配来测试和估计效果,而不考虑实际接受的治疗。然而,这种方法的批评者指出,实际接受的治疗才是生物疗效的来源,而与实际接受的治疗相比,所分配的治疗存在偏差,这种偏差不等于0。因此,IV方法提供了一种代替意向性分析这种有较大偏差的极端方法,即将治疗分配Z作为一种工具来调整传统方式分析接受的治疗X对结局Y的影响。
2.3 实验结果本文分析了123位脑卒中患者在用药组及对照组下的数据集特征,结果见表3。所选变量均为二值型,包括ASPECT评分、第14天NIHSS评分和mRS评分,当ASPECT评分小于7分、NIHSS14小于3分、mRS小于等于2分时,在各个指标的划分标准下预后表现为良好,根据该标准将其转换为二值型。同时,统计了临床上常见的各特征下的人数及占比,如表3所示。
| 表 3 病人特征 Table 3 The characteristics of patients |
表4则展示了在协变量为二分类的情况下,患者的风险差异数值。本文定义95%置信区间不包含0值时具有较强的关联性。实际用药与数据集测量的其他特征,如吸烟史和房颤,表现出较强的关联性。然而,在工具变量的调整下(表4中第3列),这些关联性被减弱了。暗示着原本这些特征具有的较强关联性可能是在未观测变量的影响下表现出的伪关联,这在计算最终的因果效应时会带来偏差,而工具变量可以在一定程度上调整协变量带来的偏差。
| 表 4 实际用药跟工具变量调整下治疗与协变量的相关性 Table 4 Correlations between treatment and covariates adjusted by using actual drug and instrumental variables |
表5展示了未经调整的估计、ITT估计和IV估计的风险差异及置信区间比较。未经调整的估计及ITT估计是根据标准的风险差异计算的,而IV估计则根据工具变量的定义计算风险差异及置信区间。在3组实验分析中,是否用药与最终的恢复都呈正相关。这表明用药对预后结果产生一定的积极影响,尽管需要注意到置信区间的范围。
| 表 5 风险差异及置信区间比较 Table 5 Comparison of risk differences and confidence intervals |
本文提出了工具变量分析方法,分析丁苯酞−急性缺血性卒中问题,调整未观测混杂变量对结局变量的影响,得到了更为无偏的因果效应估计。在实际数据集中的应用表明,这一方法在处理未观测混杂变量问题时可以一定程度上修正未观测混杂变量对结局变量带来的误差,在临床医学药效分析领域具有可行性。在对实验数据进行未调整的风险差异估计后,本文对其他变量进行了均衡的意向性分析的风险差异估计,最后进行了工具变量分析的风险差异估计。研究发现,这些分析显示出药效的估计呈现趋势性的正值,暗示药物可能对预后产生一定的积极作用,这为药效分析提供了有益的参考。
然而,工具变量分析也存在一些局限性。首先,即使数据量足够大,工具变量仍需要基于模型假设。其次,稍微违反假设(i)至(iii)可能会导致不可预测的极大偏移。第三,能够使用工具变量的理想情形相较于其他传统的方法更为罕见[20]。
在使用工具变量时,强烈建议慎重考虑模型假设,并进行敏感性分析以评估结果的稳健性。此外,为了更全面地理解工具变量的适用性,未来的研究可以进一步探讨工具变量假设的合理性,并拓展研究对象以验证方法的普适性。这将有助于深入理解药效与预后之间的关系,为临床实践提供更有针对性的指导。
| [1] |
YAO L, CHU Z, LI S, et al. A survey on causal inference[J].
ACM Transactions on Knowledge Discovery from Data (TKDD), 2021, 15(5): 1-46.
|
| [2] |
IMBENS G W, RUBIN D B. Causal inference in statistics, social, and biomedical sciences[M]. Cambridge: Cambridge University Press, 2015.
|
| [3] |
BRICK J M, KALTON G. Handling missing data in survey research[J].
Statistical Methods in Medical Research, 1996, 5(3): 215-238.
DOI: 10.1177/096228029600500302. |
| [4] |
ABADIE A, DRUKKER D, HERR J L, et al. Implementing matching estimators for average treatment effects in Stata[J].
The Stata Journal, 2004, 4(3): 290-311.
DOI: 10.1177/1536867X0400400307. |
| [5] |
LOH W Y. Classification and regression trees[J].
WIREs:Data Mining and Knowledge Discovery, 2011, 1(1): 14-23.
DOI: 10.1002/widm.8. |
| [6] |
BENGIO Y, COURVILLER A, VINCENT P. Representation learning: a review and new perspectives[J].
IEEE Transactions on Pattern Analysis and Machine Intelligence, 2013, 35(8): 1798-1828.
DOI: 10.1109/TPAMI.2013.50. |
| [7] |
CARUANA R. Multitask learning[J].
Machine Learning, 1997, 28(1): 41-75.
DOI: 10.1023/A:1007379606734. |
| [8] |
HOSPEDALES T, ANTONIOU A, MICAELLI P, et al. Meta-learning in neural networks: a survey[J].
IEEE Transactions on Pattern Analysis and Machine Intelligence, 2021, 44(9): 5149-5169.
|
| [9] |
BAIOCCHI M, CHENG J, SMALL D S. Instrumental variable methods for causal inference[J].
Statistics in Medicine, 2014, 33(13): 2297-2340.
DOI: 10.1002/sim.6128. |
| [10] |
MARTENS E P, PESTMAN W R, DE BOER A, et al. Instrumental variables: application and limitations[J].
Epidemiology, 2006, 17(3): 260-267.
DOI: 10.1097/01.ede.0000215160.88317.cb. |
| [11] |
OHLSSON H, KENDLER K S. Applying causal inference methods in psychiatric epidemiology: a review[J].
JAMA Psychiatry, 2020, 77(6): 637-644.
DOI: 10.1001/jamapsychiatry.2019.3758. |
| [12] |
BROOKHART M A, SCHNEEWEISS S. Preference-based instrumental variable methods for the estimation of treatment effects: assessing validity and interpreting results[J].
The International Journal of Biostatistics, 2007, 3(1): 14.
|
| [13] |
MUKAMAL K J, STAMPFER M J, RIMM E B. Genetic instrumental variable analysis: time to call mendelian randomization what it is. The example of alcohol and cardiovascular disease[J].
European Journal of Epidemiology, 2020, 35: 93-97.
DOI: 10.1007/s10654-019-00578-3. |
| [14] |
DAVEY SMITH G, EBRAHIM S. ‘Mendelian randomization’: can genetic epidemiology contribute to understanding environmental determinants of disease?[J].
International Journal of Epidemiology, 2003, 32(1): 1-22.
DOI: 10.1093/ije/dyg070. |
| [15] |
RASSEN J A, SCHNEEWEISS S, GLYNN R J, et al. Instrumental variable analysis for estimation of treatment effects with dichotomous outcomes[J].
American Journal of Epidemiology, 2009, 169(3): 273-284.
|
| [16] |
伍德里奇. 计量经济学导论: 现代方法[M]. 北京: 清华大学出版社, 2017.
|
| [17] |
KIM H Y. Statistical notes for clinical researchers: risk difference, risk ratio, and odds ratio[J].
Restorative Dentistry & Endodontics, 2017, 42(1): 72-76.
|
| [18] |
BROOKHART M A, WANG P, SOLOMON D H, et al. Evaluating short-term drug effects using a physician-specific prescribing preference as an instrumental variable[J].
Epidemiology, 2006, 17(3): 268.
DOI: 10.1097/01.ede.0000193606.58671.c5. |
| [19] |
MCCOY C E. Understanding the intention-to-treat principle in randomized controlled trials[J].
Western Journal of Emergency Medicine, 2017, 18(6): 1075.
DOI: 10.5811/westjem.2017.8.35985. |
| [20] |
MA H, ROBINS J M. Instruments for causal inference: an epidemiologist's dream?[J].
Epidemiology, 2006, 17(4): 360-372.
DOI: 10.1097/01.ede.0000222409.00878.37. |
 2024, Vol. 41
2024, Vol. 41

