2. 香港大学 经济与金融学院,中国 香港 999077;
3. 华南师范大学 经济与管理学院,广东 广州 510631
2. School of Economics and Finance, The University of Hong Kong, Hong Kong 999077, China;
3. School of Economics and Management, South China Normal University, Guangzhou 510631, China
社交网络研究要解决规模图计算的问题. 现代人的生活已由各种社交网络联系在一起. 近年,Facebook、Twitter等全球性社交网络快速发展,从这些社交网络数据中获取有价值的信息成为人们的努力方向. 为此,要解决两个问题,一是大规模图计算平台,二是开发适合大规模图计算的并行算法. Google提出的GFS[1]、MapReduce[2]和BigTable[3]成为分布式计算模型基础. Pregel API是Google于2010年提出的大规模分布式图计算框架,影响较大[4].
金融监管问题亟待解决. 随着金融信息化不断加深,国家金融安全形势日益严峻,这为金融监管提出了新课题. 信息安全风险已经被提上了金融监管日程,金融监管在预防金融腐败方面的重要性也逐渐增长. 在金融关系网络规模快速增长的今天,需要思考更高效的监管方法,实现覆盖整个金融关系网络的有效监管.
为了解决上述问题,本文提出一种基于Pregel平台的并行最小割算法,利用Spark集群处理大规模社交网络数据. 利用该并行算法计算得到金融社交网络图的最小割集,即可找到金融社交网络中需要监管的节点,有效实现对整个金融社交网络的监管.
1 相关工作我国的金融监管体制仍处于完善进程中. 李成等[5]提出,我国现有金融监管的目标、内容以及方式存在缺陷,缺乏统一协调与信息共享机制. 张圣[6]阐述了互联网金融监管的必要性及其原则. 王平[7]指出,我国金融监管体制已不能适应新形势下的金融业发展,需要借鉴适合我国国情的国际经验,建立统一的金融监管体制. 何剑锋[8]从法律角度给出了关于互联网金融监管的一系列建议. 赵江红[9]研究分析我国金融反腐现状,从金融监管的角度提出调整组织结构、加强现有监管职能等对策.
Spark Pregel作为基于BSP模型的并行大规模图处理平台,自诞生以来便获得了研究者的极大关注,不断有新的算法及其相关改进成果诞生. Pregel上最典型的并行算法之一是最早由美国斯坦福大学的Sergey等于1996年提出的PageRank算法. PageRank算法在搜索引擎优化和文献检索等方面得到广泛应用,不断有研究者提出改进的PageRank算法. Taher[10]提出主题敏感PageRank算法TSPR,降低了主题漂移现象带来的PageRank值不准确性.Matthew等[11]提出结合网页链接和文本信息的PageRank算法MP PageRank,降低了网页内容关联对PageRank值的干扰.张岭等[12]提出基于时间序列分析的加速PageRank算法,能够让新的高质量Web页面尽快被搜索引擎展示.
基于Spark平台的算法并行化有良好的应用前景与现实意义. 饶东宁等[13]综合考虑各种中心度指标的影响,提出基于Spark平台的社交网络在不同文化环境中的中心度加权算法. 曾雪琳等[14]针对传统协同过滤算法存在的准确率损失问题,提出一种基于位置的社会化网络的并行化推荐算法. 梁彦[15]针对k-means算法计算海量数据面临的瓶颈,提出基于Spark平台的k-means并行化算法与改进的canopy-kmeans并行化算法,得到了较高的效率以及良好的聚类效果. 陈建国等[16]基于Spark RDD与DAG模型,从数据并行以及任务并行两方面对随机森林算法进行优化,提出一种基于Spark平台的并行随机森林算法(PRF),解决了原算法的负载不均等问题,显著提高了算法表现. 邱荣财[17]考虑到CURE聚类算法适用面广泛,为将聚类算法应用于大数据处理,提出了改进的基于Spark平台的并行化ACURE算法.
此外,与Spark Pregel类似的其他平台,如Apache Giraph,GPS,Mizan以及GraphLab等,在实验中也有不俗表现[18]. 算法并行化及其相关应用具有广阔的发展前景.
2 算法背景 2.1 点割集定义定义1 设无向图G=(V, E),v为V的子集,若从图G中删去子集v的所有节点,得到的子图不连通,而删去v的任意真子集后得到的子图仍为连通图,则称v为G的一个点割集.
2.2 最大独立集定义定义2 独立集指图G=(V, E)中两两互不相邻的顶点构成的集合.
定义3 最大独立集是一个点集I,I中任意两顶点互不相邻,且图中所有不属于I的顶点均至少与I的一个顶点相邻. 也即,最大独立集是包含顶点数最多的、由两两互不相邻的顶点构成的集合. 其数学模型如下:
令
| ${v_i} = \left\{ \begin{array}{l}1,\quad i \in V' \,\, ;\\0,\quad i \notin V' \,\, .\end{array} \right.$ | (1) |
则最大独立集即为
| $\max \sum\nolimits_{i = 1}^n {{v_i}} ,\quad {v_i} \in \{ 0,1\} ,\quad i = 1,2, \cdots ,n,$ |
满足
| $\forall (i,j) \in E,\quad {v_i} + {v_j} \leqslant 1.$ | (2) |
最大独立集(MIS)并行求解算法经历了以下发展阶段. R. M. Karp等[19]首先提出求解MIS快速并行算法. 后续研究中,影响较大的是Michael G. Luby[20]提出的求解MIS并行算法. Luby证明并行算法求解MIS问题属于NC2类,并给出了确定性的NC算法(LMIS).
设图G=(V, E),v代表一个顶点(vertex),I是V的子集.
定义4 顶点v的相邻顶点集合为
| $N(v) = \{ u|(u,v) \in E\} .$ | (3) |
定义5 顶点集中所有顶点的相邻顶点集合,
| $N(I) = {\mathop \cup \limits_{u \in I}} {N(u)} .$ | (4) |
定义6 顶点的度为
| $d(v) = |N(v)|.$ | (5) |
LMIS算法核心是一系列选择步. 定义一枚有偏硬币,每次投掷这枚硬币时,正面朝上的概率
每步过程为
(1) 初始化一个集合S. 并行处理每个顶点,每个顶点被加入集合S的概率均为
(2) 对于边集E的每一条边,若其两端的顶点都在集合S中,则丢弃度较小的顶点.
3 并行最小割算法 3.1 Pregel迭代过程Spark Pregel的计算过程以顶点为中心,由一系列supersteps(超级步)组成. 其核心部分是3个函数:顶点消息处理函数vprog、消息发送函数sendMsg及消息合并函数mergeMsg. 顶点状态有两种:活跃或不活跃. 在每一个superstep中,顶点状态均可能变化:非活跃顶点收到消息后转为活跃状态,完成计算任务的顶点将被置为非活跃状态. 在第一次迭代(superstep 0)中,所有顶点均处于活跃状态,它们将接收到用户定义的初始消息.
一个superstep的执行过程为:(1) 顶点接收由上一个superstep传来的消息,若收到多个消息,则通过消息合并函数mergeMsg进行合并处理;(2) 并行地,对活跃顶点调用用户定义的顶点消息处理函数vprog,此时顶点属性值可能改变;(3) 被置为非活跃状态的顶点将不会向相邻顶点发送消息,而活跃顶点经消息发送函数sendMsg判断后,可能向相邻顶点发送消息,这些消息将在下一个superstep中被相邻顶点接收. 当所有顶点均处于非活跃状态或迭代次数达到用户设置的最大迭代次数后,迭代终止.
3.2 算法设计在LMIS算法的启发下,希望在每次迭代中判断顶点是否属于最小割集S,并将一部分顶点所属确定下来. 最后一次迭代完成时,每个顶点的属性值value标志该节点是否属于最小割集S.
首轮迭代中,对顶点度d(v)进行判断,若d(v)大于中值m,则该顶点被加入集合S的概率为1–
第二轮及其后迭代中,对未知顶点进行处理. 若顶点收到“集合S中已有相邻顶点”消息,则将该顶点标记为不属于集合S;若该顶点的所有相邻顶点均不属于集合S,则将顶点加入集合S;否则,若该顶点的度d(v)>1,则该顶点被加入集合S的概率为1–
算法设计表示为
Algorithm 1. The minimal cut set algorithm
Input: An RDD object of the original dataset.
Output: The minimal cut set.
1: while still need to iterate do
2: if one of v's neighbors is in S then
3: message = "neighbor in S";
4: else
5: count v's neighbors which are not in S;
6: end if
7: if superstep 0 then
8: if v is good then
9: put v in S with probability 1
10: else if d = 1 then
11: v is not in S;
12: end if
13: else
14: if v is not decided yet then
15: if message = "neighbor in S" then
16: v is not in S;
17: else
18: if none of v's neighbors is in S then
19: put v in S;
20: if v is good then
21: put v in S with probability 1
22: end if
23: end if
24: end if
25: if vertex is in S then
26: send message "neighbor in S" to its adjacent vertexes;
27: else if source vertex is not in S then
28: send message "one of your neighbors is not in S" to its adjacent vertexes;
29: else
30: send message "one of your neighbors has nothing to do with you" to its adjacent vertexes;
31: end if
32: end while
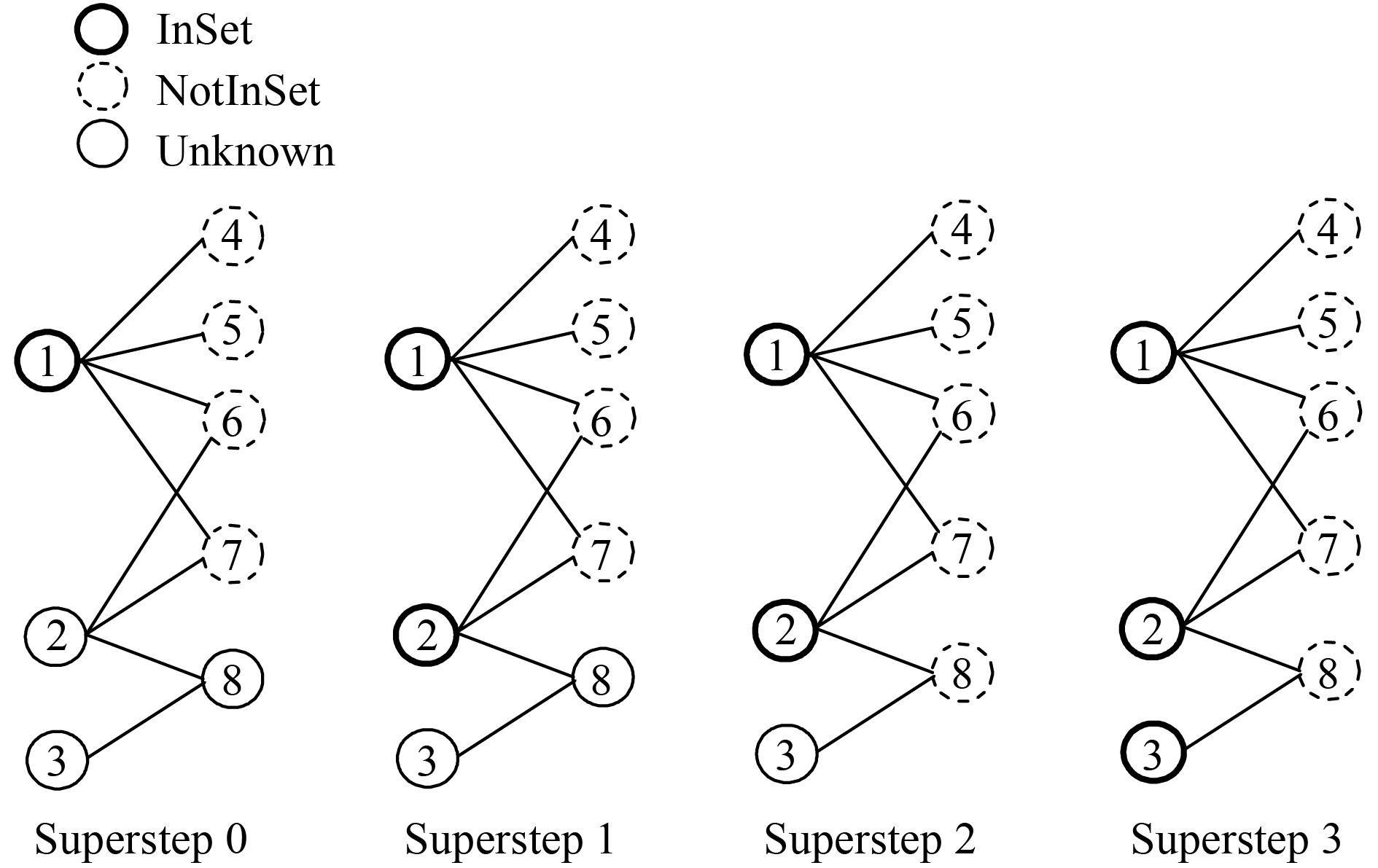
算法迭代步骤如图1所示.
|
图 1 并行最小割算法的迭代步骤 Figure 1 Supersteps of parallel minimal cut set algorithm |
使用Spark集群进行实验. Spark是美国UCBerkeley大学AMP实验室于2009年为大规模数据处理设计的快速通用计算平台. 与Hadoop MapReduce相比,Spark支持基于内存计算,中间数据在内存中读写,迭代计算效率大幅提高. Spark集群配置如表1所示.
| 表 1 Spark集群配置 Table 1 Spark cluster configuration |
实验使用香港大学提供的BoardEx数据库. BoardEx是一家总部位于伦敦的数据服务公司. BoardEx数据库包含世界上大部分董事会成员及高级执行官的详细关系信息,也包含个人教育背景和职业生涯等信息.
实验使用各个地区的董事会关系网数据. 数据以文本文件形式导入,利用数据文件中的公司标识号CompanyID与主管标识号DirectorID字段生成二分图.
4.3 实验设计实验一共使用3个BoardEx数据集,分别为欧洲地区、美国和英国的董事会关系网数据. 其中,美国的数据集规模最大,成员关系最复杂. 欧洲地区与英国的数据集规模基本相同. 基于这3个完整数据集开展并行最小割算法(PMCS)实验,结果如表2所示.
| 表 2 实验一结果 Table 2 Results of test 1 |
从表2可见,顶点间边的数量,也即不同成员之间的关系数,对时间开销的影响较大. 美国数据集成员数与英欧接近,但其成员间关系远比英欧复杂,求解时间开销远高于英欧. 主要原因是Pregel采用哈希方法进行图划分,虽能保证各节点的负载均衡,却未考虑节点间通信开销. 通信开销随各划分子图间边数增长而增大,是影响性能的关键因素. 处理具有相同数量级顶点个数的图时,由于关系边数目不同,时间开销可相差数个数量级. 基于Spark平台的并行最小割算法应用于大规模社交网络数据处理,可在时间开销较理想情况下得到实用结果.
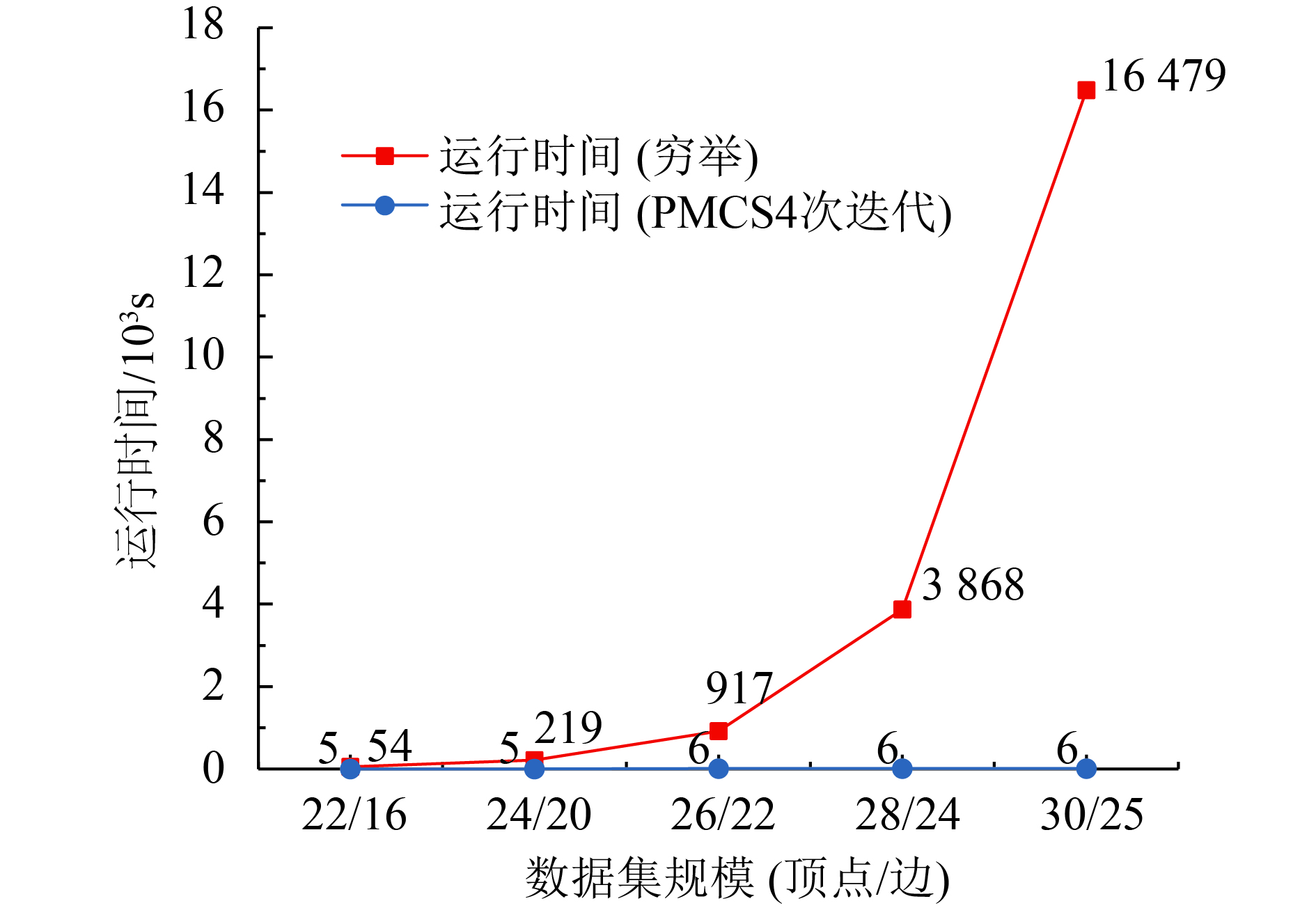
实验二使用规模较小的数据集,将穷举法与并行最小割算法(PMCS)进行对比,结果如图2所示.
|
图 2 实验二结果 Figure 2 Results of test 2 |
实验二结果表明,使用穷举法求解最小割集的时间开销呈指数增长. 这是由于顶点集的子集数目随顶点增加而呈指数增长,而穷举法须逐一判断子集是否为最小割集. 由实验二可见,使用穷举法处理仅含数十个顶点的图,其时间开销已较大. 在大规模社交网络图情境下,需处理的顶点数目可达上百万,非并行穷举法显然无法实际应用. 并行最小割算法的高效率使其相较于非并行算法具有明显优势,在数据集规模较大的情况下,并行算法是合理选择.
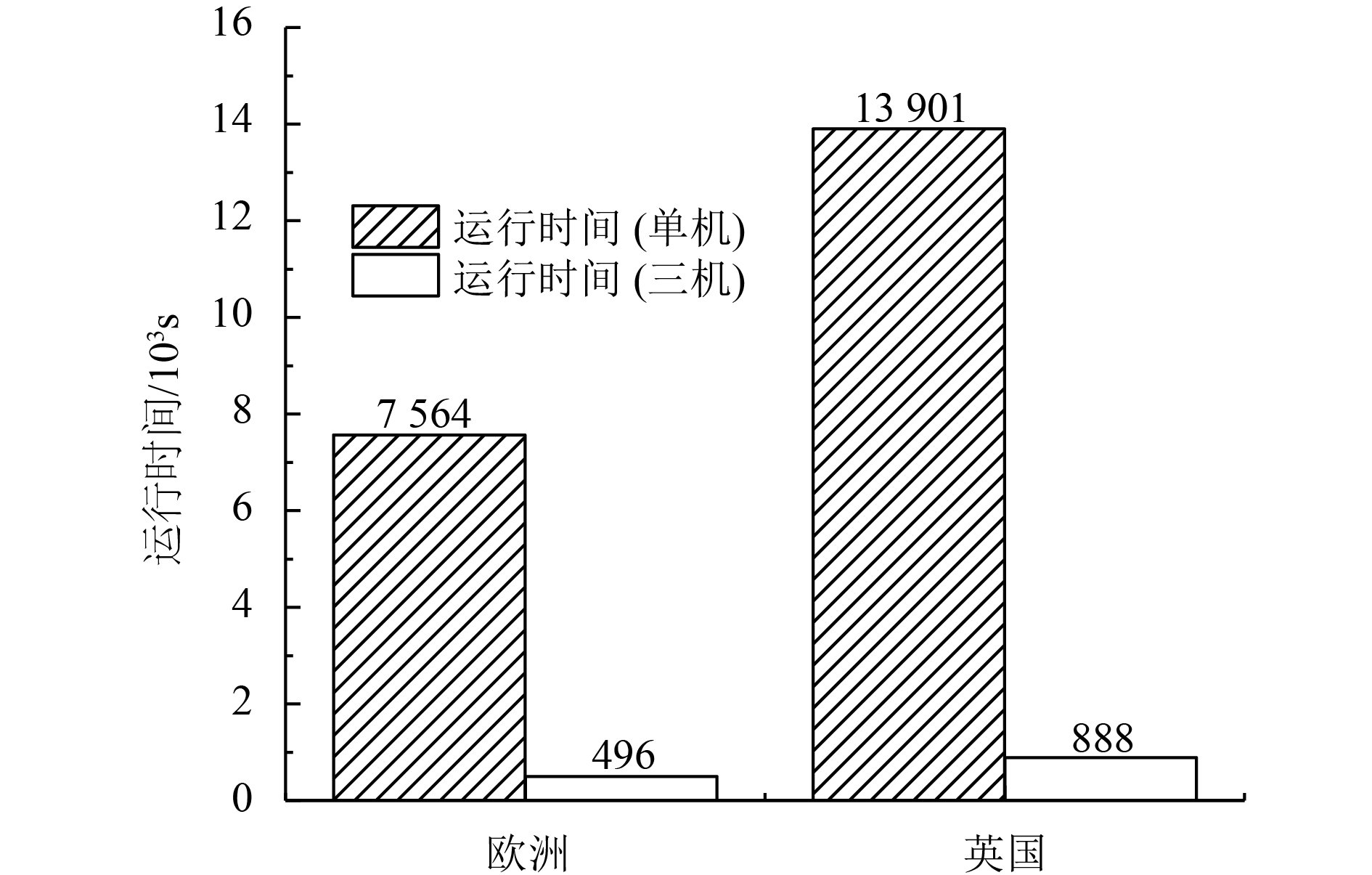
实验三使用单机运行PMCS算法,基于美国、欧洲与英国的数据集进行实验. 其中基于美国数据集的实验经过5d未完成,已终止. 单机及三机集群时间开销对比见图3,可见三机集群时间开销远低于单机.
|
图 3 实验三结果 Figure 3 Results of test 3 |
本文提出一种基于Spark Pregel平台的并行最小割算法,利用分布式Spark集群处理大规模社交网络数据,使用BoardEx数据库进行实验. 实验结果显示,在社交网络大数据计算中,该并行算法相较于非并行算法具有明显优势. 实际应用中,可借助该算法找到金融社交网络中需监管的最小割集节点,提升金融监管效率.
在未来的工作中,需要进一步探讨与完善,工作将主要在两个方面展开:(1) 尝试进一步完善算法,探讨算法的改进点,提高该并行算法的效率. (2) 结合实际,探讨具体应用情景下算法效率与精确度的取舍关系.
| [1] | GHEMAWAT S, GOBIOFF H, LEUNG S T. The Google file system[C] //ROBBERT V R. SIGOPS Operating Systems Review. NY: ACM Press, 2003, 37(5): 29-43. |
| [2] | DEAN J, GHEMAWAT S. MapReduce: simplified data processing on large clusters[J]. Communications of the ACM, 2008, 51(1): 107-113. DOI: 10.1145/1327452. |
| [3] | CHANG F, DEAN J, GHEMAWAT S, et al. Bigtable: A distributed storage system for structured data[J]. ACM Transactions on Computer Systems (TOCS), 2008, 26(2): 205-218. |
| [4] | MALEWICZ G, AUSTERN M H, BIK A J C, et al. Pregel: a system for large-scale graph processing[C] //AHMED E. Proceedings of the 2010 ACM SIGMOD International Conference on Management of Data. NY: ACM Press, 2010: 135-146. |
| [5] |
李成, 涂永前. " 后金融危机时代”我国金融监管体制的完善[J].
南京审计学院学报, 2011, 8(1): 21-26.
LI C, TU Y Q. The improvement of China's financial supervision system after the global financial crisis[J]. Journal of Nanjing Audit University, 2011, 8(1): 21-26. |
| [6] | 张圣. 互联网金融监管的必要性与核心原则[J]. 时代金融, 2016(23): 25. |
| [7] |
王平. 新形势下我国金融监管改革与完善[J].
法学杂志, 2011, 32(10): 44-47.
WANG P. Research about reform of finance supervision under new situation[J]. Law Science Magazine, 2011, 32(10): 44-47. |
| [8] |
何剑锋. 论我国互联网金融监管的法律路径[J].
暨南学报(哲学社会科学版), 2016, 38(1): 58-65.
HE J F. On the legal paths to the internet financial regulation of our country[J]. Jinan Journal(Philosophy and Social Sciences), 2016, 38(1): 58-65. |
| [9] | 赵江红. 金融腐败的对策思考[J]. 现代经济信息, 2010(7): 149+152. |
| [10] | HAVELIWALA T H. Topic-sensitive pagerank: A context-sensitive ranking algorithm for web search[J]. IEEE Transactions on Knowledge and Data Engineering, 2003, 15(4): 784-796. DOI: 10.1109/TKDE.2003.1208999. |
| [11] | RICHARDSON M, DOMINGOS P. The intelligent surfer: Probabilistic combination of link and content information in pagerank[C] //THOMAS G D. Advances in Neural Information Processing Systems.Cambridge: MIT Press, 2002: 1441-1448. |
| [12] |
张岭, 马范援. 加速评估算法: 一种提高Web结构挖掘质量的新方法[J].
计算机研究与发展, 2004, 41(1): 98-103.
ZHANG L, MA F Y. Accelerated ranking: a new method to improve Web structure mining quality[J]. Journal of Computer Research and Development, 2004, 41(1): 98-103. |
| [13] |
饶东宁, 温远丽, 魏来, 等. 基于Spark平台的社交网络在不同文化环境中的中心度加权算法[J].
广东工业大学学报, 2017, 34(3): 15-20.
RAO D N, WEN Y L, WEI L, et al. A weighted centrality algorithm for social networks based on Spark Platform in Different Cultural environments[J]. Journal of Guangdong University of Technology, 2017, 34(3): 15-20. |
| [14] |
曾雪琳, 吴斌. 基于位置的社会化网络的并行化推荐算法[J].
计算机应用, 2016, 36(2): 316-323.
ZENG X L, WU B. Parallelized recommendation algorithm in location-based social network[J]. Journal of Computer Applications, 2016, 36(2): 316-323. DOI: 10.11772/j.issn.1001-9081.2016.02.0316. |
| [15] | 梁彦. 基于分布式平台Spark和YARN的数据挖掘算法的并行化研究[D]. 广州: 中山大学数据科学与计算机学院, 2014. |
| [16] | CHEN J, LI K, TANG Z, et al. A parallel random forest algorithm for big data in a Spark cloud computing environment[J]. IEEE Transactions on Parallel and Distributed Systems, 2017, 28(4): 919-933. DOI: 10.1109/TPDS.2016.2603511. |
| [17] | 邱荣财. 基于Spark平台的CURE算法并行化设计与应用[D]. 广州: 华南理工大学计算机科学与工程学院, 2014. |
| [18] | HAN M, DAUDJEE K, AMMAR K, et al. An experimental comparison of pregel-like graph processing systems[J]. Proceedings of the VLDB Endowment, 2014, 7(12): 1047-1058. DOI: 10.14778/2732977. |
| [19] | KARP R M, WIGDERSON A. A fast parallel algorithm for the maximal independent set problem[J]. Journal of the ACM (JACM), 1985, 32(4): 762-773. DOI: 10.1145/4221.4226. |
| [20] | LUBY M. A simple parallel algorithm for the maximal independent set problem[J]. SIAM Journal on Computing, 1986, 15(4): 1036-1053. DOI: 10.1137/0215074. |
 2018, Vol. 35
2018, Vol. 35

 ,
,