过去20多年间,关于多智能体系统一致性问题的研究引起学界越来越多的关注,对一些经典多智能体系统的建模研究有助于解决自然界和人类社会中一些常见的难题[1]. 譬如:群集和蜂拥,飞行器编队控制,神经网络的稳定性控制,全球经济市场变化等[2-5]. 实际问题中系统状态一般呈非线性变化,因此对非线性多智能体系统的研究尤为必要. 文献[6]研究了一类混沌系统的控制问题,针对此问题还有其他一些有效的方法被提出,包括模糊控制法[7],自适应控制法[8]、间歇性控制法[9]、脉冲控制法[10]、切换控制法[11]等等.
传统的连续控制协议控制多智能体系统会存在一些弊端,例如有时无法连续采集各智能体的状态信息以对系统实施精确控制. 此时可以引入脉冲控制协议对系统进行离散式控制. 文献[12]研究了一类混沌系统在脉冲控制下的稳定性和同步问题. 文献[13]研究了一类二阶非线性系统脉冲控制下的平均一致性问题. 文献[14-17]则研究了在有领导者的情况下二阶非线性多智能体系统的领导跟随一致性.
受文献[13-17]启发,本文设计了不同于文献[14]的全新协议. 对文献[14]的协议作了如下改进:一是智能体自身非线性向量值函数仅与位移状态有关; 二是非脉冲时刻跟随智能体速度状态的更新仅受到邻接智能体影响; 三是在脉冲协议中位移增量仅与位移有关,而速度增量既与位移有关,又与速度有关; 四是脉冲控制协议是从文献[13, 15]的协议中推广得到,和以往协议略有不同; 五是领导者是积极领导者,即领导者和各节点的连接关系是不断变化的(领导节点无需全局可达),且任一固定节点在拓扑切换时不接受领导者信息也能和领导者保持一致; 在该协议下研究了二阶非线性多智能体系统在网络拓扑切换且无向连通时的领导跟随一致性,仿真结果验证了协议的正确性.
1 预备知识 1.1 图论通常,用有向图与无向图表示多智能体系统的网络拓扑. 令
| ${l_{ij}} = \left\{ \begin{array}{l} - {a_{ij}},\quad i \ne j;\\ - \sum\limits_{j = 1,j \ne i}^N {{l_{ij}},\quad i = j} .\end{array} \right.$ |
有积极领导者存在时,令连接矩阵
引理1[18](Rayleigh-Ritz)存在Hermite矩阵
引理2[19]符号“
(1)
(2)
(3)
(4)
引理3[20] (Gronwall)令
引理4[21]
本文引入一个二阶领导者,动力学模型如下:
| $\left\{ \begin{array}{l}{{\dot{ x}}_0}(t) = {{v}_0}(t);\\[7pt]{{\dot{ v}}_0}(t) = f({{x}_0}(t),t).\end{array} \right.$ | (1) |
其中,f表示智能体自身动力学的非线性向量值函数;x与y是n维列向量.
对含有N个智能体的二阶非线性多智能体系统,本文设计了如下动力学模型(2)与控制协议(3)、(4):
| $\left\{ \begin{array}{l}{{\dot{ x}}_i}(t) = {{v}_i}(t) + {u_{i1}}(t),\\[7pt]{{\dot{ v}}_i}(t) = f({{x}_i}(t),t) + {u_{i2}}(t);\end{array} \right.$ | (2) |
| $\begin{split}{u_{i1}}(t) = & \sum\limits_{{{k}} = 1}^{ + \infty } {\delta (t - {t_k})} ({{B}_k}a\sum\limits_{j \in {N_i}s(t)} {{a_{ij}}(s(t))({{x}_j}(t) - } \\[7pt]&{{x}_i}(t)) +{b_i}({{B}_k} - {{I}_n})({{x}_i}(t) - {{x}_0}(t)));\end{split}$ | (3) |
| $\begin{split}{u_{i2}}&(t) = a\left[ {\sum\limits_{j \in {N_I}s(t)} {{a_{ij}}(s(t))({{v}_j}(t) - {{v}_i}(t))} } \right] + \\ &\sum\limits_{k = 1}^{ + \infty } {\delta (t - {t_k}){{B}_k}a\sum\limits_{j \in {N_i}s(t)} {{a_{ij}}(s(t))} ({{x}_j}(t) - {{x}_i}(t) +} \\ & {{v}_j}(t) - {{v}_i}(t)) + \sum\limits_{k = 1}^{ + \infty } {\delta (t - {t_k}){b_i}({{B}_k} - {{I}_n})} ({{v}_i}(t) - {{v}_0}(t)) .\end{split}$ | (4) |
备注:
(1) 当多智能体系统的网络拓扑切换时,定义分段定常切换信号
(2)
结合引理4将式(2)、(3)、(4)转化为如下动力学模型
| $\left\{ \begin{aligned} &{{\dot{ x}}_i}(t) = {{v}_i}(t),t \ne {t_k};\\ & \begin{array}{l} \!\!\!\! {{{\dot v}}_i}(t) = f({{{\dot x}}_i}(t),t) + a\displaystyle\sum\limits_{j \in {N_i}s(t)} {{a_{ij}}(s(t))({{{v}}_j}(t)}- \\ \quad \!\!\!\!{{{v}}_i}(t)),t \ne {t_k}; \end{array}\\& \Delta {{x}_i}({t_k}) = {{x}_i}(t_k^ + ) - {{x}_{{i}}}(t_k^ - ) = \\ & \quad {{B}_k}a\sum\limits_{j \in {N_i}s(t)} {{a_{ij}}(s(t))({{x}_j}(t_{{k}}^ - ) - {{x}_i}(t_k^ - )) + } \\ & \quad{b_i}(\omega (t))({{B}_k} - {{I}_n})({{x}_i}(t_k^ - ) - {{x}_0}(t_k^ - )),t = {t_k};\\ & \Delta {{v}_i}({t_k}) = {{v}_i}(t_k^ + ) - {{v}_i}(t_{k}^ - ) = \\ & \quad{{B}_k}a\sum\limits_{j \in {N_i}s(t)} {{a_{ij}}(s(t))({{x}_j}(t_k^ - ) - {{x}_i}(t_k^ - ) + {{v}_j}(t_k^ - ) -} \\ & \quad{{v}_i}(t_k^ - )) + {b_i}(\omega (t))({{B}_k} - {{I}_n})({{v}_i}(t_k^ - ) - {{v}_0}(t_k^ - )),t = {t_k}. \end{aligned} \right.$ | (5) |
式(5)中,脉冲序列
同时,
定义跟随智能体和领导者之间的状态差值为
因此,由式(2)得到误差动力系统如下:
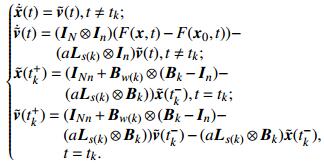
|
(6) |
其中,对于
定义:若在定理和假设条件下误差系统(6)的解使
假设1:二阶非线性多智能体系统的网络拓扑图是无向图,领导者在其中可以不是全局可达节点且与智能体的连接伴随拓扑切换而同步切换.
假设2:非线性向量值函数
定理:在假设1、假设2的条件下,若存在常数
证明 构造Lyapunov函数
| $V(t) = \frac{1}{2}{\tilde{ x}^{{T}}}(t)\tilde{ x}(t) + \frac{1}{2}{\tilde{ v}^{{T}}}(t)\tilde{ v}(t),$ | (7) |
对
| $\begin{aligned}\dot V(t) = & {{\tilde{ x}}^{{T}}}(t)\tilde{ v}(t) + {{\tilde{ v}}^{{T}}}(t)(({{I}_N} \otimes {{I}_n})(F({x},t) - F({{x}_0},t)) - \\ &(a{{L}_{s(k)}} \otimes {{I}_n})\tilde{ v}(t)).\end{aligned}$ |
由假设2得
| $\begin{aligned}\dot V(t) = & - {{\tilde{ v}}^{{T}}}(t)(a{{L}_{s(k)}} \otimes {{I}_n})\tilde{ v}(t) + {{\tilde{ x}}^{{T}}}(t)\tilde{ v}(t) + \\ &{{\tilde{ v}}^{{T}}}(t)({{I}_{Nn}}\varphi )\tilde{ x}(t).\end{aligned}$ |
由
| $\dot V(t) \leqslant {\tilde{ x}^{{T}}}(t)\tilde{ v}(t) + {\tilde{ v}^{{T}}}(t)({{I}_{Nn}}\varphi )\tilde{ x}(t).$ |
因为
| $\begin{aligned}{{\tilde{ x}}^{{T}}}(t)\tilde{ v}(t) = & {{\tilde{ v}}^{{T}}}(t)\tilde{ x}(t) = {{\tilde{ v}}_{11}}(t){{\tilde{ x}}_{11}}(t) + \\ &{{\tilde{ v}}_{12}}(t){{\tilde{ x}}_{12}}(t) + \cdots + {{\tilde{ v}}_{1n}}(t){{\tilde{ x}}_{1n}}(t) + \\ &{{\tilde{ v}}_{21}}(t){{\tilde{ x}}_{21}}(t) + \cdots + {{\tilde{ v}}_{Nn}}(t){{\tilde{ x}}_{Nn}}(t) \leqslant \\ &\frac{{{1}}}{{{2}}}(\tilde{ v}_{11}^2(t) + \tilde{ x}_{11}^2(t) + \cdots + \tilde{ v}_{Nn}^2(t) + \\ &\tilde{ x}_{Nn}^2(t)) = V(t),\end{aligned}$ |
同理可得
综上,
| $\dot V(t) \leqslant \varepsilon V(t)\text{且}\varepsilon = 1 + \phi .$ | (8) |
由引理3在时间区间
| $V(t) \leqslant V(t_{k - 1}^ + ){e^{\varepsilon (t - {t_{k - 1}})}}.$ | (9) |
在脉冲时刻tk处,可得
| $V(t_k^ + ) = \frac{1}{2}{\tilde{ x}^{{T}}}(t_k^ + )\tilde{ x}(t_k^ + ) + \frac{1}{2}{\tilde{ v}^{{T}}}(t_k^ + )\tilde{ v}(t_k^ + ).$ |
令
| $\begin{aligned}V(t_k^ + ) = & \frac{1}{2}{{\tilde{ x}}^{{T}}}(t_k^ - )({{A}^{{T}}}{A})\tilde{ x}(t_k^ - ) + \frac{1}{2}{{\tilde{ v}}^{{T}}}(t_k^ - )({{A}^{{T}}}{A})\tilde {{v}}(t_k^ - ) - \\ &\;\;\;\;\;\;\;\;\frac{1}{2}{{\tilde{ v}}^{{T}}}(t_k^ - )({E} + {{E}^{{T}}})\tilde{ x}(t_k^ - ) + \frac{1}{2}{{\tilde{ x}}^{{T}}}(t_k^ - )({{H}^{{T}}}{H})\tilde{ x}(t_k^ - ).\end{aligned}$ |
令
| $\begin{aligned}V(t_k^ + ) \leqslant & {\lambda _{k1}}(\frac{1}{2}{{\tilde{ x}}^{{T}}}(t_k^ - )\tilde{ x}(t_k^ - ) + \frac{1}{2}{{\tilde{ v}}^{{T}}}(t_k^ - )\tilde{ v}(t_k^ - )) - \\ & \frac{1}{2}{\lambda _{k2}}{{\tilde{ v}}^{{T}}}(t_k^ - )\tilde{ x}(t_k^ - ) + \frac{1}{2}{\lambda _{k3}}{{\tilde{ x}}^{{T}}}(t_k^ - )\tilde{ x}(t_k^ - ) \leqslant \\ & {\lambda _{k1}}V(t_k^ - ) - \frac{1}{2}{\lambda _{k2}}{{\tilde{ v}}^{{T}}}(t_k^ - )\tilde{ x}(t_k^ - ) + \frac{1}{2}{\lambda _{k3}}{{\tilde{ x}}^{{T}}}(t_k^ - )\tilde{ x}(t_k^ - ).\end{aligned}$ |
因为
| $\begin{aligned}{{\tilde{ x}}^{{T}}}(t_k^ - )\tilde{ v}(t_k^ - ) = & {{\tilde{ v}}^{{T}}}(t_k^ - )\tilde{ x}(t_k^ - ) \leqslant \frac{{{1}}}{{{2}}}(\tilde{ v}_{11}^2(t_k^ - ) + \tilde{ x}_{11}^2(t_k^ - ) + \cdots + \\ &\tilde{ v}_{Nn}^2(t_k^ - ) + \tilde{ x}_{Nn}^2(t_k^ - )) = V(t_k^ - ),\end{aligned}$ |
综上得
| $V(t_k^ + ) \leqslant {\lambda _k}V(t_k^ - ),\text{且}{\lambda _k} = ({\lambda _{k1}} - \frac{1}{2}{\lambda _{k2}} + {\lambda _{k3}}) \in (0,1).$ | (10) |
下面计算
由式(10)得
取k=2得
| $\begin{aligned}V(t_2^ + ) \leqslant {\lambda _2}V(t_2^ - ) = & {\lambda _2}V({t_2}) \leqslant {\lambda _2}V(t_1^ + ){{{e}}^{\varepsilon ({t_2} - {t_1})}} \leqslant \\ &{\lambda _{{1}}}{\lambda _{{2}}}V(t_0^ + ){{{e}}^{\varepsilon ({t_2} - {t_0})}}.\end{aligned}$ |
当
| $\begin{aligned}V(t) \leqslant & {\lambda _{{1}}}{\lambda _{{2}}} \cdots {\lambda _k}V(t_0^ + ){{{e}}^{\varepsilon (t - {t_0})}} = \frac{{{1}}}{{{\vartheta ^k}}}V(t_0^ + ){{{e}}^{\varepsilon (t - {t_k})}} \times \\ & \vartheta {\lambda _k}{{{e}}^{\varepsilon ({t_k} - {t_{k - 1}})}}\vartheta {\lambda _{(k - 1)}}{{{e}}^{\varepsilon ({t_{k - 1}} - {t_{k - 2}})}} \cdots \vartheta {\lambda _1}{{{e}}^{\varepsilon ({t_1} - {t_0})}}.\end{aligned}$ |
如果满足条件
| $V(t) \leqslant \frac{{{1}}}{{{\vartheta ^{{k}}}}}V(t_0^ + ){{{e}}^{\varepsilon (t - {t_k})}}.$ | (11) |
因此,当
备注:若
推论:在假设1和假设2的条件下,若脉冲增益矩阵
针对有5个多智能体的二阶非线性多智能体系统,取各智能体状态初值分别为(–15, 5)、(5, –3)、(18, –9)、(10, 7)、(3, 13),取领导者状态初值为(5, 4);令非线性函数
取耦合强度a=0.1,脉冲间隔
|
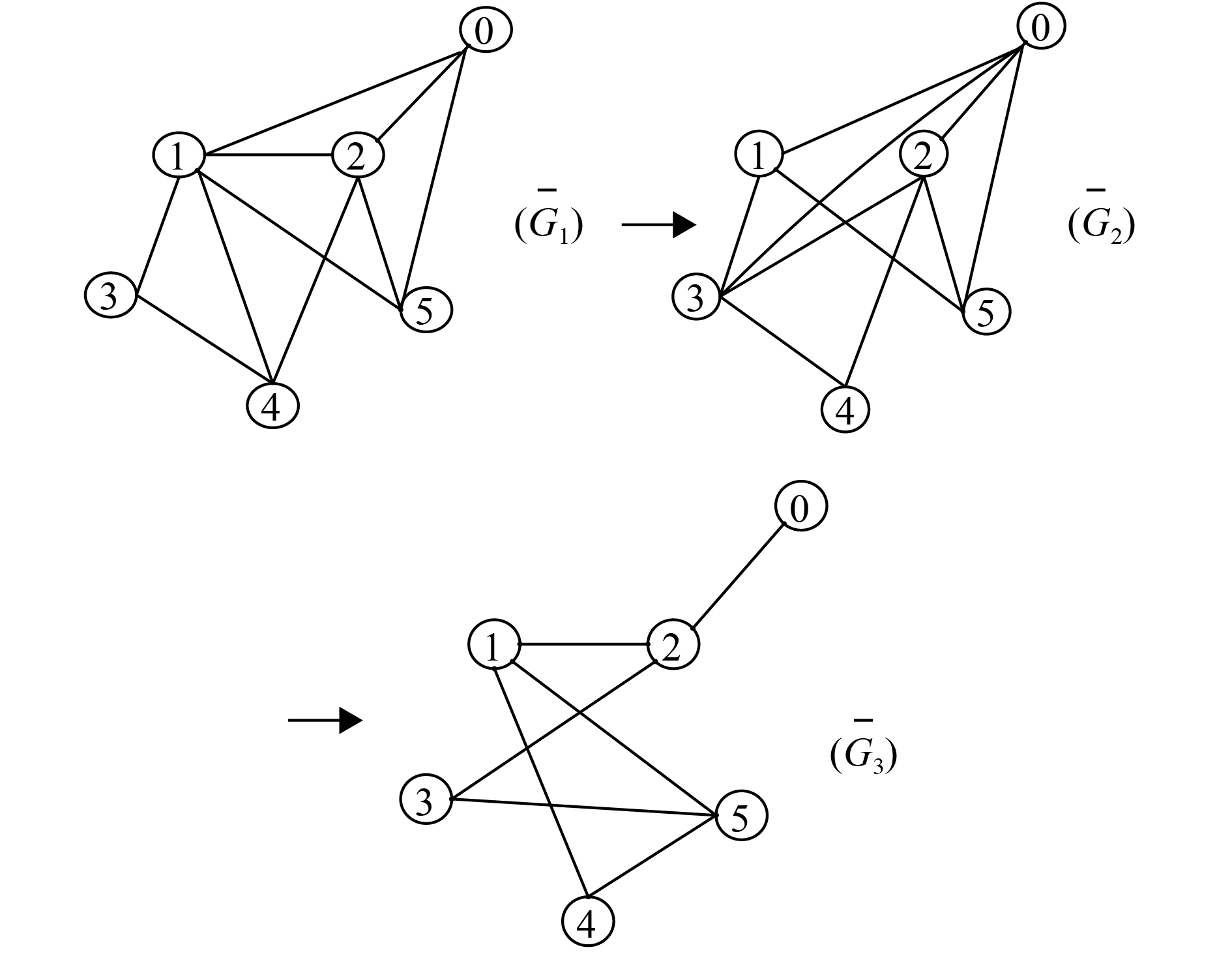
图 1 拓扑图切换顺序
|
经计算:当拓扑图为
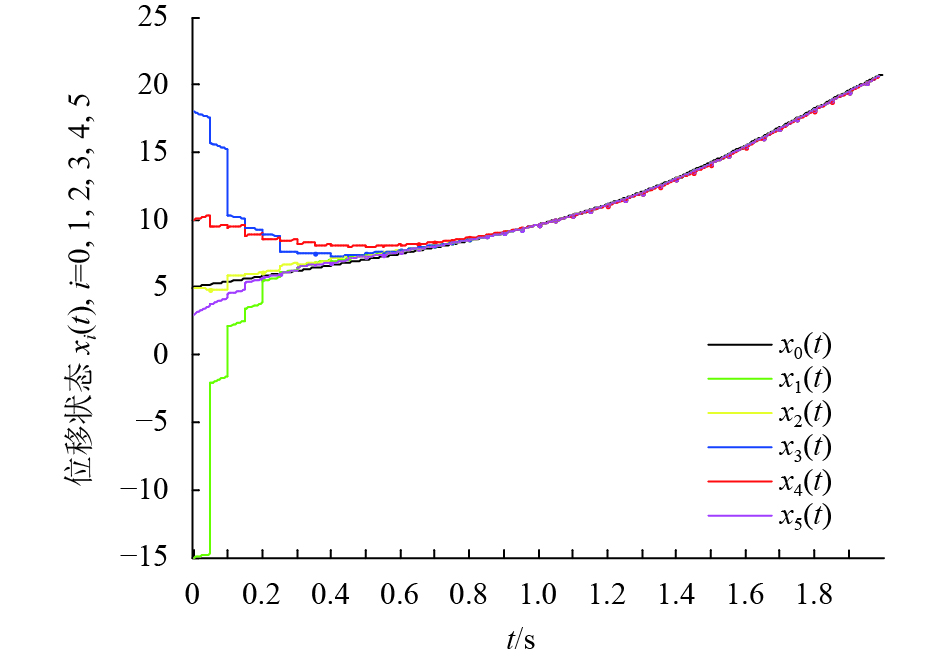
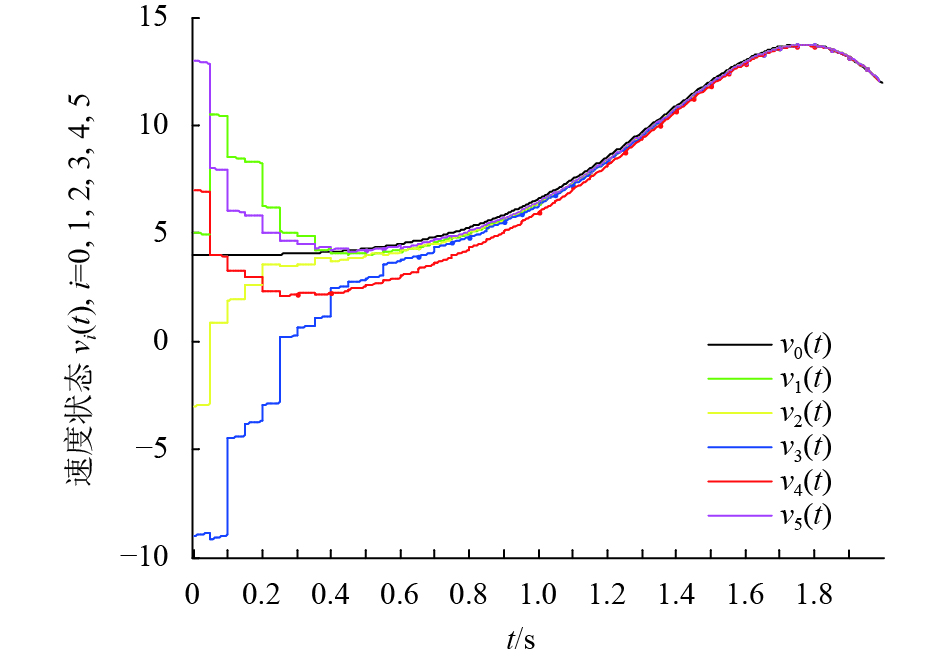
从图2、图3不难看出,随着时间不断变化在非脉冲时刻连续控制协议与脉冲时刻脉冲控制协议的双重作用下系统可以实现领导跟随一致性. 同时,在初始阶段的脉冲时刻各智能体状态变化较为剧烈,而约0.5 s以后脉冲时刻的状态增量较小并逐渐趋于0.
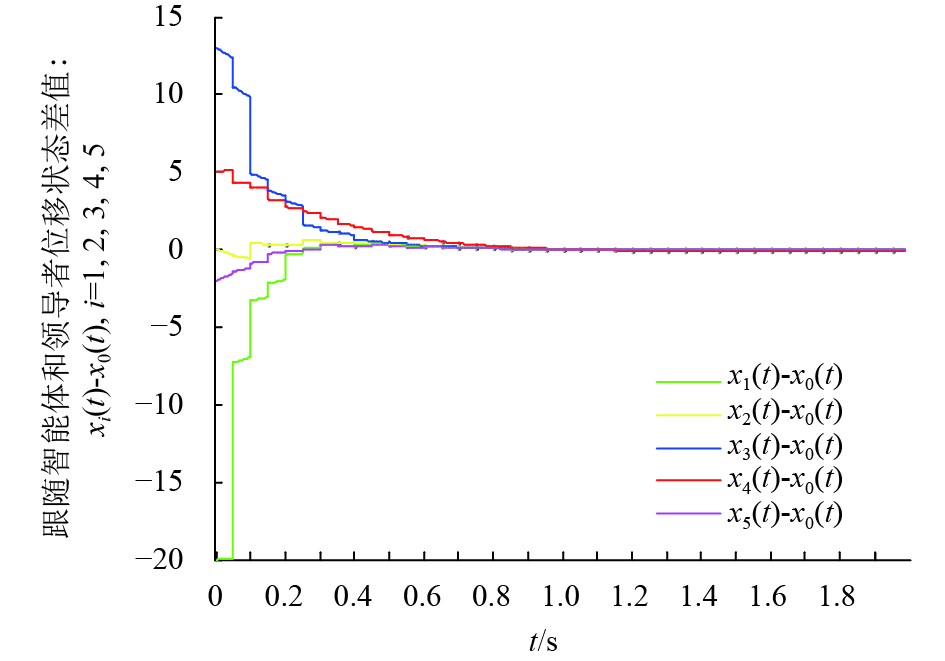
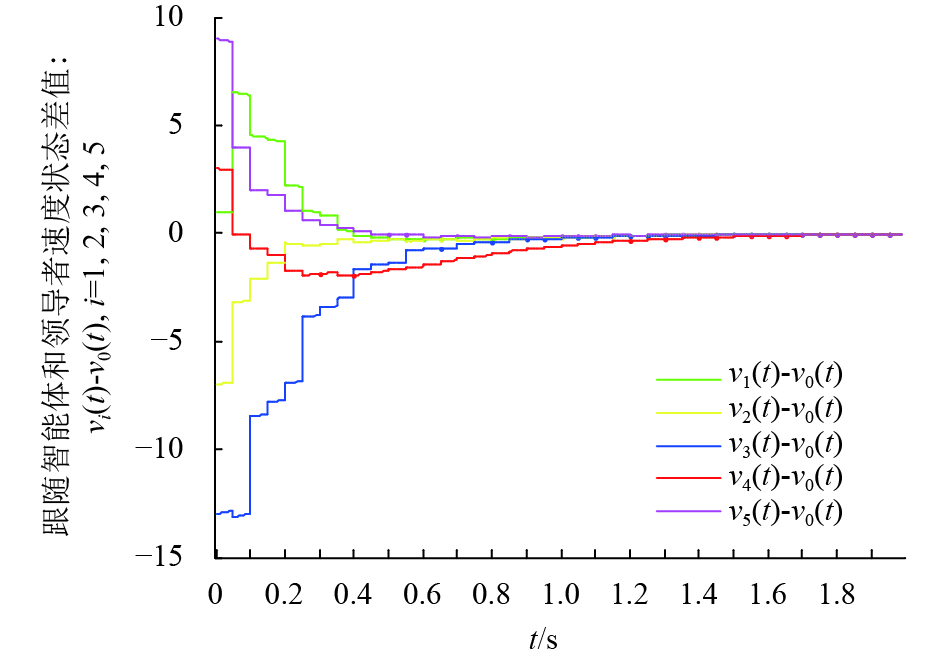
图4、图5表明:随着时间的增加,各智能体与领导者的状态误差逐渐趋于并稳定于0,实例证明了系统在脉冲控制协议作用下可以实现领导跟随一致性,即本文协议的正确性得到验证.
|
图 2 协议(3, 4)控制下跟随智能体与领导者的位移状态曲线 Figure 2 The displacement status curves of followers with leader under the control protocol (3, 4) |
|
图 3 协议(3, 4)控制下跟随智能体与领导者的速度状态曲线 Figure 3 The velocity status curves of followers with leader under the control protocol (3, 4) |
|
图 4 协议(3,4)控制下跟随智能体与领导者的位移状态误差 Figure 4 The displacement status errors of followers with leader under the control protocol (3, 4) |
本文采用一种新的控制协议对一类含有积极领导者的二阶非线性多智能体系统在网络拓扑切换情形下的领导跟随一致性进行了研究. 利用相关理论,得到系统拓扑图无向且连通时系统实现一致性必须满足的充分条件,并用Matlab软件实例仿真验证了结果的正确性.
|
图 5 协议(3, 4)控制下跟随智能体与领导者的速度状态误差 Figure 5 The velocity status errors of followers with leader under the control protocol (3, 4) |
| [1] | ZHU W, YAN C. Consensus analysis of second-order agents with active leader and time delay via impulsive control[C]//Proceedings of The 30th Chinese Control Conference. China, Yantai: IEEE, 2011: 4753-4757. |
| [2] | YAZDANI S, HAERI M. Flocking of multi-agent systems with multiple second-order uncoupled linear dynamics and virtual leader[J]. IET Control Theory & Applications, 2016, 10(8): 853-860. |
| [3] |
罗贺富, 彭世国. 多时变时滞的多智能体系统的分布式编队控制[J].
广东工业大学学报, 2017, 34(4): 89-96.
LUO H F, PENG S G. Distributed formation control of multi-agent systems with coupling time-varying delays[J]. Journal of Guangdong University of Technology, 2017, 34(4): 89-96. |
| [4] |
张治中, 彭世国. 随机变时滞神经网络的输入状态稳定性[J].
广东工业大学学报, 2017, 34(4): 84-88.
ZHANG Z Z, PENG S G. Input-to-state Stability for Stochastic Neural Networks with Time-Varying Delay[J]. Journal of Guangdong University of Technology, 2017, 34(4): 84-88. |
| [5] | HUANG C, YE X D. A nonlinear transformation for reaching dynamic consensus in multi-agent systems[J]. IEEE Transactions on Automatic Control, 2015, 60(12): 3263-3268. DOI: 10.1109/TAC.2015.2426271. |
| [6] | HEAGY J, CARROLL T L, PECORA L M. Synchronous chaos in coupled oscillator systems[J]. Physical Review E, 1994, 50(3): 1874-1885. DOI: 10.1103/PhysRevE.50.1874. |
| [7] | LI S B, ERMJ J. Distributed adaptive fuzzy control for output consensus of heterogeneous stochastic nonlinear multi-agent systems[J]. IEEE Transactions On Fuzzy Systems, 2017. DOI: 10.1109/TFUZZ.2017.2710949. |
| [8] | YIN L J, DENG Z Z, XIA Y Q, HUO B Y. Synchronization of chaotic gyros systems with adaptive sliding mode control[C]//2016 35th Chinese Control Conference(CCC). [s.n.]: Chengdu, 2016: 5509-5514. |
| [9] | ZHANG G D, SHEN Y. Exponential stabilization of memristor-based chaotic neural networks with time-varying delays via intermittent control[J]. IEEE Transactions on Neural Networks and Learning Systems, 2015, 26(7): 1431-1441. DOI: 10.1109/TNNLS.2014.2345125. |
| [10] | LI D, MA J, ZHU H M, SUN M. The consensus of multi-agent systems with uncertainties and randomly occurring nonlinearities via impulsive control[J]. International Journal of Control, Automation and systems, 2016, 14(4): 1005-1011. DOI: 10.1007/s12555-014-0366-z. |
| [11] | BORAH M, ROY B K. Switching synchronisation control between integer-order and fractional-order dynamics of a chaotic system[C]//2017 India Control Conference(ICC). India, Guwahati: IEEE, 2017: 456-461. |
| [12] | YANG T, CHUA L O. Impulsive stability for control and synchronization of chaotic systems: theory and application to secure communication[J]. IEEE Transactions on Circuits and Systems I: Fundamental Theory and Applications, 1997, 44(10): 976-988. DOI: 10.1109/81.633887. |
| [13] | QIAN Y F, WU X J, Lü J H, LU J A. Second-order consensus of multi-agent systems with nonlinear dynamics via impulsive control[J]. Neurocomputing, 2014, 125(3): 142-147. |
| [14] |
李小湄, 马中军, 刘苏雨. 二阶非线性多智能体系统的脉冲一致性[J].
桂林电子科技大学, 2013, 33(6): 502-507.
LI X M, MA Z J, LIU S Y. Second-order consensus of a nonlinear multi-agent system via impulsive control[J]. Guilin University of Electronic Technology, 2013, 33(6): 502-507. |
| [15] | ZHANG Q, CHEN S H, YU C C. Impulsive consensus problem of second-order multi-agent systems with switching topologies[J]. Commun Nonlinear Sci Number Simulat, 2012, 17(1): 9-16. DOI: 10.1016/j.cnsns.2011.04.007. |
| [16] |
颜青, 马米花, 吴海亮. 具有引导者的多智能体网络系统的脉冲一致性[J].
动力学与控制学报, 2012, 10(2): 152-155.
YAN Q, MA M H, WU H L. Impulsive consensus of networked multi-agent system with a leader[J]. Journal of Dynamics and Control, 2012, 10(2): 152-155. |
| [17] | LI Z K, DUAN Z S, HUANG L. Leader-follower consensus of multi-agent systems[C]//2009 American Control Conference. [s.n.]: St. Louis, USA, 2009: 3256-3261. |
| [18] | HORN R A, JOHNSON C. R. Matrix analysis[M]. Cambridge: Cambridge University Press, 1985. |
| [19] | HORN R A, JOHNSON C R. Topics in matrix analysis[M]. Cambridge: Cambridge University Press, 1991. |
| [20] | STARKE J, SORENSEN M P, HJORTH P, et al. An introduction to mathematical modelling, nonlinear dynamics, stochastic and complex systems[M]. [S.l]: MMC summer school Press, 2010. |
| [21] | SAICHEV A I, WOYCZYNSKI W A. Distributions in the physical and engineering science[M]. Boston: Birhhauser, 1997. |
 2018, Vol. 35
2018, Vol. 35
