随着互联时代的快速发展,众多计算密集型和时延敏感型应用兴起,如在线游戏、虚拟/增强现实、智能驾驶等。这使计算能力有限、电池电量不足和存储容量有限的移动终端设备面临着巨大的挑战。云计算可以将到达终端的任务卸载到云端服务器进行处理,其强大处理能力能有效地降低计算时延,并显著降低设备消耗电量的速度。近几年,随着无线终端设备数量的剧增,海量数据被上传到云端服务器,造成网络堵塞,服务效率降低。移动边缘计算提供了一种解决上述问题的解决方案,通过在靠近无线终端设备的网络边缘端部署服务器来处理设备卸载的计算任务,分担云端服务器的任务处理压力,进一步降低任务处理时延和设备的电量消耗[1-4]。
移动边缘计算中的计算卸载策略主要分为二进制卸载和部分卸载[5-8],二进制卸载将计算任务完整地进行卸载,而部分卸载将计算任务分割为多个部分后卸载其中部分任务。在二进制卸载策略下,文献[9]针对MEC系统网络中移动终端设备因计算能力不足,在处理低时延、高可靠应用时产生的高时延问题,提出一种基于博弈论的求解方法,用于联合优化计算卸载与资源分配;文献[10]考虑了最小化系统的执行延迟和用户能耗的加权和,通过联合优化任务卸载决策、卸载调度和功率分配,设计了一种两级交替优化框架来求解非凸混合整数优化问题;文献[11]考虑了最小化用户卸载决策下的时延,通过联合优化计算卸载和资源分配问题;文献[12]从用户的角度考虑了最小化用户能耗和传输、计算成本,通过联合优化计算卸载和资源分配问题,提出了一种基于博弈论的求解方法;文献[13]考虑了两层MEC系统,以最小化系统服务时延和用户能耗为目标,联合优化了服务缓存和计算卸载策略;文献[14]考虑了一种能量感知卸载方案,通过最小化能耗和时延之间的权衡,在能量有限和延迟敏感的条件下联合优化通信和计算资源分配。上述文献中,任务的决策会取决于终端设备的运行状态,系统的性能对设备的要求较高。
部分卸载策略下,文献[15]考虑了在随机应用请求、不可预测的无线设备状态、时变的信道状态以及计算资源等因素的基础上最小化系统的时延与能耗;联合优化多用户的部分卸载决策、传输调度和计算资源分配;并提出了一种在线资源协调与分配方案。文献[16]考虑了最小化系统总延迟,联合优化计算卸载和无线传输调度问题;文献[17]考虑了MEC服务器部署在宏基站和小型基站下的多用户场景,通过联合优化用户与基站之间的计算卸载、用户与小型基站的连接、用户的CPU (Central Processing Unit) 频率和发射功率,达到MEC系统的总能耗最小化的目的。文献[18]通过联合优化用户的任务分配比例和卸载发射功率来最小化设备之间的任务延迟。文献[19]将非正交多址技术引入到MEC系统中,通过联合优化任务卸载和资源分配以最大化系统处理能力。文献[20]在考虑卸载延迟和保密约束的前提下,通过联合优化通信和计算资源分配实现总保密卸载数据最大化的部分卸载比。文献[21]在多用户多服务器MEC系统下,利用改进的深度强化学习算法,优化服务器的选择和卸载任务比例以最小化计算时延与能耗。然而在部分卸载模式下,大部分工作仅考虑了时延或能耗的单目标优化,未考虑时延和能耗的均衡优化。
不同于以上研究,本文考虑在双MEC服务器与多用户协同场景下,以最小化系统计算时延和用户能耗加权和为目标,在有限的时间内完成用户的任务并将任务计算结果发送到远处数据驱动端进行驱动。由于用户和单MEC服务器进行卸载时会有其他MEC服务器空闲,造成资源浪费,因此考虑双服务器协同任务处理方式,最终完成数据驱动端的驱动。本文通过联合优化计算任务分割和卸载发射功率以最小化系统时延与用户能耗加权和,提出了一种较低计算复杂度的算法方案实现最优任务分割和发射功率。
本文的主要贡献总结如下:(1) 针对双MEC服务器协同多用户场景,基于用户能耗与系统计算时延加权和最小化准则,建模本地计算和双MEC服务器协同计算的联合优化问题;在计算时延和发射功率约束条件下,联合优化用户计算任务分割和计算卸载发射功率。(2) 针对该联合设计问题,提出一种较低计算复杂度的联合优化算法方案,将原问题解耦成计算卸载和计算任务分割的2个子问题,分别采用内点法和单纯形法实现快速求解。(3) 大量数值仿真实验表明,本文所提联合优化算法的系统性能优于已有启发式基准方案,并在较少的算法运行时间下,本算法方案能取得与最优拉格朗日乘子法基准方案相同的系统性能。
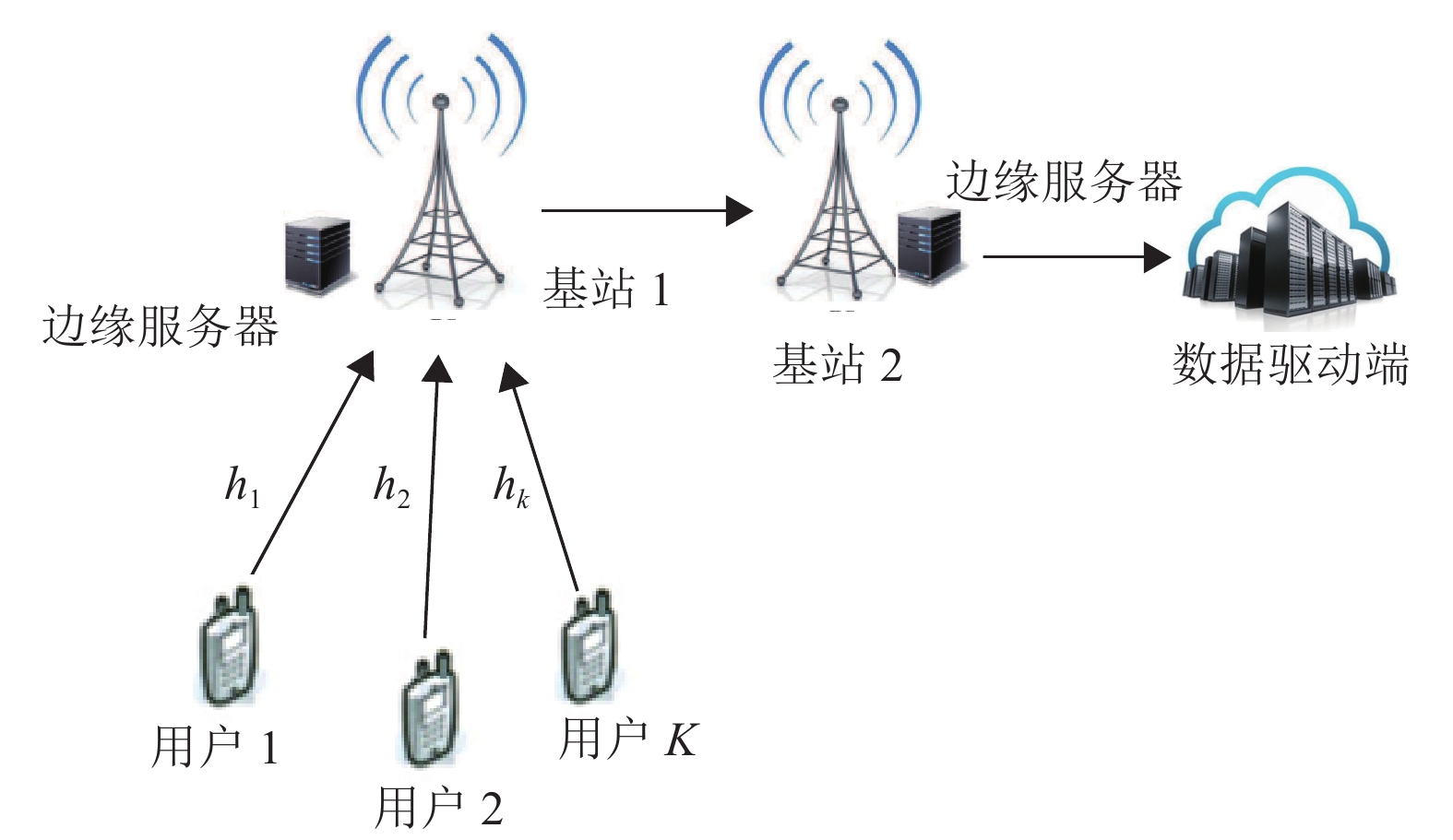
1 系统模型与问题构造考虑一个包含数据驱动端的双MEC服务器协同多用户系统。如图1所示,该模型包含
|
图 1 基于双服务器协同的多用户系统模型 Figure 1 Multi-user system model based on cooperation of two servers |
本文采用三元物理量
| $ \left\{ \begin{gathered} {x_{1,i}} + {x_{2,i}} + {x_{3,i}} = 1 \\ {x_{j,i}} \in [0,1],j \in \{ 1,2,3\} \\ \end{gathered} \right. $ | (1) |
式中:
第
| $ {t_{i,{x_{1,i}}{\beta _i}}} = \frac{{{x_{1,i}}\,{\beta _i}}}{{{f_i}}} $ | (2) |
式中:
接下来建模无线设备传输输出数据和部分输入数据所需的时间。记
| $ {r_i} = {B_i}{\log _2}\left(1 + \frac{{{p_i}{h_i}}}{{{\sigma ^2}}}\right) $ | (3) |
式中:
| $ {t_{i,{\text{tran}}}} = \frac{{({x_{2,i}} + {x_{3,i}}) {\alpha _i} + {x_{1,i}}{\gamma _i}}}{{{r_i}}} $ | (4) |
式中:
| $ {T_{{\text{W}}{{\text{D}}_i}}} = {t_{i,{x_{1,i}}{\beta _i}}} + {t_{i,{\text{tran}}}} $ | (5) |
基站1产生的时延包括计算部分任务、传输部分输入数据和传输输出数据3部分。基站1计算部分任务产生的时延为
| $ {t_{{\text{mec}}1,{\beta _i}}} = {x_{2,i}}{\beta _i}/{f_{{\text{mec}}1}} $ | (6) |
式中:
接下来分别建模基站1和基站2传输输入数据和输出数据所需的时间。本文假设基站端和数据驱动端采用光纤通信,因此,基站与基站间、基站与数据驱动端进行数据传输的传输速率都为
| $ {t_{{\text{mec}}1,{\alpha _i},{\gamma _i}}} = \frac{{({x_{1,i}} + {x_{2,i}}) {\gamma _i}}}{R} + \frac{{{x_{3,i}}{\alpha _i}}}{R} $ | (7) |
式中:
| $ {T_{{\text{mec}}1,i}} = {t_{{\text{mec}}1,{\beta _i}}} + {t_{{\text{mec}}1,{\alpha _i},{\gamma _i}}} $ | (8) |
基站2产生的时延同样包括任务计算和数据传输两部分,区别在于任务分配比例。基站2完成对应比例的任务计算量所需的时间以及传输输出数据到数据驱动端所需的时间分别为
| $ \left\{ \begin{gathered} {t_{{\text{mec}}2,{\beta _i}}} = \frac{{{x_{3,i}}{\beta _i}}}{{{f_{{\text{mec}}2}}}} \\ {t_{{\text{mec}}2,{\gamma _i}}} = \frac{{{\gamma _i}}}{r} \\ \end{gathered} \right. $ | (9) |
式中:
| $ {T_{{\text{mec}}2,i}} = {t_{{\text{mec}}2,{\beta _i}}} + {t_{{\text{mec}}2,{\gamma _i}}} $ | (10) |
式中:
结合式(5) 、(8) 和(10) 可得系统处理第
| $ {T_i} = {T_{{\text{W}}{{\text{D}}_i}}} + {T_{{\text{mec}}1,i}} + {T_{{\text{mec}}2,i}} $ | (11) |
式中:
| $ {T_i} \leqslant {T_{{\text{DL}}}} $ | (12) |
式中:
本文考虑无线设备在任务计算以及数据传输过程的能量消耗。无线设备
| $ E_i^{{\text{loc}}} = \kappa {x_{1,i}}{\beta _i}f_i^2 $ | (13) |
式中:
| $ E_i^{{\text{off}}} = {p_i}{t_{i,{\text{tran}}}} $ | (14) |
结合式(13) 和(14) ,计算第
| $ {E_i} = E_i^{{\text{loc}}} + E_i^{{\text{off}}} $ | (15) |
分别记
| $ \begin{array}{c}\underset{{x}_{1,i},{x}_{2,i},{x}_{3,i},{p}_{i}}{\mathrm{min}}{\displaystyle \sum\nolimits _{i=1}^{K}({w}_{1}{E}_{i}+{w}_{2}{T}_{i}) },\\ {\rm{s.t.}} \left\{\begin{array}{l}\text{C}1:{\displaystyle \sum\nolimits _{j=1}^{3}{x}_{j,i}}=1,\forall i\in \mathcal{K}\\ \text{C}2:{p}_{i}\le {P}^{\mathrm{max}},\forall i\in \mathcal{K}\\ \text{C}3:{T}_{i}\le {T}_{\text{DL}},\forall i\in \mathcal{K}\\ \text{C4}:0\le {x}_{j,i}\le 1,j\in \{1,2,3\},\forall i\in \mathcal{K}\end{array}\right.\end{array} $ | (16) |
式中:
由于问题(16) 目标函数中任务分配比例和发射功率是耦合的,因此该问题是一个非凸优化问题。为此,本文设计一种较低计算复杂度的算法方案,将原问题解耦成任务分割和计算卸载2个子问题,首先利用内点法求解计算卸载子问题,再利用单纯形法求解最优任务分割子问题。
2.1 传输功率优化将原问题解耦成计算卸载子问题,其中问题(16) 可以变换为子问题(17)。
| $ \begin{split} &\underset{{\left\{{p}_{i}\right\}}_{i=1}^{K}}{\mathrm{min}}{\displaystyle \sum\nolimits _{i=1}^{K}\bigg[\left(\frac{{p}_{i}}{{r}_{i}}+\frac{1}{{r}_{i}}\right) }, \\& {\rm{s.t.}} \text{C}1:{p}_{i}\le {P}^{\mathrm{max}},\forall i\in \mathcal{K} \end{split} $ | (17) |
考虑到目标函数关于传输功率的复杂性,引入辅助变量
| $ \begin{split} &\underset{{\left\{{o}_{i}\right\}}_{i=1}^{K}}{\mathrm{min}}{\displaystyle \sum\nolimits _{i=1}^{K}\bigg[\bigg(\frac{({2}^{\tfrac{1}{{o}_{i}{B}_{i}}}-1) {\sigma }^{2}}{{h}_{i}}{o}_{i}+{o}_{i}\bigg) },\\ &\qquad\quad {\rm{s.t.}} \text{C}1:{o}_{i}\ge {M}_{i},\forall i\in \mathcal{K} \end{split} $ | (18) |
式中:
证明 假设
| $ \begin{array}{c}\varphi ({o_i},{\upsilon _i}) = f({o_i}) - {\upsilon _i}{\text{ln(}}{o_i} - {M_i}) \end{array}$ | (19) |
式中:
算法1 求解问题(18) 的内点法。
(1) 输入:输入惩罚因子
(2) 迭代:令式(19) 一阶导数为零,计算函数
(3) 直到:
(4) 输出:输出问题(18) 的最优解
在取得最优发射功率
| $ \begin{array}{l}\underset{{\{{x}_{1,i},{x}_{2,i}\}}_{i=1}^{K}}{\mathrm{min}}{\displaystyle \sum\nolimits _{i=1}^{K}\left({A}_{1,i}{x}_{1,i}\text+{C}_{1,i}{x}_{2,i}\right) \text+{D}_{1,i}},\\ {\rm{s.t.}} \left\{\begin{array}{l}\text{C}1:{x}_{1,i}\text+{x}_{2,i}\le 1,\forall i\in \mathcal{K}\\ \text{C}2:{F}_{i}{x}_{1,i}\text+{G}_{i}{x}_{2,i}\le\\ \quad\quad{T}_{\text{DL}}-\dfrac{{\gamma }_{i}}{ {R}}-\left(\dfrac{{\alpha }_{i}}{R}\text+\dfrac{{\beta }_{i}}{{f}_{\text{mec}2}}\text+\dfrac{{\alpha }_{i}}{{r}_{i}}\right) ,\\ \quad\quad\forall i\in \mathcal{K}\\ \text{C}3:{x}_{1,i},{x}_{2,i}\in [0,1],\forall i\in \mathcal{K}\end{array}\right.\end{array} $ | (20) |
式中:
| $ \begin{array}{*{20}{c}} {\left\{ {\begin{array}{*{20}{l}} {{F_i} = \left(\dfrac{{{\beta _i}}}{{{f_i}}} + \dfrac{{{\gamma _i}}}{{{r_i}}} + \dfrac{{{\gamma _i}}}{R}\right) - \dfrac{{{\alpha _i}}}{R} - \dfrac{{{\beta _i}}}{{{f_{{\rm{mec}}2}}}} - \dfrac{{{\alpha _i}}}{{{r_i}}}}\\ {{G_i} = \left(\dfrac{{{\beta _i}}}{{{f_{{\rm{mec}}1}}}} + \dfrac{{{\gamma _i}}}{R}\right) - \left(\dfrac{{{\alpha _i}}}{R} + \dfrac{{{\beta _i}}}{{{f_{{\rm{mec}}2}}}}\right)} \end{array}} \right.}\;\;\;\;\\ {\left\{ {\begin{array}{*{20}{l}} {{A_{1,i}} = \left( \kappa {\beta _i}f_i^2 + \dfrac{{{p_i}{\gamma _i}}}{{{r_i}}} + \dfrac{{{\beta _i}}}{{{f_i}}} + \dfrac{{{\gamma _i}}}{{{r_i}}} + \dfrac{{{\gamma _i}}}{R}\right) - }\\ \quad\quad\;{\left(\dfrac{{{\alpha _i}{p_i}}}{{{r_i}}} + \dfrac{{{\alpha _i}}}{R} + \dfrac{{{\beta _i}}}{{{f_{{\rm{mec}}2}}}} + \dfrac{{{\alpha _i}}}{{{r_i}}}\right)}\\ {{C_{1,i}} = \left(\dfrac{{{\alpha _i}{p_i}}}{{{r_i}}} + \dfrac{{{\beta _i}}}{{{f_{{\rm{mec}}1}}}} + \dfrac{{{\gamma _i}}}{R}\right) - }\\ \quad\quad\;{{\rm{ }}\left(\dfrac{{{\alpha _i}{p_i}}}{{{r_i}}} + \dfrac{{{\alpha _i}}}{R} + \dfrac{{{\beta _i}}}{{{f_{{\rm{mec}}2}}}}\right)}\\ {{D_{1,i}} = \left(\dfrac{{{\alpha _i}{p_i}}}{{{r_i}}} + \dfrac{{{\alpha _i}}}{R} + \dfrac{{{\beta _i}}}{{{f_{{\rm{mec}}2}}}} + \dfrac{{{\alpha _i}}}{{{r_i}}}\right) + \left(\dfrac{{{\gamma _i}}}{R}\right)} \end{array}} \right.} \end{array} $ |
本文利用单纯形算法求解变换后的优化问题(20) 。
首先,设置优化问题的一个初始可行解;其次,在初始可行解条件下,如果存在非初始变量
| $ \begin{array}{c}\underset{{\{{x}_{1,i},{x}_{2,i},{s}_{i}\}}_{i=1}^{K}}{\mathrm{min}}{\displaystyle \sum\nolimits _{i=1}^{K}({w}_{1}{E}_{i}+{w}_{2}{T}_{i}) },\\ {\rm{s.t.}}\left\{\begin{array}{l}\text{C}1:{x}_{1,i}+{x}_{2,i}+{s}_{1,i}=1,\forall i\in \mathcal{K}\\ \text{C2}:{A}_{2,i}{x}_{1,i}+{C}_{2,i}{x}_{2,i}+{s}_{2,i}={D}_{2,i}, \forall i\in \mathcal{K}\\ \text{C3}:{x}_{1,i},{x}_{2,i}\in [0,1],{s}_{i}\ge 0,\forall i\in \mathcal{K}\end{array}\right.\end{array} $ | (21) |
式中:
| $ \begin{array}{*{20}{l}} {\left\{ {\begin{array}{*{20}{l}} {{A_{2,i}} = \left(\dfrac{{{\beta _i}}}{{{f_i}}} + \dfrac{{{\gamma _i}}}{{{r_i}}} + \dfrac{{{\gamma _i}}}{R}\right){{ - }}\left(\dfrac{{{\alpha _i}}}{R} + \dfrac{{{\beta _i}}}{{{f_{{\rm{mec}}2}}}} + \dfrac{{{\alpha _i}}}{{{r_i}}}\right)} \end{array}} \right.}\\ {\left\{ {\begin{array}{*{20}{l}} {{C_{2,i}} = \left(\dfrac{{{\beta _i}}}{{{f_{{\rm{mec}}1}}}} + \dfrac{{{\gamma _i}}}{R}\right){{ - }}\left(\dfrac{{{\alpha _i}}}{R} + \dfrac{{{\beta _i}}}{{{f_{{\rm{mec}}2}}}}\right)}\\ {{D_{2,i}} = {T_{{\rm{DL}}}}{{ - }}\dfrac{{{\gamma _i}}}{R}{{ - }}\left(\dfrac{{{\alpha _i}}}{R} + \dfrac{{{\beta _i}}}{{{f_{{\rm{mec}}2}}}} + \dfrac{{{\alpha _i}}}{{{r_i}}}\right)} \end{array}} \right.} \end{array} $ |
优化问题(21) 是一个标准的线性规划问题,算法2对求解问题(21) 所使用的单纯形法的求解步骤进行了总结。
算法2 求解问题(21)的单纯形法。
(1) 输入:输入初始可行解
(2) 迭代:变换初始变量并保持可行性;若
(3) 直到:
| $ { {\mu ^*} = {\mu ^{(m) }} = (x_{1,i}^{(*) },x_{2,i}^{(*) },s_{j,i}^{(*) })}$ |
(4) 输出:输出问题(21)的最优解
仿真结果验证了本模型的有效性和优越性。考虑在双MEC服务器协同多用户场景下,将系统任务计算结果发送到远处数据驱动端进行驱动,其中每个基站覆盖范围为100 m,
为了比较算法性能,本文考虑了5种已有的启发式基准方案和1种最优拉格朗日法基准方案,即:(1) 启发式基准方案1:完全本地计算,所有任务都在无线设备端进行本地计算。(2) 启发式基准方案2:单服务器卸载,所有任务仅由无线设备和第一个基站分配。(3) 启发式基准方案3:混合比例卸载,所有任务由本地和服务器按比例
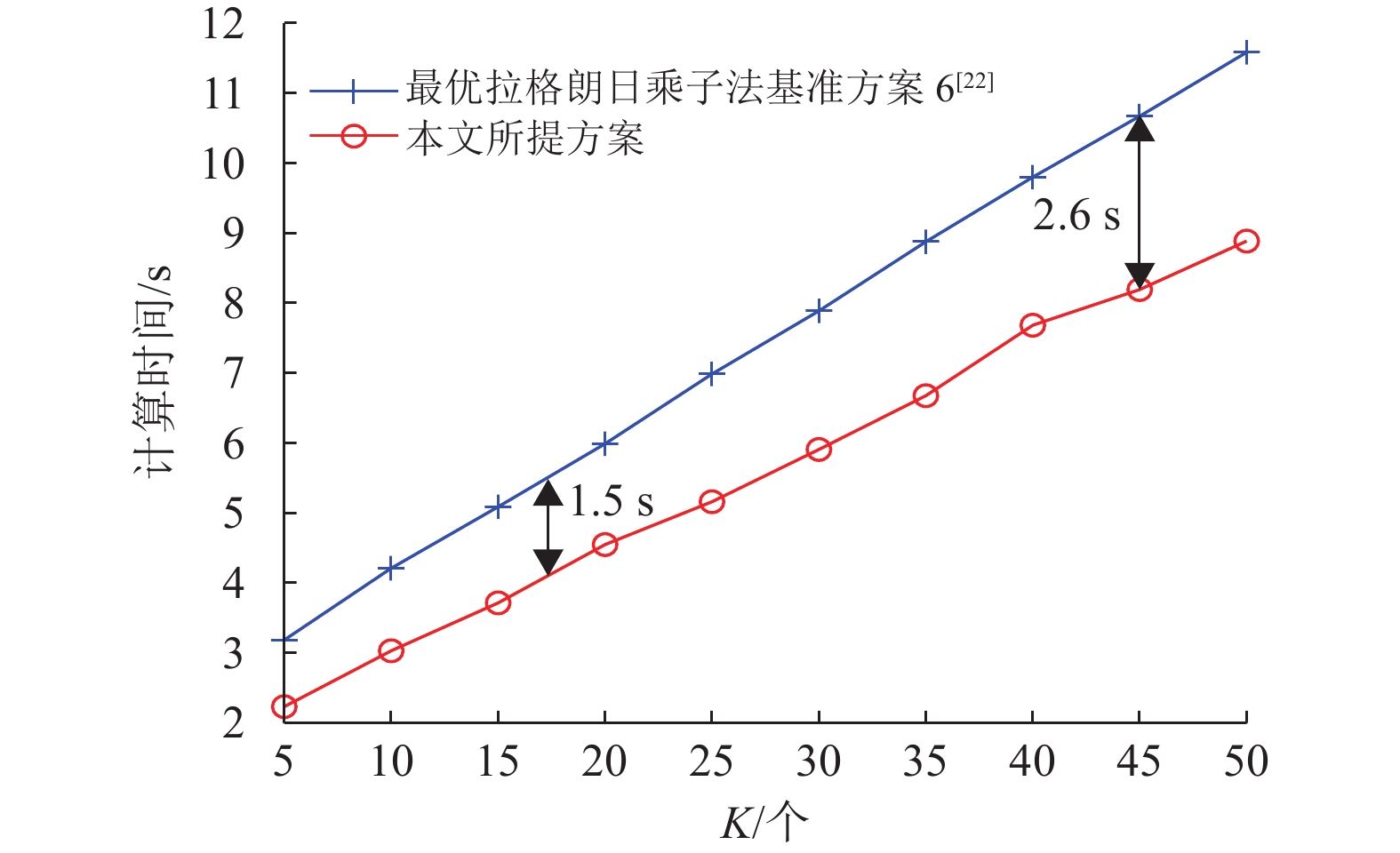
图2显示了本文所提方案与最优拉格朗日乘子法基准方案6的运行时间随不同无线设备数目变化的曲线。随着无线设备数目K的增加,本文所提方案和最优拉格朗日法基准方案6的运行时间均增加。本文所提方案的运行时间明显少于最优拉格朗日乘子法基准方案6。随着K增大,本文所提方案和最优拉格朗日法基准方案6的运行时间差距呈现增大的趋势。例如,较最优拉格朗日法基准方案6,当K=17时,本文所提算法能节省1.5 s的运行时间,当K=45时,本文所提算法能节省2.6 s的运行时间。
|
图 2 不同无线设备数目K下的系统运行时间 Figure 2 System runtime under different number of wireless device K |
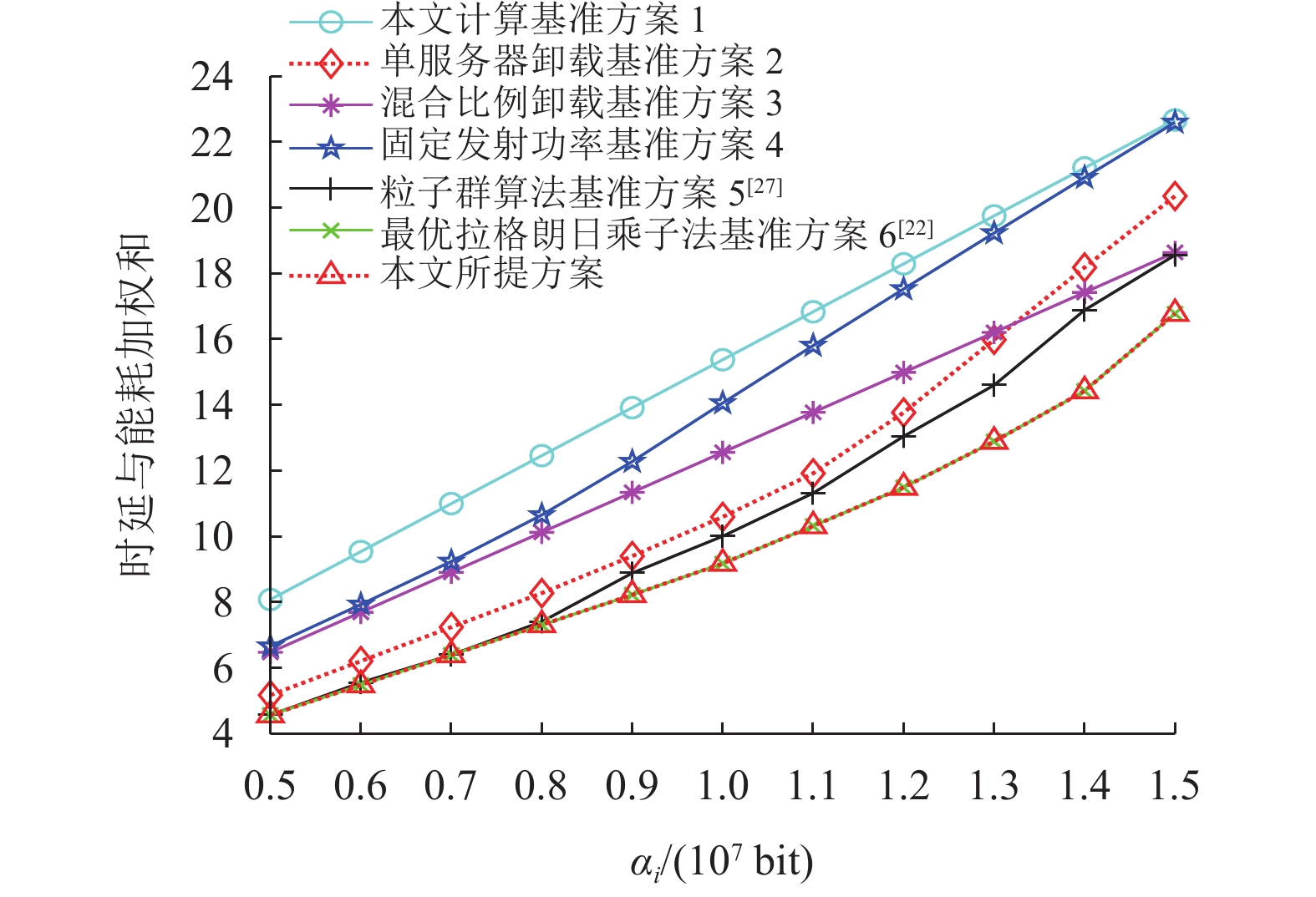
图3显示了能耗与系统时延加权和随不同输入数据量
|
图 3 不同输入数据量 |
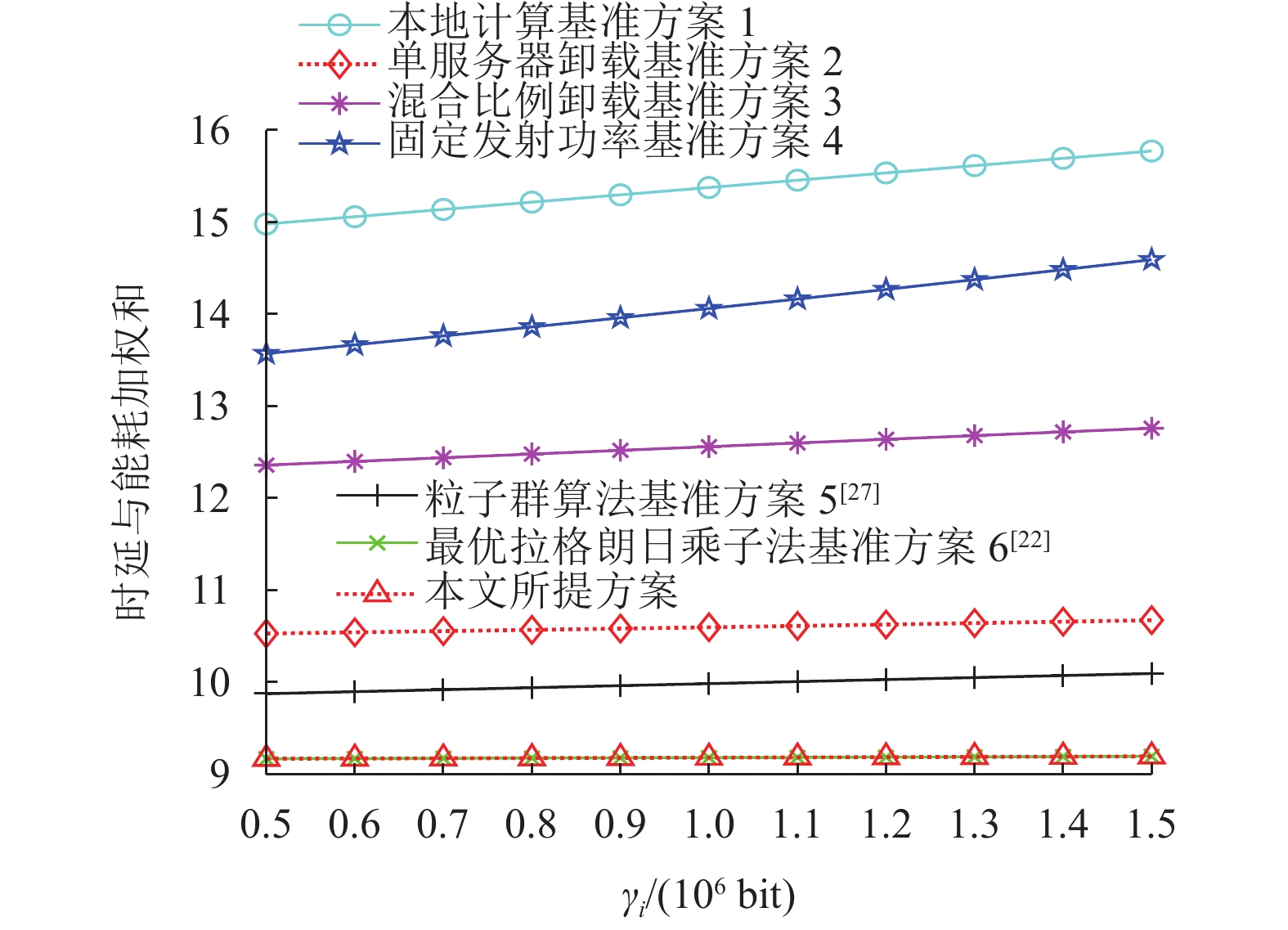
图4显示了能耗与系统时延加权和随不同输出数据量
|
图 4 不同输出数据量 |
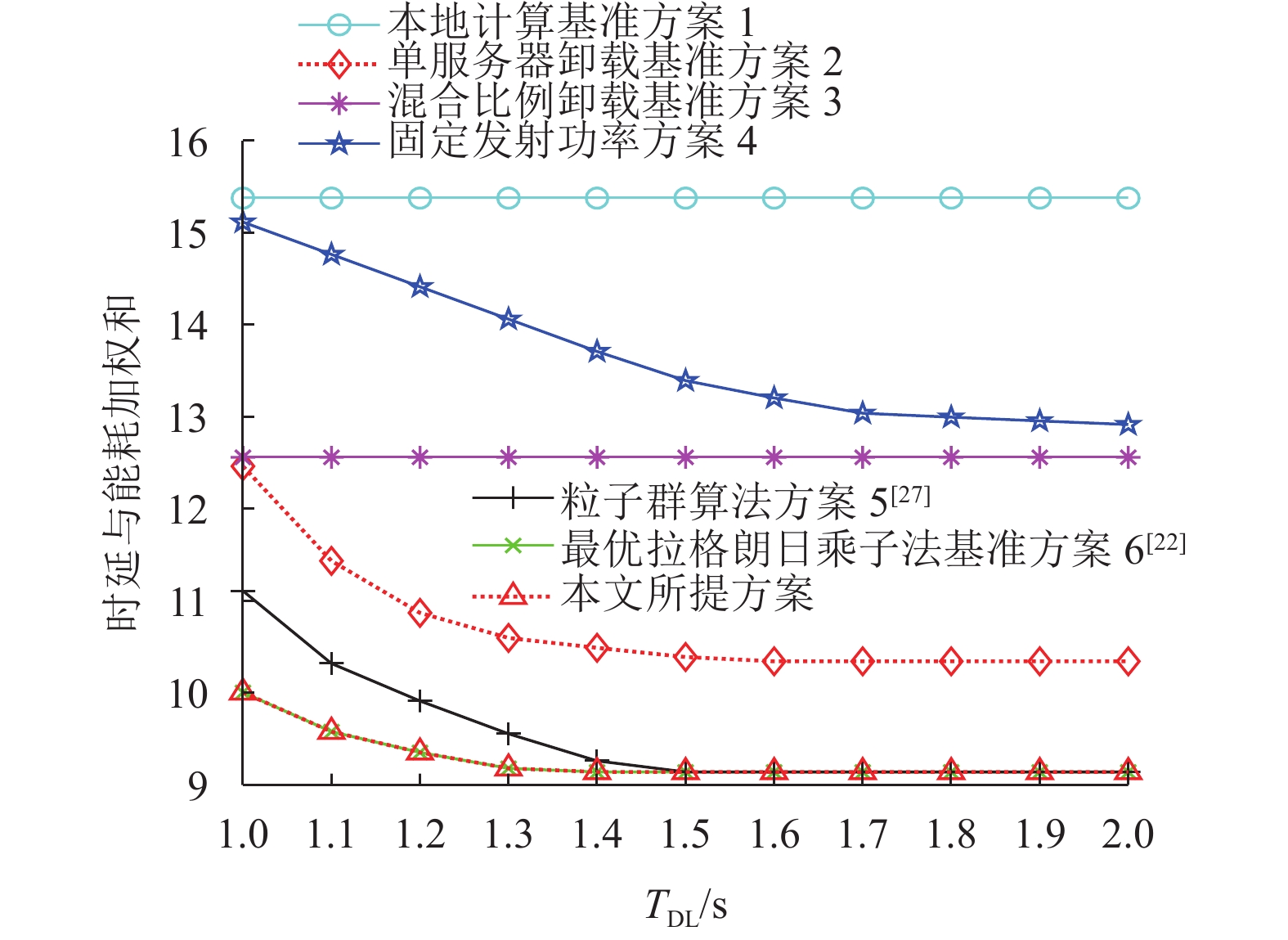
图5显示了能耗与系统时延加权和随不同时限
|
图 5 不同时延长度 |
图6显示了系统时延和能耗的加权和随着无线设备数量的增长变化的性能曲线。无线设备的数量从5增加到50,其中无线设备任务输入数据量

|
图 6 不同无线设备个数K下的时延与能耗加权和性能 Figure 6 Time delay and energy consumption weighted sum under different number of wireless device K |
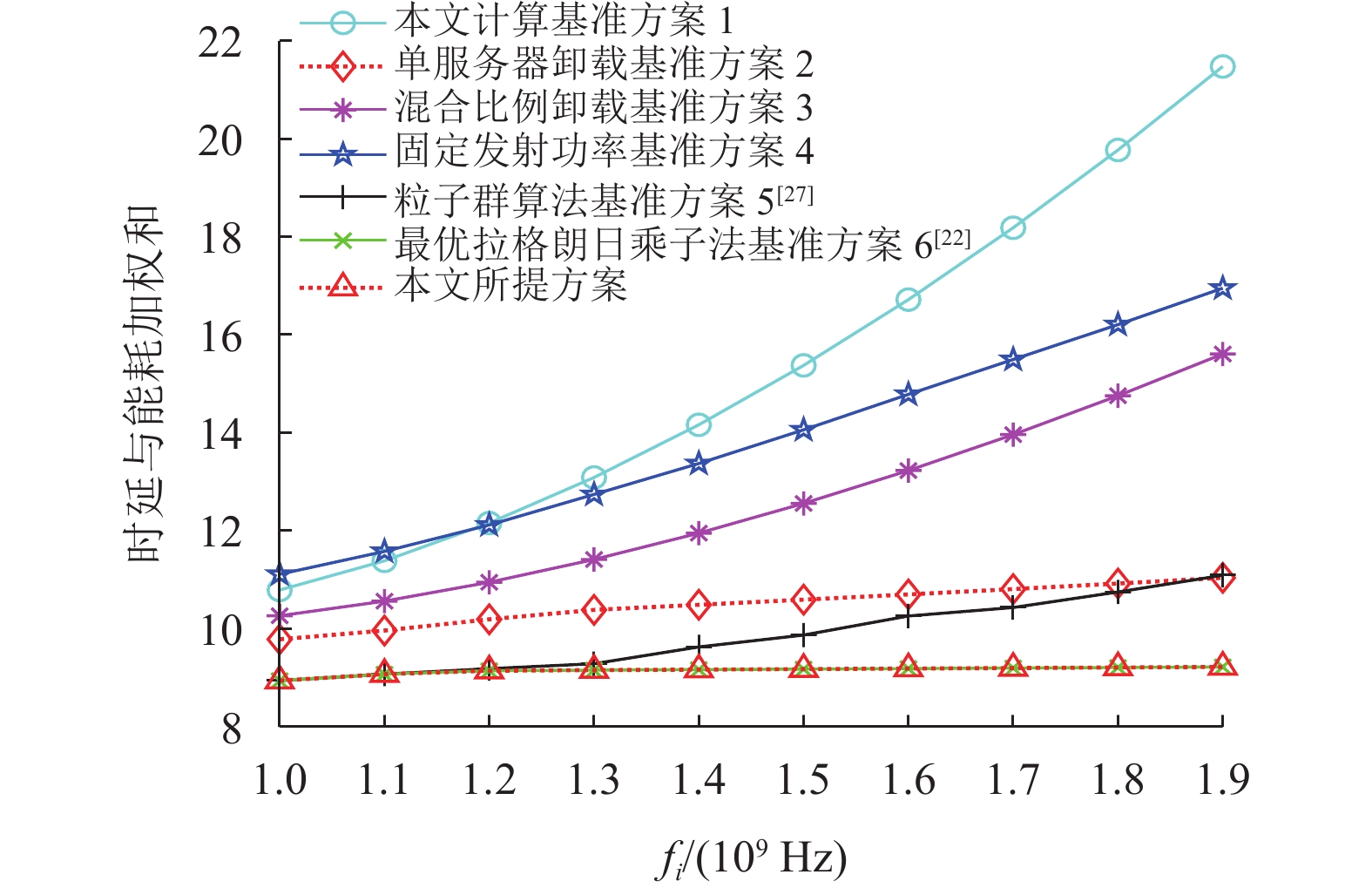
图7显示了能耗与系统时延加权和随无线设备计算能力变化的性能曲线,其中无线设备数目
|
图 7 不同无线设备计算能力 |
本文研究了双MEC服务器协同与计算通信资源联合优化设计方案,以系统计算时延和用户能耗的加权和最小化为准则,联合优化用户计算任务分割和计算卸载发射功率。本文提出一种较低计算复杂度的算法方案,将原联合设计问题解耦为计算卸载和任务分割的2个子问题,分别采用内点法和单纯形法实现快速数值求解。仿真结果表明,本文所提算法的系统性能优于已有的启发式基准方案,并在较低的算法运行时间下,本文所提方案能取得与最优拉格朗日乘子法基准方案相同的系统性能。
| [1] |
MACH P, BECVAR Z. Mobile edge computing: a survey on architecture and computation offloading[J].
IEEE Communications Surveys & Tutorials, 2017, 19(3): 1628-1656.
|
| [2] |
MAO Y, YOU C S, ZHANG J, et al. A survey on mobile edge computing: the communication perspective[J].
IEEE Communications Surveys & Tutorials, 2017, 19(4): 2322-2358.
|
| [3] |
赵竑宇. 资源受限的移动边缘计算系统中计算卸载问题研究[D]. 北京: 北京邮电大学, 2019.
|
| [4] |
WANG F, XU J, DING Z. Multi-antenna noma forcomputation offloading in multiuser mobile edge-computing systems[J].
IEEE Transactions on Communications, 2019, 67(3): 2450-2463.
DOI: 10.1109/TCOMM.2018.2881725. |
| [5] |
HUYNH L N T, PHARN Q V, PHAM O V, et al. Efficient computation offloading in multi-tier multi-access edge computing systems: a particle swarm optimization approach[J].
Applied Sciences, 2020, 10(1): 203.
|
| [6] |
景泽伟, 杨清海, 秦猛. 移动边缘计算中的时延和能耗均衡优化算法[J]. 北京邮电大学学报, 2020, 43(2) : 110-115.
JING Z W, YANG Q H, QIN M. A delay and energy tradeoff optimization algorithm for task offloading in mmobile edge computing network [J]. Journal of Beijing University of Posts and Telecommunications, 2020, 43(2) : 110-115. |
| [7] |
GONG Y. Optimal edge server and service placement in mobile edge computing [C]// 2020 IEEE 9th Joint International Information Technology and Artificial Intelligence Conference. Chongqing: IEEE, 2020: 688-691.
|
| [8] |
GUO H, LIU J. Collaborative computation offloading for multiaccess edge computing over fiberwireless networks[J].
IEEE Transactions on Vehicular Technology, 2018, 67(5): 4514-4526.
DOI: 10.1109/TVT.2018.2790421. |
| [9] |
龙隆, 刘子辰, 石晶林, 等. 移动边缘计算中计算卸载与资源分配的联合优化策略[J].
高技术通讯, 2020, 30(8): 765-773.
LONG L, LIU Z C, SHI J L, et al. Joint optimization strategy of service cache and resource allocateon in mobile edge network[J]. High Technology Tetters, 2020, 30(8): 765-773. |
| [10] |
KUANG Z, LI L, GAO J, et al. Partial offloading scheduling and power allocation for mobile edge computing systems[J].
IEEE Internet of Things Journal, 2019, 6(4): 6774-67-85.
DOI: 10.1109/JIOT.2019.2911455. |
| [11] |
TANG L, HU H. Computation offloading and resource allocation for the internet of things in energy constrained mecenabled hetnets[J].
IEEE Access, 2020, 8: 47509-47521.
DOI: 10.1109/ACCESS.2020.2979774. |
| [12] |
ZHANG J, XIA W W , ZHANG Y Y, et al. Joint offloading and resource allocation optimization for mobile edge computing[C]// IEEE Global Communications Conference. Singapore: IEEE, 2017: 1-6.
|
| [13] |
FENG H, GUO S, YANG L, et al. Collaborative data caching and computation offloading for multi-service mobile edge computing[J].
IEEE Transactions on Vehicular Technology, 2021, 70(9): 9408-9422.
DOI: 10.1109/TVT.2021.3099303. |
| [14] |
ZHANG J, HU X P, NING Z L, et al. Energy latency tradeoff for energy-aware offloading in mobile edge computing networks[J].
IEEE Internet of Things Journal, 2018, 5(4): 2633-2645.
DOI: 10.1109/JIOT.2017.2786343. |
| [15] |
PENG J, QIU H, CAI J, et al. D2D-assisted multi-user cooperative partial offloading transmission scheduling and computation allocateng for MEC[J].
IEEE Transactions on Wireless Communications, 2021, 20(8): 4858-4873.
DOI: 10.1109/TWC.2021.3062616. |
| [16] |
NING Z, DONG P, KONG X, et al. A cooperative partial computation offloading scheme for mobile edge computing enabled internet of things[J].
IEEE Internet of Things Journal, 2019, 6(3): 4804-4814.
DOI: 10.1109/JIOT.2018.2868616. |
| [17] |
BI J, YUAN H, ZHANG K, et al. Energy-minimized partial computation offloading for delay sensitive applications in heterogeneous edge networks[J].
IEEE Transactions on Emerging Topics in Computing, 2022, 10(4): 1941-1954.
DOI: 10.1109/TETC.2021.3137980. |
| [18] |
FANG F, XU Y, DING Z, et al. Optimal resource allocation for delay minimization in NOMA-MEC networks[J].
IEEE Transactions on Communications, 2020, 68(12): 7867-7881.
DOI: 10.1109/TCOMM.2020.3020068. |
| [19] |
XUE J, AN Y. Joint task offloading and resource allocation for multi-task multi-server NOMA-MEC networks[J].
IEEE Access, 2021, 9: 16152-16163.
DOI: 10.1109/ACCESS.2021.3049883. |
| [20] |
XU J, ZHU P, LI J, et al. Secure computation offloading for multi-user multi-server MEC-enabled IoT[C]// IEEE International Conference on Communications. Montreal: IEEE, 2021: 1-6.
|
| [21] |
SHANG C, SUN Y, LUO H. A hybrid deep reinforcement learning approach for dynamic task offloading in NOMA-MEC system [C]//IEEE International Conference on Sensing, Communication, and Networking (SECON) . Stockholm: IEEE, 2022: 434-442.
|
| [22] |
代美玲, 刘周斌, 郭少勇, 等. 基于终端能耗和系统时延最小化的边缘计算卸载及资源分配机制[J]. 电子与信息学报, 2019, 41(11) : 2684-2690.
DAI M L, LIU Z B, GUO S Y, et al. A computation offloading and resource allocation mechanism based on minimizing devices energy consumption and system delay [J]. Journal of Electronics & Information Technology , 2019, 41(11) : 2684-2690. |
| [23] |
FAN W H, HAN J T, YAO L, et al. Latency-energy optimization for joint wifi and cellular offloading in mobile edge computing networks[J].
Comput Networks, 2020, 181: 107570.
DOI: 10.1016/j.comnet.2020.107570. |
| [24] |
CAO X W, WANG F, XU J, et al. Joint computation and communication cooperation for energy-efficient mobile edge computing[J].
IEEE Internet of Things Journal, 2019, 6(3): 4188-4200.
DOI: 10.1109/JIOT.2018.2875246. |
| [25] |
LUO Z Q, MA W K, SO A M C, et al. Semidefinite relaxation of quadratic optimization problems[J].
IEEE Signal Processing Magazine, 2010, 27(3): 20-34.
DOI: 10.1109/MSP.2010.936019. |
| [26] |
王丰, 李宇龙, 林志飞, 等. 基于计算吞吐量最大化的能量采集边缘计算系统在线资源优化配置[J]. 广东工业大学学报, 2022, 39(4) : 17-23.
WANG F, LI Y L, LIN Z F, et al. Online resource allocation design for computation capacity maximization in energy harvesting mobile edge computing systems [J]. Journal of Guangdong University of Technology, 2022, 39(4) : 17-23. |
| [27] |
李顺, 葛海波, 刘林欢, 等. 移动边缘计算中的协同计算卸载策略[J]. 计算机工程与应用, 2022, 58(21) : 83-90.
LI S, GE H B, LIU L H, et al. Collaborative computing offloading sstrategy in mobile edge computing [J]. Computer Engineering and Applications, 2022, 58(21) : 83-90. |
 2024, Vol. 41
2024, Vol. 41

