信道极化概念在文献[1]中首次被提出,是目前唯一能够被严格证明在二进制无记忆信道中可达到信道容量上限的一种编码方式。基于这一原理,文献[1]提出一种全新的编码方式,命名为极化码。经过逐步完善,极化码被选定为5G标准中控制信道的信道编码方式。
文献[1]中同样提出了极化码编码相对应的译码算法,连续删除(Successive Cancellation, SC) 译码算法,由于SC具有低复杂度的特点,所以SC译码算法成为最主流的一类极化码译码算法之一。然而SC译码算法同时也面临着纠错性能较差、吞吐率较低等问题。为了解决这些缺陷,文献[2-3]中引入了多路径度量竞争的思路,提出连续删除列表(Successive Cancellation List, SCL) 译码和连续删除堆栈(Successive Cancellation Stack, SCS) 译码算法。SCL译码算法基于广度优先的原则对最优路径搜索,同时扩展多条译码路径。而SCS译码算法基于深度优先原则,对最优路径进行扩展。这两种改进算法具有相近的纠错性能且相较于SC译码算法有着显著的提升,而SCS在高信噪比(Signal-to-Noise-Ratio, SNR)时对比于SCL译码算法具有更低的复杂度。除此之外,部分其余的改进算法也值得关注,文献[4]提出循环冗余校验(Cyclic Redundancy Check, CRC) 级联的方法,在SC译码中加入CRC从而提高纠错性能,这一方法易于实现且未对SC算法本身做出改动,因此可以与其他许多的优化算法叠加使用,例如在文献[5-6]将CRC推广到SCL与SCS译码中,提出CRC辅助SCS(CRC Assist-SCS, CA-SCS) 译码算法和CRC辅助SCL译码算法(CRC Assist-SCL, CA-SCL) 。在非SC类译码算法中,目前关注度较高的是置信度传播(Belief Propagation, BP) 译码算法[7],并且在文献[8-9]中加入比特翻转(Bit-Flipping) 使其纠错性能得到进一步提升。BP算法本身具有高度并行性,在吞吐率方面具有较大优势,但这同样也造成了较高的运算复杂度和空间复杂度,因此在硬件实现中BP算法的应用场景较窄,并没有在硬件实现中成为一种主流的译码算法。
而极化码译码算法能否进行高效硬件实现,是以上算法得以实际应用的前提。根据SC类译码算法的递归运算原理可知,其递归运算由基本的运算单元组成。文献[10]提出了树形结构,将运算单元以树形连接。然而该结构的硬件利用率低,每个周期仅有一层的运算单元被激活。而文献[11]在这一基础上提出平行结构与半平行结构,以极小的时延为代价,将运算单元数量减少至原来的1/4,同时提高了硬件利用率。此外,提高译码器吞吐率也是在硬件设计中所面临的另一项挑战。文献[12-14]主要在硬件吞吐率上做进一步的改进,例如引入2-bits判决策略,提出矢量交叠架构实现帧间流水线等方式。文献[15]针对SCL译码提出低延迟列表译码(Reduced Latency List Decoding, RLLD) 算法,通过减少节点的访问来提高译码速度。文献[16]考虑了架构的灵活性提出可配置的SCL译码器,扩展了SCL译码器的应用场景。文献[17]则针对SCS译码排序提出双堆栈结构实现路径排序功能。然而这种双堆栈结构受到读写与比较策略的限制,其路径选择过程效率较低并且受SNR影响。而且,堆栈存储的结构使得同一路径的不同类型的数据必须进行捆包打包,对于不同类型的路径信息读写不灵活。另外,对于SC类译码算法,文献[18-19]提出的部分和更新的结构,通过寄存器存储的方式可以用较少的硬件资源实现部分和的层内并行、层间串行的更新。
针对当前SCS译码在路径选择中效率较低与路径信息存储信息不够灵活的问题,本文针对SCS译码算法提出一种基于并行比较和升调排序的路径选择方式,利用存储器组代替堆栈结构。相较于目前的SCS路径存储策略,该策略更具备灵活性,通过对不同路径值(Path Value, PV) 的独立存储,实现单条路径中不同类型的信息单独读写。另外,本文在部分和更新结构上,充分利用FPGA的并行性,直接利用组合逻辑进行运算,能够实现多层并行,提高了部分和更新的效率。
1 SC类译码算法极化码属于线性分组码,码长必须满足
| $ {{\boldsymbol{x}}}_1^N = {{\boldsymbol{u}}}_1^N{{\boldsymbol{G}}} = {{\boldsymbol{u}}}_1^N{{{\boldsymbol{F}}}^{ \otimes n}}, $ | (1) |
式中:“
现假定信道模型为二进制无记忆离散信道(Binary Discrete Memoryless Channel, B-DMC) ,用
| $ {L_i} = \ln \left( {\frac{{W_N^{(i) }({\boldsymbol{y}}_1^N,\hat {\boldsymbol{u}}_1^{i - 1}|0) }}{{W_N^{(i) }({\boldsymbol{y}}_1^N,\hat {\boldsymbol{u}}_1^{i - 1}|1) }}} \right) $ | (2) |
利用接收端所接收到的信息序列
| $ {\hat{u}}_{i}=\left\{ {\begin{array}{*{20}{l}} 0,& {L}_{i}\geqslant0 \;\;\text{or}\;\; i\in {A}^{\text{c}}\\ 1,& \text{otherwise}\end{array}} \right.$ | (3) |
式(3)中,当
SC译码算法可用满二叉树来表示译码过程。一个码长为N的SC译码流程的二叉树层数为n,LLR值从根节点向下传递为LLR值递归运算,而从叶子节点向上传递为部分和运算,每个节点都包含LLR值矢量和部分和值矢量两组值,分别用
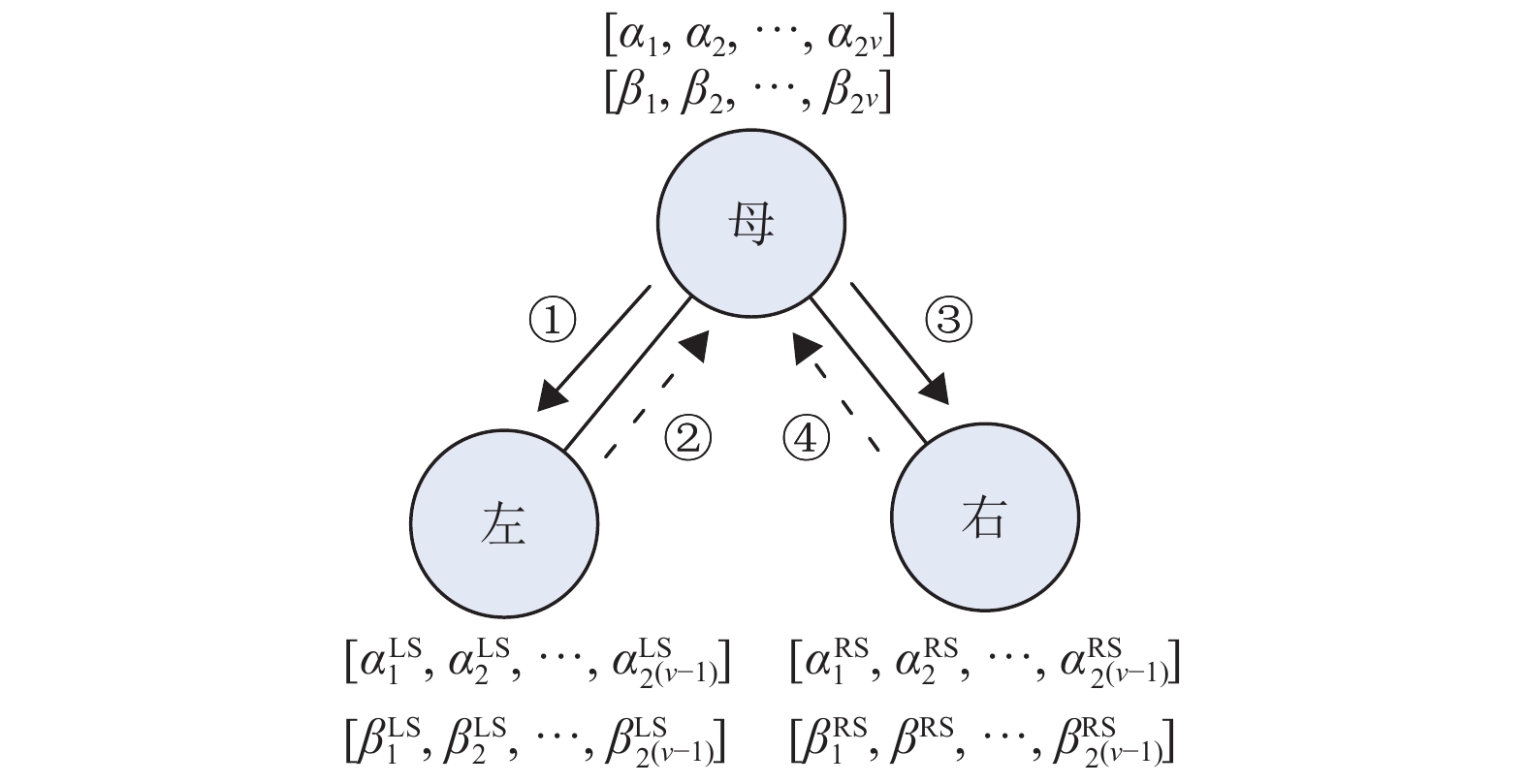
|
图 1 SC译码过程图 Figure 1 The process of SC decoding |
| $ \alpha _{^i}^{{\text{LS}}}({\alpha _i},{\alpha _{i + {2^{\lambda - 1}}}}) = {\text{sign}}({\alpha _i},{\alpha _{i + {2^{\lambda - 1}}}}) \min \{ |{\alpha _i}|,|{\alpha _{i + {2^{\lambda - 1}}}}|\} $ | (4) |
完成LLR值运算与比特判决后左子节点返回部分和
| $ \alpha _i^{{\text{RS}}}\left({\alpha _i},{\alpha _{i + {2^{\lambda - 1}}}},{\beta _i}\right) = {( - 1) ^{{\beta _i}}}{\alpha _{i + {2^{\lambda - 1}}}} + {\alpha _i}, $ | (5) |
一般地,将式(4) ~(5) 分别记作f 运算和g运算。待右子节点返回部分和值
| $ {\beta }_{i}=\left\{\begin{array}{l}{\beta }_{i}^{\text{LS}}\oplus {\beta }_{i}^{\text{RS}},\;\; i\leqslant {2}^{\lambda }\\ {\beta }_{i}^{\text{RS}},\;\; \text{otherwise}\end{array} \right.$ | (6) |
部分和值传递至上一层节点后,上层节点继续向其他未被激活的节点进行LLR值递归运算与比特判决,直至二叉树中所有叶子节点都完成比特判决即完成译码。
1.2 SCS译码算法SCS算法的主要思路是通过引入路径度量值(Path Metric,PM)计算,通过PM值大小来对每个路径的优劣程度进行度量,每次只对当前最优路径进行扩展,其余次优路径存储于堆栈中,一直扩展至路径长度(Path Length, PL) 值等于码长N结束。用p表示当前出栈的路径。PV值与比特索引值等价,可用i表示,当前出栈路径的LLR值递归运算结果用
| $ {M}_{i}^{p}=\left\{\begin{array}{l}{M}_{(i-1) }^{p},\;\; \text{if}\;\; i\in A\cap B\\ {M}_{(i-1) }^{p}+\left|{L}_{i}^{p}\right|,\;\; \text{else if}\;\; i\in A\cap \overline{B}\\ +\infty ,\;\; \text{otherwise}\end{array}\right. $ | (7) |
式中:
图2为N=4的SCS译码算法的译码过程演示图,向左扩展为比特“0”扩展,向右为比特“1”扩展,实线箭头表示被激活的路径,虚线则表示未被激活的路径,节点下方的数值为当前路径的PM值。与SCL算法中通过对多条路径同步扩展的策略不同,SCS译码算法仅对堆栈中的最优路径进行扩展,其余候选路径存于堆栈中。相当于将整个搜索过程合理“串行化”,这样做的最大好处在于可以节省大量的不必要的路径搜索,降低计算复杂度。

|
图 2 N=4下SCS译码流程图 Figure 2 The process of SCS decoding with N=4 |
SCS译码过程中涉及两个重要参数,堆栈深度和搜索宽度,分别用D和L表示,两者都对SCS译码算法的性能起到重要影响,堆栈深度D表示最多能保留下来的候选路径数量,而搜索宽度L则表示等长路径可以保留的最大数。
译码器在接收到信息矢量
在译码过程中,将当前最优PV值
算法1 SCS译码算法
1) 输入:
2) 初始化
(a) 路径扩展:出栈当前最优路径
(b) 扩展生成新路径:
(c) 入栈判定:
i. 若成立,删除栈底路径后新路径入栈
ii. 否则,新路径直接入栈
(d)
(e) 搜索宽度判断:
i. 若成立,删除堆栈中PV值小于i的路径,
ii. 否则,无操作
(f) 堆栈路径根据PM值从小到大排序,栈顶为最优 路径
(g) i=i+1
3) 直至i=N
4) 输出:
SCS译码算法的时间复杂度取决于当前信道的SNR值,但是相较于SCL译码算法,SCS译码算法避免了大量的不必要的路径扩展,特别是在高SNR的场景下,时间复杂度可以减少至
而对于空间复杂度来说,SC译码算法的空间复杂度为
在现有的SCS译码算法的硬件实现架构中,在路径排序部分,通常使用双堆栈结构进行路径排序与路径选择,一个作为候选路径存储的堆栈,另一个则作为排序过程中临时存储的数据,通过遍历堆栈中原有路径与新路径逐一比较的方式进行排序。这种排序方式在一个时刻内只能进行一次比较,效率较低,特别在堆栈存储数据量大时会造成大量时延,在最坏的情况下,排序的时延等于2D。
2 SCS译码器的硬件架构为了优化上述所提到的问题,本文提出一种新的SCS译码器硬件架构,如图3所示,总共包含4个模块:SC译码单元(SC Decode Unit) 、路径度量单元(Path Metric Unit) 、路径选择单元(Path Selection Unit) 和控制单元(Control Unit) 。下面对主要单元进行进一步详细说明和介绍。

|
图 3 SCS译码器顶层架构 Figure 3 The top architecture of SCS decoder |
SC译码单元主要包含:LLR存储器、部分和更新模块和计算单元模块。信道LLR值经过定点量化后存入LLR存储器中,在进行递归运算时根据当前路径长度读出相应LLR值。根据SC译码算法原理,SC递归运算主要包含
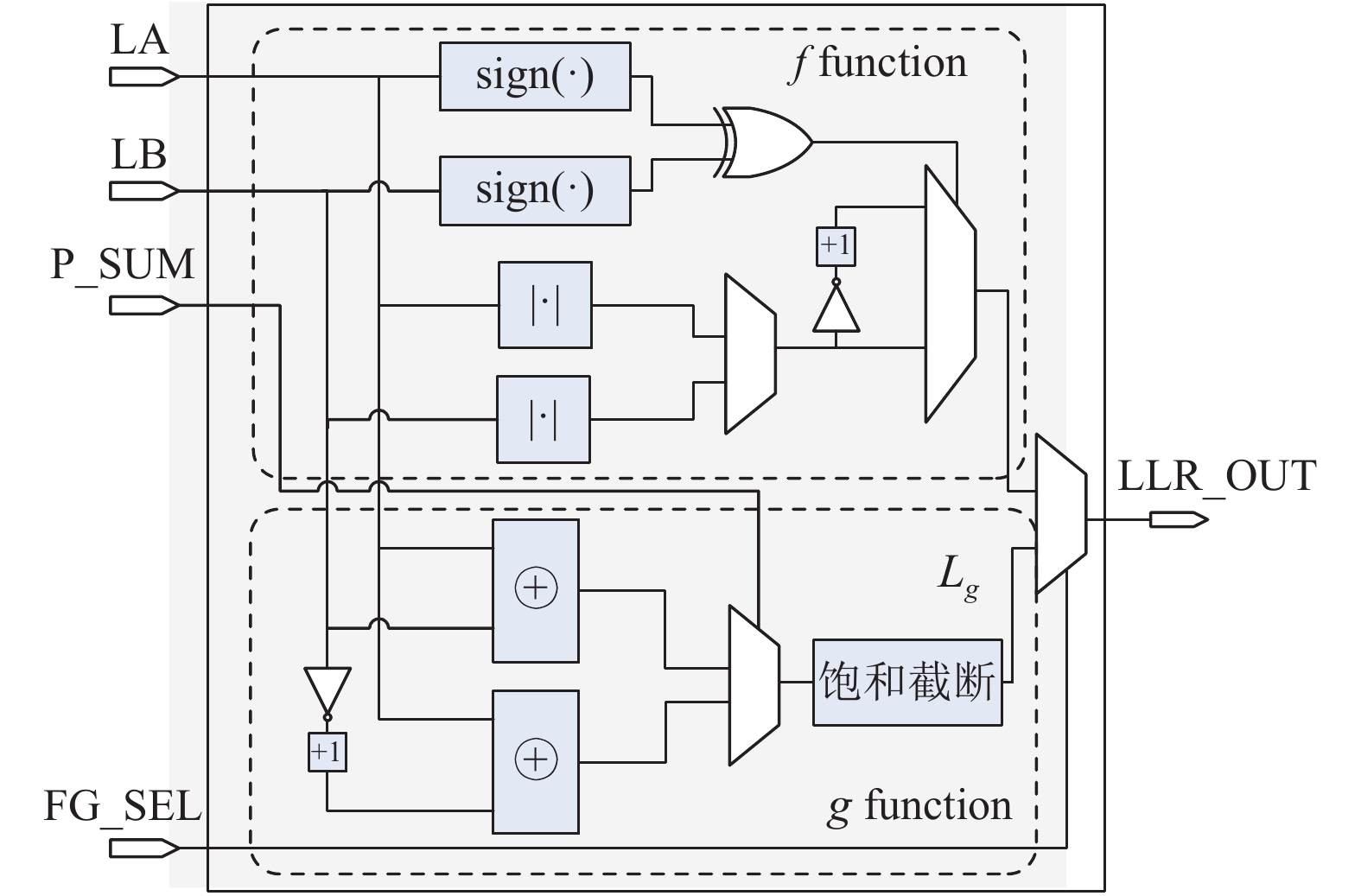
|
图 4 PE运算单元 Figure 4 The architecture of PE |
图4中,上半部分实现
| $ {L}_{g}=\left\{\begin{array}{l}\text{sign}({L}_{g}) {L}_{\mathrm{max}},\;\; \text{if}\;\; \left|{L}_{g}\right| > {L}_{\mathrm{max}}\\ {L}_{g},\;\; \text{otherwise}\end{array} \right.$ | (8) |
在递归运算结构上,基于硬件开销与运算时延的综合考虑,本文使用半平行架构实现递归运算,其结构示意如图5所示。
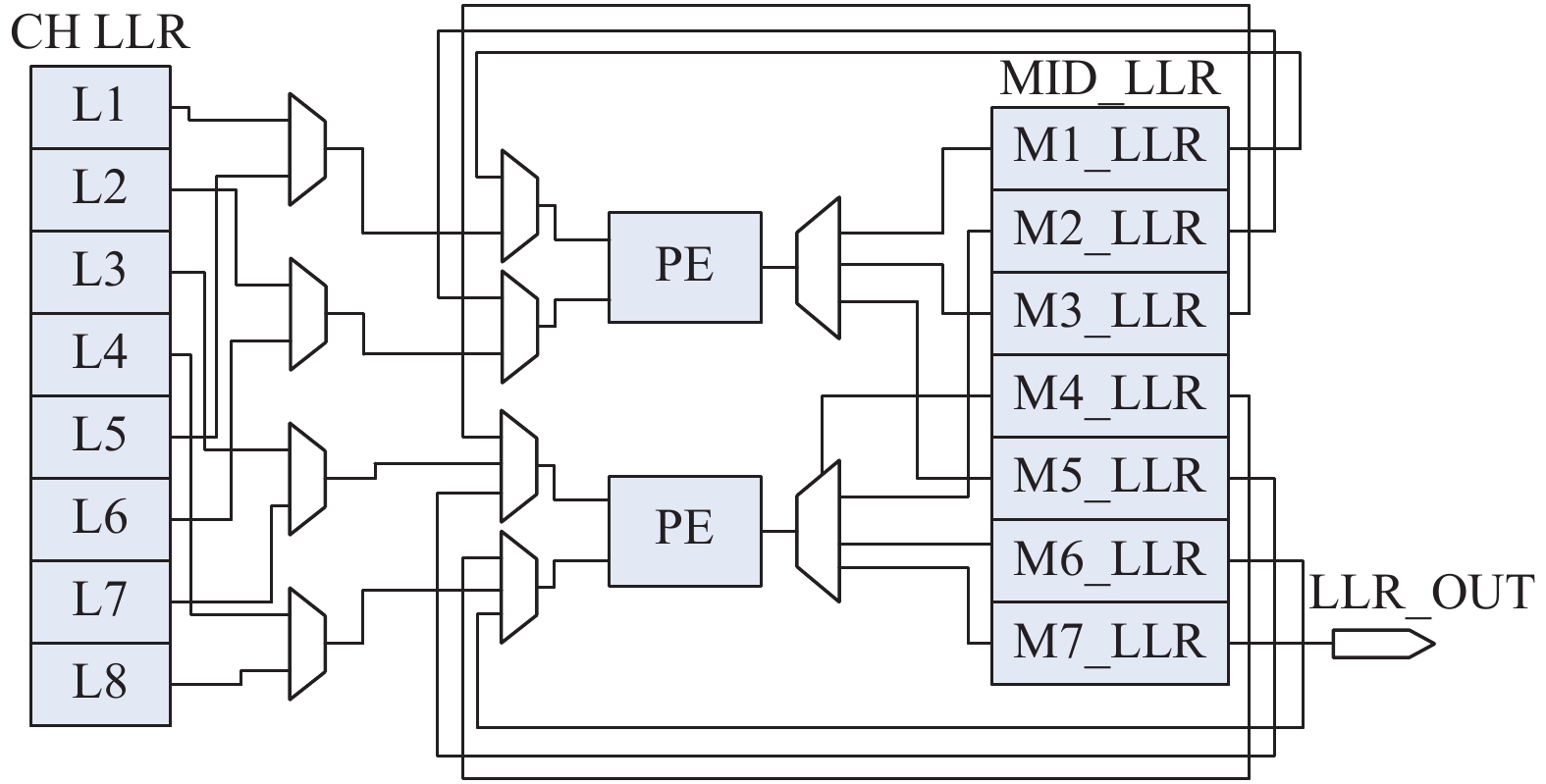
|
图 5 N=8半平行结构 Figure 5 The architecture of semi-parallel with N=8 |
图5以码长为8的递归运算结构为例,左侧CH_LLR为初始LLR值,右侧MID_LLR则为中间运算的LLR值。根据SC译码算法的递归运算原理,层内并行运算,所以每个周期内最多有N/2个PE被激活。然而继续分析可知,仅有在
传统的部分和模块都是对前一比特的部分和数据进行暂存,在暂存的部分和数据的基础上进行更新,并且这种策略每一层数据都依赖上一层的更新结果,在策略上无法实现层间并行。同时,根据SCS译码算法的特点,SCS译码算法在译码过程中由于路径不等长,存在路径回溯的情况,所以该策略不适用于SCS译码。本文的部分和更新中,利用当前最优路径的PV值,直接对下一索引的部分和进行更新,不再对前一索引的部分和数据进行暂存。同时在层间使用组合逻辑的方式进行运算,充分利用硬件的高并行性的特点,实现层间并行运算。图6为N=8的部分和更新模块,左侧ESI_U0~ESI_U7为输入PV值,PATH_LEN为路径长度值,PS_OUT为部分和输出,部分和输出选择器根据当前PL值来判断输出的对应长度值。
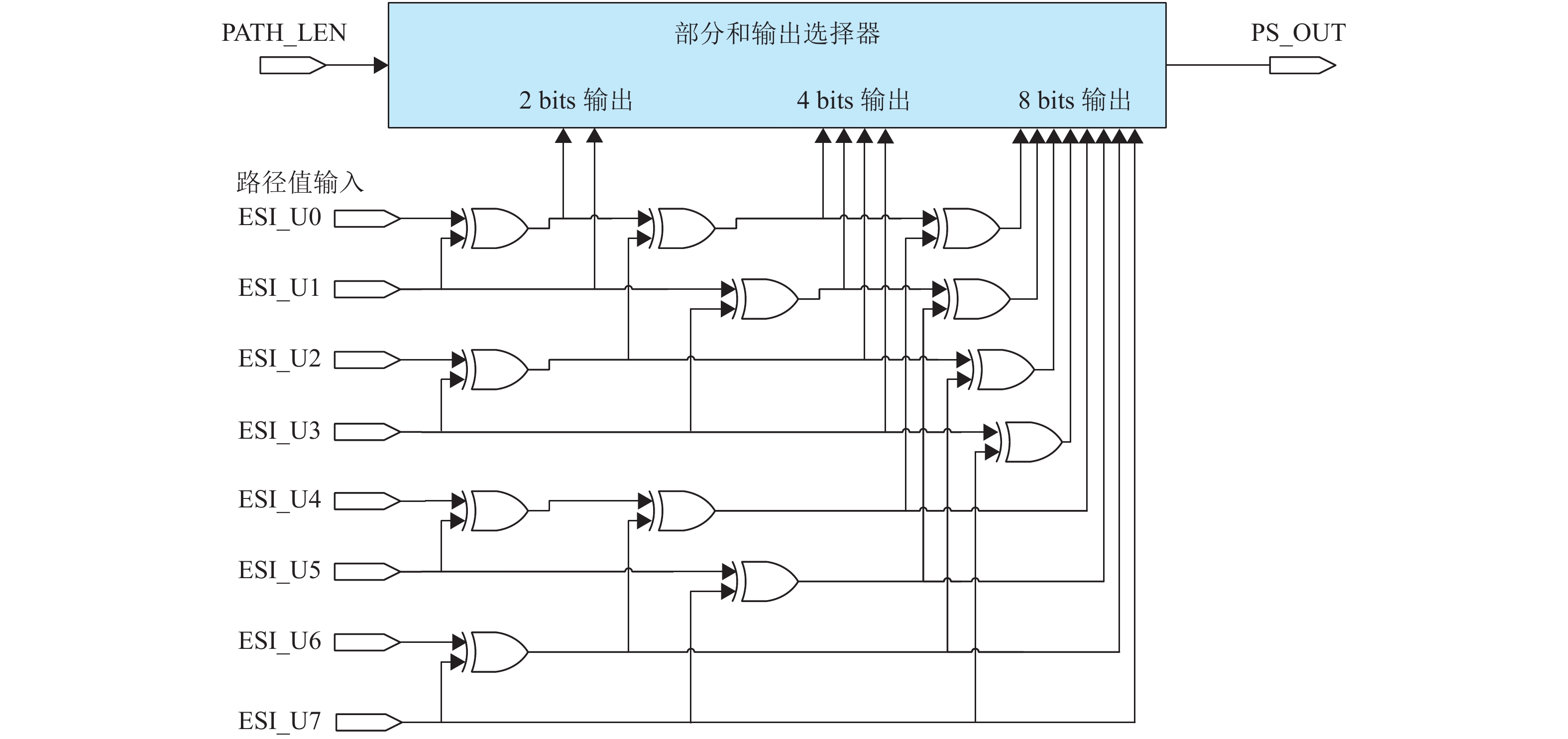
|
图 6 N=8 的部分和更新模块 Figure 6 The architecture of partial sum module with N=8 |
在经过路径值度量单元对路径进行扩展及计算出对应的PM值后,两条新路径将被输入至路径选择模块,向“0”和“1”扩展的两条新路径分别用PATH0和PATH1表示。路径选择单元包含候选路径存储器组和路径选择模块,每条候选路径都包含3种信息:路径度量值PM、路径值PV及路径长度值PL。在传统的路径选择单元中,每条候选路径的这3种信息会被打包然后送入堆栈中。在进行路径选择时,根据SCS译码原理,进行路径选择操作仅需要使用PM值数据。然而因为数据在堆栈中被打包的缘故,所对应的PV值及PL值都会被读出,造成了大量的不必要读写,增加了路径选择过程中的复杂度。针对这一问题,本文中的路径选择单元对这3种不同的信息进行单独存储,通过统一的地址读写控制来保证其信息的对应性。而在进行路径选择过程中,仅需要对PM值存储器进行单独的操作即可,在最后完成路径选择后才对其余对应的PL值和PV值进行读出,减少了在中间过程中大量不必要的读写。
在路径选择模块中,本文采用分组单调排序与并行比较相结合的方式。这种方式相较于传统的SCS译码器效率更高,其结构图如图7所示,在完成新路径写入后,将度量值存储器中所有PM值读出,读出的PM值与所对应的地址值拼接,送入路径选择模块中。在
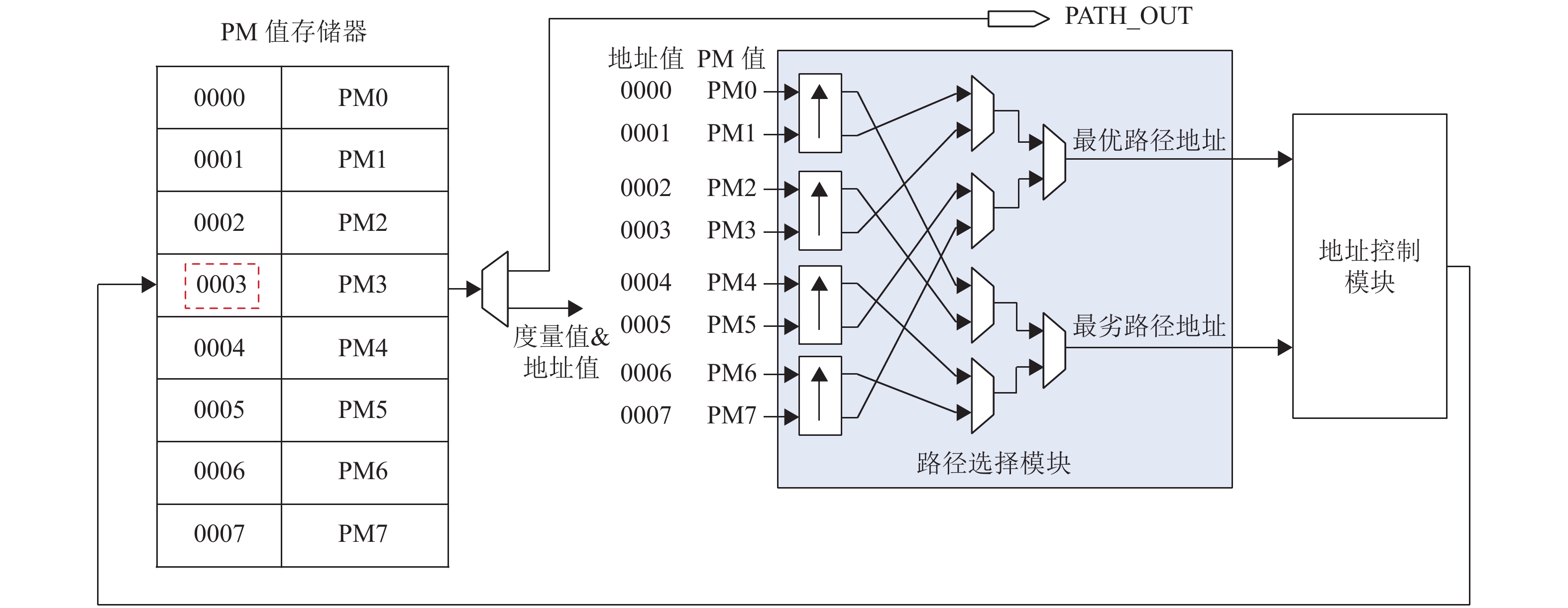
|
图 7 路径选择模块结构图 Figure 7 The architecture of path selection |
新路径写入存储器组的策略分为存储器存满和未存满两种情况,如图8所示。图8(a)为未存满情况下的存储策略,由于每次路径选择完成后,最优路径必然读出,这就意味着该最优路径POP_ADDR地址在下一次译码时处于空闲状态,所以将POP_ADDR作为下轮译码中PATH0的写入地址。同时定义一个计数器指针CNT_ADDR,该指针一直指向最小的空闲地址,该地址作为PATH1的写入地址,将PATH1按顺序存入存储器,直至存储器存满。而在存储器即将存满时,如图8(b)所示,地址控制器将使能路径选择模块中的最劣路径选择功能,此时路径选择模块则会返回两个地址值:最优路径地址POP_ADDR和最劣路径地址DEL_ADDR,设上一个译码周期返回的最优地址和最劣地址分别为
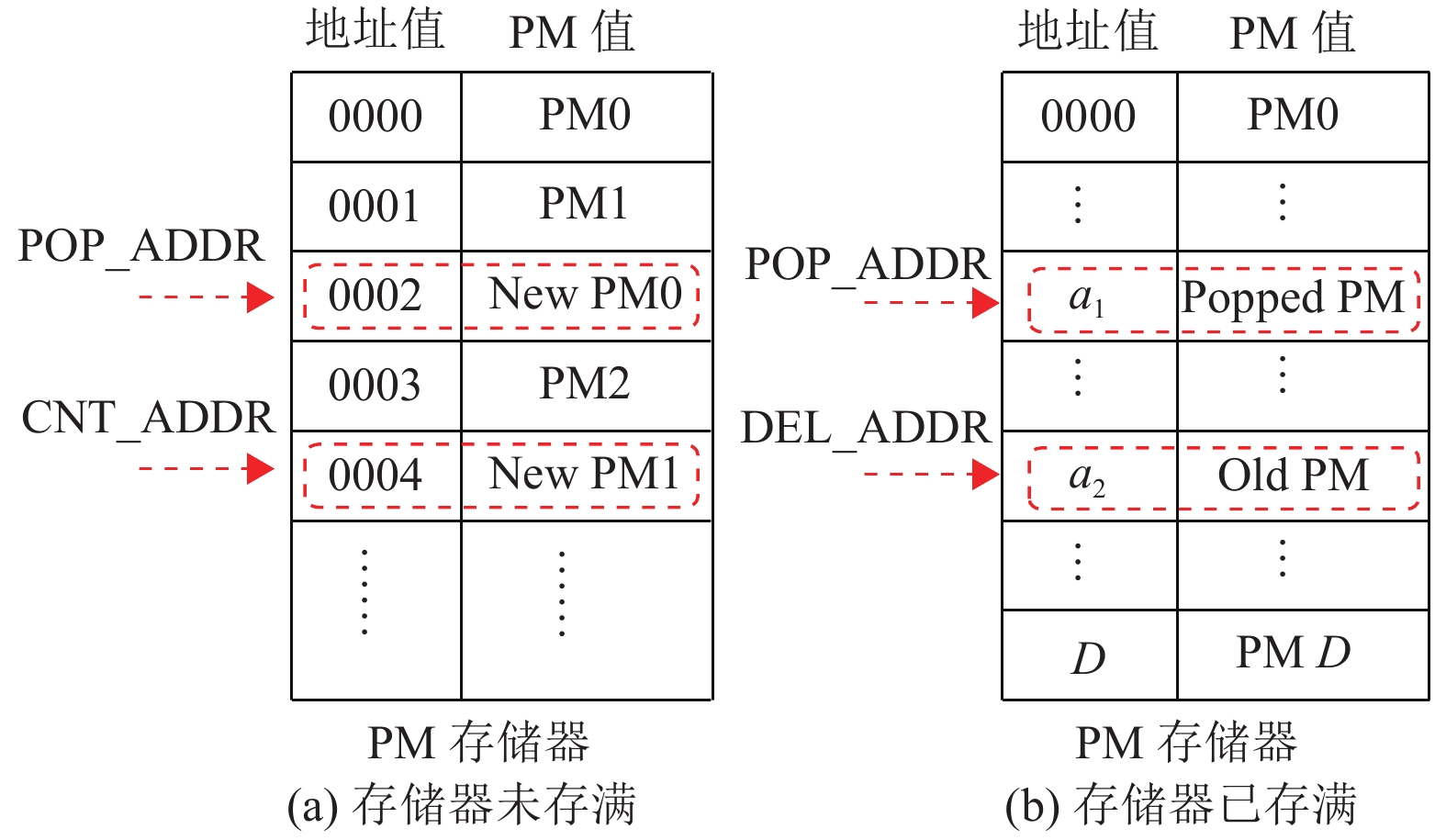
|
图 8 路径写入策略示意图 Figure 8 Examples of paths writing strategy |
在硬件实现上,本文所有硬件设计均在Xilinx系列xc7v585tffg的FPGA平台中进行,时钟频率Fclk设定为200 MHz。对码长结构(N, K) =(256, 128) 进行实现,堆栈深度D=64和搜索宽度L=16。并对文献[17]的架构在同样码长下在同平台进行复现对比,码率R均为0.5。均使用高斯近似(Gaussian Approximation, GA),仿真场景使用加性白高斯信道模型,并使用二进制相移键控(Binary Phase Shift Keying, BPSK) 调制方式。
3.1 基于MATLAB的LLR值量化分析由于LLR值为浮点数,在硬件实现中都需要将数据进行定点量化才能进行处理,而具体的量化方案将直接影响到硬件的性能以及硬件开销,所以在方案上需要做出合理的选择,使得硬件开销和性能损失都在可接受的范围内。
用
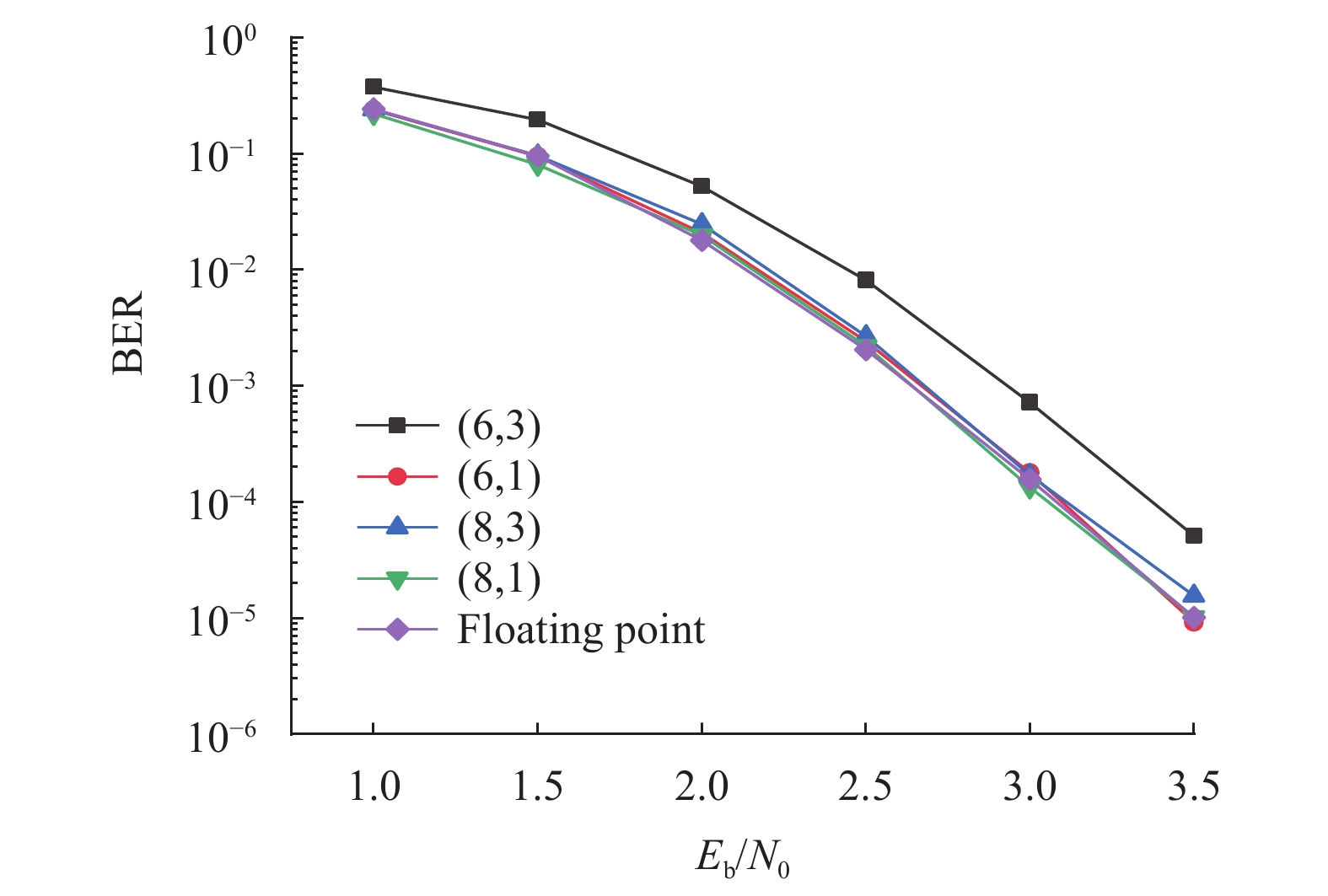
|
图 9 在不同 |
本文所提出的硬件结构资源消耗如表1所示。与文献[17]相比较,本文译码器整体资源消耗在查找表(Look Up Table, LUT)、寄存器(Register) 和块随机存储器(Block Random Access Memory, BRAM) 上分别减少了24.06%、56.42%和39.29%。特别地,将路径选择模块与部分和模块的资源消耗进行单独比较,本文的方案在路径选择模块上,LUT和Register平均多出40.65%和18.32%的开销。然而在部分和模块中,本文的方案在LUT和Register则平均减少了7.68%与77.98%的开销,并且由于没有使用到存储模块,因此BRAM消耗为0。在吞吐率方面,根据译码器吞吐率公式:
| 表 1 不同架构的性能对比情况 Table 1 The comparisons of different structures |
| $ T = \frac{{{\text{decoded\_data}}({\text{bits}}) }}{{{\text{Delay}}({\text{ms}}) }} $ | (9) |
在200 MHz的工作频率下,本文译码器的平均时延为0.046 ms,因此在此情况下吞吐率
除了硬件性能外,本文进一步验证了译码器的纠错性能,图10为本文设计的SCS译码器与同码长的SC译码器在硬件实现和MATLAB仿真中的误比特率性能对比。其中黑色线为MATLAB的仿真结果,其余为FPGA实现结果。从结果对比图可得知在FPGA上的实现与仿真结果相近,这得益于量化比特数的合理选择,从而在实现过程中未造成明显性能损失。而对比SC与SCS的FPGA实现结果可知,相较于SC译码算法,本文所提出的SCS译码器有0.6 dB的性能增益。
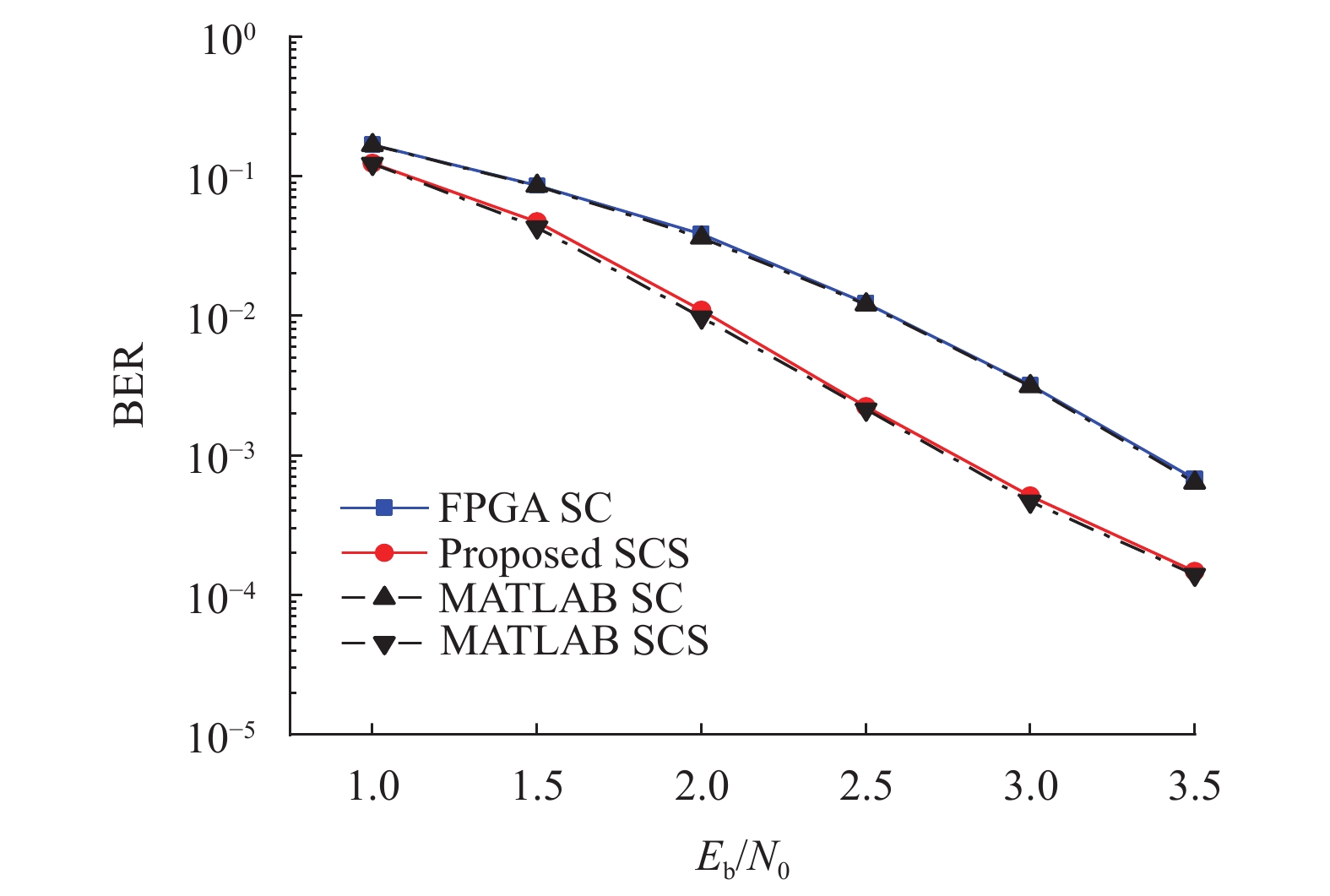
|
图 10 SCS译码器与SC译码器码长为(N,K) = (256,128) 性能比较 Figure 10 The comparison of SCS and SC with (N,K) =(256,128) |
从硬件平台实现结果看出SCS译码器在性能上明显优于SC译码器。同时合理的量化比特选取也使硬件实现中的性能损失非常小。
4 结论本文主要针对SCS译码器的路径选择模块提出了一种新的架构,从而提升路径选择模块的性能。通过硬件实现验证,本文所提出的架构通过对堆栈存储策略的改善,不同种类的路径信息读写变得更加灵活。在路径选择上利用分组单调排序与并行比较相结合的策略使得最佳路径搜索更加高效。另外,在部分和模块中本文提出用路径值实时计算部分和的方法,部分和反馈更加高效,充分利用了FPGA强大的并行性。实验结果表明,本文中所提出的硬件架构的整体资源消耗降低且吞吐率有小幅提升,在路径选择模块中需要更多的LUT和Registers,但在部分和模块中需要更少的资源。同时,本文提出的结构纠错性能优于SC译码器并与SCS译码算法的理论结果接近。
然而,SCS译码器在低SNR时会频繁出现路径回溯现象,这一现象主要由LLR量化精度损失所造成。文献[20]中所提出的通过算法模型来动态调整量化参数的策略具有一定启发性,在SCS译码中根据SNR与PL值通过一定算法来动态调整量化参数也许可以进一步提升译码器性能。
| [1] |
ARIKAN E. Channel polarization: a method for constructing capacity-achieving codes for symmetric binary-input memoryless channels[J].
IEEE Transactions on Information Theory, 2009, 55(7): 3051-3073.
DOI: 10.1109/TIT.2009.2021379. |
| [2] |
TAL I, VARDY A. List decoding of polar codes[J].
IEEE Transactions on Information Theory, 2015, 61(5): 2213-2226.
DOI: 10.1109/TIT.2015.2410251. |
| [3] |
NIU K, CHEN K. Stack decoding of polar codes[J].
Electronics Letters, 2012, 48(12): 695-697.
DOI: 10.1049/el.2012.1459. |
| [4] |
NIU K, CHEN K. CRC-aided decoding of polar codes[J].
IEEE Communications Letters, 2012, 16(10): 1668-1671.
DOI: 10.1109/LCOMM.2012.090312.121501. |
| [5] |
ZHANG Q S, LIU A J, PAN X F, et al. CRC code design for list decoding of polar codes[J].
IEEE Communications Letters, 2017, 21(6): 1229-1232.
DOI: 10.1109/LCOMM.2017.2672539. |
| [6] |
XIANG L P, EGILMEZ Z, MAUNDER R, et al. CRC-aided logarithmic stack decoding of polar codes for ultra reliable low latency communication in 3GPP new radio[J].
IEEE Access, 2019, 7: 28559-28573.
DOI: 10.1109/ACCESS.2019.2901596. |
| [7] |
ARIKAN E. A performance comparison of polar codes and reed-muller codes[J].
IEEE Communications Letters, 2008, 12(6): 447-449.
DOI: 10.1109/LCOMM.2008.080017. |
| [8] |
SHEN Y F, SONG W Q, REN Y Q, et al. Enhanced belief propagation decoder for 5G polar codes with bit-flipping[J].
IEEE Transactions on Circuits and Systems II. Express Briefs, 2020, 67(5): 901-905.
DOI: 10.1109/TCSII.2020.2984536. |
| [9] |
YU Y R, PAN Z W, LIU N, et al. Belief propagation bit-flip decoder for polar codes[J].
IEEE Access, 2019, 7: 10937-10946.
DOI: 10.1109/ACCESS.2019.2891951. |
| [10] |
LEROUX C, TAL I, VARDY A, et al. Hardware architectures for successive cancellation decoding of polar codes[C]//IEEE International Conference on Acoustics, Speech and Signal Processing. Prague, Czech Republic: IEEE, 2011: 1665-1668.
|
| [11] |
LEROUX C, RAYMOND A, SARKIS G, et al. A semi-parallel successive-cancellation decoder for polar codes[J].
IEEE Transactions on Signal Processing, 2013, 61(2): 289-299.
DOI: 10.1109/TSP.2012.2223693. |
| [12] |
ZHANG C, PARHI K. Low-latency sequential and over-lapped architectures for successive cancellation polar decoder[J].
IEEE Transactions on Signal Processing, 2013, 61(10): 2429-2441.
DOI: 10.1109/TSP.2013.2251339. |
| [13] |
ZHANG C, YUAN B, PARHI K. Reduced-latency SC polar decoder architectures[C]//IEEE International Conference on Communications. Ottawa, Canada: IEEE, 2012: 3471-3475.
|
| [14] |
ZHANG C, PARHI K. Interleaved successive cancellation polar decoders[C]//IEEE International Symposium on Circuits and Systems. Melbourne, Australia: IEEE, 2014: 401-404.
|
| [15] |
LIN J, XIONG C R, YAN Z Y. A high throughput list decoder architecture for polar codes[J].
Transactions on Very Large Scale Integration (VLSI) Systems, 2016, 24(6): 2378-2391.
|
| [16] |
TAO Y Y, CHO S G, ZHANG Z Y. A configurable successive-cancellation list polar decoder using split-tree architecture[J].
IEEE Journal of Solid-State Circuits, 2021, 56(2): 612-623.
DOI: 10.1109/JSSC.2020.3005763. |
| [17] |
SONG W Q, ZHOU H Y, NIU K, et al. Efficient successive cancellation stack decoder for polar codes[J].
IEEE Transactions on Very Large Scale Integration (VLSI) Systems, 2019, 27(11): 2608-2619.
DOI: 10.1109/TVLSI.2019.2925029. |
| [18] |
ERCAN F, TONNELLER T, GROSS W. Energy-efficient hardware architectures for fast polar decoders[J].
IEEE Transactions on Circuits and Systems I:Regular Papers, 2020, 67(1): 322-335.
DOI: 10.1109/TCSI.2019.2942833. |
| [19] |
王美芹, 仰枫帆, 赵春丽. 基于FPGA的极化码半平行CA-SCL译码器设计[J].
舰船电子工程, 2019, 39(3): 62-67.
WANG M Q, YANG F F, ZHAO C L. Implement of the CA-SCL semi-parallel decoding algorithm based on FPGA[J]. Ship Electronic Engineering, 2019, 39(3): 62-67. |
| [20] |
衡园, 吴建成, 杨志军. 基于FPGA的控制算法定点化设计[J].
广东工业大学学报, 2020, 37(3): 55-58.
HENG Y, WU J C, YANG Z J. A fixed-point design of control algorithm based on FPGA[J]. Journal of Guangdong University of Technology, 2020, 37(3): 55-58. DOI: 10.12052/gdutxb.190089. |
 2024, Vol. 41
2024, Vol. 41

