车辆导航定位技术是目前智能交通系统(Intelligent Transportation System, ITS)研究的关键内容[1-2]. 全球卫星导航系统(Global Navigation Satellite System, GNSS)在车辆定位领域的应用最为广泛[3-4],它泛指所有卫星导航系统. 技术较为成熟的有美国的全球定位(Global Positioning System, GPS),俄罗斯的格洛纳斯导航系统以及中国的北斗卫星导航系统. GNSS能够实时地为车辆提供三维位置、速度、时间等信息,实现全天候、全方位的导航定位功能[5].
目前GNSS车载定位以及GNSS-惯性组合导航已实现普遍应用[6-7]. 但是当车辆行驶在城市峡谷环境时,由于公路两旁的高层建筑有遮挡,GNSS的卫星信号易受到公路两旁建筑的遮挡和反射,多路径效应严重,若对信号反射导致的非视距卫星缺乏有效的甄别,势必引入巨大的定位误差[8-9].
多径效应是指信号通过两个或两个以上路径到达接收机天线的现象[10]. 目前针对多径误差,世界各地研究人员都尝试了不同的方法,如:(1) 基于信噪比自适应的抗多径方法;(2) 通过适当的天线设计减轻多径信号的影响;(3) 通过改进接收机内部相关器、跟踪环等方法抑制多径信号[11-12]. 以上各种方法都在不同程度上消除了一些多径误差,但都不能彻底地消除多径误差.
针对车辆在城市峡谷环境中收到多径信号的干扰的问题,本文提出了一种新颖的抑制多径卫星信号的方法,利用了建筑物只对左右方向的卫星有较大的遮挡,但对前方、上方和后方的卫星并没有遮挡这个事实,有效判断和剔除不可见卫星. 利用导航模块输出的原始数据,而不是定位数据,挑选没有被遮挡的卫星,利用它们的伪距离和多普勒进行定位,从而减弱多路径效应的影响,最终实现城市峡谷环境下的车辆高精度定位. 目前还没有在文献中看到类似本方法的技术.
1 多径信号多径效应是指信号通过两个或两个以上路径到达接收机天线的现象. GNSS信号在传播时会受到传播路径上障碍物的影响而产生多径[13-14]. 对卫星信号来说,由于多径信号的传播路径大于直达信号,导致多径信号晚于直达信号到达接收机,是直达信号的延迟信号,其功率比直达信号要弱[15]. 多径效应会导致伪距离测量误差和载波相位测量误差,进而影响卫星导航定位精度.
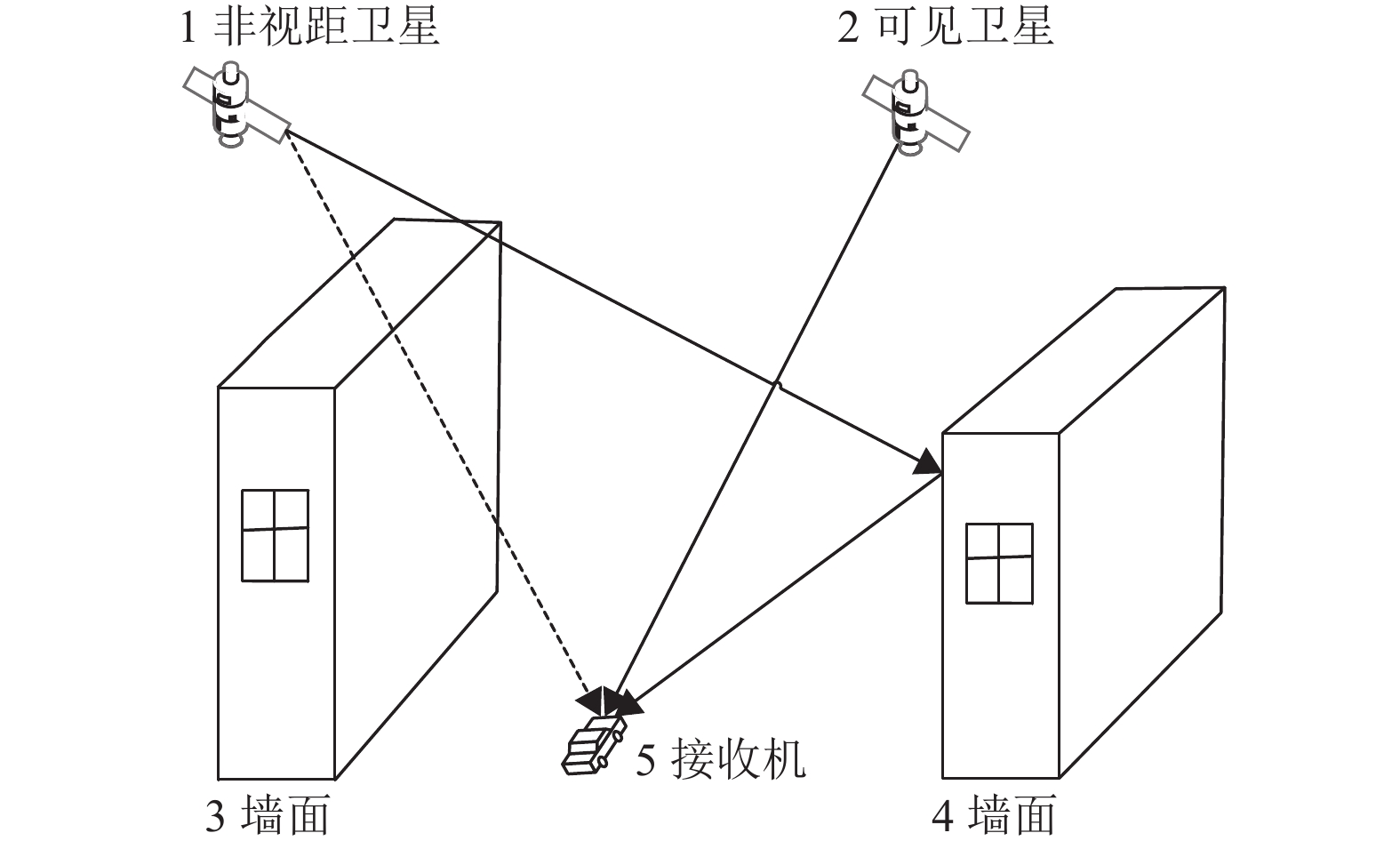
图1为卫星多径信号产生的示意图. 车辆上的接收机5可以直接接收到可见卫星2的信号,非视距卫星1的直射信号(图中虚线)被左边的墙面3遮挡,只有通过墙面4的反射(多径)信号才能被接收机5接受,这种非视距多径信号使车辆的定位精度降低.
|
图 1 多径信号产生示意图 Figure 1 Multipath signal generation diagram |
在城市峡谷环境中,道路一般都比较直而且前后都没有遮挡,但是两旁的建筑物存在遮挡,导致卫星信号被反射,车载GNSS接收机容易接收到非视距卫星的信号,由于非视距卫星的伪距测量值误差较大,若将此类卫星直接用于定位解算,将导致车辆定位精度下降. 因此为了抑制多径卫星信号,本文提出了一种抑制多径卫星信号的定位方法,该方法需要剔除非视距卫星. 剔除非视距卫星的算法,首先要推导出高度角和方向角的关系.
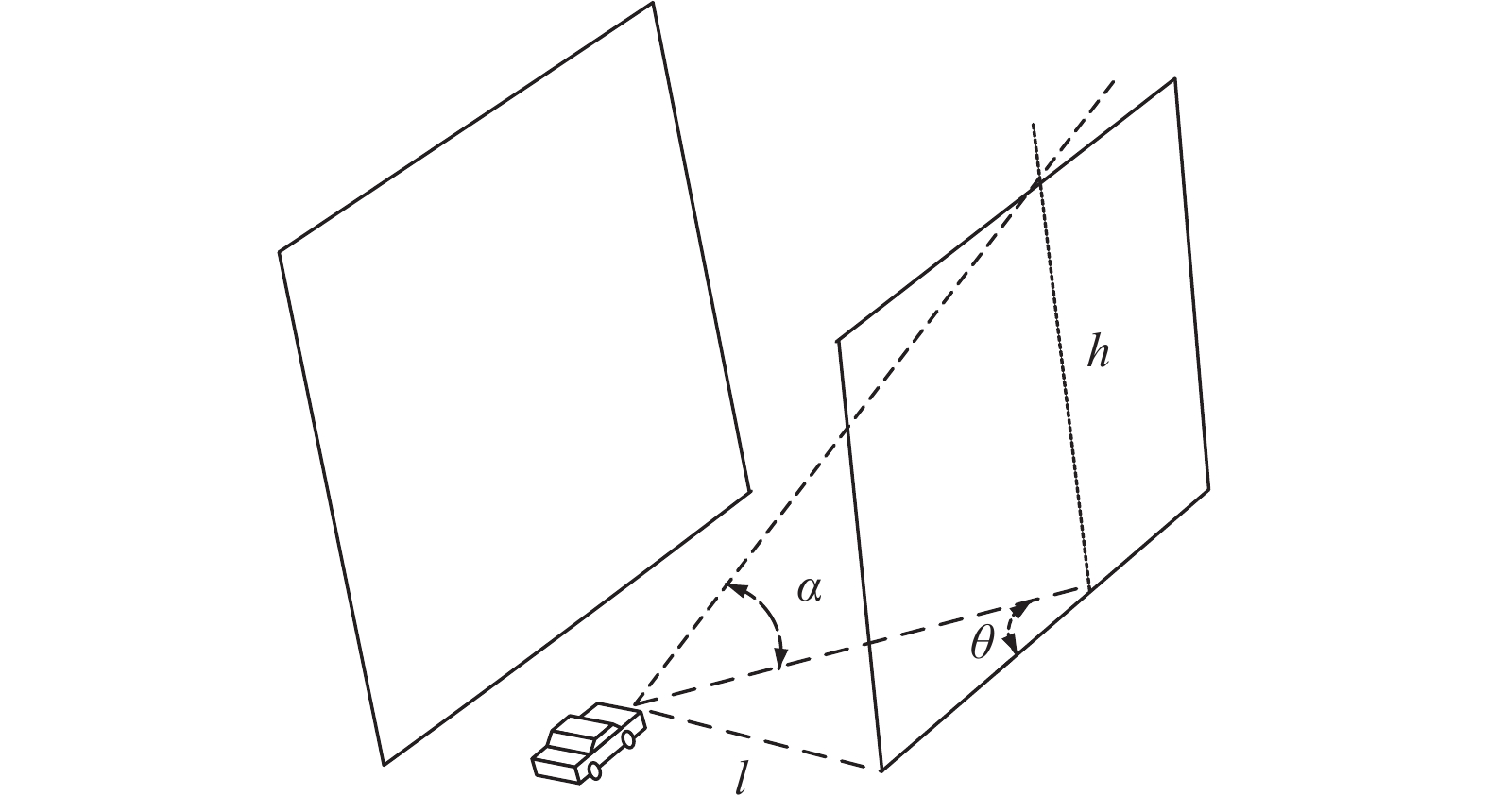
2.1 高度角和方向角的关系图2是车辆到建筑物任意临界点的高度角与方向角的示意图,h是右边建筑物的高度,l是车辆到右边建筑物的距离,α是车辆到建筑物任意临界点的高度角,θ是车辆与卫星之间相对于道路方向的方位角(0~180°). α0是临界点中的最大高度角(即方向角为90°),同时α0也是非临界点中卫星对车辆的最小高度角.
|
图 2 高度角和方向角的关系图 Figure 2 Relationship between height angle and azimuth angle |
可以得到
| $\tan {\alpha _0} = h/l. $ | (1) |
以车辆为坐标原点O,车辆的正前方为Y 轴,辆正上方为Z 轴,建立空间三维坐标系,那么建筑物顶上任意一点A 的坐标为(l, y, h),那么
| $\sin \alpha = \displaystyle\frac{h}{{\sqrt {{l^2} + {y^2} + {h^2}} }},$ | (2) |
| $\tan \theta = \displaystyle\frac{l}{y},$ | (3) |
于是由式(2)和(3)分别推出
| $\tan \alpha = \displaystyle\frac{h}{{\sqrt {{l^2} + {y^2}} }},$ | (4) |
| $y = l/\tan \theta .$ | (5) |
由式(1)、(4)和(5)推出式(6):
| $\displaystyle\begin{split}\tan \alpha = \displaystyle\frac{h}{{\sqrt {{l^2} + {l^2}/{{\tan }^2}\theta } }}{\kern 1pt} = \displaystyle\frac{{h/l}}{{\sqrt {1 + 1/{{\tan }^2}\theta } }} = \\\displaystyle\frac{{\tan {\alpha _0} \tan \theta }}{{\sqrt {1 + {{\tan }^2}\theta } }} =\tan {\alpha _0} \sin \theta ,\end{split}$ | (6) |
将式(6)变形可得
| $\alpha = {{{arc}}\tan }[\tan {\alpha _0}\sin \theta ].$ | (7) |
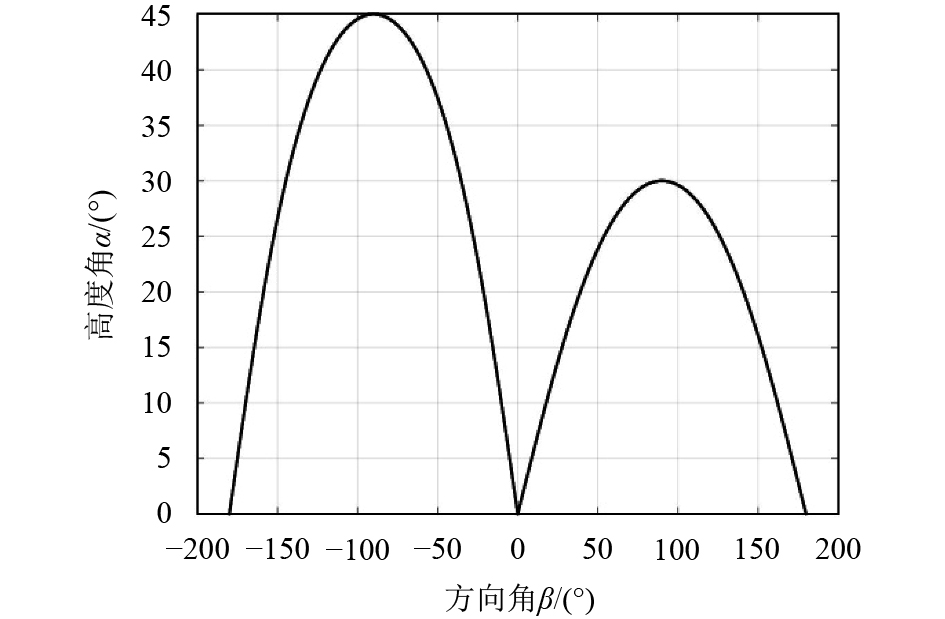
图3是卫星方向角与最低高度角的关系图,图的左半部分是车辆左边的卫星最低高度角与方向角的曲线图,图的右半部分是车辆右边的卫星最低高度角与方向角的曲线图. 曲线上方的卫星都是可见卫星,在曲线下方的是被遮挡的卫星,它们产生信号只能是多径信号,不能用于准确定位.
|
图 3 最低高度角与方向角的关系图 Figure 3 The relationship between the lowest elevation angle and the azimuth angle |
由图3可知,在曲线上方的卫星的高度角都是大于最低高度角α,曲线下方的卫星的高度角都是小于最低高度角α,即曲线上方的卫星是没有遮挡的,而曲线下方的卫星是被建筑物遮挡的.
2.2 剔除非视距卫星的具体算法车辆在道路上时,首先通过车辆的行驶速度和车辆在上一时刻的定位结果,或者用惯性导航预测车辆在当前时刻的位置. 然后利用车辆上的GNSS接收机,接受卫星的星历数据并进行星历解算,得到各卫星的位置[16].
车辆对可见卫星范围的高度角α和方向角θ有一定的曲线关系, 已经求解出α与θ的关系式为(7),其中α0(实际是车辆左右两边的最小高度角αml和αmr)是非临界点中卫星对车辆的最小高度角,未知数.
先初始化α0的最小高度角,比如15°,这样确定了初始可见卫星曲线. 根据估算的车辆位置计算每颗卫星的仰角α和相对于道路方向的方位角θ,根据方位角θ代入式(7)计算对应的最低高度角α(θ),然后求出每颗卫星的高度角与该曲线上对应的高度角之差,即
| $\Delta \alpha = \alpha - \alpha \left( \theta \right).$ | (8) |
再将这些差值从大到小排序,依次循环计算卫星的伪距残余ri,给卫星的伪距残余设定一个门限值. 然后将卫星的伪距残余依次与门限值比较,当卫星残差小于门限值时,这颗卫星是可见卫星保留下来;当有卫星伪距残余大于门限值时,终止循环,后面的就不用再比较了,并且将这个卫星的高度角αi与方向角θi代入方程式(7)可以求出α0,并且将α0加上一个较小的度数ε,即
| ${\alpha _0} = a\tan \left( {\frac{{\tan {\alpha _i}}}{{\sin {\theta _i}}}} \right) + \varepsilon ,$ | (9) |
以此来调整α0(即αml和αmr)的大小,曲线确定后那就可以确定可见卫星的范围,剔除那些因为多径发来干扰信号的非视距卫星,最后从这些可见卫星中挑选合适的几颗卫星来定出此刻车辆在道路中的位置,下一时刻重复这种方法就可以定出下一刻的位置.
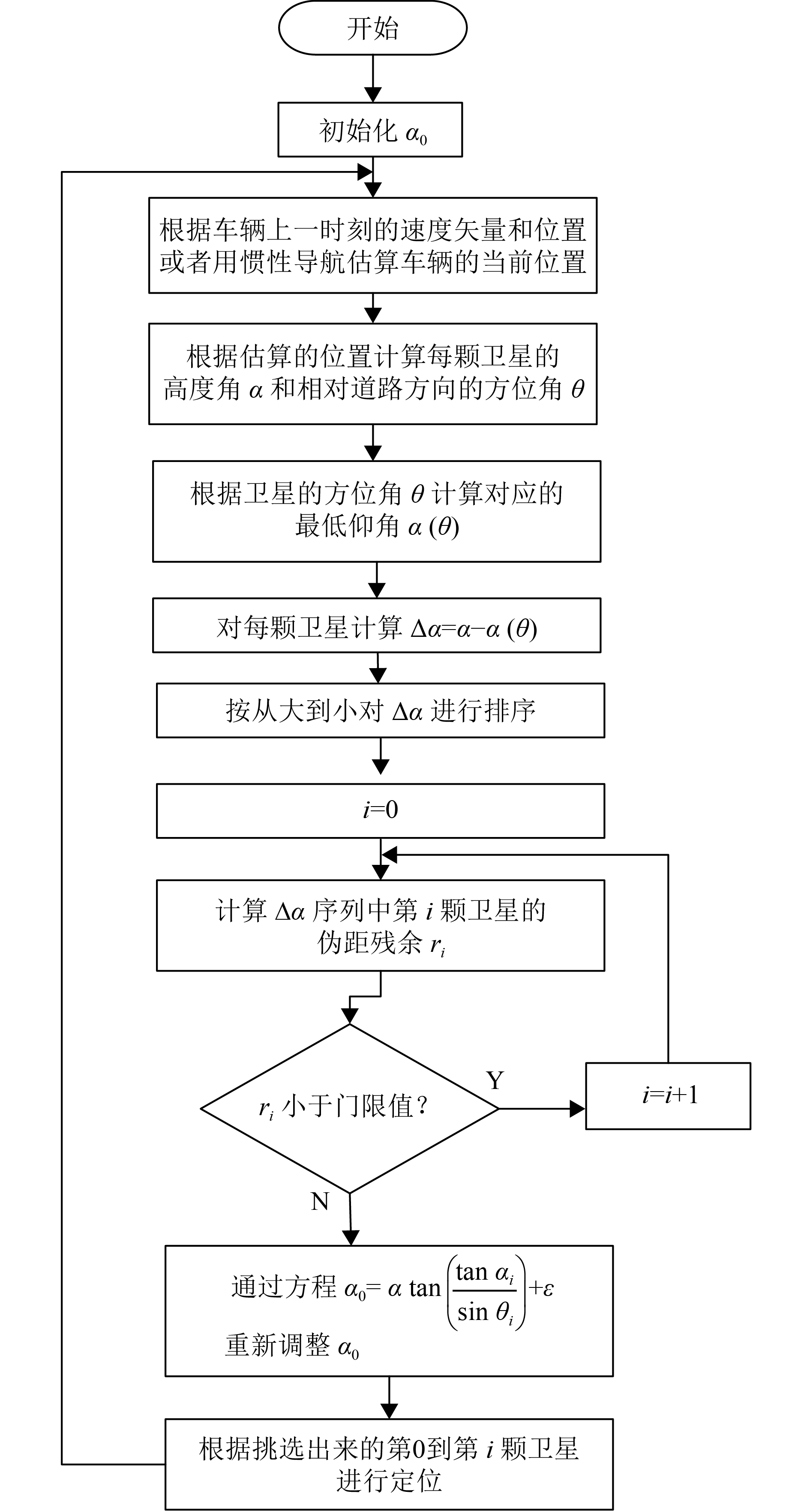
图4是该算法的具体流程图.
|
图 4 算法流程图 Figure 4 Algorithm flowchart |
本文基于成熟的GNSS技术进行研究,前期主要在Ubuntu上开发,根据实地测量的数据,编写好挑星算法的代码,然后再在树莓派与HAT测量板上实地测试验证. 接收机的天线布置在车顶的正中心位置,接收机安装在车辆质心位置,与车辆纵轴同向. 所采用的GNSS接收机具体型号是瑞士公司的ublox 8T,可输出卫星的星历以及伪距测量值和载波相位等原始数据;然后通过嵌入式电脑树莓派结合具体算法对数据进行处理. 本文使用的软件在挑选好无遮挡卫星后,计算卫星轨道,再通过伪距离方程和多普勒方程计算出车辆的位置和速度. 通过测试一些数据,已经验证了该方法能提高精度,说明是很可行的.
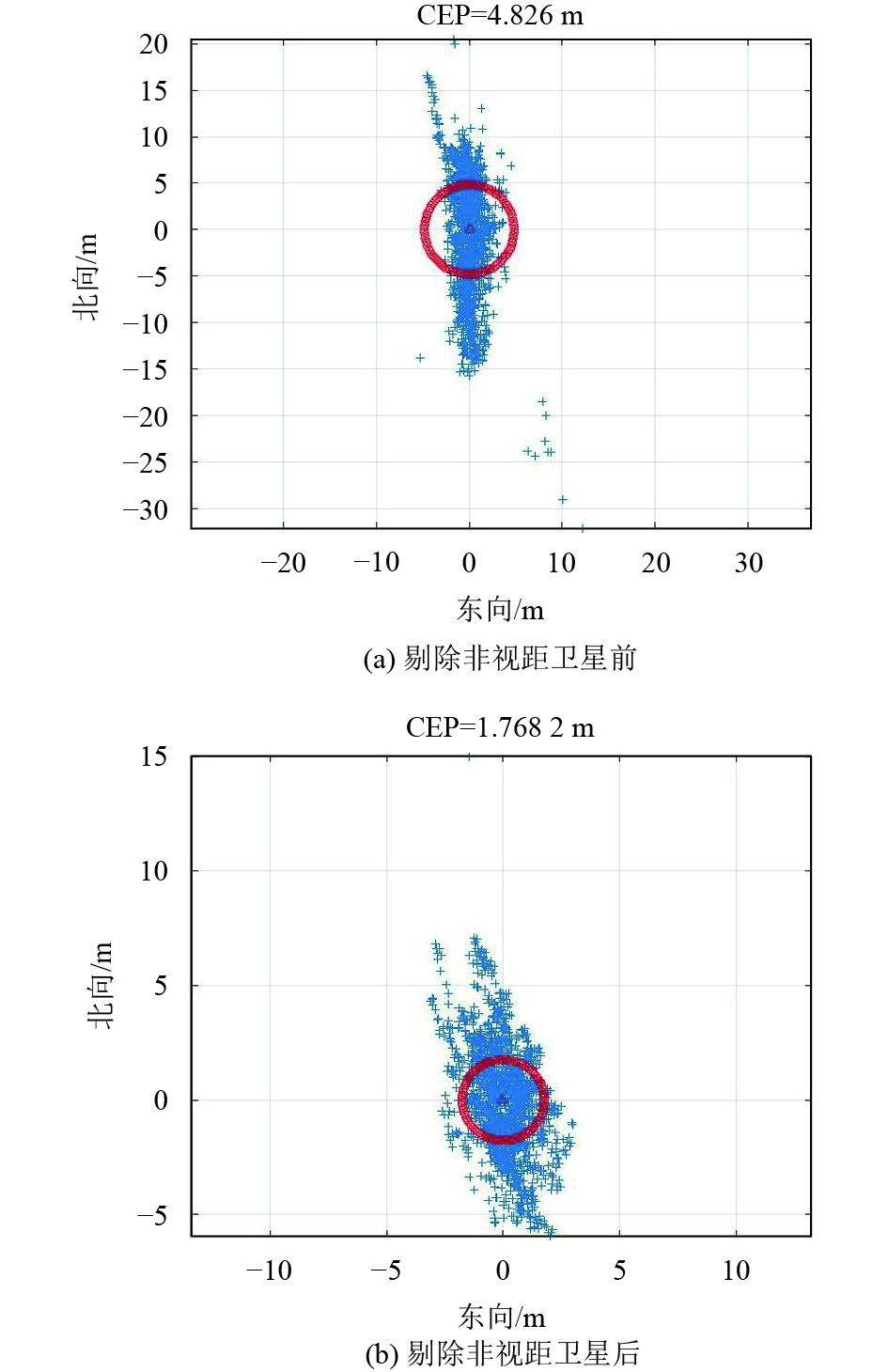
如图5所示,图5(a)是在有高大的建筑遮挡下的静态定位的精度图,CEP(circular error probable,圆概率误差)=4.826 m;图5(b)是剔除了非视距卫星后的静态定位的精度图,CEP=1.768 2 m;CEP精度明显提高,说明本方案在静态定位下是可行的.
|
图 5 静态定位精度 Figure 5 Static positioning accuracy |
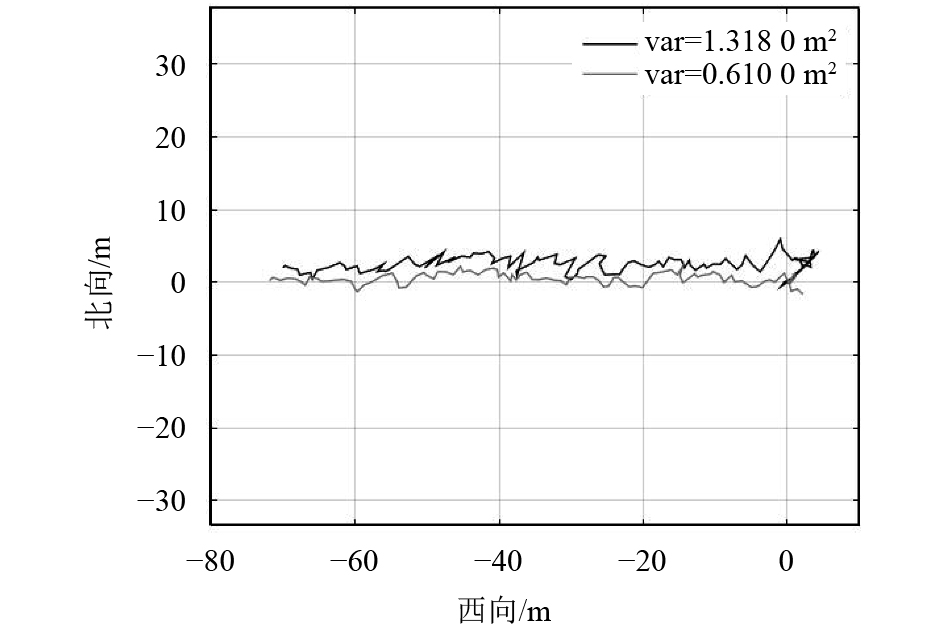
如图6所示,这是在有高大建筑物遮挡下的动态定位图,黑色实线表示剔除非视距卫星前动态定位图,方差(var)=1.318 0 m2;灰色虚线表示剔除非视距卫星后动态定位图,方差(var)=0.610 0 m2;剔除非视距卫星后的曲线明显平滑,方差变小,定位精度提高了,说明方案在动态定位下是可行的.
|
图 6 剔除非视距卫星前后动态定位精度图 Figure 6 The dynamic positioning accuracy of the non-line-of-sight satellite before and after |
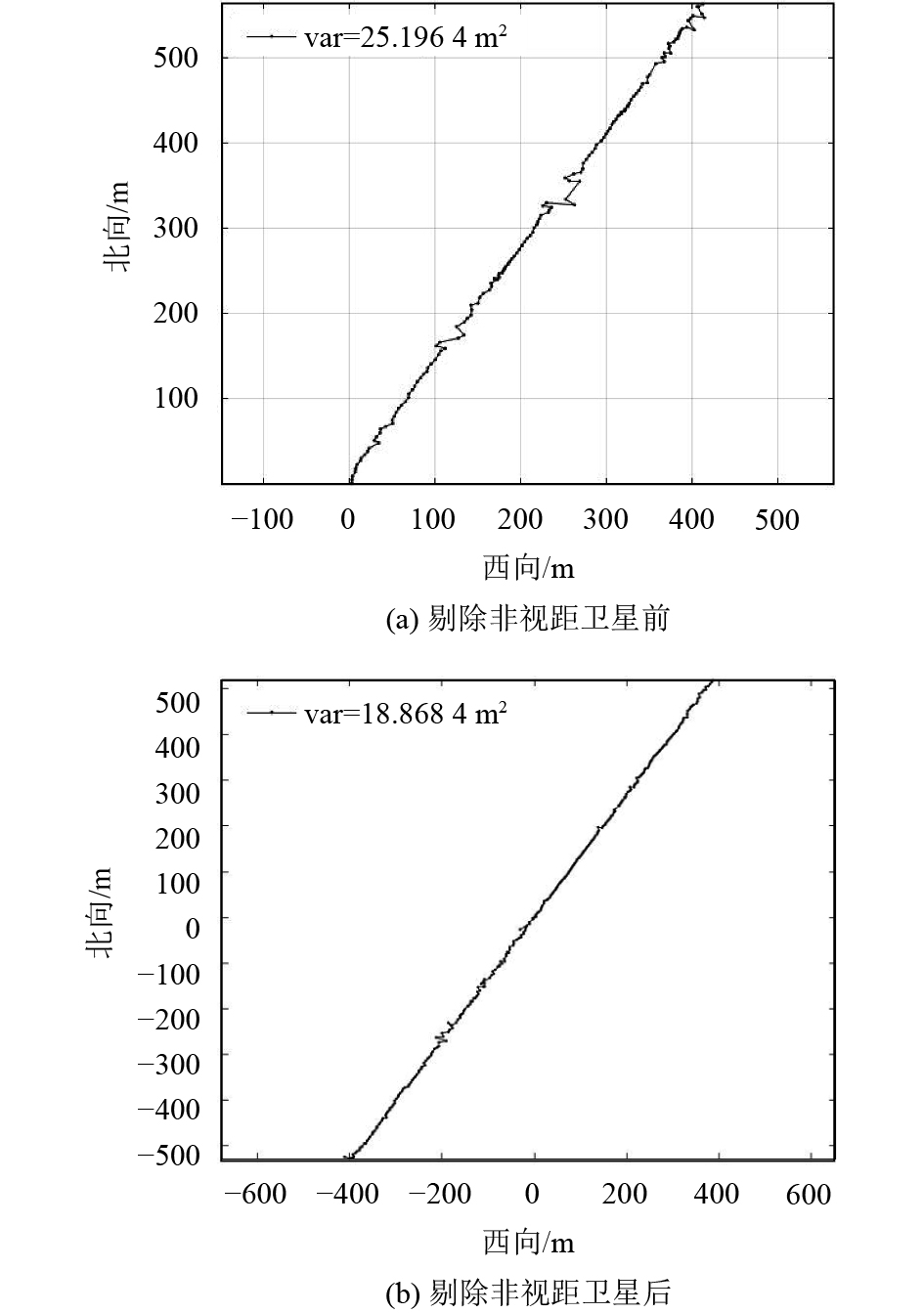
如图7所示,车辆在港口测的一段数据,道路两边都是高大的集装箱,图7(a)是剔除非视距卫星前的定位精度图,方差(var)=25.196 4 m2;图7(b)是剔除非视距卫星后的定位精度图,方差(var)=18.868 4 m2;方差变小,曲线更平滑,说明剔除非视距卫星后定位精度得到了提高.
|
图 7 港口定位精度 Figure 7 Positioning accuracy of port |
本文提出了一种新颖的抑制多径卫星信号的定位方法,应用于车辆在城市峡谷环境下的定位. 从分析的结果可以看出,图5中静态定位剔除非视距卫星后,CEP精度明显提高;图6是在有高大建筑物遮挡下的动态定位,剔除非视距卫星后,方差变小了,剔除非视距星后的曲线明显平滑;图7是车辆在港口测的一段数据,剔除非视距卫星后,方差变小了,曲线更平滑. 从这些数据说明剔除非视距卫星后定位精度得到了提高并且能满足车辆在城市峡谷环境中的实时高精度定位要求.
| [1] |
南海, 张宝龙, 刘柱. 智能车辆定位导航系统在城市交通中的应用[J].
交通世界: 运输车辆, 2013(4): 112-114.
NAN H, ZHANG B L, LIU Z. Intelligent vehicle positioning and navigation system in urbantraffic application[J]. Traffic world: transport Vehicles, 2013(4): 112-114. |
| [2] | AMINI A, VAGHEFI R M, DE L G J M, et al. Improving GPS-based vehicle positioning for Intelligent Transportation Systems[C]//Intelligent Vehicles Symposium Proceedings. [S.I.]: IEEE, 2014: 1023-1029. |
| [3] |
刘娟. 研析新形势下车载导航系统的现状与发展[J].
电子技术与软件工程, 2014(4): 56-56.
LIU J. Research on the present situation and development of Vehicle Navigation system under the new situation[J]. Electronic Technology and Software Engineering, 2014(4): 56-56. |
| [4] |
吴海锋, 袁彦玲, 张宝杰. GPS在车辆定位导航系统中的应用研究[J].
科技信息, 2011(22): 341-342.
WU H F, YUAN Y L, ZHANG B J. Researchon the application of GPS in vehicle navigation system[J]. Technology information[1], 2011(22): 341-342. DOI: 10.3969/j.issn.1001-9960.2011.22.293. |
| [5] | 常青, 杨东凯, 寇艳红, 等. 车辆导航定位方法及应用[M]. 北京: 机械工业出版社, 2005. |
| [6] |
张孝兵, 周宣赤, 夏云海, 等. 基于GPS/MEMS惯性传感器的车载组合惯导系统的设计实现[J].
传感器技术与应用, 2017, 5(1): 1-9.
ZHANG X B, ZHOU X C, XIA Y H, et al. Design and implementation of vehicle combination inertial navigation system based on GPS/MEMS inertial sensor[J]. Sensor Technology & Application, 2017, 5(1): 1-9. |
| [7] | SPANGENBERG M, CALMETTES V, TOURNEREF J Y. Fusion of GPS, INS and odometric data for automotive navigation[C]// Signal Processing Conference. European : IEEE, 2007: 886-890. |
| [8] |
朱留军, 聂久添. GPS车辆定位导航系统中多路径效应的误差分析[J].
科技视界, 2013(25): 82-82.
ZHU L J, NIE J T. Error Analysis of multipath effect in gps vehicle location navigation system[J]. Technology Horizon, 2013(25): 82-82. |
| [9] | TIAN YM, XU GH, FRANK N, et al. An approach to improve the GPS positioning performance under urban environment conditions[J]. Measurement, 2016, 93: 414-420. DOI: 10.1016/j.measurement.2016.07.021. |
| [10] |
皮姣, 刘立程, 王峰, 等. 基于阵列天线处理的GPS信号抗干扰研究[J].
广东工业大学学报, 2015, 32(4): 67-71.
PI J, LIU L C, WANG F, et al. Anti-interference study of GPS signal based on array antenna processing[J]. Journal of Guangdong University of Technology, 2015, 32(4): 67-71. |
| [11] | 侯友国. GPS接收机干扰抑制技术研究[D]. 成都: 电子科技大学通信与信息工程学院, 2010. |
| [12] |
王振岭. 车载GNSS接收机多径抑制技术[J].
全球定位系统, 2012, 37(1): 1-7.
WANG Z L. Multi-path suppression technology of vehicle GNSS receiver[J]. Global Positioning System, 2012, 37(1): 1-7. |
| [13] |
李国权, 吴玉成. 一种新的GPS系统多径抑制算法[J].
系统仿真学报, 2010, 22(7): 1588-1591.
LI G Q, WU Y C. A new multi-path suppression algorithm for GPS system[J]. Journal of System Simulation, 2010, 22(7): 1588-1591. |
| [14] | JIANG Y, ZHANG S F, SUN X W, et al. A new rake-based multipath estimation algorithm in GNSS receivers[C]//International Congress on Image and Signal Processing. [S.I.]: IEEE, 2010: 4313-4317. |
| [15] | MAO W L, DU J S, SHEEN J, et al. Adaptive multipath mitigation tracking system for GPS receiver[J]. Aerospace Science & Technology, 2013, 30(30): 66-78. |
| [16] | 谢钢. GPS原理与接收机设计[M]. 北京: 电子工业出版社, 2009. |
 2018, Vol. 35
2018, Vol. 35

