最优潮流是指当电力系统网络结构及负荷都给定时,在满足节点功率平衡及各种安全约束的条件下,通过调节系统中的控制参数使其目标函数或某一性能指标达到最优时的潮流分布. 最优潮流在电力系统的经济调度、系统规划设计及可靠性分析等方面得到了广泛应用.
在节能减排、提高能源利用率和环境效益的大背景下,以风电为代表的分布式电源得到了迅速的发展. 然而,传统的最优潮流问题并没有考虑风电等不确定性因素,在风力发电飞速发展和追求低碳电力的影响下,大规模风电并网不可避免. 由于风能具有随机性、间歇性和不可控性的特点,使风电场输出功率具有强烈的随机性和波动性,加剧了电力系统运行中不确定因素的复杂程度,使电力系统潮流优化的难度增大,因此迫切需要研究大型风电场并网后对电力系统的影响[1-3]. 含风电场电力系统最优潮流在评估风电并网对电力系统运行的经济性和环境效益上起着非常重要的作用.
含风电场最优潮流是一个复杂的非线性多约束优化问题. 近年来,学者们对含风电场最优潮流的研究主要从两个方面展开,即如何正确处理风电机组,将风电机组模型与最优潮流模型相结合以及求解这个非线性优化问题的算法. 本文从含风电场最优潮流模型、对风电机组的处理与求解方法出发,综述了近年来学者们的研究成果与方法,并对其优缺点进行分析,在此基础上对含风电场最优潮流问题的未来发展提出展望.
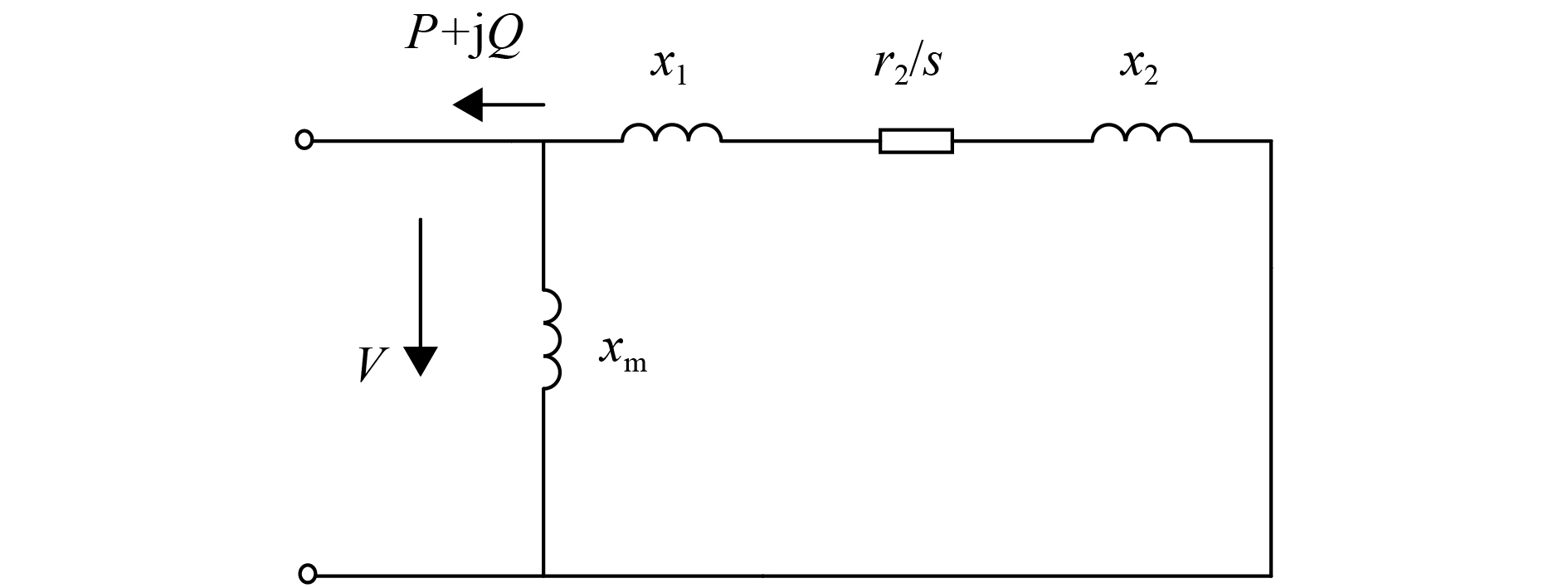
1 含风电场最优潮流模型 1.1 风电机组稳态数学模型目前实际应用中的大型风电场一般由几十甚至上百台的异步风力发电机组组成. 在进行风电机组并网后的电力系统潮流计算时,必须将风力发电机组的稳态数学模型扩展到系统的潮流方程中,联立求解. 异步风电机组的简化等值电路如图1所示,图中xm为励磁电抗,x1为定子漏抗,x2为转子漏抗,r2为转子电阻,s为转差,忽略定子电阻.
|
图 1 异步风电机组简化等值电路 Figure 1 Simplified circuit of Asynchronous wind turbine |
由图1可推导出式(1)~式(3):
| $V = \sqrt { - P({s^2}{x^2} + {r_2}^2)/{r_2}s}. $ | (1) |
| $Q = - \left( {\frac{{{V^2}}}{{{x_{{m}}}}} + \frac{{Px}}{{{r_2}}}s} \right).$ | (2) |
| $Z = {{j}}{x_{{m}}}//(\frac{{{r_2}}}{s} + {{j}}x)$ | (3) |
其中,Z为异步发电机的等值阻抗,x=x1+x2,x为发电机总阻抗,V为发电机机端电压,P为有功功率,Q为发电机无功功率.
1.2 最优潮流经典数学模型20世纪60年代,法国学者J.Carpentier在考虑电压约束等电力系统安全运行约束的基础上首次建立了经典最优潮流数学模型. 其通常的数学描述如下:
| $\left\{\begin{array}{l}\min f = f(x),\\[7pt]g(x) = 0,\\[7pt]h(x) \leqslant 0.\end{array}\right.$ | (4) |
其中,f为目标函数,通常为机组煤耗成本,也可以是系统的网络损耗、无功补偿的经济效益等;g(x)为节点注入潮流平衡方程,h(x)为不等式约束,具体如下所述.
1.3 约束条件 1.3.1 等式约束含风电场最优潮流优化必须满足基本的潮流方程式,其等式约束如式(5)所示.
| $\left\{ \begin{array}{l}\Delta {P_i} \!= \!{P_{Gi}} - \!{P_{Li}} \!=\!\!\! \displaystyle\sum\limits_{j = 1}^N {{V_i}} {V_j}({G_{ij}}\cos {\delta _{ij}} +\! {B_{ij}}\sin {\delta _{ij}});\\\Delta {Q_i} \!= \!{Q_{Gi}} - \!{Q_{Li}} \!=\!\!\! \displaystyle\sum\limits_{j = 1}^N {{V_i}} {V_j}({G_{ij}}\sin {\delta _{ij}} -\! {B_{ij}}\cos {\delta _{ij}}).\end{array} \!\!\!\!\right.$ | (5) |
其中,N为系统中的节点数;Vi、Vj分别是第i节点和第j节点电压幅值;PGi、QGi分别为第i台发电机有功功率和无功功率;PLi、QLi分别为第i节点有功功率负荷和无功功率负荷;δij为节点i和节点j之间的相角差;Gij、Bij分别为节点i和节点j之间互导纳的实部和虚部.
含风电场节点的潮流等式方程约束与式(5)相同.
1.3.2 不等式约束不等式约束包含发电机有功无功限值约束、节点电压约束、线路潮流约束和变压器变比约束等.
| $\left\{\begin{array}{l}{P_{Gi}}^{\min } \leqslant {P_{Gi}} \leqslant {P_{Gi}}^{\max };\\[6pt]{Q_{Gi}}^{\min } \leqslant {Q_{Gi}} \leqslant {Q_{Gi}}^{\max };\\[6pt]{V_i}^{\min } \leqslant {V_i} \leqslant {V_i}^{\max };\\[6pt]{S_{Li}} \leqslant {S_{Li}}^{\max }.\end{array} \right.$ | (6) |
其中,
含风电场最优潮流计算的关键问题是如何正确处理风电场节点[4-7],将机组模型与电力系统最优潮流模型相结合. 在进行风电并网后的潮流计算时,异步风电机组的节点处理方法有:P-Q简化模型,P-Q迭代模型[8]和R-X迭代模型[9]. 在早期的稳态分析中,学者们常把风电机组视为一个P-Q节点[10]. 但风电机组吸收无功与滑差和发出的有功功率有关,因此异步发电机组在潮流计算中的节点类型并不能简单地取为P-Q节点、P-V节点或平衡节点. 文献[11]根据异步风力发电机组的特性将风电机组视为Q-V节点,潮流计算时只需要修改雅克比矩阵中对应的元素
传统的最优潮流问题基于确定性模型,忽略了系统中存在的随机因素. 大规模风电以集中或分布式发电的形式接入电网,这些风电机组的出力随风速变化的影响具有较强的波动性和随机性[12-14],从而使最优潮流问题的求解面临诸多不确定因素. 目前考虑风电随机性的电力系统最优潮流模型,主要分为不确定性模型和确定性模型.
在不确定性模型中,将风电出力看成随机变量,建立机会约束规划模型[15]、随机概率模型[16]、模糊模型[17]、区间分析模型[18]求解.
文献[18]提出一种应对不确定运行环境的电力系统运行协同的区间有功优化潮流模型,模型中不确定量用服从区间分布的随机变量来表示. 文献[19]为了提高含大规模风电场的电力系统运行的经济性和稳定性,建立了基于机会约束规划的电力系统协调调度模型. 文献[20]利用无迹变换(UT)技术将概率最优潮流问题转化为少量样本点的确定性最优潮流问题. 文献[21]在模糊规划和随机规划理论的基础上将风电和负荷预测误差分别表示成模糊变量和随机变量,建立考虑多重不确定因素的混合机会约束经济调度模型,并采用混合模拟技术进行求解. 这种模型能够比较准确地描述风电的不确定性,但模型比较复杂,不能保证计算效率.
不确定性模型的约束条件本质上是不确定的,即系统约束条件仅在一定概率内能得到满足. 多数情况下,其计算结果可以保证系统安全稳定运行. 但在特殊情况下,如在短时间内风电出力发生剧烈变化,其计算结果可能会造成系统潮流越限,影响系统安全稳定运行.
在确定性模型中,调度周期被分解成若干个时间段,单个时间段中的风电输出功率为确定值,然后对整个调度周期进行潮流优化.
文献[22]和文献[11]采用分时段策略,将研究周期内的风电场风速曲线分解成若干条水平线段,每条水平线段对应1个时段,在每个时段将风电机组出力看作是确定值. 此方法对风电随机变化具有一定的适应性,能保证系统稳定可靠运行,但对风电出力变化的描述比较粗糙,且计算结果保守. 文献[23-25]根据风速随机变化的特点,应用场景分析法将风电机组输出功率分成几种典型场景,将难以用数学模型表示的不确定因素转变为容易求解的多个确定性场景问题来处理,降低了复杂问题建模和求解的难度.
2.3 含风电场最优潮流问题的计算方法如上所述,含风电场最优潮流问题是一个高维的非线性多约束的优化问题,针对这类问题的求解,众多学者提出了不同的优化算法,分为传统的经典解算法和现代人工智能优化算法.
传统的经典解算法如:简化梯度法、解耦法、牛顿法和内点法等在电力系统最优潮流问题中都得到了较好的应用. 鉴于目前介绍各类算法基本原理的文献较多,本文就不再一一赘述.
文献[26]基于常规简化梯度法,改进其搜索方向,取得了比常规简化梯度法更快的寻优速度. 文献[27]将快速解耦的思想引入常规内点法中,使其修正方程系数矩阵常数化,使每次迭代所需时间大大缩短,显著提高了计算速度. 文献[28]引入二次罚函数处理约束条件,将牛顿法和二次罚函数结合进行最优潮流问题求解,结果表明运用牛顿法优化潮流,具有较快的收敛速度,收敛性能优越. 文献[29]利用列近似最小度法对内点法牛顿方程的系数矩阵进行节点优化排序,以减少三角分解注入元的产生,从而减少优化时间,提高计算速度.
此类算法本质上都是利用目标函数对控制变量一阶或二阶梯度求解,具有收敛速度快、过程清晰等优点. 但是,此类算法对初值非常敏感且对优化目标及约束条件有一定的要求. 鉴于此类算法的不足,许多学者提出了另一类求解最优潮流问题的算法,即现代人工智能算法.
现代人工智能算法如:遗传算法[30]、粒子群优化算法[31]、差分进化算法[32]、混合蛙跳算法[22]、人工蜂群算法[33-34]和布谷鸟算法[35-36]等. 此类算法与导数无关,克服了经典算法对初值敏感的缺点,具有内在并行性,能处理非连续的、非光滑的、高度非线性解空间的复杂优化问题,是一种具有很好全局收敛性能的优化算法.
文献[22]提出一种混合蛙跳算法,采用一种洗牌策略,将其应用于含风电场电力系统动态优化潮流,结果显示混合蛙跳算法具有较强的全局搜索能力,寻优性能优于粒子群优化算法. 文献[34]提出一种基于人工蜂群的多目标算法对电力系统最优潮流问题进行求解,该算法利用外部存档技术来保存进化过程中已经找到的Pareto最优解,并在每次迭代后更新. 结果表明该算法在避免局部最优的问题上具有明显优势. 文献[35]提出一种基于量子计算和混沌局部搜索的布谷鸟算法,利用切比雪夫映射生成的混沌数列产生新的最优个体,并利用量子旋转门更新其余个体,达到使算法更快收敛并跳出局部解的效果. 文献[36]提出一种改进布谷鸟算法,对布谷鸟算法的个体进行量子位编码,通过叠加态的量子位实现多样化种群,并在算法每次迭代的优化值附近进行混沌局部搜索进而增加布谷鸟算法的局部搜索能力,同时采用量子门变换使每个个体朝最优个体进化,使算法寻优能力得到增强. 文献[37]提出了一种新的可用于安全控制最优潮流问题的遗传算法. 该算法应用一个全新的启发式搜索空间技术使算法在具有以及不具有(N-1) 断电的偶然性实例分析中,具有更好的鲁棒性和更快的收敛速度,缩减了计算的负担. 文献[38]提出基于牛顿-拉夫逊最优潮流算法的混沌粒子群优化算法, 建立了微网综合经济运行的优化模型,仿真结果表明混沌优化提高了算法的收敛速度,改善了算法对初值敏感的缺点. 文献[39]提出一种新型混合粒子群算法,将可行性更新规则引入到最优粒子位置更新过程中,同时在算法中引入模拟退火的思想,保证了算法的收敛速度及精度. 文献[40]提出改进差分进化算法,根据适应度值动态调整缩放因子和交叉控制参数,提高了算法的收敛速度和全局寻优能力. 文献[41]在差分进化算法的基础上提出一种新的动态变异算子,根据适应度值的大小形成一个有义解集合,从中随机选取一个有义解作为基向量来引导群体搜索方向,同时利用高斯分布和柯西分布产生变异因子和交叉因子,使算法在无经验知识的情况下,自动产生适合当前搜索需要的值,增强算法的收敛速度和局部抗干扰的能力.
由于各算法在不同程度上都存在一定的不足,因此,学者们结合各种算法的优缺点提出了众多不同的混合算法[42-45],在算法性能上取得了非常明显的效果.
3 含风电场最优潮流问题的研究方向与展望综上所述,如何正确处理风电场,建立合适的数学模型和选择高效、快速的计算方法是含风电场最优潮流研究的重点.
(1) 当前随机最优潮流多数只考虑单个断面下的潮流分布,而电力系统是一个动态的变化系统,并且随着风电场数量的增多和装机容量的加大,如何建立高效的考虑输入变量随机性的动态最优潮流模型已成为当今电力系统亟需解决的重要研究课题.
(2) 目前在含风电场电力系统的随机潮流研究中,大部分文献都是假设各风电场的风速相互独立,然而地形相同、位置相邻的风电场风速和出力具有较强的时空相关性,如不考虑此相关性,将会导致系统潮流计算出现较大误差,降低对系统运行的风险评估. 因此,考虑不同风电场风速相关性的含风电场最优潮流将是未来研究的又一重点.
(3) 由于风能资源具有明显的随机性、间歇性和不确定性,造成风电输出功率的极不稳定性. 提前进行风速、风电功率的精确预测是降低风电不确定性的首要工具. 但由于预测尺度、地形以及数据来源等因素的影响,当前风电预测精度还无法满足电力系统短期优化调度的需要. 因此,提出更加精确的风电预测技术对含风电场相关问题的解决意义重大.
(4) 含风电场最优潮流问题是一个高维、非线性的复杂优化问题,如用前述经典解算法进行优化会遇到许多问题. 虽然现代人工智能算法存在着数学基础不严密的问题,但其所具有的优势确是非常的明显. 因此,对现代人工智能优化算法进行深入研究以及综合各种算法的优点,提出性能更加优越的混合求解算法具有非常重要的意义.
4 结语本文通过对含风电场最优潮流有关论文的综述,阐述了含风电场最优潮流问题的模型、处理及计算方法,分析了现有研究技术的特点与不足,并在文末对含风电场最优潮流在未来的研究方向进行了展望. 随着对风电并网技术研究的进一步深入,电力系统必将实现安全、可靠、优质、高效运行和节能、环保、可持续发展的目标.
| [1] |
王天施, 苑舜. 风力发电对电网的影响及对策[J].
高压电器, 2010, 46(8): 89-92.
WANG T S, YUAN S. Effects of wind power generation on power grid with countermeasures[J]. High Voltage Apparatus, 2010, 46(8): 89-92. |
| [2] |
吴俊, 李建设, 周剑, 刘春晓. 风力发电并网对电网的影响[J].
南方电网技术, 2010, 4(5): 48-52.
WU J, LI J S, ZHOU J, LIU C X. Influence of Wind Power Generation Integrating into Power Grids[J]. Southern Power Systems Technology, 2010, 4(5): 48-52. |
| [3] |
吴林伟, 张建华, 刘若溪. 考虑风电机组故障的风电场可靠性模型及其应用[J].
电力系统自动化, 2012, 36(16): 31-35.
WU L W, ZHANG J H, LIU R X. A wind farm reliability model considering wind turbine faults and its application[J]. Automation of Electric Power Systems, 2012, 36(16): 31-35. |
| [4] | ZHANG W, WEI Z N, SUN G Q. Power flow calculation for power system including offshore wind farm grid integration[C]//International Conference on Sustainable Power Generation and Supply, 2009. SUPERGEN '09. Nanjing, China: IEEE, 2009. |
| [5] | FEIJOO A E, CIDRAS J. Modeling of wind farms in the load flow analysis[J]. IEEE Trans on Power Systems, 2000, 15(1): 110-115. DOI: 10.1109/59.852108. |
| [6] |
张伟, 卫志农, 刘玉娟. 基于混沌优化的含风电场的最优潮流计算[J].
中国电力, 2011, 44(10): 25-28.
ZHANG W, WEI Z N, LIU Y J. Chaos optimal algorithm based power flow calculation involving wind farms[J]. Electric Power, 2011, 44(10): 25-28. DOI: 10.3969/j.issn.1004-9649.2011.10.006. |
| [7] |
顾承红, 艾芊. 基于改进内点法的含风电场的系统最优潮流计算[J].
中国电力, 2007, 40(1): 89-93.
GU C H, AI Q. Optimal power flow calculation based on the improved interior method for a system integrated with wind farms[J]. Electric power, 2007, 40(1): 89-93. |
| [8] |
吴俊玲, 周双喜, 孙建锋, 等. 并网风力发电场的最大注入功率分析[J].
电网技术, 2004, 28(20): 28-32.
WU J L, ZHOU S X, SUN J F, et al. Analysis on maximum power injection of wind farm connected to power system[J]. Power System Technology, 2004, 28(20): 28-32. DOI: 10.3321/j.issn:1000-3673.2004.20.006. |
| [9] | FEIJÓO A E, CIDRÁS J. Modeling of wind farms in the load flow analysis[J]. IEEE Transactions on Power Systems, 2000, 15(1): 110-115. DOI: 10.1109/59.852108. |
| [10] | CHEN Z, SPOONER E. Grid power quality with variable speed wind turbines[J]. IEEE Transactions on Energy Conversion, 2001, 16(2): 148-154. DOI: 10.1109/60.921466. |
| [11] |
陈金富, 陈海焱, 段献忠. 含大型风电场的电力系统多时段动态优化潮流[J].
中国电机工程学报, 2006, 26(03): 31-35.
ChEN J F, ChEN H Y, DUAN X Z. Multi-period dynamic optimal power flow in wind power integrated system[J]. Proceedings of the CSEE, 2006, 26(03): 31-35. DOI: 10.3321/j.issn:0258-8013.2006.03.006. |
| [12] |
范荣奇, 陈金富, 段献忠, 等. 风速相关性对概率潮流计算的影响分析[J].
电力系统自动化, 2011, 35(04): 18-22+76.
FAN R Q, CHEN J F, DUAN X Z, et al. Impact of wind speed correlation on probabilistic load flow[J]. Automation of Electric Power Systems, 2011, 35(04): 18-22+76. |
| [13] |
邓威, 李欣然, 徐振华, 等. 考虑风速相关性的概率潮流计算及影响分析[J].
电网技术, 2012, 36(04): 45-50.
DENG W, LI X R, XU Z H, et al. Calculation of probabilistic load flow considering wind speed correlation and analysis on influence of wind speed correlation[J]. Power System Technology, 2012, 36(04): 45-50. |
| [14] | HUANG C M, HUANG Y C, HUANG K Y, et al. Deterministic and probabilistic wind power forecasting using a hybrid method[C]//2017 IEEE International Conference on Industrial Technology (ICIT). Canada, Toronto: IEEE,2017: 400-405. |
| [15] |
孙国强, 李逸驰, 向育鹏, 等. 计及风速时空相关性的含风电场电力系统动态随机最优潮流计算[J].
中国电机工程学报, 2015, 35(17): 4308-4317.
SUN G Q, LI Y C, XIANG Y P, et al. Dynamic stochastic optimal power flow of wind integrated power system considering temporal and spatial correlation of wind speed[J]. Proceedings of the CSEE, 2015, 35(17): 4308-4317. |
| [16] |
罗家勇, 鲍海波, 郭小璇. 计及风电场风速相关性的概率最优潮流计算[J].
广西电力, 2014, 37(01): 13-17.
LUO J Y, BAO H B, GUO X X. Calculation of probabilistic optimal power flow considering wind speed correlation of wind farm[J]. Guangxi Electric Power, 2014, 37(01): 13-17. DOI: 10.3969/j.issn.1671-8380.2014.01.004. |
| [17] |
廖迎晨, 甘德强, 陈星莺, 等. 考虑分布式电源出力不确定性的城市电网模糊最优潮流分析[J].
电力自动化设备, 2012, 32(9): 35-39.
LIAO Y C, GAN D Q, CHEN X Y, et al. Fuzzy optimal power flow analysis considering indeterminacy of distributed generation for urban power grid[J]. Electric Power Automation Equipment, 2012, 32(9): 35-39. |
| [18] |
蔺海明, 刘天琪, 李兴源. 考虑风电出力和负荷不确定性的电力系统有功优化潮流[J].
电网技术, 2013, 37(06): 1584-1589.
LIN H M, LIU T Q, LI X Y. Optimal active power flow considering uncertainties of wind power output and load[J]. Power System Technology, 2013, 37(06): 1584-1589. |
| [19] |
娄素华, 王志磊, 吴耀武, 等. 基于机会约束规划的含大规模风电电力系统协调经济调度(英文)[J].
电工技术学报, 2013, 28(10): 337-345.
LOU S H, WANG Z L, WU Y W, et al. Coordinated economic dispatch for power system with significant wind power generation based on chance-constrained programming[J]. Transactions of China Electrotechnical Society, 2013, 28(10): 337-345. DOI: 10.3969/j.issn.1000-6753.2013.10.040. |
| [20] |
鲍海波, 韦化. 基于无迹变换的含大规模风电场电力系统概率最优潮流计算[J].
电力系统自动化, 2014, 38(12): 46-53.
BAO H B, WEI H. Probabilistic optimal power flow computation in power systems including large-scale wind farms based on unscented transformation[J]. Automation of Electric Power Systems, 2014, 38(12): 46-53. DOI: 10.7500/AEPS20130821007. |
| [21] |
盛四清, 孙晓霞. 含风电场的混合机会约束经济调度模型[J].
电力系统及其自动化学报, 2015, 27(08): 82-86+102.
SHENG S Q, SUN X X. Hybrid chance-constrained economic dispatch model with wind farm[J]. Proceedings of the CSU-EPSA, 2015, 27(08): 82-86+102. DOI: 10.3969/j.issn.1003-8930.2015.08.15. |
| [22] |
陈功贵, 李智欢, 陈金富, 等. 含风电场电力系统动态优化潮流的混合蛙跳算法[J].
电力系统自动化, 2009, 33(04): 25-30.
CHEN G G, LI Z H, CHEN J F, et al. SFL algorithm based dynamic optimal power flow in wind power integrated system[J]. Automation of Electric Power Systems, 2009, 33(04): 25-30. DOI: 10.3321/j.issn:1000-1026.2009.04.006. |
| [23] |
陈继明, 祁丽志, 孙名妤, 等. 多场景下含风电机组的配电网无功优化的研究[J].
电力系统保护与控制, 2016, 44(09): 129-134.
CHEN J M, QI L Z, SUN M Y, et al. Reactive power optimization for distribution network with multi-scenario wind power generator[J]. Power System Protection and Control, 2016, 44(09): 129-134. |
| [24] |
陈海焱, 陈金富, 段献忠. 含风电机组的配网无功优化[J].
中国电机工程学报, 2008, 28(07): 40-45.
CHEN H Y, CHEN J F, DUAN X Z. Reactive power optimization in distribution system with wind power generators[J]. Proceedings of the CSEE, 2008, 28(07): 40-45. DOI: 10.3321/j.issn:0258-8013.2008.07.007. |
| [25] |
何健, 丁晓群, 陈光宇, 等. 基于混沌并行差分进化算法的含风电配电网无功优化[J].
电力建设, 2014, 35(11): 1-6.
HE J, DING X Q, CHEN G Y, et al. Reactive power optimization of distribution network with wind power based on chaotic parallel differential evolution algorithm[J]. Electric Power Construction, 2014, 35(11): 1-6. DOI: 10.3969/j.issn.1000-7229.2014.11.001. |
| [26] |
刘学东, 王磊, 余耀. 最优潮流改进简化梯度法的研究及应用[J].
山东电力技术, 2003(1): 19-22.
LIU X D, WANG L, YU Y. The research and application of improved simplifying gradient algorithm in the optimal power flow[J]. Shandong Dianli Jishu, 2003(1): 19-22. |
| [27] |
侯芳, 吴政球, 王良缘. 基于内点法的快速解耦最优潮流算法[J].
电力系统及其自动化学报, 2001, 13(6): 8-12.
HOU F, WU Z Q, WANG L Y. Optimal power solution based on fast decouple interior point algorithm[J]. Proceedings of the EPSA, 2001, 13(6): 8-12. |
| [28] |
朱雪凌, 张翠影, 赵臣鹏, 等. 基于牛顿法的电力系统最优潮流计算[J].
华北水利水电大学学报(自然科学版), 2014, 35(03): 71-74.
ZHU X L, ZHANG C Y, ZHAO C P, et al. Power system optimal power flow calculation based on newton's method[J]. Journal of North China University of Water Resources and Electric Power (Natural Science Edition), 2014, 35(03): 71-74. DOI: 10.3969/j.issn.1002-5634.2014.03.017. |
| [29] |
聂永辉, 肖白, 刘凤兰. 电力系统最优潮流新模型及其内点法实现[J].
电力系统及其自动化学报, 2014, 26(11): 53-57.
NIE Y H, XIAO B, LIU F L. New optimal power flow model and its solution by using nonlinear interior point method[J]. Proceedings of the CSU-EPSA, 2014, 26(11): 53-57. DOI: 10.3969/j.issn.1003-8930.2014.11.011. |
| [30] | DEVARAJ D, YEGNANARAYANA B. Genetic-algorithm-based optimal power flow for security enhancement[J]. Generation, Transmission and Distribution, IEE Proceedings, 2005, 152(6): 899-905. DOI: 10.1049/ip-gtd:20045234. |
| [31] | CHEN W N, ZHANG J, LIN Y, et al. Particle swarm optimization with an aging leader and challengers[J]. IEEE Transactions on Evolutionary Computation, 2013, 17(2): 241-258. DOI: 10.1109/TEVC.2011.2173577. |
| [32] | ELA A A E, ABIDO M A, SPEA S R. Optimal power flow using differential evolution algorithm[J]. Electrical Engineering, 2009, 91(2): 69-78. DOI: 10.1007/s00202-009-0116-z. |
| [33] | KHORSANDI A, HOSSEINIAN S H, GHAZANFARI A. Modified artificial bee colony algorithm based on fuzzy multi-objective technique for optimal power flow problem[J]. Electric Power Systems Research, 2013, 95(95): 206-213. |
| [34] |
刘前进, 许慧铭, 施超. 基于人工蜂群算法的多目标最优潮流问题的研究[J].
电力系统保护与控制, 2015, 43(08): 1-7.
LIU Q J, XU H M, SHI C. Research on power flow optimization based on multi-objective artificial bee colony algorithm[J]. Power System Protection and Control, 2015, 43(08): 1-7. |
| [35] |
周前, 卫鹏, 刘超君. 基于改进布谷鸟算法的随机最优潮流[J].
电力科学与工程, 2017, 33(02): 14-20.
ZHOU Q, WEI P, LIU C J. Stochastic optimal power flow based on modified cuckoo search algorithm[J]. Electric Power Science and Engineering, 2017, 33(02): 14-20. DOI: 10.3969/j.ISSN.1672-0792.2017.02.003. |
| [36] |
张东寅, 王澎涛, 袁艳斌, 等. 基于改进布谷鸟算法的电力系统最优潮流计算[J].
水电能源科学, 2017, 35(01): 200-204.
ZHANG D Y, WANG P T, YUAN Y B, et al. An improved cuckoo search algorithm for optimal power flow problem[J]. Water Resources and Power, 2017, 35(01): 200-204. |
| [37] |
ZHANGD Y, BENERJIM, SYDULUM. [J].
, 2011, 36(03): 46-53.
BHASSKAR M M, BENERJI M, SYDULU M. 基于启发搜索空间遗传算法的安全控制最优潮流方法(英文)[J]. 昆明理工大学学报(自然科学版), 2011, 36(03): 46-53. |
| [38] |
王晶, 陈骏宇, 蓝恺. 基于实时电价的微网PSO最优潮流算法研究[J].
电力系统保护与控制, 2013, 41(16): 34-40.
WANG J, CHEN J Y, LAN K. PSO optimal power flow algorithm for a microgrid based on spot power prices[J]. Power System Protection and Control, 2013, 41(16): 34-40. DOI: 10.7667/j.issn.1674-3415.2013.16.005. |
| [39] |
汪泳涛, 汪琳红, 罗松涛. 新型混合粒子群算法在电力系统最优潮流计算中的应用[J].
可再生能源, 2013, 31(06): 34-37.
WANG Y T, WANG L H, LUO S T. The application of novel hybrid particle swarm algorithm for optimal power flow calculation of power systems with considering wind power integration[J]. Renewable Energy Resources, 2013, 31(06): 34-37. |
| [40] |
赵树本, 张伏生. 基于改进差分进化算法的电力系统最优潮流计算[J].
电网技术, 2010, 34(08): 123-128.
ZHAO S B, ZHANG F S. Solution of optimal power flow based on differential evolution and its modified algorithm[J]. Power System Technology, 2010, 34(08): 123-128. |
| [41] |
王丛佼, 王锡淮, 陈国初, 等. 基于改进差分进化算法的潮流发电机组微观选址[J].
电工技术学报, 2016, 31(15): 99-108.
WANG C J, WANG X H, CHEN G C, et al. Tidal current turbines micrositing based on improved differential evolution algorithm[J]. Transactions of China Electrotechnical Society, 2016, 31(15): 99-108. DOI: 10.3969/j.issn.1000-6753.2016.15.012. |
| [42] |
黄琳, 周家虎. 基于混合优化算法的最优潮流计算[J].
电力学报, 2011, 26(02): 111-115+162.
HUANG L, ZHOU J H. Hybrid optimization algorithm for optimal power flow problems[J]. Journal of Electric Power, 2011, 26(02): 111-115+162. DOI: 10.3969/j.issn.1005-6548.2011.02.006. |
| [43] |
韩富春, 王晋, 杨翠茹, 等. 遗传算法与蚂蚁算法相融合的电力系统最优潮流计算[J].
电力学报, 2005, 20(04): 340-342.
HAN F C, WANG J, YANG C R, et al. The analysis of genetic algorithm and ant algorithm fusion' s electric power system optimal power flow[J]. Journal of Electric Power, 2005, 20(04): 340-342. DOI: 10.3969/j.issn.1005-6548.2005.04.005. |
| [44] |
李静文, 赵晋泉, 张勇. 基于改进差分进化-生物地理学优化算法的最优潮流问题[J].
电网技术, 2012, 36(09): 115-119.
LI J W, ZHAO J Q, ZHANG Y. Optimal power flow on basis of combining improved differential evolution algorithm with biogeography-based optimization algorithm[J]. Power System Technology, 2012, 36(09): 115-119. |
| [45] | MARCELINO C G, ALMEIDA P E M, WANNER E F, et al. Fundamentals of the C-DEEPSO algorithm and its application to the reactive power optimization of wind farms[C]//2016 IEEE Congress on Evolutionary Computation (CEC), Vancouver, BC: IEEE, 2016 : 547-1554.doi: 10.1109/CEC. 2016.7743973. |
 2018, Vol. 35
2018, Vol. 35