20世纪以来，人类对三角洲地区的开发、经济和人口的增长均对三角洲地区有着严重的影响^[1]. 珠江三角洲地区作为我国沿海的重要通商口岸之一，自改革开放以来，经济快速发展、城市人口迅猛增加、城市化水平日益提高. 不断增加的人口，加上大量的地铁等大型基础设施建设、填海造田和抽取地下水等人类活动，令原本就广泛分布喀斯特岩溶隐伏区和软土层的珠江三角洲更加不堪重负，地面沉降事故频发，连年造成巨大的生命财产损失.

及时准确地监测地面沉陷及发展过程是当前面临的重要任务. 目前沉降监测仍以水准测量等地面观测技术为主，工作量大，成本高，难以经常重复观测. 合成孔径雷达干涉测量(Interferometric Synthetic Aperture Radar，InSAR)是一种空间对地观测的新技术，它以两幅覆盖同一地区的复数SAR图像为信息源，通过干涉技术获得两幅SAR图像的相位差，进而获取地表形变^[2-4]. 利用InSAR能够监测大范围的地表形变，并且利用先进的多干涉图时间序列分析方法，可获得毫米级精度的地表形变量^[5-7]. 因此，在缺乏地面观测(如GNSS和水准测量数据)的情况下，InSAR是用来监测区域性地表沉降的最好方法^[8]. 近年来，InSAR被广泛用于地下水开采^[9-11]、构造运动^[12-13]、沉积物压实^[14]和地下油、汽开采^[15-16]等引发的沉降监测.

DInSAR数据处理中常用的方法有两轨法和多轨法^[3]. 其中两轨法可直接利用外部DEM消除干涉相位中的地形分量，现在基本成为DInSAR的通行方法. SRTM(Shuttle Radar Topography Mission)是由美国国家图像测绘局(National Imagery and Mapping Agency，NIMA)和美国国家航空航天局(National Aeronautics and Space Administration，NASA)联合完成的项目^[17]. 该项目成功获取了覆盖地表80%面积的干涉雷达数据(北纬60°到南纬57°之间)，其水平精度为7.2~12.6 m，绝对高程精度为5.6~9.0 m^[17]. 由于SRTM的DEM产品精度高、覆盖广，在InSAR数据处理中被广泛用作外部DEM的来源.

SRTM DEM包括1″(30 m)和3″(90 m)两种不同空间分辨率的产品，自2000年SRTM DEM发布以来，除美国本土数据的分辨率为30 m，全球其他地区数据的分辨率为90 m. 美国国家地理空间情报局(National Geospatial-Intelligence Agency，NGA)在2014年9月宣布30 m的SRTM DEM将数据逐步向全球用户免费开放，其中中国地区30 m DEM数据于2015年7月已经可以免费下载. 本文将选取珠江三角洲为实验区，比较两种不同分辨率的SRTM DEM对InSAR形变监测结果的差异.

本文研究范围主要是珠江三角洲地区，其地理坐标为东经112.7°至114.9°，北纬21.8°至24.0°，面积约为58 600 km². 选取了欧空局Envisat卫星在2003年至2010年采集的025、175和297三个轨道的C波段雷达影像. 使用由美国喷气推进实验室(JPL)和加州理工学院共同开发的ROI_PAC软件^[18]对雷达影像进行处理，生成多幅InSAR干涉图. 为了尽量减少轨道误差，处理时采用欧空局发布的DORIS精密轨道. 为了比较DEM在珠江三角洲地区对InSAR形变测量的差异，本文分别使用SRTM 30 m与90 m两种不同分辨率的DEM进行处理. 为了便于比较，对于90 m分辨率的DEM首先通过样条函数插值得到像素大小30 m的DEM，并且所有干涉图均进行单视处理，进而能够更加突出地显示出两种分辨率的DEM对InSAR结果的差异. 随后使用枝切法对干涉图进行相位解缠^[19]. 对于无法自动解缠的区域采用人工桥接的方式解缠. 最终对干涉图进行地理编码，获得WGS84坐标系下的解缠相位.

通常，干涉图的相干性受到垂直基线、时间间隔、季节差异等影响. 本文尽量选取垂直基线和时间间隔短、季节相同的影像组成干涉像对，最终采用了62景雷达影像，针对两种DEM各生成了168幅干涉图，其干涉组合及垂直基线分布如图1所示.

检验相位解缠误差时，可将所有干涉图组合成闭合环. 理论上每个闭合环中干涉图解缠相位的闭合差应为0，若闭合差为雷达半波长的整数倍，则说明相位解缠存在错误.

根据这一原理，使用最小距离生成树算法(MST)^[20]和Dijkstra算法^[21]检验各闭合环中的闭合差. 对于存在解缠错误的干涉图，手工进行改正，直到所有干涉图没有相位解缠错误为止^[8]. 若存在无法构成闭合环的干涉图，则通过检查解缠相位的连续性来排除解缠错误^[22].

图2为本文研究的珠江三角洲区域SRTM DEM，其中图2(b)与2(c)分别为30 m和90 m分辨率的DEM，前者明显更能显示地物的西部特征，例如珠江中江心岛的轮廓在图2(b)中清晰显现，而图2(c)中岛屿与陆地连在一起. 图2(d)的统计直方图表明高程差的绝对值小于2.5 m的像素约占70%，介于2.5~7.5 m的约占27%，大于7.5 m的约占3%.

图 1(Figure 1)

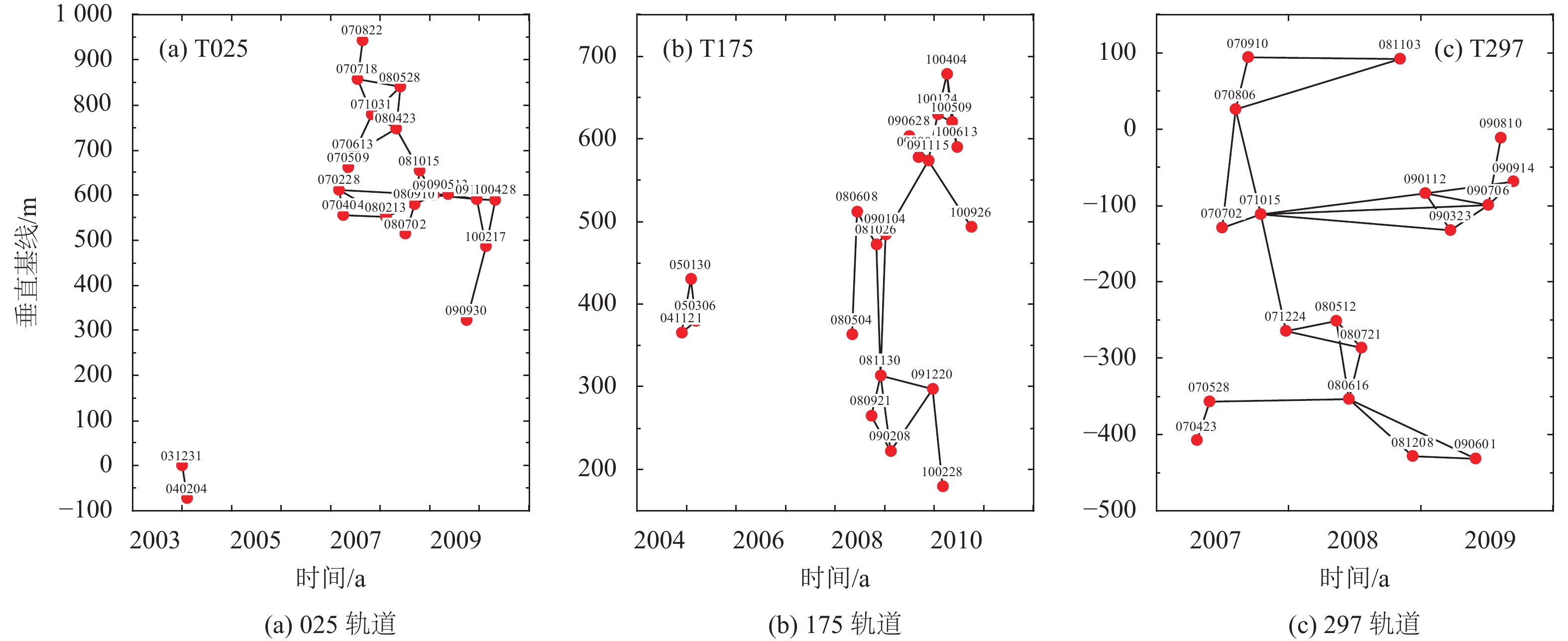
图 1 不同轨道的干涉组合及垂直基线分布 Figure 1 Interference combination and vertical baseline distribution Perpendicular Baseline(m) 垂直基线/m；Date(year) 时间/a

图 2(Figure 2)

图 2 珠江三角洲中同一地区30 m DEM与90 m DEM比较 Figure 2 Comparison of 30 m DEM and 90 m DEM in the same region of the Pearl River Delta

DInSAR中，变形相位观测值( ${\varphi _{{{defo}}}}$ )可以表示为

其中 $\varphi $ 表示干涉像对的原始差分相位， ${\varphi _{{{ref}}}}$ 表示参考相位，可以通过卫星轨道与地球的参考椭球模型计算， ${\varphi _{{{topo}}}}$ 表示地形相位，可以通过外部DEM计算，如式(2)所示.

其中， $B_ \bot ^0$ 为垂直基线， $\lambda $ 为波长， ${\, \rho _1}$ 为斜距， ${\theta _0}$ 为视角，h为高程.

鉴于变形相位与地面变形量的关系式为

外部DEM误差导致的变形误差为

由式(4)可知，在斜距 ${\rho _1}$ 和视角 ${\theta _0}$ 固定不变时，DEM产生的变形误差主要受垂直基线和高程误差的影响.

以Envisat卫星175轨道中2005/01/30与2005/03/06这两幅图组成的干涉像对为例(时间基线36 d，垂直基线50 m)，见图3. 图3(a)表示依据式(4)分别采用30 m和90 m分辨率的SRTM DEM计算的变形量之差. 从图3(a)中的直方图可以发现，两者差的绝对值小于0.5 mm的约占77%，介于0.5~1.5 mm的约占19%，介于1.5~2.5 mm的约占2%，大于2.5 mm的约占2%，最大值约为4 mm. 其中，差异较大的地区主要集中在地形起伏较明显的山区.

图3(b)为实际干涉处理时屏蔽了去相干点后两种DEM对变形量结果的差异. 由图3可以看出，图3(a)中DEM影响较大的山区往往相干性较差，难以得到有效的干涉测量结果. 在相干性较好的地区，两者差值的绝对值小于0.5 mm的约占91%，介于0.5~1.5 mm的约占7%，大于1.5 mm的约占2%.

如上所述，DEM对InSAR干涉相位的影响与垂直基线有关，在珠江三角洲地区，垂直基线小于200 m时通常能得到较好的干涉图，因此，这两种分辨率的SRTM DEM对单个干涉图变形量的影响最大可能达到图3的4倍.

图 3(Figure 3)

图 3 DEM对InSAR干涉相位的影响 Figure 3 The influence of DEM on the phase of InSAR interference

如果在同一轨道中获得了多个干涉像对，则形变速率可以通过累计的位移除以累计时间得到. 综合式(4)，可以得到DEM导致的速率误差与外部DEM的高程误差之间的关系式：

其中i为同一轨道中第i个图像对，n为干涉像对的总数.

图4(a)、4(b)和4(c)分别显示在025、175和297轨道中30 m DEM与90 m DEM对形变速率的影响. 具体影响详见表1.

由图4中的直方图可知，对于025轨道，差值的绝对值小于1 mm/a的约占81%；对于175轨道，差值的绝对值小于1 mm/a的约占99%；对于297轨道，差值的绝对值小于1 mm/a的约占89%. 综合以上3个轨道的结果，DEM对于多干涉图获得的平均速率影响分布在±4 mm/a之间，其中90%介于±1 mm/a，这意味着对于在珠江三角洲地区，30 m与90 m SRTM DEM对形变速率影响几乎可以忽略不计.

表 1(Table 1)

表 1 在025、175和297轨道中30 m DEM与90 m DEM对形变速率结果的差异 Table 1 Difference of 30 m DEM and 90 m DEM on the rate of deformation in 025, 175 and 297 orbits 差异范围/(mm·a–1) 轨道占比/% T025 T175 T297 –2.5~ –1.5 4.5 0 1 –1.5~ –0.5 20 3 18 –0.5~0.5 58 94 67 0.5~1.5 14 2 13 1.5~2.5 3 0 0.5 其余 0.5 1 0.5

表 1 在025、175和297轨道中30 m DEM与90 m DEM对形变速率结果的差异 Table 1 Difference of 30 m DEM and 90 m DEM on the rate of deformation in 025, 175 and 297 orbits

以珠江三角洲地区为试验区，本文采用欧空局Envisat卫星第175轨道2005/01/30与2005/03/06这两幅图像构成的干涉像对，分析了30 m与90 m分辨率的SRTM DEM对单个干涉图结果的差异，实验结果表明，对于50 m长度的垂直基线，干涉测量的差值介于±4 mm之间，其中89%介于±1 mm，考虑到该地区基线长度达到200 m以内能保持合理的相干性，对单个干涉图的影响值最大可以达到该实验像对的4倍. 通过对3个轨道分别获得的平均变形速率分析，得出30 m与90 m分辨率的SRTM DEM对平均速率结果的差异分布在±4 mm/a之间，其中90%介于±1 mm/a，考虑到InSAR长期形变监测的精度极限基本在1 mm/a左右，因此，本文认为30 m与90 m SRTM DEM对在珠江三角洲地区形变速率结果的差异基本可以忽略不计.

图 4(Figure 4)

图 4 不同轨道中30 m与90 m DEM对形变速率影响的比较 Figure 4 Comparison of the effects of 30 m and 90 m DEM on the rate of deformation in different orbits