2. 广州市自来水公司,广东 广州 510600
2. Guangzhou Water Supply Company, Guangzhou 510600, China
供水管网中水质恶化的原因主要是内源污染和外源污染[1]两个方面,因此供水管网水质监测点的优化选址仅考虑一个方面得到的监测点布置方案已经不能满足目前供水企业的要求. 水质监测点的优化选址俨然成为了一个多目标优化的问题. Behzadian等[2]介绍了多目标优化技术在管网优化中应用. Jonathan Berry[3]提出了多目标混合整数规划模型,用来解决多目标选址问题. 陶涛等[4]在多目标混合整数规划模型的基础上提出不同监测目标影响值的计算方法以及对根据不同目标函数得到优化布置方案结果进行评估判断. Nima Ehsani和Abbas Afshar[5] 以污染事件的监测率和平均监测期望时间为目标函数,应用非支配多目标蚁群算法求解得到平均监测时间与监测率之间的关系. NSGA-Ⅱ[6]是一种经典的多目标优化算法,可保留精英个体,实现快速的支配排序并采用拥挤度及比较算子代替了NSGA算法的共享半径,因其有效性和灵活性在地下矿运[7]、炼铁[8]、水资源优化配置和调度[9-10]等工程方面得到广泛的应用. 近年来,NSGA-Ⅱ算法有效地解决了给水管网多目标优化[11-14]的问题. 刘书明[15]以水质监测点探测到的不同污染事件的时段区间冗余度最小化和污染事件探测概率最大化为优化目标,采用NSGA-Ⅱ算法计算求解得到监测点优化选址方案.
由于NSGA-Ⅱ算法应用在非支配解的数目较大的模型求解时,种群数目的大小影响解集的完整性和求解效率. 种群数目设置较小,导致非支配解丢失;种群数目设置过大,求解效率降低. 因此,本文在NSGA-Ⅱ算法的基础上引入外部存档机制以及对父体染色体选择方式进行改进,提高NSGA-Ⅱ算法在水质监测点多目标优化求解的效率,获得完整的最优非支配解集.
1 多目标监测点优化选址数学模型构建 1.1 目标函数的设计思路水质监测点布置需要同时满足常规状况和突发污染状况的监测,因此,目标函数设置为:(1)最大化常规监测水量覆盖率;(2)最小化突发污染的监测失效率;(3)引入最小化监测点数目与管网节点数目的比值作为第三个目标函数. 其原因分析如下:研究中发现仅仅以(1)、(2)为目标函数时,在最优解的情况下,监测点的数目越大,常规监测的水量覆盖率越高和突发污染监测的监测失效率越低,如果仅仅采用两个目标函数,根据非支配理论,除了常规监测的水量覆盖率为100%,同时突发监测的失效率为0这种特殊情况外,对于任何一个监测点数目小的解,必然存在一个监测点数目大的解支配它,最终得到的非支配解集仅仅出现在监测点数目较大的位置. 因此,引入最小化监测点数目与管网节点数目的比值作为第三个目标函数,可以使不同监测点数目的最优解之间的支配关系变成了非支配关系,使得到的解集均匀分布在监测点数目区间内.
1.2 最大化常规水质监测的水量覆盖率常规水质监测中,当相连通节点i,j的平均水龄值相差不大时,说明节点i与节点j具有相似的水质,同样给定一个覆盖标准C,管网中相连通的上游节点i的节点水龄值与下游节点j的比值不小于允许覆盖标准C时,则认为节点j能够表示节点i的水质[16].
常规水质监测的目标函数可表示为
| $\max {z_1} = \frac{{\sum\limits_{{t_i}}^{{t_i} \subset S} {\sum\limits_{{M_j}}^{{M_j} \subset M} {\sum\limits_{{J_k}}^{{J_k} \subset C\left( {{t_i},{M_j}} \right)} {q\left( {{t_i},{J_k}} \right)} } } }}{{\sum\limits_{{t_i}}^{{t_i} \subset S} {\sum\limits_{{J_l}}^{{J_l} \subset J} {q\left( {{t_i},{J_l}} \right)} } }}.$ | (1) |
其中,ti为第i个时刻t;S为水力模型模拟时长输出时刻的合集,与设置的水力步长和模拟起始时间有关;Mj为第j个监测点的位置;M为布置监测点的合集;Jk为监测点Mi监测覆盖的节点;C(ti,Mj)为监测点Mj在ti时刻监测覆盖的节点合集,被覆盖的节点需满足C(ti,Mj)≥C标,在已有的关于常规水质监测点优化选址的研究中,无论是水量覆盖法还是水龄覆盖法,覆盖标准值最大设置为0.75,为了布置的监测点更具有代表性,在这里设置为0.75;q(ti,Ji)为节点Ji在ti时刻的节点流量;Ji为供水管网中第i节点;J为供水管网节点集合.
1.3 最小化突发污染水质监测的监测失效率由于突发污染事件的随机性,在整个管网拓扑结构中任意一个节点(水源点除外)任意时刻都可能发生污染物入侵,需要尽快对发生的污染事件发生预警. 对此设定一个监测时间值t,对于发生的突发污染事件(只考虑单点污染事件),如果监测点在设定的监测时间值t之内发现该污染事件认为是有效的监测;如果在监测时间值t之外发现该污染事件或者没有发现该污染事件都认为是无效的监测,即监测的失效事件.
突发水质监测的目标函数可表示为
| $\min {z_2} = \frac{{\sum\limits_{{t_i}}^{{t_i} \subset S} {\sum\limits_{{M_j}}^{{M_j} \subset M} {{{Count}}({t_i},{M_j})} } }}{{\sum\limits_{{t_i}}^{{t_i} \subset S} {{{Emount}}} }}.$ | (2) |
其中,ti为第i个时刻t;S为水力模型模拟时长输出时刻的合集,与设置的水力步长和模拟起始时间有关;Mj为第j个监测点的位置;M为布置监测点的合集;Count(ti,Mj)为监测点Mj在ti时刻监测覆盖的突发污染事件数目,被覆盖的节点需满足条件:T(ti,Ji,Mj)≤t,为了使监测点覆盖更多的污染事件以及实现对于可能发生有效的监测事件能够在30 min内预警,监测时间t设置为900 s;Emount为在ti时刻可能发生突发污染事件的集合.
1.4 最小化监测点数目与管网节点数目的比值监测点数目与管网节点数目的比值可表示为
| $\min {z_3} = \frac{{{{Mamount}}}}{{{{Jamount}}}}.$ | (3) |
其中,Mamount为水质监测点的数目;Jamount为管网节点的数目.
2 改进的NSGA-Ⅱ算法在水质监测点多目标优化中,当监测点的数目是变化的时候,优化模型必然存在多个最优非支配解. NSGA-Ⅱ算法采用的精英保留策略加速了优化速度却减少了种群的多样性,输出的解集的数目与设定的染色体数目一致. 当直接应用NSGA-Ⅱ算法求解监测点优化选址模型时,监测点布置数目变化范围大,为了获取完整的非支配解集,需要初始设置染色体的数目很大,耗费了大量的计算资源. 如果初始设置染色体的数目较小,则会导致一些监测点数目对应的解缺失. 因此,在NSGA-Ⅱ算法的基础上做出一些改进,提高求解的速率和非支配解的完整性.
2.1 NSGA-Ⅱ算法的改进策略和步骤 2.1.1 改进策略建立一个外部档案储存算法进化过程中发现的非支配解,在每一次迭代中进行更新,使输出的非支配解集的数目不再受到染色体数目的限制. 在产生下一代染色体前,先判断外部档案的数目与染色体数目的大小. 如果外部档案的数目小于染色的数目,新产生的染色体与上一代父体合并,进行支配排序和计算个体之间的拥挤距离;否则,新产生的染色体和外部档案合并,进行支配排序和计算个体之间的拥挤距离. 然后采用二进制锦标赛选出合并种群的较优个体作为父体,进行交叉、变异操作. 这样算法在前期可以避免外部档案中非支配解数目较少而陷入局部最优,后期因为外部档案中的非支配解的数目较大,可以满足种群多样性的要求,并且提高算法的收敛性.
2.1.2 改进步骤该算法的具体步骤如下:
(1) 设置染色体决策变量的范围和外部储存档案Archives的数目.
(2) 随机生成初始种群P0,令迭代次数n=0.
(3) 计算初始种群P0的目标函数适应值.
(4) 对初始种群P0进行快速支配排序,根据个体的非支配水平得到初始种群的非支配层F1,F2,…,计算出每一层Fi的拥挤距离和把第一层的个体储存在Archives中.
(5) 采用二进制锦标赛选择种群Pn的较优个体,然后进行交叉、变异操作,产生新的种群Qn.
(6) 比较外部储存档案Archives的数目与种群数的大小,如果Archives的数目大于种群数,将种群Archives与Qn合并形成混合种群Rn;否则,将种群Qn与Rn-1合并形成混合种群Rn. 对种群Rn进行快速支配排序,根据个体的非支配水平得到初始种群的非支配层F1,F2,…,更新外部储存档案Archives.
(7) 计算出每一层Fi的拥挤距离并进行排序,从Rn中选出最好的N个个体组成Pn+1,n=n+1.
(8) 如果终止条件成立,则算法终止;否则,执行步骤(4).
2.2 改进NSGA-Ⅱ算法的具体实现 2.2.1 编码设计遗传算法常用的编码方式有整数编码和二进制编码,本文采用二进制编码形式. 每一个染色体的长度为管网节点的数目,染色体每一位置只用0和1两种数值,0表示该位置不布置监测点,1表示该位置布置监测点.
2.2.2 选择操作本文采用二进制锦标赛选择方法确定算法的初始种群,通过比较两个选中的个体的排序等级和拥挤距离来确定较优的个体进入下一代种群.
2.2.3 交叉和变异操作交叉和变异操作是NSGA-Ⅱ算法产生下一代种群最重要的组成部分,它们的主要参数分别是交叉算子和变异算子. 本文采用的是两点交叉和单点变异的方式产生新的种群,交叉算子为0.9而变异算子为0.1.
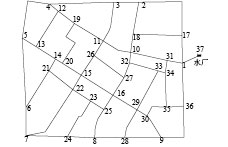
3 案例分析本文采用的案例管网是Fossolo管网,该管网有1个水源,36个节点,管网拓扑结构如图1所示.
|
图 1 Fossolo拓扑结构 Figure 1 Fossolo topology |
在EPANET平台上模拟Fossolo管网,获取管网的静态数据和动态数据. 在MATLAB平台上编写程序代码调用动态数据库,建立节点间的水龄覆盖矩阵和监测时间覆盖矩阵.
3.1.1 构建水龄覆盖矩阵在MATLAB平台上,调用Fossolo管网的动态数据库,得到管网模型在模拟周期内的水质比例矩阵,表1是在0:00时刻下的水质比例矩阵的一部分. 由于常规监测的约束条件覆盖标准值为0.75,比较水质比例值与覆盖标准值的大小,得到了常规监测的水龄覆盖矩阵,表2表示的是0:00时刻下的水龄覆盖矩阵的一部分.
| 表 1 水龄比例矩阵 Table 1 Current age proportioned matrix |
| 表 2 水龄覆盖矩阵 Table 2 Current age coverage matrix |
在MATLAB平台上,调用Fossolo管网的动态数据库,得到管网模型在模拟周期内节点间的流通时间矩阵,表3是在0:00时刻下的流通时间矩阵的一部分. 由于突发污染监测的约束条件监测时间为900 s,比较流通时间与监测时间的大小,得到了突发污染监测的监测时间覆盖矩阵,表4表示的是0:00时刻下的监测时间覆盖矩阵的一部分.
| 表 3 流通时间矩阵 Table 3 Flow time matrix |
| 表 4 监测时间覆盖矩阵 Table 4 Monitoring time coverage matrix |
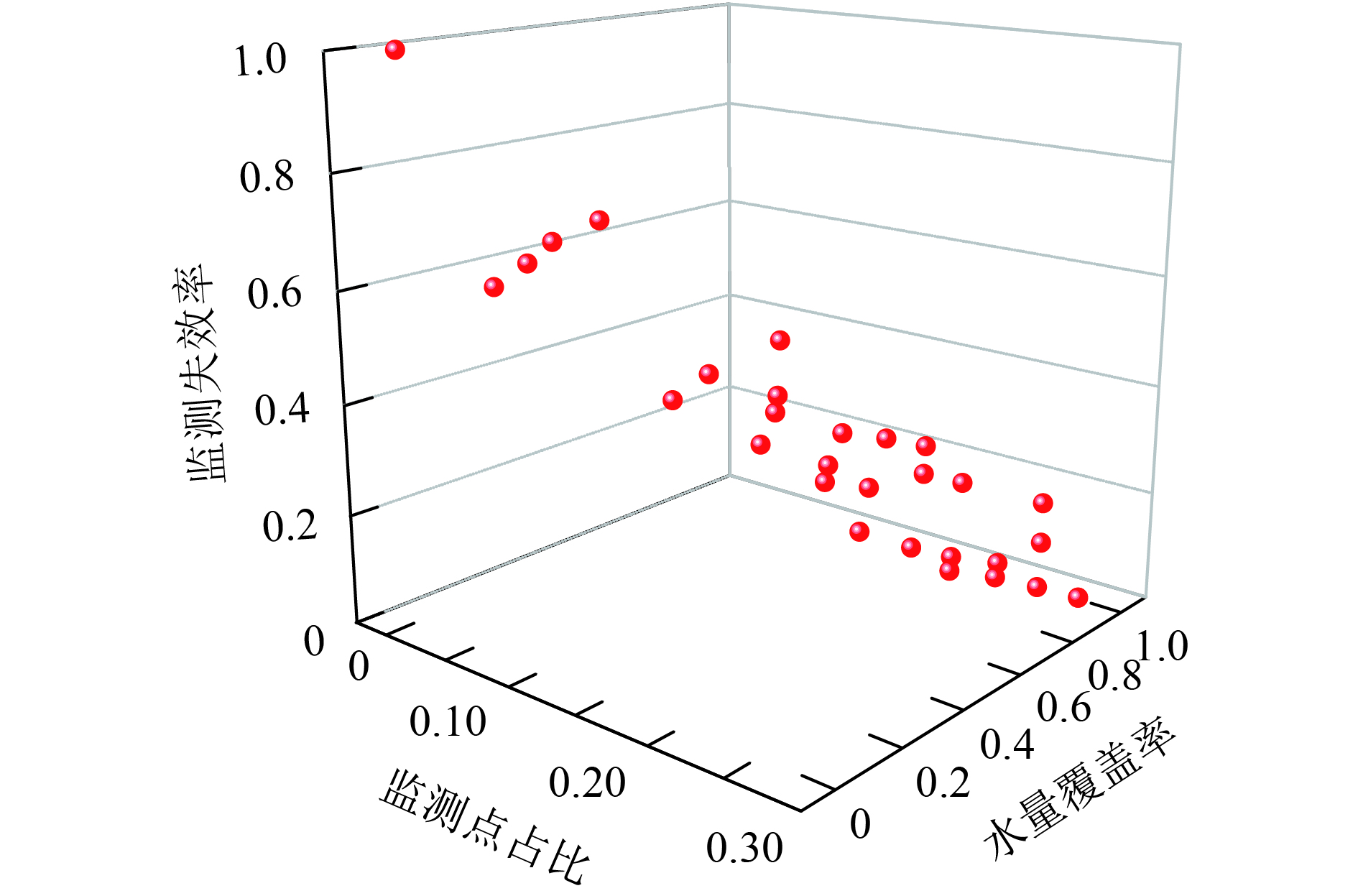
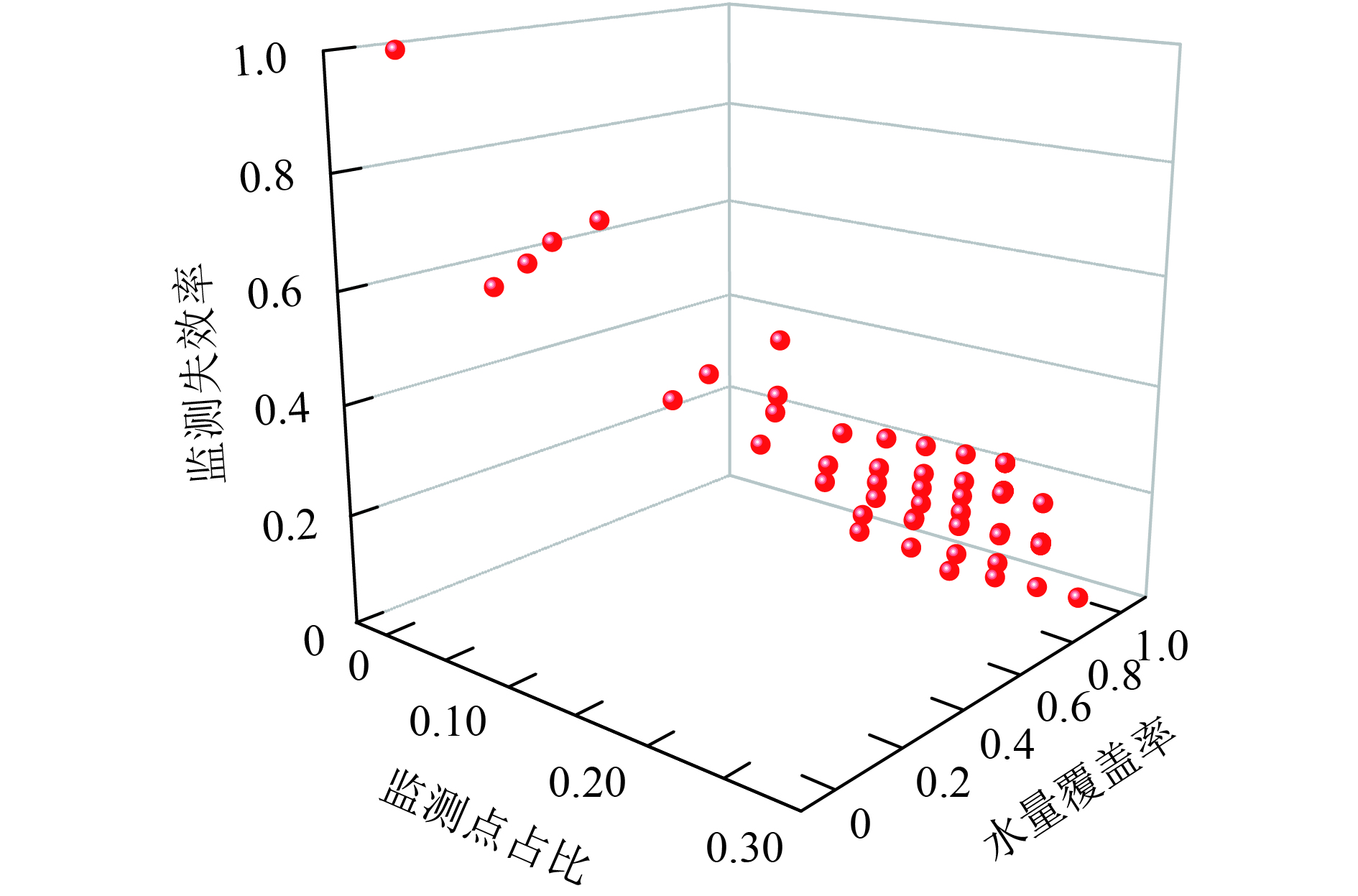
使用NSGA-Ⅱ算法对监测点多目标优化选址模型进行求解,算法的染色体数目设置为30、60,迭代次数为5 000,分别得到水质监测点多目标优化选址模型的非支配解集,非支配解Pareto如图2~3所示.
比较图2和图3的非支配解的数目和分布,由于NSGA-Ⅱ算法中非支配解保留的数目受到染色体大小的约束,导致染色体数目设置为30时非支配解出现丢失,这样会导致非支配解集中满足要求的非支配解会在运算的过程出现丢失的可能. 所以使用NSGA-Ⅱ算法时,在迭代次数设置为5 000次的情况下,种群数目设置60以上,才能够获得完整的最优非支配解集,解集中的非支配解的数目为57个. 当直接应用NSGA-Ⅱ求解监测点优化选址模型时,监测点布置数目变化范围大,为了获取完整的非支配解集,需要初始设置染色体的数目很大,耗费了大量的计算资源.
|
图 2 染色体为30的非支配解解集分布 Figure 2 The non-dominant set of 30 chromosomes |
|
图 3 染色体为60的非支配解集分布 Figure 3 The non-dominant set of 60 chromosomes |
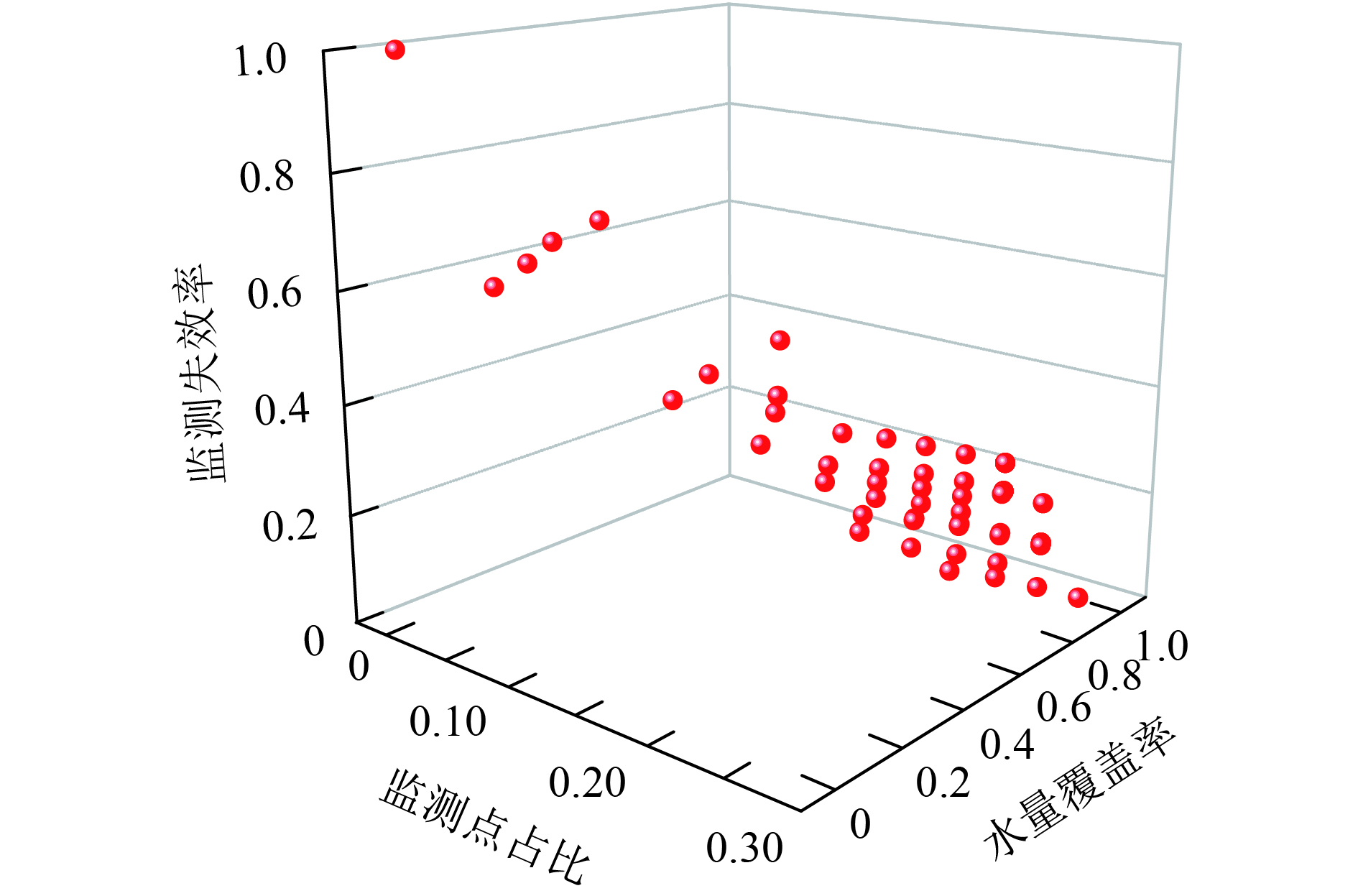
使用改进的NSGA-Ⅱ算法对水质监测点多目标优化选址模型进行求解,在迭代次数设置为5 000的条件下,算法的染色体数目大小设置为30,外部档案数目为100,得到非支配解数目为57个的完整的最优非支配解集,非支配解Pareto如下图4所示,与图3的分布一致.
|
图 4 非支配解分布 Figure 4 Non-dominant solution pareto |
在迭代次数都设置为5 000和获得最优非支配解集相同的情况下,应用NSGA-Ⅱ算法和改进NSGA-Ⅱ算法对水质监测点多目标优化选址模型求解时,计算运用的时间如表5所示. 改进的NSGA-Ⅱ算法相比于NSGA-Ⅱ算法在运算时间上减少176 s,节省了约42%的运算时间. 实际供水管网中的监测点数目的变化范围大,故解集的空间较大,改进的NSGA-Ⅱ算法在实际供水管网模型求解中能够提高运算效率.
| 表 5 算法性能比较 Table 5 Performance evaluation of algorithms |
由于目前关于水质监测点优化选址的研究,都是在监测点数目确定的情况下,对于其他监测指标的进行优化,得到的是关于某一个确定监测点数目的最优解,只是该模型最优解集的子集. 而本文引入了关于监测点数目优化这一目标函数,如图3和图4所示,监测点占比的变化范围为[0,0.3],水量覆盖率和监测失效率的变化范围为[0,1],获得了关于整个模型的最优解合集.
4 结语本文针对在NSGA-Ⅱ算法应用于水质监测点多目标优化选址模型中会出现最优非支配解缺失,占用计算资源大的缺陷,在算法的基础上引入外部存档和对父体染色体的选择方式进行改进,并且应用改进的NSGA-Ⅱ算法对水质监测点的多目标优化选址模型进行的求解,能够得到完整的最优非支配解集,改进了之前算法只能得到最优解子集的情况;同时,在采用的算例模型应用运算时间上约减少176 s,比使用NSGA-Ⅱ算法节省了约42%的运算时间. 因此,改进的NSGA-Ⅱ算法应用于实际管网的水质监测点多目标优化选址中能够提高求解计算的效率.
| [1] |
吕谋, 裘巧俊, 李乃虎, 等. 浅谈城市供水系统安全性[J].
青岛理工大学学报, 2005, 26(1): 1-4.
LYU M, QIU Q J, LI N H, et al. Study on the security of city water supply systems[J]. Journal of Qingdao Technological University, 2005, 26(1): 1-4. |
| [2] | BEHZADIAN K, KAPELAN Z, SAVIC D, et al. Stochastic sampling design using a multi-objective genetic algorithm and adaptive neural networks[J]. Environmental Modelling & Software, 2009, 24(4): 530-541. |
| [3] | BERRY J, HART W E, PHILLIPS C A Sensor placement in municipal water networks with temporal integer programming models[J], et al. Sensor placement in municipal water networks with temporal integer programming models[J]. Journal of Water Resources Planning & Management, 2006, 132(132): 218-224. |
| [4] |
陶涛, 吕存阵, 信昆仑, 等. 基于突发污染事件的管网水质监测点优化布置[J].
同济大学学报(自然科学版), 2010, 11: 1621-1625.
TAO T, LV C Z, XIN K L Optimal layout of monitoring stations for detecting acci-dental contaminations in water distribution system[J], et al. Optimal layout of monitoring stations for detecting accidental contaminations in water distribution system[J]. Journal of Tongji Univesity (natural science edition), 2010, 11: 1621-1625. DOI: 10.3969/j.issn.0253-374x.2010.11.011. |
| [5] | EHSANI N, AFSHAR A. Application of NA-ACO in multiobjective contaminant sensor network design for water distribution systems[C]//Water Distribution Systems Analysis: ASCE, 2011: 327-337. |
| [6] | DEB K, AGRAWAL S, PRATAP A, et al. A fast elitist Non-dominated sorting genetic algorithm for multi-objective optimisation: NSGA-II[C]//Parallel Problem Solving From Nature Vi. [s.n.]: Springer, 2000: 849-858. |
| [7] |
谭期仁, 王李管, 钟德云. NSGA-Ⅱ算法在井下多目标运输路径优化中的应用[J].
黄金科学技术, 2016, 24(2): 95-100.
TAN Q R, WANG L G, Zhong D Y. Application of NSGA-II in multi-objective route opt-imization of underground Mine’s Trans-portation[J]. Gold Science and Technology, 2016, 24(2): 95-100. DOI: 10.11872/j.issn.1005-2518.2016.02.095. |
| [8] |
华长春, 王雅洁, 李军朋, 等. 基于NSGA-Ⅱ算法的高炉生产配料多目标优化模型建立[J].
化工学报, 2016, 67(3): 1040-1047.
HUA C C, WANG Y J, LI J P Multi-objective optimization model for blast furnace production, et al. Multi-objective optimization model for blast furnace production and ingredients based on NSGA-Ⅱalgorithm[J]. CIESC Journal, 2016, 67(3): 1040-1047. |
| [9] |
李承红, 何英. NSGA-Ⅱ在克拉玛依市水资源优化配置应用初探[J].
地下水, 2016, 38(2): 126-129.
LI C H, HE Y The NSGA-Ⅱ application optimization allocation of water resources in Karamay[J]. The NSGA-Ⅱ application optimization allocation of water resources in Karamay[J]. Ground water, 2016, 38(2): 126-129. |
| [10] |
张忠波, 张双虎, 蒋云钟, 等. 改进的遗传算法在水库调度中的应用[J].
人民黄河, 2012, 34(8): 54-56.
ZHANG Z B, ZHANG S H, JIANG Y Z Application of improved genetic algorithm in reservoir optimal operation [J], et al. Application of improved genetic algorithm in reservoir optimal operation[J]. Yellow River, 2012, 34(8): 54-56. |
| [11] |
金溪, 高金良, 等. 利用NSGA-Ⅱ算法求解供水管网优化改造模型[J].
哈尔滨工业大学学报, 2008, 40(12): 1969-1976.
JIN X GANG J L, ZHANG J Optimal rehabilitation model of water supply network with non-dominated genetic algorithm-II [J], et al. Optimal rehabilitation model of water supply network with non-dominated genetic algorithm-II[J]. Journal of Harbin Institute of Technology University, 2008, 40(12): 1969-1976. DOI: 10.3321/j.issn:0367-6234.2008.12.025. |
| [12] |
何忠华, 袁一星. 基于剩余能量熵的供水管网可靠性优化设计[J].
浙江大学学报(工学版), 2014, 48(7): 1188-1194.
HE Z H, YUAN Y X.. Reliability optimization design of water distribution system based on surplus energy entropy[J]. Journal of Zhejiang University (engineering science), 2014, 48(7): 1188-1194. |
| [13] |
刘书明, 李明明, 王欢欢, 等. 基于NSGA-Ⅱ算法的给水管网多目标优化设计[J].
中国给水排水, 2015(5): 50-53.
LIU S M, LI M M, WANG H H, et al. Multi-objective Optimization Design of Water Distribution System Based on Non-dominated Sorting Genetic Algorithms-Ⅱ[J]. China Water & Wastewater, 2015(5): 50-53. |
| [14] |
乔俊飞, 魏静, 韩红桂. 基于改进NSGA2算法的给水管网多目标优化设计[J].
控制工程, 2016, 23(12): 1861-1866.
QIAO J F, WEI J, HAN. Multi-objective Optimization of Water Distribution System Based on an Improved NSGA2 Algorithm[J]. Control Engineering of China, 2016, 23(12): 1861-1866. |
| [15] |
刘书明. 不确定节点水量下水质监测点优化选址方法[J].
环境科学, 2013, 08: 3108-3112.
LIU S. Method for optimal sensor placement in water distribution systems with nodal demand uncertainties[J]. Environmental science, 2013, 08: 3108-3112. |
| [16] |
周书葵. 城市供水管网水质监测点优化选址的研究[J].
南华大学学报(自然科学版), 2004, 18(3): 62-66.
ZHOU S. An optimal locating of quality monitoring stations in urban water distribution systems[J]. Journal of Nanhua University of South China(natural science edition), 2004, 18(3): 62-66. |
 2018, Vol. 35
2018, Vol. 35

