恒力控制在电路板锡膏印刷、零件表面抛光打磨以及零件装配等领域大量应用。恒力控制器可以对加工过程中的接触力进行实时测量与控制,其输出的实际接触力精度决定着产品的加工质量。恒力控制器的力控制精度主要受到机械结构、控制系统的硬件性能以及控制算法的动态特性和稳态性能的影响。
目前,力控执行器的力控制精度存在着一定不足,通过研究分析大部分力控执行器在力测量阶段存在误差,主要是现有力控制执行器的机械结构存在弊端。大部分力控执行器的工作平台主要采用机械导轨、直线轴承等作为导向机构,由于受到此类导向机构存在的摩擦死区影响,作用在工作平台上的实际接触力首先要抵消导向机构上的摩擦力才能传递到力传感器上被检测,导致一部分接触力丢失,因此力传感器所检测到的接触力测量值与接触力实际值不符,出现忽大忽小的情况,故而对后续的力控制精度造成影响。众多研究机构及学者为提高力控执行器的力控制精度提出了多种解决方案,例如降低结构惯量、降低导向机构摩擦系数、提高控制算法控制性能等,但依然会受到摩擦死区等非线性因素的限制。
Mohammad等[1-3]和Li等[4]提出了一种应用于抛光机器人的高宽带力控执行器,在结构上通过延长抛光主转轴,将抛光旋转电机置于力控音圈电机之后,从而降低力控过程的移动惯性,改善控制带框,提高稳定性,但结构上同样存在直线轴承等导向机构的摩擦死区,对力控制精度造成一定的影响。Chen等[5]提出了一种应用于薄壁叶片抛光的力控执行器,在设计上采用了力控位移平台力传感器和抛光机构组成的常见结构,通过变阻尼控制,有效降低了抛光主轴的振动,但结构偏心过大,对力传感器的结构性能要求较高。Zheng等[6-7]提出了一种应用于抛光和去毛刺加工的三平移并联机构力控执行器,结构上采用3个在空间上成120°夹角的滚珠丝杆运动平台作为抛光机构及力传感器的运动执行平台,该力控执行器具有力控制响应快和分辨率高的特点,但结构和控制算法复杂且体积大。Wei等[8-9]提出了一种基于正刚度梁与负刚度梁并联的力控执行器,采用应变片来测量梁的应变而间接测量接触力大小,可以抵消惯性引起的过度位移,解决接触力的超调问题,但由于导轨滑块的存在,使得接触力的测量混杂了摩擦力,导致测量的接触力不准。Yang等[10-11]提出了一种基于平移−平移−球面关节的三自由度并联结构力控执行器,结构上采用3个空间上成120°夹角的音圈电机−被动柔性移动副−被动球面副(3-PPS)关节作为动力源,具有零扭转运动特性,但结构复杂、生产成本高且依旧受到导轨摩擦的影响。Zhang等[12]提出了一种基于柔顺恒力机构的被动力控执行器,结构上采用了抛光电机−花键轴−柔顺恒力机构−双列深沟球轴承抛光头的形式,但为了提高柔性梁的抗偏转能力依旧为柔顺恒力机构添加了导轨做导向支撑,因此在力测量及控制方面依旧会受到摩擦的影响。Chen等[13]提出了一种基于双稳态负刚度柔性铰链和线性弹簧的被动可调恒力控执行器,结构上采用步进直线电机柔性恒力机构的形式,步进直线电机输出固定位移,柔性恒力机构末端工作平台即可输出相对应的恒定接触力。但末端工作平台底部使用了导轨来保证导向性,因此导轨存在的摩擦力未知性会影响接触力的输出。Zhang等[14]提出了一种基于并联解耦柔性机构的三自由度力控执行器,结构上采用了4个8路复杂柔性铰链结构,具有良好的解耦特性,冲击和振动变得更小,但结构太过复杂,难以投入大量应用。赵亚平等[15]、刘立涛等[16]均提出了一种类似的气电混合式力控执行器,结构上采用了音圈电机和空气弹簧(或气囊式气缸)的形式,具有承载能力大、缓和冲击能力强的优点,但在力测量上受到了直线轴承的摩擦影响,精度有所损失。
在力控制技术方面,常见的力控制算法大致概括为以下几种:力/位混合控制算法、阻抗控制算法、导纳控制算法、自适应力控算法等[17-20]。力位混合控制算法是一种能够同时实现对机器人末端力控执行器的位置及接触力的跟踪控制[17],可以在保证工作方向上接触力稳定控制的情况下,其他方向上的位置控制也具有较高精度。但是该算法必须获得较为精确的机器人末端力控执行器与未知环境之间的动力学模型及刚度特性,才能保证稳定的柔顺控制和力控制精度。阻抗控制算法是一种间接力控制算法[17-18],主要包括两部分:力内环与位置外环。通过位置外环与力内环的相互结合实现间接力控制,适用于可获取关节力和位置、不需要末端力控执行器安装力传感器的设备。导纳控制与阻抗控制类似,但结构相反,主要包括力外环和位置内环,适用于只需要获取关节位置且力控执行器安装力传感器的设备。自适应力控制是一种针对未知环境下的力控制算法[18,21],可以利用力反馈作为输入来实时调整阻抗模型的参数以适应环境变化,自适应控制可应用于较为复杂的曲面抛磨场合。Lopes等[22]提出了一种基于加速度的纯弹性环境接触情况下的力阻抗控制器对并联力控执行器进行控制,该控制器能够跟踪位置和力轨迹,增加了控制器对环境建模不确定性的鲁棒性,最终具有较好的力跟踪性能。Lew等[23]提出了新型的力/位混合控制器,由力阻尼(Force Damping, FD)控制器和惯性力主动阻尼(Inertial Force Active Damping, IFAD)控制器组成。其中FD控制器将接触力调节为所需的值,IFAD控制器通过增加结构阻尼来耗散冲击前后的结构振动,具有较高的力控制精度。Bone等[24]提出了一种基于ARMAX形式平台模型的鲁棒性扩展PID直接力控制器,通过调节PID增益参数,可实现 ±1 N的力控制精度。
为了解决上述由机械结构缺陷导致的“力丢失”问题,以提高力控制精度,本文提出了一种刚柔耦合力控执行器,采用一种集缓冲与传感于一体的柔性结构将摩擦转化为弹性力,并通过测量弹性力来间接测量接触力,从而隔绝摩擦的影响,实现更高的力测量精度及力控制精度。通过以上结构的创新,理论上可测量出无摩擦扰动且准确无误的实际接触力大小,在前期力检测阶段根除摩擦扰动的影响,从而保证后续力控制过程的精度,最后配合基于自抗扰控制技术的力控制算法实现高精度恒力控制。
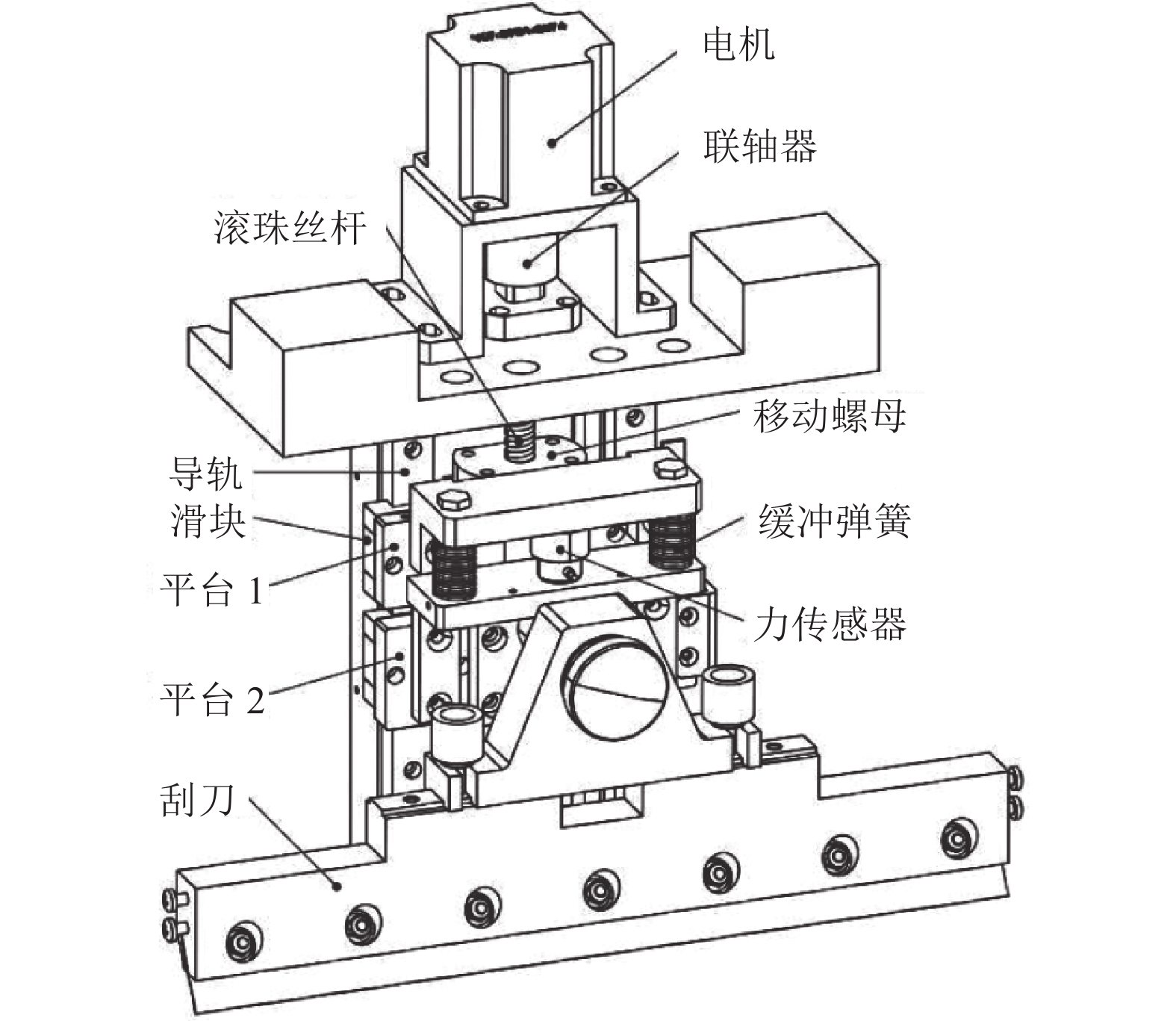
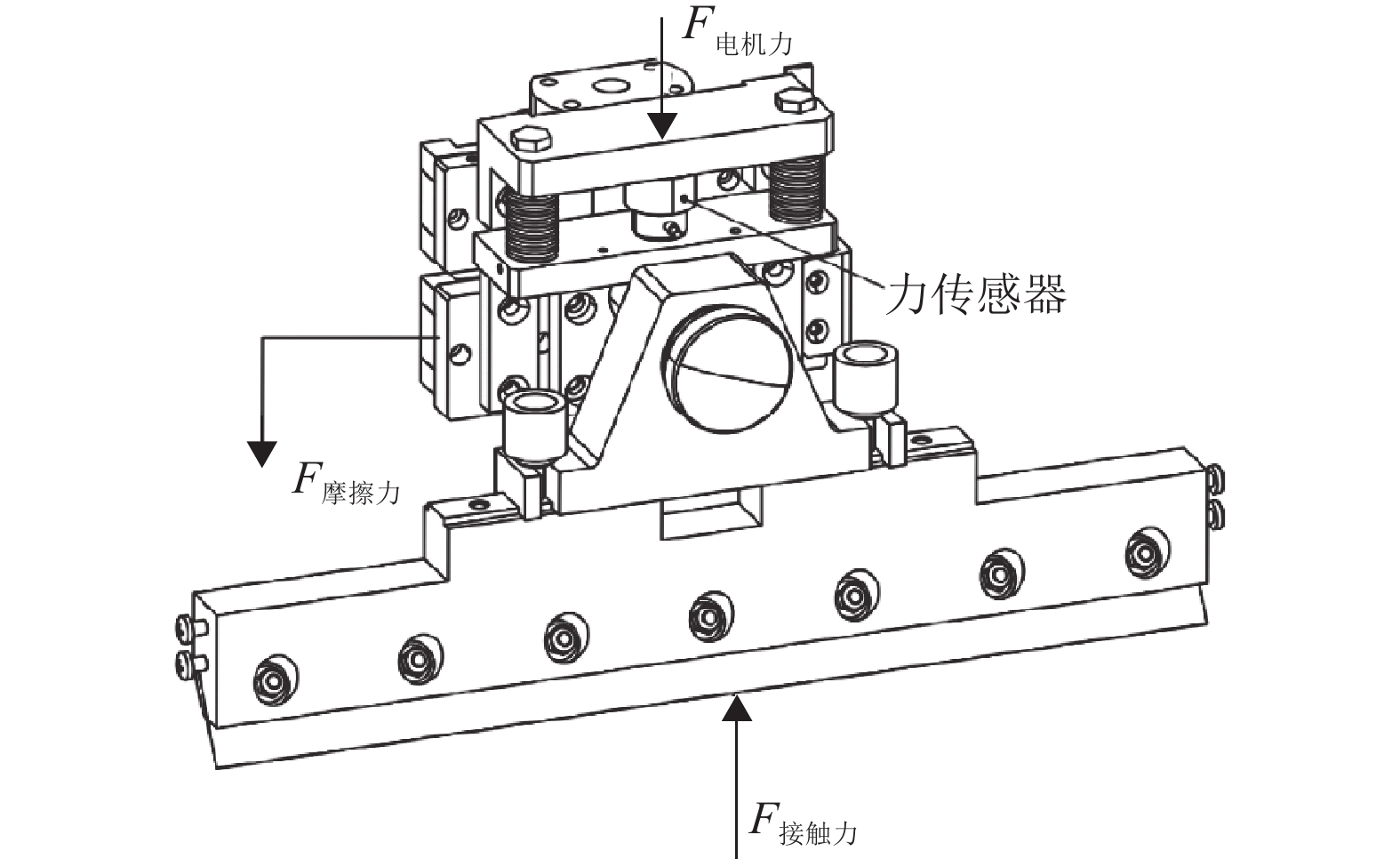
1 刚柔耦合力控制器的结构设计 1.1 问题分析图1是常见的全自动锡膏印刷机所搭载的力控执行器,主要由电机、传动装置、运动平台和刮刀组成。其中,运动平台和刮刀受力情况如图2所示。
|
图 1 全自动锡膏印刷机的力控执行器结构 Figure 1 Force-control executor structure of automatic solder paste printing machine |
|
图 2 全自动锡膏印刷机的力控执行器受力分析 Figure 2 Force analysis of force-control actuator of automatic solder paste printing machine |
由图2分析可知:整个运动平台外部仅受到电机施加在上平台上的电机力、作用在上平台及下平台上滑块与导轨之间的摩擦力和作用在与下平台相连接的刮刀的接触力,内部还有上平台与下平台之间的缓冲弹簧的弹性力,接触力由工作过程中刮刀与钢网接触时产生。力传感器主要是采用应变片检测由外力产生的结构应变并转换成电信号的变化来实现外力测量。因此,在刮刀与钢网发生接触的整个过程中接触力首先要克服上平台所受到的导轨滑块之间的摩擦力才能使上平台产生位移,最后传递到力传感器上被检测到,这种现象称为“力丢失”。由于在接触力的测量过程中,受到摩擦扰动的影响,力传感器所读取的接触力测量值与接触力实际值之间存在较大误差,这种误差也会导致后续力控制过程的力控制精度受限。
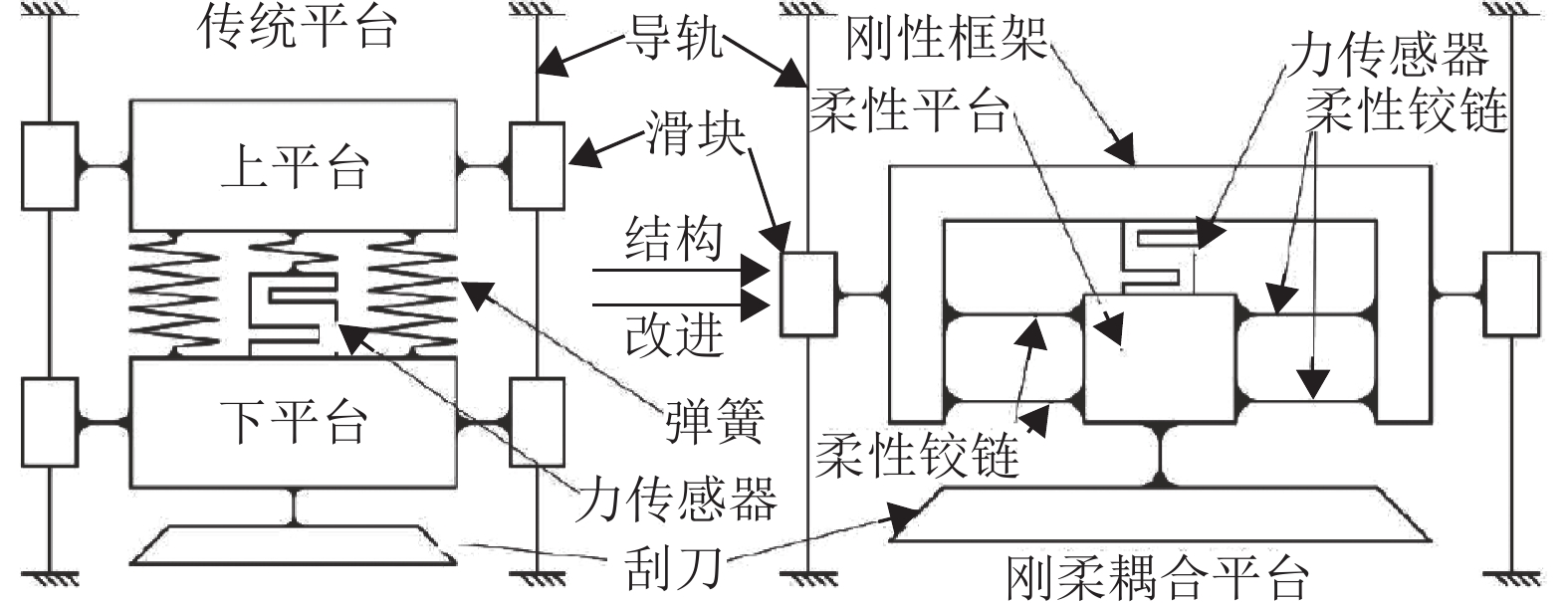
1.2 结构方案设计为了解决上述传统结构存在的“力丢失”问题,本文从结构创新的角度出发,抛弃传统的导轨、导柱、直线轴承等摩擦导向机构,设计一种不再受到摩擦影响的力控执行器结构。新结构较之原结构的改进过程如图3所示。
|
图 3 结构改进过程 Figure 3 Structure improvement process |
如图3所示,采用了由一种直梁型柔性铰链和柔性力传感器组成的柔性机构作为工作平台的导向机构,基于刚柔耦合思想,将力控执行器的传统运动平台演变成刚柔耦合平台,上述柔性机构同时综合了导向、缓冲、力传感等多方面作用。
基于图3所示方案,可以将传统的导轨导向缓冲运动平台演化成一种如图4所示的内部柔性机构导向结合外部导轨导向的刚柔耦合运动平台。

|
图 4 刚柔耦合力控执行器核心运动平台 Figure 4 Core motion stage of rigid-flexible coupling force-control actuator |
刚柔耦合力控执行器的核心运动平台,主要由刚性框架、柔性铰链、柔性力传感器和柔性平台组成,其中柔性铰链和柔性力传感器组成并联柔性机构。外部刚性框架的左右两侧与滑块连接,上侧与滚珠丝杆的移动螺母连接,因此,刚性框架用于完成大行程位移,且电机驱动力通过滚珠丝杆及移动螺母作用在刚性框架上;柔性平台作为最终的工作平台用于连接刮刀、抛光轮等末端工具,柔性平台与刚性框架之间仅通过柔性铰链和柔性力传感器并联的方式连接,由于柔性铰链的刚度较低,因此图4中柔性力传感器的安装位置可有效提高柔性平台的抗倾翻能力。并联柔性机构将原本受到的导轨滑块之间的摩擦力转换成柔性铰链和柔性力传感器的弹性力,彻底隔绝摩擦力的影响,并通过对力传感器的重新标定,直接输出柔性铰链和柔性力传感器的两个弹性力。
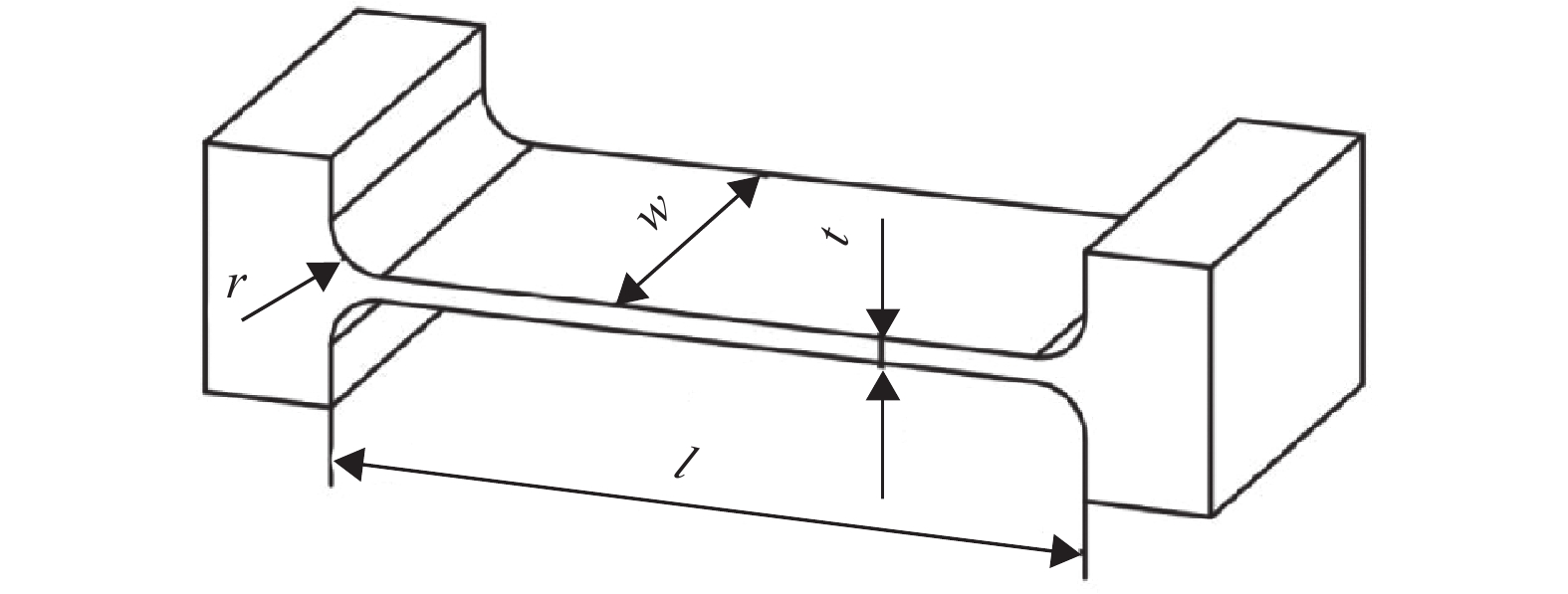
1.3 柔性铰链设计由于常见的切口式柔性铰链容易出现应力集中、疲劳寿命相对较短等不足,本文中采用如图5所示的倒圆角直梁型柔性铰链结构形式[25-27]。
|
图 5 倒圆角直梁型柔性铰链结构简图 Figure 5 Structure diagram of corner-fillet leaf-springs (CFLS) |
首先通过梁约束模型法[26]可以构建图5所示倒圆角直梁型柔性铰链的非线性变形−外力控制方程。控制方程中的载荷与位移可以表示为
| $ \begin{gathered} m = \frac{{{M_z}l}}{{EI}},\quad f = \frac{{{F_y}{l\,^2}}}{{EI}},\quad p = \frac{{{F_x}{l\,^2}}}{{EI}},\quad \\ {u_y} = \frac{{\Delta y}}{l},\quad {u_x} = \frac{{\Delta x}}{l} \\ \end{gathered} $ | (1) |
式中:参数
非线性变形外力控制方程[28],即柔性铰链的非线性变形公式可以表示为
| $ \begin{array}{*{20}{c}} {\left[ {\begin{array}{*{20}{c}} f \\ m \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} {{k'}_{11}^0}&{{k'}_{12}^0} \\ {{k'}_{12}^0}&{{k'}_{22}^0} \end{array}} \right] \left[ {\begin{array}{*{20}{c}} {{u_y}} \\ \theta \end{array}} \right] + p\left[ {\begin{array}{*{20}{c}} {\dfrac{{1.2}}{\lambda }}&{ - 0.1} \\ { - 0.1}&{\dfrac{{2\lambda }}{{15}}} \end{array}} \right] \left[ {\begin{array}{*{20}{c}} {{u_y}} \\ \theta \end{array}} \right]} \end{array} $ | (2) |
| $ \begin{array}{*{20}{c}} {{u_x} = \dfrac{{p\lambda }}{{12{b^2}}}} \end{array} - \frac{1}{2}\left[ {\begin{array}{*{20}{c}} {{u_y}}&\theta \end{array}} \right]\left[ {\begin{array}{*{20}{c}} {\dfrac{{1.2}}{\lambda }}&{ - 0.1} \\ { - 0.1}&{\dfrac{{2\lambda }}{{15}}} \end{array}} \right]\left[ {\begin{array}{*{20}{c}} {{u_y}} \\ \theta \end{array}} \right] $ | (3) |
式中:无量纲参数
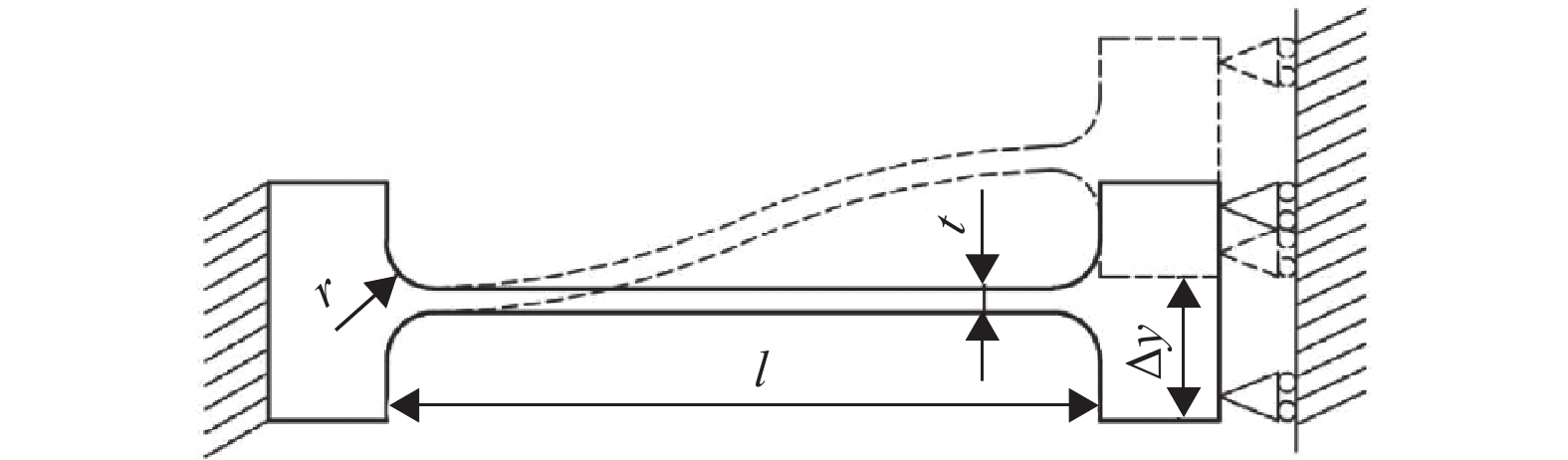
本文所设计的刚柔耦合力控执行器内部柔性铰链的约束形式属于一端固定一端导向约束类型,如图6所示。其导向端轴向位移
|
图 6 固定−导向倒圆角直梁型柔性铰链的非线性变形图 Figure 6 Nonlinear deflection of fixed-guided CFLS |
| $ \begin{array}{*{20}{c}} {f = \left( {{k'}_{11}^0 + \dfrac{{1.2}}{\lambda }p} \right) {u_y}} \end{array} $ | (4) |
| $ m = \left( {{k'}_{12}^0 - 0.1p} \right) {u_y} $ | (5) |
| $ p = \frac{{7.2{b^2}}}{{{\lambda ^2}}}u_y^2 $ | (6) |
将式(6)代入式(4),有
| $ f = \left( {{k'}_{11}^0 + \frac{{8.64}}{{{\lambda ^3}}}{b^2}u_y^2} \right) {u_y} $ | (7) |
则固定导向倒圆角直梁型柔性铰链的非线性刚度公式为
| $ {K_g} = \frac{{{F_y}}}{{\Delta y}} = \left( {{k'}_{11}^0 + {k_{{\text{non}}}}} \right) \frac{{EI}}{{{l^3}}} $ | (8) |
| $ {k_{{\text{non }}}} = \frac{{8.64}}{{{\lambda ^3}}}{\left( {\frac{{\Delta y}}{t}} \right) ^2} $ | (9) |
固定−导向倒圆角直梁型柔性铰链的非线性刚度由线性项特征系数
| $ {P_k} = \frac{{{k_{{\text{non}}}}}}{{{k'}_{11}^0 + {k_{{\text{non}}}}}} \times 100\% $ | (10) |
当
根据平台工作要求与结构尺寸限制,可以确定柔性铰链的长度为33 mm,宽度为20 mm,最大限位行程为0.5 mm,安全行程为0.4 mm,柔性铰链采用7075铝合金制造。利用式(8) 、(9)可以确定满足安全行程要求的柔性铰链厚度为1 mm,圆角半径为2 mm。
将
| $ \begin{gathered} {k'}_{11}^0 = 15.073\,2,{\text{ }}{k_{{\text{non}}}} = 1.575\,5, \\ {K_g} = 55\,592\,{\text{N/m}},{\text{ }}{P_k} = 9.46\% \lt 10\% \\ \end{gathered} $ | (11) |
由式(11)可知所设计的柔性铰链在工作过程中始终在弹性变形阶段内。通过式(8)可知
图4所示的刚柔耦合力控执行器的运动平台可等效成如图7所示的动力学等效模型,对运动平台整体进行分析,当刚柔耦合力控执行器受到环境外力作用时,其动力学方程表示为

|
图 7 刚柔耦合力控执行器运动平台力学模型 Figure 7 Mechanical model of rigid-flexible coupling force-control actuator |
| $ {m_1}{\ddot x_1} + {m_2}{\ddot x_2} = {F_{\rm{m}}} - {F_{\rm{c}}} - {F_{\rm{u}}} + \left( {{m_1} + {m_2}} \right) g $ | (12) |
式中:
对柔性平台进行动力学分析,有
| $ {m_2}{\ddot x_2} = {F_{\rm{s}}} - {F_{\rm{c}}} + {m_2}g $ | (13) |
根据柔性机构的刚度
| $ {F_{\rm{s}}} = k\left( {{x_1} - {x_2}} \right) + c\left( {{{\dot x}_1} - {{\dot x}_2}} \right) $ | (14) |
在
自抗扰控制技术(Active Disturbance Rejection Control, ADRC)基于传统的PID控制系统结合现代控制系统中的扰动观测器来估计补偿控制系统中扰动误差,具有调参方便、控制精度高等特点,本文采用ADRC来构建力控制系统。
ADRC算法的核心在于扩张状态观测器(Extended State Observer, ESO) 的设计,当系统中某些变量不易于检测时,就需要利用状态观测器设计一个新系统来观测原系统的状态
| $ \left\{ \begin{array}{l} \hat x = {\boldsymbol{A}}\hat x + {\boldsymbol{B}}u + {\boldsymbol{L}}(y - \hat y) \\ \hat y = {\boldsymbol{C}}\hat x \\ \end{array} \right. $ | (15) |
式(15)即为ESO扩张状态观测器,
根据式(12)的刚柔耦合力控执行器的动力学方程,求解出状态矩阵
| $ \left\{ \begin{array}{l} {{\dot z}_1} = {z_2} + {L_1}(y - {z_1}) \\ {{\dot z}_2} = {z_3} + {L_2}(y - {z_1}) + {b_0}u \\ {{\dot z}_3} = {L_3}(y - {z_1}) \\ \end{array} \right. $ | (16) |
在刚柔耦合力控执行器中,
| $ \left\{ \begin{gathered} E(n) = {F_{\rm{c}}}(n) - {z_1}(n) \\ {z_1}(n) = (3{\omega _0}E(n) + {z_2}(n) ) T + {z_1}(n - 1) \\ {z_2}(n) = (3\omega _0^2E(n) + {z_3}(n) + {b_0}u(n) ) T + {z_2}(n - 1) \\ {z_3}(n) = \omega _0^3E(n) T + {z_3}(n - 1) \\ {u_0} = {k_{\rm{p}}}E(n) + {k_{\rm{d}}}(E(n) - E(n - 1) ) \\ u(n) = ({u_0} - {z_3}(n) ) /{b_0} \\ \end{gathered} \right. $ | (17) |
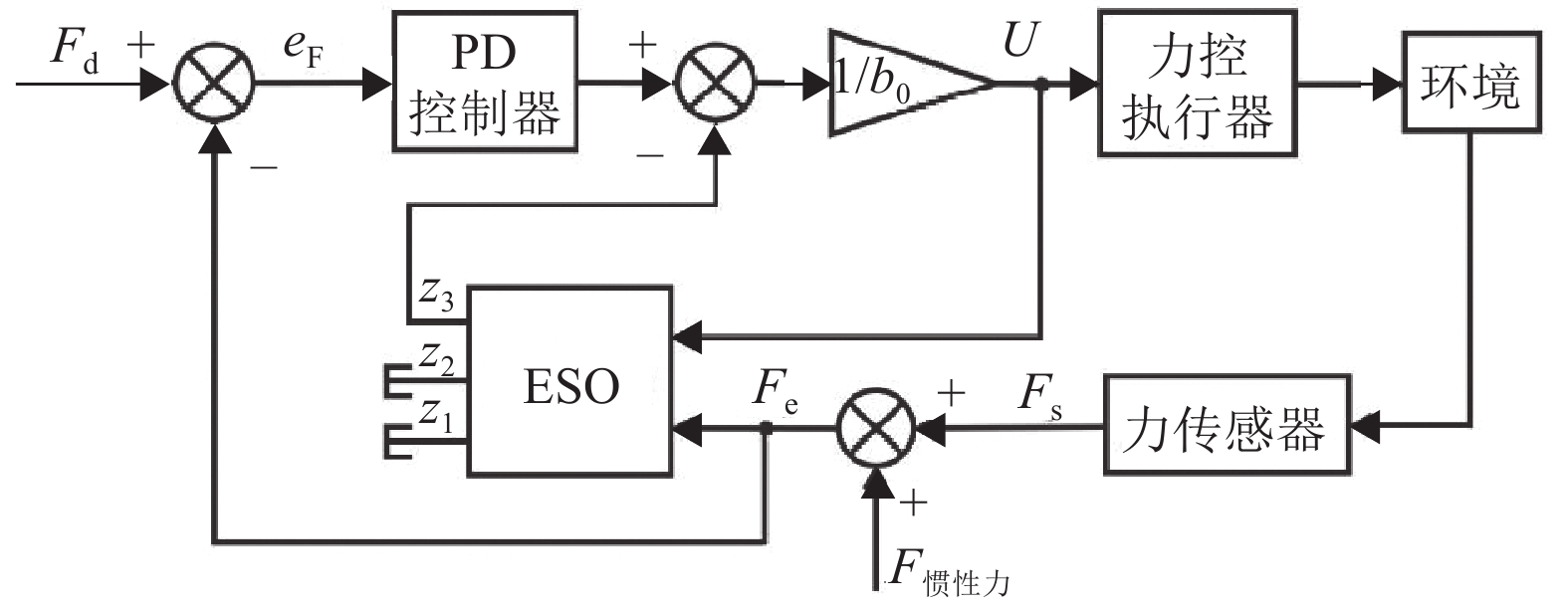
因此ADRC直接力控制的原理可简化为如图8所示的控制系统。
|
图 8 ADRC直接力控制原理 Figure 8 Direct force control principle by ADRC |
根据图8在 simulink中建立ADRC直接力控制的仿真模型,如图9所示。

|
图 9 ADRC直接力控制simulink仿真模型 Figure 9 Simulink model of force controller by ADRC |
为了验证所述的理论设计方法和控制方法,本文搭建了刚柔耦合力控执行器实验平台,包括硬件系统、软件上位机等,随后完成力传感器的标定实验,获得接触力反馈信号,最后在刚柔耦合力控执行器中进行ADRC直接力控制实验,探讨其力控制精度及抗扰性能。
3.1 刚柔耦合力控执行器实验平台的搭建本文所搭建的刚柔耦合力控执行器实验平台如图10 所示,主要包括刚柔耦合力控执行器、外扰动凸轮机构、力传感器信号采集模块、计算机、Servotronix(高创)公司的CDHD2-006-2A-AP1型号的伺服驱动器、固高科技公司的GT2-400-ACC2-VB-G型号的端子板和GTS-400-PG-VB型号的主卡,其中主卡安装在计算机主板的PCI插槽中。图中的外扰动凸轮机构由一个旋转电机和凸轮组成,凸轮转动时,会产生一个竖直方向的正弦周期循环推力,用以模拟图11所示的外部扰动。

|
图 10 刚柔耦合力控执行器实验平台实物图 Figure 10 Experiment setup of rigid-flexible coupling force-control actuator |
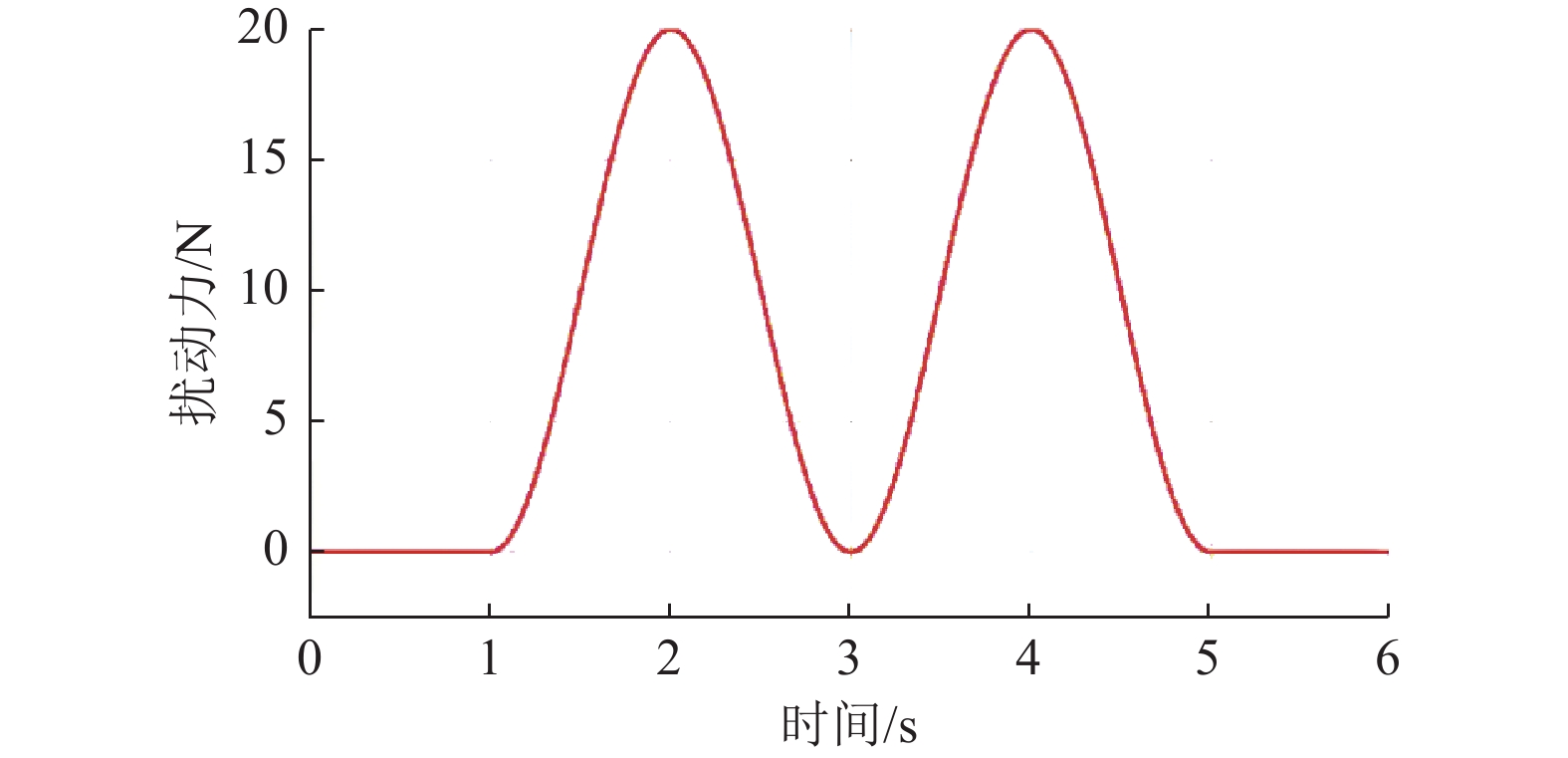
|
图 11 外部扰动力的模拟 Figure 11 Simulation of external disturbing force |
整个实验平台的详细连接方式、工作原理、工作流程如图12所示,首先在计算机中利用QT Creator开发出力控制算法上位机软件,该软件可用于控制刚柔耦合力控执行器和外扰动凸轮机构,在接线方面,固高控制卡(端子板)的通讯线与计算机中的主卡卡槽相连接,轴信号线与2个高创驱动器接收端连接,两个高创驱动器的通讯线与电脑连接,力传感器信号采集模块的输入端、输出端分别与力传感器和计算机连接。在控制方面,计算机接收到力传感器信号采集模块的接触力信号反馈和固高控制卡接收到的力控执行器末端位置反馈,并通过上位机软件计算出输出电压,控制固高输出电压,完成刚柔耦合力控执行器的闭环控制。
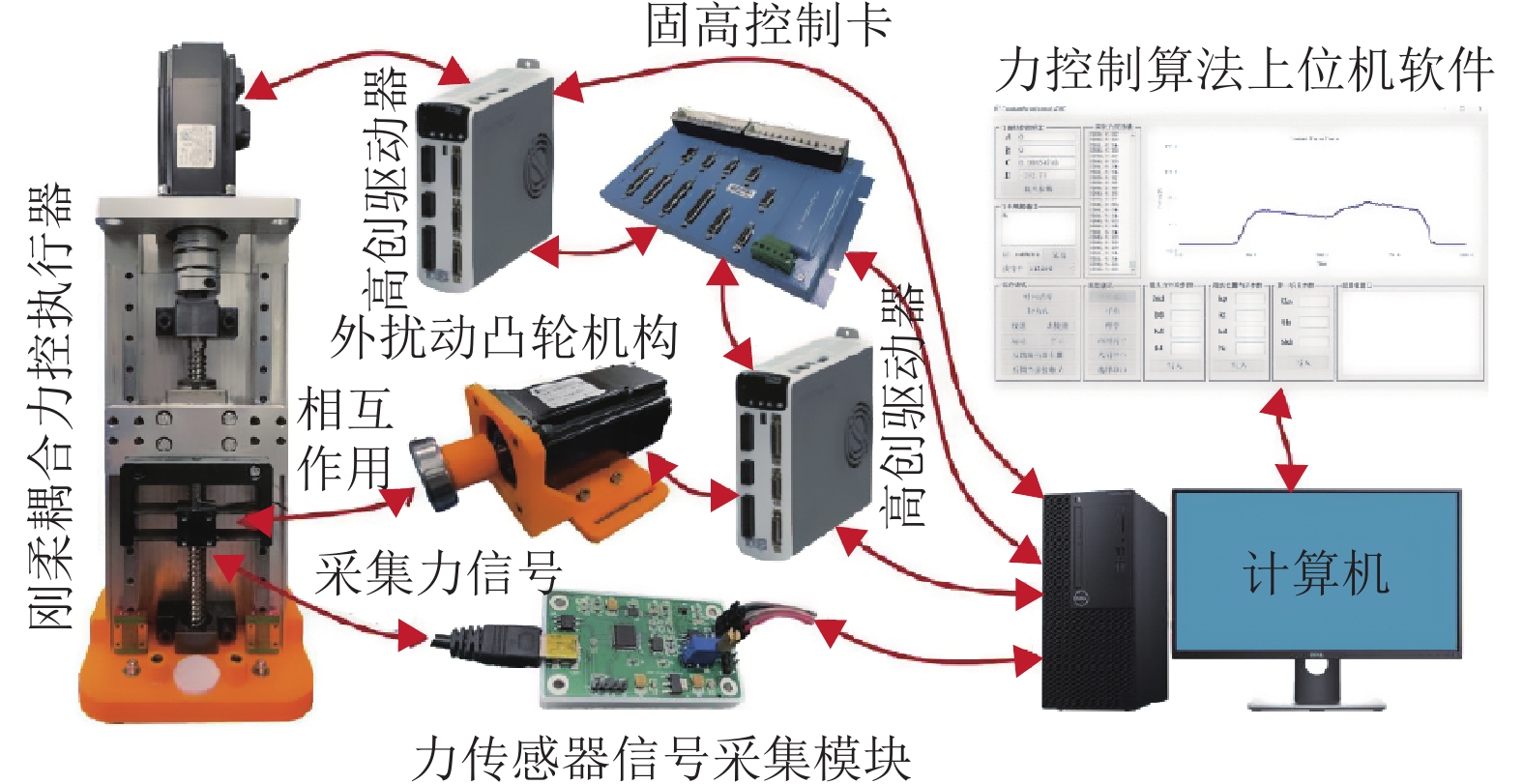
|
图 12 实验平台控制系统工作流程 Figure 12 Workflow of experimental stage control system |
力传感器内部的全桥应变片电路电阻变化非常微小,输出的模拟电压十分微小,需要采用图12中的力传感器信号采集模块中的 A/D转换模块和放大器对力传感器输出电压进行处理,转换为0~65536范围的数字量且在无外力作用,即零应变的情况下输出信号为30000左右。
为了获得刚柔耦合力控执行器末端与环境之间的接触力

|
图 13 力传感器标定实验实物图 Figure 13 Calibration setup of force sensor |
|
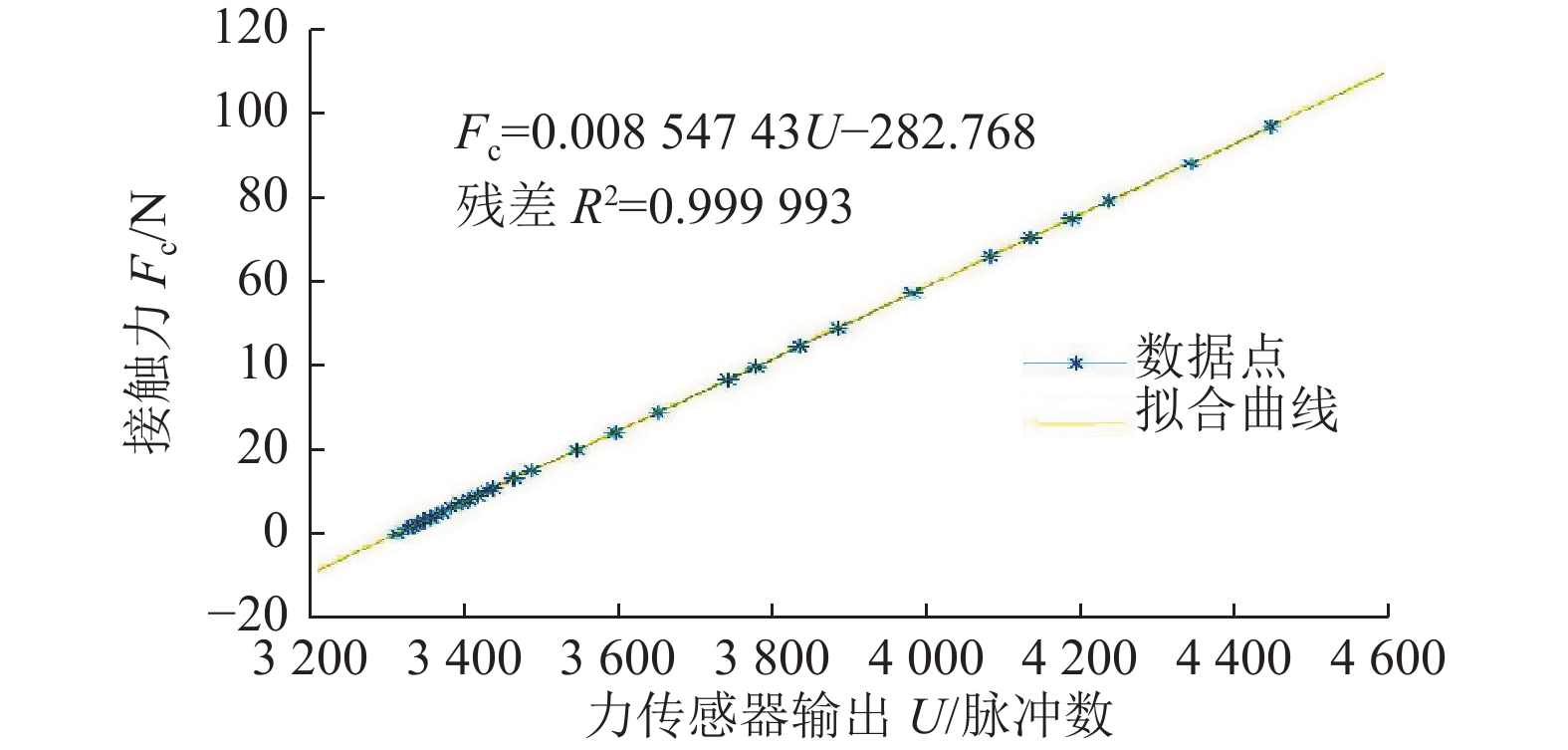
图 14 力传感器标定曲线 Figure 14 Calibration curve of force sensor |
最终得到力传感器标定函数为
| $ {F_{\rm{c}}} = 0.008\,547\,34U - 282.768 $ | (18) |
根据拟合结果可知,拟合函数的残差R2=0.999993,证明拟合函数线性度很高,这一点也验证了所设计的由力传感器和柔性铰链组成的柔性机构并没有发生非线性变形,依旧处在弹性变形阶段,可以将其看作理想弹簧。因此无论柔性平台安装任何重量的末端工具都不会改变式(18)力传感器标定函数中的1次项系数,只需修改常数项对所安装末端工具重量进行补偿即可,并且标定后的力传感器读数与WD−100数显推拉力计的读数最大差值仅为0.02 N,可认定力传感器所输出的力与实际接触力大小相等,力测量阶段不再存在由摩擦引起的“力丢失”问题。
4 力控制实验刚柔耦合力控执行器的实验过程主要分为两部分。
(1) 无扰动静态实验:通过跟踪各种跃变值、接触力的阶跃力实验来分析上升时间、超调量;通过跟踪不同接触力的静态实验来分析稳态误差。
(2) 有扰动动态实验:通过外扰动凸轮机构对刚柔耦合力控执行器末端施加正弦外部扰动力,分析其动态误差及其抗扰性能。
其中,无扰动静态实验工况见表1。连续多段力跃变实验工况条件为实验⑦:分别跟踪10,30,60,100 N接触力的实验;有扰动动态实验工况条件为实验⑧:在跟踪20 N接触力的情况下,通过外扰动凸轮机构施加外部扰动。
| 表 1 无扰动静态实验工况 Table 1 Static experimental conditions without disturbance |
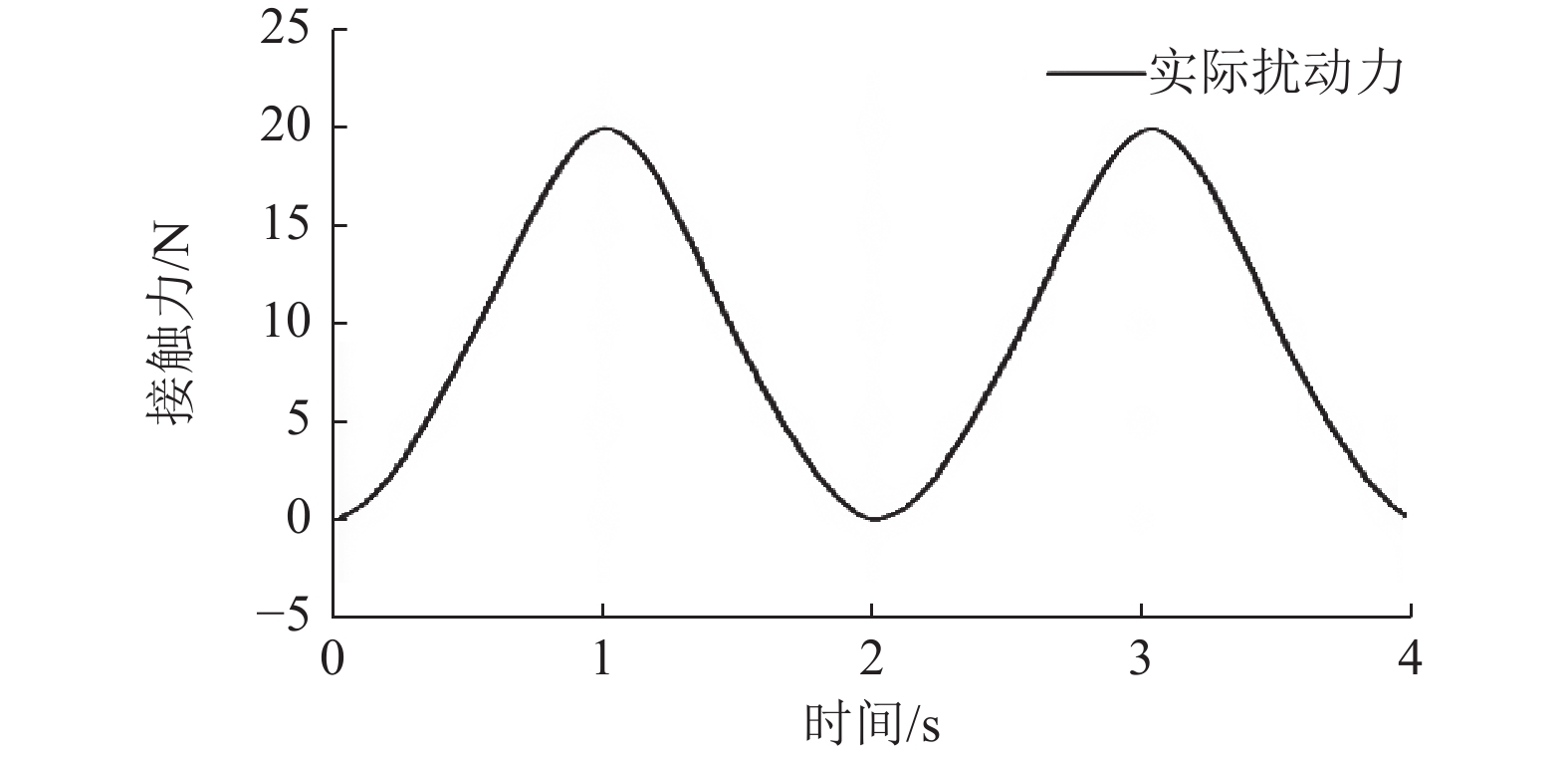
通过固定运动平台,使柔性平台底部与凸轮最低点刚接触时,控制外扰动凸轮机构的电机以30 r/min速度转动,同时采集力传感器数据,可得到如图15所示的实际外部扰动力。
|
图 15 外扰动凸轮机构所产生的外部扰动力 Figure 15 External disturbing force generated by cam |
通过ADRC直接力控制上位机软件,调节
|
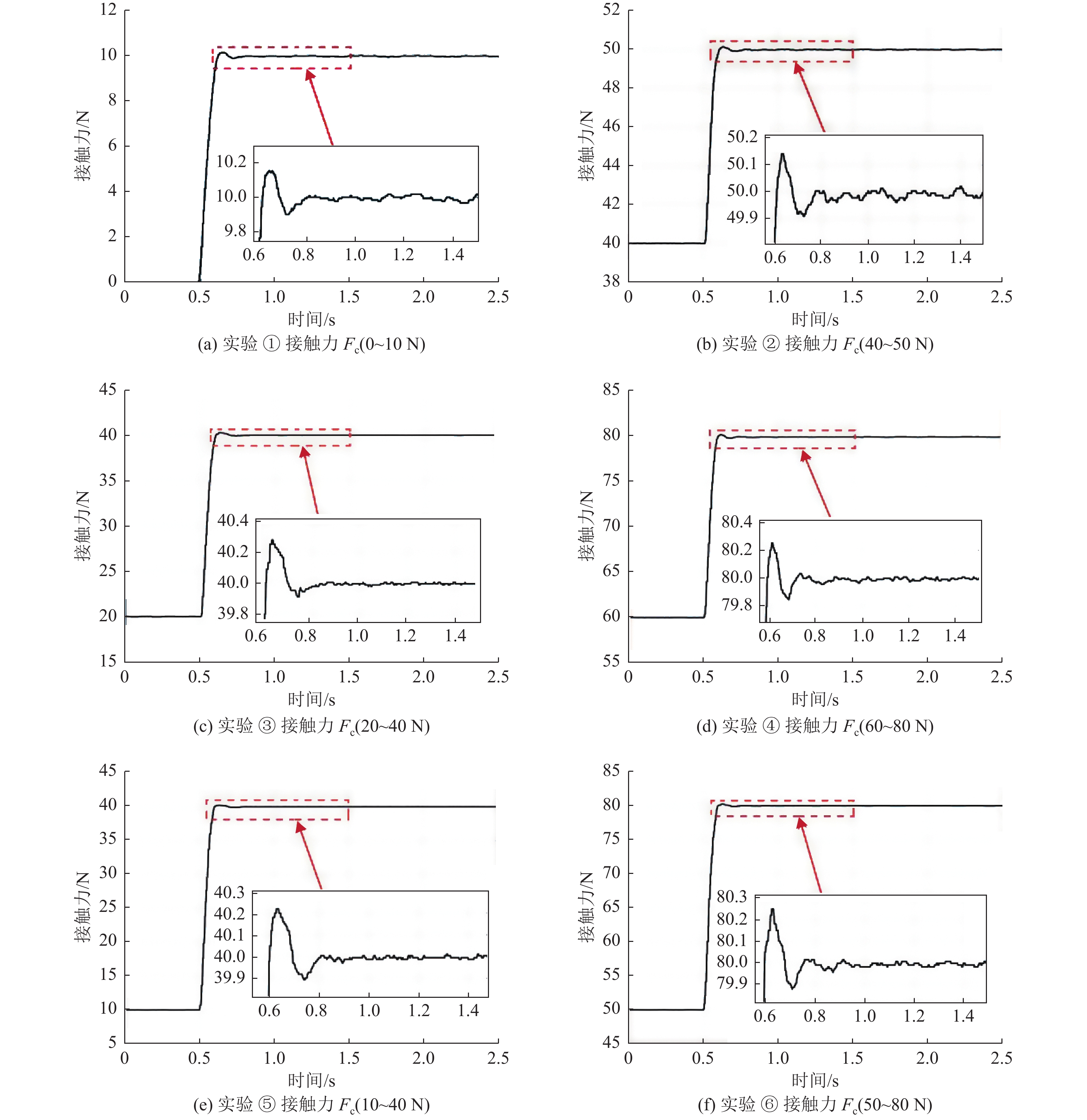
图 16 ADRC直接力控制实验①至实验⑥的实验结果 Figure 16 Experimental results of ADRC direct force control experiments ① through ⑥ |
根据图16可知,实验①至实验⑥的上升时间分别为 102,101,99,100,96,98 ms,超调量分别为0.18,0.14,0.24,0.23,0.22,0.25 N。
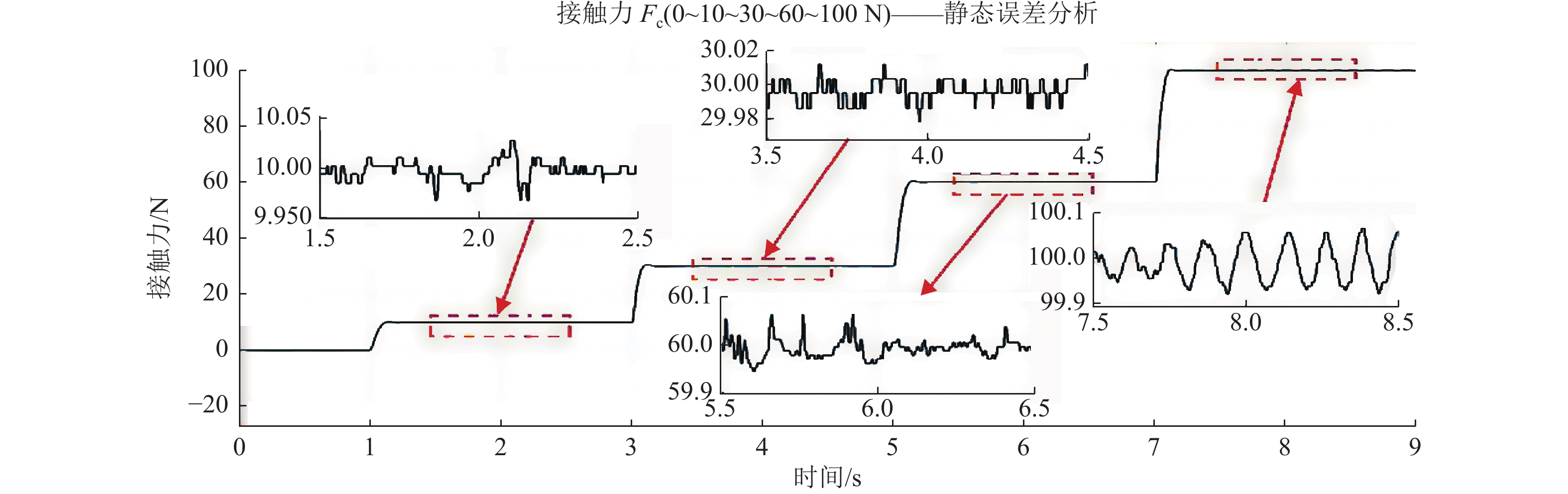
下面通过实验⑦,控制刚柔耦合力控执行器接触力从0~10~30~60~100 N变化,得到如图17所示实验结果,根据实验结果可知力跟踪稳态误差在 ± 0.08 N 以内。
|
图 17 ADRC直接力控制实验⑦实验结果 Figure 17 Experimental results of ADRC direct force control experiment ⑦ |
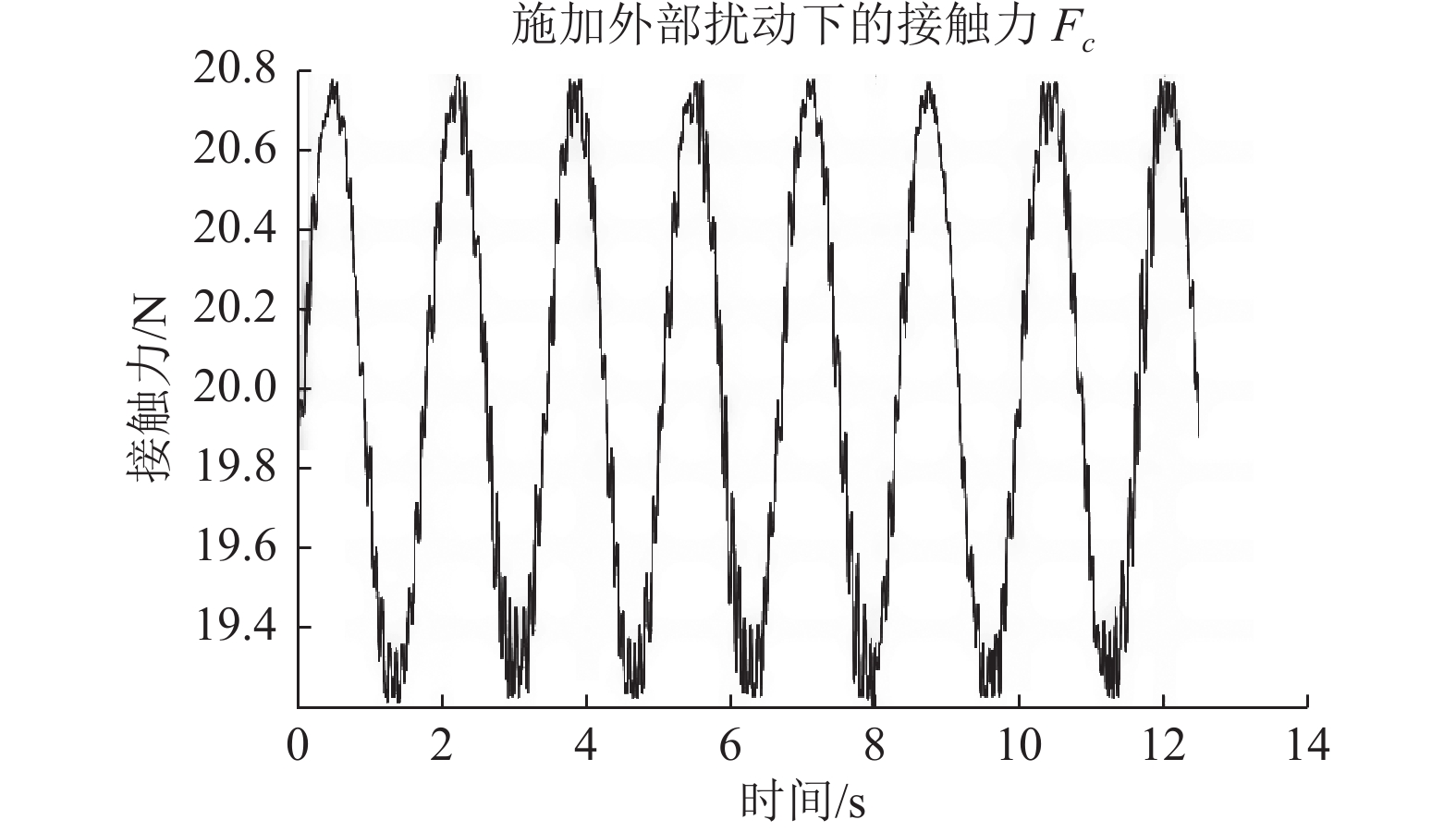
最后进行实验⑧,有扰动动态实验的实验结果如图18所示。
|
图 18 ADRC直接力控制实验⑧实验结果 Figure 18 Experimental results of ADRC direct force control experiment ⑧ |
根据图18实验结果,在图15所示外部扰动力的干扰下,其跟踪 20 N接触力的动态误差为 ± 0.8 N,其抗扰性能用扰动抑制率
| $ {R_{\rm{f}}} = \frac{{20 - 0.7}}{{20}} \times 100\% = 96.5\% $ | (19) |
对于目前市场上现有的力控执行器,由于受到摩擦影响,存在“力丢失”问题,使得所测量的接触力偏离实际值,其力控制性能指标应由力测量误差与力控制误差共同决定,因此,其最终的力控制精度往往有所降低。然而对于本文所设计的刚柔耦合力控执行器,在力传感器标定实验中已证明在力测量阶段将不再受到摩擦影响。因此根据实验数据可认定本文所设计的刚柔耦合力控执行器的力跟踪稳态误差为 ± 0.08 N,扰动抑制率为96.5%,完全满足全自动锡膏印刷、抛光打磨、智能装配等领域的要求,为各类自动化接触作业提供解决方案。
5 结论本文针对现有力控执行器存在由摩擦死区引起的力测量精度及力控制精度受限的难题,提出了一种基于柔性铰链的刚柔耦合缓冲传感一体力控执行器的设计方案。利用由柔性铰链及柔性力传感器并联组成的柔性机构作为力控执行器末端的导向单元、缓冲单元及力测量单元,利用其弹性变形有效解决了摩擦问题。为了验证理论的准确性,进行了ADRC直接力控制实验,实验结果表明刚柔耦合力控执行器的力跟踪稳态误差为 ± 0.08 N,扰动抑制率为96.5%,精度高且抗扰性能优越,可广泛应用于全自动锡膏印刷机、打磨机器人、装配机器人等设备中。
| [1] |
MOHAMMAD A E K, HONG J, WANG D, et al. Synergistic integrated design of an electrochemical mechanical polishing end-effector for robotic polishing applications[J].
Robotics and Computer-Integrated Manufacturing, 2019, 55: 65-75.
DOI: 10.1016/j.rcim.2018.07.005. |
| [2] |
HONG J, MOHAMMAD A E K, WANG D. Improved design of the end-effector for macro-mini robotic polishing systems[C]// Proceedings of the 3rd International Conference on Mechatronics and Robotics Engineering. Paris: ACM, 2017: 36-41.
|
| [3] |
MOHAMMAD A E K, HONG J, WANG D. Design of a force-controlled end-effector with low-inertia effect for robotic polishing using macro-mini robot approach[J].
Robotics and Computer-Integrated Manufacturing, 2018, 49: 54-65.
DOI: 10.1016/j.rcim.2017.05.011. |
| [4] |
LI J, GUAN Y, CHEN H, et al. A high-bandwidth end-effector with active force control for robotic polishing[J].
IEEE Access, 2020, 8: 169122-169135.
DOI: 10.1109/ACCESS.2020.3022930. |
| [5] |
CHEN F, ZHAO H, LI D, et al. Contact force control and vibration suppression in robotic polishing with a smart end effector[J].
Robotics and Computer-Integrated Manufacturing, 2019, 57: 391-403.
DOI: 10.1016/j.rcim.2018.12.019. |
| [6] |
MA Z, HONG G S, ANG M H, et al. Design and control of an end-effector module for industrial finishing applications[C]//2016 IEEE International Conference on Advanced Intelligent Mechatronics (AIM) . Banff, AB: IEEE, 2016: 339-344.
|
| [7] |
MA Z, SEE H H, HONG G S, et al. Control and modeling of an end-effector in a macro-mini manipulator system for industrial applications[C]//2017 IEEE International Conference on Advanced Intelligent Mechatronics (AIM) . Munich: IEEE, 2017: 676-681.
|
| [8] |
WEI Y, XU Q. Design of a new robot end-effector based on compliant constant-force mechanism[C]//2021 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS) . Prague, Czech Republic: IEEE, 2021: 7601-7606.
|
| [9] |
WEI Y, XU Q. Design of a new passive end-effector based on constant-force mechanism for robotic polishing[J].
Robotics and Computer-Integrated Manufacturing, 2022, 74: 102278.
DOI: 10.1016/j.rcim.2021.102278. |
| [10] |
ZHU R, YANG G, FANG Z, et al. Kinematic design of a 3-DOF force-controlled end-effector with flexure joints for robotic finishing applications[C]//2019 IEEE/ASME International Conference on Advanced Intelligent Mechatronics (AIM) . Hong Kong: IEEE, 2019: 1473-1478.
|
| [11] |
YANG G, ZHU R, FANG Z, et al. Kinematic design of a 2R1T robotic end-effector with flexure joints[J].
IEEE Access, 2020, 8: 57204-57213.
DOI: 10.1109/ACCESS.2020.2982185. |
| [12] |
ZHANG J, ZHAO L, LI L, et al. Design of passive constant-force end-effector for robotic polishing of optical reflective mirrors[J].
Chinese Journal of Mechanical Engineering, 2022, 35(1): 141.
DOI: 10.1186/s10033-022-00811-3. |
| [13] |
CHEN Y H, LAN C C. An adjustable constant-force mechanism for adaptive end-effector operations[J].
Journal of Mechanical Design, 2012, 134(3): 031005.
DOI: 10.1115/1.4005865. |
| [14] |
ZHANG X, FU Z, WANG G. Design and development of a novel 3-DOF parallel robotic polishing end-effector[C]//2021 6th IEEE International Conference on Advanced Robotics and Mechatronics (ICARM) . Chongqing: IEEE, 2021: 352-357.
|
| [15] |
赵亚平, 杨桂林, 杨巍, 等. 气电混合式机器人力控末端执行器研究[J].
组合机床与自动化加工技术, 2016(12): 103-106.
ZHAO Y P, YANG G L, YANG W, et al. Research on a pneumoelectric robotic end-effector with force control[J]. Modular Machine Tool & Automatic Manufacturing Technique, 2016(12): 103-106. |
| [16] |
刘立涛, 杨桂林, 柳丽, 等. 气电混合式力控末端执行器接触力控制研究[J]. 机械设计与研究, 2020, 36(5) : 33-37.
LIU L T, YANG G L, LIU L, et al. Research on the contact force control of pneumatic-electric hybrid force-controlled end-effector[J], Machine Design and Research, 2020, 36(5) : 33-37. |
| [17] |
WHITNEY D E. Historical perspective and state of the art in robot force control[J].
The International Journal of Robotics Research, 1987, 6(1): 3-14.
DOI: 10.1177/027836498700600101. |
| [18] |
李正义. 机器人与环境间力/位置控制技术研究与应用[D]. 武汉: 华中科技大学, 2011.
|
| [19] |
SCHUMACHER M, WOJTUSCH J, BECKERLE P, et al. An introductory review of active compliant control[J].
Robotics and Autonomous Systems, 2019, 119: 185-200.
DOI: 10.1016/j.robot.2019.06.009. |
| [20] |
葛吉民, 邓朝晖, 李尉, 等. 机器人磨抛力柔顺控制研究进展[J].
中国机械工程, 2021, 32(18): 2217-2230.
GE J M, DENG Z H, LI W, el al. Research progresses of robot grinding and polishing force compliance controls[J]. China Mechanical Engineering, 2021, 32(18): 2217-2230. |
| [21] |
甘亚辉, 段晋军, 戴先中. 非结构环境下的机器人自适应变阻抗力跟踪控制方法[J].
控制与决策, 2019, 34(10): 2134-2142.
GAN Y H, DUAN J J, DAI X Z. Adaptive variable impedance control for robot force tracking in unstructured environment[J]. Control and Decision, 2019, 34(10): 2134-2142. |
| [22] |
LOPES A, ALMEIDA F. A force-impedance controlled industrial robot using an active robotic auxiliarydevice[J].
Robotics and Computer-Integrated Manufacturing, 2008, 24(3): 299-309.
DOI: 10.1016/j.rcim.2007.04.002. |
| [23] |
LEW J Y. Contact control of flexible micro/macro-manipulators[C]// Proceedings of International Conference on Robotics and Automation. Albuquerque, NM: IEEE, 1997: 2850-2855.
|
| [24] |
BONE G M, ELBESTAWI M A. Active end effector control of a low precision robot in deburring[J].
Robotics and Computer-Integrated Manufacturing, 1991, 8(2): 87-96.
DOI: 10.1016/0736-5845(91)90024-M. |
| [25] |
TIAN Y, SHIRINZADEH B, ZHANG D. Closed-form compliance equations of filleted V-shaped flexure hinges for compliant mechanism design[J].
Precision Engineering, 2010, 34(3): 408-418.
DOI: 10.1016/j.precisioneng.2009.10.002. |
| [26] |
LI R, YANG Z, CHEN G, et al. Analytical solutions for nonlinear deflections of corner-fillet leaf-springs[J].
Mechanism and Machine Theory, 2021, 157: 104182.
DOI: 10.1016/j.mechmachtheory.2020.104182. |
| [27] |
LI R, YANG Z, CAI B, et al. A compliant guiding mechanism utilizing orthogonally oriented flexures with enhanced stiffness in Degrees-of-Constraint[J].
Mechanism and Machine Theory, 2022, 167: 104555.
DOI: 10.1016/j.mechmachtheory.2021.104555. |
| [28] |
李瑞奇. 倒圆角弹片式柔性铰链非线性变形分析、优化与应用[D]. 广州: 广东工业大学, 2021.
|
 2023, Vol. 40
2023, Vol. 40

