2. 高性能工具全国重点实验室, 广东 广州 510006
2. State Key Laboratory for High Performance Tools, Guangzhou 510006, China
齿轮是一种传递运动和动力的机械零件。作为机械装备的关键基础零件,齿轮在汽车制造、轨道交通、工业机床、医疗器械、国防装备以及航空航天等领域被广泛使用,是现代机械产品中不可或缺的零件,在机械设备传动以及整个机械领域中具有举足轻重的作用。
工业机器人、多轴数控机床等机械设备对齿轮性能的要求逐渐提高,齿轮的加工精度和质量对机械设备的整体性能起着重要甚至决定性的作用。齿轮磨削通常作为齿轮加工的精加工工序,不仅适用于淬硬齿轮的精加工,而且能够消除齿轮预加工的各项误差,将齿轮的加工精度提升一级到两级[1-2]。齿轮磨削加工主要分为展成法和成形法。齿轮成形磨削凭借成形磨齿机床结构简单、成形加工简便、加工效率高、可磨削高精度渐开线齿轮以及适合任意模数、各种齿形的齿轮和内齿轮加工等优点[3-4],在齿轮制造中广泛应用。在成形磨削齿轮时,齿轮的齿形加工精度主要取决于成形砂轮的轮廓修整精度[5]。在磨削加工齿轮时,砂轮表面容易发生不均匀磨损,产生的砂轮轮廓误差将直接复映在齿轮上。为了保持磨削过程中砂轮表面有足够的锐度和正确的几何形状,必须对成形砂轮进行定期修整[6]。成形砂轮修整技术是齿轮成形磨削的关键技术之一。
针对成形砂轮的修整,任小钟等[7]对渐开线廓形的成形砂轮修整进行了计算研究,采用了等误差直线逼近渐开线的算法实现成形砂轮修整,但该方法的砂轮修整精度有限,而且数控修整程序繁琐。刘贵祥[8]研究了摆线轮成形磨削砂轮的修整方法,建立了摆线轮齿廓曲线的数学模型,然后使用双圆弧拟合砂轮廓形数据点。相比于直线逼近法,该方法可以提高砂轮修整精度,但精度提升有限。早期数控成形磨齿机在砂轮修整过程需要将成形砂轮的轮廓曲线离散成一系列小线段或者圆弧段,导致砂轮轮廓曲线出现不连续和波动现象,甚至会改变原来轮廓曲线的凹凸性[8],使修整后的成形砂轮加工出的齿轮精度有限,并且修整程序繁琐、数据量大。
B样条曲线具有灵活性好、局部可修改等优点。使用B样条曲线拟合成形砂轮轮廓曲线有利于后续磨齿机的数控系统使用样条插补功能修整成形砂轮,省去成形砂轮轮廓离散为小线段的步骤,可有效提高成形砂轮的修整精度和修整效率,避免了直线和圆弧逼近成形砂轮轮廓所产生的问题。韩江等[9]提出了一种适用于稠密采样数据点的 B 样条曲线拟合算法,该算法根据离散数据点曲率分布情况选定轮廓关键点进行拟合,并且采用邻域点比较法计算拟合误差。但是该算法中特征点的选取是根据曲率平均值来选取的,这将导致在采样数据点曲率不复杂的区域也会产生较多的特征点,并且拟合误差计算方法的计算精度也不高,尤其是当原始数据点不稠密时,误差计算精确度将极大降低。Park 等[10]提出一种基于误差自适应控制的 B 样条曲线拟合方法,该方法在平坦区域选择较少的特征点,而在复杂区域选择较多的特征点,尽可能用较少数目的控制点得到满足预设精度的B样条曲线。此方法在特征点的选取时需要提前得到一条基准曲线来计算曲率,并且采用的是最小二乘法逼近数据点,计算过程较为费时繁琐。当数据点复杂,曲率变化较大时,该方法还将产生较多的特征点。陶浩等[11]采用依据主导点的拟合方法对复杂刀具轨迹进行平滑压缩,该算法首先对原始数据点进行预处理,选取出主导点,然后进行主导点的在线插值以及利用轮廓误差跟随法对非主导点进行误差检测,进而生成一条满足拟合精度要求的B样条曲线。
本文采用B样条曲线在满足指定误差要求下用较少的控制点拟合成形砂轮轮廓。以渐开线斜齿轮为例,通过建立渐开线斜齿轮齿面模型计算出成形砂轮的轮廓截面形状,提出采用B样条曲线拟合成形砂轮轮廓曲线的方法,并利用差分演化算法计算拟合误差,保证了砂轮轮廓的拟合精度。
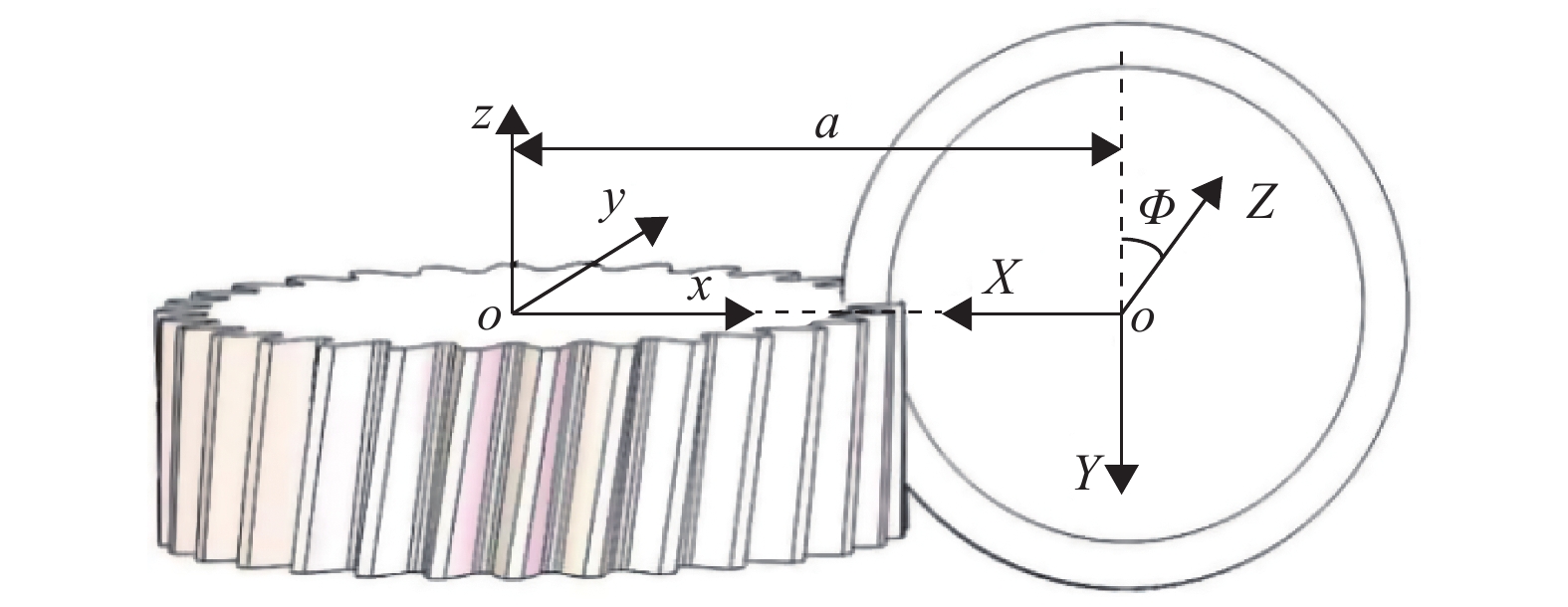
1 渐开线斜齿轮齿面建模 1.1 建立齿轮磨削坐标系在进行齿轮成形磨削砂轮轮廓研究前需要建立齿轮成形磨削坐标系,根据磨削时斜齿轮与成形砂轮的相对位置关系建立图1所示的坐标系,其中坐标系o-xyz为斜齿轮坐标系,z轴通过齿轮轴线,x轴通过齿轮齿槽中线,xoy平面为齿轮端面;坐标系O-XYZ为成形砂轮坐标系,Z轴通过砂轮轴线,X轴与斜齿轮坐标系x轴反向共线,两坐标系符合右手定则。成形砂轮轴线与斜齿轮轴线的夹角为Φ=90°−β,β为斜齿轮螺旋角,两轴线的中心距离为a。
|
图 1 斜齿轮成形磨削坐标系 Figure 1 Grinding coordinate system of helical gear forming grinding |
根据图1所示的斜齿轮成形磨削坐标系,斜齿轮坐标系与成形砂轮坐标系的变换关系为
| $ \left\{ \begin{gathered} X = a - x \\ Y = - y\cos \varPhi - z\sin \varPhi \\ Z = - y\sin \varPhi - z\cos \varPhi \\ \end{gathered} \right. $ | (1) |
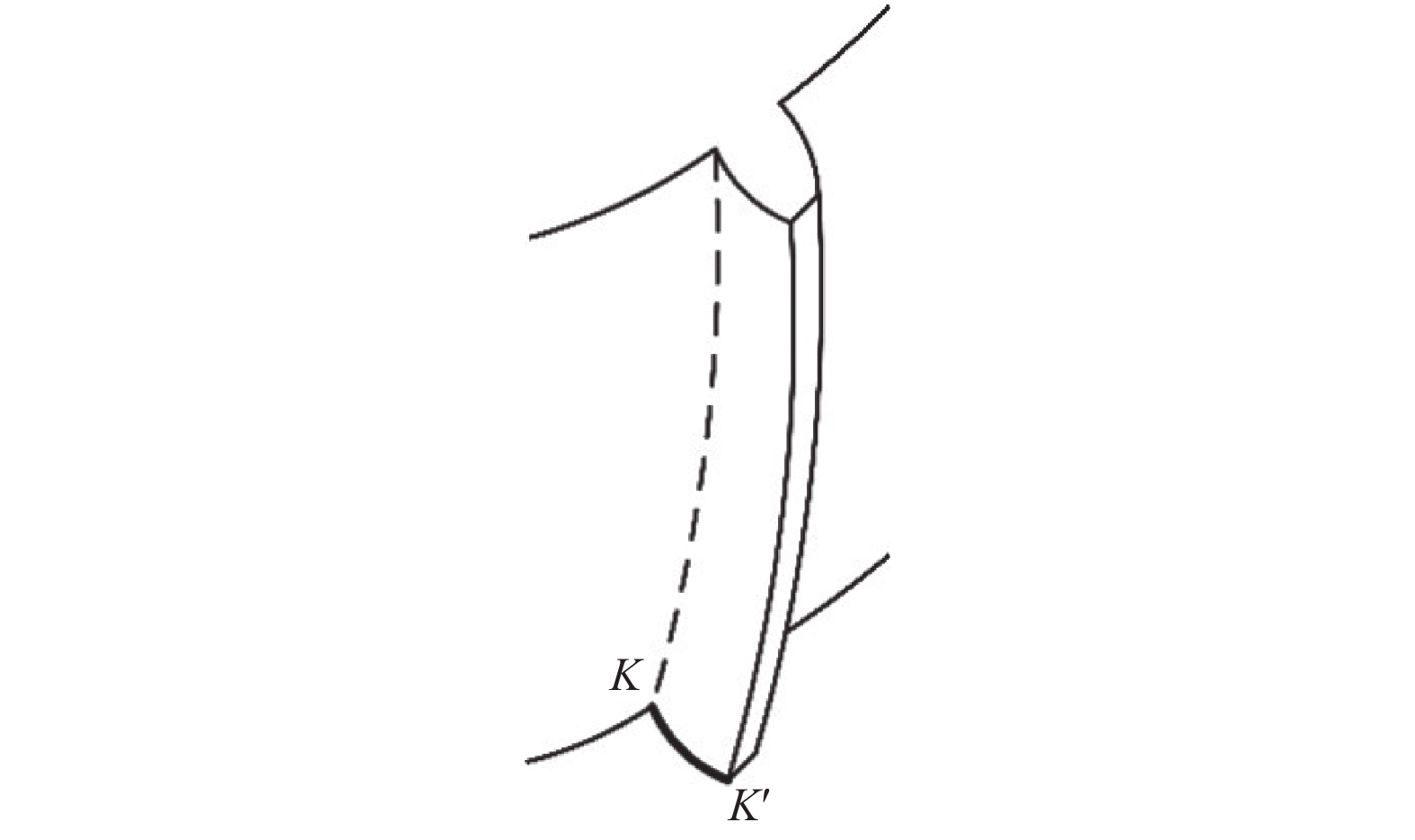
渐开线斜齿轮的齿面也称为渐开螺旋面,如图2所示。已知一条渐开线KK',当渐开线上的每一点都绕z轴作相同的螺旋运动时,即同时绕z轴作等速旋转运动和沿z轴作等速直线运动,此时渐开线KK'在空间形成的轨迹曲面就是一个渐开螺旋面,即为渐开线斜齿轮的齿面[12]。
|
图 2 渐开螺旋面 Figure 2 Involute helicoid surface |
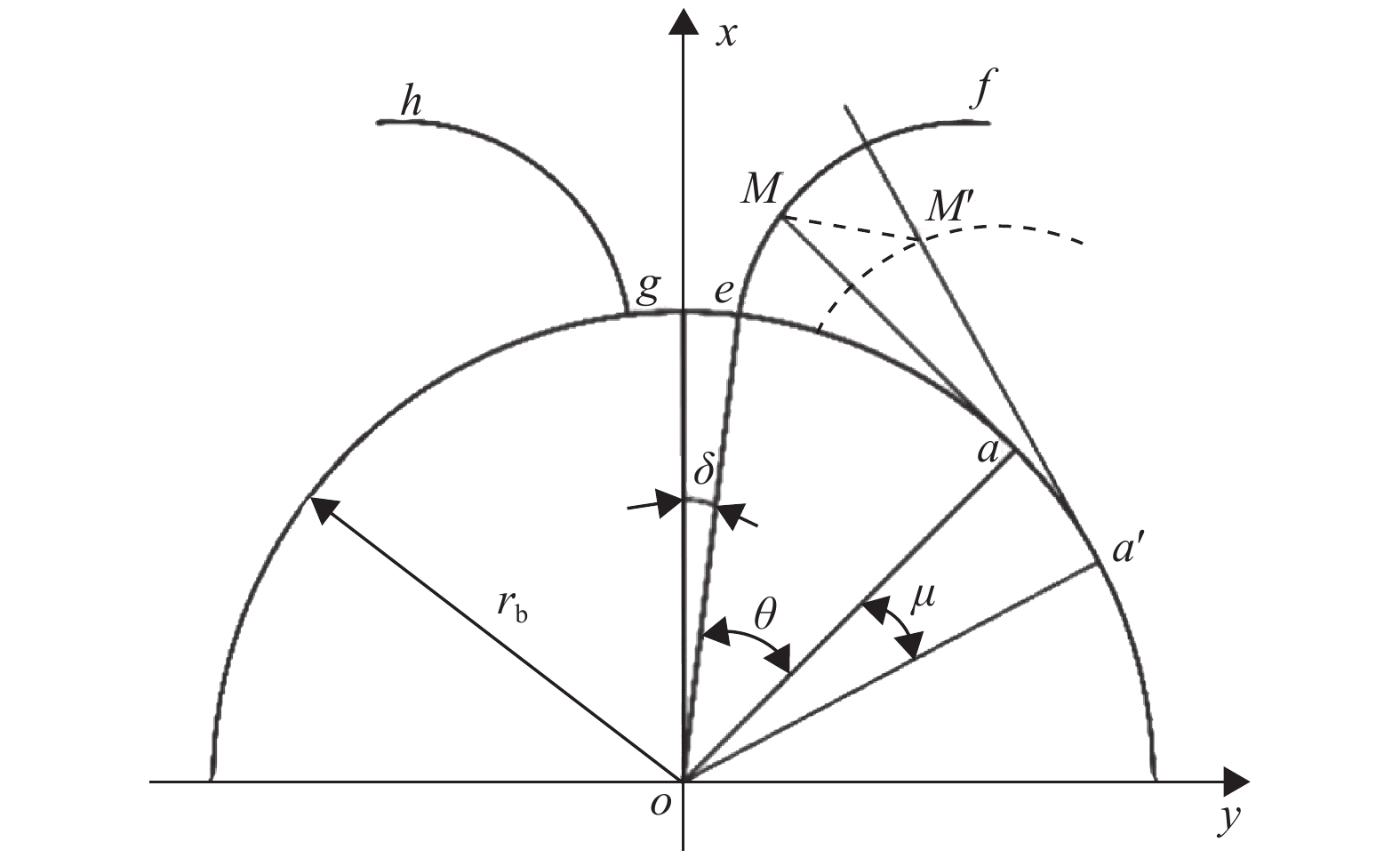
在斜齿轮坐标系的端面xoy平面内建立齿轮端面标准渐开线廓形,其参数如图3所示,其中x轴通过齿轮端面齿槽中点,曲线ef为齿槽右侧渐开线,曲线gh为齿槽左侧渐开线,M为右侧渐开线ef上任意一点,点M的法线与基圆相切于a点,δ为基圆齿槽半角,rb为基圆半径,点M绕z轴旋转到点M'时所转过的角度为μ。取∠eoa=θ作为参变量,则根据渐开线的性质可得:
|
图 3 齿轮端面标准渐开线 Figure 3 Standard involute profile of gear end face |
| $ Ma = {r_{\rm{b}}}\theta $ | (2) |
可求得齿轮端面渐开线ef在平面直角坐标系的方程为
| $ \left\{ \begin{gathered} x = {r_{\rm{b}}} \cos (\theta + \delta ) + \theta {r_{\rm{b}}} \sin (\theta + \delta ) \\ y = {r_{\rm{b}}} \sin (\theta + \delta ) - \theta {r_{\rm{b}}} \cos (\theta + \delta ) \\ \end{gathered} \right. $ | (3) |
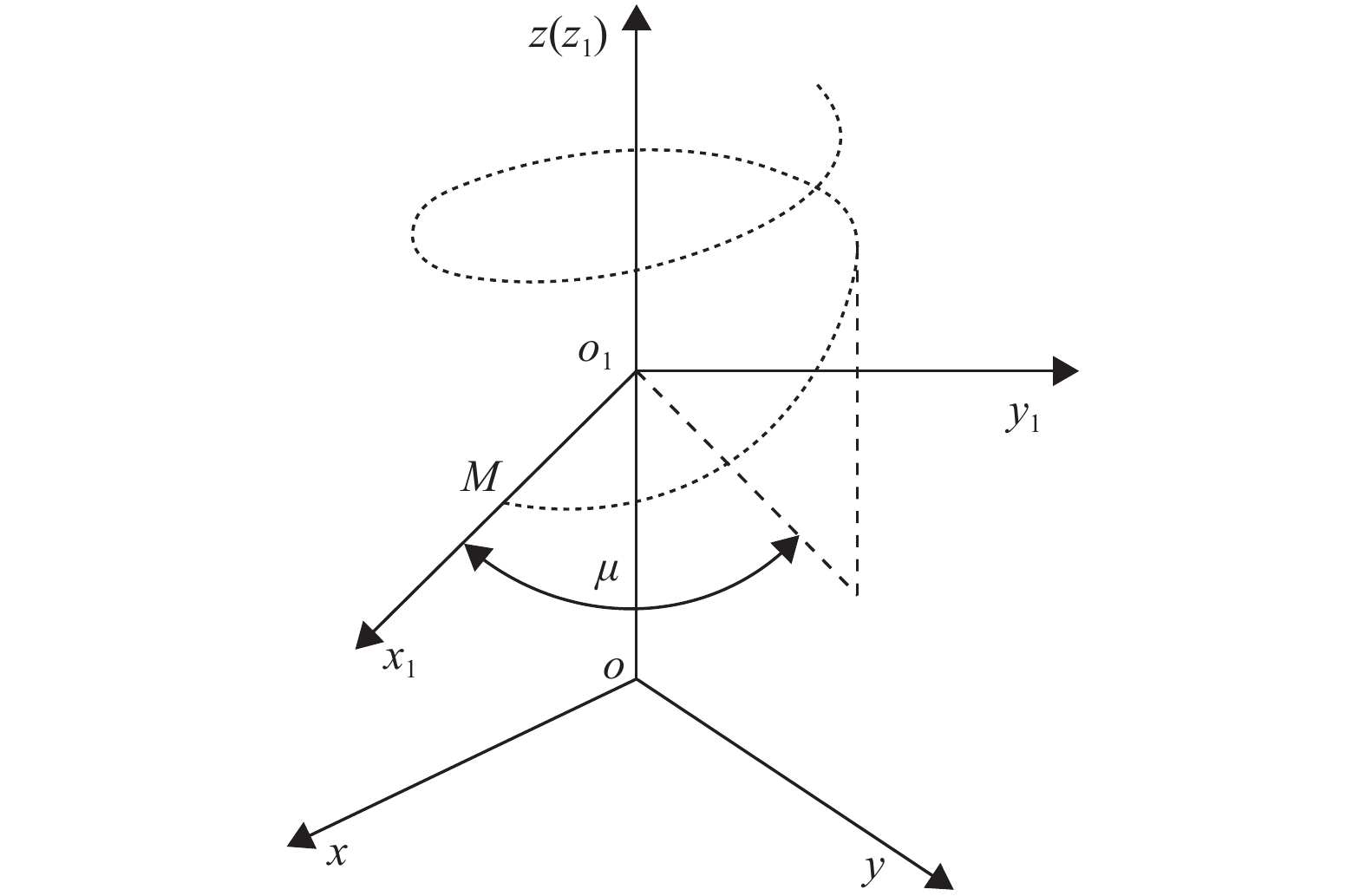
将渐开线ef绕z轴作螺旋运动,则可得到斜齿轮渐开螺旋面。求出齿轮端面渐开线方程后,若要继续求得齿轮渐开螺旋面方程,则需要知道渐开线上任意一点的螺旋线方程。设点M(x0,y0,z0) 是空间坐标系o-xyz中的一点,当点M绕z轴作螺旋运动时,其轨迹为一条螺旋线,如图4所示。过点M(x0,y0,z0) 作z轴的垂直平面,与z轴的交点为o1,以o1M为x1轴正方向、z轴为z1轴建立直角坐标系o1-x1y1z1,在坐标系o1-x1y1z1中,过点M的螺旋线方程为
|
图 4 螺旋线 Figure 4 Helical curve |
| $ {x_1} = | {\overline {{o_1}M} } |\cos \mu ,\;\;\;{y_1} = | {\overline {{o_1}M} } |\sin \mu ,\;\;\;\;{z_1} = \frac{h}{{2\text{π} }}\mu = q\mu $ | (4) |
式中:
将坐标系o1-x1y1z1与坐标系o-xyz进行坐标变换,最终计算得到螺旋线在坐标系o-xyz中的方程为
| $ \left\{ \begin{gathered} x = {x_0}\cos \mu - {y_0}\sin \mu \\ y = {x_0}\sin \mu + {y_0}\cos \mu \\ z = {z_0} + q\mu \\ \end{gathered} \right. $ | (5) |
将点M的渐开线方程式(3) 代入螺旋线方程式(5) 即可得到渐开线的螺旋线方程,所有渐开线的螺旋线组合起来就形成渐开螺旋面,此时得到齿槽右侧渐开螺旋面的方程式为
| $ \left\{ \begin{gathered} x = {r_{\rm{b}}}\cos (\theta + \delta + \mu ) + \theta {\kern 1pt} {r_{\rm{b}}}\sin (\theta + \delta + \mu ) \\ y = {r_{\rm{b}}}\sin (\theta + \delta + \mu ) - \theta {\kern 1pt} {r_{\rm{b}}}\cos (\theta + \delta + \mu ) \\ z = q\mu \\ \end{gathered} \right. $ | (6) |
设斜齿轮渐开螺旋面方程为
| $ {\boldsymbol{r}} = {\boldsymbol{r}}(\theta ,\mu ) = x(\theta ,\mu ) {\boldsymbol{i}} + y(\theta ,\mu ) {\boldsymbol{j}} + z(\theta ,\mu ) {\boldsymbol{k}} $ | (7) |
则齿轮渐开螺旋面上任意一点的法线矢量n为
| $ {\boldsymbol{n}} = \frac{{\text{∂} {\boldsymbol{r}}}}{{\text{∂} \theta }} \times \frac{{\text{∂} {\boldsymbol{r}}}}{{\text{∂} \mu }} $ | (8) |
其中有
| $ \left\{ \begin{gathered} \frac{{\text{∂} {\boldsymbol{r}}}}{{\text{∂} \theta }} = \frac{{\text{∂} x}}{{\text{∂} \theta }}{\boldsymbol{i}} + \frac{{\text{∂} y}}{{\text{∂} \theta }}{\boldsymbol{j}} + \frac{{\text{∂} z}}{{\text{∂} \theta }}{\boldsymbol{k}} \\ \frac{{\text{∂} {\boldsymbol{r}}}}{{\text{∂} \mu }} = \frac{{\text{∂} x}}{{\text{∂} \mu }}{\boldsymbol{i}} + \frac{{\text{∂} y}}{{\text{∂} \mu }}{\boldsymbol{j}} + \frac{{\text{∂} z}}{{\text{∂} \mu }}{\boldsymbol{k}} \\ \end{gathered} \right. $ | (9) |
令
| $ {\boldsymbol{n}} = {n_x}{\boldsymbol{i}} + {n_y}{\boldsymbol{j}} + {n_z}{\boldsymbol{k}} $ | (10) |
根据矢量计算法则,由式(8) 和(9) 可得
| $ {n_x} = \left| {\begin{array}{*{20}{c}} {\dfrac{{\text{∂} y}}{{\text{∂} \theta }}} & {\dfrac{{\text{∂} z}}{{\text{∂} \theta }}} \\ {\dfrac{{\text{∂} y}}{{\text{∂} \mu }}} & {\dfrac{{\text{∂} z}}{{\text{∂} \mu }}} \end{array}} \right|,{n_y} = \left| {\begin{array}{*{20}{c}} {\dfrac{{\text{∂} z}}{{\text{∂} \theta }}} & {\dfrac{{\text{∂} x}}{{\text{∂} \theta }}} \\ {\dfrac{{\text{∂} z}}{{\text{∂} \mu }}} & {\dfrac{{\text{∂} x}}{{\text{∂} \mu }}} \end{array}} \right|,{n_z} = \left| {\begin{array}{*{20}{c}} {\dfrac{{\text{∂} x}}{{\text{∂} \theta }}} & {\dfrac{{\text{∂} y}}{{\text{∂} \theta }}} \\ {\dfrac{{\text{∂} x}}{{\text{∂} \mu }}} & {\dfrac{{\text{∂} y}}{{\text{∂} \mu }}} \end{array}} \right| $ | (11) |
对式(6) 中的θ和μ分别求偏导,可得
| $ \left\{ \begin{gathered} \frac{{\text{∂} x}}{{\text{∂} \theta }} = \theta {r_{\rm{b}}}\cos (\theta + \delta + \mu ) \\ \frac{{\text{∂} y}}{{\text{∂} \theta }} = \theta {r_{\rm{b}}}\sin (\theta + \delta + \mu ) \\ \frac{{\text{∂} z}}{{\text{∂} \theta }} = 0 \\ \end{gathered} \right. $ | (12) |
| $ \left\{ \begin{gathered} \frac{{\text{∂} x}}{{\text{∂} \mu }} = - {r_{\rm{b}}}\sin (\theta + \delta + \mu ) + \theta {r_{\rm{b}}}\cos (\theta + \delta + \mu ) = - y \\ \frac{{\text{∂} y}}{{\text{∂} \mu }} = {r_{\rm{b}}}\cos (\theta + \delta + \mu ) + \theta {r_{\rm{b}}}\sin (\theta + \delta + \mu ) = x \\ \frac{{\text{∂} z}}{{\text{∂} \mu }} = q \\ \end{gathered} \right. $ | (13) |
将式(12) 、(13) 代入式(11) 可得到右旋渐开螺旋面上任意一点的法线矢量的3个分量为
| $ \left\{ \begin{gathered} {n_x} = q{r_{\rm{b}}}\theta \sin (\theta + \delta + \mu ) \\ {n_y} = - q{r_{\rm{b}}}\theta \cos (\theta + \delta + \mu ) \\ {n_z} = \frac{1}{q}({n_x}y - {n_y}x) = r_{\rm{b}}^2\theta \\ \end{gathered} \right. $ | (14) |
成形砂轮磨削加工齿轮时,在砂轮和齿轮的相对磨削运动中,成形砂轮绕自身轴线高速旋转,齿轮齿面也绕自身轴线做螺旋运动。在啮合磨削过程中,成形砂轮与斜齿轮齿面之间在任何时刻都存在一条相切且位置不变的空间接触线[13],将此接触线绕砂轮回转轴线旋转即可得到成形砂轮的回转表面。
根据图1 斜齿轮成形磨削坐标系,设空间任意一点在成形砂轮坐标系O-XYZ中相对原点的径矢为R′。成形砂轮与斜齿轮螺旋面在接触线上一点的公共法线矢量为n,当齿轮螺旋面已知时,根据齿轮啮合原理[14],成形砂轮与斜齿轮螺旋面的接触条件为
| $ ({\boldsymbol{k'}} \times {\boldsymbol{R'}}) {\boldsymbol{n}} = 0 $ | (15) |
式中:
根据斜齿轮与成形砂轮的坐标关系,可得
| $ {\boldsymbol{R'}} = (x - a) {\boldsymbol{i}} + y{\boldsymbol{j}} + z{\boldsymbol{k}} $ | (16) |
| $ {\boldsymbol{k'}} = - {\boldsymbol{j}}\sin \varPhi + {\boldsymbol{k}}\cos \varPhi $ | (17) |
式中:i、j、k为斜齿轮坐标系o-xyz中坐标轴x、y、z方向的单位矢量。将式(10) 、(16) 、(17) 代入接触条件式(15) ,得到成形砂轮与斜齿轮螺旋面的接触条件为
| $ (a - x) \left(\frac{{{n_y} + {n_z}\tan \varPhi }}{{{n_x}}}\right) + y + z\tan \varPhi = 0 $ | (18) |
将斜齿轮齿槽右侧渐开螺旋面的方程式(6) 以及其法线矢量的3个分量式(14) 代入齿轮与砂轮接触条件式(18) ,最终得到斜齿轮齿槽右侧渐开线形成的螺旋面与成形砂轮的接触条件为
| $ \mu - \frac{{r_{\rm{b}}^2\theta }}{{{q^2}}} - \frac{{(qa\cot \varPhi + r_{\rm{b}}^2) \cot (\theta + \delta + \mu ) }}{{{q^2}}} + \frac{{{r_{\rm{b}}}(q\cot \varPhi + a) }}{{{q^2}\sin (\theta + \delta + \mu ) }} = 0 $ | (19) |
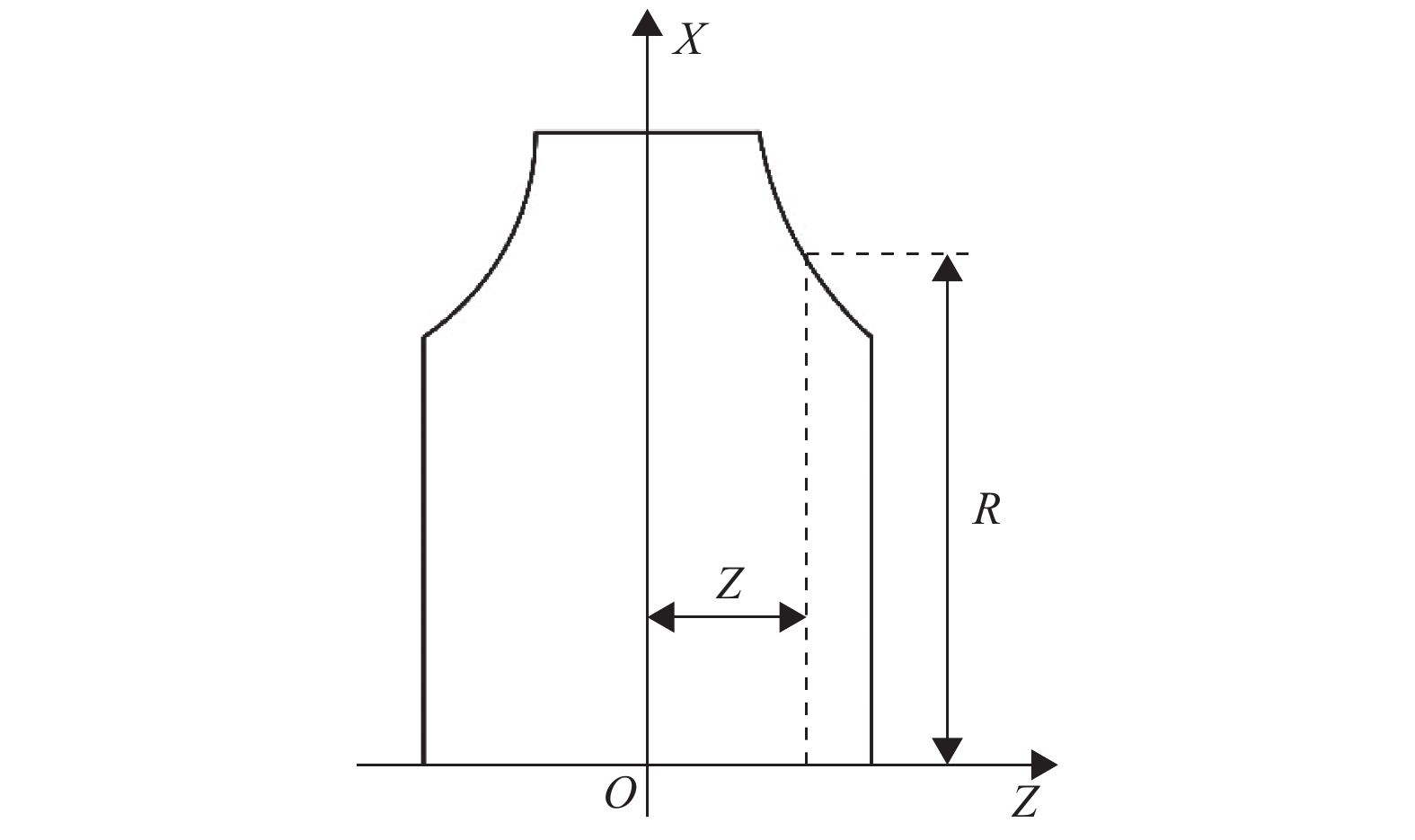
最后将斜齿轮螺旋面方程式(6) 和接触条件式(19) 联立计算,即可求出成形砂轮与斜齿轮齿面之间在斜齿轮坐标系o-xyz中的空间接触线,将接触线绕砂轮回转轴线旋转即可得到成形砂轮的回转面,图5所示为成形砂轮轴向截面轮廓。
|
图 5 成形砂轮轴向截面轮廓 Figure 5 Axial cross-sectional profile of formed grinding wheel |
利用斜齿轮坐标系与成形砂轮坐标系变换关系式(1) 将接触线坐标变换到成形砂轮坐标系O-XYZ中,得到成形砂轮轮廓轴向截面方程式为
| $ \left\{ \begin{gathered} R = \sqrt {{X^2} + {Y^2}} \\ Z = Z \\ \end{gathered} \right. $ | (20) |
p次B样条曲线的数学表达式为[15]
| $ C(u) = \sum\limits_{t = 0}^s {{N_{t,{\kern 1pt} p}}(u) {{\boldsymbol{P}}_t}}, {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {l_1} \leqslant u \leqslant {l_2} $ | (21) |
式中:p为样条曲线次数,{Pt}为控制点,由控制点构成的多边形称为控制多边形,并且通常取l1=0,l2=1。Nt,p(u) 为第t个p次B样条基函数,它是由节点矢量U=[u0,u1,···,um]确定的分段多项式函数,其定义为
| $ \left\{ \begin{array}{l}{N}_{t,0}(u) =\left\{\begin{array}{l}1\text{,}{u}_{t}\le u < {u}_{t+1}\\ 0\text{,}其他\end{array}\right.\\ {N}_{t,p}(u) = \dfrac{u - {u}_{t}}{{u}_{t+p} - {u}_{t}}{N}_{t,p-1}(u) + \dfrac{{u}_{t+p+1} - u}{{u}_{t+p+1} - {u}_{t+1}}{N}_{t+1,p-1}(u) \end{array}\right. $ | (22) |
式中:特别约定0/0=0,并且次数p、控制点个数s+1和节点个数m+1满足关系m=s+p+1,确定样条曲线次数p和节点矢量U后即可计算出B样条基函数。
3.2 B样条曲线初始拟合在B样条曲线拟合成形砂轮轮廓问题中,拟合曲线无需精准通过砂轮轮廓的所有数据点,只需在指定拟合误差约束下通过原始数据中的一些特定的点集来拟合逼近所有轮廓数据点,特定的点集称为特征点。B样条曲线拟合精度主要与控制点个数有关,一般而言,控制点数目越多,拟合精度越高。为了减少B样条曲线的控制点计算量,需要尽可能减少所需通过的特征点个数。因此,本文由最少的特征点个数开始拟合成形砂轮轮廓,然后逐渐增加特征点数目以提高拟合精度,最终满足指定误差约束要求,整个B样条曲线拟合成形砂轮轮廓过程属于一个迭代计算过程。
3.2.1 特征点的选取特征点主要反映曲线的基本外形特征,初始特征点的选取对拟合的样条曲线影响重大,合理的特征点选取可以有效提高拟合效率,减少迭代次数。特征点的选取主要根据原始数据点曲率、拐点以及弓高误差等信息确定[16]。原始数据点曲率信息可以判断曲线的平滑情况,曲率极值点通常为曲线弯曲点,可以作为拟合的B样条曲线的特征点。拐点定义为曲线凹凸性发生变化的转折点,是决定曲线几何形状的主要特征之一。除拐点和曲率极值点外,最大弓高误差点也可以作为特征点。
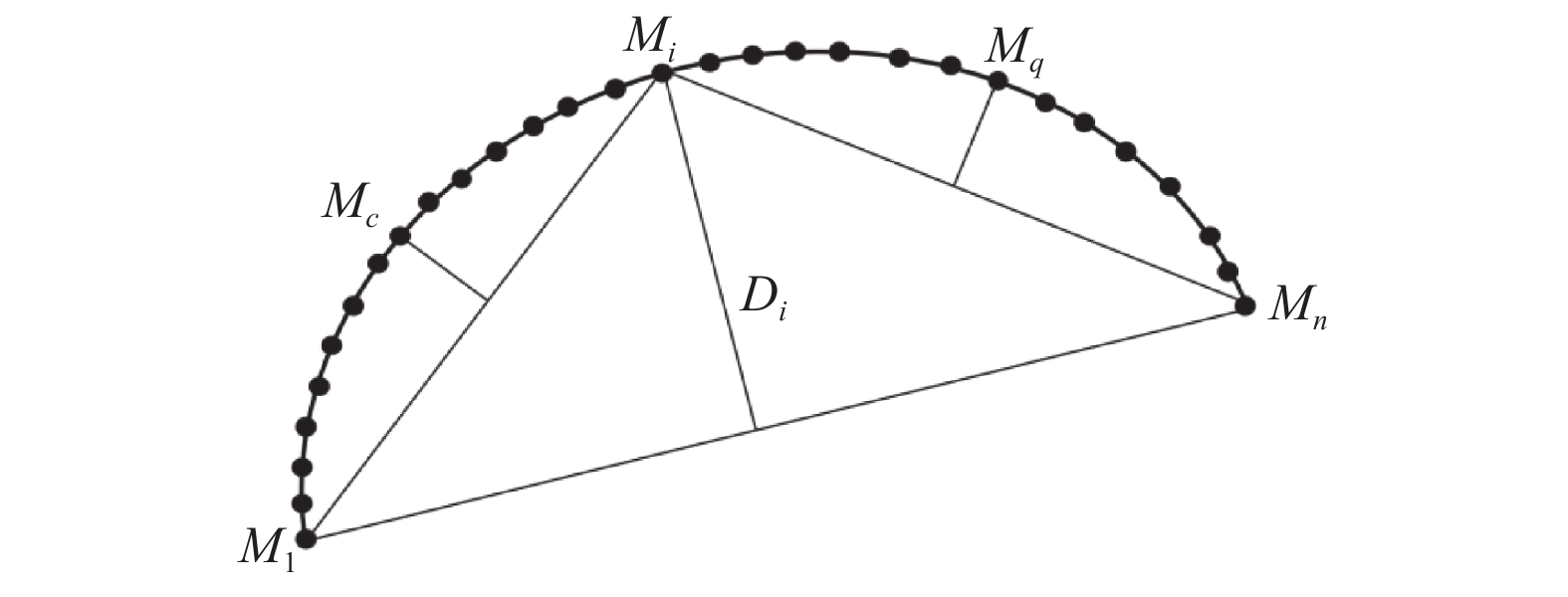
由于成形砂轮的理论轮廓是一条平滑的曲线,不存在明显弯曲点和拐点,因此本文选择最大弓高误差点作为初始特征点。最大弓高误差点计算方法如下:如图6所示,设M1和Mn为一段圆弧数据点的起点和终点,计算两点之间的其他数据点到直线M1Mn的距离,当距离最大值为Di时,则点Mi为最大弓高误差点。同理,可计算出另外2个最大弓高误差点Mc和Mq。
|
图 6 弓高误差计算示意图 Figure 6 Schematic diagram of chord error calculation |
假设选取出一组特征点集{Qe},e=0,1,···,s,则需要对选取的特征点进行参数化处理,常用的参数化计算方式主要有均匀参数化、弦长参数化和向心参数化[15]。
3种参数化计算方式中均匀参数化在特征分布不均匀时容易产生打圈自交等奇怪的形状;弦长参数化是常用的方法,能够满足常见的曲线拟合;向心参数化在特征点急转弯变化时,计算结果优于弦长参数化。由于本文中的成形砂轮形状轮廓不属于复杂曲线,其形状不会出现急转弯现象,因此本文选择弦长参数化方法计算特征点参数,弦长参数化计算方法如下:
设d为总弦长,其计算公式为
| $ d = \sum\limits_{e = 1}^s {\left| {{Q_e} - {Q_{e - 1}}} \right|} $ |
则有
| $ \left\{\begin{array}{l}{\overline{u}}_{0}=0\text{,}{\overline{u}}_{s}=1\\ {\overline{u}}_{{}_{e}}={\overline{u}}_{{}_{e-1}}+\dfrac{\left|{Q}_{e}-{Q}_{e-1}\right|}{d},e=1,2,\cdots,s-1\end{array}\right. $ | (23) |
对特征点进行参数化处理之后,需要计算节点矢量U,采用平均值计算方法:
| $ \left\{\begin{array}{l}{u}_{0}=\cdots ={u}_{p}=0\\ {u}_{m-p}=\cdots ={u}_{m}=1\\ {u}_{g+p}=\dfrac{1}{p}{\displaystyle \sum _{e=j}^{g+p-1}{\overline{u}}_{e}},g=1,2,\cdots \text{,}s-p\end{array}\right. $ | (24) |
根据B样条曲线表达式(21) 建立一个系数矩阵为(s+1) ×(s+1) 的线性方程组:
| $ {{\boldsymbol{Q}}_e} = C({\overline u _{_e}}) = \sum\limits_{t = 0}^s {{N_{t,{\kern 1pt} p}}({{\overline u }_e}) {{\boldsymbol{P}}_t}} $ | (25) |
利用式(23)、(24)计算出特征点对应参数值
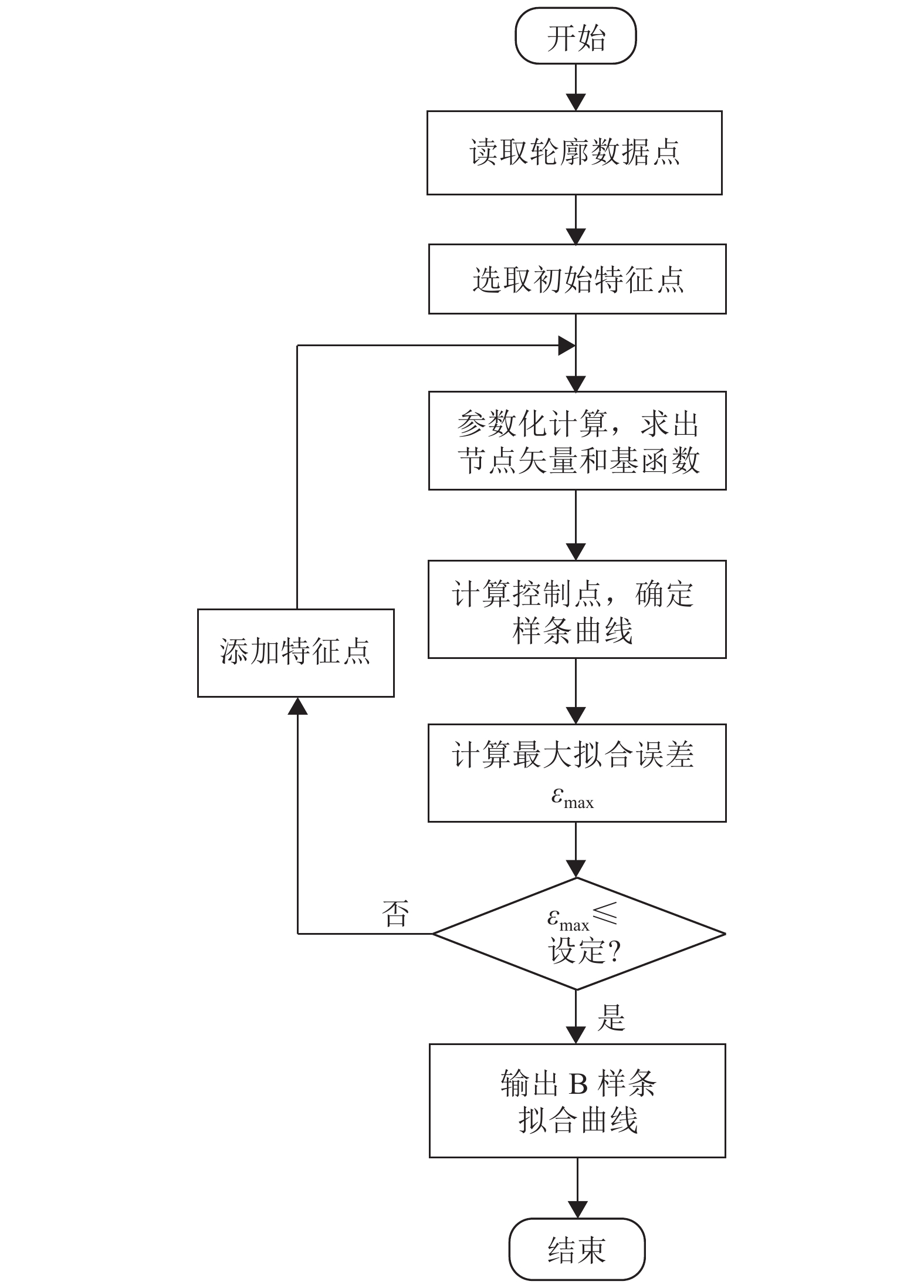
|
图 7 B样条曲线拟合成形砂轮轮廓流程图 Figure 7 Flowchart of B-spline curve fitting method for formed grinding wheel profile |
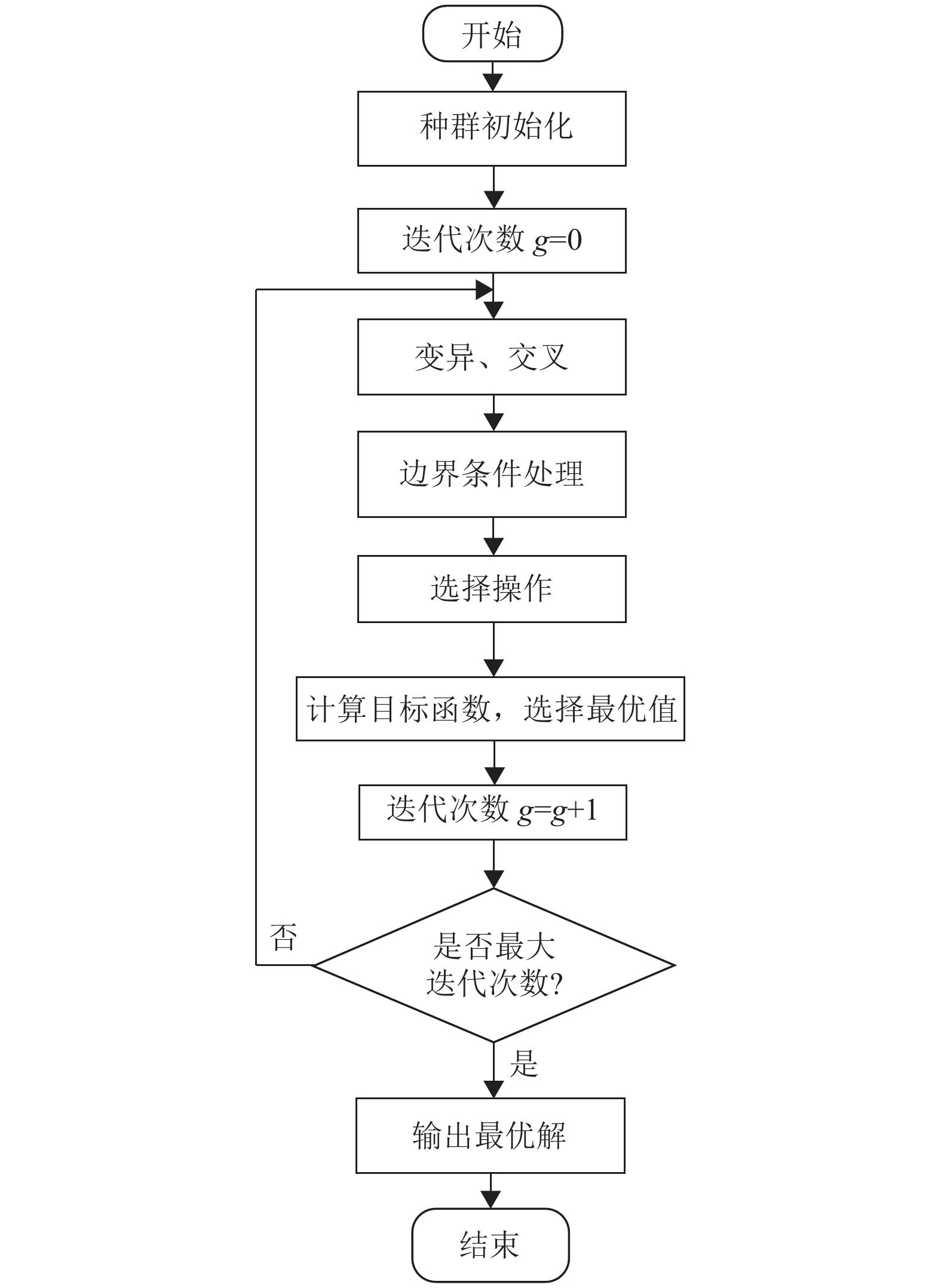
根据上述方法计算得到初始拟合的B样条曲线后,还需计算原始数据点中非特征点的拟合误差,根据最大拟合误差判断拟合精度是否满足预定要求。若拟合误差不满足要求,则把最大拟合误差处数据点添加到特征点继续迭代拟合,直至最终拟合误差满足预定精度要求。拟合误差定义为成形砂轮原始数据点到B样条曲线的最短距离。为了准确计算出非特征点的拟合误差,本文采用差分演化算法依次计算非特征点的拟合误差,流程图如图8所示,计算步骤如下:
|
图 8 差分演化算法流程图 Figure 8 The flowchart of differential evolution algorithm |
(1) 确定算法参数,进行种群初始化。
| $ u_{{{m}}}={\rm{rand}}({\rm{NP}},{\rm{Dim}}) \times (X_{{\rm{max}}} - X_{{\rm{min}}}) + X_{{\rm{min}}} ,m=1,\cdots, {\rm{NP}}$ |
式中:NP为种群个体规模,Dim为变量维数,本文变量为一维,Xmax和Xmin分别为种群值的上限和下限,本文中上限取值为1,下限取值为0。um为(0,1) 内的随机值。
(2) 建立目标函数。
| $ \varepsilon (u) {\text{ = }}|{{M_i} - C(u) }| $ |
式中:ε为拟合误差值,Mi为砂轮轮廓原始离散数据点,C(u) 为种群个体所对应的B样条曲线上的点。
(3) 进行变异处理,产生个体vm。
| $ {v_m} = u_{{r_{{\kern 1pt} 1}}}^{g - 1} + F \times ({u_{{r_{{\kern 1pt} 2}}}} - {u_{{r_{{\kern 1pt} 3}}}}) $ |
(4) 进行交叉处理,产生新个体wm。
| $ {w_m} = \left\{{{\begin{array}{*{20}{l}} {{v_m}},&{{\rm{if}}}&{{\rm{cr}}<{\rm{CR}}}\\ {{u_m}},&{{\rm{if}}}&{其他}\\ \end{array}} } \right. $ |
cr为(0,1) 内的随机数,CR为交叉算子。
(5) 边界条件处理,若个体wm和vm超出上下限范围,则重新赋值。
(6) 选择操作,对个体um和wm进行选择,获得下一代种群个体
| $ u_m^g = \left\{ \begin{gathered} {w_m},{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\text{if}}{\kern 1pt} {\kern 1pt} {\kern 1pt} \varepsilon \left( {{w_m}} \right) < \varepsilon \left( {{u_m}} \right) \\ {u_m},{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\text{if}}{\kern 1pt} {\kern 1pt} {\kern 1pt} \varepsilon \left( {{w_m}} \right) \geqslant \varepsilon \left( {{u_m}} \right) \\ \end{gathered} \right. $ |
(7) 选择最优值,选择最小值作为当前迭代的最优值。
| $ \varepsilon = \min (\varepsilon (u_1^g) , \cdots ,\varepsilon (u_{{\text{NP}}}^g) ) $ |
(8) 判断是否达到最大迭代次数,若达到,则输出最优值,差分演化算法结束;若没达到最大迭代次数,则返回步骤(3) 继续进行迭代计算,直至迭代结束。
4 仿真计算为验证本文提出的采用B样条曲线拟合成形砂轮轮廓方法的可行性和准确性,在指定拟合误差为ε=0.001 mm的条件下,通过编程仿真对计算出的砂轮轮廓进行B样条曲线拟合,本文中B样条曲线的次数设为3。仿真计算的斜齿轮参数如表1所示。
| 表 1 斜齿轮参数 Table 1 Helical gear parameters |
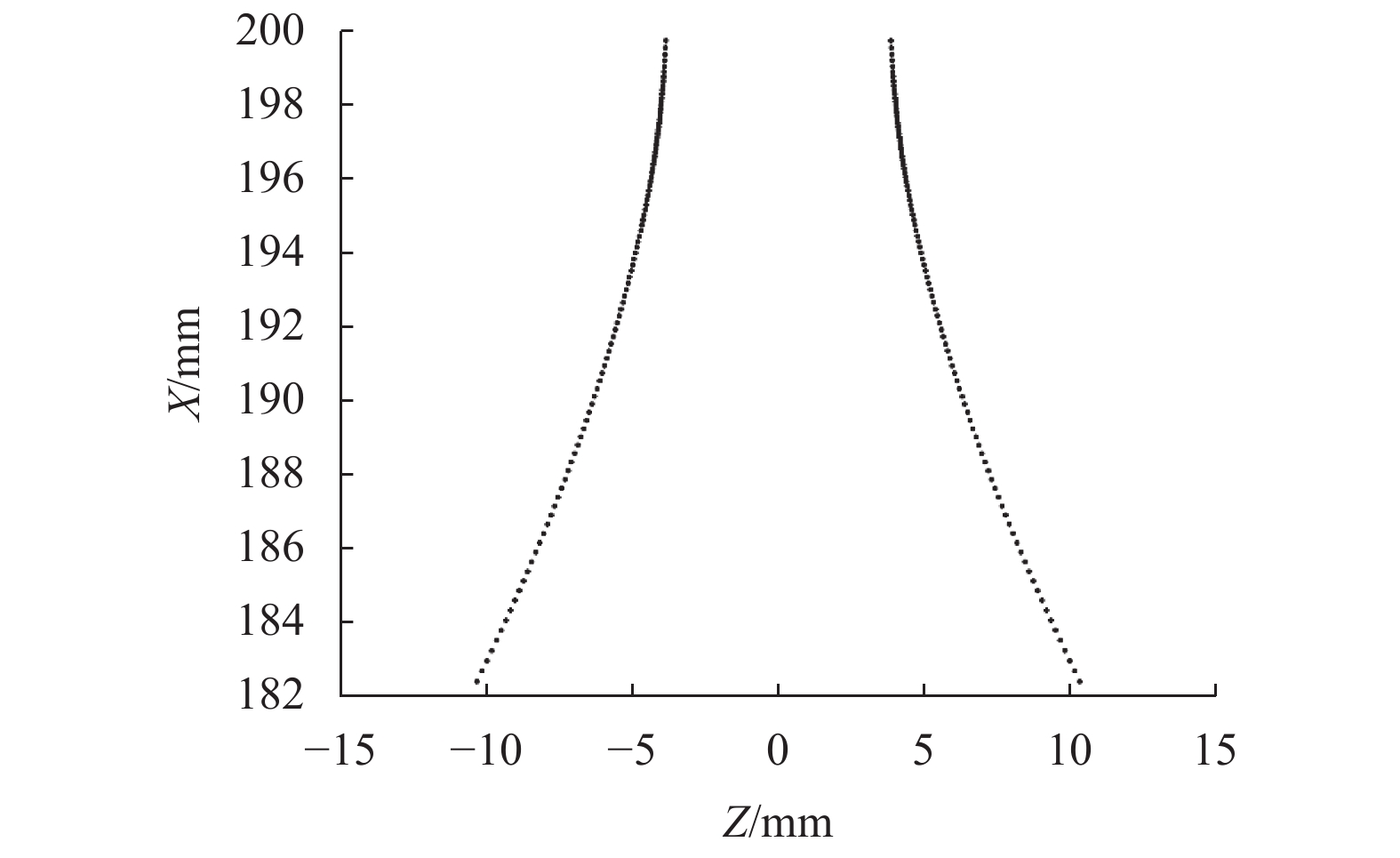
根据渐开线斜齿轮成形砂轮轮廓计算式(6) 和式(19) 以及坐标变换式(1) 和式(20) ,在Matlab软件中编程计算出成形砂轮轮廓,其计算结果为一系列离散数据点,如图9所示,其中单侧共有100个离散数据点。
|
图 9 成形砂轮轮廓 Figure 9 Profile of the formed grinding wheel |
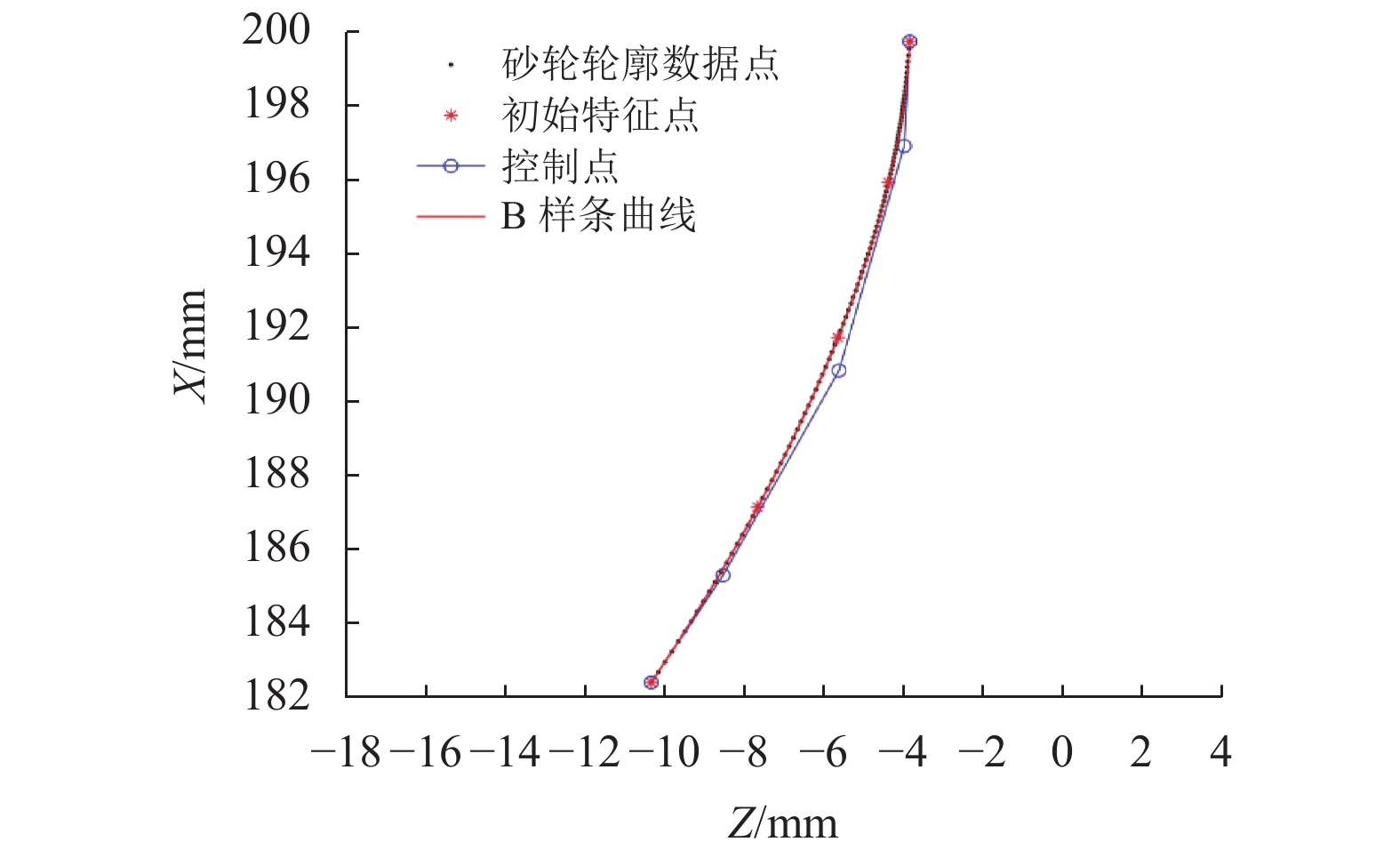
本文以砂轮单侧轮廓为例,由最少的特征点个数开始拟合,根据特征点选择方法,选取砂轮轮廓中3个最大弓高误差点以及轮廓曲线的起始点和终点,总共5个点作为初始特征点进行B样条曲线拟合,其拟合结果如图10所示。
|
图 10 初始拟合的 B样条曲线 Figure 10 The initial fitted B-spline curve |
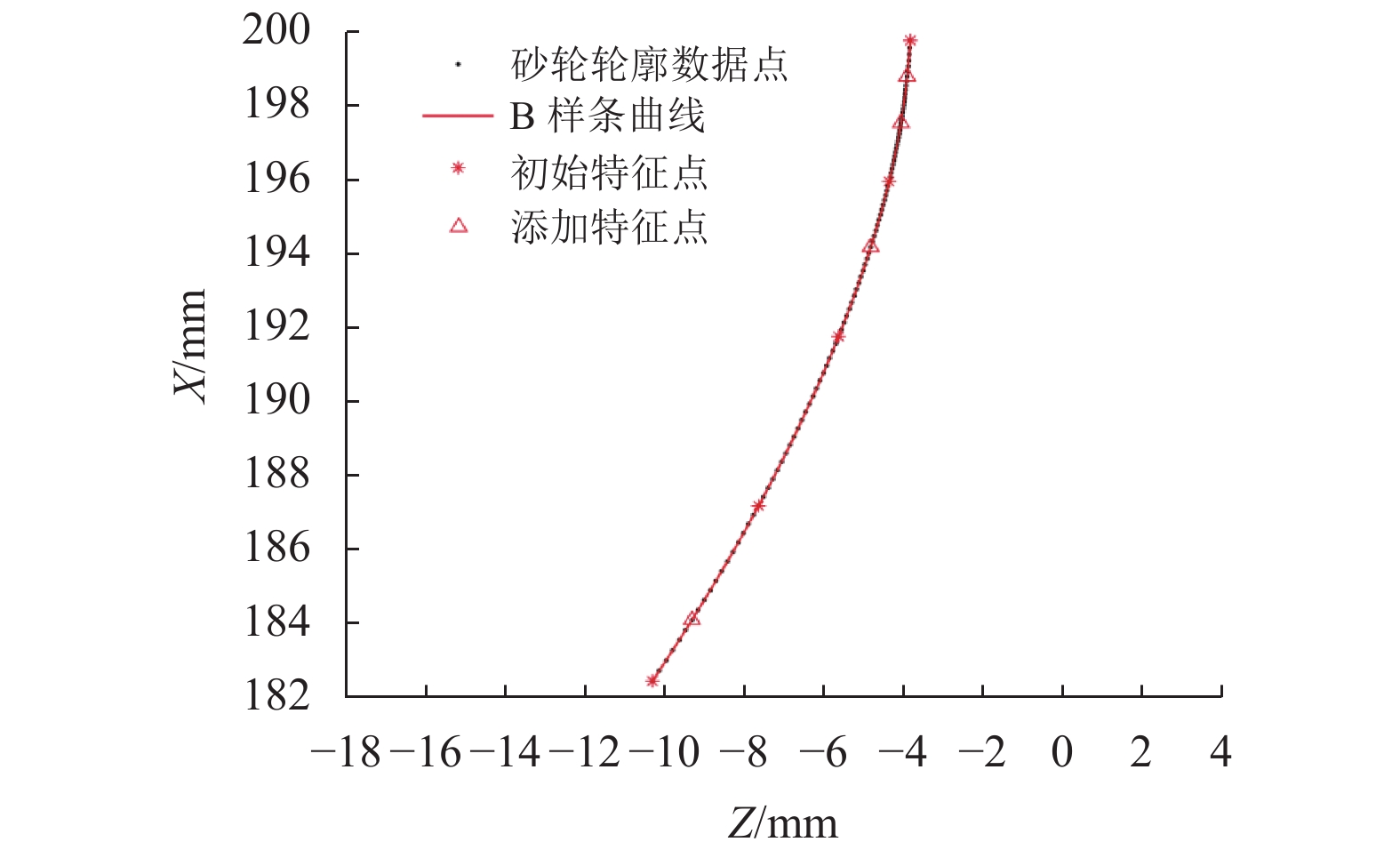
利用差分演化算法计算初始拟合的B样条曲线的拟合误差,最大误差εmax为 0.011 mm,不满足指定拟合误差ε为0.001 mm的要求。添加最大误差处的原始数据点作为特征点继续进行迭代拟合计算,最终经过5次迭代后得到满足指定拟合误差要求的B样条曲线,如图11所示。经计算得到最大拟合误差εmax,5为3.390×10−4 mm,满足指定拟合误差要求。
|
图 11 最终拟合的B样条曲线 Figure 11 The final fitted B-spline curve |
本文首先建立了斜齿轮成形磨削中砂轮轮廓的数学计算模型,获得成形磨齿砂轮的轮廓形状,然后提出了一种采用B样条曲线对砂轮轮廓进行拟合的方法,在拟合过程中利用差分演化算法计算拟合误差,保证了B样条曲线拟合成形磨齿砂轮轮廓能够满足指定精度要求。
为了验证提出的用B样条曲线在满足指定误差要求下用较少的控制点拟合成形砂轮轮廓方法的正确性,选取了具体参数的斜齿轮进行了仿真实验。仿真实验证明 ,在计算得到的成形砂轮100个原始数据点中,最终通过9个控制点即可实现对成形砂轮轮廓的B样条拟合,极大地降低了数据量,满足了用较少控制点拟合砂轮轮廓的目的,并且拟合误差为3.390×10−4 mm,具有较高的拟合精度。
| [1] |
唐平. 普及型成形磨齿机砂轮修整技术研究与应用[D]. 重庆: 重庆大学, 2015.
|
| [2] |
张四弟, 左键民, 张兆祥, 等. 成形砂轮高精度修整技术研究[J].
机床与液压, 2011, 39(17): 39-41.
ZHANG S D, ZUO J M, ZHANG Z X, et al. Research on the high-accuracy dressing technology of form grinding wheel[J]. Machine Tool & Hydraulics, 2011, 39(17): 39-41. DOI: 10.3969/j.issn.1001-3881.2011.17.012. |
| [3] |
李先冲. 普及型数控成形磨齿机关键技术开发及应用[D]. 重庆: 重庆大学, 2015.
|
| [4] |
YI J, JIN T, DEENG Z. The temperature field study on the three-dimensional surface moving heat source model in involute gear form grinding[J].
International Journal of Advanced Manufacturing Technology, 2019, 103(2): 3097-3108.
|
| [5] |
任小中, 李昊凯, 苏建新, 等. 修形内斜齿轮成形磨削砂轮廓形优化研究[J].
机械设计与制造, 2021(8): 149-151.
REN X Z, LI H K, SU J X, et al. Profile optimization of grinding wheel for form-grinding modified inner helical gear[J]. Machinery Design & Manufacture, 2021(8): 149-151. DOI: 10.3969/j.issn.1001-3997.2021.08.035. |
| [6] |
DENG H, XU Z. Dressing methods of superabrasive grinding wheels: a review[J].
Journal of Manufacturing Processes, 2019, 45: 46-69.
DOI: 10.1016/j.jmapro.2019.06.020. |
| [7] |
任小中, 丁军鹏, 谢丰坤. 渐开线廓形砂轮数控修整实验系统的开发[J].
实验室科学, 2011, 14(6): 107-109.
REN X Z, DING J P, XIE F K. Development of experimental system for CNC dressing involute grinding wheel[J]. Laboratory Science, 2011, 14(6): 107-109. DOI: 10.3969/j.issn.1672-4305.2011.06.033. |
| [8] |
刘贵祥. 基于NUM Flexium的摆线轮成形磨削CAM系统开发[D]. 西安: 西安工业大学, 2018.
|
| [9] |
韩江, 江本赤, 夏链, 等. 基于轮廓关键点的B样条曲线拟合算法[J].
应用数学和力学, 2015, 36(4): 423-431.
HAN J, JIANG B C, XIA L, et al. A B-spline curve fitting algorithm based on contour key points[J]. Applied Mathematics and Mechanics, 2015, 36(4): 423-431. DOI: 10.3879/j.issn.1000-0887.2015.04.010. |
| [10] |
PARK H, LEE J H. B-spline curve fitting based on adaptive curve refinement using dominant points[J].
Computer-aided Design, 2007, 39(6): 439-451.
DOI: 10.1016/j.cad.2006.12.006. |
| [11] |
陶浩, 何改云, 王太勇, 等. 一种基于插值拟合的复杂刀具轨迹在线平滑压缩算法[J].
中国机械工程, 2018, 29(13): 1524-1530.
TAO H, HE G Y, WANG T Y, et al. An online complex tool path smooth compression algorithm based on interpolation curve fitting method[J]. China Mechanical Engineering, 2018, 29(13): 1524-1530. |
| [12] |
张展. 渐开线圆柱齿轮传动[M]. 北京: 机械工业出版社, 2011: 103.
|
| [13] |
何文涛. 成形磨齿机运动轨迹规划及控制系统设计[D]. 重庆: 重庆大学, 2015.
|
| [14] |
吴序堂. 齿轮啮合原理[M]. 2版. 西安: 西安交通大学出版社, 2009: 98-99.
|
| [15] |
LES P, WAYNE T. 非均匀有理B样条[M]. 赵罡, 穆国旺, 王拉柱, 译. 2版. 北京: 清华大学出版社, 2010: 256-257.
|
| [16] |
李钱宽. 连续微小线段NURBS曲线拟合及插补算法研究[D]. 镇江: 江苏科技大学, 2020.
|
 2023, Vol. 40
2023, Vol. 40

