经济市场中，投资者的效用水平不仅受个人财富的影响，还受到对手财富或者社会平均财富的影响，前者称为绝对财富关注，后者称为相对财富关注。相对财富关注偏好的研究源于经济学中的攀比效应，这种攀比现象在机构投资者中更为明显。决策者在选择金融机构时通常会参考行业排名报告，金融机构需要相对业绩优势来凸显竞争力。在经济学领域，我们习惯用博弈描述上述竞争关系。另一方面，机构投资者由于资金量大等特点，风险控制尤为重要。显然，在相对财富的关注下研究投资与风险控制问题具有重要意义。

针对投资组合选择问题，很多学者利用不同方法在不同视角下展开了研究。Markowitz^[1]最早使用均值和方差度量投资的收益和风险，研究了离散时间的投资组合选择问题，开创了现代投资组合选择问题研究的先河，为一般风险资产的收益−风险分析提供了一种可行的量化思路。此后，大量学者在这基础上展开研究。Sharpe^[2]在Markowitz^[1]提出了均值−方差模型的基础上研究了资本资产定价问题。Collin等^[3]假设资产的预期收益、波动率和交易成本服从状态转移模型，在连续时间模型下研究了投资组合选择问题。

上述研究是在均值−方差准则下做出的，在投资组合选择问题中，期望效用最大化是另一个常用的准则。Merton^[4]在连续时间框架下研究了投资与消费问题，以终端时刻期望效用的最大化为目标，系统探讨了投资与消费问题，学术界称之为经典的Merton问题。Liu^[5]在CARA(Constant Absolute Risk Aversion)效用函数下，考虑风险资产交易成本，研究了最优跨期消费和投资策略问题。Campbell和Sigalov^[6]在效用函数最大化准则下，考虑可持续支出约束，对无限寿命投资者的最优投资消费问题进行研究，发现无风险利率降低时，投资者会增加风险资产投资；可持续支出约束会影响风险偏好对风险溢价变化的反应。Baltas等^[7]在考虑模型不确定的条件下研究了机构投资者的鲁棒投资组合选择问题，基于零和博弈思想求得了最优投资策略与风险控制策略的解析表达。

上述研究都是针对单个投资者而言的，没有考虑投资者之间的竞争关系和攀比现象。学者们把投资者之间的竞争关系具体为博弈关系，在博弈框架下对投资组合选择问题展开研究。Espinosa和Touzi^[8]最早在连续时间下对相对财富关注的投资组合决策问题进行了分析，使用投资者自身财富与竞争对手财富的差值来衡量相对财富，采用非零和随机微分博弈理论解决了多个相互作用的投资管理者最优投资组合决策问题，证明了CARA效用函数下Nash均衡解的存在性，为策略互动情形下的投资组合决策研究建立了系统的理论框架。Basak和Makarov^[9]采用投资者自身财富与竞争对手财富的比值来刻画相对业绩，建立了连续时间框架下的两人非零和随机微分投资博弈模型，运用动态规划原理求得了博弈的Nash均衡策略。Kraft等^[10]则在非完备市场模型下构建了包含两个投资管理者的非零和随机微分投资博弈模型，他们采用扩展的Heston模型描述非完备市场，运用动态规划原理求得了CRRA(Constant Relative Risk Aversion)效用函数下博弈Nash均衡策略的解析表达。更多的关于非零和投资组合博弈的研究，可参见文献[11-13]及其所引文献。

上述研究都是基于两人博弈展开的，但是在实际市场中，远不止两个投资者。平均场博弈理论主要研究大量同质化个体之间的策略互动问题，该理论为研究大量机构投资者之间竞争性投资策略选择问题提供了有益的思路。在多人最优投资与风险控制平均场博弈问题中，一个投资者的行为并不直接影响另一个投资者，但大量投资者的行为会影响市场环境，而市场环境会影响每一个投资决策者。无疑，上述竞争环境更符合真实市场。近年来，部分学者在多人博弈和平均场博弈模型框架下研究了投资组合选择问题。Lacker和Zariphopoulou^[14]在考虑策略互动情形下，构建了包含n个投资者的非零和投资博弈模型，分别在CARA效用和CRRA效用下利用随机微分博弈理论和平均场博弈理论求得了博弈的Nash均衡策略。Lacker和Soret^[15]在Lacker和Zariphopoulou^[14]的基础上，增加考虑了消费行为，构建了包含n个投资者的非零和投资与消费博弈模型，在CARA效用函数下利用随机微分博弈理论和平均场博弈理论求得了博弈的Nash均衡策略。Guan和Xu^[16]、Yang等^[17]在均值−方差准则下利用随机微分博弈理论和平均场博弈理论研究了n家保险公司的非零和投资与再保险博弈问题，得到了博弈Nash均衡策略的解析表达。

受上述研究的启发，本文在期望效用最大化准则下研究投资与风险控制问题。使用机构投资者财富与行业平均财富之差来刻画相对财富，运用风险转移方法进行风险控制，建立 $ n $ 个机构投资者的非零和投资与风险控制博弈模型。在CARA效用函数下，利用随机微分博弈理论和平均场博弈理论求得了博弈的Nash均衡策略，并进行参数的敏感性分析。

需要指出的是，本文所使用的模型是对文献[14]中的模型进行拓展得到的。文献[14]在期望效用最大化准则下，基于相对财富关注效应构建了多人投资组合选择博弈模型和平均场博弈模型。但文中财富过程只考虑了投资组合的收益，没有考虑公司经营业务所造成的现金流动，与金融机构的真实情况存在偏差。针对上述问题，本文把金融机构支出现金流纳入财富过程，基于业务经营与投资收益的双重考虑，寻找最优的投资策略；进一步地，增加风险转移手段，对经营业务中的支出风险进行控制，更符合金融机构的风险管理要求。本文综合考虑投资与风险控制，构建多人非零和博弈模型及平均场博弈模型。此外，本文所使用模型与文献[15-17]也有相近之处，但均不相同，具体体现在：第一，文献[15]在文献[14]的基础上增加考虑了消费问题，即在模型中把消费纳入财富过程，且增加考虑消费效用，主要研究投资与消费问题；本文在文献[14]的基础上增加考虑金融机构经营业务中的支出风险，把支出现金流纳入财富过程，通过风险转移手段控制风险，主要研究投资与风险控制问题。第二，文献[16]和[17]基于均值−方差准则构建投资与再保险多人博弈模型与平均场博弈模型，寻找Nash均衡投资再保险策略；本文基于期望效用最大化准则构建投资与风险控制多人博弈模型与平均场博弈模型，二者互补共同构成了投资组合选择问题中最常用的两个重要准则。

本文的主要贡献概括起来包括：(1) 在考虑市场竞争的情形下，基于非零和博弈理论构建了多人最优投资与风险控制博弈模型和平均场博弈模型；(2) 在期望效用最大化准则下，以CARA效用函数为例，运用随机控制理论得到了Nash均衡状态下最优投资与风险控制策略的解析表达。

1 模型假设

考虑一个完备的赋流概率空间 $(\varOmega ,F,P,\left\{{F}_{t}\right\}{\text{}}_{t\in [0,T]})$ ，其中 $ P $ 为一个参考概率测度，域流 $ \text{}{\left\{{F}_{t}\right\}}_{t\in [0,T]} $ 满足通常条件，即 $ {\left\{ {{F_t}} \right\}_{t \geqslant 0}} $ 右连续且 $P$ −完备， ${F_t} = \sigma ( {W\left( s \right) ,{B_l}\left( s \right) ,} {{B_i}\left( s \right) ,B\left( s \right) , s \leqslant t,i = 1, \cdots ,n} )$ 是包含4个相互独立的一维布朗运动 $ \left\{ {W\left( t \right) ,t \geqslant 0} \right\} $ ， $ {\left\{ {{B_i}\left( t \right) ,t \geqslant 0} \right\}_{i = 1,2, \cdots ,n}} $ ， $ \left\{ {{B_l}\left( t \right) ,t \geqslant 0} \right\} $ 和 $ \left\{ {B\left( t \right) ,t \geqslant 0} \right\} $ 的自然滤波， $\varOmega$ 为样本空间。假设金融市场中所有交易可连续进行且容许卖空，不考虑交易费用和税收。

考虑市场上有 $ n $ 个金融机构，互为竞争关系。金融机构在开展业务(例如：基金管理、企业年金管理、资产管理等)的过程中，产生一系列的支出现金流(例如：各种长期或短期的支付、业务相关运营成本、所得税等)。假设金融机构 $ i $ ， $ i = 1, \cdots ,n $ 在日常业务中的支出现金流动态 $ \left\{ {{L_i}(t) } \right\} $ 服从如式(1)微分方程。

$ {\text{d}}{L_i}(t) = {a_i}{\text{d}}t + {b_i}{\text{d}}{B_i}(t) + {c_i}{\text{d}}{B_l}(t) $

(1)

式中：系数 $ {a_i} > 0 $ ，系数 $ {b_i} \geqslant 0 $ ，系数 $ {c_i} \geqslant 0 $ ，且 $ {b_i} + {c_i} > 0 $ 。且支出现金流动态包含一个漂移项和两个波动项，第一个波动项用各不相同的一维布朗运动 $ {B_i}(t) ,i = 1, \cdots , n $ 描述，表示每个金融机构独立的支出波动；第二个波动项用一个共同的一维布朗运动 $ {B_l}(t) $ 描述，表示不同的金融机构受到同一个经济环境和共同的业务影响带来的支出波动， $ {c_i} $ 越大，表示金融机构对市场的依赖程度越大。

支出现金流的随机过程为金融机构带来了一定的风险敞口，风险控制势在必行。风险转移(例如购买保险)是金融机构管理风险的重要手段之一。本文假定金融机构借助风险转移方式进行风险控制，把每一笔经营业务产生的风险都按照一定的比例转移给第三方机构(如外部投资者、保险公司或其他金融机构)，自身承担剩余比例的风险。假设金融机构 $ i $ 把 $ {q_i}\left( t \right) ,{q_i}\left( t \right) \in [0,1] $ 比例的风险转移给第三方机构，风险自留比例为 $ \left( {1 - {q_i}\left( t \right) } \right) $ 。当该笔业务面临支出时，金融机构需要承担亏损额的 $ \left( {1 - {q_i}\left( t \right) } \right) \times 100\% $ ，接受风险的第三方机构承担支出额的 $ {q_i}\left( t \right) \times 100\% $ 。金融机构 $ i $ 的盈余过程 $ \left\{ {{H_i}(t) } \right\} $ 可以描述成

$ \begin{aligned} {\text{d}}{H_i}(t) = & \left\{ {{p_i}{\rm{E}}[{L_i}(t) ] - {\lambda _i}{q_i}(t) {\rm{E}}[{L_i}(t) ]} \right\}{\text{d}}t - [1 - {q_i}(t) ]{\text{d}}{L_i}(t) = \\ & {a_i}[{q_i}(t) (1 - {\lambda _i}) - (1 - {p_i}) ]{\text{d}}t - {b_i}[1 - {q_i}(t) ]{\text{d}}{B_i}(t) - \\ &{c_i}[1 - {q_i}(t) ]{\text{d}}{B_l}(t) \\[-10pt] \end{aligned} $

(2)

式中： $ {p_i} > 0 $ 表示金融机构提供金融服务收取的管理费率， $ {\lambda _i} > 0 $ 表示承担风险的第三方机构收取的费率， $ {\lambda _i} > {p_i} $ ； ${\rm{E}}[ \cdot ] $ 表示数学期望。假设金融机构可以把财富投资于由一种无风险债券和一种股票构成的金融市场中，无风险债券价格动态 $ \left\{ {{S_0}(t) } \right\} $ 和风险股票的价格动态 $ \left\{ {{S_1}(t) } \right\} $ 由式(3)描述：

$ \left\{ \begin{gathered} {\text{d}}{S_0}(t) = r{S_0}(t) {\text{d}}t,{\text{ }}{S_0}(0) = {s_0} \\ {\text{d}}{S_1}(t) = \mu {S_1}(t) {\text{d}}t + \sigma {S_1}(t) {\text{d}}W(t) {\text{, }}{S_1}(0) = {s_1} \\ \end{gathered} \right. $

(3)

式中： $ r \geqslant 0 $ ，为无风险利率； $ \mu > r $ ，为股票的预期收益率； $ \sigma \geqslant 0 $ ，为股票收益的波动率。

将金融机构 $ i $ 在 $t$ 时刻的财富记为 $ {X_i}\left( t \right) $ ，用 $ {\pi _i}\left( t \right) $ 表示金融机构 $ i $ 在 $t$ 时刻投资于股票的金额，余下的财富 $ \left( {{X_i}\left( t \right) - {\pi _i}\left( t \right) } \right) $ 投资于无风险债券。将金融机构 $ i $ 在 $t$ 时刻的交易策略记为 $ {\eta _i}: = \left( {{\pi _i}(t) ,{q_i}(t) } \right) $ ， $ {\pi _i}\left( t \right) \in R $ 为投资策略； $ {q_i}\left( t \right) \in R $ 为风险控制策略。金融机构 $ i $ 的财富过程可以表示为

$ \begin{aligned} {\text{d}}{X_i}(t) = & \left\{ {{\pi _i}(t) \left(\mu - r\right) + r{X_i}(t) + {a_i}\left[{q_i}(t) (1 - {\lambda _i}) - (1 - {p_i}) \right]} \right\}{\text{d}}t + \\ & \sigma {\pi _i}(t) {\text{d}}W(t) - {b_i}[1 - {q_i}(t) ]{\text{d}}{B_i}(t) - \\ &{c_i}[1 - {q_i}(t) ]{\text{d}}{B_l}(t) \\[-10pt] \end{aligned} $

(4)

式中： $ {X_i}\left( 0 \right) = {\xi _i} $ 表示金融机构 $ i $ 的初始财富。

定义1(可行策略)　对于金融机构 $ i $ ，策略 $ {\eta _i} = \left( {{\pi _i}(t) ,{q_i}(t) } \right) $ 称为可行策略，如果

(i) $ {\eta _i} = \left( {{\pi _i}(t) ,{q_i}(t) } \right) $ 是 $ {F_t} - $ 循序可测过程，满足 ${\rm{E}}\left[ {\int_0^T {\left\| {\pi _i^2(t) } \right\|} + \left\| {q_i^2(t) } \right\|{\text{d}}t} \right] < \infty$ ；(ii) 对 $ \forall {x_i} \in R $ ，随机微分方程(4) 存在唯一的强解 $ {X_i}(t) $ ，满足 ${\rm{E}}\left[ {\mathop {\sup }\limits_{0 \leqslant t \leqslant T} \left\| {{X_i}(t) } \right\|} \right] < \infty$ 。将金融机构 $ i $ 所有可行策略构成的集合记为 $ {\varPi _i},i = 1, \cdots ,n $ 。

假定金融机构的目标为预期效用最大化，金融机构的效用取决于终端时刻自身的财富值，以及其财富与行业平均财富的差值。使用指数效用(CARA Utility) 来描述金融机构 $ i $ 的风险偏好。

$ {U_i}(x) = - \exp \left( - \frac{1}{{{\delta _i}}}x\right) ,{\text{ }}{\delta _i} > 0 $

(5)

式中： $ {\delta _i} > 0 $ ，表示对风险的容忍程度。 $ {\delta _i} $ 越大，表示金融机构 $ i $ 越偏好风险；反之亦然。

2 多人博弈

假设金融市场中机构投资者的数量 $ n $ 有限，每个金融机构在市场竞争中都希望自身财富高于同行所有竞争者的财富，但这一希望难以实现，退而求其次，每个金融机构旨在追求自身财富高于行业平均财富。金融机构 $ i $ 通过选择最优策略 $ {\eta _i}(t) : = \left( {{\pi _i}(t) ,{q_i}(t) } \right) \in {\varPi _i} $ ，最大化预期效用。其优化目标可描述为：

$ \begin{split} &\mathop {\sup }\limits_{{\eta _i} \in {\varPi _i}} {J_i}\left( {{\eta _1}, \cdots ,{\eta _{i - 1}},{\eta _i},{\eta _{i + 1}}, \cdots ,{\eta _n}} \right) =\\ &\qquad {J_i}\left( {{\eta _1}, \cdots ,{\eta _{i - 1}},{\eta _i}^*,{\eta _{i + 1}}, \cdots ,{\eta _n}} \right) \end{split}$

(6)

式中，支付函数为

$ \begin{aligned}{J_i}\left( {{\eta _1}, \cdots ,{\eta _n}} \right) : =& {\rm{E}}\left\{ {{U_i}\left[ {\left( {1 - {\theta _i}} \right) {X_i}\left( T \right) + {\theta _i}\left( {{X_i}\left( T \right) - \overline X \left( T \right) } \right) } \right]} \right\} = \\ &{\rm{E}}\left\{ { - \exp \left[ { - \frac{1}{{{\delta _i}}}\left( {{X_i}\left( T \right) - {\theta _i}\overline X \left( T \right) } \right) } \right]} \right\} \end{aligned}$

$i = 1,2, \cdots , n$ ， $ {X_i}\left( T \right) $ 表示金融机构 $ i $ 的终端财富值， $\overline X \left( T \right) = \dfrac{1}{n}\displaystyle\sum\nolimits_{k = 1}^n {{X_k}\left( T \right) }$ 表示市场中所有金融机构在终端时刻的平均财富， $ \left( {{X_i}\left( T \right) - \overline X \left( T \right) } \right) $ 表示金融机构 $ i $ 与行业平均财富的差值，描述相对财富。 $ {\theta _i} \in [0,1] $ 表示金融机构 $ i $ 对相对财富的关注程度，也可以反映市场竞争的激烈程度， $ {\theta _i} $ 越大，表示金融机构 $ i $ 越关注相对财富，市场竞争越激烈；反之亦然。特别地，当 $ {\theta _i} = 0 $ 时，问题退化为单个投资者的最优投资与风险控制问题。

定义2 (Nash均衡)　对于所有 ${\eta _i}(t) = \left( {{\pi _i}(t) , {q_i}(t) } \right) \in {\varPi _i},i = 1, \cdots ,n$ ，如果策略组合 $ \left( {{\eta _1}^*, \cdots ,{\eta _n}^*} \right) $ 满足

$ {J_i}\left( {{\eta _1}^*, \cdots ,{\eta _i}^*, \cdots ,{\eta _n}^*} \right) \geqslant {J_i}\left( {{\eta _1}^*, \cdots ,{\eta _{i - 1}}^*,{\eta _i},{\eta _{i + 1}}^*, \cdots ,{\eta _n}^*} \right) $

(7)

则称 $ \left( {{\eta _1}^*, \cdots ,{\eta _n}^*} \right) $ 为Nash均衡。一个恒定的Nash均衡策略是指，对于每一个金融机构 $ i $ ，在博弈的持续期 $[0,T]$ 内，其最优策略 $ {\eta _i}^* $ 都不随时间 $t$ 而变动，即 $ {\eta _i}^*\left( t \right) = {\eta _i}^*\left( 0 \right) ,\forall t \in \left[ {0,T} \right] $ 。

下述定理给出了本节内容的主要结论。

定理1 　假定对于所有的 $ i = 1, \cdots ,n $ ，在 $ {\delta _i} > 0 $ ， $ {\theta _i} \in [0,1] $ ， $ \mu > 0 $ ， $ \sigma > 0 $ ， $ {b_i} \geqslant 0 $ ， $ {c_i} \geqslant 0 $ ， $ {b_i} + {c_i} > 0 $ 成立的条件下，定义常数 $\overline \delta : = \dfrac{1}{n}\displaystyle\sum\nolimits_{k = 1}^n {{\delta _k}}$ ， $\overline \theta : = \dfrac{1}{n}\displaystyle\sum\nolimits_{k = 1}^n {{\theta _k}}$ ，均衡投资策略存在下述两种情况：

(i) 当 $ \overline \theta < 1 $ 时，存在唯一的Nash均衡投资策略，由式(8)给出：

$ {\pi _i}^*\left( t \right) = \frac{{\left( {\mu - r} \right) }}{{{\sigma ^2}}}\left[ {{\delta _i} + {\theta _i}\frac{{\overline \delta }}{{\left( {1 - \theta } \right) }}} \right] $

(8)

(ii) 当 $ \overline \theta = 1 $ 时，Nash均衡投资策略不存在。

定义常数 ${\varepsilon _n}: = \dfrac{1}{n}\displaystyle\sum\nolimits_{k = 1}^n {\dfrac{{{a_k}\left( {1 - {\lambda _k}} \right) {\delta _k}{c_k}}}{{{c_k}^2 + {b_k}^2\left( {1 - \dfrac{{{\theta _k}}}{n}} \right) }}}$ ， ${\phi _n}: = \dfrac{1}{n}\displaystyle\sum\nolimits_{k = 1}^n {\dfrac{{{c_k}^2{\theta _k}}}{{{c_k}^2 + {b_k}^2\left( {1 - \dfrac{{{\theta _k}}}{n}} \right) }}}$ ， $\overline c : = \dfrac{1}{n}\displaystyle\sum\nolimits_{k = 1}^n {{c_k}}$ ，风险控制策略存在下述两种情况：

(i) 当 $ {\phi _n} < 1 $ 时，存在唯一的Nash均衡风险控制策略，由式(9)给出：

$ {q_i}^*\left( t \right) = 1 + \frac{{{a_i}\left( {1 - {\lambda _i}} \right) {\delta _i}}}{{{c_i}^2 + {b_i}^2\left( {1 - \dfrac{{{\theta _i}}}{n}} \right) }} + \frac{{{c_i}{\theta _i}}}{{{c_i}^2 + {b_i}^2\left( {1 - \dfrac{{{\theta _i}}}{n}} \right) }}\dfrac{{{\varepsilon _n}}}{{\left( {1 - {\phi _n}} \right) }} $

(9)

(ii) 当 $ {\phi _n} = 1 $ 时，Nash均衡风险控制策略不存在。

证明 　考虑金融机构 $ i $ 的最优决策问题，假设其他金融机构 $ k \ne i \in \{ 1, \cdots ,n\} $ 都使用恒定投资与风险控制策略 ${\varphi _k}\left( t \right) : = \left( {{\alpha _k}\left( t \right) ,{\beta _k}\left( t \right) } \right) \in {\varPi _k} = R \times R$ ，其中 $ {\alpha _k}\left( t \right) \in R $ 表示机构 $ k $ 的投资策略， $ {\beta _k}\left( t \right) \in R $ 表示机构 $k$ 的风险控制策略。定义变量 $Y\left( t \right) : = \dfrac{1}{n}\displaystyle\sum\limits_{k \ne i} {{X_k}\left( t \right) }$ ，则有

$ \begin{aligned} {\text{d}}Y(t) =& \left[ {\widehat \alpha (\mu - r) + rY(t) + \widehat {a\beta } - \widehat {a\beta \lambda } - \widehat a + \widehat {ap}} \right]{\text{d}}t + \\ &\sigma {\widehat \alpha \text{d}}W\left( t \right) {\text{ }} - \left( {\widehat c - \widehat {c\beta }} \right) {\text{d}}{B_l}\left( t \right) - \frac{1}{n}\sum\limits_{k \ne i} {{b_k}\left( {1 - {\beta _k}} \right) } {\text{d}}{B_k}(t) \\ \end{aligned} $

(10)

式中： $Y(0) = \dfrac{1}{n}\displaystyle\sum\limits_{k \ne i} {{X_k}} (0)$ ， $\widehat {a\beta }: = \dfrac{1}{n}\displaystyle\sum\limits_{k \ne i} {{a_k}} {\beta _k}$ ， $\widehat {a\beta \lambda }: = \dfrac{1}{n} \displaystyle\sum\limits_{k \ne i} {{a_k}} {\beta _k}{\lambda _k}$ ， $\widehat a: = \dfrac{1}{n}\displaystyle\sum\limits_{k \ne i} {{a_k}}$ ， $\widehat {ap}: = \dfrac{1}{n}\displaystyle\sum\limits_{k \ne i} {{a_k}} {p_k}$ ， $\widehat c: = \dfrac{1}{n}\displaystyle\sum\limits_{k \ne i} {{c_k}}$ ， $\widehat {c\beta }: = \dfrac{1}{n}\displaystyle\sum\limits_{k \ne i} {{c_k}} {\beta _k}$ ， $\widehat {{b^2}{{\left( {1 - \beta } \right) }^2}}: = \dfrac{1}{n}{\displaystyle\sum\limits_{k \ne i} {\left[ {{b_k}\left( {1 - {\beta _k}} \right) } \right]} ^2}$ ， $\widehat \alpha : = \dfrac{1}{n} \displaystyle\sum\limits_{k \ne i} {{\alpha _k}}$ 。

机构 $ i $ 的优化目标可转化为

$ \mathop {\sup }\limits_{{\eta _i} \in {\varPi _i}} {\rm{E}}\left\{ { - \exp \left( { - \frac{1}{{{\delta _i}}}} \right) \left[ {\left( {1 - \frac{{{\theta _i}}}{n}} \right) {X_i}\left( T \right) - {\theta _i}Y\left( T \right) } \right]} \right\},{\text{ }}i = 1, \cdots ,n $

(11)

金融机构 $ i $ 的值函数可表示为

$ \begin{aligned}&V\left( {t,x,y} \right) = \\ &\mathop {\sup }\limits_{{\eta _i} \in {\varPi _i}} {\rm{E}}\left\{ {{U_i}\left[ {\left( {1 - \frac{{{\theta _i}}}{n}} \right) {X_i}\left( T \right) - {\theta _i}Y\left( T \right) } \right]\left| {{X_i}\left( t \right) = x,Y\left( t \right) } \right. = y} \right\} \end{aligned}$

由动态规划原理可知，值函数 $ V\left( {t,x,y} \right) $ 满足HJB方程，如式(12)所示。

$ \begin{split} 0 = &{V_t} + {V_x}\left\{ {{\pi _i}\left( {\mu - r} \right) + rx + {a_i}\left[ {{q_i}\left( {1 - {\lambda _i}} \right) - \left( {1 - {p_i}} \right) } \right]} \right\}+ \\ &{V_y}\left[ {\left( {\mu - r} \right) \widehat \alpha + ry + \widehat {a\beta } - \widehat {a\beta \lambda } - \widehat a + \widehat {ap}} \right] + \\ &\frac{1}{2}{V_{xx}}\left[ {{\sigma ^2}{\pi _i}^2 + {b_i}^2{{\left( {1 - {q_i}} \right) }^2} + {c_i}^2{{\left( {1 - {q_i}} \right) }^2}} \right] + \\ &\frac{1}{2}{V_{yy}}\left[ {{\sigma ^2}{{\widehat \alpha }^2} + \frac{1}{n}\widehat {{b^2}{{\left( {1 - \beta } \right) }^2}} + {{\left( {\widehat c - \widehat {c\beta }} \right) }^2}} \right] + \\ &{V_{xy}}\left[ {{\sigma ^2}{\pi _i}\widehat \alpha + {c_i}\left( {1 - {q_i}} \right) \left( {\widehat c - \widehat {c\beta }} \right) } \right] \\[-10pt] \end{split} $

(12)

为了求解式(12) ，假设值函数形式为

$ V\left( {t,x,y} \right) = - f\left( t \right)\exp \left\{ { - \dfrac{1}{{{\delta _i}}}\left[ {\left( {1 - \dfrac{{{\theta _i}}}{n}} \right) x - {\theta _i}y} \right]} \right\}$

终端条件为 $ f\left( T \right) = 1 $ 。

式(12) 分别对 $ {\pi _i} $ 和 $ {q_i} $ 求一阶条件：

$ {\pi }_{i}{}^{*}\left(t\right) :=\frac{{\delta }_{i}\left(\mu -r\right) }{{\sigma }^{2}\left(1-\dfrac{{\theta }_{i}}{n}\right) }+\widehat{\alpha }\dfrac{{\theta }_{i}}{\left(1-\dfrac{{\theta }_{i}}{n}\right) } $

(13)

$ {q}_{i}{}^{*}\left(t\right) :=1+\frac{{a}_{i}\left(1-{\lambda }_{i}\right) {\delta }_{i}-{c}_{i}\left(\widehat{c}-\widehat{c\beta }\right) {\theta }_{i}}{\left({b}_{i}{}^{2}+{c}_{i}{}^{2}\right) \left(1-\dfrac{{\theta }_{i}}{n}\right) } $

(14)

把式(13) 和(14)代回HJB方程(12) 中，得到

$ {f_t}\left( t \right) - \rho f\left( t \right) = 0 $

式中：

$ \begin{split} \rho : = & \frac{1}{{{\delta _i}}}\left( {1 - \frac{{{\theta _i}}}{n}} \right) \left[ {rx - {a_i}\left( {1 - {p_i}} \right) } \right] - \\ &\frac{{{\theta _i}}}{{{\delta _i}}}\left[ {ry + \widehat {a\beta } - \widehat {a\beta \lambda } - \widehat a + \widehat {ap}} \right]{\text{ + }}\frac{1}{2}\frac{{{{\left( {\mu - r} \right) }^2}}}{{{\sigma ^2}}} + \\ &\frac{1}{2}\frac{{{a_i}^2{{\left( {1 - {\lambda _i}} \right) }^2}}}{{{b_i}^2 + {c_i}^2}} - \frac{1}{{2n}}\frac{{{\theta _i}^2\widehat{{{b^2}{{\left( {1 - \beta } \right) }^2}}}}}{{{\delta _i}^2}} - \\ &\frac{{{\theta _i}^2{b_i}^2{{\left( {\widehat c - \widehat {c\beta }} \right) }^2}}}{{2{\delta _i}^2\left( {{b_i}^2 + {c_i}^2} \right) }} - \frac{{{a_i}\left( {1 - {\lambda _i}} \right) {\theta _i}{c_i}\left( {\widehat c - \widehat {c\beta }} \right) }}{{{\delta _i}^2\left( {{b_i}^2 + {c_i}^2} \right) }} \end{split}$

(15)

结合终端条件 $ f\left( T \right) = 1 $ 解得 $ f\left( t \right) = {{\rm{e}}^{ - \rho \left( {T - t} \right) }} $ 。

策略组合 $ \left( {\eta _1^*, \cdots ,\eta _n^*} \right) $ 要成为Nash均衡策略，必须满足 $ {\eta _i}^* = \left( {\pi _i^ * ,q_i^ * } \right) = {\varphi _i} = \left( {{\alpha _i},{\beta _i}} \right) $ ， $ \forall i = 1, \cdots ,n $ ，即 $ {\pi _i}^*\left( t \right) = {\alpha _i}\left( t \right) $ ， $ {q_i}^*\left( t \right) = {\beta _i}\left( t \right) $ 。把 $ {\pi _i}^*\left( t \right) = {\alpha _i}\left( t \right) $ 代入式(13) ，两边在 $ i = 1, \cdots ,n $ 的基础上取均值得式(16) ；把 ${q_i}^*\left( t \right) = {\beta _i}\left( t \right)$ 代入式(14) ，两边乘上 $ {c_i} $ ，并在 $ i = 1, \cdots ,n $ 的基础上取均值得式(17) 。

$ \overline \alpha = \frac{1}{n}\sum\nolimits_{k = 1}^n {{\alpha _k}} = \frac{{\left( {\mu - r} \right) }}{{{\sigma ^2}}}\overline \delta + \overline \theta \overline \alpha $

(16)

$ \overline {c\beta } = \frac{1}{n}\sum\nolimits_{k = 1}^n {{c_k}} {\beta _k} = \overline c \left( {1 - {\phi _n}} \right) + {\varepsilon _n} + {\phi _n}\overline {c\beta } $

(17)

式中： $\overline \alpha : = \dfrac{1}{n}\displaystyle\sum\nolimits_{k = 1}^n {{\alpha _k}} = \widehat \alpha + \frac{1}{n}{\alpha _i}$ ， $\overline c : = \dfrac{1}{n}\displaystyle\sum\nolimits_{k = 1}^n {{c_k}} = \widehat c + \frac{1}{n}{c_i}$ ， $\overline {c\beta } : = \dfrac{1}{n}\displaystyle\sum\nolimits_{k = 1}^n {{c_k}} {\beta _k} = \widehat {c\beta } + \frac{1}{n}{c_i}{\beta _i}$ ， $ \overline \delta $ ， $ \overline \theta $ ， $ {\varepsilon _n} $ ， $ {\phi _n} $ 在定理1中给出。至此，均衡投资策略存在下述3种情况：

(i) 当 $ \overline \theta < 1 $ 时，由式(16) 可以得到 $\overline \alpha = \dfrac{{\left( {\mu - r} \right) \overline \delta }}{{{\sigma ^2}\left( {1 - \overline \theta } \right) }}$ ，Nash均衡投资策略由(8) 确定。

(ii) 当 $ \overline \theta = 1 $ 且 $\dfrac{{\left( {\mu - r} \right) \overline \delta }}{{{\sigma ^2}}} > 0$ 时，式(16) 无解，故不存在Nash均衡投资策略。

(iii) 当 $ \overline \theta = 1 $ 且 $\dfrac{{\left( {\mu - r} \right) \overline \delta }}{{{\sigma ^2}}} = 0$ 时，式(16) 有无穷多个解，但这种情况不可能发生。因为当 $ \forall i = 1, \cdots ,n $ ，有 $ {\delta _i} > 0 $ ， $ \mu > r $ ，故 $\dfrac{{\left( {\mu - r} \right) \overline \delta }}{{{\sigma ^2}}} > 0$ 恒成立。

均衡风险控制策略存在下述3种情况：

(i) 当 $ {\phi _n} < 1 $ 时，由式(17) 可以得到 $\overline {c\beta } = \overline c + \dfrac{{{\varepsilon _n}}}{{\left( {1 - {\phi _n}} \right) }}$ ，Nash均衡风险控制策略由式(9) 确定。

(ii) 当 $ \overline \phi = 1 $ 且 $ {\varepsilon _n} < 1 $ 时，式(17) 无解，故不存在Nash均衡风险控制策略。

(iii) 当 $ \overline \phi = 1 $ 且 $ {\varepsilon _n} = 1 $ 时，式(17) 有无穷多个解，但这种情况不可能发生。因为当 $ \forall i = 1, \cdots ,n $ ，有 ${a_i} > 0$ ， $ {\lambda _i} > 0 $ ， $ {\delta _i} > 0 $ ， $ {b_i} \geqslant 0 $ ， $ {c_i} \geqslant 0 $ ， $ {b_i} + {c_i} > 0 $ 且 $ \mu > r $ ，当 ${\phi _n} = 1$ 时，表示 $ {c_i} $ 不恒等于0，故 $ {\varepsilon _n} < 0 $ 恒成立。

定理1证毕。

3 平均场博弈

上一节，本文在 $ n $ 有限的基础上，研究了 $ n $ 个竞争性的金融机构之间的投资与风险控制博弈。在这一节，对上述模型进行拓展，研究 $ n \to \infty $ 的情形。

在 $ n \to \infty $ 的 $ n $ 人博弈中，对于每一个金融机构 $ i = 1, \cdots ,n $ ，都有类型向量

$ {{\boldsymbol{\zeta}} _i}: = \left( {{x_i}(0) ,{\delta _i},{\theta _i},{a_i},{b_i},{c_i},{\lambda _i},{p_i},\mu ,r,\sigma } \right) $

这些类型向量包含一种经验测度，称为类型分布，即类型空间上的概率测度

$ {G^e}: = R \times \left( {0,\infty } \right) \times \left[ {0,1} \right] \times {[0,\infty ) ^3} \times {[1,\infty ) ^2} \times \left( {0,\infty } \right) \times {[0,\infty ) ^2} $

(18)

式(18) 由下式给出。

$ {m_n}\left( A \right) = \frac{1}{n}\sum\nolimits_{i = 1}^n {{1_A}\left( {{{\boldsymbol{\zeta}} _i}} \right) ,{\text{ }}{\rm{for}}{\text{ }}{\rm{Borel}}{\text{ }}{\rm{sets}}} {\text{ }}A \subset {G^e} $

其中， $ {m_n} $ 代表行业中 $ n $ 家金融机构的平均财富， ${m_n} = \dfrac{1}{n}\displaystyle\sum\nolimits_{i = 1}^n {{\delta _{{{\boldsymbol{\zeta}} _i}}}}$ 。可以看到，对于每一个金融机构 $ i $ ，其由定理1所计算出来的 $ {\eta _i}^* $ 只决定于其自身的类型向量 $ {{\boldsymbol{\zeta }}_i} $ 和所有类型向量的分布 $ {m_n} $ 。实际上，在 $ {m_n} $ 下积分相应函数便可容易得到式(9) 中的 $ \overline \delta $ ， $ \overline \theta $ ， $ {\varepsilon _n} $ 和 $ {\phi _n} $ 。

现在假设金融机构的数量增加， $ n \to \infty $ ，上述经验测度 $ {m_n} $ 在弱收敛下的极限为 $ m $ ，即对于所有定义在 $ {G^e} $ 上的有界连续函数 $ f $ 都有 $\displaystyle\int_{{G^e}} f {\rm{d}}{m_n} \to \displaystyle\int_{{G^e}} f {\rm{d}}m$ 。 $ n \to \infty $ 时，用概率测度 $ m $ 代替经验测度 $ {m_n} $ 。 ${\boldsymbol{\zeta }}= ( {\xi ,\delta ,\theta ,a,} {b,c,\lambda ,p,\mu ,r,\sigma } )$ 表示一个在 $ {G^e} $ 测度空间上测度为 $ m $ 的随机变量。概率空间记为 $ \left( {{G^e},{F_G},m} \right) $ 。根据定理1可得，最优投资策略和风险控制策略可表示为

$ \mathop {\lim }\limits_{n \to \infty } {\pi _i}^*\left( t \right) = \frac{{\left( {\mu - r} \right) }}{{{\sigma ^2}}}\left[ {{\delta _i} + {\theta _i}\frac{{\overline \delta }}{{\left( {1 - \bar \theta } \right) }}} \right] $

(19)

$ \mathop {\lim }\limits_{n \to \infty } {q_i}^*\left( t \right) = 1 + \frac{{{a_i}\left( {1 - {\lambda _i}} \right) {\delta _i}}}{{{c_i}^2 + {b_i}^2}} + \frac{{{c_i}{\theta _i}}}{{{c_i}^2 + {b_i}^2}}\frac{\varepsilon }{{\left( {1 - \phi } \right) }} $

(20)

其中常数 $\overline \delta : = {\rm{E}}\left[ \delta \right]$ ， $\overline \theta : = {\rm{E}}\left[ \theta \right]$ ， $\varepsilon : = \mathop {\lim }\limits_{n \to \infty } {\varepsilon _n} = {\rm{E}}\left[ {\dfrac{{a\left( {1 - \lambda } \right) \delta c}}{{{c^2} + {b^2}}}} \right]$ ， $\phi : = \mathop {\lim }\limits_{n \to \infty } {\phi _n} = {\rm{E}}\left[ {\dfrac{{{c^2}\theta }}{{{c^2} + {b^2}}}} \right]$ 。

接下来本文定义的平均场博弈允许将极限策略(19) 和(20) 化为一个独立的均衡问题，这个均衡问题直观地反映了一个金融机构与一个拥有 $ m $ 分布的众多机构集体的博弈问题。与其让一个金融机构与一系列的机构建立博弈模型，不如依照平均场博弈的范式，对一个随机选择的代表性的金融机构建模。概率测度 $ m $ 表示类型参数在众多机构的集体中的分布；相应地，金融机构的类型向量是一个服从规律 $ m $ 的随机变量。在集体中的每一个金融机构的盈余过程都是相互独立的。

为了描述平均场博弈问题，考虑在完备的概率空间 $(\varOmega ,F,P,\left\{{F}_{t}\right\}{\text{}}_{t\in [0,T]})$ ，存在3个独立同分布的一维布朗运动 $ W\left( t \right) $ ， $ {B_l}\left( t \right) $ 和 $ B\left( t \right) $ ，以及随机变量 ${\boldsymbol{\zeta}} =( \xi ,\delta ,\theta , a,b,c,\lambda ,p,\mu ,r,\sigma )$ 。 $ {\boldsymbol{\zeta}} $ 称为类型向量，其分布称为类型分布。 $ {\boldsymbol{\zeta}} $ 定义在式(18) 中的 $ {G^e} $ 空间上，独立于 $ W\left( t \right) $ ， $ {B_l}\left( t \right) $ 和 $ B\left( t \right) $ 。 $ {F^{{\rm{MF}}}} = {\left\{ {F_t^{{\rm{MF}}}} \right\}_{t \in \left[ {0,T} \right]}} $ 表示满足一般假设的最小的滤波，即 $ {\boldsymbol{\zeta}} $ 是 $ F_0^{{\rm{MF}}} $ 可测的，且一维布朗运动 $ W\left( t \right) $ ， $ {B_l}\left( t \right) $ 和 $ B\left( t \right) $ 满足 $ {F^{{\rm{MF}}}} = {\left\{ {F_t^{{\rm{MF}}}} \right\}_{t \in \left[ {0,T} \right]}} $ 。 ${F^{B \times W \times {B_l}}} =$ $ {\left\{ {F_t^{B \times W \times {B_l}}} \right\}_{t \in \left[ {0,T} \right]}} $ 表示由布朗运动 $ W\left( t \right) $ ， $ {B_l}\left( t \right) $ 和 $ B\left( t \right) $ 产生的的自然滤波。

根据式(4) 可知，代表性的金融机构的财富过程可以表示为

$ \begin{aligned} {\text{d}}X(t) = &\left\{ {\pi (t) (\mu - r) + rX(t) + a[q(t) (1 - \lambda ) - (1 - p) ]} \right\}{\text{d}}t + \\ &\sigma \pi (t) {\text{d}}W(t) - b[1 - q(t) ]{\text{d}}B(t) - c[1 - q(t) ]{\text{d}}{B_l}(t) \\ \end{aligned}$

(21)

式中： $ X(0) = \xi $ 。金融机构使用的策略表示为 $\eta (t) : = \left( {\pi (t) ,q(t) } \right) \in R \times R$ ， $ \pi \left( t \right) \in R $ 为投资策略， $ q\left( t \right) \in R $ 为风险控制策略。

定义3(可行策略)　对于金融机构，策略 $ \eta (t) = \left( {\pi (t) ,q(t) } \right) $ 称为可行策略，如果

(i) $ \eta (t) = \left( {\pi (t) ,q(t) } \right) $ 是 $F_t^{{\rm{MF}}} -$ 循序可测过程，满足 ${\rm{E}}\left[ {\int_0^T {\left\| {{\pi ^2}(t) } \right\|} + \left\| {{q^2}(t) } \right\|{\rm{d}}t} \right] < \infty$ ；(ii) 对 $ \forall x \in R $ ，式(21) 存在唯一的强解 $ X(t) > 0 $ ，满足 ${\rm{E}}\left[ {\mathop {\sup }\limits_{0 \leqslant t \leqslant T} \left\| {X(t) } \right\|} \right] < \infty$ 。将金融机构所有可行策略构成的集合记为 ${\varPi _{{\rm{MF}}}}$ 。

在平均场博弈中，平均财富过程服从 $ {F^{B \times W \times {B_l}}} = {\left\{ {F_t^{B \times W \times {B_l}}} \right\}_{t \in \left[ {0,T} \right]}} $ 。假设代表性的金融机构知道其他机构集体由 $ {F^{B \times W \times {B_l}}} $ 适应过程 $ \overline X $ 控制的几何平均财富，即 $ \overline X $ 是给定的。显然，代表性金融机构的优化目标可描述成最大化下述预期回报

$ \mathop {\sup }\limits_{\eta \in {\varPi _{{\rm{MF}}}}} {\rm{E}}\left\{ { - \exp \left( { - \frac{1}{\delta }} \right) \left[ {X\left( T \right) - \theta \bar X} \right]} \right\} $

(22)

其中 $ X(t) ,t \in \left[ {0,T} \right] $ 由式(21) 给出。

定义4 (Nash均衡)　假定 $ {\eta ^*} \in {F^{{\rm{MF}}}} $ 是一个可行的策略，考虑 $ F_T^{B \times W \times {B_l}} $ 可测的随机变量 $\overline X : = {\rm{E}}\left[ {{X^*}\left( T \right) |F_T^{B \times W \times {B_l}}} \right]$ ，其中 $ {X^*}\left( t \right) ,t \in \left[ {0,T} \right] $ 是式(22) 中对应最优策略 $ {\eta ^*} = \left( {{\pi ^*},{q^*}} \right) $ 的财富状态。如果 $ {\eta ^*} $ 是问题(22) 的最优解，则认为在给定 $ \bar X $ 的情况下， $ {\eta ^*} $ 是平均场博弈的Nash均衡策略。恒定平均场博弈均衡是 $ F_T^{B \times W \times {B_l}} $ 可测随机变量 $ {\pi ^*}\left( t \right) $ ，如果 $ \eta \left( t \right) : = {\eta ^*},\forall t \in \left[ {0,T} \right] $ ，则 $ \eta \left( t \right) $ 是平均场博弈的Nash均衡策略。

接下来，我们将构造出平均场博弈的Nash均衡策略，并证明。

定理2 　假定 $ \delta > 0 $ ， $ \theta \in \left[ {0,1} \right] $ ， $ \mu > r \geqslant 0 $ ， $ \sigma \geqslant 0 $ ， $ b \geqslant 0 $ ， $ c \geqslant 0 $ ， $ b + c > 0 $ ，引入两个常数表示 $\overline \delta = {\rm{E}}\left[ \delta \right]$ 和 $\overline \theta = {\rm{E}}\left[ \theta \right]$ ，在上述两个常数皆存在且有限的情况下，均衡投资策略存在下述两种情况：

(i) 当 $ \bar \theta < 1 $ 时，存在唯一的恒定Nash均衡，Nash均衡投资策略由式(23)给出。

$ {\pi ^*}\left( t \right) = \frac{{\left( {\mu - r} \right) }}{{{\sigma ^2}}}\left[ {\delta + \frac{{\theta \bar \delta }}{{\left( {1 - \bar \theta } \right) }}} \right] $

(23)

(ii) 当 $ \bar \theta = 1 $ 时，Nash均衡投资策略不存在。

引入两个常数 $\varepsilon = {\rm{E}}\left[ {\dfrac{{a\left( {1 - \lambda } \right) \delta c}}{{{c^2} + {b^2}}}} \right]$ 和 $\phi = {\rm{E}}\left[ {\dfrac{{{c^2}\theta }}{{{c^2} + {b^2}}}} \right]$ ，在上述两个常数皆存在且有限的情况下，均衡风险控制策略存在下述两种情况：

(i) 当 $ \phi < 1 $ 时，存在唯一的恒定平均场博弈Nash均衡，均衡时最优风险控制策略由式(24)给出。

$ {q^*}\left( t \right) = 1 + \frac{{a\left( {1 - \lambda } \right) \delta }}{{{c^2} + {b^2}}} + \frac{{c\theta }}{{{c^2} + {b^2}}}\frac{\varepsilon }{{\left( {1 - \phi } \right) }} $

(24)

(ii) 当 $ \phi = 1 $ 时，Nash均衡风险控制策略不存在。

证明 　在给定 $ \bar X $ 的情况下，构造一个恒定的平均场博弈均衡来解决式(22) 中的随机最优化问题。由于 $ \left( {\xi ,a,\lambda ,p,\mu ,r,\sigma ,\alpha ,\beta } \right) $ 与 $ W\left( t \right) $ ， $ {B_l}\left( t \right) $ 和 $ B\left( t \right) $ 相互独立，对 $ t \in \left[ {0,T} \right] $ ，有

$ \begin{aligned}\bar X(t) = &\bar \xi + \left[ {(\mu - r) \bar \alpha + r\bar X(t) + \overline {a\beta } - \overline {a\lambda \beta } - \bar \alpha + \overline {ap} } \right]t +\\ & \overline {\sigma \alpha } W(t) - \left( {\bar c - \overline {c\beta } } \right) {B_l}(t) \end{aligned}$

对任意的 $ t \in \left[ {0,T} \right] $ ，定义 $ {Z^\eta }(t) : = X(t) - \theta \bar X(t) $ ，结合式(21) 的财富过程有

$ \begin{aligned} {\text{d}}{Z^\eta }(t) =&\big\{ {\pi (t) (\mu - r) + rX(t) + a[q(t) (1 - \lambda ) - (1 - p) ]} - \\ &{\theta \left[ {(\mu - r) \bar \alpha + r\bar X(t) + \overline {a\beta } - \overline {a\lambda \beta } - \bar \alpha + \overline {ap} } \right]} \big\}{\text{d}}t + \\ &\left[ {\sigma \pi (t) - \theta \overline {\sigma \alpha } } \right]{\text{d}}W(t) - b[1 - q(t) ]{\text{d}}B(t) -\\ &\left\{ {c[1 - q(t) ] - \theta (\bar c - \overline {c\beta } ) } \right\}{\text{d}}{B_l}(t) \\ \end{aligned}$

其中 $ {Z^\eta }(0) = \xi - \theta \bar \xi $ 。把 $ \bar X $ 纳入优化目标式(22) 中，优化目标可化为

$ \mathop {\sup }\limits_{\eta \in {\varPi _{{\rm{MF}}}}} {\rm{E}}\left\{ { - \exp \left[ { - \frac{1}{\delta }{Z^\eta }\left( T \right) } \right]} \right\} $

(25)

值函数 $ V\left( {t,z} \right) $ 是式(26)HJB方程唯一解：

$ \begin{split} 0 =& {V_t} + {V_z}\Big\{ {\pi (\mu - r) + rx + a[(1 - \lambda ) - (1 - p) ]} - \\ &\theta \left[ {(\mu - r) \bar \alpha + r\bar x + \overline {a\beta } -\overline {a\lambda \beta } - \bar a + \overline {ap} } \right] \Big\}+ \\ &\frac{1}{2}{V_{zz}}\bigg[{{{\left( {\sigma \pi - \theta \overline {\sigma \alpha } } \right) }^2} + \left( {{b^2} + {c^2}} \right) {{\left( {1 - q} \right) }^2} + }\\ &{ {\theta ^2}{{\left( {\bar c - \overline {c\beta } } \right) }^2} - 2c\theta \left( {1 - q} \right) \left( {\bar c - \overline {c\beta } } \right) } \bigg] \end{split} $

(26)

假设满足HJB方程(26) 的值函数形式为 $V\left( {t,z} \right) = - {{\rm{e}}^{ - \frac{z}{\delta }}}f\left( t \right)$ ，终端条件为 $ f\left( T \right) = 1 $ 。式(26) 分别对 $ \pi $ 和 $ q $ 求一阶条件得

$ {\pi ^*}\left( t \right) : = \frac{\theta }{\sigma }\overline {\sigma \alpha } + \frac{{\left( {\mu - r} \right) }}{{{\sigma ^2}}}\delta $

(27)

$ {q^*}\left( t \right) : = 1 + \frac{{a\left( {1 - \lambda } \right) \delta - c\theta \left( {\overline c - \overline {c\beta } } \right) }}{{{b^2} + {c^2}}} $

(28)

投资与风险控制策略 $ {\eta ^*}(t) = \left( {{\pi ^*}\left( t \right) ,{q^*}\left( t \right) } \right) $ 要成为平均场博弈的均衡，需满足： $ {\pi ^*}\left( t \right) = \alpha \left( t \right) $ ， $ {q^*}\left( t \right) = \beta \left( t \right) $ 。把 $ {\pi ^*}\left( t \right) = \alpha \left( t \right) $ 代入式(27) ，两边同时乘以 $ \sigma $ ，然后取均值得到式(29) ；把 $ {q^*}\left( t \right) = \beta \left( t \right) $ 代入式(28) ，两边同时乘以 $ c $ ，然后取均值得到式(30) 。

$ \overline {\sigma {\pi ^*}} = \overline \theta \overline {\sigma {\pi ^*}} + \frac{{\left( {\mu - r} \right) }}{{{\sigma ^2}}}\overline \delta $

(29)

$ \overline {c{q^*}} = \overline c \left( {1 - \phi } \right) + \varepsilon + \phi \overline {c{q^*}} $

(30)

至此，均衡投资策略存在下述3种情况：

(i) 当 $ \bar \theta < 1 $ 时，有 $\overline {\sigma {\pi ^*}} = \dfrac{{\left( {\mu - r} \right) }}{{\sigma \left( {1 - \theta } \right) }}\overline \delta$ ，根据式(27) 和式(29) ，可以证明定理2中式(23) 。

(ii) 当 $ \bar \theta = 1 $ 且 $\dfrac{{\left( {\mu - r} \right) }}{\sigma }\overline \delta \ne 0$ 时，方程(29) 没有解，即不存在该问题下的均衡投资策略。

(iii) 当 $ \bar \theta = 1 $ 且 $\dfrac{{\left( {\mu - r} \right) }}{\sigma }\overline \delta = 0$ 时，此情形不存在。因为 $ \delta > 0 $ , $ \mu > r \geqslant 0 $ , $ \sigma \geqslant 0 $ ，故 $\dfrac{{\left( {\mu - r} \right) }}{\sigma }\overline \delta > 0$ 恒成立。

均衡风险控制策略存在下述3种情况：

(i) 当 $ \phi < 1 $ 时，有 $\overline {c{q^*}} = \bar c + \dfrac{\varepsilon }{{1 - \phi }}$ ，根据式(28) 和式(30) ，可以证明定理2中式(24) 。

(ii) 当 $ \phi = 1 $ 且 $ \varepsilon \ne 0 $ 时，方程(30) 没有解，即不存在该问题下的均衡风险控制策略。

(iii) 还有一种情况： $ \phi = 1 $ ， $ \varepsilon = 0 $ 。但这种情况不存在，因为 $ \delta > 0 $ ， $ a > 0 $ ， $ \lambda > 0 $ ， $ \mu > r $ ， $ b \geqslant 0 $ ， $ c \geqslant 0 $ ， $b + c > 0$ ，当 $ \phi = 1 $ 时，表示 $ c $ 不恒等于0， $ \varepsilon < 0 $ 恒成立。

把式(27) ～式(30)代回HJB方程(26) ，得到

$ {f_t}\left( t \right) - \rho f\left( t \right) = 0 $

其中

$ \begin{aligned} \rho : = &\frac{1}{\delta }\left\{ {rz - a(p - \lambda ) - \theta \left[ {\overline {a\beta } - \overline {a\lambda \beta } - \bar a + \overline {ap} } \right]} \right\} -\\ &\frac{{a(1 - \lambda ) c\theta }}{{\left( {{b^2} + {c^2}} \right) \delta }}\left( {\bar c - \frac{\varepsilon }{{1 - \phi }}} \right) + \frac{{\theta {{\left( {\mu - r} \right) }^2}\overline \delta }}{{{\sigma ^2}\left( {1 - \overline \theta } \right) \delta }} + \\ & \frac{1}{2}\left[ {\frac{{{{(\mu - r) }^2}}}{{{\sigma ^2}}} + \frac{{{a^2}{{(1 - \lambda ) }^2}}}{{{b^2} + {c^2}}} - \frac{{{b^2}{\theta ^2}}}{{({b^2} + {c^2}) {\delta ^2}}}{{\left( {\bar c - \frac{\varepsilon }{{1 - \phi }}} \right) }^2}} \right] \\ \end{aligned} $

(31)

结合终端条件 $ f\left( T \right) = 1 $ 得 $ f\left( t \right) = {{\rm{e}}^{ - \rho \left( {T - t} \right) }} $ 。定理2证毕。

4 敏感性分析

本文从金融市场中提取真实交易数据，对金融市场模型中的参数进行校准，根据参数估计的结果进行敏感性分析。

首先估计金融市场中风险股票价格模型和无风险债券价格模型中的参数。根据式(4) ，运用极大似然估计法，股票预期收益率的估计量 $ \hat \mu $ 和股票收益波动率的估计量 $ \hat \sigma $ 可表示为

$\begin{array}{c} \hat \mu = \dfrac{1}{T}\ln \dfrac{{{S_1}(T) }}{{{S_1}(0) }} + \dfrac{1}{2}{\hat \sigma ^2}{\text{ }},\\ \quad \hat \sigma = {\left\{ {\dfrac{1}{T}\displaystyle\sum\limits_{j = 1}^n {{{\left[\ln \dfrac{{{S_1}(t_n^j) }}{{{S_1}(t_n^{j - 1}) }} - \dfrac{1}{n}\displaystyle\sum\nolimits_{i = 1}^n {\ln \dfrac{{{S_1}(t_n^j) }}{{{S_1}(t_n^{j - 1}) }}} \right]}^2}} } \right\}^{\textstyle\frac{1}{2}}} \end{array}$

沪深300指数(代码：399300) 是中国股票市场的晴雨表，其行情可以反映中国股市大盘走势。故使用2012年5月28日至2022年05月05日沪深300指数日频数据，共计2416个样本观测值，即 $ n = 2\;416 $ ，对风险资产价格模型中的预期收益率和波动率参数进行拟合， $ T = n \times (1/252) $ 。考虑数据的平稳性，对指数价格进行对数化处理。相应地，无风险收益率采用Shibor一年期利率均值对应的对数收益率。金融市场相关参数设置：μ为0.0725，σ为0.2291，r为0.0405。

参考Baltas等^[12]，Lacker和Zariphopoulou^[14]，Guan和Hu^[16]，金融机构相关参数取值如表1所示。

本文主要对平均场博弈中的均衡策略，即定理2中展示的主要结论进行分析。

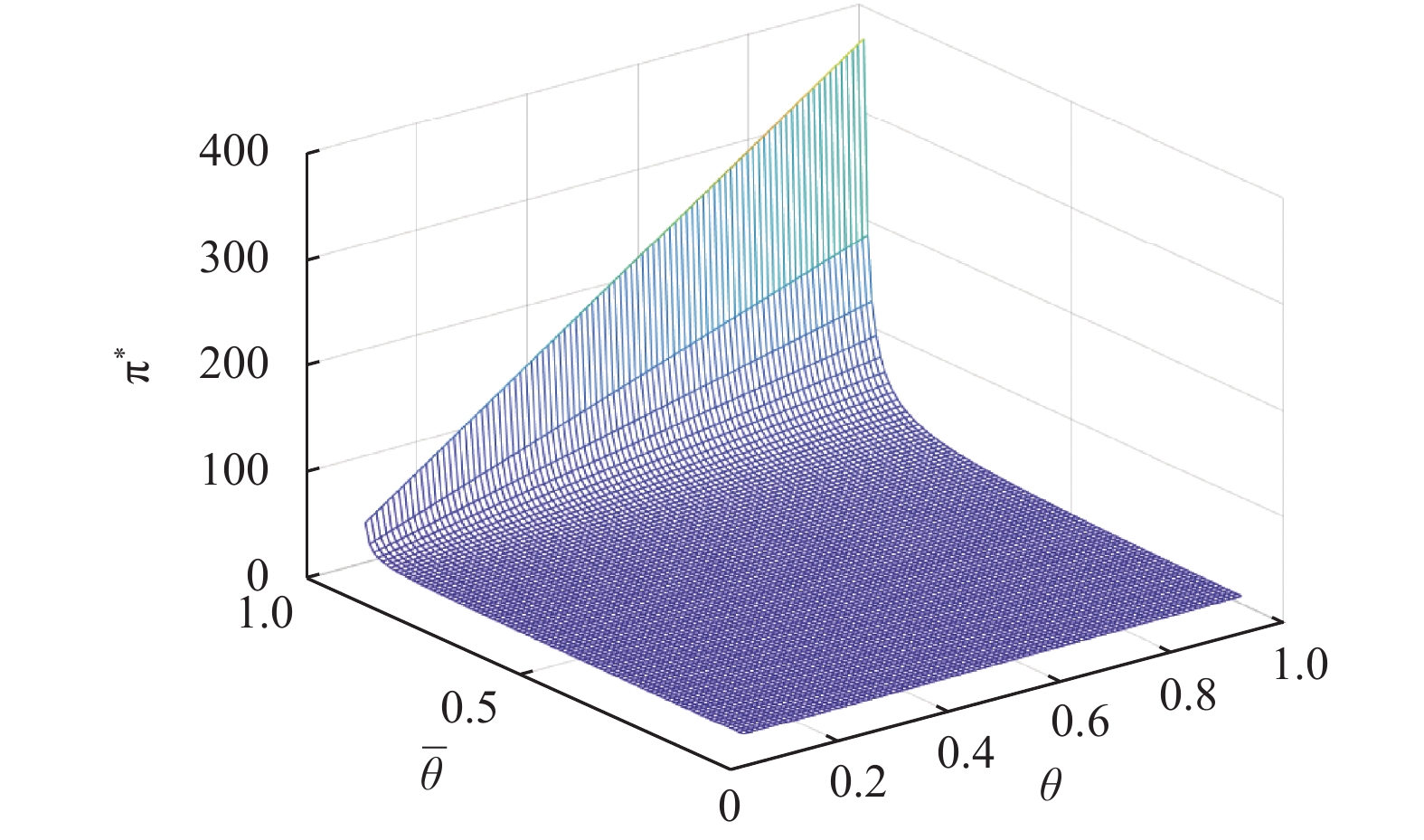
图1刻画了金融机构的均衡投资策略 $ {\pi ^*} $ 与其竞争参数 $ \theta $ 以及行业竞争参数的均值 $ \overline \theta $ 的关系，竞争将导致风险投资攀升。显然，当 $ \theta $ 和 $ \overline \theta $ 接近1的时候，均衡投资策略 $ {\pi ^*} $ 呈爆炸式增长。这反映了，在竞争激烈的群体中，投资者都投资了大量的风险资产。一方面，均衡投资策略 $ {\pi ^*} $ 与竞争参数 $ \theta $ 成正相关。这表明，在激烈的竞争环境中，金融机构希望在行业排名中脱颖而出，会增加风险资产的投资额，通过争取更高的风险报酬在与同行的博弈中获胜。另一方面，均衡投资策略 $ {\pi ^*} $ 与市场竞争参数的均值 $ \overline \theta $ 成正相关。这表明，投资者的均衡投资策略会受到环境和对手的影响。若其他金融机构都具有强烈的相对财富关注，进行大量风险资产投资，市场竞争就会变得异常激烈。金融机构为了跟上市场和同行，只能增加风险资产的投资额，通过高风险高回报的投资保持行业地位。

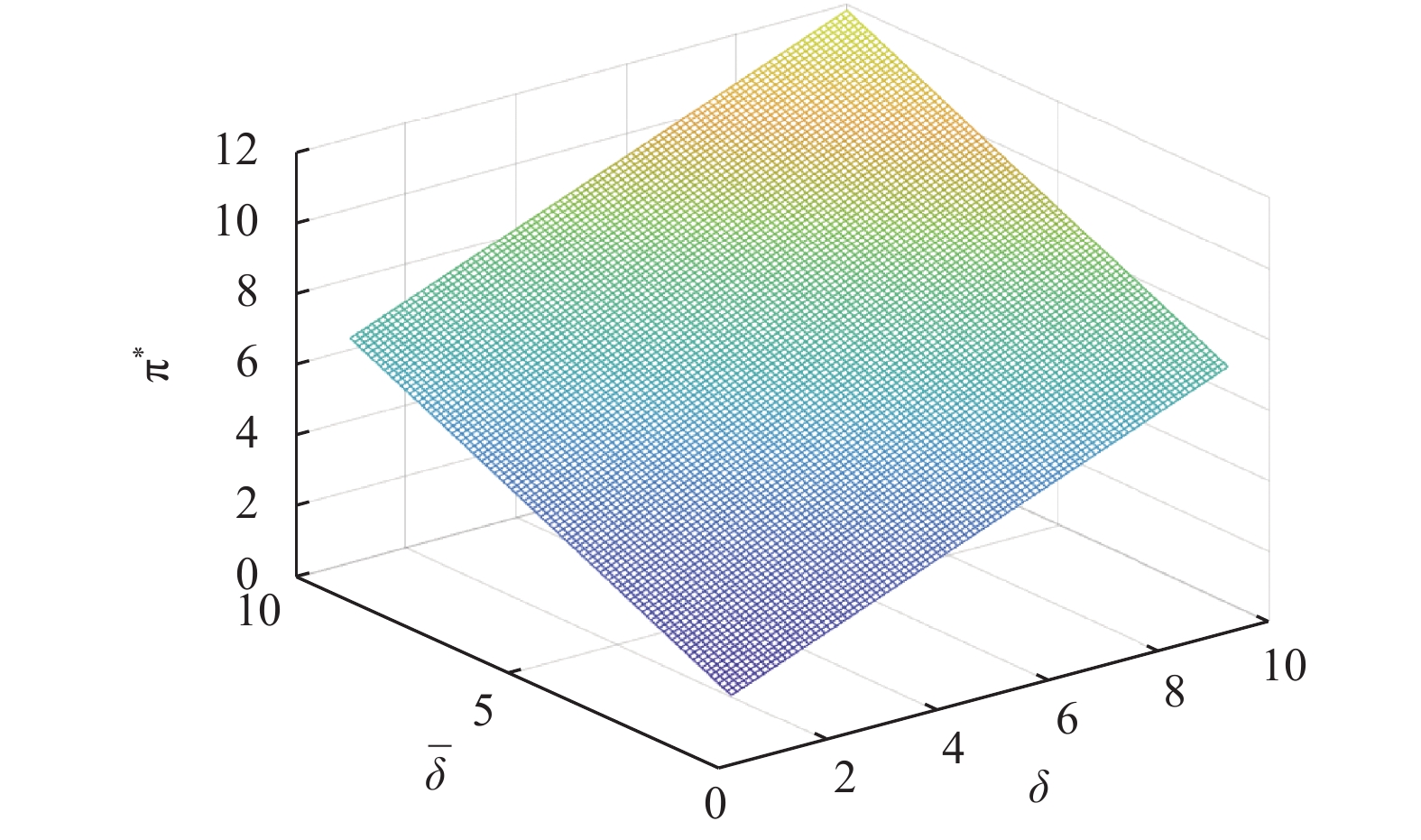
图2描绘了金融机构的均衡投资策略 $ {\pi ^*} $ 与 $ \delta $ 以及其市场均值 $ \overline \delta $ 的关系。 $ \delta $ 越大，金融机构对风险的容忍程度越强。一方面，均衡投资策略 $ {\pi ^*} $ 与 $ \delta $ 成正相关。这表明，当金融机构偏好风险时，会增加风险资产的投资。另一方面，均衡投资策略 $ {\pi ^*} $ 与 $ \overline \delta $ 成正相关。这可以理解为，当市场中的大部分机构投资者偏好风险，采取激进投资策略，为了在收益上追上对手，金融机构不得不增加风险资产的投资，竞争使得风险资产投资增加；当市场中的大部分机构投资者都对风险恐惧，采取保守的投资策略时，由于羊群效应，金融机构也会采取保守的投资策略，减少对风险资产的投资，把更多资金投资于无风险资产。

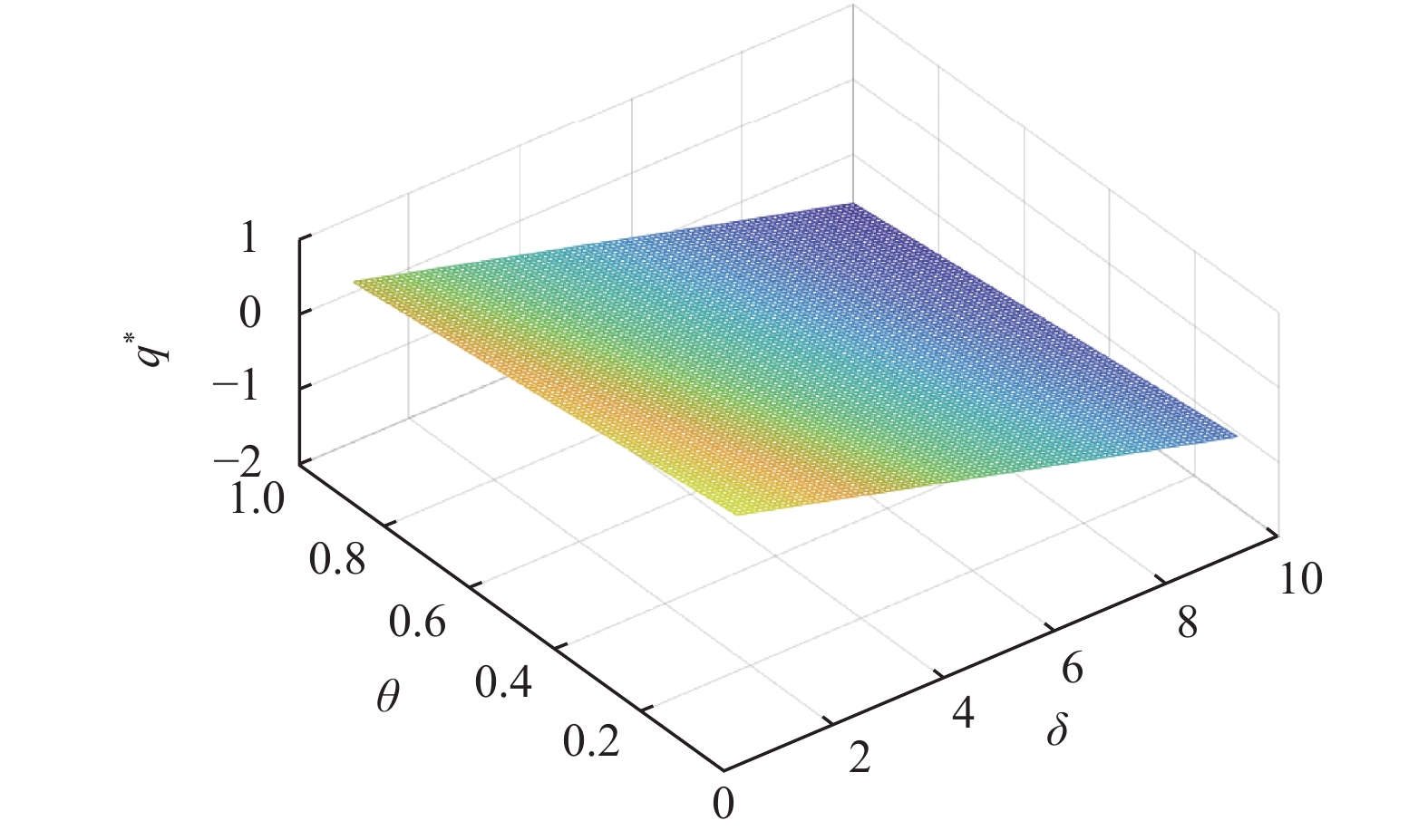
图3描述了金融机构的均衡风险控制策略 $ {q^*} $ 与其竞争参数 $ \theta $ 以及其风险容忍程度 $ \delta $ 的关系。一方面，均衡风险控制策略 $ {q^*} $ 与竞争参数 $ \theta $ 成负相关。这表明，竞争会导致风险控制的减弱。金融市场竞争激烈，金融机构会降低保险购买的比例，降低风险转移的比例和费用，搏取更高的风险报酬，在财富上超越对手。另一方面，均衡风险控制策略 $ {q^*} $ 与 $ \delta $ 成负相关。显然，金融机构对风险越厌恶，恐惧风险带来亏损，会提高风险转移的比例，控制风险。当 $ {q^*} < 0 $ 时，表示金融机构主动承担由其他金融机构转出的风险。从图3可以看出，即使存在保险等风险转移手段，但具有偏好风险的金融机构不仅不会转移风险，还会主动作为第三方机构，接受由其他金融机构转出的风险，赚取风险转移费用。显然，竞争使得风险控制减弱。

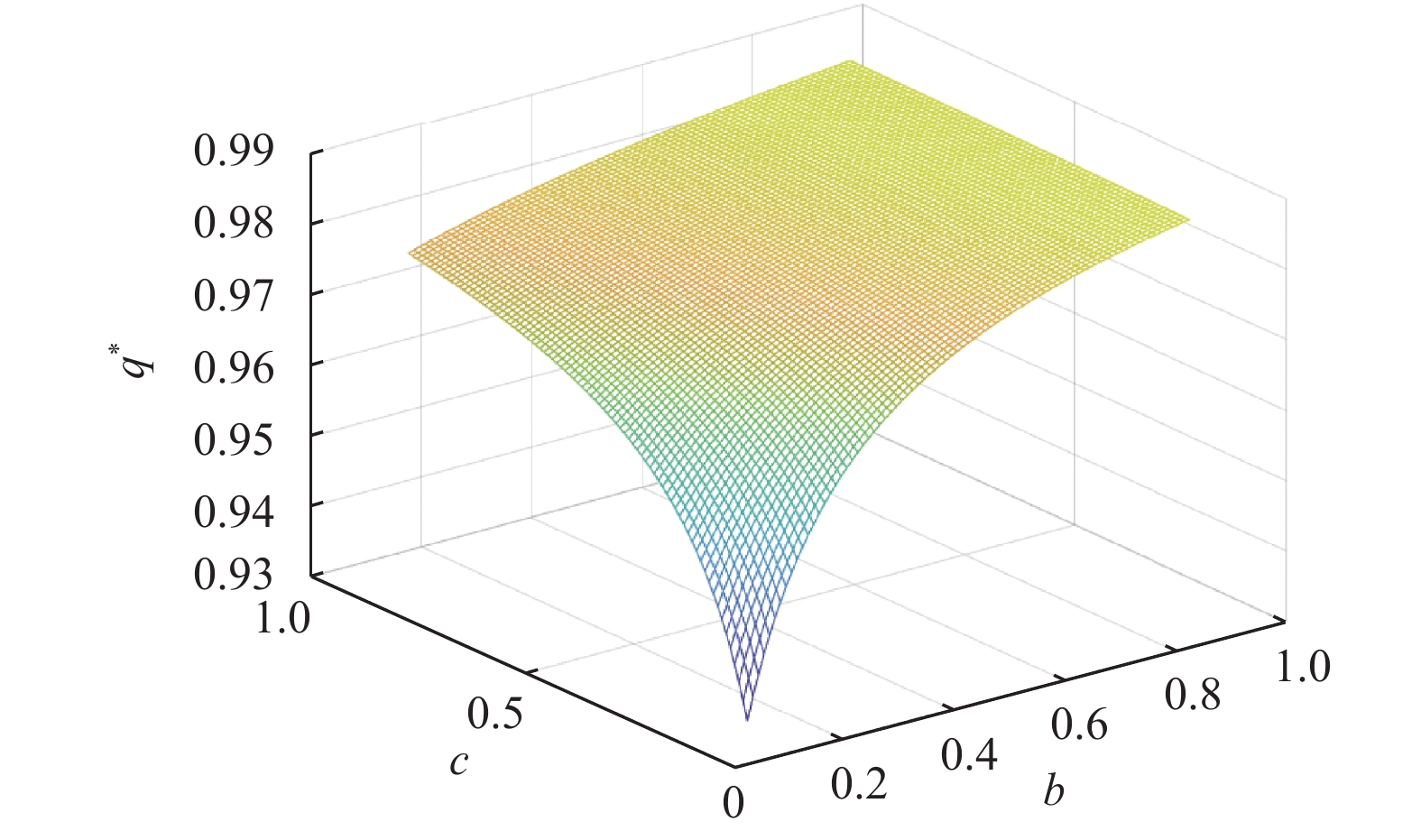
图4描述了金融机构的均衡风险控制策略 $ {q^*} $ 与其盈余过程的独立波动 $ b $ 和公共波动 $ c $ 之间的关系。可以看出，盈余过程的波动会影响其均衡风险转移策略，但这种影响在波动小的时候较为明显，即当盈余过程的波动率较小的时候，均衡风险控制策略对盈余波动较为敏感；当波动超过一定程度的时候，金融机构倾向于把绝大部分风险转移出去，此后波动的改变，不会引起均衡风险控制策略的大幅度调整。一方面，金融机构的均衡投资策略 $ {q^*} $ 与其盈余过程的独立波动 $ b $ 成正相关。这表明，当盈余过程波动增大，金融机构会提高风险转移比例，使风险的自留比例降低，发生亏损时，可减少损失。另一方面，金融机构的均衡投资策略 $ {q^*} $ 与其盈余过程的公共波动 $ c $ 成正相关。这可以解释为，当盈余过程与市场的相关程度越高，当市场的波动越大时，金融机构会选择提高风险转移比例以控制风险。

5 结语

金融机构作为盈利性机构，如何对自有和筹集到的资金进行合理有效的运用，实现财富保值增值，是金融机构所关注的核心内容。在经营和投资过程中，金融机构面临支出和投资两方面的风险。为了稳健公司经营，金融机构需要进行风险控制。金融市场竞争激烈，金融机构在进行决策时关注相对绩效，以提高竞争力。金融机构作为金融市场的重要参与者，其资金安全和良好运营对市场稳定有重要作用。因此，在相对绩效关注下对金融机构投资与风险控制问题进行研究，有利于金融机构健康发展，稳定金融市场，促进经济社会有序运行。研究结论为金融机构经营决策者，以及金融行业发展的引导者提供理论参考，具有重要的现实意义。

本文研究了策略互动下多个相互竞争的机构投资者之间的最优投资与风险控制问题。使用经典的Black-Scholes模型描述风险资产的价格动态，采用购买保险等方法进行风险控制，使用投资者自身财富与行业平均财富之间的差值描述相对财富，在CARA效用函数下构建非零和博弈模型，运用多人博弈理论和平均场博弈理论求出Nash均衡时最优投资与风险控制策略的解析表达，并对参数进行敏感性分析。

研究结果表明：(1) 竞争将导致风险投资攀升，风险控制减弱。市场中竞争越激烈，金融机构希望业绩优于同行，就会增加风险资产的投资额，降低风险转移比例，博取高额风险报酬，减少风险转移费用，提高相对绩效；同时，当同行都为了提高业绩而采取激进的投资策略和风险控制策略时，金融机构为了在财富上追赶上对手，不得不增加风险资产的投资，削弱风险控制。(2) 金融机构的投资与风险控制策略受到对手风险偏好的影响。金融机构自身和对手风险的偏好都会导致其降低风险转移的比例。由于羊群效应，当同行都厌恶风险而采取保守的投资策略时，该金融机构也会降低对风险资产的投资。(3) 盈余波动的变化影响风险转移策略发生同向改变。当金融机构盈余过程的波动越大时，为了控制风险，金融机构会增加风险转移比例；当金融机构的盈余过程对市场的依赖越强，且市场的波动增大时，金融机构也会增加风险转移的比例，降低损失风险。但这种影响在波动较小时较为明显；当波动超过一定程度时，金融机构倾向于把绝大部分风险转移，波动对风险转移策略影响甚微。