随着电力电子技术的快速发展,非线性负载使得电网电流产生畸变,造成严重的谐波污染[1]。有源电力滤波器(Active Power Filter,APF)作为一种有效的谐波抑制、无功补偿手段,被广泛应用于谐波治理场合[2-4]。传统APF由三相桥式电压源逆变器和直流电容组成,其拓扑需要匹配变压器和大量的有源开关器件,导致补偿装置体积大、成本高昂,使其应用受到限制[5-6],因此简化APF结构,降低其成本具有重要的研究意义。
文献[7-8]提出了一种两相三线制的变流器,通过两个电感与三相三线制变流器连接,简化了拓扑结构,但该结构需要匹配大型变压器,工程造价高且仅适用于电力机车负载等场合。文献[9-11]提出了一种新型的三相四开关拓扑结构用于三相并联型APF,减少了开关器件的数量,降低系统成本,但这种拓扑结构的直流侧电压必须高于两倍电网线电压的峰值,电压过高会加大系统的运行负担。文献[12-13]采用了将多组无源滤波器(Passive Filter,PF)与APF结合来进行补偿,弥补了PF只能补偿特定次谐波的缺点,但该拓扑所需PF器件较多,系统较为复杂,装置体积大。
针对上述APF拓扑复杂以及装置成本过高的问题,本文提出一种不对称拓扑的单调谐混合有源电力滤波器,该拓扑结构由两相单调谐的LC式无源滤波器与三相变流器串联后并入带有非线性负载的电网,减少了一相LC无源滤波器,在保留原有补偿能力的情况下,降低装置成本并简化拓扑结构,也使得控制设计变得简单,降低系统复杂度。最后,仿真和实验结果验证了所提出的拓扑结构的可行性。
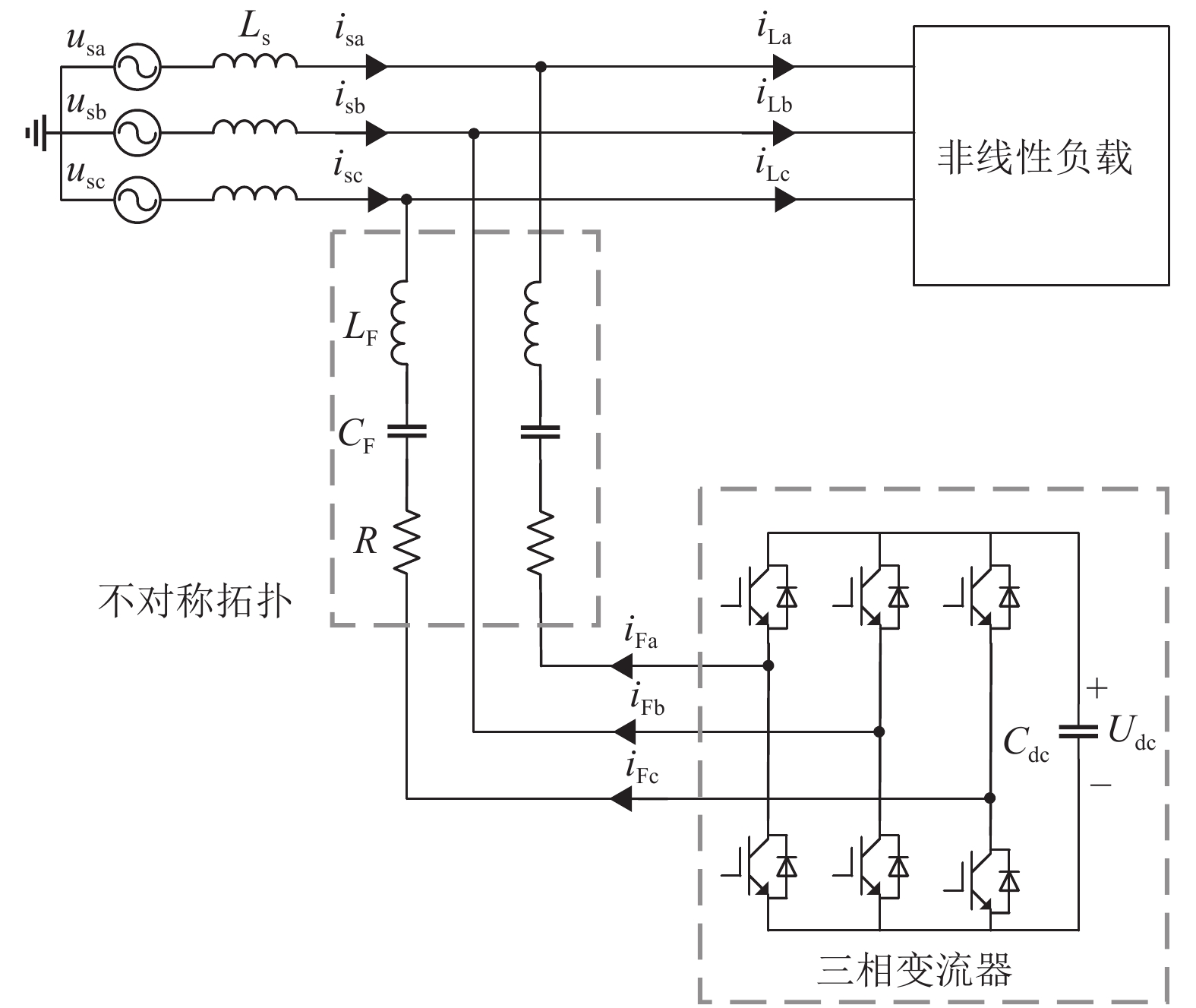
1 不对称拓扑结构分析 1.1 拓扑不对称的HAPF结构本文提出一种不对称拓扑的单调谐混合有源滤波器,如图1所示。不对称拓扑可选取三相中的任一相作为缺少滤波器件的支路,本文选取B相支路作为不对称相。该结构由两相LC串联式的无源滤波器与三相变流器串联而成,其中变流器的B相直接与电网B相连接。LC无源滤波器对于基波而言阻抗较大,能承受大部分基波电压,使变流器承受的基波电压减小,相比于单电感结构,降低了APF的容量和直流侧电压。
|
图 1 拓扑不对称的混合型有源电力滤波器 Figure 1 Asymmetric topology of hybrid active power filter |
图1中usa、usb、usc表示电网侧三相电压,Ls表示等效电网电感,isa、isb、isc表示网侧三相电流,iLa、iLb、iLc为负载三相电流,Cdc表示直流侧电容,Udc为直流侧电容电压,电感LF与电容CF共同组成LC无源滤波器,R表示器件内阻,补偿电流为iFa、iFb、iFc。
1.2 LC无源滤波器的调谐次数选取LC无源滤波器在特定频率下发生串联谐振,呈现低阻抗,适当选取LF和CF的参数能够实现更好的补偿性能。在三相不控整流电路接入电网时,主要产生6k±1次的谐波,调谐频率选取公式为
| $ {f_n} = \frac{1}{{2{\text{π }}\sqrt {{L_{\text{F}}}{C_{\text{F}}}} }} $ | (1) |
式中:fn是n次谐波频率,由于5次谐波最高,为得到更好的补偿效果,本文选取5次调谐频率f5=250 Hz,在该频率下,无源滤波器有较高的基波阻抗和较低的5次谐波阻抗,对高频谐波呈高阻抗,能够有效减少变流器的开关纹波(20 kHz)注入电网,无需加装高频谐波滤波器。
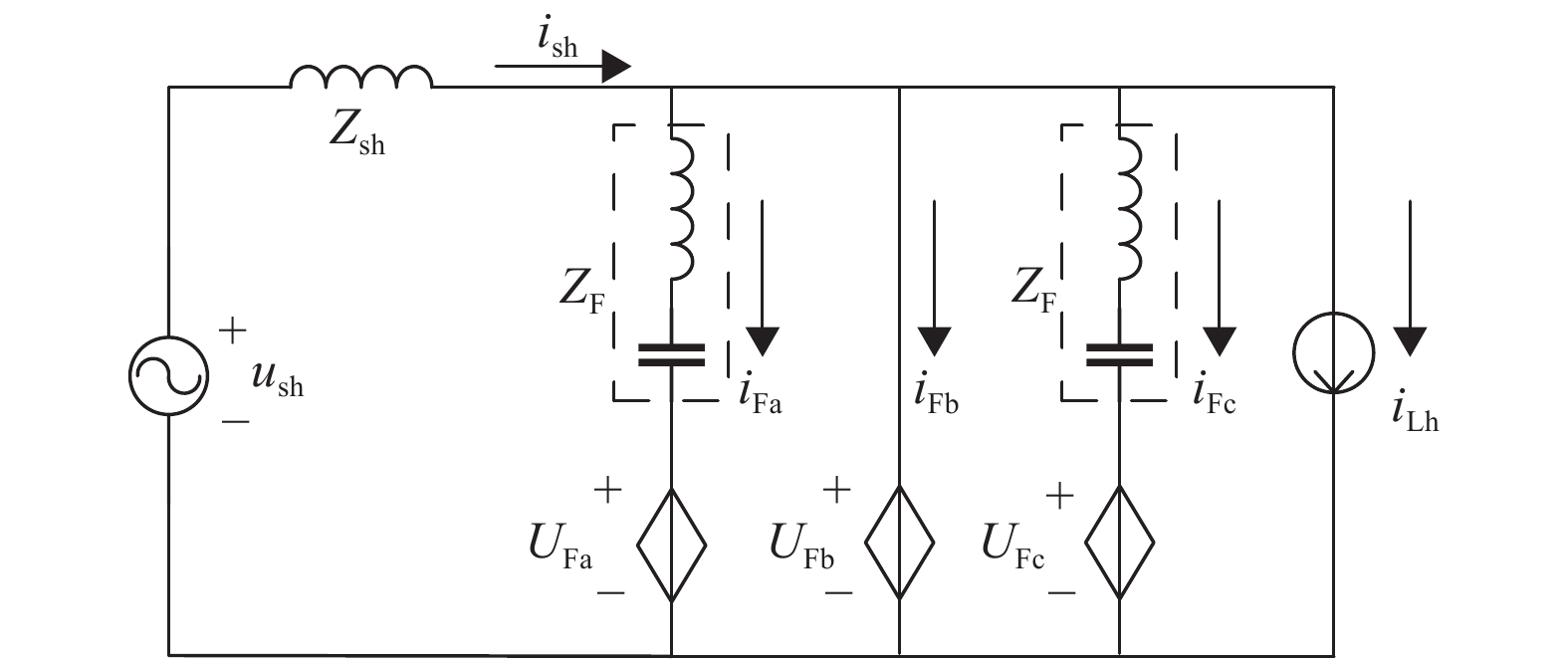
1.3 工作原理及滤波特性图2为不对称拓扑的HAPF谐波等效电路,其中ush为电网电压us的谐波电压分量。Zsh为电网侧的等效阻抗,ish为电网侧的谐波电流,iLh为负载谐波电流,iFa、iFb、iFc为补偿电流,ZF为滤波电路阻抗,UFa、UFb、UFc为变流器交流侧输出电压。
|
图 2 不对称拓扑的HAPF谐波等效电路 Figure 2 Harmonic equivalent circuit of HAPF with Asymmetric topology |
将变流器侧等效为一个受控电压源,其电压UF=Kish,其中K为增益系数。由等效图可得,A、C两相具有相同的结构,根据基尔霍夫电压电流定律可得
| $ \left\{\begin{split} &{U}_{\text{sh}x}={i}_{\text{sh}x}{Z}_{\text{sh}}+{i}_{\text{F}x}{Z}_{\text{F}}+{U}_{\text{F}x}\\ &{i}_{\text{sh}x}={i}_{\text{F}x}+{i}_{\text{Lh}x}\end{split}\text{ }\text{,}\text{ }(x=\text{a},\text{c})\right. $ | (2) |
当只补偿电网电压谐波时,iLh=0,由式(2)得
| $ {i}_{\text{sh}x}=\frac{{u}_{\text{sh}x}}{{Z}_{\text{sh}}+{Z}_{\text{F}}+K}\text{ }\text{,}\text{ }(x=\text{a},\text{c}) $ | (3) |
当只补偿电网电流谐波时,ush=0,由式(2)得
| $ {i}_{\text{sh}x}=\frac{{Z}_{\text{F}}}{{Z}_{\text{F}}+{Z}_{\text{sh}}+K}{i}_{\text{Lh}x}\text{ }\text{,}\text{ }(x=\text{a},\text{c}) $ | (4) |
式(3)和式(4)由叠加定理得
| $ {i_{{\text{sh}}x}} = \frac{{{u_{{\text{sh}}x}}}}{{{Z_{{\text{sh}}}} + {Z_{\text{F}}} + K}} + \frac{{{Z_{\text{F}}}}}{{{Z_{\text{F}}} + {Z_{{\text{sh}}}} + K}}{i_{{\text{Lh}}x}}{\text{ , }}(x = {\text{a}},{\text{c}}) $ | (5) |
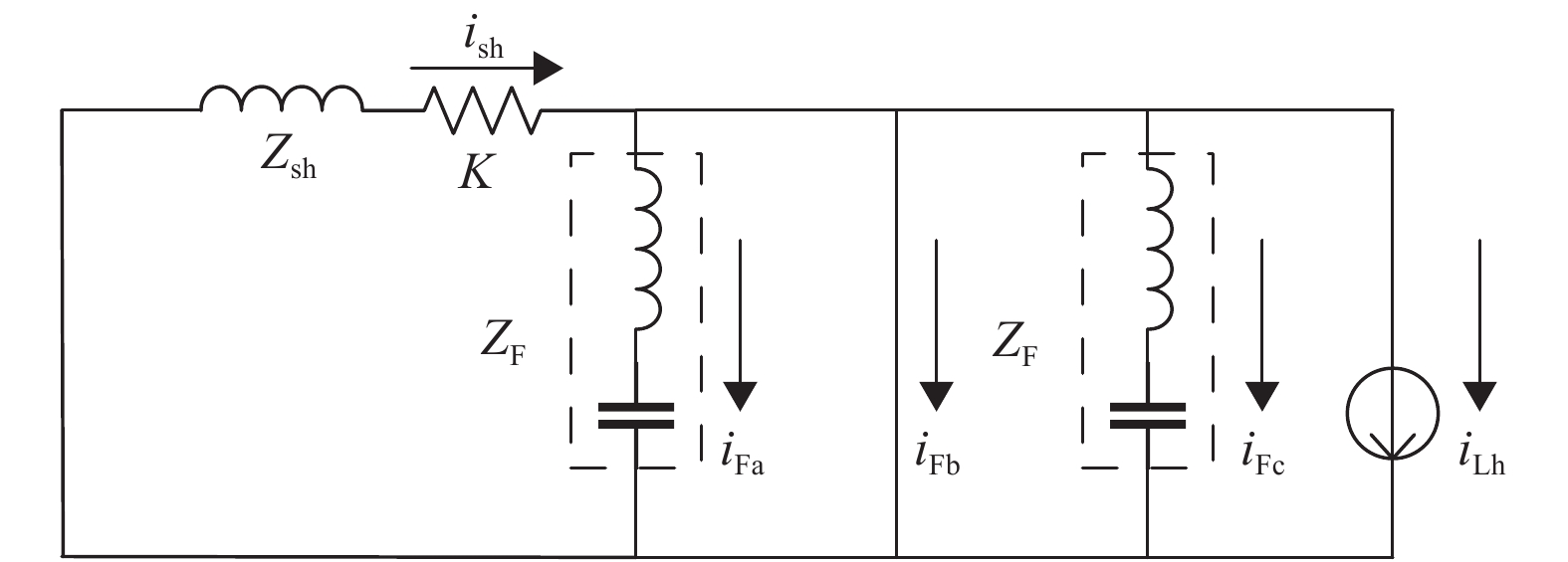
式中:ZF=sLF+1/(sCF) ,Zsh=sLs,并联型的APF主要补偿电网电流谐波,在不考虑电网电压畸变下,电网电压谐波ush=0。由式(5)可知,将变流器控制成电压源后,相当于在电网侧串联一个阻值为K的电阻,迫使电网中的谐波电流流入PF支路,达到补偿电网谐波的目的,其等效图如图3所示。要使电网电流的谐波ish得到抑制,则需增大K值,理想状态下K趋于无穷大时,ish=0。
|
图 3 K值谐波等效电路图 Figure 3 Harmonic equivalent circuit of K value |
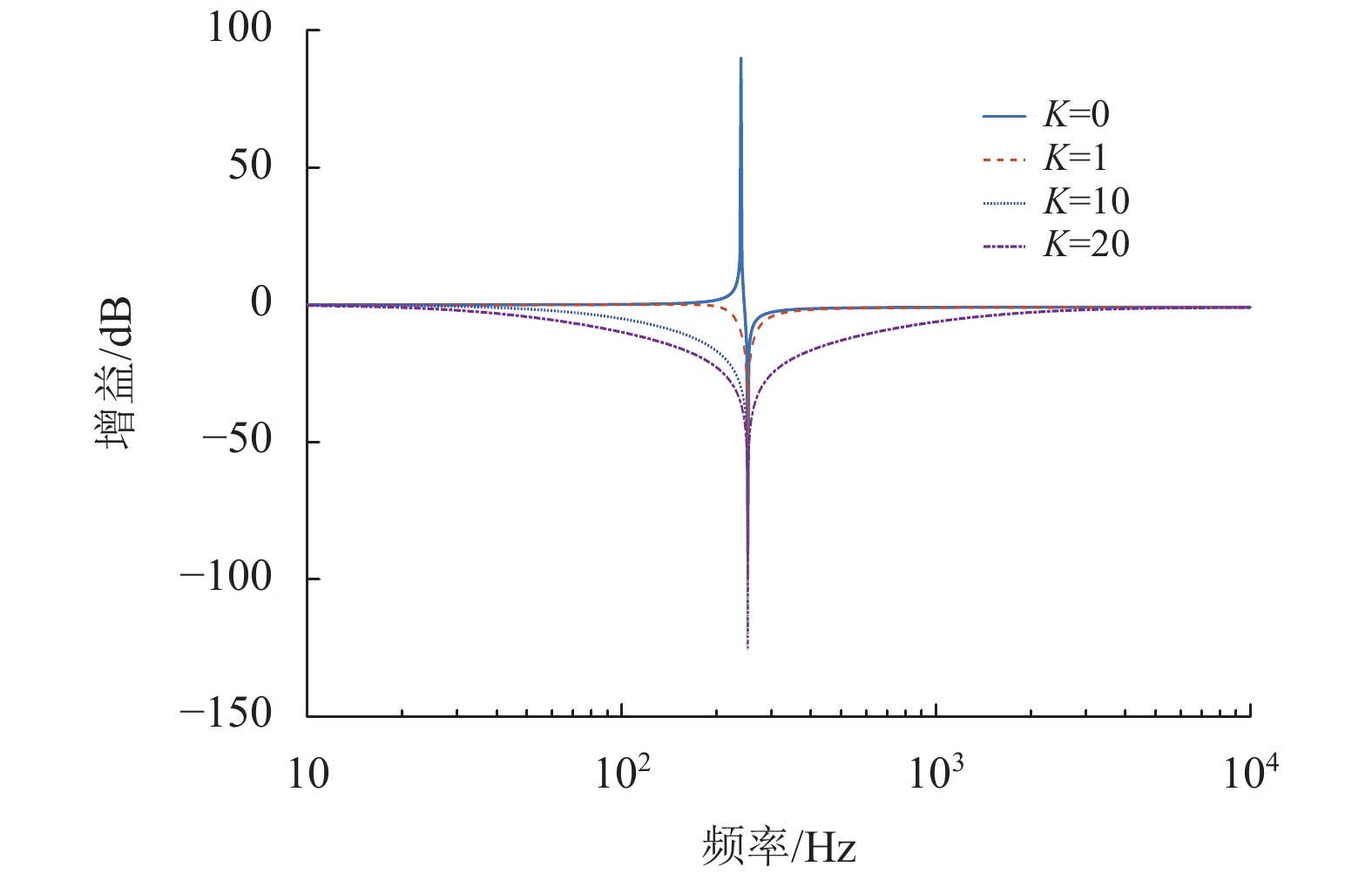
取LF=2 mH,CF=200 μF,由式(4)可得如图4所示的滤波特性图,当仅使用PF补偿时,K=0,在250 Hz频率处增益大于零,发生谐波放大现象,对电网谐波的补偿效果差;当K>0时,电网侧的谐波阻尼增加,增益小于零,对ish的抑制变大。由图4可看出在5次谐振频率抑制最大,当K值越大,抑制效果越明显。
|
图 4 滤波特性 Figure 4 Filtering characteristics |
以上情况为不对称拓扑HAPF的A、C两相的等效分析,B相支路缺少LC滤波器,可以根据另外两相求得补偿量,在三相对称的电网下,三相电流有以下约束关系,即三相电流之和为零。
| $ {i_{{\rm{sa}}}} + {i_{{\rm{sb}}}} + {i_{{\rm{sc}}}} = 0 $ | (6) |
对于谐波等效电路,也有
| $ {i_{{\rm{sha}}}} + {i_{{\rm{shb}}}} + {i_{{\rm{shc}}}} = 0 $ | (7) |
当A、C两相的电流得到补偿后,isha和ishc为零,由式(7)知ishb也相应为零,此时B相APF的控制电压可表示为
| $ {U_{{\rm{Fb}}}} = K( - {i_{{\rm{sha}}}} - {i_{{\rm{shc}}}}) $ | (8) |
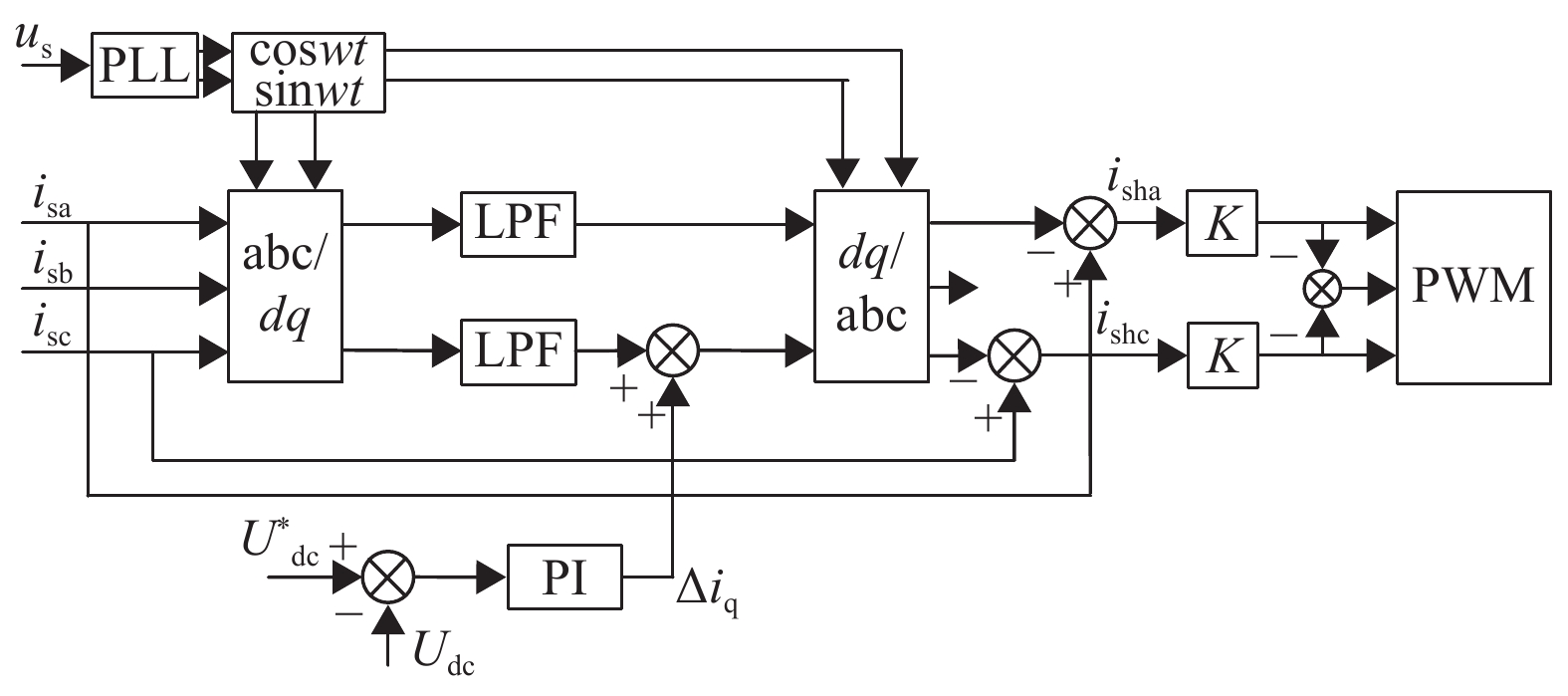
本文采用一种电网电流反馈的控制策略[14],通过ip-iq谐波检测法[15]检测电网谐波isha、ishb、ishc,再使A、C两相的谐波isha、ishc乘以系数K,得到A相和C相的调制电压量后,再由式(8)求出B相的调制电压,最后通过脉冲宽度调制发出脉冲信号驱动开关管通断,系统控制框图如图5所示。
|
图 5 系统控制结构框图 Figure 5 Block diagram of the system control |
直流侧采用PI控制器来维持电容电压的稳定,控制框图如图5所示,PI控制器的公式为
| $ \Delta {i_{\rm{q}}} = ({K_{\rm{p}}} + {K_{\rm{i}}}\frac{1}{s}) \Delta {U_{{\rm{dc}}}} $ | (9) |
式中:Kp为比例系数,Ki为积分系数。直流侧电压期望值U*dc减去Udc后的差值输入PI控制器,由于LC滤波器对基波呈容性,导致补偿电流超前于耦合点电压,故PI控制器输出的Δiq要叠加到谐波检测中无功电流的直流分量上,再通过坐标反变换得到含有一定有功分量的谐波指令值,使APF输出一个与补偿电流同相位的电压,从而产生有功功率控制直流侧电压。
3 仿真与实验验证 3.1 仿真验证用Matlab/Simulink搭建系统仿真模型,验证该拓扑及其控制的可行性,仿真中电网线电压为380V,电网分布电感为0.21 mH,主电路电感LF=2 mH,电容CF=200 μF,非线性负载为不控整流桥带15 Ω纯电阻负载,直流侧电容Cdc=3300 μF,直流侧电压控制在500 V。
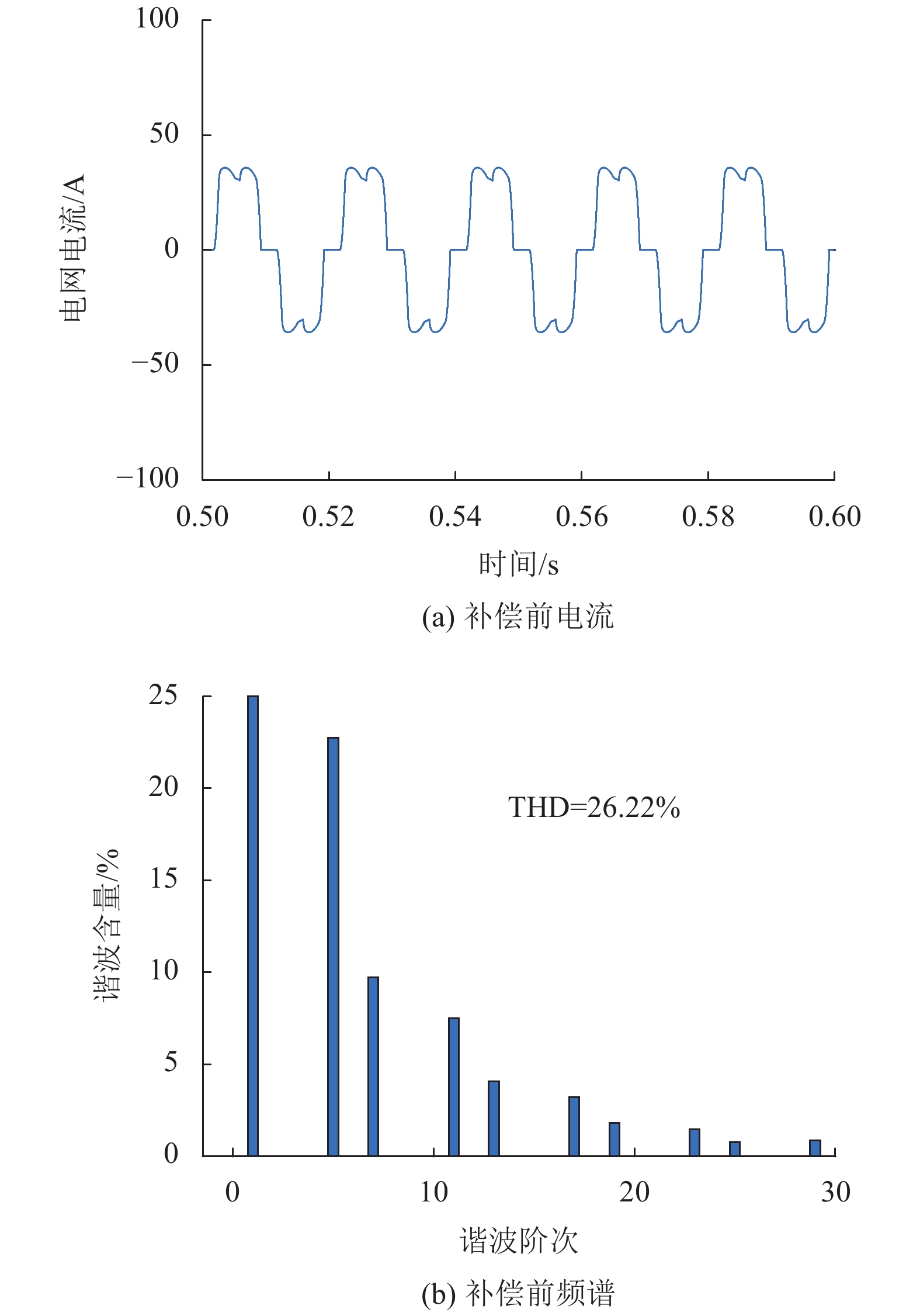
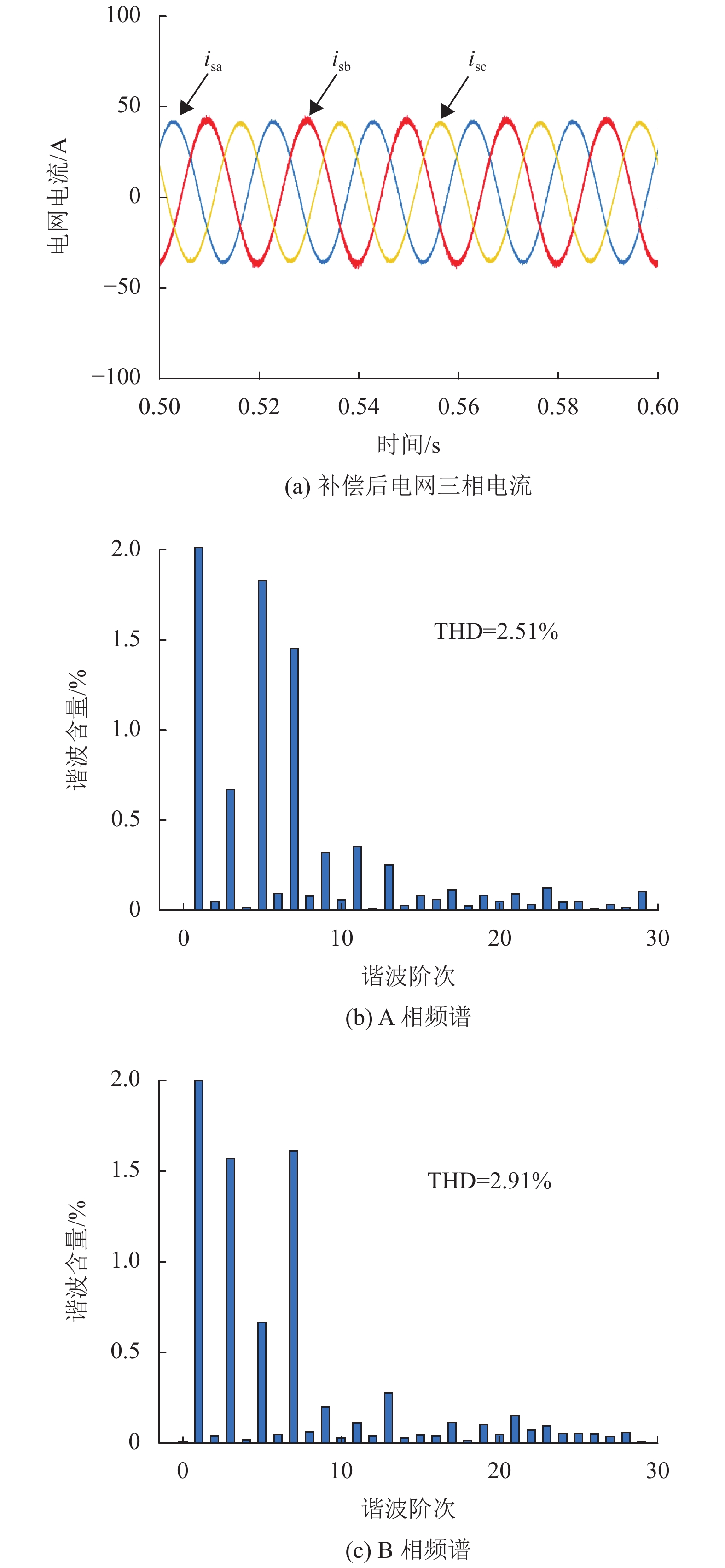
由图6知,补偿前电网电流畸变严重,谐波畸变率达到26.22%。图7为补偿后电流波形及频谱,补偿后三相电流为正弦波,A相和B相的总谐波畸变率(Total Harmonic Distortion,THD)分别为2.51%、2.91%,可见在拓扑不对称的情况下,该装置仍具有补偿谐波的能力,且三相电流的THD均满足5%以下的标准。
|
图 6 补偿前电网电流及频谱 Figure 6 Grid side current waveform without compensation and frequency spectrum |
|
图 7 补偿后电网电流及频谱 Figure 7 Grid side current with compensation and frequency spectrum |
为了进一步验证该不对称拓扑的可行性,搭建一套实验样机进行实验验证,实验样机如图8所示。控制模块采用TMS320F28335浮点型DSP处理器,非线性负载采用三相不控整流带25Ω纯电阻负载,样机参数如表1所示。

|
图 8 实验样机 Figure 8 Experiment prototype |
| 表 1 实验参数 Table 1 experiment parameters |
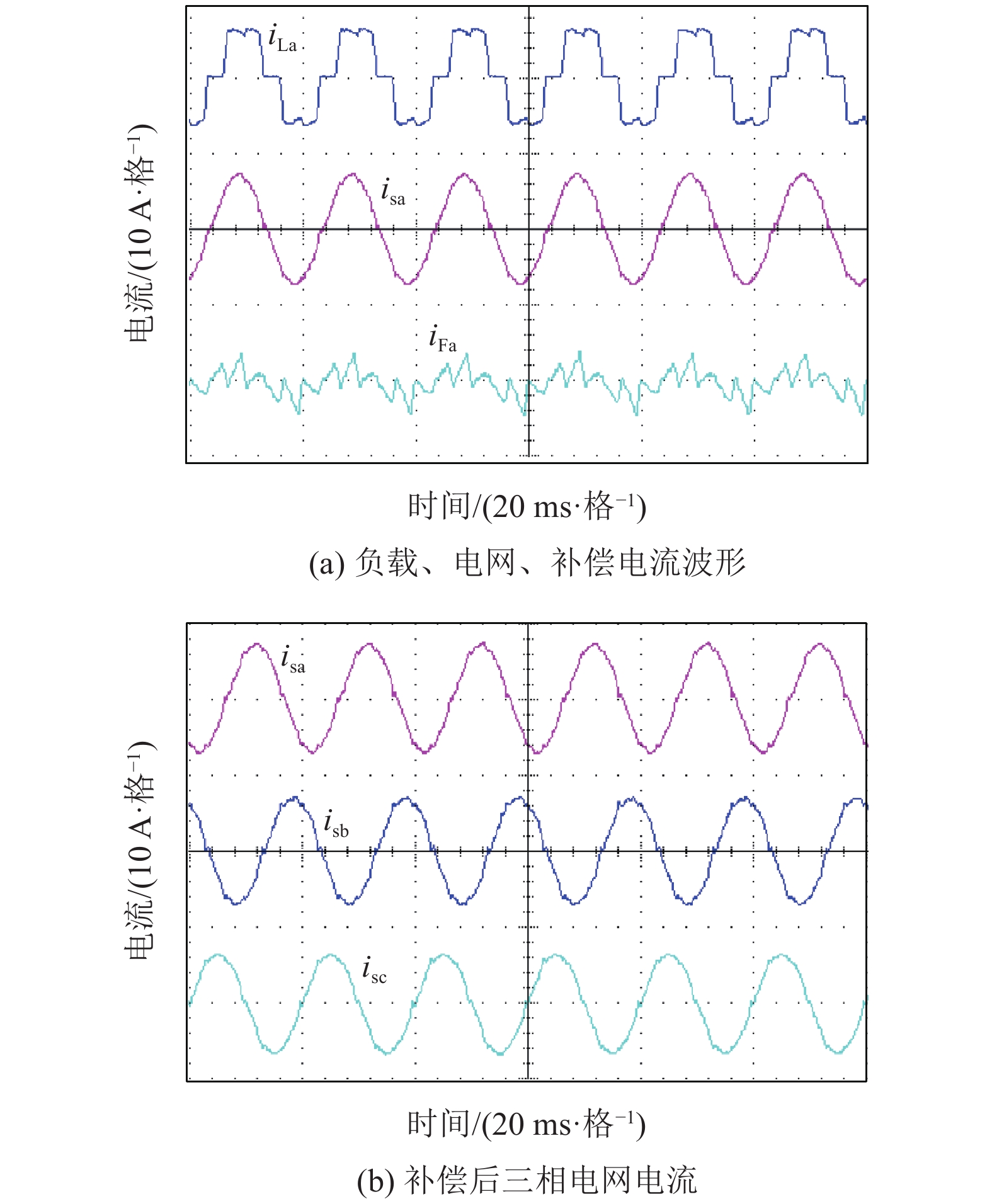
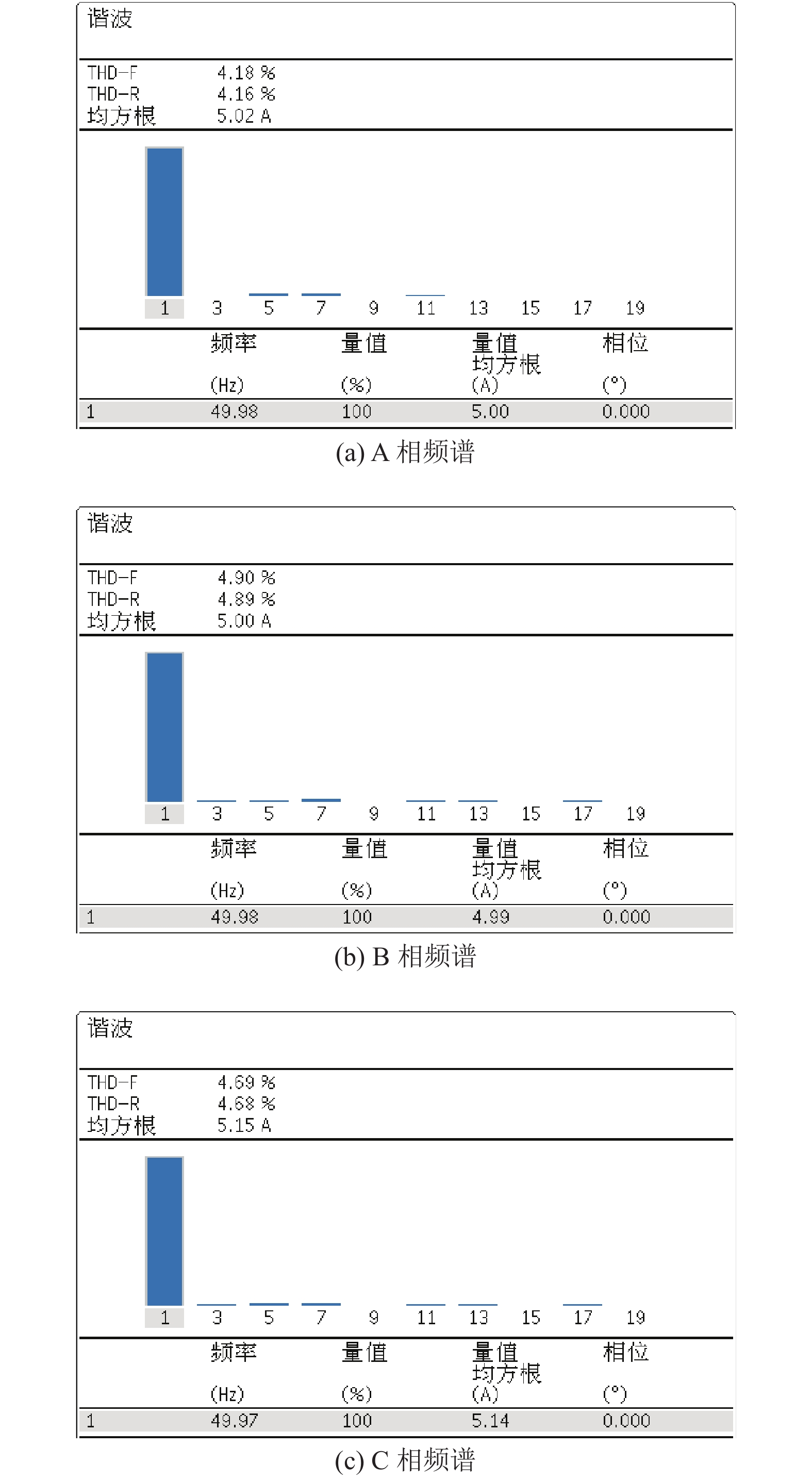
图9(a) 给出的实验波形分别是A相负载电流iLa、电网电流isa和APF注入的谐波电流iFa。补偿前电网电流波形畸变严重,THD达到25.9%。图9(b)为补偿后三相电流波形,可见三相波形呈正弦波,三相对称。由图10知A相、B相和C相的THD分别为4.16%、4.89%、4.68%,电流畸变率大大降低,证明了不对称拓扑的HAPF在缺少B相滤波器件的情况下,具备谐波补偿能力。
|
图 9 实验波形 Figure 9 Experimental waveforms |
|
图 10 补偿后电网电流频谱 Figure 10 Grid side current with compensation and frequency spectrum |
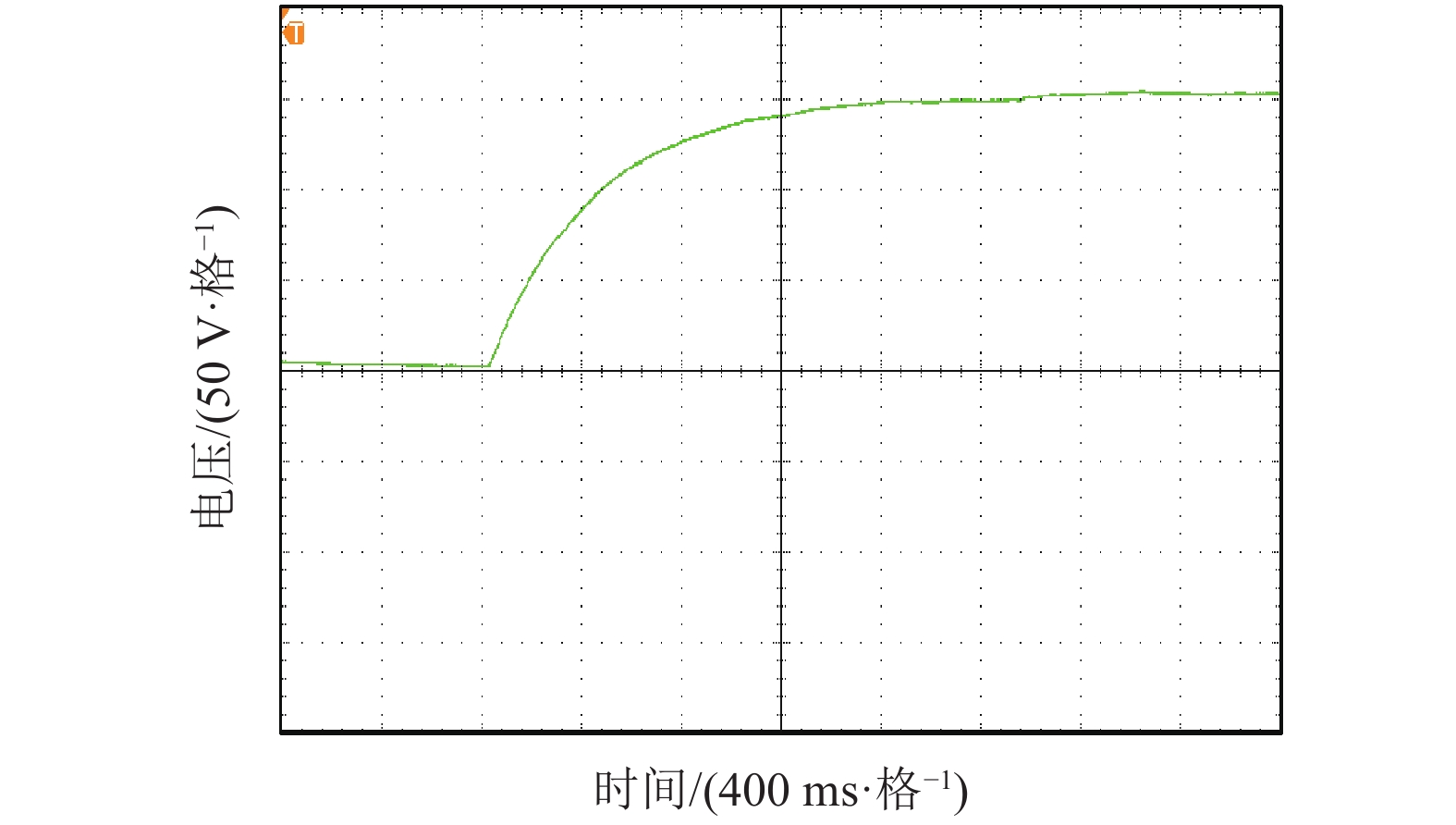
图11为直流侧电容电压波形图,开启装置后电容充电使电压逐渐上升,在PI控制器调节下,上升平稳,无超调,最终稳定于150V,波动幅度很小。
|
图 11 直流侧电压 Figure 11 DC-link voltage |
本文提出了一种不对称拓扑的HAPF,与传统的三相HAPF相比,减少了其中一相滤波电路的器件,使系统结构更加简单,降低了整个系统的成本;文中详细分析不对称HAPF的滤波原理和特性,并利用三相电流的约束关系,控制上仅需考虑两相电流,简化了控制器的设计,提高系统性能,仿真和实验结果验证了所提出拓扑结构可行性。补偿后电网电流THD降低到5%以内,达到电网运行标准。
| [1] |
KALAIR A, ABAS N, KALAIR A R, et al. Review of harmonic analysis, modeling and mitigation techniques[J].
Renewable and Sustainable Energy Reviews, 2017, 78: 1152-1187.
DOI: 10.1016/j.rser.2017.04.121. |
| [2] |
王雪, 高云广, 吝伶艳, 等. 有源电力滤波器的研究现状与展望[J].
电力系统保护与控制, 2019, 47(1): 177-186.
WANG X, GAO Y G, LIN L Y, et al. Research status and prospect of active power filter[J]. Power System Protection and Control, 2019, 47(1): 177-186. DOI: 10.7667/PSPC171873. |
| [3] |
张淼, 庞卓标, 郝雪冬, 等. 一种无变压器型并联混合有源电力滤波器研究[J].
广东工业大学学报, 2019, 36(5): 33-37.
ZHANG M, PANG Z B, HAO X D, et al. A research on a transformerless parallel hybrid active power filter[J]. Journal of Guangdong University of Technology, 2019, 36(5): 33-37. DOI: 10.12052/gdutxb.190011. |
| [4] |
李双健, 杜夏冰, 贾秀芳, 等. 一种应用于LCC高压直流输电的级联H桥混合型有源滤波器[J].
电网技术, 2021, 45(4): 1409-1416.
LI S J, DU X B, JIA X F, et al. A cascaded H-bridge hybrid active power filter applied to LCC-HVDC[J]. Power System Technology, 2021, 45(4): 1409-1416. DOI: 10.13335/j.1000-3673.pst.2020.0281. |
| [5] |
LI D, WANG T, PAN W, et al. A comprehensive review of improving power quality using active power filters[J].
Electric Power Systems Research, 2021, 199(3): 107389.
|
| [6] |
TAREEN W U, MEKHILEF S, SEYEDMAHMOUDIAN M, et al. Active power filter (APF) for mitigation of power quality issues in grid integration of wind and photovoltaic energy conversion system[J].
Renewable and Sustainable Energy Reviews, 2017, 70: 635-655.
DOI: 10.1016/j.rser.2016.11.091. |
| [7] |
施大发, 吴传平. 基于两相三线制变流器的高速铁路负序和谐波综合补偿新方法[J].
电工技术学报, 2012, 27(7): 257-266.
SHI D F, WU C P. A novel integrated compensation method of negative sequence and harmonic for high-speed railway based on two-phase three-wire converter[J]. Transactions of China Electrotechnical Society, 2012, 27(7): 257-266. DOI: 10.19595/j.cnki.1000-6753.tces.2012.07.034. |
| [8] |
夏焰坤. 基于两相三线制变流器的高速铁路新型同相供电系统仿真计算[J].
铁道学报, 2018, 40(8): 68-72.
XIA Y K. Simulative calculation of novel cophase power supply system based on two-phase three wire converter for high-speed railway[J]. Journal of the China Railway Society, 2018, 40(8): 68-72. DOI: 10.3969/j.issn.1001-8360.2018.08.009. |
| [9] |
郭亚男, 孟庆达, 刘培忠, 等. 三相四开关并联型有源电力滤波器选择性谐波补偿方法[J].
电力电容器与无功补偿, 2018, 39(3): 5-10.
GUO Y N, MENG Q D, LIU P Z, et al. Selective harmonic compensation method for three-phase four-switch SAPF[J]. Power Capacitor & Reactive Power Compensation, 2018, 39(3): 5-10. DOI: 10.14044/j.1674-1757.pcrpc.2018.03.002. |
| [10] |
LUO Z, SU M, SUN Y, et al. Analysis and control of a reduced switch hybrid active power filter[J].
IET Power Electronics, 2016, 9(7): 1416-1425.
DOI: 10.1049/iet-pel.2015.0027. |
| [11] |
TAREEN W K, MEKHIELF S. Three-phase transformerless shunt active power filter with reduced switch count for harmonic compensation in grid-connected applications[J].
IEEE Transactions on Power Electronics, 2018, 33(2): 4868-4881.
|
| [12] |
牛庆, 邵蕾, 蔡华洵, 等. 基于微网有源滤波装置谐波检测与抑制的研究[J].
智慧电力, 2020, 48(12): 46-50.
NIU Q, SHAO L, CAI H X, et al. Harmonic detection and suppression of active filter device based on microgrid[J]. Smart Power, 2020, 48(12): 46-50. DOI: 10.3969/j.issn.1673-7598.2020.12.009. |
| [13] |
何克成, 温润, 李璐, 等. 改进型并联混合有源滤波器设计研究[J].
实验室研究与探索, 2021, 40(11): 94-100.
HE K C, WEN R, LI L, et al. Research on the design of improved shunt hybrid active power filter[J]. Research and Exploration in Laboratory, 2021, 40(11): 94-100. DOI: 10.19927/j.cnki.syyt.2021.11.021. |
| [14] |
时晓洁, 王智强, 张军明, 等. 单调谐并联混合有源电力滤波器控制策略研究[J].
电机与控制学报, 2012, 16(4): 64-71.
SHI X J, WANG Z Q, ZHANG J M, et al. Study on the control strategy for single-tuned hybrid active power filters[J]. Electric Machines and Control, 2012, 16(4): 64-71. DOI: 10.3969/j.issn.1007-449X.2012.04.011. |
| [15] |
古超帆, 张新燕, 童涛, 等. 基于二阶广义积分器的改进型ip-iq谐波检测算法
[J].
电测与仪表, 2020, 57(10): 88-93.
GU C F, ZHANG X Y, TONG T, et al. An improved ip-iq harmonic detection algorithm based on second-order generalized integrator [J]. Electrical Measurement and Instrumentation, 2020, 57(10): 88-93. |
 2023, Vol. 40
2023, Vol. 40

