多智能体系统的协同控制因其在无人机作战、机器人编队等方面的广泛应用而得到关注。作为其中一个重要的研究分支,领导跟随一致性问题在近几年取得了大量的研究成果[1-6]。
多智能体系统中大多数一致性控制算法是根据各智能体状态信息设计的,当这些信息不可用时,此类控制器的设计将会受到限制。为解决上述问题,基于状态观测器的控制方法被提出,如文献[7]根据滑模观测器估计的状态信息构建了分布式控制协议。类似地,如果在领导跟随多智能体系统中领导者状态信息不可用时,需要设计相应的观测器来观测[8]。值得注意的是,上述观测器的设计依赖于输出向量的连续测量,这样会造成信道的拥堵和较高的控制成本。
输出向量是否能够只在某些离散时刻获取,同时设计出相应的观测器?答案是肯定的。脉冲观测器于2007年首次被Raff [9]提出,它只需要观测器状态在离散时刻进行更新。相比连续测量的观测器,这大大减少了观测器与系统之间的信息交互,节省了通信带宽。近年来,脉冲观测器逐步得到重视。例如,为实现时滞系统的稳定,文献[10]设计了一类基于脉冲观测器的脉冲控制器;文献[11]对不确定线性系统给出了基于脉冲观测器的镇定方法;文献[12]研究了不确定交换信息的带有脉冲观测器的神经网络的同步;文献[13]研究了基于脉冲观测器的时滞多智能体系统的一致性问题。虽然脉冲观测器的前景较好,但是基于此的多智能体系统一致性控制的相关研究成果仍然较少。
本文旨在设计合适的多智能体脉冲观测器以估计领导者的信息,再根据估计的信息设计相应的控制方法,实现系统的领导跟随一致性。通过构造合适的Lyapunov函数和线性矩阵不等式理论,给出了系统实现领导跟随一致性的充分条件。
1 预备知识及问题描述 1.1 图论多智能体系统可用有向图
考虑具有一个领导者和
| $ \left\{ \begin{gathered} {{{\dot {\boldsymbol{x}}}}_0}(t) = {{{{\boldsymbol{A}}}{{{\boldsymbol{x}}}}}_0}(t) + {{\boldsymbol{B}}}{{{\boldsymbol{u}}}_0}(t) \\ {{{\boldsymbol{y}}}_0}(t) = {{\boldsymbol{C}}}{{{\boldsymbol{x}}}_0}(t) \\ \end{gathered} \right. $ | (1) |
式中:
| $ \left\{ \begin{gathered} {{{\dot {\boldsymbol{x}}}}_i}(t) = {{\boldsymbol{A}}}{{{\boldsymbol{x}}}_i}(t) + {{\boldsymbol{B}}}{{{\boldsymbol{u}}}_i}(t) \\ {{{\boldsymbol{y}}}_i}(t) = {{\boldsymbol{C}}}{{{\boldsymbol{x}}}_i}(t) \\ \end{gathered} \right. $ | (2) |
式中:
令序列
| $ \left\{ \begin{array}{l} {{\dot{ \hat {\boldsymbol{x}}}}_{{i}}}( {t}) = {\boldsymbol{A}}{{\hat {\boldsymbol{x}}}_{i}}( {t}) + {\boldsymbol{B}}{{\boldsymbol{u}}_0}({t}) {\rm{, }} \; {t} \ne { {t}_{k}}\\ {{\hat {\boldsymbol{x}}}_{i}}({t}_{k}^ { + }) = {{\hat {\boldsymbol{x}}}_{i}}({t}_{k}^{ - }) + {\boldsymbol{G}}\left[{l_{ {ij}}}({{\hat y}_{i}}({t}_ {k}^{ - }) - {{\hat y}_{j}}({t}_{k}^{ - }) ) + \right. \\ \left. \quad\qquad{{\boldsymbol{d}}_{i}}({{\hat {\boldsymbol{y}}}_ {i}}( {t}_{k}^{ - }) - {{\boldsymbol{y}}_0}({t}_ {k}^ { - }) ) \right]{\rm{, }}\;{t} = {{t}_{k}}\\ {{\hat {\boldsymbol{y}}}_{i}}({t}) = {\boldsymbol{C}}{{\hat {\boldsymbol{x}}}_{i}}( {t}) \end{array} \right. $ | (3) |
式中:
本文的一致性控制协议设计为
| $ {{\boldsymbol{u}}_{i}}({t}) = {{\boldsymbol{u}}_{0}}({t}) - {\boldsymbol{K}}({{\boldsymbol{x}}_{i}}({t}) - {\hat {\boldsymbol{x}}_{i}}({t}) ) $ | (4) |
式中:
定义
| $ \left\{ \begin{gathered} {{\dot {\boldsymbol{\varepsilon}} }_{i}}({t}) = ({{\boldsymbol{A}}} - {{\boldsymbol{BK}}}) {{\boldsymbol{\varepsilon}} _{i}}({t}) + {\boldsymbol{BK}}{{\boldsymbol{e}}_{i}}({t}) ,\quad {t} \ne {{t}_{k}} \\ {{\dot {\boldsymbol{e}}}_{i}}({t}) = {\boldsymbol{A}}{{\boldsymbol{e}}_{i}}({t}) {\text{ }} \\ {{\boldsymbol{\varepsilon}} _{i}}({t}_{k}^{ + }) = {{\boldsymbol{\varepsilon}} _{i}}({t}_{k}^{ - }) ,\quad {t} = {{t}_{k}} \\ {{\boldsymbol{e}}_{i}}({t}_{k}^{ + }) = {{\boldsymbol{e}}_{i}}({t}_{k}^ - ) + {\boldsymbol{GC}}\sum\limits_{{j = 1}}^{N} {\big[({{\boldsymbol{l}}_{{ij}}}({{\boldsymbol{e}}_{i}}({t}_{k}^ - ) } - {{\boldsymbol{e}}_{j}}({t}_{k}^ - ) + {{\boldsymbol{d}}_{i}}{{\boldsymbol{e}}_{i}}({t}_{k}^ - ) \big] \\ \end{gathered} \right. $ | (5) |
此外,基于引理3,上述误差动力学模型可改写为
| $ \left\{ \begin{gathered} \dot {\boldsymbol{\varepsilon}} ({t}) = \left[{{\boldsymbol{I}}_{N}} \otimes \left({\boldsymbol{A}} - {\boldsymbol{BK}}\right) \right]{\boldsymbol{\varepsilon}} ({t}) + ({{\boldsymbol{I}}_{N}} \otimes {\boldsymbol{BK}}) {\boldsymbol{e}}({t}) \\ \dot {\boldsymbol{e}}({t}) = ({{\boldsymbol{I}}_{N}} \otimes {\boldsymbol{A}}) {\boldsymbol{e}}({t}) ,{\text{ }}{t} \ne {{t}_{k}} \\ {\boldsymbol{\varepsilon}} ({t}_{k}^{ + }) = {\boldsymbol{\varepsilon}} ({{t}_{k}}) \\ {\boldsymbol{e}}({t}_{k}^{ + }) = [{{\boldsymbol{I}}_{{Nn}}} + {\boldsymbol{GC}} \otimes {\boldsymbol{H}}]{\boldsymbol{e}}({t}_{k}^ - ) ,{\text{ }}{t = }{{t}_{k}} \\ \end{gathered} \right. $ | (6) |
式中:
| $ \begin{gathered} {\boldsymbol{\varepsilon}} ({t}) = {[{\boldsymbol{\varepsilon}} _{1}^{{\rm{{\rm{T}}}}}({t}) ,{\boldsymbol{\varepsilon}} _{2}^{{\rm{T}}}({t}) ,\cdots,{\boldsymbol{\varepsilon}} _{N}^{{\rm{T}}}({t}) ]^{{\rm{T}}}} \\ {\boldsymbol{e}}({t}) = {[{\boldsymbol{e}}_{1}^{{\rm{T}}}({t}) ,{\boldsymbol{e}}_{2}^{{\rm{T}}}({t}) ,\cdots,{\boldsymbol{e}}_{N}^{{\rm{T}}}({t}) ]^{{\rm{T}}}} \\ \end{gathered} $ |
以下是本文所需要用到的定义、引理和假设。
定义1 如果对系统(1) ~(2)的任意初始条件,有下式成立:
| $ \mathop {\lim }\limits_{{t} \to + \infty } ||{\boldsymbol{e}}({t}) || = 0 $ |
则称领导跟随多智能体系统(1) ~(2)实现了领导跟随一致。
引理1[14] 给定对称矩阵
| $ {{\boldsymbol{{\boldsymbol{X}}}}} = \left[ {\begin{array}{*{20}{c}} {{{{\boldsymbol{X}}}_{11}}}&{{{{\boldsymbol{X}}}_{12}}} \\ {{{\boldsymbol{X}}}_{12}^{\rm{T}}}&{{{{\boldsymbol{X}}}_{22}}} \end{array}} \right] $ |
若
(1)
(2)
(3)
引理2[15] 若矩阵
| $ {\lambda _{\min }} = {\lambda _1} \leqslant {\lambda _2} \leqslant \cdots \leqslant {\lambda _{n - 1}} \leqslant {\lambda _n} = {\lambda _{\max }} $ |
则对任意
引理3[16] 符号“
(1)
(2)
(3)
(4)
假设1
假设2 领导跟随多智能体系统的通信拓扑具有一棵以领导者为根节点的有向生成树。
2 主要结果本节定义了一个分段连续函数
定义函数:
| $ {\phi _k}(t) = \frac{c}{{{{({t_{k + 1}} - {t_k}) }^2}}}\left(1 - \frac{1}{\mu }\right) {\left(t - {t_k}\right) ^2} + \frac{c}{\mu },{\text{ }}t \in \left[{t_k},{t_{k + 1}}\right] $ |
和分段连续函数
| $ \phi (t) = \left\{ \begin{gathered} {\phi _k}(t) ,{\text{ }}t \in ({t_k},{t_{k + 1}}) \\ \phi (t_k^ + ) = {\phi _k}({t_k}) ,{\text{ }}t = {t_k} \\ \end{gathered} \right. $ |
则对任意
| $ \phi ({t_k}) = \frac{c}{\mu },\quad \phi \left(t_{k + 1}^ - \right) = c $ | (7) |
此外,
| $ \phi ({t_k}) \leqslant \phi (t) \leqslant \phi \left(t_{k + 1}^ - \right) $ | (8) |
| $ 0 \leqslant \dot \phi (t) \leqslant \frac{{2c}}{h}\left(1 - \frac{1}{\mu }\right) $ | (9) |
式中:
定理1 在假设1和2成立的情况下,如果存在
| $ \left[ {\begin{array}{*{20}{c}} { - \mu {{{\bar {\boldsymbol{P}}}}_2}}&{{{\left({{{\boldsymbol{I}}}_{Nn}} + {{\boldsymbol{GC}}} \otimes {{\boldsymbol{H}}}\right) }^{\rm{T}}}{{{\bar {\boldsymbol{P}}}}_2}} \\ &{ - {{{\bar {\boldsymbol{P}}}}_2}} \end{array}} \right] < 0 $ | (10) |
| $ {{\boldsymbol{\varPsi}} } = \left[ {\begin{array}{*{20}{c}} {{{{\boldsymbol{\varGamma}} }_1}}&0&{{{{\boldsymbol{\varGamma}} }_3}}&{{{{\bar {\boldsymbol{P}}}}_1}{\bar {\boldsymbol{B}}\bar {\boldsymbol{K}}}} \\ &{{{{\boldsymbol{\varGamma}} }_2}}&0&{{{{\bar {\boldsymbol{P}}}}_2}{\bar {\boldsymbol{A}}} + \left(\dfrac{c}{2} + \dfrac{c}{{2\mu }}\right) {{{\boldsymbol{W}}}_2}} \\ & &{ - {{{\boldsymbol{W}}}_1}}&0 \\ & & &{ - {{{\boldsymbol{W}}}_2}} \end{array}} \right] < 0 $ | (11) |
式中:
| $ {{{\boldsymbol{\varGamma}} }_1} = \frac{{2c}}{h}\left(1 - \frac{1}{\mu }\right) {{\bar {\boldsymbol{P}}}_1} - \frac{{{c^2}}}{\mu }{{{\boldsymbol{W}}}_1} $ |
| $ {{{\boldsymbol{\varGamma}} }_2} = \frac{{2c}}{h}\left(1 - \frac{1}{\mu }\right) {{\bar {\boldsymbol{P}}}_2} - \frac{{{c^2}}}{\mu }{{{\boldsymbol{W}}}_2} $ |
| $ {{{\boldsymbol{\varGamma}} }_3} = {{\bar {\boldsymbol{P}}}_1}\left({\bar {\boldsymbol{A}}} - {\bar {\boldsymbol{B}}\bar {\boldsymbol{K}}}\right) + \left(\frac{c}{2} + \frac{c}{{2\mu }}\right) {{{\boldsymbol{W}}}_1} $ |
则多智能体系统(1) ~(2)在脉冲观测器(3)和控制器(4)的作用下实现了领导跟随一致。
证明 选取Lyapunov函数:
| $ V(t) = {e^{{\delta _0}t}}\phi (t) {{{\boldsymbol{\varepsilon}} }^{\rm{T}}}(t) {{\bar {\boldsymbol{P}}}_1}{{\boldsymbol{\varepsilon}} }(t) + {{{e}}^{{\delta _0}t}}\phi (t) {{{\boldsymbol{e}}}^{\rm{T}}}(t) {{\bar {\boldsymbol{P}}}_2}{{\boldsymbol{e}}}(t) $ | (12) |
式中:
| $ \begin{gathered} V(t_k^ + ) = {e^{{\delta _0}{t_k}}}\phi (t_k^ + ) {{{\boldsymbol{\varepsilon }}}^{\rm{{\rm{T}}}}}(t_k^ + ) {{{\bar {\boldsymbol{{\boldsymbol{P}}}}}}_1}{{\boldsymbol{\varepsilon}} }(t_k^ + ) + {e^{{\delta _0}{t_k}}}\phi (t_k^ + ) {{{\boldsymbol{e}}}^{\rm{T}}}(t_k^ + ) {{{\bar {\boldsymbol{P}}}}_2}{{\boldsymbol{e}}}(t_k^ + ) = \\ \quad\quad\quad\; {e^{{\delta _0}{t_k}}}\phi ({t_k}) {{{\boldsymbol{\varepsilon}} }^{\rm{T}}}(t_k^ - ) {{{\bar {\boldsymbol{P}}}}_1}{{\boldsymbol{\varepsilon}} }(t_k^ - ) + {e^{{\delta _0}{t_k}}}\phi ({t_k}) {{{\boldsymbol{e}}}^{\rm{T}}}(t_k^ - ) ({{{\boldsymbol{I}}}_{Nn}} + \\ \quad\quad\quad\; {{\boldsymbol{GC}}} \otimes {{\boldsymbol{H}}}{) ^{\rm{T}}}{{{\bar {\boldsymbol{P}}}}_2}({{{\boldsymbol{I}}}_{Nn}} + {{\boldsymbol{GC}}} \otimes {{\boldsymbol{H}}}) {{\boldsymbol{e}}}(t_k^ - ) \leqslant {e^{{\delta _0}{t_k}}} \times \frac{c}{\mu } \times \mu \times \\ \quad\quad\quad\; ({{{\boldsymbol{\varepsilon}} }^{\rm{T}}}(t_k^ - ) {{{\bar {\boldsymbol{P}}}}_1}{{\boldsymbol{\varepsilon}} }(t_k^ - ) + {{{\boldsymbol{e}}}^{\rm{T}}}(t_k^ - ) {{{\bar {\boldsymbol{P}}}}_2}{{\boldsymbol{e}}}(t_k^ - ) ) {\text{ = }}V(t_k^ - ) \\ \end{gathered} $ |
即对任意
| $ V(t_k^ + ) \leqslant V(t_k^ - ) $ | (13) |
另一方面,当
| $ \begin{gathered} {D^ + }V(t) - {\delta _0}V(t) = {\delta _0}{e^{{\delta _0}t}}\phi (t) {{{\boldsymbol{\varepsilon}} }^{\rm{T}}}(t) {{{\bar {\boldsymbol{P}}}}_1}{{\boldsymbol{\varepsilon}} }(t) + {e^{{\delta _0}t}}\dot \phi (t) {{{\boldsymbol{\varepsilon}} }^{\rm{T}}}(t) {{{\bar {\boldsymbol{P}}}}_1}{{\boldsymbol{\varepsilon}} }(t) + \\ \quad\quad\quad 2{e^{{\delta _0}t}}\phi (t) {{{\boldsymbol{\varepsilon}} }^{\rm{T}}}(t) {{{\bar {\boldsymbol{P}}}}_1}{\dot {\boldsymbol{\varepsilon}} }(t) - {\delta _0}{e^{{\delta _0}t}}\phi (t) {{{\boldsymbol{\varepsilon}} }^{\rm{T}}}(t) {{{\bar {\boldsymbol{P}}}}_1}{{\boldsymbol{\varepsilon}} }(t) + \\ \quad\quad\quad {\delta _0}{e^{{\delta _0}t}}\phi (t) {{{\boldsymbol{e}}}^{\rm{T}}}(t) {{{\bar {\boldsymbol{P}}}}_2}{{\boldsymbol{e}}}(t) + {e^{{\delta _0}t}}\dot \phi (t) {{{\boldsymbol{e}}}^{\rm{T}}}(t) {{{\bar {\boldsymbol{P}}}}_2}{{\boldsymbol{e}}}(t) + \\ \quad\quad\quad 2{e^{{\delta _0}t}}\phi (t) {{{\boldsymbol{e}}}^{\rm{T}}}(t) {{{\bar {\boldsymbol{P}}}}_2}{\dot {\boldsymbol{e}}}(t) - {\delta _0}{e^{{\delta _0}t}}\phi (t) {{{\boldsymbol{e}}}^{\rm{T}}}(t) {{{\bar {\boldsymbol{P}}}}_2}{{\boldsymbol{e}}}(t) = \\ \quad\quad\quad {e^{{\delta _0}t}}\dot \phi (t) {{{\boldsymbol{\varepsilon}} }^{\rm{T}}}(t) {{{\bar {\boldsymbol{P}}}}_1}{{\boldsymbol{\varepsilon}} }(t) + 2{e^{{\delta _0}t}}\phi (t) {{{\boldsymbol{\varepsilon}} }^{\rm{T}}}(t) {{{\bar {\boldsymbol{P}}}}_1}{\dot {\boldsymbol{\varepsilon}} }(t) + \\ \quad\quad\quad {e^{{\delta _0}t}}\dot \phi (t) {{{\boldsymbol{e}}}^{\rm{T}}}(t) {{{\bar {\boldsymbol{P}}}}_2}{{\boldsymbol{e}}}(t) + 2{e^{{\delta _0}t}}\phi (t) {{{\boldsymbol{e}}}^{\rm{T}}}(t) {{{\bar {\boldsymbol{P}}}}_2}{\dot {\boldsymbol{e}}}(t) \leqslant {e^{{\delta _0}t}} \times \\ \quad\quad\quad \frac{{2c}}{h} \times \left(1 - \frac{1}{\mu }\right) \times {{{\boldsymbol{\varepsilon}} }^{\rm{T}}}(t) {{{\bar {\boldsymbol{P}}}}_1}{{\boldsymbol{\varepsilon}} }(t) + \\ \quad\quad\quad 2{e^{{\delta _0}t}}\phi (t) {{{\boldsymbol{\varepsilon}} }^{\rm{T}}}(t) {{{\bar {\boldsymbol{P}}}}_1}\left[({\bar {\boldsymbol{A}}} - {\bar {\boldsymbol{B}}\bar {\boldsymbol{K}}}) {{\boldsymbol{\varepsilon}} }(t) + {\bar {\boldsymbol{B}}\bar {\boldsymbol{Ke}}}(t) \right] + \\ \quad\quad\quad {e^{{\delta _0}t}} \times \frac{{2c}}{h} \times \left(1 - \frac{1}{\mu }\right) \times {{{\boldsymbol{e}}}^{\rm{T}}}(t) {{{\bar {\boldsymbol{P}}}}_2}{{\boldsymbol{e}}}(t) + \\ \quad\quad\quad 2{e^{{\delta _0}t}}\phi (t) {{{\boldsymbol{e}}}^{\rm{T}}}(t) {{{\bar {\boldsymbol{P}}}}_2}{\bar {\boldsymbol{Ae}}}(t) \\ \end{gathered} $ |
因为
| $ \begin{gathered} \left(c - \phi (t) \right) \left(\phi (t) - \frac{c}{\mu }\right) {{{\boldsymbol{\varepsilon}} }^{\rm{T}}}(t) {{{\boldsymbol{W}}}_1}{{\boldsymbol{\varepsilon}} }(t) \geqslant 0 \\ \left(c - \phi (t) \right) \left(\phi (t) - \frac{c}{\mu }\right) {{{\boldsymbol{e}}}^{\rm{T}}}(t) {{{\boldsymbol{W}}}_2}{{\boldsymbol{e}}}(t) \geqslant 0 \\ \end{gathered} $ |
故有
| $ \begin{gathered} {D^ + }V(t) - {\delta _0}V(t) \leqslant {e^{{\delta _0}t}} \times \dfrac{{2c}}{h} \times \left(1 - \dfrac{1}{\mu }\right) \times {{{\boldsymbol{\varepsilon}} }^{{\rm{T}}}}(t) {{{\bar {\boldsymbol{P}}}}_1}{{\boldsymbol{\varepsilon}} }(t) + \\ \quad\quad\quad 2{e^{{\delta _0}t}} \times \phi (t) \times {{{\boldsymbol{\varepsilon}} }^{{\rm{T}}}}(t) {{{\bar {\boldsymbol{P}}}}_1}\left[({\bar {\boldsymbol{A}}} - {\bar {\boldsymbol{B}}\bar {\boldsymbol{K}}}) {{\boldsymbol{\varepsilon}} }(t) + {\bar {\boldsymbol{B}}\bar {\boldsymbol{Ke}}}(t) \right] + \\ \quad\quad\quad \left(c + \dfrac{c}{\mu }\right) \times \phi (t) \times {e^{{\delta _0}t}} \times {{{\boldsymbol{\varepsilon}} }^{{\rm{T}}}}(t) {{{\boldsymbol{W}}}_{1}}{{\boldsymbol{\varepsilon}} }(t) - \dfrac{{{c^2}}}{\mu } \times \\ \quad\quad\quad {e^{{\delta _0}t}} \times {{{\boldsymbol{\varepsilon}} }^{{\rm{T}}}}(t) {{{\boldsymbol{W}}}_{1}}{{\boldsymbol{\varepsilon}} }(t) + {e^{{\delta _0}t}} \times \dfrac{{2c}}{h} \times \left(1 - \dfrac{1}{\mu }\right) \times \\ \quad\quad\quad {{{\boldsymbol{e}}}^{{\rm{T}}}}(t) {{{\bar {\boldsymbol{P}}}}_{2}}{{\boldsymbol{e}}}(t) +2{e^{{\delta _0}t}}\phi (t) {{{\boldsymbol{e}}}^{{\rm{T}}}}(t) {{{\bar {\boldsymbol{P}}}}_{2}}{\bar {\boldsymbol{Ae}}}(t) + \\ \quad\quad\quad \left(c + \dfrac{c}{\mu }\right) \phi (t) \times {e^{{\delta _0}t}} \times{{{\boldsymbol{e}}}^{{\rm{T}}}}(t) {{{\boldsymbol{W}}}_{2}}{{\boldsymbol{e}}}(t) -\dfrac{{{c^2}}}{\mu } \times \\ \quad\quad\quad {e^{{\delta _0}t}} \times {{{\boldsymbol{e}}}^{{\rm{T}}}}(t) {{{\boldsymbol{W}}}_{2}}{{\boldsymbol{e}}}(t) ={e^{{\delta _0}t}}{{{\boldsymbol{\zeta}} }^{{\rm{T}}}}(t) {{\boldsymbol{\varPsi}} {\boldsymbol{\zeta}} }(t) \lt 0 \\ \end{gathered} $ |
式中:
因此,对任意
| $ V(t) \leqslant {e^{{\delta _0}(t - {t_k}) }}V({t_k}) $ | (14) |
对任意
| $ V(t) \leqslant V({t_0}) {e^{{\delta _0}(t - {t_0}) }} \leqslant {\lambda _2}||{{\boldsymbol{\eta}} }({t_0}) |{|^2}{e^{{\delta _0}t}} $ | (15) |
式中:
| $ \begin{gathered} {{\boldsymbol{\eta}} }(t) = {[{{{\boldsymbol{\varepsilon}} }^{{\rm{T}}}}(t) ,{{{\boldsymbol{e}}}^{{\rm{T}}}}(t) ]^{{\rm{T}}}} \\ {\lambda _2} = c\, \max ({\lambda _{\max }}({{{\boldsymbol{P}}}_1}) ,{\lambda _{\max }}({{{\boldsymbol{P}}}_2}) ) \\ \end{gathered} $ |
对任意
| $ \begin{gathered} V(t) \leqslant V({t_1}) {e^{{\delta _0}(t - {t_1}) }} \leqslant V(t_1^ - ) {e^{{\delta _0}(t - {t_1}) }} \leqslant V({t_0}) {e^{{\delta _0}({t_1} - {t_0}) }}{e^{{\delta _0}(t - {t_1}) }} = \\ \qquad\qquad\quad V({t_0}) {e^{{\delta _0}(t - {t_0}) }} \leqslant {\lambda _2}||{{\boldsymbol{\eta}} }({t_0}) |{|^2}{e^{{\delta _0}t}} \\ \end{gathered} $ | (16) |
假设对任意
| $ V(t) \leqslant V(t_{k - 1}^ - ) {e^{{\delta _0}(t - {t_{k - 1}}) }} \leqslant V({t_0}) {e^{{\delta _0}(t - {t_0}) }} \leqslant {\lambda _2}||{{\boldsymbol{\eta}} }({t_0}) |{|^2}{e^{{\delta _0}t}} $ |
现证明对任意
| $ V(t) \leqslant {\lambda _2}||{{\boldsymbol{\eta}} }({t_0}) |{|^2}{e^{{\delta _0}t}} $ | (17) |
对任意
| $ \begin{aligned} V(t) \leqslant & V({t_k}) {e^{{\delta _0}(t - {t_k}) }} \leqslant V(t_k^ - ) {e^{{\delta _0}(t - {t_k}) }} \leqslant V({t_{k - 1}}) {e^{{\delta _0}(t - {t_{k - 1}}) }} \leqslant \\ &V(t_{k - 1}^ - ) {e^{{\delta _0}(t - {t_k}) }} \leqslant \cdots \leqslant V({t_0}) {e^{{\delta _0}(t - {t_0}) }} \leqslant {\lambda _2}||{{\boldsymbol{\eta}} }({t_0}) |{|^2}{e^{{\delta _0}t}} \\ \end{aligned} $ |
即有式(17)成立。由式(14) ~(17) ,通过数学归纳法可得,对任意
注解1 与文献[10]中单个系统的分析不同,本文为基于网络交流的智能体系统的协同控制提供了一种有效的方案。
注解2 在多智能体系统的实际应用中,基于连续测量的观测器会造成较高的资源负载[6-7]。为了克服这一缺点,脉冲技术被采纳到观测器的设计中。脉冲观测器有效地减少了智能体间的通信负担,因为该观测器只需要智能体在
定理1是在假设矩阵K和G已知的情况下得到的。如果这些矩阵事先不可得知,则难以应用该定理。对此,本文给出定理2。该定理可设计合适的矩阵K和G,并基于脉冲观测器(3)与控制器(4),实现多智能体系统(1) ~(2)领导跟随一致。
定理2 在假设1和2成立的情况下,如果存在
| $ \left[ {\begin{array}{*{20}{c}} { - \mu {{{\bar {\boldsymbol{P}}}}_2}}&{{{{\bar {\boldsymbol{P}}}}_2} + {{{\boldsymbol{C}}}^{{\rm{T}}}}{{\boldsymbol{Z}}} \otimes {{{\boldsymbol{H}}}^{{\rm{T}}}}} \\ &{ - {{{\bar {\boldsymbol{P}}}}_2}} \end{array}} \right] \lt 0 $ | (18) |
| $ \left[ {\begin{array}{*{20}{c}} {{{{\bar {\boldsymbol{\varGamma}} }}_1}}&0&{{{{\bar {\boldsymbol{\varGamma}} }}_3}}&{{\bar {\boldsymbol{B}}\bar {\boldsymbol{K}}}} \\ &{{{{\boldsymbol{\varGamma}} }_2}}&0&{{{{\bar {\boldsymbol{P}}}}_2}{\bar {\boldsymbol{A}}} + \left(\dfrac{c}{2} + \dfrac{c}{{2\mu }}\right) {{{\boldsymbol{W}}}_2}} \\ & &{ - {{{\bar {\boldsymbol{W}}}}_1}}&0 \\ & & &{ - {{{\boldsymbol{W}}}_2}} \end{array}} \right] \lt 0 $ | (19) |
式中:
| $ {{\bar {\boldsymbol{\varGamma}} }_1} = \frac{{2c}}{h}\left(1 - \frac{1}{\mu }\right) {{\boldsymbol{X}}} - \frac{{{c^2}}}{\mu }{{\bar {\boldsymbol{W}}}_1} $ |
| $ {{{\boldsymbol{\varGamma}} }_2} = \frac{{2c}}{h}\left(1 - \frac{1}{\mu }\right) {{\bar {\boldsymbol{P}}}_2} - \frac{{{c^2}}}{\mu }{{{\boldsymbol{W}}}_2} $ |
| $ {{\bar {\boldsymbol{\varGamma}} }_3} = {\bar {\boldsymbol{A}}{\boldsymbol{X}}} - {\bar {\boldsymbol{B}}{\boldsymbol{Y}}} + \left(\frac{c}{2} + \frac{c}{{2\mu }}\right) {{\bar {\boldsymbol{W}}}_1} $ |
则多智能体系统(1) ~(2) 在脉冲观测器(3) 和控制器(4) 的作用下可实现领导跟随一致。
证明 令
另外,令
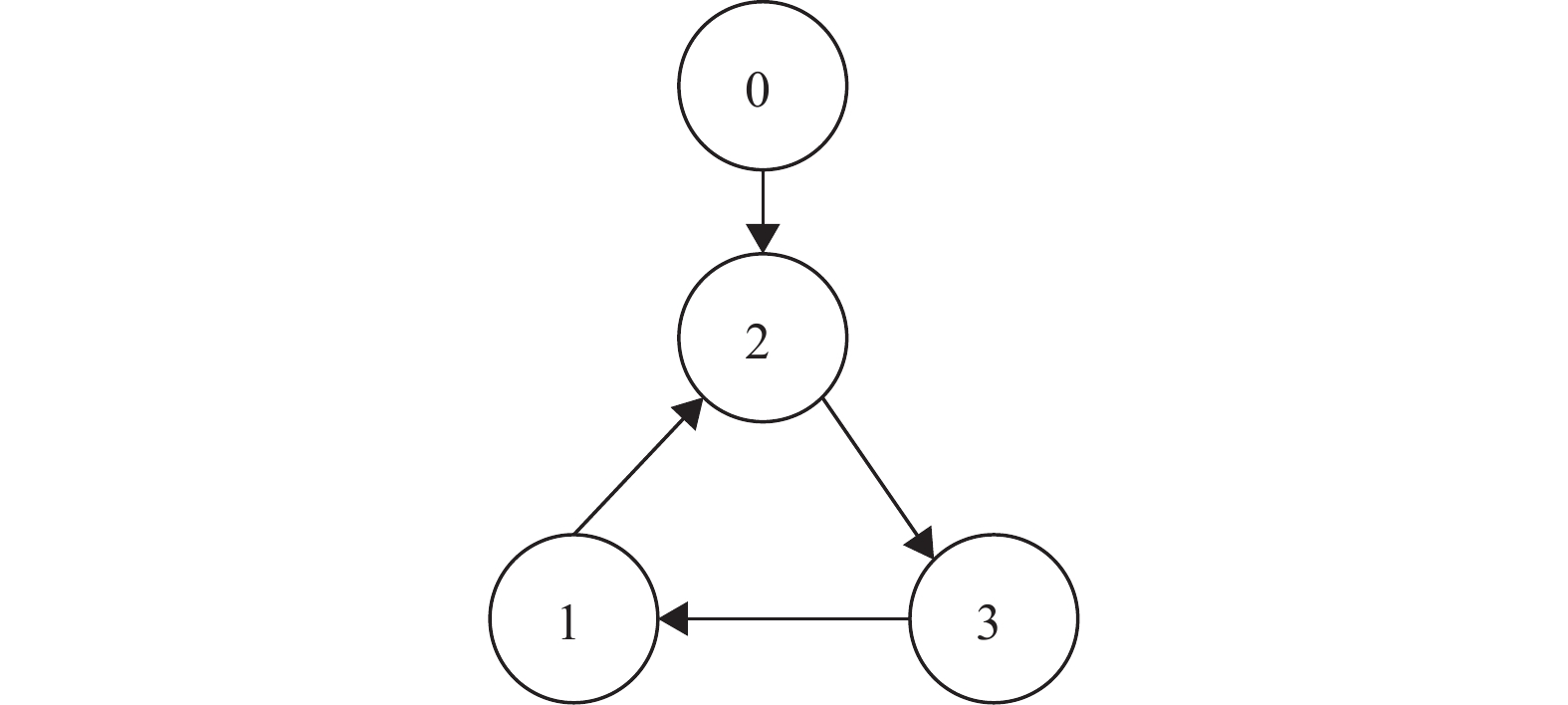
考虑3个跟随者和1个领导者组成的线性多智能体系统,其拓扑图如图1所示。
|
图 1 线性多智能体系统拓扑图 Figure 1 Topology of the linear multi-agent system |
由图1可知,Laplacian矩阵
| $ {\boldsymbol{L}} = \left[ {\begin{array}{*{20}{c}} 1&0&{ - 1} \\ { - 1}&1&0 \\ 0&{ - 1}&1 \end{array}} \right] \text{,} {\boldsymbol{D}} = \left[ {\begin{array}{*{20}{c}} 0&0&0 \\ 0&1&0 \\ 0&0&0 \end{array}} \right] $ |
则有
| $ {\boldsymbol{H}} = {\boldsymbol{L}} + {\boldsymbol{D}} = \left[ {\begin{array}{*{20}{c}} 1&0&{ - 1} \\ { - 1}&2&0 \\ 0&{ - 1}&1 \end{array}} \right] $ |
各智能体状态初值在
| $ {\boldsymbol{A}} = \left[ {\begin{array}{*{20}{c}} { - 1}&0 \\ 0&{ - 1.5} \end{array}} \right],\quad {\boldsymbol{B}} = \left[ {\begin{array}{*{20}{c}} { - 0.5} \\ { - 0.5} \end{array}} \right],\quad {\boldsymbol{C}} = [\begin{array}{*{20}{c}} {1.2}&{2.1} \end{array}] $ |
选择
| $ {{\boldsymbol{X}}} = {\text{1}}{{\text{0}}^3}\left[ \begin{gathered} {\text{1}}{\text{.634\;4 }}\quad{\text{1.049\;6}} \\ {\text{1}}{\text{.049\;6 }}\quad{\text{0.677\;7}} \\ \end{gathered} \right] $ |
| $ {{\boldsymbol{Y}}} = {\text{1}}{{\text{0}}^3}\left[ {{\text{2}}{\text{.944\;4 }}\quad{\text{1.894\;9}}} \right] $ |
| $ {{\boldsymbol{Z}}} = \left[ { - {\text{0}}{\text{.604\;3 }} \quad -{\text{1}}{\text{.035\;0}}} \right] $ |
| $ {{{\boldsymbol{P}}}_2} = \left[ \begin{gathered} {\text{6}}{\text{.759\;1 }}\quad {\text{0.698\;3}} \\ {\text{0}}{\text{.698\;3 }}\quad {\text{5.659\;7}} \\ \end{gathered} \right] $ |
另外,由
| $ \begin{gathered} {{\boldsymbol{K}}} = [{\text{1}}{\text{.089\;2 }}\quad {\text{1.109\;3}}] \\ {{\boldsymbol{G}}} = \left[ {\begin{array}{*{20}{c}} { - {\text{0}}{\text{.071\;4}}} \\ { - {\text{0}}{\text{.174\;1}}} \end{array}} \right] \\ \end{gathered} $ |
假设脉冲观测器的观测频率是周期的,
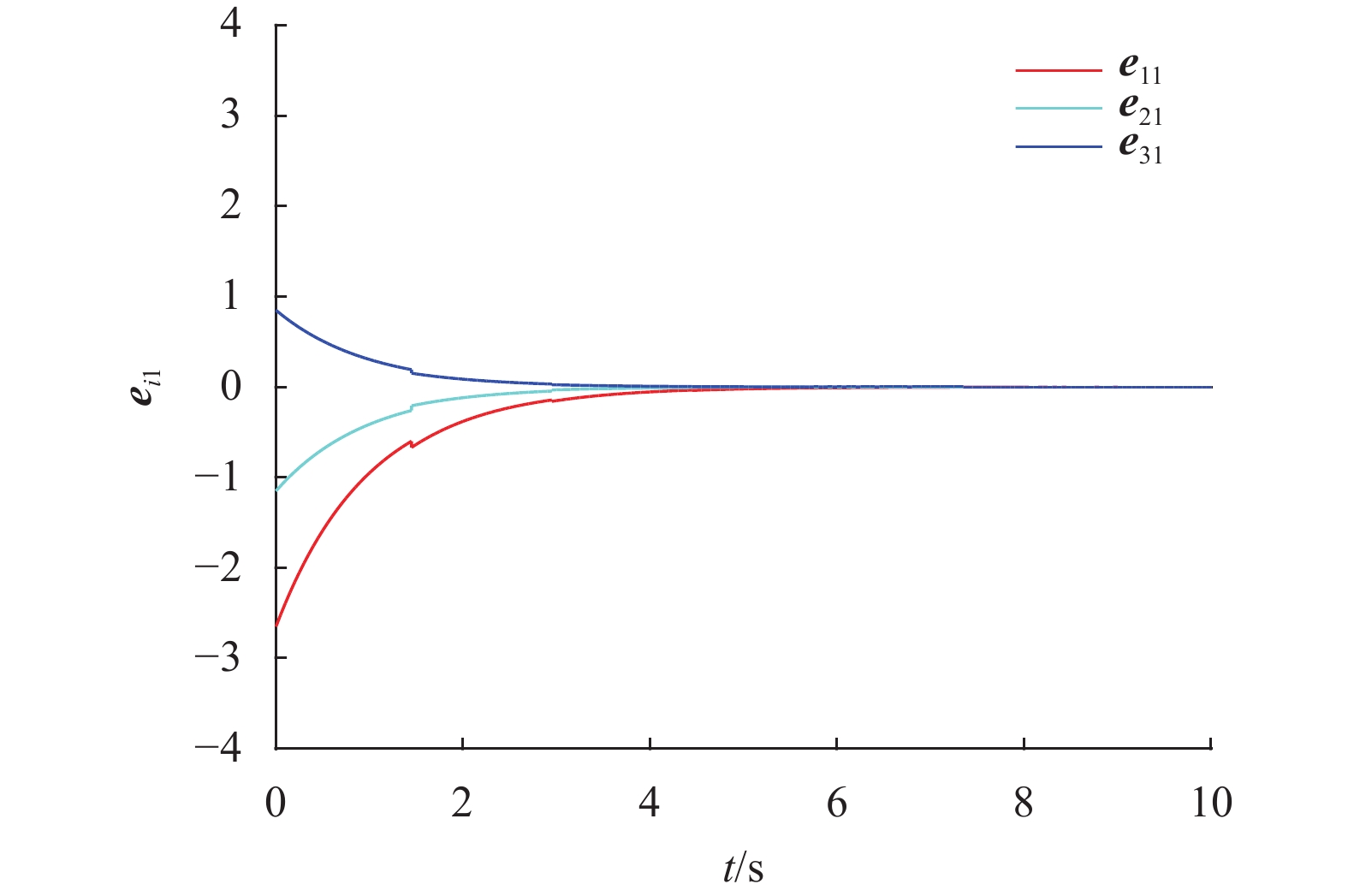
|
图 2 观测误差
|
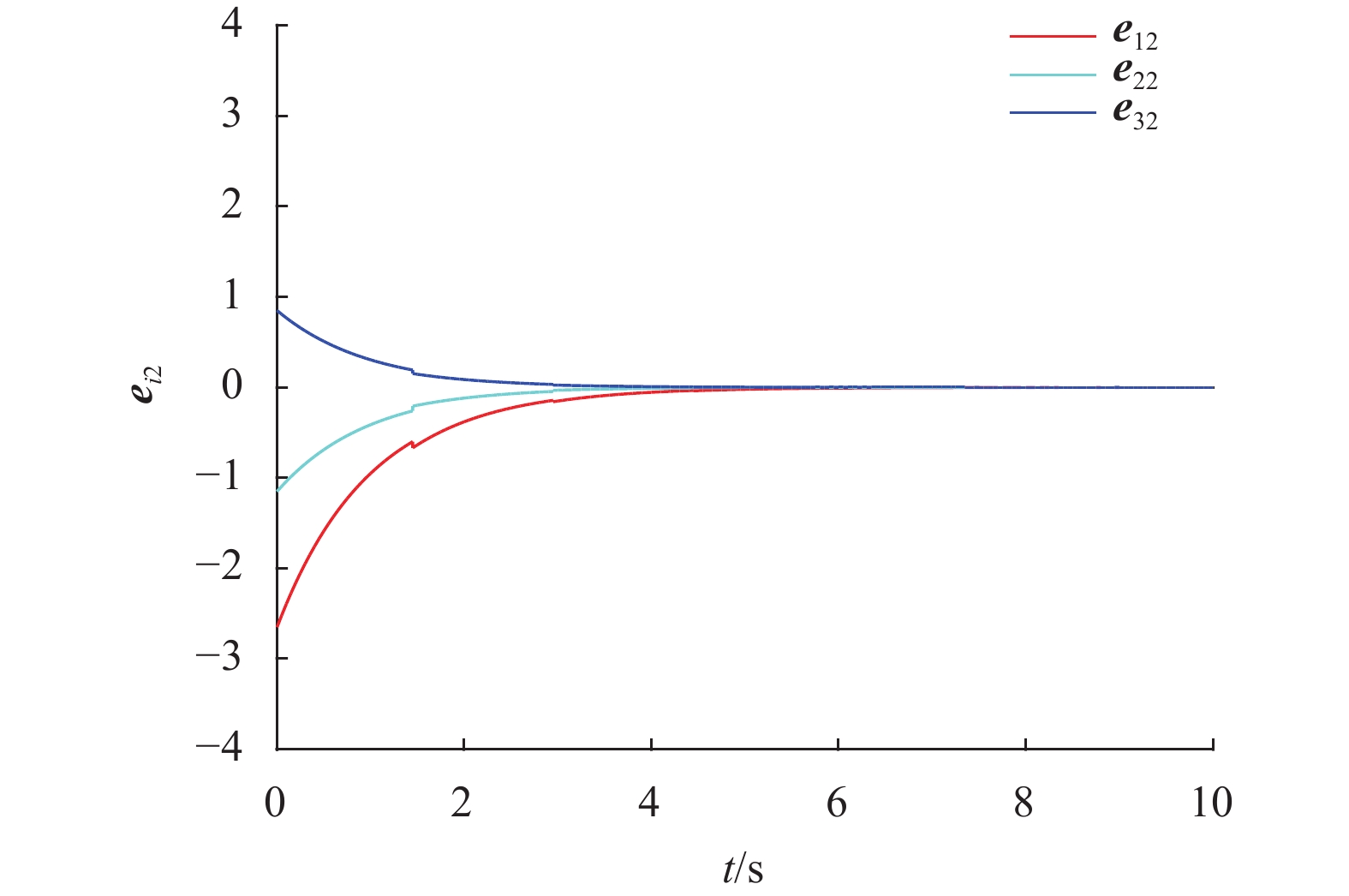
|
图 3 观测误差
|
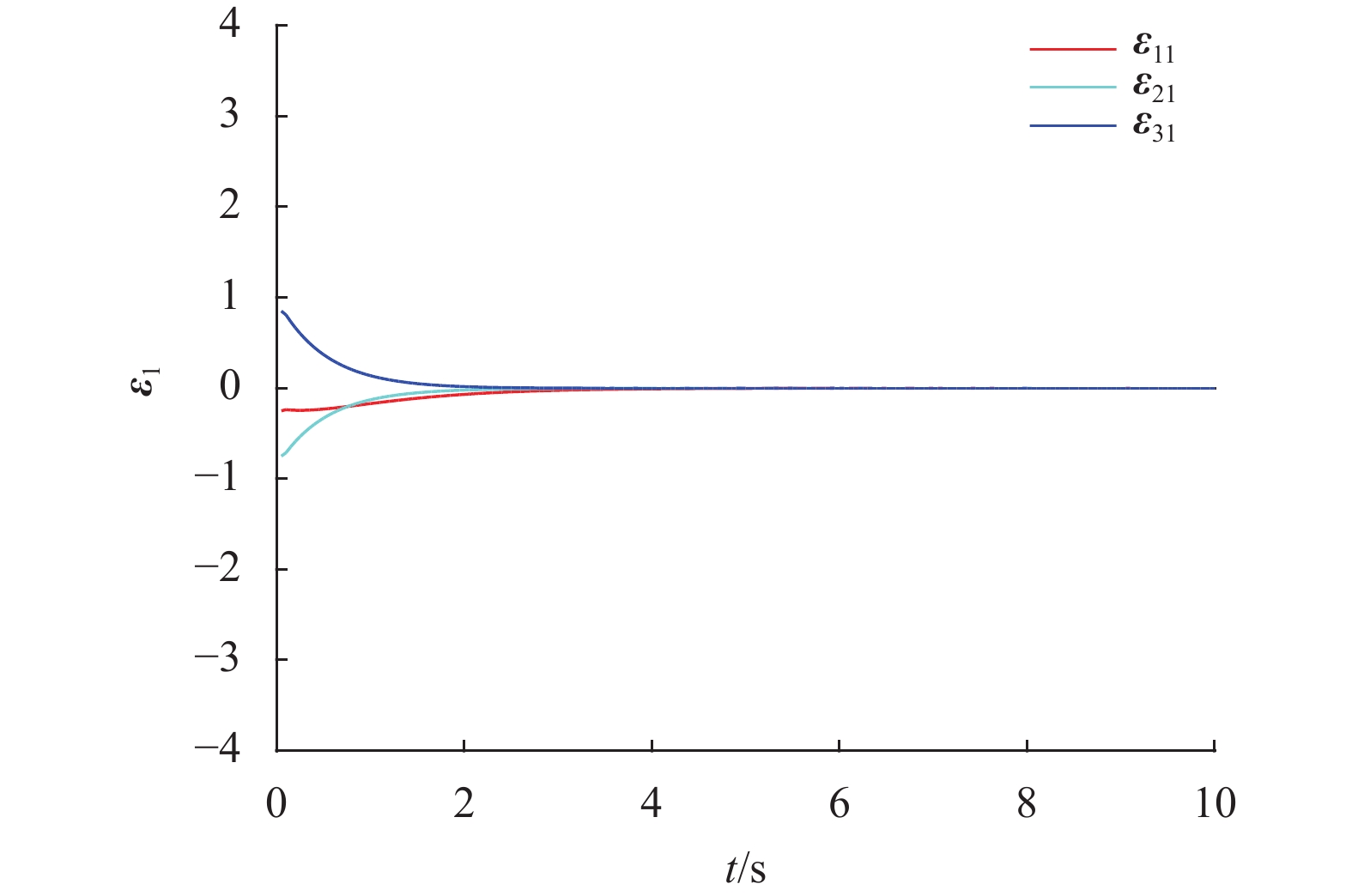
|
图 4 追踪误差
|
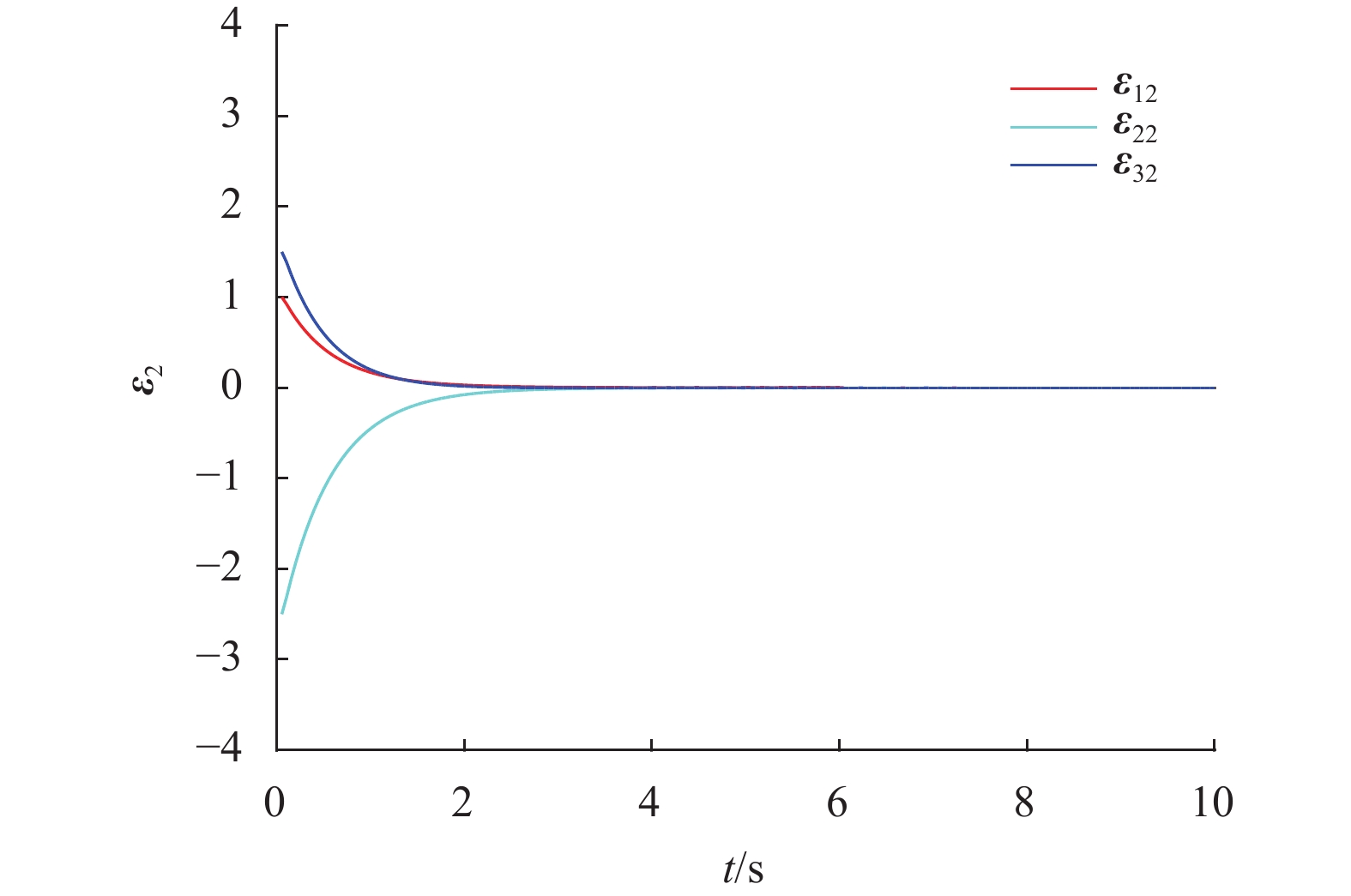
|
图 5 追踪误差
|
当
本文设计了可估计领导者状态的脉冲全维观测器,并在此基础上解决了领导跟随一致性问题,利用分段Lyapunov函数和线性矩阵不等式理论,给出了跟随者准确估计领导者状态且系统实现领导跟随一致性的条件。未来,将对事件触发脉冲观测器进行深入研究。
| [1] |
ZOU W, ZHOU C, XIANG Z. Sampled-data leader-following consensus of nonlinear multi-agent systems subject to impulsive perturbations[J].
Communications in Nonlinear Science and Numerical Simulation, 2019, 78: 104884.
DOI: 10.1016/j.cnsns.2019.104884. |
| [2] |
SHI Y, YIN Y, WANG S, et al. Distributed leader-following consensus of nonlinear multi-agent systems with nonlinear input dynamics[J].
Neurocomputing, 2018, 286: 193-197.
DOI: 10.1016/j.neucom.2018.01.059. |
| [3] |
WANG Y, CHENG Z, XIAO M. UAVs’ formation keeping control based on multi-agent system consensus[J].
IEEE Access, 2020, 8: 49000-49012.
DOI: 10.1109/ACCESS.2020.2979996. |
| [4] |
张振华, 彭世国. 二阶多智能体系统拓扑切换下的领导跟随一致性[J].
广东工业大学学报, 2018, 35(2): 75-80.
ZHANG Z H, PENG S G. Leader-following consensus of second-order multi-agent systems with switching topology[J]. Journal of Guangdong University of Technology, 2018, 35(2): 75-80. |
| [5] |
HU X, ZHANG Z, LI C, et al. Leader-following consensus of multi-agent systems via a hybrid protocol with saturation effects[J].
International Journal of Control, Automation and Systems, 2021, 19(1): 124-136.
DOI: 10.1007/s12555-019-1042-0. |
| [6] |
ZHANG Y, LI R, ZHAO W, et al. Stochastic leader-following consensus of multi-agent systems with measurement noises and communication time-delays[J].
Neurocomputing, 2018, 282: 136-145.
DOI: 10.1016/j.neucom.2017.12.024. |
| [7] |
JIANG Y, ZHANG Y, WANG H, et al. Sliding-mode observers based distributed consensus control for nonlinear multi-agent systems with disturbances[J].
Complex & Intelligent Systems, 2022, 8(3): 1889-1897.
|
| [8] |
HONG Y, CHEN G, BUSHNELL L. Distributed observers design for leader-following control of multi-agent networks[J].
Automatica, 2008, 44(3): 846-850.
DOI: 10.1016/j.automatica.2007.07.004. |
| [9] |
RAFF T, ALLGOWER F. An impulsive observer that estimates the exact state of a linear continuous-time system in predetermined finite time[C]//2007 Mediterranean Conference on Control & Automation. Athens: IEEE, 2007: 1-3.
|
| [10] |
WANG Y, LI X. Impulsive observer and impulsive control for timedelay systems[J].
Journal of the Franklin Institute, 2020, 357(13): 8529-8542.
DOI: 10.1016/j.jfranklin.2020.05.009. |
| [11] |
CHEN W H, YANG W, LU X. Impulsive observer-based stabilisation of uncertain linear systems[J].
IET Control Theory & Applications, 2014, 8(3): 149-159.
|
| [12] |
RAO H, LIU F, PENG H, et al. Observer-based impulsive synchronization for neural networks with uncertain exchanging information[J].
IEEE Transactions on Neural Networks and Learning Systems, 2019, 31(10): 3777-3787.
|
| [13] |
QIN W, LIU Z, CHEN Z. Impulsive observer-based consensus control for multi-agent systems with time delay[J].
International Journal of Control, 2015, 88(9): 1789-1804.
DOI: 10.1080/00207179.2015.1017738. |
| [14] |
BOYD S, GHAOUI L, FERON E, et al. Linear matrix inequalities in system and control theory[M]. Philadelphia:Society for Industrial and Applied Mathematics, 1994.
|
| [15] |
HORN R A, JOHNSON C R. Matrix analysis[M]. Cambridge:Cambridge University Press, 2012.
|
| [16] |
MERINO D I. Topics in matrix analysis[M]. Baltimore:The Johns Hopkins University, 1992.
|
 2023, Vol. 40
2023, Vol. 40

