离散事件系统(Discrete Event Systems,DES) 是一种在离散事件和状态上建模的系统。DES已经成功地运用到许多实际应用中，例如生产系统、工程系统、计算机网络等都能够在某种抽象水平上构建为一个DES。为保障系统的安全运行，近年来DES的故障诊断问题受到了许多国内外研究学者的关注^[1-3]。

在大多数工程应用中，DES的状态和事件都是明确的。然而在一些其他应用中，DES的状态和事件不是明确的而是模糊的。例如，在生物医学领域中，含糊、不准确性和主观性都是模糊典型的特征。为了解决这类问题，美国著名教授Lin等^[4]把经典DES模型和模糊集理论结合起来，并提出了模糊离散事件系统(Fuzzy Discrete Event Systems,FDES) 这一概念。FDES成功地应用在生物医学领域上^[5-7]。

虽然运用这些故障诊断方法都可以在故障事件或模式故障发生后的一定时延内将故障诊断出来，但是故障事件从发生到被诊断期间，系统仍有可能会执行一些被禁止的非法操作，这对于已经发生故障的系统来说是很危险的。为此，Paoli 等^[8]在经典DES故障诊断问题中提出了安全性要求，并得到了一种安全诊断的方法。文献[9-10]又将经典DES的安全诊断方法扩展到了FDES中。一个安全可诊断的模糊系统不但要求系统中发生的故障能够以一定的诊断程度诊断出来，而且这种诊断应该在不执行任何被禁止的非法操作之前完成。

上述文献中的故障诊断方法都只是对单个事件而引发的故障进行诊断。而在现实的系统中，故障往往是由多个事件相继发生而引起的(称为模式故障) 。文献[11]研究了经典DES的模式故障诊断问题，提出了模式故障诊断性的验证算法。文献[12]研究了DES的模式故障在线诊断问题，并提出了在线诊断算法。文献[13-14]研究了随机离散事件系统的模式故障诊断问题。文献[15]则进一步将经典DES的模式故障诊断方法扩展到了FDES中，提出了一种模式故障诊断的方法。然而，这种模式故障诊断方法由于在故障诊断期间仍然可能会执行一些被禁止的非法操作而存在安全隐患。

本文主要研究分布式模糊离散事件系统的模式故障安全诊断的问题，提出一种基于模式故障安全协同诊断器的模式故障安全诊断方法，此方法不同于文献[10]和文献[15]的方法。文献[10]研究的是故障事件(非模式故障)的安全协同诊断，它是通过构造故障诊断器来实现的。文献[15]研究的是模式故障的故障诊断问题(非安全诊断问题)，它是通过构造模式故障诊断器来实现的。而本文考虑的是分布式FDES模式故障的安全诊断问题，通过构造一个模式故障安全协同诊断器，并得到模式故障安全可诊断的充分必要条件，从而实现分布式FDES的模式故障安全诊断。

1 模糊离散事件系统(FDES)

一个经典DES能够用一个四元组 $ G = (Q,E,\delta ,{q_0}) $ 来表示，其中 $Q{\text{ = \{ }}{q_0},{q_1}, \cdot \cdot \cdot ,{q_{{{n - 1}}}}{\text{\} }}$ 是状态集合，E是事件集合，在事件集E上的每一个序列叫做一个字符串。 ${E^*}$ ( $ E $ 的克林闭包) 表示在事件集E上的所有有限字符串的集合。对于 $ s \in {E^*} $ ， $ |s| $ 表示 $ s $ 的长度。当 $ |s| $ =0时， $ s $ 是空字符串，用 $ \varepsilon $ 表示。 $ {q_0} $ 是初始状态。 $ \delta :Q \times E \to Q $ 是状态转移函数。

设一个在语言L中的字符串 $ u = stv $ ，如果 $ s $ , $ t $ , $ v $ 也是在语言L中的字符串，那么 $ s $ 叫做 $ u $ 的一个前缀， $ t $ 叫做 $ u $ 的一个子串， $ v $ 叫做 $ u $ 的一个后缀。给定一个字符串 $ s \in L $ ， $ s $ 的一个子序列通过删除字符串 $ s $ 中0个或者更多的事件得到。

如果经典DES中状态集合 $Q{\text{ = \{ }}{q_0},{q_1}, \cdot \cdot \cdot ,{q_{{{n - 1}}}}{\text{\} }}$ ，那么在FDES中，每一个模糊状态 $\tilde {\boldsymbol{q}}$ 是一个经典状态集合的向量，用 $\left[ {{a_0},{a_1}, \cdots ,{a_{n - 1}}} \right]$ 来表示，其中 $ {a_i} \in \left[ {0,1} \right] $ 表示当前状态在 $ {q_i} $ 的可能性。一个模糊事件 $\tilde {\boldsymbol{\sigma}}$ 是一个矩阵 $ {[{a_{ij}}]_{nn}} $ ，其中 $ [{a_{ij}}] \in [0,1] $ 表示当模糊事件 $\tilde {\boldsymbol{\sigma}}$ 发生时经典DES从状态 $ {q_i} $ 转移到状态 $ {q_j} $ 的概率。一个FDES 用一个四元组 $\tilde G = (\tilde Q,\tilde E,\tilde \delta ,{\tilde {\boldsymbol{q}}_0})$ 来表示，其中 $ \tilde Q $ 是模糊状态集合， $ \tilde E $ 是模糊事件集合， ${\tilde {\boldsymbol{q}}_0}$ 是模糊初始状态， $ \tilde \delta :\tilde Q \times \tilde E \to \tilde Q $ 是模糊状态转移函数，定义为 $\tilde \delta \left(\tilde {\boldsymbol{q}},\tilde {\boldsymbol{\sigma}} \right) = \tilde {\boldsymbol{q}} \odot \tilde {\boldsymbol{\sigma}}$ 。对于矩阵 ${\boldsymbol{A}} = {[{a_{ij}}]_{nm}}$ 和矩阵 ${\boldsymbol{B}} = {[{b_{ij}}]_{mk}}$ ， ${\boldsymbol{A}} \odot {\boldsymbol{B}} = {[{c_{ij}}]_{nk}}$ ,其中

$ {c_{ij}} = \mathop {{\rm{max}}}\limits_{l = 1}^m {\rm{min}}\{ {a_{il}},{b_{lj}}\} $

(1)

设 $\tilde G = (\tilde Q,\tilde E,\tilde \delta ,{\tilde {\boldsymbol{q}}_0})$ 是一个FDES，每一个模糊事件同属于可观事件集合、不可观事件集合、模式故障集合，只是同属于这些集合的程度可能不同。因此引进了3个模糊子集：不可观事件模糊子集 ${ \tilde \varSigma _{{\rm{uo}}}}$ ，可观事件模糊子集 ${ \tilde \varSigma _{\rm{o}}}$ ，模式故障 $ \tilde K $ 的模糊子集 $ { \tilde \varSigma _{\tilde K}} $ 。 ${ \tilde \varSigma _{\tilde K}}(\tilde {\boldsymbol{\sigma}} )$ 表示模糊事件 $\tilde {\boldsymbol{\sigma}}$ 在模式故障 $ \tilde K $ 中发生的可能性。 ${ \tilde \varSigma _{\rm{o}}}(\tilde {\boldsymbol{\sigma}} )$ 和 ${ \tilde \varSigma _{{\rm{uo}}}}(\tilde {\boldsymbol{\sigma}} )$ 表明模糊事件 $ \tilde \sigma $ 的观测程度，并且满足： ${ \tilde \varSigma _{\rm{o}}}(\tilde {\boldsymbol{\sigma}} )$ + ${ \tilde \varSigma _{{\rm{uo}}}}(\tilde {\boldsymbol{\sigma}} )$ =1。

对于每一个 $\tilde {\boldsymbol{\sigma}} \in \tilde E$ ，引入了最大可观事件集合 ${\tilde E_{{\text{max-o}}}}$ ， ${\tilde E_{{\text{max-o}}}}$ 是由最大可观度的事件所构成，定义为

$ {\tilde E_{{\text{max-o}}}} \left\{ \tilde{\boldsymbol{ \sigma}} \in \tilde E : \left(\forall {{\tilde{\boldsymbol{ \sigma}}} {'}}\in \tilde E\right) { { \tilde \varSigma} _{\rm{o}}}\left(\tilde{\boldsymbol{ \sigma}} \right) \ge { \tilde \varSigma _{\rm{o}}}({\tilde{\boldsymbol{ \sigma}} {'}}) \right\} $

(2)

模糊离散事件系统 $ \tilde G $ 的生成语言用 $ \tilde L $ 表示， $\tilde L = \{ \tilde s \in {\tilde E^ * }:(\exists \tilde {\boldsymbol{q}} \in \tilde Q) \tilde \delta ({\tilde {\boldsymbol{q}}_0},\tilde s) = \tilde {\boldsymbol{q}}\}$ 。在语言 $ \tilde L $ 中模糊事件串 $ \tilde s $ 的后续定义为 $\tilde L/\tilde s = \{ \tilde t \in {\tilde E^ * }:\tilde \delta ({\tilde {\boldsymbol{q}}_0},\tilde s\tilde t) = \tilde {\boldsymbol{q}}\}$ 。

对于模糊事件 $\tilde {\boldsymbol{\sigma}} \in \tilde E$ ， $\tilde {\boldsymbol{\sigma}}$ 的投影 ${P_{\tilde {\boldsymbol{\sigma}} }}$ 定义为

${P_{\tilde {\boldsymbol{\sigma}} }}(\tilde {\boldsymbol{a}})\left\{ {\begin{array}{*{20}{l}} {\tilde {\boldsymbol{a}}\;,\;{\text{如果}}\;\tilde {\boldsymbol{a}} \in {\tilde E_{{\text{max-o}}}}\;或者{{\tilde \varSigma}_{\rm{o}}}(\tilde {\boldsymbol{a}}) > {{\tilde \varSigma}_{\rm{o}}}(\tilde {\boldsymbol{\sigma}} )}\\ {\varepsilon \;,\;}其他 \end{array}} \right. $

(3)

$\tilde {\boldsymbol{\sigma}}$ 逆投影 $P_{\tilde {\boldsymbol{\sigma}} }^{ - 1}$ 定义为 $P_{\tilde {\boldsymbol{\sigma}} }^{ - 1}(\;\tilde t\;) = \{ \tilde s \in {\tilde E^*}:(\exists \tilde {\boldsymbol{q}} \in \tilde Q) \tilde \delta ({\tilde {\boldsymbol{q}}_0},\tilde s) = \tilde {\boldsymbol{q}} \wedge {P_{\tilde {\boldsymbol{\sigma}} }}(\tilde s) = \tilde t \; \}$ 。

设 ${\tilde L_{{\rm{pa}}}}$ 表示在FDES中含有模式故障 $ \tilde K $ 的语言。对于 $ \tilde u \in \tilde K $ ， ${\tilde L_{{\rm{pa}}}}$ 定义为 ${\tilde L_{{\rm{pa}}}} = \left\{ \tilde u \in {\tilde E^ * }|{ \tilde \varSigma _{\tilde K}}(\tilde u) > 0\right\}$ 。对于 $ \tilde s \in {\tilde L_{{\rm{pa}}}} $ ，模式故障 $ \tilde K $ 发生的可能性定义为 $\tilde \varSigma_{\tilde K}^{\tilde S}(\tilde s) = \left\{ {\tilde \varSigma_{\tilde K}}(\tilde u)|\tilde u \in {\tilde L_{{\rm{pa}}}}，\tilde u是\tilde s的子序列\right\}$ 。

${\varPsi _{\tilde S}}(\tilde K)$ 表示以模式故障事件串结尾的集合，即

$ {\varPsi _{\tilde S}}(\tilde K) ={ \tilde s\tilde {\boldsymbol{\sigma}} \in \tilde S | \tilde k\tilde {\boldsymbol{\sigma}} 是 \tilde s\tilde {\boldsymbol{\sigma}} 的子序列且 \tilde \varSigma _{\tilde K}^{\tilde S}(\tilde s\tilde {\boldsymbol{\sigma}} ) \geqslant { \tilde \varSigma _{\tilde K}}(\tilde u) } $

(4)

2 模糊离散事件系统的模式故障安全协同诊断的定义

一个安全诊断的FDES不但要求系统中发生的模式故障事件串能够以一定的程度诊断出来，而且这种诊断应该在不执行任何被禁止的非法操作之前完成。设 $\varGamma$ 是系统中给定的被禁止事件串集合。当系统模式故障发生后，所有包含来自集合 $\varGamma$ 的元素都是必须被禁止的非法操作，即非法语言集合 $ {\tilde L^I} $ 定义为

$ {\tilde L^I} =\{ \tilde \omega \in \tilde L/\tilde s:\tilde s \in {\varPsi _{\tilde S}}(\tilde u) , \tilde t \in \varGamma \; , \; \tilde t \text{是} \tilde \omega \text{的一个子序列}\} $

(5)

为了识别系统中非法语言字符串，引入一个标识符集合 ${ O} = \{ {S^1},{S^2},B\}$ ,其中标识符 $ {S^1} $ 表示系统 $ \tilde G $ 还没有发生模式故障；标识符 $ {S^2} $ 表示系统 $ \tilde G $ 发生了模式故障，但还没有执行被禁止的非法操作；标识符B表示系统 $ \tilde G $ 发生了模式故障，并且执行了被禁止的非法操作。

定义1 　设 $ \tilde G $ 是一个FDES， $ \tilde K $ 是一个模式故障集合， $ \tilde L $ 是 $ \tilde G $ 的生成语言。如果满足

$ \begin{gathered} (\exists {n_0} \in N) (\forall \tilde s \in {\varPsi _{\tilde S}}(\tilde K) ) (\forall \tilde t \in \tilde L/\tilde s) (|\tilde t\,| \geqslant {n_0} \Rightarrow (\exists i \in I) \\ (\exists \tilde v \in {\text{pre}}(\tilde t\,) ) ({\text{pre}}(\tilde {v}) \cap {{\tilde L}^I} = \emptyset ) \wedge ({\lambda _i} = {\text{FPD}}_{i,\tilde K}^{\tilde S}(\tilde s\tilde {v}) \geqslant \lambda > 0) ) \\ \end{gathered} $

(6)

则称系统 $ \tilde G $ 是程度为 $ \lambda $ 的模式故障安全协同可诊断的，其中 ${\text{FPD}}_{i,\tilde K}^{\tilde S}(\tilde s\tilde t\,) = \mathop {\min }\limits_{\tilde u \in \tilde K}\Big(\dfrac{{{D_i}}}{{{{\tilde \varSigma}_{\tilde K}}(\tilde u) }}\Big)$ 为模式故障协同诊断函数， ${D_i} = {\rm{min}}\left\{ {\tilde \varSigma_{\tilde K}}(\tilde u) ,\tilde \varSigma_{\tilde K}^{\tilde S}(\tilde \omega ) |\tilde \omega \in P_{i,\tilde {\boldsymbol{\sigma}} }^{ - 1}{P_{i,\tilde {\boldsymbol{\sigma}} }}(\tilde s\tilde {v}) \subseteq \tilde S\right\}$ 为诊断条件， $i \in I = \{ 1,2,\cdots,n\}$ ， $\;0 < \lambda \leqslant {\lambda _i} \leqslant 1$ 。

直观上，系统 $ \tilde G $ 是程度为 $ \lambda $ 的模式故障安全协同可诊断的，对于任何以模式故障结尾的事件串 $ \tilde s $ (即 $\forall \tilde s \in {\varPsi _{\tilde S}}(\tilde K)$ )及其有限长的后续 $ \tilde t $ (即 $ \forall \tilde t \in \tilde L/\tilde s $ , $ |\tilde t| \geqslant {n_0} $ )，至少存在一个本地站点 $ i $ 和一个 $ \tilde t $ 的前缀 $ \tilde v $ ，使得模式故障不但能够通过本地站点 $ i $ 诊断出来(即 $ {\text{FPD}}_{i,\tilde K}^{\tilde S}(\tilde s\tilde v) \geqslant \lambda $ )，而且 $ \tilde v $ 中不包含任何被禁止事件串(即 $ {\text{pre}}(\tilde v) \cap {\tilde L^I} = \emptyset $ )；也就算说，一旦模式故障发生，至少存在一个本地站点能够及时对其进行诊断，并且在诊断期间没有执行任何被禁止的非法操作。

例1 　假设某地近期爆发一种不明原因的动物疾病。医生对这种新型疾病不是很了解，根据现有的知识认为抗生素、茶碱、奥氟沙星、多巴胺、琥珀酸红霉素乙脂、溴化异丙托溴铵(分别用 $\tilde {\boldsymbol{a}}、\tilde {\boldsymbol{b}}、\tilde {\boldsymbol{c}}、\tilde {\boldsymbol{d}}、\tilde {\boldsymbol{e}}、\tilde {\boldsymbol{f}}$ 来表示)这6种药物对该疾病有一定的治疗效果。

假设根据临床经验，白细胞数量过高可以看作是病情可能恶化的一个特征，而在服用完多巴胺后再服用抗生素将会导致白细胞数量过高。因此，可以把服用完多巴胺后再服用抗生素看作是模式故障 $\tilde K = \left\{ \tilde {\boldsymbol{a}}\tilde {\boldsymbol{d}}\right\}$ 。如果出现白细胞数量过高后，继续服用某药物将会产生更危险的副作用。一旦模式故障发生(即服用完多巴胺后再服用抗生素而导致白细胞数量过高)，需要在产生更危险的副作用之前将该模式故障及时诊断出来。

通过对动物的治疗过程来分析这6种药物的使用情况。因为动物的身体状况可能同时属于“好”“一般”和“差”这3种状态但却带有不同的隶属度，因此可以把治疗过程看作是一个FDES。当动物服用某种药物后，不能准确地判断出动物的身体状况从一个状态转移到另一个状态，因此一个模糊事件可以用一个3×3矩阵来表示。

假设在动物的整个治疗过程能够构建一个FDES，用 $\tilde G = (\tilde Q,\tilde E,\tilde \delta ,{\tilde {\boldsymbol{q}}_0})$ 来表示，如图1所示。初始状态 ${\tilde {\boldsymbol{q}}_0} = {\tilde {\boldsymbol{x}}_0} = [ {\begin{array}{*{20}{c}} {0.6}&{0.2}&{0.3} \end{array}}]$ ，模糊状态集合 $\tilde Q = \left\{ {\tilde {\boldsymbol{x}}_0},{\tilde {\boldsymbol{x}}_1},{\tilde {\boldsymbol{x}}_2},{\tilde {\boldsymbol{x}}_3},{\tilde {\boldsymbol{x}}_4},{\tilde {\boldsymbol{x}}_5},{\tilde {\boldsymbol{x}}_6}\right\}$ ，模糊事件集合 $\tilde E = \{ \tilde {\boldsymbol{a}},\tilde {\boldsymbol{b}},\tilde {\boldsymbol{c}},\tilde {\boldsymbol{d}},\tilde {\boldsymbol{e}},\tilde {\boldsymbol{f}}\}$ 。根据医生对这些药物的经验，模糊事件用矩阵表示为

$ \tilde {\boldsymbol{a}} = \left[ {\begin{array}{*{20}{c}} {0.9}& 0& 0 \\ {0.7}&{0.3}& 0 \\ {0.2}&{0.1}&{0.4} \end{array}} \right] \;,\; \tilde {\boldsymbol{b}} = \left[ {\begin{array}{*{20}{c}} {0.7}&{0.3}&{0.2} \\ 0&{0.4}&{0.3} \\ 0& 0&{0.6} \end{array}} \right] $

$ \tilde {\boldsymbol{c}} = \left[ {\begin{array}{*{20}{c}} {0.6}& 0& 0 \\ {0.1}&{0.3}& 0 \\ {0.7}&{0.2}&{0.2} \end{array}} \right] \;,\;\tilde {\boldsymbol{d}} = \left[ {\begin{array}{*{20}{c}} {0.5}&{0.3}&{0.6} \\ 0&{0.6}&{0.5} \\ 0& 0&{0.4} \end{array}} \right] $

$ \tilde {\boldsymbol{e}} = \left[ {\begin{array}{*{20}{c}} {0.6}& 0& 0 \\ {0.2}&{0.4}& 0 \\ {0.7}&{0.5}&{0.1} \end{array}} \right] \;,\; \tilde {\boldsymbol{f}} = \left[ {\begin{array}{*{20}{c}} {0.8}&{0.3}&{0.1} \\ 0&{0.3}&{0.1} \\ 0& 0&{0.4} \end{array}} \right] $

由于动物服用某种药物后，效果特征并不是很明显，所以可以用模糊事件的可观测程度来表示动物服用药物后效果特征的明显程度。假设有2个治疗团队同时对该动物进行联合会诊。假设这2个治疗团队对每个模糊事件的可观测程度为

$ {\tilde \varSigma_{1,{\text{o}}}}(\tilde {\boldsymbol{a}}) = 0.8,{\text{ }}{\tilde \varSigma_{1,{\text{o}}}}(\tilde {\boldsymbol{b}}) = 0.3,{\text{ }}{\tilde \varSigma_{1,{\text{o}}}}(\tilde {\boldsymbol{c}}) = 0.1 $

$ {\tilde \varSigma_{1,{\text{o}}}}(\tilde {\boldsymbol{d}}) = 0.5,{\text{ }}{\tilde \varSigma_{1,{\text{o}}}}(\tilde {\boldsymbol{e}}) = 0.7,{\text{ }}{\tilde \varSigma_{1,{\text{o}}}}(\tilde {\boldsymbol{f}}) = 0.2 $

$ {\tilde \varSigma_{2,{\text{o}}}}(\tilde {\boldsymbol{a}}) = 0.7,{\text{ }}{\tilde \varSigma_{2,{\text{o}}}}(\tilde {\boldsymbol{b}}) = 0.3,{\text{ }}{\tilde \varSigma_{2,{\text{o}}}}(\tilde {\boldsymbol{c}}) = 0.8 $

$ {\tilde \varSigma_{2,{\text{o}}}}(\tilde {\boldsymbol{d}}) = 0.6,{\text{ }}{\tilde \varSigma_{2,{\text{o}}}}(\tilde {\boldsymbol{e}}) = 0.5,{\text{ }}{\tilde \varSigma_{2,{\text{o}}}}(\tilde {\boldsymbol{f}}) = 0.4 $

假设每一种药物在模式故障 $ \tilde K $ 中产生的副作用程度为 ${\tilde \varSigma_{\tilde {{K}}}}(\tilde {\boldsymbol{a}}) = 0.5$ ， ${\tilde \varSigma_{\tilde K}}(\tilde {\boldsymbol{b}}) = 0.3$ ， ${\tilde \varSigma_{\tilde K}}(\tilde {\boldsymbol{c}}) = 0.2$ ， ${\tilde \varSigma_{\tilde K}}(\tilde {\boldsymbol{d}}) = 0.4$ ， ${\tilde \varSigma_{\tilde K}}(\tilde {\boldsymbol{e}}) = 0.1$ ， ${\tilde \varSigma_{\tilde K}}(\tilde {\boldsymbol{f}}) = 0.6$ 。并且第一个治疗团队对模式故障 $ \tilde K $ 的诊断情况用 $ {P_{1,\tilde K}} $ 表示，第二个治疗团队对模式故障 $ \tilde K $ 的诊断情况用 $ {P_{2,\tilde K}} $ 表示。下面用定义的方法来判断FDES模型 $ \tilde G $ 对于 $\left\{ {P_{1,\tilde K}},{P_{2,\tilde K}}\right\}$ 是否实现了模式故障安全协同可诊断。

根据图1得出 $ \tilde G $ 的生成语言 $\tilde L = \tilde {\boldsymbol{a}} [ \tilde {\boldsymbol{b}}\tilde {\boldsymbol{d}}(\tilde {\boldsymbol{e}}\tilde {\boldsymbol{f}} + \tilde {\boldsymbol{c}}\tilde {\boldsymbol{e}}) + \tilde {\boldsymbol{c}}\tilde {\boldsymbol{e}} ]{\tilde {\boldsymbol{a}}^ * }$ ，并且 ${\tilde \varSigma_{\tilde K}}(\tilde {\boldsymbol{\sigma}} )$ = ${\rm{min}}({\tilde \varSigma_{\tilde K}}(\tilde {\boldsymbol{a}}) ,{\tilde \varSigma_{\tilde K}}(\tilde {\boldsymbol{d}}) )$ = ${\tilde \varSigma_{\tilde K}}(\tilde {\boldsymbol{d}})$ =0.4， $\tilde s = {\varPsi _{\tilde S}}(\tilde K) = \tilde {\boldsymbol{a}}\tilde {\boldsymbol{b}}\tilde {\boldsymbol{d}}$ 。

假设模式故障发生(即服用完多巴胺后再服用抗生素而导致白细胞数量过高)之后，连续服用琥珀酸红霉素乙脂和溴化异丙托溴铵(即 $\tilde {\boldsymbol{e}}\tilde {\boldsymbol{f}}$ )或者奥氟沙星和琥珀酸红霉素乙脂(即 $\tilde {\boldsymbol{c}}\tilde {\boldsymbol{e}}$ )将使病情严重恶化，即被禁止事件串集合 $\varGamma = \{ \tilde {\boldsymbol{e}}\tilde {\boldsymbol{f}},\tilde {\boldsymbol{c}}\tilde {\boldsymbol{e}}\}$ 。

取n₀=3， $\tilde t \in \tilde L/\tilde s = \{ \tilde {\boldsymbol{e}}\tilde {\boldsymbol{f}}\tilde {\boldsymbol{a}},\tilde {\boldsymbol{c}}\tilde {\boldsymbol{e}}\tilde {\boldsymbol{a}}\}$ 得

$ \begin{gathered}{\lambda _1} = \frac{{{\rm{min}}\left\{ {{\tilde \varSigma}_{\tilde K}}(\tilde u) ,\tilde \varSigma_{\tilde K}^{\tilde S}(\tilde \omega ) |\tilde \omega \in P_{1,\tilde {\boldsymbol{\sigma}} }^{ - 1}{P_{1,\tilde {\boldsymbol{\sigma}} }}(\tilde s\tilde t) \subseteq \tilde S\right\} }}{{{{\tilde \varSigma}_{\tilde K}}(\tilde u) }} =\\ \frac{{{\rm{min}}\left\{ {{\tilde \varSigma}_{\tilde K}}(\tilde {\boldsymbol{a}}\tilde {\boldsymbol{d}}) ,{{\tilde \varSigma}_{\tilde K}}(\tilde {\boldsymbol{a}}\tilde {\boldsymbol{b}}\tilde {\boldsymbol{d}}\tilde {\boldsymbol{e}}) \right\} }}{{{{\tilde \varSigma}_{\tilde K}}(\tilde {\boldsymbol{a}}\tilde {\boldsymbol{d}}) }} = \frac{{0.1}}{{0.4}} =0.25 \end{gathered}$

并且存在一个 $\tilde {v} = \tilde {\boldsymbol{e}} \in {\text{pre}}(\tilde t\;)$ ，使得

$ {\text{pre}}(\tilde {v}) \cap {\tilde L^I} = \emptyset $

$ \begin{gathered}{\lambda _2} = \frac{{{\rm{min}}\left\{ {{\tilde \varSigma}_{\tilde K}}(\tilde u) ,\tilde \varSigma_{\tilde K}^{\tilde S}(\tilde \omega ) |\tilde \omega \in P_{2,\tilde {\boldsymbol{\sigma}} }^{ - 1}{P_{2,\tilde {\boldsymbol{\sigma}} }}\left(\tilde s\tilde t\right) \subseteq \tilde S\right\} }}{{{{\tilde \varSigma}_{\tilde K}}(\tilde u) }} =\\ \frac{{{\rm{min}}\left\{ {{\tilde \varSigma}_{\tilde K}}(\tilde {\boldsymbol{a}}\tilde {\boldsymbol{d}}) ,{{\tilde \varSigma}_{\tilde K}}(\tilde {\boldsymbol{a}}\tilde {\boldsymbol{b}}\tilde {\boldsymbol{d}}\tilde {\boldsymbol{c}}) \right\} }}{{{{\tilde \varSigma}_{\tilde K}}(\tilde {\boldsymbol{a}}\tilde {\boldsymbol{d}}) }} = \frac{{0.2}}{{0.4}} =0.5 \end{gathered}$

并且也存在一个 $\tilde {v} = \tilde {\boldsymbol{c}} \in {\text{pre}}(\tilde t)$ ，使得 ${\text{pre}}(\tilde {v}) \cap {\tilde L^I} = \emptyset$ 。因此， $ \lambda = 0.25 $ ，即 $ \tilde G $ 是程度为0.25的模式故障安全协同可诊断的，这表明一旦模式故障发生(即服用完多巴胺后再服用抗生素而导致白细胞数量过高)，能以25%的可能性在产生更危险的副作用之前将该模式故障及时诊断出来。

3 模式故障安全协同诊断器的构建

下面给出模式故障安全协同诊断器的构建方法。

步骤1：模式故障识别器的构建。

给定一个 $ \tilde G $ 和一个模式故障串集合 $ \tilde K $ ， $\tilde s = {\tilde {\boldsymbol{\sigma}} _1}{\tilde {\boldsymbol{\sigma}} _2}\cdots {\tilde {\boldsymbol{\sigma}} _m} \in \tilde K$ ，构建一台模式故障自动机 ${H_{\tilde S}} = ({\tilde Q_{\tilde S}},\tilde E, {\tilde \delta _{\tilde S}}, \tilde q_0^{\tilde S},{\tilde F_{\tilde S}})$ ，其中 ${\tilde Q_{\tilde S}} = \{ 0,1,2,\cdots,m\}$ ， $ \tilde q_0^{\tilde S} = 0 $ , $ {\tilde F_{\tilde S}} = |\tilde s| = m $ 。对于所有的 $ {\tilde q^{\tilde S}} \in {\tilde Q_{\tilde S}}/{\tilde F_{\tilde S}} $ 和 $\tilde {\boldsymbol{\sigma}} \in \tilde E$

$ {\tilde{\delta }}_{\tilde{S}}({\tilde{q}}^{\tilde{S}},\tilde{{\boldsymbol{\sigma}} }) =\left\{\begin{split}&{\tilde{q}}^{\tilde{S}}+1,\;如果\tilde{{\boldsymbol{\sigma}} }={\tilde{{\boldsymbol{\sigma}} }}_{{\tilde{q}}^{\tilde{S}}+1} \\ &{\tilde{q}}^{\tilde{S}},\;其他 \end{split} \right.$

(7)

并且 ${\tilde \delta _{\tilde S}}(m,\tilde {\boldsymbol{\sigma}} ) = m$ 。

模式故障识别器 ${\tilde G_{{\rm{pa}}}}$ = ${U_{\tilde u \in \tilde K}}({H_{\tilde S}} \times \tilde G)$ = $({\tilde Q_{{\rm{pa}}}},{\tilde E_{{\rm{pa}}}},{\tilde \delta _{{\rm{pa}}}}, \tilde q_{{\rm{pa}}}^0)$ ， ${\tilde Q_{{\rm{pa}}}} \subseteq {2^{\tilde Q \times {{\tilde Q}_{\tilde S}}}}$ 为状态空间， ${\tilde E_{{\rm{pa}}}} = \tilde E$ ，初始状态 $\tilde q_{{\rm{pa}}}^0 = ({\tilde {\boldsymbol{q}}_0},0)$ ，状态转移函数 ${\tilde \delta _{{\rm{pa}}}}:{\tilde Q_{{\rm{pa}}}} \times {\tilde E_{{\rm{pa}}}} \to {\tilde Q_{{\rm{pa}}}}$ ， ${\tilde \delta _{{\rm{pa}}}}((\tilde {\boldsymbol{q}},{l_1}) , {\tilde {\boldsymbol{\sigma}} _{{\rm{pa}}}}) = (\tilde \delta (\tilde {\boldsymbol{q}},{\tilde {\boldsymbol{\sigma}} _{{\rm{pa}}}}) ,{\tilde \delta _{\tilde S}}({l_1},{\tilde {\boldsymbol{\sigma}} _{{\rm{pa}}}}) )$ ，其中 $\tilde {\boldsymbol{q}} \in \tilde Q,{l_1} \in {\tilde Q_{\tilde S}},{\tilde {\boldsymbol{\sigma}} _{{\rm{pa}}}} \in {\tilde E_{{\rm{pa}}}}$ 。

步骤2：非法语言识别器的构建。

给定一个 $ \tilde G $ 和非法字符串集合 $\varGamma$ ，非法语言集合 $ {\tilde L^I} $ 的识别器 ${\tilde G_{{\rm{la}}}} = ({\tilde Q_{{\rm{la}}}},{\tilde E_{{\rm{la}}}},{\tilde \delta _{{\rm{la}}}},\tilde q_{{\rm{la}}}^0)$ ，其中 ${\tilde Q_{{\rm{la}}}} \subseteq {2^{{{\tilde Q}_{{\rm{pa}}}} \times O}}$ 是状态空间； ${\tilde E_{{\rm{la}}}} = \tilde E$ ； $\tilde q_{{\rm{la}}}^0 = \left({\tilde {\boldsymbol{q}}_0},0,{S^1}\right)$ 是初始状态； ${\tilde \delta _{{\rm{la}}}}:{\tilde Q_{{\rm{la}}}} \times \tilde E_{{\rm{la}}}^ * \to {\tilde Q_{{\rm{la}}}}$ 是状态转移函数， ${\tilde \delta _{{\rm{{\rm{la}}}}}}\left({\tilde q_{{\rm{la}}}},{\tilde {\boldsymbol{\sigma}} _{{\rm{la}}}}\right) = {\tilde \delta _{{\rm{la}}}}((\tilde {\boldsymbol{q}},{l_1},{l_2}) , {\tilde {\boldsymbol{\sigma}} _{{\rm{la}}}}) = (\tilde \delta \left(\tilde {\boldsymbol{q}},{\tilde {\boldsymbol{\sigma}} _{{\rm{la}}}}\right) ,{\tilde \delta _{\tilde S}}\left({l_1},{\tilde {\boldsymbol{\sigma}} _{{\rm{la}}}}\right) ,\varOmega ({\tilde {\boldsymbol{\sigma}} _{{\rm{la}}}}) )$ ， ${\tilde \sigma _{{\rm{la}}}} \in {\tilde E_{{\rm{la}}}},{\tilde q_{{\rm{la}}}} \in {\tilde Q_{{\rm{la}}}}, {l_2} \in { O}$ ，并且 $\varOmega$ 是标识符转移函数。非法语言 $ {\tilde L^I} $ 的标识符转移函数 $\varOmega :{\tilde E^ * } \to { O}$ 定义为

$ \varOmega (\tilde{s}) =\left\{\begin{array}{l}{S}^{1},如果\text{pre}(\tilde{s}) \cap {\varPsi }_{\tilde{S}}(\tilde{K}) \text=\varnothing \\ {S}^{2},如果\tilde{s}\in {\varPsi }_{\tilde{S}}(\tilde{K}) ({\tilde{E}}^{\ast }-{\tilde{L}}^{I}) \\ B\text{ },如果\tilde{s}\in {\varPsi }_{\tilde{S}}(\tilde{K}) {\tilde{L}}^{I} \end{array}\right. $

(8)

步骤3：本地模式故障安全诊断器的构建。

设 ${\tilde G_{{\rm{la}}}} = ({\tilde Q_{{\rm{la}}}},{\tilde E_{{\rm{la}}}},{\tilde \delta _{{\rm{la}}}},\tilde q_{{\rm{la}}}^0)$ 为非法语言识别器， ${\tilde G_{{\rm{pa}}}} = ({\tilde Q_{{\rm{pa}}}},{\tilde E_{{\rm{pa}}}},{\tilde \delta _{{\rm{pa}}}},\tilde q_{{\rm{pa}}}^0)$ 为模式故障识别器，每个 $ i \in I $ 都有相对应的本地投影 ${P_{i,\tilde {\boldsymbol{\sigma}} }}$ ， $ \tilde G $ 的一个本地模式故障安全诊断器构建为一个有限状态自动机 ${\tilde G_{i,{\rm{d}}}} = ({\tilde Q_{i,{\rm{d}}}}, {\tilde E_{i,{\rm{d}}}},{\tilde \delta _{i,{\rm{d}}}},\tilde p_0^i)$ ，其中 $\tilde p_0^i = ({\tilde {\boldsymbol{q}}_0},0,{S^1},{N^0})$ 为初始状态； ${\tilde Q_{i,{\rm{d}}}} \subseteq {2^{{{\tilde Q}_{{\rm{la}}}} \times \varDelta }}$ 为状态空间集合，其中 $\varDelta = \left\{ {F^\gamma }:\gamma = {\tilde \varSigma_{\tilde K}}(\tilde s) \right\} \cup \{ {N^u}:u = {\tilde \varSigma _{\tilde K}}(\tilde s) \}$ 为故障标签集合； ${\tilde E_{i,{\rm{d}}}}$ 为模糊事件集合并且

$ {\tilde E_{i,{\rm{d}}}} = {\tilde E_{i,\max {\text{-o}}}} \cup \left\{ \tilde {\boldsymbol{a}} \in \tilde E:{\tilde \varSigma_{i,{\text{o}}}}(\tilde {\boldsymbol{a}}) > {\tilde \varSigma_{i,{\text{o}}}}(\tilde {\boldsymbol{\sigma}} ) \right\} $

${\tilde \delta _{i,{\rm{d}}}}:{\tilde Q_{i,{\rm{d}}}} \times {\tilde E_{i,{\rm{d}}}} \to {\tilde Q_{i,{\rm{d}}}}$ 为状态转移函数，对于 ${\tilde p^i} \in {\tilde Q_{i,{\rm{d}}}}$ 和 $\tilde {\boldsymbol{a}} \in {\tilde E_{i,{\rm{d}}}}$ ， ${\tilde \delta _{i,{\rm{d}}}}$ 定义为

$ {\tilde \delta _{i,{\rm{d}}}}({\tilde p^i},\tilde {\boldsymbol{a}}) = \mathop \cup \limits_{({{\tilde q}_{{\rm{la}}}},{l_3}) \in {{\tilde p}^i}} \mathop \cup \limits_{\tilde s \in {{\tilde L}_{\tilde {{{\boldsymbol{a}}}}}}({{\tilde p}^i},\tilde {\boldsymbol{a}}) } \{ {\tilde \delta _{{\rm{la}}}}\left({\tilde q_{{\rm{la}}}},\tilde s\right) ,{\rm{LP}}\left({\tilde q_{{\rm{la}}}},{l_3},\tilde s\right) \} $

${\tilde L_{\tilde {\boldsymbol{a}}}}({\tilde p^i},\tilde {\boldsymbol{a}})$ 是从状态 $ {\tilde p^i} $ 出发并且以模糊事件 $\tilde {\boldsymbol{a}}$ 结尾的字符串集合。LP是标签传播函数，定义为

如果 ${l_3} = {F^{\gamma} } $ ，并且 ${{\gamma} {'}} = {\tilde \varSigma_{{\tilde K}}}(\tilde s)$ ，那么

$ \text{LP}\left({\tilde{p}}^{i},{l}_{3},\tilde{s}\right) =\left\{\begin{array}{l}{F}^{\gamma },\text{如果}{l}_{3}\text=B \\ {F}^{{\gamma'}},如果{l}_{2}={S}^{2}并且{\gamma'} < \gamma \\ {F}^{\gamma },如果{l}_{2}={S}^{2}并且{\gamma'}\ge \gamma \end{array}\right. $

(9)

如果 $ {l_3} = {N^\gamma } $ 并且 ${\gamma {'}} = {\tilde \varSigma_{\tilde K}}(\tilde s)$ ，那么

$ \text{LP}\left({\tilde{p}}^{i},{l}_{3},\tilde{s}\right) =\left\{\begin{array}{l}{F}^{{\gamma'}}\text{ },如果{l}_{1}\text=m\text{,}{l}_{2}\text={S}^{2}并且{\gamma '} < \gamma \\ {F}^{\gamma }\text{ },如果{l}_{1}\text=m\text{,}{l}_{2}\text={S}^{2}并且{\gamma'}\ge \gamma \\ {N}^{{\gamma'}},如果{l}_{1}\ne m\text{,}{l}_{2}={S}^{1}并且{\gamma '} < \gamma \\ {N}^{\gamma },如果{l}_{1}\ne m\text{,}{l}_{2}={S}^{1}并且{\gamma '}\ge \gamma \end{array}\right. $

(10)

步骤4：全局模式故障安全诊断器的构建。

$ \tilde G $ 的全局模式故障安全诊断器构建为一个有限状态自动机 ${\tilde G_{\rm{D}}} = ({\tilde Q_{\rm{D}}},{\tilde E_{\rm{D}}},{\tilde \delta _{\rm{D}}},\tilde p_0^{\rm{D}})$ ，其中 ${\tilde E_{\rm{D}}}$ 为所有 ${\tilde E_{i,{\rm{d}}}}$ 的并集； $\tilde p_0^{\rm{D}} = ({\tilde {\boldsymbol{q}}_0},0,{S^1},{N^0})$ 为初始状态； ${\tilde Q_{\rm{D}}} \subseteq {2^{{{\tilde Q}_{{\rm{la}}}} \times \varDelta }}$ 为状态空间集合； ${\tilde \delta _{\rm{D}}}:{\tilde Q_{\rm{D}}} \times \tilde E_{\rm{D}}^ * \to {\tilde Q_{\rm{D}}}$ 为状态转移函数，对于 ${\tilde p^{\rm{D}}} \in {\tilde Q_{\rm{D}}}$ 和 $\tilde {\boldsymbol{a}} \in {\tilde E_{\rm{D}}}$ ， ${\tilde \delta _{\rm{D}}}$ 定义为

$ {\tilde \delta _{\rm{D}}}({\tilde p^{\rm{D}}},\tilde {\boldsymbol{a}}) = \mathop \cup \limits_{({{\tilde q}_{{\rm{la}}}},{l_3}) \in {{\tilde p}^{\rm{D}}}} \mathop \cup \limits_{\tilde s \in {{\tilde L}_{\tilde {\boldsymbol{a}}}}({{\tilde p}^{\rm{D}}},\tilde {\boldsymbol{a}}) } \{ {\tilde \delta _{{\rm{la}}}}\left({\tilde q_{{\rm{la}}}},\tilde s\right) ,{\text{LP}}({\tilde q_{{\rm{la}}}},{l_3},\tilde s) \} $

步骤5：模式故障安全协同诊断器的构建。

$ \tilde G $ 的模式故障安全协同诊断器构建为一个有限状态自动机 ${\tilde G_{\rm{T}}} = ({\tilde Q_{\rm{T}}},{\tilde E_{\rm{T}}},{\tilde \delta _{\rm{T}}},\tilde p_0^{\rm{T}})$ ， ${\tilde G_{\rm{T}}}$ 的初始状态 $\tilde p_0^{\rm{T}} = \left\{ \tilde p_0^{\rm{D}},\tilde p_0^1,\cdots,\tilde p_0^n\right\}$ 由全局模式故障安全诊断器的初始状态以及所有本地模式故障安全诊断器的初始状态所构成的集合； ${\tilde Q_{\rm{T}}} = {\tilde Q_{\rm{D}}} \times {\tilde Q_{1,{\rm{d}}}} \times {\tilde Q_{2,{\rm{d}}}} \times \cdots \times {\tilde Q_{n,{\rm{d}}}}$ 为状态空间集合； ${\tilde E_{\rm{T}}} \subseteq ({\tilde E_{\rm{D}}} \cup \left\{ \varepsilon \right\} ) \times ({\tilde E_{1,{\rm{d}}}} \cup \left\{ \varepsilon \right\} ) \times \cdots \times ({\tilde E_{n,{\rm{d}}}} \cup \left\{ \varepsilon \right\} )$ 为事件集合； ${\tilde {\boldsymbol{\sigma}} ^{\rm{T}}} = ({\tilde {\boldsymbol{\sigma}} ^{\rm{D}}},{\tilde {\boldsymbol{\sigma}} ^1},\cdots,{\tilde {\boldsymbol{\sigma}} ^n})$ 表示在 ${\tilde E_{\rm{T}}}$ 中的一个事件，对于每一个 $i \in \left\{ 1,2,\cdots,n\right\}$ 有

$ {\tilde{{\boldsymbol{\sigma}} }}^{i}=\left\{\begin{array}{l}{\tilde{{\boldsymbol{\sigma}} }}^{{\rm{D}}},如果{\tilde{{\boldsymbol{\sigma}} }}^{{\rm{D}}}\in {\tilde{E}}_{i,{\rm{d}}} \\ \varepsilon \text{ },其他 \end{array} \right.$

(11)

转移函数 ${\tilde \delta _{\rm{T}}}:{\tilde Q_{\rm{T}}} \times {\tilde E_{\rm{T}}} \to {\tilde Q_{\rm{T}}}$ 定义为 ${\tilde{\delta }}_{{\rm{T}}}({\tilde{p}}_{{\rm{T}}},{\tilde {\boldsymbol{\sigma}} }^{{\rm{T}}}) ={\tilde{p}}_{{\rm{T}}}{'}$ ，其中 ${\tilde p_{\rm{T}}} = ({\tilde p^{\rm{D}}},{\tilde p^1},\cdots,{\tilde p^n})$ ， $\tilde p_{\rm{T}}{'} = ({\tilde p^{{{\rm{D'}}{}}}},{\tilde p^{{1{'}}}},\cdots,{\tilde p^{{n{'}}}})$

$ {\tilde{p}}^{{{\rm{D}}}{{'}}}=\left\{\begin{array}{l}{\tilde{\delta }}_{{\rm{D}}}({\tilde{p}}^{{\rm{D}}},{\tilde{{\boldsymbol{\sigma}} }}^{{\rm{D}}}) ,如果{\tilde{\delta }}_{{\rm{D}}}({\tilde{p}}^{{\rm{D}}},{\tilde{{\boldsymbol{\sigma}} }}^{{\rm{D}}}) 有定义 \\ {\tilde{p}}^{{\rm{D}}},其他 \end{array}\right. $

(12)

对于每一个 $i \in \{ 1,2,\cdots,n\}$ ，有

$ {\tilde{p}}^{{i'}}=\left\{\begin{array}{l}{\tilde{\delta }}_{i,{\rm{d}}}({\tilde{p}}^{i},{\tilde{{\boldsymbol{\sigma}} }}^{i}) ,如果{\tilde{\delta }}_{i,{\rm{d}}}({\tilde{p}}^{i},{\tilde{{\boldsymbol{\sigma}} }}^{i}) 有定义 \\ {\tilde{p}}^{i},其他 \end{array} \right.$

(13)

注释1 　上述步骤1构建的模式故障识别器 ${\tilde G_{{\rm{pa}}}}$ 用于识别系统 $ \tilde G $ 是否发生了模式故障。通过步骤2构建的非法语言识别器 ${\tilde G_{{\rm{la}}}}$ 以识别当系统 $ \tilde G $ 发生了模式故障之后，是否执行了被禁止的非法操作。在步骤2的基础上，通过步骤3构建 $ \tilde G $ 的所有本地模式故障安全诊断器 ${\tilde G_{1,{\rm{d}}}},{\tilde G_{2,{\rm{d}}}}, \cdots ,{\tilde G_{n,{\rm{d}}}}$ ，以实现本地站点的模式故障安全诊断。再通过步骤4，构建 $ \tilde G $ 的全局模式故障安全诊断器 ${\tilde G_{\rm{D}}}$ 。步骤5则在上述全局模式故障安全诊断器 ${\tilde G_{\rm{D}}}$ 和所有本地模式故障安全诊断器 ${\tilde G_{1,{\rm{d}}}},{\tilde G_{2,{\rm{d}}}}, \cdots , {\tilde G_{n,{\rm{d}}}}$ 的基础上构建模式故障安全协同诊断器 ${\tilde G_{\rm{T}}}$ ，以实现分布式FDES的模式故障安全协同诊断。其框架图如图2所示。

4 模式故障安全协同诊断的充分必要条件

定义2 　设 ${\tilde G_{\rm{T}}}$ 是 $ \tilde G $ 的模式故障安全协同诊断器并且 ${\tilde p_{\rm{T}}} = ({\tilde p^{\rm{D}}},{\tilde p^1},\cdots,{\tilde p^n}) \in {\tilde Q_{\rm{T}}}$ 是 ${\tilde G_{\rm{T}}}$ 的一个状态，如果 $\left(\tilde {\boldsymbol{q}},{l_1},{l_2},{l_3}\right) \in {\tilde p^i}$ 满足 $ {l_2} = {S^2} $ 并且 $ {l_3} = {F^\gamma } $ ，那么 $ {\tilde p^i} $ 叫做 ${\tilde p_{\rm{T}}}$ 的第 $ i $ 分量的 $ {S^2} - {F^\gamma } $ 状态。

定义3 　设 ${\tilde p_{\rm{T}}} = ({\tilde p^{\rm{D}}},{\tilde p^1},\cdots,{\tilde p^n}) \in {\tilde Q_{\rm{T}}}$ 是 $ {\tilde G_T} $ 的一个状态，如果对于任何 $\left(\tilde {\boldsymbol{q}},{l_1},{l_2},{l_3}\right) \in {\tilde p^i}$ ，总满足 $ {l_3} = {F^\gamma } $ 或者 $ {l_3} = {N^u} $ ，那么 ${\tilde p_{\rm{T}}}$ 是一个第 $ i $ 分量的确定性状态。如果存在 $\left(\tilde {\boldsymbol{q}},{l_1},{l_2},{l_3}\right) \in {\tilde p^i}$ 、 $\left({\tilde {\boldsymbol{q}}{{'}}},l_1{'},l_2{'},l_3{'}\right) \in {\tilde p^i}$ 满足 $ {l_3} = {F^{\gamma} } $ 、 $l_3{'} = {N^u}$ 或者 $ {l_3} = {N^u} $ 、 $l_3{'} = {F^\gamma }$ ，那么 ${\tilde p_{\rm{T}}}$ 是一个第 $ i $ 分量的不确定性状态。

在定义2和定义3引入第 $ i $ 分量的不确定性状态之后，可以得到如下分布式FDES的模式故障安全协同诊断的一个充分必要条件。

定理1 　设 $\tilde G = (\tilde Q,\tilde E,\tilde \delta ,{\tilde {\boldsymbol{q}}_0})$ 是一个FDES，并且 ${\tilde G_{\rm{T}}} = ({\tilde Q_{\rm{T}}},{\tilde E_{\rm{T}}},{\tilde \delta _{\rm{T}}},\tilde \tau _{\rm{T}}^0)$ 是相应的模式故障安全协同诊断器。当且仅当下列条件成立， $ \tilde G $ 是程度为 $ \lambda $ 的模式故障安全协同可诊断的。

(1) ${\tilde G_{\rm{T}}}$ 存在一个第 $ i $ 分量的不确定性状态循环。

(2) ${\tilde G_{\rm{T}}}$ 存在一个第 $ i $ 分量的 $ {S^2} - {F^\gamma } $ 状态，并且 $\lambda = \dfrac{{{\rm{min}}{(}\gamma {) }}}{{{{\tilde \varSigma}_{\tilde K}}{(}\tilde {\boldsymbol{\sigma}} {) }}}$ 。

证明 　充分性：假设 $ \tilde G $ 是程度为 $ \lambda $ 的模式故障安全协同可诊断的。根据定义1，存在 $ {n_0} \in N $ ，对于任意 $\tilde s \in {\varPsi _{\tilde S}}(\tilde K)$ 且 $ \tilde t \in \tilde L/\tilde s $ ，当 $|\tilde t\,| \geqslant {n_0}$ ，有

$\begin{gathered} \left(\exists i \in I\right) \left(\exists \tilde v \in {\text{pre}}(\tilde t) \right) ({\text{pre}}\left(\tilde v\right) \cap {\tilde L^I} = \emptyset ) \wedge \\ \left({\lambda _i} = {{\rm{min}}_{\tilde u \in \tilde K}}\left(\frac{{{D_i}}}{{{{\tilde \varSigma}_{\tilde K}}\left(\tilde u\right) }}\right) \geqslant \lambda > 0\right) \end{gathered}$

所以存在 $\tilde \omega \in P_{i,\tilde{\boldsymbol{ \sigma}} }^{ - 1}{P_{i,\tilde {\boldsymbol{\sigma}} }}(\tilde s\tilde v)$ 满足 $\tilde \varSigma_{\tilde K}^{\tilde S}(\tilde \omega ) = {\lambda _i}{\tilde \varSigma_{\tilde K}}(\tilde u) \leqslant {\tilde \varSigma_{\tilde K}}(\tilde u)$ 。记 $\tilde \delta ({\tilde {\boldsymbol{q}}_0},\tilde s\tilde v) = \tilde {\boldsymbol{q}}$ 和 $\tilde \delta ({\tilde {\boldsymbol{q}}_0},\tilde \omega ) = {\tilde {\boldsymbol{q}}{{{'}}}}$ 。 $ \tilde G $ 的状态不是无限的，并且当后续状态数足够多时，在模式故障安全协同诊断器 ${\tilde G_{\rm{T}}}$ 中存在一个第 $ i $ 分量的不确定性状态循环。 $(\left(\exists i \in I\right) (\exists \tilde v \in {\text{pre}}\left(\tilde t\right) ) {\text{pre}}\left(\tilde v\right) \cap {\tilde L^I} = \emptyset)$ 根据式(8)可以得到 $ {l_2}{\text{ = }}{S^2} $ 。所以在模式故障安全协同诊断器 ${\tilde G_{\rm{T}}}$ 中存在一个第 $ i $ 分量 $ {S^2} - {F^\gamma } $ 状态。如果对于任意 ${\tilde \omega {{{'}}}} \in P_{i,\tilde {\boldsymbol{\sigma}} }^{ - 1}{P_{i,\tilde {\boldsymbol{\sigma}} }}(\tilde s\tilde v)$ ，满足 $\tilde \varSigma _{\tilde K}^{\tilde S}(\tilde \omega ) \leqslant \tilde \varSigma _{\tilde K}^{\tilde S}({\tilde \omega {{{'}}}})$ 且对于任意 ${\tilde u{{{'}}}} \in \tilde K$ 都有

$ \frac{{\min \left\{ {{\tilde \varSigma }_{\tilde K}}(\tilde u) ,\tilde \varSigma _{\tilde K}^{\tilde S}(\tilde \omega ) \right\} }}{{{{\tilde \varSigma }_{\tilde K}}(\tilde u) }} \leqslant \frac{{\min \left\{ {{\tilde \varSigma }_{\tilde K}}({{\tilde u}^{'}}) ,\tilde \varSigma _{\tilde K}^{\tilde S}(\tilde \omega ) \right\} }}{{{{\tilde \varSigma }_{\tilde K}}({{\tilde u}^{'}}) }} $

即 ${\tilde \varSigma _{\tilde K}}(\tilde u) \leqslant {\tilde \varSigma _{\tilde K}}({\tilde u^{'}})$ ，所以 $\lambda = {\rm{min}}{(}{\lambda _i}{) } = \dfrac{{{\rm{min}}{(}\gamma {) }}}{{{{\tilde \varSigma }_{\tilde K}}{(}\tilde {\boldsymbol{\sigma}} {) }}}$ 。

必要性：下面用反证法证明必要性。假设 $ \tilde G $ 是程度为 $ \lambda $ 的模式故障安全协同可诊断的，但不符合定理1中的条件(1)或条件(2)。

若不满足条件(1)，则在 ${\tilde G_{\rm{T}}}$ 中不存在不确定性状态循环。记 $\tilde \delta ({\tilde {\boldsymbol{q}}_0},\tilde s\tilde v) = \tilde {\boldsymbol{q}}$ 和 $\tilde \delta ({\tilde {\boldsymbol{q}}_0},\tilde \omega ) = {\tilde {\boldsymbol{q}}{'}}$ 。因为 ${\tilde G_{\rm{T}}}$ 中不存在不确定性状态循环，所以对于任意 $ i \in I $ 来说，都不存在 $\tilde \omega \in P_{i,\tilde {\boldsymbol{\sigma}} }^{ - 1}{P_{i,\tilde {\boldsymbol{\sigma}} }}(\tilde s\tilde v) \subseteq \tilde S$ ，因此可以得到 ${\tilde G_{\rm{T}}}$ 不是模式故障可诊断的，所以 $ \tilde G $ 不是程度为 $ \lambda $ 的模式故障安全协同可诊断的，这与假设相矛盾。

若不满足条件(2)，则在 ${\tilde G_{\rm{T}}}$ 中不存在 $ {S^2} - {F^\gamma } $ 状态。设 $\tilde s \in {\varPsi _{\tilde S}}(\tilde K)$ 且 $ \tilde t \in \tilde L/\tilde s $ ，因为在 ${\tilde G_{\rm{T}}}$ 中不存在 $ {S^2} - {F^\gamma } $ 状态，当 $ |\tilde t| \geqslant {n_0} $ 有对于任意 $ i \in I $ 和 $\tilde v \in {\text{pre}}(\tilde t\,)$ ，总是可以得到 $ {\text{pre}}(\tilde v) \cap {\tilde L^I} \ne \emptyset $ ，所以 $ \tilde G $ 不是程度为 $ \lambda $ 的模式故障安全协同可诊断的，这与假设相矛盾。

下面通过一个例子来说明第3部分构建模式故障安全协同诊断器的具体步骤以及用定理1中的方法来判断例1中构建的FDES模型 $ \tilde G $ 是否模式故障安全协同可诊断的。

例2 　考虑例1中的FDES模型 $ \tilde G $ 以及模式故障 $\tilde K = \{ \tilde {\boldsymbol{a}}\tilde {\boldsymbol{d}}\}$ 和被禁止事件串集合 $\varGamma = \left\{ \tilde {\boldsymbol{e}}\tilde {\boldsymbol{f}},\tilde {\boldsymbol{c}}\tilde {\boldsymbol{e}}\right\}$ ，在例1中用定义的方法得到 $ \tilde G $ 是程度为0.25的模式故障安全协同可诊断的。

首先由获得模式故障 $\tilde K = \left\{ \tilde {\boldsymbol{a}}\tilde {\boldsymbol{d}}\right\}$ ，再根据步骤1和步骤2，分别构建模式故障识别器 ${\tilde G_{{\rm{pa}}}}$ 和非法语言识别器 ${\tilde G_{{\rm{la}}}}$ 如图3和图4所示。

再根据步骤3构建本地模式故障安全诊断器 ${\tilde G_{1,{\rm{d}}}}$ 如图5所示。本地模式故障安全诊断器 ${\tilde G_{2,{\rm{d}}}}$ 和全局模式故障安全诊断器 ${\tilde G_{\rm{D}}}$ 能够类似得到。

根据步骤5，模式故障安全协同诊断器 ${\tilde G_{\rm{T}}}$ 如图6所示。

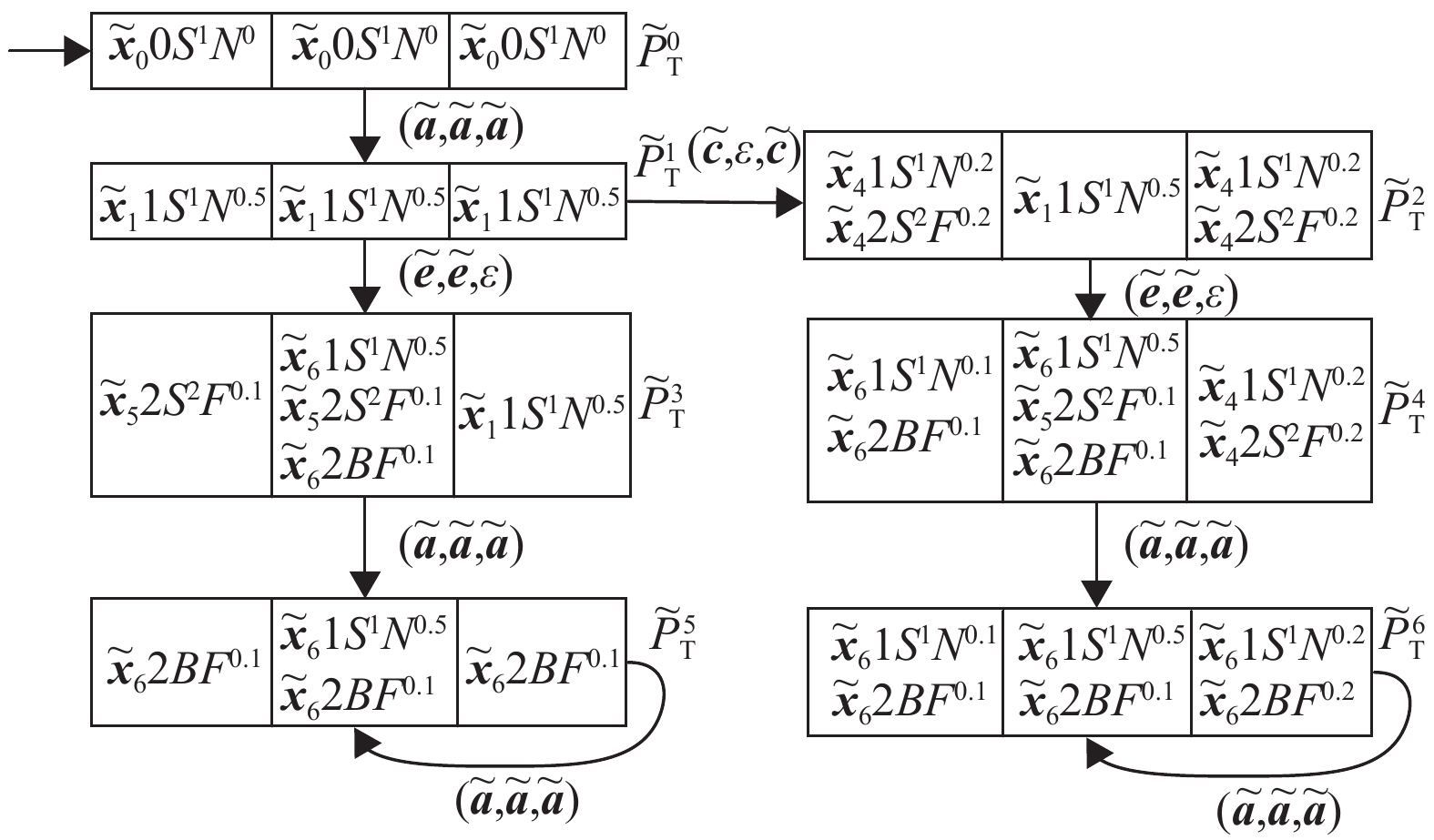
在 ${\tilde G_{\rm{T}}}$ 中 $\tilde p_{\rm{T}}^5$ 的第1分量形成了一个不确定性状态循环， $\tilde p_{\rm{T}}^6$ 的第1分量和第2分量都形成了一个不确定性状态循环。在 ${\tilde G_{\rm{T}}}$ 中 $\tilde p_{\rm{T}}^2$ 的第2分量是 $ {S^2} - {F^{0.2}} $ 状态， $\tilde p_{\rm{T}}^3$ 的第1分量是 $ {S^2} - {F^{0.1}} $ 状态， $\tilde p_{\rm{T}}^4$ 的第1分量是 $ {S^2} - {F^{0.1}} $ 状态并且第2分量是 $ {S^2} - {F^{0.2}} $ 状态。根据定理1可知， $ \tilde G $ 是模式故障安全协同可诊断的并且诊断程度为

$ \lambda=\dfrac{{{\rm{min}}{(}\gamma {) }}}{{{{\tilde \varSigma}_{\tilde K}}{(}\tilde {\boldsymbol{\sigma}} {) }}}=\dfrac{{{\rm{min}}{(}0.2,0.1{) }}}{{0.4}}=\dfrac{{0.1}}{{0.4}}=0.25 $

这与例1用定义的方法得到的结论相吻合。

5 总结

本文在FDES的框架下，提出了一种模式故障安全协同诊断的定义方法。并且通过构建模式故障安全协同诊断器，得到了一个判定分布式FDES的模式故障安全诊断的充分必要条件。在本文研究的基础上，还可以进一步考虑赋时DES的模式故障安全诊断和FDES的模式故障安全预测等问题。