近年来，随着有低时延需求的智能应用(如虚拟现实技术和增强现实技术)的发展，这些有低时延需求的应用要求无线设备(如智能手机和便携式设备等)具有低时延通信和计算的能力^[1-3]。因此，移动边缘计算(Mobile Edge Computing，MEC)的研究日益受到关注^[4-5]，而在MEC系统的缓存设计中，部署了MEC服务器的无线接入点(Access Points，APs)和基站(Base Stations，BSs)能提前缓存计算任务或计算结果，无线设备因此能直接从AP端获取计算结果而无需进行计算卸载和本地计算。联合设计计算任务缓存、计算资源分配和计算卸载能有效地提高MEC系统的性能^[6-7]。

国内外很多研究团队对移动边缘计算的缓存设计进行了深入的研究。文献[8-9]研究多MEC系统的缓存设计和任务路由问题，部署MEC服务器的AP需要从多个MEC服务器中选择其中一个服务器，将来自无线设备的计算任务卸载到被选定服务器中进行计算；针对物联网设备中存储的内容面临着安全威胁的问题，文献[10]研究物联网设备缓存内容的安全和隐私问题；文献[11]针对单个用户的场景进行缓存和计算卸载设计；文献[12]基于Lyapunov优化方法提出一种动态缓存方案为车联网用户提供高质量视频流服务；文献[13]提出一种两阶段的随机博弈框架以优化MEC系统的缓存决策和资源分配；文献[14-15]针对MEC系统的资源匮乏问题提出了联合任务/内容缓存和资源分配方法；文献[16-18]基于Lyapunov优化方法研究MEC系统给定缓存方案在大时间尺度下的稳定性和性能。以上工作都在计算任务可能重复的情况下进行缓存设计，缺乏每个任务都不相同情况下的缓存研究，基于任务热度的缓存方案未必是最优节能方案；此外，缺乏在多用户MEC系统缓存设计中以降低系统能耗为目的的研究。

针对上述问题，基于加权能耗和最小化的系统性能准则，本文研究多用户多时隙的MEC系统计算任务缓存优化设计。考虑的多用户多时隙MEC系统由一个部署了MEC服务器的AP和多个无线设备构成，无线设备通过计算卸载和本地计算在任务完成期限内执行动态到达的计算任务，部署在AP侧的MEC服务器通过缓存和代理计算协助无线设备在完成期限内处理到达的计算任务。本文排除了计算任务的热度信息，考虑在不同时隙到达无线设备的计算任务互不相同的场景下进行任务缓存研究，探索任务热度以外影响缓存决策的因素。此外，本文考虑部分计算卸载技术，计算任务可以任意地分割为两个部分，分别由无线设备进行本地计算和通过计算卸载到AP端进行任务计算。

本文的主要贡献总结如下：(1) 在多时隙计算框架下，建立了计算任务动态到达多用户的MEC系统缓存设计的数学模型，基于加权能耗和最小化准则，优化MEC服务器缓存决策、MEC服务器计算量、无线设备本地计算量和计算卸载量，约束条件包括缓存容量限制、任务因果性限制和任务完成期限限制。(2) 为了刻画系统性能下界，考虑信道状态信息和计算任务已知的离线场景，利用分支定界法获得系统最优性能。(3) 为降低计算复杂度，提出基于凸松弛的求解方案，数值结果表明该求解方案的性能接近分支定界法给出的最优解。(4) 数值仿真实验验证了本文提出的联合设计缓存方案的有效性，基于凸松弛的求解方案的性能接近由分支定界法给出的最优解；相较于考虑的基准设计方案，本文所提方案具有显著的性能增益。

1 系统模型与问题构造

如图1所示，本文考虑多用户多时隙移动边缘计算系统，该系统包括一个部署了MEC服务器的AP和K个无线设备。令 $\mathcal{K} = \{ 1, \cdots ,K\} $ 为K个无线设备组成的集合，每个无线设备需要完成在各个时隙开始时刻随机到达的计算任务，到达无线设备的所有计算任务都需要在给定的任务完成期限内完成。MEC服务器能通过计算任务缓存提前缓存到达无线设备的计算任务，无线设备因此能从MEC服务器中直接获取计算结果而无需上传输入数据以及本地计算。但对于没有被缓存的计算任务，无线设备需要通过本地计算和计算卸载来在时间期限内完成这些计算任务。

1.1 缓存模型

MEC服务器能将可能到达无线设备的计算任务进行缓存并完成计算任务。本文采用多时隙计算框架，记 $\mathcal{N} \buildrel \Delta \over = \{ 1, \cdots ,N\}$ 为N个时隙组成的集合, 每个时隙记为τ，在第n个时隙开始时刻到达第k个无线设备的任务序列的输入数据的比特数记为 ${S}_{k,n}\geqslant 0$ 。记布尔变量 ${a_{k,n}} \in \{ 0,1\} $ 为MEC服务器的缓存决策，当MEC服务器缓存第n个时隙开始时刻到达第k个无线设备的计算任务时，则取 ${a_{k,n}} = 1$ ；否则取 ${a_{k,n}} = 0$ 。建模计算任务缓存约束条件

$ {\displaystyle \sum _{k=1}^{K}{\displaystyle \sum _{n=1}^{N}{a }_{k,n}}}{S}_{k,n} \leqslant {S}_{0} $

(1)

式中： ${S_0}$ 为MEC服务器的最大缓存容量。在实际场景中，不同用户在不同时间的请求可能是重复的，本文在没有任务热度信息情况下研究计算缓存，挖掘热度信息以外影响缓存决策的因素，因此假设到达的计算任务不重复。值得注意的是，本文是在计算任务已知的离线场景中进行缓存决策研究，离线场景的缓存设计可以作为在线设计方案的系统性能下界，为在线设计时的任务序列预测算法提供先验知识。

1.2 无线设备端的计算卸载和本地计算

本文首先描述了用于无线设备计算卸载和本地计算的任务输入比特调度方案，然后对该调度方案的能耗进行了建模。

通过使用计算任务卸载，MEC成为延长无线设备电池寿命的一个有前景的解决方案。具体而言，无线设备可以将计算密集型任务卸载给AP以减少其能耗。通过计算任务部分卸载技术，无线设备将计算任务划分为两部分，一部分在无线设备端进行计算，而另一部分通过计算卸载到MEC服务器进行计算。记 ${d}_{k,n}^{\text{loc}} \geqslant 0$ 为第k个无线设备在第n个时隙进行本地计算的任务输入数据的比特数，另一部分计算任务记为 ${d}_{k,n}^{\text{off}} \geqslant 0$ ，为卸载到MEC服务器的任务输入数据的比特数。由于到达的计算任务、任务卸载量以及执行的计算任务三者存在因果性，该因果性指的是无线设备在前n个时隙计算和卸载比特数总和不能多于前n个时隙到达的未缓存的计算任务输入数据的比特数总和。建模无线设备端的计算任务因果性约束条件

$ {\displaystyle \sum _{i=1}^{n}{d}_{k,i}^{\text{loc}}}+{\displaystyle \sum _{i=1}^{n}{d}_{k,i}^{\text{off}}} \leqslant {\displaystyle \sum _{i=1}^{n}(1-{a }_{k,i}) }{S}_{k,i} $

(2)

式中： $ k = 1, \cdots ,K $ ； $ n = 1, \cdots ,N - 1 $ 。

每个无线设备都必须在任务完成期限内完成所有到达的未被缓存的计算任务。建模计算完成期限约束条件

$ \sum\limits_{i = 1}^N {d_{k,i}^{{\text{loc}}}} + \sum\limits_{i = 1}^{N - 1} {d_{k,i}^{{\text{off}}}} = \sum\limits_{i = 1}^N {(1 - {a _{k,i}}) } {S_{k,i}} $

(3)

式中： $ k = 1, \cdots ,K $ 。值得注意的是，因为在第N个时隙卸载的计算任务将在时隙(N+1) 的开始时刻到达MEC服务器，故 $d_{k,N}^{{\text{off}}} = 0$ 。

1.2.1 无线设备本地计算的能耗

无线设备本地计算所产生的能耗与需要完成的计算任务的比特数相关。已知第k个无线设备在第n个时隙需要完成的计算任务的比特数为 $d_{k,n}^{{\text{loc}}}$ ，因此需要总数目为 ${C_k}d_{k,n}^{{\text{loc}}}$ 的CPU周期数，其中 ${C_k}$ 是该无线设备本地计算单位比特所需要的CPU周期数。本文假设无线设备采用动态电压频率调整技术^[1,5]动态地调节在无线设备的CPU频率，因此，第k个无线设备在第n个时隙将CPU频率调整为 ${f_{k,n}} = {C_k}d_{k,n}^{{\text{loc}}}/\tau $ ，假设上述所需的CPU频率 ${f_{k,n}}$ 总是不大于无线设备允许的最大频率值。建模无线设备本地计算的能耗^[19]

$ E_{k,n}^{{\text{loc}}} = {\zeta _k}{C_k}d_{k,n}^{{\text{loc}}}f_{k,n}^2 = \frac{{{\zeta _k}C_k^3{{(d_{k,n}^{{\text{loc}}}) }^3}}}{{{\tau ^2}}} $

(4)

式中： $ k = 1, \cdots ,K $ ； $ n = 1, \cdots ,N $ ； $ {\zeta _k} $ 是由第k个无线设备的CPU芯片架构决定的电容系数。

1.2.2 无线设备计算卸载的能耗

为计算无线设备计算卸载产生的能耗，建模上行链路传输的传输速率(以bits/s为单位)

$ {r_{k,n}} = {B_{k,n}}{\log _2}\left( {1 + \frac{{{p_{k,n}}{{\left| {{h_{k,n}}} \right|}^2}}}{{{\sigma ^2}}}} \right) $

式中： ${p_{k,n}}$ 和 ${h_{k,n}}$ 分别为第k个无线设备在第n个时隙的向AP进行计算卸载的传输功率和信道功率增益^[19] ；B_k,n为第k个无线设备在第n个时隙进行计算卸载的上行链路传输的频谱带宽； ${\sigma ^2}$ 为AP接收端的加性噪声功率。为确保卸载的计算任务输入数据在下一时隙开始时候到达AP端，第k个无线设备在第n个时隙计算卸载的输入数据的比特数为 $d_{k,n}^{{\text{off}}}$ ，所需的传输速率满足等式 ${r_{k,n}}\tau = d_{k,n}^{{\text{off}}}$ 。建模无线设备计算卸载的能耗

$ E_{k,n}^{{\text{off}}} = {p_{k,n}}\tau = \frac{{{\sigma ^2}\tau ({2^{\frac{{d_{k,n}^{{\text{off}}}}}{{{B_{k,n}}\tau }}}} - 1) }}{{{{\left| {{h_{k,n}}} \right|}^2}}} $

(5)

式中： $ k = 1, \cdots ,K $ ； $ n = 1, \cdots ,N - 1 $ 。

1.3 AP端的任务计算模型

为建模AP端的计算任务因果性，记 $d_n^{{\text{mec}}}$ 为MEC服务器在第n个时隙要完成的输入数据的比特数。MEC服务器执行的计算任务量和因缓存而需要的计算量，以及从无线设备卸载而来的任务量三者存在计算任务因果性，即MEC服务器在第n个时隙执行的计算任务量不大于因缓存而需进行的任务计算量和卸载而来的计算任务量。建模AP端的计算任务因果性限制条件

$ {\displaystyle \sum _{i=1}^{n}{d}_{i}^{\text{mec}}} \leqslant {\displaystyle \sum _{k=1}^{K}{\displaystyle \sum _{i=1}^{N}{a }_{k,i}}}{S}_{k,i}+{\displaystyle \sum _{k=1}^{K}{\displaystyle \sum _{i=1}^{n-1}{d}_{k,i}^{\text{off}}}} $

(6)

式中： $ n = 1, \cdots ,N - 1 $ 。

部署在AP端的MEC服务器必须在任务完成期限内完成被缓存的计算任务以及从K个无线设备计算卸载而来的计算任务。建模MEC服务器的计算任务完成期限限制条件

$ \sum\limits_{i = 1}^N {d_i^{{\text{mec}}}} = \sum\limits_{k = 1}^K {\sum\limits_{i = 1}^N {{a _{k,i}}} } {S_{k,i}} + \sum\limits_{k = 1}^K {\sum\limits_{i = 1}^{N - 1} {d_{k,i}^{{\text{off}}}} } $

(7)

为建模MEC服务器的任务计算能耗，记 ${C_0}$ 为MEC服务器执行单位比特所需的CPU周期数，记 $f_n^{{\text{mec}}}$ 为MEC服务器在第n个时隙进行任务计算的CPU频率，其值可由表达式 $f_n^{{\text{mec}}} = {C_0}d_n^{{\text{mec}}}/\tau $ 计算而得。建模MEC服务器在第n个时隙进行计算的能耗

$ E_n^{{\text{mec}}} = {\zeta _0}{C_0}d_n^{{\text{mec}}}{(f_n^{{\text{mec}}}) ^2} = \frac{{{\zeta _0}C_0^3{{(d_n^{{\text{mec}}}) }^3}}}{{{\tau ^2}}} $

(8)

式中： $ n = 1, \cdots ,N $ ； $ {\zeta _0} $ 为由MEC服务器的CPU芯片架构决定的电容系数。

1.4 优化问题构造

构造多用户多时隙MEC系统的计算节能缓存优化设计问题，该优化设计问题以MEC系统的加权能耗和为目标函数，所述的目标函数的表达式为

$ E \buildrel \Delta \over = \sum\limits_{n = 1}^N {{w_0}} E_n^{{\text{mec}}} + \sum\limits_{k = 1}^K {\sum\limits_{n = 1}^N {{w _{k,n}}} } (E_{k,n}^{{\text{loc}}} + E_{k,n}^{{\text{off}}}) $

(9)

式中： $ {w_0} > 0 $ 和 ${w_{k,n}} > 0$ 分别为在不同时隙MEC服务器和各无线设备的能耗权值。

本文以最小化MEC系统的加权能耗和为目标，以MEC服务器缓存容量限制、计算任务因果性以及计算任务完成期限限制为限制条件，在上述优化目标和约束条件下优化MEC服务器缓存决策和计算量、无线设备的本地计算量和计算卸载量。构造的多用户多时隙MEC系统的节能缓存与计算卸载优化问题表示为

$\tag{10a} \mathop {\min }\limits_{{{\{ {a_{k,n}},d_{k,n}^{{\text{loc}}},d_{k,n}^{{\text{off}}}\} }_{\forall k,n}},{{\{ d_n^{{\text{mec}}}\} }_{\forall n}}} {\text{ }}E $

$ {\text{s}}{\text{.t}}{\text{.}} $ (1), (2), (3), (6), (7)

$ \tag{10b} {d}_{k,n}^{\text{off}} \geqslant 0,\forall k\in \mathcal{K}\,,n\in \mathcal{N}\backslash \left\{N\,\right\} $

$\tag{10c} {d}_{k,n}^{\text{loc}}\geqslant 0,{d}_{k,n}^{\text{mec}}\geqslant 0,\forall k\in \mathcal{K},n\in \mathcal{N} $

$\tag{10d} {a}_{k,n}\in \{0,1\},\forall k\in \mathcal{K},n\in \mathcal{N} $

优化问题(10)是一个混合整数非线性规划问题，该类问题是一个NP难问题^[20]。记 $ \{ {\{ a_{k,n}^*,d_{k,n}^{{\text{loc*}}},d_{k,n}^{{\text{off*}}}\} _{\forall k,n}}, {\{ d_n^{{\text{mec*}}}\} _{\forall n}}\} $ 为问题(10)的最优解。

2 优化问题求解

本文首先使用分支定界法求得问题(10) 的全局最优解，然后基于凸松弛提出一种低计算复杂度的算法快速求解问题(10) 。

2.1 基于分支定界法的最优解

本文首先使用分支定界法获得问题(10)的全局最优解以描述系统最优性能，分支定界法是求解混合整数非线性规划问题的一种常用算法^[20]。

分支定界方法的最大优点是，如果问题全局最优解存在，它可以保证收敛到最优全局解。然而应该注意的是，这种保证是由于问题的凸性^[20]。分支定界法通过维护一个全局上界和一个全局下界逼近原问题最优解，算法在全局上界和全局下界的差不大于给定精确度时停止。分支定界法将原问题分解成多个凸的子问题进行求解，因此首先需要对求解的子问题进行说明。首先是为获得下界需要求解的问题

$\tag{11a} \begin{gathered} \mathcal{P}\,\,({\mathcal{B}_1},{\mathcal{B}_0}) :\mathop {\min }\limits_{{{\{ {a_{k,n}}\} }_{\forall k,n}},{{\{ d_{k,n}^{{\rm{loc}}},d_{k,n}^{{\rm{off}}}\} }_{\forall k,n}},{{\{ d_n^{{\rm{mec}}}\} }_{\forall n}}} {\text{ }}E \\ {\text{ }} \\ \end{gathered} $

$ {\text{s}}{\text{.t}}{\text{.}} $ (1), (2), (3), (6), (7), (10b), (10c)

$\tag{11b} {a_{k,n}} \in [0,1],\forall (k,n) \in \mathcal{B}\backslash ({\mathcal{B}_1} \cup {\mathcal{B}_0}) $

$\tag{11c} {a_{k,n}} = 0,\forall (k,n) \in {\mathcal{B}_0} $

$\tag{11d} {a_{k,n}} = 1,\forall (k,n) \in {\mathcal{B}_1} $

式中： ${\mathcal{B}_0} = \{ (k,n) :{a_{k,n}} = 0,k \in \mathcal{K},n \in \mathcal{N}\} $ 和 ${\mathcal{B}_1} = \{ (k,n) : {a_{k,n}} = 1, k \in \mathcal{K},n \in \mathcal{N}\} $ 分别为最优值取值为0的缓存决策下标对集合和最优值取值为1的缓存决策下标对集合，用集合 $\mathcal{B}$ $ = \{ $ $(k,n) $ | $\forall k \in \mathcal{K},$ $\forall n \in \mathcal{N}\} $ 表示所有缓存决策的下标对集合。用 $ {a'_{k,n}} $ 表示求解问题 $\mathcal{P}\,\,({\mathcal{B}_1},{\mathcal{B}_0})$ 后得到的最优缓存决策，记 $ {\tilde{ \mathcal{B}_0}} = \{ (k,n) :{a'_{k,n}} \in [0,0.5) $ $,\forall (k,n) $ $ \in \mathcal{B}\backslash ({\mathcal{B}_1} \cup {\mathcal{B}_0}) \} $ 为求解 $\mathcal{P}\,\,({\mathcal{B}_1},{\mathcal{B}_0})$ 后取值范围为 $[0,0.5) $ 的缓存决策 $ {a'_{k,n}} $ 的下标对，类似地，记 ${\tilde{\mathcal{B}_1}} = $ $\{ (k,n) :$ ${a'_{k,n}} \in (0.5,1],$ $\forall (k,n) $ $ \in \mathcal{B}\backslash ({\mathcal{B}_1} \cup {\mathcal{B}_0}) \} $ 为求解问题 $\mathcal{P}\,\,({\mathcal{B}_1},{\mathcal{B}_0})$ 后得到的 $ {a'_{k,n}} $ 取值范围为 $(0.5,1]$ 的缓存决策下标对集合。

然后是为了获得上界而需要求解的问题

$\tag{12a} \begin{gathered} \tilde {\mathcal{P}}\,\,({\mathcal{B}_1},{\mathcal{B}_0}) :\mathop {\min }\limits_{{{\{ d_{k,n}^{{\text{loc}}},d_{k,n}^{{\text{off}}}\} }_{\forall k,n}},{{\{ d_n^{{\text{mec}}}\} }_{\forall n}}} {\text{ }}E \\ {\text{ }} \\ \end{gathered} $

$ {\text{s}}{\text{.t}}{\text{.}} $ (1), (2), (3), (6), (7), (10b), (10c)

$\tag{12b} {a_{k,n}} = 0,\forall (k,n) \in {\mathcal{B}_0} $

$\tag{12c} {a_{k,n}} = 1,\forall (k,n) \in {\mathcal{B}_1} $

$\tilde{ \mathcal{P}}\,\,({\mathcal{B}_1},{\mathcal{B}_0})$ 的下标对集合必须满足 $ {\mathcal{B}_1} \cup {\mathcal{B}_0} = \mathcal{B} $ 。问题 $\mathcal{P}\,\,({\mathcal{B}_1},{\mathcal{B}_0})$ 和 $\tilde {\mathcal{P}}\,\,({\mathcal{B}_1},{\mathcal{B}_0})$ 都是凸问题，通过CVX工具箱可进行求解。

分支定界法通过迭代逐一确定每个缓存决策的取值，假设 ${\mathcal B\,'_0}$ 和 ${\mathcal B\,'_1}$ 是某一次迭代中节点下界最小的节点的下标对集合，则这次迭代需要确定取值的缓存决策变量的下标对(k, n)通过式(13) 确定。

$ (k,n) = \mathop {\arg \min }\limits_{(i,j) \in \mathcal{B}\backslash \left( {\mathcal B\,'_1} \cup {\mathcal B\,'_0} \right) } |a_{i,j}^{} - 0.5| $

(13)

最后需要说明的是，分支定界法求解问题的过程会逐一确定每个缓存决策的取值，这类似于展开一棵分支定界二叉树，该树中深度为i的节点对应有i个缓存决策的取值已固定，即 $|{\mathcal{B}'_0} \cup {\mathcal{B}'_1}| = i$ 。

为分析该算法的复杂度，假设分支定界法在第L次迭代后收敛至给定的可容忍误差，其中1 $\leqslant$ L $\leqslant$ 2^KN。则此时总共进行了L(L+1) 次子问题的求解，求解这样的子问题采用内点法，故算法需要不少于 $O(\sqrt {N + KN} $ ${\mathrm{log}}_{2}({\scriptstyle \dfrac{\sqrt{N+KN}}{{t}^{(0) }\varepsilon}}) (1+L) L)$ 次牛顿迭代收敛至给定的可容忍误差，其中 $\varepsilon$ 为使用内点法时给定的求解精度， $ {t}^{\left(0\right) } $ 为内点法时的初始障碍参数^[20]， $ O(·) $ 为描述函数渐近上界的数学符号。求解问题(10) 的分支定界法如算法1所示。

算法1 求解问题(10) 的分支定界法

(1) 输入：精确度 $ \varepsilon $ ，任务序列S_k,n。

(2) 初始化： $ {{\mathcal{B}_1}{\text{ = }}{\mathcal{B}_0}{\text{ = }}\phi}$ ；求解问题 $ {\mathcal{P}\,\,({\mathcal{B}_1},{\mathcal{B}_0})}$ ， $ {\mathcal{P}\,\,({\mathcal{B}_1},{\mathcal{B}_0})}$ 的最优解用于初始化全局下界Λ；基于问题 $ {\mathcal{P}\,\,({\mathcal{B}_1},{\mathcal{B}_0})}$ 的最优缓存决策求解问题 $ {\widetilde {\mathcal{P}}\,\,({\tilde {\mathcal{B}_1}},{\tilde {\mathcal{B}_0}}) }$ ，并用问题 $ { \widetilde {\mathcal{P}}\,\,({\tilde {\mathcal{B}_1}},{\tilde {\mathcal{B}_0}}) }$ 的最优解初始化全局上界Υ。

(3) 迭代：

(a) 选定节点下界最小的节点，假设该节点已确定缓存决策取值的下标对的集合分别为 $ {{\mathcal{B}'_0} }$ 和 $ {{\mathcal{B}'_1}}$ ；

(b) 分支：根据式(13) 选定下标对(k,n) 后得 $ { \{ {\mathcal{B}'_0} \cup (k,n) ,{\mathcal{B}'_1}\}}$ 和 $ {\{ {\mathcal{B}'_0},{\mathcal{B}'_1} \cup (k,n) \} }$ 两条新分支；

(c) 求新分支的下界：求解 $ {\mathcal{P}\,\,({\mathcal{B}'_0} \cup \{ (k,n) \} ,{\mathcal{B}'_1})}$ 和 $ {\mathcal{P}\,\,({\mathcal{B}'_0},{\mathcal{B}'_1} \cup }$ $\{ (k,n) \} ) $ 获得两个新分支的节点下界以及两个下标对集合 $ {\tilde {\mathcal{B}}_0} $ 和 $ {\tilde {\mathcal{B}_1}} $ ；

(d) 求新分支的上界：分别求解 $ {\tilde {\mathcal{P}}\,\,({\mathcal{B}'_1} \cup \{ (k,n) \} }$ $ {\cup {\tilde {\mathcal{B}_1}})}$ $ { ,{\mathcal{B}'_0} \cup {\tilde {\mathcal{B}_0}}) }$ 和 $ { \tilde{ \mathcal{P}}\,\,({\mathcal{B}'_1} \cup {\tilde {\mathcal{B}_1}},{\mathcal{B}'_0} \cup \{ (k,n) \} \cup {\tilde {\mathcal{B}_0}}) }$ 获得两个新分支的节点上界；

(e) 更新： $\mathcal{L} $ ←所有叶节点中最小的节点下界值；

$ \mathscr{U} $ ←所有叶节点中最小的节点上界值。

(4) 直到： $ \mathscr{U}-\mathcal{L} $ $\leqslant$ $ \varepsilon $ 。

(5) 输出： $ \{ {\{a_{k,n}^*,d_{k,n}^{{\text{loc*}}},d_{k,n}^{{\text{off*}}}\} _{\forall k,n}},{\{ d_n^{{\text{mec*}}}\} _{\forall n}}\} $ 。

2.2 基于凸松弛的算法方案

本节提出基于凸松弛的低复杂度算法来求解问题(10) 。基于凸松弛的算法方案首先求解凸问题 $\mathcal{P}\,\,(\emptyset ,\emptyset )$ ，然后将求解后得到的缓存决策转换为布尔值，最后基于先验知识修正缓存决策后得到次优的缓存决策。

算法2展示了基于凸松弛的算法过程,其中 $ a_{k,n}^{'} \in [0,1] $ 为求解 $\mathcal{P}\,\,(\emptyset ,\emptyset )$ 后得到的缓存决策；而 ${\hat {\mathcal{B}_0}} \buildrel \Delta \over = \{ (k,n) |$ $ {a'_{k,n}} \in [0,0.5) , $ $ \forall k \in \mathcal{K}, $ $ n \in \mathcal{N}\} $ 为求解 $\mathcal{P}\,\,(\emptyset ,\emptyset )$ 后取值范围在[0,0.5) 的缓存决策下标对集合； ${\hat {\mathcal{B}_1}}\buildrel \Delta \over = \{(k,n) |{{a}^{\prime }}_{k,n}\in [0.5,1],$ $ \forall k \in \mathcal{K} $ $ ,n \in \mathcal{N}\} $ 为求解后取值范围在[0.5,1]的缓存决策下标对集合。由于 $ {\hat {\mathcal{B}_0}} $ $ \cup $ $ {\hat{\mathcal{B}_1}} $ 中的元素对应的缓存决策并不保证满足问题的缓存容量约束条件(1)，为保证满足缓存容量约束(1) ，算法2中的步骤5对缓存决策进行了修正，即将指定缓存决策的值从1设为0。修正依据是我们注意到分支定界法给出的最优解中，到达时隙更晚的计算任务将有更大的可能被MEC服务器缓存。所以在调整缓存决策的过程中，应优先将到达时隙早且计算任务比特数目最少的缓存决策值设为0，直到满足限制条件(1) 。

与分支定界法相比，基于凸松弛的算法方案只需要使用两次内点法即可，此算法需要不少于 $O(\sqrt {N + KN} $ $ {\mathrm{log}}_{2}({\scriptstyle \dfrac{2\sqrt{N+KN}}{{t}^{(0) } \varepsilon }}) ) $ 次牛顿迭代收敛至给定的允许误差。基于凸松弛的算法如算法2所示。

算法2 基于凸松弛的算法

(1) 输入：任务序列S_k,n。

(2) 初始化 $ {{\mathcal{B}_1} = {\mathcal{B}_0} = \emptyset }$ 。

(3) 使用CVX工具箱求解问题 $ {\mathcal{P}\,\,({\mathcal{B}_1},{\mathcal{B}_0}) }$ 。

(4) 将步骤2的最优缓存决策 $ {a'_{k,n}} $ 进行分类得 $ {{\hat {\mathcal{B}_0}} }$ 和 $ {{\hat {\mathcal{B}_1}}}$ 。

(5) 若 $ {{\displaystyle {\sum }_{(k,n) \in {{\hat {\mathcal{B}_1}}}}{a}_{k,n}}\leqslant{S}_{0} }$ ，则执行步骤5，否则迭代：

迭代：i取值从1到N。

(a) 找出第i个时隙时缓存决策取值为1且计算任务比特数最少的用户k，记录下标对(k,i) ；

(b) $ { {\hat {\mathcal{B}_1}} \leftarrow }$ $ {{\hat {\mathcal{B}_1}}\backslash \{ (k,i) \}}$ ， $ {{\hat {\mathcal{B}_0}} \leftarrow }$ $ {{\hat {\mathcal{B}_0}} \cup \{ (k,i) \}}$ ；

(c) 直到：满足 $ { {\displaystyle {\sum }_{(k,n) \in { {\hat {\mathcal{B}_1}}}}{a}_{k,n}}\leqslant{S}_{0} }$ 。

(6) 使用CVX工具箱求解问题 $ { \tilde {\mathcal{P}}\,\,({\tilde {\mathcal{B}_1}},{\tilde {\mathcal{B}_0}}) }$ 。

(7) 输出： $ {a_{k,n}^* = 1,\forall (k,n) \in {\tilde {\mathcal{B}_1}}}$ ； $ {a_{k,n}^* = 0,\forall (k,n) \in {\tilde {\mathcal{B}_0}} }$ ； $ {\{ d_{k,n}^{{\text{loc*}}}, } { d_{k,n}^{{\text{off*}}}\} _{\forall k,n}, {\{ d_n^{{\text{mec*}}}\} _{\forall n}} }$ 。

3 仿真结果

本节将提供数值仿真来验证所提出的设计方案。本文仿真的参数设置如下：无线设备用于卸载计算任务到MEC服务器的带宽B_k,n=1 MHz；由第k个无线设备的CPU芯片架构决定的电容系数 ${\zeta _k} = {10^{ - 27}}$ ；第k个无线设备计算单位比特计算任务所需的CPU周期数设置为C_k=3×10³；各计算任务的输入比特数服从均匀分布^[17]S_k,n $\sim \mathscr{U}$ (1,5) ×10³ bits；第k个无线设备在第n个时隙的权值 $ {w_{k,n}} = 0.9 $ 。在AP端，由MEC服务器的CPU芯片架构决定的系数 ${\zeta _k} = {10^{ - 23}}$ ；MEC服务器完成单位比特的计算任务所需的CPU周期数C₀=3×10³；AP接收端的噪声功率 $ {\sigma }^{2}={10}^{-9} $ W；MEC服务器的权值为 $ {w_0} = 0.1 $ 。本文采用莱斯衰落信道模型^[6]作为无线设备卸载计算任务到AP的过程中的信道，即 $ {h_{k,n}} = $ $\sqrt {\dfrac{{{{\mathcal{X}}_{R}}{\Omega _0}D_k^{ - \alpha }}}{{1 + {{\mathcal{X}_R}}}}} {h_0}$ $+ \sqrt {\dfrac{{{\Omega _0}D_k^{ - \alpha }}}{{1 + {\mathcal{X}_R}}}} h$ ，其中D_k为第k个无线设备和AP之间的距离； ${\mathcal{X}_R} = 1$ 为莱斯因子；h₀=1为视距因子；参考距离为一米时的路径损耗Ω₀=−32 dB； $ \alpha $ =3为路径损耗因子；h为小尺度信道衰落系数，该系数服从 $h \sim \mathcal{C}\mathcal{N}\,\,(0,1) $ 。

表1对比了分支定界法和基于凸松弛的求解方案给出的缓存决策。其中，无线设备个数K=5，时隙个数N=10，时隙的长度τ=0.2 s，第k个无线设备和AP的距离D_k=5k m；MEC服务器最大缓存容量 $ {S}_{0} $ =30×10³ bits，因此平均可以缓存10个计算任务。表1中的百分数表示在50次仿真的过程中，该计算任务被缓存的频率。由表1可见，两个算法方案都倾向于缓存最后若干个时隙到达无线设备的计算任务。到达时隙更晚的计算任务将有更大可能被缓存，这是因为最后若干个时隙到达的计算任务用于完成计算任务所剩余的的时隙数更少，将这些计算任务进行缓存可以让MEC服务器有更多时隙进行调度，从而有效地降低了系统的加权能耗和。同时可以观察到相距AP更远的无线设备的计算任务将有更大的可能被缓存，这是因为这些无线设备卸载计算任务到AP消耗更多的能量，在AP端将这些无线设备的计算任务进行缓存能有效地降低系统的加权能耗和。

本文考虑以下4个多用户MEC系统基准方案进行性能对比：

(1) 联合设计无缓存方案：MEC服务器不进行任务缓存，该方案对应求解问题(10) 时，令 ${a _{k,n}} = 0$ ， $ k = 1, \cdots ,K $ ； $ n = 1, \cdots ,N $ 。

(2) 计算卸载缓存方案：每个无线设备仅通过将计算卸载到AP端的方式处理到达的计算任务，该方案对应求解问题(10) 时，令 $ d_{k,n}^{{\text{loc}}} = 0 $ ， $ k = 1, \cdots ,K $ ； $n = 1, \cdots ,N$ 。

(3) 本地计算缓存方案：每个无线设备仅通过本地计算完成到达的计算任务，该方案对应求解问题(10) 时，令 $ d_{k,n}^{{\text{off}}} = 0 $ ， $ k = 1, \cdots ,K $ ； $ n = 1, \cdots ,N - 1 $ 。

(4) 本地计算无缓存方案：每个无线设备仅通过本地计算完成到达的计算任务，MEC服务器不提供缓存服务，该方案对应求解问题(10) 时，令 $ d_{k,n}^{{\text{off}}} = 0 $ ， $ {a _{k,n}} = 0 $ ， $ k = 1, $ $ \cdots ,K $ ； $ n = 1, \cdots ,N $ 。

注意到对于计算卸载方案，在最后一个时隙到达的计算任务无法进行处理导致无解，本文在仿真的过程中令S_k,N =0， $ k = 1, \cdots ,K $ 。

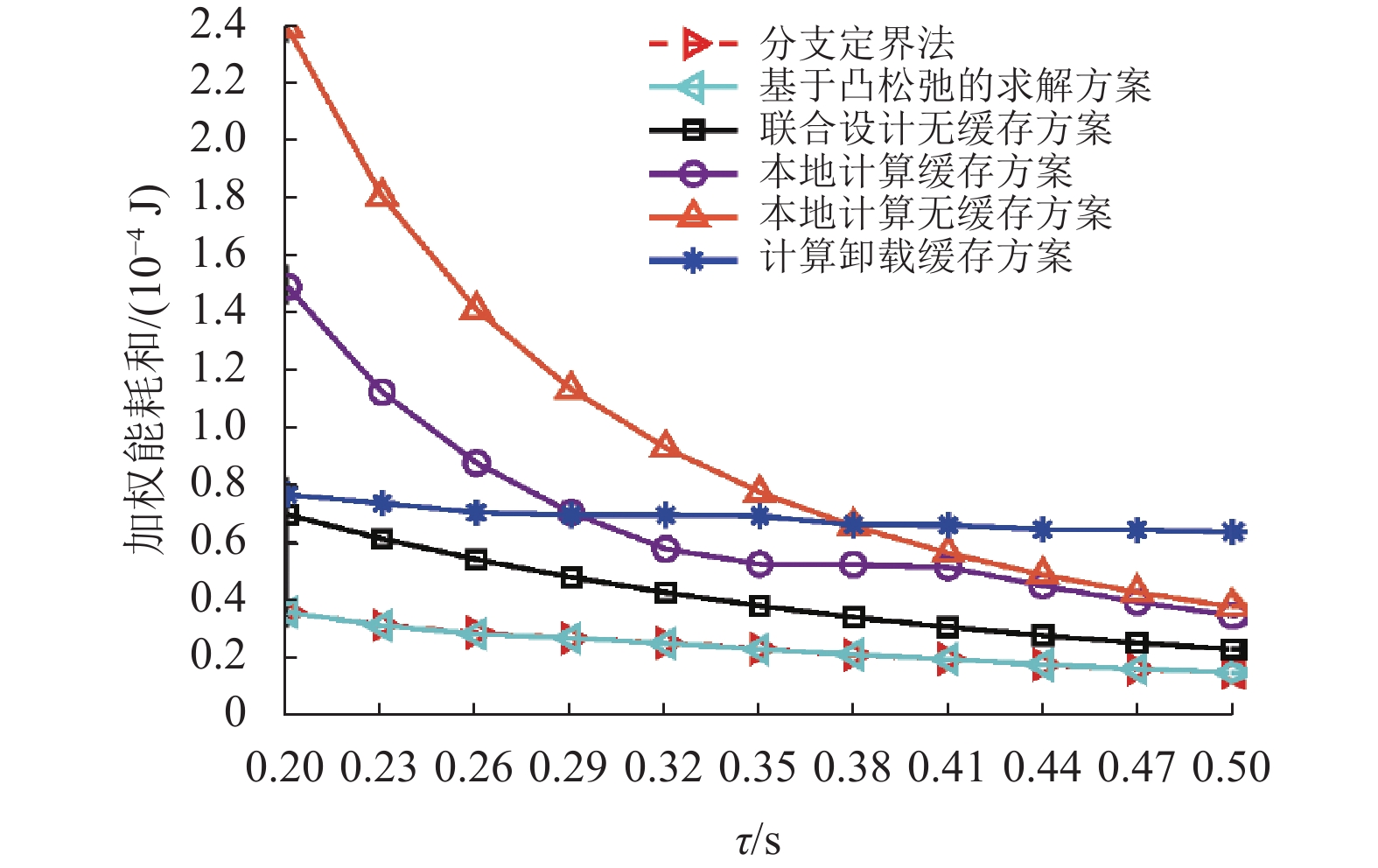
图2展示了τ和加权能耗和的变化关系。其中K=10，N=15， $ {S}_{0} $ =60×10³ bits，AP和第K个无线设备的距离服从均匀分布D_k $\sim \mathscr{U}$ (1,10) m。由图2可见，各个方案的加权能耗和随着时隙长度的增加而减少，这是因为AP端的MEC服务器和无线设备有更多时间以能耗更小的方式处理到达的计算任务。对比分支定界法和基于凸松弛的算法方案的性能曲线，基于凸松弛的求解方案逼近基于分支定界法的最优性能曲线。此外，由图可见基于凸松弛的求解方案的性能优于所有基准方案。本地计算缓存方案的性能优于本地计算无缓存方案，这展现了缓存在MEC系统在节能方面的效益。联合设计无缓存方案的性能优于其他3个基准方案，这说明联合设计对于节约MEC系统的加权能耗和具有重大作用。此外，计算卸载缓存方案在τ $\geqslant $ 0.29 s后不如本地计算缓存方案，这说明在仅由MEC服务器或仅由无线设备完成所有计算任务的情况下，若时隙的持续时间较长，则所有计算任务都交由MEC服务器进行计算的加权能耗高于将计算任务交由各个无线设备进行计算的加权能耗，若时隙的持续时间较短则交由MEC服务器进行计算能降低系统加权能耗和。

图3展示了无线设备数量和加权能耗和的变化关系。其中N=5， ${S}_{0}$ =60×10³ bits，τ=0.2 m，AP和无线设备k的距离服从均匀分布D_k $\sim \mathscr{U}$ (1,10) m。由图3可见，加权能耗和随着无线设备数量的增加而增加，这是因为无线设备的增加使得到达的计算任务增加，计算这些增加的计算任务需要更多的能量进行计算。所提的基于凸松弛的求解方案的性能接近分支定界法给出的最优解，且优于其余4个基准方案。联合设计无缓存方案在K为 $ ⩾ $ 22后加权能耗和性能才优于本地计算缓存方案和计算卸载缓存方案，这是因为缓存容量有限，本地计算缓存方案和计算卸载缓存方案的缓存容量已经用完，没有进一步降低系统加权能耗和的方法；虽然联合设计无缓存方案没有缓存功能，但联合设计在计算任务量大的时候能有效降低系统加权能耗和。

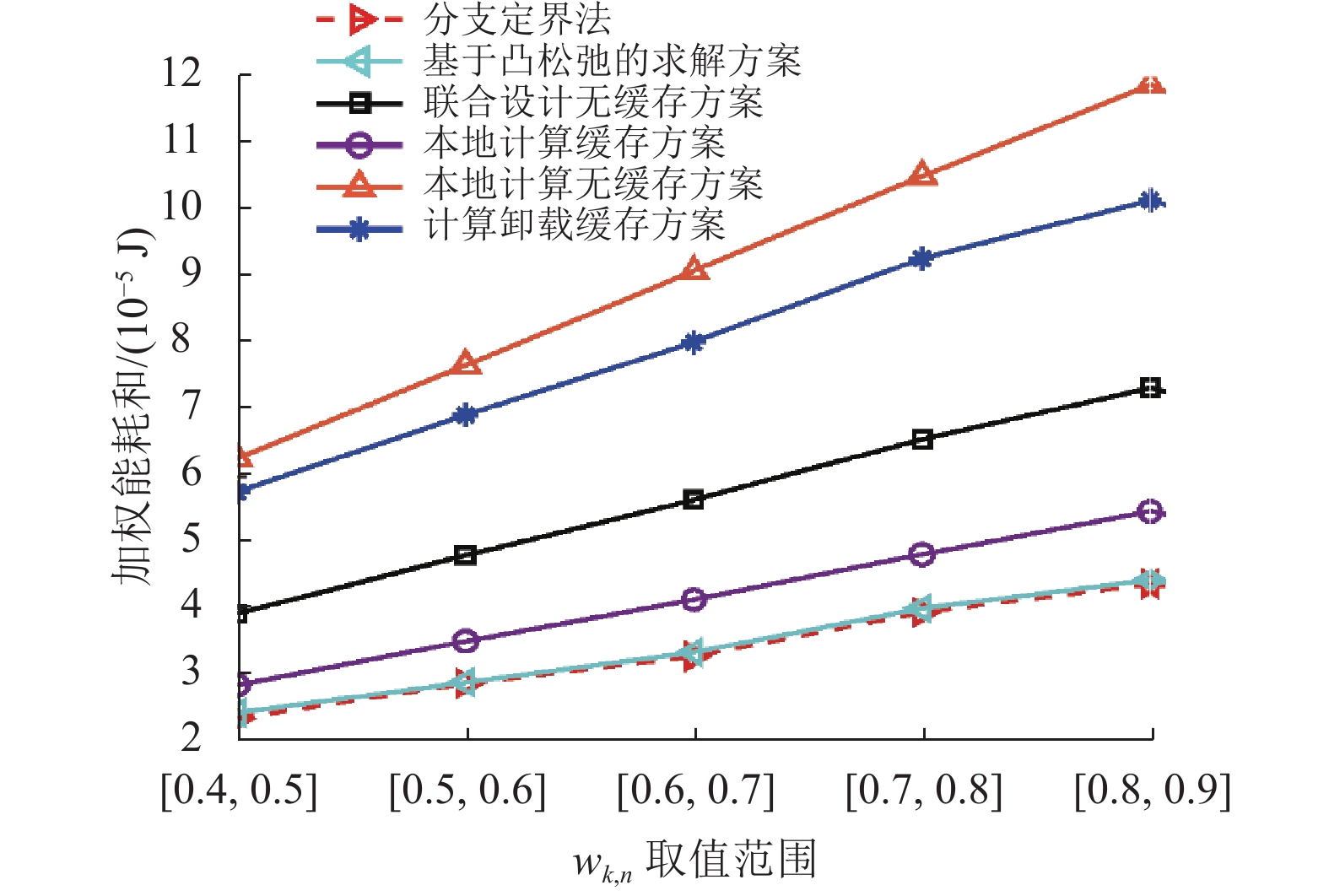
图4展示了无线设备的权值 ${w_{k,n}}$ 和加权能耗和的变化关系。其中N=10，K=10，S₀=60×10³ bits，τ=0.2 s，AP到第k个无线设备的距离服从均匀分布D_k =10 m, 不同设备在不同时隙的权值服从给定取值范围的均匀分布。实验仿真中无线设备的能耗的权值高于边缘服务器的权值，这是因为本文更关注无线设备的能耗，因此给予无线设备更高的能耗权值；其次，单个无线设备的能耗与边缘服务器的能耗相比非常小，需要对两者能耗进行平衡考虑。在不同权值的取值范围下，所提的基于凸松弛的求解方案的性能接近分支定界法给出的最优解，且优于其余4个基准方案。

4 结语

本文研究了多用户多时隙移动边缘计算系统优化设计。通过建立数学模型，该数学模型以最小化MEC系统加权能耗和为目标，建立MEC缓存容量和计算任务因果性约束模型作为约束条件，联合优化MEC服务器的缓存决策和任务计算量，以及无线设备的本地计算量和计算卸载量。为求解提出的优化问题，首先采用分支定界法获得全局最优解用以得到系统的最优性能，然后基于凸松弛提出一种低复杂度的算法方案。数值结果展示了所提设计方案相对于其他基准方案的优越性，而且基于凸松弛的求解方案逼近基于分支定界法的最优性能曲线。