随着物联网、智能电子设备以及定位系统的快速发展，交通探头、交通刷卡机等智能设备更容易生成和收集轨迹数据。这些轨迹由一系列位置组成，代表着用户的日常轨迹活动。虽然轨迹数据具有很大的应用价值，但轨迹数据中包含的敏感信息^[1]，例如家庭住址、工作地点等，一旦泄露，对用户的生命财产安全会构成极大的威胁。然而传统的数据收集方法，例如k-匿名^[2]，攻击者可以通过获取额外的背景知识来分析用户在某段时间内的轨迹数据、行动路线等，导致无法抵御背景知识攻击^[3]。传统的k-匿名方法即使采用了唯一标志符，仍无法阻止用户的行为被追溯。因此，迫切需要实现隐私保护的轨迹数据发布方案。

Dwork^[4]于2006年提出了差分隐私的概念，通过在查询或分析结果添加噪声的方式，防止数据库中的信息被泄露。由于差分隐私严格的数学统计模型与可量化的噪声机制，研究者们开始将其应用在轨迹发布领域，并取得了良好的效果。Chen等^[5]首次提出基于前缀树的数据发布模型，随后扩展了前缀树的工作，提出了基于可长度n-gram的方法^[6]。Zhao等^[7]也提出了一种r树结构，由轨迹序列组成r树，从而保证轨迹的时空完整性。上述工作都需要满足轨迹必须要有相同前缀的假设，这并不符合大多数轨迹的特性。

因此，Hua等^[8]提出了一种基于聚类的轨迹泛化方法，Li等^[9]拓展了该方法，提出了一种具有有界拉普拉斯噪声的轨迹发布方法，但是Kmeans聚类受初始值影响较大，且在有限的迭代次数中无法提供终止聚类算法有效解。并且，已有工作表明，在复杂高维数据面前，拉普拉斯机制并不是最优的噪声添加机制。Quan等^[10]提出一种优化的阶梯机制，与拉普拉斯机制相比，在同等隐私预算下，阶梯机制的噪声添加量会更小。现有的轨迹隐私保护工作，Kmeans方法受初始点和离群点的影响，迭代过程无法保证质心的收敛，从而结果不稳定，对随后的轨迹映射的准确性也会造成影响。同时，在提高发布轨迹的统计，保证发布的轨迹数据的隐私效用时，会在一定程度上忽略掉数据的可用性。

为此，本文提出了一种差分隐私轨迹数据发布方法(Differential Privacy Data Publishing with SKmeans||, SKTDP) ，集成了方向控制机制的SKmeans||聚类轨迹泛化算法和阶梯有界噪声机制的轨迹发布算法。首先，结合SKmeans||聚类和指数机制对轨迹点进行区域划分以及泛化映射。其次，提出了一种方向控制机制来保证聚类的迭代收敛，实验结果表明，本文的方法提高了聚类的质量。

本文的主要工作与贡献如下：

(1) 提出了一种基于SKmeans||聚类的轨迹泛化算法(Trajectory Generalization Based on SKmeans|| Clustering, TGSC)，通过在SKmeans||算法中添加方向控制机制，确保了聚类泛化质量，消除了现有机制对隐式假设的依赖，提高了聚类效果和数据效用。

(2) 设计了基于阶梯有界噪声机制的轨迹发布算法(Differentially Private Publishing with Bounded Staircase Noise, SNDP)，该算法相较于传统的拉普拉斯机制，添加的噪声量更小。阶梯有界噪声机制基于一般的效用最大化或成本最小化框架，在具有阶梯分布的机制中添加查询输出的噪声是最优的，且该分布在原点附近对称，在x $\geqslant $ 0时是单调递减且几何衰减的阶梯形概率密度函数。

(3) 在真实轨迹数据集上验证了该方法的可行性，发布后轨迹数据具有较好的可用性。

1 相关工作与问题描述 1.1 相关工作

差分隐私^[4]的提出是为了解决隐私保护的数据分析问题。采用基于差分隐私的隐私保护模型，不仅可以有效防止背景知识攻击，还在一定程度保证了数据的统计学特性。Chen等^[5]首次提出了基于混合粒度前缀树结构的SeqPT模型，用前缀树表示轨迹序列数据，并利用前缀树的节点来保存轨迹子序列的噪声计数，对轨迹数据有很好的可用性。后来，Chen等^[6]拓展了基于前缀树的工作，提出了一种可变长度n-gram模型来处理序列数据。Li等^[11]提出的前缀树结构，取消了每一层的分类树，并设计了增量隐私预算分配模型和时空维度缩减方法，提高了算法的运行效率和数据效用。Gursoy等^[12]提出了当前较为先进的DP-Star框架，利用特征提取、特征学习、噪声扰动和合成来实现隐私保护。然而，上述工作假设原始轨迹包含相同的前缀或长度为n的公共子序列，这在许多应用中都很难满足。

为了消除文献[5-6]中的轨迹数据必须要有相同前缀的假设，Hua等^[8]提出了基于Kmeans聚类与指数机制结合的位置泛化算法。随后，Li等^[9]拓展了该方法，提出了一种具有有界拉普拉斯噪声的轨迹发布方法。由于Kmeans聚类受初始值影响较大，且在有限的迭代次数中无法提供终止聚类算法的有效解，Ni等^[13]提出了一种新的聚类算法DP-KCCM，通过添加自适应噪声以及合并聚类，显著提高了聚类的效用。而Lu等^[14]提出了一种基于交互式差分隐私的Kmeans聚类方法，该方法在质心迭代中的受控方向上应用ExpDP方法，然后注入有界拉普拉斯噪声，以保护数据隐私免受推理攻击，从而保证了聚类的收敛。与该文献不同的是，本文采用非交互式差分隐私，同时为了适应高维数据的特征，在SKmeans||聚类中设计指数机制来保证收敛。Liu等^[15]在提出了两种基于Kmeans||聚类的轨迹合并方案，使用Kmeans||聚类算法对定位区域进行聚类，聚类中的所有点都被聚类的中心所取代以及利用楼梯机制来扰乱集群中心，以提高隐私保护的水平。Joonas等^[16]提出了两种新的Kmeans||聚类初始化方法，通过采样、子采样和降维来减少数据处理，适用于初始化大规模问题。

此外，随着机器学习的不断发展，越来越多机器学习与差分隐私的融合技术产生。Xu等^[17]提出了一种差异隐私潜在轨迹组发现方案(DP-LTOD) ，将原始轨迹序列模糊为差异隐私保证的轨迹序列，以保持轨迹隐私，并通过对上传的轨迹序列组进行聚类来发现潜在的轨迹。陈思等^[18]通过建立新的基于时间泛化和空间分割的高效采样模型,并利用Kmeans聚类算法进行抽样数据处理,同时借助差分隐私保护机制对轨迹数据进行双重扰动,有效解决了具有强大背景知识的攻击者窃取用户隐私的问题。Zhao等^[19]提出了一种基于聚类的差异隐私轨迹保护方法，首先将拉普拉斯噪声添加到集群中的轨迹位置计数中，然后在聚类中的轨迹位置数据中加入有限半径的拉普拉斯噪声，以避免过度的噪声影响聚类。

1.2 理论基础

差分隐私是建立在数学理论基础上，严格且可证明的数学模型。对于两个相邻数据集，经过差分隐私的处理，可以发布两个不存在明显差异的数据集，即无法识别数据集中的单条轨迹。因此，可以有效防止背景知识攻击，保护用户的隐私。

定义1^[4] 　对相邻数据集 $ {D}_{1},{D}_{2} $ ，一种随机算法A， $ \mathrm{R}\mathrm{a}\mathrm{n}\mathrm{g}\mathrm{e}\left(A\right) $ 表示算法A所有可能的输出集合，有 $ S\in \mathrm{R}\mathrm{a}\mathrm{n}\mathrm{g}\mathrm{e}\left(A\right) $ 。若对于所有的S，算法A输出S的概率为 $ \mathrm{Pr}[A\left({D}_{1}\right) =S] $ ，都有

$ \mathrm{Pr}[A\left({D}_{1}\right) =S] \leqslant {\mathrm{e}}^{\varepsilon }\times \mathrm{Pr}[A\left({D}_{2}\right) =S] $

(1)

则随机算法A满足 $\varepsilon -$ 差分隐私。式中：隐私预算 $\varepsilon$ 越小，噪声添加量越大，隐私级别越高；隐私预算越大则相反；e为自然对数的底。

定义2^[4] 　用敏感度表示查询结果变化的最大值，对函数 $ f:{D}_{1}\to {R}^{m} $ ，输入为数据集 $ {D}_{1} $ ，输出为 $ m $ 维向量。则敏感度 $ \Delta f $ 为

$ \Delta f={\mathrm{m}\mathrm{a}\mathrm{x}}_{{D}_{1},{D}_{2}}\left|\left|f\left({D}_{1}\right) -f\left({D}_{2}\right) \right|\right| $

(2)

式中： $ {D}_{1},{D}_{2} $ 互为相邻数据集，|| ||表示一阶范式。

定理1^[10](阶梯机制)　对一个多维查询函数 $ f:D\to {R}^{d} $ ,staircase-shaped机制会输出

$ A\left(D\right) =f\left(D\right) +{\mathrm{s}\mathrm{t}\mathrm{a}\mathrm{i}\mathrm{r}\mathrm{c}\mathrm{a}\mathrm{s}\mathrm{e}\text{-}\mathrm{s}\mathrm{h}\mathrm{a}\mathrm{p}\mathrm{e}\mathrm{d}\left(\Delta f,\varepsilon ,\gamma \right) }^{d} $

(3)

令 $\mathrm{s}\mathrm{t}\mathrm{a}\mathrm{i}\mathrm{r}\mathrm{c}\mathrm{a}\mathrm{s}\mathrm{e}\text{-}\mathrm{s}\mathrm{h}\mathrm{a}\mathrm{p}\mathrm{e}\mathrm{d}(\Delta f,\varepsilon ,\gamma )$ 表示要添加的噪声，它是具有阶梯概率密度函数的随机变量，阶梯概率密度函数表示为

$ {f}_{\gamma }\left(x\right) = \left\{\begin{array}{l}a\left(\gamma \right) , x\in [0,\gamma \Delta f]\\ {\mathrm{e}}^{-\varepsilon }a\left(\gamma \right) , x\in [\gamma \Delta f,\Delta f]\\ {\mathrm{e}}^{-h\varepsilon }{f}_{\gamma }\left(x-h\Delta f\right) , x\in [h\Delta f,\left(h+1\right) \Delta f]\\ {f}_{\gamma }\left(-x\right) , x < 0\end{array}\right. $

(4)

式中： $ h $ 为比例系数， $ \Delta f $ 为敏感度， $ a\left(\gamma \right) $ 是一个归一化常数， $ \gamma $ 是损失函数的最优值，计算方法为

$ a\left(\gamma \right) \triangleq \frac{1-{\mathrm{e}}^{-\varepsilon }}{2\Delta f\left(\gamma +{\mathrm{e}}^{-\varepsilon }\left(1-\gamma \right) \right) } $

(5)

$ \gamma =-\frac{b}{1-b}+\frac{{(b-2{b}^{2}+2{b}^{4}-{b}^{5}) }^{\frac{1}{3}}}{{2}^{\frac{1}{3}}{\left(1-b\right) }^{2}},b={\mathrm{e}}^{-\varepsilon } $

(6)

定理2(指数机制)　设得分函数 $q \left(D,R\right) $ ，输入数据集D，输出为一实体集 $ R $ ，若对一随机算法A以正比于 ${\mathrm{exp}}({\varepsilon q(D,R) / ({2\Delta q}}))$ 的概率输出结果 $ y\in R $ ，则称随机算法A满足 $ \varepsilon - $ 差分隐私。

1.3 问题描述

本文研究的问题是在给定的轨迹数据集 $ D $ 和隐私预算 $ \varepsilon $ 下,构建差分隐私下基于SKmeans||聚类的轨迹泛化算法，然后构建基于有界阶梯噪声机制的轨迹数据发布算法，使得发布的数据集 $ {D}^{{'}} $ 在满足差分隐私的同时，保证聚类最后的集群质量，同时保证发布轨迹集具有较高的数据可用性。数据效用的衡量主要是以下两个方面，一是衡量原始数据集与重构轨迹数据集之间的相似性，二是范围查询准确度。在本文中，数据集相似性通过豪斯多夫聚类来衡量，而范围查询准确度则通过 $ \mathrm{F}-\mathrm{m}\mathrm{e}\mathrm{a}\mathrm{s}\mathrm{u}\mathrm{r}\mathrm{e} $ 分数来衡量。最后，在这里介绍关于轨迹的定义。

定义3 　轨迹是按时间顺序排列的时间地点戳对，即 $ T=\left({t}_{1},{l}_{1}\right) \to \dots \to \left({t}_{i},{l}_{i}\right) \to \dots \to ({t}_{\left|T\right|},{l}_{\left|T\right|}) $ ，其中 $ {l}_{i}(1\ll i\ll T) $ 是由经度和纬度坐标表示的离散空间点， $ \left|T\right| $ 是轨迹的数量。

2 方法描述及分析

本文提出的满足差分隐私保护的轨迹数据发布方法包括两个算法，基于Skmeans||聚类的轨迹泛化算法(TGSC)和基于阶梯有界噪声机制的轨迹发布算法(SNDP)。

由于传统Kmeans聚类在初始点选择和质心迭代的过程中存在局限性，无法在有限的迭代次数内提供终止聚类的有效解，从而影响泛化的质量。因此，TGSC算法使用SKmeans||算法，先获取一组候选质心集合，然后基于该集合再生成k个质心，形成k个分组，保证了选取的初始点距离较远且都落在密集区域。在聚类迭代过程中加入了方向控制机制，设计了指数机制中的打分函数选择偏移后的质心，确保聚类一定能够收敛，从而提高聚类的质量和泛化的效果。

其次，传统的拉普拉斯机制在轨迹等高维数据中存在噪声添加量过大的问题，SNDP算法结合阶梯有界噪声添加机制，设计了噪声添加阈值，在同等的隐私保护级别下添加的噪声量更小，保护数据隐私的同时提高了数据的可用性。

实验结果表明，该方法发布的重构数据集在满足差分隐私保护的同时，有效降低了轨迹合并的时间成本，具有较高的数据可用性。

2.1 基于SKmeans||聚类的轨迹泛化算法(TGSC)

TGSC算法使用SKmeans||算法对每个时间戳下的轨迹点进行聚类划分。为提高聚类的效果，在迭代质心更新的过程中，加入了方向控制机制，使用指数机制对质心进行距离和方向偏移，期间设计了指数机制的打分函数，更契合高维轨迹数据。

算法1：TGSC算法流程

输入：原始数据集 $ { D }$ ，时间域 $ { {D}_{t} }$ ,候选划分数量 $ { \varphi}$ ，隐私预算 $ {{\varepsilon }_{1}}$

输出：泛化后的轨迹集 $ { {D}_{1} }$

01. $ { {D}_{1}=\left[ \right]}$

02. For i = 1:len( $ {{\boldsymbol{}} {D}_{t} }$ ) do

03. 　 $ { {D}_{i} }$ = [ $ {{T}_{i} }$ for T in D]

04. init_k = SKmeans||( $ {{D}_{i} }$ , k)

05. 　For t = 1:max_iter do

06. 　　For cluster i in t do

07. 　　　 c[i] = each $ {{D}_{i}} $ closest with cent[t-1]

08. 　　　cent_k[t] = means of c[i]

09. 　　　Szone = TSZG(cent_k[t],cent_k[t-1])

10. 　　　New_k = ExpDP(Szone, $ {{\epsilon }_{1}} $ )

11. 　　End for

12. 　End for

13. End for

14. Temp = map(D,New_k)

15. For $ { {T}_{i}} $ in temp

16. 　while Haud( $ {{T}_{i}\left[i\right] }$ , $ { {T}_{i}[j]}$ ) ≤threshold

17. $ { {D}_{1}} $ .add( $ { {T}_{i} }$ )

18. 　End while

19. End for

20. return $ {{D}_{1}}$

算法1首先对每一个时间戳下的轨迹点聚类(02~13行) ，先通过SKmeans||生成初始点(04行) ，其次在聚类的每轮迭代中(05~12行) ，采用文献[14]中的 $ \mathrm{T}\mathrm{S}\mathrm{Z}\mathrm{G} $ 算法，设计概率函数得到采样区的中心点以及半径，建立收敛区和采样区(09行) 。设本轮迭代得到的簇质心为 $ {c}_{t} $ ,上一轮迭代得到的簇质心为 $ {c}_{t-1} $ ,通过指数机制偏移得到的质心为 $ {c}_{t}^\prime $ ,可以重新设计得到距离偏移函数和角度偏移函数为

$ {d}_{t}=\frac{||{c}_{t}-{c}_{t}^\prime||}{\left|\left|{c}_{t}-{c}_{t-1}\right|\right|} $

(7)

$ {\theta }_{t}=\angle {c}_{t}^\prime{c}_{t}{c}_{t-1} $

(8)

式中： $ {d}_{t}\in \left(\mathrm{0,1}\right) $ , ${\theta }_{t}\in (-{\text{π} }/2,{\text{π} }/2)$ 。对聚类当前迭代的任意一个簇t，可以得到打分函数为

$ \mathrm{s}\mathrm{c}\mathrm{o}\mathrm{r}\mathrm{e}\left({d}_{t},{\theta }_{t}\right) =\left(1-{d}_{t}\right) +\left(1-\frac{2{\theta }_{t}}{{\text{π} }}\right) $

(9)

通过打分函数得到簇中的偏移质心(10行) ，与文献^[14]不同的是没有在当前迭代过程中再利用聚类重新迭代，去除了冗余的操作，缩短了迭代时间，从而有效提高了聚类的效率，具有更好的聚类质量。然后将簇中的其他轨迹点映射为质心，再将不同时间戳下的轨迹连接起来(14行) ，得到重构的泛化轨迹。为了保持轨迹集的种类一致，以及连续两个位置之间的距离受到速度的限制，将不满足速度限制的n条轨迹筛选掉(15~19行) 。

2.2 基于阶梯有界噪声机制的轨迹发布算法(SNDP)

SNDP算法包括有界阶梯噪声添加模块和一致性约束模块。首先，有界阶梯噪声添加模块假设有n个包含原始轨迹的泛化轨迹，通过在真实计数上添加有界阶梯分布的噪声，得到相应的噪声计数。然后，通过一致性约束模块，对轨迹进行后处理并发布，使轨迹更符合真实情况。

算法2：SNDP算法流程

输入：泛化轨迹 $ { {D}_{1} }$ ，隐私预算 $ {{\varepsilon }_{2}}$ ，敏感度 $ { \Delta f }$ ，每条轨迹的真实计数{ $ { {t}_{1},{t}_{2},\cdots ,{t}_{n} }$ }, $ { \alpha }$ , $ { \beta }$

输出：重构发布的轨迹数据集 $ { {D}^\prime }$

01. $ { \Delta f={\mathrm{m}\mathrm{a}\mathrm{x}}_{p,q}\left\{\right|{t}_{p}-{t}_{q}\left|\right\} }$

02. For p, q from 1 to n do

03. 　 $ { \mu =\mathrm{a}\mathrm{v}\mathrm{g}({t}_{p}) ,\eta =\mathrm{min}\{{t}_{p}\} }$

04. End for

05. $ { \alpha =\eta /2，\beta =2\mu }$

06. For i in N do

07.　 if i<n:

08.　 　 $ {{s}_{i}={t}_{i}+\mathrm{s}\mathrm{t}\mathrm{a}\mathrm{i}\mathrm{r}\mathrm{c}\mathrm{a}\mathrm{s}\mathrm{e}\_\mathrm{s}\mathrm{h}\mathrm{a}\mathrm{p}\mathrm{e}\mathrm{d}(\Delta f,{\varepsilon }_{2},\gamma )}$

09. else if

10. 　　 $ {{s}_{i}=\mathrm{s}\mathrm{t}\mathrm{a}\mathrm{i}\mathrm{r}\mathrm{c}\mathrm{a}\mathrm{s}\mathrm{e}\_\mathrm{s}\mathrm{h}\mathrm{a}\mathrm{p}\mathrm{e}\mathrm{d}(\Delta f,{\varepsilon }_{2},\gamma ) }$

11. 　End if

12. 　　if $ {{s}_{i} \geqslant}$ $ {\beta}$ then $ { {s}_{i}=\beta }$

13. 　　if $ {{s}_{i} \leqslant}$ $ {\alpha}$ then $ { {s}_{i}=\alpha }$

14. End for

15. $ {\mathrm{N}\mathrm{C}= < {s}_{1},{s}_{2},\cdots ,{s}_{N} > }$

16. Sorted NC and $ {S= < S_1^\prime ,S_2^\prime ,\cdots ,{s}_{N}^\prime >}$

17. $ {{Q}_{m}={\mathrm{m}\mathrm{a}\mathrm{x}}_{i\in [1,m]}{\mathrm{m}\mathrm{i}\mathrm{n}}_{j\in [i,n]}\dfrac{{\sum }_{m=1}^{j}tc\left({v}_{m}\right) }{j-i+1}}$

18. $ { {S}^\prime= < {Q}_{1},{Q}_{2},\cdots ,{Q}_{N} > }$

19. For i in N do

20. 　　 $ {{s}_{i}^\prime={Q}_{i}}$

21. End for

22. for i=1:N do

23. 　　 $ { {D}^\prime.\mathrm{a}\mathrm{d}\mathrm{d}\left(T\right) }$ based on $ {P\left({s}_{i}^\prime/\mathrm{s}\mathrm{u}\mathrm{m}\left({S}^\prime\right) \right)}$

24. End for

25. Return $ {{D}^\prime }$

算法2包括有界阶梯噪声添加和一致性约束两个模块。前半部分(01~11行) 为噪声添加模块，先计算出敏感度(01行) ，由敏感度定义可知这里敏感度为1。假设轨迹范围属于 $ [\alpha ,\beta ] $ ，而阶梯机制噪声属于 $ [\gamma ,\eta ] $ ，噪声计数等于t加阶梯噪声sn，如果 $ t+\mathrm{s}\mathrm{n} < 0 $ ，则噪声计数为负，这会是一个毫无意义的轨迹发布。虽然噪声计数可以超过轨迹上限 $ \beta $ ，但如果 $ t+\mathrm{s}\mathrm{n} > \beta $ ，则这种泛化轨迹已经很拥挤了。因此，噪声阈值设置模块(02~04行) 先计算轨迹真实计数的平均值和最小值(03行) ，并将噪声上界设为平均值的2倍，噪声下界设为最小值的1/2(05行) 。有界阶梯噪声添加模块(06-14行) 通过定理1给出的staircase-shaped机制对轨迹的真实计数进行加噪，若噪声计数超过阈值，则用阈值替换噪声计数。

假设一对邻近轨迹数据集 $ D\mathrm{和}D^\prime $ 不同的那条轨迹为 $ {T}_{0} $ , ${T}_{0}^\prime$ 为 $ {T}_{0} $ 对应的泛化轨迹，则从序列 $ {s}_{i}\left(D\right) $ 中输出候选项 $o=\{{o}_{1},{o}_{2},\cdots ,{o}_{\left|\varOmega \right|}\}$ 的概率为 $ \mathrm{P}\mathrm{r}[s\left(D\right) =o]= \prod _{i}\mathrm{P}\mathrm{r}[{s}_{i}\left(D\right) ={o}_{i}] $ ；对于任何泛化轨迹 $ {T}_{i}^\prime \ne {T}_{0}^\prime $ ，有 $\mathrm{Pr}\left[{s}_{i}\left(D\right) ={o}_{i}\right]=\mathrm{P}\mathrm{r}[{s}_{i}\left(D^\prime \right) ={o}_{i}]$ ；对于任何 ${T}_{i}^\prime \ne {T}_{0}^\prime \wedge {T}_{0}^\prime \in D^\prime$ ， $ {T}_{0}^\prime $ 的噪声计数等于真实计数加staircase-shaped噪音,有 $\mathrm{Pr}\left[s\left(D\right) =o\right] < {\mathrm{e}}^{{\varepsilon }_{2}}\cdot \mathrm{P}\mathrm{r}[s\left(D^\prime \right) =o]$ ；对任意 ${T}_{i}^\prime \ne {T}_{0}^\prime \wedge {T}_{0}^\prime \notin D^\prime \wedge o\ne \varnothing$ ，有 $\mathrm{Pr}\left[s\left(D\right) =o\right]=\mathrm{P}\mathrm{r}[s\left(D^\prime \right) =o]$ ，因此有界的staircase-shaped噪声是符合差分隐私定义的。

后半部分(15~21行) 为一致性约束模块，在无噪声图中，对于任意的两条边 $ v,u $ ，如果边 $ v $ 的轨迹多于边 $ u $ ，则有 $ t\left(v\right) > t\left(u\right) $ 。因此，对于有噪声的轨迹，也通过图来映射轨迹集，基于文献[9]的方法，先生成图G中每条边的噪声计数，并组成序列S，令 $ \mathrm{m}\mathrm{e}\mathrm{a}\mathrm{n}[i,j] $ 表示其中一条子序列的平均数

$ \mathrm{m}\mathrm{e}\mathrm{a}\mathrm{n}[i,j]=\frac{{\Sigma }_{m=1}^{j}t\left({v}_{m}\right) }{j-i+1} $

(10)

$ {Q}_{m}={\mathrm{m}\mathrm{a}\mathrm{x}}_{i\in \left[1,m\right]}{\mathrm{m}\mathrm{i}\mathrm{n}}_{j\in \left[i,\left|E\left(G\right) \right|\right]}\mathrm{m}\mathrm{e}\mathrm{a}\mathrm{n}[i,j] $

(11)

然后可以得到预期序列 $ {S}^\prime $

$ {S}^\prime = < {Q}_{1},{Q}_{2},\cdots ,{Q}_{\left|E\left(G\right) \right|} > $

(12)

最后，按照噪声计数与序列和的比值输出与原轨迹同样数量的重构轨迹并发布。

2.3 隐私分析

在本文提出的方法中，主要包括两个算法。TGSC算法对每个时间戳下的地点域进行聚类，运用指数机制获取更符合实际情况的聚类质心，然后映射得到泛化轨迹。SNDP算法采用有界的staircase-shaped机制进行加噪，设计噪声阈值，防止添加噪声过大或者过小。可以得到以下定理。

定理3 　TGSC算法满足 $ {\varepsilon }_{1}-\mathrm{差}\mathrm{分}\mathrm{隐}\mathrm{私} $ 。

证明 　对于得到聚类中心的指数机制，有

$ \begin{gathered} \frac{\mathrm{Pr}\left[{{c}^\prime }_{i}^{t}=c\right]}{\mathrm{Pr}\left[{{c}^{\prime\prime}}_{i}^{t}=c\right]}=\frac{\mathrm{Pr}\left[c,{c}_{i}^{t},{{c}^\prime}_{i}^{t}\right]\times \mathrm{exp}\left(\dfrac{{\varepsilon }_{i}^{t}q({d}_{i}^{t},{\theta }_{i}^{t}) }{2\Delta q}\right) }{\mathrm{Pr}\left[c,{c}_{i}^{t},{{c}^{{\prime }}}_{i}^{t}\right]\times \mathrm{exp}\left(\dfrac{{\varepsilon }_{i}^{t}q({{d}^{{\prime }}}_{i}^{t},{{\theta }^{{\prime }}}_{i}^{t}) }{2\Delta q}\right) } =\\\qquad\qquad\qquad \mathrm{exp}\left({\varepsilon }_{i}^{t}\cdot \frac{q({d}_{i}^{t},{\theta }_{i}^{t}) -q({{d}^{{\prime }}}_{i}^{t},{{\theta }^{{\prime }}}_{i}^{t}) }{2\Delta q} \right)\leqslant\\ {\rm{exp}}({\varepsilon }_{i}^{t})\end{gathered} $

(13)

式中： ${c}_{i}^{t}$ 为第i次迭代t簇的质心， ${{c}^\prime }_{i}^{t}$ 为第i次迭代t簇的加噪质心。在一轮迭代中，均满足 ${\varepsilon }_{i}^{t}-$ 差分隐私。因为在每次迭代中，所有地点域都被分成 $ k $ 个簇,基于顺序组合特性，泛化方法满足 ${\varepsilon }_{1}-\mathrm{差}\mathrm{分}\mathrm{隐}\mathrm{私}$ ，其中 ${\varepsilon }_{1}= { \sum }_{t=1}^{T}{\mathrm{m}\mathrm{a}\mathrm{x}}_{i=1}^{k}\left\{{\varepsilon }_{i}^{t}\right\}$ 。

定理4 　SNDP算法满足 ${\varepsilon }_{2}-\mathrm{差}\mathrm{分}\mathrm{隐}\mathrm{私}$ 。

证明 　在轨迹发布过程，隐私分析集中在加噪声的发布。根据并行组合特性，消耗总预算为 ${\varepsilon }_{2}$ ，有

$ \frac{\mathrm{Pr}\left[s\left(D\right) =s\right]}{\mathrm{Pr}\left[s\left({D}^{{\prime }}\right) =s\right]}=\frac{\frac{1}{\beta -\alpha }{\int }_{\alpha }^{\beta }\mathrm{p}\mathrm{d}\mathrm{f}\left(x\right) {\rm{d}}x}{\frac{1}{\beta -\alpha }{\int }_{\alpha }^{\beta }\mathrm{p}\mathrm{d}\mathrm{f}\left(x\right) {\rm{d}}x} =1\leqslant {\mathrm{e}}^{{\varepsilon }_{2}}\cdot\mathrm{Pr}\left[s\left({D}^{{\prime }}\right) =s\right] $

(14)

式中：pdf(x) 为有界噪声函数， $ \alpha 、\beta $ 为噪声的上下界。因此，SKTDP方法总体满足 ${\varepsilon }_{1}+{\varepsilon }_{2}-$ 差分隐私。

3 实验分析

本文提出的方法基于Python实现。实验的硬件环境为双核Intel Core i5 1.60 GHz，内存为16 GB。本文使用的数据集为微软提供的公开数据集T-Drive^[20]，包含了北京地区10 357辆出租车一周的出行轨迹数据，由出租车ID、时间、经纬度位置组成，从中选取850条轨迹，并进行预处理。选取每天上午8:30到下午14:30的时间段，并离散为32个时间点，其中任意相邻的两个时间点相差大概10 min。在接下来的实验中，用SKTDP表示本文提出的方法，通过文献[9]和文献[15]的IS17方法和DP21方法，对比验证本文提出方法的有效性。

3.1 评估指标 3.1.1 轨迹相似度

豪斯多夫距离是度量空间中任意两个集合之间定义的一种距离，本文使用豪斯多夫距离来衡量原始轨迹集与重构轨迹集之间的轨迹相似度。

$ H\left(D\right) =\mathrm{max}\left\{h\left(D,{D}^{{\prime }}\right) ,h\left({D}^{{\prime }},D\right) \right\} $

(15)

式中：

$ h\left(D,{D}^{{\prime }}\right) ={\mathrm{m}\mathrm{a}\mathrm{x}}_{T\in D}\left\{{\mathrm{m}\mathrm{i}\mathrm{n}}_{{T}^{{\prime }}\in {D}^{{\prime }}}\left\{\mathrm{D}\mathrm{i}\mathrm{s}\mathrm{t}\mathrm{a}\mathrm{n}\mathrm{c}\mathrm{e}\left(T,{T}^{{\prime }}\right) \right\}\right\} $

(16)

式中： $\mathrm{D}\mathrm{i}\mathrm{s}\mathrm{t}\mathrm{a}\mathrm{n}\mathrm{c}\mathrm{e}\left(T,{T}^{{\prime }}\right)$ 为距离函数。如果豪斯多夫距离越小，则说明两个数据集的相似度越高，对应数据可用性也越高。

3.1.2 计数查询误差

为了评价重构数据集的可用性，可以通过计数查询来定义相对误差，计数查询的结果是轨迹集中拥有相同前缀的子轨迹的数量。因此，本文规定，计数查询 $ q\left(D\right) $ ，在地图上任取一点为圆心作圆，计算轨迹集 $ D $ 中经过该圆的轨迹数。则相对误差定义为

$ e=\frac{\left|q\left({D}^{{\prime }}\right) -q\left(D\right) \right|}{\mathrm{max}\left\{q\left(D\right) ,\eta \right\}} $

(17)

式中： $ \eta $ 为阈值，为原轨迹数据集数量的 $ 0.1\% $ 。实验运行100次，并取平均值为最终结果。

3.1.3 范围查询精度

因为发布重构轨迹集的目的是为了对其进行查询，采用窗口范围查询对轨迹数据集 $ D $ 和 ${D}^{{\prime }}$ 的查询结果进行比较。给定一个范围查询 $ \mathrm{R}\mathrm{Q} $ ， $ {R}_{d} $ 为原始轨迹集的查询结果， ${R}_{{d}^{\prime }}$ 为重构轨迹集的查询结果，则范围查询的查询精度和召回率定义为

$ \mathrm{p}\mathrm{r}\mathrm{e}\mathrm{c}=\frac{\left|{R}_{d}\cap {R}_{{d}^{{\prime }}}\right|}{{R}_{d}} $

(18)

$ \mathrm{r}\mathrm{e}\mathrm{c}\mathrm{a}\mathrm{l}\mathrm{l}=\frac{\left|{R}_{d}\cap {R}_{{d}^{{\prime }}}\right|}{{R}_{{d}^{{\prime }}}} $

(19)

将二者进行加权，可以得到

$ \mathrm{F}\text{-}\mathrm{m}\mathrm{e}\mathrm{a}\mathrm{s}\mathrm{u}\mathrm{r}\mathrm{e}=\frac{2\times \mathrm{p}\mathrm{r}\mathrm{e}\mathrm{c}\times \mathrm{r}\mathrm{e}\mathrm{c}\mathrm{a}\mathrm{l}\mathrm{l}}{\mathrm{p}\mathrm{r}\mathrm{e}\mathrm{c}+\mathrm{r}\mathrm{e}\mathrm{c}\mathrm{a}\mathrm{l}\mathrm{l}} $

(20)

使用F-measure作为指标，随机运行100次，取平均值为最终结果。

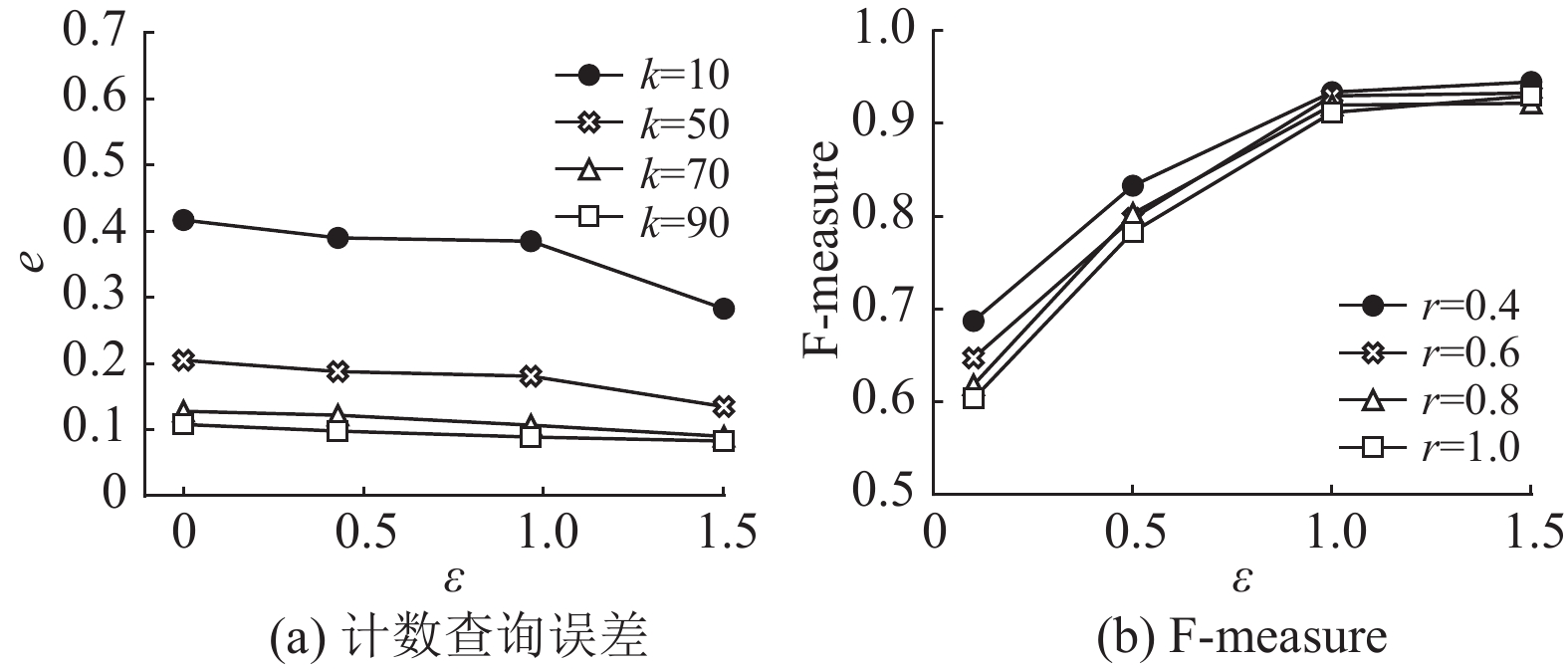
3.2 结果分析 3.2.1 方法评估

图1为本文提出的方法在不同隐私预算下的计数查询误差和F-measure度量。从图1(a) 可以看出，随着分组数k和隐私预算的增加，计数查询误差是逐渐降低的。从图1(b) 可以看出，随着隐私预算的增加，对于不同的查询半径r，F-measure度量也随之增加，但随着查询窗口的增加而减小。从两个图中可以看出，随着隐私预算的增加，计数查询误差呈减小的趋势，F-measure度量呈增加的趋势，都满足差分隐私的定义。

3.2.2 对比分析

本文在不同隐私预算和不同聚类分组数下，对比方法IS17和DP21进行实验，并分析评价指标的差异。

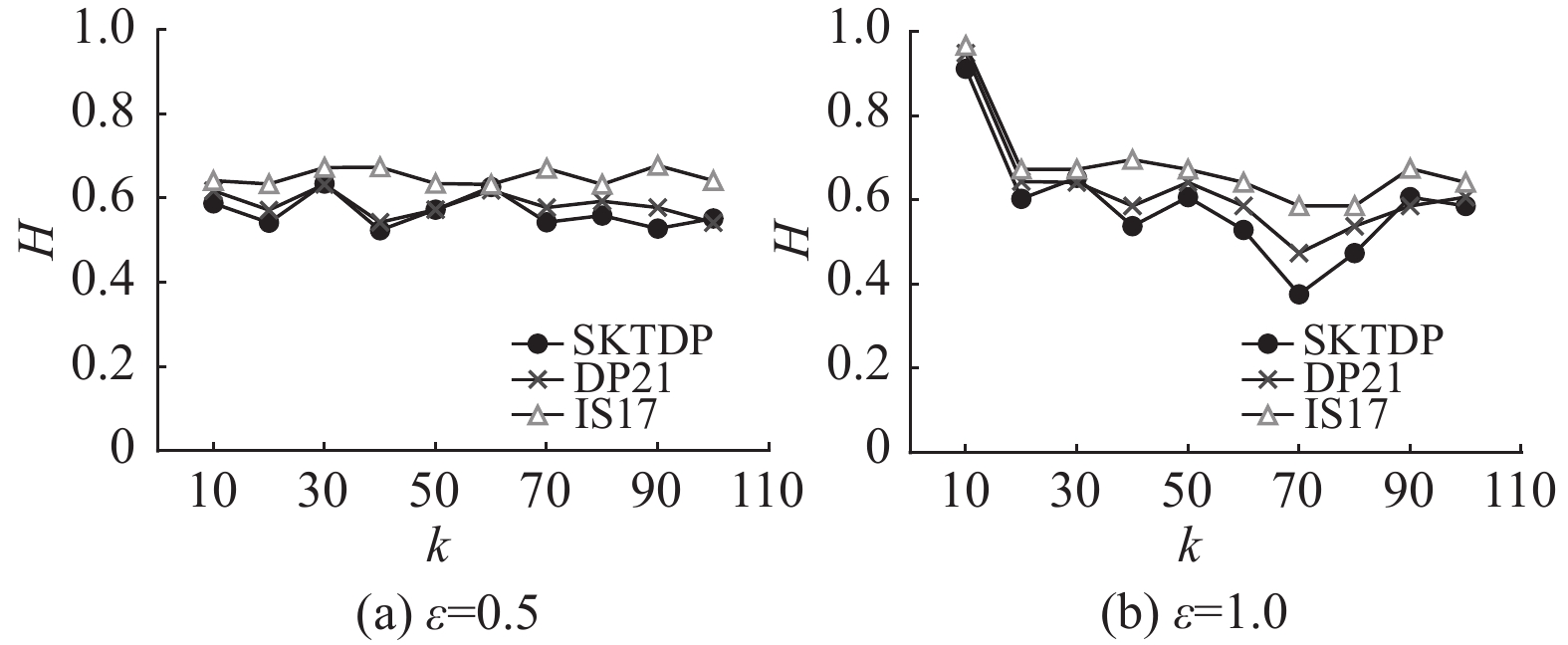
图2为隐私预算为0.5和1，组数为10、20、30、40、50、60、70、80、90、100的情况下，本方法与方法IS17和DP21的豪斯多夫距离对比图。可以看出，在大多数的隐私预算和分组数下，本方法得到的豪斯多夫距离小于方法IS17和DP21，且随着差分隐私预算的增加，豪斯多夫距离越来越低，符合差分隐私的定义，所以本方法得到的数据可用性较高。

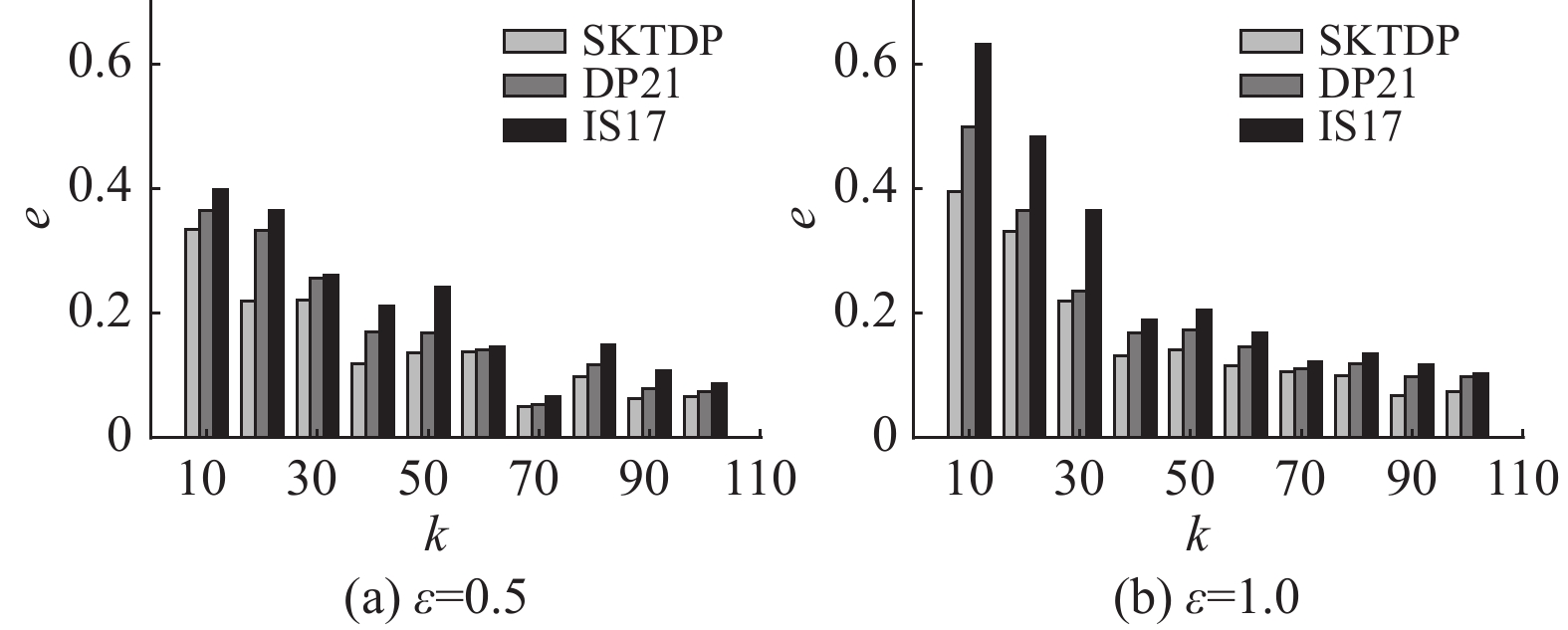
图3分别为隐私预算0.5和1.0，组数为10、20、30、40、50、60、70、80、90、100的情况下，本方法与方法IS17和DP21的计数查询误差对比图。在隐私预算为0.5时，分组数为70时计数查询误差最小，在隐私预算为1.0，分组数为100时计数查询误差最小，且均小于方法IS17和DP21。可以看出，在不同的隐私预算下，本方法都具有更低的计数查询误差，这说明本方法可以更好地拟合原始轨迹数据的稀疏性，更大程度上保存了轨迹数据信息。

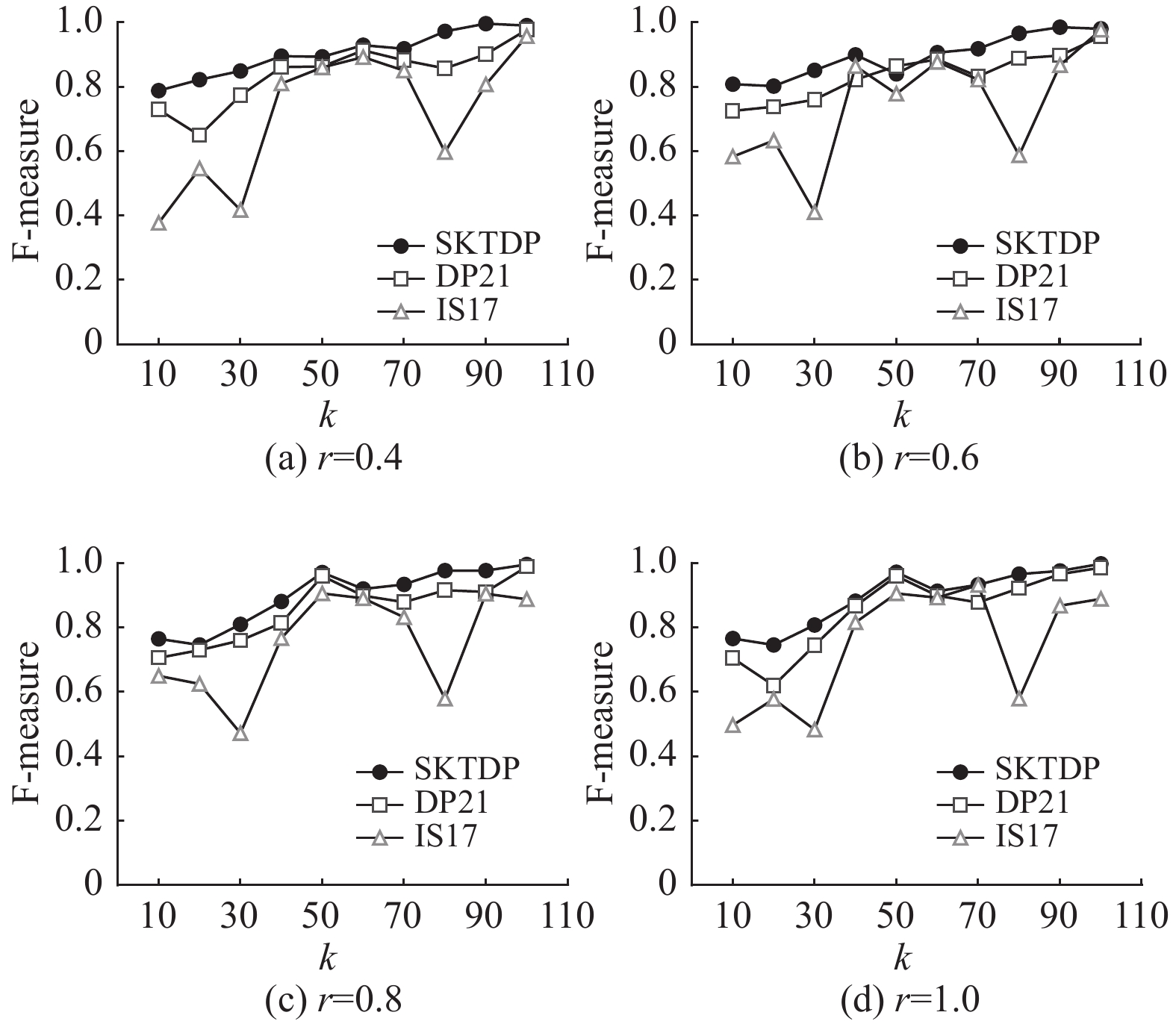
图4分别为在同一隐私预算( $ \varepsilon $ =1.0)下，查询半径分别为0.4、0.6、0.8、1.0 km的F-measure得分。可以看出，在不同的分组数和查询半径下，本方法比方法IS17和DP21具有更高的数据效用。此外，从图中可以发现，随着分组数的增加，数据效用也呈现一个增加的趋势,这是因为分组数的增加会导致合并在集群中的轨迹数量减少，从而提高数据效用。

4 结论

本文针对时间序列轨迹数据发布存在的数据可用性低和聚类效果质量差的问题，提出一种基于SKmeans||聚类和最优噪声机制的轨迹重构方法，在提高数据可用性的同时保证差分隐私。本文的方法包括基于Skmeans||聚类的轨迹泛化算法(TGSC)和基于有界噪声机制的轨迹发布算法(SNDP)。在TGSC算法中，在聚类中加入方向控制机制来控制聚类的收敛，保证聚类的质量，并针对质心的更新设计了新的指数机制的打分函数，然后将聚类得到的簇心映射到该簇内所有的点。对比常用的Kmeans聚类，本文提出的方法具有更好的聚类效果，也更适用于高维稀疏的轨迹集。实验表明，本文提出的方法在保证差分隐私的同时，具有更好的数据可用性。下一步将拓展差分隐私在其他新兴领域的应用，并尝试与机器学习和深度学习方法相结合，来提高数据可用性。