2. 深圳市启灵图像科技有限公司,广东 深圳 518114
2. Shenzhen QiLing Image Technology Co., Ltd., Shenzhen 518114, China
智能制造在全球范围内快速发展,已成为制造业重要发展趋势[1]。机器视觉技术因其作为实现智能制造的重要技术[2],成为了工业自动化领域的关注重点。在机器视觉技术中,图像分割是关键的预处理操作,被广泛应用于工业自动化、在线产品检测、文档图像处理等方面。图像分割的作用是提取出具有独特性质的区域,供后续图像分析、特征提取与模式识别所用。图像阈值化分割是一种传统的最常用的图像分割方法,因其实现简单、性能较稳定而成为图像分割中最基本和应用最广泛的分割方法[3-4],主要包括大津法、最小误差法以及最大Kapur熵法等分割方法[5]。但是当图像中存在多个目标或多个灰度不同的区域时,使用传统的单阈值分割方法并不能把图像中的目标有效地分割出来,而常见的多阈值分割方法是通过穷举所有阈值来获得图像分割的最佳阈值,随着阈值数的增多,分割算法的计算时间大大增加,不能满足工业使用当中的实时性要求[6]。因此,如何快速且准确地获得最佳阈值成为图像多阈值分割问题的研究重点。
近年来,众多学者把图像多阈值分割问题作为参数最优化问题,将群体智能优化算法或群体智能优化算法的改进算法应用于图像多阈值分割问题的最佳阈值搜索上,降低了最佳阈值的搜索时间。吴亮等[7]使用改进蝴蝶优化算法对Otsu多阈值分割方法进行快速寻优;于洋等[8]提出了一种自适应粒子群优化二维Otsu的阈值分割算法,利用图像的灰度级和邻域灰度级构成二元组,建立二维最大类间方差模型,结合自适应粒子群算法估计出图像最佳阈值;陈恺等[9]分析了二维熵分割原理,将二维熵扩展至多阈值形式,并引入萤火虫算法,提高了最佳阈值的搜索速度。但以上方法对多阈值图像的分割处理时间仍需数秒。
为进一步提升图像二维熵多阈值分割的分割效率,本文尝试引入麻雀搜索算法(Sparrow Search Algorithm, SSA)[10]并对标准麻雀搜索算法进行分析研究,针对其存在的缺陷提出了一种改进麻雀搜索算法(Improved Sparrow Search Algorithm, ISSA)。接着,通过引入积分图方法,降低二维熵多阈值图像分割中总信息熵的运算量,并将总信息熵作为ISSA的适应度函数进行最佳阈值寻优,提出了基于ISSA并结合积分图的二维熵图像多阈值分割快速算法,最后将该算法与穷举法以及基于粒子群优化算法(Particle Swarm Optimization, PSO) 的二维熵方法进行图像分割对比实验。实验结果表明相较于穷举法,本文方法在图像双阈值分割和三阈值分割的速度上分别提升了1077.76倍和1317635.53倍;相较于基于PSO的二维熵方法,本文方法仍取得了6.47倍和4.48倍的速度优势,极大地提升了图像二维熵多阈值分割的分割效率,同时在工业应用场景仍能够获得相同的效果。
1 麻雀搜索算法麻雀搜索算法是根据麻雀觅食并逃避捕食者的行为而提出的群体智能优化算法[10]。麻雀搜索算法主要模拟了麻雀群觅食的过程。麻雀群觅食过程也是发现者−跟随者模型的一种,同时还叠加了侦查预警机制。在麻雀搜索算法中,每只麻雀的位置代表一个可行解。麻雀种群中的个体被划分为3类,分别肩负不同的觅食职责,其中包括:(1) 发现较好食物的个体作为发现者;(2) 跟随发现者进行觅食活动的跟随者;(3) 在觅食过程中遇到危险进行反捕食行为的侦查者。麻雀种群中的发现者、跟随者以及侦查者的个体数量保持恒定的比例。麻雀种群中的发现者是种群中适应度较高的个体,拥有更广的搜索范围,为跟随者提供觅食方向。跟随者能够发现适应度最高的发现者,跟随发现者的引导,不断更新自身位置以获得更高的适应度。而发现者与跟随者之间的身份是动态变化的,只要跟随者获得更高的适应度,就有机会成为发现者。在觅食过程中,麻雀种群中一定比例的个体作为侦查者,在意识到危险时,会移向安全区作出反捕食行为,以获得更高的适应度。
发现者的位置更新公式为
| $ {x}_{ij}^{t+1}=\left\{ \begin{array}{l} {x}_{ij}^{t}\cdot \mathrm{exp}\left(\dfrac{-i}{\alpha \cdot {\text{iter}}_{\mathrm{max}}}\right) ,\;{R}_{2} < T\\ {x}_{ij}^{t}+Q,\;{R}_{2}\ge T \end{array} \right.$ | (1) |
式中:
跟随者位置更新公式为
| $ {x}_{ij}^{t+1}=\left\{ \begin{array}{l} Q\cdot \mathrm{exp}\left(\dfrac{{x}_{{\rm{w}}j}^{t}-{x}_{ij}^{t}}{{i}^{2}}\right) ,\;i > \dfrac{n}{2}\\ {x}_{{\rm{p}}j}^{t}+\left|{x}_{ij}^{t}-{x}_{{\rm{p}}j}^{t}\right|\cdot {{\boldsymbol{A}}}^+{\boldsymbol{L}},\;其他 \end{array} \right.$ | (2) |
式中:
侦查者的位置更新公式为
| $ x_{ij}^{t + 1} = \left\{ \begin{gathered} x_{{\rm{b}}j}^t + \beta \cdot \left| {x_{ij}^t - x_{{\rm{b}}j}^t} \right|{\text{ , }}{f_i} \ne {f_{\rm{g}}} \\ x_{ij}^t + k \cdot \frac{{\left| {x_{ij}^t - x_{{\rm{w}}j}^t} \right|}}{{\left( {{f_i} - {f_{\rm{w}}}} \right) + \varepsilon }}{\text{ , }}{f_i} = {f_{\rm{g}}} \\ \end{gathered} \right. $ | (3) |
式中:
由式(1)可知在SSA中,当
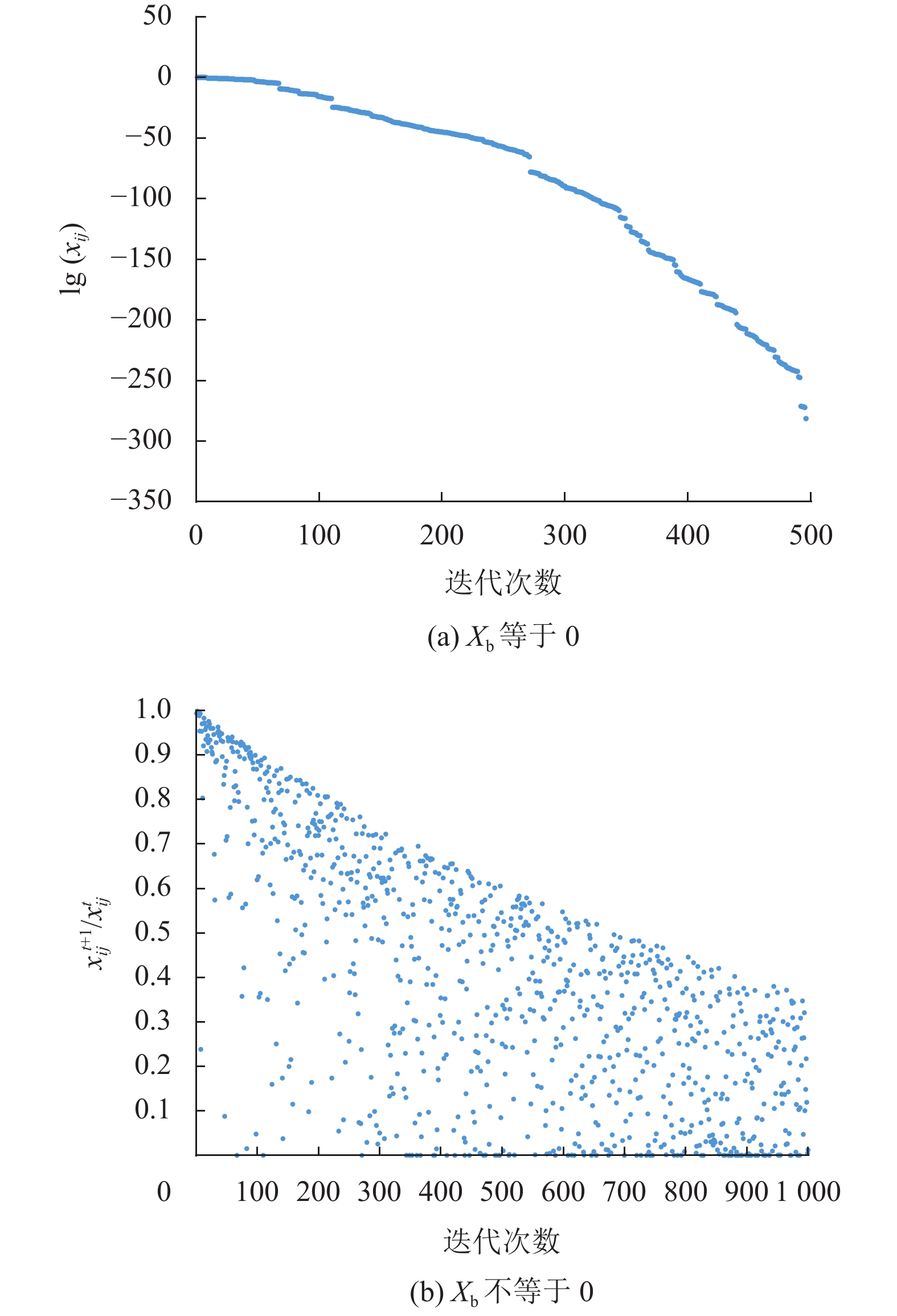
|
图 1 发现者位置变化趋势 Figure 1 Change trend of discoverer's position |
为解决麻雀搜索算法在迭代过程之中,因发现者所有维度有向原点靠拢或跳跃的趋势所造成的全局搜索能力不高的问题,本文采用方差线性递减的高斯扰动策略,即去除式(1)中
| $ x_{ij}^{t + 1} = x_{ij}^t + {\text{normrnd}}\left( {0,{\text{sigma}}} \right) $ | (4) |
式中:
| $ {\text{sigma}} = \left( {{s_{{\text{start}}}} - {s_{{\text{end}}}}} \right) \frac{{{t_{\max }} - t}}{{{t_{\max }}}} + {s_{{\text{end}}}} $ | (5) |
式中:
| $ 3{s_{{\text{start}}}} = \frac{{b - a}}{2} $ | (6) |
从式(2)中可以看出,在迭代过程中,当
| $ x_{ij}^{t + 1} = x_{{\rm{p}}j}^t + \frac{1}{D}\sum\limits_{d = 1}^D {\left( {2 \cdot {\text{randi}}\left( {\left[ {0,1} \right]} \right) - 1} \right) \cdot \left| {x_{ij}^t - x_{{\rm{p}}j}^t} \right|} $ | (7) |
式中:
为解决以上问题,本文提出随机步长移动策略,将算法中发现者的位置更新公式改进为
| $ x_{ij}^{t + 1} = x_{ij}^t + \left( {{\text{rand}} \cdot \left( {u - l} \right) + l} \right) \cdot \left( {x_{{\rm{p}}j}^t - x_{ij}^t} \right) $ | (8) |
式中:
改进的麻雀搜索算法流程为:
步骤1:初始化,包括初始化种群的规模
步骤2:计算每只麻雀的适应度
步骤3:选取适应度最优的前
步骤4:根据各麻雀个体所处的位置重新计算适应度值
步骤5:若算法的迭代次数达到最大迭代次数,则算法结束,否则跳转到步骤3。
3 基于改进麻雀搜索算法的多阈值图像分割 3.1 二维熵多阈值分割方法基于一维直方图可分离判据的阈值分割方法在图像信噪比下降时,图像的分割质量急剧下降[11]。因此出现了一些利用图像的二维直方图进行阈值分割的方法[12-13],其中就包括二维熵的阈值分割方法。可将二维熵阈值分割方法扩展为二维熵多阈值分割方法。
二维熵多阈值分割方法的原理为:假设一幅尺寸为
| $ {p_{ij}} = \frac{{r\left( {i,j} \right) }}{{M \times N}} $ | (9) |
式中:
如此得到了一个关于
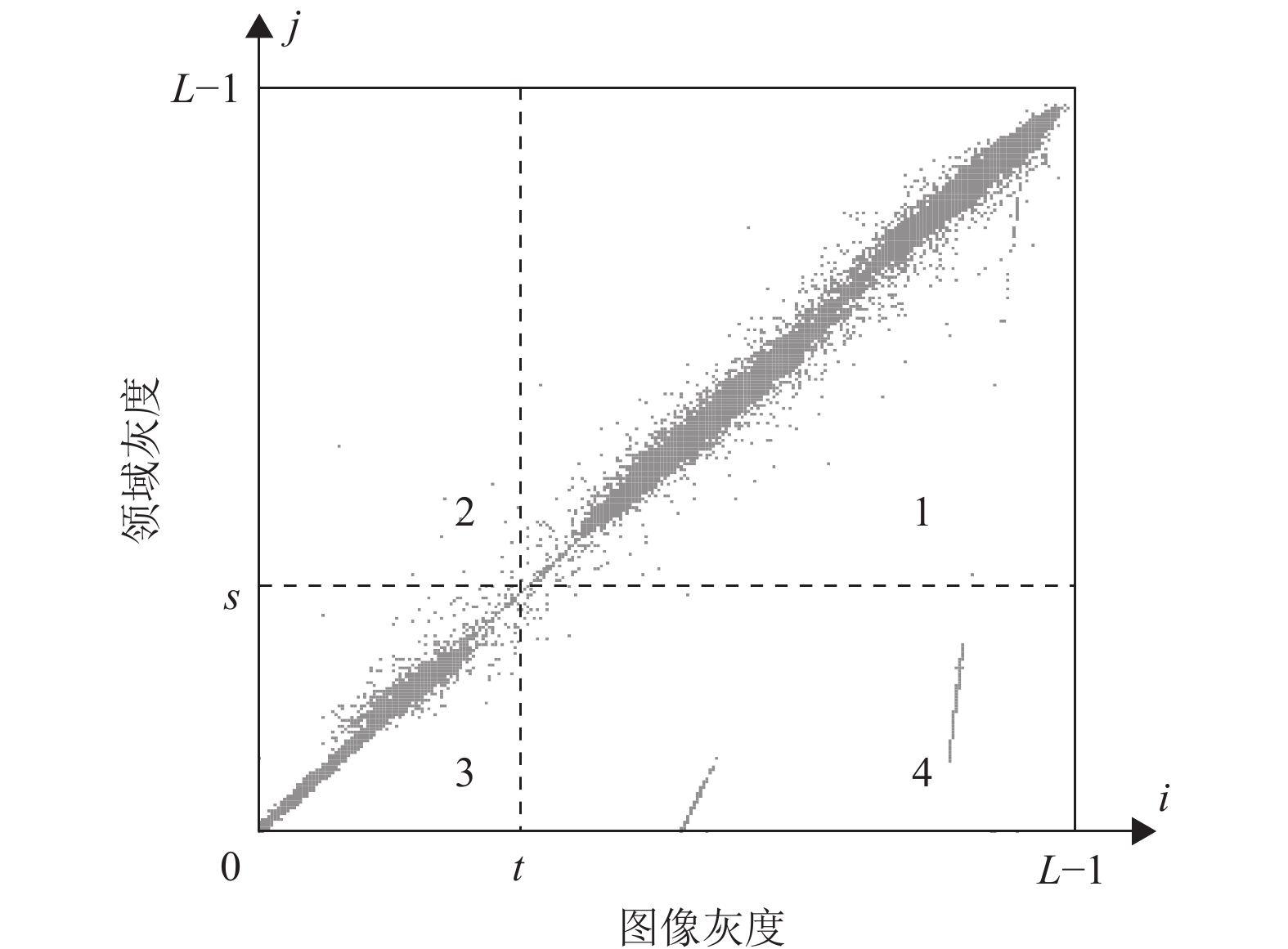
|
图 2 二维直方图 Figure 2 Two-dimensional histogram |
区域1和区域3的概率分别为
| $ {p_1}\left( {t,s} \right) = \sum\limits_{i = t + 1}^L {\sum\limits_{j = s + 1}^L {{p_{ij}}} } $ | (10) |
| $ {p_3}\left( {t,s} \right) = \sum\limits_{i = 0}^t {\sum\limits_{j = 0}^s {{p_{ij}}} } $ | (11) |
区域1与区域3的总信息熵为[14]
| $ H\left( {t,s} \right) = \ln \left( {{p_1}\left( {t,s} \right) {p_3}\left( {t,s} \right) } \right) + \frac{{{h_1}\left( {t,s} \right) }}{{{p_1}\left( {t,s} \right) }} + \frac{{{h_3}\left( {t,s} \right) }}{{{p_3}\left( {t,s} \right) }} $ | (12) |
式中:
| $ {h_i}\left( {t,s} \right) = - \sum\limits_{i = t + 1}^L {\sum\limits_{j = s + 1}^L {{p_{ij}}} } \ln \left( {{p_{ij}}} \right) $ | (13) |
| $ {h_3}\left( {t,s} \right) = - \sum\limits_{i = 0}^L {\sum\limits_{j = 0}^L {{p_{ij}}} } \ln \left( {{p_{ij}}} \right) $ | (14) |
最大二维熵则是要获得最佳阈值
| $ \left( {{t^*},{s^*}} \right) = \arg \mathop {\max }\limits_{0 \leqslant t < L} \mathop {\max }\limits_{0 \leqslant t < L} \left( {H\left( {t,s} \right) } \right) $ | (15) |
将最大二维熵扩展至多阈值形式,则设有n对阈值
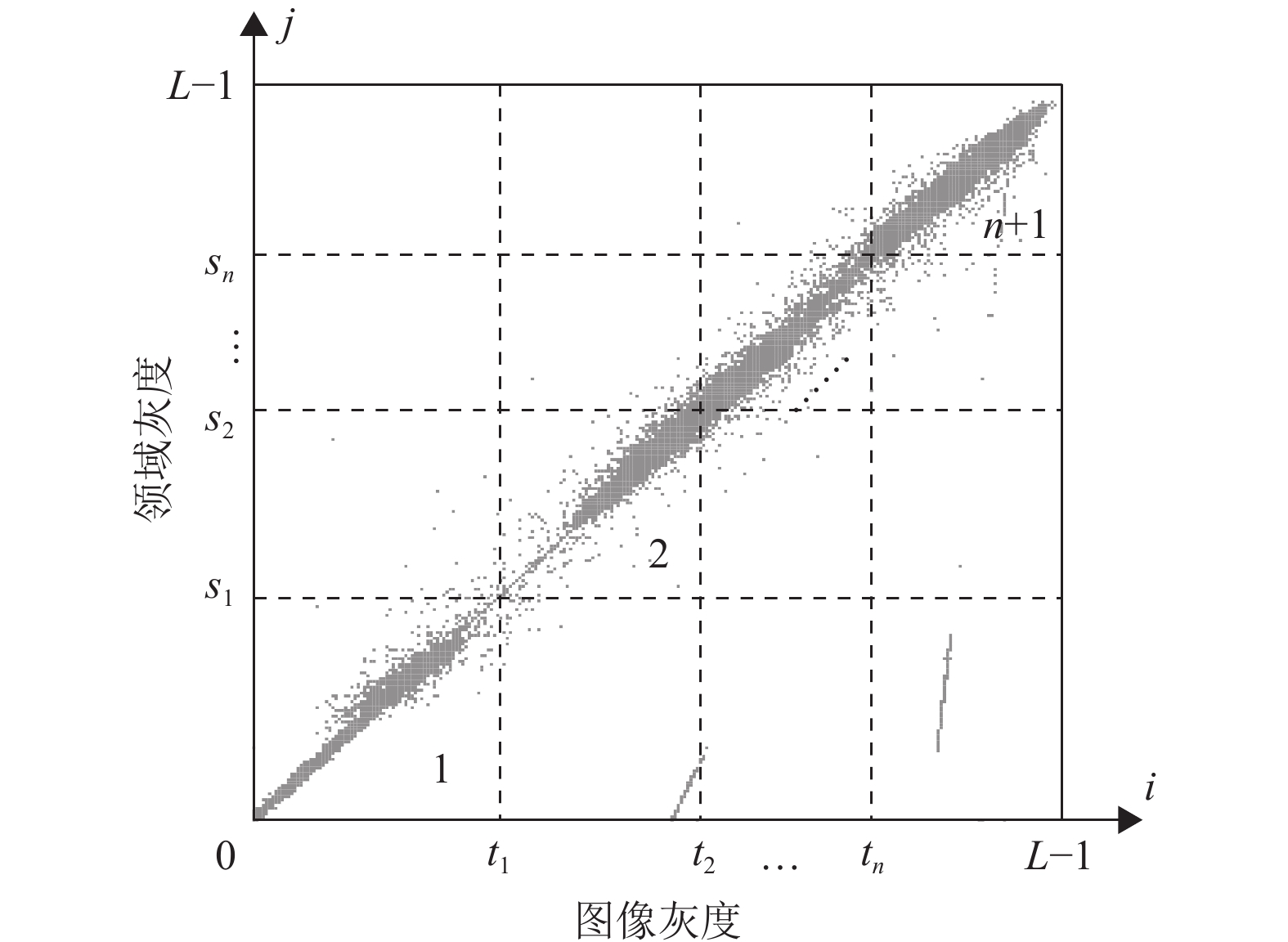
|
图 3 多阈值二维直方图 Figure 3 Two-dimensional multi-threshold histogram |
| $ H\left( {{t_1},{s_1},{t_2},{s_2} ,\cdots, {t_n},{s_n}} \right) = \ln \left( {\prod\limits_{i = 1}^{n + 1} {{p_i}} } \right) - \sum\limits_{i = 1}^{n + 1} {\frac{{{h_i}}}{{{p_i}}}} $ | (16) |
令
| $ {p_k} = \sum\limits_{i = {t_{k - 1}} + 1}^{{t_k}} {\sum\limits_{j = {s_{k - 1}} + 1}^{{s_k}} {{p_{ij}}} } $ | (17) |
| $ {h_k} = \sum\limits_{i = {t_{k - 1}} + 1}^{{t_k}} {\sum\limits_{j = {s_{k - 1}} + 1}^{{s_k}} {{p_{ij}}} } \ln \left( {{p_{ij}}} \right) $ | (18) |
式中:
通过二维直方图计算总信息熵
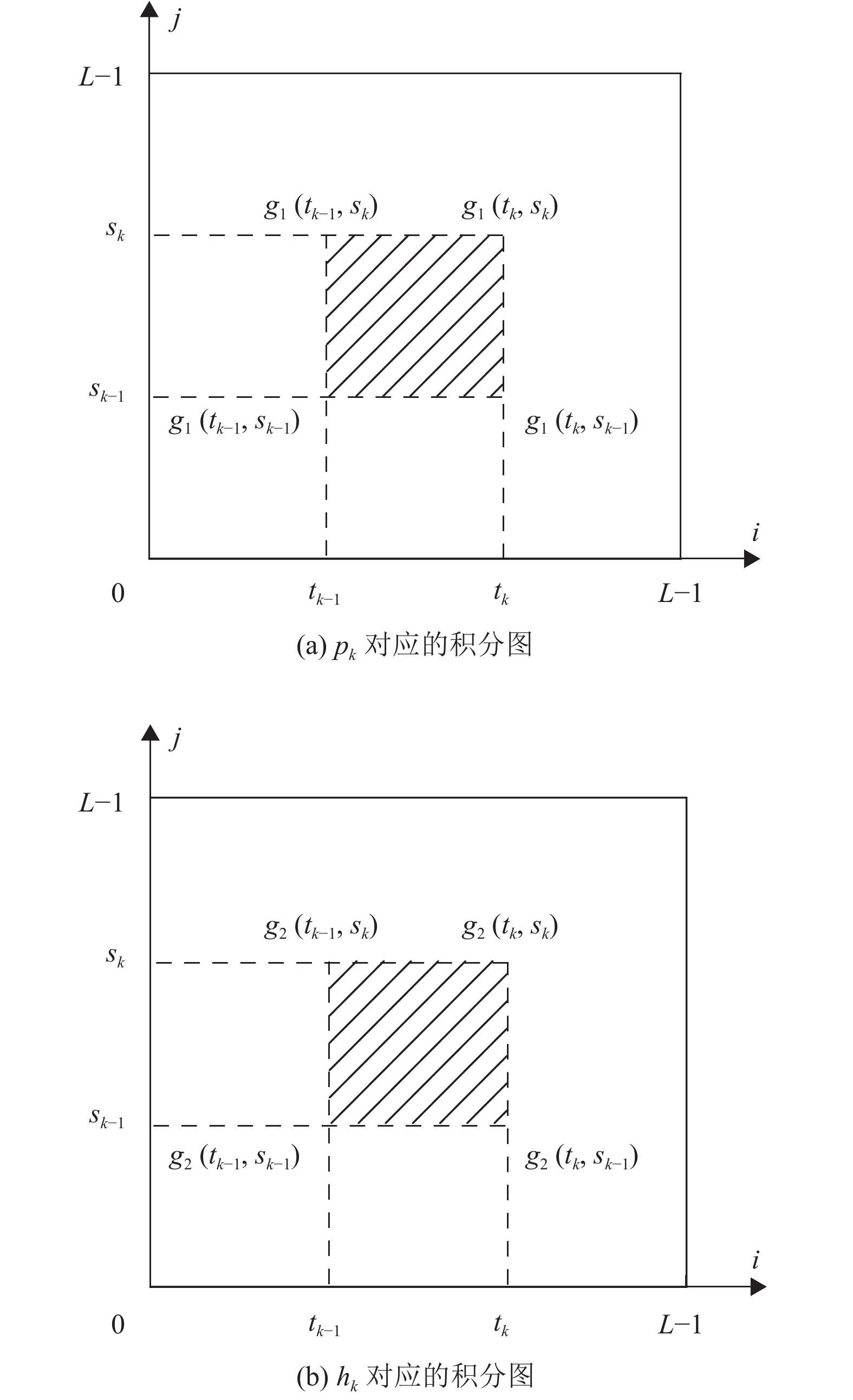
|
图 4 |
| $ {g_1}\left( {i,j} \right) = \sum\limits_{x = 0}^i {\sum\limits_{y = 0}^j {{p_{ij}}} } $ | (19) |
| $ {g_2}\left( {i,j} \right) = \sum\limits_{x = 0}^i {\sum\limits_{y = 0}^j {{p_{ij}}} } \ln \left( {{p_{ij}}} \right) $ | (20) |
运用积分图,可将式(17)和式(18)的计算简化为:
| $ \begin{gathered} {p_k} = {g_1}\left( {{t_k},{s_k}} \right) - {g_1}\left( {{t_{k - 1}},{s_k}} \right) -\\ {g_1}\left( {{t_k},{s_{k - 1}}} \right) + {g_1}\left( {{t_{k - 1}},{s_{k - 1}}} \right) \\ \end{gathered} $ | (21) |
| $ \begin{gathered} {h_k} = {g_2}\left( {{t_k},{s_k}} \right) - {g_2}\left( {{t_{k - 1}},{s_k}} \right) - \\ {g_2}\left( {{t_k},{s_{k - 1}}} \right) + {g_2}\left( {{t_{k - 1}},{s_{k - 1}}} \right) \\ \end{gathered} $ | (22) |
设分割图像的阈值向量T为
步骤1:读取待分割灰度图
步骤2:根据灰度图
步骤3:根据步骤2中的二维直方图求得
步骤4:初始化麻雀种群,其中每个麻雀个体的位置代表一个阈值向量,并利用积分图及根据式(16)、式(21)和式(22)计算所有麻雀个体的适应度值。
步骤5:利用改进麻雀搜索算法对阈值向量进行寻优迭代,直至达到最大迭代次数。
步骤6:通过使用寻优得到的最优阈值对待分割图像进行阈值分割,输出分割后的图像。
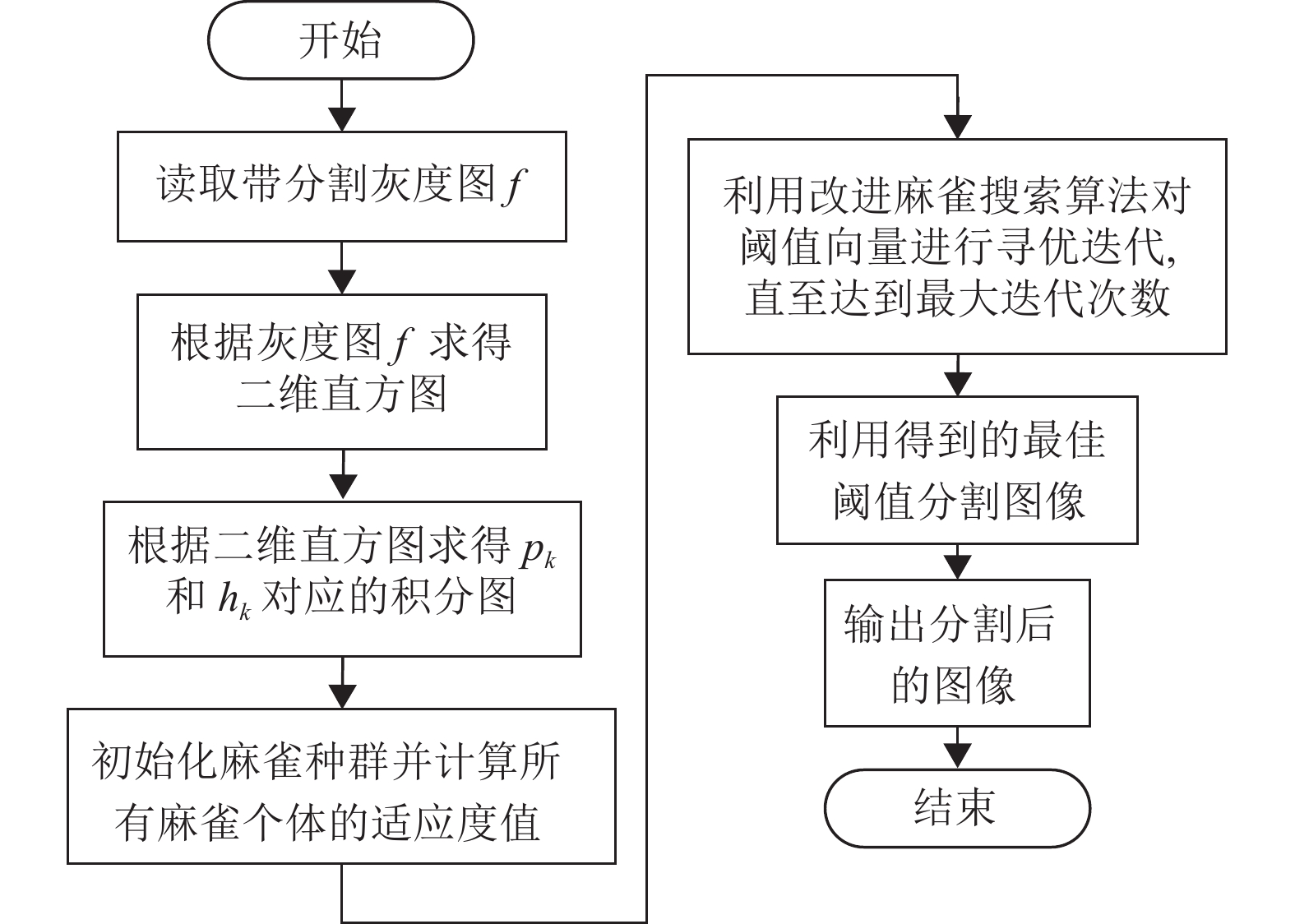
流程图如图5所示。
|
图 5 分割算法流程图 Figure 5 Flow chart of segmentation algorithm |
通过设计基准函数对比实验来验证改进算法的性能提升,设计二维熵图像多阈值分割对比实验来验证基于改进麻雀搜索算法的二维熵多阈值分割方法在运行速度上的优越性。本文实验均基于Windows1064位操作系统,CPU为Intel(R)Core(TM) i5-4210 M和16 GB内存的PC机,实验软件为Matlab R2018a。
为测试改进麻雀搜索算法的搜索能力,本文采用4个不同特征的基准测试函数作为实验对象,如表1所示。表1中特征“U”代表该函数是单峰函数,函数在定义域内没有局部极值,只有全局最优解;特征“M”代表函数是多峰函数,多峰函数相对于单峰函数具有多个局部极值,用于检验算法的全局搜索能力;特征“S”代表函数是可分离的,即该函数可由N个单变量函数之和表示;特征“N”代表函数是不可分离的,与可分离函数相对,不可分离函数变量之间存在复杂的关系,因此此类函数的寻优较为困难[16]。实验中算法的通用参数分别设置为:种群的规模
| 表 1 基准测试函数 Table 1 Benchmark functions |
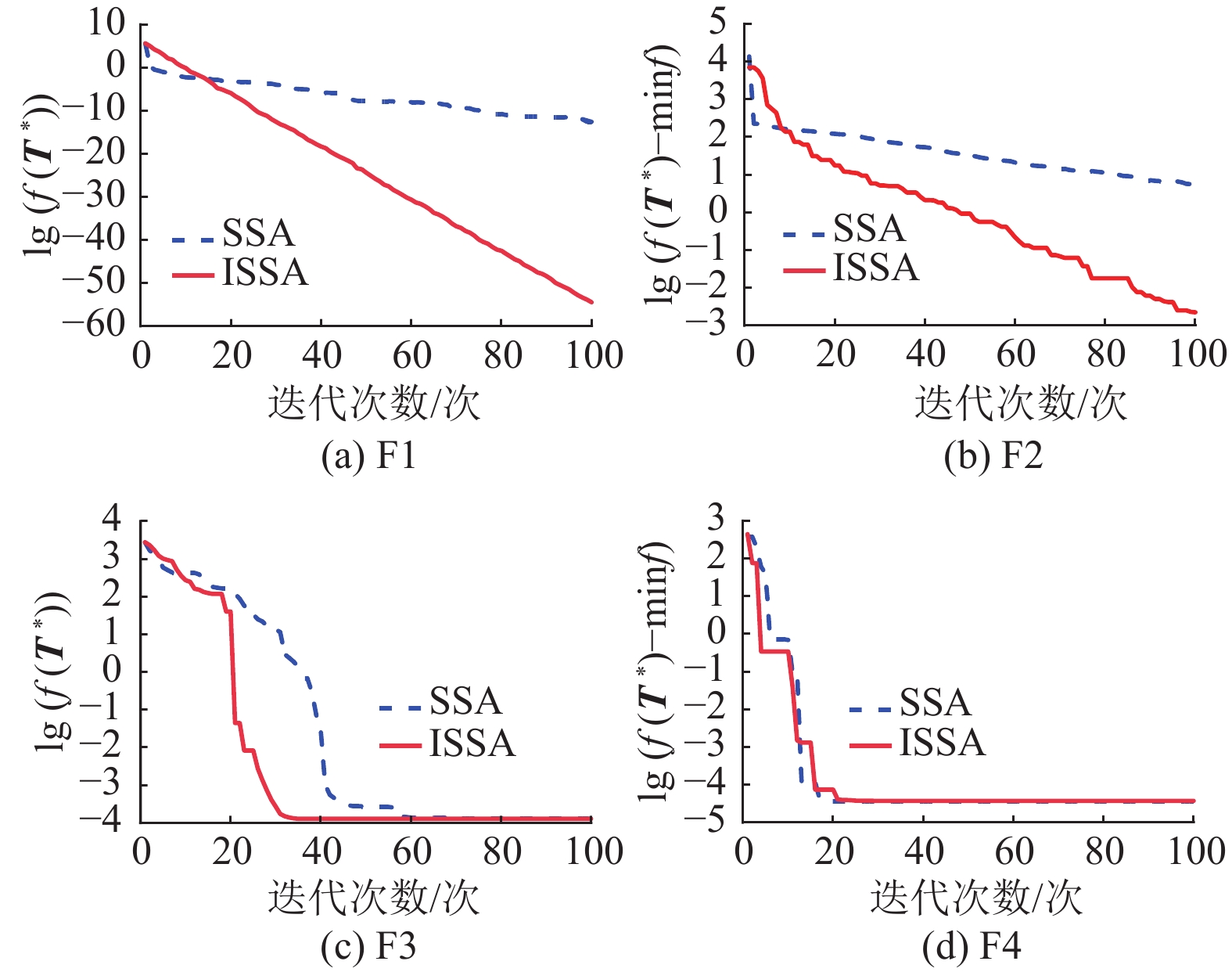
标准麻雀搜索算法和改进麻雀搜索算法在4个基准测试函数上的收敛曲线如图6所示,从图中可以看出改进后的麻雀搜索算法在F1上表现出了更优的收敛精度;在F2上表现出了更优的全局搜索能力;在F3上表现出更优的收敛速度;在F4上表现出与标准麻雀搜索算法相似的寻优能力。
|
图 6 基准函数收敛图 Figure 6 Convergence graph of benchmark function |
为避免实验结果的随机性,定量分析改进后算法的寻优性能,标准麻雀搜索算法(SSA)和改进麻雀搜索算法(ISSA) 对表1中的4个基准函数各独立运行30次,选取运行结果中的最差值、最优值、平均值和标准差作为对比指标进行比较,如表2所示。
| 表 2 算法性能比较 Table 2 Comparison of performance among different algorithms |
从寻优结果的比较中可发现,在F1上,ISSA极大地提高了寻优精度;在F2上SSA没有能够搜寻到最优解,体现了ISSA相较于SSA在全局搜索能力上的提升;在F3和F4上,ISSA相较于SSA,其寻优结果的标准差更低,表现出了更好的寻优稳定性,具有更高的寻优能力。
5.2 基于改进麻雀搜索算法的二维熵多阈值图像分割方法实验本文实验选取了Lenna图、Camera man图、Rice图以及工业生产当中的齿轮图和刹车盘图分别进行基于改进麻雀搜索算法的二维熵多阈值图像分割方法的单阈值分割、双阈值分割以及三阈值分割。算法的参数设置为:种群的规模

|
图 7 分割结果 Figure 7 Segmentation results |
为验证本文方法的优越性,将其与基于粒子群优化算法(Particle Swarm optimization,PSO) 的二维熵分割方法进行对比实验。基于粒子群优化算法(PSO) 的二维熵分割方法是直接利用粒子群优化算法对图像的二维熵最优阈值进行寻优的方法。
以上2种算法对前述5幅原始图像进行分割实验,分割后的阈值与计算时间如表3所示。由表3可知,相较于基于PSO的二维熵方法,本文方法在双阈值分割及三阈值分割中取得了6.47倍及4.48倍的速度优势。将改进麻雀搜索算法应用在二维熵图像多阈值分割上,提高了图像分割的速度。
| 表 3 两种算法的结果对比 Table 3 Comparison of the results between two algorithms |
本文针对图像二维熵多阈值分割时存在的计算量过大,计算时间过长的问题,提出了基于ISSA并结合积分图的二维熵图像多阈值分割快速算法。首先,引入麻雀搜索算法(SSA)并对该算法的算法性能进行分析研究,针对SSA存在的全局搜索能力差、容易陷入局部最优解的缺点,提出了基于方差线性递减的高斯扰动策略和随机步长移动策略的ISSA。相较于SSA,ISSA在4种不同类型的基准函数上表现出更优的寻优能力。接着,通过引入积分图方法,降低总信息熵的运算量,最终提出了基于改进麻雀搜索算法并结合积分图的二维熵图像多阈值分割快速算法。最后,使用该方法与基于PSO的二维熵方法进行图像分割对比实验,实验结果表明,相较于基于PSO的二维熵方法,本文方法仍取得了6.47倍和4.48倍的速度优势,提升了图像二维熵多阈值分割的分割效率。
| [1] |
陈百红, 张华, 高恩运, 等. 鞍钢热轧带钢厂智慧制造发展研究[J].
鞍钢技术, 2020(2): 67-70.
CHEN B H, ZHANG H, GAO E Y, et al. Study on development of smart manufacturing in hot rolled strip steel mill of ansteel[J]. Angang Technology, 2020(2): 67-70. DOI: 10.3969/j.issn.1006-4613.2020.02.015. |
| [2] |
王成军, 韦志文, 严晨. 基于机器视觉技术的分拣机器人研究综述[J].
科学技术与工程, 2022, 22(3): 893-902.
WANG C J, WEI Z W, YAN C. Review on sorting robot based on machine vision technology[J]. Science Technology and Engineering, 2022, 22(3): 893-902. DOI: 10.3969/j.issn.1671-1815.2022.03.004. |
| [3] |
SARKAR S, DAS S, CHAUDHURI S S. Multi-level thresholding with a decomposition-based multi-objective evolutionary algorithm for segmenting natural and medical images[J].
Applied Soft Computing, 2017, 50: 142-157.
DOI: 10.1016/j.asoc.2016.10.032. |
| [4] |
MALA C, SRIDEVI M. Multilevel threshold selection for image segmentation using soft computing techniques[J].
Soft Computing, 2016, 20(5): 1793-1810.
DOI: 10.1007/s00500-015-1677-6. |
| [5] |
宋佳声, 王永坚, 戴乐阳. 基于不同自适应阈值法的铁谱图像分割效果比较[J].
润滑与密封, 2021, 46(4): 111-115.
SONG J S, WANG Y J, DAI L Y. Comparison of ferrographic image segmentation by difference adaptive thresholding methods[J]. Lubrication Engineering, 2021, 46(4): 111-115. DOI: 10.3969/j.issn.0254-0150.2021.04.018. |
| [6] |
吴禄慎, 程伟, 胡赟. 应用改进布谷鸟算法优化多阈值图像分割[J].
吉林大学学报(工学版), 2021, 51(1): 358-369.
WU L S, CHENG W, HU Y. Image segmentation of multilevel threshold based on improved cuckoo search algorithm[J]. Journal of Jilin University(Engineering and Technology Edition), 2021, 51(1): 358-369. DOI: 10.13229/j.cnki.jdxbgxb20190858. |
| [7] |
吴亮, 杜灵彬, 汤显峰. 基于改进蝴蝶优化算法的多阈值图像分割[J].
中国科技论文, 2021, 16(11): 1174-1180.
WU L, DU L B, TANG X F. Multi-level threshold image segmentation based on improved butterfly optimization algorithm[J]. China Sciencepaper, 2021, 16(11): 1174-1180. DOI: 10.3969/j.issn.2095-2783.2021.11.004. |
| [8] |
于洋, 孔琳, 虞闯. 自适应粒子群集优化二维OSTU的图像阈值分割算法[J].
电子测量与仪器学报, 2017, 31(6): 827-832.
YU Y, KONG L, YU C. Image threshold segmentation algorithm based on adaptive particle swarm optimization of two-dimensional OSTU[J]. Journal of Electronic Measurement and Instrumentation, 2017, 31(6): 827-832. DOI: 10.13382/j.jemi.2017.06.002. |
| [9] |
陈恺, 陈芳, 戴敏, 等. 基于萤火虫算法的二维熵多阈值快速图像分割[J].
光学精密工程, 2014, 22(2): 517-523.
CHEN K, CHEN F, DAI M, et al. Fast image segmentation with multilevel threshold of two-dimensional entropy based on firefly algorithm[J]. Optics and Precision Engineering, 2014, 22(2): 517-523. DOI: 10.3788/OPE.20142202.0517. |
| [10] |
XUE J K, SHEN B. A novel swarm intelligence optimization approach: sparrow search algorithm[J].
Systems Science & Control Engineering, 2020, 8(1): 22-34.
|
| [11] |
阳树洪. 灰度图像阈值分割的自适应和快速算法研究[D]. 重庆: 重庆大学, 2014.
|
| [12] |
AHMED S A. Automatic thresholding of gray-level pictures using two-dimensional entropy[J].
Computer Vision, Graphics, and Image Processing, 1989, 47(1): 22-32.
|
| [13] |
刘健庄, 栗文青. 灰度图象的二维Otsu自动阈值分割法[J].
自动化学报, 1993(1): 101-105.
LIU J Z, LI W Q. The automatic thresholding of gray-level pictures via two-dimensional Otsu method[J]. Acta Automatica Sinica, 1993(1): 101-105. DOI: 10.16383/j.aas.1993.01.015. |
| [14] |
张新明, 张爱丽, 郑延斌, 等. 改进的最大熵阈值分割及其快速实现[J].
计算机科学, 2011, 38(8): 278-283.
ZHANG X M, ZHANG A L, ZHENG Y B, et al. Improved two-dimensional maximum entropy image thresholding and its fast recursive realization[J]. Computer Science, 2011, 38(8): 278-283. DOI: 10.3969/j.issn.1002-137X.2011.08.068. |
| [15] |
VIOLA P, JONES M. Rapid object detection using a boosted cascade of simple features[C]// Proceedings of the 2001 IEEE Computer Society Conference on Computer Vision and Pattern Recognition. CVPR 2001. Kauai: IEEE, 2001.
|
| [16] |
吴虎胜, 张凤鸣, 吴庐山. 一种新的群体智能算法——狼群算法[J].
系统工程与电子技术, 2013, 35(11): 2430-2438.
WU H S, ZHANG F M, WU L S, et al. New swarm intelligence algorithm—wolf pack algorithm[J]. Systems Engineering and Electronics, 2013, 35(11): 2430-2438. |
 2023, Vol. 40
2023, Vol. 40

