2. 广东工业大学 信息工程学院,广东 广州 510006
2. School of Information Engineering, Guangdong University of Technology, Guangzhou 510006, China
医疗体制改革后,医疗机构需要自负盈亏,不仅要解决医疗资源供给与医疗需求不平衡的矛盾,还面临着市场竞争带来的压力,医院的管理者十分重视医疗成本控制以及医疗资源的高效利用。分配并调度重要的医疗资源是提高利用率和成本控制的关键。我国现行手术调度方法大多采用人工调度,在实施调度过程中只追求提高资源利用率,忽视了对手术室、医护人员、医疗设备和耗材等相关医疗资源的综合调配[1]。
目前,我国仍然停留在通过经验来完成手术预估及排程的阶段,即使在大型综合医疗机构,手术室的信息系统也只能实现手术申请、患者信息传输和采集、传递接送患者指令、手术数据简单统计等功能。医院管理者需要凭借个人经验综合考虑各种影响因素,例如手术难度级别、手术医生习惯、手术间洁净度的级别、医疗设备数量、外科技术、护理人员加班情况等进行手术调度,缺乏科学的调度运营方法、理论或模型作为技术支持,缺少对影响手术调度所有因素的全面整合[2-4]。
目前对医院调度优化的研究主要有3个方面,分别是门诊预约调度、手术调度和护士排班。门诊预约调度的目的是为了缩短患者等待就诊的时间,优化预约流程,改善就医体验,提高就诊满意度。Anvaryazdi等[5]提出了一个两阶段的随机混合整数线性规划模型,并结合模拟模型,最终生成预约调度模板,以此来为病人分配资源。Song等[6]提出了一个关联的嵌入式马尔可夫链来推导稳态分布,并且基于插槽利用率、预约成功率和患者等待时间3个评价指标平衡等待时间和获得医疗机会的可能性,在中国北京的一家实际医院进行验证,在缩减患者等待时间以及增加高到达率的患者获得医疗机会的提升超过60%。Xie等[7]考虑到患者由于没有遵守门诊预约时间而导致医院出现患者在同一时间大量积压问题,引入了离散时间批量服务队列来模拟积压动态,考虑患者的未出现行为,并考虑不同的超额预订策略,以在加班风险最小的情况下减少积压。
手术调度与门诊调度类似,都是要求合理分配医疗资源,其区别主要在于手术调度涉及到多个科室的协同合作,手术所需的相关资源的不确定性显著。Elkhattabi等[8]提出了一种新的通过主动/被动方法来解决外科手术计划和调度问题,主动阶段使用禁忌搜索算法最大限度地增加手术室占用率并最大限度地减少加班相关成本,被动阶段使用多智能体系统去适应计划的不确定性。Wang等[9]提出基于列生成的启发式算法,解决外科医生与手术的联合调度问题。Pang等[10]同时考虑手术取消和手术时间2个不确定因素,提出多手术室调度的随机整数规划模型。
针对护士排班问题,Ngoo等[11]提出了一种改进的灰狼算法,使用变异和交叉算子取代原灰狼算法中位置的更新操作,提高了灰狼算法的性能,使用INRC-II比赛提供的问题实例进行测试,证明改进后的灰狼算法优于爬山算法。王陟等[12]提出了一种新的智能高效两步并行护士排班算法,通过采用启发式调整排序随机生成问题的初始解和并行智能多样化变邻域搜索和增量式计算,提高算法在大规模护士排班问题上的平均解质量和缩短运行时间。
智能优化算法[13]是受到人类智能、生物群体社会性或自然现象规律的启发而设计的算法。智能优化算法已经成功应用于解决连续优化[14]、组合优化[15]、调度优化[16]等问题。通过智能优化算法能够优化系统效率、降低能耗、合理地利用资源,并且随着处理对象规模的增加,智能优化算法的效果会更加明显。陈蒙蒙等[17]定义了护士排班问题中的多种约束条件,提出了一种多约束粒子群算法。Rurifandho等[18]提出了一种使用遗传算法求解门诊、住院和手术的医生调度和重新规划的方法。
上述3类医院调度优化问题其本质都在于医生、护士及相关医疗资源如何更高效地进行协作,从而提高为病人提供医疗服务的质量。本文将医生、护士和病人之间的治疗活动看作一个多角色的协同控制问题,协作治疗的过程即为医生、护士和病人3种角色之间的相互协同的过程,并将三者相互协同的问题场景通过Abstract Swarm图形化建模方法[19]进行建模。现有的Abstract Swarm模拟系统中存在random、minDistance、maxFreeSpace这3种基准评估策略。角色在访问目标站点前需要通过评估策略选择当前最适合访问的目标站点。random策略生成一个随机值作为该目标站点的评估值。minDistance策略将当前角色所在的站点与目标站点的距离作为对该目标站点的评估值。maxFreeSpace策略则将目标站点剩余的空闲空间作为该目标站点的评估值。上述3种策略在复杂的场景中可能出现多个角色在不同站点上相互等待而导致无法继续协同,故而无法生成可行的调度图。
因此本文提出了一种由多个决策组组成的决策模型,每个决策组负责一类角色的决策,如不同类型的病人、医生和护士角色,每个决策组均有4个基本决策指标及对应的权重值组成。这4个基本决策指标分别为站点间的距离、空闲度、紧急度和吞吐量。设计该决策模型的目的是为了在目标站点选择的决策过程中能综合多个因素进行考虑,指导角色做出最优的访问行为。
针对算法优化结果的评价,本文采用模拟仿真的方式,设计并实现了场景模拟程序。为了更好地应用决策模型,确定各个决策指标在场景调度中所占的权重,本文引入了智能优化技术优化决策模型中各个指标的权重。其中,分别采用了差分演化算法、粒子群算法、遗传算法、模拟退化算法4种智能优化算法来优化决策模型中的各个决策指标的权重值。通过对比实验,差分演化算法表现最佳,能够找到更优的决策模型从而得到更优的调度结果。
1 医院协作治疗调度问题协作治疗调度是一个由多种医疗资源与病人协作完成治疗任务的调度问题。协作治疗调度问题的描述如下:k名医生和l名护士在有限的医疗资源约束下,需要为r名病人提供不同类型的医疗服务。本文将原本医疗机构为病人提供医疗服务的调度问题看成病人与各种医疗资源的协作调度问题,即将医院为病人提供医疗服务看成是一个需要由医生、护士和病人协作完成的医疗任务。此外,在协作的过程中还需要满足下面的约束条件。
(1) 同一个角色同一时刻只能参与一个医疗任务。
(2) 每个医疗任务在执行过程中不能中断。
(3) 所有满足执行条件的医疗任务在0时刻都可以开始执行。
(4) 每一个医疗任务需要在指定的服务站点完成。
1.1 优化目标假设所有病人从同一个时间开始进入医院,本文的优化目标是最小化所有用户完成所有检查的完成时间,优化目标公式为
| $ f = \min (\mathop {\max }\limits_{1 < j \leqslant r} (C_{j}) ) $ | (1) |
式中:r为病人的个数,Cj为第j个病人完成其参与的所有医疗任务的总用时。
1.2 问题表示图1给出了协作治疗场景中的角色、站点和关系的基本图例。角色和站点均使用矩形表示。其中,角色中的数量和速度属性分别表示角色的个数以及角色每个单位时间可以移动的距离,站点中的数量、最大被访问次数、必须被访问次数、被访问时间、被访问空间分别表示站点的个数、站点累计可以被访问的次数、与站点具有访问关系的角色必须访问站点的次数、角色访问站点所需的时间、站点可以同时被多少个角色访问。访问关系由实线表示,表示角色需要访问与其具有访问关系的站点。距离关系由带菱形的实线表示,该关系表示站点间的距离,具体距离由菱形中的数值表示,比如图中的数字2表示2个站点间的距离为2。并行关系由带菱形的双实线表示,该关系相连的2个对象必须同时发生。

|
图 1 协作治疗场景中的角色、站点和关系的基本图例 Figure 1 Basic illustrations of roles, sites, and relationships in collaborative therapy scenarios |
图2给出的场景示例图中,有5名病人、1名护士和3个站点。护士和服务1存在访问关系,每次访问需要12个单位时间;5名病人角色与站点1和站点2均存在访问关系,每次访问分别需要12和10个单位时间;服务1站点与站点1存在并行关系,3个站点的被访问空间均为1,初始时所有病人均在站点1。

|
图 2 场景示例图 Figure 2 Scenario of the example |
决策模型的作用是在医疗资源紧缺的条件下,指导医生、护士和病人前往合适的站点执行对应的医疗任务,其目标在于通过决策模型使得医疗机构在更短的时间内充分利用现有的医疗资源为病人提供更加高效的医疗服务。文中提出了影响决策的4个指标,分别是距离度(D) 、空闲度(V) 、紧急度(C) 以及吞吐量(T) 。根据问题场景的不同,上述4个指标对于决策的影响均不相同。决策模型的计算如式 (2) 所示。
| $ \begin{gathered} M(o) = p{}_1D(c,o) + {p_2}V(o) + \\ {p_3}C(o) + {p_4}T(o) \\ \end{gathered} $ | (2) |
式中:
(1) 站点之间的距离度(D):距离度D(c,o) 表示角色从其当前所在的站点c到达目标站点o的最短距离,距离度的取值范围为[0,+∞) 。
(2) 站点的空闲度(V):站点的空闲度表示站点所剩余的被访问空间大小,即除去正在访问站点的角色,站点剩余的被访问空间大小,空闲度V(o) 具体的计算如式(3) 所示。
| $ V(o)={s}_{o}-{a}_{o} $ | (3) |
式中:
(3) 站点的紧急度(C):若目标站点与某一站点存在并行关系,且该站点处于运行状态,则目标站点的紧急度值为0,否则目标站点的紧急度C(o) 的计算如式(4) 所示。
| $ C(o) = \mathop {\max }\limits_{1 < {a_j} < |{\boldsymbol{A}}|} ({w_{{a_j}}}) $ | (4) |
式中:A为当前所有处于与站点o存在依赖关系的站点的角色集合,
(4) 站点的吞吐量(T):站点的吞吐量T(o) 的计算如式(5) 所示。
| $ T(o) = \frac{{{t_o}}}{{{s_o}}} $ | (5) |
式中:
场景模拟程序的作用是应用决策模型的关键,场景模拟程序通过决策模型模拟协作治疗场景的调度过程。下文将详细介绍场景模拟程序的设计与实现。
3.1 角色状态如图3所示,角色拥有6种状态,分别为初始、等待、就绪、访问、移动、完成。当角色处于初始状态时,表示角色刚刚被创建;当角色处于等待状态时,表示处于目标站点的等待队列;当角色处于就绪状态时,表示角色无任何前置约束随时可以进入工作空间;当角色处于访问状态时,表示角色在目标站点的工作空间中已经开始运行;当角色处于移动状态时,表示角色正在向目标站点移动;当角色处于完成状态时,表示角色已经没有任何站点需要访问。

|
图 3 角色状态图 Figure 3 State diagram of roles |
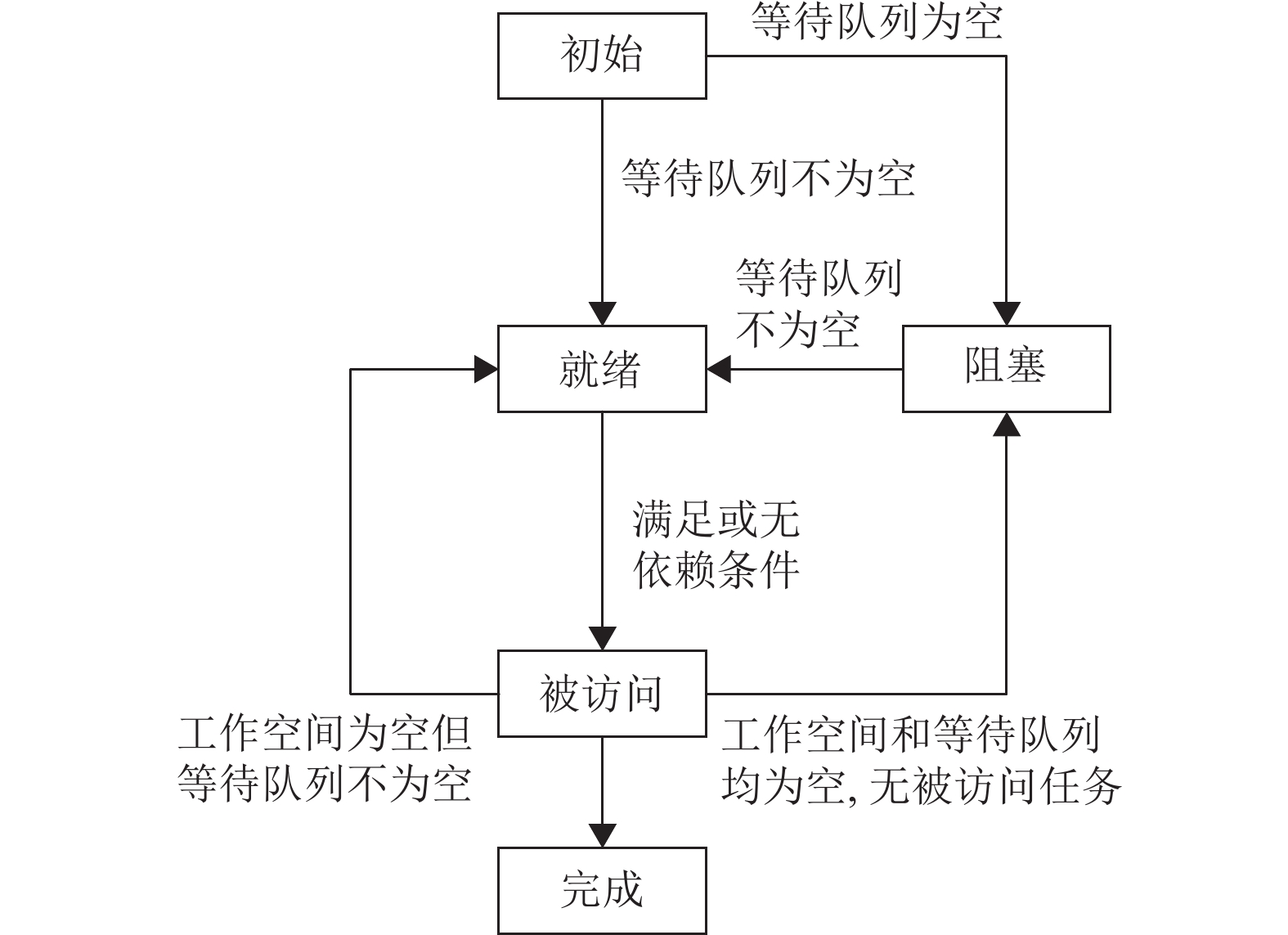
如图4所示,站点拥有5种状态,分别为初始、就绪、被访问、阻塞、完成。当站点处于初始状态时,表示站点刚刚被创建;当站点处于就绪状态时,表示站点的等待队列中已经存在角色正在等待;当站点处于被访问状态时,表示有角色正在访问该站点;当站点处于阻塞状态时,表示工作空间和等待队列均为空;当站点处于完成状态时,表示该站点已经完成其所需要被访问的任务,不再允许任何角色访问该站点。
|
图 4 站点状态图 Figure 4 State diagram of stations |
模拟程序根据决策模型模拟协作治疗病人的调度模型,该决策模型在模拟场景中运行的时间作为该调度方案的适应度值。模拟场景的具体流程如下:
(1) 初始化场景。初始化所有参与调度角色(例如r个病人、k个医生和l个护士) ,初始时所有的角色状态均为初始状态。
(2) 所有目标站点集合不为空且当前无目标站点的角色,根据给定的策略从目标站点集合中选择一个站点作为当前的目标站点。
(3) 所有未到达目标站点的角色向各自的目标站点移动一个单位时间。
(4) 检查角色是否就绪,当角色抵达目标站点的等待队列并且无任何前置约束或前置约束均已满足则该角色置为就绪状态。
(5) 检查站点是否就绪,若站点无任何前置约束或前置约束均已满足则该站点置为就绪状态。
(6) 所有处于被访问状态的站点分别被访问一个单位时间。
(7) 当所有角色均已访问完成所有给定的待访问的站点时或场景模拟出现死锁现象,则判定场景模拟结束,否则执行步骤(2) 。
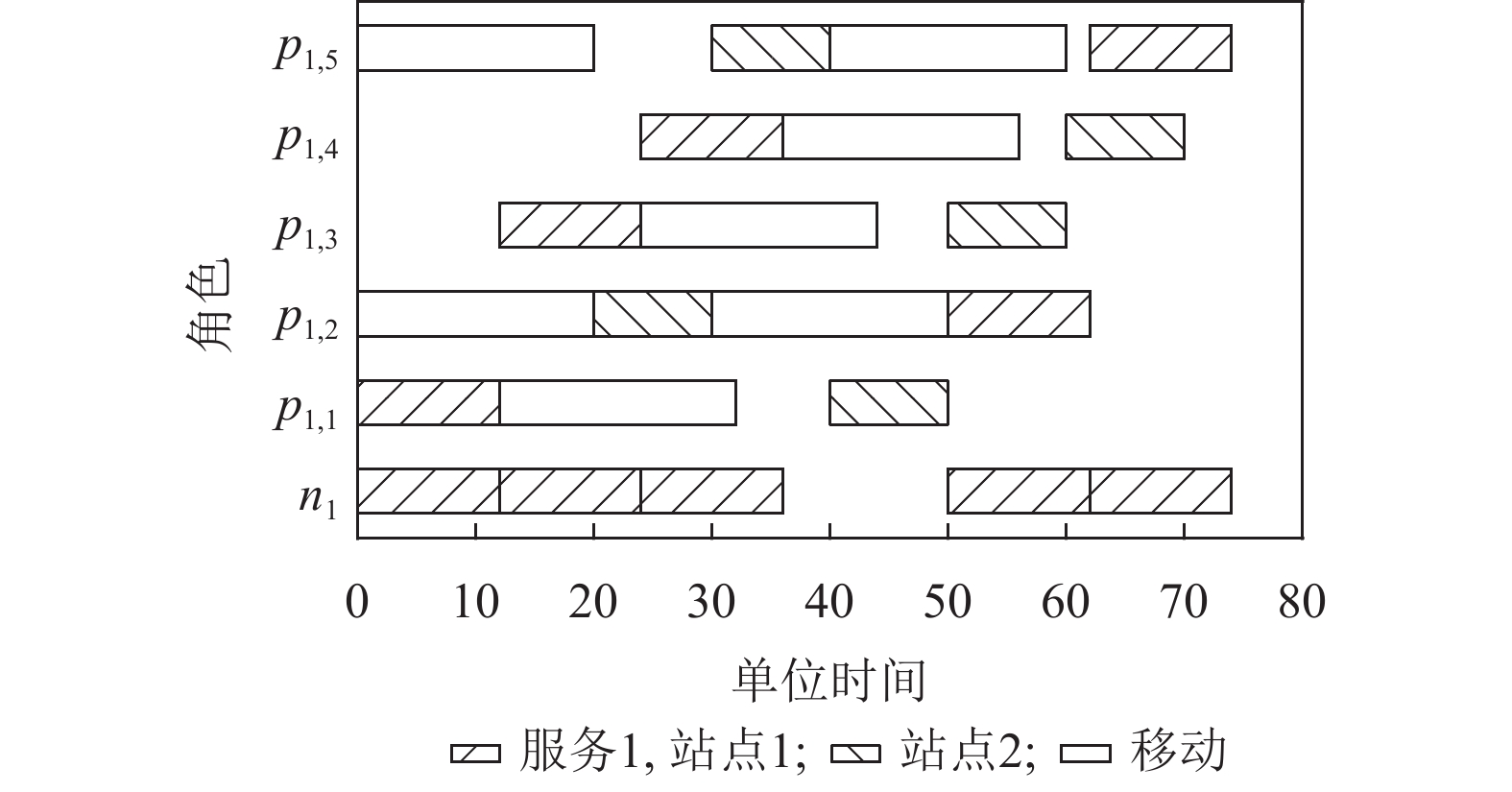
3.4 场景模拟示例图2的场景模拟调度过程如图5所示,其中横坐标表示时间片,p1,1~5分别为1~5号病人,n1为一号护士,角色正在移动由内部空白的矩形区域表示,护士访问服务1站点和病人访问站点1由内部斜杠填充的矩形区域表示,病人访问站点2由内部反斜杠填充的矩形区域表示。
|
图 5 示例场景调度图 Figure 5 An scheduling diagram for example scenario |
时间片1时,假设5名病人均处于站点1,1名护士处于服务1站点且所有角色均为初始状态。5名病人均需访问站点1和站点2站点各1次,护士需访问服务1站点5次,服务1站点、站点1和站点2均为初始状态。此时所有角色均没有目标站点,若根据决策模型,1号、3号、4号病人均选择先访问站点1,2号和5号病人选择先访问站点2,1号护士选择访问服务1站点。由于1号、3号、4号病人和1号护士均已经处于目标站点,故分别进入目标站点的等待队列且他们均无任何前置约束,故均置为就绪状态,而2号、5号病人尚未抵达目标站点,故分别向目标站点移动一个单位时间并置为移动状态。服务1站点与站点1的等待队列不为空,均从初始状态置为就绪状态,而站点2的等待队列为空,从初始状态置为阻塞状态。服务1站点当前处于就绪状态且其依赖的站点1处于就绪状态时,将服务1站点从就绪状态更新为被访问状态,站点1当前处于就绪状态且其依赖的服务1站点处于被访问状态时,将站点1从就绪状态更新为被访问状态。站点1的工作空间大小为1,根据排队原则1号病人先进入工作空间执行一个单位时间,3号病人和4号病人继续在等待队列等待,服务1站点的工作空间大小为1,1号护士进入工作空间执行一个单位时间。
当所有处于访问状态的站点均工作完一个单位时间后,此时时间片为2,且当前所有角色所领取的任务均未完成,无法领取新任务,需继续执行当前的访问任务。
直到时间片13时,1号病人和1号护士完成访问任务,领取下一个访问任务。此时,1号病人只剩下访问站点2的任务故领取访问站点2的任务,1号护士继续领取访问服务1站点的任务。2号病人进入站点1的工作空间开始执行,1号护士进入服务1站点的工作空间开始执行。
时间片21时,2号病人和5号病人到达站点2的等待队列。站点2状态从初始状态置为就绪状态且站点2不存在依赖站点故直接置为被访问状态,2号病人进入站点2的工作空间开始执行。
时间片25时,3号病人完成站点1的访问任务,领取其最后一个访问站点2的任务并开始向站点2移动,1号护士完成服务1站点的访问任务,继续领取访问服务1站点的任务并开始工作,4号病人进入站点1的工作空间开始执行。
时间片31时,2号病人完成访问任务,领取其最后一个访问站点1的访问任务并开始向站点1移动。5号病人进入站点2的工作空间开始执行。
时间片33时,1号病人抵达站点2的等待队列。
时间片37时,4号病人完成站点1的访问任务,领取其最后一个访问站点2的任务并开始向站点2移动,1号护士完成服务1站点的访问任务,继续领取访问服务1站点的任务。
时间片41时,5号病人完成站点2的访问任务,领取其最后一个访问站点1的任务并开始向站点1移动。
时间片45时,3号病人抵达站点2的等待的队列。
时间片51时,2号病人抵达站点1的等待队列,站点1从阻塞状态变成就绪状态;服务1站点与站点1站点均处于就绪状态,故服务1站点和站点1均从就绪状态置为被访问状态;3号病人进入站点2的工作空间开始执行。1号病人完成访问站点2的任务,且1号病人已经完成其需要访问的所有任务,将1号病人置为完成状态。
时间片57时,4号病人抵达站点2的等待队列。
时间片61时,3号病人完成访问站点2的任务,且3号病人已经完成其需要访问的所有任务,将3号病人置为完成状态。4号病人进入站点2的工作空间开始访问。5号病人抵达站点1等待队列。
时间片63时,1号护士完成访问任务,领取下一个访问任务。2号病人完成访问站点1的任务,且2号病人已经完成其需要访问的所有任务,将2号病人置为完成状态。
时间片71时,4号病人完成访问站点2的任务,且4号病人已经完成其需要访问的所有任务,将4号病人置为完成状态。
时间片75时,1号护士和5号病人各自完成其所需访问的最后一个站点,将1号护士和5号病人均置为完成状态。此时所有角色的状态均为完成,场景模拟结束。
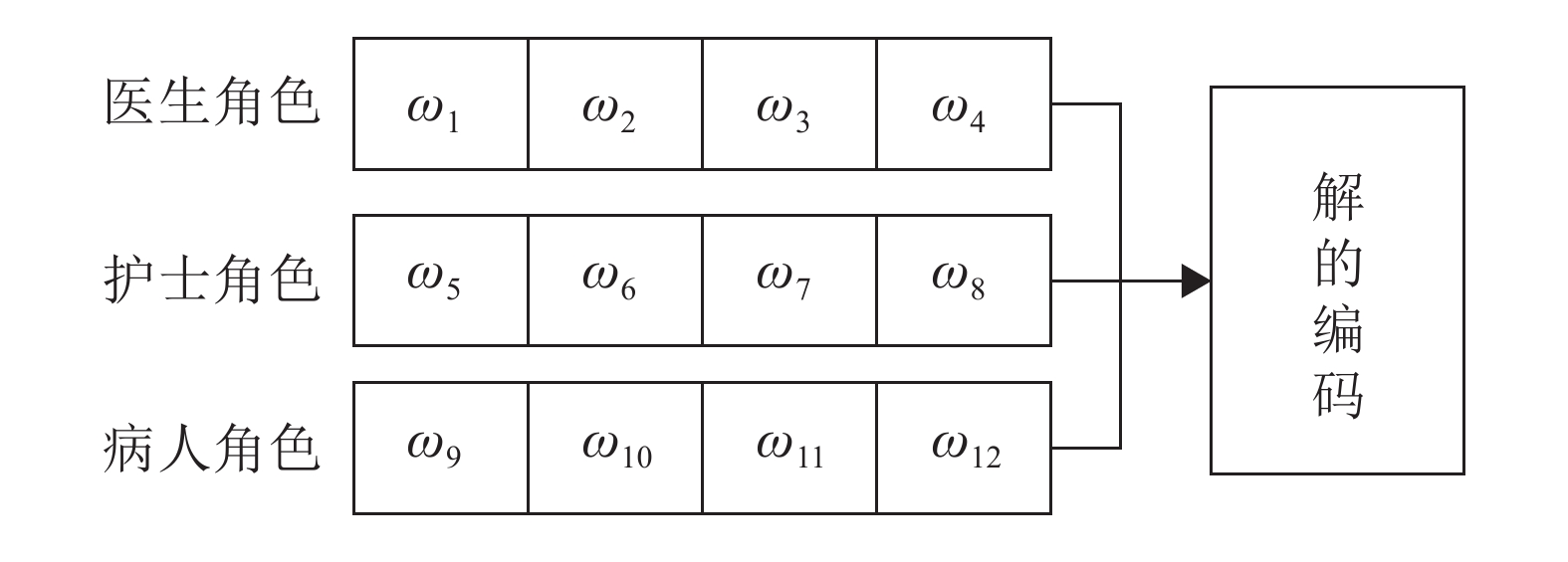
4 优化决策模型算法 4.1 编码方案及初始化编码和解码是指解与染色体之间的相互转换,是应用智能算法的首要和关键问题。基于文中所提出的决策模型,编码方案由距离度、空闲度、紧急度、吞吐量4个决策指标的权重值组成且每种角色均独立拥有一组决策模型。若问题场景中存在医生、护士和病人3种角色,则编码方案由医生、护士和病人的决策模型权重值组成,编码方案的长度为12。如图6所示,上4个权重值、中间4个权重值、下4个权重值分别为医生、护士和病人决策模型的权重值。其中每个部分的权重值依次为距离度、空闲度、紧急度和吞吐量4个决策指标的权重值。
|
图 6 编码方案示例图 Figure 6 An example of the coding scheme |
根据编码方案的长度初始化,在
评价操作是用于衡量个体的优劣情况。根据场景模拟程序,模拟每一个个体所生成的调度方案,并将模拟时所经历的时间作为该个体的适应度值。
4.3 产生新解的操作产生新解的操作是不同智能优化算法的主要区别,同时也是决定算法在优化目标问题上性能表现的根本原因。下面将分别介绍差分演化算法、粒子群算法、遗传算法和模拟退火算法产生新解的具体操作。
4.3.1 差分演化算法产生新解的策略差分演化算法通过差分变异产生变异向量,将产生的变异向量与目标向量进行二项式交叉变成试验向量,最后从目标向量和试验向量中选择最优的向量作为下一代演化的目标向量。变异向量v、试验向量u的产生如式(6) 、(7) 所示。
| $ {\boldsymbol{v}}_{i,t+1}={\boldsymbol{x}}_{{r}_{1},t}+F({\boldsymbol{x}}_{{r}_{2},t}-{\boldsymbol{x}}_{{r}_{3},t}) $ | (6) |
| $ {{\boldsymbol{u}}_{{ji}{,}{t+1}}}=\left\{\begin{array}{cc}{\boldsymbol{v}}_{ji,t+1},& \mathrm{r}\mathrm{a}\mathrm{n}\mathrm{d}\left(\right) < R\\ {\boldsymbol{x}}_{ji,t+1},& \mathrm{r}\mathrm{a}\mathrm{n}\mathrm{d}\left(\right) \ge R\end{array}\right. $ | (7) |
| $ (i = 1,2,\cdots,{Z_{\text{p}}};j = 1,2,\cdots,{Z_{\text{d}}}) $ |
式中:随机选择的序号
粒子群算法通过更新粒子的位置状态作为新的解。粒子位置状态更新主要分为两步,首先更新粒子的速度向量,具体的更新方式如式(8) 所示。
| $ \begin{split} {{\boldsymbol{v}}_i}(t + 1) = &w{{\boldsymbol{v}}_i}(t) + {c_1}{r_1}({{\boldsymbol{p}}_i}(t) - {{\boldsymbol{x}}_i}(t) + \\ &{c_2}{r_2}({\boldsymbol{g}}(t) - {{\boldsymbol{x}}_i}(t) ) ) \end{split} $ | (8) |
式中:
然后根据速度向量更新粒子的位置向量,具体的更新方式如式(9) 所示。
| $ {\boldsymbol{x}}_{i}(t+1) ={\boldsymbol{x}}_{i}\left(t\right) +{\boldsymbol{v}}_{i}(t+1) $ | (9) |
在更新粒子速度向量和位置向量的过程中,均会对速度向量和位置向量进行越界处理,即若发生越界,则随机产生一个符合取值范围的值替代。
4.3.3 遗传算法产生新解的策略遗传算法通过交叉、变异和轮盘赌选择产生新解。其中交叉操作是根据选中的成对个体,在给定的交叉概率下,对满足交叉概率的位置进行交换。变异操作是在给定的变异概率下,对满足变异概率的位置,根据取值范围重新生成该位置上的值,文中遗传算法交叉概率取值为0.8,变异概率取值为0.1。轮盘赌选择是根据种群中每个个体的适应度值,计算出每个个体被选为下一代个体的概率,其中适应度越好的个体被选中的概率越高,最后以轮盘赌选择的方式随机选择并将选择到的个体作为下一代种群中的个体。
4.3.4 模拟退火算法产生新解的策略模拟退火算法是通过从解的领域中搜索出M次候选解,然后通过Metropolis抽样准则选择一个解作为新解。文中初始温度取值为100,温度衰减因子取值为0.998,领域搜索的步长为0.05,领域搜索的次数M为50。
5 案例研究 5.1 协作治疗病人场景(A)协作治疗病人案例场景如图7所示。图中包含8名一类病人,8名二类病人,2名医生以及4名护士。医生和护士需要协作为病人提供医疗服务。初始时,所有病人的默认起点为站点2、所有医生的默认起点为服务7站点、所有护士的默认起点为服务3站点。

|
图 7 协作治疗病人场景图 Figure 7 Scene diagram of patients in collaborative treatment |
一类病人需要进行6项医疗服务,分别要到站点1~6进行;二类病人也同样需要进行6项医疗服务,分别要到站点1~5和站点7进行;医生需要提供3项医疗服务;护士需要提供5项医疗服务。当病人到达站点3或站点4或站点5准备接受医疗服务时,必须要求存在一名护士为其服务,即当病人到达站点3进行医疗服务与护士到达服务3站点提供医疗服务必须同时发生。同理当病人准备接受站点1的医疗服务时,必须要求存在一名医生提供该项医疗服务,即病人到达站点1开始接受医疗服务与医生到达服务1站点开始提供医疗服务必须同时发生。当病人准备接受站点6或站点7的医疗服务时,必须要求存在一名医生和护士共同为其提供医疗服务,即病人到达站点6或站点7准备接受医疗服务,与医生到达服务6站点或服务7站点、护士到达服务6站点或服务7站点提供医疗服务必须同时发生。
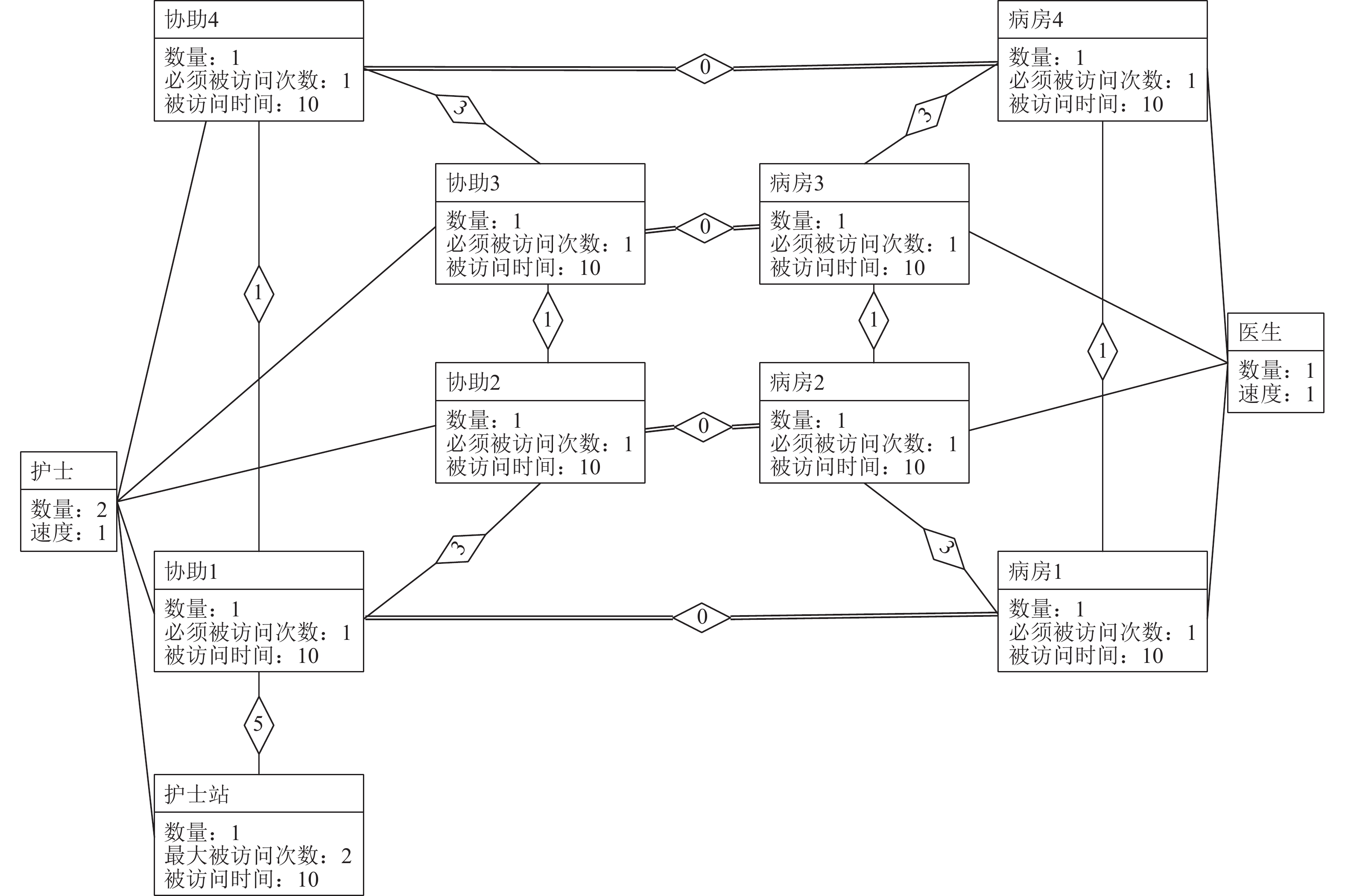
5.2 医生探查病房场景(B)医生探查病房案例场景如图8所示。图中有1名医生和2名护士需要一起去4个病房中查看病人身体状况,在图中表示为医生访问病房1~4,护士访问协助1~4站点。而护士除了在陪同医生探查病房外,还需要在护士站处理一些事务,在图中表示为护士访问护士站。初始时,医生的默认起点为病房2,护士的默认起点为护士站。
|
图 8 医生探查病房场景图 Figure 8 Scene diagram of doctor exploring ward |
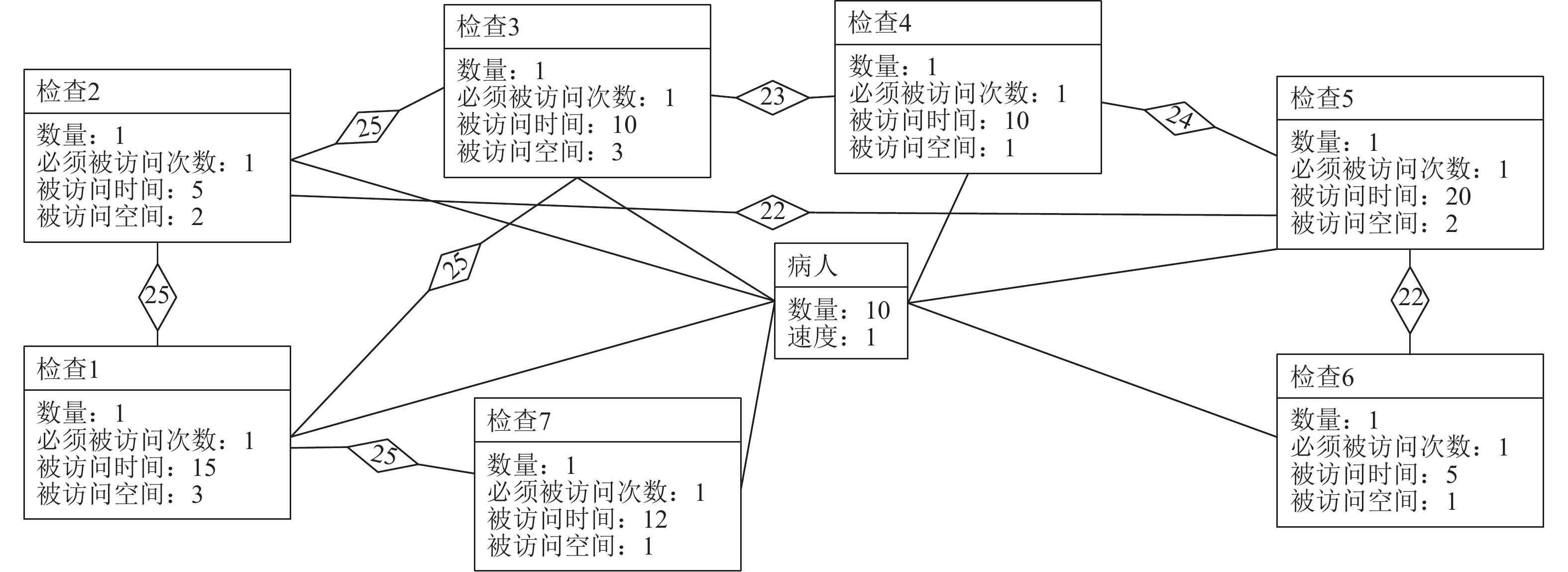
病人体检案例场景如图9所示。图中有10名病人分别需要参加7项体检项目,在图中表示为病人访问检查1~7站点。
|
图 9 病人体检场景图 Figure 9 Scene diagram of patient physical examinations |
实验参数如表1所示,算法中的种群大小为100,种群中每个个体的维度为12,个体中每一维分量的取值上界和下界分别为1和−1,协作治疗病人场景累计评价106次结束运行,医生探查病房场景和病人体检场景累计评价105次结束运行。文中协作治疗病人场景、医生探查病房场景和病人体检场景分别使用A、B、C表示。
| 表 1 实验参数 Table 1 Experimental parameters |
针对于不同规模协作治疗病人场景、医生查房场景和病人体检场景,对比基于随机、最短距离、最大空闲空间和决策模型4种调度算法独立测试30次的平均调度用时如表2所示。其中,平均调度用时旁边括号中的数值表示独立重复运行30次可行解的个数;random、minDistance、maxFreeSpace分别表示基于随机、基于最短距离、基于最大空闲空间;DM_GA、DM_PSO、DM_SA、DM_DE分别表示使用遗传算法(Genetic Algorithm,GA) 、粒子群算法(Particle Swarm Optimization, PSO) 、模拟退火算法(Simulated Annealing,SA) 、差分演化(Differential Evolution Algorithm,DE) 所优化得出的决策模型。
| 表 2 独立测试30次平均调度用时结果 Table 2 Average results of repeating 30 times based ondifferent algorithms |
从能否找到可行解的角度上分析,基于random、minDistance、maxFreeSpace的调度策略在部分场景中无法找到或鲜能找到可行解。相比之下,基于决策模型的调度策略在所有场景中都能找到可行解。从平均调度用时结果的角度分析,基于决策模型的调度策略整体明显优于基于random、minDistance、maxFreeSpace的调度策略。在B1、B2、B3、C1、C1、C3场景中,使用GA、DE和PSO算法优化的决策模型的性能和稳定性基本一致,而A1、A2、A3场景中DE算法优化的决策模型的性能和稳定性明显优于GA、PSO、SA算法。
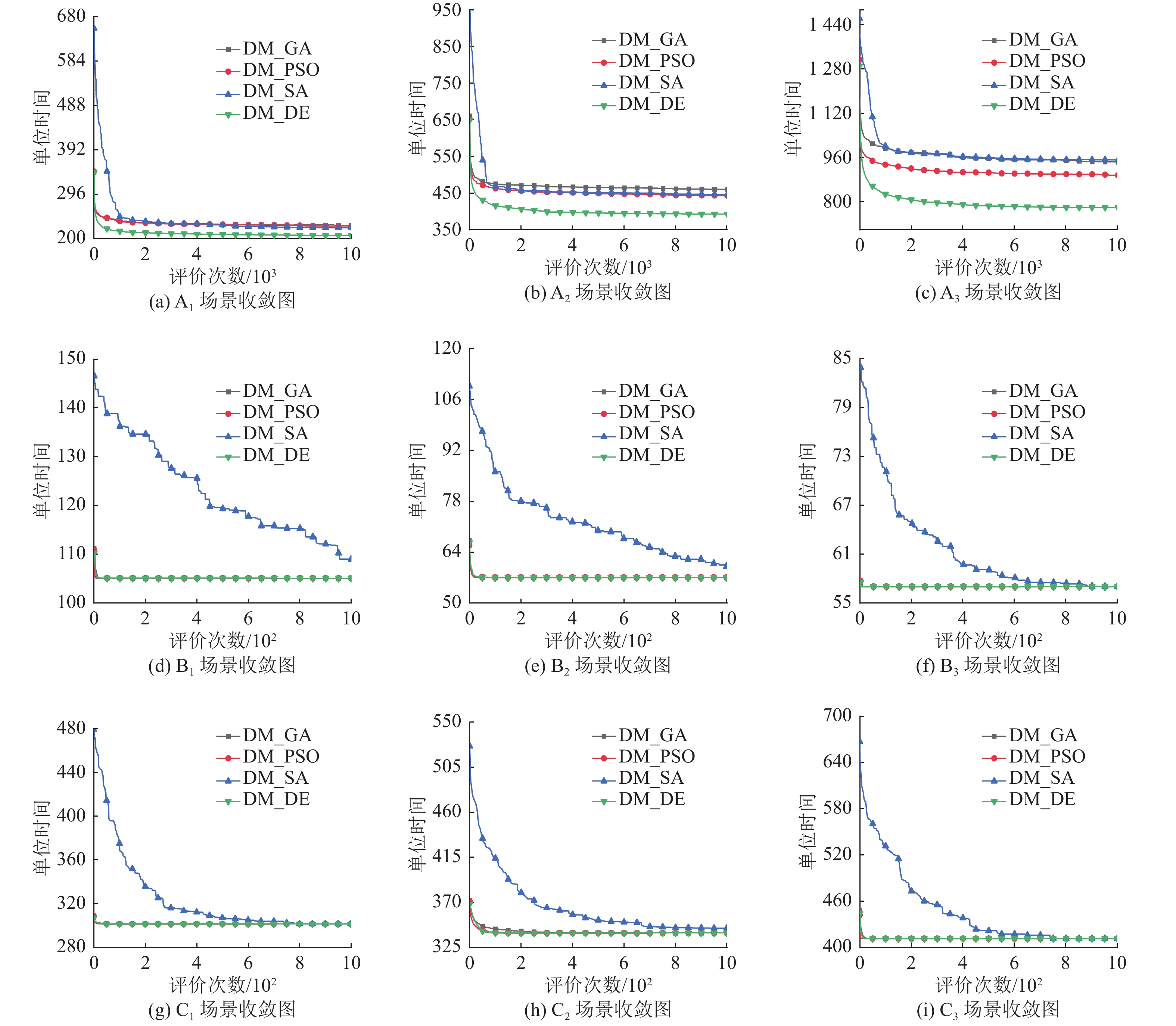
6.3 收敛性分析在不同场景的不同规模下独立测试GA、PSO、SA、DE优化决策模型30次的平均收敛结果如图10所示。在A1、A2、A3、B1、B2、B3、C1、C2、C3场景中,在优化决策模型时,基于GA、PSO和DE算法优化的决策模型整体上都有着较快的收敛速度且收敛速度基本一致。相比之下,SA算法收敛速度相对较慢,经分析由于SA算法局部搜索的特性,初始生成的解的附近往往难以找到可行解,需要经过不断的迭代才能找到可行的决策模型,故而影响了其收敛速度。在A1、A2、A3场景中,DE算法相较于其他智能优化算法有着更快的收敛速度。
|
图 10 独立测试30次平均收敛图 Figure 10 Average convergence curves of different algorithms with running 30 times |
独立测试30次最优调度用时结果如表3所示。其中,括号内中的数值表示在30次独立测试中得到该最优调度的次数。根据表3中的结果可以看出,基于决策模型调度策略所找到的最优调度结果均明显优于random、minDistance、maxFreeSpace调度策略。对比GA、PSO、SA、DE这4种算法优化得出的决策模型,从所找到最优决策模型的角度分析,在B1、B2、C1、C2、C3场景下GA、PSO、SA、DE算法所优化得出的决策模型性能基本一致。在B3场景下即有足够的护士参与调度时SA算法才能找到最优的调度结果。在A1、A2、A3场景中,只有DE算法优化得出的决策模型表现最优。综合性能、稳定性、收敛性和最优结果分析,DE算法优化的决策模型整体表现最优。
| 表 3 独立测试30次最优调度用时结果 Table 3 The optimal time taken of different algorithms with running 30 times |
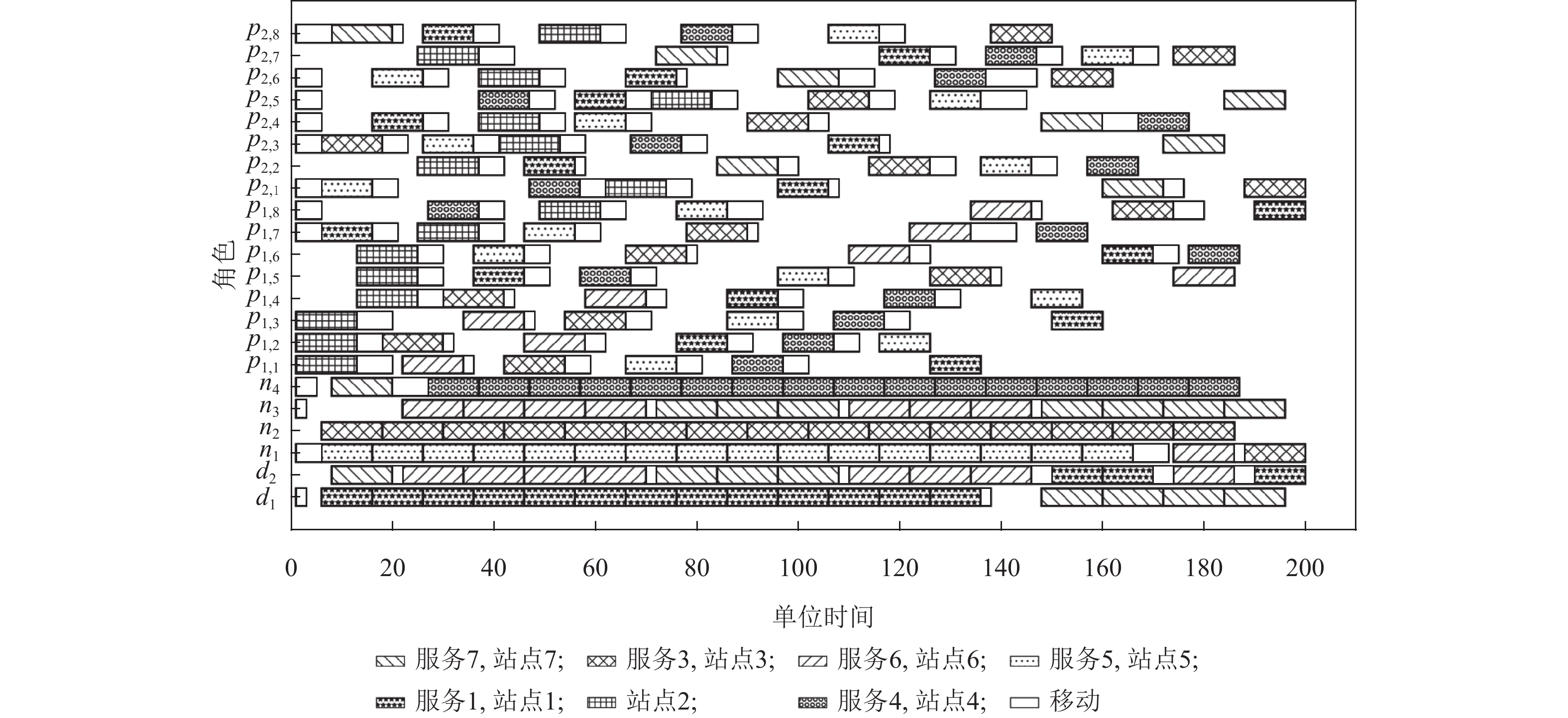
在协作治疗病人场景中,使用最优的决策模型的调度结果如图11所示。其中,纵坐标pi.j为第i类的j号病人,ni为第i号护士,di为第i号医生;使用空白填充的矩形区域表示角色正在移动;对于病人角色而言,使用五角星填充的矩形区域表示正在访问站点1,使用十字填充的矩形区域表示正在访问站点2,使用乘号填充的矩形区域表示正在访问站点3,使用空心圆填充的区域表示正在访问站点4,使用点填充的矩形区域表示正在访问站点5,使用反斜杠填充的矩形区域表示正在访问站点6,使用斜杠填充的矩形区域表示正在访问站点7;对于医生而言,使用反斜杠填充的矩形区域表示正在访问服务6站点,使用斜杠填充的矩形区域表示正在访问服务7站点,使用五角星填充的矩形区域表示正在访问服务1站点;对于护士而言,使用乘号填充的矩形区域表示正在访问服务3站点,使用空心圆填充的区域表示正在访问服务4站点,使用点填充的矩形区域表示正在访问服务5站点,使用反斜杠填充的矩形区域表示正在访问服务6站点,使用斜杠填充的矩形区域表示正在访问服务7站点。
|
图 11 最优决策模型在协作治疗病人场景调度图 Figure 11 Scheduling diagrams of the optimal decision-making model in collaborative treatment |
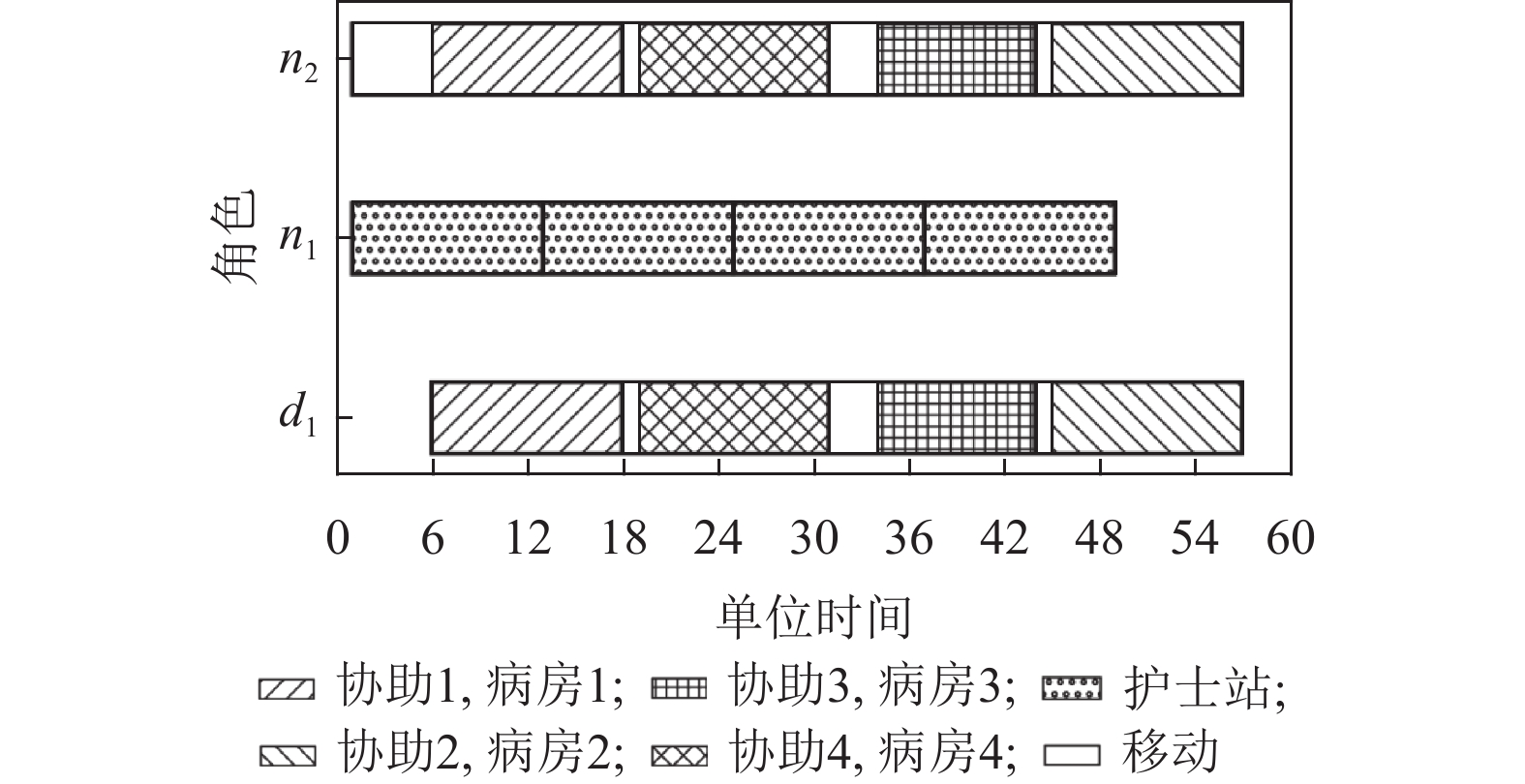
在医生探查病房场景中,使用最优的决策模型的调度结果如图12所示。其中,纵坐标ni为第i号护士,di为第i号医生;使用空白填充的矩形区域表示角色正在移动;对于护士而言,使用空心圆填充的矩形区域表示访问护士站,使用斜杠填充的矩形区域表示正在访问协助1站点,使用反斜杠填充的矩形区域表示正在访问协助2站点,使用十字填充的矩形区域表示正在访问协助3站点,使用乘号填充的矩形区域表示正在访问协助4站点;对于医生而言,使用斜杠填充的矩形区域表示正在访问病房1,使用反斜杠填充的矩形区域表示正在访问病房2,使用十字填充的矩形区域表示正在访问病房3,使用乘号填充的矩形区域表示正在访问病房4。
|
图 12 最优决策模型在医生探查病房场景调度图 Figure 12 Scheduling diagrams of the optimal decision-making model in patient physical examinations |
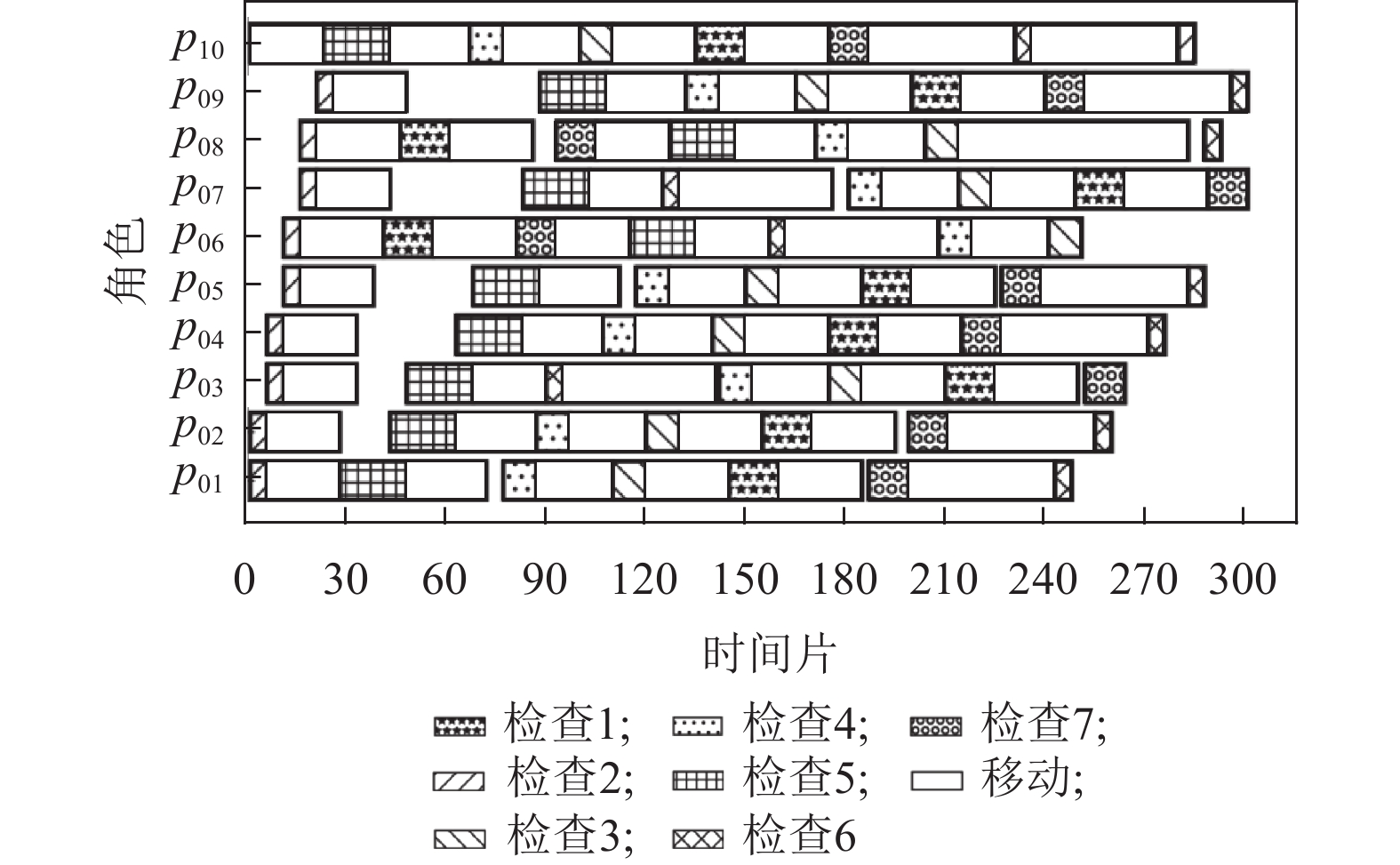
在病人体检场景中,使用最优的决策模型的调度结果如图13所示。其中,纵坐标pi为第i号病人;使用五角星填充的矩形区域表示病人正在访问检查1;使用斜杠填充的矩形区域表示病人正在访问检查2;使用反斜杠填充的区域表示病人正在访问检查3;使用点填充的矩形区域表示病人正在访问检查4;使用十字填充的矩形区域表示病人正在访问检查5;使用五角星填充的矩形区域表示病人正在访问检查6;使用空心圆填充的矩形区域表示病人正在访问检查7;使用空白填充的矩形区域表示病人正在移动。
|
图 13 最优决策模型在病人体检场景调度图 Figure 13 Scheduling diagrams of the optimal decision-making model in patient physical examinations |
协作治疗调度是一个应用性很强的研究,它包含了医生、护士和患者三者的联合调度。随着医疗改革的不断推进,以及人们对于医疗服务的需求逐渐增加,如何在有限的医疗资源下提高医疗服务质量和医院管理水平成为医院管理者关注的重要问题。文中将医生和护士为患者提供医疗服务,将提供医疗服务的场景定义成一个协作治疗调度问题,提出了解决该问题决策模型以及决策模型的推荐的智能优化算法。
| [1] |
韩通, 徐梅. 手术调度的研究进展[J].
中国护理管理, 2021, 21(10): 1587-1589.
HAN T, XU M. Research progress of operation scheduling[J]. Chinese Nursing Management, 2021, 21(10): 1587-1589. DOI: 10.3969/j.issn.1672-1756.2021.10.031. |
| [2] |
叶燕, 高彪, 方丹, 等. 信息化转运交接对手术室工作效率影响[J].
解放军医院管理杂志, 2019, 26(7): 651-654.
YE Y, GAO B, FANG D, et al. Effect of informatization transfer and handover on efficiency of the operating room[J]. Hospital Administration Journal of Chinese People's Liberation Army, 2019, 26(7): 651-654. DOI: 10.16770/j.cnki.1008-9985.2019.07.015. |
| [3] |
张海洋, 王英丽, 徐梅. 基于重点环节质量改进的手术进程发布系统的应用[J].
中国护理管理, 2018, 18(8): 1086-1089.
ZHANG H Y, WANG Y L, XU M. The practice of the improved surgical process publishing system[J]. Chinese Nursing Management, 2018, 18(8): 1086-1089. DOI: 10.3969/j.issn.1672-1756.2018.08.017. |
| [4] |
张海洋, 徐梅, 李莉. 手术室接送患者信息系统的设计与应用[J].
中国护理管理, 2019, 19(5): 740-743.
ZHANG H Y, XU M, LI L. Design and evaluation of patient transport information system in operating room[J]. Chinese Nursing Management, 2019, 19(5): 740-743. DOI: 10.3969/j.issn.1672-1756.2019.05.020. |
| [5] |
ANVARYAZDI S F, VENKATACHALAM S, CHINNAM R B. Appointment scheduling at outpatient clinics using two-stage stochastic programming approach[J]. IEEE Access, 2020, 8: 175297-175305.
|
| [6] |
SONG J, BAI Y, WEN J. Optimal appointment rule design in an outpatient department[J].
IEEE Transactions on Automation Science and Engineering, 2019, 16(1): 100-114.
DOI: 10.1109/TASE.2018.2794335. |
| [7] |
XIE X, FAN Z, ZHONG X. Appointment capacity planning with overbooking for outpatient clinics with patient no-shows[J].
IEEE Transactions on Automation Science and Engineering, 2022, 19(2): 864-883.
DOI: 10.1109/TASE.2021.3060567. |
| [8] |
ELKHATTABI S, CHRAIBI A, BENABBOU R. MAS for planning and scheduling of the surgical operations under uncertainties using taboo search[C]//2018 IEEE International Conference on Technology Management, Operations and Decisions (ICTMOD) . Marrakech: IEEE, 2018. 303-308.
|
| [9] |
WANG Y, ZHANG G, ZHANG L, et al. A column-generation based approach for integrating surgeon and surgery scheduling[J]. IEEE Access, 2018, 6: 41578-41589.
|
| [10] |
PANG B, XIE X, SONG Y, et al. Surgery scheduling under case cancellation and surgery duration uncertainty[J].
IEEE Transactions on Automation Science and Engineering, 2019, 16(1): 74-86.
DOI: 10.1109/TASE.2018.2834486. |
| [11] |
NGOO C M, GOH S L, LIKOH J. Grey wolf optimizer for the nurse rostering problem[C]//2022 IEEE 13th Control and System Graduate Research Colloquium (ICSGRC) . Shah Alam: IEEE, 2022. 11-15.
|
| [12] |
王陟, 李雁妮. 一种智能高效的并行护士排班算法[J].
西安电子科技大学学报, 2019, 46(2): 47-53.
WANG Z, LI Y N. Algorithm for intelligent and efficient parallel rostering of nurses[J]. Journal of Xidian University, 2019, 46(2): 47-53. DOI: 10.19665/j.issn1001-2400.2019.02.009. |
| [13] |
包子阳. 智能优化算法及其MATLAB实例[M]. 北京: 电子工业出版社, 2018: 7-175.
|
| [14] |
LI Z, TAM V, YEUNG L K. An adaptive multi-population optimization algorithm for global continuous optimization[J]. IEEE Access, 2021, 9: 19960-19989.
|
| [15] |
YAKOVLEV S, KARTASHOV O, YAROVAYA O. On class of genetic algorithms in optimization problems on combinatorial configurations[C]//2018 IEEE 13th International Scientific and Technical Conference on Computer Sciences and Information Technologies (CSIT) . Lviv: IEEE, 2018. 374-377.
|
| [16] |
MAHDI M A, DAWOOD L M. A grey wolf optimization algorithm for integrating process planning and scheduling problem[C]//2022 International Congress on Human-Computer Interaction, Optimization and Robotic Applications (HORA) . Ankara: IEEE, 2022. 1-5.
|
| [17] |
陈蒙蒙, 方振红, 温伟伟, 等. 基于多约束粒子群算法的护士智能排班模式及效果研究[J].
医院管理论坛, 2021, 38(10): 35-38.
CHEN M M, FANG Z H, WEN W W, et al. Research on intelligent nurse scheduling mode and effect based on multi-constraint particle swarm algorithm[J]. Hospital Management Forum, 2021, 38(10): 35-38. DOI: 10.3969/j.issn.1671-9069.2021.10.010. |
| [18] |
RURIFANDHO A, RENALDI F, SANTIKARAMA I. Doctors dynamic scheduling for outpatient, inpatient, and surgery using genetic algorithm[C]//2022 International Conference on Science and Technology (ICOSTECH) . Batam City: IEEE, 2022. 1-8.
|
| [19] |
APELDOORN D. AbstractSwarm – a generic graphical modeling language for multi-agent systems[C]//German Conference on Multiagent System Technologies. Berlin: Springer, 2013. 180-192.
|
 2023, Vol. 40
2023, Vol. 40

