2. 广东工业大学 计算机学院,广东 广州 510006
2. School of Computer Science and Technology, Guangdong University of Technology, Guangzhou 510006, China
衡量2个对象之间的距离和相似度在数据挖掘[1]和机器学习[2]任务中起着重要作用,它往往只是算法[3]嵌入式的一个小步骤,却能对整个学习算法效果产生巨大影响。所以,确定一个合适的距离度量是数据挖掘和机器学习的重要研究内容。
当对象数据是数值数据,常用闵可夫斯基距离、欧氏距离和马氏距离[4]衡量对象的距离。但当对象数据是分类数据[5],它的属性值是类别属性而不是数字,因此数值数据的距离度量不能在分类数据上使用。为了解决这个问题,最简单的方法就是将分类数据转化成数值数据,然后运用数值数据的距离度量。
然而将分类数据转化成数值数据的方法会丢失分类数据原有的数据分布和结构特点,因此很多学者利用分类数据的特点来衡量分类数据的距离和相似度。文献[6]提出汉明距离(Hamming Distance Metric, HDM) ,它给相同属性值距离定义为0,不同属性值距离定义为1。这种简单的方式不仅忽略了属性值的分布特征,而且平等地对待每一个属性。所以越来越多的学者从分类数据的分布特征和属性之间关系定义分类数据的距离度量。如Ahmad等[7]提出了一种无监督分类数据距离度量(Ahmad’s Distance Metric, ADM) ,Ienco等[8-9]提出基于上下文的距离(Context-Based Distance Metric, CBDM) ,这些度量在定义一个属性的2个值之间的距离时利用了相关属性的数据信息,所以它们都不适用于独立属性数据集。Jia等[10]利用目标属性的频率信息提出了一个新的距离度量(Jia’s Distance Metric, JDM),Chen等[11]提出了一个概率分布函数来衡量属性的距离,Jian等[12]基于分类数据的内在异构关系,针对非独立同分布数据提出了分类数据耦合相似度量(Coupled Metric Similarity, CMS) ,但是,这些度量方法都没有区分分类数据的有序属性[13-14],而是将有序属性当作标称属性来对待。
针对这一问题,有学者提出了区分有序属性的分类数据距离度量方法。其中最简单的方式是在汉明距离的基础上用连续的整数来编码有序属性的等级结构,并用数字之间的距离除以最大整数与最小整数差的商来衡量2个有序值的距离[15]。但这样的定义方式同样忽略了属性之间的影响。近几年来,既区分有序属性又考虑属性之间关系的分类数据距离度量方法被提出[16-18]。其中文献[16]提出了一种基于熵的距离度量(Entropy-Based Distance Metric, EBDM) ,EBDM利用了信息熵的和来定义同一个属性中的2个属性值之间的距离;文献[17]提出了一种统一的分类数据距离度量(Unified Distance Metric, UDM) ,UDM在定义同一个属性中的2个属性值之间的距离不仅考虑了这个属性的影响,还考虑了其他属性的影响。EBDM和UDM都考虑了有序属性的顺序结构关系,并提出了有序属性和标称属性统一的分类数据距离度量。但是这2种度量方法都利用信息熵来定义分类数据距离,而信息熵是从数据的概率分布中得到的,它依赖于数据的概率分布,间接地描述了分类数据的特征,并没有直接从分类数据的数据特征中定义距离。
因此针对这个问题,本文提出了一种基于图结构的分类数据距离度量(New Distance Metric, NewDM) 。它利用有序属性和标称属性的图结构,定义了2个概率分布列之间的距离,并利用平均信息熵占总体平均信息熵的比值来衡量属性的重要性。NewDM同时兼备了概率和信息熵的优点,使异构属性距离的度量更准确且更具可比性。NewDM是无参数的,在6个数据集上的实验结果验证了NewDM的度量性能优于其他度量方法。同时本文总结了区分有序属性的分类数据距离定义的基本框架公式,使分类数据的距离定义更加简单明了。
1 相关工作 1.1 分类属性的图结构分类数据按属性划分为有序属性和标称属性,有序属性和标称属性的相同点是它们都由类别属性值构成,不同点是有序属性的属性值之间具有等级关系,例如学生成绩的属性值:优秀、良好、及格、不及格。这些属性值都是由类别属性构成,但是很明显它们之间还具有等级顺序关系,所以有序属性也可以看作是特殊的标称属性。
在数学领域中,图论[19]是一个以图为研究对象的重要分支。其中图论中的图是由若干给定的点及连接两点的线所构成的图形,这种图形通常用来描述某些事物之间的某种特定关系,用点代表事物,用连接两点的线表示相应两个事物间具有这种关系。由于有序属性中的属性值之间具有等级关系,当有序属性的属性值按等级从高到低排列并用线将每一个属性值与邻近的属性值连接,同时将属性值当作是顶点,则有序属性的图结构是单链状的树[20]。对于标称属性,标称属性值之间没有等级关系,所以每两个属性之间都可以连接起来,因此标称属性值之间的图结构是完全图[21]。若有序属性的属性值按等级从高到低排列分别为
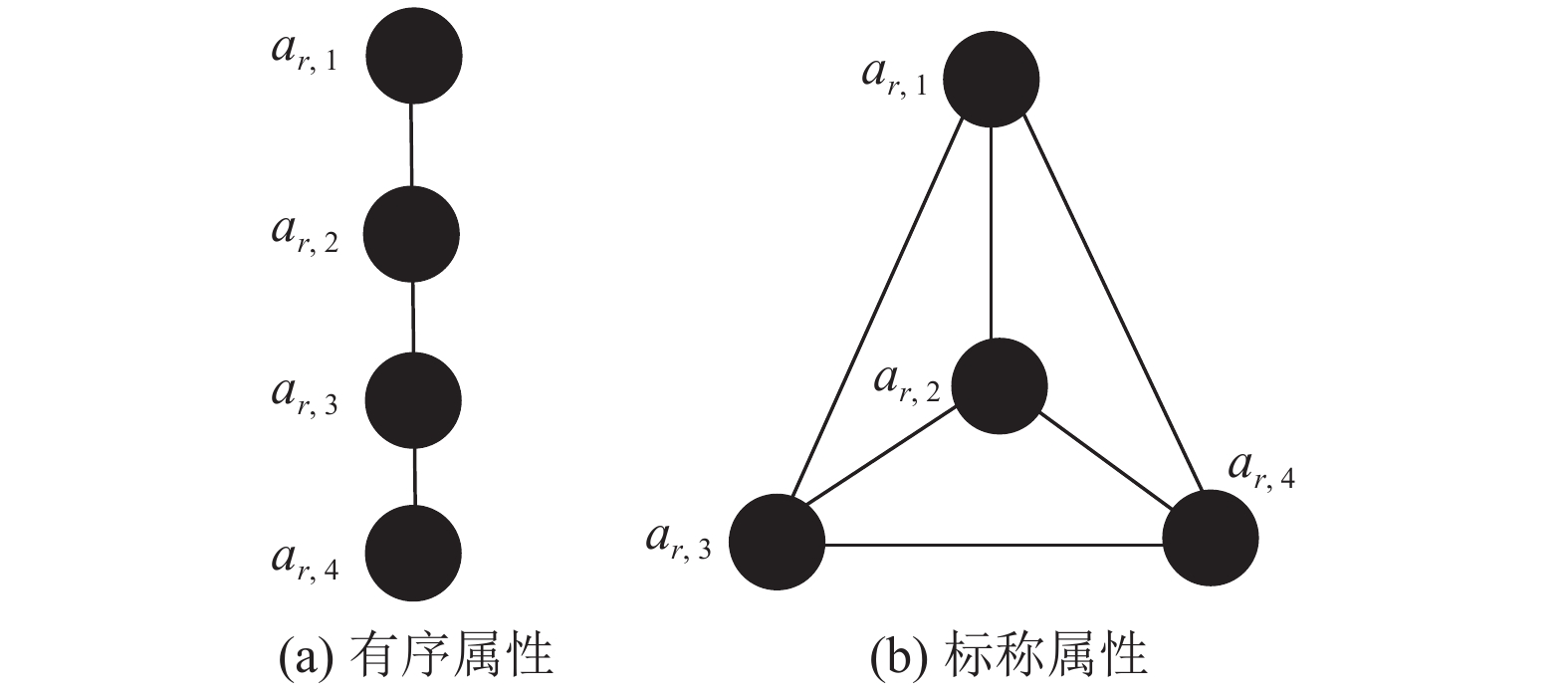
|
图 1 图结构
Figure 1 Graph structure
|
目前区分有序属性的分类距离度量的方式可分成2种。第1种,仅利用有序属性之间具有等级结构的思路出发,在原有不区分有序属性的分类距离度量中单独定义有序属性值之间的距离。例如文献[15]中将有序属性编码数值后,用数值数据的方法来定义有序属性之间的距离。第2种,利用有序属性是特殊的标称属性的思路,在原有不区分有序属性的分类距离度量中将有序属性的结构特点融入到距离定义中加以区分[16-18]。
对于这2种区分有序属性的思路,第1种单独区分的方式,容易造成标称属性和有序属性尺度之间的差异,不能很好地揭示分类数据的数据特征。第2种区分的方式既考虑到有序属性和标称属性之间的共同特性,又考虑到这2种不同属性之间的差异,所以第2种区分的方式会优于第1种。由于文献[16-18]中区分有序属性的思路大致相同,所以这些度量方法在定义分类数据任意属性下2个属性值之间距离的基本框架公式也大致相同。不同的是它们量化2个属性值之间距离的方法和属性之间权重的定义。
因此将同一个属性下2个属性值之间距离的基本框架公式进行梳理。先给定第
| $ D(m,h) =\left\{\begin{array}{l}w{\displaystyle \sum _{s=\mathrm{min}(m,h) }^{\mathrm{max}(m,h) -1}\varphi (s,s+1) ,\;\;当{r}为有序属性}\\ w\varphi (m,h) ,\;\;当{r}为标称属性\end{array} \right.$ | (1) |
给定分类数据
对任意2个数据对象
| $ {\text{Dist}}\left( {{{\boldsymbol{x}}_i},{{\boldsymbol{x}}_j}} \right) = \sqrt {{{\sum\nolimits_{r = 1}^d {{\text{dist}}( {{x_{ir}},{x_{jr}}} ) } }^2}} $ | (2) |
子距离
| $ {\text{dist}}( {{x_{ir}},{x_{jr}}} ) = {\text{dist}}( {{a_{r,t}},{a_{r,h}}} ) $ | (3) |
文献[17]中提出了
在
首先将
定义1 当
当2个分布列分别为
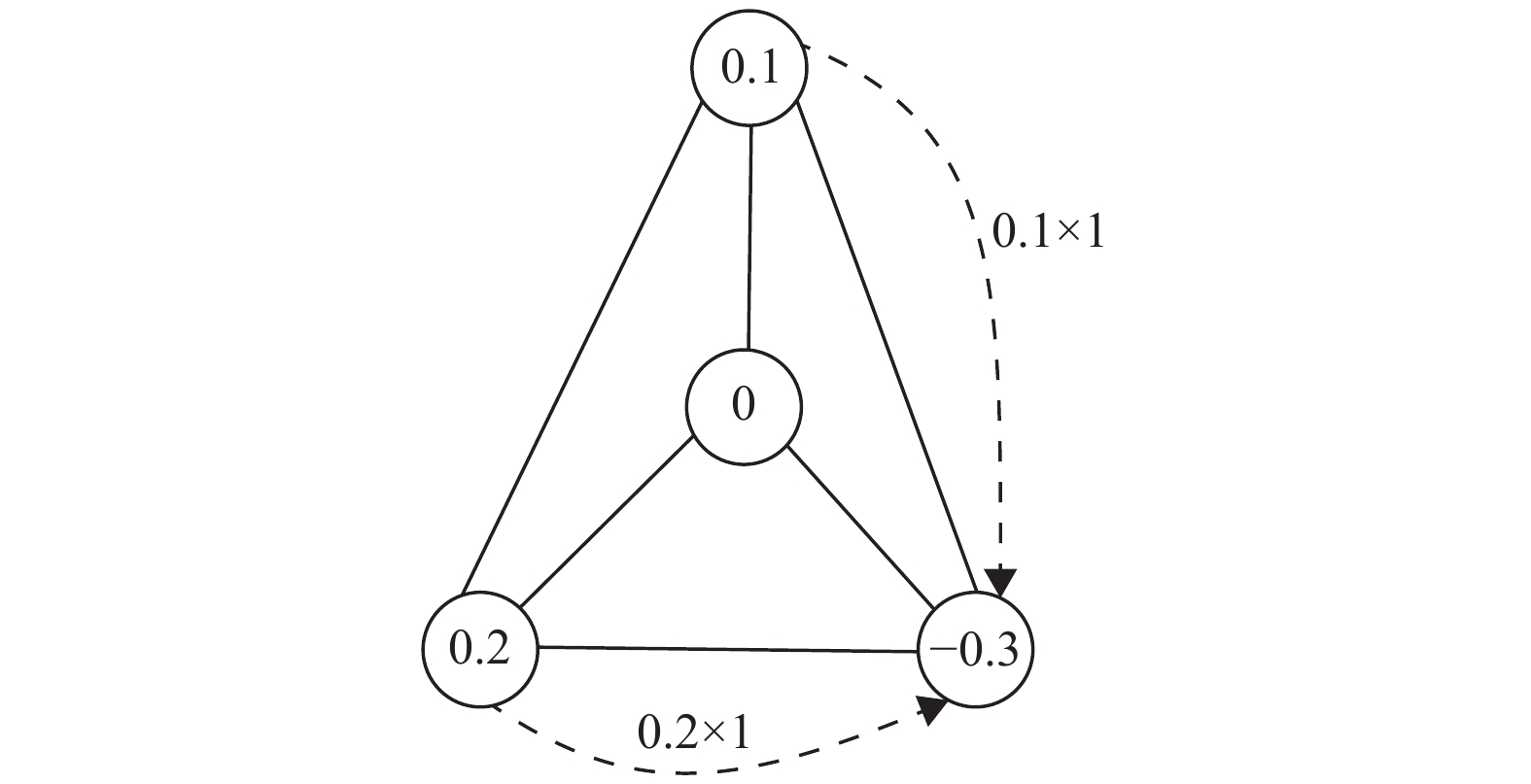
|
图 2 标称属性转化过程 Figure 2 The process of nominal attribute conversion |
定义2 当
当
也就是说当
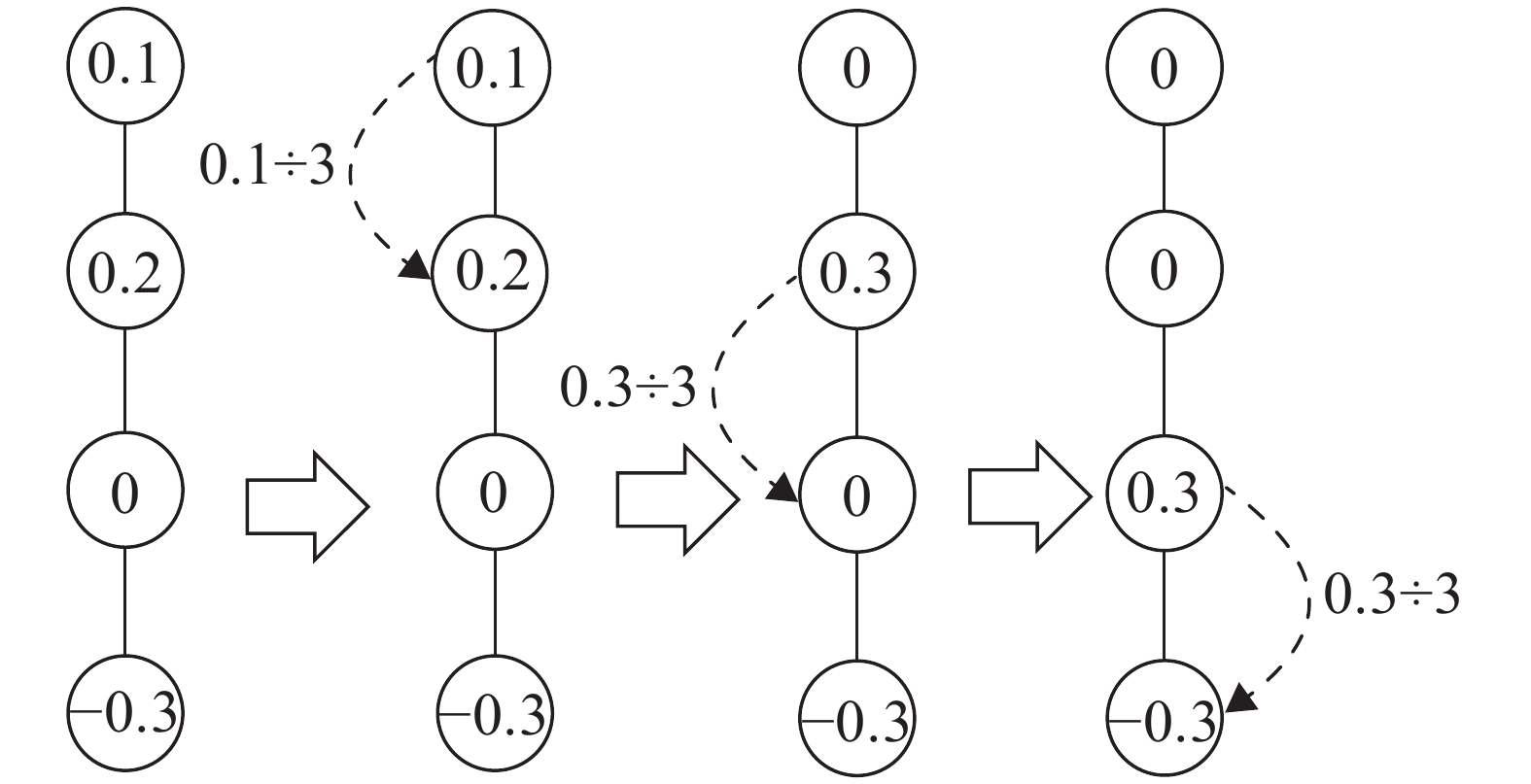
|
图 3 有序属性转化过程 Figure 3 The process of ordered attribute conversion |
综上所述,
| $ \begin{array}{l}{\psi }_{r,m}\left({a}_{r,t},{a}_{r,h}\right) \text=\\ \left\{ \begin{array}{l}\dfrac{1}{{{v^m} - 1}}{{\displaystyle \sum _{i=1}^{{v}^{m}-1}\left|{\displaystyle \sum _{w=1}^{i}\left({p}_{w}^{{a}_{r,t}}-{p}_{w}^{{a}_{r,h}}\right) }\right|}}\text{,} 当{a}_{r,t} \ne {a}_{r,h},m \le {d}_{{\rm{ord}}}\\ \;0,当{a}_{r,t}={a}_{r,h}\\\dfrac{1}{{2}} {{\displaystyle \sum _{i=1}^{{v}^{m}}\left|{p}_{i}^{a{}_{r,t}}-{p}_{i}^{a{}_{r,h}}\right|}}\text{,}当{a}_{r,t}\ne {a}_{r,h},m > {d}_{{\rm{ord}}}\end{array} \right.\end{array}$ | (4) |
式中:
在同一个数据集中,每一个属性的重要程度是不一样的,信息理论用信息熵来描述数据的不确定性,不确定越大代表着数据的信息量越大,信息量越大也代表着这个数据是更重要的,因此可用信息熵来量化每个属性的重要程度。
若属性
| $ W({A_r}) = \sum\limits_{s = 1}^{{v^r}} { - {p_s}\ln {p_s}} $ | (5) |
但是,一个属性的属性值的类别数量越多,信息熵
定义3 若
| $ H\left( {{A_r}} \right) =\frac{1}{{{ - \ln ({1}/{{{v^r}}})}}}{{\displaystyle\sum\limits_{s = 1}^{{v^r}} { - {p_s}\ln {p_s}} }} $ | (6) |
式中:
所以属性
| $ {w_r} = {{H\left( {{A_r}} \right) }}\Bigg/{{\displaystyle\sum\limits_{{{i}} = 1}^d {H\left( {{A_i}} \right) } }} $ | (7) |
本文利用有序属性和标称属性的图结构特征定义了
| $ \text{dist}({a}_{r,t},{a}_{r,h} ) = \left\{ \begin{array}{l}{w}_{r}\displaystyle \sum _{s=\mathrm{min}(t,h) }^{\mathrm{max}(t,h) -1}{\displaystyle \sum _{m=1}^{d}{\psi }_{r,m}({a}_{r,s},{a}_{r,s+1} ) , 当t \ne h且r \leqslant {d}_{{\rm{ord}}}}\\ {w}_{r}{\displaystyle \sum _{m=1}^{d}{\psi }_{r,m}({a}_{r,t},{a}_{r,h}),当t\ne h且r > {d}_{{\rm{ord}}}}\\ 0,当t=h\end{array}\right. $ | (8) |
本文提出的NewDM计算步骤详见算法1。
算法1 NewDM
输入:数据集
输出:
1.for
2. 根据式(6)和(7)计算
3.end for
4.for
5. for
6. 根据式(4)计算
7. end for
8. 根据式(8)计算
9.end for
10.根据式(2)计算
首先利用式(6)、(7)计算出每个属性的权重
为了验证NewDM在分类数据中的有效性,使用6个公开的分类数据集,利用3种聚类评价指标,设计2个实验来验证NewDM的有效性。
3.1 实验设置 3.1.1 数据集说明本文使用6个分类数据集来进行实验,这6个数据集都来自美国加州大学UCI机器学习数据库,它们分别是Qualitative、Car、Zoo、Solar、Hayes、Student。其中 Qualitative、Car是只有有序属性的分类数据,Zoo、Solar 是只有标称属性的分类数据,Hayes、Student是既有有序属性又有标称属性的混合型分类数据,所有数据集中缺失属性值的数据都被忽略,具体数据集信息如表1所示。其中
| 表 1 数据集属性说明 Table 1 Statistics of the 6 data sets |
为了衡量不同分类数据距离度量的聚类效果,采用3种评价指标,分别是聚类精度(Clustering Accuracy, CA)[22],调整的兰德指数(Adjusted Rand Index, ARI)[23]和归一化信息(Normalized Mutual Information, NMI)[24]。
CA为分类正确的数据对象的百分比,表达式为
| $ {\text{CA}} =\frac{1}{n} {{\displaystyle\sum\nolimits_{i = 1}^n {\delta ( {{c_i},{\text{map}}\left( {{l_i}} \right) } ) } } } $ |
式中:
ARI比RI更有区分度,表达式为
| $ {\text{ARI}} = {{\left( {{\text{RI}} - E\left( {{\text{RI}}} \right) } \right) } \mathord{\left/ {\vphantom {{\left( {{\text{RI}} - E\left( {{\text{RI}}} \right) } \right) } {\left( {{\text{max}}\left( {{\text{RI}}} \right) - E\left( {{\text{RI}}} \right) } \right) }}} \right. } {\left( {{\text{max}}\left( {{\text{RI}}} \right) - E\left( {{\text{RI}}} \right) } \right) }}$ |
式中:
NMI从信息理论角度来衡量预测标签和真实标签的一致性,表达式为
| $ {\rm{NMI}} = \frac{{\left( {\displaystyle\sum\nolimits_{r = 1}^k {\displaystyle\sum\nolimits_{t = 1}^k {{{{c_{r,t}}\lg ( {n {c_{r,t}}} ) } \mathord{\left/ {\vphantom {{{c_{r,t}}\lg \left( {n \cdot {c_{r,t}}} \right) } {{c_r} \cdot {c_t}}}} \right. } {{c_r} {c_t}}}} } } \right) }}{{\left( {\left( {\displaystyle\sum\nolimits_{r = 1}^k {{c_r}\lg {{{c_r}} \mathord{\left/ {\vphantom {{{c_r}} N}} \right. } N}} } \right) \left( {\displaystyle\sum\nolimits_{t = 1}^k {{c_t}\lg {{{c_t}} \mathord{\left/ {\vphantom {{{c_t}} N}} \right. } N}} } \right) } \right) }} $ |
式中:
为了验证NewDM的有效性,设置了2个实验。实验1将分类数据距离度量HDM、JDM、EBDM、UDM和NewDM分别嵌入到K-Modes算法[25],比较这5种度量方法的聚类效果,来验证NewDM的有效性。其中以HDM为度量基准,JDM是未区分有序属性的度量中较为经典的一种分类数据距离度量。EBDM和UDM都是区分有序属性和标称属性的分类数据距离度量方法,所以NewDM的主要对比距离是EBDM和UDM。
实验2将NewDM嵌入到不同的分类数据聚类算法中,与原有算法的聚类效果进行比较,来验证NewDM在不同聚类算法的有效性。选择K-Modes算法作为算法基准,基于子空间的聚类算法有较好的聚类效果,所以选择文献[26]中的熵加权聚类算法(Entropy Weighting K-Means, EWKM) 和文献[27] 中的加权 OCIL聚类算法(Weighted Object-cluster Similarity metric, WOCIL) 作为经典的聚类算法。为了实验的公平,所有算法都随机选取聚类中心,其中聚类中心数从真实标签中获取,并对每个数据集运行10次后取平均值及其标准差作为最后结果,用“平均值±标准差”来表示。对实验1的结果用黑体、“ _” “
实验1的结果如表2所示。在只有有序属性的数据集Qualitative和Car中,NewDM的优势非常明显,表明了基于有序属性图结构的概率分布列距离比利用信息熵的度量方法更好地揭示和量化了有序属性数据的特征。在只有标称属性的数据集Zoo和Solar中,NewDM效果不如有序属性中显著,但在其他4种分类数据距离度量中的效果仍是最好的。它表明了在纯标称属性的分类数据中利用2个概率分布列之间的距离和利用平均信息熵信息作为权重也是可行的。在既有有序属性又有标称属性的数据集Hayes和Student中,NewDM效果仍然优于其他几种距离度量,这表明了NewDM分别利用有序属性和标称属性图结构定义的概率分布列距离,使异构属性距离的度量更加准确。综上所述,在每个数据集中,NewDM在K-Modes聚类算法中的3个指标的结果都是最好的,它验证了NewDM不仅优于不区分有序属性的距离度量,也优于区分有序属性中利用熵来定义距离的EBDM和UDM。
| 表 2 不同距离度量在K-Modes算法中实验结果 Table 2 Experimental results of different distance metrics in K-Modes algorithm |
实验2用来验证NewDM嵌入到3个不同聚类算法的有效性。表3的实验结果表明,嵌入了NewDM的聚类算法的聚类效果整体上都优于原有的聚类算法距离或相似度量,这验证了将NewDM嵌入到分类数据聚类算法中不仅可行而且可以提升聚类的效果。同时也验证了NewDM兼备了概率和信息熵的优点,使异构属性距离的度量更准确且更具可比性。
| 表 3 NewDM在不同聚类算法中的实验结果 Table 3 Experimental results of the NewDM in different clustering algorithms |
为了更好地揭示和量化分类数据中不同属性的数据特点,本文利用标称属性和有序属性的图结构定义了2种概率分布列之间的距离,并利用平均信息熵占总体平均信息熵的比值作为权重,提出了一种新的分类数据距离度量方法NewDM,通过与现有的几种分类数据距离度量方法和聚类算法进行对比,验证了NewDM的度量性能优于其他度量方法。同时本文还总结了2个属性值之间距离的基本框架公式,它为区分有序属性的分类数据距离度量提供了更加清晰的定义思路和改进方向。
| [1] |
SONG S, SUN Y, ZHANG A, et al. Enriching data imputation under similarity rule constraints[J].
IEEE Transactions on Knowledge and Data Engineering, 2020, 32(2): 275-287.
DOI: 10.1109/TKDE.2018.2883103. |
| [2] |
ALABDULMOHSIN I, CISSE M, GAO X, et al. Large margin classification with indefinite similarities[J].
Machine Learning, 2016, 103(2): 215-237.
DOI: 10.1007/s10994-015-5542-8. |
| [3] |
张巍, 张圳彬. 联合图嵌入与特征加权的无监督特征选择[J].
广东工业大学学报, 2021, 38(5): 16-23.
ZHANG W, ZHANG Z B. Joint graph embedding and feature weighting for unsupervised feature selection[J]. Journal of Guangdong University of Technology, 2021, 38(5): 16-23. DOI: 10.12052/gdutxb.210053. |
| [4] |
ZENG S, WANG X, DUAN X, et al. Kernelized mahalanobis distance for fuzzy clustering[J].
IEEE Transactions on Fuzzy Systems, 2021, 29(10): 3103-3117.
DOI: 10.1109/TFUZZ.2020.3012765. |
| [5] |
AGRESTI A. An introduction to categorical data analysis[M]. New York: John Wiley & Sons, 2018.
|
| [6] |
HAMMING R W. Error detecting and error correcting codes[J].
Bell Labs Technical Journal, 2014, 29(2): 147-160.
|
| [7] |
AHMAD A, DEY L. A method to compute distance between two categorical values of same attribute in unsupervised learning for categorical data set[J].
Pattern Recognition Letters, 2007, 28(1): 110-118.
DOI: 10.1016/j.patrec.2006.06.006. |
| [8] |
IENCO D, PENSA R G, MEO R. Context-based distance learning for categorical data clustering[C]//Advances in Intelligent Data Analysis VIII: 8th International Symposium on Intelligent Data Analysis. Lyon: Springer, 2009: 83-94.
|
| [9] |
IENCO D, PENSA R G, MEO R. From context to distance: learning dissimilarity for categorical data clustering[J].
ACM Transactions on Knowledge Discovery from Data, 2012, 6(1): 1-25.
|
| [10] |
JIA H, CHEUNG Y, LIU J. A new distance metric for unsupervised learning of categorical data[J].
IEEE Transactions on Neural Networks Learning Systems, 2015, 27(5): 1065-1079.
|
| [11] |
CHEN L, WANG S, WANG K, et al. Soft subspace clustering of categorical data with probabilistic distance[J].
Pattern Recognition, 2016, 51(3): 322-332.
|
| [12] |
JIAN S, CAO L, LU K, et al. Unsupervised coupled metric similarity for non-iid categorical data[J].
IEEE Transactions on Knowledge and Data Engineering, 2018, 30(9): 1810-1823.
DOI: 10.1109/TKDE.2018.2808532. |
| [13] |
AGRESTI A. Analysis of ordinal categorical data[M]. New York: John Wiley & Sons, 2010.
|
| [14] |
ZHANG Y, CHEUNG Y. An ordinal data clustering algorithm with automated distance learning[C]//Proceedings of the AAAI Conference on Artificial Intelligence. New York: AAAI Press, 2020: 6869-6876.
|
| [15] |
林 强, 唐加山. 一种适用于混合型分类数据的聚类算法[J].
计算机工程与应用, 2019, 55(1): 168-173.
LIN Q, TANG J S. Clustering algorithm for mixed categorical data[J]. Computer Engineering and Applications, 2019, 55(1): 168-173. |
| [16] |
ZHANG Y, CHEUNG Y M, TAN K C. A unified entropy-based distance metric for ordinal-and-nominal-attribute data clustering[J].
IEEE Transactions on Neural Networks and Learning Systems, 2019, 31(1): 39-52.
|
| [17] |
ZHANG Y, CHEUNG Y M. A new distance metric exploiting heterogeneous interattribute relationship for ordinal-and-nominal-attribute data clustering[J].
IEEE Transactions on Cybernetics, 2022, 52(2): 758-771.
DOI: 10.1109/TCYB.2020.2983073. |
| [18] |
ZHANG Y, CHEUNG Y M, ZHANG Y, et al. Learnable weighting of intra-attribute distances for categorical data clustering with nominal and ordinal attributes[J].
IEEE Transactions on Pattern Analysis and Machine Intelligence, 2021, 44(7): 3560-3576.
|
| [19] |
WEST D B. Introduction to graph theory[M]. Upper Saddle River: Prentice hall, 2001.
|
| [20] |
CHAKRABORTY M, CHOWDHURY S, CHAKRABORTY J, et al. Algorithms for generating all possible spanning trees of a simple undirected connected graph: an extensive review[J].
Complex & Intelligent Systems, 2019, 5(3): 265-281.
|
| [21] |
DEVRIENDT K, VAN M P. The simplex geometry of graphs[J].
Journal of Complex Networks, 2019, 7(4): 469-490.
DOI: 10.1093/comnet/cny036. |
| [22] |
CAI D, ZHANG C, HE X. Unsupervised feature selection for multi-cluster data[C]//Proceedings of the 16th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining. New York: Association for Computing Machinery, 2010: 333-342.
|
| [23] |
SANTOS J M, EMBRECHTS M. On the use of the adjusted rand index as a metric for evaluating supervised classification[C]//Artificial Neural Networks–ICANN 2009: 19th International Conference. Cyprus: Springer, 2009: 175-184.
|
| [24] |
ESTÉVEZ P A, TESMER M, PEREZ C A, et al. Normalized mutual information feature selection[J].
IEEE Transactions on Neural Networks, 2009, 20(2): 189-201.
DOI: 10.1109/TNN.2008.2005601. |
| [25] |
HUANG Z. Extensions to the k-means algorithm for clustering large data sets with categorical values[J].
Data Mining and Knowledge Discovery, 1998, 2(3): 283-304.
DOI: 10.1023/A:1009769707641. |
| [26] |
JING L, NG M K, HUANG J Z. An entropy weighting k-means algorithm for subspace clustering of high-dimensional sparse data[J].
IEEE Transactions on Knowledge and Data Engineering, 2007, 19(8): 1026-1041.
DOI: 10.1109/TKDE.2007.1048. |
| [27] |
JIA H, CHEUNG Y M. Subspace clustering of categorical and numerical data with an unknown number of clusters[J].
IEEE Transactions on Neural Networks and Learning Systems, 2017, 29(8): 3308-3325.
|
 2023, Vol. 40
2023, Vol. 40

