离散事件系统(Discrete-Event Systems, DES) 是离散事件按照一定运行规则相互作用而触发状态演化的一类动态系统,在军事国防、交通控制、计算机集成制造系统、电子通讯网络、机器人技术等领域有着广泛应用。为保障系统的安全运行,离散事件系统的故障诊断问题近年来成为了国内外学者的研究热点[1-4]。
离散事件系统的故障诊断最早是由Sampath等[5]提出,并用构造诊断器的方法验证离散事件系统的故障可诊断性,但该方法的复杂度是关于系统状态数的指数时间,这将耗费大量时间和空间。为此,Jiang等[6]和Yoo等[7]提出了一种多项式时间复杂度的故障可诊断性检验算法,该算法能更快捷地对离散事件系统进行故障诊断。为了诊断系统中的故障事件,需要使用传感器捕获相关事件信息,即当事件发生时,有对应的传感器捕获该事件信息并反馈给系统。为了节约构造可诊断性系统的成本,减少传感器的开销,Cassez等[8]在保证系统具有故障可诊断性的前提下,研究了传感器的最小化问题。
然而,上述故障诊断方法对系统要求过高,它要求可诊断的系统必须在故障事件发生之后的所有后继操作中,对系统的每一条运行轨迹都能够在一定时延内将所发生的故障事件诊断出来。这对于一个复杂的系统来说,必须使用大量传感器以获得更多事件发生的信息,也势必增加构造可诊断性系统的成本。为了达到系统故障可诊断能力和传感器开销的平衡,Cao等[9]提出了一个新属性——弱故障可诊断性,这种弱故障可诊断性将Sampath等[5]提出的故障诊断条件适当放宽,只要求系统在故障事件发生之后的任一后继操作中,至少存在一条轨迹(而不是所有轨迹)能够在一定时延内将所发生的故障事件诊断出来即可。因此,对于无法用Sampath等[5]提出的故障诊断方法进行故障诊断的系统,在不增加传感器开销的前提下,可用弱故障诊断解决系统的故障诊断问题。此外,Cao等[9]把弱故障可诊断性推广到网格化离散事件系统(Networked Discrete Event Systems, NDES),提出网格化系统的弱故障诊断方法。事实上,弱故障诊断的概念在文献[10]中也被应用于Petri网。
尽管在大多数工程应用中,DES的状态和事件都是十分明确的。然而,在生物医学等许多其他应用中,情况并非如此,因为模糊性、不精确性和主观性是其典型特征。例如,当一个人的身体状况被称为“好”或“差”时,它是模糊的。此外,也很难定义身体状况到底何时从“好”状态变为“差”状态。为了更有效地处理这类问题,Lin等[11-12]将模糊集理论[13]与传统DES相结合,提出了模糊离散事件系统(Fuzzy Discrete Event Systems, FDES)。此后,许多学者相继致力于FDES的研究,文献[14-15]研究了FDES的监督控制和分布式控制,Huq等[16]则运用FDES理论研究了移动机器人的行为调制技术。Benmessahel等[17]把DES的故障预测推广到FDES,提出了模糊故障预测。
本文把Cao等[9]提出的上述经典离散事件系统的弱故障可诊断方法拓展至模糊系统,研究模糊离散事件系统的弱故障诊断,提出一种弱模糊故障诊断方法[8-9]。先对模糊离散事件系统的弱模糊故障可诊断性进行形式化;为验证模糊系统的弱模糊故障可诊断性,构造了一个验证器自动机。这种验证器的构造方法是多项式时间复杂度算法,它不同于文献[9]的指数时间复杂度方法。在验证器自动机的基础上,得到了一个模糊离散事件系统弱模糊故障可诊断性的充分必要条件,实现了对模糊离散事件系统的弱模糊故障诊断。值得指出的是,该方法既适用于模糊离散事件系统的故障诊断,又适用于经典离散事件系统的弱故障诊断。
1 模糊离散事件系统
设经典离散事件系统的状态集
${Q = \{ {q_0}, {q_1},\cdots, } {{q_{n - 1}}\}}$
,则在模糊离散事件系统中,每个模糊状态表示为向量
$\tilde {\boldsymbol{q}} = [{a_0},{a_1},\cdots,{a_{n - 1}}]$
,其中
$ {a_i} \in [0,1] $
,表示当前状态隶属于状态
${q_i}$
的可能性;每个模糊事件
$\tilde \varSigma$
表示为矩阵
$ {[{a_{ij}}]_{n \times n}} $
,其中
$ {a_{ij}} \in [0,1] $
,表示该事件发生后从状态
${q_i}$
转移到状态
${q_j}$
的可能性;具体形式化定义如下:模糊离散事件系统表示为模糊自动机[18]
$\tilde G = \{ \tilde Q, \tilde E, \tilde {{\delta}} ,{\tilde {\boldsymbol{q}}_{\rm{0}}}\}$
,其中
$\tilde Q$
是模糊状态集,
${\tilde {\boldsymbol{q}}_{\rm{0}}}$
是初始模糊状态,
$\tilde E$
是模糊事件集,
$\tilde \delta $
是转移函数
$\tilde \delta :\tilde Q \times \tilde E \to \tilde Q$
,定义为
$\tilde \delta (\tilde {\boldsymbol{q}},\tilde {\boldsymbol{\sigma}} ) = \tilde{\boldsymbol{ q}} \oplus \tilde {\boldsymbol{\sigma}}$
,这里
$ \oplus $
指max-min运算:对于矩阵
${\boldsymbol{A}} = {[{a_{ij}}]_{n \times m}}$
和
${\boldsymbol{B}} = {[{b_{ij}}]_{m \times k}}$
,定义
${\boldsymbol{A}} \oplus {\boldsymbol{B}} = {[{c_{ij}}]_{n \times k}}$
,其中
$ {c_{ij}} = \mathop {\max }\limits_{l = 1}^m \min \{ {a_{il}},{b_{lj}}\} $
。
例1 设
$\tilde G$
是一个模糊离散事件系统,如果模糊状态
$\tilde {\boldsymbol{q}} = [0.7,0.3]$
,模糊事件
$\tilde {\boldsymbol{\sigma}} = \left[ \begin{gathered} 0.4{\text{ }}0,5 \\ 0.8{\text{ }}0.1 \\ \end{gathered} \right]$
,那么在状态
$\tilde {\boldsymbol{q}}$
发生事件
$\tilde {\boldsymbol{\sigma}}$
,则
$\tilde \delta (\tilde {\boldsymbol{q}},\tilde{\boldsymbol{\sigma}} ) = \tilde {\boldsymbol{q}} \oplus \tilde {\boldsymbol{\sigma}} = [0.7,0.3] \oplus \left[ \begin{gathered} 0.4{\text{ }}0,5 \\ 0.8{\text{ }}0.1 \\ \end{gathered} \right] = [0.4,0.5]$
。
分别记可观事件集、不可观事件集和故障事件集为
${\tilde \varSigma _{\rm{o}}}$
、
${\tilde \varSigma _{{\rm{uo}}}}$
和
${\tilde \varSigma _{\rm{f}}}$
,对于模糊事件
$\tilde {\boldsymbol{\sigma}} \in \tilde E$
,
${\tilde \varSigma _{\rm{o}}}(\tilde {\boldsymbol{\sigma}} )$
、
${\tilde \varSigma _{{\rm{uo}}}}(\tilde {\boldsymbol{\sigma}} )$
和
${\tilde \varSigma _{\rm{f}}}(\tilde {\boldsymbol{\sigma}} )$
分别表示事件
$\tilde {\boldsymbol{\sigma}}$
是可观事件、不可观事件和故障事件的隶属度,它们满足
${\tilde \varSigma _{\rm{o}}}(\tilde {\boldsymbol{\sigma}} ) + {\tilde \varSigma _{{\rm{uo}}}}(\tilde {\boldsymbol{\sigma}} ) = 1$
。另外,对于
${\tilde {\boldsymbol{\sigma}} _1}{\tilde {\boldsymbol{\sigma}} _2}\cdots{\tilde {\boldsymbol{\sigma}} _m} \in {\tilde E^*}$
,定义
${\tilde \varSigma _{\rm{o}}}({\tilde {\boldsymbol{\sigma}} _1}{\tilde {\boldsymbol{\sigma}} _2}\cdots{\tilde {\boldsymbol{\sigma}} _m}) = \min \{ {\tilde \varSigma _{\rm{o}}}({\tilde {\boldsymbol{\sigma}} _i}) : i = 1,2,\cdots,m\}$
,
${\tilde \varSigma _{\rm{f}}}({\tilde {\boldsymbol{\sigma}} _1}{\tilde {\boldsymbol{\sigma}} _2}\cdots{\tilde {\boldsymbol{\sigma}} _m}) = \max \{ {\tilde \varSigma _{\rm{f}}}({\tilde {\boldsymbol{\sigma}} _i}) :i = 1, 2,\cdots, m\}$
。对于
$\tilde {\boldsymbol{\sigma}} \in \tilde E$
,用
${\varPsi _{\tilde {\boldsymbol{\sigma}} }}({\tilde \varSigma _{\rm{f}}})$
表示所有以故障度不小于
${\tilde \varSigma _{\rm{f}}}(\tilde {\boldsymbol{\sigma}} )$
的事件为结尾的事件串集。记
${\tilde E_{\max - {\rm{o}}}} = \{ \tilde {\boldsymbol{\sigma}} \in \tilde E:(\forall \tilde {\boldsymbol{\sigma}} ' \in \tilde E) {\tilde \varSigma _{\rm{o}}}(\tilde {\boldsymbol{\sigma}}) \geqslant {\tilde \varSigma _{\rm{o}}}(\tilde {\boldsymbol{\sigma}} ') \}$
。对于
$\tilde {\boldsymbol{\sigma}} \in \tilde E$
,
$\tilde {\boldsymbol{\sigma}}$
投影
${P_{\tilde {\boldsymbol{\sigma}} }}:{\tilde E^*} \to {\tilde E^*}$
定义为
${P_{\tilde {\boldsymbol{\sigma}} }}({\boldsymbol{\varepsilon}} ) = {\boldsymbol{\varepsilon}}$
,且当
$\tilde s \in {\tilde E^*}$
时
${P_{\tilde {\boldsymbol{\sigma}}}} (\tilde s\tilde t) = {P_{\tilde {\boldsymbol{\sigma}} }}(\tilde s) {P_{\tilde {\boldsymbol{\sigma}} }}(\tilde t)$
,其中
|
$ {P}_{\tilde {\boldsymbol{\sigma}} }(\tilde{t}) =\left\{\begin{array}{l}\tilde{t}\text{ },\text{ }\tilde{t}\in {\tilde{E}}_{\mathrm{max}-{\rm{o}}}\vee {\tilde \varSigma}_{{\rm{o}}}(\tilde{t}) > {\tilde \varSigma }_{{\rm{o}}}(\tilde{\boldsymbol{\sigma}}) \\ \varepsilon \text{ },否则\end{array}\right. $
|
2 模糊离散事件系统的弱模糊故障可诊断性
设
$\tilde G = \{ \tilde Q,\tilde E,\tilde \delta ,{\tilde {\boldsymbol{q}}_0}\}$
是一个模糊离散事件系统且
$\tilde \varSigma \in \tilde E$
,模糊可诊断函数[18]定义为
${\rm{F}}{{\rm{D}}_{\tilde{\boldsymbol{\sigma}} }}:{\tilde E^*} \to [0,1]$
,对于
$\tilde s \in {\varPsi _{\tilde{\boldsymbol{\sigma}}}}({\tilde \varSigma _{\rm{f}}})$
,
$\tilde t \in L/\tilde s$
,
|
$ {\rm{F}}{{\rm{D}}_{\tilde{\boldsymbol{\sigma}}}}(\tilde s\tilde t) = \frac{{\min \{ {{\tilde \varSigma }_{\rm{f}}}(\tilde{\boldsymbol{\sigma}} ) ,{{\tilde \varSigma }_{\rm{f}}}(\tilde \omega ) :\tilde \omega \in P_{\tilde{\boldsymbol{\sigma}} }^{ - 1}{P_{\tilde{\boldsymbol{\sigma}} }}(\tilde s\tilde t) \} }}{{{{\tilde \varSigma }_{\rm{f}}}(\tilde{\boldsymbol{\sigma}} ) }} $
|
定义1 设
$\tilde G = \{ \tilde Q,\tilde E,\tilde \delta ,{\tilde {\boldsymbol{q}}_0}\}$
为一个模糊离散事件系统且
$ 0 \leqslant \lambda < 1 $
。
(1) 称
$\tilde G$
对于
$\tilde{\boldsymbol{\sigma}}$
是弱模糊故障可诊断(或称
$\tilde G$
对于
$\tilde{\boldsymbol{\sigma}}$
的弱模糊故障可诊断度为1),如果式(1)成立:
|
$ (\forall \tilde s \in {\varPsi _{\tilde{\boldsymbol{\sigma}}}}({\tilde \varSigma _{\rm{f}}}) ) (\forall \tilde t \in L/\tilde s) (\exists \tilde t' \in L/\tilde s\tilde t) \Rightarrow {\rm{F}}{{\rm{D}}_{\tilde{\boldsymbol{\sigma}} }}(\tilde s\tilde t\tilde t') = 1 $
|
(1) |
(2) 称
$\tilde G$
对于
$\tilde{\boldsymbol{\sigma}}$
是
$ \lambda $
弱模糊故障可诊断(或称
$\tilde G$
对于
$\tilde{\boldsymbol{\sigma}}$
的弱模糊故障可诊断度为
$ \lambda $
),如果式(2)成立:
|
$ \min \{ \max \{ {\rm{F}}{{\rm{D}}_{\tilde{\boldsymbol{\sigma}} }}(\tilde s\tilde t\tilde t') :\tilde t' \in L/\tilde s\tilde t\} :\tilde s \in {\varPsi _{\tilde {\boldsymbol{\sigma}} }}({\tilde \varSigma _{\rm{f}}}) ,\tilde t \in L/\tilde s\} = \lambda $
|
(2) |
(3) 特别地,当
$ \lambda = 0 $
时称
$\tilde G$
对于
$\tilde{\boldsymbol{\sigma}}$
是弱故障不可诊断(或称
$\tilde G$
对于
$\tilde{\boldsymbol{\sigma}}$
的弱模糊故障可诊断度为0)。
注1 直观上,定义1情况(2)的含义为对于任意故障事件串
${\tilde s_i}$
和任意后续事件串
${\tilde t_i}$
,如果存在一个发生在
${\tilde s_i}{\tilde t_i}$
之后的事件串
${\tilde t_i}'$
使得
${\rm{F}}{{\rm{D}}_{\tilde{\boldsymbol{\sigma}} }}({\tilde s_i}{\tilde t_i}{\tilde t_i}') = {\lambda _i}$
,那么
$\tilde G$
对于
$\tilde{\boldsymbol{\sigma}}$
的弱模糊可诊断度
$ \lambda $
为所有这些
$ {\lambda _i} $
的最小值,即
$ \lambda = \min \{ {\lambda _i}:i = 1,2,\cdots\} $
。显然,情况(1) 和情况(3) 是情况(2) 分别在
$\lambda = {\text{1}}$
和
$\lambda = {\text{0}}$
的特殊情况。
3 模糊离散事件系统弱模糊故障可诊断验证器的构造
下面提出一种验证器的构造方法,该方法既可用于FDES的弱模糊故障诊断(见第4节),又可用于经典DES的弱故障诊断(见第5节),并且时间复杂度是多项式时间,优于文献[9]中的指数时间复杂度。
定义2 设模糊离散事件系统为
$\tilde G = \{ \tilde Q,\tilde E,\tilde \delta ,{\tilde {\boldsymbol{q}}_0}\}$
,构造验证器为
${\tilde G_{\rm{V}}} = \{ {\tilde Q_{\rm{V}}},\tilde E,{\tilde \delta _{\rm{V}}},{\tilde {\boldsymbol{q}}_{{\rm{V}}0}},\tilde{\boldsymbol{\sigma}} \}$
,其中
${\tilde Q_{\rm{V}}}$
是验证器的状态集,每一个状态
${\tilde {\boldsymbol{q}}_{\rm{V}}} = ({\tilde {\boldsymbol{q}}_1},{l_1},{\tilde {\boldsymbol{q}}_2},{l_2})$
,其中
${\tilde {\boldsymbol{q}}_1}, {\tilde {\boldsymbol{q}}_2} \in \tilde Q$
且
$ {l_1},{l_2} \in \{ F,{N^\mu }\} $
,标签
$ F $
表示发生故障的概率超过
${\tilde \varSigma _{\rm{f}}}(\tilde{\boldsymbol{\sigma}} )$
,标签
$ {N^\mu } $
表示发生故障的概率为
$ \mu $
且小于
${\tilde \varSigma _{\rm{f}}}(\tilde{\boldsymbol{\sigma}} )$
;
${\tilde {\boldsymbol{q}}_{{\rm{V}}{\text{0}}}} = ({\tilde {\boldsymbol{q}}_0},{N^0},{\tilde {\boldsymbol{q}}_0},{N^0})$
是初始状态,表示验证器从正常状态开始运行;并分别用
$\tilde \delta (\tilde {\boldsymbol{q}},\tilde{\boldsymbol{\sigma}} ) !$
和
$\neg \tilde \delta (\tilde {\boldsymbol{q}},\tilde {\boldsymbol{\sigma}}) !$
表示
$\tilde \delta (\tilde {\boldsymbol{q}},\tilde {\boldsymbol{\sigma}} )$
有定义和
$\tilde \delta (\tilde {\boldsymbol{q}},\tilde{\boldsymbol{\sigma}} )$
无定义。
转移函数
$ {\tilde \delta _V} $
定义如下:对于
${\tilde {\boldsymbol{q}}_{\rm{V}}} = ({\tilde {\boldsymbol{q}}_1},{l_1},{\tilde {\boldsymbol{q}}_2},{l_2})$
,
$\tilde {\boldsymbol{a}} \in \tilde E$
,则
${\tilde \delta _{\rm{V}}}(({\tilde {\boldsymbol{q}}_1},{l_1},{\tilde {\boldsymbol{q}}_2},{l_2}) ,\tilde {\boldsymbol{a}})$
分以下4种情况定义:
(1)如果
${\tilde \varSigma _{\rm{o}}}(\tilde {\boldsymbol{a}}) > {\tilde \varSigma _{\rm{o}}}(\tilde{\boldsymbol{\sigma}} )$
,且
${\tilde \varSigma _{\rm{f}}}(\tilde {\boldsymbol{a}}) \geqslant {\tilde \varSigma _{\rm{f}}}(\tilde{\boldsymbol{\sigma}} )$
,则
|
$ {\tilde{\delta }}_{{\rm{V}}}(({\tilde{{\boldsymbol{q}}}}_{1},{l}_{1},{\tilde{{\boldsymbol{q}}}}_{2},{l}_{2}) ,\tilde{{\boldsymbol{a}}}) =\left\{\begin{gathered} (\tilde{\delta }({\tilde{{\boldsymbol{q}}}}_{1},\tilde{{\boldsymbol{a}}}) ,F,\tilde{\delta }({\tilde{{\boldsymbol{q}}}}_{2},\tilde{{\boldsymbol{a}}}) ,F) \text{ },\\ \tilde{\delta }({\tilde{{\boldsymbol{q}}}}_{1},\tilde{{\boldsymbol{a}}}) !\wedge \tilde{\delta }({\tilde{{\boldsymbol{q}}}}_{2},\tilde{{\boldsymbol{a}}}) !\\ (\tilde{\delta }({\tilde{{\boldsymbol{q}}}}_{1},\tilde{{\boldsymbol{a}}}) ,F,\tilde{\delta }({\tilde{{\boldsymbol{q}}}}_{1},\tilde{{\boldsymbol{a}}}) ,F) \text{ },\\ \tilde{\delta }({\tilde{{\boldsymbol{q}}}}_{1},\tilde{{\boldsymbol{a}}}) ! \wedge \neg \tilde{\delta }({\tilde{{\boldsymbol{q}}}}_{2},\tilde{{\boldsymbol{a}}}) !\\ 无定义,\text{ }否则 \end{gathered}\right. $
|
(2) 如果
${\tilde \varSigma _{\rm{o}}}(\tilde {\boldsymbol{a}}) > {\tilde \varSigma _{\rm{o}}}(\tilde{\boldsymbol{\sigma}} )$
,且
${\tilde \varSigma _{\rm{f}}}(\tilde {\boldsymbol{a}}) < {\tilde \varSigma _{\rm{f}}}(\tilde{\boldsymbol{\sigma}} )$
,则
|
$ {\tilde{\delta }}_{{\rm{V}}}(({\tilde{{\boldsymbol{q}}}}_{1},F,{\tilde{{\boldsymbol{q}}}}_{2},F) ,\tilde{{\boldsymbol{a}}}) =\left\{ \begin{array}{l}(\tilde{\delta }({\tilde{{\boldsymbol{q}}}}_{1},\tilde{{\boldsymbol{a}}}) ,F,\tilde{\delta }({\tilde{{\boldsymbol{q}}}}_{2},\tilde{{\boldsymbol{a}}}) ,F) ,\\ \tilde{\delta }({\tilde{{\boldsymbol{q}}}}_{1},\tilde{{\boldsymbol{a}}}) !\wedge \tilde{\delta }({\tilde{{\boldsymbol{q}}}}_{2},\tilde{{\boldsymbol{a}}}) !\\ (\tilde{\delta }({\tilde{{\boldsymbol{q}}}}_{1},\tilde{{\boldsymbol{a}}}) ,F,\tilde{\delta }({\tilde{{\boldsymbol{q}}}}_{1},\tilde{{\boldsymbol{a}}}) ,F) ,\\ \tilde{\delta }({\tilde{{\boldsymbol{q}}}}_{1},\tilde{{\boldsymbol{a}}}) !\wedge \neg \tilde{\delta }({\tilde{{\boldsymbol{q}}}}_{2},\tilde{{\boldsymbol{a}}}) !\\ 无定义,否则\end{array} \right. $
|
|
$ {\tilde{\delta }}_{{\rm{V}}}(({\tilde{{\boldsymbol{q}}}}_{1},F,{\tilde{{\boldsymbol{q}}}}_{2},{N}^{{\mu }_{2}}) ,\tilde{{\boldsymbol{a}}}) =\left\{\begin{split}&(\tilde{\delta }({\tilde{{\boldsymbol{q}}}}_{1},\tilde{{\boldsymbol{a}}}) ,F,\tilde{\delta }({\tilde{{\boldsymbol{q}}}}_{2},\tilde{{\boldsymbol{a}}}) ,{N}^{{\boldsymbol{\sigma}}{'}}) \text{ },\text{ }\\ &\tilde{\delta }({\tilde{{\boldsymbol{q}}}}_{1},\tilde{{\boldsymbol{a}}}) !\wedge \tilde{\delta }({\tilde{{\boldsymbol{q}}}}_{2},\tilde{{\boldsymbol{a}}}) !\\ &(\tilde{\delta }({\tilde{{\boldsymbol{q}}}}_{1},\tilde{{\boldsymbol{a}}}) ,F,\tilde{\delta }({\tilde{{\boldsymbol{q}}}}_{1},\tilde{{\boldsymbol{a}}}) ,F) \text{ },\text{ }\\ &\tilde{\delta }({\tilde{{\boldsymbol{q}}}}_{1},\tilde{{\boldsymbol{a}}}) !\wedge \neg \tilde{\delta }({\tilde{{\boldsymbol{q}}}}_{2},\tilde{{\boldsymbol{a}}}) !\\ &无定义,\text{ }否则\end{split}\right. $
|
|
$ {\tilde{\delta }}_{{\rm{V}}}(({\tilde{{\boldsymbol{q}}}}_{1},{N}^{{\mu }_{1}},{\tilde{{\boldsymbol{q}}}}_{2},{N}^{{\mu }_{2}}) ,\tilde{{\boldsymbol{a}}}) =\left\{\begin{split}&(\tilde{\delta }({\tilde{{\boldsymbol{q}}}}_{1},\tilde{{\boldsymbol{a}}}) ,{N}^{{\boldsymbol{\sigma}}{'}}, \tilde{\delta }({\tilde{{\boldsymbol{q}}}}_{2},\tilde{{\boldsymbol{a}}}) ,{N}^{{\boldsymbol{\sigma}}{'}}) \text{ },\text{ }\\ &\tilde{\delta }({\tilde{{\boldsymbol{q}}}}_{1},\tilde{{\boldsymbol{a}}}) !\wedge \tilde{\delta }({\tilde{{\boldsymbol{q}}}}_{2},\tilde{{\boldsymbol{a}}}) !\\ &(\tilde{\delta }({\tilde{{\boldsymbol{q}}}}_{1},\tilde{{\boldsymbol{a}}}) ,{N}^{{\boldsymbol{\sigma}}{'}},\tilde{\delta }({\tilde{{\boldsymbol{q}}}}_{1},\tilde{{\boldsymbol{a}}}) ,{N}^{{\boldsymbol{\sigma}}{'}}) \text{ },\text{ }\\ &\tilde{\delta }({\tilde{{\boldsymbol{q}}}}_{1},\tilde{{\boldsymbol{a}}}) !\wedge \neg \tilde{\delta }({\tilde{{\boldsymbol{q}}}}_{2},\tilde{{\boldsymbol{a}}}) !\\ &无定义,\text{ }否则\end{split} \right.$
|
这里
${{\boldsymbol{\sigma}}}' = \max \{ {\mu _1},{\tilde \varSigma _{\rm{f}}}(\tilde {\boldsymbol{a}}) \}$
,
${{\boldsymbol{\sigma}}}' = \max \{ {\mu _2},{\tilde \varSigma _{\rm{f}}}(\tilde {\boldsymbol{a}}) \}$
。
(3) 如果
${\tilde \varSigma _{\rm{o}}}(\tilde {\boldsymbol{a}}) \leqslant {\tilde \varSigma _{\rm{o}}}(\tilde{\boldsymbol{\sigma}})$
,且
${\tilde \varSigma _{\rm{f}}}(\tilde {\boldsymbol{a}}) \geqslant {\tilde \varSigma _{\rm{f}}}(\tilde{\boldsymbol{\sigma}} )$
:
若
$\tilde{\delta }({\tilde{{\boldsymbol{q}}}}_{1},\tilde{{\boldsymbol{a}}}) !$
且
$\tilde{\delta }({\tilde{{\boldsymbol{q}}}}_{2},\tilde{{\boldsymbol{a}}}) !$
,则
|
$ {\tilde \delta _{\rm{V}}}(({\tilde {\boldsymbol{q}}_1},{l_1},{\tilde {\boldsymbol{q}}_2},{l_2}) ,\tilde {\boldsymbol{a}}) = \left\{ \begin{gathered} (\tilde \delta ({{\tilde {\boldsymbol{q}}}_1},\tilde {\boldsymbol{a}}) ,F,{{\tilde {\boldsymbol{q}}}_2},{l_2}) \\ (\tilde \delta ({{\tilde {\boldsymbol{q}}}_1},\tilde {\boldsymbol{a}}) ,F,\tilde \delta ({{\tilde {\boldsymbol{q}}}_2},\tilde {\boldsymbol{a}}) ,F) \\ \end{gathered} \right. $
|
否则,
${\tilde \delta _{\rm{V}}}(({\tilde {\boldsymbol{q}}_1},{l_1},{\tilde {\boldsymbol{q}}_2},{l_2}) ,\tilde {\boldsymbol{a}})$
无定义。
(4) 如果
${\tilde \varSigma _{\rm{o}}}(\tilde {\boldsymbol{a}}) \leqslant {\tilde \varSigma _{\rm{o}}}(\tilde{\boldsymbol{\sigma}} )$
,且
${\tilde \varSigma _{\rm{f}}}(\tilde {\boldsymbol{a}}) < {\tilde \varSigma _{\rm{f}}}(\tilde{\boldsymbol{\sigma}} )$
:
若
$\tilde \delta ({\tilde {\boldsymbol{q}}_1},\tilde {\boldsymbol{a}}) !$
且
$\tilde \delta ({\tilde {\boldsymbol{q}}_2},\tilde {\boldsymbol{a}}) !$
,则
|
$ {\tilde \delta _{\rm{V}}}(({\tilde {\boldsymbol{q}}_1},F,{\tilde {\boldsymbol{q}}_2},F) ,\tilde {\boldsymbol{a}}) = \left\{ \begin{gathered} (\tilde \delta ({{\tilde {\boldsymbol{q}}}_1},\tilde {\boldsymbol{a}}) ,F,{{\tilde {\boldsymbol{q}}}_2},F) \\ (\tilde \delta ({{\tilde {\boldsymbol{q}}}_1},\tilde {\boldsymbol{a}}) ,F,\tilde \delta ({{\tilde {\boldsymbol{q}}}_2},\tilde {\boldsymbol{a}}) ,F) \\ \end{gathered} \right. $
|
|
$ {\tilde \delta _{\rm{V}}}(({\tilde {\boldsymbol{q}}_1},F,{\tilde {\boldsymbol{q}}_2},{N^{{\mu _{\text{2}}}}}) ,\tilde {\boldsymbol{a}}) = \left\{ \begin{gathered} (\tilde \delta ({{\tilde {\boldsymbol{q}}}_1},\tilde {\boldsymbol{a}}) ,F,{{\tilde {\boldsymbol{q}}}_2},{N^{{\mu _{\text{2}}}}}) \\ (\tilde \delta ({{\tilde {\boldsymbol{q}}}_1},\tilde {\boldsymbol{a}}) ,F,\tilde \delta ({{\tilde {\boldsymbol{q}}}_2},\tilde {\boldsymbol{a}}) ,{N^{{{\boldsymbol{\sigma}}}'}}) \\ \end{gathered} \right. $
|
|
$ {\tilde \delta _{\rm{V}}}(({\tilde {\boldsymbol{q}}_1},{N^{{\mu _1}}},{\tilde {\boldsymbol{q}}_2},{N^{{\mu _{\text{2}}}}}) ,\tilde {\boldsymbol{a}}) = \left\{ \begin{gathered} (\tilde \delta ({{\tilde {\boldsymbol{q}}}_1},\tilde {\boldsymbol{a}}) ,{N^{{{\boldsymbol{\sigma}}}'}},{{\tilde {\boldsymbol{q}}}_2},{N^{{\mu _{\text{2}}}}}) \\ (\tilde \delta ({{\tilde {\boldsymbol{q}}}_1},\tilde {\boldsymbol{a}}) ,{N^{{{\boldsymbol{\sigma}}}'}},\tilde \delta ({{\tilde {\boldsymbol{q}}}_2},\tilde {\boldsymbol{a}}) ,{N^{{{\boldsymbol{\sigma}}}'}}) \\ \end{gathered} \right. $
|
若
$\neg \tilde{\delta }({\tilde{{\boldsymbol{q}}}}_{1},\tilde{{\boldsymbol{a}}}) !$
且
$\tilde \delta ({\tilde {\boldsymbol{q}}_2},\tilde {\boldsymbol{a}}) !$
,则
|
$ {\tilde \delta _{\rm{V}}}(({\tilde {\boldsymbol{q}}_1},F,{\tilde {\boldsymbol{q}}_2},F) ,\tilde {\boldsymbol{a}}) = ({\tilde {\boldsymbol{q}}_1},F,\tilde \delta ({\tilde {\boldsymbol{q}}_2},\tilde {\boldsymbol{a}}) ,F) $
|
|
$ {\tilde \delta _{\rm{V}}}(({\tilde {\boldsymbol{q}}_1},F,{\tilde {\boldsymbol{q}}_2},{N^{{\mu _{\text{2}}}}}) ,\tilde {\boldsymbol{a}}) = ({\tilde {\boldsymbol{q}}_1},F,\tilde \delta ({\tilde {\boldsymbol{q}}_2},\tilde {\boldsymbol{a}}) ,{N^{{{\boldsymbol{\sigma}}}'}}) $
|
|
$ {\tilde \delta _{\rm{V}}}(({\tilde {\boldsymbol{q}}_1},{N^{{\mu _1}}},{\tilde {\boldsymbol{q}}_2},{N^{{\mu _{\text{2}}}}}) ,\tilde {\boldsymbol{a}}) = ({\tilde {\boldsymbol{q}}_1},{N^{{\mu _1}}},\tilde \delta ({\tilde {\boldsymbol{q}}_2},\tilde {\boldsymbol{a}}) ,{N^{{{\boldsymbol{\sigma}}}'}}) $
|
若
$\tilde \delta ({\tilde {\boldsymbol{q}}_1},\tilde {\boldsymbol{a}}) !$
且
$\neg \tilde{\delta }({\tilde{{\boldsymbol{q}}}}_{2},\tilde{{\boldsymbol{a}}}) !$
,则
|
$ {\tilde \delta _{\rm{V}}}(({\tilde {\boldsymbol{q}}_1},F,{\tilde {\boldsymbol{q}}_2},{l_2}) ,\tilde {\boldsymbol{a}}) = (\tilde \delta ({\tilde {\boldsymbol{q}}_1},\tilde {\boldsymbol{a}}) ,F,{\tilde {\boldsymbol{q}}_2},{l_2}) $
|
|
$ {\tilde \delta _{\rm{V}}}(({\tilde{\boldsymbol{ q}}_1},{N^{{\mu _1}}},{\tilde {\boldsymbol{q}}_2},{l_2}) ,\tilde {\boldsymbol{a}}) = (\tilde \delta ({\tilde {\boldsymbol{q}}_1},\tilde {\boldsymbol{a}}) ,{N^{{{\boldsymbol{\sigma}}}'}},{\tilde {\boldsymbol{q}}_2},{l_2}) $
|
若
$\neg \tilde \delta ({\tilde {\boldsymbol{q}}_1},\tilde {\boldsymbol{a}}) !$
和
$\neg \tilde{\delta }({\tilde{{\boldsymbol{q}}}}_{2},\tilde{{\boldsymbol{a}}}) !$
,则
${\tilde \delta _{\rm{V}}}(({\tilde {\boldsymbol{q}}_1},{l_1},{\tilde {\boldsymbol{q}}_2},{l_2}) ,\tilde {\boldsymbol{a}})$
无定义。
这里
${{\boldsymbol{\sigma}}}' = \max \{ {\mu _1},{\tilde \varSigma _{\rm{f}}}(\tilde {\boldsymbol{a}}) \}$
,
${{\boldsymbol{\sigma}}}' = \max \{ {\mu _2},{\tilde \varSigma _{\rm{f}}}(\tilde {\boldsymbol{a}}) \}$
。
直观地,上述转移函数
${\tilde \delta _{\rm{V}}}$
的定义是为了保证
${\tilde G_{\rm{V}}}$
中的每个状态
${\tilde {\boldsymbol{q}}_{\rm{V}}} = ({\tilde {\boldsymbol{q}}_1},{l_1},{\tilde {\boldsymbol{q}}_2},{l_2})$
都存在
${\tilde s_1},{\tilde s_2} \in {\tilde E^*}$
,满足
${\tilde {\boldsymbol{q}}_1} = \tilde \delta ({\tilde {\boldsymbol{q}}_0},{\tilde s_1})$
,
${\tilde {\boldsymbol{q}}_2} = \tilde \delta ({\tilde {\boldsymbol{q}}_0},{\tilde s_2})$
且
${P_{\tilde {\boldsymbol{\sigma}} }}({\tilde s_1}) = {P_{\tilde{\boldsymbol{\sigma}} }}({\tilde s_2})$
。
注2 设
$\tilde G$
的状态数为
$|\tilde Q|$
,事件数为
$|\tilde E|$
,则根据上述构造可知,验证器
${\tilde G_{\rm{V}}}$
的每个状态最多有
$2|\tilde E|$
个转移,且最多有
$|\tilde Q{|^2}(|\tilde E{|^2} + |\tilde E|) $
个状态,所以构造验证器
${\tilde G_{\rm{V}}}$
的复杂度为
$O(|\tilde Q{|^2}|\tilde E{|^3}) $
。而在文献[9]的验证器构造方法中,每个状态有2个分量,第1个分量代表当前状态,第2个分量代表当前状态估计,所以最多有
$|\tilde Q| \cdot {{\text{2}}^{|\tilde Q|}}$
个状态,且每个状态最多有
$|\tilde E|$
个转移,所以构造验证器的复杂度为
$O(|\tilde Q| \cdot {{\text{2}}^{|\tilde Q|}}|\tilde E|) $
。因此,本文构造验证器的方法是多项式复杂度,明显优于文献[9]中的指数复杂度。
4 弱模糊故障可诊断性的充分必要条件
给出弱模糊故障可诊断性的充分必要条件之前,先补充相关定义。
如果状态
${\tilde {\boldsymbol{q}}_{\rm{V}}} = ({\tilde {\boldsymbol{q}}_1},{l_1},{\tilde {\boldsymbol{q}}_2},{l_2}) \in {\tilde Q_{\rm{V}}}$
满足
$ {l_1} = F $
且
$ {l_2} = {N^\mu } $
,则
${\tilde {\boldsymbol{q}}_{\rm{V}}}$
称为
$ \mu F $
不确定状态[19]。如果状态
${\tilde {\boldsymbol{q}}_{\rm{V}}} =({\tilde {\boldsymbol{q}}_1}, {l_1},{\tilde {\boldsymbol{q}}_2},{l_2}) \in {\tilde Q_{\rm{V}}}$
满足
$ {l_1} = F $
且
$ {l_2} = F $
,则
${\tilde q_{\rm{V}}}$
称为
$ F $
确定状态。如果状态转移
${\tilde {\boldsymbol{q}}_{{{\rm{V}}_1}}}\mathop \to \limits^{{{\tilde{\boldsymbol{\sigma}} }_1}} {\tilde {\boldsymbol{q}}_{{{\rm{V}}_2}}}\mathop \to \limits^{{{\tilde {\boldsymbol{\sigma}} }_2}}\cdots\mathop \to \limits^{{{\tilde{\boldsymbol{\sigma}}}_{n - 1}}} {\tilde {\boldsymbol{q}}_{{{\rm{V}}_n}}}$
满足
${\tilde {\boldsymbol{q}}_{{{\rm{V}}_1}}} = {\tilde {\boldsymbol{q}}_{{{\rm{V}}_n}}}$
,则称之为一个环。如果环的每个状态都是
$ \mu F $
不确定状态,则称之为
$ \mu F $
不确定环[19];如果环的每个状态都是
$ F $
确定状态,则称之为
$ F $
确定环。
定义3 设
$C:{\tilde {\boldsymbol{q}}_{{{\rm{V}}_1}}}\mathop \to \limits^{{{\tilde{\boldsymbol{\sigma}} }_1}} {\tilde {\boldsymbol{q}}_{{{\rm{V}}_2}}}\mathop \to \limits^{{{\tilde {\boldsymbol{\sigma}} }_2}} \cdots\mathop \to \limits^{{{\tilde {\boldsymbol{\sigma}} }_{n - 1}}} {\tilde {\boldsymbol{q}}_{{{\rm{V}}_n}}}$
是一个
$ \mu F $
不确定环,如果由
$C$
可到达一个
$ F $
确定环,则定义
$R(C) = {\tilde \varSigma _{\rm{f}}}(\tilde{\boldsymbol{\sigma}} )$
;如果由
$C$
无法到达一个
$ F $
确定环,但由
$C$
可到达一个极大
$ \mu 'F $
不确定环,则定义
$ R(C) = $
$ \mu ' $
。
注3
${\tilde G_{\rm{V}}}$
中出现
$ \mu F $
不确定环,意味着存在某事件串的可诊断度为
$ \lambda $
,且
$\lambda = \dfrac{\mu }{{{{\tilde \varSigma }_{\rm{f}}}(\tilde{\boldsymbol{\sigma}} ) }}$
。定义3计算
$ R(C) $
就是为了计算该事件串
$\tilde s\tilde t$
后续事件串的最大可诊断度。
$R(C) = {\tilde \varSigma _{\rm{f}}}(\tilde{\boldsymbol{\sigma}})$
意味着
${\tilde G_V}$
中存在某事件串使得
$ C $
转移到
$ F $
确定环;当
$ R(C) = \mu ' $
,意味着
${\tilde G_{\rm{V}}}$
中不存在事件串使得
$ C $
转移到
$ F $
确定环,但存在某事件串使得
$ C $
转移到一个
$ \mu 'F $
不确定环,
$ \mu ' $
为所有可转移到达的
$ \mu F $
不确定环中的最大值。
定理1 对于
${\tilde G_{\rm{V}}}$
中所有的
$ F $
不确定环
$ {C_i} $
,如果
$ \mu = \min \{ R({C_i}) ,i = 1,2,\cdots\} $
,那么
$\tilde G$
对于
$\tilde{\boldsymbol{\sigma}}$
是
$ \lambda $
弱模糊故障可诊断当且仅当
$\mu = \lambda {\tilde \varSigma _{\rm{f}}}(\tilde{\boldsymbol{\sigma}} )$
。
证明 假设
${\tilde G_{\rm{V}}}$
中
$ F $
不确定环
$ {C_i} $
有
$ n $
个,由注记3可知
$ R({C_i}) $
必定存在,设
$R({C_i}) = {\mu _i},i = 1,2,\cdots$
,不失一般性,假设
$ R({C_1}) $
为最小值,即
$ \mu = R({C_1}) $
,设
${C_{\text{1}}}:{\tilde {\boldsymbol{q}}_{{{\rm{V}}_1}}}\mathop \to \limits^{{{\tilde {\boldsymbol{\sigma}} }_1}} {\tilde {\boldsymbol{q}}_{{{\rm{V}}_2}}}\mathop \to \limits^{{{\tilde{\boldsymbol{\sigma}} }_2}}\cdots\mathop \to \limits^{{{\tilde {\boldsymbol{\sigma}} }_{n - 1}}} {\tilde {\boldsymbol{q}}_{{{\rm{V}}_n}}}$
是一个
$ {\mu _1}F $
不确定环。
必要性证明:(1) 如果
$R({C_1}) = {\tilde \varSigma _{\rm{f}}}(\tilde{\boldsymbol{\sigma}} )$
,则存在
$\tilde s \in L, {\tilde {\boldsymbol{q}}_{{{\rm{V}}_1}}}' = {\tilde \delta _{\rm{V}}}({\tilde {\boldsymbol{q}}_{{{\rm{V}}_1}}},\tilde s)$
,存在
$C':{\tilde {\boldsymbol{q}}_{{{\rm{V}}_1}}}'\mathop \to \limits^{{{\tilde {\boldsymbol{\sigma}} }_1}'} {\tilde {\boldsymbol{q}}_{{{\rm{V}}_2}}}'\mathop \to \limits^{{{\tilde {\boldsymbol{\sigma}} }_2}'} \cdots\mathop \to \limits^{{{\tilde {\boldsymbol{\sigma}} }_{n - 1}}'}$
${\tilde {\boldsymbol{q}}_{{{\rm{V}}_{\rm{n}}}}}'$
的
$ F $
确定环。因为
${\tilde {\boldsymbol{q}}_{{{\rm{V}}_i}}} = ({\tilde {\boldsymbol{q}}_{i1}},F,{\tilde {\boldsymbol{q}}_{i2}},{N^{{\mu _{\text{1}}}}}) \in {\tilde Q_{\rm{V}}}$
,故存在
${\tilde s_1} \in L$
满足
${\tilde \varSigma _{\rm{f}}}({\tilde s_1}) \geqslant {\tilde \varSigma _{\rm{f}}}(\tilde{\boldsymbol{\sigma}} )$
且
${\tilde {\boldsymbol{q}}_{11}} = \tilde \delta ({\tilde {\boldsymbol{q}}_0},{\tilde s_1})$
,取
${\tilde s_1}' \in {\rm{pre}}({\tilde s_1})$
且
${\tilde s_1}' \in {\varPsi _{\tilde{\boldsymbol{\sigma}} }} ({\tilde \varSigma _{\rm{f}}})$
,
$ {\tilde t_1}' \in L/{\tilde s_1}' $
且
$ {\tilde s_1} = {\tilde s_1}'{\tilde t_1}' $
,令
${\tilde t_1}'' = \tilde s$
,则
${\tilde {\boldsymbol{q}}_{11}}' = \tilde \delta ({\tilde {\boldsymbol{q}}_0},{\tilde s_1}'$
${\tilde t_1}'{\tilde t_1}'') $
,因为
$ C' $
是
$ F $
确定环,所以任意
$\tilde \omega \in P_{\tilde{\boldsymbol{\sigma}} }^{ - 1}{P_{\tilde {\boldsymbol{\sigma}} }}({\tilde s_1}'{\tilde t_1}'{\tilde t_1}'')$
,都有
${\tilde \varSigma _{\rm{f}}}(\tilde \omega ) \geqslant {\tilde \varSigma _{\rm{f}}}(\tilde{\boldsymbol{\sigma}} )$
,根据模糊可诊断函数可得
${\rm{F}}{{\rm{D}}_{\tilde{\boldsymbol{\sigma}} }}({\tilde s_1}'{\tilde t_1}'{\tilde t_1}'') = 1$
,又
$ \mu = R({C_1}) $
为最小值,故
$R({C_i}) = {\tilde \varSigma _{\rm{f}}}(\tilde{\boldsymbol{\sigma}} )$
对所有的
$ i $
均成立,即对任意
${\tilde s_i} \in {\varPsi _{\tilde{\boldsymbol{\sigma}} }}({\tilde \varSigma _{\rm{f}}}) ,{\tilde t_i} \in L/{\tilde s_i}$
,
$\max \{ {\rm{F}}{{\rm{D}}_{\tilde{\boldsymbol{\sigma}} }}({\tilde s_i}{\tilde t_i}{\tilde t_i}') :{\tilde t_i}' \in L/{\tilde s_i}{\tilde t_i}\} = 1$
恒成立。
$\tilde G$
对于
$\tilde {\boldsymbol{\sigma}}$
是
$ \lambda $
弱模糊故障可诊断,根据定义1可得
$\min \{ \max \{ {\rm{F}}{{\rm{D}}_{\tilde{\boldsymbol{\sigma}} }}(\tilde s\tilde t\tilde t') : \tilde t' \in L/\tilde s\tilde t\} : \tilde s \in {\varPsi _{\tilde {\boldsymbol{\sigma}} }}({\tilde \varSigma _{\rm{f}}}) , \tilde t \in L/\tilde s\} = \lambda$
。故
$ \lambda = 1 $
,又
$R({C_1}) = {\tilde \varSigma _{\rm{f}}}(\tilde{\boldsymbol{\sigma}} )$
,则
$\mu = {\tilde \varSigma _{\rm{f}}}$
$(\tilde {\boldsymbol{\sigma}} )$
,所以
$\mu = \lambda {\tilde \varSigma _{\rm{f}}}(\tilde {\boldsymbol{\sigma}} )$
。
(2) 如果
$R({C_1}) = {\mu _1} < {\tilde \varSigma _{\rm{f}}}(\tilde {\boldsymbol{\sigma}} )$
,则存在
$\tilde s \in L$
满足
${\tilde {\boldsymbol{q}}_{{{\rm{V}}_1}}}' = {\tilde \delta _{\rm{V}}}({\tilde {\boldsymbol{q}}_{{{\rm{V}}_1}}},\tilde s)$
,存在
$C':{\tilde {\boldsymbol{q}}_{{{\rm{V}}_1}}}'\mathop \to \limits^{{{\tilde {\boldsymbol{\sigma}} }_1}'} {\tilde {\boldsymbol{q}}_{{{\rm{V}}_2}}}'\mathop \to \limits^{{{\tilde{\boldsymbol{\sigma}} }_2}'}$
$\cdots\mathop \to \limits^{{{\tilde{\boldsymbol{\sigma}} }_{n - 1}}'} {\tilde {\boldsymbol{q}}_{{{\rm{V}}_n}}}'$
的
$ {\mu _1}F $
不确定环,对于任意的
$C'':{\tilde {\boldsymbol{q}}_{{{\rm{V}}_1}}}''\mathop \to \limits^{{{\tilde {\boldsymbol{\sigma}} }_1}''} {\tilde {\boldsymbol{q}}_{{{\rm{V}}_2}}}''\mathop \to \limits^{{{\tilde{\boldsymbol{\sigma}} }_2}''} \cdots\mathop \to \limits^{{{\tilde{\boldsymbol{\sigma}} }_{n - 1}}''} {\tilde {\boldsymbol{q}}_{{{\rm{V}}_n}}}''$
的
${\mu' _1}F$
不确定环,存在
$\tilde s \in L$
满足
${\tilde {\boldsymbol{q}}_{{{\rm{V}}_1}}}' = {\tilde \delta _{\rm{V}}}({\tilde {\boldsymbol{q}}_{{{\rm{V}}_1}}},\tilde s)$
且
${\mu _1} \geqslant {\mu' _1}$
。因为
${\tilde {\boldsymbol{q}}_{{{\rm{V}}_i}}} = ({\tilde {\boldsymbol{q}}_{i1}},F,{\tilde {\boldsymbol{q}}_{i2}},{N^{{\mu _1}}}) \in {\tilde Q_{\rm{V}}}$
,故存在
${\tilde s_1} \in L$
满足
${\tilde \varSigma _{\rm{f}}}({\tilde s_1}) \geqslant {\tilde \varSigma _{\rm{f}}}(\tilde {\boldsymbol{\sigma}})$
且
${\tilde {\boldsymbol{q}}_{11}} = r \tilde \delta ({\tilde {\boldsymbol{q}}_0},{\tilde s_1})$
,取
${\tilde s_1}' \in {\rm{pre}}({\tilde s_1})$
且
${\tilde s_1}' \in {\varPsi _{\tilde{\boldsymbol{\sigma}}}({\tilde \varSigma _{\rm{f}}})}$
,
${\tilde t_1}' \in L/{\tilde s_1}'$
且
${\tilde s_1} = {\tilde s_1}'{\tilde t_1}'$
,令
${\tilde t_1}'' = \tilde s$
,则
${\tilde {\boldsymbol{q}}_{11}}' = \tilde \delta ({\tilde {\boldsymbol{q}}_0},{\tilde s_1}'{\tilde t_1}'{\tilde t_1}'')$
,故对于任意
$ {\tilde t_1}''' \in L/{\tilde s_1}'{\tilde t_1}' $
,都有
${\rm{F}}{{\rm{D}}_{\tilde{\boldsymbol{\sigma}}}}({\tilde s_1}'{\tilde t_1}'{\tilde t_1}'') \geqslant {\rm{F}}{{\rm{D}}_{\tilde {\boldsymbol{\sigma}} }}({\tilde s_1}'{\tilde t_1}'{\tilde t_1}''')$
,根据模糊可诊断函数可得
${\rm{F}}{{\rm{D}}_{\tilde{\boldsymbol{\sigma}}}}({\tilde s_1}'{\tilde t_1}'{\tilde t_1}'')$
$= \dfrac{{{\mu _1}}}{{{{\tilde \varSigma }_{\rm{f}}}(\tilde{\boldsymbol{\sigma}}) }}$
。所以
${\mu _1} = \max \{ {\rm{F}}{{\rm{D}}_{\tilde{\boldsymbol{\sigma}} }} ({\tilde s_1}'{\tilde t_1}'{\tilde t_1}'') : {\tilde t_1}'' \in L/{\tilde s_1}'{\tilde t_1}'\} {\tilde \varSigma _{\rm{f}}}(\tilde{\boldsymbol{\sigma}} )$
,同理得
${\mu _i} = \max \{ {\rm{F}}{{\rm{D}}_{\tilde {\boldsymbol{\sigma}} }}({\tilde s_i}'{\tilde t_i}' {\tilde t_i}'') : {\tilde t_i}'' \in L/{\tilde s_i}'{\tilde t_i}'\} {\tilde \varSigma _{\rm{f}}}(\tilde {\boldsymbol{\sigma}} )$
,对所有的
$ i $
均成立,又
$\mu = \min \{ R({C_i}) ,i = 1,2,\cdots\} {\text{ = }}$
$\min \{ {\mu _i},i = 1,2,\cdots\}$
。
$\tilde G$
对于
$\tilde {\boldsymbol{\sigma}}$
是
$ \lambda $
弱模糊故障可诊断,根据定义1可得
$ \min \{ \max $
$\{ {\rm{F}}{{\rm{D}}_{\tilde{\boldsymbol{\sigma}} }}(\tilde s\tilde t\tilde t') :\tilde t' \in L/\tilde s\tilde t\} : \tilde s \in {\Psi _{\tilde {\boldsymbol{\sigma}} }}({\tilde \varSigma _{\rm{f}}}) ,\tilde t \in L/\tilde s\} = \lambda$
。又
${\mu _1} = R({C_1}) $
为最小值,故
$ R({C_i}) \geqslant {\mu _1} $
对所有的
$ i $
均成立,即对于任意
${\tilde s_i} \in {\varPsi _{\tilde{\boldsymbol{\sigma}} }}({\tilde \varSigma _{\rm{f}}}) ,{\tilde t_i} \in L/{\tilde s_i}$
,
$\max \{ {\rm{F}}{{\rm{D}}_{\tilde {\boldsymbol{\sigma}} }}({\tilde s_i}{\tilde t_i}{\tilde t_i}') :{\tilde t_i}' \in L/{\tilde s_i}{\tilde t_i}\} \geqslant \dfrac{{{\mu _1}}}{{{{\tilde \varSigma }_{\rm{f}}}(\tilde {\boldsymbol{\sigma}} ) }}$
恒成立,故
$\lambda = \dfrac{{{\mu _1}}}{{{{\tilde \varSigma }_{\rm{f}}}(\tilde {\boldsymbol{\sigma}} ) }}$
,即
${\mu _1} = \lambda {\tilde \varSigma _{\rm{f}}}(\tilde{\boldsymbol{\sigma}} )$
,又
$ \mu = R({C_1}) = {\mu _1} $
,所以
$\mu = \lambda {\tilde \varSigma _{\rm{f}}}(\tilde{\boldsymbol{\sigma}} )$
。
充分性证明:(1) 如果
$R({C_1}) = {\tilde \varSigma _{\rm{f}}}(\tilde {\boldsymbol{\sigma}})$
,与必要性证明类似可得
$R({C_i}) = {\tilde \varSigma _{\rm{f}}}(\tilde {\boldsymbol{\sigma}} )$
对所有的
$ i $
均成立,即对任意
${\tilde s_i} \in {\varPsi _{\tilde{\boldsymbol{\sigma}} }}({\tilde \varSigma _{\rm{f}}}) ,{\tilde t_i} \in L/{\tilde s_i}$
,
$\max \{ {\rm{F}}{{\rm{D}}_{\tilde{\boldsymbol{\sigma}} }}({\tilde s_i}{\tilde t_i}{\tilde t_i}') :{\tilde t_i}' \in L/{\tilde s_i}{\tilde t_i}\} = 1$
恒成立。因为
$ \mu = R({C_1}) $
且
$R({C_1}) = {\tilde \varSigma _{\rm{f}}}(\tilde {\boldsymbol{\sigma}} )$
,所以
$\mu = {\tilde \varSigma _{\rm{f}}}(\tilde {\boldsymbol{\sigma}} )$
,又
$\mu = \lambda {\tilde \varSigma _{\rm{f}}}(\tilde{\boldsymbol{\sigma}} )$
,故
$ \lambda = 1 $
。所以
$\min \{ \max \{ {\rm{F}}{{\rm{D}}_{\tilde {\boldsymbol{\sigma}} }}(\tilde s\tilde t\tilde t') : \tilde t' \in L/ \tilde s\tilde t\} : \tilde s \in {\varPsi _{\tilde {\boldsymbol{\sigma}} }}({\tilde \varSigma _{\rm{f}}}) ,\tilde t \in$
$L/\tilde s\} = \lambda {\text{ = 1}}$
,所以
$\tilde G$
对于
$\tilde {\boldsymbol{\sigma}}$
是
$ \lambda $
弱模糊故障可诊断。
(2) 如果
$R({C_1}) = {\mu _1} < {\tilde \varSigma _{\rm{f}}}(\tilde {\boldsymbol{\sigma}} )$
,与必要性证明类似可得
${\mu _i} = \max \{ {\rm{F}}{{\rm{D}}_{\tilde{\boldsymbol{\sigma}} }}({\tilde s_i}'{\tilde t_i}'{\tilde t_i}'') :{\tilde t_i}'' \in L/{\tilde s_i}'{\tilde t_i}'\} {\tilde \varSigma _{\rm{f}}}$
$(\tilde {\boldsymbol{\sigma}} )$
,对所有的
$ i $
均成立,又
$\mu = \min \{ R({C_i}) ,i = 1,2,\cdots\} {\text{ = }}$
$\min \{ {\mu _i},i = 1, 2,\cdots\}$
,且
$\mu = \lambda {\tilde \varSigma _{\rm{f}}}(\tilde {\boldsymbol{\sigma}} )$
,则
$\lambda = \dfrac{{\min \{ {\mu _i},i = 1,2,\cdots\} }}{{{{\tilde \varSigma }_{\rm{f}}}(\tilde{\boldsymbol{\sigma}} ) }} = \min \{ \max \{ {\rm{F}}{{\rm{D}}_{\tilde {\boldsymbol{\sigma}} }}(\tilde s\tilde t\tilde t') : \tilde t' \in L/ \tilde s$
$\tilde t\} \} $
,所以
$\tilde G$
对于
$\tilde {\boldsymbol{\sigma}}$
是
$ \lambda $
弱模糊故障可诊断。
推论1
$\tilde G$
对于
$\tilde {\boldsymbol{\sigma}}$
是弱模糊故障不可诊断当且仅当对于
${\tilde G_{\rm{V}}}$
中所有的
$ F $
不确定环
$ {C_i} $
,有
$\mu = \min \{ R({C_i}) , i = 1,2,\cdots\}$
$ = {\text{0}} $
。
证明 在定理1中令
$ \lambda = {\text{0}} $
即可。
推论2
$\tilde G$
对于
$\tilde {\boldsymbol{\sigma}}$
是弱模糊故障可诊断当且仅当对于
${\tilde G_{\rm{V}}}$
中所有的
$ F $
不确定环
$ {C_i} $
,有
$\mu = \min \{ R({C_i}) ,i = 1, 2,\cdots\} = {\tilde \varSigma _{\rm{f}}}(\tilde {\boldsymbol{\sigma}} )$
;或者
${\tilde G_{\rm{V}}}$
中不存在
$ F $
不确定环。
证明 在定理1中令
$ \lambda = {\text{1}} $
即可。特别地,当
${\tilde G_{\rm{V}}}$
中不存在
$ F $
不确定环,则对于任意故障事件串
${\tilde s_i}$
和任意后续事件串
${\tilde t_i}$
,都有
${\rm{F}}{{\rm{D}}_{\tilde {\boldsymbol{\sigma}} }}({\tilde s_i}{\tilde t_i}) = 1$
,故定义1的(1)显然成立,故
$\tilde G$
对于
$\tilde {\boldsymbol{\sigma}}$
是弱故障可诊断。
5 应用
在这一节中,将用2个例子来说明本文提出的上述方法既可用于经典DES的弱故障诊断,又可用于FDES的弱模糊故障诊断。
5.1 在经典DES弱故障诊断的应用实例
例2 考虑文献[9]中的经典离散事件系统
$ G $
,如图1所示,文献[9]中已经证明
$ G $
是弱故障可诊断的。下面用本文提出的模糊离散事件系统的弱模糊故障诊断方法验证该结论。
根据文献[18],经典离散事件系统按照如下方法可视为一个特殊的模糊离散事件系统:状态向量的分量
$ {a_i} \in \{ 0,1\} $
,事件矩阵的分量
$ {a_{ij}} \in \{ 0,1\} $
,而对于每个事件
${\boldsymbol{\sigma}} \in E$
,
${\tilde \varSigma _{\rm{o}}}({\boldsymbol{\sigma}} ) \in \{ 0,1\}$
,
${\tilde \varSigma _{\rm{f}}}({\boldsymbol{\sigma}} )$
$ \in \{ 0,1\} $
。
由于
${\tilde \varSigma _{\rm{o}}} = \{ {\boldsymbol{a}},{\boldsymbol{b}},{\boldsymbol{c}},{\boldsymbol{d}},{\boldsymbol{e}}\}$
,
${ \tilde \varSigma _{{\rm{uo}}}} = \{ {{\boldsymbol{\sigma}} _{\rm{f}}},{{\boldsymbol{\sigma}} _{{\rm{uo}}}}\}$
,
${ \tilde \varSigma _{\rm{f}}} = \{ {{\boldsymbol{\sigma}} _{\rm{f}}}\}$
,因此各事件的可观隶属度和故障隶属度如下:
|
$ \begin{split}&{\tilde \varSigma _{\rm{o}}}({\boldsymbol{a}}) = {\tilde \varSigma _{\rm{o}}}({\boldsymbol{b}}) = {\tilde \varSigma _{\rm{o}}}({\boldsymbol{c}}) = {\tilde \varSigma _{\rm{o}}}({\boldsymbol{d}}) = {\tilde \varSigma _{\rm{o}}}({\boldsymbol{e}}) = 1\text{,}\\&\qquad\quad {\tilde \varSigma _{\rm{o}}}({{\boldsymbol{\sigma}} _{\rm{f}}}) = {\tilde \varSigma _{\rm{o}}}({{\boldsymbol{\sigma}} _{{\rm{uo}}}}) = 0\end{split}$
|
|
$ \quad\;\;\begin{split}&{\tilde \varSigma _{\rm{f}}}({\boldsymbol{a}}) = {\tilde \varSigma _{\rm{f}}}({\boldsymbol{b}}) = {\tilde \varSigma _{\rm{f}}}({\boldsymbol{c}}) = {\tilde \varSigma _{\rm{f}}}({\boldsymbol{d}}) = {\tilde \varSigma _{\rm{f}}}({\boldsymbol{e}}) = {\tilde \varSigma _{\rm{f}}}({{\boldsymbol{\sigma}} _{{\rm{uo}}}}) = 0\text{,}\\&\qquad\qquad\qquad {\tilde \varSigma _{\rm{f}}}({{\boldsymbol{\sigma}} _{\rm{f}}}) = 1\end{split} $
|
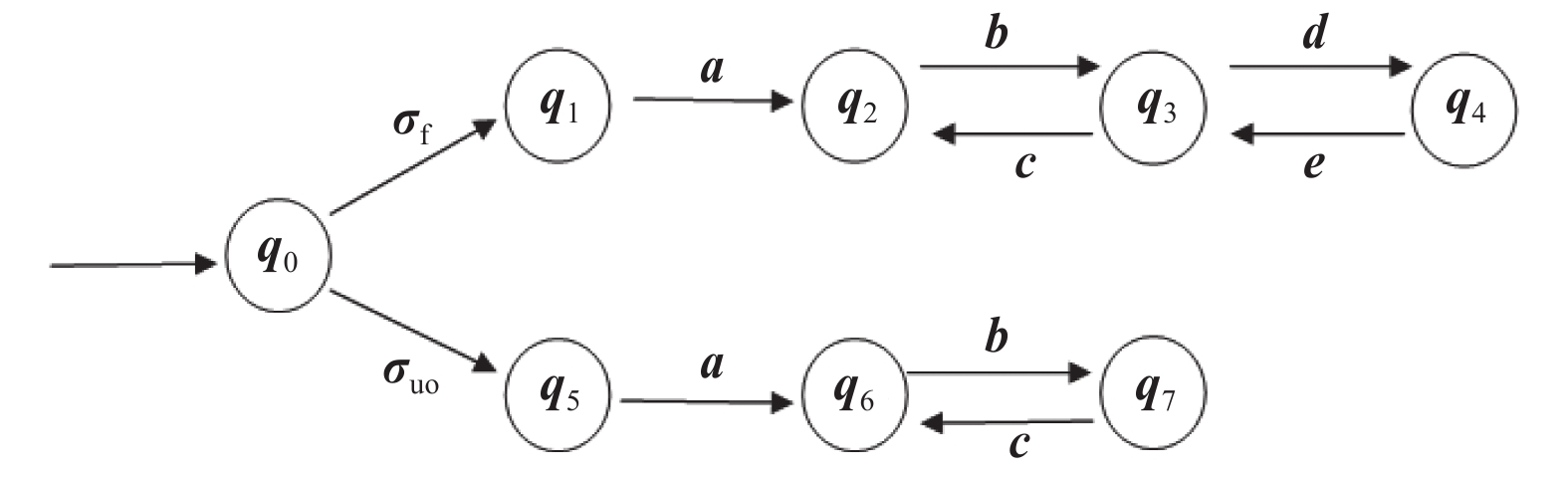
根据第4节对
${\boldsymbol{\sigma}} = {{\boldsymbol{\sigma}} _{\rm{f}}}$
构造相应的验证器自动机,如图2所示。
由图2可知,
${G_{\rm{V}}}$
中只存在一个
$ 0F $
不确定环
$C: ({{\boldsymbol{q}}_2},F,{{\boldsymbol{q}}_6},{N^0}) \mathop \to \limits^{\boldsymbol{b}} ({{\boldsymbol{q}}_3},F,{{\boldsymbol{q}}_7},{N^0}) \mathop \to \limits^{\boldsymbol{c}} ({{\boldsymbol{q}}_2},F,{{\boldsymbol{q}}_6},{N^0})$
。由于存在事件串
${\boldsymbol{bd}}$
使得
$ 0F $
不确定环
$ C $
到达
$F$
确定环
$C':({{\boldsymbol{q}}_4}, F,{{\boldsymbol{q}}_4},F) \mathop \to \limits^{\boldsymbol{e}} ({{\boldsymbol{q}}_3},F,{{\boldsymbol{q}}_3},F) \mathop \to \limits^{\boldsymbol{d}} ({{\boldsymbol{q}}_4},F,{{\boldsymbol{q}}_4},F)$
。根据定义3可得
$R(C) = 1$
,再根据推论2得
$ \mu = 1 $
,即
$ G $
对于
${\boldsymbol{\sigma}} = {{\boldsymbol{\sigma}} _{\rm{f}}}$
是弱故障可诊断,这与文献[9]得到的结论相吻合。
5.2 在FDES弱模糊故障诊断的应用实例
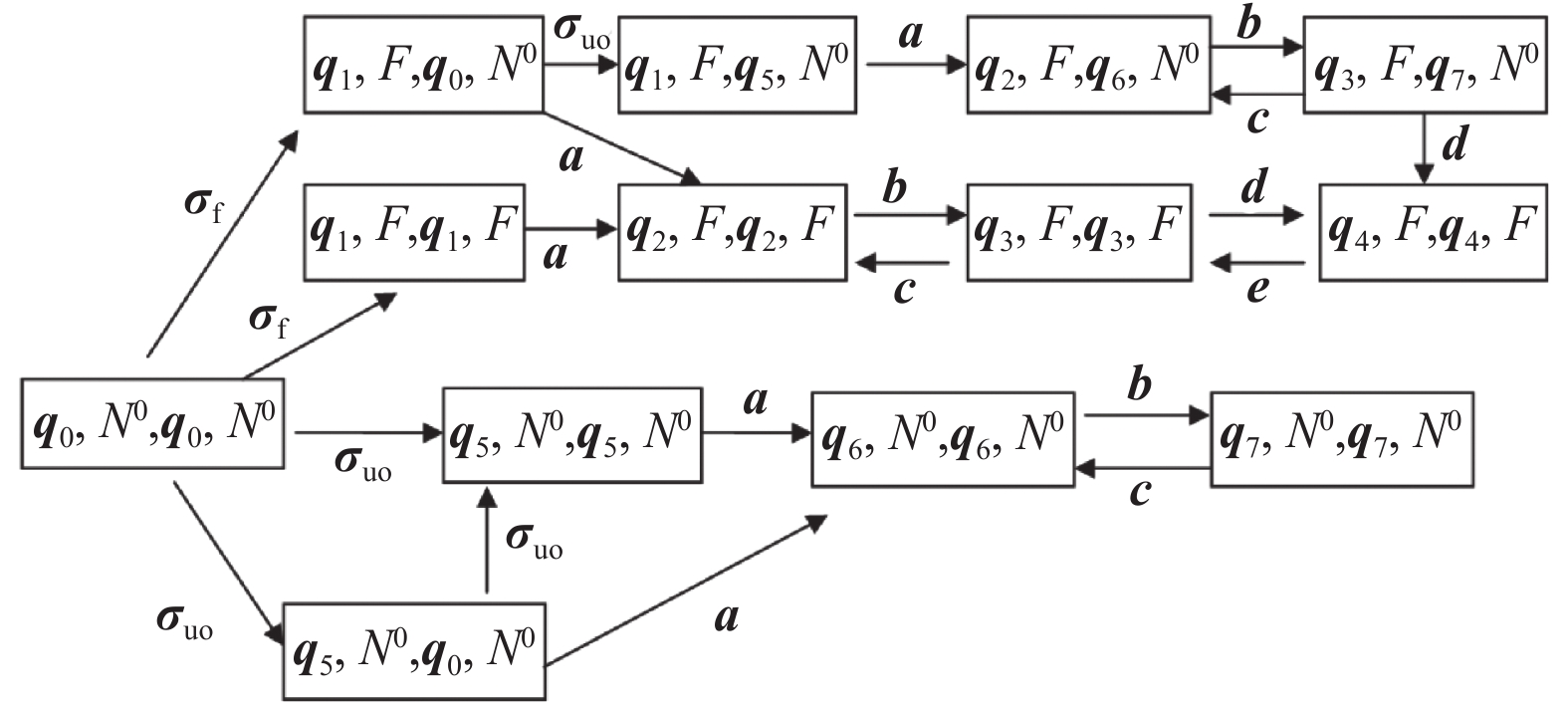
例3 下面以一个动物治疗过程进行建模,构建一个模糊离散事件系统并考虑其弱模糊故障可诊断性。
如果把“药物的副作用”视为一个故障事件,要考虑的问题是:对于一个已设计的动物治疗过程(如图3所示),能否在故障发生后将其及时检测出来(即在动物服用具有副作用药物后通过观测药物症状检测出动物是否服用了具有副作用的药物)?
为简单起见,假设医生将动物的状况划分为“好”“一般”和“虚弱”3个状态。由于“好”“一般”和“虚弱”3个状态划分的模糊或不确定性,动物的各个状态可以用一个三维向量
$\tilde{{\boldsymbol{q}}}={[{a}_{1}}{{a}_{2}}{{a}_{3}]}$
表示,其中
$ {a_1} $
、
$ {a_{\text{2}}} $
和
$ {a_{\text{3}}} $
分别代表动物处于“好”“一般”和“虚弱”3个状态的隶属度。假设医生根据医学理论和经验获知这4种药物——茶碱、溴化异丙托品、琥珀酸乙酯红霉素和多巴胺可能对治疗有用(如表1所示)。同样地,由于药物治疗后动物从一种状态转变为另一种状态也是不精确的[18-19]。因此,每种药物可用如下3×3矩阵表示
表 1(Table 1)
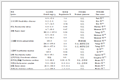
表 1 动物治疗过程各事件描述
Table 1 Description of each event during animal treatment
| 事件 |
描述 |
|
$\tilde{\boldsymbol{ \alpha}}$
|
对动物使用茶碱 |
|
$\tilde {\boldsymbol{\beta}}$
|
对动物使用溴化异丙托品 |
|
$\tilde {\boldsymbol{\gamma}} $
|
对动物使用琥珀酸乙酯红霉素 |
|
$\tilde{\boldsymbol{ \theta}}$
|
对动物使用多巴胺 |
|
表 1 动物治疗过程各事件描述
Table 1 Description of each event during animal treatment
|
|
$\tilde {\boldsymbol{\sigma}} = \left[ {\begin{array}{*{20}{c}} {{a_{11}}({\boldsymbol{\sigma}} )}&{{a_{1{\rm{2}}}}({\boldsymbol{\sigma}} )}&{{a_{1{\rm{3}}}}({\boldsymbol{\sigma}} )}\\ {{a_{21}}({\boldsymbol{\sigma}} )}&{{a_{{\rm{22}}}}({\boldsymbol{\sigma}} )}&{{a_{{\rm{23}}}}({\boldsymbol{\sigma}} )}\\ {{a_{31}}({\boldsymbol{\sigma}} )}&{{a_{{\rm{32}}}}({\boldsymbol{\sigma}} )}&{{a_{{\rm{33}}}}({\boldsymbol{\sigma}} )} \end{array}} \right] $
|
其中每个
${a_{ij}}({\boldsymbol{\sigma}} ) \in [0,1]$
表示动物服用该种药物
$\tilde{\boldsymbol{\sigma}}$
后,动物从“好”“一般”和“虚弱”状态转变为“好”“一般”和“虚弱”状态的隶属度。假设根据医学理论和医生经验各药物对应的模糊事件如下:
|
$\quad\tilde {\boldsymbol{\alpha}} = \left[ {\begin{array}{*{10}{l}} &0.4 &0.9 &0.4 \\ &0 &0.4 &0.4 \\ &0 &0 &0 \end{array}} \right] \\ \text{,}\tilde {\boldsymbol{\beta}} = \left[ {\begin{array}{*{10}{l}} &0.4 &0 &0 \\ &0.9 &0.4 &0 \\ &0.4 &0.4 &0.4 \end{array}} \right] $
|
|
$ \tilde {\boldsymbol{\gamma}} = \left[ {\begin{array}{*{10}{l}} &0.9&0.9&0.4 \\ &0&0.4&0.4 \\ &0&0&0.4 \end{array}} \right] \\ \text{,}\tilde {\boldsymbol{\theta}} = \left[ {\begin{array}{*{10}{l}} &0.5&0&0 \\ &0.1&0.1&0 \\ &0.1&0.1&0.1 \end{array}} \right]$
|
根据文献 [20],每个模糊事件在FDES框架中都具有一定的可观察隶属度。例如,有些药物的症状,如皮肤变白,医生可以清楚地看到,但有些症状只有通过特殊的医疗器械才能观察到。假设医生对各药物的可观察程度和药物副作用发生的可能性(即可观隶属度和故障隶属度)进行评估如下:
|
$ {\tilde \varSigma _{\rm{o}}}(\tilde {\boldsymbol{\alpha}} ) = 0.5 , {\tilde \varSigma _{\rm{o}}}(\tilde {\boldsymbol{\beta}} ) = 0.4 ,{\tilde \varSigma _{\rm{o}}}(\tilde {\boldsymbol{\gamma}} ) = 0.6,{\tilde \varSigma _{\rm{o}}}(\tilde {\boldsymbol{\theta}} ) = 0.3\text{;} $
|
|
$ {\tilde \varSigma _{\rm{f}}}(\tilde {\boldsymbol{\alpha}} ) = 0.1,{\tilde \varSigma _{\rm{f}}}(\tilde {\boldsymbol{\beta }}) = 0.2, {\tilde \varSigma _{\rm{f}}}(\tilde {\boldsymbol{\gamma}} ) = 0.3 ,{\tilde \varSigma _{\rm{f}}}(\tilde {\boldsymbol{\theta}} ) = 0.4 $
|
因为各种药物都有其可观隶属度和故障隶属度,无法确定哪些药物的症状在治疗过程中必定能观测到或必定存在副作用,因此需要分别以不同药物的可观隶属度和故障隶属度作为参照物,可观隶属度大于参照药物的可观隶属度的药物可视为可观事件;故障隶属度不小于参照药物的故障隶属度的药物视为具有副作用的药物(即故障事件)。
需要解决的问题是:以不同药物作为参照物(
$\tilde {\boldsymbol{\alpha}}$
,
$\tilde{\boldsymbol{ \beta}}$
,
$\tilde{\boldsymbol{ \gamma}}$
或
$\tilde {\boldsymbol{\theta}}$
),通过观察治疗过程中所使用药物的症状,是否能在动物服用具有副作用药物后将其检测出来?
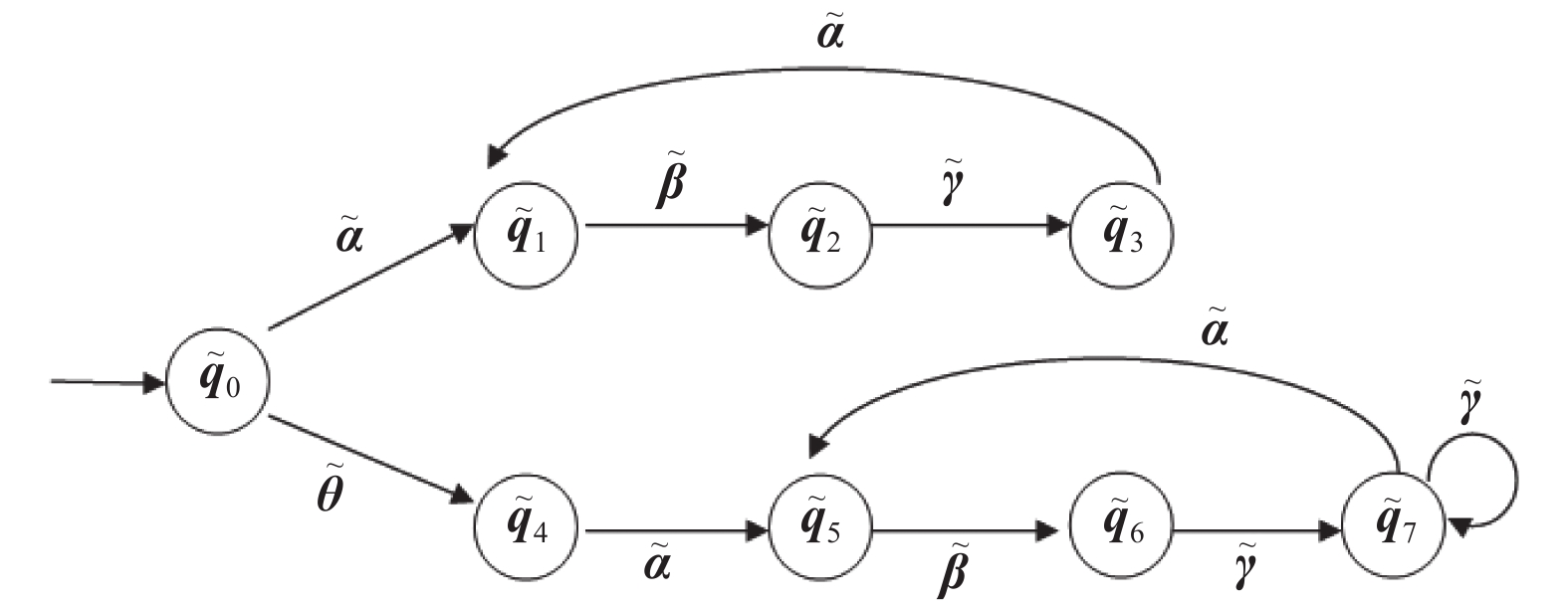
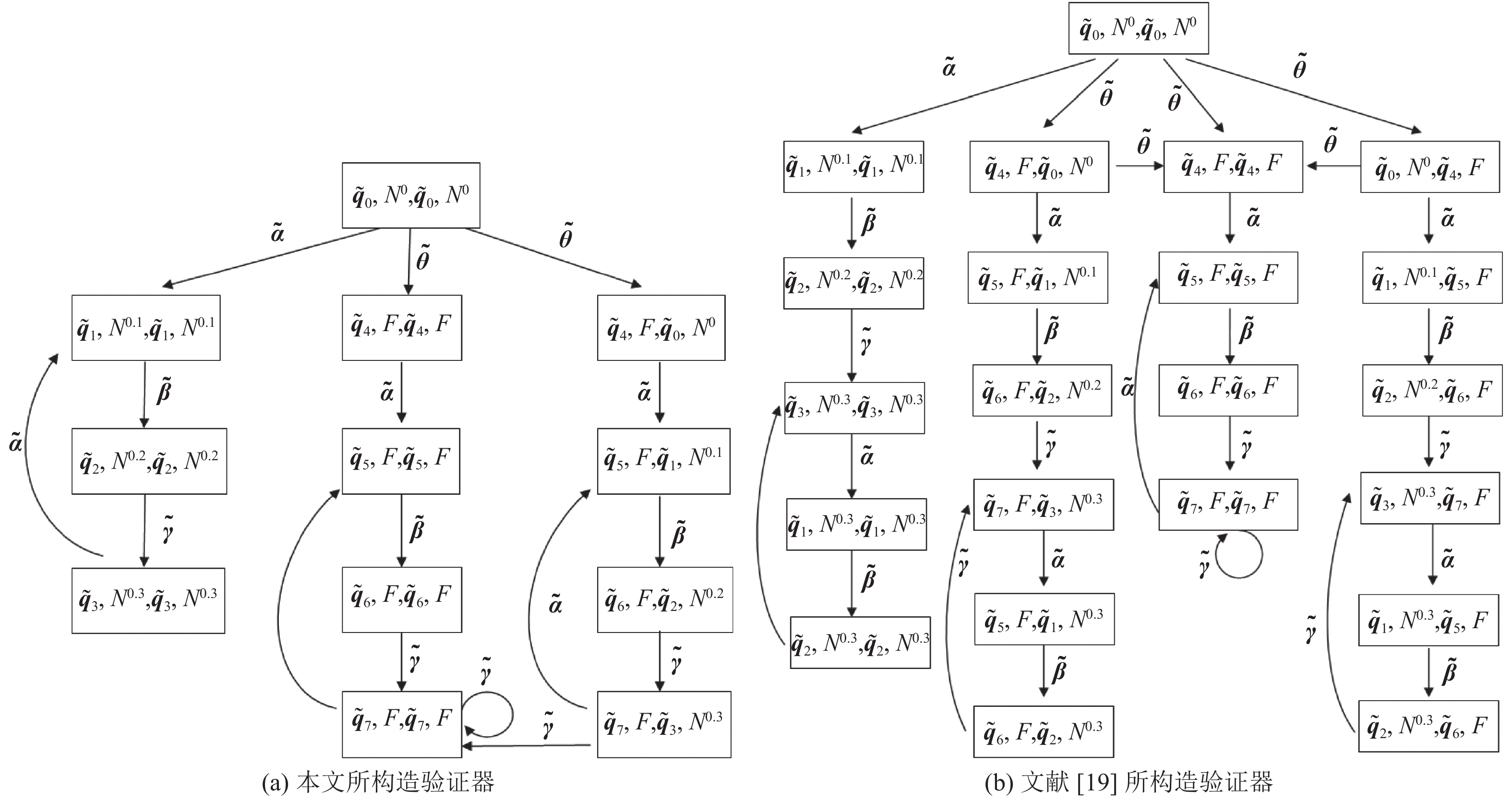
(1)根据本文第4节构造验证器的方法:对于
$\tilde {\boldsymbol{\sigma}} = \tilde {\boldsymbol{\theta}}$
构造的验证器如图4(a)所示,由于
${\tilde G_{\rm{V}}}$
中只存在一个
$ 0.3F $
不确定环
$C:({\tilde {\boldsymbol{q}}_7},F,{\tilde {\boldsymbol{q}}_3},{N^{0.3}}) \mathop \to \limits^{\tilde {\boldsymbol{\alpha}} }$
$({\tilde {\boldsymbol{q}}_5},F,{\tilde {\boldsymbol{q}}_1},{N^{0.3}}) \mathop \to \limits^{\tilde {\boldsymbol{\beta}} } ({\tilde {\boldsymbol{q}}_6},F,{\tilde {\boldsymbol{q}}_2},{N^{0.3}}) \mathop \to \limits^{\tilde {\boldsymbol{\gamma}} } ({\tilde {\boldsymbol{q}}_7},F,{\tilde {\boldsymbol{q}}_3},{N^{0.3}})$
。由于
$ 0.3F $
不确定环
$ C $
可到达
$F$
确定环
$C':({\tilde {\boldsymbol{q}}_{\text{7}}},F,{\tilde {\boldsymbol{q}}_{\text{7}}},F) \mathop \to \limits^{\tilde {\boldsymbol{\gamma}} } ({\tilde {\boldsymbol{q}}_{\text{7}}},F,{\tilde {\boldsymbol{q}}_{\text{7}}},F)$
,根据定义3可得
$R(C) = {\tilde \varSigma _{\rm{f}}}(\tilde {\boldsymbol{\theta}} ) = 0.4$
,再根据推理2得
$\mu {\text{ = }} {\tilde \varSigma _{\rm{f}}}(\tilde {\boldsymbol{\theta}} ) = {\text{0}}{\text{.4}}$
,所以
$\tilde G$
对于
$\tilde {\boldsymbol{\theta}}$
是弱模糊故障可诊断,这表明该治疗过程能够以100%的概率将动物服用多巴胺后的副作用检测出来。
(2)采用文献[19]构造验证器的方法:对于
$\tilde{\boldsymbol{\sigma}} = \tilde {\boldsymbol{\theta}}$
构造验证器如图4(b)所示。由于
${\tilde G_{\rm{V}}}$
中存在两个
$ 0.3F $
不确定环:
$({\tilde{\boldsymbol{ q}}_7},F,{\tilde {\boldsymbol{q}}_3},{N^{0.3}}) \mathop \to \limits^{\tilde {\boldsymbol{\alpha}} }$
$({\tilde {\boldsymbol{q}}_5},F,{\tilde {\boldsymbol{q}}_1},{N^{0.3}}) \mathop \to \limits^{\tilde {\boldsymbol{\beta}} } \left({\tilde {\boldsymbol{q}}_6},F,{\tilde {\boldsymbol{q}}_2},\right. {N^{0.3}}) \mathop \to \limits^{\tilde {\boldsymbol{\gamma}} } ({\tilde {\boldsymbol{q}}_7}, F, {\tilde {\boldsymbol{q}}_3},{N^{0.3}})$
和
$({\tilde {\boldsymbol{q}}_3},{N^{0.3}},{\tilde {\boldsymbol{q}}_7},F) \mathop \to \limits^{\tilde {\boldsymbol{\alpha}} } ({\tilde {\boldsymbol{q}}_1},{N^{0.3}},{\tilde {\boldsymbol{q}}_5}, F) \mathop \to \limits^{\tilde {\boldsymbol{\beta}} } ({\tilde {\boldsymbol{q}}_2},{N^{0.3}}, {\tilde {\boldsymbol{q}}_6}, F) \mathop \to \limits^{\tilde {\boldsymbol{\gamma}} } ({\tilde {\boldsymbol{q}}_3},{N^{0.3}}, {\tilde {\boldsymbol{q}}_7},F)$
。根据文献[19]的定理2,
$\tilde G$
对于
$\tilde {\boldsymbol{\theta}}$
的模糊故障诊断度为
$\lambda {\text{ = }}\dfrac{{{\text{0}}{\text{.3}}}}{{{{\tilde \varSigma }_{\rm{f}}}(\tilde {\boldsymbol{\theta}} ) }} = {\text{0}}{\text{.75}}$
,这表明该治疗过程能够以75%的概率将动物服用多巴胺后的副作用检测出来。
由此可知,对于同一个治疗过程,本文提出的弱模糊故障诊断相较于文献[19]的模糊故障诊断具有更高的概率将动物服用多巴胺后的副作用检测出来。
6 总结
本文研究了模糊离散事件系统的弱模糊故障诊断问题。对模糊离散事件系统的弱模糊故障可诊断性进行了形式化,构造了相应的验证器,推导出弱模糊故障可诊断性的充分必要条件,得到了验证模糊离散事件系统弱模糊故障诊断的方法。在本文的基础上,可进一步将集中系统推广到分布式系统。另外,本文是把经典离散事件系统的弱故障诊断推广到模糊离散事件系统,能否以类似的方法将其推广至弱故障预测也是很有意义的研究,这些问题将在后续研究中进一步深入探讨。
 2023, Vol. 40
2023, Vol. 40

