在现实世界中，复杂动态网络无时不在、无处不在。许多自然或者人造系统都可以通过复杂动态网络来进行建模和描述，例如万维网、遗传网络、电力网络、社会交际网络、交通网络等^[1-4]。除此之外，可以通过研究复杂网络拓扑结构，来解决实际网络中的问题，譬如电力网络大面积停电、病毒在网络中传播等。

在复杂动态网络中，存在一种有趣的集体性行为——同步。它不仅能够很好地解释一些神奇的自然现象(如萤火虫的同步闪烁) ，在工程中也有大量的应用(如多桩锤振动系统中的振动桩锤之间相位与速度需保持一致^[5]) 。由此，网络同步得到了一大批学者的关注。近年来，多种同步现象已被提出，譬如完全同步^[6]、簇同步^[7]、指数同步^[8]、外同步^[9]、有限时间同步^[10]等。有限时间同步是指网络中节点的运动轨迹与参考轨迹在有限时间内达到一致。因此，它可以加快同步的收敛速度以此来节约同步时间和成本。然而，大部分网络都不能自发地实现同步。因此，控制常常作为有效的手段来实现网络的同步。例如文献[10]提出了非周期间歇控制策略使得一类具有相同节点的驱动响应网络实现了有限时间完全同步；文献[11]提出了基于观测器的滑模控制策略使得一类具有未知扰动的复杂动态网络实现了同步；文献[12]提出了一种事件触发分散控制策略使得一类具有非周期拒绝服务式攻击的复杂动态网络达到同步。

然而，大多数现有文献中的同步考虑的是节点的所有状态分量达到一致。而在现实网络中，存在着网络节点的部分状态分量达到同步的现象与需求，并且所需关注的状态分量不限于节点状态的前一部分。例如：在交通网络中，同一车道行驶的汽车要求其行驶方向相同，而其行驶速度可以不同^[13]；在传染病网络中，医生关注点为个体中病毒的状态而不是个体的所有状态(例如身高、体重等) 。除此之外，对于由高维节点组成的网络来说，在一些特殊情况下，只需要关注每个节点部分状态分量的时间演化^[14]。因此，在这些情况下，只关注网络节点部分状态分量比关注其所有状态分量更具有经济效益并且更节约成本。针对上述现实与需求，已有一些关于部分状态分量同步的研究成果^[13-19]。例如：文献[15]提出了一种分布式同步策略使得一类二阶多智能体系统实现了部分状态分量同步；文献[16]得出了一类具有相同节点的复杂动态网络实现部分状态分量同步的两个充分条件；文献[17]研究了一类离散时间多智能体系统部分状态分量一致性问题。但值得注意的是，文献[13-14,16-19]中的部分状态分量同步策略，都是针对每个节点状态的前一部分状态分量而得出的。而在现实需求中，这一情况是极为特殊的。除此之外，文献[4,6,8-10,12-14,16-19]研究的成果都是基于由相同节点组成的网络或系统。而在现实网络中，网络节点的动力学可能不同(参数不同或者结构有差异) ，例如在电力网络中，不同的发电机可能具有不同的物理参数^[20]。综上所述，研究由不同节点组成的复杂动态网络部分状态分量同步是有实际意义和需求的。

目前，有关部分状态分量同步的研究^[13-19]均是在理论意义上当时间趋于无穷大时实现的。但在实际工程中，人们更希望网络能够在有限时间内实现同步(即有限时间同步) ，以此节约时间和成本。对此，已有大量关于有限时间同步的研究成果^[10,21-27]。例如文献[21]研究了一类具有不确定扰动的驱动响应混沌系统实现有限时间投影同步；文献[22]探究了一类具有混合耦合时滞的复杂动态网络实现有限时间同步问题。然而，目前尚缺乏有关复杂动态网络有限时间部分状态分量同步的研究成果。

根据上述讨论分析，本文主要研究一类具有不同节点的复杂动态网络有限时间部分状态分量同步问题。本文的主要贡献如下：(1) 引入了一个特殊对角矩阵来表述节点所需关注的状态分量(不限定于节点状态的前一部分状态分量) 并给出了有限时间部分状态分量同步的定义，这一方法比文献[13-19]的方法更加简便灵活；(2) 在一个较弱的假设下，提出了一个分散控制策略使得网络实现有限时间部分状态分量同步。

符号说明： ${{{{\boldsymbol{R}}}}^n}$ 和 ${{{{\boldsymbol{R}}}}^{m \times n}}$ 分别表示n维向量集和 $ m \times n $ 型矩阵集； ${{{{\boldsymbol{I}}}}_n}$ 代表n阶单位矩阵； ${{{{{{\boldsymbol{O}}}}}}_n}$ 表示n维零向量； ${{{{\boldsymbol{X}}}}^{\text{T}}}$ 表示向量 ${{{\boldsymbol{X}}}}$ 或矩阵 ${{{\boldsymbol{X}}}}$ 的转置； $ {{\bf{Z}}^ + } $ 代表正整数集； $ \left\| {{\text{ }} \cdot {\text{ }}} \right\| $ 表示一个向量的欧几里得范数或者一个矩阵的F范数； ${{{\boldsymbol{A}}}} \otimes {{{\boldsymbol{B}}}}$ 表示矩阵A和B的Kronecker积； $ {\lambda _{\max }}( * ) $ 表示 $ * $ 的最大特征值。

1 模型描述及前言

考虑如下由N个不同节点组成的复杂动态网络：

$ {\dot{{ {\boldsymbol{x}}}}_i} = {{{{\boldsymbol{f}}}}_i}({{{{\boldsymbol{x}}}}_i}) + \sigma \sum\limits_{j = 1}^N {{c_{ij}}{{{\boldsymbol{A}}}}{{{{\boldsymbol{x}}}}_j}} + {{{{\boldsymbol{u}}}}_i} \text{，} i = 1,\;2, \cdots ,N $

(1)

式中： ${{{{\boldsymbol{x}}}}_i} = {({x_{i1}},{x_{i2}}, \cdots ,{x_{in}}) ^{\text{T}}} \in {{{{\boldsymbol{R}}}}^n}$ 与 ${{{{\boldsymbol{u}}}}_i} \in {{{{\boldsymbol{R}}}}^n}$ 分别表示第i个节点的状态向量和控制输入， $ {x_{ik}} $ ( $ k = 1,\;2, \cdots ,\;n $ ) 表示节点i的第k个状态分量； ${{{{\boldsymbol{f}}}}_i}({{{{\boldsymbol{x}}}}_i}) \in {{{{\boldsymbol{R}}}}^n}$ 为非线性向量值函数； $ \sigma \gt 0 $ 为整体耦合强度； ${{{\boldsymbol{A}}}} \in {{{{\boldsymbol{R}}}}^{n \times n}}$ 为内部耦合矩阵且为对角阵。定义 ${{{\boldsymbol{C}}}} = {({c_{ij}}) _{N \times N}} \in {{{{\boldsymbol{R}}}}^{N \times N}}$ 为外部耦合结构矩阵，表示网络(1) 的拓扑结构和节点间的耦合强度。耦合系数 $ {c_{ij}} $ 定义如下： $ {c_{ij}} = {c_{ji}} $ 并且满足耗散条件 ${c_{ii}} = - \displaystyle\sum\limits_{\scriptstyle j = 1\atop\scriptstyle j \ne i}^N {{c_{ij}}}$ ，即考虑的网络(1)为无向网络。

不失一般性，本文考虑每个节点 $ m $ ( $ m \in {{\bf{Z}}^ + } $ ， $ 1 \leqslant m \leqslant n $ ) 个状态分量 $ {x_{i{n_1}}},{x_{i{n_2}}}, \cdots ,{x_{i{n_m}}} $ 的动态轨迹与参考目标的相应状态分量的动态轨迹实现同步，其中 $ {n}_{k} \in {{\bf{Z}}}^{+} $ ， $1 \leqslant {n_1} \lt {n_2} \lt \cdots \lt {n_m} \leqslant n,$ $ i = 1,\,2, \cdots ,N,$ $ k = 1,\,2, \cdots , m $ 。特别地，如果 $ m = n $ ，那么 $ {n_n} = n $ 。

为了给出部分状态分量同步的定义以及方便理论分析，引入一个特殊矩阵 ${{{\boldsymbol{P}}}} = {\rm{diag}}\,({p_1},{p_2}, \cdots ,{p_n})$ ，其中 $ {p_{{n_k}}} = 1 $ ( $ k = 1,\,2, \cdots ,m $ ) ，其余对角元素值为0。

记向量 $ {\bar {\boldsymbol{x}}_i} \in {{\boldsymbol{R}}^n}$ 为

$ {\bar{{ {\boldsymbol{x}}}}_i} = {{{\boldsymbol{P}}}}{{{{\boldsymbol{x}}}}_i} $

(2)

其中，向量 ${\bar {\boldsymbol{x}}_i}$ 只保留下被关注的状态分量 ${x_{i{n_1}}}, {x_{i{n_2}}}, \cdots , {x_{i{n_m}}} $ 的信息，并把不需要关注的状态分量信息置为0。

注1特殊对角矩阵P的作用，在于保留了节点状态向量 ${{{{\boldsymbol{x}}}}_i}$ 中被关注的状态分量信息，同时把不需要被关注的状态分量信息置为0。下面以一个由五维节点组成的复杂动态网络为例说明，假设 ${{{{\boldsymbol{x}}}}_i} = {({x_{i1}},{x_{i2}},{x_{i3}},{x_{i4}},{x_{i5}}) ^{\text{T}}}$ ，其需关注的是第1和第3个状态分量，即 $ {x_{i{n_1}}} = {x_{i1}} $ ( $ {n_1} = 1 $ ) ， $ {x_{i{n_2}}} = {x_{i3}} $ ( $ {n_2} = 3 $ ) ， ${{{\bar {\boldsymbol{x}}}}_i} = {({x_{i1}},\, 0, {x_{i3}},\,0,\, 0) ^{\text{T}}}$ 。此时特殊矩阵 ${{{\boldsymbol{P}}}} = {\rm{diag}}(1,\,0,\,1,\,0,\,0)$ ，使得(2) 式成立。

设 ${\boldsymbol{s}}={({{\boldsymbol{s}}}_{1},{s}_{2},\cdots ,{s}_{n}) }^{\text{T}}�{R{\boldsymbol{}}}^{n}$ 为参考轨迹的状态向量，且其动力学为 ${\dot{ {\boldsymbol{s}}}}$ ，其中 ${{s}_i}$ 为参考轨迹 ${{{\boldsymbol{s}}}}$ 的第i个状态分量， $ i = 1,\;2, \cdots ,\;n $ 。记 ${\bar{ {\boldsymbol{s}}}} = {{{\boldsymbol{Ps}}}}$ 。

定义1^[22,24] 　考虑复杂动态网络(1)。对于所有的节点i ( $ i = 1,\;2, \cdots ,\;N $ ) ，如果存在一个有限时刻 $ T \gt 0 $ ，满足

$ \mathop {\lim }\limits_{t \to T} \left\| {{{{{\bar {\boldsymbol{x}}}}}_i} - {{\bar {\boldsymbol{s}}}}} \right\| = \mathop {\lim }\limits_{t \to T} \left\| {{{{\boldsymbol{P}}}}({{{{\boldsymbol{x}}}}_i} - {{{\boldsymbol{s}}}}) } \right\| = 0 $

并且

$ \left\| {{{{{\bar {\boldsymbol{x}}}}}_i} - {{\bar {\boldsymbol{s}}}}} \right\| = 0 \text{，} \forall t \geqslant T $

则称复杂动态网络(1)实现了有限时间部分状态分量同步。

注2　定义1所描述的有限时间部分状态分量同步是借鉴文献[22,24]中的有限时间完全同步定义的。当定义1中的 ${{{\boldsymbol{P}}}} = {{{{\boldsymbol{I}}}}_n}$ 时，定义1即为[22,24]中的有限时间完全同步。

注3　可以从定义1看出，有限时间部分状态分量同步只关注节点i中部分状态分量 $ {x_{i{n_k}}} $ ( $ i = 1,\;2, \cdots ,\;N $ ， $ k = 1,\;2, \cdots ,\;m $ ) 在有限时间内分别收敛到相应的参考轨迹，而不考虑其他状态分量的时间演化，这与文献[10,21-27]中的有限时间同步不同。

引理1^[28] 　假设 $ V(t) $ 是连续的正定函数，且满足以下微分不等式条件：

$ \dot V(t) \leqslant - \alpha {V^\xi }(t) \text{，} \forall t \geqslant {t_0} \text{，} V({t_0}) \geqslant 0 $

式中： $ \alpha \gt 0 $ 和 $ \xi \in (0,\,1) $ 为两个常数。那么，对于任意给定的 $ {t_0} $ ， $ V(t) $ 满足以下不等式：

$ {V^{1 - \xi }}(t) \leqslant {V^{1 - \xi }}({t_0}) - \alpha (1 - \xi ) (t - {t_0}) \text{，} {t_0} \leqslant t \leqslant {t_1} $

并且

$ V(t) = 0 \text{，} \forall t \geqslant {t_1} $

式中： $t{}_1 = t{}_0 + \dfrac{{{V^{(1 - \xi ) }}(t{}_0) }}{{\alpha (1 - \xi ) }}$ 。

引理2^[29] 　若实数 ${{\textit{z}}_1},\,{{\textit{z}}_2}, \cdots ,\,{{\textit{z}}_n} \gt 0$ ， $ {l_1} $ ， $ {l_2} $ 为实数且满足 $ 0 \lt {l_1} \lt {l_2} $ ，则以下不等式成立：

$ {\left(\sum\limits_{i = 1}^n {{{\textit{z}}_i}^{{l_2}}} \right) ^{{1}/{{{l_2}}}}} \leqslant {\left(\sum\limits_{i = 1}^n {{{\textit{z}}_i}^{{l_1}}} \right) ^{{1}/{{{l_1}}}}} $

假设1 　假设网络(1) 中的非线性向量值函数 ${{{{\boldsymbol{f}}}}_i}({{{{\boldsymbol{x}}}}_i})$ ( $ i = 1,\,2, \cdots ,N $ ) 是有界的。即，存在正常数 $ {\eta _i} \in R $ ，使得 $\left\| {{{{{\boldsymbol{f}}}}_i}({{{\boldsymbol{x}}}}{}_i) } \right\| \leqslant \eta {}_i$ 。

2 控制器设计

在这一小节中，设计有效的分散控制器，保证复杂动态网络(1) 实现定义1意义下的有限时间部分状态分量同步。

为方便，记网络(1) 中节点i ( $ i = 1,\;2, \cdots ,\;N $ ) 的误差向量为 ${{{{\boldsymbol{r}}}}_i} = {{{{\boldsymbol{x}}}}_i} - {{{\boldsymbol{s}}}}$ ，并且记 ${{{\bar {\boldsymbol{r}}}}_i} = {{{\boldsymbol{P}}}}{{{{\boldsymbol{r}}}}_i} = {{{\bar {\boldsymbol{x}}}}_i} - {{\bar {\boldsymbol{s}}}}$ ，其中P为式(2)中的特殊对角矩阵。为简洁，记

$ {\text{sign}}({{{\bar {\boldsymbol{r}}}}_i}) = \left\{ {\begin{array}{*{20}{l}} \dfrac{{{{{{\bar {\boldsymbol{r}}}}}_i}}}{{\left\| {{{{{\bar {\boldsymbol{r}}}}}_i}} \right\|}},& {{{{\bar {\boldsymbol{r}}}}}_i} \ne {{{{\boldsymbol{O}}}}_n} \\ {{{{\boldsymbol{O}}}}_n},&{{{{\bar {\boldsymbol{r}}}}}_i} = {{{{\boldsymbol{O}}}}_n} \\ \end{array}} \right. $

控制目标：考虑复杂动态网络(1) 。设计控制器 ${{{{\boldsymbol{u}}}}_i}$ ，使得 $\left\| {{{{{\bar {\boldsymbol{x}}}}}_i} - {{\bar {\boldsymbol{s}}}}} \right\|\mathop \to \limits^{t \to {T_0}} 0$ 对所有的 $ i = 1,\;2, \cdots ,\;N $ 都成立，并且对于任意的 $ t \geqslant {T_0} $ ，都有 $\left\| {{{{{\bar {\boldsymbol{x}}}}}_i} - {{\bar {\boldsymbol{s}}}}} \right\| = 0$ 。其中 $ {T_0} $ 为某一有限时刻。

为了实现上述控制目标，本节提出如下分散控制器：

$ {{{{\boldsymbol{u}}}}_i} = - ({\eta _i} + K) {\text{sign}}({{{\bar {\boldsymbol{r}}}}_i}) + {{\dot {\boldsymbol{s}}}} - {\gamma _i}{{{{\boldsymbol{r}}}}_i} $

(3)

式中： $ {\eta _i} $ 为假设1中的正常数，K和 $ {\gamma _i} $ 为待定可调的正常数，并且 $ {\gamma _i} $ 满足 ${\gamma _i} \gt {\lambda _{\max }}(\sigma {{{\boldsymbol{C}}}} \otimes {{{\boldsymbol{A}}}})$ 。

定理1 　考虑复杂动态网络(1)。在定义1的意义下，如果假设1成立，则分散控制器(3)能够保证网络(1)在 $ {T_0} $ 时刻内实现部分状态分量同步，其中 ${T_0} = {t_0} + $ $\dfrac{{\sqrt 2 {V^{\tfrac{1}{2}}}({t_0}) }}{K}$ ， $V({t_0}) = \dfrac{1}{2}\displaystyle\sum\limits_{i = 1}^N {{{\bar {\boldsymbol{r}} }}_i^{\text{T}}({t_0}) {{{{\bar {\boldsymbol{r}} }}}_i}({t_0}) }$ 。

证明 　注意到外部耦合结构矩阵 ${{{\boldsymbol{C}}}} = {({c_{ij}}) _{N \times N}} \in {{{{\boldsymbol{R}}}}^{N \times N}}$ 满足零行和条件，因此可以得到 $\displaystyle\sum\limits_{j = 1}^N {{c_{ij}}{{{\boldsymbol{As}}}}} = {{{{\boldsymbol{O}}}}_n}$ 对所有的i ( $i = 1,\,2, \cdots, N$ ) 都成立。进一步，根据网络(1) 和控制器(3) ，可以得到误差系统：

$ {{{\dot {\boldsymbol{r}}}}_i} = {{{\dot {\boldsymbol{x}}}}_i} - {{\dot {\boldsymbol{s}}}}= {{{{\boldsymbol{f}}}}_i}({{{{\boldsymbol{x}}}}_i}) + \sigma \sum\limits_{j = 1}^N {{c_{ij}}{{{\boldsymbol{A}}}}{{{{\boldsymbol{x}}}}_j}} - ({\eta _i} + K) {\text{sign}}({{{\bar {\boldsymbol{r}}}}_i}) + {{\dot {\boldsymbol{s}}}}- $

$ {\gamma _i}{{{{\boldsymbol{r}}}}_i} - {{\dot {\boldsymbol{s}}}}= {{{{\boldsymbol{f}}}}_i}({{{{\boldsymbol{x}}}}_i}) + \sigma \sum\limits_{j = 1}^N {{c_{ij}}{{{\boldsymbol{A}}}}{{{{\boldsymbol{r}}}}_j}} - {\gamma _i}{{{{\boldsymbol{r}}}}_i} - ({\eta _i} + K) {\text{sign}}({{{\bar {\boldsymbol{r}}}}_i}) $

(4)

考虑以下正定函数：

$ V(t) = \frac{1}{2}\sum\limits_{i = 1}^N {{{\bar {\boldsymbol{r}}}}_i^{\text{T}}{{{{\bar {\boldsymbol{r}}}}}_i}} $

(5)

由于A为对角阵且P是一个对角元为0或1的对角矩阵，故有 ${{{\boldsymbol{PA}}}} = {{{\boldsymbol{AP}}}}$ ，且 ${{\bar {\boldsymbol{r}}}}_i^{\text{T}}{{{\boldsymbol{P}}}} = {({{{\boldsymbol{P}}}}{{{{\boldsymbol{r}}}}_i}) ^{\text{T}}}{{{\boldsymbol{P}}}} =$ ${{{\boldsymbol{r}}}}_i^{\text{T}}{{{{\boldsymbol{P}}}}^{\text{T}}}{{{\boldsymbol{P}}}} = {{{\boldsymbol{r}}}}_i^{\text{T}}{{{{\boldsymbol{P}}}}^{\text{T}}} = {{\bar {\boldsymbol{r}}}}_i^{\text{T}}$ 成立。并且，结合 ${\text{sign}}({{{\bar {\boldsymbol{r}}}}_i})$ 的定义，可以得出 ${{{\boldsymbol{P}}}}\,{\text{sign}}({{{\bar {\boldsymbol{r}}}}_i}) = {\text{sign}}({{{\bar {\boldsymbol{r}}}}_i})$ 。于是，正定函数 $ V(t) $ 沿误差方程(4)的导数为：

$\begin{split} &\dot V(t) = \sum\limits_{i = 1}^N {{{\bar {\boldsymbol{r}}}}_i^{\text{T}}{{\dot{\boldsymbol{ \bar r}}}_i}} = \sum\limits_{i = 1}^N {{{\bar {\boldsymbol{r}}}}_i^{\text{T}}{{{\boldsymbol{P}}}}\,{{{{\dot {\boldsymbol{r}}}}}_i}}= \sum\limits_{i = 1}^N {{\bar {\boldsymbol{r}}}}_i^{\text{T}}{{{\boldsymbol{P}}}}\,({{{{\boldsymbol{f}}}}_i}({{{{\boldsymbol{x}}}}_i}) + \\ & \sigma \sum\limits_{j = 1}^N {{c_{ij}}{{{\boldsymbol{A}}}}{{{{\boldsymbol{r}}}}_j}} - {\gamma _i}{{{{\boldsymbol{r}}}}_i}- ({\eta _i} + K) {\text{sign}}({{{\bar {\boldsymbol{r}}}}_i}) )=\\ & \sum\limits_{i = 1}^N {{{\bar {\boldsymbol{r}}}}_i^{\text{T}}({{{\boldsymbol{P}}}}\,{{{{\boldsymbol{f}}}}_i}({{{{\boldsymbol{x}}}}_i}) + \sigma \sum\limits_{j = 1}^N {{c_{ij}}{{{\boldsymbol{AP}}}}\,{{{{\boldsymbol{r}}}}_j}} - {\gamma _i}{{{\boldsymbol{P}}}}\,{{\boldsymbol{r}}_i}}-\\ & ({\eta _i} + K) {{{\boldsymbol{P}}}}\,{\text{sign}}({{{\bar {\boldsymbol{r}}}}_i}) )= \sum\limits_{i = 1}^N {{\bar {\boldsymbol{r}}}}_i^{\text{T}}({{{\boldsymbol{P}}}}{{{{\boldsymbol{f}}}}_i}({{{{\boldsymbol{x}}}}_i}) +\\ & \sigma \sum\limits_{j = 1}^N {{c_{ij}}{{{\boldsymbol{A}}}}\,{{{{\bar {\boldsymbol{r}}}}}_j}} - {\gamma _i}{{{\boldsymbol{\bar r}}}_i}- ({\eta _i} + K) {\text{sign}}({{{\bar {\boldsymbol{r}}}}_i}) )=\\ & \sum\limits_{i = 1}^N {{{\bar {\boldsymbol{r}}}}_i^{\text{T}}{{{\boldsymbol{P}}}}{{{{\boldsymbol{f}}}}_i}({{{{\boldsymbol{x}}}}_i}) } + \sigma \sum\limits_{i = 1}^N {\sum\limits_{j = 1}^N {{c_{ij}}{{\bar {\boldsymbol{r}}}}_i^{\text{T}}{{{\boldsymbol{A}}}}{{{{\bar {\boldsymbol{r}}}}}_j}} } - \sum\limits_{i = 1}^N {{\gamma _i}{{\bar{\boldsymbol{ r}}}}_i^{\text{T}}{{{{\bar {\boldsymbol{r}}}}}_i}}-\\ &\sum\limits_{i = 1}^N {({\eta _i} + K) {{\bar {\boldsymbol{r}}}}_i^{\text{T}}{\text{sign}}({{{{\bar {\boldsymbol{r}}}}}_i}) } =\sum\limits_{i = 1}^N {{{\bar {\boldsymbol{r}}}}_i^{\text{T}}{{{{\boldsymbol{f}}}}_i}({{{{\boldsymbol{x}}}}_i}) } +\\ & \sigma \sum\limits_{i = 1}^N {\sum\limits_{j = 1}^N {{c_{ij}}{{\bar {\boldsymbol{r}}}}_i^{\text{T}}{{{\boldsymbol{A}}}}{{{{\bar {\boldsymbol{r}}}}}_j}} } - \sum\limits_{i = 1}^N {{\gamma _i}{{\bar {\boldsymbol{r}}}}_i^{\text{T}}{{{{\bar {\boldsymbol{r}}}}}_i}}- \sum\limits_{i = 1}^N {({\eta _i} + K) \left\| {{{{{\bar {\boldsymbol{r}}}}}_i}} \right\|}\end{split}$

(6)

为方便，记 ${{\boldsymbol{r}}^{\boldsymbol{c}}} = {({\boldsymbol{\bar r}}_1^{\text{T}},{\boldsymbol{\bar r}}_2^{\text{T}}, \cdots ,{\boldsymbol{\bar r}}_N^{\text{T}}) ^{\text{T}}}$ 。进一步，结合假设1与式(6) ，可以推出

$\begin{split} & \dot V(t) \leqslant \sum\limits_{i = 1}^N {\left\| {{{{{\bar {\boldsymbol{r}}}}}_i}} \right\| \left\| {{{{{\boldsymbol{f}}}}_i}({{{{\boldsymbol{x}}}}_i}) } \right\|} + \sigma \sum\limits_{i = 1}^N {\sum\limits_{j = 1}^N {{c_{ij}}{{\bar {\boldsymbol{r}}}}_i^{\text{T}}{{{\boldsymbol{A}}}}{{{{\bar {\boldsymbol{r}}}}}_j}} } - \\& \sum\limits_{i = 1}^N {{\gamma _i}{{\bar {\boldsymbol{r}}}}_i^{\text{T}}{{{{\bar {\boldsymbol{r}}}}}_i}}-\sum\limits_{i = 1}^N {({\eta _i} + K) \left\| {{{{{\bar {\boldsymbol{r}}}}}_i}} \right\|}\leqslant \end{split}$

$ \begin{split} &\sum\limits_{i = 1}^N {{\eta _i}\left\| {{{{{\bar {\boldsymbol{r}}}}}_i}} \right\|} + {({{{{\boldsymbol{r}}}}^{{{\boldsymbol{c}}}}}) ^{\text{T}}}(\sigma {{{\boldsymbol{C}}}} \otimes {{{\boldsymbol{A}}}}) {{{{\boldsymbol{r}}}}^{{{\boldsymbol{c}}}}} - \sum\limits_{i = 1}^N {{\gamma _i}{{\bar {\boldsymbol{r}}}}_i^{\text{T}}{{{{\bar {\boldsymbol{r}}}}}_i}}-\\ &\sum\limits_{i = 1}^N {({\eta _i} + K) \left\| {{{{{\bar {\boldsymbol{r}}}}}_i}} \right\|}\leqslant \\ &{\lambda _{\max }}(\sigma {{{\boldsymbol{C}}}} \otimes {{{ {\boldsymbol{A}}}}}) {({{{{\boldsymbol{r}}}}^{{{\boldsymbol{c}}}}}) ^{\text{T}}}{{{{\boldsymbol{r}}}}^{{{\boldsymbol{c}}}}} - \sum\limits_{i = 1}^N {{\gamma _i}{{\bar {\boldsymbol{r}}}}_i^{\text{T}}{{{{\bar {\boldsymbol{r}}}}}_i}} - K\sum\limits_{i = 1}^N {\left\| {{{{{\bar {\boldsymbol{r}}}}}_i}} \right\|}=\\& {\lambda _{\max }}(\sigma {\boldsymbol{C}} \otimes {\boldsymbol{A}}) \sum\limits_{i = 1}^N {{\boldsymbol{\bar r}}_i^{\text{T}}{{{\boldsymbol{\bar r}}}_i}} - \sum\limits_{i = 1}^N {{\gamma _i}{\boldsymbol{\bar r}}_i^{\text{T}}{{{\boldsymbol{\bar r}}}_i}} - K\sum\limits_{i = 1}^N {\left\| {{{{\boldsymbol{\bar r}}}_i}} \right\|} \end{split}$

(7)

由于 $ {\gamma _i} \gt {\lambda _{\max }}(\sigma {\boldsymbol{C}} \otimes {\boldsymbol{A}}) $ ，故有

$ {\lambda _{\max }}(\sigma {\boldsymbol{C}} \otimes {\boldsymbol{A}}) \sum\limits_{i = 1}^N {{\boldsymbol{\bar r}}_i^{\text{T}}{{{\boldsymbol{\bar r}}}_i}} - \sum\limits_{i = 1}^N {{\gamma _i}{\boldsymbol{\bar r}}_i^{\text{T}}{{{\boldsymbol{\bar r}}}_i}} \leqslant 0 $

(8)

据引理2，可得 ${(\displaystyle\sum\limits_{i = 1}^N {{\boldsymbol{\bar r}}_i^{\text{T}}{{{\boldsymbol{\bar r}}}_i}} ) ^{{1}/{2}}} = {(\displaystyle\sum\limits_{i = 1}^N {{{\left\| {{{{\boldsymbol{\bar r}}}_i}} \right\|}^2}} ) ^{{1}/{2}}} \leqslant \displaystyle\sum\limits_{i = 1}^N {\left\| {{{{\boldsymbol{\bar r}}}_i}} \right\|}$ 。由于K为正常数，因此可以推出

$ - K\sum\limits_{i = 1}^N {\left\| {{{{\boldsymbol{\bar r}}}_i}} \right\|} \leqslant - K{(\sum\limits_{i = 1}^N {{\boldsymbol{\bar r}}_i^{\text{T}}{{{\boldsymbol{\bar r}}}_i}} ) ^{{1}/{2}}} $

(9)

结合式(5)、式(7)和式(9) ，可以得到

$ \dot V(t) \leqslant - K{(\sum\limits_{i = 1}^N {{\boldsymbol{\bar r}}_i^{\text{T}}{{{\boldsymbol{\bar r}}}_i}} ) ^{{1}/{2}}} = - K{(2V(t) ) ^{{1}/{2}}} = - \sqrt 2 K{V^{{1}/{2}}}(t) $

(10)

根据引理1，当 ${T_0} = {t_0} + \dfrac{{\sqrt 2 {V^{{1}/{2}}}({t_0}) }}{K}$ 时， $ V({T_0}) = 0 $ ，且对于 $ \forall t \geqslant {T_0} $ ，有 $ V(t) = 0 $ 成立。由式(5) 和式(10) 可知， $ V(t) \geqslant 0 $ 且 $ \dot V(t) \leqslant 0 $ 。因此 $ \mathop {\lim }\limits_{t \to {T_0}} V(t) = V({T_0}) = 0 $ ，故 $\mathop {\lim }\limits_{t \to {T_0}} \left\| {{{{\boldsymbol{\bar r}}}_i}} \right\| = \mathop {\lim }\limits_{t \to {T_0}} \left\| {{{{\boldsymbol{\bar x}}}_i} - {\boldsymbol{\bar s}}} \right\| = 0$ ，并且对于 $ \forall t \geqslant {T_0} $ ，有 $ \left\| {{{{\boldsymbol{\bar x}}}_i} - {\boldsymbol{\bar s}}} \right\| = 0 $ 。于是，在定义1的意义上，网络(1) 实现了有限时间部分状态分量同步。

证毕。

注4　从式(3) 可以看出，分散控制器 ${{{{\boldsymbol{u}}}}_i}$ 只需要节点i和参考轨迹的信息，并不需要网络中其他节点的信息。因此，本文的有限时间部分状态分量同步控制器具有维数低、成本低和易实现的优点。

注5　值得注意的是，文献[10,22,25-27]所提出的有限时间同步控制器不仅需要自身节点和参考轨迹的信息，还需要网络中其他节点的信息，这与本文所设计的分散控制器不同。除此之外，文献[10,22,24-27]提出的有限时间同步控制结论是针对由相同节点组成的复杂网络，而本文所探讨的有限时间同步是针对由不同节点组成的复杂网络。

注6　定理1的使用步骤如下。

步骤1：针对网络模型(1) ，判断外部耦合结构矩阵 $ {\boldsymbol{C}} = {({c_{ij}}) _{N \times N}} $ 是否为对称矩阵并且满足耗散条件，判断网络(1) 中的非线性向量值函数 $ {{\boldsymbol{f}}_i}({{\boldsymbol{x}}_i}) $ 是否满足假设1，若满足，则进行步骤2，否则停止；

步骤2：根据实际情况，给出每个节点所关注的部分状态分量，定出特殊矩阵P；

步骤3：计算 $ \sigma {\boldsymbol{C}} \otimes {\boldsymbol{A}} $ 的最大特征值，根据定理1，给出在分散控制器(3) 中的参量 $ {\eta _i} $ 、 $ {\gamma _i} $ 和 $ K $ 。

3 数值仿真

在这一小节，借助Matlab数值仿真来验证本文理论结果的有效性及正确性。

考虑10个分别由Lorenz混沌系统与Rössler混沌系统组成的复杂动态网络。

第 $ i $ 个孤立节点为Lorenz混沌系统^[30]，其中

$ \begin{split} &{{\boldsymbol{f}}_i}({{\boldsymbol{x}}_i}) = {[{b_1}({x_{i2}} - {x_{i1}}) ,\,{d_1}{x_{i1}} - {x_{i1}}{x_{i3}} - {x_{i2}},\,{x_{i1}}{x_{i2}} - {h_1}{x_{i3}}]^{\text{T}}}\\ & \end{split}$

(11)

式中： $ {b_1} = 10 $ ， $ {d_1} = 28 $ ， ${h_1} = \dfrac{8}{3}$ ， $ i = 1,\,2,\,3,\,4,\,5 $ 。

第 $ j $ 个孤立节点为Rössler混沌系统^[31]，其中

$ {{\boldsymbol{f}}_j}({{\boldsymbol{x}}_j}) = {[ - {x_{j2}} - {x_{j3}},\;{x_{j1}} + {b_2}{x_{j2}},\;({x_{j1}} - {d_2}) {x_{j3}} + 0.2]^{\text{T}}} $

(12)

式中： $ {b_2} = 0.2 $ ， $ {d_2} = 5.7 $ ， $ j = 6,\,7,\,8,\,9,\,10 $ 。

不失一般性，网络(1) 的其他参量选取如下：

$ \begin{split} &{\boldsymbol{C}} = \left[ {\begin{array}{*{20}{r}} { - 7}&1&3&{ - 1}&0&2&0&1&{ - 3}&4 \\ 1&{ - 3}&{ - 1}&0&1&0&2&{ - 2}&{ - 1}&3 \\ 3&{ - 1}&{ - 4}&1&1&{ - 1}&1&1&{ - 2}&1 \\ { - 1}&0&1&{ - 1}&2&{ - 2}&{ - 1}&{ - 1}&1&2 \\ 0&1&1&2&{ - 9}&{ - 1}&0&2&0&4 \\ 2&0&{ - 1}&{ - 2}&{ - 1}&3&0&{ - 1}&2&{ - 2} \\ 0&2&1&{ - 1}&0&0&{ - 5}&0&1&2 \\ 1&{ - 2}&1&{ - 1}&2&{ - 1}&0&{ - 2}&0&2 \\ { - 3}&{ - 1}&{ - 2}&1&0&2&1&0&1&1 \\ 4&3&1&2&4&{ - 2}&2&2&1&{ - 17} \end{array}} \right]\\ & \end{split} $

(13)

$ {\boldsymbol{A}} = {\text{diag}}(2,\,0,\, - 1) \text{，} \sigma = 2 $

(14)

给出参考轨迹s的动力学方程^[32]为

$ {{\dot {\boldsymbol{s}}}} = {[{s_2}, - {s_1},\sin t \cdot {s_3}]^{\text{T}}} $

(15)

在接下来的仿真中，选取以下初始值：

$ {{\boldsymbol{x}}_i}(0) = 2{\text{rand}}(3,\,1) - 1 \text{，} {\boldsymbol{s}}(0) = 2{\text{rand}}(3,\,1) - 1 $

(16)

其中 $ {\text{rand}}(3,1) $ 表示一个服从均匀分布的3维随机向量，其每个分量的取值区间为(0,1) 。

由文献[30-31]可知，Lorenz混沌系统和Rössler混沌系统是有界的。因此，假设1成立。

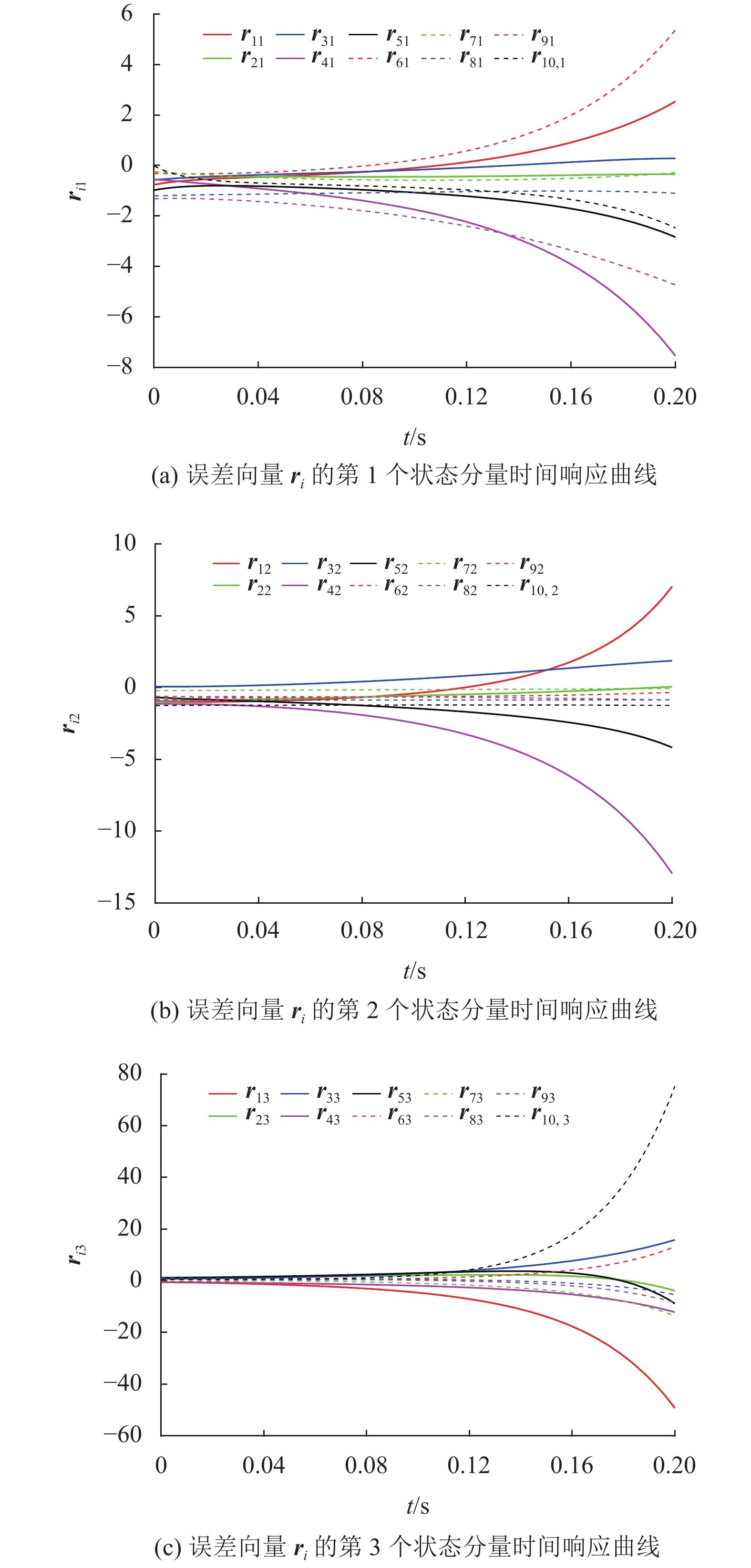
当复杂动态网络(1) 中的节点不受控制，即(1) 中的 $ {{{{\boldsymbol{u}}}}_i} $ 为零向量时，具有参数(11)~(16) 的网络(1)的同步误差仿真结果如图1所示。

从图1可以看出具有参数(11)~(16)的复杂动态网络(1)不能自发地实现部分状态分量同步。下面，利用控制器(3)来协助网络(1)实现有限时间部分状态分量同步。

控制器(3)中的参数选取如下：

$ {\eta _i} = 50 \text{，} {\gamma _i} = 70 \text{，} K = 2 \text{，} i = 1,\,2, \cdots ,\,10 $

(17)

下面给出2种网络(1)所需关注同步状态分量的情形，并且在图2和图3给出相应的仿真结果。

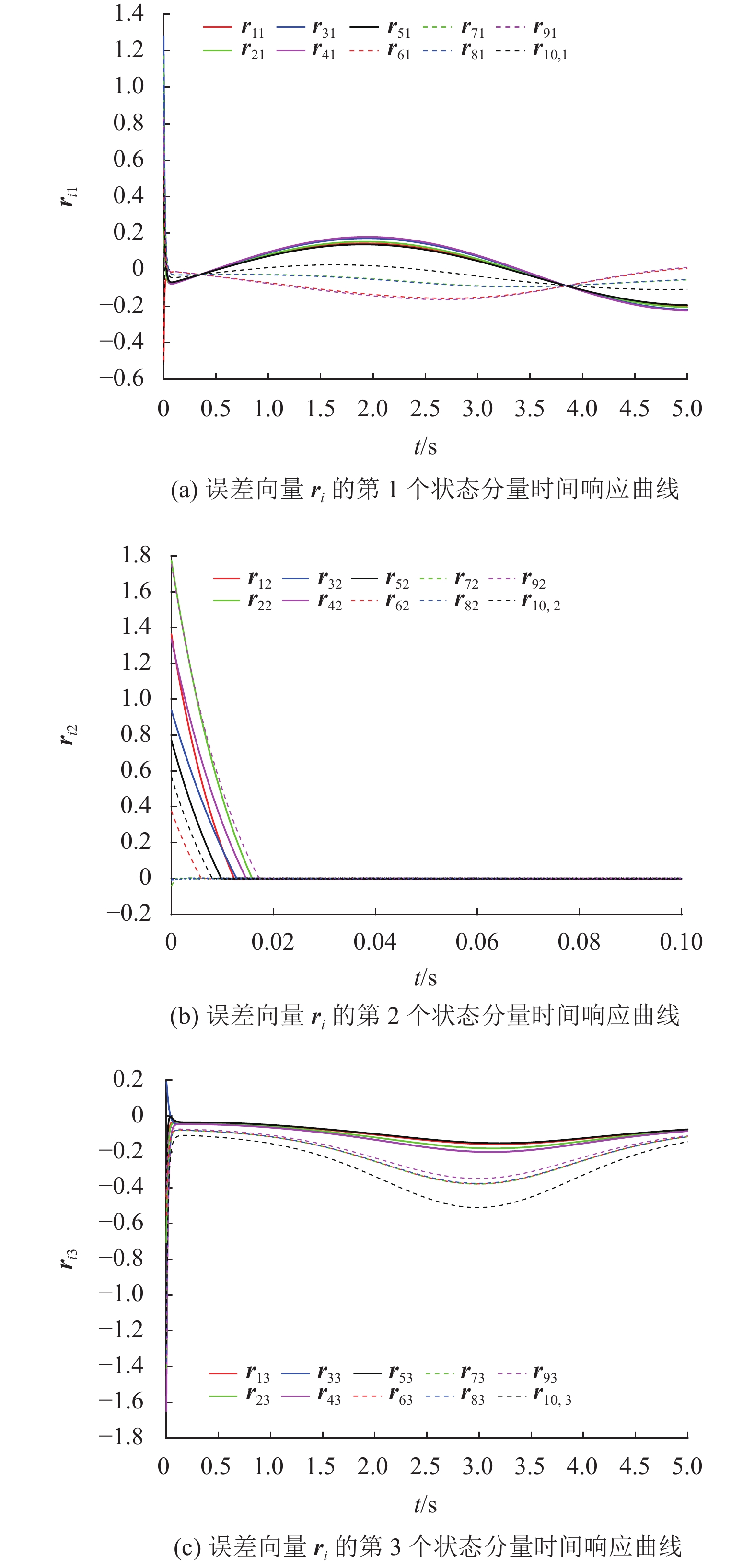
情形1考虑网络(1) 中每个节点的第2个状态分量实现同步，即选取

$ {{{\boldsymbol{P}}}} = {\text{diag}}(0,\,1,\,0) $

(18)

由图2可以观察到，网络中每个节点的第2个状态分量实现了有限时间同步，而每个节点的第1和第3个状态分量没有实现同步。

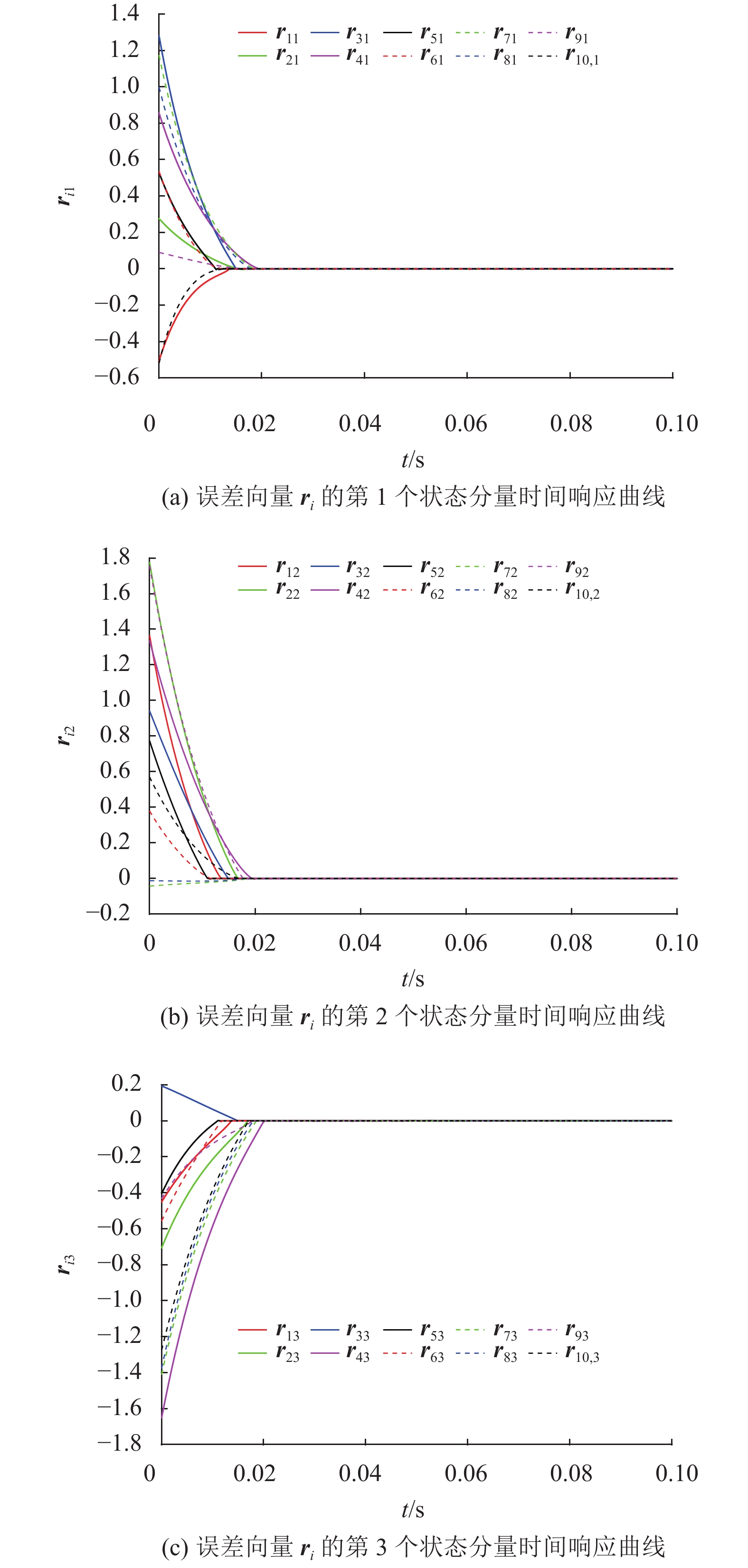
情形2考虑网络(1) 中每个节点的所有状态分量实现同步，即选取

$ {{{\boldsymbol{P}}}} = {\text{diag}}(1,\,1,\,1) $

(19)

由图3可以观察到，网络中每个节点所有状态分量均实现了有限时间同步。即网络实现了有限时间完全同步，借此也可以说明完全同步是部分状态分量同步的特例。

图1～3充分展示了具有参数(11)~(17) 的复杂动态网络(1)通过分散控制器(3)实现了有限时间部分状态分量同步，从而验证了定理1的有效性。从情形1和情形2可以看出，根据实际情况，所需关注的状态分量可以通过不同的特殊矩阵P来体现。

4 结论

本文主要探讨了一类具有不同节点的无向网络有限时间部分状态分量同步问题。首先，确定所需关注的状态分量，引入一个特殊对角矩阵来表述这些状态分量，并且可以根据实际情况，通过更改特殊矩阵来改变所需关注的状态分量。基于这一特殊矩阵，给出了有限时间部分状态分量同步的定义。进一步，基于有限时间稳定性定理以及控制理论，设计分散控制器，使得网络实现了有限时间部分状态分量同步。最后，通过了一个数值仿真例子，验证了理论结果的正确性和有效性。在未来的研究中，将进一步研究有向时变时滞复杂网络有限时间部分状态分量同步问题，并且将考虑使用滑模控制、脉冲控制、间歇控制等不同的控制手段使网络实现同步。