近年来，随着无线设备和移动应用的不断普及，数据流量呈爆炸式增长，有效利用频谱资源是未来无线通信网络应对这种数据流量高速增长的关键。为了应对频谱通信资源短缺的问题，动态频谱接入(Dynamic Spectrum Access, DSA) 技术可以发挥有效的作用。动态频谱接入模型主要分为3种：动态开放模型、开放共享模型和分层接入模型^[1]。3种模型之中分层接入模型与现有频谱接入方式兼容性较好，其侧重点在于将频谱资源划分给主用户(Primary User, PU) 与次用户(Secondary User, SU) ，主用户在进行频谱通信时候拥有优先权。在分层接入模型之中的覆盖式模式即机会式频谱接入，可以帮助次用户在感知频谱空穴之后接入空闲频谱，这样可以有效地降低频谱资源短缺带来的压力。

DSA技术作为频谱共享、提高频谱利用率的关键技术之一，近年来备受关注。研究人员已经为提升频谱效率提出了不少解决办法。文献[2-4]介绍了基于图论和博弈论方法来解决频谱分配问题，但是这类方法需要所有用户提前知道所处环境的频谱信道状态信息，而大多时候次用户是无法获取系统的完整信息的，只能基于部分感知信息选择信道。不过强化学习中基于无模型策略的学习方法，可以在不需要系统环境的先验知识基础上，通过智能体与环境不断交互学习使得智能体找到最优策略，比如文献[5-6]将Q学习方法运用到物联网通信中，但Q学习方法收敛缓慢且不能处理高维度的状态和动作空间，为此研究人员通过结合了深度学习与Q学习的深度Q学习方法来满足对于认知无线环境的自适应管理^[7-8]。目前深度Q学习在频谱接入技术研究中已经取得了一些进展。例如：文献[9]提出了一种基于深度Q学习的频谱分配方法，以支持D2D用户无线接入网络的子信道分配和模式选择。文献[10]也提出了基于深度Q学习的频谱分配方法，帮助次用户在多个微信蜂窝基站中进行关联和资源分配。虽然文献[9-10]中深度Q学习方法一定程度上克服了Q学习方法所带来的缺点，但是该类方法主要使用了集中式的深度强化学习算法来帮助次用户进行频谱分配，并没有考虑到随着次用户数量增加、动作空间变大的情况带来的“维数灾难”问题^[11-12]。并且这类方法在训练神经网络过程中对于数据的采集方式为传统的均匀采样，没有充分利用数据池中比较“有效”的数据以帮助智能体进行更高效的学习。

因此本文提出了一种基于分布式优先经验池结合双深度Q网络(Distributed Priority Experience Pool and Double Deep Q Network, DPEP-DDQN) 的多用户动态频谱接入方法，用来帮助次用户根据自己的通信需求和所处环境信息来进行信道选择。其贡献如下。

(1) 为了解决动作空间增大带来的维数灾难问题，采用了分布式强化学习框架，将每个次用户视为一个智能体来对动态频谱接入进行建模分析。

(2) 为了使神经网络模型可以更充分利用有效数据来进行训练，采用优先经验回放算法对神经网络中的训练样本进行优化，加快收敛速度。

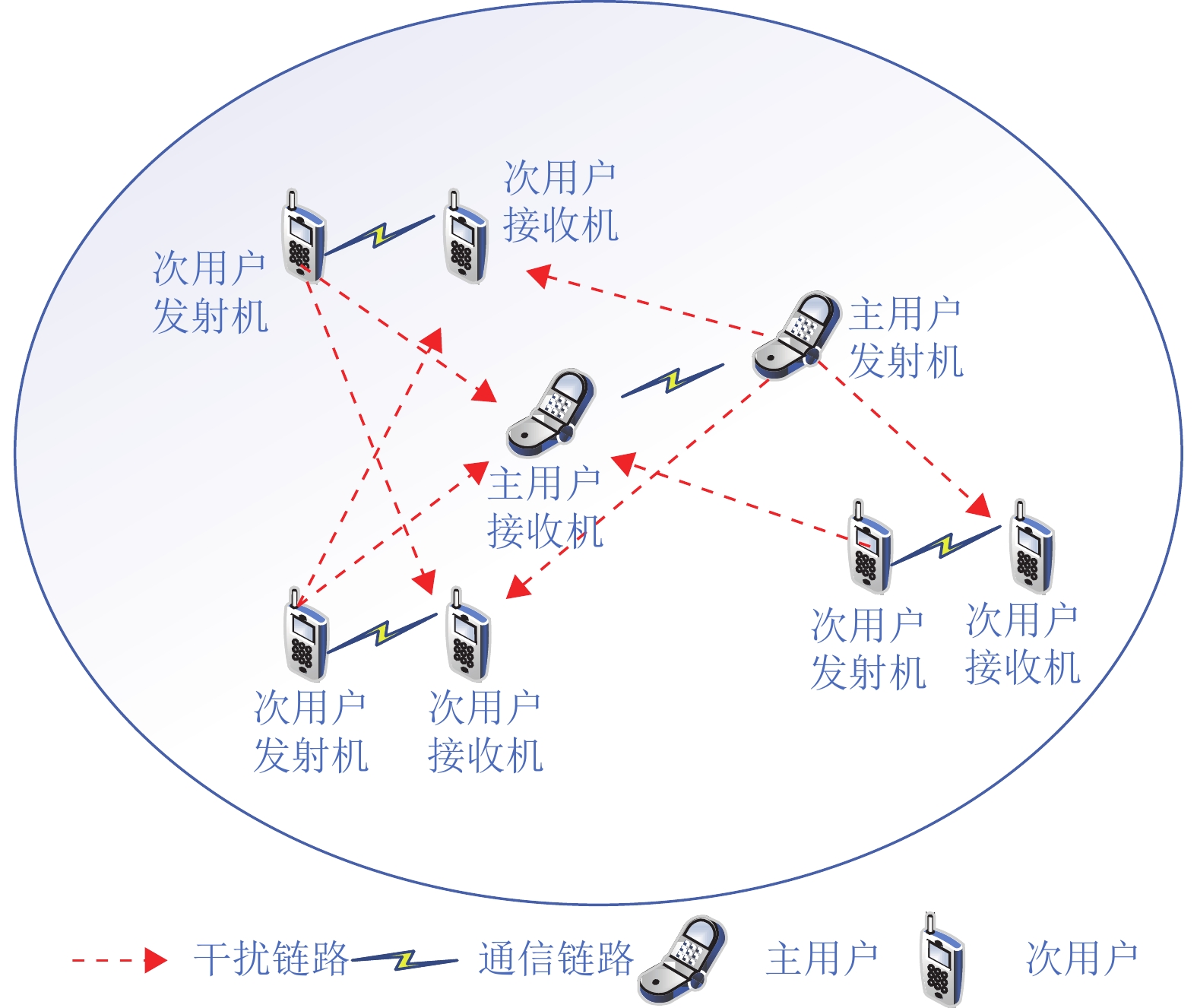
1 系统模型

如图1所示，假设一个微小区的环境中随机分布若干主用户和次用户。主用户集合为 $ {M}=\{{m}_{1},{m}_{2},\cdots ,{m}_{J}\} $ 一个主用户由一个主用户发射机和主用户接收机组成， $ J $ 为主用户总数。次用户集合为 $ {N}= \{{n}_{1},{n}_{2},\cdots ,{n}_{L}\} $ ，其中一个次用户由一个次用户发射机和次用户接收机组成， $ L $ 为次用户总数。假设存在 $ J $ 条信道正交授权可以均匀分配给各个主用户正常数据通信，主用户通信时不需要考虑其余次用户是否存在，只需根据自身传输需求进行传输即可。次用户在进行频谱接入的时候不可以打扰到主用户的正常通信，即主用户在该条信道进行数据通信时次用户不可以接入，只有当主用户不使用该频谱信道的情况下次用户才可以通过机会式接入主用户的授权信道进行通信。此外，若主用户所在信道发生碰撞，主用户会将信道碰撞的相关警告信息广播给次用户以对自身保护。因此次用户需要根据自身感知情况所获得的信息，通过自身学习来选择信道。

1.1 信道状态模型

次用户要想成功接入信道，需要感知想选择信道的状态。每条信道可能处于两种状态：空闲状态(1) 或者活跃状态(0) 。若信道处于活跃状态，表明有主用户在使用这条信道，次用户在此期间不能接入该条信道，否则该时间段主用户没有使用这条信道，这时候次用户可以采用机会式接入该条信道进行通信。第 $ j $ 条信道的活动状态可被描述为马尔科夫链，如图2所示，其状态转移概率可表示为

$ \begin{array}{c}{{\boldsymbol{\xi}} }_{j}=\left[\begin{array}{cc}{\xi }_{00}^{j}& {\xi }_{01}^{j}\\ {\xi }_{10}^{j}& {\xi }_{11}^{j}\end{array}\right]\end{array} $

(1)

式中： $ {\xi }_{ab}^{j}=\mathrm{P}\mathrm{r}\{\mathrm{下}\mathrm{一}\mathrm{状}\mathrm{态}b|\mathrm{当}\mathrm{前}\mathrm{状}\mathrm{态}a\},( a,b\in {0,1})$ 。

1.2 传输速率模型

涉及到的系统模型参数如表1所示。

从图1可知 $ J $ 个主用户和 $ L $ 个次用户在一个微小区的二维的空间中随机分布，且在知道发射机和接收机位置距离的情况下，可以通过统计信息的方法来建立信道模型^[13]，即在已知传播距离的情况下，根据不同场景的概率分布，通过WINNER II模型^[14]来定义其中的路径损耗：

$ \begin{array}{c}{Z}\left(d,{f}_{c}\right) ={{\overline Z}}+{A}_{W} \lg d+{\mathcal{B}}_{W} \lg\left(f_c/5\right) \end{array} $

(2)

因此可以获得期望信号的路径损耗 $ Z\left({d}_{ll},{f}_{c}\right) $ ，以及干扰信号的路径损耗 $ Z\left({d}_{jl},{f}_{c}\right) $ 和 $ {Z}\left({d}_{kl},{f}_{c}\right) $ ，其中 $ {d}_{ll} $ 、 $ {d}_{jl} $ 、 $ {d}_{kl} $ 分别为第 $ l $ 个次用户发射机与接收机之间的通信链路距离，第 $ j $ 个主用户发射机对第 $ l $ 个次用户接收机的干扰链路距离和第 $ k $ 个次用户发射机对第 $ l $ 个次用户接收机的干扰链路距离。假设发射机和接收机之间存在强视线路径(Line of Sight, LoS) ，则可采用Rician信道模型推导信道增益，可表示为

$ \begin{array}{c}h=\sqrt{\dfrac{\kappa }{\kappa +1}}\sigma {\mathrm{e}}^{j\theta }+\sqrt{\dfrac{1}{\kappa +1}}{\rm{CN}}\left(0,{\sigma }^{2}\right) \end{array} $

(3)

$ \begin{array}{c}{\sigma }^{2}={10}\Large^{{-[{({\overline Z}+{A}_{w} \mathrm{l}\mathrm{g}d +{\mathcal{B}}_{w}\;{{\rm{lg}}}\left({f}_{c} /5\right) ) }/{10}]} }\end{array} $

(4)

式中： $ {\sigma }^{2} $ 取决于路径损耗， $ \kappa $ 为视线路径和散射路径的接收机信号功率之间的比率。 $\theta \sim U\left(\mathrm{0,1}\right)$ 为强视线路径上到达信号的相位，取值于0和1之间的均匀分布。 $\mathrm{C}\mathrm{N}( \cdot)$ 表示一个圆对称的复高斯随机变量。

因此，第 $ l $ 个次用户选择信道 $ j $ 后接收机收到信号的信干噪比(Signal to Interference plus Noise Ratio, SINR)可表示为

$ \begin{array}{c}{\delta }_{j}^{l}=\dfrac{{p}_{lj} {|{h}_{ll}|}^{2}}{{p}_{jj} {|{h}_{jl}|}^{2}+\displaystyle\sum\nolimits _{k=1,k\ne l}^{L}{p}_{kj} {\left|{h}_{kl}\right|}^{2}+B \mathrm{\vartheta }} \end{array} $

(5)

根据香农定理，第 $ l $ 个次用户的理论传输速率为

$ \begin{array}{c}{T}_{l}=B{\rm{lb}}\left(1+{\delta }_{j}^{l}\right) \end{array} $

(6)

式中： $ B $ 为信道的带宽。本文研究目的是最大化所有次用户的总传输速率，故研究问题的优化目标可简化为

$ \begin{array}{c}\max\displaystyle\sum\nolimits _{l=1}^{L}{T}_{l} \end{array} $

(7)

2 基于强化学习的频谱接入建模

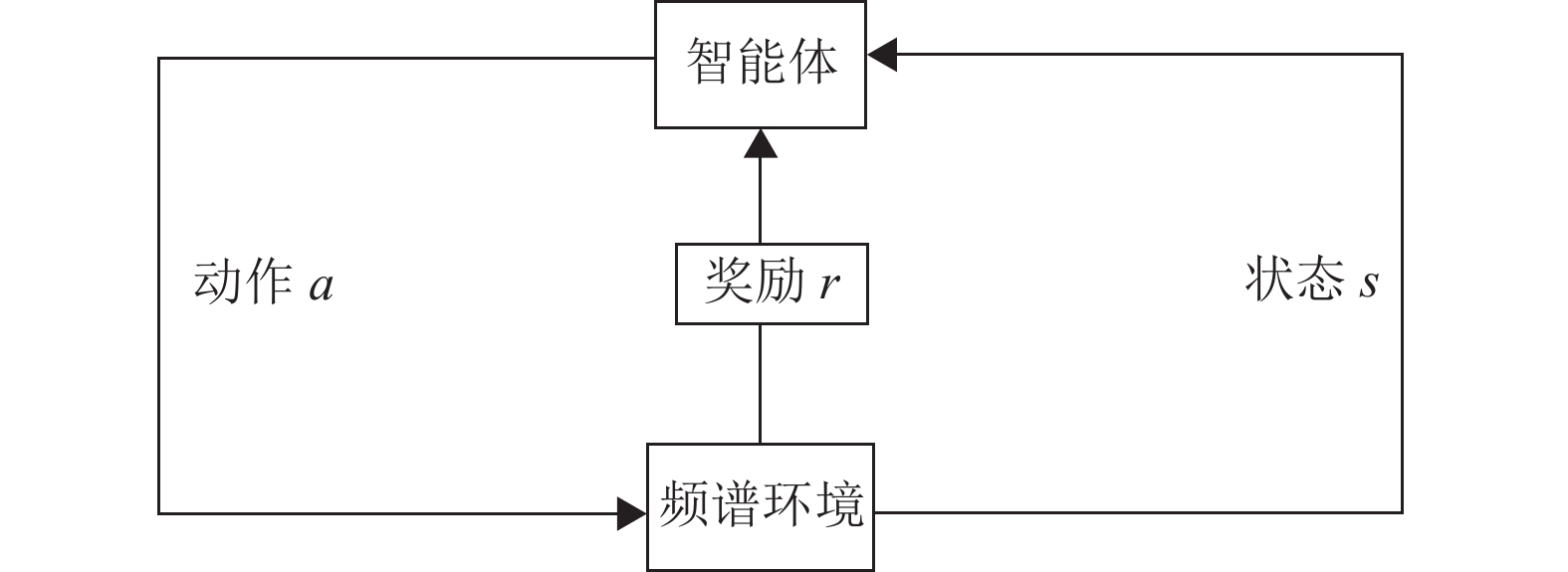
强化学习是一种通过让智能体与环境不断交互进行学习的方法^[15]，深度强化学习是在强化学习的基础上引入深度学习，使得强化学习拥有强大的算力，从而帮助智能体适应动态环境进行自行学习。如图3所示，强化学习主要有5大要素：环境、智能体、状态 $ s $ 、动作 $ a $ 和奖励 $ r $ 。智能体想要得到的策略是由环境给出的状态 $ s $ 和智能体所做出的动作 $ a $ 以及得到的奖励 $ r $ 所决定的，而强化学习的目的就在于通过对环境进行有限的交互次数找到最优策略 $ {\pi }_{*}\left(s\right) $ ，最大化奖励值，其中 $ {\pi }_{*}\left(s\right) $ 可表示为

$ \begin{array}{c}{\pi }_{*}\left(s\right) ={\mathrm{a}\mathrm{r}\mathrm{g}\mathrm{m}\mathrm{a}\mathrm{x}}_{a}Q\left(s,a\right) \end{array} $

(8)

式中： $ Q $ 为值函数。

本文研究的动态频谱接入过程的本质是一个马尔可夫决策过程，可以利用强化学习来帮助解决。次用户机会式访问决策过程如图4所示，次用户接入策略是由双深度Q网络和当前频谱感知结果共同决定的。次用户根据自身频谱接入策略接入无线信道进行数据传输，然后次用户接收机根据实际无线传输质量得到反馈奖励，反馈奖励由次用户发射机存储，并作为双深度Q网络的训练数据用来更新频谱接入策略。

2.1 状态集合

在每个时刻开始时，信道状态感知结果可作为状态值，则在 $ t $ 时刻状态集合可以表示为

$ \begin{array}{c}{\boldsymbol{S}}\left(t\right) =\left[{S}_{1}\left(t\right) ,\cdots{,S}_{l}\left(t\right) ,\cdots,{S}_{L}\left(t\right) \right] \end{array} $

(9)

式中： $ {{\boldsymbol{S}}}_{l}\left(t\right) $ 为 $ l $ 个次用户所感知到的信道状态，是一个 $ J $ 维向量 $ {[{s}_{l}^{1}\left(t\right) ,\cdots,{s}_{l}^{j}\left(t\right) ,\cdots,{s}_{l}^{J}\left(t\right) ]}^{\mathrm{T}} $ ，并且 $ {s}_{l}^{j}\left(t\right) \in \left\{\mathrm{0,1}\right\} $ ， $ {s}_{l}^{j}\left(t\right) =0 $ 表示第 $ l $ 个次用户感知到第 $ j $ 条信道处于活跃状态；反之 $ {s}_{l}^{j}\left(t\right) =1 $ 表示第 $ l $ 个次用户感知到第 $ j $ 条信道处于空闲状态，次用户可以选择机会式接入该信道。并且考虑到次用户在进行频谱感知的时候可能会存在一定的误差，因此给 $ {s}_{l}^{j}\left(t\right) $ 的感知结果加上一定错误的概率 $ {E}_{l}^{j} $ ，故假设第 $ l $ 个次用户在第 $ j $ 个信道的真实情况为

$ \begin{array}{c}P\left\{{T}_{l}^{j}\left(t\right) ={s}_{l}^{j}\left(t\right) \right\}=1-{E}_{l}^{j} \end{array} $

(10)

2.2 动作集合

在次用户感知完信道状态后，次用户可以基于感知结果进行信道访问，但是每个次用户最多访问一个信道，其中次用户 $ t $ 时刻访问的动作集合表示为

$ \begin{array}{c}A\left(t\right) =\left[{A}_{1}\left(t\right) ,\cdots{,A}_{l}\left(t\right) ,\cdots,{A}_{L}\left(t\right) \right] \end{array} $

(11)

式中： $ {A}_{l}\left(t\right) \in \left\{0,\cdots,j,\cdots,J\right\},{A}_{l}\left(t\right) =j $ 为 $ l $ 个次用户选择了第 $ j $ 个信道，若 $ {A}_{l}\left(t\right) =0 $ ，则第 $ l $ 个次用户没有选择任何信道。

2.3 奖励函数

次用户 $ l $ 在 $ t $ 时刻根据信道状态做出信道 $ j $ 选择后，为了实现传输速率最大化，可以将奖励函数按照如下方法建立，如式(12) 所示。

$ \begin{array}{l}{R}_{l}\left(t\right) =\left\{\begin{array}{l}-2 ，与主用户发生碰撞\\ 0，不做任何选择\\ B{\rm{lb}}\left(1+{\delta }_{j}^{l}\right) ，否则\end{array}\right. \end{array} $

(12)

(1) 次用户访问信道时没有主用户正在使用，并且只有一个次用户接入信道，可以用理论传输速率 $ B\mathrm{l}\mathrm{b}\left(1+{\delta }_{j}^{l}\right) $ 当作奖励，并且记成功接入一次。

(2) 次用户访问信道时主用户正在使用，与主用户发生碰撞，给予−2作为惩罚，并记碰撞一次。

(3) 次用户访问信道时没有主用户正在使用，但同时有多个次用户访问相同信道，给予 $ B\mathrm{l}\mathrm{b}(1+{\delta }_{j}^{l}) $ 作为奖励，记碰撞一次。

(4) 次用户决定不访问任何信道，不给予奖励，成功次数和碰撞均不记。

3 DPEP-DDQN算法描述

本文提出的DPEP-DDQN算法，是在进行强化学习建模的基础上结合了分布式独立Q学习、优先经验回放算法和双深度Q网络的方法形成的。

3.1 分布式独立Q学习

为了减少集中式训练所带来的底层开销，本文在进行强化学习建模的基础上加入分布式独立Q学习方法。在此方法中，每个智能体都是独立学习的主体，它们将其他智能体视为环境的一部分，并认为联合状态可观测，采用标准单智能体强化学习方法进行学习^[16]。如图5所示，在与环境互动的过程中，每个智能体可以只需要考虑自己的状态对环境做出回馈，而不需考虑其余智能体的动作选择，故这种情况更贴近于认知无线网络环境中次用户不会在选择信道之前进行相互协商的情况。其中分布式独立Q学习方法的主要目标可简化为在满足次用户不对主用户造成干扰的情况下，提高所有次用户的传输速率。故需要系统找到最优策略 ${\pi }_{*}={\pi }_{*}^{1}+{\pi }_{*}^{2}\cdots+ {\pi }_{*}^{l}+\cdots {\pi }_{*}^{L}$ ，其中 $ {\pi }_{*}^{l} $ 为第 $ l $ 个次用户信道选择的最优策略。

3.2 双深度Q网络

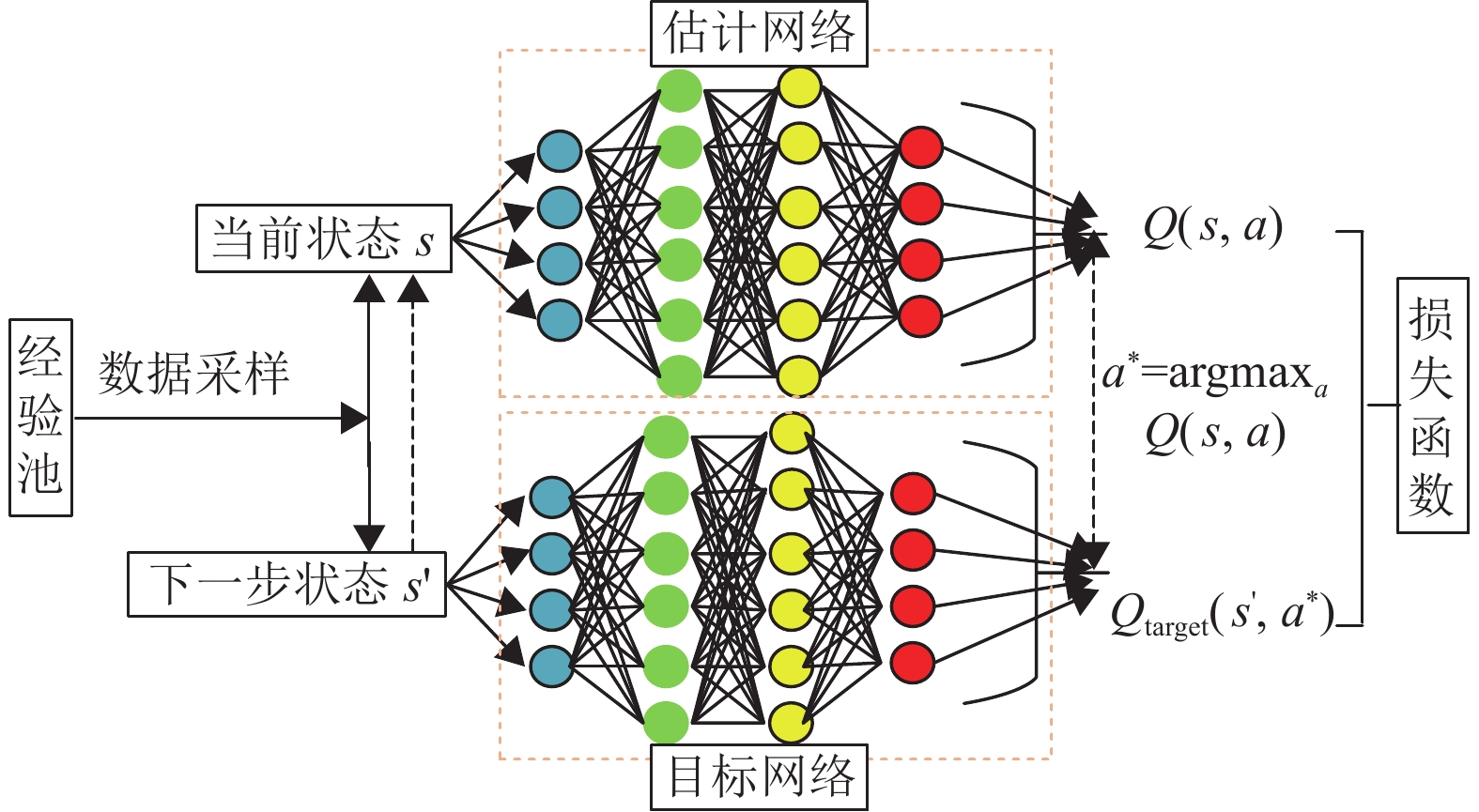
在准备分布式训练框架之后，神经网络将采用双深度Q网络(Double Deep Q Network, Double DQN) ，该神经网络属于深度Q网络(Deep Q Network, DQN) 的一种变体，相对于DQN其特点就是使用2次Q学习来寻找最优动作，通过解耦目标Q值动作的选择和目标Q值的计算，达到消除过度估计的目的^[17]。神经网络结构图如图6所示。

3.3 优先经验回放

为了提升神经网络训练效率，本文采用了优先经验回放算法。在传统DQN算法中，为了打破样本之间的关联，通常的做法是在经验池中随机抽取样本训练进而更新参数来构建神经网络，但是这常常会出现奖励稀疏的情况，例如智能体需要进行很多步探索才得到奖励，使得经验池中能让智能体学习的有效经验十分缺少，这个时候如果仍然采取随机抽取经验池样本的方式会使得效率降低。因此，本文将采取一种二叉树的结构来对数据进行存储，该数据存储结构在一定程度上可以在数据采样的时候节省时间，而且可以定义出便于神经网络训练的采样规则，比如可以对样本设置不同的优先级。

如图7所示，本文将采用一种基于SumTree即累计求和的二叉树来作为经验池储存结构。SumTree中每个底层的叶子节点存储样本数据以及对应的优先级，中继节点和根节点不储存样本数据而储存下级节点的优先级之和。叶子节点中存储的数据值区间的数值越大意味着优先级越高，能够存储的数字区间越长。在保证优先级采样的情况下也需要保障最低优先级非零概率采样，故设定次用户 $ l $ 选择采样概率计算方法为

$ \begin{array}{c}{H}_{l}\left(x\right) =\dfrac{{\left[{h}_{l}\right(x\left) \right]}^{\alpha }}{\displaystyle\sum\nolimits _{y}{\left[{h}_{l}\right(y\left) \right]}^{\alpha }} \end{array} $

(13)

式中： $ {\left[{h}_{l}\right(x\left) \right]}^{\alpha } $ 和 $ {\left[{h}_{l}\right(y\left) \right]}^{\alpha } $ 为样本 $ x $ 和样本 $ y $ 的优先级， $ \alpha $ 为优先级指数， $ \alpha =0 $ 时为均匀采样。 $ {\left[{h}_{l}\right(x\left) \right]}^{\alpha } $ 的计算方法为

$ \begin{array}{c}{\left[{h}_{l}\right(x\left) \right]}^{\alpha }=\left|{\varPhi }_{l}\left(x\right) \right|+\varepsilon \end{array} $

(14)

$ \begin{split}&{\varPhi }_{l}\left(x\right) ={R}_{l}\left(x\right) -Q\left({S}_{l}\left(x-1\right) ,{A}_{l}\left(x-1\right) \right)+ \\ &{\gamma Q}_{\mathrm{t}\mathrm{a}\mathrm{r}\mathrm{g}\mathrm{e}\mathrm{t}}({S}_{l}\left(x\right) ,{\mathrm{a}\mathrm{r}\mathrm{g}\mathrm{m}\mathrm{a}\mathrm{x}}_{a}Q\left({S}_{l}\left(x\right) ,{A}_{l}\left(x\right) \right) ) \end{split}$

(15)

式中： ${\varPhi }_{l}\left(x\right)$ 为样本 $ x $ 的时序差分(Temporal Difference，TD) 误差， $ Q $ 和 $ {Q}_{\mathrm{t}\mathrm{a}\mathrm{r}\mathrm{g}\mathrm{e}\mathrm{t}} $ 分别为估计网络和目标网络输出的Q值， $ {R}_{l}\left(x\right) $ 为样本 $ x $ 的奖励。 $\varepsilon$ 为一个非常小的正数，其目的是为了保证采样概率 $ {H}_{l}\left(x\right) $ 大于0。

但是该采样机制可能会带来偏差，为了使系统更加稳定，故设定样本重要权重来纠正偏差：

$ \begin{array}{c}{w}_{l}\left(x\right) ={\left(\dfrac{1}{{O}_{l}} \times \dfrac{1}{{H}_{l}\left(x\right) }\right) }^{\beta } \end{array} $

(16)

式中： $ {w}_{l}\left(x\right) $ 为次用户 $ l $ 的标识权重系数， $ {O}_{l} $ 为次用户 $ l $ 的经验池大小， $ \beta $ 为标识非均匀补偿系数，当 $ \beta =1 $ 时就完全补偿了 $ {H}_{l}\left(x\right) $ 。

3.4 DPEP-DDQN算法流程

算法1　DPEP-DDQN算法伪代码

1. 初始化：主次用户的发射机与接收机位置，各次用户 神经网络和经验池的超参数

2. For 次用户 l = 1 to L do

3. 　次用户 $ { l} $ 感知频谱环境，初始化状态 $ {{S}_{l}\left(0\right) }$ 和选择动 作A_l(0)

4. 　For 训练步数 t = 1 to T do

5. 　　次用户 $ { l} $ 以贪婪算法选择动作， $ { 1-\varepsilon} $ 概率选择动 作 $ { {A}_{l}\left(t\right) ={\mathrm{a}\mathrm{r}\mathrm{g}\mathrm{m}\mathrm{a}\mathrm{x}}_{a}Q\left({S}_{l}\left(t\right) ,{A}_{l}\left(t\right) \right) }$ ，否则随机选择动作 $ { {A}_{l}\left(t\right)} $

6. 　　获取环境反馈即时奖励 $ { {R}_{l}\left(t\right) }$ 和下一时刻状态 $ { {S}_{l}\left(t+1\right) }$

7. 　　将样本数据 $ { \{ ({S_l}\left( t \right),{A_l}\left( t \right),{R_l}\left( t \right),{S_l}\left( {t + 1} \right)\} }$ 存入到 经验池 $ { {D}_{l} }$ 并赋予优先级

8. 　　状态迭代 $ { {S}_{l}\left(t\right)} $ = $ { {S}_{l}\left(t+1\right) }$

9. 　　IF t到达训练点then

10. 　　　For x = 1 to y do

11. 　　　　从经验池从 $ { {D}_{l} }$ 中抽取样本并遵循 $ {x\sim H_l}$ $ { \left(x\right) = \dfrac{{\left[{h}_{l}\right(x\left) \right]}^{\alpha }}{\displaystyle\sum\nolimits _{y}{\left[{h}_{l}\right(y\left) \right]}^{\alpha }} }$ 的规律

12. 　　　　计算采样权重：

$ {\qquad\;\;\;{w}_{l}\left(x\right) ={\left(\dfrac{1}{{O}_{l}} \times \dfrac{1}{{H}_{l}\left(x\right) }\right) }^{\beta }{\mathrm{m}\mathrm{a}\mathrm{x}}_{y}{w}_{l}\left(y\right)} $

13. 　　　　计算TD误差：

$ { \begin{split} \qquad\quad {\Phi }_{l}\left(x\right) =&{R}_{l}\left(x\right) +{\gamma Q}_{\mathrm{t}\mathrm{a}\mathrm{r}\mathrm{g}\mathrm{e}\mathrm{t}}\left({S}_{l}\left(x\right) ,{\mathrm{a}\mathrm{r}\mathrm{g}\mathrm{m}\mathrm{a}\mathrm{x}}_{a}Q\left({S}_{l}\left(x\right) ,{A}_{l}\left(x\right) \right) \right) -\\ & Q\left({S}_{l}\left(x-1\right) ,{A}_{l}\left(x-1\right) \right) \end{split} }$

14.　　　　 更新样本优级： $ { {h}_{l}\left(x\right) =\left|{\Phi }_{l}\left(x\right) \right| }$

15. 　　　　 累计权重变化： $ { {\Delta}_{l}={\Delta}_{l}+{w}_{l}\left(x\right) \cdot {\Phi }_{l}\left(x\right) \cdot {\nabla }_{\theta }Q }$ $ {({S}_{l}(x-1)}$ , $ {{A}_{l}(x-1)} $ )

16.　　　End For

17. 　　　更新神经网络权重 $ { {\theta }_{l}={\theta }_{l}+{\eta}_{l}\cdot{\Delta}_{l} }$ ，重置权重差值 $ { {\Delta}_{l}=0 }$

18. 　　　更新目标网络参数 $ { \widehat{{\theta }_{l}}={\theta }_{l} }$

19. 　　End IF

20. 　　每隔一定步数随机更新环境的参数

21.　 End For

22.End For

4 实验环境介绍

本节中将设置系统模型的仿真参数。参考文献[14]中关于城市微小区场景中的WINNER II模型，假设超参数 $ {f}_{c}\text{=}2.4\;\mathrm{G}\mathrm{H}\mathrm{z} $ ， $ \overline{{Z}}=41 $ ， $ {A}_{W}=22.7 $ ， $ {\mathcal{B}}_{W}=20 $ ， $ \kappa =8 $ ， $ {\sigma }^{2} $ 由路径损耗所决定。其中次用户接收机所接收到的SINR由式(5) 给出，其中信道带宽 $ B=1\;\mathrm{M}\mathrm{H}\mathrm{z} $ ，次用户的传输功率设置为50 mW，主用户的传输功率设置为65 mW。

如动态频谱接入模型即信道状态模型(见图2)，将主用户的状态分割成2个独立的马尔科夫链：主用户不在使用(1) 和主用户已经在使用(0)。为了初始化每个马尔科夫链，分别从[0.7,1]，[0,0.3]区间上的均匀分布中随机选取 $ {\xi }_{11} $ 和 $ {\xi }_{00} $ ，那么 $ {\xi }_{10}=1-{\xi }_{11} $ ， $ {\xi }_{01}=1-{\xi }_{00} $ 就可以计算得出。之所以选择这2个区间范围的原因是 $ {\xi }_{11} $ 和 $ {\xi }_{00} $ 大多数授权频段的利用率偏低，所以 $ {\xi }_{00} $ 的值是偏低的，并且 $ {\xi }_{11} $ 的值偏高。

为了更好地实验演示，本次仿真还加入了myopic方法作为参考方法进行对比。在myopic方法中，智能体将选择最大的即时奖励。为了计算预期的即时回报，myopic方法需要信道的转移概率和感知错误概率的信息。在myopic中，第 $ l $ 个次用户首先计算信道状态概率，其中 $ {G}_{j}(t $ ) =Pr{在 $ t $ 时刻第 $ j $ 个信道状态=1}，其表达式为

$ {G}_{j}\left(t\right) ={s}_{l}^{j}\left(t\right) (1-{E}_{l}^{j}) +(1-{s}_{l}^{j}\left(t\right) ) {E}_{l}^{j} $

(17)

式中： $ {s}_{l}^{j}\left(t\right) $ 为第 $ l $ 个次用户于第 $ j $ 个信道的感应结果， $ {E}_{l}^{j} $ 为第 $ l $ 个次用户于第 $ j $ 个信道感知错误的概率，假设其为0.2。因此myopic方法可以计算第 $ j $ 个信道的奖励函数为

$ \begin{split}&{R}_{j}\left(t\right) ={G}_{j}\left(t\right) [{\xi }_{10}^{j} \left(-2\right) +{\xi }_{11}^{j} B\mathrm{l}\mathrm{b}(1+{\delta }_{j}^{l}) ]+\\ &(1-{G}_{j}\left(t\right) ) [{\xi }_{00}^{j} \left(-2\right) +{\xi }_{01}^{j} B\mathrm{l}\mathrm{b}(1+{\delta }_{j}^{l}) ] \end{split}$

(18)

5 实验仿真与分析

本节将对所提方案进行仿真实验和性能评估，实验将以myopic方法为参考基准，此外，需要注意的是，每个主用户都拥有自己的信道，并且假设所有主用户不会同时使用信道。实验使用python语言编写，以Tensorflow进行建模，构建如图6所示的神经网络结构。构建的神经网络有2个隐藏层，每个隐藏层中的神经元数目都是64，激活函数都是tanh函数。训练总次数是378 000，记忆库D的容量O为5400。

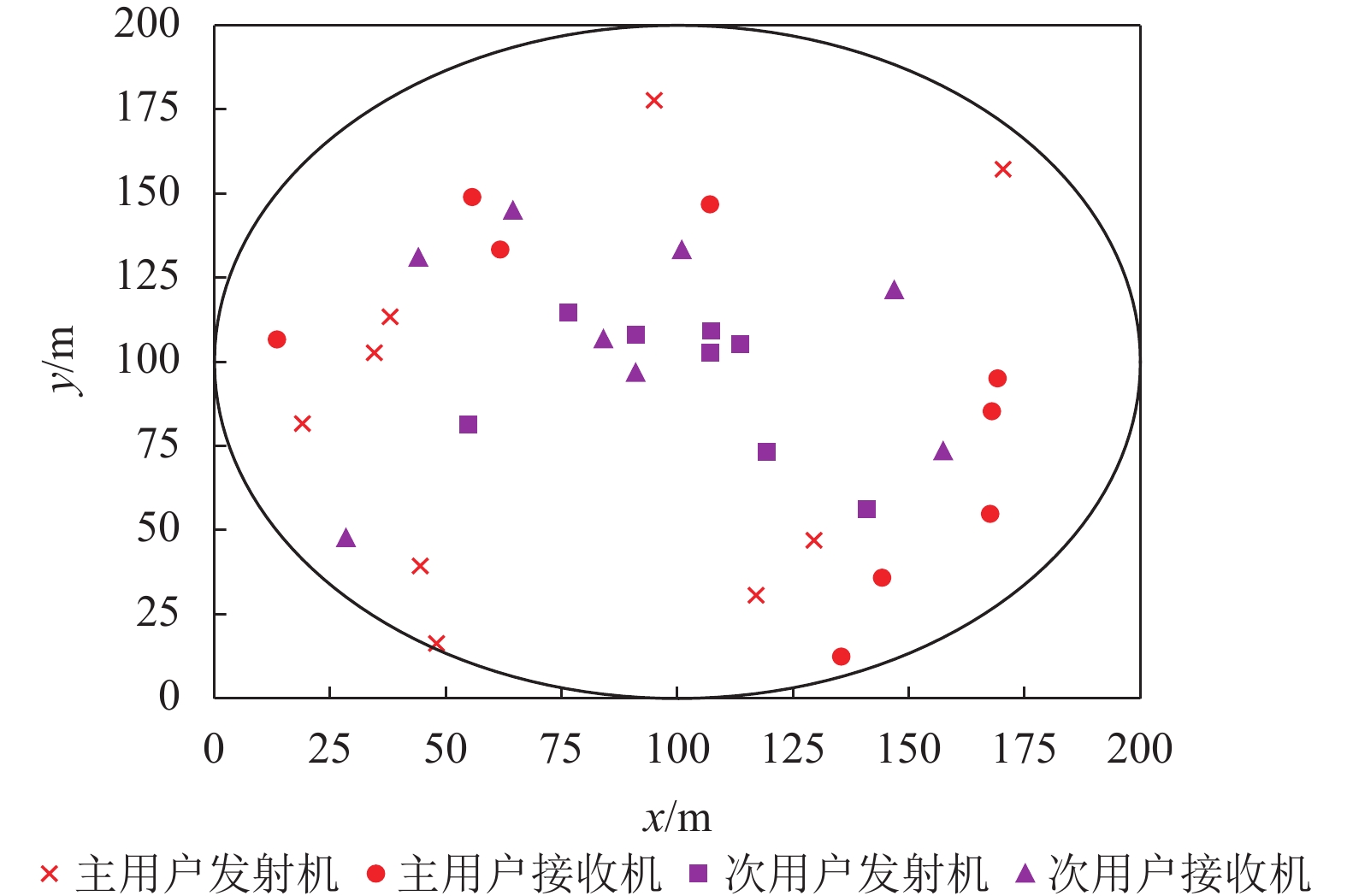
5.1 位置分布

图8描述了在假设的一个半径为100 m的圆形二维空间中，9个主用户和8个次用户随机位置的分布，其中主用户发射机、接收机随机分布，次用户接收机与发射机之间的距离在20~50 m之间随机选择。

5.2 平均成功率

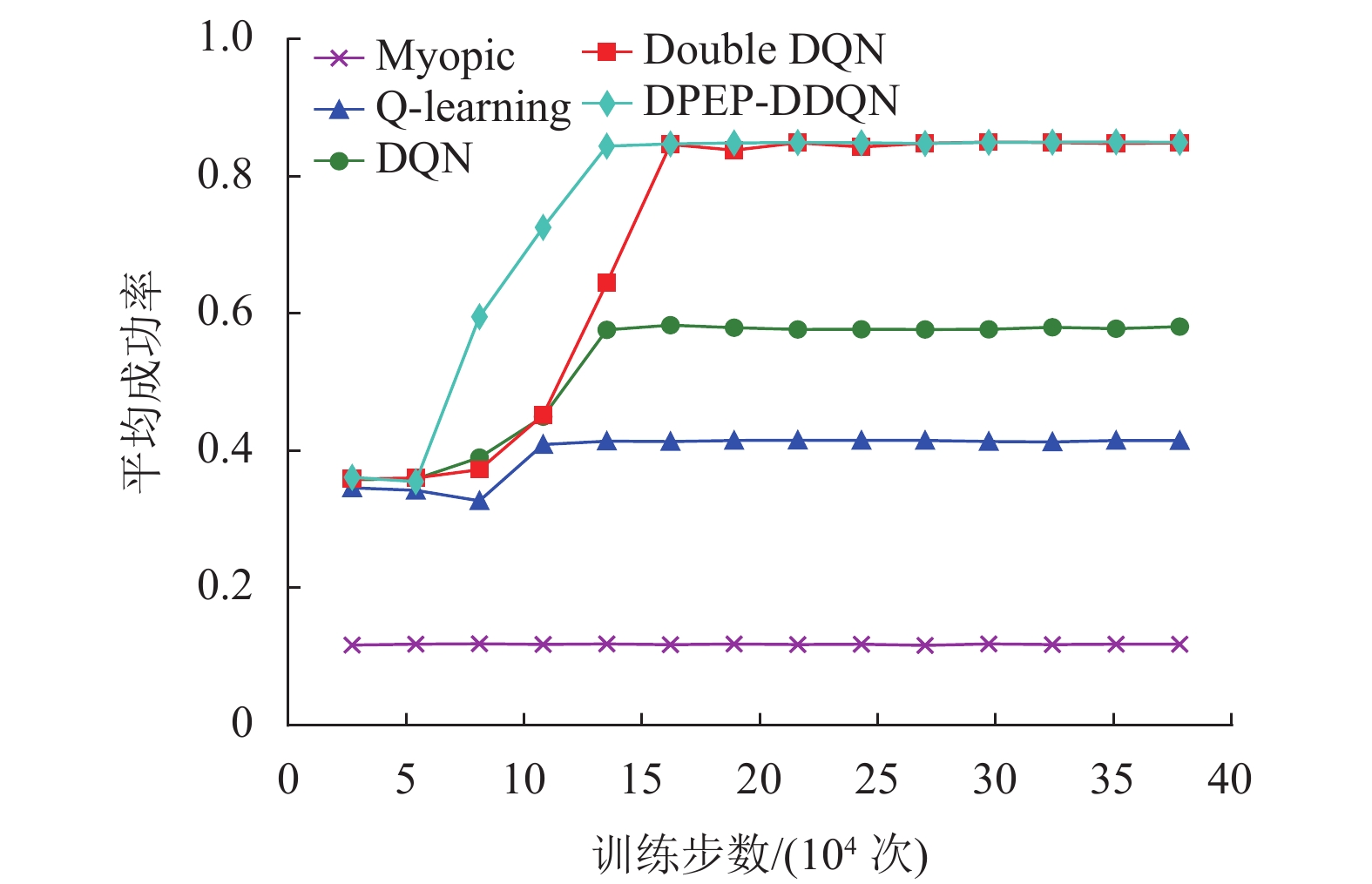
图9描述了在378 000次迭代中，次用户在进行频谱接入时的平均成功率，每隔27 000次进行一次平均统计。从图中比较算法可以得出：当存在感知错误可能性时，作为参考的Myopic表现得不太好。虽然Myopic算法将信道的转移概率和感知误差概率视为已知信息，但是该算法完全不考虑未来奖励，故成功率一直维持在较低水平。Q-learning需要密集的Q表更新，故其在面对传输数据较大时，环境反馈的复杂性提高，智能体难以理解环境，从而达不到好的效果，其成功率也仅在0.41左右波动。相比较于加入神经网络进行训练的深度Q学习算法，在神经网络的优化下，深度Q学习算法可以取得一个很好的学习结果，其中按照性能升序排序依次是：DQN，Double DQN，DPEP-DDQN。DQN 算法由于本身的神经网络学习效果差，使得接入成功功率只能提升到0.58左右。当训练网络更换成Double DQN后，每个智能体变成使用2次Q学习来寻找最优动作，这使得智能体可以更好地学习，使得成功率可以达到0.85左右。虽然DPEP-DDQN与Double DQN在收敛的时候达到了相似的成功率，但是加上了优先经验回放的DPEP-DDQN算法的收敛速度会比普通Double DQN快。

5.3 平均碰撞率

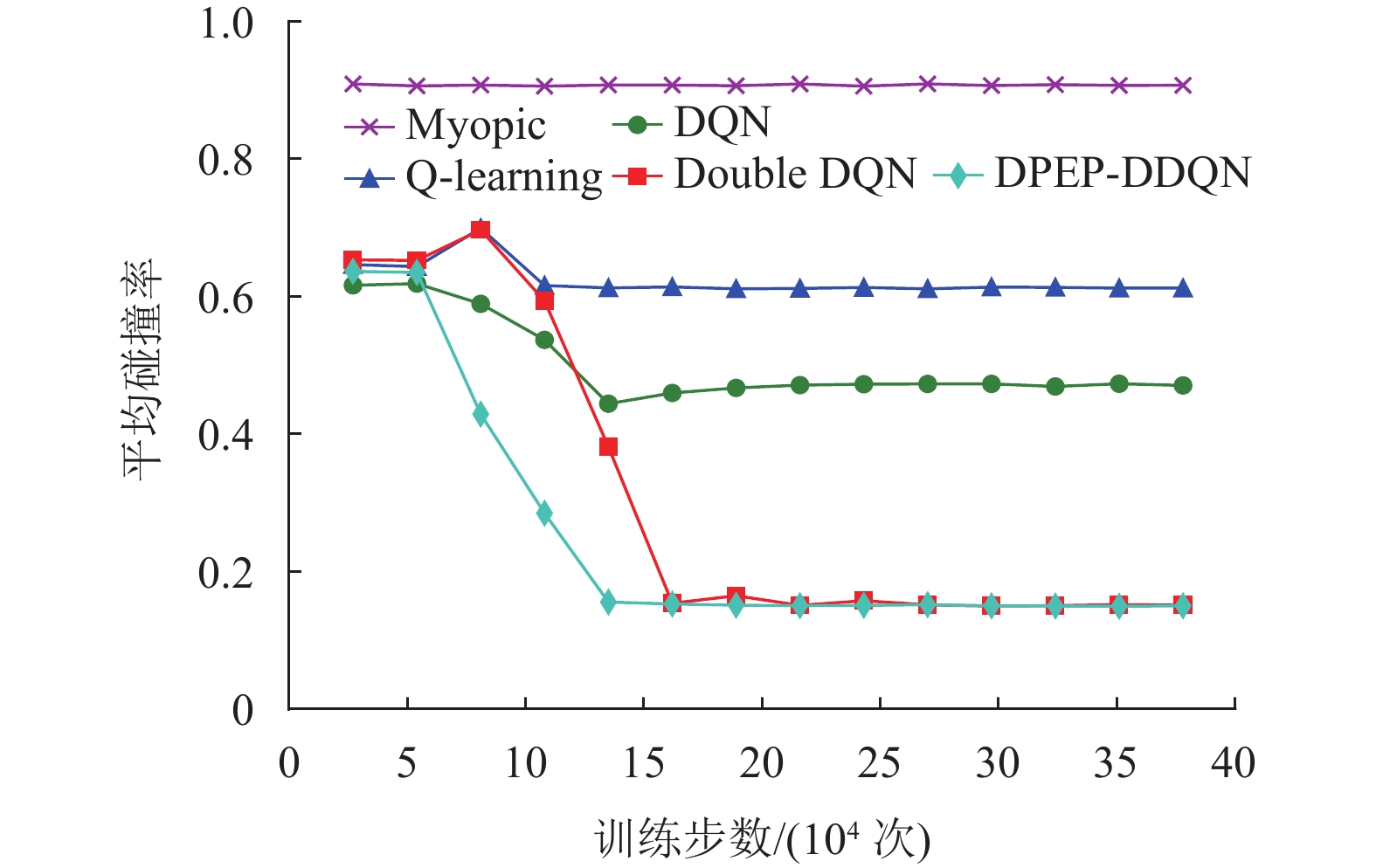
图10描述了次用户在进行信道争夺时产生的平均碰撞率。对比图9可以发现虽然用户可以选择不接入信道，但是在以传输速率为期望回报的情况下，次用户都会努力尝试接入信道，故成功率和碰撞率总和接近1。从图中可知Myopic算法和Q-learning算法都表现得不太好，信道的碰撞率较高，这种情况下会造成整个认知无线网络环境通信的干扰加深，影响整个网络的传输速率。相比之下DPEP-DDQN和Double DQN算法虽然存在差异但是最终都可达到一个较低的碰撞率，尤其是DPEP-DDQN算法，不仅最终收敛的碰撞率维持最小，而且最终曲线收敛最快。

5.4 平均奖励

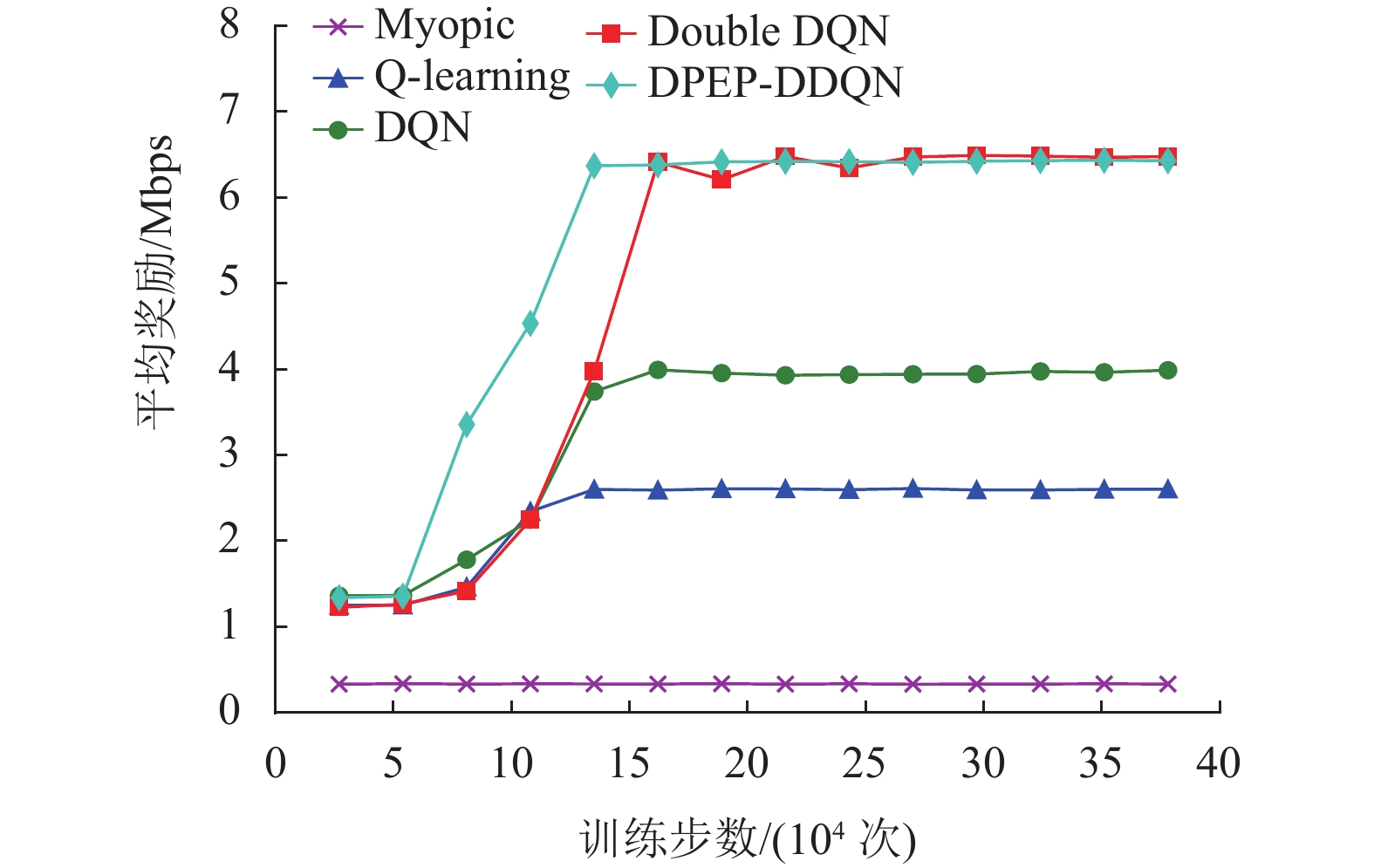
图11描述了次用户在进行信道争夺时产生的平均奖励值，即信道通信的理论传输速率。在参数相同的模拟环境下DPEP-DDQN可以以最快的速度达到最大奖励。这是因为加入了SumTree累计求和的二叉树作为经验池储存结构之后，智能体就不会像传统模型那样进行随机采样，而是对数据加入相应的优先级，这使得神经网络训练时能够更加有效地采集样本，不仅可以优化数据库的容量，而且可以更好地保证整个网络的传输速率。

5.5 不同次用户数目下的最终平均奖励

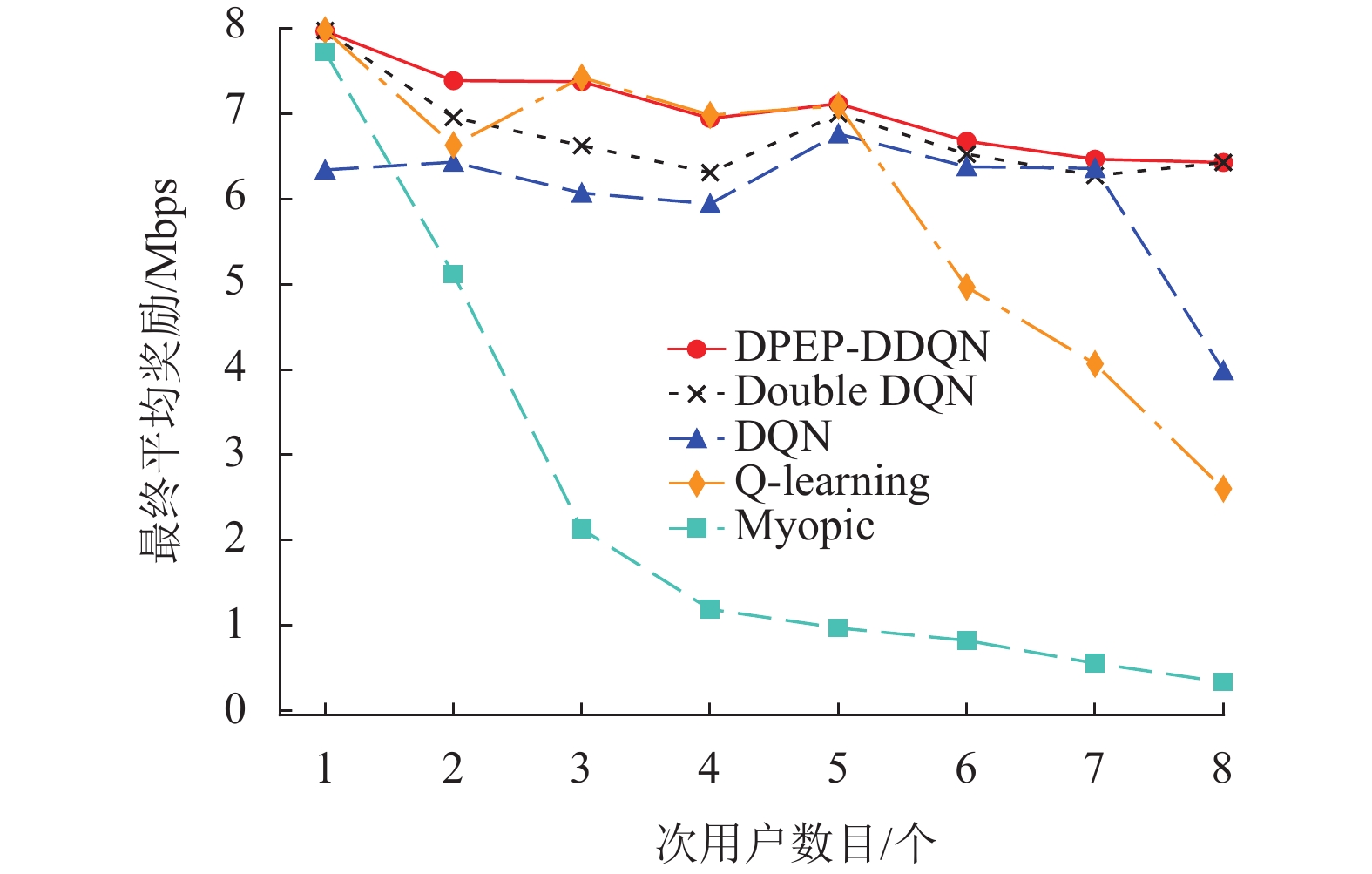
图12描述了在存在9个主用户的情况下，次用户的数目分别从1增加到8时次用户最终收敛时的平均奖励。可以看出，在这5种算法中最终平均奖励都随着次用户数目的增加而呈现减少趋势。这是因为随着次用户数目的增加，通信资源逐渐短缺，可以使用的信道数目也会逐渐减少，因此理论传输速率就会随之下降。不难看出，在通信资源充足的情况下，各类算法最终都可以达到较好的奖励值，可是随着频谱资源的逐渐减少，各类算法之间的差距也开始渐渐增加。由此可以看出本文提出的DPEP-DDQN算法在面临通信资源减少的时候仍然可以保持一个较好的传输速率。

6 结论

为了解决认知无线网络中多个次用户需要快速且准确接入频谱信道的问题，本文提出了一种基于分布式优先经验池结合双深度Q网络的多用户动态频谱接入方法，用来帮助次用户在不完美感知频谱环境的情况下，机会式地做出适当的频谱访问决策。实验结果表明，该方法不仅可以保证最高的接入成功率和传输速率，并且在次用户数目不增加的情况下，该算法的最大化理论传输速率和收敛速度仍然可以保持良好水平。不仅可以帮助认知无线网络降低干扰，还有效地提高了整个网络的传输速率。