近年来，由于无人机的高机动性、自主性和灵活性，无人机得到了广泛的关注，并已应用在生活中许多领域。例如，通过无人机观察实时路况，从而控制城市交通，以及使用无人机进行地震后的搜救工作^[1-2]。文献[3]研究通过无人机来实现图像采集以及高分辨率的地形探测。除此之外，由于无人机可以通过安装小型通信设备，作为中继节点为地面用户提供通信服务，或者作为移动基站采集地面无线传感网络的数据，通过优化无人机轨迹来最大化地对地面设备进行数据收集。目前无人机辅助无线通信已经成为研究热点，跨越了多个方向，如缓存网络^[4]、无线传感器网络^[5]、异构蜂窝网络^[6]、大规模多输入多输出^[7]、设备到设备通信^[8]和灾难通信^[9-10]。

对于单无人机辅助数据收集的问题，前人进行了诸多研究。文献[11]考虑了一种无人机对多个地面用户进行数据收集的场景，通过对无人机轨迹和数据采集时间等进行联合优化，最大化最小数据量。文献[12]在无人机支持的无线传感器网络中对节能数据收集进行了研究，通过联合优化无人机轨迹和传感器节点唤醒时间以最小化所有传感器节点的最大能耗，同时确保能可靠地收集数据。文献[13]考虑一个无人机支持的无线传感器网络，其中无人机用于从多个传感器节点收集数据，研究联合优化无人机轨迹和通信调度，最大化所有传感器节点的最小平均数据收集率。已有研究表明，用无人机辅助无线通信对地面用户或传感器节点进行数据收集具有可行性和高效性。

尽管与无人机路径和数据收集相关的优化问题可以通过数学优化方法来解决^[11-13]，但是计算复杂度较高，计算量较大。由于强化学习可以提供低复杂度的解决方案，目前被用作一种新型工具来解决以上问题。例如，文献[14]研究了无人机作为一个移动基站服务多个用户时的最优轨迹问题，利用Q-learning算法优化轨迹，最大限度地提高了传输速率。文献[15]研究了无人机数据采集场景下的轨迹优化问题，利用DQN(Deep Q-network)算法通过优化无人机轨迹采集所需数据。事实证明，利用强化学习方法可以大大减少计算量，降低计算复杂度^[14-15]。

但是面对用户分布广阔且分散的情况，单无人机则显得力不从心，难以很好地完成数据收集任务，因此有必要研究使用多架无人机辅助数据收集。文献[16]研究了在分布式物联网环境下利用多无人机进行数据收集时的路径规划问题，在飞行时间和避碰约束的条件下，引入了一种基于DDQN(Double DQN)的强化学习方法解决了以上轨迹优化问题，同时最大限度地收集了物联网节点的数据。文献[17]研究通过规划多个无人机的轨迹对物联网节点的数据进行采集，为了在避免碰撞和通信干扰等约束下最小化任务时间，提出了一种三步式方法来求解这个问题，包括基于任务分配的K-means算法以及基于深度强化学习的分布式和集中式轨迹设计方法。

然而，无人机机载能量是有限的，它决定了无人机的飞行时间，而无人机的飞行时间直接影响数据采集的性能。现有的研究大多忽略了实际应用中无人机严格的飞行时间限制。同时，通常假设地面用户为静止状态且环境已知。实际上，用户往往具有移动性，且移动目的无法精确预测。传统的优化决策方法一般用来解决静态规划问题，如旅行商问题^[18]。为了解决这些难题，本文使用一种新型深度强化学习算法——Dueling-DDQN来优化多无人机路径，最大化收集数据。强化学习算法相比传统优化决策方法可以更好地解决无模型动态规划问题，同时此算法既结合了DDQN将TD(Temporal-Difference)目标的动作选择和动作评估分别用不同的值函数来实现的优点，又采用了Dueling网络架构，使估算的函数值更准确，很好地解决了传统DQN算法的过估计问题^[19]。

本文主要贡献：(1) 本文在吞吐量的获取、无人机轨迹和无人机成功到达终点之间取得了良好的权衡，解决了严格的飞行时间限制下无人机的路径规划问题。(2) 目前关于动态用户的研究较少，在系统模型中本文考虑用户随机分布，同时遵循随机游走模型移动，在实际应用中具有较大的适用范围。(3) 本文考虑无人机起点和终点约束、边界碰撞约束、无人机防碰撞约束、通信距离约束以及用户通信约束，为了使无人机在最短时间内到达终点，同时最大化采集地面用户数据，本文提出了基于Dueling-DDQN的多无人机辅助数据收集系统智能路径规划算法。该算法既结合了DDQN的优点，同时又采用了独特的对抗式架构，具有良好的学习能力、收敛速度以及稳定性。(4) 仿真结果表明，所提算法可以很好地完成本文研究目标，相比两个基准算法具有最优的收敛性和鲁棒性。

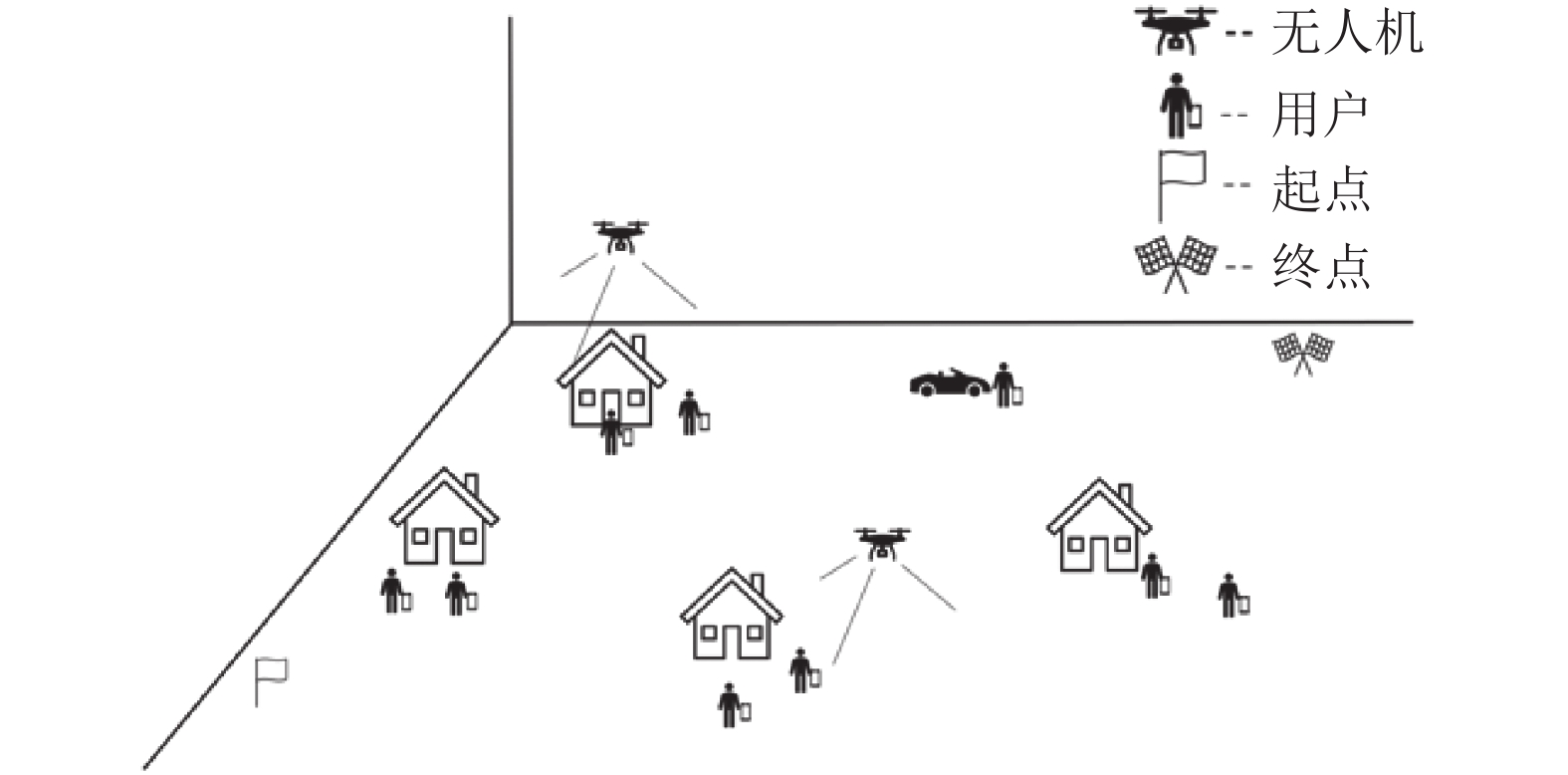
1 系统模型

如图1所示，本文考虑一个多无人机辅助数据收集系统， $ N $ 架无人机在目标区域内同时服务 $ P $ 个用户。用户能以低于 $ v $ 的速度自由移动，初始位置坐标从目标区域内 $ M $ 个半径为 $ {R}_{\mathrm{r}\mathrm{e}\mathrm{g}} $ 的集群中随机生成，其中每个集群存在 $ K $ 个用户。第 $ m $ 个集群中第 $ k $ 个用户在第 $ t $ 时隙的位置坐标用 $ {X}_{m,k}^{t}= $ ( $ {x}_{m,k}^{t},{y}_{m,k}^{t} $ ) 表示。

由于尺寸限制，考虑无人机和用户都具有单天线，所有无人机起点和终点位置的水平坐标分别为( $ {X}_{0},{Y}_{0} $ ) ，( ${X}_{{\rm{f}}},{Y}_{{\rm{f}}}$ ) ，飞行高度固定为 $ H $ ，能与其覆盖范围内的用户进行通信，其中地面覆盖范围的半径 $ {R}_{\mathrm{u}\mathrm{a}\mathrm{v}} $ 由无人机的飞行高度 $ H $ 和天线发射角度 $ {\textit{ϴ}} $ 决定，即 ${R}_{\mathrm{u}\mathrm{a}\mathrm{v}}=H\cdot \mathrm{t}\mathrm{a}\mathrm{n}\left({\textit{ϴ}}\right)$ 。在第 $ t $ 时隙，无人机 $ i $ 的三维坐标用 ${X}_{i}^{t}= ({x}_{i}^{t},{y}_{i}^{t},H)$ 表示， $i=\mathrm{1,2},\cdots,N$ 。 $ {X}_{\mathrm{b}\mathrm{o}\mathrm{u}\mathrm{n}\mathrm{d}} $ 和 $ {Y}_{\mathrm{b}\mathrm{o}\mathrm{u}\mathrm{n}\mathrm{d}} $ 表示目标区域长度和宽度，假设在任意时刻用户和无人机不能离开目标区域，即0 $ < {x}_{i}^{t},{x}_{m,k}^{t} < {X}_{\mathrm{b}\mathrm{o}\mathrm{u}\mathrm{n}\mathrm{d}} $ ，0 $ < {y}_{i}^{t},{y}_{m,k}^{t} < {Y}_{\mathrm{b}\mathrm{o}\mathrm{u}\mathrm{n}\mathrm{d}} $ 。无人机两两之间的距离为

$ {d}_{i,j}^{t}=\sqrt{{({x}_{i}^{t}-{x}_{j}^{t}) }^{2}+{({y}_{i}^{t}-{y}_{j}^{t}) }^{2}} $

(1)

式中： $ j\in \left\{\mathrm{1,2},\cdots,N\right\} $ ，且 $ i\ne j $ ，为避免无人机之间发生碰撞，假设 $ {d}_{i,j}^{t}\ge L $ 。

在第 $ t $ 时隙，第 $ m $ 个集群中第 $ k $ 个用户到无人机 $ i $ 的距离为

$ {d}_{m,k,i}^{t}=\sqrt{{({x}_{i}^{t}-{x}_{m,k}^{t}) }^{2}+{({y}_{i}^{t}-{y}_{m,k}^{t}) }^{2}+{H}^{2}} $

(2)

由于无人机与用户之间的通信信道由视线链路主导，在第 $ t $ 时隙，无人机 $ i $ 与第 $ m $ 个集群中的第 $ k $ 个用户之间的信道遵循自由空间路径损耗模型，可表示为

$ {h}_{m,k,i}^{t}={\beta }_{0}{{d}_{m,k,i}^{t}}^{-2}=\frac{{\beta }_{0}}{{({x}_{i}^{t}-{x}_{m,k}^{t}) }^{2}+{({y}_{i}^{t}-{y}_{m,k}^{t}) }^{2}+{H}^{2}} $

(3)

式中： $ {\beta }_{0} $ 表示信道在参考距离d为1 m时的功率增益。

当用户处于无人机覆盖范围内，即满足通信距离约束时，第 $ m $ 个集群中的第 $ k $ 个用户在第 $ t $ 时隙到第 $ i $ 个无人机的吞吐量定义为

$ {R}_{m,k,i}^{t} = B{\mathrm{l}\mathrm{o}\mathrm{g}}_{2}\Biggr(1+\frac{{p}_{m,k}^{t}{h}_{m,k,i}^{t}}{\displaystyle\sum _{a\ne m}^{M}\displaystyle\sum _{b}^{K}{p}_{a,b}^{t}{h}_{a,b}^{t}+\displaystyle\sum _{c\ne k}^{K}{p}_{m,c}^{t}{h}_{m,c}^{t}+{\alpha }^{2}}\Biggr) ,\forall m,k $

(4)

式中： $ {p}_{m,k} $ 为传输功率， $ B $ 和 $ {\alpha }^{2} $ 分别是带宽和噪声功率。在第 $ t $ 时隙，若用户处于多个无人机覆盖范围内，则其吞吐量是与多个无人机通信产生的吞吐量之和：

$ {R}_{m,k}^{t}={\displaystyle{\sum }}_{i=1}^{N}{R}_{m,k,i}^{t} $

(5)

若仅被无人机 $ i $ 覆盖，其吞吐量为 $ {R}_{m,k}^{t}={R}_{m,k,i}^{t} $ 。因此，从无人机起飞到第 $ t $ 个时隙，集群 $ m $ 中的第 $ k $ 个用户与无人机通信的总吞吐量为

$ {R}_{m,k}={{\displaystyle\sum }}_{t=1}^{t}{R}_{m,k}^{t},\forall m,k $

(6)

本文考虑用户通信约束 $ P\left(m,k\right) =\left\{\mathrm{0,1}\right\} $ ， $ P\left(m,k\right) $ 初始值为0。当总吞吐量 $ {R}_{m,k} $ 大于吞吐量阈值 $ {r}_{{\rm{min}}} $ 时， $ P\left(m,k\right) =1 $ ，表示此用户和无人机已完成通信，同时被标记为“已覆盖用户”且在此轮任务中不再被无人机访问。定义用户平均吞吐量为

$ {T}_{\mathrm{a}\mathrm{v}\mathrm{e}\mathrm{r}\mathrm{a}\mathrm{g}\mathrm{e}}=\frac{{{\displaystyle\sum }}_{m}^{M}{{\displaystyle\sum }}_{k}^{K}P\left(m,k\right) {R}_{m,k}}{MK},P\left(m,k\right) =\left\{\mathrm{0,1}\right\} $

(7)

2 问题构建

为了最大化用户平均吞吐量，保证无人机的最短飞行时间，本文在所有无人机的飞行起点和终点约束、边界碰撞约束、无人机防碰撞约束、通信距离约束以及用户通信约束下，研究了多无人机路径规划问题，优化问题可以表述为

$ \mathrm{max}\;\;{T}_{\mathrm{a}\mathrm{v}\mathrm{e}\mathrm{r}\mathrm{a}\mathrm{g}\mathrm{e}}\qquad\qquad $

(8)

$ \qquad\qquad\qquad\qquad {\rm{s}}.{\rm{t}}.\left\{ \begin{array}{l} {X}_{i}^{\mathrm{u}\mathrm{a}\mathrm{v}\mathrm{f}}={X}_{\mathrm{f}}\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;(9)\\ {Y}_{i}^{\mathrm{u}\mathrm{a}\mathrm{v}\mathrm{f}}={Y}_{\mathrm{f}}\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\,(10)\\ 0\le {X}_{i}\left(t\right) \le {X}_{\mathrm{b}\mathrm{o}\mathrm{u}\mathrm{n}\mathrm{d}}\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\,(11)\\ 0\le {Y}_{i}\left(t\right) \le {Y}_{\mathrm{b}\mathrm{o}\mathrm{u}\mathrm{n}\mathrm{d}}\,\,\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\,(12)\\ {d}_{i,j}^{t}\ge L\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;(13)\\ {d}_{m,k,i}^{t}\le {d}_{\mathrm{c}\mathrm{o}\mathrm{n}\mathrm{s}}\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\,(14)\\ {R}_{m,k}\ge {r}_{\mathrm{m}\mathrm{i}\mathrm{n}}\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\,(15)\\ P\left(m,k\right) =\left\{\mathrm{0,1}\right\}\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\,(16) \end{array} \right.$

式中： $ {T}_{\mathrm{a}\mathrm{v}\mathrm{e}\mathrm{r}\mathrm{a}\mathrm{g}\mathrm{e}} $ 表示本文需要优化的用户平均吞吐量；式(9) 与(10) 为多无人机终点约束， $ {X}_{i}^{\mathrm{u}\mathrm{a}\mathrm{v}\mathrm{f}} $ 和 $ {Y}_{i}^{\mathrm{u}\mathrm{a}\mathrm{v}\mathrm{f}} $ 分别表示无人机终点位置的横坐标和纵坐标， $ {X}_{\mathrm{f}} $ 和 $ {Y}_{\mathrm{f}} $ 为终点水平位置的横坐标和纵坐标；式(11) 与(12) 为无人机边界约束， $ {X}_{i}\left(t\right) $ 和 $ {Y}_{i}\left(t\right) $ 分别表示无人机 $ i $ 在当前水平位置的横坐标和纵坐标， $ {X}_{\mathrm{b}\mathrm{o}\mathrm{u}\mathrm{n}\mathrm{d}} $ 和 $ {Y}_{\mathrm{b}\mathrm{o}\mathrm{u}\mathrm{n}\mathrm{d}} $ 为该区域的长度和宽度；式(13) 为无人机防碰撞约束， $ {d}_{i,j}^{t} $ 为 $ t $ 时隙无人机 $ i $ 与无人机 $ j $ 之间的距离， $ L $ 为最小安全距离；式(14) 为用户与无人机的通信距离约束， ${d}_{\mathrm{c}\mathrm{o}\mathrm{n}\mathrm{s}}= \sqrt{{{R}_{\mathrm{u}\mathrm{a}\mathrm{v}}}^{2}+{H}^{2}}$ 表示用户与无人机通信的最大有效距离；式(15) 表示用户吞吐量 $ {R}_{m,k} $ 需要大于最小阈值 ${r}_{{\rm{min}}}；$ 式(16) 为用户通信约束， $ P\left(m,k\right) $ 初始值为0，当式(15) 满足时， $ P\left(m,k\right) =1 $ ，届时此用户将不再被无人机访问。

问题(8)～(16) 是一个非凸的优化问题，使用传统的优化决策方法需要进行复杂的数学分析和数学推导，随着无人机数量的增加，计算成本也可能会增加，且不能保证求得最优解。深度强化学习作为机器学习的一个重要分支，可为复杂系统的感知和决策问题提供低复杂度的解决方案，具有强大的数据处理能力^[20-21]。

3 基于深度强化学习的多无人机路径规划

本文提出使用Dueling-DDQN算法设计多无人机轨迹，解决上述优化问题。Dueling-DDQN算法采用Dueling网络架构，同时结合了DDQN算法的优势，有效避免了因过大估计 $ Q $ 值而导致的过优化问题，具有很强的探索性、鲁棒性和收敛性，可应用于复杂任务中搜索可能的最优策略。

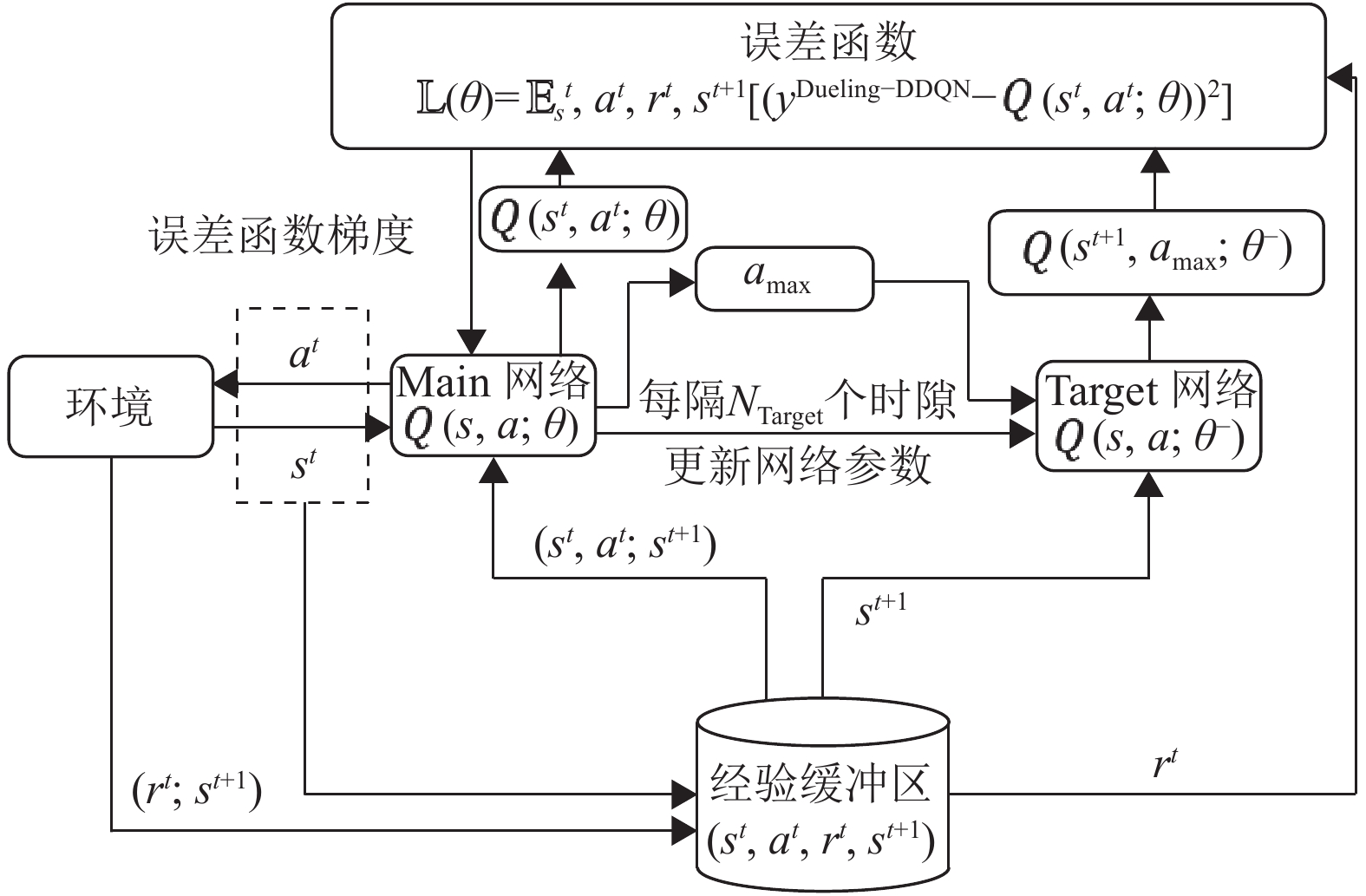
Dueling-DDQN算法的框架如图2所示，它主要由Main网络、Target网络、环境和经验缓冲区组成，在第t时隙，智能体通过与环境交互观察到状态 $ {s}^{t} $ ，并将状态输入到Main网络，然后根据策略选择动作 $ {a}^{t} $ ，得到当前奖励 $ {r}^{t} $ ，随后转移至下一个状态 $ {s}^{t+1} $ ，最后将经验 $ ({s}^{t},{a}^{t},{r}^{t},{s}^{t+1}) $ 存储在经验缓冲区中用于网络的训练。

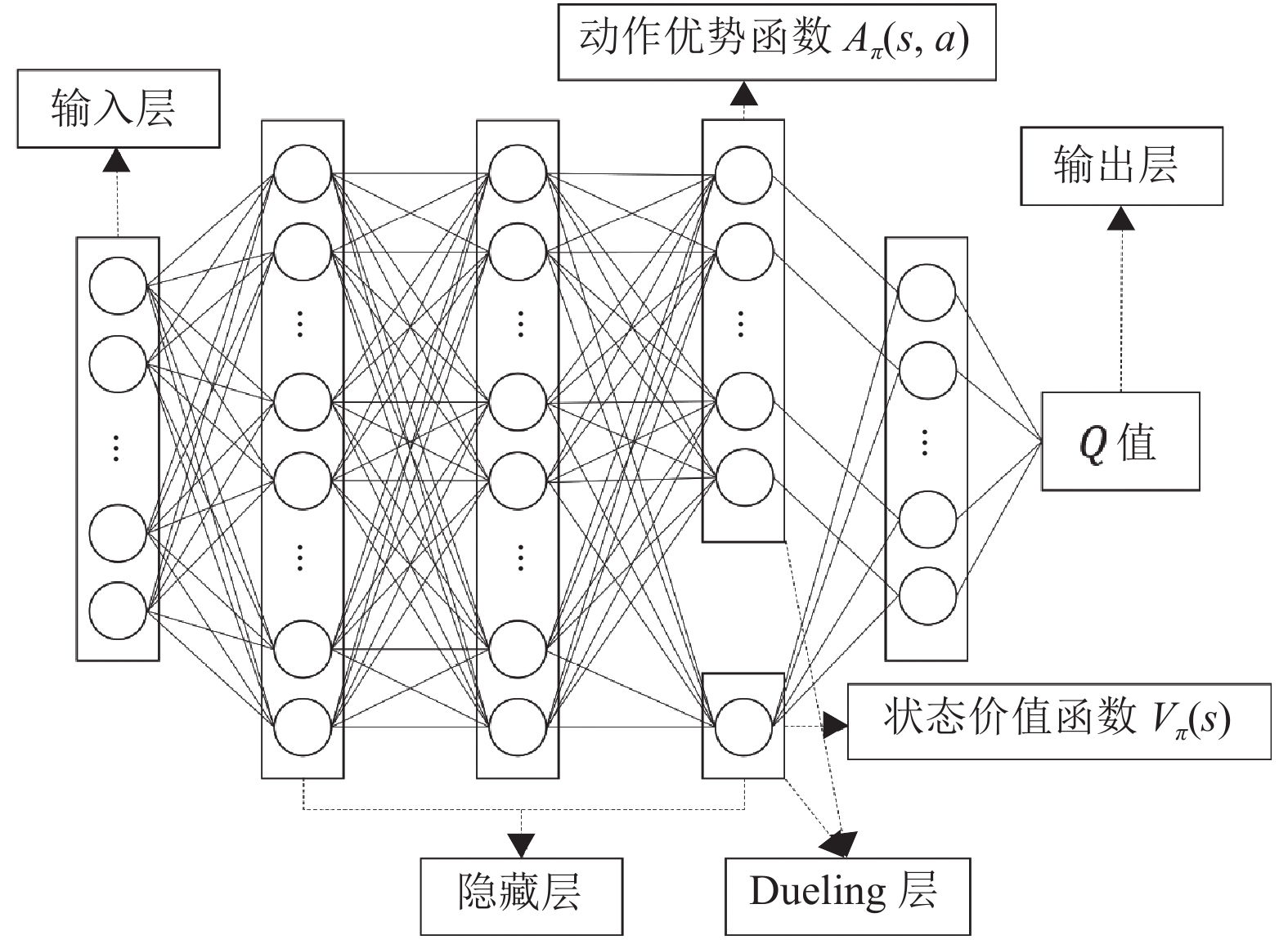
Dueling-DDQN算法采用双网络结构，包括参数为 $ \theta $ 的Main网络 $ Q(s,a;\theta ) $ 和参数为 $ {\theta }^{-} $ 的Target网络 $ Q(s,a;{\theta }^{-}) $ 。每隔 $ {N}_{\mathrm{T}\mathrm{a}\mathrm{r}\mathrm{g}\mathrm{e}\mathrm{t}} $ 个时隙，Target网络通过Main网络更新网络参数，使得Target网络的参数 $ {\theta }^{-} $ 更新频率较慢，这有助于保持TD目标相对稳定，从而提高训练的收敛性。图3为Main网络(Target网络)的神经网络图，该网络是一个6层全连接层的网络，即一个输入层、4个隐藏层和一个输出层。图中输入层对应无人机位置状态 $ {s}^{t} $ ，其神经元个数与状态信息维数相同，输出层输出采取不同动作 $ {a}^{t} $ 时获得的 $ Q $ 值，输出层神经元个数与动作空间维数相同。Dueling层使用两个全连接序列层，而非单一序列的全连接层。其中一个序列称为状态价值函数 $ {V}_{\pi }\left(s\right) $ ，包含1个神经元，用于预测状态值；另一个序列称为依赖于状态的动作优势函数 $ {A}_{\pi }(s,a) $ ，神经元个数与动作空间维数一致，用于预测当前状态下采取不同动作的优势。与单一序列的全连接层相比，Dueling架构的优点是可以在不受动作影响的情况下学习环境的状态价值，使估算的函数值更准确。此外，还可以在不改变底层强化学习算法的情况下，跨动作进行泛化学习。

Dueling-DDQN是一种迭代求解贝尔曼方程的无模型强化学习算法,其状态动作价值函数定义为

$ {Q}_{\pi }({s}^{t},{a}^{t}) ={r}^{t}+\gamma \sum _{{s}^{t+1}\in S}{P}_{{s}^{t}{s}^{t+1}}^{{a}^{t}}\Bigg[\sum _{{a}^{t+1}\in A}\pi ({a}^{t+1}|{s}^{t+1}) {Q}_{\pi }({s}^{t+1},{a}^{t+1}) \Bigg] $

(17)

式中： $ {P}_{{s}^{t}{s}^{t+1}}^{{a}^{t}} $ 表示智能体在状态 $ {s}^{t} $ 采取动作 $ {a}^{t} $ 后转移到状态 $ {s}^{t+1} $ 的概率， $ \pi \left(\cdot \right) $ 表示智能体的选择策略。Dueling-DDQN算法先通过Main网络选择 $ Q $ 值最大的一个动作 $ {a}_{\mathrm{m}\mathrm{a}\mathrm{x}} $ 作为下一步无人机的移动方向，之后再由 Target网络来评估 $ {a}_{\mathrm{m}\mathrm{a}\mathrm{x}} $ ：Target网络将 $ {a}_{\mathrm{m}\mathrm{a}\mathrm{x}} $ 作为最优动作计算 $ Q({s}^{t+1},{a}_{\mathrm{m}\mathrm{a}\mathrm{x}};{\theta }^{-}) $ 的值，而非根据Target网络的参数 $ {\theta }^{-} $ 来选择最优动作计算 $ Q $ 值，这样做可以避免由于状态值过高而导致的过估计问题。

$ \left\{ \begin{aligned} & {a}_{\mathrm{m}\mathrm{a}\mathrm{x}}=\mathrm{arg}\;\underset{a}{\mathrm{m}\mathrm{a}\mathrm{x}}Q\left({s}^{t+1},a;\theta \right) \\& {y}^{\mathrm{D}\mathrm{u}\mathrm{e}\mathrm{l}\mathrm{i}\mathrm{n}\mathrm{g}-\mathrm{D}\mathrm{D}\mathrm{Q}\mathrm{N}}={r}^{t}+\gamma Q({s}^{t+1},{a}_{\mathrm{m}\mathrm{a}\mathrm{x}};{\theta }^-) \end{aligned}\right. $

(18)

同时，此算法把动作价值函数 $ {Q}_{\pi }\left(s,a\right) $ 分为了两个部分，包括状态价值函数 $ {V}_{\pi }\left(s\right) $ 和动作优势函数 $ {A}_{\pi }(s,a) $ ，有效提高了算法学习效率和鲁棒性。

$ {Q}_{\pi }\left(s,a;\theta ,\alpha ,\beta \right) ={V}_{\pi }\left(s;\theta ,\alpha \right) +{A}_{\pi }(s,a;\theta ,\beta ) $

(19)

式中： $ \theta $ 表示 $ {V}_{\pi }\left(s\right) $ 和 $ {A}_{\pi }(s,a) $ 的互参数， $ \alpha $ 和 $ \beta $ 分别为 $ {V}_{\pi }\left(s\right) $ 和 $ {A}_{\pi }(s,a) $ 的参数。

Dueling-DDQN算法设置了经验缓冲区，将经验 $ ({s}^{t},{a}^{t},{r}^{t},{s}^{t+1}) $ 存储在其中，然后通过小批量随机采样对网络进行更新。这样可以避免连续更新的高度相关数据，有助于减少参数更新时的方差。

为了实现用户平均吞吐量最大化，本文依次对智能体、状态、动作和奖励进行定义。

智能体：多无人机整体充当一个智能体，通过不断与环境进行交互寻找最优策略。

状态 $ {s}^{t} $ ：本文把多无人机的位置定义为状态空间，即 $S=\{{x}_{1},{y}_{1},H,{x}_{2},{y}_{2},H,\cdots,{x}_{i},{y}_{i},H\}$ 。在第 $ t $ 时隙，智能体的状态为 ${s}^{t}=\{{x}_{1}^{t},{y}_{1}^{t},H,{x}_{2}^{t},{y}_{2}^{t},H,\cdots,{x}_{i}^{t},{y}_{i}^{t},H\}$ 。

动作 $ {a}^{t} $ ：每一个无人机可以根据策略选择属于动作空间 $ A $ 的一个动作：

$ A=\{\mathrm{l}\mathrm{e}\mathrm{f}\mathrm{t},\mathrm{r}\mathrm{i}\mathrm{g}\mathrm{h}\mathrm{t},\mathrm{f}\mathrm{o}\mathrm{r}\mathrm{w}\mathrm{a}\mathrm{r}\mathrm{d},\mathrm{b}\mathrm{a}\mathrm{c}\mathrm{k}\mathrm{w}\mathrm{a}\mathrm{r}\mathrm{d}\} $

(20)

式中： $ \mathrm{l}\mathrm{e}\mathrm{f}\mathrm{t} $ 和 $ \mathrm{r}\mathrm{i}\mathrm{g}\mathrm{h}\mathrm{t} $ 分别指无人机向左和向右飞行， $ \mathrm{f}\mathrm{o}\mathrm{r}\mathrm{w}\mathrm{a}\mathrm{r}\mathrm{d} $ 和 $ \mathrm{b}\mathrm{a}\mathrm{c}\mathrm{k}\mathrm{w}\mathrm{a}\mathrm{r}\mathrm{d} $ 分别指向前和向后飞行。例如，假设目标区域内存在两个无人机，即 $ N=2 $ 时有

$ {a}^{t}=\{\mathrm{f}\mathrm{o}\mathrm{r}\mathrm{w}\mathrm{a}\mathrm{r}\mathrm{d},\mathrm{r}\mathrm{i}\mathrm{g}\mathrm{h}\mathrm{t}\} $

(21)

表示无人机1向前移动，同时无人机2向右移动。

奖励 $ {r}^{t} $ ：在深度强化学习中，奖励用于评估智能体在当前状态下采取的动作的好坏。本文设计的奖励功能既依赖于用户平均吞吐量 $ {T}_{\mathrm{a}\mathrm{v}\mathrm{e}\mathrm{r}\mathrm{a}\mathrm{g}\mathrm{e}} $ ，同时也跟无人机整条路径上所收集的其他奖励有关。当所有无人机都到达终点(不要求同时到达)时获得终点奖励 $ {R}_{\mathrm{f}\mathrm{i}\mathrm{n}\mathrm{a}\mathrm{l}} $ 。

$ {R}_{\mathrm{f}\mathrm{i}\mathrm{n}\mathrm{a}\mathrm{l}}=\left\{ \begin{aligned} & 2\;000\text{，}{X}_{i}\left(t\right) ={X}_{\mathrm{f}}\;{\rm{and}}\;{Y}_{i}\left(t\right) ={Y}_{\mathrm{f}}\\& 0\text{，}{\rm{otherwise}} \end{aligned}\right. $

(22)

无人机飞行轨迹越长，整条路径上获得的步数惩罚 $ {R}_{\mathrm{s}\mathrm{p}} $ 越大，若有无人机飞出目标区域，智能体将返回上一个状态且受到边界惩罚 $ {R}_{\mathrm{b}\mathrm{p}} $ 。同时，若无人机之间发生碰撞将被给予碰撞惩罚 $ {R}_{\mathrm{c}\mathrm{p}} $ 。

因此，在第 $ t $ 时隙，多无人机总奖励 $ {r}^{t} $ 表达式为

$ {r}^{t}={T}_{\mathrm{a}\mathrm{v}\mathrm{e}\mathrm{r}\mathrm{a}\mathrm{g}\mathrm{e}}+{R}_{\mathrm{s}\mathrm{p}}+{R}_{\mathrm{b}\mathrm{p}}+{R}_{\mathrm{c}\mathrm{p}}+{R}_{\mathrm{f}\mathrm{i}\mathrm{n}\mathrm{a}\mathrm{l}} $

(23)

当 $ {s}^{t+1} $ 为终止状态：

$ {y}^{\mathrm{D}\mathrm{u}\mathrm{l}\mathrm{i}\mathrm{n}\mathrm{g}-\mathrm{D}\mathrm{D}\mathrm{Q}\mathrm{N}}{=r}^{t} $

(24)

当 $ {s}^{t+1} $ 不是终止状态：

$ {y}^{\mathrm{D}\mathrm{u}\mathrm{l}\mathrm{i}\mathrm{n}\mathrm{g}-\mathrm{D}\mathrm{D}\mathrm{Q}\mathrm{N}}=\begin{array}{c}\\ {r}^{t}+\gamma Q({s}^{t+1},{\rm{arg}}\,\underset{a}{\mathrm{m}\mathrm{a}\mathrm{x}}Q({s}^{t+1},a;\theta ) ,{\theta }^-) \end{array} $

(25)

本文所提的基于Dueling-DDQN的多无人机辅助数据收集系统智能路径规划的完整算法见算法1。

算法1 　基于Dueling-DDQN的多无人机辅助数据收集系统智能路径规划算法

1. 初始化：Main网络的参数 $ {\theta }$ 、Target 网络的参数 $ {{\theta }^{-} }$ 和经　　　验回放池，随机初始化用户坐标。

2. 对于每一个episode：

3. 　　初始化多无人机坐标以及系统状态；

4. 　　在当前系统状态 $ {{s}^{t} }$ 下，基于 $ {\varepsilon }$ -贪婪策略，根据式　　　　(20)和式(21) 选择一个动作 $ { {a}^{t}\in A}$ ：

$ {{a}^{t}=\left\{\begin{aligned} & {\rm{random\;action}},\varepsilon \\& {\rm{arg}}\;\;\underset{a}{\mathrm{m}\mathrm{a}\mathrm{x}}Q({s}^{t},a) ,1-\varepsilon \end{aligned} \right.} $

5.　　执行动作 $ {{a}^{t}}$ ，根据式(4) 计算多无人机覆盖范围内　　　与每个用户的吞吐量，根据式(23) 估计当前奖励 $ {{r}^{t}}$ ；

6. 　　获得下一个环境状态 $ {{s}^{t+1}}$ ；

7. 　　将元组 $ {({s}^{t},{a}^{t},{r}^{t},{s}^{t+1})}$ 存入到经验回放池；

8. 　　如果经验回放池R储存经验数量大于容量阈值　　　　 $ { {C}_{{\rm{batch}}} }$ ；

9. 　　随机从经验回放池中抽取 $ {{N}_{\mathrm{b}\mathrm{a}\mathrm{t}\mathrm{c}\mathrm{h}}}$ 个样本，计算样本　　　 $ { ({s}^{t},{a}^{t},{r}^{t},{s}^{t+1})}$ 的目标值；

10. 　　用梯度下降法更新网络参数，使损失最小化：

$ {\mathbb{L}(\theta ) ={\mathbb{E}}_{{s}^{t},{a}^{t},{r}^{t},{s}^{t+1}}[{({y}^{\mathrm{D}\mathrm{u}\mathrm{e}\mathrm{l}\mathrm{i}\mathrm{n}\mathrm{g}-\mathrm{D}\mathrm{D}\mathrm{Q}\mathrm{N}}-Q({s}^{t},{a}^{t};\theta ) ) }^{2}] \text{，} }$

　梯度更新为：

$ {\qquad\quad {\nabla }_{\theta }\mathbb{L}(\theta ) ={\mathbb{E}}_{{s}^{t},{a}^{t},{r}^{t},{s}^{t+1}}[({y}^{\mathrm{D}\mathrm{u}\mathrm{e}\mathrm{l}\mathrm{i}\mathrm{n}\mathrm{g}-\mathrm{D}\mathrm{D}\mathrm{Q}\mathrm{N}}-Q({s}^{t},{a}^{t};\theta ) ) {\nabla }_{\theta }Q({s}^{t},{a}^{t};\theta ) ] \text{，}} $

11. 　更新状态 $ { {s}^{t}={s}^{t+1}}$ ；

12. 　每隔一定步数更新Target网络参数 $ { {\theta }^{-}=\theta }$ ；

13. 　如果所有无人机均到达终点，进入下一个episode，　　　返回3；如果所有的episode都已经执行完，则训练过程　　　结束；否则返回4。

4 仿真结果

本文设定无人机在 $1\;000\;\mathrm{m}\times 1\;000\;\mathrm{m}$ 的目标区域内飞行，即 ${X}_{\mathrm{b}\mathrm{o}\mathrm{u}\mathrm{n}\mathrm{d}}={Y}_{\mathrm{b}\mathrm{o}\mathrm{u}\mathrm{n}\mathrm{d}}=1\;000$ m，同时无人机飞行高度 $ H $ 固定为200 m，无人机的起点和终点位置水平坐标分别为(0,0) 和(1000,1000) 。该目标区域内存在5个集群，每个集群中随机分布了10个用户。训练时目标区域被离散为 $ 25\;\mathrm{m}\times 25\;\mathrm{m} $ 的栅格，因此无人机每一步移动距离为40 m。训练阶段的算法迭代次数episode为3000次，当所有无人机到达终点则当前episode结束，为便于分析，本文在仿真中每10个episode对无人机每步均覆盖率取一次平均。本文设置经验缓冲区R的容量 $ {C}_{\mathrm{m}\mathrm{a}\mathrm{x}} $ 为 $ 2\times {10}^{5} $ ，容量阈值 $ {C}_{\mathrm{b}\mathrm{a}\mathrm{t}\mathrm{c}\mathrm{h}} $ 为200。本文其他参数如表1所示。

仿真考虑两个场景——“单无人机场景”与“两无人机场景”。在两个场景下将本文所提方案简称为“基于Dueling-DDQN的数据收集方案”。为进行比较，在两个场景中将DQN和DDQN算法辅助数据收集作为对比方案。这两种对比方案的状态、动作和奖励等的定义与“基于Dueling-DDQN的数据收集方案”一致。DDQN和DQN算法同样采用双网络结构，不同之处在于DDQN算法通过解耦目标 $ Q $ 值动作选择和计算目标 $ Q $ 值这两步来消除过度估计的问题，这与本文所提算法一致，但两种基准算法均未采用Dueling网络架构。本文将DDQN和DQN算法分别称为“基于DDQN的数据收集方案”和“基于DQN的数据收集方案”。此外，在“单无人机场景”中增设一个没有优化轨迹的对比方案，采用固定的无人机飞行轨迹。在固定无人机飞行轨迹的对比方案中，取所有用户的坐标中心点( $ {X}_{c},{Y}_{c} $ ) ，即 $ P $ 个用户的初始水平坐标之和的均值， ${X}_{c}={{\displaystyle\sum }}_{m}^{M}{{\displaystyle\sum }}_{k}^{K}{x}_{m,k}^{0}/P$ ， ${Y}_{c}= {{\displaystyle\sum }}_{m}^{M}{{\displaystyle\sum }}_{k}^{K}{y}_{m,k}^{t}/P$ 。无人机从起点起飞，径直穿过坐标中心点大致位置，最后到达终点，同时在飞行途中计算满足通信距离约束的用户的吞吐量。将该方案称为“固定轨迹数据收集方案”，与基于强化学习的方案作对比。

由于当用户总吞吐量 $ {R}_{m,k} $ 大于吞吐量阈值 $ {r}_{\mathrm{m}\mathrm{i}\mathrm{n}} $ 时， $ P\left(m,k\right) =1 $ ，此用户被标记为“已覆盖用户”且在此幕中不再与无人机通信，因此，“已覆盖用户”越多则表示已收集平均吞吐量 ${T}_{\mathrm{a}\mathrm{v}\mathrm{e}\mathrm{r}\mathrm{a}\mathrm{g}\mathrm{e}}=$ $\displaystyle\frac{{{\displaystyle\sum }}_{m}^{M}{{\displaystyle\sum }}_{k}^{K}P\left(m,k\right) {R}_{m,k}}{MK} $ 越大。为了使数据更直观且易于分析，本文考虑将以无人机每步均覆盖率 $C= \displaystyle\frac{{{\rm{Users}}}_{\mathrm{c}}}{{\rm{Steps}}}$ 来衡量系统性能的好坏，其中的 ${{\rm{Users}}}_{\mathrm{c}}$ 表示每一幕“已覆盖用户”的数量， ${\rm{Steps}}$ 表示在每一幕中无人机从起点飞往终点所用总步数。最大化每步均覆盖率即最大化用户平均吞吐量的同时最小化无人机到达终点总步数，用每步均覆盖率作为性能指标刚好满足本文研究目的。

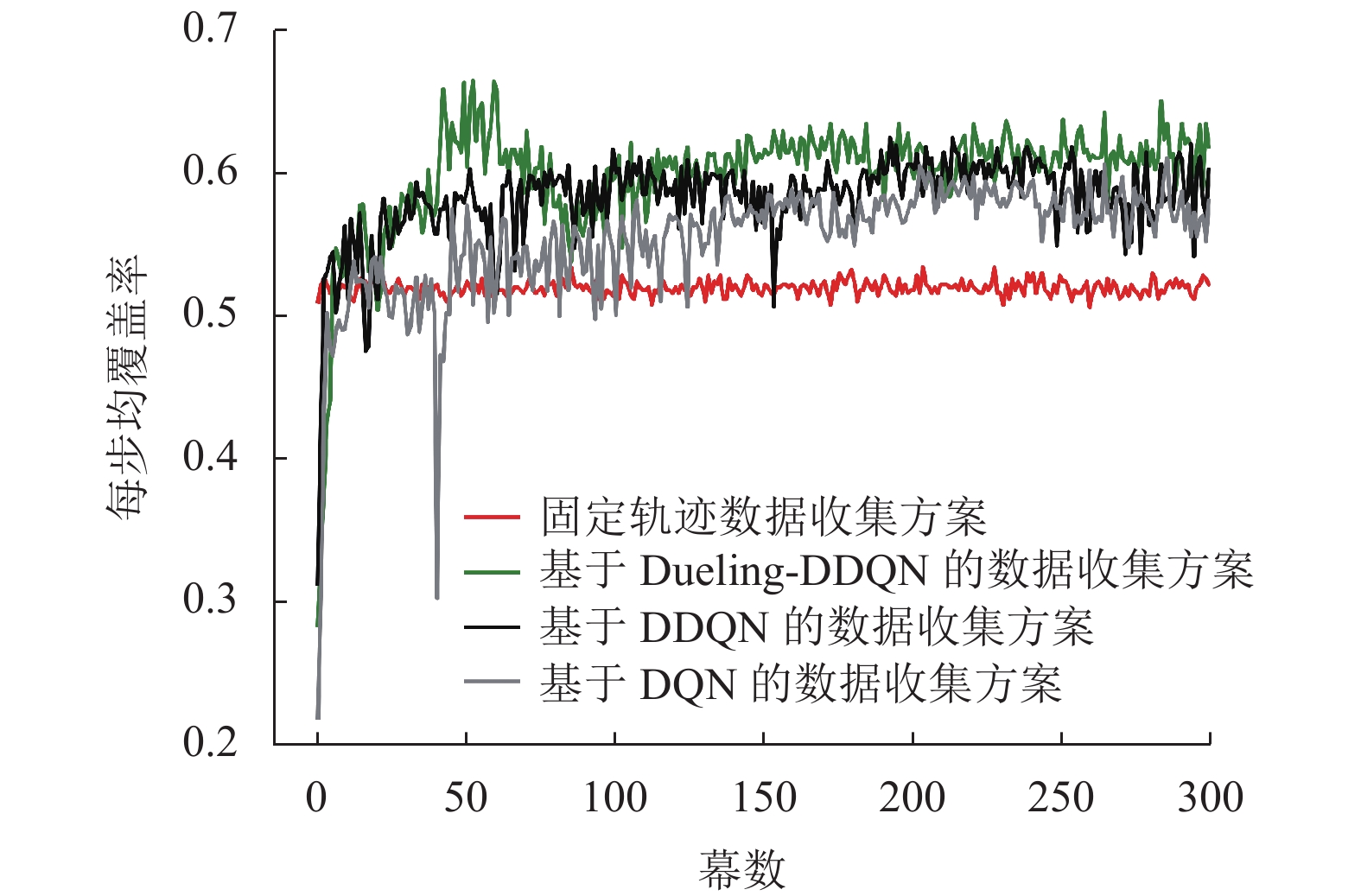
图4给出了“单无人机场景”下不同方案的无人机每步均覆盖率对比图。可以看出，“固定轨迹数据收集方案”无人机每步均覆盖率基本保持不变且低于其他3种方案，这是因为在每一幕中无人机飞行的轨迹相同，所服务的地面用户基本固定不变。这说明强化学习算法具备自主学习的能力，在训练时会通过与环境交互最大化本文优化目标。在“基于DQN的数据收集方案”中，无人机每步均覆盖率在50幕之前较低，这是由于DQN算法在网络训练初期对 $ Q $ 值计算尚不准确时，在Target网络中遍历取最大 $ Q $ 值导致过估计。此方案无人机每步均覆盖率在200幕之后不再上升，训练开始收敛。同时，可以观察到“基于DDQN的数据收集方案”和本文所提方案在训练初期无人机每步均覆盖率增长速度比“基于DQN的数据收集方案”更快，这体现了目标的动作选择和动作评估分别用不同的值函数来实现的优势。但是，在整个训练过程中，“基于DDQN的数据收集方案”的每步均覆盖率波动较大，特别是在第153幕出现较大幅度下降，然后回升，在190幕左右开始收敛。在本文所提方案中，每步均覆盖率在140幕之后趋于收敛，且在训练后期具备最优的收敛值。同时，通过对各方案在训练后期(200～300幕)无人机每步均覆盖率的方差进行了计算，“基于DQN的数据收集方案”和“基于DDQN的数据收集方案”的覆盖率方差分别为1.7×10⁻⁴和3.4×10⁻⁴，而本文所提方案的覆盖率方差为1.5×10⁻⁴，较两种基准方案更稳定，这体现了Dueling-DDQN算法采用Dueling网络架构的优势。上述结果显示，与其他3个对比方案相比，本文所提方案在“单无人机场景”下具有很好的学习能力、鲁棒性和收敛速度。

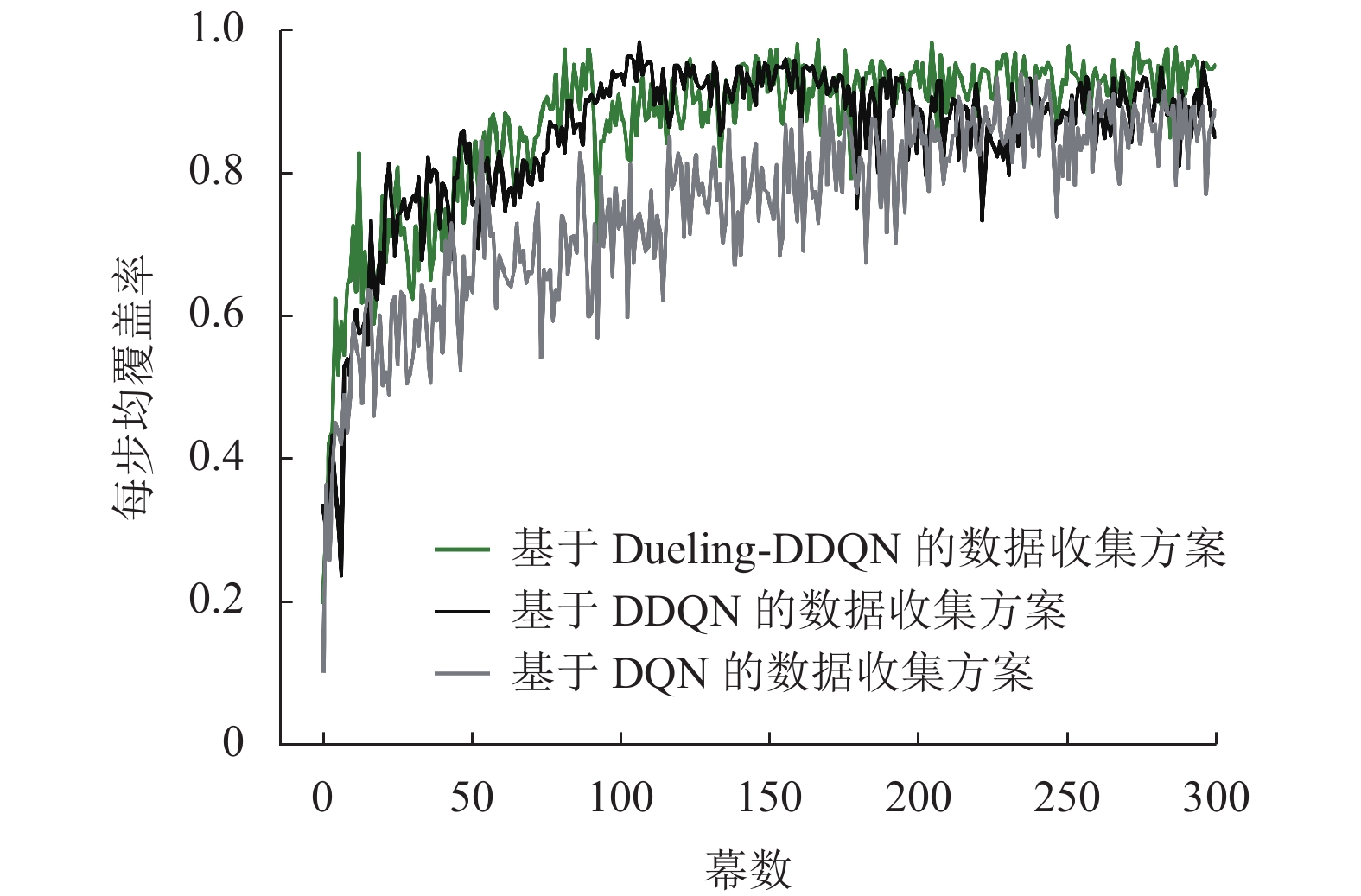
图5给出了“两无人机场景”下不同方案的无人机每步均覆盖率对比图。从图中可以观察到，“基于DQN的数据收集方案”在训练初期依旧存在过估计问题，同时训练过程波动较大，在200幕左右开始收敛。“基于DDQN的数据收集方案”虽然解决了DQN方案训练初期的过估计问题，但是由于存在网络训练波动较大的问题，在150～230幕之间无人机每步均覆盖率下滑严重，最终在230幕之后开始收敛。本文所提方案在训练初期每步均覆盖率增长迅速，在第123幕之后开始收敛，且相比上述两种基准方案具有更佳的收敛值。经计算，上述3种方案在训练后期(200～300幕)的覆盖率方差分别为1.7×10⁻³、1.4×10⁻³、8×10⁻⁴，可以发现本文所提方案方差最小，具有更加稳定的性能。综合图4和图5分析得出，本文所提算法优于两种基准算法，既能很好地解决DQN算法的过估计问题，又能克服两种对比算法波动较大的问题，具有更好的学习能力、收敛速度和鲁棒性，更适合用于解决无人机路径规划和数据收集问题。

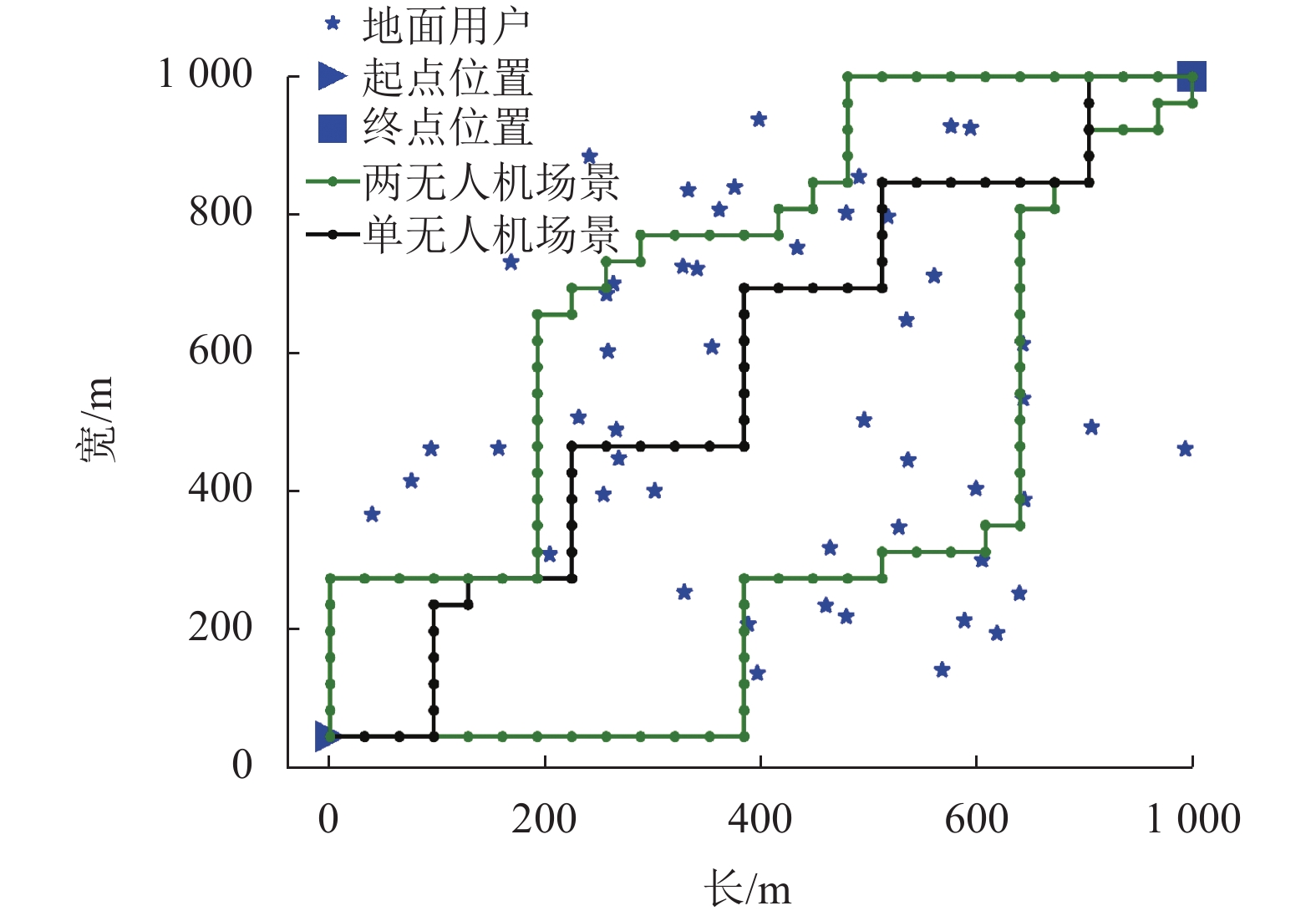
图6为本文所提算法在“单无人机场景”和“两无人机场景”下的无人机二维飞行轨迹对比图。可以观察到，在这两种场景下无人机都能在最短时间内到达终点。在“单无人机场景”下无人机轨迹分布居中呈“之”字型，这样可以充分利用单个无人机的覆盖范围最大化数据收集。“两无人机场景”下无人机路径未出现重合现象，能够很好地避免无人机之间产生碰撞。同时轨迹分散在两侧，这样能扩大无人机对用户的覆盖范围，充分利用无人机的数量优势最大化收集数据。

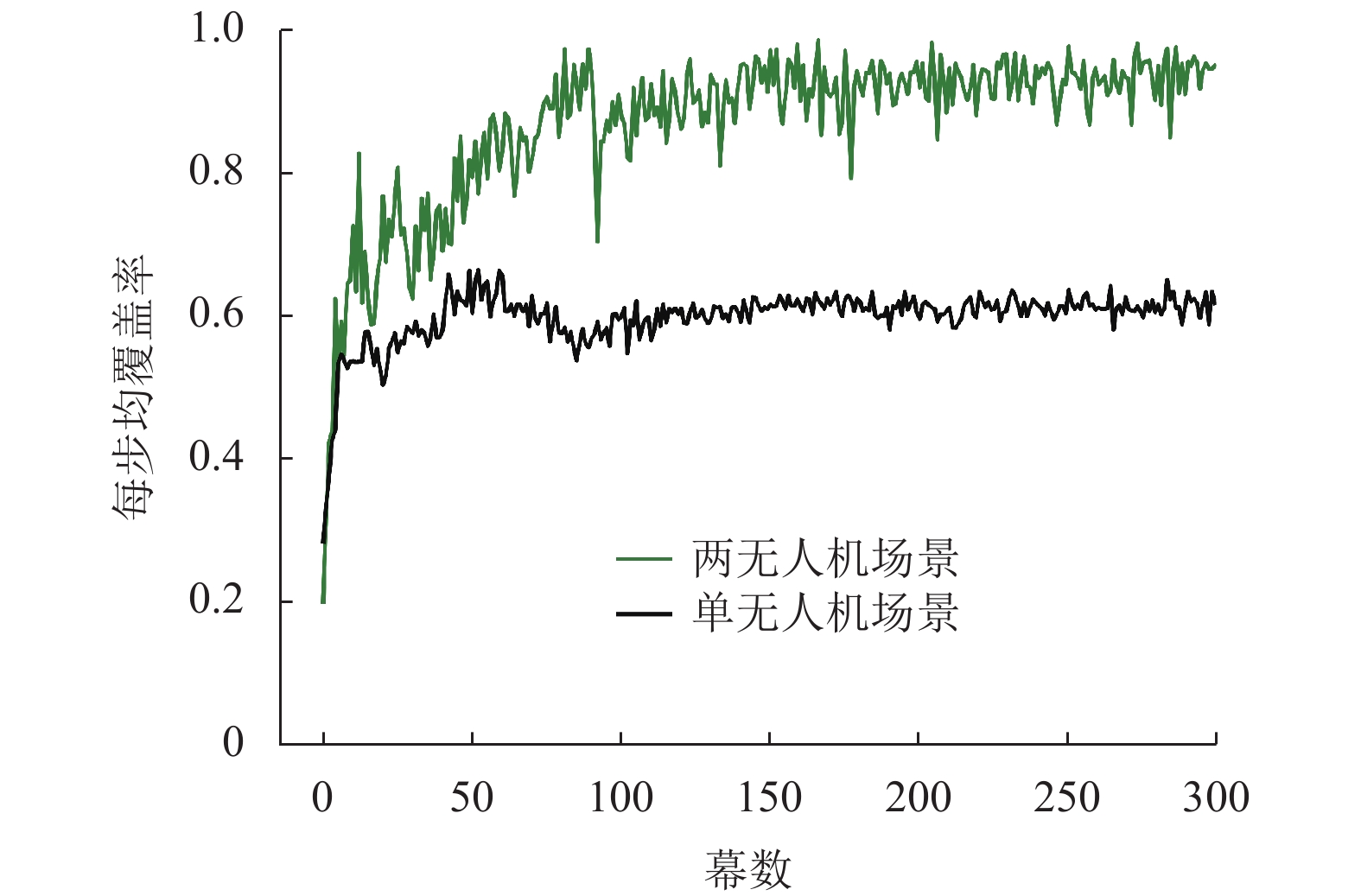
图7给出了本文所提算法在不同场景下的无人机每步均覆盖率对比图。可以发现，在“两无人机场景”无人机每步均覆盖率的值接近1.0，而“单无人机场景”下每步均覆盖率在0.6左右，远低于前者。结合图6无人机轨迹可以发现，本文所提算法在两种场景下都能使无人机在最短时间内到达终点。经简单计算可以得出，在“两无人机场景”下无人机可以覆盖约50个用户，接近饱和，而“单无人机场景”下在训练收敛以后无人机覆盖用户数约为30。分析得出，本文所提算法可以很好地完成研究目标，能够使无人机在最短时间内从起点飞往终点，并在此过程中最大化收集用户平均吞吐量。同时，在本文所考虑的系统模型中两无人机辅助数据收集相比单无人机性能提升明显，基本可以实现用户全覆盖，解决了单无人机在用户分布分散且具备移动能力时覆盖不全的问题，体现了研究多无人机辅助数据收集的有效性和必要性。

5 结论

本文研究了一种多无人机辅助数据收集系统的智能路径规划算法，无人机作为移动基站为地面用户提供通信服务。本文的研究目标是通过规划多架无人机的轨迹，使无人机在最短时间内到达终点的同时最大化收集数据。考虑到飞行时间限制、用户分布分散等问题，本文提出了基于Dueling-DDQN的多无人机辅助数据收集系统智能路径规划算法。仿真结果表明，所提算法可以实现本文研究目标，在本文所考虑的系统模型中解决了单无人机辅助数据收集时用户覆盖不全的问题。同时，所提算法与两种基准算法相比具有更好的收敛性、鲁棒性和学习能力。