随着老龄化人口不断增加,老年人医疗健康日益成为社会关注问题。跌倒已成为65岁及以上老年人意外死亡和受伤的最大威胁[1]。现有的跌倒检测方法主要分为三类[2]:基于可穿戴设备[3-4]、基于环境设备[5]和基于视觉。基于视觉的方法是目前研究主流,比前两种方法具有更高检测精度和鲁棒性。在计算机视觉中,许多研究人员使用卷积神经网络(Convolutional Neural Network, CNN) 来实现跌倒检测,其主要工作包括:(1) 将动作视频编码为图像,最常见方法是对3D骨架序列进行编码,这种方法可以明显减少参数。(2) 利用CNN对编码后的图像进行分类以实现跌倒检测。文献[6]将骨架序列编码为RGB图像,将其输入到轻量级卷积网络进行跌倒判决。文献[7]计算关节点位移和高度,将其编码为RGB图像中的像素值,构造关节运动图,设计双流卷积网络用于跌倒判断。文献[8]提出分层网络用来提取关节点之间的共现特征,根据这些特征识别不同动作。文献[9]提出自适应推理框架,通过该框架学习关节点之间的依赖关系,生成骨架图并送到CNN网络进行动作识别。
上述文献提出的算法存在如下问题:所生成的图像没能很好保存骨架序列空间结构以及使用的CNN网络只能提取局部特征,无法获取全局特征信息。针对这一问题,本文提出一种人体跌倒检测方法。该方法首先利用姿态估计算法生成人体骨架序列;然后使用基于DFS方法将骨架序列编码为能够保存骨架数据空间结构的TSSI;最后设计一个可学习STB-CNN提取TSSI中多尺度特征及进行跌倒检测。
1 方法本文跌倒检测算法主要流程如图1所示,图中虚框部分为所提出的可学习时空块卷积神经网络(STB-CNN) 。

|
图 1 跌倒检测算法流程 Figure 1 Fall detection algorithm flow |
姿态估计算法主要从每帧图像中提取关节点,将RGB视频数据转化为骨架序列。本文使用基于图注意力时空卷积网络(Craph Attention Spatio Temproal Convolutional Network,GAST-Net) [10]获取人体关节点,该网络由交错的时空卷积和图注意块组成。通过GAST-Net得到17个人体关节点坐标,若序列中某一帧出现关节点缺失问题,本文使用相邻两帧对应关节点坐标均值进行填充,若首尾两帧缺失,则将其删除。
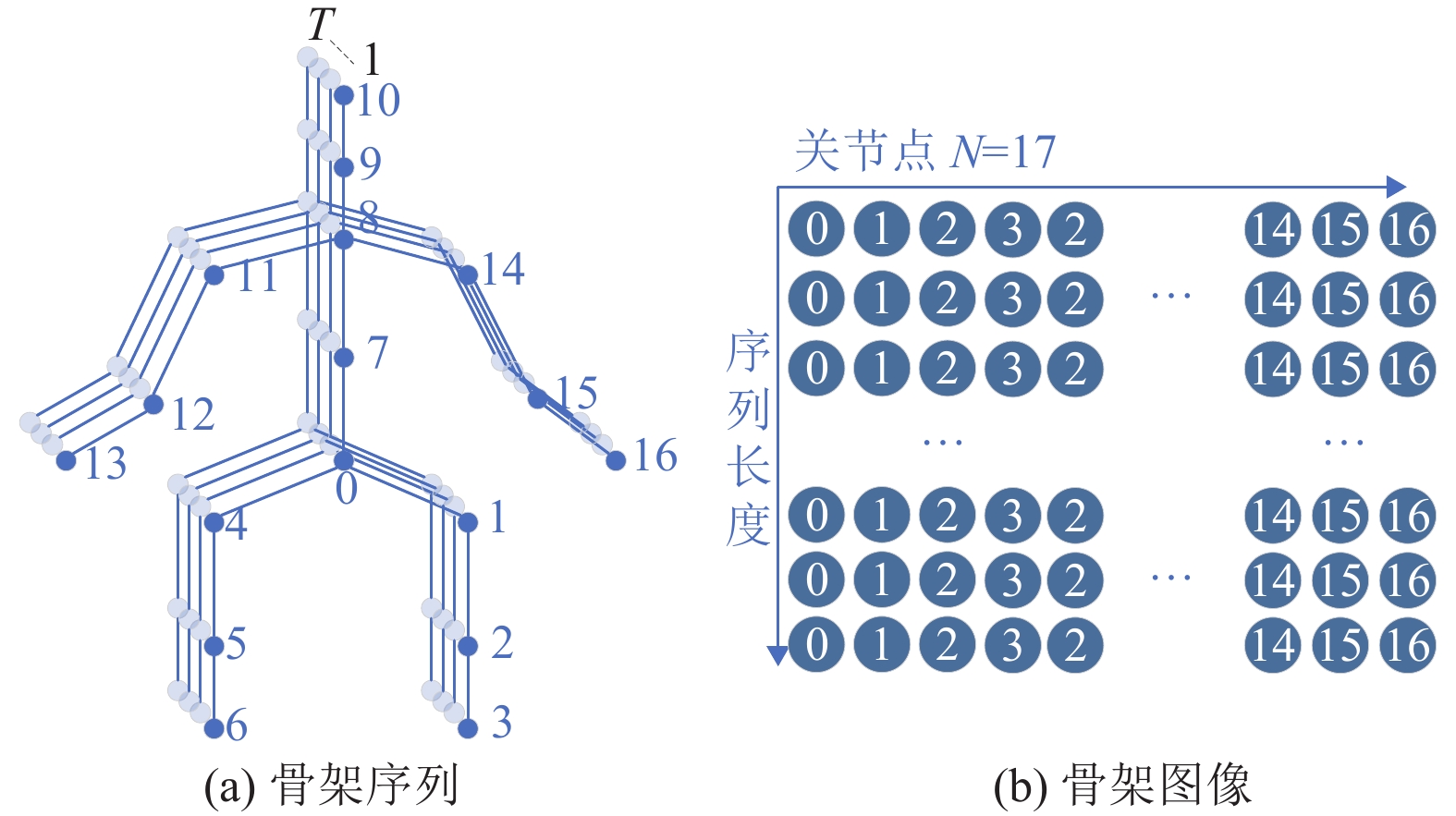
1.2 构建骨架图像早期构建方法是将骨架序列每帧内的所有关节点按索引顺序排成一行[11-12],所有帧按时间顺序排列,从而将整个骨架序列(见图2(a))编码成大小为
|
图 2 骨架序列和骨架图像 Figure 2 Skeleton sequence and skeleton image |
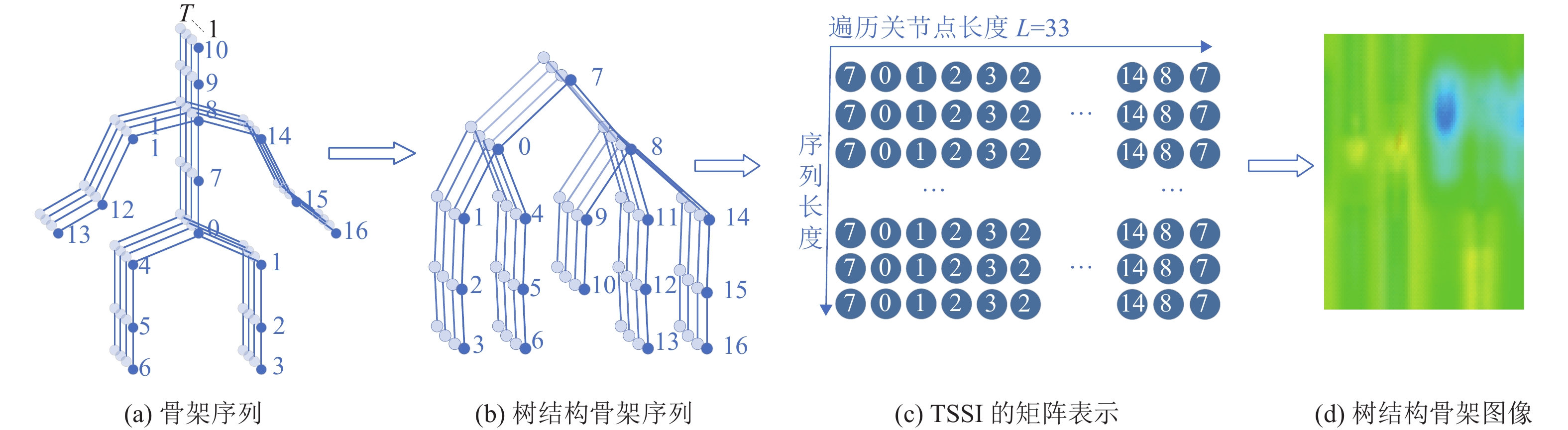
|
图 3 TSSI构建过程 Figure 3 The construction process of TSSI |
本文将TSSI表示为
本文采用基于DFS方法将骨架序列转化为TSSI,该方法较好地保留了骨架序列的空间信息。考虑到TSSI的结构,本文设计一个可学习STB-CNN学习TSSI的空间和时间信息。STB-CNN网络结构如图4所示。网络包括时空差分模块、时空可学习框架、时空多分支卷积模块和分类模块。
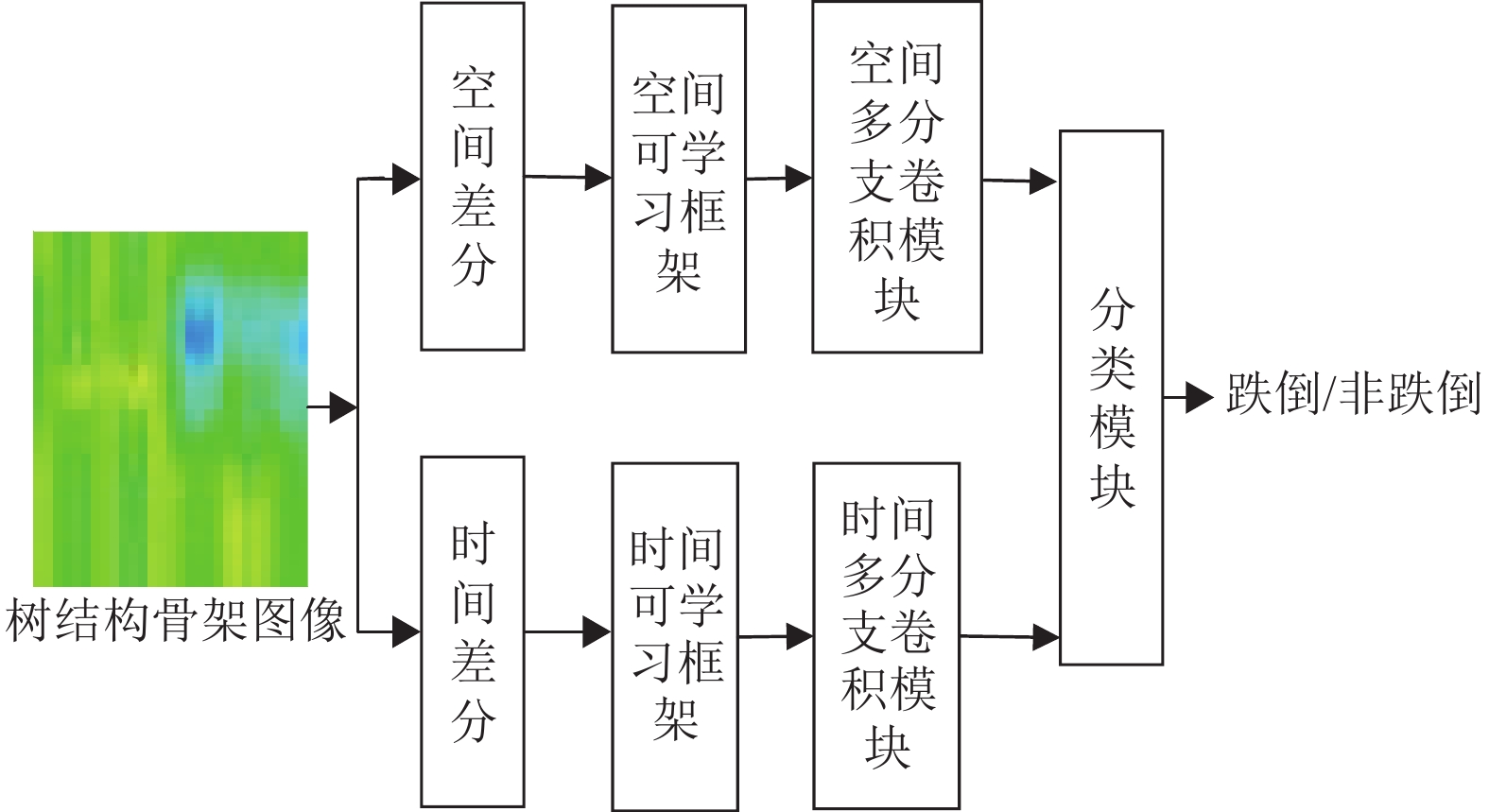
|
图 4 STB-CNN网络 Figure 4 STB-CNN network |
为降低周围环境噪声对识别结果的影响,针对TSSI的时空特性,本文采用空间差分和时间差分操作来初步提取输入骨架数据的时空特征信息,得到空间差分特征图像
| $ \begin{array}{c}{\boldsymbol{s}}_{i,j}=\left\{\begin{array}{l}{\boldsymbol{v}}_{i,j},j=1,\;\;i\in \left(\mathrm{1,2},\cdots,T\right)\\ {\boldsymbol{v}}_{i,j}-{\boldsymbol{v}}_{i,j-1},j\in \left(2,\cdots,L\right) ,\;\;i\in \left(\mathrm{1,2},\cdots,T\right)\end{array}\right. \end{array} $ | (1) |
| $ \begin{array}{c}{\boldsymbol{m}}_{i,j}=\left\{\begin{array}{l}{\boldsymbol{v}}_{i,j},i=1,\;\;j\in \left(\mathrm{1,2},\cdots,L\right)\\ {\boldsymbol{v}}_{i,j}-{\boldsymbol{v}}_{i-1,j},i\in \left(2,\cdots,T\right) ,\;\;j\in \left(\mathrm{1,2},\cdots,L\right)\end{array}\right. \end{array} $ | (2) |
关节点之间的依赖性对于跌倒判别至关重要。
如图5和图6所示,本文将
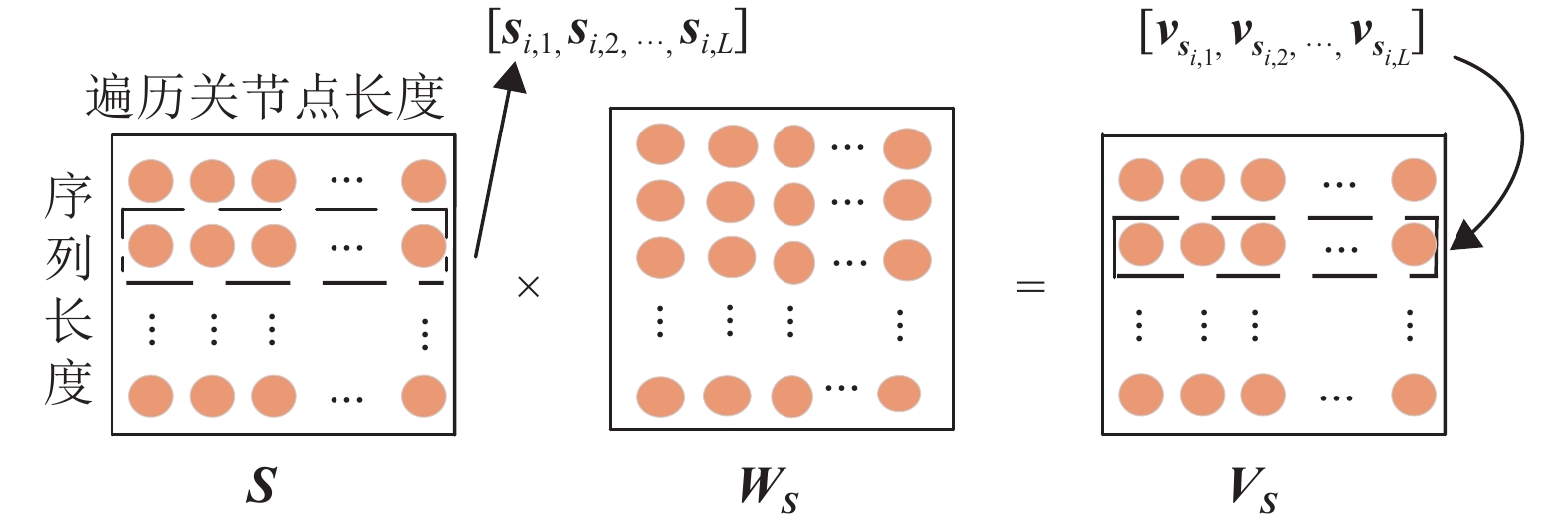
|
图 5 空间可学习框架 Figure 5 Spatial learnable framework |
|
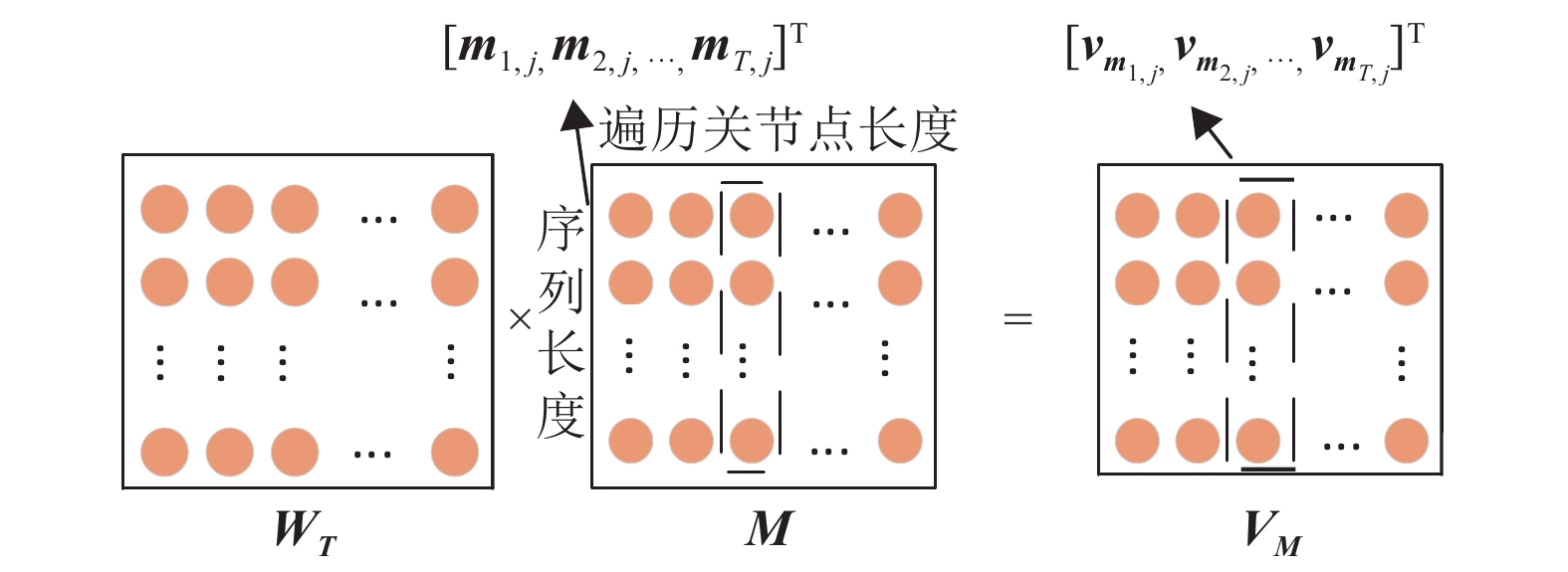
图 6 时间可学习框架 Figure 6 Temporal learnable framework |
| $ \begin{split} &{{\boldsymbol{v}}_{\boldsymbol{s}_{i,j}}^{c}}=\sum _{k=1}^{L}{s}_{i,k}^{c}\cdot {{w}_{{\boldsymbol{s}}_{k,j}}},c\in \left(\mathrm{1,2},3\right),\\ &\qquad {{\boldsymbol{v}}_{\boldsymbol{s}_{i,j}}}=\left[{{v}_{{\boldsymbol{s}}_{i,j}}^{1}},{{v}_{{\boldsymbol{s}}_{i,j}}^{2}},{{v}_{{\boldsymbol{s}}_{i,j}}^{3}}\right] \end{split}$ | (3) |
式中:
从式(3) 中可以看出,关节点空间特征
跌倒动作是一个连续过程,关节点时间相关性信息对于动作判断也十分重要。本文采用时间可学习框架来生成具有较强关节点时间相关性信息的特征图像,有效地对骨架序列的时间关系进行建模。时间可学习框架处理过程如图6所示。
| $\begin{split} &{{\boldsymbol{v}}_{\boldsymbol{m}_{i,j}}^{c}}=\sum _{k=1}^{T}{{w}_{{t}_{i,k}}}\cdot {m}_{k,j}^{c},c\in \left(\mathrm{1,2},3\right),\\ &\qquad{{\boldsymbol{v}}_{\boldsymbol{m}_{i,j}}}=[{{v}_{{\boldsymbol{m}}_{i,j}}^{1}},{{v}_{{\boldsymbol{m}}_{i,j}}^{2}},{{v}_{{\boldsymbol{m}}_{i,j}}^{3}}] \end{split}$ | (4) |
式中:
通过时空可学习模块获得了能有效模拟关节点之间空间和时间依赖性的特征图像。由于单一的、时间或空间尺度上的卷积操作无法获取全面的时空信息,借鉴Inception 模块[14],本文设计时空多分支卷积模块来学习骨架数据间的时空关联信息,该模块包括两个部分:空间多分支卷积模块和时间多分支卷积模块。
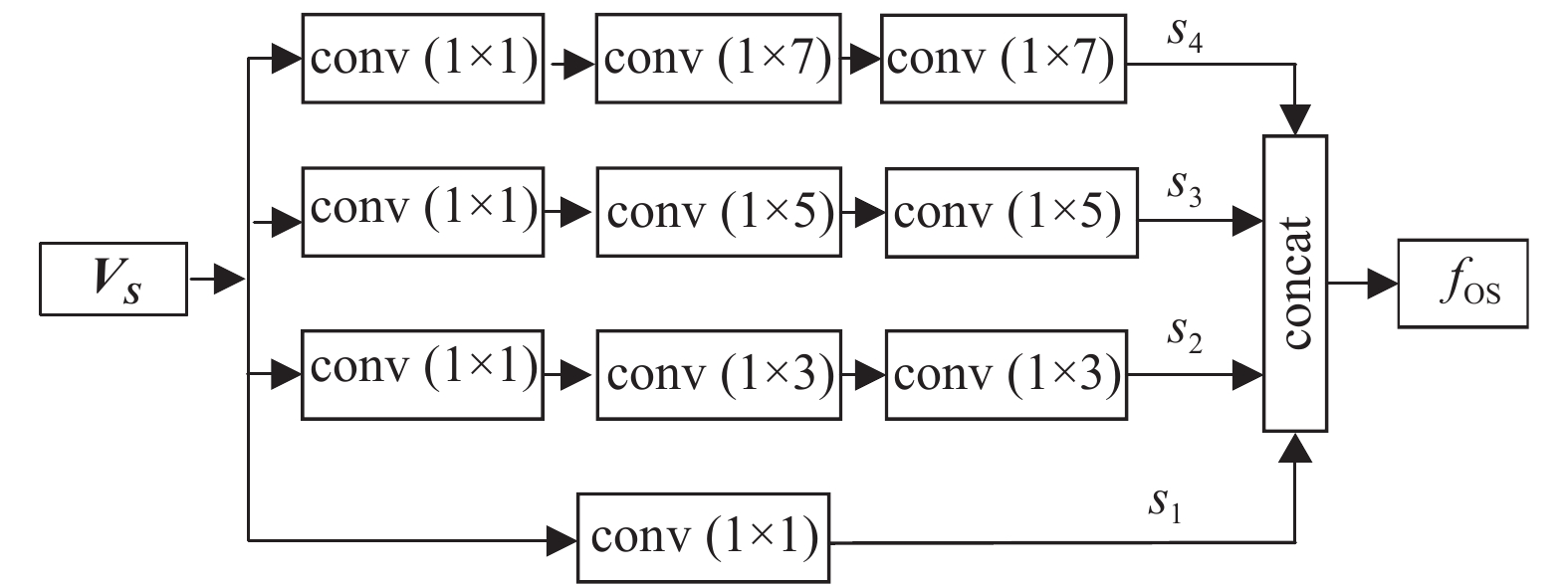
空间多分支卷积模块包含4个空间卷积分支,如图7所示。每个分支分别在骨架数据空间维度(即输入图像每一行)上执行一维卷积操作,从不同感受野上提取空间特征。具体实现过程为:(1) 在4个分支都进行
|
图 7 空间多分支卷积模块结构 Figure 7 Spatial multi-branch convolution module structure |
| ${s}_{1}={f}_{\mathrm{c}\mathrm{o}\mathrm{n}\mathrm{v}\left(1\times 1\right) }\left({\boldsymbol{V}}_{\boldsymbol{S}}\right), $ |
| ${s}_{2}={f}_{\mathrm{c}\mathrm{o}\mathrm{n}\mathrm{v}(1\times 3) }({f}_{\mathrm{c}\mathrm{o}\mathrm{n}\mathrm{v}(1\times 3) }({f}_{\mathrm{c}\mathrm{o}\mathrm{n}\mathrm{v}(1\times 1) }({\boldsymbol{V}}_{\boldsymbol{S}}) ) ), $ |
| ${s}_{3}={f}_{\mathrm{c}\mathrm{o}\mathrm{n}\mathrm{v}(1\times 5) }({f}_{\mathrm{c}\mathrm{o}\mathrm{n}\mathrm{v}(1\times 5) }({f}_{\mathrm{c}\mathrm{o}\mathrm{n}\mathrm{v}(1\times 1) }({\boldsymbol{V}}_{\boldsymbol{S}}) ) ) , $ |
| $ {s}_{4}={f}_{\mathrm{c}\mathrm{o}\mathrm{n}\mathrm{v}(1\times 7) }({f}_{\mathrm{c}\mathrm{o}\mathrm{n}\mathrm{v}(1\times 7) }({f}_{\mathrm{c}\mathrm{o}\mathrm{n}\mathrm{v}(1\times 1) }({\boldsymbol{V}}_{\boldsymbol{S}}) ) ), $ |
| $ {f}_{\mathrm{O}\mathrm{S}}={\rm{concat}}\left({s}_{1},{s}_{2},{s}_{3},{s}_{4}\right) $ | (5) |
式中:
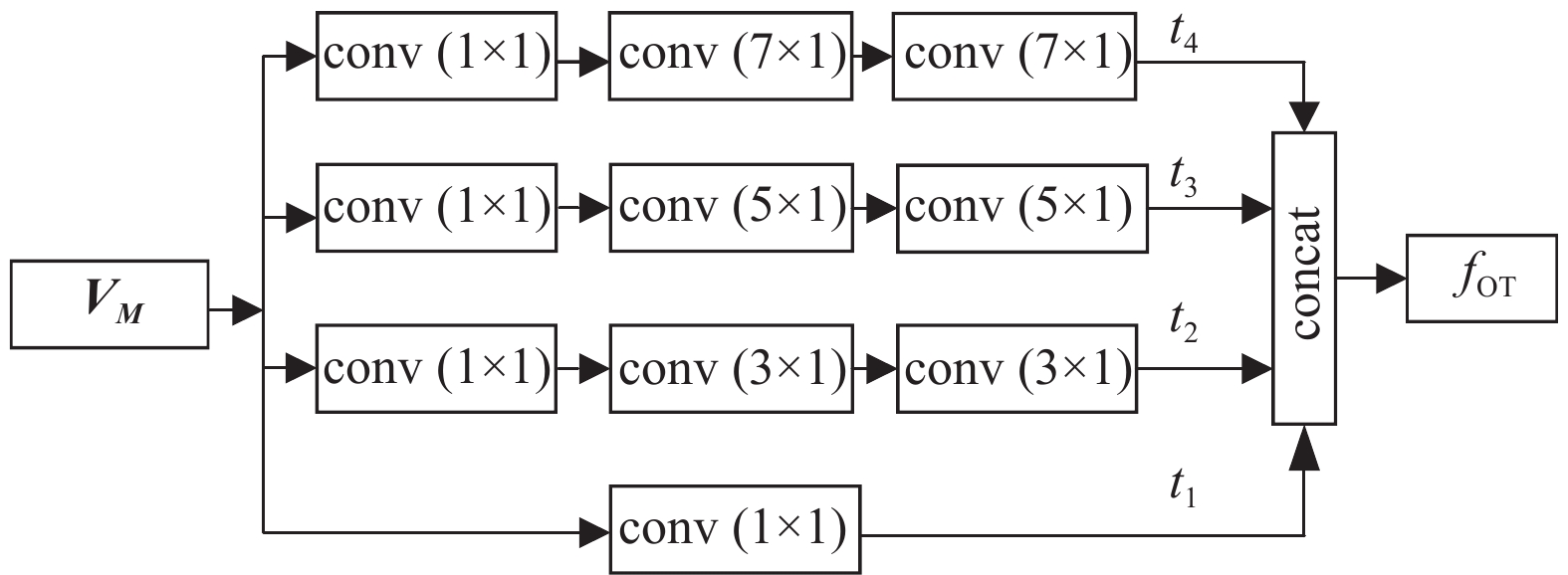
与空间多分支卷积模块类似,时间多分支卷积模块利用4个时间卷积分支提取骨架数据时间维度上的特征,其结构如图8所示,公式见式(6)。
|
图 8 时间多分支卷积模块结构 Figure 8 Temporal multi-branch convolution module structure |
| ${t}_{1}={f}_{\mathrm{c}\mathrm{o}\mathrm{n}\mathrm{v}\left(1\times 1\right) }\left({\boldsymbol{V}}_{\boldsymbol{M}}\right) , $ |
| ${t}_{2}={f}_{\mathrm{c}\mathrm{o}\mathrm{n}\mathrm{v}(3\times 1) }({f}_{\mathrm{c}\mathrm{o}\mathrm{n}\mathrm{v}(3\times 1) }({f}_{\mathrm{c}\mathrm{o}\mathrm{n}\mathrm{v}(1\times 1) }({\boldsymbol{V}}_{\boldsymbol{M}}) ) ),$ |
| ${t}_{3}={f}_{\mathrm{c}\mathrm{o}\mathrm{n}\mathrm{v}(5\times 1) }({f}_{\mathrm{c}\mathrm{o}\mathrm{n}\mathrm{v}(5\times 1) }({f}_{\mathrm{c}\mathrm{o}\mathrm{n}\mathrm{v}(1\times 1) }({\boldsymbol{V}}_{\boldsymbol{M}}) ) ) , $ |
| ${t}_{4}={f}_{\mathrm{c}\mathrm{o}\mathrm{n}\mathrm{v}(7\times 1) }({f}_{\mathrm{c}\mathrm{o}\mathrm{n}\mathrm{v}(7\times 1) }({f}_{\mathrm{c}\mathrm{o}\mathrm{n}\mathrm{v}(1\times 1) }({\boldsymbol{V}}_{\boldsymbol{M}}) ) ),$ |
| $ {f}_{\mathrm{O}\mathrm{T}}={\rm{concat}}\left({t}_{1},{t}_{2},{t}_{3},{t}_{4}\right) $ | (6) |
式中:
时空多分支卷积模块分别在空间、时间上对输入数据进行多尺度一维卷积操作,获得更加全面的时空信息。这种处理方法能够减少由于大量二维卷积而导致的时空信息过度交流,进而避免过拟合现象。
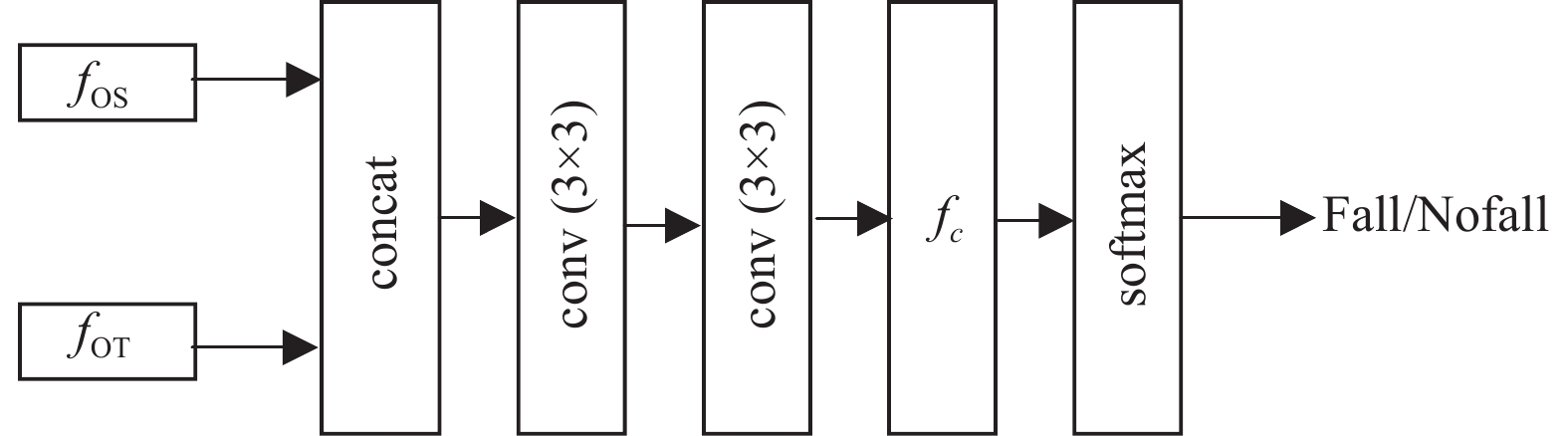
1.3.4 分类模块分类模块结构如图9所示。该模块实现对特征图像进行分类,识别出跌倒动作。实现步骤为:(1) 将多分支卷积得到结果
|
图 9 分类模块结构 Figure 9 Classification module structure |
| $ {f}_{\mathrm{S}\mathrm{T}}={\rm{concat}}\left({f}_{\mathrm{O}\mathrm{S}},{f}_{\mathrm{O}\mathrm{T}}\right) ,\qquad\; $ |
| ${f}_{\mathrm{O}1}={f}_{\mathrm{c}\mathrm{o}\mathrm{n}\mathrm{v}\left(3\times 3\right) }({f}_{\mathrm{c}\mathrm{o}\mathrm{n}\mathrm{v}\left(3\times 3\right) }({f}_{\mathrm{S}\mathrm{T}})), $ |
| $ {f}_{\mathrm{O}}=\mathrm{s}\mathrm{o}\mathrm{f}\mathrm{t}\mathrm{max}(f_{c}\left({f}_{\mathrm{O}1}\right) )\qquad\; $ | (7) |
本文所使用的实验数据包括两个数据集:公共跌倒数据集UR FALL Detection Datasets (URFD) [15]和自建跌倒数据集。
URFD数据集包含30个跌倒动作和40个日常行为动作视频数据。跌倒视频包括行走跌倒、坐着跌倒及站立跌倒3种形式,日常生活视频包括坐下、蹲下、躺下和弯腰等日常动作。
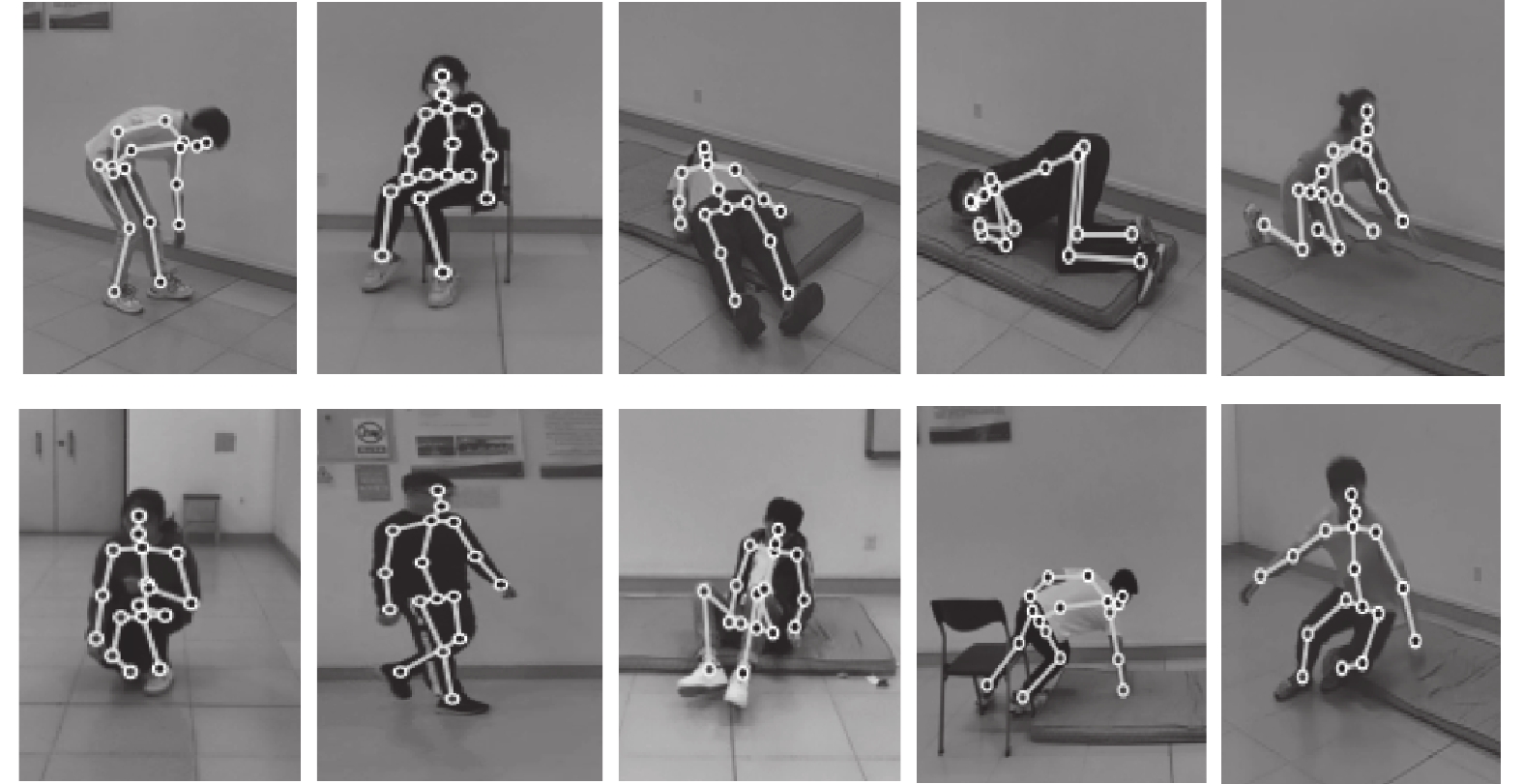
自建数据集包括10类动作,其中6类为日常行为:行走、弯腰、躺下、坐、趴和蹲下;4类为跌倒动作:行走跌倒、坐着跌倒、蹲下跌倒和绊倒,各类动作骨架检测图如图10所示。共9人参与数据采集,每类动作每人做3次。每类动作包含81个视频,共810个视频。视频采样频率为30,分辨率为
|
图 10 各类动作骨架检测图 Figure 10 The skeleton detection results of various actions |
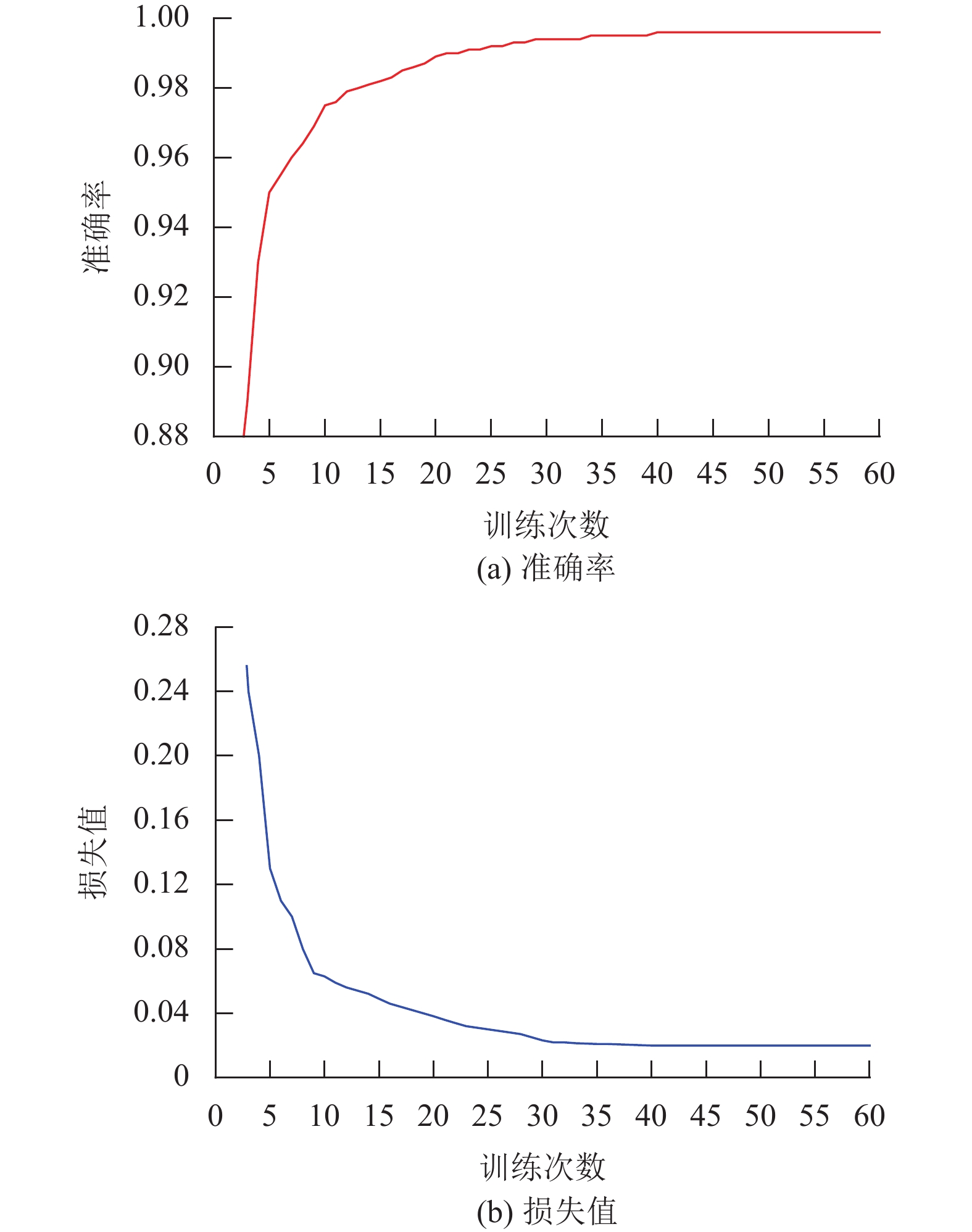
本文实验开发环境为Windows10操作系统、NVIDIA Quadro RTX 5000显卡、Intel(R) Xeon(R) W-2225处理器及32G 内存,用pytorch框架搭建并训练网络模型,选取数据集中的70%作为训练集,30%作为测试集。模型的参数设置会影响最终识别效果,经过实验,确定训练模型参数设置如下:batch=64,epoch=60,学习率初始化为0.0001,损失函数使用交叉熵,优化算法为Adam,跌倒动作持续时间约3.4 s,骨架序列长度T为100帧,其余参数均为默认值。如图11所示,模型到40个epoch后基本收敛,准确率在训练集上接近100%,损失值接近于0。
|
图 11 模型训练结果 Figure 11 The training results |
使用准确率(Accuracy) 、召回率(Recall) 、精确度(Precision) 作为实验评价标准。准确率表示跌倒检测算法正确识别的样本个数占全部样本的比值,召回率表示正确识别为跌倒的样本占所有跌倒样本的比值,精确度表示准确判断为跌倒的样本与全部被判断为跌倒样本的比值。
本节在自建跌倒数据集上分别比较TSSI和各个模块对跌倒检测结果的影响。
在这部分实验中,本文将原始骨架图像和TSSI分别输入可学习STB-CNN网络中,学习时空特征并进行跌倒行为识别,实验结果如表1所示。与原始骨架图像相比,TSSI在准确率、召回率、精确度分别提高了5.37%、6.25%、7.03%。TSSI较好保留了骨架序列的结构信息,如骨盆节点和脊部节点间的连接强度和方向,有利于模型更好识别跌倒行为。
| 表 1 TSSI对跌倒检测结果影响 Table 1 Effect of TSSI on fall recognition results |
本文将原始数据和经过时空差分模块提取的数据分别输入神经网络进行跌倒检测。相比于原始数据,后者的准确率、召回率、精确度分别提高了6.66%、5.21%、8.69%,如表2所示。这是因为时空差分数据比原始数据包含更多的行为特征信息,有助于跌倒行为识别,上述客观结论与主观感受是一致的。
| 表 2 时空差分模块对跌倒检测结果影响 Table 2 Effect of space-time difference module on fall detection results |
本文分别使用包含、不包含时空可学习框架的STB-CNN进行跌倒检测,结果如表3所示。相比于STB-CNN,可学习STB-CNN的准确率、召回率、精确度分别提高6.25%、4.17%、10.26%。实验结果说明时空可学习框架能较好提高跌倒检测效果,其原因是可学习框架可以在关节点之间学习更多空间和时间依赖关系,如头部与双腿关节点间的空间依赖关系、头部关节点第一帧和最后一帧时间依赖关系等。这些额外时空依赖关系,可以帮助STB-CNN了解关节点间的空间和时间特征。
| 表 3 时空可学习框架对跌倒检测结果影响 Table 3 Effect of spatio-temporal learnable framework on fall detection results |
本文分别使用包含、不包含多分支卷积模块的可学习STB-CNN进行跌倒检测实验,结果如表4所示。前者在准确率、召回率、精确度上分别比后者高5%、3.15%、8.47%。实验结果表明多分支卷积模块能够有效提高神经网络模型跌倒检测效果。
| 表 4 时空多分支卷积模块对跌倒检测结果影响 Table 4 Effect of spatio-temporal multi branch convolution module on fall detection results |
如表5所示,本文算法在跌倒动作方面表现良好,但在“趴下”“躺下”“绊倒”等动作方面出现一定偏差。对错误样本进行检查,确定原因是“趴下”“躺下”动作与“绊倒”动作具有高度相似性,在TSSI中表现较为相似,导致算法出现错误判断,这是今后需解决问题。
| 表 5 本文算法在自建数据集的实验结果 Table 5 Experimental results of our algorithm in self-built dataset |
为了验证算法的有效性和适用性,在URFD和自建跌倒数据集上,将本文算法与其他方法分别进行比较,所选方法都是基于骨架图像和CNN的经典算法,其中数据集都采用同样预处理方式,且各个模型超参数以及运行设备统一。实验结果如表6所示。
| 表 6 不同算法在URFD和自建跌倒数据集上的实验结果 Table 6 Experimental results of different algorithms in URFD and self-built falling datasets |
在URFD上,本文算法在召回率和精确度上取得较好的结果,分别为100%和97.56%,准确率与其他算法相比分别提高了4.29%、2.86%、1.43%、1.43%;在自建跌倒数据集上,本文算法准确率相较于其他算法分别提高了7.08%、4.58%、5.83%、1.66%;在时间复杂度方面,本文算法仅高于文献[16]的算法,远低于其他算法。
本文算法能获得较好跌倒识别效果,但对于“趴下”“躺下”等类似跌倒等动作具有一定误判性,同时对于动作识别需要一定时间,暂时无法达到实时检测,这些均是未来工作需要解决的问题。
4 总结本文提出了一种基于TSSI和可学习STB-CNN的跌倒检测方法。TSSI能够有效保存骨架序列结构信息;STB-CNN利用差分模块提取时空差分特征,使用可学习框架学习关节点之间的时空依赖性;通过使用多尺度卷积操作提取时空特征,可以有效地提高识别准确率。实验表明:与其他相关算法相比,本文算法具有较高准确率和更好的适用性。
| [1] |
FOX J A, FOX M A. Falls in older people–an overview for the acute physician[J].
Acute Med, 2011, 10(2): 99-102.
DOI: 10.52964/AMJA.0481. |
| [2] |
MUBASHIR M, SHAO L, SEED L. A survey on fall detection: principles and approaches[J].
Neurocomputing, 2013, 100: 144-152.
DOI: 10.1016/j.neucom.2011.09.037. |
| [3] |
LIU K C, HSIEH C Y, HUANG H Y, et al. An analysis of segmentation approaches and window sizes in wearable-based critical fall detection systems with machine learning models[J].
IEEE Sensors Journal, 2019, 20(6): 3303-3313.
|
| [4] |
CHEN X, XUE H, KIM M, et al. Detection of falls with smartphone using machine learning technique[C]//2019 8th International Congress on Advanced Applied Informatics. Toyama: IEEE, 2019: 611-616.
|
| [5] |
DROGHINI D, FERRETTI D, PRINCIPI E, et al. A combined one-class SVM and template-matching approach for user-aided human fall detection by means of floor acoustic features[J].
Computational Intelligence and Neuroscience, 2017, 2017(8): 1512670.
|
| [6] |
WU J, WANG K, CHENG B, et al. Skeleton based fall detection with convolutional neural network[C]//2019 Chinese Control And Decision Conference (CCDC) . Nanchang: IEEE, 2019: 5266-5271.
|
| [7] |
YAO L, YANG W, HUANG W. A fall detection method based on a joint motion map using double convolutional neural networks[J].
Multimedia Tools and Applications, 2020, 81(4): 4551-4568.
|
| [8] |
LI C, ZHONG Q, XIE D, et al. Co-occurrence feature learning from skeleton data for action recognition and detection with hierarchical aggregation[C]// Proceedings of the 27th International Joint Conference on Artificial Intelligence. Stockholm: ACM, 2018: 786-792.
|
| [9] |
SU H, CHANG Z, YU M, et al. Convolutional neural network with adaptive inferential framework for skeleton-based action recognition[J].
Journal of Visual Communication and Image Representation, 2020, 73: 102925.
DOI: 10.1016/j.jvcir.2020.102925. |
| [10] |
LIU J, ROJAS J, LI Y, et al. A graph attention spatio-temporal convolutional network for 3D human pose estimation in video[C]//2021 IEEE International Conference on Robotics and Automation (ICRA) . Xi'an: IEEE, 2021: 3374-3380.
|
| [11] |
KE Q, BENNAMOUN M, AN S, et al. A new representation of skeleton sequences for 3D action recognition[C]//Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition. Los Alamitos: IEEE, 2017: 3288-3297.
|
| [12] |
KIM T S, REITER A. Interpretable 3D human action analysis with temporal convolutional networks[C]//2017 IEEE Conference on Computer Vision and Pattern Recognition Workshops (CVPRW) . Honolulu: IEEE, 2017: 1623-1631.
|
| [13] |
YANG Z, LI Y, YANG J, et al. Action recognition with spatio–temporal visual attention on skeleton image sequences[J].
IEEE Transactions on Circuits and Systems for Video Technology, 2018, 29(8): 2405-2415.
|
| [14] |
SZEGEDY C, VANHOUCKE V, IOFFE S, et al. Rethinking the inception architecture for computer vision[C]//Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition. Las Vegas: IEEE, 2016: 2818-2826.
|
| [15] |
KWOLEK B, KEPSLI M. Human fall detection on embedded platform using depth maps and wireless accelerometer[J].
Neurocomputing, 2015, 168(3): 637-645.
|
| [16] |
TAN T H, HUS J H, LIU S H, et al. Using direct acyclic graphs to enhance skeleton-based action recognition with a linear-map convolution neural network[J].
Sensors, 2021, 21(9): 3112-3118.
DOI: 10.3390/s21093112. |
 2023, Vol. 40
2023, Vol. 40

