2. 广东工业大学 自动化学院, 广东 广州 510006
2. School of Automation, Guangdong University of Technology, Guangzhou 510006, China
在机器学习领域中,一个重要的假设是训练数据和目标数据必须在相同的特征空间中并且具有相同的分布,但是在真实世界中,这种假设很难满足,例如有的时候对于感兴趣的目标领域缺乏足量的数据,或者是标记的数据太少,但是在与之相关的领域中却有大量的训练数据,能否利用与目标领域相关领域的训练数据得到训练模型,从而将相关任务训练数据中的可泛化知识迁移到目标领域的分类和回归任务中,在这种情况下,如果成功地进行知识转移,就可以避免昂贵的数据标记工作,从而大大提高学习的性能。近年来,迁移学习作为一种新的学习框架应运而生,它的出现就是为了解决目标领域中训练数据匮乏,但其相关领域有大量训练数据的问题。
本文提出了一种基于自步学习策略的归纳式迁移学习模型,在自步学习策略中引入自步学习函数,设置自步学习率来调整多个相关源任务中样本的学习速率。在迭代的过程中,通过计算预测值和标签的差别来选择置信度高的样本,也即损失较小的样本,更新自步学习函数的相关参数,并且根据选择的样本加入到下一次的迭代过程中,更新多个源任务的迁移学习模型的相关参数。当迭代到一定次数并到达某个阈值的时候就会得到每一个源任务的分类器,可以将得到的分类器应用到与之相关的目标领域的分类任务中。本文的主要贡献如下。
(1) 提出了一种新的基于自步学习策略的迁移学习模型,该模型引入了自步学习策略,在学习多个相关源任务的过程中充分考虑到了相关源任务中样本的复杂性;(2) 利用了拉格朗日函数将原问题转化为对偶问题,通过对拉格朗日函数进行求导,将偏导值代入到原问题中进一步优化迁移学习模型从而得到更好的分类器;(3) 实验结果表明在相同的实验条件下,通过与现有的模型进行比较,本文提出的模型能够获得比较好的分类效果。
1 相关工作 1.1 自步学习现有的机器学习方法都会面临非凸优化问题,传统的优化方法在避免非凸优化问题陷入较差局部解时,往往采用多次随机初始化方式训练模型,然后选择其中效果最好的初始化结果构建模型,但这种方法只能够针对具体的问题,并且花费的代价过高。为了解决这个问题,课程学习和自步学习被提出来,以更好地解决非凸优化问题,Bengio等[1]在2009年提出了课程学习。为了进一步改进课程学习只是针对特定问题的不足,Kumar等[2]在2010提出了自步学习,并且给出了自步学习的数学表达形式。课程学习[3-5] 和自步学习[6-8] 的核心思想是通过模拟人的认知机理,首先学习简单的、普适性的知识结构,然后逐渐增加难度,过渡到学习更复杂的知识。在机器学习领域中,可以使用这种按学习目标的难易程度从易到难开展学习的方式。自步学习研究的关键是假设样本的选择并不是随机的,在一次迭代中不是将全部样本纳入训练过程中,而是通过一种由简到难的有意义的方式来选择样本,所以自步学习的过程实际上是一个从简单到复杂的样本选择过程,简单样本可以理解为具有较小的损失或较大似然函数值的样本,复杂的样本为具有较大损失的样本。
1.2 迁移学习迁移学习是一种机器学习的方法[9],其目标是将某个领域或任务上学习到的知识或模式应用到不同但相关的领域或问题中。与半监督学习、主动学习等不同的是迁移学习放宽了对训练数据和测试数据需要服从独立同分布这一假设的要求,从而使得参与学习的领域或任务可以服从不同的边缘概率分布或条件概率分布。迁移学习的主要思想是:从相关的辅助领域中迁移标注数据或知识结构,完成或改进目标领域或任务的学习效果。根据标注数据的情况,迁移学习可以分成3大类:归纳式迁移学习[10-13]、直推式迁移学习[14-16] 和无监督迁移学习[17-19]。归纳式迁移学习是从已观测到的数据到一般数据的迁移,归纳式学习也即平时所说的监督学习,使用带有标签的数据进行模型训练,然后使用训练好的模型预测测试集数据的标签,训练集数据不包含测试集数据。直推式迁移学习是从观测到的特定数据到特定数据的推理,训练数据和测试数据在之前都已经可以观测,并且可以根据已知的训练数据学习特征来预测测试集标签。即使不知道测试集的标签,也可以在学习过程中利用数据中的特征或其他信息来进行推理。直推式迁移学习利用训练集数据和测试集数据共同训练模型,然后使用测试集数据进行测试。无监督迁移学习与归纳式迁移学习的源域和目标域类似,但是任务不同,标记数据在任一域中都不可用。
2 基于自步学习策略的归纳式迁移学习模型本节提出了基于自步学习策略的归纳式迁移学习模型,然后使用拉格朗日函数结合卡鲁什−库恩−塔克条件(Karush-Kuhn-Tucker,KKT)优化原问题对应的目标模型从而获得更好的分类器,在2.1节中展示目标模型的构建,在2.2节中展示使用拉格朗日函数优化目标模型的过程和具体算法的实现框架。
2.1 目标模型假定现在有
| $ {w_t} = {w_0} + {v_t} $ | (1) |
本文在提出的目标模型中引入了自步学习的策略,使用自步学习的策略可以将多个相关源任务中损失较小的样本到损失较大的样本加入到迭代过程中,挑选出合适的样本从而提高分类器的分类性能。自步学习策略一般包含2个函数,分别为自步学习函数以及对应的损失函数,不同问题的自步学习函数与损失函数一般不同,本文提出的目标模型对应的自步学习函数如式(2) 所示。
| $ f(v,\lambda ,\mu ) = - \lambda \sum\limits_{t = 1}^T {\sum\limits_{i = 1}^{{m_t}} {{p_{ti}}} } + \mu \sum\limits_{t = 1}^T {\sqrt {\frac{1}{{{m_t}}}\sum\limits_{i = 1}^{{m_t}} {{{({p_{ti}}) }^2}} } } $ | (2) |
式中:
| $\begin{split}& \qquad l({x_{ti}},{y_{ti}}) = - {p_{ti}}{y_{ti}}({w_0} + {v_t}) \phi ({x_{ti}}) , \\& t = 1,2,\cdots,T,i = 1,2,\cdots,{m_t},{p_{ti}} \in \{ 0,1\} \end{split}$ | (3) |
根据上面的分析可以构建目标模型,如式(4) 所示。
| $ \begin{split}& {\min _{{w_0},{v_t},{\xi _{ti}}}}\frac{1}{2}||{w_0}|{|^2}\; + \frac{k}{2}\mathop \sum \limits_{t = 1}^T ||{v_t}|{|^2}\; + C\sum\limits_{t = 1}^T {\sum\limits_{i = 1}^{{m_t}} {{\xi _{ti}}} } + \\&\qquad f(v,\lambda ,\mu ) \; + \sum\limits_{t = 1}^T {\sum\limits_{i = 1}^{{m_t}} l } ({x_{ti}},{y_{ti}}) ,\\& {\rm{s}}.{\rm{t}}.\;\;\;{y_{ti}}({w_0} + {v_t}) \cdot \phi ({x_{ti}}) \geqslant 1 - {\xi _{ti}},{\xi _{ti}} \geqslant 0, \\ & \qquad i = 1,2,\cdots,{m_t},t = 1,2,\cdots,T \\ \end{split} $ | (4) |
式中:
为了优化式(4) 的目标模型,本文引入拉格朗日函数对其进行优化,根据式(4) 的不等式约束条件,分别引入拉格朗日乘数子
| $ \begin{split} L =& \frac{1}{2}||{w_0}|{|^2} + \frac{k}{2}\mathop \sum \limits_{t = 1}^T ||{v_t}|{|^2} - \sum\limits_{t = 1}^T {\sum\limits_{i = 1}^{{m_t}} \; } {p_{ti}}{y_{ti}}({w_0} + {v_t}) \phi ({x_{ti}})- \\& \sum\limits_{t = 1}^T {\sum\limits_{i = 1}^{{m_t}} \; } {\alpha _{ti}}[{y_{ti}}({w_0} + {v_t}) \cdot \phi ({x_{ti}}) - 1 + \;{\xi _{ti}}] -\\& \sum\limits_{t = 1}^T {\sum\limits_{i = 1}^{{m_t}} \; } {\beta _{ti}}{\xi _{ti}} + C\sum\limits_{t = 1}^T {\sum\limits_{i = 1}^{{m_t}} \; } {\xi _{ti}} + f(v,\lambda ,\mu )\\[-15pt] \end{split} $ | (5) |
令拉格朗日函数等于0求解
| $ { \begin{split} {\text{max}}L =& \frac{{1 + k}}{{2k}}\sum\limits_{i = 1}^T {\sum\limits_{u = 1}^{{m_t}} {\sum\limits_{j = 1}^T {\sum\limits_{s = 1}^{{m_t}} {{p_{iu}}} } } } {p_{js}}{y_{iu}}{y_{js}} < \phi ({x_{iu}}) ,\phi ({x_{js}}) >+ \\& \frac{{1 + k}}{k}\sum\limits_{i = 1}^T {\sum\limits_{u = 1}^{{m_t}} {\sum\limits_{j = 1}^T {\sum\limits_{s = 1}^{{m_t}} {{p_{iu}}} } } } {\alpha _{iu}}{y_{iu}}{y_{js}} < \phi ({x_{iu}}) ,\phi ({x_{js}}) >+\\& \frac{{1 + k}}{{2k}}\sum\limits_{i = 1}^T {\sum\limits_{u = 1}^{{m_t}} {\sum\limits_{j = 1}^T {\sum\limits_{s = 1}^{{m_t}} {{\alpha _{iu}}} } } } {\alpha _{js}}{y_{iu}}{y_{js}} < \phi ({x_{iu}}) ,\phi ({x_{js}}) >-\\& \frac{{1 + k}}{k}\sum\limits_{i = 1}^T {\sum\limits_{u = 1}^{{m_t}} {\sum\limits_{j = 1}^T {\sum\limits_{s = 1}^{{m_t}} {{y_{iu}}} } } } {y_{js}}({p_{iu}} + {\alpha _{iu}}) ({p_{js}} + {\alpha _{js}}) < \\& \phi ({x_{iu}}) ,\phi ({x_{js}}) > + \sum\limits_{t = 1}^T {\sum\limits_{i = 1}^{{m_t}} {{\alpha _{ti}}} } + f(v,\lambda ,\mu ) ,\\& {\text{s}}{\text{.t}}{\text{.}}\;\;\;C - {\alpha _{ti}} - {\beta _{ti}} = 0,0 \leqslant {\alpha _{ti}} \leqslant C \\[-12pt] \end{split}} $ | (6) |
通过求解式(6)最大值的结果来更新参数
| $ {f_t} = {\text{sgn}}[({w_0} + {v_t}) \phi (x) ] $ | (7) |
式中:
根据上面的分析定义具体的算法框架如下:
算法1 SP-DTL
输入:需要训练的
输出:
1. 初始化参数
2. 设置训练过程中的最大迭代次数,例如可以设置
3. 通过式(2) 构建凸优化二次方程;
4. 重复:
5.
6. 更新
7. 计算式(5)、(6)结果,更新
8. 直到
9. 返回
本节主要是选择现有的推导式迁移学习模型和自步学习模型在不同的数据集中进行比较,验证分类的效果。
3.1 实验对比方法与设置实验选择了自步学习模型[7](Self-paced Learning for K-means Clustering Algorithm,SPKC) 和基于孪生支持向量机的多任务学习模型[20](Multi-task Least Squares Twin Support Vector Machine, MTLS-TWSVM) 与本文提出的方法SP-DTL在文本数据集和图像数据集上进行实验对比,比较分类器的分类性能,其中自步学习模型采用一种从简单到复杂的方式来选择样本从而实现对文本和图像数据集的分类,而基于孪生支持向量机的多任务学习模型通过共享多个相关的任务参数,而每一个任务都有其特殊的部分,从而实现对文本和图像数据集的分类任务。
3.2 数据集(1) 文本数据集。文本数据集分别为 20 Newsgroup 和Reuters-21578 数据集。20 Newsgroup数据集主要用于文本分类、文本挖掘和信息检索,数据集收集了大约20000个的新闻组文档,分为20个不同主题的新闻组集合,一些新闻组的主题特别类似,例如comp.sys.ibm.pc.hardware,comp.sys.mac.hardware,还有一些是完全不相关的主题,例如misc.forsale 和soc.religion.christian。Reuters-21578 数据集是文本分类研究的数据集,该数据集主要包含“exchanges”“orgs”“people”“places”和“topic”5个顶级类别,每个顶级类别还包含许多子类别,非常适合于做文本分类的相关问题。
(2) 图像数据集。图像数据集分别为MINIST和CIFAR-10 数据集,其中MINIST数据集为手写数字的图片数据集,一共统计了来自250个不同的人手写的数字图片,其中50% 是高中生,50% 来自人口普查局的工作人员,该数据集主要用来实现对手写数字的识别。CIFAR-10数据集一共包含10个类别的彩色图片,分别为飞机、汽车、鸟类、猫、鹿、狗、蛙类、马、船和卡车,图片的尺寸为 32×32,数据集中共有 50000张训练图片和 10000 张测试图片。表1根据源任务中的任务数量和不同的数据集设置了不同的子数据集。
| 表 1 数据集的设置 Table 1 Dataset settings |
表2列出了本文模型与对比方法的平均精度和标准差,从表2可以看出本文提出的模型在大部分情况下的精度优于其他2个对比的模型,例如对于dataset1,SP-DTL的精度为78.6%,高于对比模型SPKC和MTLS-TWSVM的精度(72.2%,74.3%)。
| 表 2 在不同数据集上各个模型的实验精度和标准差 Table 2 Precisions and standard deviations of different models on different datasets |
在这一部分研究了目标模型对应的式(2) 中参数
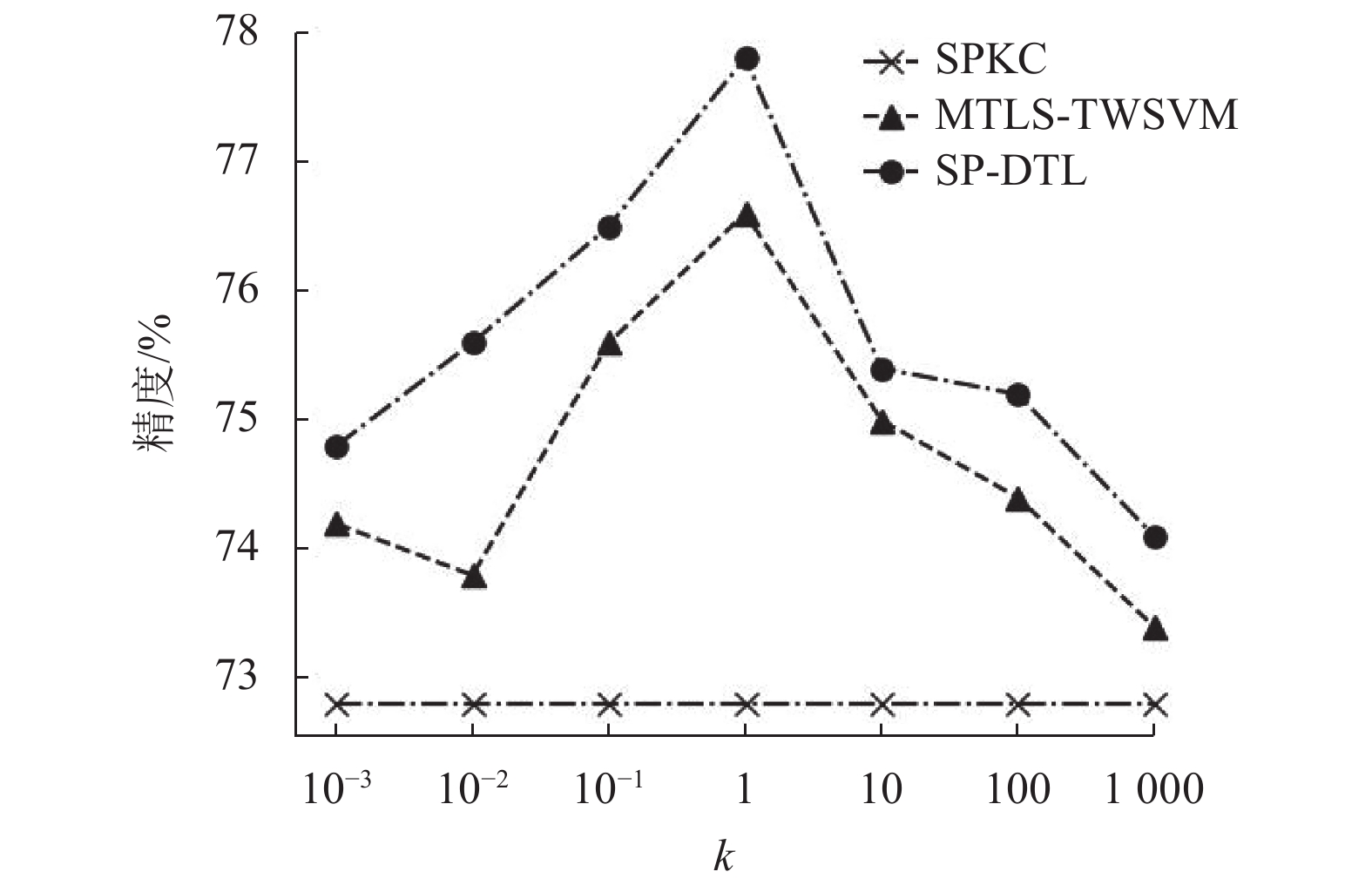
|
图 1 参数
|
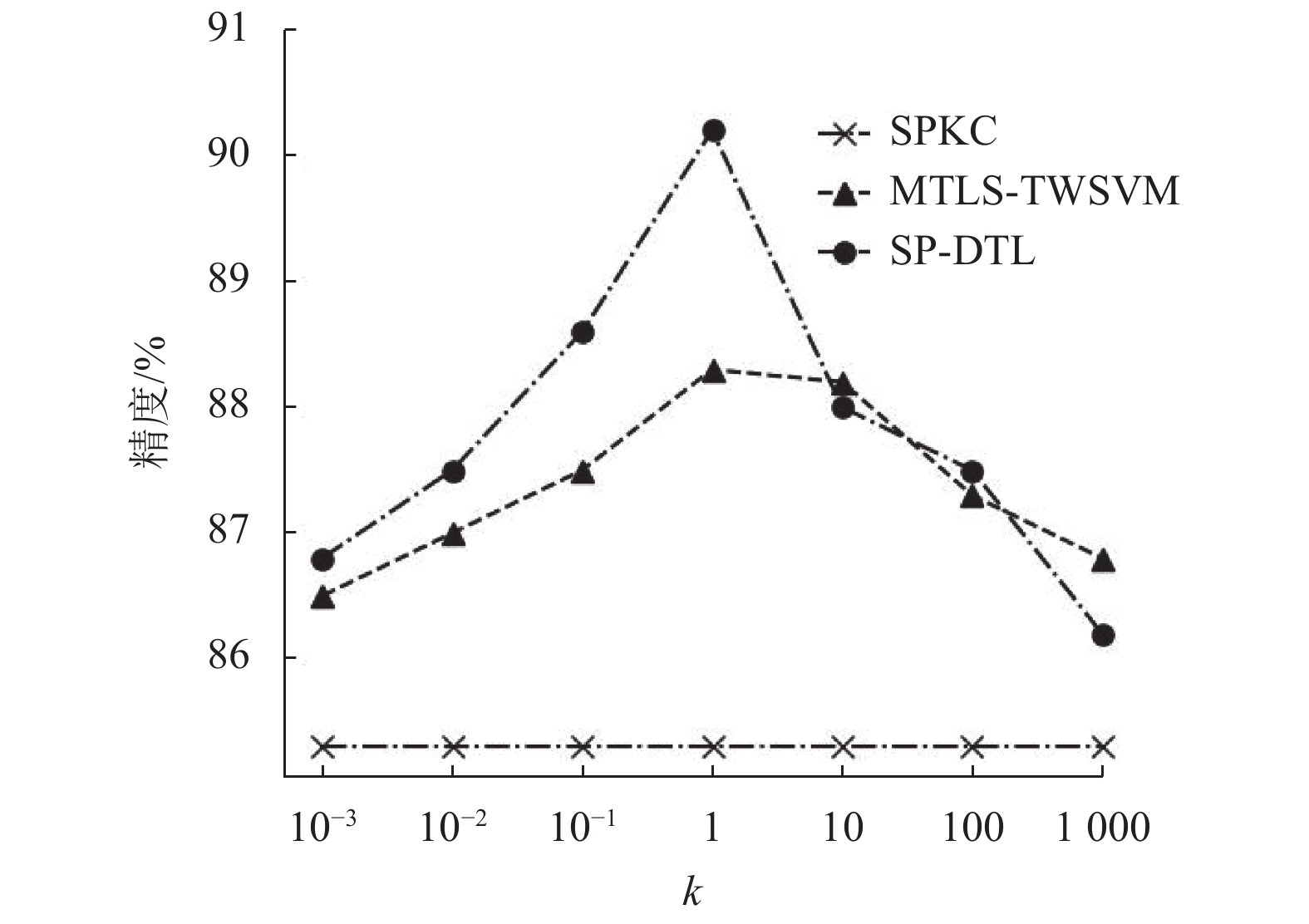
|
图 2 参数
|
本文提出了一种新的基于自步学习策略的推导式迁移学习模型,通过引入自步学习的策略,充分考虑到了多个相关源任务中样本的复杂性。在迭代的过程中,通过从“简单”到“复杂”的学习过程学习源任务中的样本,通过计算预测值和标签的差别来选择置信度高的样本,也即损失较小的样本。通过自步学习策略调整学习速率,在迭代的过程中更新多个相关源任务中的共享参数和每一个源任务中的特有参数,最终使每一个源任务获得一个比较好的分类器。通过相关源任务的学习可以将源任务目标模型迁移到目标任务中,解决目标任务中文本分类和图像分类的问题。将现有的模型与本文提出的模型进行对比,发现本文提出的模型的实验效果优于现有的迁移学习模型。
| [1] |
BENGIO Y, LOURADOUR J, COLLOBERT R, et al. Curriculum learning[C]//Proceedings of the 26th Annual International Conference on Machine Learning. Montreal: ACM, 2009, 382: 41-48.
|
| [2] |
KUMAR M, PACKER B, KOLLER D. Self-paced learning for latent variable models[C]//Advances in Neural Information Processing Systems 23: 24th Annual Conference on Neural Information Processing Systems 2010. Vancouver: Curran Associates, Inc., 2010: 1189-1197.
|
| [3] |
BENGIO Y, COURVILLE A C, VINCENT P. Representation learning: a review and new perspectives[J].
Journal of Electronic Imaging, IEEE Transactions on Pattern Analysis and Machine Intelligence, 2013, 35(8): 1798-1828.
DOI: 10.1109/TPAMI.2013.50. |
| [4] |
WANG Y, GAN W, YANG J, et al. Dynamic curriculum learning for imbalanced data classification[C]//Proceedings of the IEEE/CVF International Conference on Computer Vision. Seoul: IEEE, 2019: 5017-5026.
|
| [5] |
SOVIANY P, TUDOR R, IONESCU. Curriculum learning: a survey[J].
International Journal of Computer Vision, 2022, 130(6): 1526-1565.
DOI: 10.1007/s11263-022-01611-x. |
| [6] |
YIN T, LIU N, SUN H. Self-paced active learning for deep CNNs via effective loss function[J].
Neurocomputing, 2021, 424: 1-8.
DOI: 10.1016/j.neucom.2020.11.019. |
| [7] |
YU H, WEN G, GAN J. Self-paced learning for K-means clustering algorithm[J].
Pattern Recognition Letters, 2020, 132: 69-75.
DOI: 10.1016/j.patrec.2018.08.028. |
| [8] |
XIAO Y, YANG X, LIU B. A new self-paced method for multiple instance boosting learning[J].
Information Sciences, 2020, 515: 80-90.
DOI: 10.1016/j.ins.2019.12.015. |
| [9] |
PAN S J, YANG Q. A Survey on transfer learning[J].
IEEE Transactions on Knowledge and Data Engineering, 2010, 22(10): 1345-1359.
DOI: 10.1109/TKDE.2009.191. |
| [10] |
CRAWFORD M, KHOSHGOFTAAR T M. Using inductive transfer learning to improve hotel review spam detection[C]//2021 IEEE 22nd International Conference on Information Reuse and Integration for Data Science (IRI) . Las Vegas, NV: IEEE, 2021: 248-254.
|
| [11] |
YUN H, ZHANG C, HOU H, et al. An adaptive approach for ice detection in wind turbine with inductive transfer learning[J].
IEEE Access, 2019, 7: 122205-122213.
DOI: 10.1109/ACCESS.2019.2926575. |
| [12] |
DENG Z, JIANG Y, WANG S, et al. Enhanced knowledge leverage-based TSK fuzzy system modeling for inductive transfer learning[J]. ACM Transactions on Intelligent Systems and Technology, 2016, 8(1) : 11: 1-11: 21.
|
| [13] |
黎启祥, 肖燕珊, 郝志峰, 等. 基于抗噪声的多任务多示例学习算法研究[J].
广东工业大学学报, 2018, 35(3): 47-53.
LI Q X, XIAO Y S, HAO Z F, et al. An algorithm based on multi-task multi-instance anti-noise learning.[J]. Journal of Guangdong University of Technology, 2018, 35(3): 47-53. DOI: 10.12052/gdutxb.180036. |
| [14] |
XIAO Y, FENG J, LIU B. A new transductive learning method with universum data[J].
Applied Intelligence, 2021, 51(8): 5571-5583.
DOI: 10.1007/s10489-020-02113-4. |
| [15] |
XIAO F, PANG L, LAN Y, et al. Transductive learning for unsupervised text style transfer[C]// Proceedings of the 2021 Conference on Empirical Methods in Natural Language Processing. Punta Cana: Association for Computational Linguistics, 2021, 2510-2521.
|
| [16] |
ZHAO P, WU G, YAO S, et al. A transductive transfer learning approach based on manifold learning[J].
Computing in Science and Engineering, 2020, 22(1): 77-87.
DOI: 10.1109/MCSE.2018.2882699. |
| [17] |
MICHAU G, FINK O. Unsupervised transfer learning for anomaly detection: application to complementary operating condition transfer[J].
Knowledge-Based Systems, 2021, 216: 106816.
DOI: 10.1016/j.knosys.2021.106816. |
| [18] |
CHEN X, YANG R, WEN H. Transfer learning with unsupervised domain adaptation method for bearing fault diagnosis[C]//2021 CAA Symposium on Fault Detection, Supervision, and Safety for Technical Processes (SAFEPROCESS) . Chengdu: IEEE, 2021: 1-6.
|
| [19] |
ROCHA G, CARDOSO H L. Improving transfer learning in unsupervised language adaptation[C]//International Conference on Artificial Neural Networks. Bratislava: Springer, 2021, 12895: 588-599.
|
| [20] |
MEI B, XU Y. Multi-task least squares twin support vector machine for classification[J].
Neurocomputing, 2019, 338: 26-33.
DOI: 10.1016/j.neucom.2018.12.079. |
 2023, Vol. 40
2023, Vol. 40

